An Adaptive Neuro-Fuzzy Inference System to Improve Fractional Order Controller Performance

1  Introduction

Conventional controllers such as PID, PI, and PD are widely used in most industrial control applications to control different processes. These controllers are selected because of their simple structure, which makes them easy to understand and implement [1–3]. The performance of traditional controllers is satisfactory for systems that are simple and have a linear input-output relationship [4]. However, real-world industrial processes are highly dynamic, nonlinear, and more complex. Conventional controllers are not good enough to provide better control performance for those industrial processes due to the various constraints [5]. Besides, conventional controller-based closed-loop systems are more sensitive to system parameter change and load disturbances [6]. Hence, most recent researchers are focusing on the fractional order control (FOC) as an alternative, the integral and derivative terms of the conventional PID controller are replaced by fractional order numbers (PIλDµ) then the controller becomes a fractional order controller [7]. In the past, several research studies have confirmed that FOCs can exhibit better performance than classical controllers [8–11]. If the integral and derivate parts order of a fractional order controller is equal to unity (i.e., λ = µ = 1) then the FOPID controller will work as a conventional PID controller. The FOC technique can be used for integer order or fractional order plant models in a particular control application [12].

Many fields, particularly engineering, biology, physics, and medicine, have expanded their usage of FOCs in recent years [13–15]. The accurate model of a real-time system can be developed with the help of FOC, which is necessary to achieve precise and reliable control action. The traditional PID controller only has three adjustable parameters: Kp, Ki, and Kd, however, the FOPID controller has two extra adjustable fractional order factors (λ and µ) by which greater system design and improved control will be possible [16]. Unfortunately, parameter tuning in fractional order controllers is a difficult part of system design, and there is currently no easy and effective tuning solution. Caponetto et al. [17] suggested a design strategy for the PIλDµ controller tuning. For the PIλDµ controller design, Hwang et al. [18] used the minimal error criterion method. Intelligent algorithms such as fuzzy logic control (FLC), neural network (NN), ANFIS etc. have increased the flexibility of controller tuning and system design. Recent studies show that intelligent algorithms combined with fractional order controllers provide a better outcome in closed-loop control [19–22]. Controller tuning is an important component of the system design, and it becomes difficult as the number of controller parameters increases. On the other hand, intelligent algorithm combined with closed-loop control schemes will reduce the challenges in system design. In the past, only a few investigations on controller adaptation employing intelligent techniques were documented in connection with the FOC. Nooshin and Hossein introduced an adaptive intelligent robust controller for stabilizing uncertain fractional order chaotic systems in [23], demonstrating that the controller is more robust against external disturbances and process uncertainties. Gholamreza et al. [24] used a fuzzy-neural controller to fine-tune the settings of a PID controller for controlling the speed of a DC motor; improved results were reported in terms of settling time and rising time.

An intelligent ANFIS combined FOC design and its performance validation for a first order plus delay time plant is discussed in the present study. The ANFIS model has been developed to adjust the value of the FOC parameters dynamically based on system conditions. To enhance controller performance, a modified structure of the FOPID controller is proposed in this work. In the modified FOPID controller structure, the order of the integral part (λ) is used for the combined proportional and integral part (i.e., [PI]λDµ). The ANFIS part of the controller block will closely monitor process dynamics by utilizing error and changes in error inputs. The designed system performance is validated under different operating conditions. The suggested controller results are compared to those of conventional PID and classical PIλDµ controllers to confirm the advantages.

The following sections make up this paper: Section 2 provides an overview of fractional order control. The controller design technique is discussed in Section 3. The structure and functions of the ANFIS are detailed in Section 4. Section 5 explains how the suggested controller is implemented in the proposed system. In Section 6, the outcomes of the simulation study are discussed. The research findings are presented in Section 7 as a conclusion.

2  Fractional Order Control an Overview

The fractional calculus is a non-integer order variation of standard differentiation and integration [25]. In the literature, different forms of fractional order calculus definitions have been reported; the most popular are the Grunwald-Letnikov (GL) and Riemann Liouville (RL) methods [26–28]. As per the GL definition, the fundamental fractional operator is expressed as

p.Dxγf(x)=limq→0⁡q−γ∑k=0[x−pq]⁡(−1)k(γk)f(x−kq), (1)

where p and x are the limits, γ is the order of operation, while in RL definition the fractional operator is expressed as

p.Dxγf(x)=1Γ(m−γ)dmdtm∫pxf(τ)(x−τ)γ−m+1dτ, (2)

for (m − 1 < γ < m), where Γ(⋅) Euler’s gamma function. The Laplace transform of the GL and RL fractional derivative/integral is provided as under a zero initial condition which is expressed as

L{0.Dxγf(x)}=SγH(s). (3)

The transfer function in the case of a commensurate order system is stated as

H(s)=∑q=0m⁡bqSγq∑q=0n⁡aqSγq, (4)

where γq=qγ,βq=qγandγ∈(0,1),∀q∈Z+

3  Controller Design Procedure

The design approach for the classical PIλDµ and proposed [PI]λDµ controllers are described in this section. For FOC with an integer-order pole, Luo et al. [29] have proposed the controller design method. Malek et al. [30] have combined this fractional order pole controller design method with a time-delay mechanism. A fractional first order plus delay time plant model general transfer function is given as

G(s)=KTsα+1e−Ls, (5)

where K denotes the plant gain, T denotes the time constant, L denotes the delay, and α denotes the plant order. The transfer function of the classical PIλDµ controller and the proposed [PI]λDµ are expressed respectively, as follows

Cg(s)=Kp+KiSλ+Kdsμ, (6)

Cmfoc(s)=[Kp+Kis]λ+Kdsμ, (7)

where λ is the order of the integral part and µ is the order derivative part, Ki, Kp and Kd are the coefficients of integral, proportional, and derivative terms, respectively. In this paper, the range of fractional order numbers (λ, µ) are chosen between 0 and 2.

Phase margin, gain crossover frequency, and robustness to changes in plant parameter are the three key characteristics that are frequently addressed for fractional order controller design [30–32]. The fractional order controller must meet the following parameters based on the fundamental definitions of gain crossover frequency and phase margin.

•   Phase margin (ɸm)

arg[Hg(jω)]ω=ωc=arg[Cg(jω)G(jω)]ω=ωc=−π+ϕm, (8)

where ω and ϕm are the required gain crossover frequency and phase margin, respectively.

•   Gain crossover frequency (ω)

In the logarithmic frequency domain, the magnitude of the open-loop transfer function should be zero at the gain crossover frequency point

|Hg(jω)|ω=ωc=|Cg(jω)G(jω)|ω=ωc=1. (9)

•   Robustness to changes in the plant parameter

The phase Bode plot is flat for a certain value of the ω, as mentioned in [9], indicating that the system is more robust to changes in the parameter. As a result, the controller must meet this requirement,

|d[arg(Hg(jω)]dω|ω=ωc=0. (10)

Besides in the above three requirements, the controller’s noise rejection and disturbance elimination abilities are also considered during the design process to maintain system stability. The specifications for noise rejection and disturbance elimination are presented in the following formulations.

•   Noise rejection

In the case of noise rejection specifications, the sensitive function N can be given as

|R(jω)=Cg(jω)G(jω)1+Cg(jω)G(jω)|dB≤NdB,∀ω≥ωrrads⇒|R(jωr)|dB=NdB, (11)

where N is the preferred reduction in noise for frequencies ω≥ωr rad/sec.

•   Rejection of disturbance

The constraint related output disturbance rejection sensitive function D can be given as

|D(jω)=11+Cg(jω)G(jω)|dB≤MdB,∀ω≥ωdrads⇒|D(jωd)|dB=MdB, (12)

where M is the preferred value of the sensitivity function for frequencies ω≥ωd rad/sec.

3.1 Classical PIλ Dµ Controller Design

The transfer function of the system under open-loop condition using the plant Eq. (5) and the classical PIλDµ controller Eq. (6) is given as

Hfoc(s)=Cg(s)G(s)=K[Kp+Kisλ+Kdsμ]Tsα+1e−Ls. (13)

The Eq. (13) can be written as

Hfoc(jω)=K[Kp+KiM+KdN+i(−KiJ+KdQ)]×[cosLωπ2−isinLωπ2]P+iR, (14)

where P=1+Tωαcosαπ2,R=Tωαsinαπ2 , M=ω−1cosλπ2,J=ω−λsinλπ2

N=ωμcosμπ2Q=ωμsinμπ2

Argument part of Eq. (14) is

arg[Hfoc(jω)]=tan−1(−KiJ+KdQKp+KiM+KdN)−tan−1(RP)−Lω=−π+ϕm. (15)

The Eq. (15) can be rewritten as

−KiJ+KdQKp+KiM+KdN=tan[tan−1(RP)+Lω−π+ϕm]. (16)

The magnitude of Eq. (14) yields

|Hfoc(jω)|=(Kp+KiM+KdN)2+(KiJ−KdQ)2P2+R2=1K. (17)

According to the robustness to plant parameters variation constraint Eq. (10), the open-loop phase is expressed as

(d(arg⁡(Hfoc(jω)))dω)=λKpKiJ+μKpKdQ+ωKdiKi(λ+μ)sin(λ+μ)π2Kp2+Ki2M2+Kd2N2+2KpKiM+2KpKdN+2KpKdNM=αRT2ω2α+2P−1−L. (18)

Using Eqs. (16)–(18) the parameters Kp, Ki, Kd, λ, and µ of the classical PIλDµ controller can be obtained.

3.2 [PI]λ D µ Controller Design

This research proposes a modified version of the classical PIλDµ controller in which the proportional and integral coefficients of the controller will use a common fractional order number(λ). The system’s open-loop transfer function employing the plant Eq. (5) and the suggested [PI]λDµ controller Eq. (7) is written as

Hmfoc(s)=Cmfoc(s)G(s). (19)

In the frequency domain, the Eq. (19) can be represented in the following form by replacing s with jω

Hmfoc(jω)=Cmfoc(jω)G(jω), (20)

where Cmfoc(jω)=[Kp+Ki(jω)−1]λ+Kd(jω)μ

=(Kp−Kijω)λ+Kdωμ(cosμπ2+jsinμπ2)=(Kpλ−λKiKpλ−1ω)+Kdωμ(cosμπ2+jsinμπ2) (21)

arg⁡[Cmfoc(jω)]=tan−1(−λKiKpλ−1+Kdωμ+1sinμπ2ωKpλ+Kdωμ+1cosμπ2), (22)

andG(jω)=KT(jω)α+1e−Ld(jω). (23)

arg|G(jω)|=−tan−1(Tωαsinαπ21+Tωαcosαπ2)−Lω. (24)

Open-loop phase at ω frequency can be expressed as

arg|Hmfoc(jω)|=arg|Cmfoc(jω)|arg|G(jω)| (25)

=tan−1(−λKiKpλ−1+Kdωμ+1sinμπ2ωKpλ+Kdωμ+1cosμπ2)−tan−1(Tωαsinαπ21+Tωαcosαπ2)−Lω (26)

arg|Hmfoc(jω)|=tan−1[−λKiKpλ−1+Kdωμ+1sinμπ2ωKpλ+Kdωμ+1cosμπ2]−tan−1(BA)−Lω, (27)

where A=1+Tωαcosαπ2,B=Tωαsinαπ2

According to the phase margin constraint Eq. (8), the open-loop phase could satisfy the following expression

arg[Hmfoc(jω)]=tan−1[−λKiKpλ−1+Kdωμ+1sinμπ2ωKpλ+Kdωμ+1cosμπ2]−tan−1(BA)−Lω=−π+ϕm. (28)

According to the gain crossover frequency constraint Eq. (9), the open-loop gain at the gain crossover frequency satisfies the following equation

arg[Hmfoc(jω)]=K(−λKiKpλ−1+Kdωμ+1sinμπ2)2+(ωKpλ+Kdωμ+1cosμπ2)2A2+B2=1, (29)

=λ2Ki2Kp2(λ−1)+Kd2(μ+1)−2Kp−1λKiC−2ω2D+ω2Kp2λ=E, (30)

where C=ωμ+1KpλKdsinμπ2,D=ωμKpλKdcosμπ2,E=1+T2ω2α+2Tωαcosμπ2

According to the robustness to plant parameters variation constraint Eq. (10), the open-loop phase is expressed as

(d(arg⁡(Hmfoc(jω)))dω)=μC+λKp−1Ki[Kp2λ+(μ+1)D]ω2Kp2λ+ωμ+1(Kd2ωμ+1+2D)=F+λKp−1Ki(λKp2λ−1Ki−2C), (31)

where F=αTωα−1sinαπ21+T2ω2α+2Tωαcosαπ2−L.

Using Eqs. (28), (30) and (31) the parameters Kp, Ki, Kd, λ, and µ of the proposed [PI]λDµ controller can be achieved.

4  Adaptive Neuro-Fuzzy Inference System

The expert knowledge is expressed in terms of linguistic description in the traditional FLC, which is utilized to produce the necessary control action. The range of each input is partitioned by fuzzy membership functions with a specified boundary in traditional fuzzy system design to decide local conclusions based on fuzzy rules. However, ANFIS is a modified fuzzy inference system (FIS) architecture in which membership function ranges are adapted using neuro-adaptive learning approaches. The ANFIS combines the benefits of FLS and NN, with the FLS’ inference ability and the NN’s learning ability performing the tuning process. In NN, parameter optimization is made by back-propagation and the least-squares technique. Fig. 1 depicts the internal design of a typical ANFIS. The structure consists of five layers; the input layer is followed by a membership layer, the rule layer, the normalization layer, and the output layer. The first layer, which is made up of nodes for each input, will just transfer data to the second layer and will not do any calculations. For the second layer, the type of membership function and the number of input membership functions are specified in advance by the designer. The membership value to a specific fuzzy set is expressed as

yij=exp(−[yi−nij]22σij2),i=1,2,…,m;j=1,2,…,n (32)

where σij and nij are denotes the variance and mean of the Gaussian membership function. The nodes in the third layer represent the preconditioned part of a fuzzy rule. In this method, the layer two nodes are used to determine the degree of membership of the applicable rule. The output function of the inference node and the product (AND) operation that is commonly done in this layer are depicted as

Sj=yj=∏i⁡yij,i=1,2,…,m;j=1,2,…,n (33)

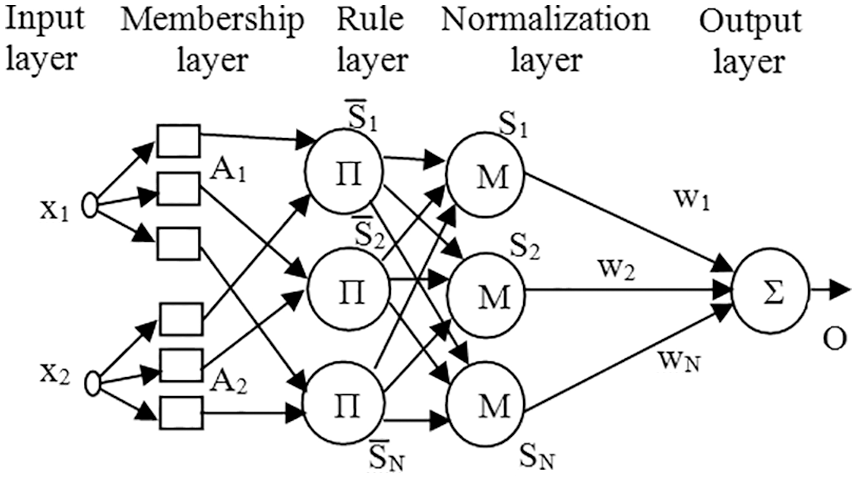
Figure 1: The internal architecture of ANFIS

The output from the third layer is received by normalization nodes, which are normalization layers. The fourth layer node function can be expressed as

Sj=yj/(∑k=1n⁡yk),j=1,2,…,n (34)

Layer five combines the several actions advised in layer four to create a single output which is expressed as

O=∑k=1n⁡wkyk (35)

5  Implementation of the Proposed Control Configuration

The fractional order numbers (λ and µ) are dynamically updated based on the system parameters in the ANFIS combined modified FOC (which is designated as ANF[PI]λDµ). To test the effectiveness of the suggested control approach, the model of the pressure control plant [32] was chosen and is given in Eq. (36),

G(s)=2.154.803s1.2+1e−1.4s. (36)

The initial parameters of the proposed [PI]λDµ controller can be determined using Eqs. (28), (30), and (31). Using the controller tuning procedure in [33], the controller parameters’ value has been determined with the following specifications: phase margin (ɸm) = 70°, gain margin = 10 dB, gain crossover frequency (ω) = 0.001 rad/sec., high-frequency noise rejection = 10 rad/sec., and disturbance elimination sensitivity function = 0.001 rad/sec. In addition, to acquire the optimal controller parameters, the Nelder-Mead optimization approach discussed in [34] and integral absolute error (IAE) performance metrics are used. To ensure the applicability of the identified system, the system stability and controller design specifications described in Eqs. (8)–(12) are validated using the MATLAB software toolbox. To assess the usefulness of the suggested control strategy, a classical PIλDµ and a conventional PID control method are also evaluated for the same plant. The classical PIλDµ controller parameters are obtained using Eqs. (16)–(18). Tab. 1 lists the parameters of the three distinct controllers used in this research.

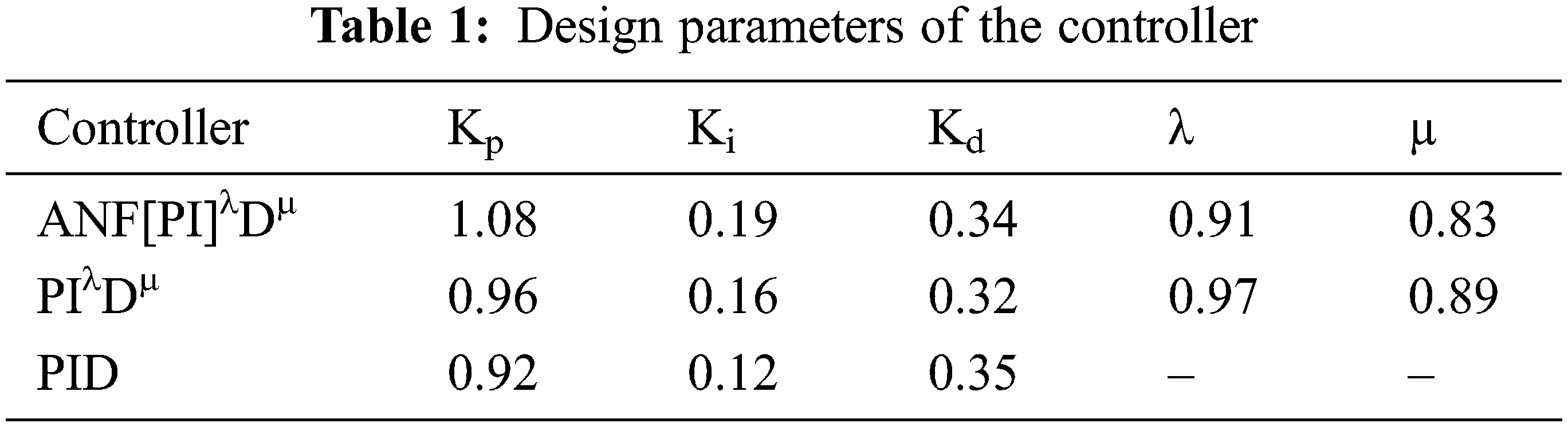
Fig. 2 depicts the suggested ANF[PI]λDµ control scheme in schematic form. The ANFIS component of the system is initially trained with a precise dataset linking the research model’s inputs and outputs. The Sugeno fuzzy model with three fuzzy membership functions of Gaussian type is utilized for both inputs and outputs throughout the ANFIS design process, and the hybrid (i.e., least-squares and back-propagation combined) optimization approach with an error tolerance of 0.001 is selected. The relationship between inputs and outputs is represented in the form of a surface view as shown in Fig. 3. The trained ANFIS will adjust λ and µ parameters to accomplish adaptability. The fuzzy rules for creating the outputs λ and µ have their own ANFIS block, as shown in Fig. 2. The process error e(t) and change in error Δe(t) are used as inputs by both ANFIS parts of the controller to fix the value of fractional factors λ and µ in the range of 0 to 2.

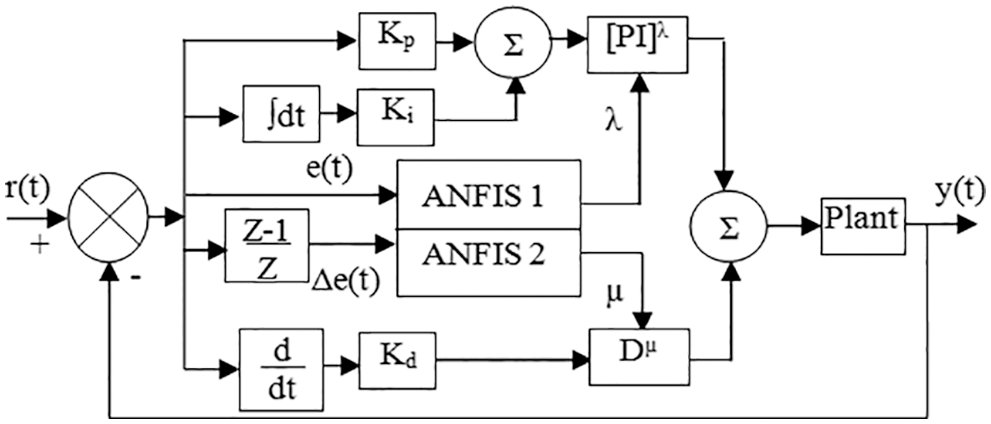
Figure 2: The proposed ANF[PI]λDµ controller structure

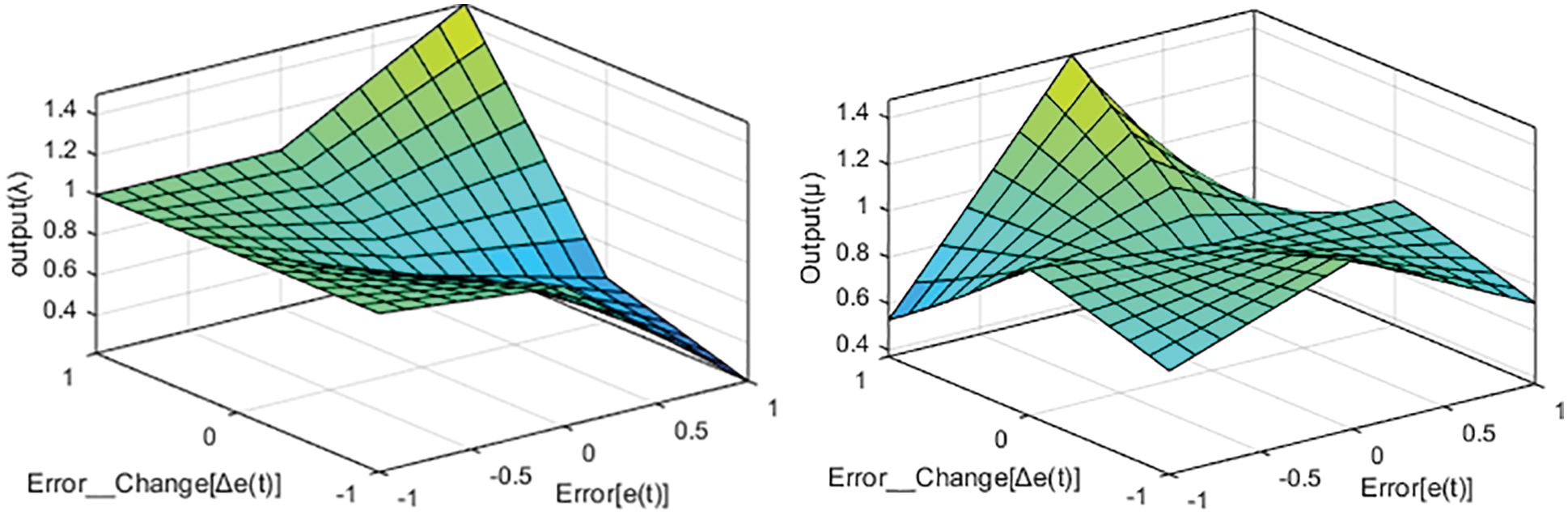
Figure 3: The surface view of the fuzzy control rules (a) Output λ (b) Output µ

6  Results and Discussion from the Simulation Study

The performance of the developed ANF[PI]λDµ, classical PIλDµ, and conventional PID controllers were examined under various operating conditions for the chosen fractional first-order plant model (36). In the initial part of the study, the effectiveness of the controllers has been validated for the unit step input. From the study results shown in Fig. 4, one can understand that the designed ANF[PI]λDµ controller performance is comparatively better in terms of rise-time and settling time. The proposed system with ANF[PI]λDµ controller reached the target level quickly than the classical PIλDµ and conventional PID controller-based system. When compared to PIλDµ and PID controllers, the suggested control approach has a better overall transient performance since the ANFIS modifies the controller parameters dynamically, which results in the system performing well for the unit step input. Fig. 5 depicts the time response of the proposed controller’s adaptive settings for the unit step input study corresponds to Fig. 4. This result illustrates that the controller’s ANFIS rightly changes the controller’s parameters and ensures the system responds quickly without any oscillation or overshoot. Therefore, the designed FOC with modified structure exhibit better transient performance than traditional control methods. External load disturbances and changes in input test have been performed to confirm the robustness of the proposed controller. When the system is at a steady-state level, load disturbances have been applied. The external load disturbances at 10 and 20 s and the associated system output using three different control schemes are shown in Fig. 6. When compared to the traditional controllers, the present fractional order controller with ANFIS control scheme outperforms for the load disturbances. The ANFIS section of the proposed controller immediately detects load disturbances and thereby modifies the controller parameters accurately, which results a better performance. Fig. 7 depicts adaptive parameter changes during load disturbances.

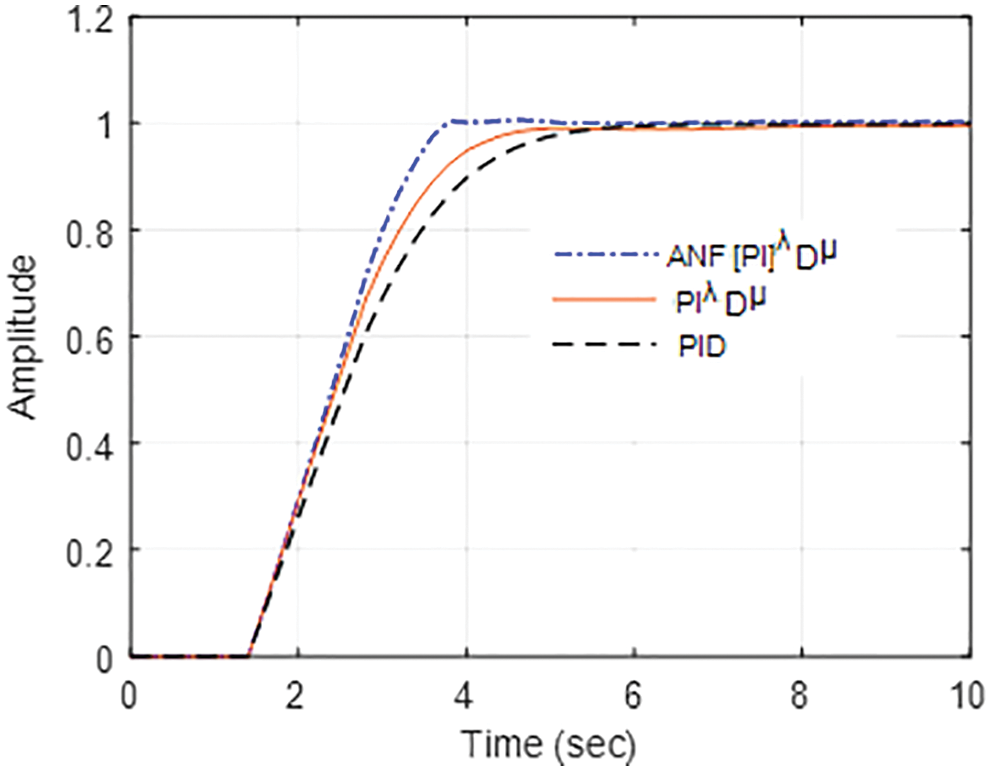
Figure 4: System response for the step input

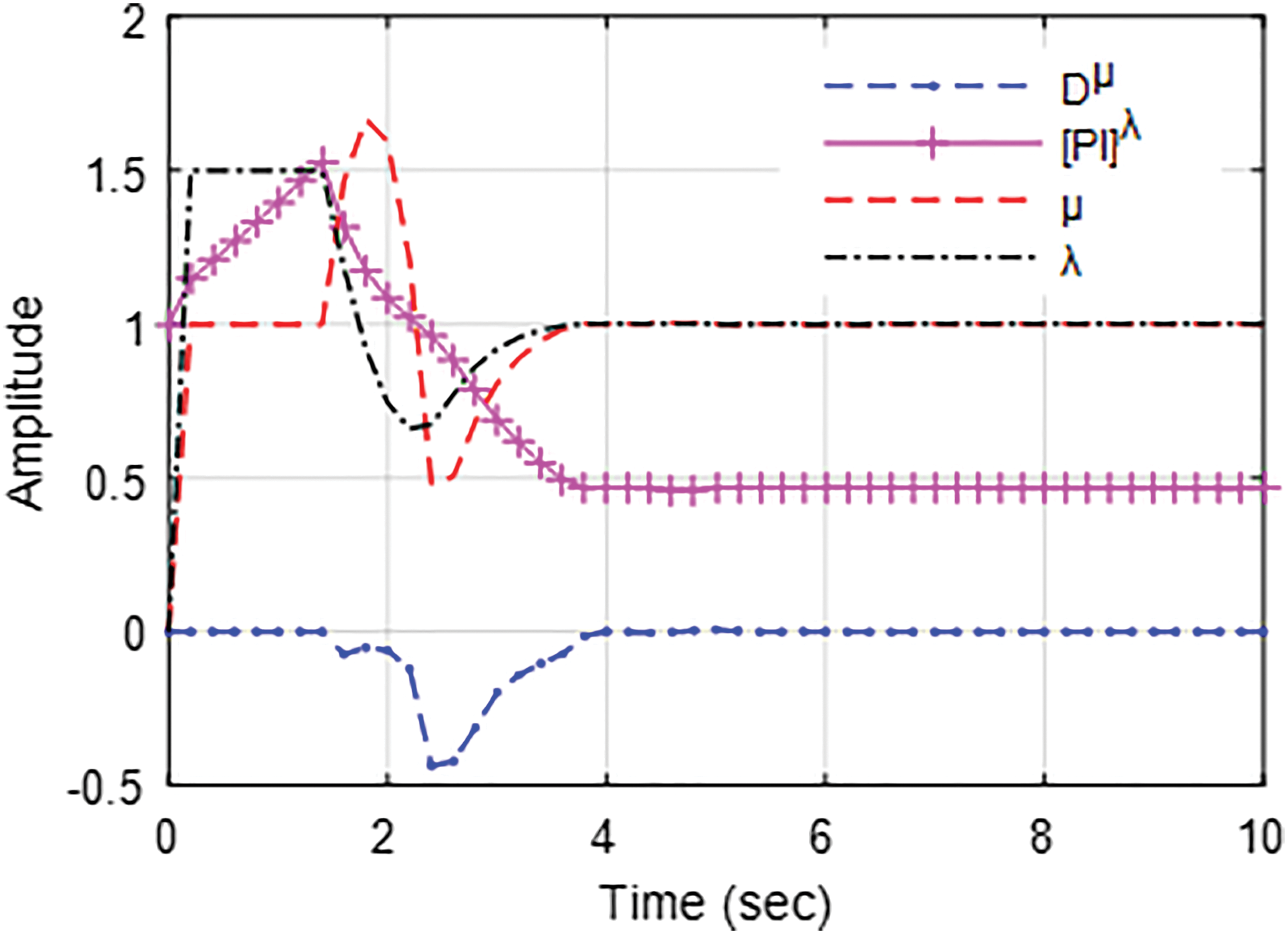
Figure 5: Adaptive parameters of ANF[PI]λDµ controller for the step input

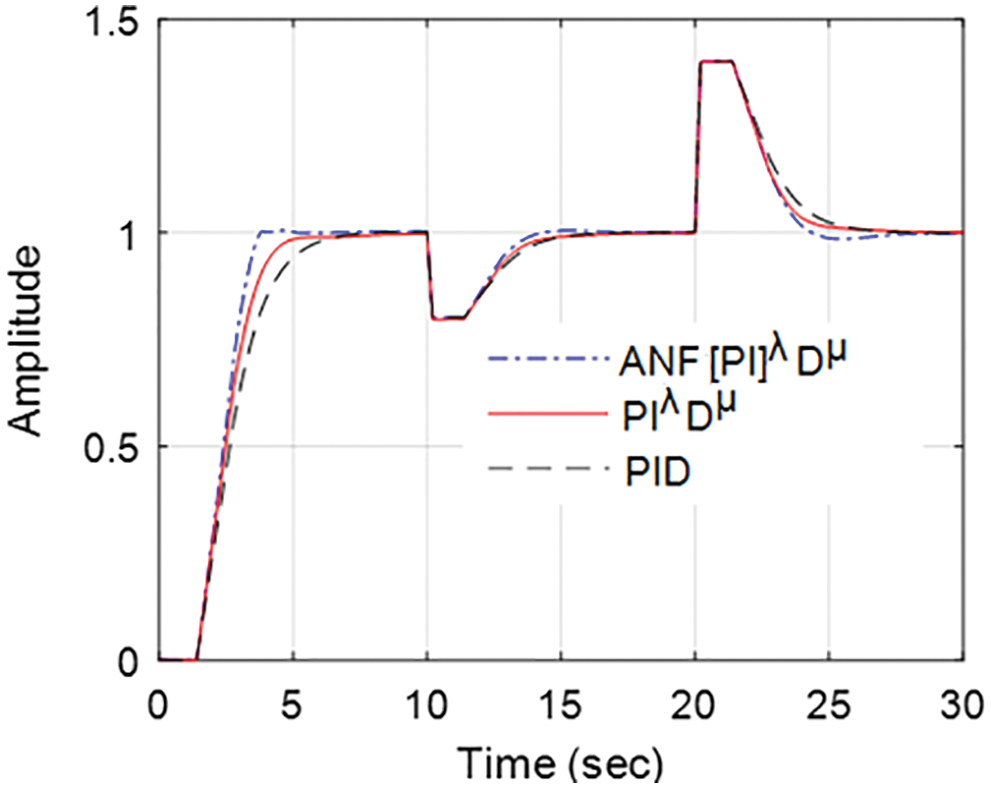
Figure 6: Load disturbances response comparison of different controller

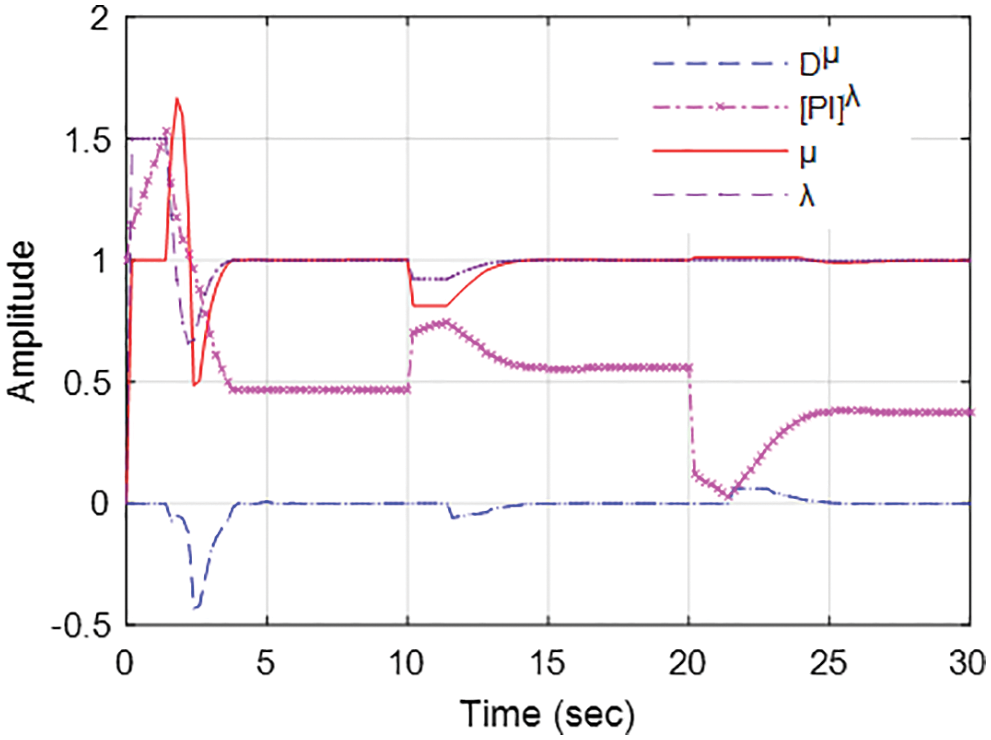
Figure 7: Time response of the ANF[PI]λDµ controller parameters during load disturbances

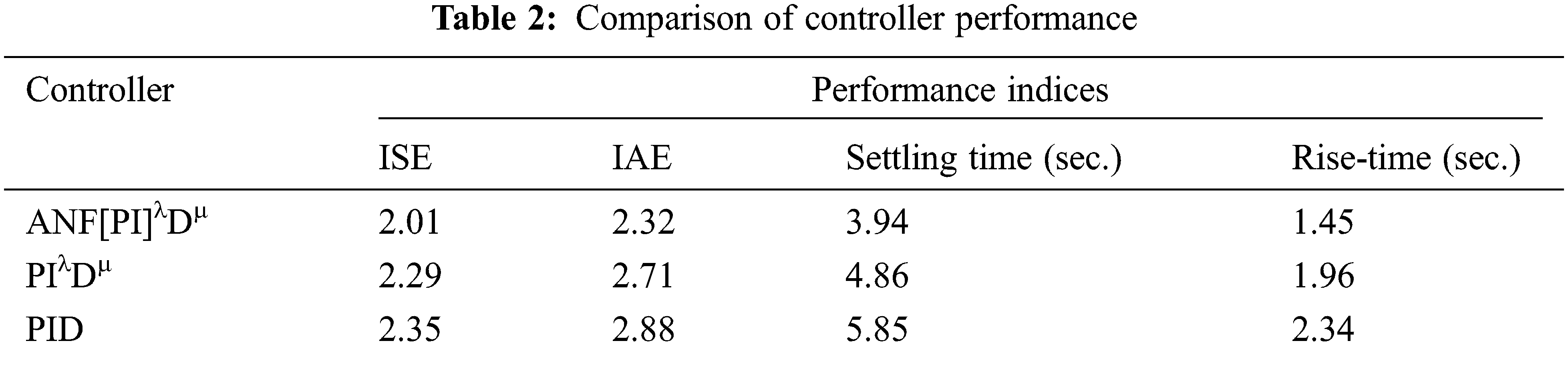
By adjusting the system’s set-point level, the closed-loop system’s response to the input change was tested and the result is shown in Fig. 8. The input change test has been carried out using three distinct controllers for the input to the system reduced by 20% from its normal level after 10 s and then boosted by 40% after 20 s. The system with ANF[PI]λDµ controller senses input changes promptly and then modify the FOC controller’s parameters, which makes the system output to a new steady-state level within a short time. On the other hand, traditional controllers take longer to reach the new steady-state output. Therefore, the ANFIS-based adaptation technique proposed in this study improves the controller performance and thereby the system’s robustness. Fig. 9 depicts the ANF[PI]λDµ controller’s adaptive parameters change corresponding to the study results of Fig. 8. Tab. 2 shows a numerical comparison of the performance of three different controllers using various metrics such as rise time, settling time, IAE and integral square error (ISE). In all these performance metrics, the adaptive mechanism using ANFIS for the fractional order controller outperforms when compared to other controllers. Therefore, the proposed ANFIS-based adaptive control scheme will be a better option to enhance controller action for non-linear and complex systems.

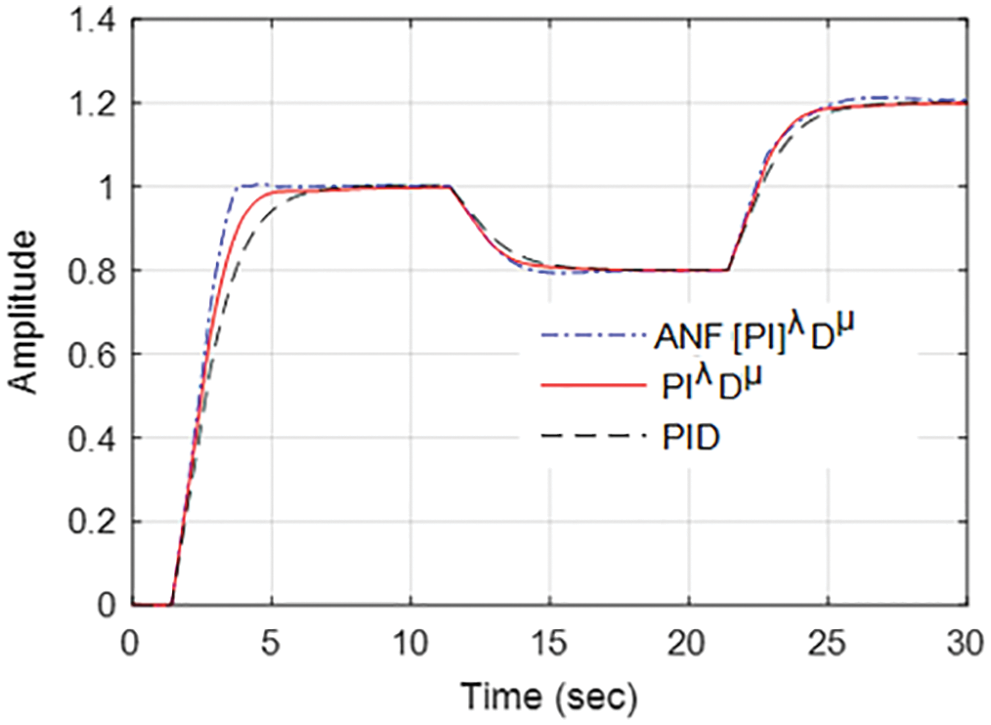
Figure 8: Input change response comparison of different controller

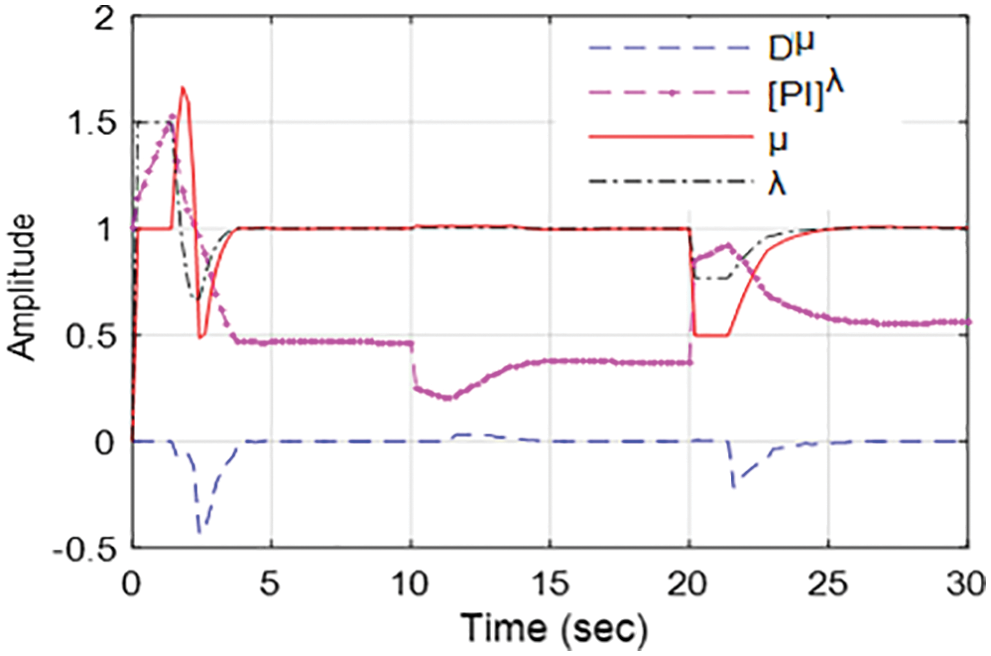
Figure 9: Time response of the ANF[PI]λDµ controller parameters during input change

7  Conclusions

A modified fractional order PID controller integrated with ANFIS control scheme was investigated for a fractional first order pressure regulating plant model. The ANFIS was created for the proposed control scheme to keep track of the system parameters and thereby modify the fractional order PID controller coefficients to achieve a better control action on the system. The designed ANF[PI]λDµ controller performance was studied and compared to classical PIλDµ and conventional PID controllers under various operating conditions. The study’s findings indicated that when the system encounters input parameter change and external load disturbances, the designed controller performs effectively to bring back the output of the system quickly to the desired level. Compared to traditional PIλDµ and PID controllers, the suggested control strategy greatly reduced the settling time and rise time of the system, which is essential for a good controller. Also, the modified fractional order PID controller integrated with ANFIS can improve the closed-loop system’s stability and robustness. The study results confirm that the present control technique will be a better option for nonlinear and complex industrial systems. Computational time and controller identification are the big challenges in this type of ANFIS combined adaptive fractional order control schemes.

Funding Statement: The author extends their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number (IF-PSAU-2021/ 01/18128).

Conflicts of Interest: The author declares that he has no conflicts of interest to report regarding the present study.

References

 1.  K. H. Ang, G. Chong and Y. Li, “PID control system analysis, design and technology,” IEEE Transaction on Control Systems Technology, vol. 13, no. 4, pp. 559–576, 2005. [Google Scholar]

 2.  K. J. Astrom and T. Hagglund, Advanced PID control. Research Triangle Park, USA: ISA, 2005. [Google Scholar]

 3.  J. Zhang, N. Wang and S. Wang, “A developed method of tuning PID controllers with fuzzy rules for integrating process,” in Proc. of the American Control Conf., Massachusetts, pp. 1109–1114, 2004. [Google Scholar]

 4.  B. Del-Muro-Cuellar, M. Velasco-Villa, J. J. Alvarez Ramirez, F. Marquez-Rubio and O. Jimenez-Ramiirez, “Control scheme based on internal prediction for unstable linear time-delay systems,” in Proc. of 8th Int. IFAC Symp. on Dynamics and Control of Process System, Mexico, vol. 2, 2007. [Google Scholar]

 5.  B. Verma and P. K. Padhy, “Robust fine tuning of optimal PID controller with guaranteed robustness,” IEEE Transactions on Industrial Electronics, vol. 67, no. 6, pp. 4911–4920, 2020. [Google Scholar]

 6.  K. Jezernik and M. Rodic, “High precision motion control of servo drives,” IEEE Transactions on Industrial Electronics, vol. 56, pp. 3810–3816, 2009. [Google Scholar]

 7.  I. Podlubny, “Fractional-order systems and PIλDμ controller,” IEEE Transaction on Automatic Control, vol. 440, no. 1, pp. 208–214, 1999. [Google Scholar]

 8.  N. Kanagaraj and V. N. Jha, “Design and performance evaluation of an improved fractional order PID controller for a class of second order plant,” International Journal for Computation and Mathematics in Electrical and Electronic Engineering, vol. 40, no. 3, pp. 579–592, 2021. [Google Scholar]

 9.  M. Z. Fardila, M. Saad and M. Marizan, “Application of fractional order sliding mode control for speed control of permanent magnet synchronous motor,” IEEE Access, vol. 7, pp. 101765–101774, 2019. [Google Scholar]

10. M. Dhaifallah, N. Kanagaraj and K. S. Nisar, “Fuzzy fractional-order PID controller for fractional model of pneumatic pressure system,” Mathematical Problems in Engineering, 5478781, 2018. [Google Scholar]

11. B. T. Zhang and Y. Pi, “Robust fractional order proportion-plus-differential controller based on fuzzy inference for permanent magnet synchronous motor,” IET Control Theory & Applications, vol. 6, no. 6, pp. 829–837, 2012. [Google Scholar]

12. Y. Q. Chen, “Ubiquitous fractional order controls,” in Proc. of 2nd IFAC Symp. on Fractional Derivatives and Applications, Portugal, 2, pp. 168–173, 2006. [Google Scholar]

13. H. S. Ramadan, S. Padmanaban and M. I. Mosaad, “Metaheuristic-based near-optimal fractional order PI controller for on-grid fuel cell dynamic performance enhancement,” Electric Power Systems Research, vol. 208, no. 6, pp. 107897, 2022. [Google Scholar]

14. M. I. Mosaad, “Direct power control of SRG based-wind energy conversion systems using optimized fractional order PI,” IET Electric Power Applications, vol. 14, no. 3, pp. 409–417, 2020. [Google Scholar]

15. M. Ghorbani, M. Tavakoli-Kakhki, A. Tepljakov, E. Petlenkov, A. Farnam et al., “Robust stability analysis of interval fractional-order plants with interval time delay and general form of fractional-order controllers,” IEEE Control Systems Letters, vol. 6, pp. 1268–1273, 2022. [Google Scholar]

16. F. Padula and A. Visioli, “Tuning rules for optimal PID and fractional-order PID controllers,” Journal of Process Control, vol. 21, pp. 69–81, 2011. [Google Scholar]

17. R. Caponetto, L. Fortuna and D. Porto, “A new tuning strategy for a non-integer order PID controller,” in Proc. of the IFAC Workshop on Fractional Differentiation and its Application, Bordeaux, France, pp. 168–173, 2004. [Google Scholar]

18. C. Hwang, J. F. Leu and S. Y. Tsay, “A note on time-domain simulation of feedback fractional order systems,” IEEE Transaction on Automatic Control, vol. 47, no. 4, pp. 625–631, 2002. [Google Scholar]

19. N. Kanagaraj, “Design and performance evaluation of fuzzy variable fractional-order [PI]λDμ controller for a class of first-order delay-time systems,” Studies in Informatics and Control, vol. 28, no. 4, pp. 443–452, 2019. [Google Scholar]

20. M. I. Mossad, F. A. banakhr, S. S. M. Ghoneim, T. A. Abdulfattah and M. M. Samy, “Self-regulated single-phase induction generator for variable speed stand-alone WECS,” Intelligent Automation & Soft Computing, vol. 28, no. 3, pp. 715–727, 2021. [Google Scholar]

21. C. Wang, M. Liang and J. Gao, “Adaptive fuzzy output tracking control of a class of uncertain fractional order systems subject to unknown disturbance,” IEEE Access, vol. 6, pp. 70655–70665, 2018. [Google Scholar]

22. N. Kanagaraj, “An enhanced maximum power point tracking method for thermoelectric generator using adaptive neuro‐fuzzy inference system,” Journal of Electrical Engineering & Technology, vol. 16, no. 3, pp. 1207–1218, 2021. [Google Scholar]

23. B. Nooshin and A. Z. Hossein, “Design of fractional robust adaptive intelligent controller for uncertain fractional-order chaotic systems based on active control technique,” Nonlinear Dynamics, vol. 87, no. 3, pp. 1703–1719, 2017. [Google Scholar]

24. F. Gholamreza and R. Karim, “Speed control of a separately excited dc motor using new proposed fuzzy neural algorithm based on FOPID controller,” Journal of Control Automation and Electrical Systems, vol. 30, no. 5, pp. 728–740, 2019. [Google Scholar]

25. B. M. Vinagre, Y. Q. Chen and I. Petras, “Two direct Tustin discretization methods for fractional-order differentiator/integrator,” Journal of the Franklin Institute, vol. 340, no. 5, pp. 349–362, 2003. [Google Scholar]

26. C. A. Monje, Y. Q. Chen, B. M. Vinagre, D. Xue and V. Feliu-Batlle, Fundamentals of fractional-order systems. London: Springer, 2010. [Google Scholar]

27. G. Franklin, J. Powell and A. Naeini, Feedback control of dynamic systems. USA: Addison-Wesley, 1986. [Google Scholar]

28. R. E. Gutiérrez, J. M. Rosário and J. T. Machado, “Fractional order calculus: Basic concepts and engineering applications,” Mathematical Problems in Engineering, vol. 2010, no. 1, pp. 1–19, 2010. [Google Scholar]

29. Y. Luo, Y. Q. Chen, C. Y. Wang and Y. G. Pi, “Tuning fractional order proportional integral controllers for fractional order systems,” Journal of Process Control, vol. 20, no. 7, pp. 823–831, 2010. [Google Scholar]

30. H. Malek, Y. Luo and Y. Q. Chen, “Identification and tuning fractional order proportional integral controllers for time delayed systems with a fractional pole,” Mechatronics, vol. 237, no. 7, pp. 746–754, 2013. [Google Scholar]

31. Y. Chen and K. L. Moore, “Relay feedback tuning of robust PID controllers with ISO-damping property,” IEEE Transactions on Systems, Man and Cybernetics Systems, vol. 35, no. 1, pp. 23–31, 2005. [Google Scholar]

32. N. Kanagaraj, M. A.Dhaifalla and K. S. Nisar, “Design of intelligent fuzzy fractional-order PID controller for pressure control application,” in Proc. of IEEE Int. Conf. on Intelligent Computing, Instrumentation and Control Technologies, Kerala, India, pp. 525–530, 2017. [Google Scholar]

33. T. Aleksei, P. Eduard and B. Juri, “FOMCON fractional-order modeling and control toolbox for MATLAB,” in Proc. of 18th Int. Conf. Mixed Design of Integrated Circuits and Systems, Poland, pp. 684–689, 2011. [Google Scholar]

34. S. Stefanescu, “Applying Nelder-Mead’s optimization algorithm for multiple global minima,” Romanian Journal of Economic Forecasting, vol. 4, no. 4, pp. 97–103, 2007. [Google Scholar]