Explainable Heart Disease Prediction Using Ensemble-Quantum Machine Learning Approach

1  Introduction

Healthcare is one of the most influential fields on the global population’s safety. The continuous evolution of the healthcare sector facilitates disease prediction, treatment, diagnosis, and cure. The advancement of research and technologies in healthcare and public health has significantly decreased global mortality, with the advanced healthcare system helping in the prevention of disease progression and improvement of life quality. However, the healthcare sector has recently experienced an explosion of data and increased system complexity. The scope and quality of healthcare data open up new opportunities for healthcare practitioners to utilize advances in data science to extract valuable insights from these enormous databases. Advancements in data analytics, computing power, and algorithms are rapidly changing the prospect of healthcare by improving clinical and operational decision-making [1]. Artificial intelligence’s (AI) ability to derive conclusions from input data has the potential to revolutionize the delivery of care and assist in addressing a variety of healthcare challenges. Indeed, AI can improve healthcare outcomes, healthcare systems, patient experience, and treatment. The investment of AI in healthcare is growing rapidly, as it increases the efficiency and effectiveness of care delivery and enables healthcare systems to provide care to more people [1]. Machine learning (ML) is a subfield of artificial intelligence used to solve specific problems, such as predictive problems, by teaching a model to learn from an input dataset to predict the output. Machine learning plays a crucial role in the healthcare industry, where it is primarily used to assist in decision-making for a variety of diseases involving prediction, diagnosis, and medical image analysis [2]. Ensemble learning (EL) is a notable technique for enhancing the performance of these machine learning models. EL refers to the application of ensemble methods in which multiple ML models individually contribute to the prediction task. They have been demonstrated to be a successful addition to the field of predictive ML models, as their predictive performance is superior to that of their constituents. On another side, quantum machine learning (QML), the intersection of classical machine learning and quantum computing, is a recently developed field that has attracted researchers from a variety of disciplines due to its flexibility, representation power, and promising scalability and speed results. Quantum computers take advantage of quantum mechanical properties to improve the processing efficiency of classical computers. Consequently, QML algorithms running on quantum computers have the potential to perform extremely rapid calculations for problems that are challenging to solve with classical computers. QML can handle complex medical situations and improve system performance, thereby providing substantial benefits to the healthcare industry. Quantum computing can enable a variety of quantum use cases that are essential to the ongoing transformation of healthcare, such as diagnostic assistance, precision medicine, and price optimization. Numerous studies have demonstrated that QML algorithms offer substantial advantages over traditional machine learning algorithms for a variety of applications, including healthcare [3,4].

Cardiovascular diseases (CDVs) is a medical term that refers to diseases that affect both the heart and blood vessels and can lead to heart attack, stroke, and heart failure. According to the World Health Organization (WHO), CDVs cause approximately 17.9 million deaths annually, or 32% of all deaths worldwide. Among the risk factors for these diseases are high blood pressure, high blood glucose levels, obesity, and high blood lipid levels [5]. Heart disease is among the most prevalent cardiovascular diseases that threaten global public health. The prevalence of heart disease and consequently the increased risk of death pose a grave threat to human security. In order to prevent the disease’s progression and lessen its long-term effects, it is crucial to investigate the early detection of heart disease through specific physical indicators. The treatment of heart disease has been an active area of research for a very long time, so that preventative measures can be taken in the early stages. Consequently, a number of researchers utilized machine learning techniques to predict heart disease risks. A variety of medical fields have adopted machine learning strategies, as researchers strive to enhance and optimize medical decision-making. Methods of machine learning are primarily used to automatically detect patterns in the intended dataset, without the need for human intervention. However, classical machine learning approaches can be enhanced to obtain better results and more reliable models by employing various machine learning techniques, such as ensemble learning, which has been shown to improve the performance of models in predicting heart disease [6–10]. Alternatively, quantum computing can provide a more efficient framework for machine learning than classical approaches. Quantum machine learning is a relatively new field of study that has made considerable progress in recent years. Motivated by the development of various machine learning models to predict the risk of heart disease and in an effort to improve classification performance, the objective of this study was to explore the potential of ensemble learning in addition to quantum machine learning for predicting the risk of heart disease by designing an ensemble learning model based on a quantum machine learning model. Given the fact that machine learning methods can provide accurate solutions for predicting the presence of heart disease, the research was conducted using both well-known classical machine learning algorithms and quantum machine learning algorithms.

This research utilized a four-step methodology: Initially, the data are prepared using multiple pre-processing techniques, including feature selection, feature extraction, and normalization. Second, analyzing the performance of classical machine learning classifiers such as Support Vector Classifier (SVC) and Artificial Neural Network (ANN) and quantum machine learning classifiers to investigate the potential of QML models in comparison to traditional ones. Then, applying three distinct quantum machine learning classifiers namely Quantum Support Vector Classifier (QSVC), Quantum Neural Network (QNN), and Variational Quantum Classifier (VQC)). The objective of this step is to identify the best performing QML model for the given dataset. Finally, designing, applying and evaluating a Quantum Support Vector Classifier-based bagging ensemble learning model (Bagging-QSVC). In addition to explaining the significance and indication of the findings, the interpretation of a machine learning model facilitates the understanding of why a particular decision was made. The interpretability of the proposed model, where the importance and contribution of each feature to the prediction are computed and visualized using the SHapley Additive exPlanations (SHAP) framework, is thus another novel aspect of this work. To evaluate the models, several performance metrics, including accuracy, recall, precision, F1-score, and ROC, were calculated, with the results indicating that the quantum classifiers outperform the classical classifiers in terms of performance. In addition, the study demonstrated that ensemble learning yields superior predictive performance for quantum classifiers compared to classical classifiers. In addition, it can be deduced that combining ensemble learning with quantum classifiers can produce successful results.

The remaining sections are organized as follows. In Section 2, a review of related work is presented. Section 3 is devoted to the description of the background material used in this study, which is comprised of the two main ingredients EL and QML, as well as the methodology employed, with a focus on the data set, the investigated models, and the proposed ensemble model. Section 4 provides the experimental study, obtained results, and model interpretation. In Section 5, conclusions and future work are drawn.

2  Related Work

Machine learning classification algorithms are vastly utilized in many fields to solve numerous problems. A field such as healthcare is considered a rich machine learning domain, where machine learning can be employed to tackle various medical decisions. Heart disease is a major health problem investigated by researchers using novel machine learning methods. Ensemble learning is one of the machine learning methods that has proven to boost machine learning performance. A remarkable number of previous works utilized ensemble learning to improve the accuracy of heart disease prediction using multiple methodologies. In the light of recent past studies, Gao et al. [6] used boosting and bagging ensemble learning methods besides Principal Component Analysis (PCA) and Linear Discriminant Analysis (LDA) feature extraction algorithms to improve heart disease prediction. The study also applied five different classical machine learning algorithms and compared their performance with the performance of the ensemble learning methods. The results of the experiment indicated that the bagging ensemble learning method based on the decision tree classifier and principal component analysis feature selection achieved the highest accuracy. Another study conducted by Mienye et al. [7] proposed an enhanced machine learning method that splits up the dataset randomly into smaller subsets, and the different subsets are then modelled by making use of the Classification and Regression Tree (CART). An ensemble learning model is then generated from the different CART models using a modified version of the Weighted Aging classifier Ensemble approach (WAE) known as Accuracy-Based Weighted Aging classifier Ensemble (AB-WAE). Latha et al. [8] presented a more comprehensive study that applied to the Cleveland heart disease dataset using bagging, boosting, majority voting, and stacking ensemble learning techniques. The result of the study showed that the majority voting approach induced the highest improvement of accuracy. In a slightly different manner, Anuradha et al. [9] modelled eXtreme Gradient Boosting (XGBoost), and Category Boosting (CatBoost) classifiers together with hard majority voting ensemble classifier on three different datasets, namely, Cleveland, Statlog, and South African heart disease. The outcomes of the study revealed that the hard majority vote ensemble classifier achieved the best performance on the Statlog dataset. Practically, Uddin et al. [10] evolved an intelligent agent using an ensemble method-based Multilayer Dynamic System (MLDS) to predict cardiovascular disease. In every layer, three classification algorithms (i.e., Random Forest (RF), Naïve Bayes (NB), and Gradient Boosting (GB)) were applied to construct the ensemble model. Uddin and Halder used a realistic dataset consisting of 70,000 instances to test the proposed model effectively. The test results showed that MLDS has proven to be able to efficiently predict the risk of cardiovascular disease compared to five other different models. In the same context, Rahim et al. [11] suggested a Machine Learning-based Cardiovascular Disease Diagnosis framework (MaLCaDD) to improve the prediction accuracy of cardiovascular diseases. Rahim et al. stated that increasing the accuracy of the prediction using various feature selection and classification methods has taken the most attention of the researchers. However, handling missing values and class imbalance problems gained less attention while improving accuracy. In a more improved manner, Ali et al. [12] enhanced the automation process of heart disease prediction by developing a smart monitoring framework that consists of a heart disease prediction system based on an ensemble deep learning approach in addition to an ontology-based recommendation system. The ensemble deep learning model comprises a feed-forward neural network along with back-propagation techniques and gradient algorithms to minimize the errors. In the past decade, Das et al. [13] investigated the performance of bagging, Adaptive Boosting (Adaboost), and random subspace ensemble learning methods for diagnosing valvular heart disease. The empirical results of the study proved the efficiency of the ensemble learning approach over the single classifiers.

Among several studies, the majority voting ensemble learning approach is largely used in the literature of heart disease [2,8,10,14]. Raza [2] ensembled three different classifiers (i.e., Logistic Regression (LR), Naïve Bayes (NB), and Artificial Neural Network (ANN)), and combined the results of these classifiers using a majority voting combiner which provided better performance over other combiners. Raza mentioned the three different forms of majority voting approach, which are unanimous voting, simple majority, and plurality voting. Likewise, Mehanović et al. [14] applied an ensemble learning model using Artificial Neural Network (ANN), k-Nearest Neighbour (KNN), and Support Vector Machine (SVM) classifiers to predict heart disease in patients using binary classification (0 for the absence of disease and 1 for the presence), and multi-classification (0 for the absence of disease and 1, 2, 3, 4 for the presence). In both classification cases, the highest accuracies were gained by using the majority voting approach.

On other hand, few researchers have addressed the ensemble learning approach besides quantum machine learning to solve the heart disease prediction problem [4]. Schuld et al. [15] applied quantum ensemble learning on quantum classifiers, where quantum classifiers were assessed in parallel, and their integrated decision was accessed by a qubit measurement. Kumar et al. [4] utilized QML to detect heart failure on the Cleveland dataset. The empirical study proved that quantum-enhanced machine learning algorithms such as Quantum K-Nearest Neighbour (QKNN), Quantum Gaussian Naïve Bayes (QGNB), Quantum Decision Tree (QDT), and Quantum Random Forest (QRF) present better results than traditional machine learning algorithms in heart failure detection. In another context, Maheshwari et al. [16] implemented multiple ensemble learning models that combine classical and quantum methods on a diabetes dataset. The classical ensemble learning methods used in the study were Random Forest (RF), XGBoost, and Adaboost, whereas, the Quantum Boosting (QBoost) classifier was the quantum ensemble learning method that uses Quantum Annealing (QA) to find the best learners collection. Our work expands on these efforts by investigating the potential of quantum machine learning-based ensemble learning in heart disease prediction while explaining the model’s outcomes. This study investigates several classical and quantum machine learning classifiers as well as a novel heart disease prediction model to achieve accurate heart disease prediction. The novel model combines ensemble learning with quantum machine learning. In addition, this is the first study to propose an interpretation of the heart disease prediction model using the Cleveland data set and the proposed model based on the SHapley Additive exPlanations (SHAP) framework. To the best of our knowledge, no previous studies have looked into this.

3  Materials and Methods

3.1 Ensemble Learning

The field of machine learning investigates algorithms and techniques that allow computers to automatically find solutions to complex problems that traditional programming methods cannot solve. Machine learning can be leveraged to provide insights into the pattern in a dataset by trying to design an efficient model that learns from a training dataset to predict outcomes [17,18]. Typically, the success of machine learning algorithms is determined by the structure of the data, which can be learned in a variety of ways. However, the ML model’s balanced complexity is critical for obtaining accurate results. All ML algorithms have some level of bias and variance, where a model with higher bias does not fit training and test data well due to the model’s low complexity, whereas a model with higher variance does not fit test data well but has a much lower error on training data due to the model’s high complexity. In general, there are four learning models in machine learning, namely, supervised learning, unsupervised learning, semi-supervised learning, and reinforcement learning [17]. Machine learning applications are used in a wide range of fields, including Natural Language Processing (NLP), speech processing, computer vision, text classification, and computational biology [18].

Ensemble learning is a popular machine learning approach that combines several models and then assembles their outputs to make more accurate predictions [18,19]. In fact, each learning algorithm has strengths and weaknesses since it is not expected for a single model to fit all scenarios correctly. As a result, rather than creating a single model that may result in poor performance, ensemble learning techniques aggregate various models to achieve better generalization performance than any of the ensemble model’s single basic components [19,20]. Ensemble learning was initially developed to reduce variance in automated decision-making systems, but it has since gained widespread attention due to its flexibility and effectiveness in a variety of machine learning areas and experimental applications. A variety of machine learning problems, including feature selection, class imbalanced data, confidence estimation, incremental learning, missing feature, and error correction, have been addressed using ensemble learning systems [21]. In general, three approaches are commonly used to generate ensemble systems: bagging, boosting, and stacking, as well as improved versions of these methods that developed to solve specific problems [22].

The bagging or (bootstrap aggregation) method produces one model at a time from a random sample or (bootstrap sample) that has the same size as the dataset [19]. As a result, models trained on dissimilar bootstrap samples will differ depending on the random bootstrap sample used to train the model [2]. The final prediction is generated after fitting and aggregating the models by calculating the average or majority voting of the overall prediction models. When results from multiple models are combined, the bagging ensemble model can produce an optimal model with higher confidence, lower variance, and lower bias error than single models. Random Forests (RF), which is based on the decision-tree algorithm, and K-Nearest Neighbour (KNN) subspace bagging, which is based on the k-Nearest Neighbour algorithm, are two significant extensions of the bagging approach [22].

3.2 Quantum Machine Learning

Personal computers are working on the concept of classical mechanics, which uses a bit of 0 or 1 as a fundamental unit of electronic circuits. However, quantum machines employ a quantum bit (or qubit) that can simultaneously occupy two fundamental states, 0 and 1 [23]. This property of quantum machines is known as the superposition of states, in which a qubit can be in both |0⟩ and |1⟩ states at the same time. The superposition of the states allows the operations to run in parallel rather than sequentially, reducing the number of operations required in any algorithm [24]. Furthermore, quantum computers make use of the entanglement property, which allows quantum particles to gain a stronger correlation by connecting to the properties of other particles. As a result, despite large physical distances, the qubits can be correlated with each other [25]. These quantum physics behaviours give quantum machines an advantage over classical machines by speeding up many tasks that would otherwise take a very long time using classical algorithms [23]. In quantum mechanics, the basis states 0 and 1 are represented by two-dimensional vectors, where:

0→=[10]1→=[01] (1)

The state of a quantum system is given by a vector that has a particular notation in quantum systems called the Dirac notation which is denoted by ∣ψ⟩ [20]. The state ∣ψ⟩ can demonstrate the linear combination of the basis states |0⟩ and |1⟩ as presented in Eq. (2).

|ψ⟩=α|0⟩+β|1⟩ (2)

The linear coefficients alpha (α), and beta (β) belong to the complex numbers, i.e., α, β ∈ ℂ. The complex numbers α and β indicate that the qubit has a probability of |α|2 to appear in state |0⟩ and a probability of to appear in state |1⟩ [23]. Thus, the sum of the probabilities of a qubit to appear in each one of the basis states is equal to 1 as shown in Eq. (3).

|α|2+|β|2=1 (3)

A qubit can be visualized using a Bloch sphere which is a geometric representation of the qubit states. The continuous combination of the two states |0⟩ and |1⟩ can be placed in any potential points on the Bloch sphere. A qubit is represented on a Bloch sphere as a point on the surface of the sphere. Hence, a generic quantum state |ψ⟩ can be represented by the three parameters θ, γ and ϕ of real numbers, Where, 0 ≤ θ ≤ π and 0 ≤ ϕ ≤ 2π, as shown in Eq. (4).

|ψ⟩=eiγ(cos⁡(θ2)|0⟩+ei∅sin⁡(θ2)|1⟩) (4)

The global factor eiγ has no noticeable impact among other factors, thus it can be neglected in the equation. Therefore, Eq. (5) illustrates the final equation after omitting the eiγ factor [26].

|ψ⟩=cos⁡(θ2)|0⟩+ei∅|1⟩ (5)

The states in quantum computing can be represented in the Bloch sphere as a vector that starts at the original centre and ends on the sphere surface, where the vector is represented by an arrow pointing to a location on a sphere. The three-dimensional graphical representation of a single qubit using the Bloch sphere is represented in Fig. 1.

Figure 1: Qubit representation using Bloch sphere

Quantum Machine Learning (QML) field represents the intersection between the concepts of machine learning and quantum computing [25]. Quantum algorithms were developed in quantum machine learning to handle classical algorithms using quantum computers [27]. Quantum machine learning offers a great opportunity to improve the computational proficiency of classical machine learning algorithms and handle some of the more computationally complex problems that classical machine learning algorithms cannot effectively solve [23,28]. Quantum machine learning applies classical machine learning methods in quantum systems by using various quantum properties such as superposition and entanglement that were mentioned previously. The superposition of states property produces parallelism in quantum computers, allowing the evaluation of multiple input functions at the same time. Furthermore, the entanglement property provides a method for increasing storage capacity [27]. These two and other QML properties improve the performance of classical machine learning algorithms by providing significant computational acceleration at run-time based on complexity. Grover’s Algorithm and the Harrow-Hassidim-Lloyd (HHL) Algorithm [25] are the two main quantum algorithms used by machine learning techniques to gain speedup. Regardless of the speedup property of QML, research on quantum machine learning focuses on other types of QML properties that represent advancements in quantum machine learning techniques over classical ML, such as model complexity, sample complexity, and robustness to noise [29]. Furthermore, several quantum algorithms, such as the Quantum Support Vector Machine (QSVC), Quantum Clustering technique, Quantum Neural Network (QNN), and Quantum Decision Tree, were developed to run classical algorithms on quantum computers (QDT). As a result, using supervised and unsupervised quantum algorithms implemented through quantum models, the data can be classified, categorized, and analysed [27].

3.3 Methodology

The purpose of this study is to investigate the potential of quantum machine learning algorithms for predicting heart disease. As a result, the research was divided into four distinct phases, the first of which dealt with the Cleveland dataset using various pre-processing techniques, including Recursive Feature Elimination (RFE) for feature selection, Principal Component Analysis (PCA) for feature extraction, and Min-Max normalization. In the second phase, classical classifiers (SVC and ANN) were compared to quantum classifiers. Three different quantum machine learning classifiers (QSVC, QNN, and VQC) were investigated in the third phase. Finally, a bagging ensemble learning model based on Quantum Support Vector Classifier (Bagging-QSVC) has been designed and implemented.

3.3.1 Dataset

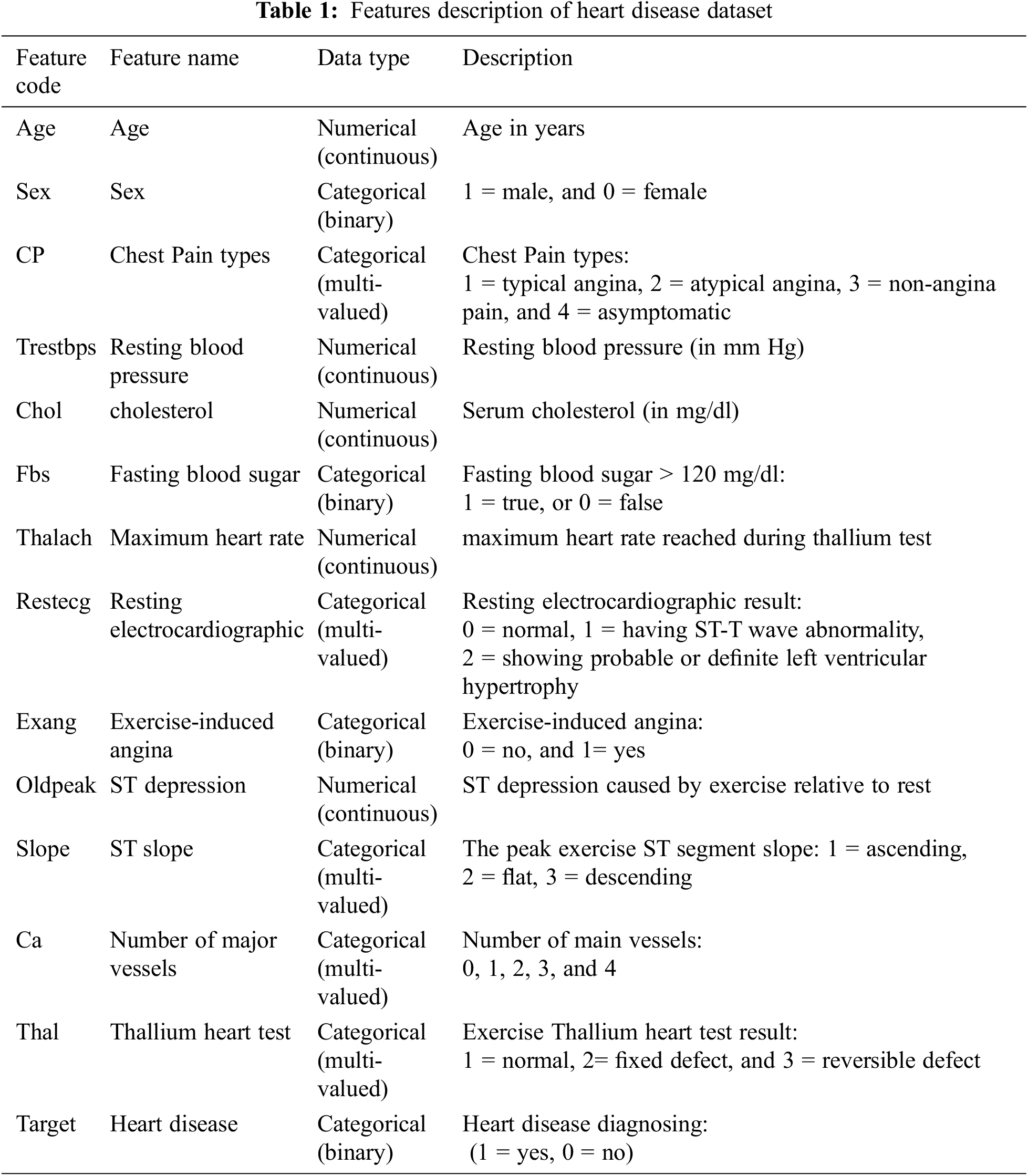
This research uses the UCI machine learning repository’s [30] Cleveland benchmark dataset. The Cleveland dataset consists of 303 instances and 14 attributes, with a two-level target attribute representing a binary classification where label 1 indicates patients with heart diseases and 0 indicates patients without heart disease. Since 165 instances have label 1 and 138 instances have label 0, the dataset is roughly balanced. Tab. 1 describes the Cleveland dataset’s features.

3.3.2 Quantum Support Vector Classifier (QSVC)

In quantum computers, Quantum SVC is the quantum counterpart of the classical SVC. Since the classical SVC handles problems in higher dimension space, the computational resources required to solve them on classical computers can be costly and time-consuming [26]. The QSVC has a quantum advantage over the classical SVC in situations where it is difficult to estimate the feature map classically. Using a quantum kernel in QSVC algorithms, quantum computers can accelerate learning in SVC by using a quantum kernel. To investigate the potential of QSVC, the classical-quantum (CQ) method was used, which entails utilizing a classical dataset on quantum computers. Using quantum feature maps that map data points to quantum states, classical data can be encoded to be processed by a quantum computer [24]. Fig. 2 depicts the structure of the QSVC algorithm, in which the dataset was divided into training and testing datasets with ratios of 80:20 respectively, and pre-processed with RFE and Min-max normalization. The classical feature vectors were subsequently mapped to quantum spaces using a 5-qubit feature map (the number of qubits in the circuit is equal to the number of selected features namely Number of major vessels, Chest Pain types, Thallium heart test, Exercise-induced angina, and ST-slope. By taking the inner product of the quantum feature maps, the quantum kernel maps the quantum state data points into higher-dimensional space. After fitting the QSVC classifier to the training data and evaluating the performance of the model using the test data, for each classical input, the binary measurements decode the quantum data into the corresponding classical output data (a classical value of 0 or 1).

Figure 2: QSVC outline

3.3.3 Quantum Neural Network (QNN)

Quantum Neural Networks combine the fundamentals of conventional ANN with quantum computation models that outperform conventional ANN [31]. QNN is an algorithm for machine learning that employs quantum computers to classify datasets by training various parameters within quantum circuits. QNN can be used to solve problems requiring a large amount of memory and capacity [24]. Fig. 3 depicts the structure of the QNN algorithm where the dataset was divided into training and testing datasets using 8-fold cross-validation, and pre-processed using RFE, PCA and Min-max normalization. Thereafter, the classical feature vectors are mapped to quantum spaces using a feature map of 2 qubits (the number of qubits in the circuit is equal to the number of PCA components). A CircuitQNN network that is based on a parametrized quantum circuit was constructed after that to get the input data and weights as parameters and produces a batch of binary output. After fitting the QNN classifier with the training data and testing the model performance using cross-validation iterators, the binary measurements decode back the quantum data into appropriate output data (a classical value of 0 or 1).

Figure 3: QNN classifier outline

3.3.4 Variational Quantum Classifier (VQC)

Variational Quantum Classifier [24] is a quantum supervised learning algorithm that employs variational circuits to perform classification tasks. In quantum variational classification, the data is mapped to a quantum state using the feature map circuit, and a parameterized and trained short-depth quantum circuit is applied to the feature state [32]. Fig. 4 presents the outline of the VQC algorithm where the dataset was divided into training and testing datasets with ratios of 80:20 respectively, and pre-processed using RFE, PCA and Min-max normalization. Thereafter, the classical feature vectors are mapped to quantum spaces using a feature map of 2 qubits (the number of qubits in the circuit is equal to the number of PCA components). After fitting the VQC classifier with the training data and testing the model performance using the test data, the binary measurements decode the quantum data into a classical value of 0 or 1.

Figure 4: VQC outline

3.3.5 The Proposed Bagging Model for Heart Disease Prediction

Since it has been proven that ensemble learning enhances the performance of the models, the model proposed in this work consists of a bagging ensemble model with QSVC Classifier (Bagging-QSVC). QSVC was chosen with the bagging model because it achieved the highest performance among the three quantum classifiers. Nevertheless, in the bagging ensemble method, each model was trained on a random sample of the dataset, where the random samples (or bootstrap samples) have the same size as the original dataset. Bagging models make use of sampling with a replacement that duplicates or ignores some instances from the original dataset in each bootstrap sample. Therefore, each subsample had different instances, and these subsamples were used to train 100 different QSVC models that fitted in parallel. Subsequently, once the separated models in the ensemble had been trained, the ensemble aggregated their predictions by returning the class that gained the majority of the votes to get the final output of the ensemble model. The proposed Bagging-QSVC model is illustrated in Fig. 5.

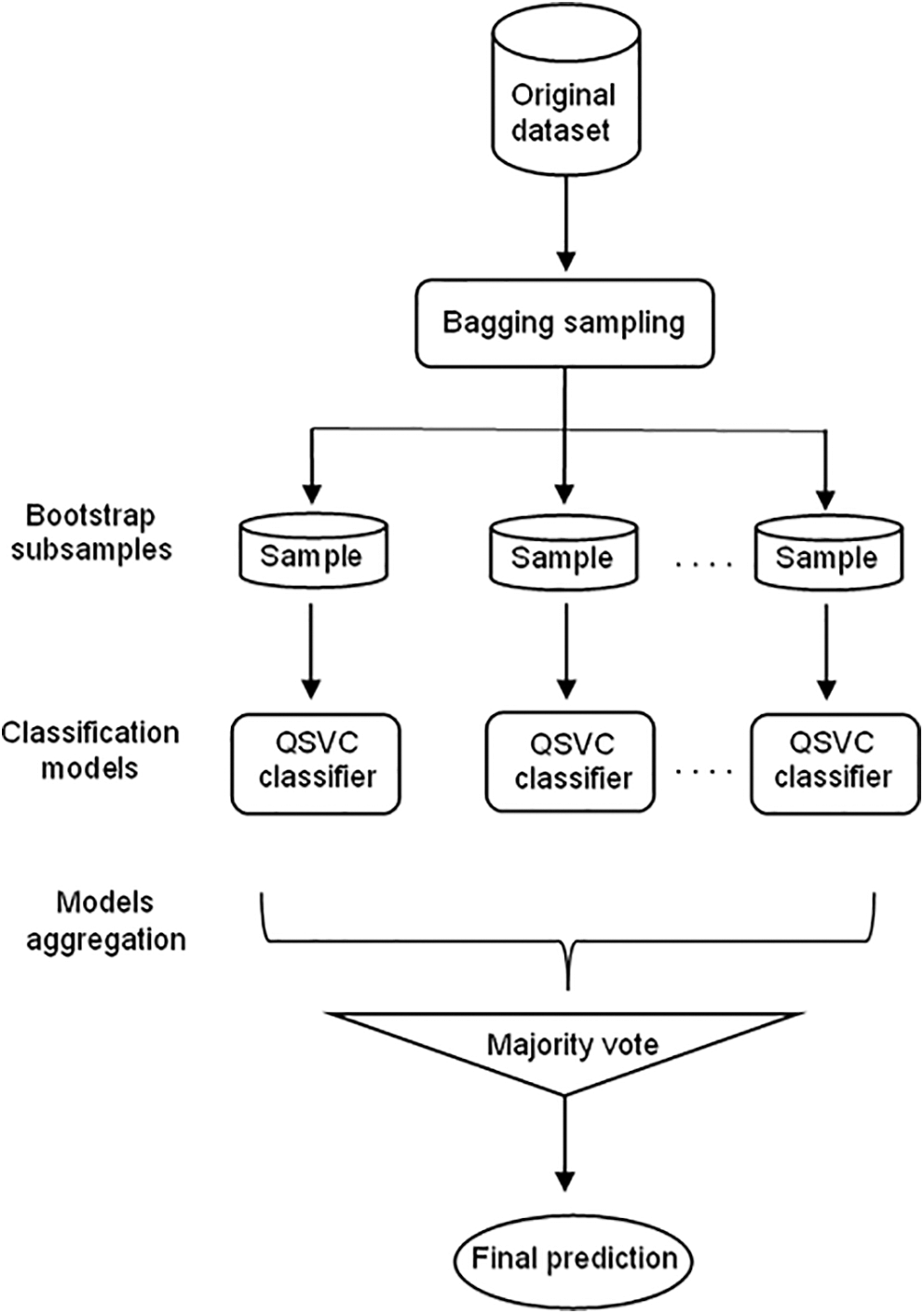
Figure 5: Bagging-QSVC architecture

4  Experimental Study and Results

4.1 Experimental Setups

The experimental study was conducted using qiskit in jupyter notebook and python. The code is accessible at [33]. In addition to quantum and classical classifiers, the Bagging-QSVC model was implemented on a simulator. The simulator was operating on a computer system with a 7th generation Core i7 processor and 8 GB of RAM.

4.2 Results and Discussion

To evaluate the performance of the predictive models applied in this work (QSVC, SVC, QNN, ANN, VQC, and Bagging-QSVC), a set of performance measures including accuracy, precision, recall, F1-measure and area under the curve (AUC) or ROC index have been used. The definitions and equations of these performance measures are provided below Eqs. (6)–(9), where True Positive (TP) represents the positive instances classified correctly, True Negative (TN) represents the negative instances classified correctly, False Positive (FP) represents the positive instances classified incorrectly, and False Negative (FN) represents the negative instances classified incorrectly.

– Accuracy: The percentage of the total number of instances that are correctly classified relative to the number of all tested instances.

Accuracy=TP+TNTP+FP+TN+FN (6)

– Precision: The ratio between the number of positive instances that are correctly classified and all instances predicted as positive. The precision presents how confident an instance predicted with a positive target actually has a positive target level.

Precision=TPTP+FP (7)

– Recall (or sensitivity): The ratio between the positive instances and the number of all actual positive instances. The recall presents how confident all the instances with a positive target the model found.

Recall=TPTP+FN (8)

– F1-measure: The harmonic mean of precision and recall measures. The F-measure, precision, and recall can assume values in the range [0,1], where the larger values indicate better performance.

F1measure=2×(Precision×Recall)(Precision+Recall) (9)

– The ROC index (or Area Under the Curve): The ROC curve relates the True Positive Rate (TPR) (the positive points correctly predicted as positive) to the False Positive Rate (FPR). The diagonal of the ROC curve represents the expected performance of a model with random predictions, while the closer the curve is to the upper left corner (or a higher AUC value), the more predictive the model. The ROC index or AUC can take on values between 0 and 1, with larger values indicating superior model performance [19].

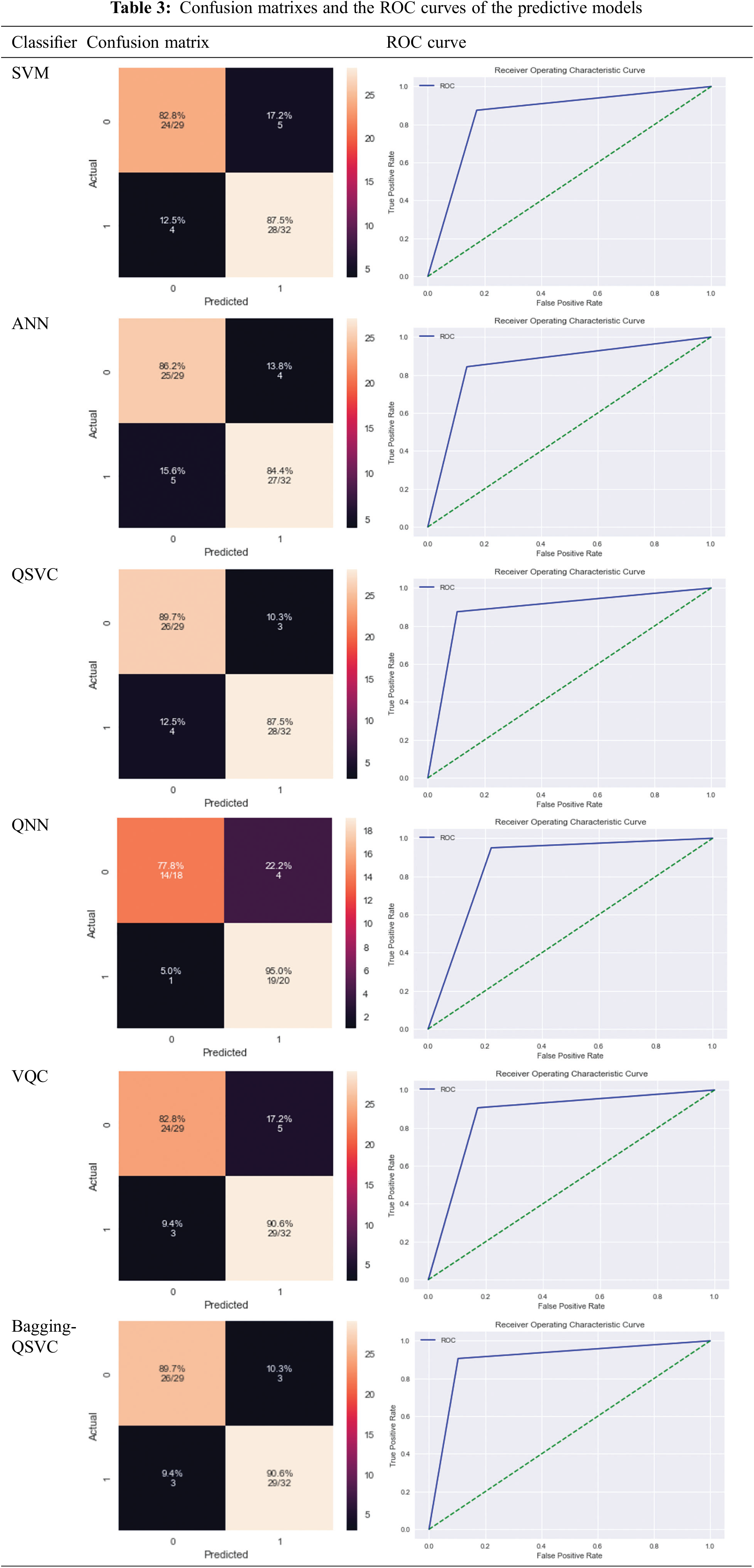
Tab. 2 shows the results based on the aforementioned performance measures of the classical and quantum classifiers, as well as the proposed model (Bagging-QSVC). According to the results of the experiment, QSVC achieved an accuracy of 88.52%, while traditional SVC achieved 85.24%. Similarly, QNN achieved an accuracy of 86.84%, whereas ANN only achieved 85.24%. QSVC, QNN, and VQC achieved the highest performance for quantum classifiers with 88.52%, 86.84%, and 85.25%, respectively. This indicates that quantum classifiers are capable of producing better results than their counterpart classical classifiers. On the other hand, Tab. 2 depicts the improvement of the proposed model (or Bagging-QSVC) relative to other quantum and classical classifiers through the use of ensemble learning. The Bagging-QSVC outperformed all other classifiers with an accuracy of 90.16%, indicating that ensemble learning improves the performance of quantum classifiers. Tab. 3 also depicts the confusion matrix and the ROC curve of the predictive models.

The comparative analysis shows that the proposed Bagging-QSVC outperforms some previous studies in predicting heart disease with improved accuracy. Tab. 4 compares the results of our proposed model and models of other studies applied to the same dataset using different ensemble learning approaches.

4.3 Model Interpretation

The SHapley Additive exPlanations (SHAP) framework was used to interpret and explain the model results [36]. As a result, the SHAP python library was used to compute and visualize the significance of each and every feature in the prediction. The calculation of SHAP values is the foundation of this framework. A SHAP value is a feature contribution measure that is used to improve the interpretability of machine learning models. SHAP values explain how to get from the predicted or base value E[f(x)] to the actual output f if the features are unknown (x). These values also show how features influence prediction by indicating the direction of the relationship between the features and the target variable. A feature with a SHAP value closer to 1 or −1 has a strong positive or strong negative contribution to the prediction of a specific data point, whereas a feature with a SHAP value closer to 0 has a small contribution to the prediction [36]. Several plots that help to understand the contribution of features can be obtained using this framework.

4.3.1 SHAP Beeswarm Plot

The Beeswarm plot represents feature importance in descending order, as well as feature impacts on prediction, whether positive or negative. The SHAP values are used to depict the impact of higher and lower feature values on the model output. The feature determines the position on the y-axis, and positive and negative SHAP values determine the position on the x-axis. Each point in the plot represents a single observation, and the colour represents how the higher and lower values of the feature affect the result, with red representing a higher value and blue representing a lower value of a feature. Fig. 6 shows the Beeswarm plot for our model. It can be observed clearly that the number of major vessels has the greatest influence on the predictions, followed by the thallium heart scan. Exercise-induced angina, on the other hand, has the smallest change in the prediction of heart disease probability and thus has the least importance. The feature values are also shown in Fig. 6 to represent the impact of each feature on the prediction. For example, ST slop values (1 = ascending, 2 = flat, and 3 = descending) indicate that ascending and flat ST slop are associated with a lower risk of heart disease, whereas descending ST slop is associated with a higher risk of heart disease.

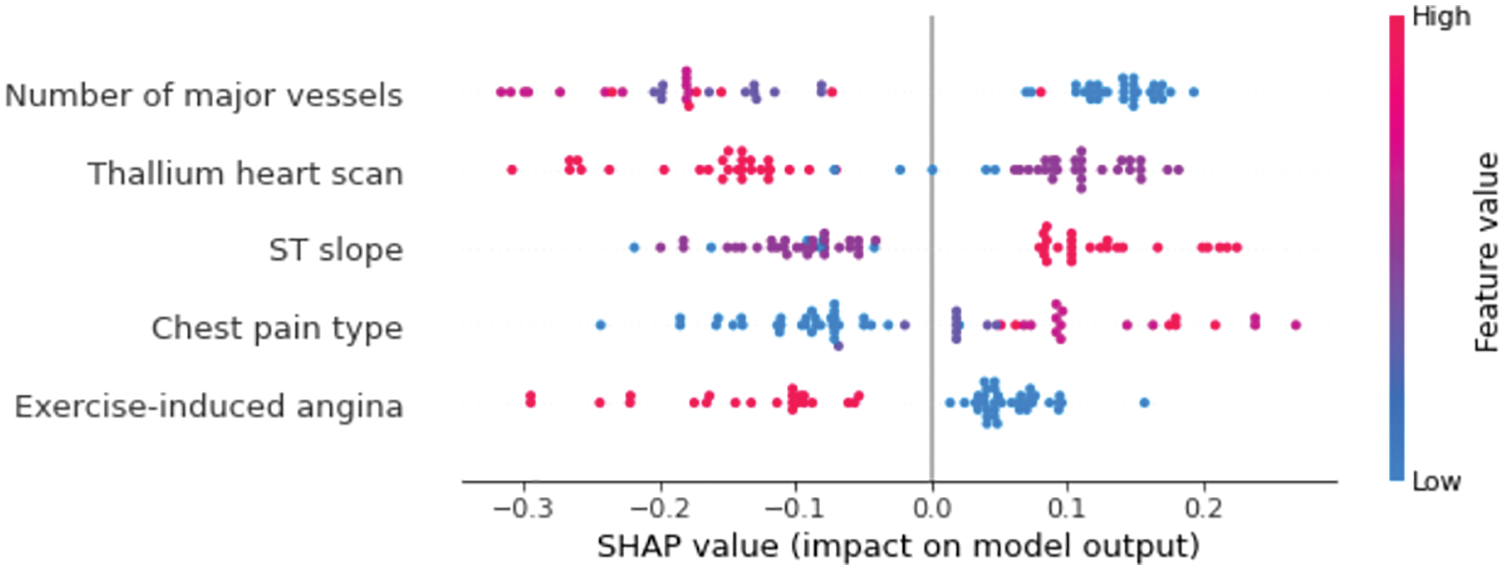
Figure 6: SHAP Beeswarm plot

4.3.2 SHAP Force Plot

The SHAP force plot visualizes the SHAP values of each feature as a force that either increases or decreases the prediction, representing the contribution of each feature to the model’s prediction of a particular observation. Each feature's force is represented by a red or blue arrow, depending on whether it increases or decreases the model's score. The features that have a greater influence on the prediction are located closer to the dividing line, and the size of the arrow represents the magnitude of this influence. The force plot illustrates the significance of each feature in adjusting the model to increase or decrease the prediction based on a SHAP value baseline. These characteristics counterbalance one another to determine the final prediction of the data instance. Fig. 7 shows our model’s force plot for a random observation. As can be seen, it reveals that the Chest Pain type has the greatest influence on the prediction, followed by Number of major vessels and Exercise-induced angina, respectively. These three predictive characteristics raise the model’s score (to the right), which should result in a final prediction of 1. Otherwise, Thallium heart scan and ST slop have less influence, which reduces the model’s predictive accuracy (to the left).

Figure 7: SHAP force plot

4.3.3 Stacked SHAP Force Plot

As implied by its name, the Stacked SHAP force plot combines multiple force plots, each of which depicts the prediction of an instance in the dataset. The Staked plot depicts the predictions for all samples in the dataset in a single plot by rotating the force plots of each instance by 90 degrees and stacking them vertically next to one another based on their clustering similarity. Each x-axis position represents an instance of the data, while each y-axis position represents the baseline prediction. The red SHAP values result in a higher prediction, whereas the blue SHAP values result in a lower prediction, and the values at the top of the vertical axis indicate a higher probability of being classified as class 1, whereas the values at the bottom of the vertical axis indicate a higher probability of being classified as class 0. Fig. 8 shows the model stacked SHAP force plot. Higher values on the vertical axis denote a greater likelihood of heart disease risk, whereas lower values denote a lesser likelihood of heart disease. Features that appear in red raise the model score (to the top), while features that appear in blue lower it (to the bottom).

Figure 8: Stacked SHAP force plot

5  Conclusion

Heart disease is a major cause of death, and early detection can help prevent the disease’s progression. Consequently, the objective of this study was to investigate the potential of quantum machine learning for predicting the risk of cardiovascular disease by developing an ensemble learning model based on quantum machine learning algorithms. The Bagging-QSVC model involves randomly subdividing the dataset into smaller subsets and modelling each subset using QSVC. Afterwards, an ensemble was formed using the majority voting method. On the Cleveland dataset, the proposed ensemble model achieved a higher classification accuracy of 90.16%, compared to 88.52%, 86.84%, and 85.25% for QSVC, QNN, and VQC, respectively, and 85.24% for both SVC and ANN. Accordingly, the various performance measures and ROC curves showed that the proposed model performed better than other machine learning models. According to the findings of this study, quantum classifiers are more effective than classical classifiers. Furthermore, results showed also that ensemble learning models can enhance the performance of quantum classifiers. In addition to predicting and diagnosing other cardiovascular diseases and aiding in medical decision-making, the model proposed in this study can be used for the early prediction of heart disease risk to avoid any serious consequences, as well as for predicting and diagnosing other cardiovascular diseases.

Acknowledgement: The authors would like to acknowledge the Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R196), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Data Availability: The data is publicly available at https://archive.ics.uci.edu/ml/datasets/heart+disease (accessed on 8 Feb 2022).

Funding Statement: This work is supported by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R196), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  EIT Health and McKinsey & Company, “Transforming healthcare with AI,” 2020. [Online]. Available: https://eithealth.eu/wp-content/uploads/2020/03/EIT-Health-and-McKinsey_Transforming-Healthcare-with-AI.pdf. [Google Scholar]

 2.  K. Raza, Improving the prediction accuracy of heart disease with ensemble learning and majority voting rule. In: U-Healthcare Monitoring Systems, 1st ed., vol. 1. New Delhi, India: Elsevier Inc, pp. 179–196, 2019. [Google Scholar]

 3.  IBM Institute for Business Value, “Exploring computing quantum use cases for healthcare,” 2020. [Online]. Available: https://www.ibm.com/thought-leadership/institute-business-value/report/exploring-quantum-financial#. [Google Scholar]

 4.  Y. Kumar, A. Koul, P. S. Sisodia, J. Shafi, K. Verma et al., “Heart failure detection using quantum-enhanced machine learning and traditional machine learning techniques for internet of artificially intelligent medical things,” Wireless Communications and Mobile Computing, vol. 2021, no. 1, pp. 1–16, 2021. [Google Scholar]

 5.  World Health Organization, “Cardiovascular diseases,” 2020. [Online]. Available: https://www.who.int/health-topics/cardiovascular-diseases#tab=tab_1. [Google Scholar]

 6.  X. Gao, A. A. Ali, H. S. Hassan and E. M. Anwar, “Improving the accuracy for analyzing heart diseases prediction based on the ensemble method,” Complexity, vol. 2021, pp. 1–10, 2021. [Google Scholar]

 7.  I. D. Mienye, Y. Sun and Z. Wang, “An improved ensemble learning approach for the prediction of heart disease risk,” Informatics in Medicine Unlocked, vol. 20, no. 8, pp. 1–5, 2020. [Google Scholar]

 8.  C. B. C. Latha and S. C. Jeeva, “Improving the accuracy of prediction of heart disease risk based on ensemble classification techniques,” Informatics in Medicine Unlocked, vol. 16, pp. 1–9, 2019. [Google Scholar]

 9.  P. Anuradha and V. K. David, “Feature selection and prediction of heart diseases using gradient boosting algorithms,” in Int. Conf. on Artificial Intelligence and Smart Systems (ICAIS 2021), Coimbatore, India, pp. 711–717, 2021. [Google Scholar]

10. M. N. Uddin and R. K. Halder, “An ensemble method based multilayer dynamic system to predict cardiovascular disease using machine learning approach,” Informatics in Medicine Unlocked, vol. 24, no. 7, pp. 1–19, 2021. [Google Scholar]

11. A. Rahim, Y. Rasheed, F. Azam, M. W. Anwar, M. A. Rahim et al., “An integrated machine learning framework for effective prediction of cardiovascular diseases,” IEEE Access, vol. 9, pp. 106575–106588, 2021. [Google Scholar]

12. F. Ali, S. El-Sappagh, S. M. R. Islam, D. Kwak, A. Ali et al., “A smart healthcare monitoring system for heart disease prediction based on ensemble deep learning and feature fusion,” Information Fusion, vol. 63, pp. 208–222, 2020. [Google Scholar]

13. R. Das and A. Sengur, “Evaluation of ensemble methods for diagnosing of valvular heart disease,” Expert Systems with Applications, vol. 37, no. 7, pp. 5110–5115, 2010. [Google Scholar]

14. D. Mehanović, Z. Mašetić and D. Kečo, “Prediction of heart diseases using majority voting ensemble method,” in IFMBE Proc., Banja Luka, Bosnia & Herzegovina, pp. 491–498, 2020. [Google Scholar]

15. M. Schuld and F. Petruccione, “Quantum ensembles of quantum classifiers,” Scientific Reports, vol. 8, no. 1, pp. 1–12, 2018. [Google Scholar]

16. D. Maheshwari, B. G. Zapirain and D. S. Soso, “Machine learning applied to diabetes dataset using quantum versus classical computation,” in IEEE Int. Symp. on Signal Processing and Information Technology (ISSPIT 2020), Louisville, KY, USA, pp. 1–6, 2020. [Google Scholar]

17. G. Rebala, A. Ravi and S. Churiwala, “Machine learning definition and basics,” in An Introduction to Machine Learning. Vol. 975. Cham, Switzerland: Springer Nature,1, pp. 1–16, 2019. [Google Scholar]

18. M. Mohri, A. Rostamizadeh and A. Talwalkar, “Introduction,” in Foundations of Machine Learning, 2nd ed., vol. 1. Cambridge, Massachusetts: The MIT Press, pp. 1–7, 2018. [Google Scholar]

19. J. D. Kelleher, B. M. Namee and A. D’Arcy, “Machine learning for predictive data analytics,” in Fundamentals of Machine Learning for Predictive Data Analytics: Algorithms, Worked Examples, And Case Studies, 2nd ed., vol. 1. Cambridge, Massachusetts: The MIT Press, pp. 3–21, 2020. [Google Scholar]

20. P. Wittek, Quantum computing. In: Quantum Machine Learning What Quantum Computing Means to Data Mining, 1st ed., vol. 34. Sweden: Elsevier Inc, pp. 41–52, 2014. [Google Scholar]

21. C. Zhang and Y. Ma, “Ensemble learning,” in Ensemble Machine Learning Methods and Applications. Vol. 1. USA: Springer, pp. 1–34, 2012. [Google Scholar]

22. A. Dixit, “Introduction to ensemble learning,” in Ensemble Machine Learning. Vol. 1. Birmingham, UK: Packt Publishing Ltd., pp. 32–55, 2017. [Google Scholar]

23. S. Pattanayak, “Introduction to quantum computing,” in Quantum Machine Learning with Python. Vol. 1. Bangalore, India: Apress, pp. 1–43, 2021. [Google Scholar]

24. S. Ganguly, “Rise of the quantum machines: fundamentals,” in Quantum Machine Learning: An Applied Approach. Vol. 1. Ashford, UK: Apress, pp. 1–39, 2021. [Google Scholar]

25. A. Jhanwar and M. J. Nene, “Enhanced machine learning using quantum computing,” in 2nd Int. Conf. on Electronics and Sustainable Communication Systems (ICESC 2021), Coimbatore, India, pp. 1407–1413, 2021. [Google Scholar]

26. M. Senekane, Getting started with quantum information processing. In: Hands-On Quantum Information Processing With Python. Vol. 1. Birmingham, UK: Packt Publishing Ltd., pp. 4–10, 2021. [Google Scholar]

27. N. Mishra, M. Kapil, H. Rakesh, A. Anand, N. Mishra et al., “Quantum machine learning: A review and current status,” in Data Management, Analytics and Innovation. Advances in Intelligent Systems and Computing. Vol. 1175. New Delhi, India: Springer, pp. 101–145, 2021. [Google Scholar]

28. J. Biamonte, P. Wittek, N. Pancotti, P. Rebentrost, N. Wiebe et al., “Quantum machine learning,” Nature, vol. 549, no. 7671, pp. 195–202, 2017. [Google Scholar]

29. L. Alchieri, D. Badalotti, P. Bonardi and S. Bianco, “An introduction to quantum machine learning: From quantum logic to quantum deep learning,” Quantum Machine Intelligence, vol. 3, no. 2, pp. 1–30, 2021. [Google Scholar]

30. UCI Machine Learning Repository, “Heart disease data set,” 1988. [Online]. Available: https://archive.ics.uci.edu/ml/datasets/heart+disease. [Google Scholar]

31. S. K. Jeswal and S. Chakraverty, “Recent developments and applications in quantum neural network: A review,” Archives of Computational Methods in Engineering, vol. 26, no. 4, pp. 793–807, 2019. [Google Scholar]

32. V. Havlíček, A. D. Córcoles, K. Temme, A. W. Harrow, A. Kandala et al., “Supervised learning with quantum-enhanced feature spaces,” Nature, vol. 567, no. 7747, pp. 209–212, 2019. [Google Scholar]

33. G. Abdulsalam, “Heart disease prediction using ensemble-quantum ML,” 2022. [Online]. Available: https://github.com/ghada000/Heart_Disease_Prediction_Using_Ensemble-Quantum_ML. [Google Scholar]

34. B. A. Tama, S. Im and S. Lee, “Improving an intelligent detection system for coronary heart disease using a two-tier classifier ensemble,” BioMed Research International, vol. 2020, pp. 1–10, 2020. [Google Scholar]

35. M. A. Alim, S. Habib, Y. Farooq and A. Rafay, “Robust heart disease prediction: a novel approach based on significant feature and ensemble learning model,” in 3rd Int. Conf. on Computing, Mathematics and Engineering Technologies (iCoMET 2020), Sukkur, Pakistan, pp. 1–5, 2020. [Google Scholar]

36. S. Lundberg and S. Lee, “A Unified approach to interpreting model predictions,” in 31st Conf. on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, pp. 1–10, 2017. [Google Scholar]