Implementation of Hybrid Particle Swarm Optimization for Optimized Regression Testing

1  Introduction

Software systems are irreplaceable and an integral part of many engineering systems that assists in various tasks. Software testing is the process of finding errors in the given program in the execution of a system or program. Software testing is a process of evaluating or exercising a system component or system in automated or manual means to verify specified requirements and provides actual results [1]. Features combination provides faults in the system that implies exponential search space for fault detection using feature combinations. Various methods were applied for solving test case problems in software that are mainly classified into three classes: meta-heuristic algorithms, greedy algorithms, and constraint encoding algorithms [2]. Software testing is considered an expensive and time-consuming process that leads to the reliable formation and effective software systems. The testing process is provided with high software development resources due to its significance. The conventional software testing methods are cleared in the modules due to high data-intensive software [3]. The existing research explored various optimization and Constraint Satisfaction Problem for typical Software Product Line (SPL) problems due to the scare of SPL. Optimization-based solutions were applied in various types of research to solve cost problems in test case optimization [4]. The Target Software Project is compared with the completed project to find similar projects to predict software effort in Case-Based Reasoning (CBR) [5].

Regression testing is considered an important activity, time-taking, and costliest activity in an environment for certain restrictions to ensure modified software validity [6]. A test case sequence is necessary to select in case optimization that provides an efficient solution and transverse faults in minimum execution time [7]. Test case prioritization helps to provide efficient performance in which important test cases are executed first and later lower important test cases are executed. The studies show that prioritization methods based on test factors like Coverage, Time, Fault Rate, Complexity, Volatility, and importance have good results, and optimization methods like Genetic Algorithm (GA), and Ant Colony provide efficient performance in test case optimization [8]. In the software testing process, automatic test case generation is an optimization problem. Test cases are automatically generated with help of optimization methods like GA. Some researchers apply hybrid methods like Cuckoo search optimization and GA for better-optimized test cases. GA method is used by many researchers in software test case optimization due to its efficiency. The test cases are automatically generated for the structural test such as search space operations and parallelism which are important characteristics. GA method efficiently solves many optimization problems to provide near a global optimum solution and lacks exploitation [9,10]. The contribution of the TW-GA method in software test case optimization is given as follows:

The TW-GA method is proposed in software test case optimization for fault diagnosis and test case optimization. The Tournament winner in the GA method selects instances with higher fitness value for search and increases the exploitation.

The HIS software is applied to test the performance of the TW-GA method for software test case optimization. The TW-GA method is compared with conventional GA and existing methods for optimization.

The TW-GA method has higher performance in fault detection, average size, and average time in test case optimization. The TW-GA method increases the exploitation process which improves the performance.

The organization of the paper is given as follows: Recent research on software test case optimization was reviewed in Section 2 and related work is explained in Section 3. The TW-GA method explanation is given in Section 4. The simulation setup is given in Section 5 and the results are shown in Section 6. The conclusion of this research work is given in Section 7.

2  Literature Review

Much automated software is used in the real-time system and defect-free software is required for effective performance. Test case optimization technique is required in software reliability and software reusability. Some recent methods in software test case optimization research were reviewed in this section.

Mishra et al. [11] applied genetic algorithm-based software test case optimization that considers execution time, risk exposure, requirement factors, and statement coverage data. Regression testing of three processes such as test case selection, test case prioritization, and test case minimization was carried out. Test cases are optimized based on given constraints in the software model. Agrawal et al. [12] applied ant colony and hybrid Particle Swarm Optimization (PSO) models for software test case optimization. The SIR repository of standard flex objects was applied to test the performance of the developed model. The quality measure was calculated using fault coverage and execution time of the process. Panwar et al. [13] applied a cuckoo search algorithm and modified ant colony optimization for software test case optimization in a time constraint scenario. The hybrid algorithm was applied to the triangle categorization problem and prioritizes test case generation using the DD-path graph.

Chen et al. [14] applied Adaptive Random Sequences (ARS) with clustering techniques on black-box information for regression testing on object-oriented software. The K-means and K-medoids techniques cluster the test case based on several objects and methods. The K-medoids clustering method with similarity metrics was applied for the optimization of test cases. A neighboring test case is considered in ARS for optimization. Banias et al. [15] developed a dynamic programming method for test case optimization for selection-prioritization in software. The dynamic programming method was applied as an objective method and empiric human decision was applied for the prioritization task. The model requires less memory for the software test case optimization. proposed regression test case prioritization for generating the test case and Kernel Fuzzy C Means (KFCM) method was applied for the generated test case. The KFCM clusters relevant and irrelevant test cases, then relevant test cases are used for the prioritization task. The Whale Optimization Algorithm was applied for weight optimization and Modified Artificial Neural Network was applied for test case prioritization. The developed model selects the optimal selection for test suites at better convergence. The model has considerable performance in terms of average time and average size.

3  Related Methods

The Hill climbing optimization technique performs local search optimization to find the solution.

Hill Climbing

Hill climbing is an optimization technique and iterative technique in the local search method developed from a random solution and then continues to a trajectory search for finding better positions in search space. This process is iterated till a higher solution is achieved.

Original hill climb consists of many challenges and the most vital one is movement uphill accepts. Local optima have occurred in the model for getting trapped is an important problem in optimization. To solve the local optima trap problem, many extensions are applied and β-hill climbing is a considerable method in which exploration-exploitation is balanced using the β-factor, such that β∈[0, 1].

The local search method of βhill-climbing optimizer starts the process with a unique solution. At each iteration, the present solution is changed to randomly generate a solution utilizing two factors β-factor and Z-factor, which are highly responsible for the exploration-exploitation process. A neighborhood search is carried out using Z-factor and a mutation operator is carried out using β-factor. The Z-factor or β-factor at every iteration provides the best solution.

The β-hill climbing process generates a single solution x∈Rn, randomly that further evaluates the objective function f(x). Once Z-factor updates the solution, a new individual ‘x’ is generated in x vicinity, as in Eq. (1).

xj′=xj±rnd×bw (1)

where the new solution to the current solution bandwidth is denoted as bw , and randomly selected value is j∈{1, 2, …, n} . In case f(x′)<f(x) , then x←x′ .

A decision variable j is selected randomly for the new solution considering the β -operator, as given in Eq. (2).

xi′←{lj+(uj×lj)×U(0, 1)r≤βxiotherwise (2)

where r∼U(0, 1) . The current solution is replaced with a new solution as x←x′ in the case of f(x′)<f(x) .

The β-hill-climbing method is effectively applied to various real-world problems such as engineering optimization, feature extraction, signal processing, and gene selection problem.

4  Proposed Method

Hospital Information System (HIS) software is used in the research for test case optimization in the model. Test case information of software is analyzed with test case requirement, test case subset, and test case coverage. Tournament selection with a genetic algorithm is applied to the extracted information for optimal selection of test cases. The flow of the Tournament Winner Genetic Algorithm (TW-GA) is shown in Fig. 1.

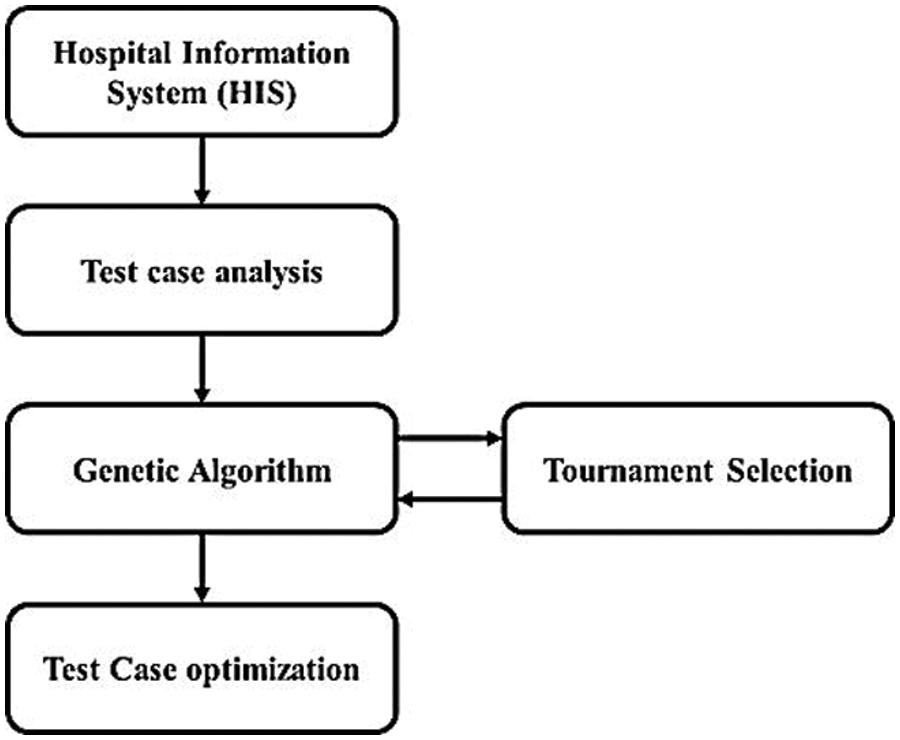
Figure 1: Tournament winner genetic algorithm for test case optimization

4.1 Hospital Information System (HIS)

HospitalRun is offline-enable, open-source, and easy-to-use Electronic Medical Record (EMR) or Hospital Information System (HIS) software to assist in the healthcare system.

The HIS system integrates solutions designed to manage hospital operations including medical operations, legal, inventory, human resources, administrative, financial, and clinical workflow. HIS is developed to assist in the hospital and for every user with an active role in hospital operations such as lab technicians, pharmacists, accountants, staff nurses, doctors, and managers. The HIS basic features are

Human resources management

Ward management

Accounting and Financial management

Pharmacy management

Laboratory management

Inpatient management

Patient records management

Appointment management

Patient admissions

An electronic medical record system adoption is the primary goal of modern health organizations and this aim is to increase the efficiency of treating patient information and make it available in an accurate and timely form at the point of service.

More information is available on mobile phones, traditional computers, and other mobile devices as the system progresses to the final stage in terms of maturity. This system operates as storage for all patient information and offers complete medical records available online and when in human contact with the patient. Several characteristics are present in influencing factors and various functions required to build a complete and exhaustive electronic medical record for the patient.

The screenshot of the HospitalRun HIS software is given below in Figs. 2 and 3.

Figure 2: Sample screenshot of the software

Figure 3: Sample screenshot of the software

4.2 Problem Statement

Minimization: Given a test suite T s and test case requirements set r1, r2, r3, …, rn that is to be satisfied for software test coverage. The Ts subsets T1,  T2,  T3, …, Tn are related to the Traceability matrix in such a way each test case Tj belongs to Ti used for test ri .

Problem: Test cases set representative from Ts that satisfies all ri 's where program all requirements represent ri′ s or requirements related to the modified program.

Prioritization: A number of ways test cases are selected based on Torder and a test suite T. The test suite T fitness f is based on real value criteria.

Problem: Find T′ based on T′∈Torder for all T, where f(T′)≥f(T) and T!=T′ .

4.3 Genetic Algorithm

Genetic algorithm optimization starts with a solution set (chromosome) called population. The selected solutions create new solutions (offspring) using fitness value and a higher chance of reproduction if the fitness value is more. Algorithm 1 explains the TW-GA method.

The TW-GA method is an improved version of GA, where selected values are used for increases the exploitation in the search to achieve desired optimizing results. The conventional GA method applies mutation to the chromosome of each parent for random interchanging of genes to occur. The chromosome’s fitness is used to measure mutation calculation and the rate of mutation is based on mutation performance. A solution set is generated using chromosomes for TW-GA functioning. Every chromosome is related to TW-GA steps.

The TW-GA method steps are explained below.

The GA is a popular soft computing method and the Tournament winner technique is introduced in GA to increase the exploitation capacity to find faults in test case optimization. The TW-GA steps are given as follows.

Chromosomes generation

Fitness function calculation

Crossover

Mutation

Tournament Selection

The fuzzy classifier generates the rules for optimization and every rule is considered a chromosome. Randomly generates the chromosome pools and every chromosome is applied for the TW process. Chromosomes are evaluated using fitness values and chromosomes with higher fitness values are available at the output. The crossover and mutation are vital steps in the GA method.

Solution pre-defined ways of containing information are represented by chromosomes. Chromosome information is commonly encoded using binary strings.

String every bit retains correspondence of solution’s characteristic and a complete string are used to represent by a number. Solution encoding is presented by many coding techniques and this is based on the problem solved. The integer is directly applied for encoded and certain permutations are encoded.

Step 1 Chromosome Generation: The initial stage of the TW-GA method generates chromosomes and those are used to generate rules based on the rule parameters. Count C chromosomes at the solution space are generated randomly and Eq. (3) provides the term.

Chk=[G0kG1k…GCL−1k]0≤k≤M−1; 0≤i≤CL−1 (3)

where chromosome length is denoted as CL , the total population is denoted as M, and jth gene chromosome is denoted as Gik .

Step 2 Calculating Fitness Function: The fitness function is used to optimize the rules for selecting solutions and better fitness solutions are selected using Eq. (4).

ft=∑K=1M⁡Rs/M (4)

where the rules’ total count is denoted as M, the selected rule is denoted as Rs , summation term is denoted as s and mk .

Each chromosome’s fitness value ft is measured using selected rules and every chromosome is verified against fitness function. Solutions that satisfy the fitness function are selected to participate in reproduction as either mutation or crossover.

Step 3 Crossover: Crossover is applied for two-parent chromosomes to generate a new chromosome. Offspring is a newly generated chromosome and crossover is measured based on selected genes and offspring production on crossover rate. The crossover point is given in Eq. (5).

CPrate=CGCL (5)

where the length of the chromosome is denoted as CL , the number of genes generated is denoted as CG and the crossover rate is denoted as CPrate .

The parent chromosomes perform crossover generation based on crossover rate and new chromosomes set named of spring. The crossover point is found using crossover rate and genes are interchanged from both parent chromosomes to generate springs of both parent’s chromosomes. The better fitness function is applied for chromosome generation compared to older chromosome generation.

Step 4 Adaptive Mutation: Some random genes are changed from a single parent and mutation is performed using the rate of mutation. Eq. (6) provides the mutation rate.

MUr=PmCL (6)

where chromosome length is denoted as CL , mutation point is denoted as Pm , and mutation rate is denoted as MUr .

Mutation rate selection is based on estimated fitness value and generated rules are used to measure the fitness value. Mutation rate compared with fitness-stated values is used to measure resultant and threshold values that are selected as the final mutation rate. The mutation points of the vector are used in Eq. (7).

MUr={mp1, mp2, …, mpl} (7)

Fitness value ft is measured using the Rate of mutation r and chromosome length is denoted as l, as in Eq. (8).

MUr={1; if ft≤T0; else (8)

where mutation rules are used to compute T and every mutating point extraction is used for mutating. Every chromosome with the iteration of mutation rate is based on fitness value.

Step 5 Selection

The TW-GA method is applied for the selection of solution and new chromosomes (Np) are applied in the selection pool based on fitness value. The fitness value in the selection pool chromosome is the best and topmost Np chromosome stored in the selection pool in next-generation between 2Np chromosomes. The flow chart of the GA method is given in Fig. 4.

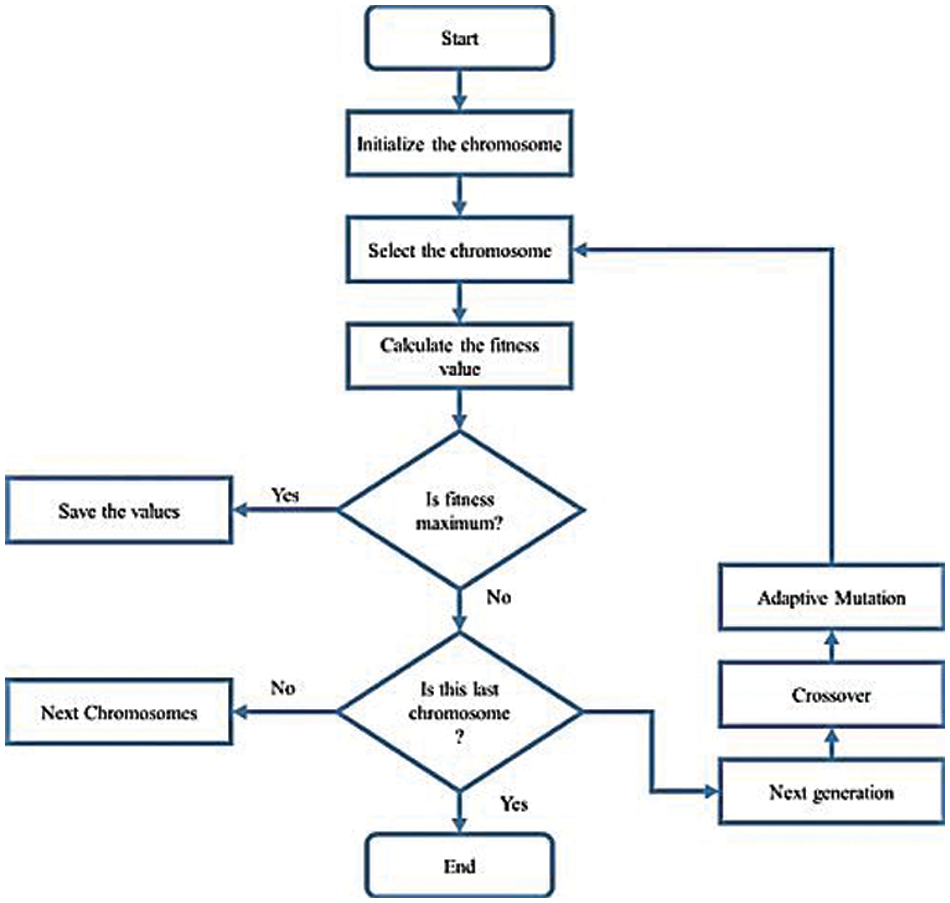
Figure 4: Flow chart of genetic algorithm

Tournament selection is a selection process to select the fittest candidates in the GA method in the current generation. The selected candidate is applied for the next generation. The k-individuals are selected in k-way tournament selection and compute the tournament. The Fittest candidate is applied for a selected candidate for next-generation passing the candidates. Many tournaments are applied and the candidate’s final selection is processed to the next generation. Selection pressure is used as a parameter for the probabilistic measure of candidates for participation likelihood in a tournament. Weak candidates have a smaller selection chance if the tournament size is larger than competing with a stronger candidate. GA convergence rate is measured based on a parameter of selection pressure. More convergence rate is applied for more selection pressure. Near-optimal solutions or identifying optimal GA are selected over selection pressures wide range. The TW also considers negative fitness values.

The individual candidate is selected from the population of GA based on fitness value.

Several ‘Tournaments’ are selected among a few individuals selected randomly from the population.

The candidate with the best fitness or each tournament winner is selected for crossover.

Tournament selection provides a chance to all individuals if tournament size is small and diversely preserves that degrades convergence rate.

Weak individuals have less chance for selection if the tournament size is larger.

5  Simulation Setup

The implementation details of the TW-GA algorithm in test case optimization for software were discussed below.

5.1 System Requirement

The system configuration for the implemented proposed method is given as follows.

Intel i9 processor

22 GB graphics card

128 GB RAM

Windows 10 64-bit OS

The Python 3.7 tool is used to analyze the test case from the software and apply optimization for test case optimization.

5.2 Metrics

Mutation score, average size, and average time were measured from the optimized test case in the developed method. Average size and average time are requirements of size and time for the model.

Mutation score is test suite adequacy measured based on dead mutants, equivalent mutants, and a total number of mutants, as given in Eq. (9).

Mutation Score(MS)=(|DM|M−|E|)×100 (9)

where killed mutants are denoted as |DM| , the equivalent mutants are denoted as |E| , and the total number of mutants is denoted as |M| .

6  Results

The TW-GA method is proposed for software test case optimization in HIS software. The TW-GA method is compared with existing methods in the software test case optimization process, discussed in this section. Mutation score, average time, and average size were measured from TW-GA and existing methods.

The mutation is fault applying method in the software and is commonly used to evaluate the test case optimization method. The mutation operator is applied in the software to lead to various faults such faults are mutant and alternations are mutations. If the optimization method detects the mutations in the software based on the behavior change then the mutation is removed from the software. Some mutations are difficult to find due to the mutants being similar to original test cases and these are known as equivalent mutants. Table 1 shows the mutants applied for each subject in a test case and the detection performance of the TW-GA model is measured by mutation score. The S1 and S11 subjects are difficult to find mutants due to subjects consisting of more equivalent mutants.

The mutation score of TW-GA and existing methods were measured, as shown in Fig. 5 and Table 2. The TW-GA method has a higher mutation score than existing methods in software test case optimization. TW-GA model applies the tournament winner method to further selects the best values based on fitness value in the optimization. This process tends to increase the exploitation and convergence of the TW-GA method in software test case optimization. The exploitation performance is need to be improved in the GA method that helps to find the equivalent mutation in the model. The equivalent mutation is difficult to find in the software test case optimization due to its similarity to the original test case. The Hill climbing method has a second higher performance in mutation score and this fails to find the equivalent mutation in the test case. GA method has a limitation of lower convergence and the BGA method has trap into local optima that have lower exploration process. The SGO model has lower performance in strings and dynamic arrays in the software. The random search and BGA method has lower performance in the software test case optimization due to lower convergence in the optimization.

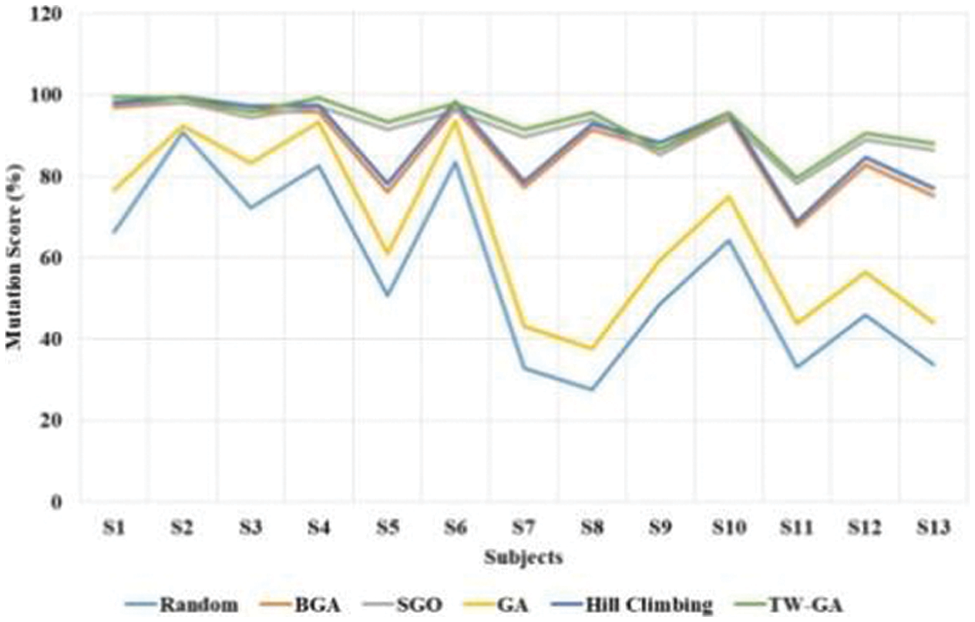
Figure 5: TW-GA and existing methods mutation score in software test case optimization

The average size of the TW-GA model in software test case optimization was measured and compared with existing models, as given in Fig. 6 and Table 3. The tournament winner in the GA method helps to discard the information of lower fitness value which helps to reduce the memory requirement of the model. The TW-GA method has a higher exploration and exploitation capacity that requires a minimum population for searching for the optimal solution. The MOCSFO method has considerable performance in software test case optimization. The MOCSFO method generates more data related to search due to Crow Search and the fruitfly algorithm. The MOPSO method has a lower exploration process and lower convergence in the search process. The existing methods have lower performance when the number of test cases in software is high.

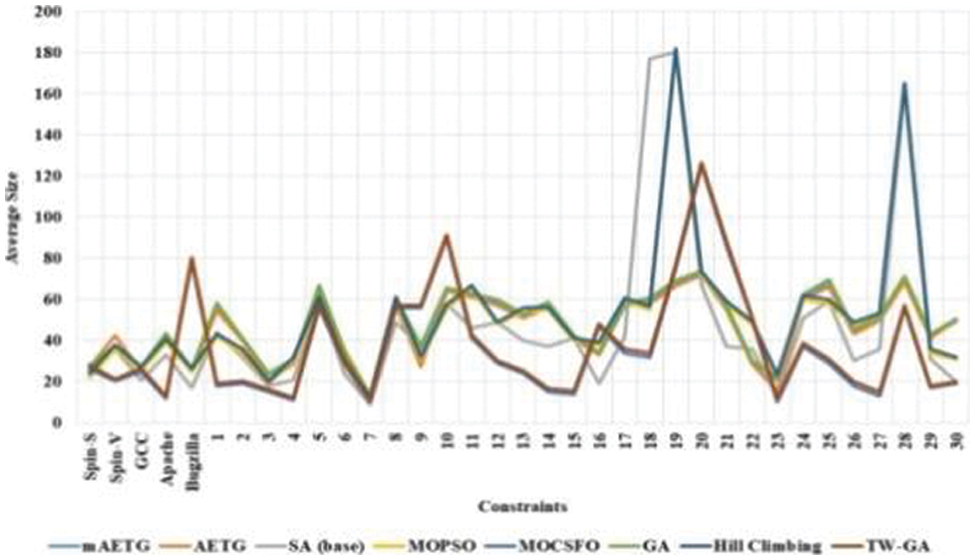
Figure 6: The average size of TW-GA and existing methods in software test case optimization

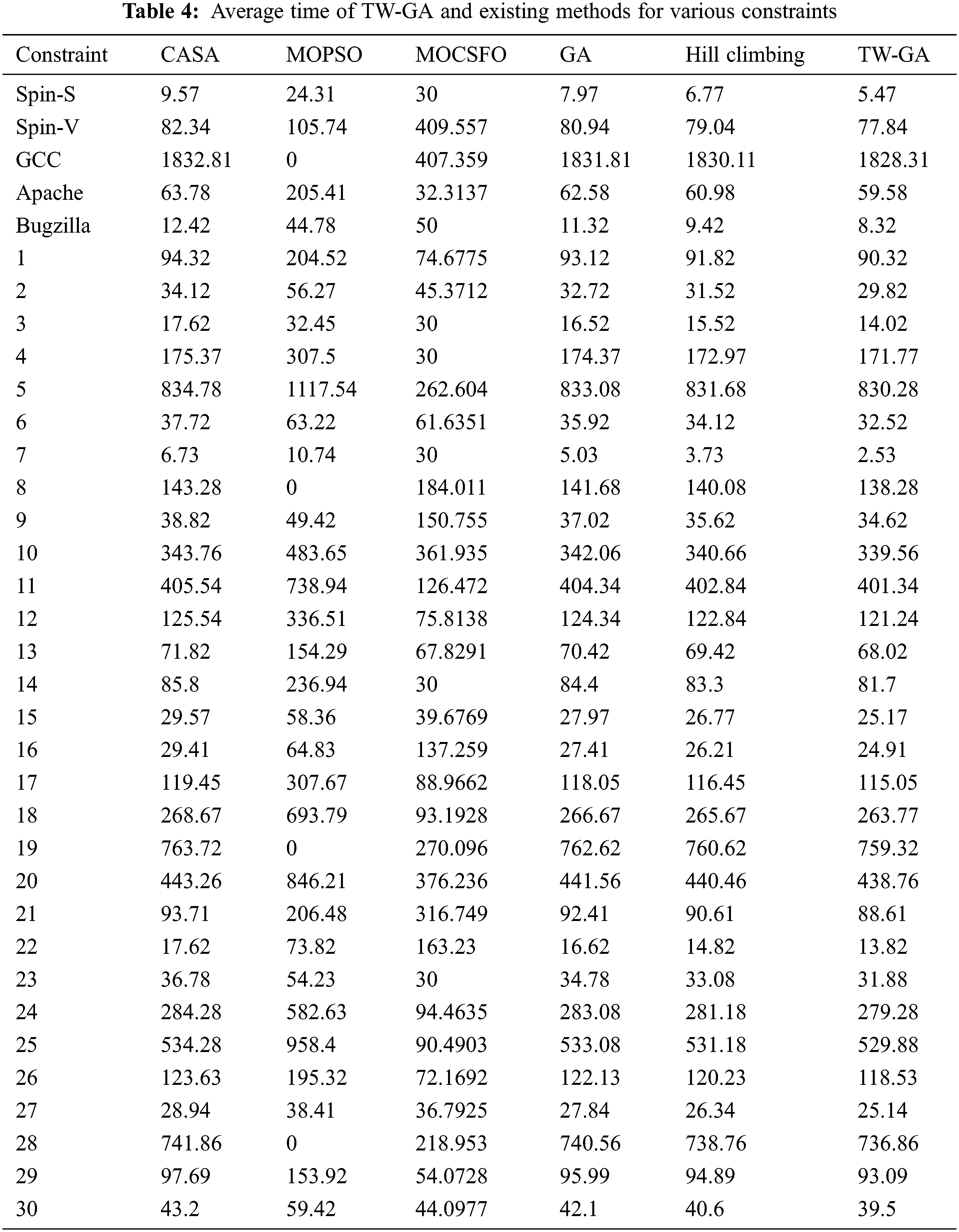
The average time of TW-GA and existing methods in software test case optimization for various constrains are measured, as in Fig. 7 and Table 4. The TW-GA method has a lower average time for various constraints due to this method finding the potential region for search and increasing the exploitation in the region. The TW-GA method discards the information with a lower fitness value that helps to increase the search speed. The convergence rate of the proposed method is increased using the tournament winner in the optimization process. The MOCSFO method has a limitation of lower convergence and is easily trapped into local optima. The MOCSFO method is a hybrid method and has high computational complexity.

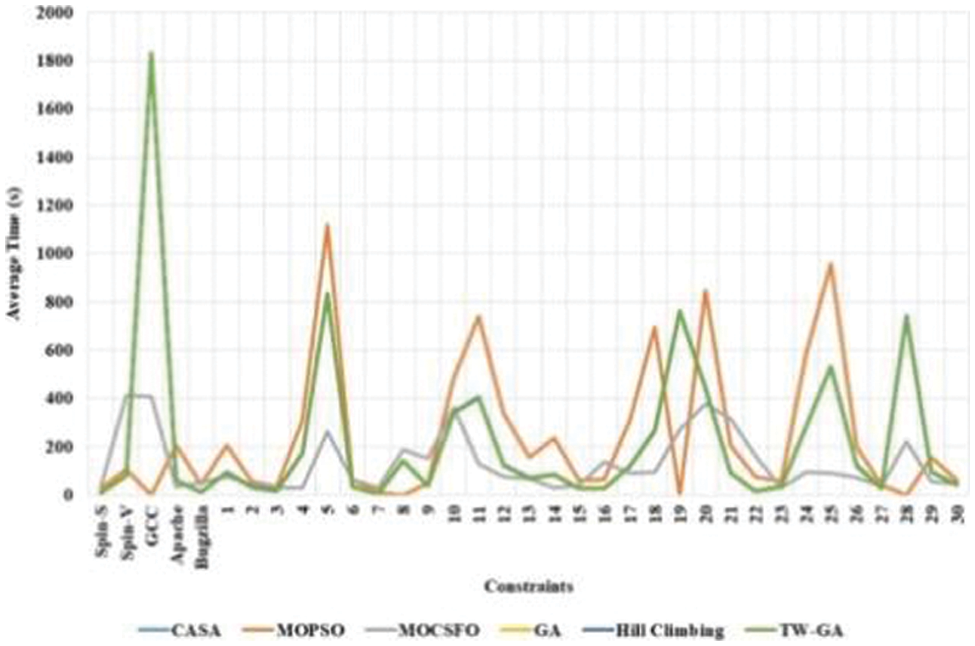
Figure 7: Average time of TW-GA and existing method in software test case optimization

7  Conclusion

Software test case optimization finds the fault in the software, provides proper structure, and increases the reusability of the software. The existing methods have limitations and lower efficiency in software test case optimization due to lower convergence. This research proposes the TW-GA method to find a potential region in search and increases the exploitation in the search process. The TW-GA method has higher exploitation that helps find mutant and equivalent mutant in software for fault diagnosis. The TW-GA method discards information with a lower fitness value that reduces the computational time and memory requirement. The MOCSFO method has lower exploitation, convergence rate, and higher complexity that affects the performance of optimization. The TW-GA method has a 99.43% mutation score and the SGO method has a 97.93% mutation score. The future work of this research is to apply recent optimization methods to increase the convergence rate.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. M. Khari, P. Kumar, D. Burgos and R. G. Crespo, “Optimized test suites for automated testing using different optimization techniques,” Soft Computing, vol. 22, no. 24, pp. 8341–8352, 2018. [Google Scholar]

2. Y. Fu, Z. Lei, S. Cai, J. Lin and H. Wang, “WCA: A weighting local search for constrained combinatorial test optimization,” in Information and Software Technology, vol. 122, China: Elsevier, pp. 106288, 2019. [Google Scholar]

3. P. Ramgouda and V. Chandraprakash, “Constraints handling in combinatorial interaction testing using multi-objective crow search and fruitfly optimization,” Soft Computing, vol. 23, no. 8, pp. 2713–2726, 2019. [Google Scholar]

4. U. Afzal, T. Mahmood, A. H. Khan, S. Jan, R. U. Rasool et al., “Feature selection optimization in software product lines,” IEEE Access, vol. 8, pp. 160231–160250, 2020. https://doi.org/10.1109/ACCESS.2020.3020795 [Google Scholar] [CrossRef]

5. D. Wu, J. Li and C. Bao, “Case-based reasoning with optimized weight derived by particle swarm optimization for software effort estimation,” Soft Computing, vol. 22, no. 16, pp. 5299–5310, 2018. [Google Scholar]

6. S. F. Ahmad, D. K. Singh and P. Suman, “Prioritization for regression testing using ant colony optimization based on test factors,” in Intelligent Communication, Control and Devices, vol. 624, Singapore: Springer, pp. 1353–1360, 2018. https://doi.org/10.1007/978-981-10-5903-2_142 [Google Scholar] [CrossRef]

7. T. Yaghoobi,” “Parameter optimization of software reliability models using improved differential evolution algorithm,” in Mathematics and Computers in Simulation, vol. 177, Iran: Elsevier, pp. 46–62, 2020. [Google Scholar]

8. K. Raimond and J. Lovesum, “A novel approach for automatic remodularization of software systems using extended ant colony optimization algorithm,” in Information and Software Technology, vol. 114, India: Elsevier, pp. 107–120, 2019. https://doi.org/10.1016/j.infsof.2019.06.002 [Google Scholar] [CrossRef]

9. D. B. Mishra, R. Mishra, K. N. Das and A. A. Acharya, “Test case generation and optimization for critical path testing using genetic algorithm,” in Soft Computing for Problem Solving, vol. 817, Singapore: Springer, pp. 67–80, 2019. https://doi.org/10.1007/978-981-13-1595-4_6 [Google Scholar] [CrossRef]

10. R. Khan, M. Amjad and A. K. Srivastava, “Optimization of automatic test case generation with cuckoo search and genetic algorithm approaches,” in Advances in Computer and Computational Sciences, vol. 554, Singapore: Springer, pp. 413–423, 2018. https://doi.org/10.1007/978-981-10-3773-3_40 [Google Scholar] [CrossRef]

11. D. B. Mishra, R. Mishra, A. A. Acharya and K. N. Das, “Test case optimization and prioritization based on multi-objective genetic algorithm,” in Harmony Search and Nature Inspired Optimization Algorithms, vol. 741, Singapore: Springer, pp. 371–381, 2019. https://doi.org/10.1007/978-981-13-0761-4_36 [Google Scholar] [CrossRef]

12. A. P. Agrawal and A. Kaur, “A comprehensive comparison of ant colony and hybrid particle swarm optimization algorithms through test case selection,” in Data Engineering and Intelligent Computing, vol. 542, Singapore: Springer, pp. 397–405, 2018. https://doi.org/10.1007/978-981-10-3223-3_38 [Google Scholar] [CrossRef]

13. D. Panwar, P. Tomar and V. Singh, “Hybridization of cuckoo-ACO algorithm for test case prioritization,” Journal of Statistics and Management Systems, vol. 21, no. 4, pp. 539–546, 2018. [Google Scholar]

14. J. Chen, L. Zhu, T. Y. Chen, D. Towey, F. C. Kuo et al., “Test case prioritization for object-oriented software: An adaptive random sequence approach based on clustering,” Journal of Systems and Software, vol. 135, China: Elsevier, pp. 107–125, 2018. https://doi.org/10.1016/j.jss.2017.09.031 [Google Scholar] [CrossRef]

15. O. Banias, “Test case selection-prioritization approach based on memoization dynamic programming algorithm,” in Information and Software Technology, vol. 115, Romania: Elsevier, pp. 119–130, 2019. [Google Scholar]