Accurate Phase Detection for ZigBee Using Artificial Neural Network

1  Introduction

IEEE802.15.4 has brought the industrial community’s attention because of its features in power consumption [1], wireless sensor mesh networks [2], home automation, and the Internet of Things (IoT). IEEE802.15.4 physical layer uses BPSK modulation with two options of frequency bands which are 868 and 915 MHz. Many wireless sensor network protocols are built on top of IEEE802.15.4 physical and medium access control (MAC) layers, such as ZigBee, WirelessHart, 6LoWPAN, and MiWi [3]. However, BPSK is susceptible to noise, leading to several issues, such as low detection performance of BPSK signal and weak signal energy [4–10]. Moreover, noise can be initiated by human or natural phenomena, and in both cases, it is considered a big challenge for signal reception [11–15]. Therefore, removing noise in the BPSK signal is necessary to mitigate its negative sequences and increase its capability in industrial wireless sensor networks.

Artificial neural networks (ANNs) have shown a great success in solving different problems such as image recognition [16,17], semantic segmentation [18], object detection [19,20], cell segmentation and counting [21,22]. Initially, ANN was inspired by biological brain neurons and connections between multiple neuron activities [23]. Although ANN has existed since the 1970s, recent progress in artificial neural networks is due to the big data, the computation resources advances, and the development of algorithms and optimizers that advanced the learning process of artificial neural networks [22].

A recurrent neural network (RNN) is an artificial neural network algorithm that is used to learn from sequential data. It has a different architecture than the classical neural network algorithm, such as feedforward, because the internal state at time t is input at time t + 1, which allows RNNs to learn from a sequence of data that is related to each other [24]. RNN can be expressed as in Eq. (1), where ht is the hidden state at time t, xt is the input at time t, and θ is the parameters for the RNN. Therefore, learning at each time step t is based on the hidden state at earlier time step ht−1, which allows RNN to learn from subsequent input data [25].

ht=f(ht−1;xt;θ) (1)

In this research, first, we injected Gaussian noise into the BPSK signal. Second, we collected the data from the BPSK simulation model. Third, we used an RNN technique to detect noise that interfered with the BPSK signal based on supervised learning. In addition, the BPSK signal will be recovered from the noise by predicting the noisy BPSK signal. Furthermore, this research uses the RNN to learn from BPSK sequential data because RNN has shown extraordinary performance in capturing nonlinear relationships on sequential data [26]. The experiment results confirm that the implemented RNN used in this research has shown the expected results in detecting and recovering the BPSK signal.

1.1 Contributions

This research enhances the BPSK phase signals at the receiver side by:

•   Reducing the noise interfered with the BPSK signal at the receiver side of ZigBee.

•   To do that, we implemented the RNN model to detect the noisy signal of the BPSK system via predicting the phase.

•   We evaluated our RNN model using MSE, correlation coefficient, recall, and F1-Score metrics. As a result, our model shows better performance than the existing model, in which we scored 8.0621e-13 on MSE, 98.71% on recall, and 96.34% on F1-Score.

1.2 Paper Structure

This paper is structured as follows; Section 2 discusses the related works associated with modulated signal detection and ML. Section 3 represents the design and method of the proposed RNN based-phase detection. Section 4 presents our findings’ results and discussion, respectively. Finally, Section 5 discusses the conclusion and highlights some recommendations for improvements.

2  Related Works

AI has been used widely to detect the modulated signal on different modulation schemes. In [27], the research studies the performance of utilizing the deep belief network (DBN)-support vector machine (SVM) on detecting the M-QAM, and the performance of the experimental studies shows a significant improvement with 100% accuracy when 15 SNR values occur. In [28] deep convolutional neural network (DCNN) is used in detecting the frequency shift keying (FSK) modulated signal to overcome the effect of fading channel. DCNN has shown superiority in terms of error probability among the other ML classifiers, including Support Vector Machine (SVM), Linear Discriminant Analysis (LDA), and Multi-Layer Perceptron (MLP).

The research study conducted by Xiang et al. [29] has provided brief information regarding the frequency offset carrier phase estimation. In the research study, a carrier recovery scheme was proposed by the researchers. The proposed scheme in the study is based on the Adaptive Kalman Filter (AKF). Through the proposed scheme, the researchers have identified that frequency offset can be estimated efficiently. Through this scheme, the estimation range and estimation accuracy showed enhancement. Overall the results of the study have shown that the proposed scheme improves the estimation accuracy and configuration capability. The researchers have provided detailed information in the study and contributed lots of new information to the literature; however, future research is required to understand more about the adaptive Kalman filter and its uses.

The research in [30] introduces a technique for nonzero staircase modulation to switch single-switched PWM DC-DC boost converters to reduce the effect of harmonics. The methodology is based on forming two pulse train signals if comparing a 50 Hz nonzero wave with a 1.5 Hz train wave. They achieved good performance, which led to an appropriate efficiency compared to the existing techniques presented in the literature.

The research in [31] has provided detailed insights into deep learning methods. In the research study, the researchers have discussed the neural network-based technique for demodulating digital signals. Researchers have shed light on the importance of digital signal modulation in communication systems. There is a need for such demodulation techniques through which existing errors can be eliminated. Neural networks are utilized for various types of problems. The results of the study show that the neural network model performed way better than the conventional demodulation method. The performance of the proposed model is much better than the old method of demodulation. The researchers have said that such models should be implemented to improve the performance of the communication system. Future research is required so that more information regarding the proposed model can be gathered.

Researchers in [32] have proposed a method that uses a one-dimensional Convolutional Neural network. In the research study, the researchers have proposed a binary phase-shift keying demodulator. This demodulator is based on a 1-dimensional neural network. Through this proposed model, the overall performance of the communication system can be enhanced. The error rates through the proposed model can be reduced significantly. Through conventional models, the error rate is higher; however, with new technology, the errors can be mitigated. There is a need for such a model through which errors can be reduced and the overall performance of the systems can be enhanced. This research study has a huge contribution to the literature; however, future research is required so that more data can be gathered for the proposed model.

Researchers in [33] have discussed the use of 2 steps stochastic hybrid estimation for global navigation satellite systems (GNSS). In the study, a new algorithm was proposed which enhanced the performance of the system, and existing errors were eliminated. In the research study, the theoretical performance of the proposed algorithm is analyzed. The results of the study have shown many benefits of the proposed algorithm. The first benefit is the high accuracy in the estimation of GNSS signals, and the second benefit is the rapid recovery of carrier base observation.

The researchers Kalade et al. [34] have discussed sequence learning in detail in the research study. Sequence learning is being used for digital QPSK and BPSK demodulation. The researchers in the study have discussed that over the years, machine learning has experienced immense growth. Machine learning is now being used in different fields and provides many opportunities to individuals. In the field of wireless communication, machine learning can also be applied. In this study, sequence to sequence, a model has been proposed. The proposed model has the capability to work efficiently with PSK data. Overall, it can be said that in the future, this model can provide many benefits and opportunities to the wireless communication industry. It can be applied to next-generation networks. Although significant detail has been provided in this study, future research is still required to gather more information about the proposed model and its future applications.

In the research study [29], the researchers have provided detailed information about machine learning and its application in the modulation format transparent carrier recovery. The researchers in the study have stated that the usage of the internet has increased up to a lot of extents in recent years. In the future, it is expected that internet usage will grow further. Internet traffic in recent years has become unpredictable due to cloud-related applications. The conventional modulation might not work as perfectly as the proposed machine learning enhanced modulation. Through the proposed modulation, the issues regarding internet traffic can be resolved up to a lot of extents. In the future, internet traffic will further increase, and there will be a need for such technology through which internet traffic can be efficiently managed. However, future research should be performed to know how the proposed model can be further improved.

Researchers [35] Xiang et al. have discussed the application of the Kalman Filter. In this research study, self-learning, the Kalman filter is proposed by the researchers. Through the proposed technique, the modulation can be improved up to a lot of extents. In recent years technology is becoming advanced day by day. New methodologies and techniques are required for resolving complex issues. The errors that occur in the transition cause huge problems in the communication process. The methods such as the self-learning Kalman filter are the solution to the latest problems. Through such solutions communication system can be improved effectively.

Researchers in [36] LeCun et al. (2015) have discussed deep learning in detail according to the researchers, through deep learning, the communication systems can be improved. Today technology is required to resolve the issues that occur in the transmission. If such issues are not resolved, the transfer of data from one place to another cannot be done accurately. Over the years, many new methods and algorithms have emerged that have revolutionized the communication system machine learning technology is also playing its role in the improvement of the transmission. Overall, it can be said that machine learning can improve communication systems.

The researchers in [37] have discussed neural networks for demodulation Methods. In the research study, the researchers have discussed the neural network-based technique for demodulating digital signals. Researchers have shed light on the importance of digital signal modulation in the communication system. There is a need for such a demodulation technique through which existing errors can be eliminated. Neural networks are utilized for various types of problems. The error rates through the proposed model can be reduced significantly. Through conventional models, the error rate is higher; however, with new technology, the errors can be mitigated. There is a need for such a model through which errors can be reduced and the overall performance of the systems can be enhanced.

None of the previous works highlighted the accuracy of applying machine learning or deep learning to detect phase changes. In this paper, we investigate using a neural network-based phase signal detection method to optimize the performance of Binary Phase Shift Keying (BPSK). Therefore, we integrate a Recurrent Neural Network (RNN) to detect the BPSK’s phase signal at the receiver side. Furthermore, we test the performance of the proposed method to check its superiority against the existing model by trying the system for different Signal-to-Noise (SNR) values.

3  Methodology

3.1 BPSK System Model

The mathematical representation of the BPSK waveform Sm(t) is described below with a deep concentration on the carrier phase changes ∅m and the number of possible carrier phases M [38,39]:

Sm(t)=Re[g(t)ei2π(m−1)M ei2πfct] (2)

Sm(t)=g(t)cos(2πfc(t)+2πM (m−1)) (3)

Sm(t)=g(t)cos⁡(∅m)cos(2πfc(t)−g(t)sin⁡(∅m) sin(2πfc(t)) (4)

∅m=2π(m−1)M (5)

where ∅m is the carrier phase, g(t) is the signal pulse shape, fc is the carrier frequency, is the number of possible carrier phases. In BPSK, the number of carrier phases is M = 2. The mathematical representation of the BPSK can be defined as follows:

S1(t)=Accos(2πfct),                 0≤t ≤Tb (6)

S0(t)=Accos(2πfct+π),                 0≤t ≤Tb (7)

Eq. (6) is used to transmit 1, and Eq. (7) is used to transmit 0. In general, the BPSK modulated signal can be represented as:

S(t)=Accos(ωt+φ(t))  (8)

where φ(t) defines the phase changes of the carrier in BPSK waveform, Ac is the amplitude of the carrier, and it does not carry any information in PSK. Fig. 1 displays the BPSK waveform generation in IEEE802.15.4 standard [3,40]. Binary bits are encoded deferentially and then mapped to chips (spreading) and then get passed through BPSK modulation with pulse shaping named as normal raised cosine filtering.

Figure 1: BPSK modulated signal in IEEE802.15.4 standard

3.2 Proposed Method: RNN-Based Phase Detection Model

We developed an RNN model to predict the actual carrier phase of the BPSK waveform with the effect of Gaussian noise. In Fig. 2, we illustrate the system pipeline used in this research. Initially, the dataset was collected in the first two components: BPSK modulation and phase detection using the ZigBee software simulation. The dataset size is (60480 × 5); each column has a different SNR value (5, 7, 11, 13, 15) respectively. Then the collected dataset was split into two parts; the first part was used to train the RNN model, and the second part was used to test the model.

Figure 2: The proposed approach, where the BPSK modulation signal is used for phase detection followed by splitting the data into training and testing. The training data is used to train the RNN model, followed by testing and obtaining the predicted phase

In the training phase, we trained the RNN with a noisy phase signal with an 11 SNR value. The dataset was divided into three partitions during the training procedure: 80% of the data was used for training, 10% used for validation, and 10% used for testing. We used the Levenberg-Marquardt algorithm to train our model. Finally, we tested our model with the above SNR values in the testing procedure.

3.3 Architecture of RNN

We briefly showed Recurrent Neural Network (RNN) in architecture Fig. 3. It consists of three layers: input, hidden, and output layer. The input layer is fed with the input signal x(t), which is the noisy phase signal of the BPSK system. The hidden layer has ten nodes to perform the required calculation to predict the actual signals of BPSK. After that, the estimated value is delivered to the output layer y(t). The feedback node is an essential part of the RNN because it feeds the input layer with the previous prediction y(t − 1), which leads to an increase in the accuracy of the prediction procedure.

Figure 3: Architecture of RNN

A full architecture of our proposed RNN model is shown in Fig. 4. The input layer has two neurons; one receives the input value, and another receives the feedback value. The feedback value is fed with an input value to the hidden layer to increase the accuracy of the prediction. The hidden layer has ten neurons, and the output layer has a single neuron that produces the predicted BPSK value.

Figure 4: Architecture of RNN

4  Results and Discussion

4.1 Evaluation of RNN

We used two methods to evaluate the training of the RNN model: Mean Squared Error (MSE) and correlation coefficient (R-value). MSE is a metric calculated using two parameters, the target data (true BPSK signal) and RNN output (predicted BPSK signal) [41]. Therefore the smaller value of MSE means a similarity between the target data and the network output data, which is what we are looking for in this case [42]. Fig. 5 shows the MSE performance of the RNN model while the SNR value equals 11 during the training procedure. The best validation performance was reached when the epoch was equal to 42. Table 1 shows the performance of the correlation coefficient (R-value) along with MSE values.

Figure 5: MSE with SNR = 11

The R-value is also calculated between the target data and the RNN output. If the R-value between the target (true BPSK signal) and the predicted BPSK signals (output) is close to 1, that means they have comparable results [43]. Therefore, by looking at Fig. 6, the R-values for training, validation, and test are equal to 1.

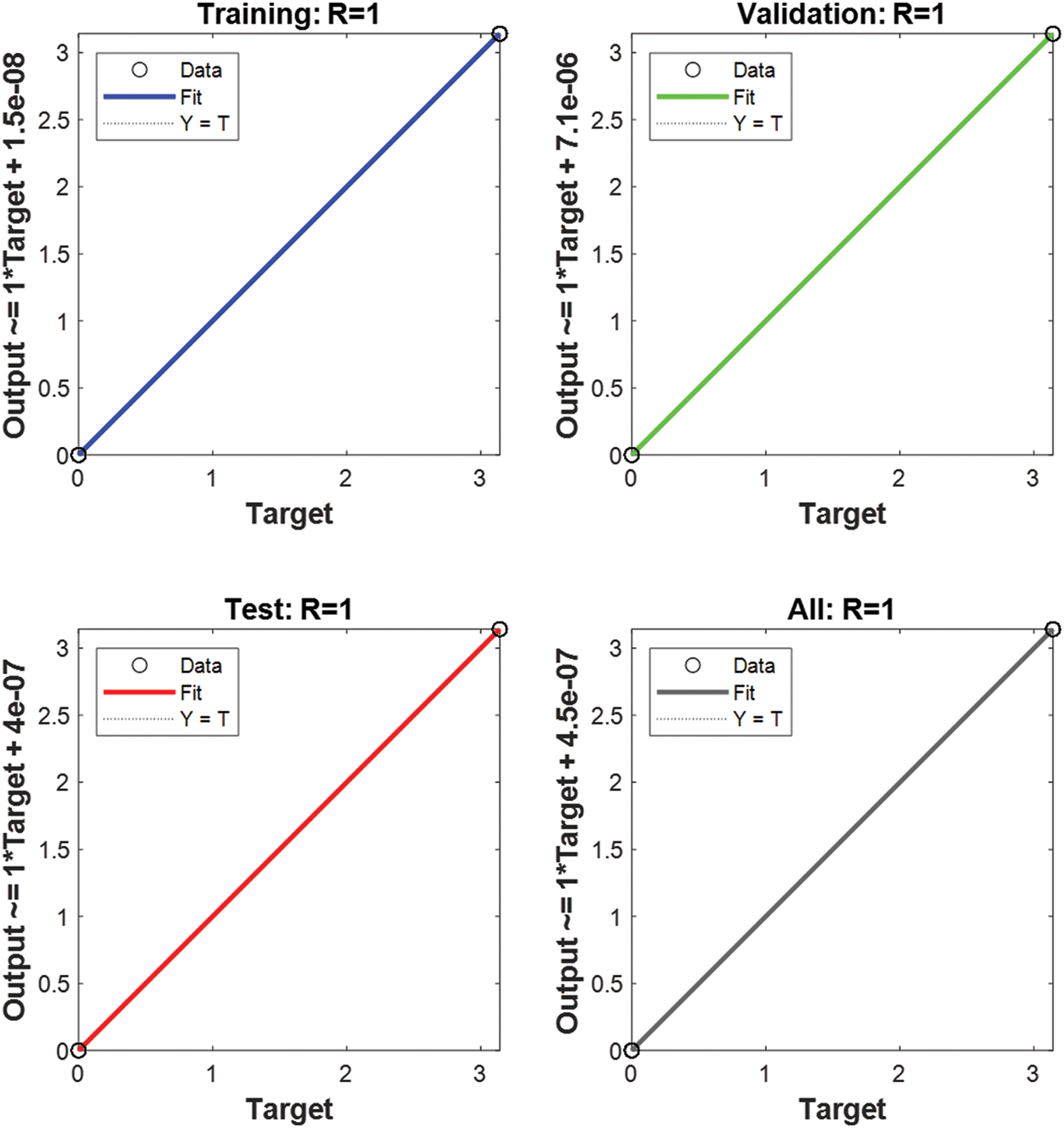
Figure 6: Training results

We also evaluated the testing of the RNN model. We calculated the accuracy using two parameters, recall, and F1-score. The recall is calculated using Eq. (9) [44]. In classification, TP represents the true positive rate, TN represents the true negative rate, FP represents the false positive rate, and FN represents the false negative rate. The precision is calculated using Eq. (10), and the F1-score is calculated in Eq. (11). Our model achieved 98.71% of recall and 96.34% of F1-score.

Recall =TPTP+FN (9)

Precision =TPTP+FP  (10)

F1−Score =2∗Precision × RecallPrecision + Recall  (11)

4.2 Comparison Results

We illustrated the design of the artificial neural network receiver and discussed its architecture in the previous Section 3. This section discusses the evaluation of the proposed method against the existing model of BPSK in IEEE802.15.4 standard in the presence of Gaussian noise. Furthermore, we obtained the response of the BPSK signal waveform without using the proposed method, and second, we recorded the system’s response in the presence of the proposed method. The simulation of the BPSK system was recorded for different SNR values = 7, 11, 13, 15, as depicted in Figs. 7–11. The reason for showing that is to confirm the effectiveness of the proposed method. Figs. 7a, 8a, 9a, 10a, and 11a illustrate the performance of the BPSK system without using the proposed method for different SNR values. However, Figs. 7b, 8b, 9b, 10b, and 11b show the performance of the BPSK system using the proposed method. For example, Fig. 7a illustrates the response of the noise and true phases of the BPSK system. The red line represents the noise phase, and the blue line represents the true phase. We recorded the simulation for the first 100 s. By comparing the response of the noisy and true phases, we notice the differentiation between the two signals. However, Fig. 7b represents the performance of the predicted phase compared with the phase of the BPSK system using the proposed method. We can conclude that the predicted and true phases of the BPSK system have identical results.

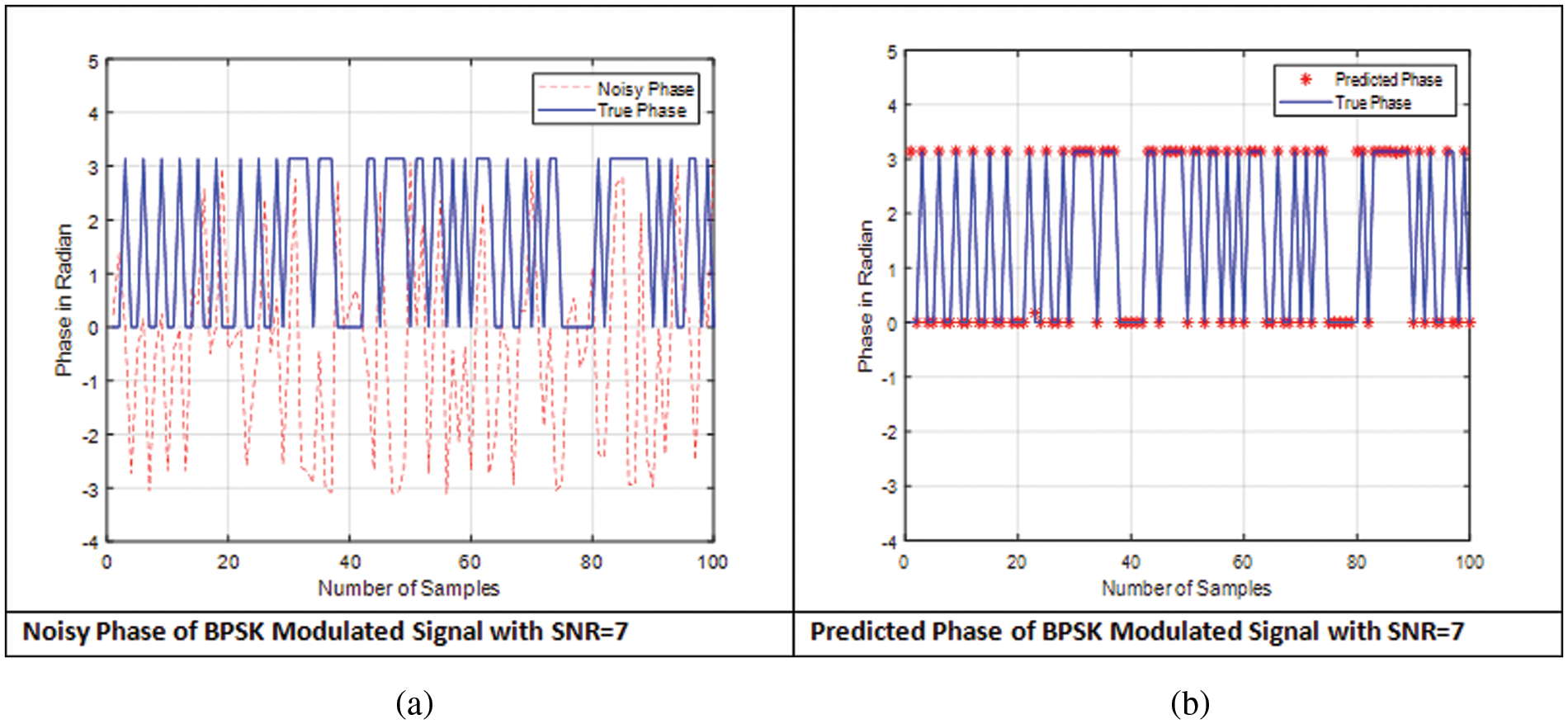
Figure 7: SNR = 7

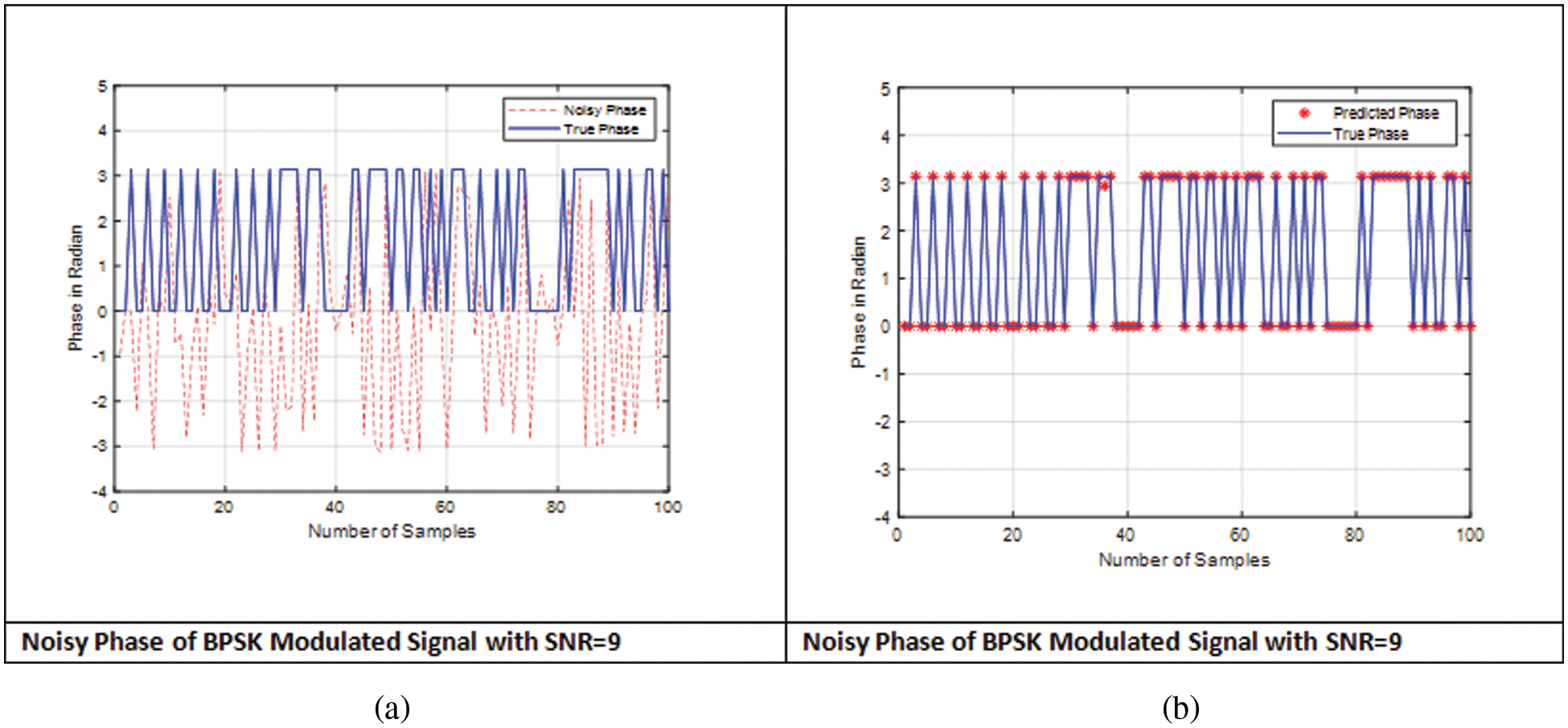
Figure 8: SNR = 9

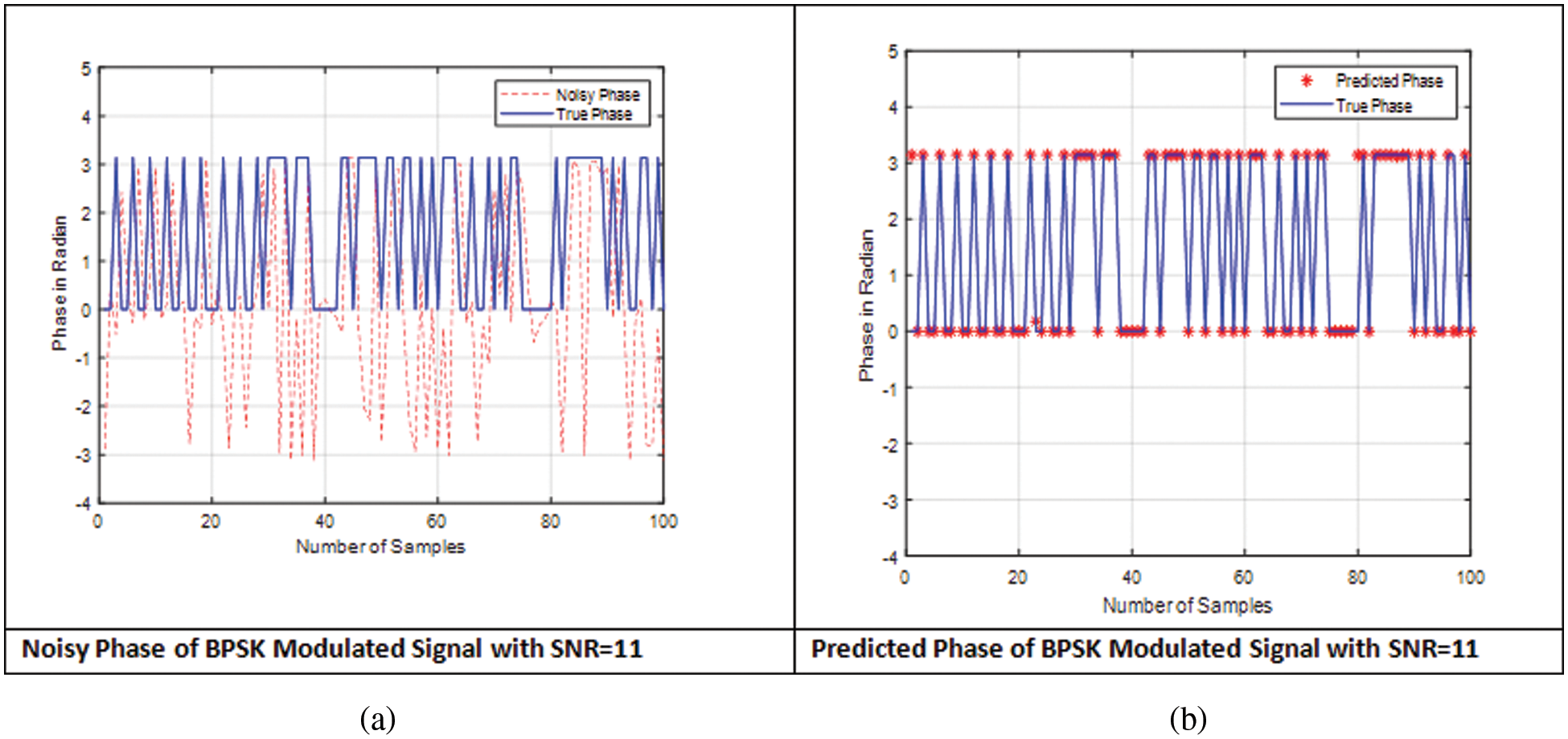
Figure 9: SNR = 11

Figure 10: SNR = 13

Figure 11: SNR = 15

5  Conclusions and Recommendations

In our proposed method, we focused on reducing the noise of the BPSK system. First, we integrated Gaussian noise into the BPSK simulation model. Second, we collected the data from the BPSK simulation model. Third, we implemented an RNN supervised learning-based model to detect the noisy BPSK phase signal and then predict the phase signal. The proposed RNN-based phase signal detection shows the potential to optimize the performance of BPSK modulated signal. The proposed method is optimal due to its low MSE for different SNR values. We achieved 8.0621e-13 of MSE when the SNR value is equal to 11. Furthermore, we evaluated our RNN model using recall and F1-score metrics. Our model showed a recall of 98.71% and an F1-score of 96.34%. The proposed RNN model can be integrated at the receiver side for different mobile and WPAN standards to detect different phase signals. In addition, we recommend testing the proposed method applied in IEEE802.15.4 standard under different nominal propagation such as non-Gaussian noise and co-channel interference (CCI) with Bluetooth, WiFi, or other IEEE802.15.4 networks to test its robustness.

Acknowledgement: The authors are thankful to the Deanship of Scientific Research at Najran University, Kingdom of Saudi Arabia, for funding this work under the General Research Funding program grant code (NU/-/SERC/10/641).

Funding Statement: This research was funded by the ministry of education and the deanship of scientific research at Najran University, Kingdom of Saudi Arabia, for financial and technical support under code number (NU/-/SERC/10/641).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. K. Bao, J. D. Matyjas, F. Hu and S. Kumar, “Intelligent software-defined mesh networks with link-failure adaptive traffic balancing,” IEEE Transactions on Cognitive Communications and Networking, vol. 4, no. 2, pp. 266–276, 2018. [Google Scholar]

2. D. Yang, Y. Xu and M. Gidlund, “Coexistence of IEEE802.15.4 based networks: A survey,” in IECON, 2010-36th Annual Conf. on IEEE Industrial Electronics Society, Glendale, AZ, USA, pp. 2107–2113, 2010. [Google Scholar]

3. End-to-End IEEE 802.15.4 PHY Simulation-MATLAB & Simulink. (n.d.2022. [Online]. Available: https://www.mathworks.com/help//comm/ug/end-to-end-ieee-802-15-4-phy-simulation.html. [Google Scholar]

4. X. Fan, P. Bai, X. Liang, J. Zhang and B. Liu, “Detection algorithm of BPSK signal of parameter-adjusted bistable stochastic resonance model based on scale change,” IEEE Access, vol. 8, pp. 97643–97657, 2020. [Google Scholar]

5. N. V. Kuznetsov, G. A. Leonov, S. M. Seledzhi, M. V. Yuldashev and R. V. Yuldashev, “Elegant computation of phase-detector characteristics of BPSK Costas loop with non-sinusoidal signals,” in 2017 IEEE European Conf. on Circuit Theory and Design (ECCTD), Catania, Italy, pp. 1–4, 2017. [Google Scholar]

6. J. Y. Oh, B. J. Kwak and J. Y. Kim, “Carrier frequency recovery for in non-coherent demodulation for IEEE802. 15.4 system,” in IEEE Vehicular Technology Conf., Montreal, QC, Canada, pp. 1–5, 2006. [Google Scholar]

7. S. Olonbayar, D. Kreiser and R. Kraemer, “Performance and implementation of a multi-rate ir-uwb baseband transceiver for ieee802. 15.4 a,” in 2013 IEEE Int. Conf. on Ultra-Wideband (ICUWB), Sydney, NSW, Australia, pp. 231–237, 2013. [Google Scholar]

8. S. Olonbayar, D. Kreiser and R. Kraemer, “FPGA and ASIC implementation and testing of IR-UWB baseband transceiver for IEEE802. 15.4 a,” in 2014 IEEE Int. Conf. on Ultra-WideBand (ICUWB), Paris, France, pp. 456–461, 2014. [Google Scholar]

9. S. Sun, L. Xu, Z. Cao, A. Huang and W. Yang, “Digital recursive demodulator based on Kalman filter,” IEEE Transactions on Instrumentation and Measurement, vol. 66, no. 12, pp. 3138–3147, 2017. [Google Scholar]

10. H. J. Jeon, T. Demeechai, W. G. Lee, D. H. Kim and T. G. Chang, “IEEE 802.15. 4 BPSK receiver architecture based on a new efficient detection scheme,” IEEE Transactions on Signal Processing, vol. 58, no. 9, pp. 4711–4719, 2010. [Google Scholar]

11. U. Ashraf and G. R. Begh, “Performance evaluation of Nakagami-m fading with impulsive noise,” IET Communications, vol. 15, no. 3, pp. 364–373, 2021. [Google Scholar]

12. A. K. Gogoi, R. K. Mallik, A. Mahanta and R. Raghuram, “Performance of a coherent BPSK receiver in an impulsive noise environment,” in 1999 IEEE Int. Conf. on Personal Wireless Communications (Cat. No. 99TH8366), Jaipur, India, pp. 471–475, 1999. [Google Scholar]

13. A. Mathur, M. Bhatnagar and B. Panigrahi, “Performance evaluation of PLC under the combined effect of background and impulsive noises,” IEEE Communications Letters, vol. 19, no. 7, pp. 1117–1120, 2015. [Google Scholar]

14. S. A. Bhatti, Q. Shan, R. Atkinson, M. Vieira and I. A. Glover, “Vulnerability of Zigbee to impulsive noise in electricity substations,” in 2011 IEEE URSI General Assembly and Scientific Symp., Istanbul, Turkey, pp. 1–4, 2011. [Google Scholar]

15. M. Cheffena, “Industrial wireless sensor networks: Channel modeling and performance evaluation,” EURASIP Journal on Wireless Communications and Networking, vol. 2012, no. 1, pp. 1–8, 2012. [Google Scholar]

16. A. Krizhevsky, I. Sutskever and G. E. Hinton, “Imagenet classification with deep convolutional neural networks,” in Advances in Neural Information Processing Systems, Lake Tahoe, Nevada, USA, vol. 25, 2012. [Google Scholar]

17. K. Simonyan and A. Zisserman, “Very deep convolutional networks for large-scale image recognition,” arXiv preprint arXiv:1409.1556, 2014. [Google Scholar]

18. K. He, G. Gkioxari, P. Dollár and R. Girshick, “Mask R-cnn,” in Proc. of the IEEE Int. Conf. on Computer Vision, Venice, Italy, pp. 2961–2969, 2017. [Google Scholar]

19. R. Girshick, “Fast R-cnn,” in Proc. of the IEEE Int. Conf. on Computer Vision, Santiago, Chile, pp. 1440–1448, 2015. [Google Scholar]

20. S. Ren, K. He, R. Girshick and J. Sun, “Faster R-CNN: Towards real-time object detection with region proposal networks,” in Advances in Neural Information Processing Systems, Montreal, Quebec, Canada, vol. 28, 2015. [Google Scholar]

21. O. Ronneberger, P. Fischer and T. Brox, “U-net: Convolutional networks for biomedical image segmentation,” in Int. Conf. on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, pp. 234–241, 2015. [Google Scholar]

22. S. S. Alahmari, D. Goldgofa, L. Hall and H. A. Phoulady, “Automated cell counts on tissue sections by deep learning and unbiased stereology,” Journal of Chemical Neuroanatomy, vol. 96, pp. 94–101, 2019. [Google Scholar] [PubMed]

23. I. J. Goodfellow, Y. Bengio and A. Courville, “Deep Learning.” Cambridge, MA, USA: MIT Press, 2016. [Google Scholar]

24. J. Yu, Z. Yi and J. Zhou, “Continuous attractors of Lotka–Volterra recurrent neural networks with infinite neurons,” IEEE Transactions on Neural Networks, vol. 21, no. 10, pp. 1690–1695, 2010. [Google Scholar] [PubMed]

25. D. E. Rumelhart, G. E. Hinton and R. J. Williams, “Learning representations by back-propagating errors,” Nature, vol. 323, no. 6088, pp. 533–536, 1986. [Google Scholar]

26. Y. Qin, D. Song, H. Chen, W. Cheng, G. Jiang et al., “A dual-stage attention-based recurrent neural network for time series prediction,” arXiv preprint arXiv:1704.02971, 2017. [Google Scholar]

27. H. Wang, Z. Wu, S. Ma, S. Lu, H. Zhang et al., “Deep learning for signal demodulation in physical layer wireless communications: Prototype platform, open dataset, and analytics,” IEEE Access, vol. 7, pp. 30792–30801, 2019. [Google Scholar]

28. A. S. Mohammad, N. Reddy, F. James and C. Beard, “Demodulation of faded wireless signals using deep convolutional neural networks,” in 2018 IEEE 8th Annual Computing and Communication Workshop and Conf. (CCWC), Las Vegas, NV, USA, pp. 969–975, 2018. [Google Scholar]

29. Q. Xiang, Y. Yang, Q. Zhang, J. Cao and Y. Yao, “Adaptive and joint frequency offset and carrier phase estimation based on Kalman filter for 16QAM signals,” Optics Communications, vol. 430, no. 2, pp. 336–341, 2019. [Google Scholar]

30. A. O. Salau, C. U. Eya and O. C. Onyebuchi, “Nonzero staircase modulation scheme for switching DC-DC boost converter,” Journal of Control Science and Engineering, vol. 2020, no. 16, pp. 1–15, 2020. [Google Scholar]

31. T. Wu, “CNN and RNN-based deep learning methods for digital signal demodulation,” in Proc. of the 2019 Int. Conf. on Image, Video and Signal Processing, New York, United States, pp. 122–127, 2019. [Google Scholar]

32. M. Zhang, Z. Liu, L. Li and H. Wang, “Enhanced efficiency BPSK demodulator based on one-dimensional convolutional neural network,” IEEE Access, vol. 6, pp. 26939–26948, 2018. [Google Scholar]

33. P. Fan, X. Cui, S. Zhao, G. Liu and M. Lu, “A two-step stochastic hybrid estimation for GNSS carrier phase tracking in Urban environments,” IEEE Transactions on Instrumentation and Measurement, vol. 70, pp. 1–18, 2021. [Google Scholar]

34. S. Kalade, L. Crockett and W. R. Stewart, “Using sequence to sequence learning for digital BPSK and QPSK demodulation,” in 2018 IEEE 5G World Forum (5GWF), Silicon Valley, CA, USA, pp. 317–320, 2018. [Google Scholar]

35. Q. Xiang, Y. Yang, Q. Zhang, Q. Fan and Y. Yao, “Machine learning enhanced modulation format transparent carrier recovery based on high order statistics,” in 45th European Conf. on Optical Communication (ECOC 2019), Dublin, Ireland, pp. 1–4, 2019. [Google Scholar]

36. Y. LeCun, Y. Bengio and G. Hinton, “Deep learning,” Nature, vol. 521, no. 7553, pp. 436–444, 2015. [Google Scholar] [PubMed]

37. X. Li, C. Zhao and M. Jiang, “Neural network for demodulating the output signals of nonlinear systems with memory,” in 2017 IEEE 9th Int. Conf. on Wireless Communications and Signal Processing (WCSP), Nanjing, China, pp. 1–5, 2017. [Google Scholar]

38. A. Alqahtani and M. Zohdy, “An investigation into using Kalman filtering for phase estimation in IEEE 802.15. 4/zigbee receivers running on adjacent channel interference,” in 2019 IEEE Int. Conf. on Electro Information Technology (EIT), Brookings, SD, USA, pp. 58–62, 2019. [Google Scholar]

39. A. Alqahtani, S. Ganesan, M. Zohdy and R. Olawoyin, “A novel non-coherent OQPSK detection based on interactive Kalman filtering with applications in Zigbee receiver,” in 2020 IEEE Int. Conf. on Electro Information Technology (EIT), Chicago, IL, USA, pp. 601–608, 2020. [Google Scholar]

40. I. Howitt and J. A. Gutierrez, “IEEE 802.15. 4 low rate-wireless personal area network coexistence issues,” in 2003 IEEE Conf. on Wireless Communications and Networking (WCNC 2003), New Orleans, LA, USA, pp. 1481–1486, 2003. [Google Scholar]

41. F. A. Almeida, G. F. Gomes, V. R. Paula, J. E. Correa, A. P. Paiva et al., “A weighted mean square error approach to the robust optimization of the surface roughness in an AISI 12L14 free-machining steel-turning process,” Journal of Mechanical Engineering, vol. 64, no. 3, pp. 147–156, 2018. [Google Scholar]

42. B. O. Adame and A. O. Salau, “Genetic algorithm based optimum finger selection for adaptive minimum mean square error rake receivers discrete sequence-CDMA ultra-wide band systems,” Wireless Personal Communications, vol. 123, no. 2, pp. 1537–1551, 2022. [Google Scholar]

43. N. X. Thao, “A new correlation coefficient of the Pythagorean fuzzy sets and its applications,” Soft Computing, vol. 24, no. 13, pp. 9467–9478, 2020. [Google Scholar]

44. A. A. Alsulami, Q. Abu Al-Haija, A. Alqahtani and R. Alsini, “Symmetrical simulation scheme for anomaly detection in autonomous vehicles based on LSTM model,” Symmetry, vol. 14, no. 7, pp. 1450, 2022. [Google Scholar]