An Efficient Approach Based on Remora Optimization Algorithm and Levy Flight for Intrusion Detection

1  Introduction

With the increased use of internet services, cybersecurity issues have become one of the most serious challenges that pose specific risks not only to individuals but also to business operations [1]. A variety of security mechanisms, such as firewalls, intrusion detection prevention systems, encryptions, and antivirus, are used by organizations and enterprises to deal with such cybersecurity attacks on their networks [2–4]. These mechanisms prove themselves as powerful methods for preventing many types of attacks. However, they cannot perform analysis for every network packet, and thus they cannot reach the desired detection performance [5]. To overcome these shortcomings and achieve optimal security requirements for a network, researchers employed Machine Learning (ML) approaches to look inside packet payloads and detect such attacks with high accuracy and a low false positive rate [6].

Selecting an Optimal Feature Subset (OFS) assists the learning process by ML techniques to achieve better performance results. Nature-inspired algorithms are mostly Meta-Heuristics (MH) optimization methods inspired by nature. These methods gained special attention from many scholars in different applications due to their great potential to specify OFS [7]. They are also effective, reliable, and gradient-free stochastic optimization techniques that have successfully solved various numerical and combinatorial optimization problems with diverse frameworks [8,9].

MH inspiration sources are broken down into three types [10,11]: swarm-based algorithms, evolutionary-based algorithms, and physics-based algorithms. Some popular MH methods, including Multi-Verse Optimizer (MVO) [12], Particle Swarm Optimization (PSO) [13], Salp Swarm Algorithm (SSA) [14], genetic algorithm [15], whale optimization algorithm [16], Snake Optimizer (SO) [17], ROA [18], are some examples of applied MH methods for Feature Selection (FS).

MH algorithms can be combined to achieve better results in different applications. The authors in [19] combined the reptile search algorithm with ROA for data clustering. In another work [20], a modified version of the ROA method using Brownian motion is introduced for image segmentation. In [21], ROA with an autonomous foraging mechanism is used to explore search space and effectively enhance global optimization solutions of the ROA. In [22], the authors combined Gorilla Troops Optimizer (GTO) with Bird Swarms (BS) to boost the capability of the GTO for FS. They evaluated their proposed GTO-BS using several evaluation measures on four Intrusion Detection (ID) datasets: Network Security Laboratory Knowledge Discovery and Data Mining (NSL-KDD), Block out traffic network (Botnet), Canadian Institute of Cybersecurity (CIC-IDS-2017), University of New South Wales Network Botnet (UNSW-NB15) and Botnet-IoT. In [23], an efficient FS method named Dynamic Feature Selector (DFS) is introduced for filtering insignificant variables. The DFS used statistical analysis and feature importance tests to reduce model complexity and improve prediction accuracy using two ID datasets.

MH methods use two principles that are characteristic of all optimization techniques, which are exploration and exploitation. In the first principle, the algorithm attempts to discover different regions in the search area, while the exploitation searches around the obtained solution from the first phase to find the best candidates. However, experiment results show that ROA is weak in exploring search space broadly. In this paper, an improved version of ROA, namely ROA-LF, is presented for the purpose of selecting OFS for the application of ID. The ROA-LF combines the original ROA with LF to enhance the exploration process and maintain a balance between exploration and exploitation in the original ROA method’s structure. The main contributions of this work could be summarized as follows:

■   An improved version of ROA using LF, named ROA-LF, is proposed for ID,

■   LF strategy is applied to enhance the ability of the ROA to explore search space more effectively and avoid getting stuck in local optima,

■   The ROA-LF is examined using five open-access datasets for ID and three well-known engineering optimization problems,

■   The ROA-LF’s efficacy is confirmed when compared to other MH methods and the tested engineering problems.

The remainder of this paper is organized as follows: Section 2 provides a brief overview of ROA and LF. Section 3 describes the developed ROA-LF method, followed by the experimental results and statistical comparison with other popular FS methods shown in Section 4. Section 5 presents the conclusion of this work.

2  Method

This section provides an overview of the ROA and LF.

2.1 ROA

ROA [18] is a new MH method that mimics the concept of parasitism of Remora. Exploration and exploitation of ROA are briefly described in this section.

2.1.1 Exploration (Free Travel)

■ Swordfish Optimization Strategy (SFO)

In the case where the Remora sticks to the swordfish, its location is updated using the following:

Rit+1=Ribestt−(rand(0,1))(Ribestt− Rrandt2−Rrandt)(1)

where t  is the number of current iterations; Ribestt  refers to the best-obtained solution and Rrandt indicates a random location, and rand(0,1) is a random number in the range of 0–1.

■ Attack experience

Remora takes small steps in the vicinity of the host end to identify whether to change or not change the host based on fitness. This behavior mathematically can be presented as:

Ratt=Rit+(Rit−Rpre)∗randn(2)

where Ratt and Rpre are the position of the previous generation and the test step, respectively, and randn is the small global random step of the Remora.

Then Remora randomly checks the change in the fitness values between the current response (f(Rit)) and the tested response  (f(Ratt)). If (f(Rit) > f(Ratt), then the Remora selects one of the feeding methods for local optimization, while if (f(Rit) < f(Ratt), Remora picks the host.

2.1.2 Exploitation (Thoughtful Nutrition)

■ WOA Strategy

According to the WOA, the position of the Remora attached to the whale is updated as follows:

Ri+1=D∗expα∗cos⁡(2πx)+Ri(3)

α=rand(0,1)∗(α−1)+1(4)

α=−(1+tT)(5)

D=⌈Rbest−Ri⌉∗R(6)

where D presents the distance between the hunter and prey, α is a random number [−1, 1], α is a linear number [=1 and −2], and t is the number of iterations.

■ Host nutrition

“Host feeding” is a small step in the exploitation process, which creates a solution space that converges gradually around the host, refining and enhancing the ability of local optimization. This stage can be mathematically modeled as follows:

Rit=Rit+A(7)

     =B∗(Rit−C∗Rbest)(8)

B=2∗V∗rand (0,1)−V(9)

V=2(1−tT)(10)

where A is a small step between the fish adhesive and the host, C is the coefficient of stickiness to indicate its position, and it is within the range of [0, 0.3].

2.2 LF

LF is a linear combination of two random independent variables (y1,y2), identically distributed with the same Probability Density Function (PDF) and is defined as [24–29]:

Ly,ld(y)=y2π 1(y−ld)32 exp(−y2y−ld), ⋯ld<y<∞(11)

where y  is a scale parameter and ld is the location parameter of the Levy distribution.

LF, which is used to produce a random walk, has step lengths (Sl) that are drawn from a Levy distribution length density distribution, and it can be given as:

Lα(Sl)≈1Sβ+1 ⋯⌊S⌋"1(12)

where β is a power law.

In the first stage of LF, stochastic variables σy1 and σy2 with standard deviations are generated

σy1(α)=[G(1+β)sin[πβ/2]G(1+β/2)β2β−1/2]1β    and    σy2=1(13)

where G(.) is the gamma function, and then the variable V is generated using,

V=y1|t2|1/β        1<β<2(14)

3  Proposed Method

This section explains the structure of the developed ROA-LF, which combines ROA and LF. Like any MH, ROA suffers from a balance between exploration and exploitation, which leads to it being trapped in a local optimum. To tackle this weakness and to enhance the global and local searching capability of the ROA, LF is used. The LF is integrated into the ROA’s structure to extend its search ability and make it capable of visiting new locations in the search space. This helps the ROA to avoid becoming trapped in locally optimal solutions and balance between exploration and exploitation. The flowchart of the introduced ROA-LF is provided in Fig. 1, and the pseudocode is in Algorithm 1.

Figure 1: Structure of the ROA-LF approach

Initially, the dataset is divided into two mutually exclusive and exhaustive subsets: training and testing. The training data is used for optimization and classifier training, while the testing data is used for performance evaluation. The entire method can be understood in two phases: the training phase and the testing phase. The training phase starts by initializing hyper-parameters of the method, such as the maximum number of iterations T, problem dimensionality M, and some constants of ROA and LF methods. The training data’s lower LB and upper UB limits are calculated for each dimension. Further, N Romera positions are initialized randomly in the range LB–UB, as in Eq. (1).

Fitness values for all candidate solutions are calculated using Eq. (9). If Romera’s previous position is better than the updated positions, then the Whale position update is implemented. Else Sailfish position update is implemented. To check if the uodate is optimum or not, a small step is taken in the test direction. The fitness value of Romera’s position and the newly tested position is calculated. If the new test direction results in a larger fitness value, then Host feeding is implemented. If the test direction provides a smaller fitness value, then Romera’s position is updated using LF.

LF is introduced into the exploration phase of the ROA to enhance its exploration ability further. For tth iteration and ith Romera is updated after LF as follows:

Ri(t)=Ri(t)+V(t) ⊙ Ri(t)(15)

where Ri(t) is candidate solution of ith Romera at tth iteration, V is the LF parameter, and ⊙ indicates the dot product. The above process is repeated for all Romeras. When all Romera positions are updated, the global best solution is saved, and the next iteration starts. For new iterations, the entire process is repeated. The optimization stops when the maximum number of iterations T is reached.

The performance of the updated Romera position fitness is calculated by using the Fitness Function (FF), which is a K-Nearest Neighbor (KNN) classifier with five neighbors and a threshold value of 0.5, as recommended by the work of [30]. The Romera with the smallest fitness as a result of the least number of selected features and maximum accuracy is the best one and is defined as:

FF(Ri)=λ×E+(λ−1)× |OFSi|M(16)

where E is the classification error rate of the KNN classifier with five neighbors, |OFSi| is the number of selected features and M is the total number of features in the dataset, and λ controls the relative importance of classification error and the number of selected features. The value of α varies in the range of [0,1] and is set to 0.99, as recommended by [31].

The global best Romera’s position is used to generate OFS by simple thresholding. It can be noted that a universal threshold of 0.5 is used during optimization, and the absolute value of the threshold used during the optimization does not change the OFS.

The testing phase starts with test data. The number of features is optimized using the position of the final global-best Romera received at the end of the training phase. The OFS of the test data is given as input to the trained classifier for performance evaluation.

4  Experimental Results

For assessing the effectiveness of the introduced ROA-LF, its capability is compared with other methods comprising PSO [13], SSA [14], SO [17], and ROA [18] on five ID datasets, and the results are provided in this section. Python scikit-learn environment setup on Windows 10 operating system with 32 GB RAM and 3.13 GHz processor speed is used to implement the experiments.

4.1 Parameter Settings

The ROA-LF is compared with other popular FS methods, with the number of expected candidate solutions and the maximum iterations set to 20 and 100, respectively. Also, each method is executed for 20 independent runs for statistically significant results. The MH methods used for comparison include PSO, SSA, SO, and ROA. The parameter setup of these MAs is detailed in Table 2. The parameter selection was based on the parameters used by the original author in the article or the parameters widely used by various researchers.

4.2 Standard Datasets

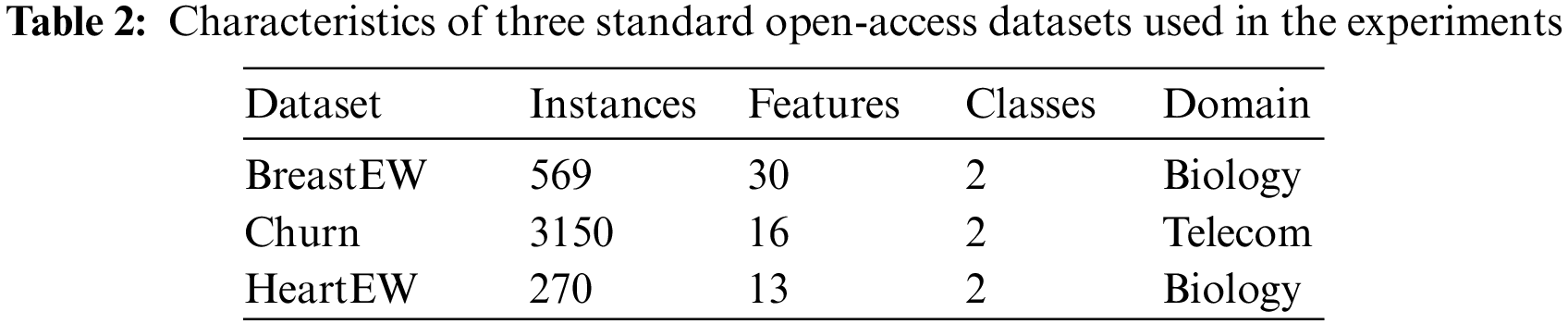
For quantitative and qualitative evaluation of the introduced ROA-LF, three standard open-access datasets from the UCI repository, suggested by several researchers in the literature, are used. Table 2 summarizes the details of the used datasets. For optimization experiments, each dataset is grouped into 80%–20% of the samples used for training and testing, respectively.

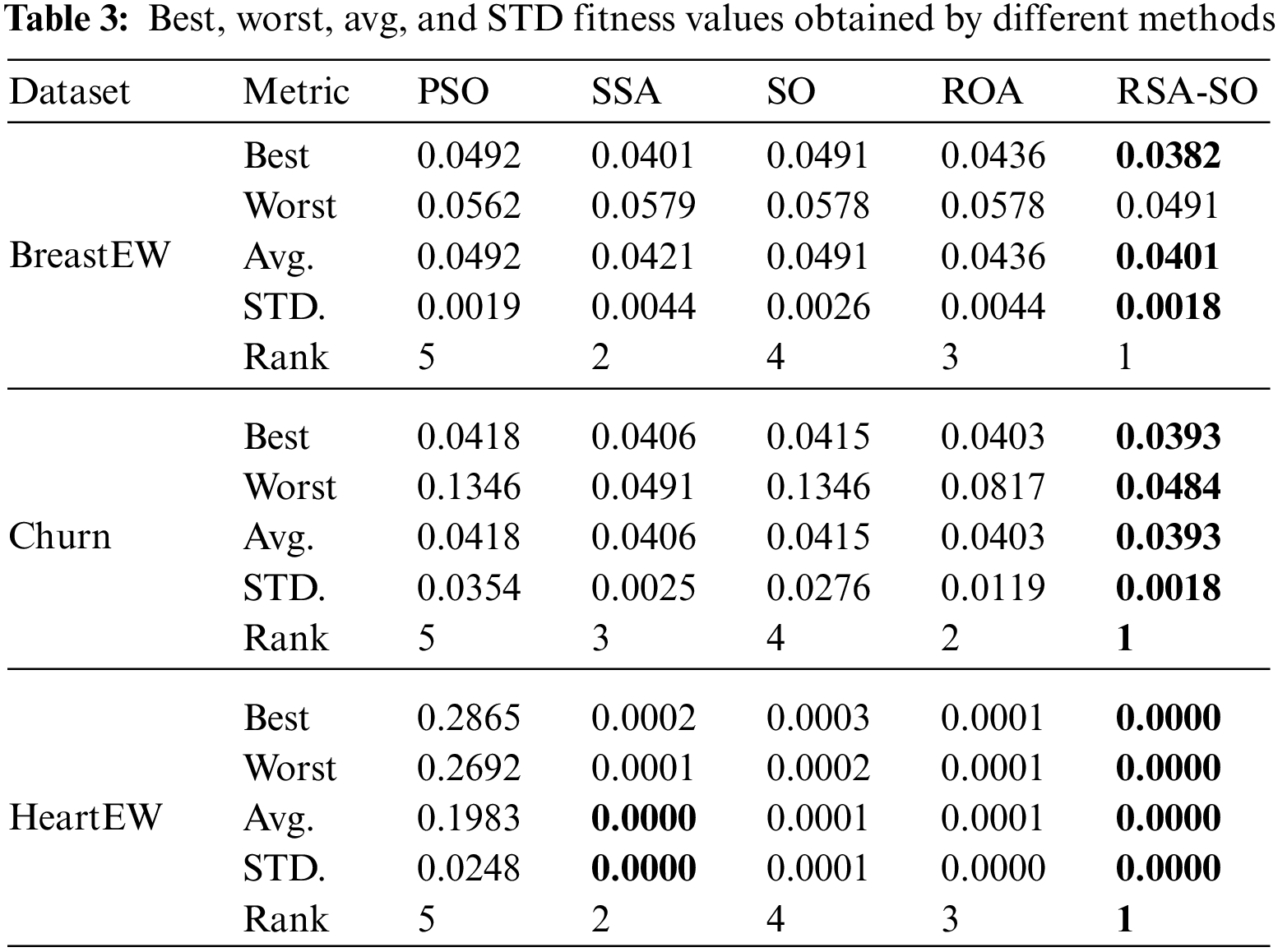
Table 3 summarizes the performance comparison of the ROA-LF and other methods in terms of statistical inferences of fitness values for three standard datasets. All methods are also ranked based on average, STD, best, fitness, and worst fitness values, in that order. Remember that a method with the smallest fitness value will be ranked first and vice versa. The table shows that the ROA-LF gained the first rank in all three datasets, indicating its superior performance over other methods. On average, SSA shows the second-best performance for all three datasets, followed by ROA and SO, respectively. PSO obtained the worst rank for all three datasets, indicating poor performance compared to other methods. These results prove the ROA-LF’s capability to sustain a stable balance between the two main principles of MH methods.

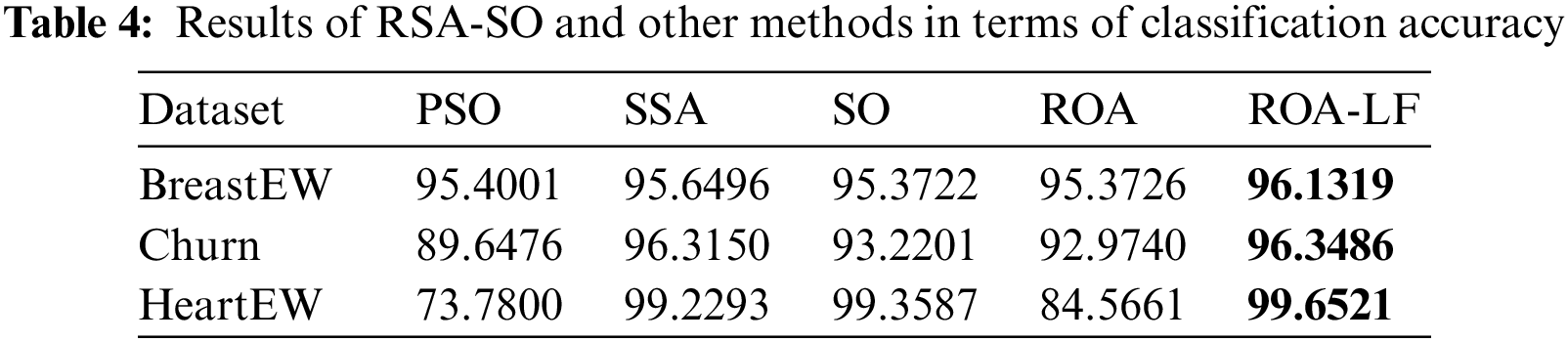
Tables 4 and 5 compare all methods in terms of the testing accuracy and the number of selected features i.e., OFS. In Table 4, the ROA-LF shows the highest accuracy compared to other methods for all three datasets. The improved exploration of ROA can interpret as this because of LF integration. SO performs the second best, followed by SSA, ROA, and PSO.

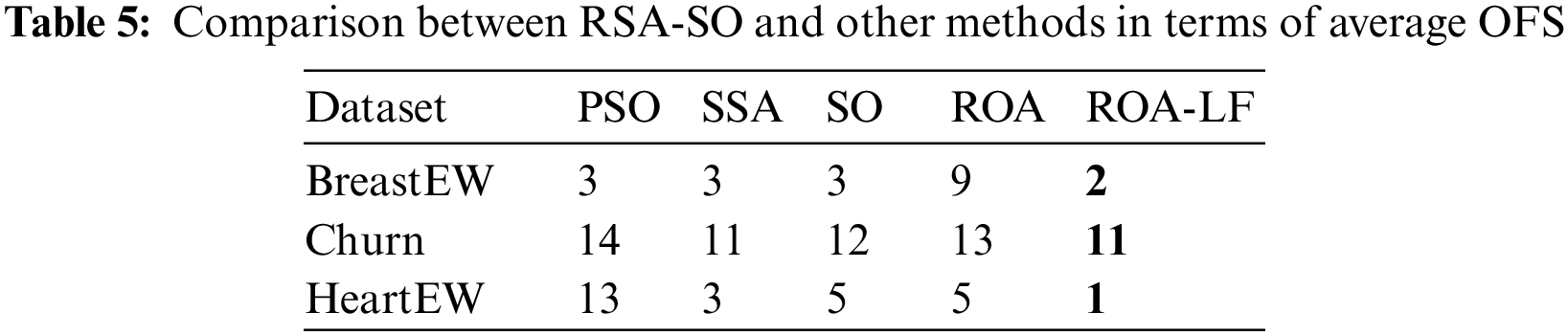
The comparative analysis using OFS is shown in Table 5 for all three datasets. The ROA-LF selected the least number of features in OFS for all three datasets. This confirms the efficiency of the proposed ROA-LF in eliminating features that are not significant for binary classification. SSA shows the second smallest OFS, followed by SO and ROA. PSO selects the highest number of features in OFS and hence, the least perming method.

4.3 ID Datasets Descriptions

Five real datasets from ID applications are selected to assess ROA-LF efficiency. These datasets are widely used for ID [22,23], and they include Knowledge Discovery and Data Mining Tools Competition (KDD-CUP99), NSL-KDD, Intrusion Detection Evaluation Dataset (ISCXIDS2012), Botnet, and CIC-IDS2018. The main characteristics of those datasets are given in Table 6.

4.4 Experimental Results and Discussion

In order to examine the effectiveness of the ROA-LF as an FS method, the real-world datasets provided in Table 1 are used, and its efficacy is evaluated using fitness values (best, worst, average (Avg.), standard deviation (STD.)), classification accuracy, and the number of the OFS.

Table 7 provides a summary of the obtained results by the ROA-LF against the other methods. The Friedman test is performed for ranking the MH methods, and ranks are presented in the table. The ROA-LF gives the best fitness values in four datasets and the smallest, worst fitness value in three out of five datasets, while the original ROA achieved both the best and worse fitness values on the CIC-IDS2018 dataset. Also, the ROA-LF has both better Avg and STD of fitness values in four datasets and achieved the first rank in four datasets. The PSO ranked first in one dataset, while SSA achieved the best STD result for the ISCXIDS2012 dataset. These results prove the ROA-LF’s stability in balancing the exploration and exploitation principles.

Table 8 compares different MH algorithms in terms of mean and Std of accuracy. The developed ROA-LF shows the least STD accuracy in all used datasets, which reflects the stability of the ROA-LF compared to PSO, SSA, SO, and ROA. The mean of accuracy is the highest for the developed ROA-LF in three out of five datasets. The SSA method gained the best mean accuracy result in the ISCXIDS2012 dataset and PSO in the CIC-IDS2018 dataset. Overall results indicate that the LF strategy improves the ROA’s performance.

The results of the proposed ROA-LF and the other MH algorithms based on the mean and STD of the OFS selected by the corresponding MH algorithm are shown in Table 9. The ROA-LF selected the least mean OFS in four out of five datasets, while for ISCXIDS2012 dataset, PSO, SA, ROA, and the developed ROA-LF selected the same mean number of OFS. Similarly, the STD of the number of OFS is the least by ROA-LF in four of five datasets, indicating better stability. For the ISCXIDS2012 dataset, SO, ROA and ROA-LF show similar STD of OFS.

The convergence behavior of the developed ROA-LF is shown in Fig. 2. The ROA-LF shows a faster convergence rate than the other methods on four out of five datasets, while the original ROA needs fewer iterations to reach the optimal solution on the CIC-IDS2018 dataset. This indicates that the use of LF can effectively improve the convergence ability of ROA and thus obtain better optimization results. These results prove the suitability of the developed ROA-LF as an FS for ID.

Figure 2: Convergence curves of the ROA-LF and the other MH algorithms for (a) KDD-CUP99, (b) NSL-KDD, (c) ISCXIDS2012, (d) Botnet, and (e) CIC-IDS2018

Boxplot is a visual representation of data distribution of the results in terms of accuracy in three quartiles: lower, middle, and upper. A boxplot of all the methods over five datasets is shown in Fig. 3. This Figure shows that the median accuracy of ROA-LF is higher than other MH methods in three out of five datasets, while upper accuracy is higher for four out of five datasets. This confirms the stability of the developed ROA-LF compared to the other comparison algorithms.

Figure 3: Box plots of the ROA-LF and the other MH algorithms for (a) KDD-CUP99, (b) NSL-KDD, (c) ISCXIDS2012, (d) Botnet, and (e) CIC-IDS2018

4.5 Real-World Engineering Problems

In this section, the ROA-LF method is applied to solve two real-world engineering problems with constraints, and these problems include Cantilever Beam Design [37], Three-Bar Truss Design [38], and Pressure Vessel Design [39].

4.5.1 Cantilever Beam Design (CBD) Problem

The proposed ROA-LF is applied to solve the CBD problem, which has five main parameters that need to be specified during the optimization process. Fig. 4 shows the CBD problem design. The mathematical representation of this problem can be formulated as follows:

Figure 4: The CBD problem

Minimize

f(x)=0.6224(x1+x2+x3+x4+x5)(17)

Subject to:

g(x)=60x13+27x23+19x33+7x43+1x53−1≤0(18)

where (0.01≤xi≤100,i=1,2,3,4,5).

Table 10 gives the results of the ROA-LF and the other methods for solving the problem of CBD. The ROA-LF has the smallest weight compared to PSO, SSA, SO, and ROA, while SO ranked second.

4.5.2 Three-Bar Truss Design (TBTD) Problem

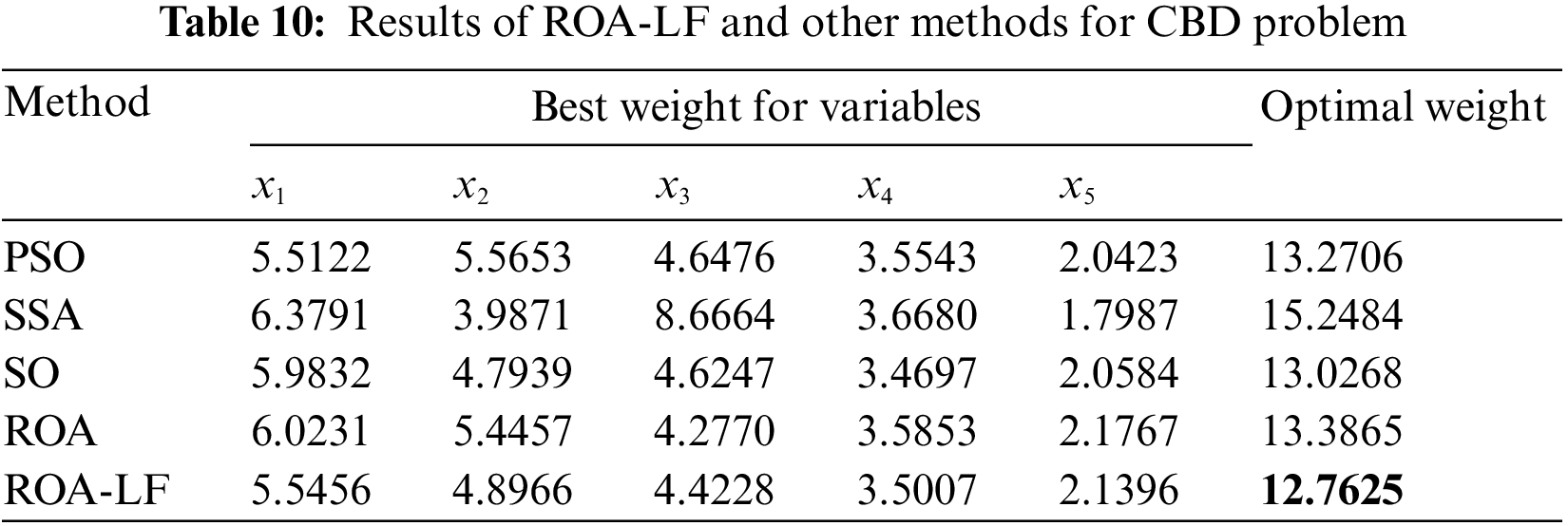
The optimal design of a TBTD seeks to minimize the structure weight subject to supporting a total load acting vertically downward. Two design variables and the structural geometry of the problem are given in Fig. 5. The objective function of this problem can be written as follows:

Figure 5: TBTD problem

Minimize

f(x)=(22x1+x2)∗l(19)

Subject to:

g1(x)=x1x1+x22x12+2x1x2P−σ≤0g2(x)=x22x12+2x1x2P−σ≤0g3(x)=12x2+x1P−σ≤0(20)

where l=100 cm, P=2kNcm2, σ=2kNcm2,and  0≤xi≤1,i=1.2.

The results of the ROA-LF for solving the problem of TBTD are provided in Table 11. The ROA-LF provides the best solution since it gained the smallest weight in comparison to PSO, SSA, SO, and ROA methods. This indicates the suitability of the developed ROA-LF for the TBTD engineering problem.

4.5.3 Pressure Vessel Design (PVD) Problem

In this problem, the PVD seeks to minimize the total pressure constrained by material, shaping, and welding costs. This problem consists of four variables, as illustrated in Fig. 6, where Ts denotes the thickness of the shell, Th is the head thickness, R represents the inner radius, and L is the length of the cylindrical section of the vessel. The objective function of the PVD can be written as follows:

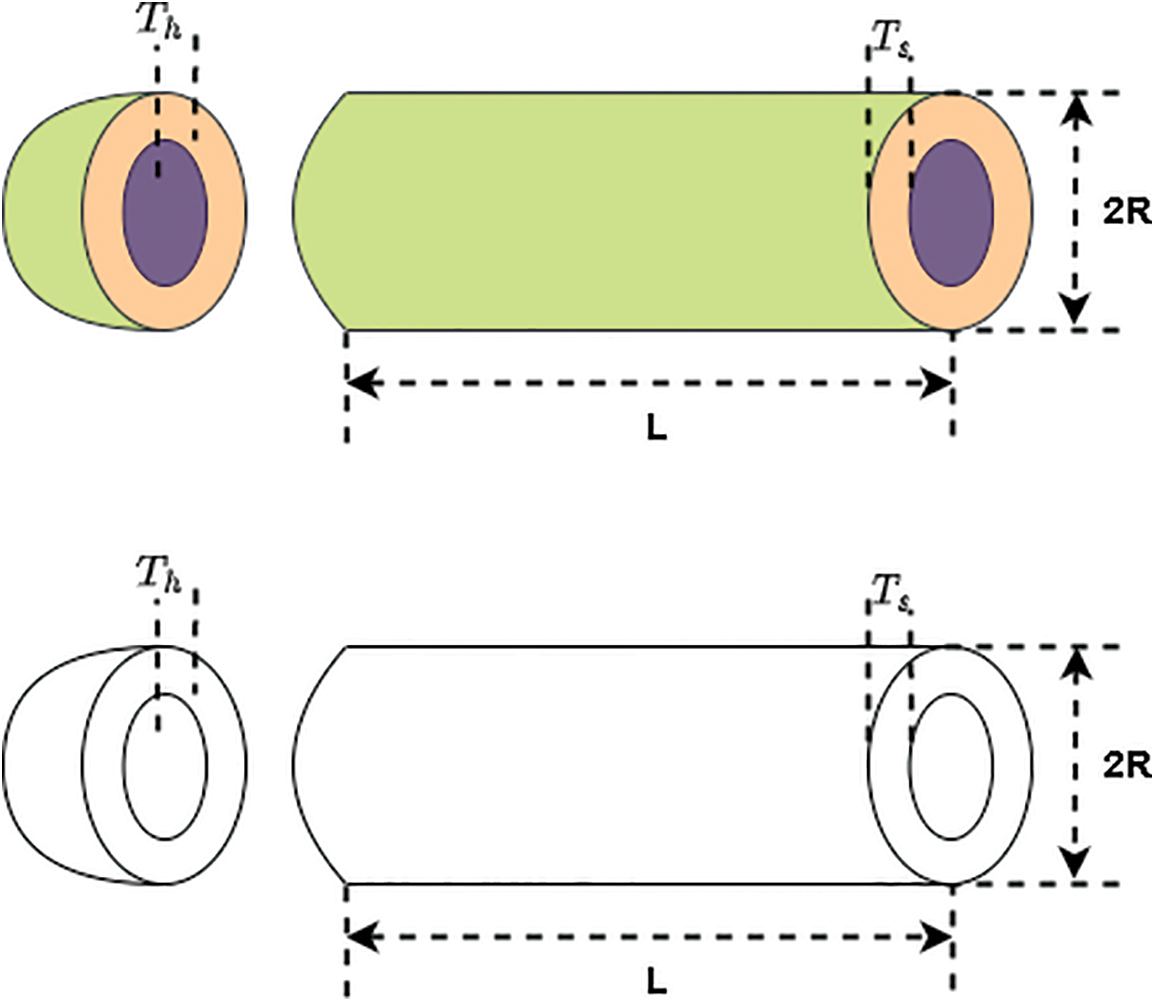
Figure 6: The PVD problem

Minimize

f(x)=0.6224x1x2x3+1.7781x2x32+3.1661x12x4+19.84x12x3(21)

Subject to:

g1(x)=−x1+0.0193x3≤0g2(x)=−x3+0.00954x3≤0g3(x)=−πx32x4− 43πx33+1,296,000 ≤0g4(x)=x4−240≤0(22)

where (0≤xi≤100,i=1.2) and (10≤xi≤200,i=3.4).

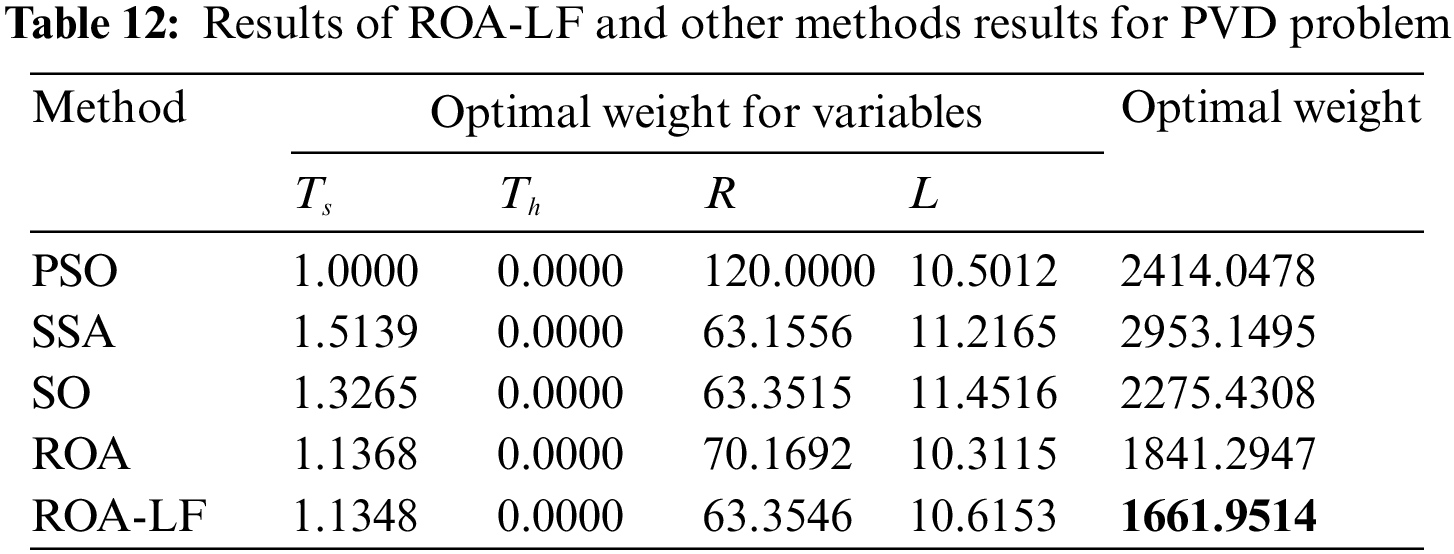
The results of the ROA-LF and the other comparative methods for the problem of PVD are given in Table 12. The ROA-LF has the smallest weight compared to PSO, SSA, SO, and the original ROA, while the SSA ranked second. The results reveal that ROA-LF can obtain excellent optimal values in this engineering problem, reflecting the applicability of ROA-LF to engineering problems.

5  Conclusion and Future Work

The existence of irrelevant or redundant data affects the performance of ML methods. This paper presents a novel FS method to improve the capability of the original ROA in exploration and exploitation using LF. The developed ROA-LF efficiency is validated using five open-access datasets in the ID domain: KDD-CUP99, NSL-KDD, ISCXIDS2012, Botnet, CIC-IDS2018, and three engineering problems. The developed ROA-LF performance is compared with the PSO, SSA, SO, and original ROA. The experimental results showed that the adaptive LF could improve ROA, thus improving its performance capability. The developed ROA-LF performs better than the other comparative methods in terms of fitness values, accuracy, number of the selected OFS, and convergence speed evaluation metrics. The statistical results show that ROA-LF is significantly more effective than the comparison algorithm.

Moreover, the results demonstrate that ROA-LF is applicable to the tested engineering optimization problems in real life with satisfactory optimization results compared to PSO, SSA, SO, and ROA alone. In future work, we will attempt to use developed ROA-LF as an FS method in other applications such as text mining, image segmentation, industry, and IoT. The introduced FS method can be improved by applying chaotic maps or combining it with other MH methods to speed up ROA’s capability when searching for OFS and avoid getting stuck in the local optima. Moreover, the developed ROA-LF can be used for deep learning and ML model parameter tuning in medical applications such as Pancreatic Nodule Detection [40], and brain tumors [41].

Funding Statement: The author received no specific funding for this study.

Conflicts of Interest: The author declares that he has no conflicts of interest to report regarding the present study.

References

1. K. K. R. Choo, K. Gai, L. Chiaraviglio and Q. Yang, “A multidisciplinary approach to internet of things (IoT) cybersecurity and risk management,” Computer Security, vol. 102, pp. 102136, 2021. [Google Scholar]

2. E. Jaw and X. Wang, “Feature selection and ensemble-based intrusion detection system: An efficient and comprehensive approach,” Symmetry, vol. 13, no. 10, pp. 1764, 2021. [Google Scholar]

3. S. Krishnaveni, S. Sivamohan, S. S. Sridhar and S. Prabakaran, “Efficient feature selection and classification through ensemble method for network intrusion detection on cloud computing,” Cluster Computing, vol. 24, no. 3, pp. 1761–1779, 2021. [Google Scholar]

4. V. R. Balasaraswathi, L. Mary Shamala, Y. Hamid, M. Pachhaiammal Alias Priya, M. Shobana et al., “An efficient feature selection for intrusion detection system using B-HKNN and C2 search based learning model,” Neural Process Letter, vol. 54, no. 1, pp. 1–25, 2022. [Google Scholar]

5. V. Ford and A. Siraj, “Applications of machine learning in cyber security,” in Proc. of the. 27th Int. Conf. on Computer Applications in Industry and Engineering, Kota Kinabalu, Malaysia, vol. 118, pp. 64–82, 2014. [Google Scholar]

6. A. Gupta, R. Gupta and G. Kukreja, “Cyber security using machine learning: Techniques and business applications,” Applications of Artificial Intelligence in Business Education and Healthcare, vol. 954, pp. 385–406, 2021. [Google Scholar]

7. H. Varaee and M. R. Ghasemi, “Engineering optimization based on ideal gas molecular movement algorithm,” Engineering and Computers, vol. 33, no. 1, pp. 71–93, 2017. [Google Scholar]

8. S. S. Band, S. Ardabili, A. S. Danesh, Z. Mansor, I. AlShourbaji et al., “Colonial competitive evolutionary rao algorithm for optimal engineering design,” Alexandria Engineering Journal, vol. 61, no. 12, pp. 11537–11563, 2022. [Google Scholar]

9. M. Banaie-Dezfouli, M. H. Nadimi-Shahraki and Z. Beheshti, “R-GWO: Representative-based grey wolf optimizer for solving engineering problems,” Applied Soft Computing, vol. 106, pp. 107328, 2021. [Google Scholar]

10. R. Khalid and N. Javaid, “A survey on hyperparameters optimization algorithms of forecasting models in smart grid,” Sustain Cities Soc., vol. 61, pp. 102275, 2020. [Google Scholar]

11. L. Abualigah and A. Diabat, “A comprehensive survey of the grasshopper optimization algorithm: Results, variants, and applications,” Neural Computing and Applications, vol. 32, pp. 15533–15556, 2020. [Google Scholar]

12. S. Mirjalili, S. M. Mirjalili and A. Hatamlou, “Multi-verse optimizer: A nature-inspired algorithm for global optimization,” Neural Computing and Applications, vol. 27, pp. 495–513, 2016. [Google Scholar]

13. J. Kennedy and R. Eberhart, “Particle swarm optimization,” in Proc. of Int. Conf. on Neural Networks, Perth, WA, Australia, vol. 1, no. 1, pp. 1942–1948, 1995. [Google Scholar]

14. S. Mirjalili, A. H. Gandomi, S. Z. Mirjalili, S. Saremi, H. Faris et al., “Salp swarm algorithm: A bio-inspired optimizer for engineering design problems,” Advances in Engineering Software, vol. 114, pp. 163–191, 2017. [Google Scholar]

15. J. H. Holland, “Genetic algorithms,” Scientific Am., vol. 267, pp. 66–73, 1992. [Google Scholar]

16. S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Advances in Engineering Software, vol. 95, pp. 51–67, 2016. [Google Scholar]

17. F. A. Hashim and A. G. Hussien, “Snake optimizer: A novel meta-heuristic optimization algorithm,” Knowledge-Based Systems, vol. 242, pp. 108320, 2022. [Google Scholar]

18. H. Jia, X. Peng, and C. Lang, “Remora optimization algorithm,” Expert Syst. Appl., vol. 185, pp. 46–61, 2021. [Google Scholar]

19. K. H. Almotairi and L. Abualigah, “Hybrid reptile search algorithm and remora optimization algorithm for optimization tasks and data clustering,” Symmetry, vol. 14, no. 3, pp. 458, 2022. [Google Scholar]

20. Q. Liu, N. Li, H. Jia, Q. Qi and L. Abualigah, “Modified remora optimization algorithm for global optimization and multilevel thresholding image segmentation,” Mathematics, vol. 10, no. 7, pp. 1014, 2022. [Google Scholar]

21. R. Zheng, H. Jia, L. Abualigah, S. Wang and D. Wu, “An improved remora optimization algorithm with autonomous foraging mechanism for global optimization problems,” Mathematical Biosciences and Engineering, vol. 19, no. 4, pp. 3994–4037, 2022. [Google Scholar] [PubMed]

22. S. S. Kareem, R. R. Mostafa, F. A. Hashim and H. M. El-Bakry, “An effective feature selection model using hybrid metaheuristic algorithms for iot intrusion detection,” Sensors, vol. 22, no. 4, pp. 1396, 2022. [Google Scholar] [PubMed]

23. M. Ahsan, R. Gomes, M. M. Chowdhury and K. E. Nygard, “Enhancing machine learning prediction in cybersecurity using dynamic feature selector,” Journal of Cybersecurity and Privacy, vol. 1, no. 1, pp. 199–218. 2021. [Google Scholar]

24. Z. Manbari, F. AkhlaghianTab and C. Salavati, “Hybrid fast unsupervised feature selection for high-dimensional data,” Expert Systems with Applications, vol. 124, pp. 97–118, 2019. [Google Scholar]

25. M. Shehab and L. Abualigah, “Opposition-based learning multi-verse optimizer with disruption operator for optimization problems,” Soft Computing, vol. 26, pp. 11669–11693, 2021. [Google Scholar]

26. A. G. Hussien and M. Amin, “A self-adaptive Harris Hawks optimization algorithm with opposition-based learning and chaotic local search strategy for global optimization and feature selection,” International Journal of Machine Learning and Cybernetics, vol. 13, no. 2, pp. 309–336, 2022. [Google Scholar]

27. Y. Yuan, X. Mu, X. Shao, J. Ren, Y. Zhao et al., “Optimization of an auto drum fashioned brake using the elite opposition-based learning and chaotic k-best gravitational search strategy based grey wolf optimizer algorithm,” Applied Soft Computing, vol. 123, pp. 108947, 2022. [Google Scholar]

28. J. P. Nolan, “Modeling with stable distributions,” in Univariate Stable Distributions, Cham: Springer, pp. 25–52, 2020. [Google Scholar]

29. Y. Li, Y. Zhao and J. Liu, “A levy flight sine cosine algorithm for global optimization problems,” International Journal of Distributed Systems and Technologies, vol. 12, no. 1, pp. 49–66, 2021. [Google Scholar]

30. I. Al-Shourbaji, P. H. Kachare, S. Alshathri, S. Duraibi, B. Elnaim et al., “An efficient parallel reptile search algorithm and snake optimizer approach for feature selection,” Mathematics, vol. 10, pp. 2351, 2022. [Google Scholar]

31. I. Al-Shourbaji, N. Helian, Y. Sun, S. Alshathri and M. Abd Elaziz, “Boosting ant colony optimization with reptile search algorithm for churn prediction,” Mathematics, vol. 10, pp. 1031, 2021. [Google Scholar]

32. M. Tavallaee, E. Bagheri, W. Lu and A. A. Ghorbani, “A detailed analysis of the KDD CUP 99 data set,” in Proc. of IEEE Conf. on Symp. on Computational Intelligence for Security and Defense, Ottawa, ON, Canada, pp. 1–6, 2009. [Google Scholar]

33. S. Sapre, P. Ahmadi and K. Islam, “A robust comparison of the KDDCup99 and NSL-KDD IoT network intrusion detection datasets through various machine learning algorithms,” arXiv preprint, pp. 1–8, 2019. [Google Scholar]

34. A. Shiravi, H. Shiravi, M. Tavallaee and A. A. Ghorbani, “Toward developing a systematic approach to generate benchmark datasets for intrusion detection,” Computer Security, vol. 31, no. 3, pp. 357–374, 2012. [Google Scholar]

35. E. B. Beigi, H. H. Jazi, N. Stakhanova and A. A. Ghorbani, “Towards effective feature selection in machine learning-based botnet detection approaches,” in Proc. of IEEE Conf. on Communications and Network Security, San Francisco, CA, USA, pp. 247–255, 2014. [Google Scholar]

36. I. Sharafaldin, A. H. Lashkari and A. A. Ghorbani, “Toward generating a new intrusion detection dataset and intrusion traffic characterization,” in Proc. of the 4th Int. Conf. on Information Systems Security and Privacy, Funchal, Portugal, vol. 1, no. 2, pp. 108–116, 2018. [Google Scholar]

37. H. Chickermane and H. C. Gea, “Structural optimization using a new local approximation method,” Int. J. Numerical Methods in Engineering, vol. 39, no. 5, pp. 829–846, 1996. [Google Scholar]

38. T. Ray and K. M. Liew, “Society and civilization: An optimization algorithm based on the simulation of social behavior,” IEEE Trans. Evolutionary Computation, vol. 7, no. 4, pp. 386–396, 2003. [Google Scholar]

39. S. Mirjalili, “Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm,” Knowledge Based Systems, vol. 89, pp. 228–249, 2015. [Google Scholar]

40. T. Thanya and S. W. Franklin, “Grey wolf optimizer based deep learning for pancreatic nodule detection,” Intelligent Automation and Soft Computing, vol. 36, no. 1, pp. 97–112, 2023. [Google Scholar]

41. S. Keerthi and P. Santhi, “Precise multi-class classification of brain tumor via optimization based relevance vector machine,” Intelligent Automation and Soft Computing, vol. 36, no. 1, pp. 1173–1188, 2023. [Google Scholar]