A Novel Attack on Complex APUFs Using the Evolutionary Deep Convolutional Neural Network

1  Introduction

The Internet of Things (IoT) is a wide network of different nodes that are connected using the Internet. Nowadays, the existence of many telecommunication networks with limited computing, power, and communication capacity has made the necessity of IoT inevitable in many infrastructures [1–3]. Security is one of the major concerns that needs to be considered for IoT to be practically available in the near future, as it is with all communication networks, especially given the unique features of IoT. Many efforts have been made so far to address security issues in the IoT, though providing a suitable security solution considering the limitations of the IoT has been an open problem [4–7]. Among all proposed security solutions for the IoT, physically unclonable functions (PUFs) [8] are among the most popular primitives because they provide lightweight authentication as well as security against physical attacks, which are among the most important attacks in IoT networks [9–14].

PUFs work as challenge-response black boxes and can be utilized to extract unique random bits by using the unique manufacturing-related physical properties of an electronic device. In this way, many challenge-response pairs (CRPs) can be generated as cryptographic keys for device authentication purposes in IoT networks using the embedded PUF in IoT devices [15–17]. These responses are typically extremely difficult for an adversary to replicate or predict. Several authentication schemes have been introduced to eliminate the practical restrictions where a server with high computational capacity authenticates a low-power device [18].

The Arbiter PUF (APUF) was proposed and implemented at the very beginning of PUFs as a low-power device-oriented secret key generator [19] with a simple structure and functionality and low implementation costs. However, it has been shown that APUFs are assailable to different modeling threats. For example, an adversary who can get access to a set of CRPs from a PUF instance attempts to build a mathematical framework using the gathered CRPs and predict a PUF response with a high probability. Among all modeling attack techniques, machine learning (ML) algorithms like support vector machine (SVM) and logistic regression (LR) have been the most favorite attacks that could have broken the resistance of APUF. More importantly, multiple-layer perceptron neural networks (MLPNN) have been recently employed to break the security of APUF [20–25]. On the other hand, XOR APUFs (XAPUFs) have been recently proposed to increase the security of APUFs against modeling attacks [26]. Although some efforts have shown that XAPUFs can be modeled by some ML-based approaches [27–31], breaking the security of the more complex XAPUF is still an open problem. Furthermore, the majority of the proposed XAPUF attacks place a high computational burden on the attacker’s side. Therefore, another motivation for this paper is to propose more practical attacks for breaking the security of complex XAPUFs structures.

According to the literature [32–43], different ML algorithms have been proposed to break the security of XAPUFs, containing deep learning (DL), neural networks (NNs), and SVMs. Although the most effective approach is uncertain, since 2006, DL has gained popularity in the ML field. DL models have surpassed conventional ML models because of advancements in information availability. The popularity of DL techniques has also gained due to improvements in decreasing execution time and enhancing the convergence rate. Therefore, this paper uses a deep convolutional neural network (DCNN) to bypass the security of XAPUFs. However, an effective DL training approach is known to be one of the major ML tasks. Gradient-based methods have significant limitations, such as becoming stuck at local extremums in multi-objective loss functions, considerable computational cost, and requiring continuous objective functions [44–46]. To address this challenge, researchers have delved into the application of MH algorithms for parameter optimization in DL. In this paper, a new migration-based multi-parent genetic algorithm (MBMPGA) has been developed to train DCNN. MH algorithms are able to greatly enhance the training of DL models by enhancing the learning process, leading to better accuracy and decreased computational complexity.

1.1 Paper Contributions

We intend to develop a deep architecture by proposing a novel MBMPGA to train the fully connected NN in the proposed deep structure for achieving higher attack accuracy. The major contributions of this paper can be summarized as follows:

•   A new MH algorithm named MBMPGA is introduced to enhance the exploitation and exploration abilities of GA by using the non-linear migration operator in BBO and multi-parent crossover, respectively.

•   The performance of a deep CNN as an attacking tool is improved by tuning the weights and biases in its NN using the proposed MBMPGA in order to reach a high rate of accuracy for modeling complex XAPUFs.

•   The performance of the proposed MBMPGA-DCNN is compared against eight different models, namely GA-DCNN, particle swarm optimization (PSO)-DCNN, BBO-DCNN, improved crow search algorithm (I-CSA)-DCNN, black widow optimization (BWO)-DCNN, DCNN, MLPNN, and SVM.

•   The performance of MBMPGA is evaluated using several real-word datasets, namely tension spring design, three-bar truss design, and complex XAPUFs problems. To compare the models, various metrics were utilized, including sensitivity, accuracy, specificity, mean square error (MSE), receiver operating characteristic (ROC) curve, convergence curve, execution time, best fitness function, mean fitness function, and standard deviation.

•   Compared to previous attacking models, the simulation results of the proposed model on some simulated CRPs [33] show a significant improvement in computational cost and the number of CRPs needed for training the model.

1.2 Paper Organization

The remainder of this paper is formed as follows: Section 2 presents the related works. Section 3 presents the proposed MBMPGA algorithm. Section 4 elaborates on the DL model improved by MBMPGA. Section 5 first measures the performance of MBMPGA using different benchmark datasets, then compares the performance of the proposed DL architecture in modeling different complex XAPUFs, and finally draws a conclusion about this work in Section 6.

2  Related Works

In typical modeling attacks on PUFs, by using a CRP sub-related to a PUF instance, an adversary can drive a numerical PUF structure. Accordingly, many efforts have been made to study the resistance of XAPUFs against machine-learning-based attacks. These efforts have usually utilized various attack models. Ruhrmair et al. [27] employed LR to model 4-XAPUF, 5-XAPUF, and 6-XAPUF with 64-bit 128-bit challenges, and the attack models could predict the PUF responses with 99% accuracy. With the exception of 4-XAPUF, their attacks took some time to train their model. Tobisch et al. [30] suggested parallelizing the LR-based technique according to [27]. By having 2 × 107 and 1.5 × 108 CRPs, a better accuracy was achieved for 7-XAPUF and 8-XAPUF with 64-bit challenge bits. However, the suggested modeling attack needed a long-time training process.

For the first time, Hospodar et al. [32] used an MLP neural network to attack XAPUFs. They achieved approximately 90% accuracy when attacking the 2-XAPUF with a challenge-bit length of 64 bits. Santikellur et al. [28] introduced the earliest effective employment of DL in modeling different types of APUF. Their modeling results have shown 98% accuracy on 5-XAPUF and 6-XAPUF with 64-bit challenge-bit length. In [29], Aseeri et al. proposed an MLP NN for the 4to8-XOR-APUF for different challenge bits. By employing just 3 × 107 CRPs, they were able to predict the testing CRPs of the 8-XOR-APUF with 64-bit challenge-bit length with 99% accuracy.

Mursi et al. [33] have proposed MLP-based attacks on 5to9-XOR-APUFs. Their attack’s structure followed the Aseeri techniques, though the number of used hidden layers in NN was 50% reduced. Shi et al. have proposed two novel modeling attacks, the logical approximation and the global approximation, which utilize an ANN for modeling the nonlinear nature of the XOR-APUFs [34]. In addition, an effective attack entitled CANDECOMP/PARAFAC-Tensor Regression Network (CP-TRN) has been introduced by Santikellur et al. [31] to reduce the computational complexity of the attack on XAPUFs. This is important to mention that CP-TRN is a type of CP-decomposition-based TRN. Cui et al. [35] proposed an ML-based attack on different types of strong PUFs. To achieve this, XORs in the XOR-based Multi-PUF were substituted with multiplexers [36]. According to the literature, different ML algorithms have been proposed to break the security of XAPUFs. However, these attacks have typically failed to model the more complex structure of XAPUF, necessitating a large set of CRPs as well as significant computational power.

Based on the review of the papers, it becomes evident that in order to achieve more precise modeling of complex XAPUFs problem, the utilization of more robust DL algorithms is necessary. The optimization of parameters in DLs is a challenging task owing to their NP-hard nature. To address this challenge, researchers have delved into the application of MH algorithms for parameter optimization in DL. Although MH-based methods have been effective in finding optimal solutions for complex problems, the use of MH for optimizing different DL structures is a relatively new research area. The first attempt to employ a GA to train a DCNN was proposed in [47]. This method used the advantages of various GA operators to train the DCNN by treating the parameters of the NN as chromosomes. Fan et al. proposed an approach using progressive unsupervised learning (PUL) to optimize the variables of a pre-trained DCNN [48]. Their scheme demonstrated efficient implementation and was employed as an optimized principle for unsupervised learning. Sun et al. presented a GA-trained DCNN in order to classify image features without requiring extra information about the used DCNN. However, the major drawback of the mentioned scheme was that the training algorithm becomes slow when the deep architecture is relatively large due to the large size of the GA’s chromosomes [49]. In recent years, several other training algorithms have been introduced to enhance the performance of different DL models [44,50].

In the context of complex APUFs, several technical gaps have been identified, leading to the development of the proposed methodology utilizing MBMPGA for training DCNNs. The following technical gaps have motivated the design of this novel approach:

•   Existing methodologies lack effective attack strategies specifically tailored for complex APUFs. This gap highlights the need for an innovative algorithm that can successfully exploit vulnerabilities in these systems.

•   Optimizing the parameters of DL models is a difficult task. To tackle this challenge, researchers have explored the use of MHs for DL parameter optimization. Over the years, a plethora of MH algorithms have been proposed and shown promising results in solving various engineering problems. As problems become more intricate, the demand for new MH algorithms becomes more apparent than ever. There are five main motivations that drive this need a) flexibility; b) derivation-free mechanisms; c) simple and effective implementation; d) simple structure and concepts; e) local optima avoidance. Addressing the exploration and exploitation aspects of complex optimization problems is recognized as a challenging endeavor. To overcome these difficulties, in this paper, a new MBMPGA algorithm has been developed to train DCNN.

•   Traditional genetic algorithms often rely on a single parent population, limiting the exploration and exploitation of diverse solutions. The proposed MBMPGA addresses this gap by incorporating multiple parent populations and migration strategies to enhance diversity and convergence speed.

3  Migration-Based Multi-Parent Genetic Algorithm (MBMPGA)

GA is a type of search algorithm that takes inspiration from Charles Darwin’s theory of natural evolution. First presented by Holland in 1975 [37], the aim of GA is to produce offspring that are biologically superior to their parents. The algorithm works by selecting the most competent individuals from the population and allowing them to reproduce by producing offspring. During the reproduction process, the genes from both parents’ crossover, leading to a genetic mutation. The offspring then reproduce, and the cycle continues, resulting in the production of healthier generations. GA consists of four distinct phases [38].

At the beginning of the genetic algorithm, a collection of solutions called the “initial population” is generated. Each solution is represented by a chromosome, consisting of a set of genes that define the variables of the problem. The next step involves selecting two pairs of chromosomes (parents) based on their fitness values using a selection method such as the roulette wheel. The most important step in the algorithm is the crossover operator, which involves randomly selecting a crossover point within the genes and exchanging them between the parents to create offspring. This operator is used to enhance the exploitation of GA by searching the space around a chromosome. The mutation is also introduced to enhance exploration by randomly modifying the genes of some newly formed offspring.

There are several drawbacks known for the original GA e.g., weaker exploitation ability and getting stuck in local extremums. However, if chromosomes suddenly and rapidly change their motion space to move in the desired direction, the GA algorithm converges faster. Fig. 1 indicates the single-point crossover operator of the normal GA. As it is observed, in this method, only two parents are mixed, thus the chromosomes generated (offspring) are not very distinct from the parents [39].

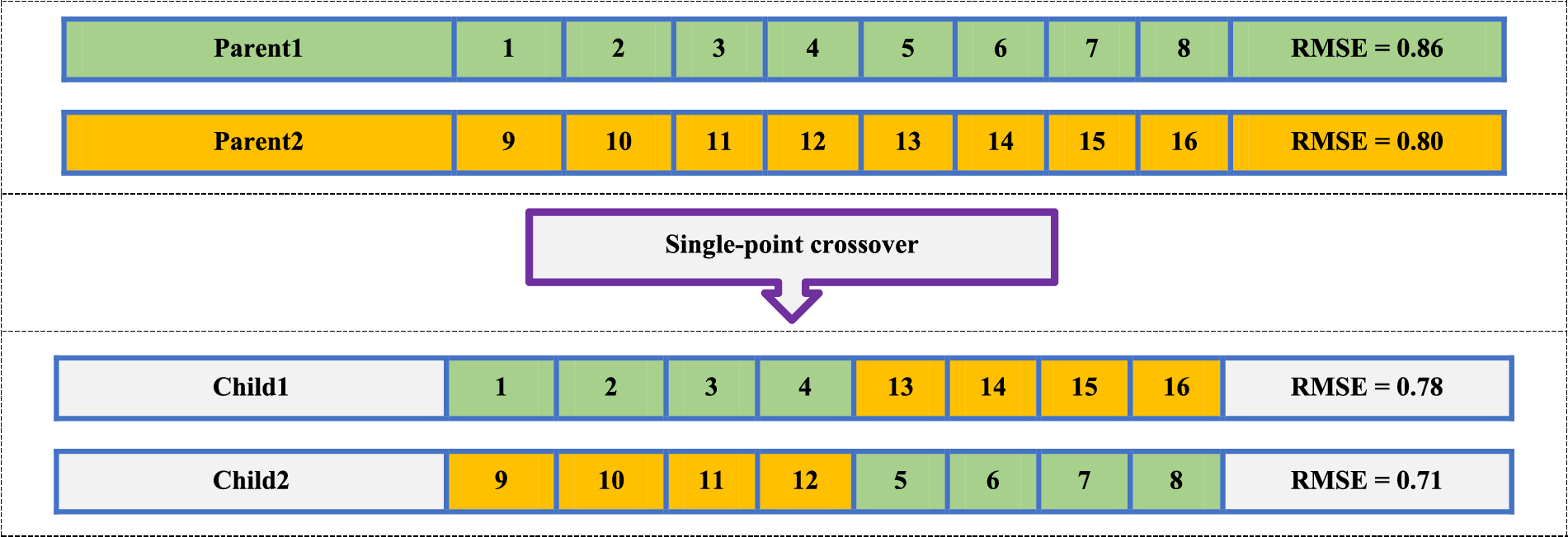
Figure 1: An example of a single-point crossover

Another disadvantage of standard single-point crossover is that it only searches the space between two parents. If a better global search is done in GA, in addition to diversifying the answers, the convergence curve of the GA will also improve. In this article, a novel MBMPGA algorithm is presented as an innovative operator to enhance the exploitation and exploration of GA. In MBMPGA, the migration operator of the BBO is employed to enhance the exploitation of GA. Multi-parent crossover (as a new operator) is then introduced to develop the exploration ability of GA. Considering the comparison of the performances of different migration models, in this paper, the generalized sinusoidal model has been used. Emigration (μk(j)) and immigration rates (λk(j)) are defined as Eqs. (1) and (2).

μk(j)=E2×(−cos cos(k(j)πN+φ)+1)(1)

λk(j)=I2×(cos cos(k(j)πN+φ)+1)(2)

where k(j) denotes the rank of species in the jth habitat. E and I show the maximum rates of emigration and immigration, respectively. Figs. 2 and 3 show examples of multi-parent crossover and migration-based multi-parent crossover in the MBMPGA, respectively. As is observed, the value of RMSE is like the objective function, and the lower the RMSE, the better the approach. In MBMPGA, when several of the best parents are selected to generate a new offspring simultaneously, the resulting offspring bears less resemblance to one parent, i.e., the offspring is more diverse (improving exploration). However, since the offspring have obtained all of their genes from multiple chromosomes, the exploitation of the algorithm improves. Fig. 4 shows the flowchart of the MBMPGA. The pseudo-codes of the MBMPGA are also shown in Algorithm 1.

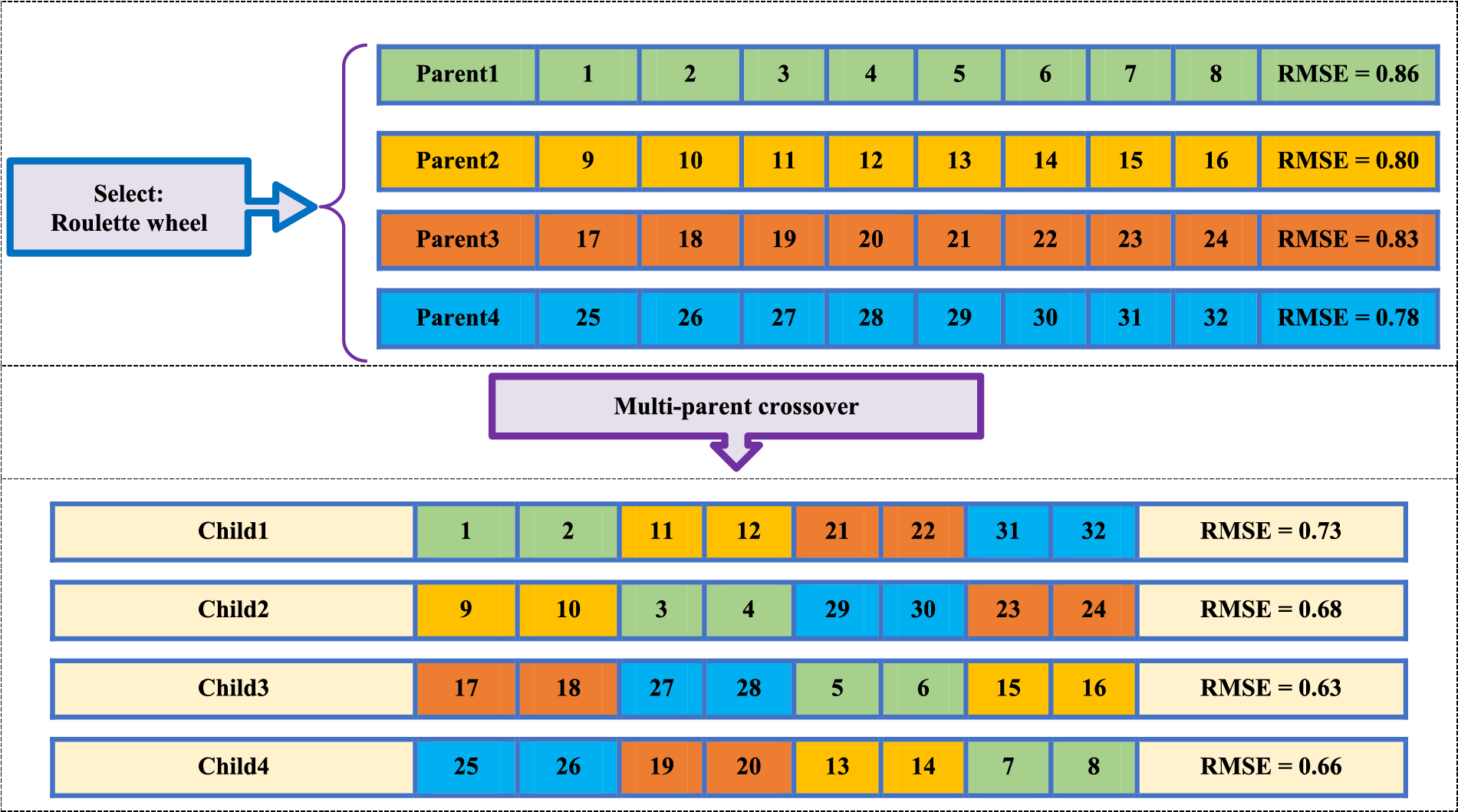
Figure 2: An example of multi-parent crossover

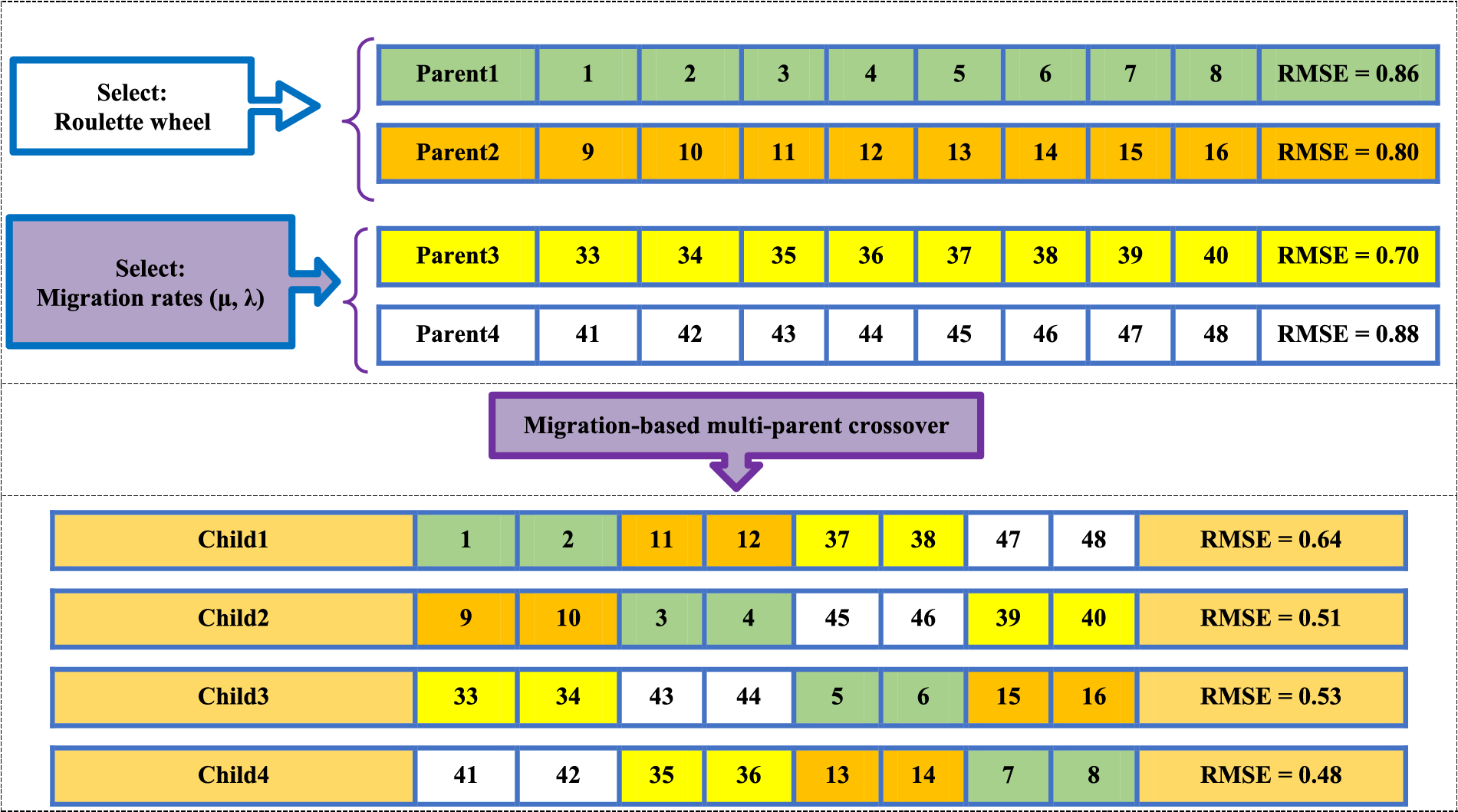
Figure 3: An example of multi-parent crossover

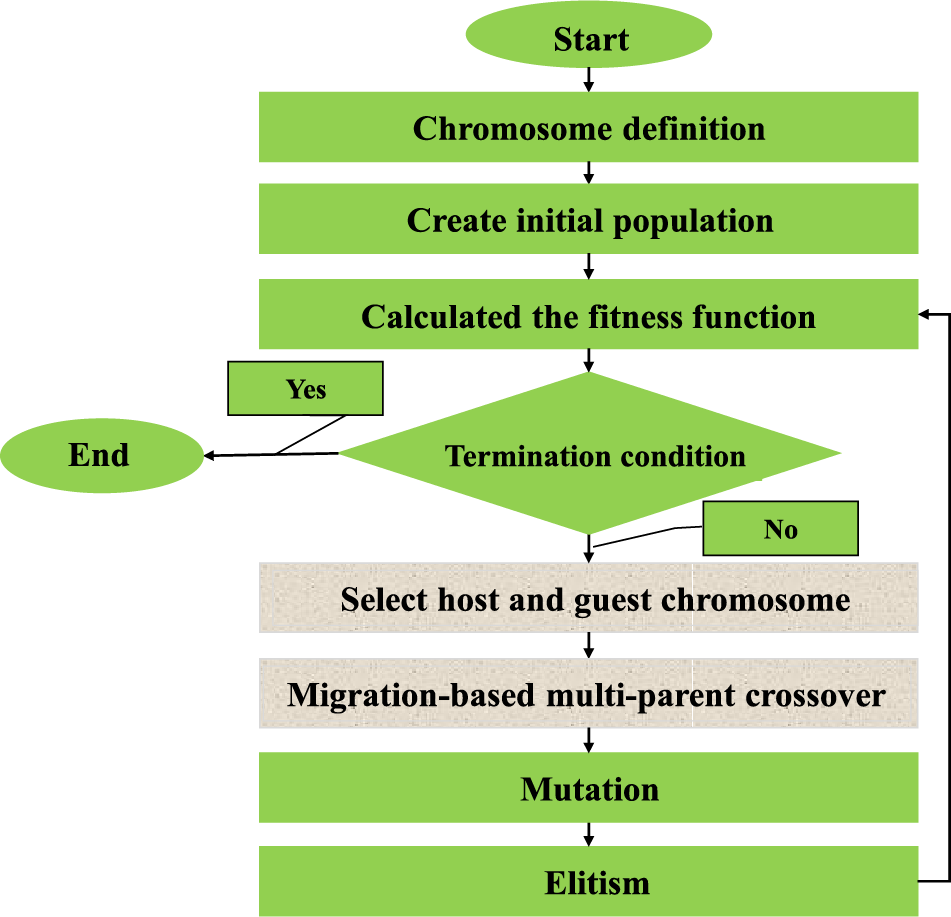
Figure 4: The flowchart of the proposed MBMPGA

4  Training DCNN Architecture

A DCNN is built upon four main layers: convolution, pooling, activation, and fully connected layers. In the convolution layer, a convolution filter is applied to the input data to extract features. This involves multiplying the input data with a set of values determined by the filter. The kernel then bypasses the image multiple times, with the weights being multiplied by the input data at each position. The kernel moves from top to bottom and from left to right to mask all the input data before an operation is applied. The results of this process are summed up to produce a distinctive value for each kernel position.

In the subsequent step, the output of the convolution operation is passed through a nonlinear activation function known as the Rectified Linear Unit (ReLU). This function replaces all negative values with zeros, which helps to further process the data. The pooling layer then performs the task of reducing the input data size while retaining the most useful information. For instance, in a group of eight pixels, max pooling selects the most noteworthy ones. This layer plays a vital role in deep learning as it helps to reduce computational costs and minimize over fitting. Following the convolution and pooling stages, the fully connected layer comes into play, which mainly consists of an MLP NN.

In our experiment setup, the deep architecture has four 1D convolutional layers with increasing numbers of filters (32, 64, 128, and 256, respectively) with a kernel size of 5, followed by max-pooling layers with pool sizes of 2 to reduce the dimensionality of the feature maps. Each convolutional layer is followed by a dropout layer (0.25) to prevent overfitting. The output of the fourth convolutional layer is flattened and passed through two fully connected layers (with 512 and 256 units, respectively) each of which is also followed by a dropout layer (0.5). The output layer consists of a single Sigmoid unit representing the predicted output of the XOR Arbiter PUF. The model uses the Adam optimizer and binary cross-entropy loss function, and accuracy is used as the evaluation metric. We have used 106 CRPs of which 80% have been used for training and 20% have been used for testing.

In this paper, MBMPGA is used to train DCNN. In the suggested approach, MBMPGA tunes the weights and biases of the DCNN. When it comes to MBMPGA modeling, a crucial objective is to establish a chromosome-based solution. Fig. 5 demonstrates the structure of a chromosome in MBMPGA. The cost function of the algorithm can be shown in Eq. (3).

Figure 5: Chromosome definition in proposed MBMPGA-DCNN

Mean Square Error (MSE)=1k∑i=1k(Oi−Di)2(3)

where, k shows the number of samples, Oi shows the output, and Di shows the desired value. Many chromosomes are randomly produced to build an initial population. The roulette wheel method (Eq. (4)) and Migration rates (μ, λ) are also used to select parent chromosomes.

Pr=F(Xr)∑k=1nF(Xk)(4)

where, Pr is the probability of choosing chromosome r, F(Xr)is the cost function, and n is the total number of the initial population. The migration-based multi-parent crossover operator is the same as Fig. 3. Finally, Fig. 6 shows the mutation operator of MBMPGA.

Figure 6: Example of the mutation operator in MBMPGA-DCNN

5  MBMPGA-DCNN Performance Evaluation

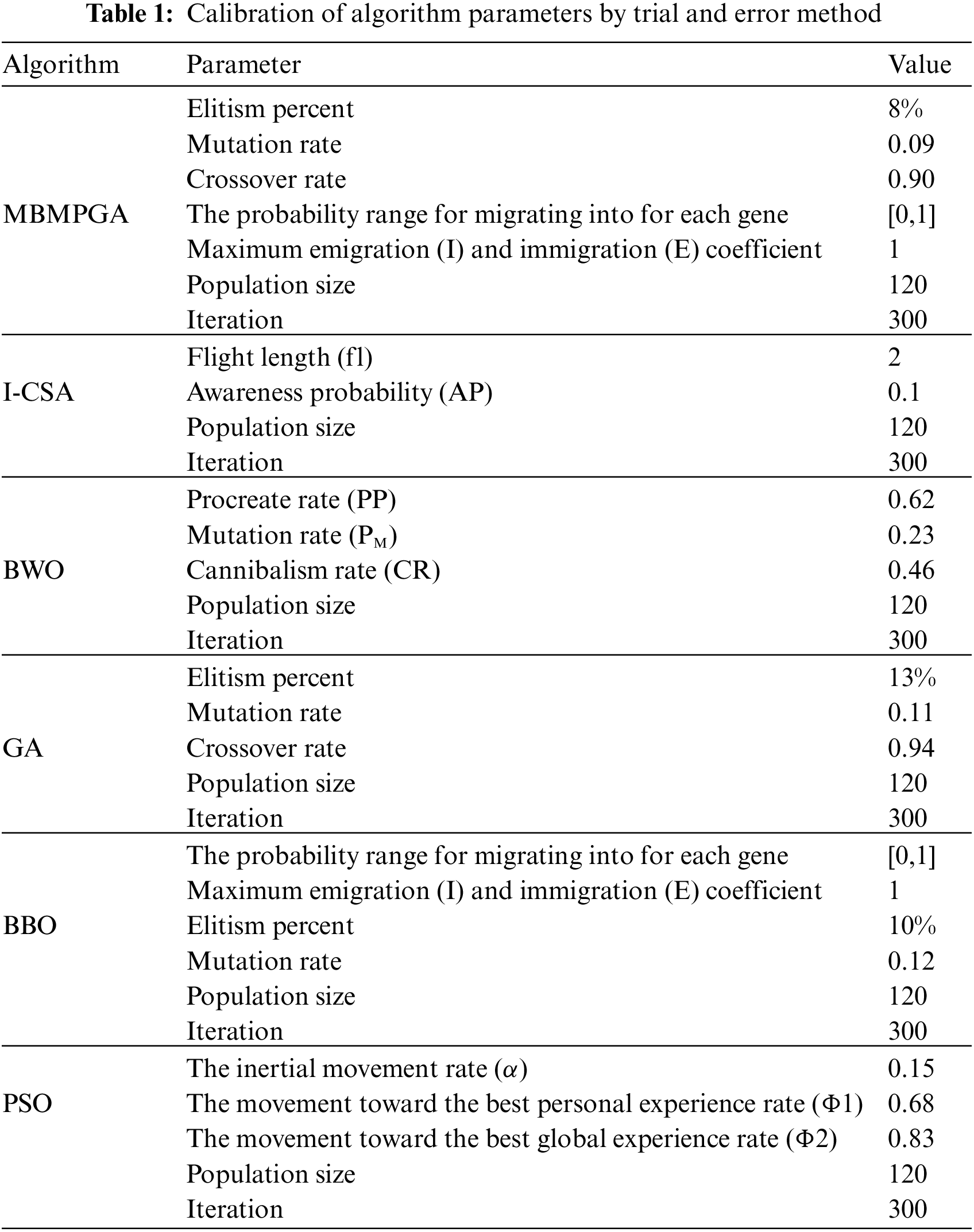
In this section, the performance of the proposed MBMPGA on two benchmark engineering problems is measured in compared to some MHs, including GA, PSO, BBO, I-CSA, and BWO. In the following subsection, the performance of the proposed MBMPGA-DCNN for modeling complex XAPUFs is evaluated. All algorithms were coded in MATLAB software and the calibration variables of the MHs are demonstrated in Table 1. In this paper trial and error method has been used. The objective function defines the main criterion for resetting the parameters.

5.1 Tension Spring Design

In this part, the performance of the proposed MBMPGA on a tension spring design is evaluated. Fig. 7 provides a schematic of the problem, and its formulation can be expressed throughEqs. (5)–(10) [46].

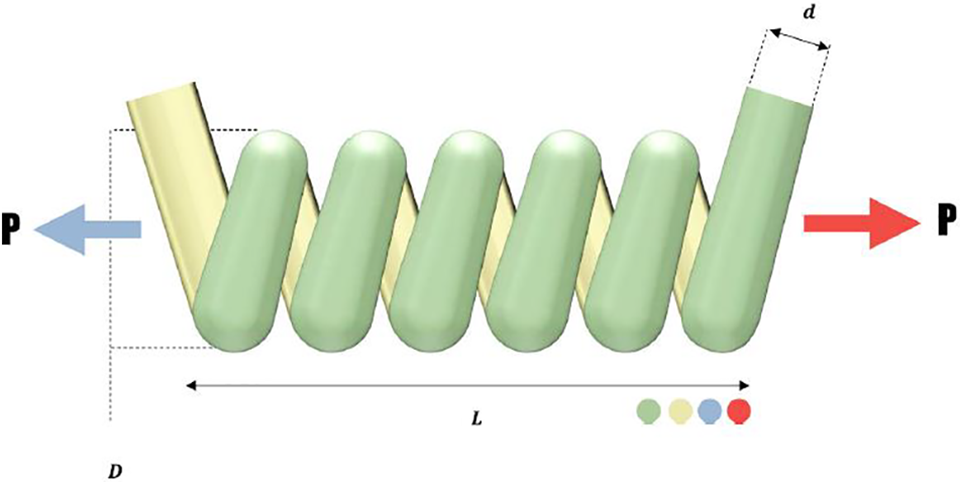
Figure 7: A schematic view of the design of the tension spring

f(X)=(x3+2)x2x12(5)

Subjected to

g1(X)=1−x3x2371785x14≤0(6)

g2(X)=4x22−x1x212566(x2x13−x14)+15108x12−1≤0(7)

g3(X)=1−140.45x1x22x3≤0(8)

g4(X)=x1+x21.5−1≤0(9)

0.05≤x1≤2.00,0.25≤x2≤1.30,2≤x3≤15(10)

where, x1 = Wire diameter (d), x2 = Mean coil diameter (D), x3 = number of active coils (N).

Table 2 indicates the results of the algorithms on the tension spring problem. The table consists of four columns: Best of fitness, mean of fitness, standard deviation, and iteration. As is observed, MBMPGA achieved the best objective function value (Best fitness). The best solution (by MBMPGA) for this problem is 0.012666. MBMPGA also has the best standard deviation, as seen in the table. Fig. 8 shows the convergence curve of MBMPGA for this problem. The x-axis represents the iterations, while the y-axis shows the value of best fitness function. According to Fig. 8, MBMPGA has the best convergence rate. MBMPGA, in its 75th iteration, has achieved significant advancements and emerged with the most optimal solutions.

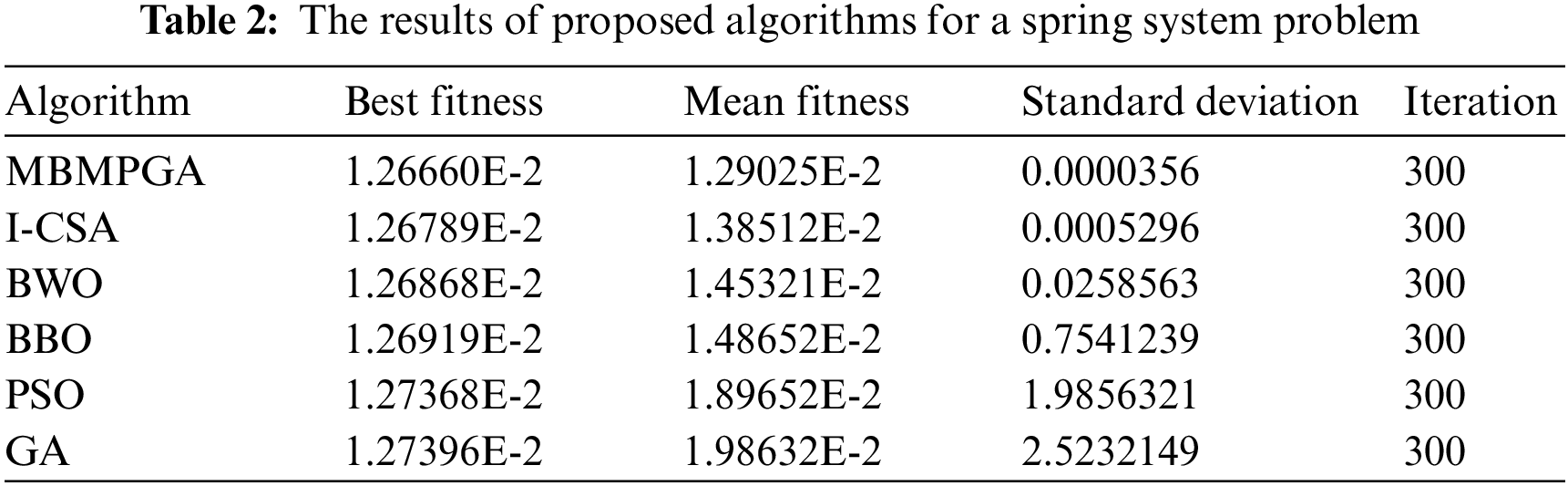
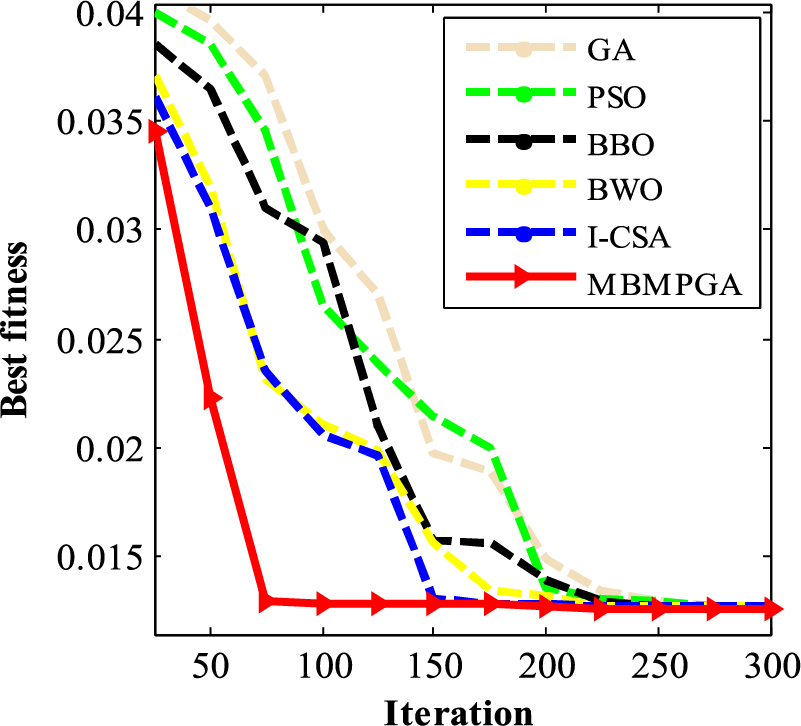
Figure 8: The convergence curve of algorithms for spring system design problem

5.2 Three-Bar Truss Design Problem

Here, we aim to obtain the minimum weight of the three-bar truss. Fig. 9 shows an overview of this problem and can be formulated as Eqs. (11)–(15).

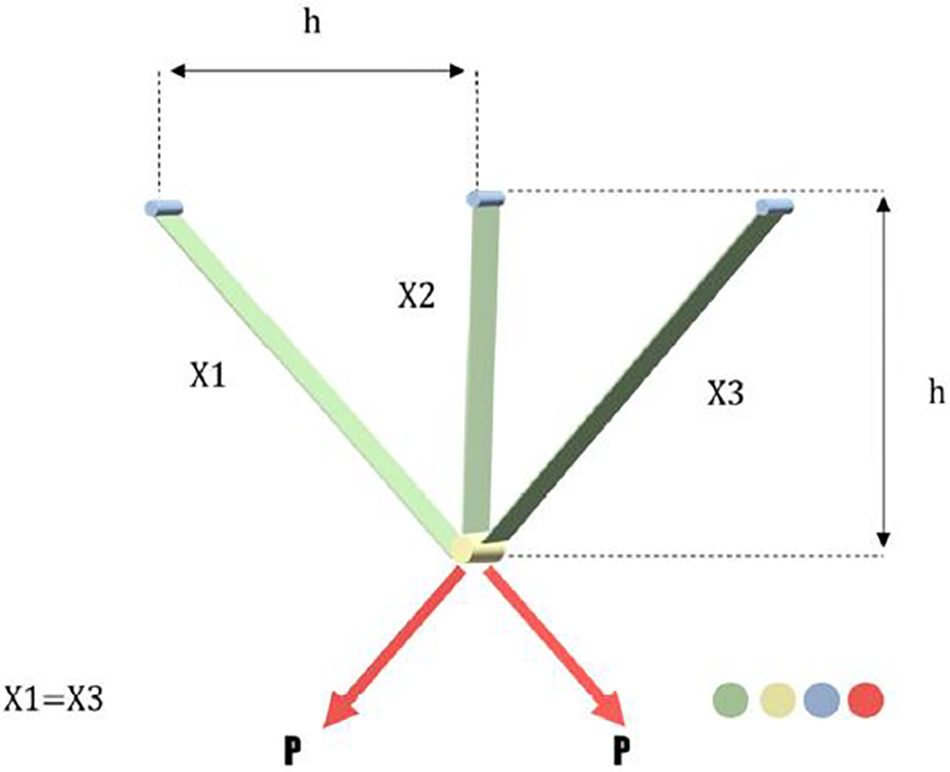
Figure 9: A schematic view of the truss design problem

f(X)=(22x1+x2)×l(11)

Subjected to

g1(X)=2x1+x22x12+2x1x2P−σ≤0(12)

g2(X)=x22x12+2x1x2P−σ≤0(13)

g3(X)=12x2+x1P−σ≤0(14)

0≤x1,x2≤1(15)

where, l=100 cm, P=2KN/cm2 ,σ=2KN/cm2

The outcomes of various algorithms are displayed in Table 3. The table consists of four columns: Best of fitness, mean of fitness, standard deviation, and iteration. It is evident that MBMPGA has the best value for the cost function, resulting in a solution of 263.921453. Furthermore, MBMPGA has the best standard deviation, as seen in the table. Fig. 10 depicts the convergence rate for MBMPGA and other MHs. The x-axis represents the iterations, while the y-axis shows the value of best fitness function. MBMPGA’s convergence rate is better than those of other MHs. MBMPGA, in its 100th iteration, has achieved significant advancements and emerged with the most optimal solutions.

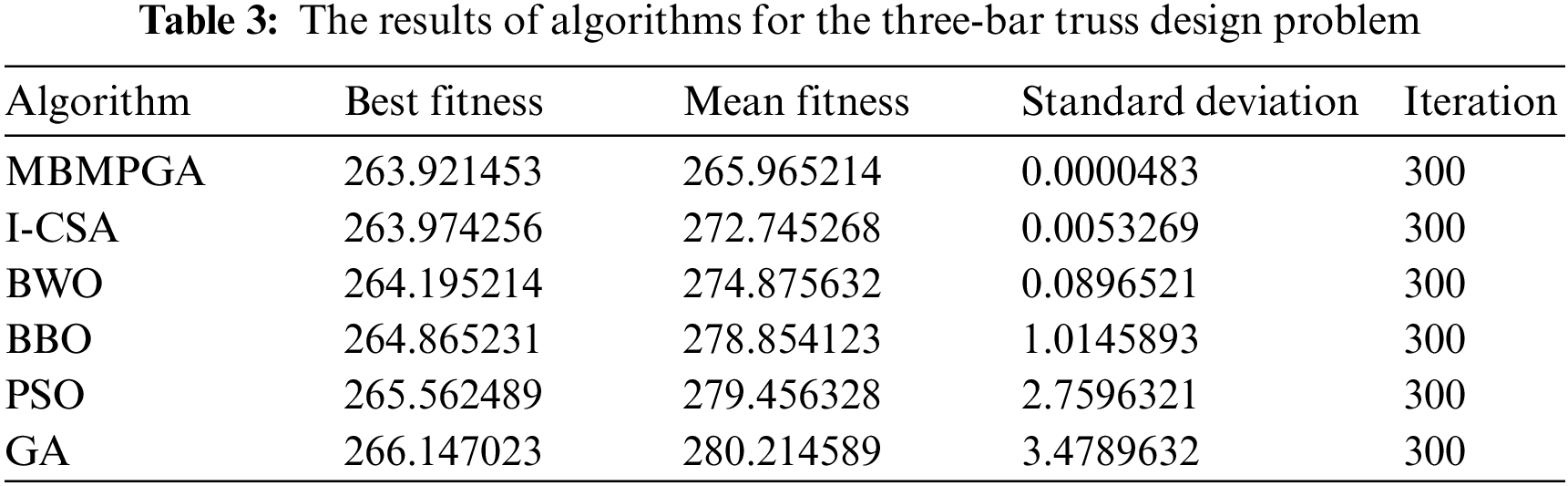
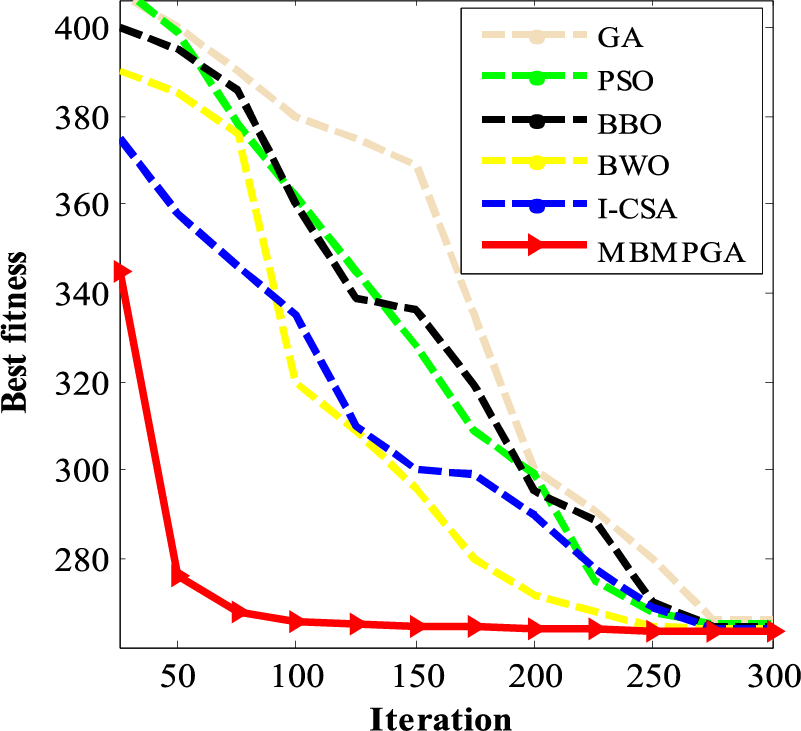
Figure 10: The convergence curve of algorithms for spring system design problem

5.3 Simulation Results for Modeling the Complex XAPUFs

In this section, the performance of the MBMPGA-DCNN and other ML architectures for XAPUFs is evaluated. To do so, we exploited the generated CRPs from [33] to model complex XAPUFs. The CRPs were generated in an additive delay model (ADM)-based simulator [40]. The APUFs used in XAPUFs are 64-bit APUFs, and the corresponding challenges within each simulation were randomly determined from 0 to 264. Gaussian distribution with a standard deviation of σ = 40 and a mean of µ = 300 has also been utilized to uniformly determine the MUX delays in APUFs. For this comparison, sensitivity, accuracy, and specificity analyses are utilized. These analyses are derived from the confusion matrix and are computable as Eqs. (16)–(18).

Sensitivity=TPTP+FN(16)

Specificity=TNTN+FP(17)

Accuracy=TP+TNTP+FN+FP+TN(18)

where, TP = True positive, TN = True negative, FN = False negative, FP = False positive.

Table 4 indicates the sensitivity, specificity, and accuracy of different evolutionary DL structures for complex XAPUF. As is observed, the MBMPGA-DCNN architecture shows the best performance in sensitivity, specificity, and accuracy for training and validation datasets. SVM also shows the worst performance in training and validation datasets. MBMPGA-DCNN reached 99.41% and 98.86% accuracy in the test and training datasets, respectively. Figs. 11 and 12 indicate the comparison of proposed structures in training and validation datasets, respectively (According to Table 4).

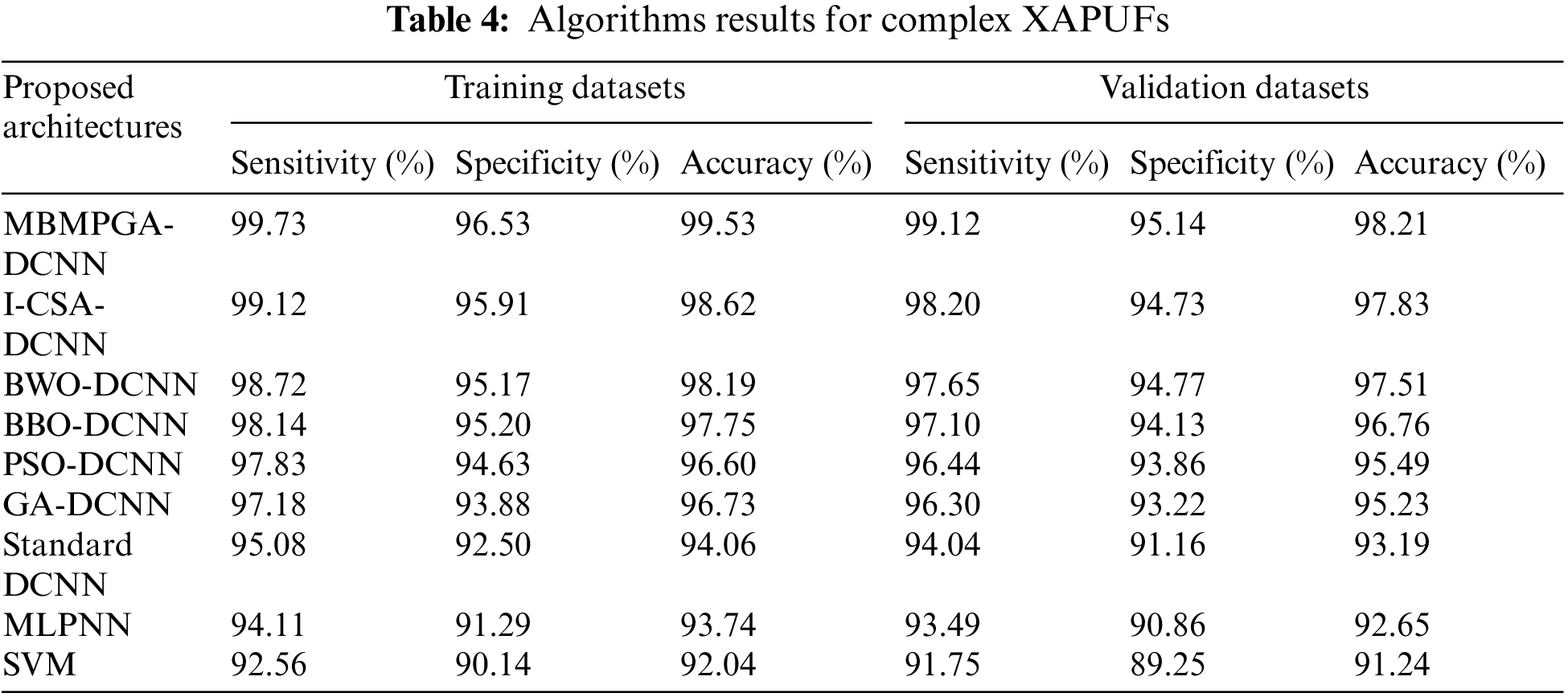
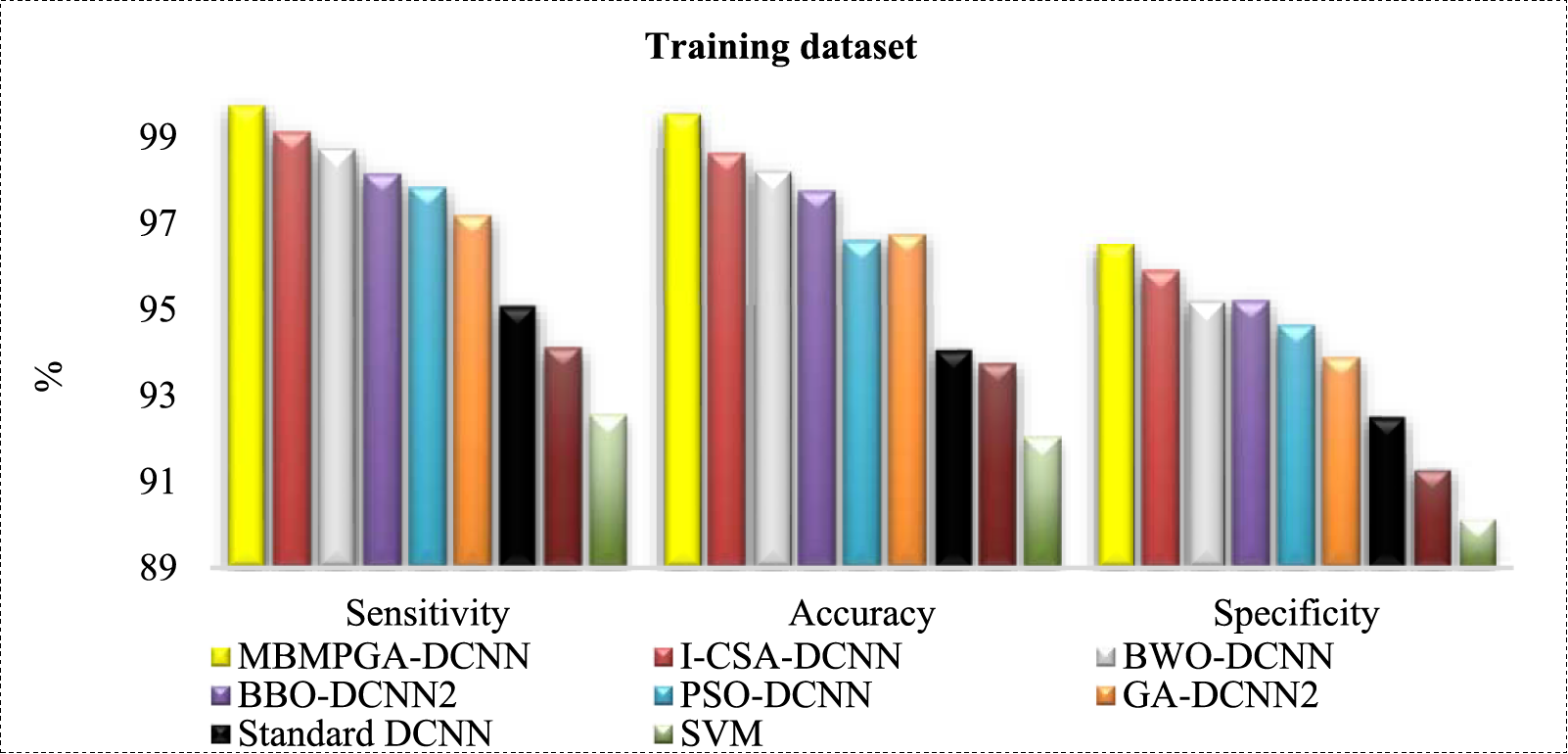
Figure 11: Comparison of ML approaches in training datasets

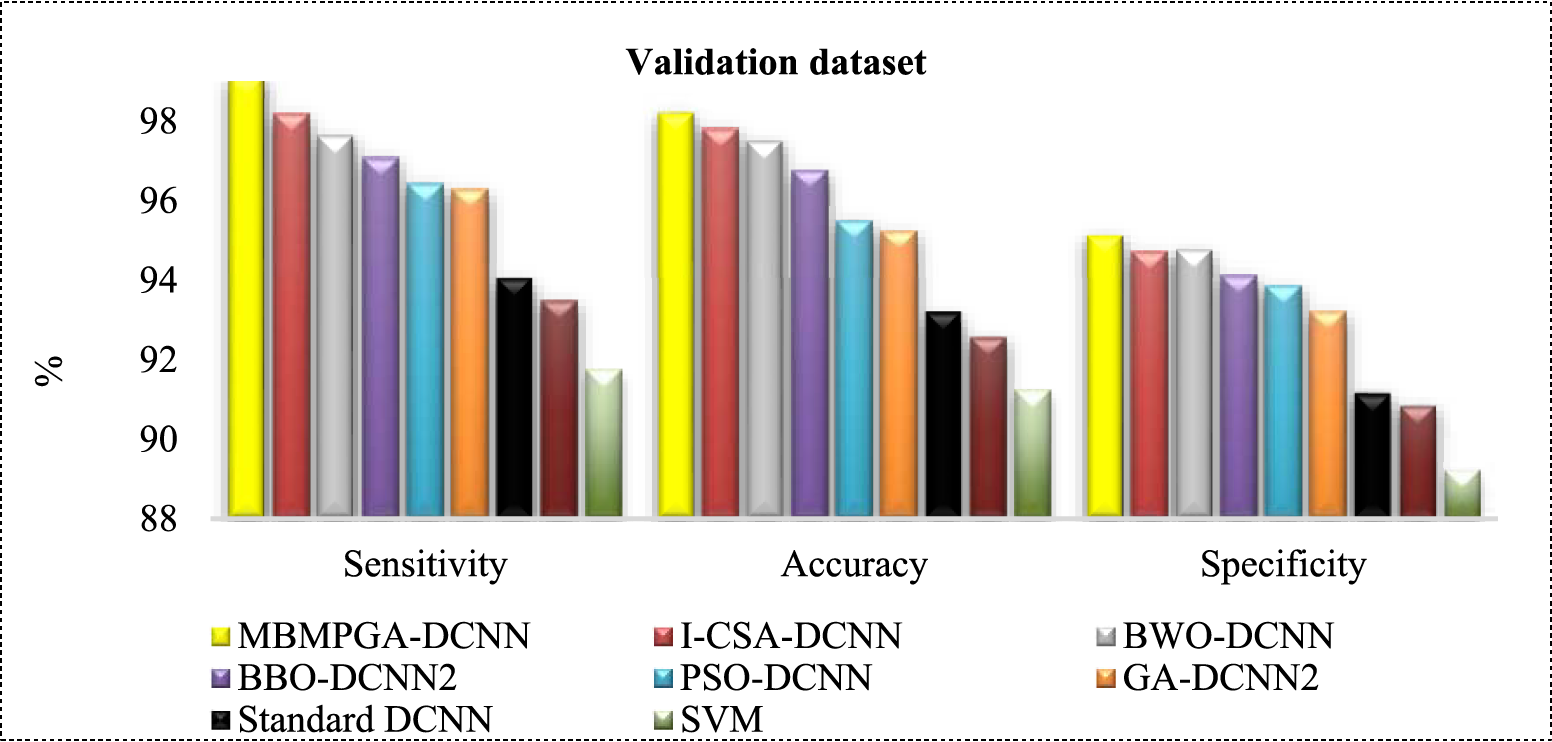
Figure 12: Comparison of ML approaches in validation datasets

Fig. 13 shows the ROC curve of architectures. The ROC Curve is valuable not only because it gives us an overview of our model’s performance, but because it also gives us an easy visual to compare the performance of different classifiers to one another. As can be seen, the area under the curve (AUC) of MBMPGA-DCNN is better than other architectures. Table 5 shows a comparison of the proposed models using MSE criteria. MSE is lower in the MBMPGA-DCNN architecture than in other architectures. Thus, the introduced approach has been useful for solving this problem.

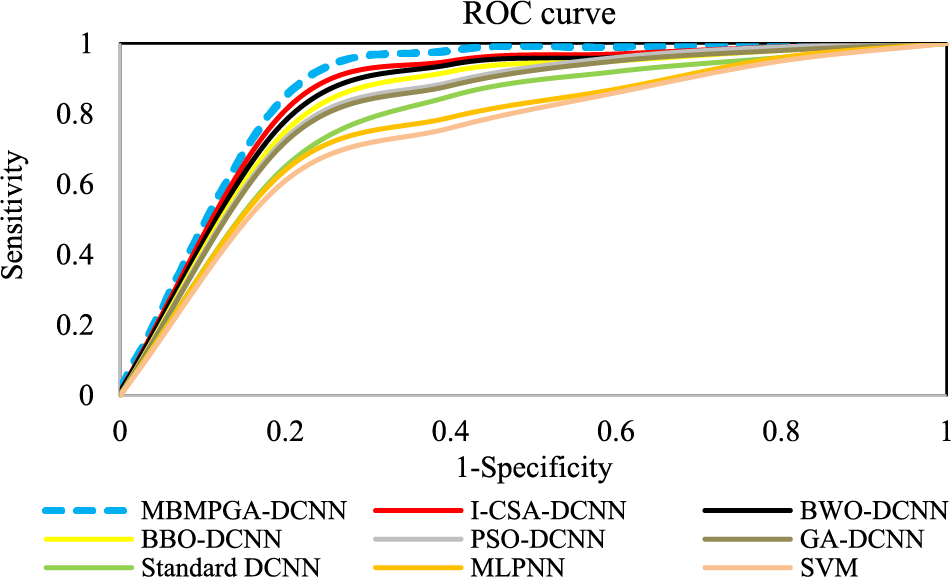
Figure 13: The ROC curve of architectures

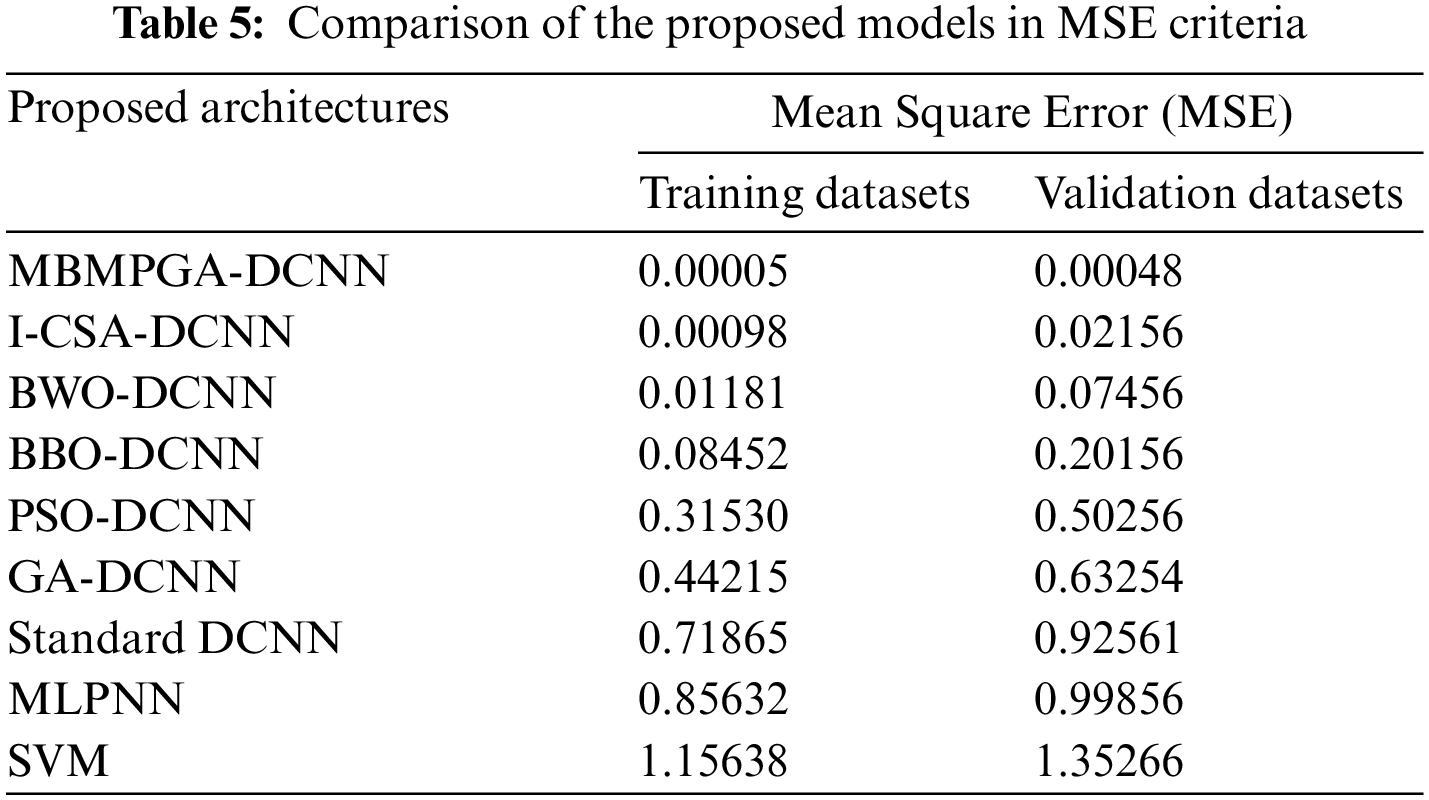
Fig. 14 indicates the convergence of MBMPGA-DCNN and other architectures in the accuracy criterion. The x-axis represents the epochs, while the y-axis shows the value of MSE. In MBMPGA, when several of the best chromosomes are selected to generate a new offspring, the resulting offspring bears less resemblance to one parent, i.e., the offspring is more diverse. However, since the offspring have obtained all of their genes from multiple chromosomes, the exploitation of the algorithm improves.

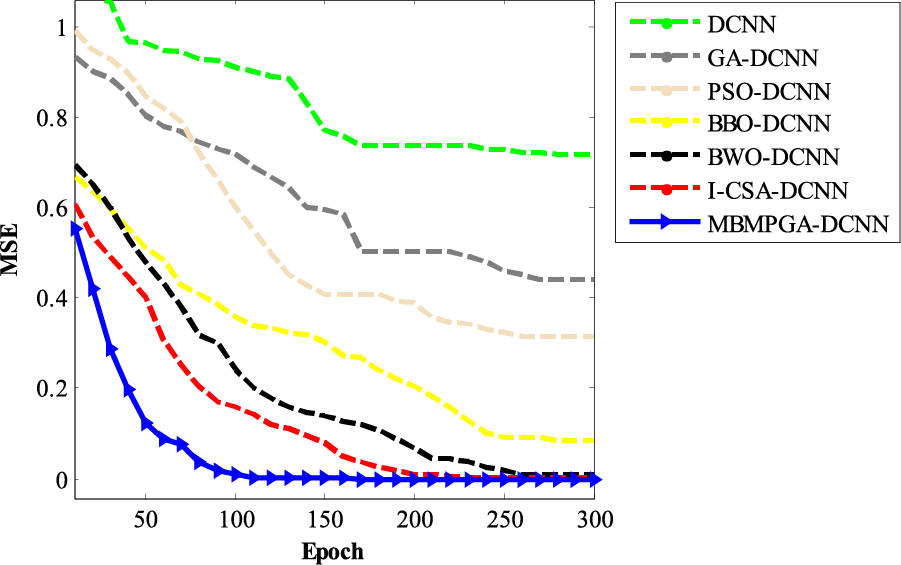
Figure 14: The convergence of architectures in the accuracy criterion

Table 6 demonstrates the trend of accuracy and execution time of all architectures in different epochs. Based on the results, the MBMPGA-DCNN has obtained the best accuracy (99.53%) in the shortest execution time. The accuracy of the I-CSA-DCNN, BWO-DCNN, BBO-DCNN, PSO-DCNN, GA-DCNN, DCNN, MLPNN, and SVM is 98.62%, 98.19%, 97.75%, 96.60%, 96.73%, 94.06%, 93.74%, and 92.04%, respectively. Fig. 15 compares the total “Runtime (s)” of the different models. As can be observed, the execution time of MBMPGA-DCNN is shorter than other models.

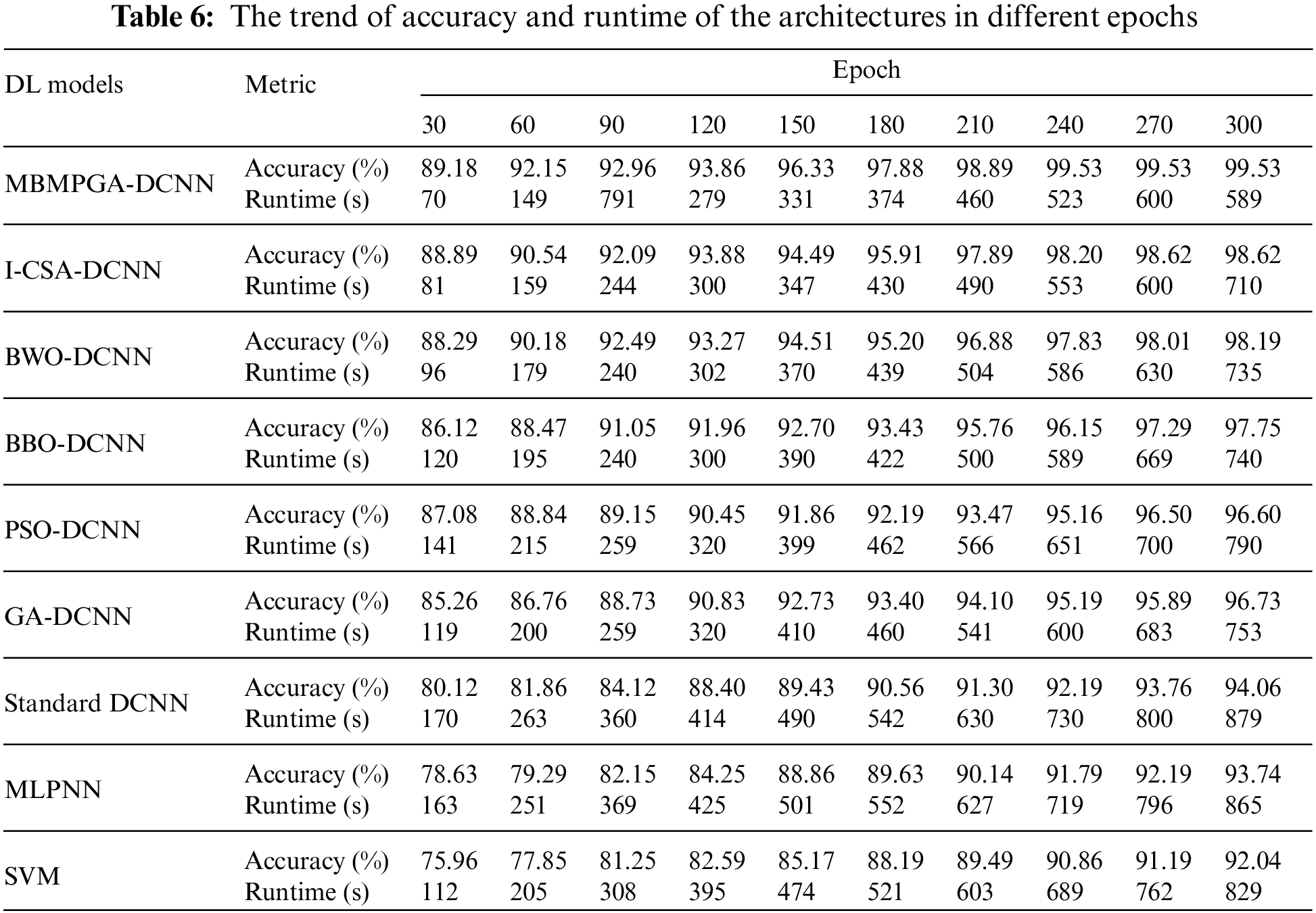
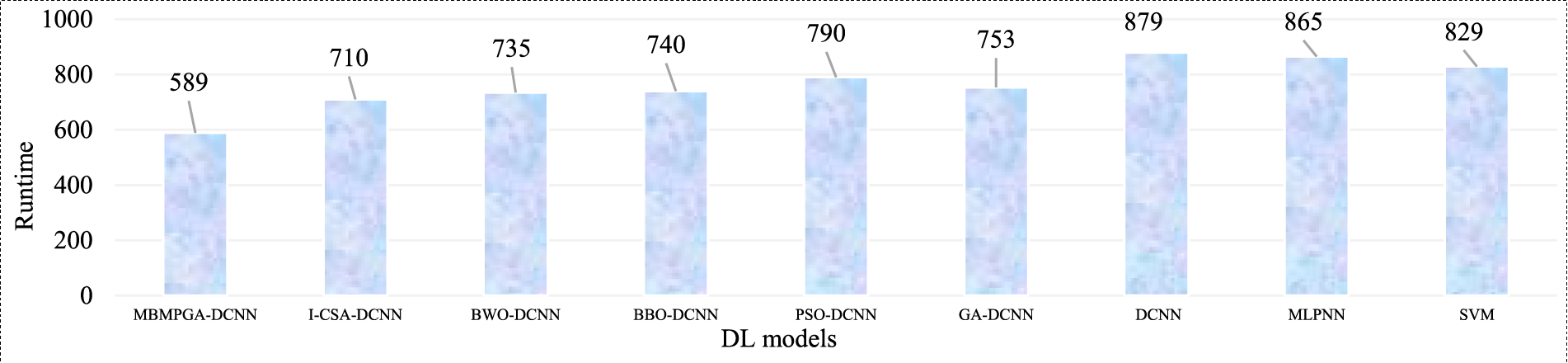
Figure 15: Total runtime of DL models

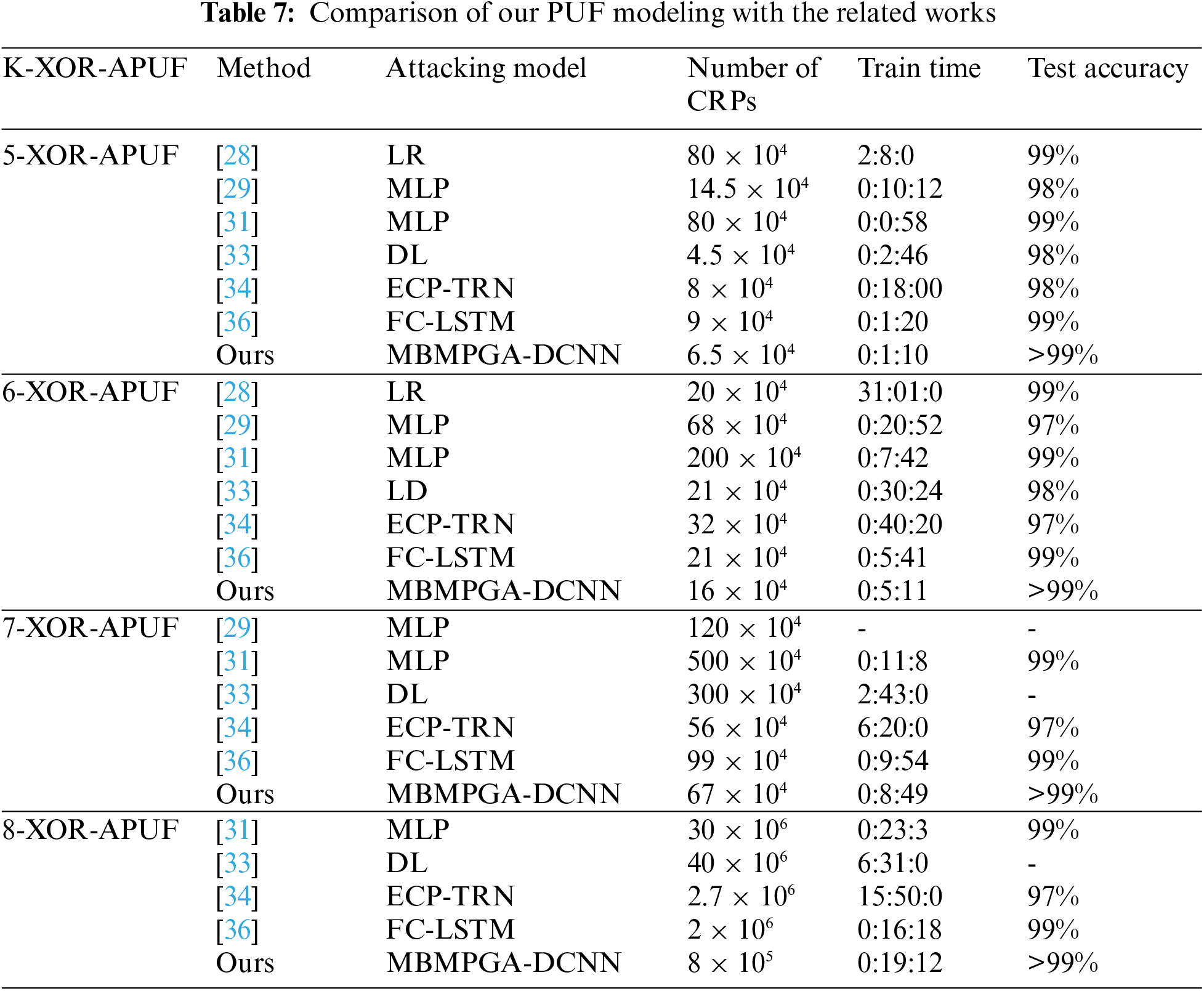
Table 7 exhibits how effective the proposed MBMPGA-DCNN model is in attacking XOR-APUF in comparison to other methods. The “Number of CRPs” column indicates the size of the training datasets required for successful machine learning training of the models, and the “Attacking Model” column mentions the machine learning methods used. As demonstrated in Table 7, our approach is more efficient than other related works in terms of the number of CRPs utilized, the needed time, and the accuracy of the results.

6  Conclusion and Future Research Direction

In this paper, we propose a novel DL-based modeling attack to break the resistance of complex XAPUFs. More specifically, we introduce a new algorithm named MBMPGA to train the deep architecture for obtaining a higher rate of accuracy and convergence speed while decreasing the run-time of the attack. First, we evaluated the performance of MBMPGA on some well-known benchmark datasets. After successfully passing the benchmark tests, we used the generated CRPs from [33] to model complex XAPUFs using the proposed MBMPGA-based deep architecture. The simulation results on the XAPUF dataset show that the suggested modeling attack obtains more than 99% modeling accuracy and a high rate of specificity and sensitivity. The accuracy of MBMPGA-DCNN on the training and validation datasets was 99.53% and 98.21%, respectively, which were the highest accuracy rates.

The precise configuration of the MBMPGA’s initial parameters can pose a constraint, and it may be necessary to utilize specific techniques, such as the Taguchi method. Another issue in practical applications can the computational overhead of MBMPGA. For instance, in a single generation of the MBMPGA, many chromosomes are produced. Typically, the computation of the loss function for all possible solutions and selecting the best one is a complex process that requires significant computing resources, especially for solving real-world problems, e.g., modeling more complex PUF structures.

There are several avenues for future research that can be recommended. Firstly, exploring the adaptation of variants of MBMPGA to address a wide range of real-world problems, including multi-objective and discrete problems, would be valuable. This would expand the applicability and versatility of the methodology. Moreover, further work can focus on optimizing specific thresholds within the equations of MBMPGA to enhance its efficiency. Fine-tuning these aspects can lead to more effective optimization outcomes. The utilization of hybrid algorithms is another promising direction for future research. Incorporating elements from different algorithms can enhance the operators within MBMPGA and potentially improve its overall effectiveness. Considering the challenges posed by limited training data in big data problems, future research should address this issue by proposing DL-based approaches that utilize multiple training datasets. By leveraging diverse datasets, DLs can overcome the limitations imposed by data scarcity and enhance their performance. Furthermore, the next generation of DL methods is anticipated to be semi-supervised and unsupervised. Future research should explore incorporating clustering concepts and techniques into DLs to improve their performance and efficiency.

As APUFs become more prevalent in security-critical applications, the development of effective defense mechanisms against adversarial attacks becomes crucial. Future research can focus on designing and evaluating robust defense mechanisms that can withstand the proposed attack methodology and mitigate its impact. While the proposed methodology primarily focuses on complex APUFs, future research could explore the applicability of the developed MBMPGA and DCNN-based attack techniques to other security-sensitive domains. This could involve investigating their effectiveness in attacking other hardware security primitives or cryptographic systems.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. X. Yang, L. Shu, Y. Liu, G. P. Hancke, M. A. Ferrag et al., “Physical security and safety of IoT equipment: A survey of recent advances and opportunities,” IEEE Transactions on Industrial Informatics, vol. 18, no. 7, pp. 4319–4330, 2022. [Google Scholar]

2. E. Lee, Y. D. Seo, S. R. Oh and Y. G. Kim, “A survey on standards for interoperability and security in the internet of things,” IEEE Communications Surveys & Tutorials, vol. 23, no. 2, pp. 1020–1047, 2021. [Google Scholar]

3. M. Stoyanova, Y. Nikoloudakis, S. Panagiotakis, E. Pallis and E. K. Markakis, “A survey on the internet of things (IoT) forensics: Challenges, approaches, and open issues,” IEEE Communications Surveys & Tutorials, vol. 22, no. 2, pp. 1191–1221, 2020. [Google Scholar]

4. J. Zhang, C. Shen, H. Su, M. T. Arafin and G. Qu, “Voltage over-scaling-based lightweight authentication for IoT security,” IEEE Transactions on Computers, vol. 71, no. 2, pp. 323–336, 2021. [Google Scholar]

5. M. Kaveh, S. Aghapour, D. Martin and M. R. Mosavi, “A secure lightweight signcryption scheme for smart grid communications using reliable physically unclonable function,” in IEEE Int. Conf. on Environment and Electrical Engineering and IEEE Industrial and Commercial Power Systems, Europe, pp. 1–6, 2020. [Google Scholar]

6. X. Jiang, X. Liu, J. Fan, X. Ye, C. Dai et al., “Enhancing IoT security via cancelable HD-sEMG-based biometric authentication password, encoded by gesture,” IEEE Internet of Things Journal, vol. 8, no. 22, pp. 16535–16547, 2021. [Google Scholar]

7. S. Aghakhani, A. Larijani, F. Sadeghi, D. Martín and A. A. Shahrakht, “A novel hybrid artificial bee colony-based deep convolutional neural network to improve the detection performance of backscatter communication systems,” Electronics, vol. 12, no. 10, pp. 2263, 2023. [Google Scholar]

8. V. Vijay, K. Chaitanya, C. S. Pittala, S. S. Susmitha, J. Tanusha et al., “Physically unclonable functions using two-level finite state machine,” Journal of VLSI Circuits and Systems, vol. 4, no. 1, pp. 33–41, 2022. [Google Scholar]

9. P. Mall, R. Amin, A. K. Das, M. T. Leung and K. K. R. Choo, “PUF-based authentication and key agreement protocols for IoT, WSNs and smart grids: A comprehensive survey,” IEEE Internet of Things Journal, vol. 9, no. 11, pp. 8205–8228, 2022. [Google Scholar]

10. W. Lalouani, M. Younis, M. Ebrahimabadi and N. Karimi, “Countering modeling attacks in puf-based iot security solutions,” ACM Journal on Emerging Technologies in Computing Systems (JETC), vol. 18, no. 3, pp. 1–28, 2022. [Google Scholar]

11. B. Gao, B. Lin, X. Li, J. Tang, H. Qian et al., “A unified PUF and TRNG design based on 40-nm RRAM with high entropy and robustness for IoT security,” IEEE Transactions on Electron Devices, vol. 69, no. 2, pp. 536–542, 2022. [Google Scholar]

12. A. Shamsoshoara, A. Korenda, F. Afghah and S. Zeadally, “A survey on physical unclonable function (PUF)-based security solutions for Internet of Things,” Computer Networks, vol. 183, no. 1, pp. 107593, 2020. [Google Scholar]

13. Y. Zheng, W. Liu, C. Gu and C. H. Chang, “PUF-based mutual authentication and key exchange protocol for peer-to-peer IoT applications,” IEEE Transactions on Dependable and Secure Computing, vol. 2022, pp. 1–18, 2022. [Google Scholar]

14. M. El-Hajj, A. Fadlallah, M. Chamoun and A. Serhrouchni, “A taxonomy of PUF schemes with a novel Arbiter-based PUF resisting machine learning attacks,” Computer Networks, vol. 194, no. 1, pp. 108133, 2021. [Google Scholar]

15. P. Gope and B. Sikdar, “A comparative study of design paradigms for PUF-based security protocols for IoT devices: Current progress, challenges, and future expectation,” Computer, vol. 54, no. 11, pp. 36–46, 2021. [Google Scholar]

16. M. Kaveh and A. Falahati, “An improved Merkle hash tree based secure scheme for bionic underwater acoustic communication,” Frontiers of Information Technology & Electronic Engineering, vol. 22, no. 7, pp. 1010–1019, 2021. [Google Scholar]

17. X. Zhao, T. Xu, C. Xie, X. Pan, W. He et al., “A CRP-space-extended RRAM PUF with in-cell zero-overhead salicide-blocked contact,” IEEE Transactions on Electron Devices, vol. 68, no. 7, pp. 3702–3705, 2021. [Google Scholar]

18. H. Rabiei, M. Kaveh, M. R. Mosavi and D. Martín, “MCRO-PUF: A novel modified crossover RO-PUF with an ultra-expanded CRP space,” Computers, Materials and Continua, vol. 74, no. 3, pp. 4831–4845, 2023. [Google Scholar]

19. N. Wisiol, B. Thapaliya, K. T. Mursi, J. P. Seifert and Y. Zhuang, “Neural network modeling attacks on Arbiter-PUF-based designs,” IEEE Transactions on Information Forensics and Security, vol. 17, pp. 2719–2731, 2022. [Google Scholar]

20. A. Lotfy, M. Kaveh, D. Martín and M. R. Mosavi, “An efficient design of Anderson PUF by utilization of the Xilinx primitives in the SLICEM,” IEEE Access, vol. 9, pp. 23025–23034, 2021. [Google Scholar]

21. S. Aghapour, M. Kaveh, M. R. Mosavi and D. Martín, “An ultra-lightweight mutual authentication scheme for smart grid two-way communications,” IEEE Access, vol. 9, pp. 74562–74573, 2021. [Google Scholar]

22. P. Afrasyabi, M. S. Mesgari, M. Razban and M. Kaveh, “Multi-modal routing using NSGA-II algorithm considering COVID-19 protocols: A case study in Tehran,” Earth Observation and Geomatics Engineering, vol. 6, no. 1, pp. 1–14, 2022. [Google Scholar]

23. M. Kaveh, M. S. Mesgari and A. Khosravi, “Solving the local positioning problem using a four-layer artificial neural network,” Engineering Journal of Geospatial Information Technology, vol. 7, no. 4, pp. 21–40, 2020. [Google Scholar]

24. O. Rostami and M. Kaveh, “Optimal feature selection for SAR image classification using biogeography-based optimization (BBOartificial bee colony (ABC) and support vector machine (SVMA combined approach of optimization and machine learning,” Computational Geosciences, vol. 25, no. 3, pp. 911–930, 2021. [Google Scholar]

25. S. Baniasadi, O. Rostami, D. Martín and M. Kaveh, “A novel deep supervised learning-based approach for intrusion detection in IoT systems,” Sensors, vol. 22, no. 12, pp. 4459, 2022. [Google Scholar] [PubMed]

26. P. Gope, Y. Wang, Z. Li and B. Sikdar, “QR-PUF: Design and implementation of A RFID-based secure inpatient management system using XOR-Arbiter-PUF and QR-Code,” IEEE Transactions on Network Science and Engineering, vol. 2022, pp. 1–9, 2022. [Google Scholar]

27. U. Ruhrmair, F. Sehnke, J. Solter, G. Dror, S. Devadas et al., “Modeling attacks on physical unclonable functions,” in Proc. of the 17th ACM Int. Conf. on Computer and Communications Security, Chicago, USA, pp. 237–249, 2010. [Google Scholar]

28. P. Santikellur, A. Bhattacharyay and R. S. Chakraborty, “Deep learning-based model building attacks on Arbiter PUF compositions,” Cryptology ePrint Archive, vol. 2019, pp. 566, 2019. [Google Scholar]

29. A. O. Aseeri, Y. Zhuang and M. S. Alkatheiri, “A Machine learning-based security vulnerability study on XOR PUFs for Resource-constraint Internet of Things,” in Proc. of the 2018 IEEE Int. Conf. on Internet of Things (ICIOT), San Francisco, CA, USA, pp. 49–56, 2018. [Google Scholar]

30. J. Tobisch and G. T. Becker, “On the scaling of machine learning attacks on PUFs with application to noise bifurcation,” in Proc. of the 11th RFIDsec Int. Conf. on Radio Frequency Identification: Security and Privacy Issues, New York, NY, USA, pp. 17–31, 2015. [Google Scholar]

31. P. Santikellur and R. S. Chakraborty, “A computationally efficient tensor regression network-based modeling attack on XOR Arbiter PUF and its variants,” IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 40, no. 6, pp. 1197–1206, 2020. [Google Scholar]

32. G. Hospodar, R. Maes and I. Verbauwhede, “Machine learning attacks on 65 nm Arbiter PUFs: Accurate modeling poses strict bounds on usability,” in Proc. of the 2012 IEEE Int. Conf. on Information forensics and security (WIFS), Costa Adeje, Spain, pp. 37–42, 2012. [Google Scholar]

33. K. T. Mursi, B. Thapaliya, Y. Zhuang, A. O. Aseeri and M. S. Alkatheiri, “A fast deep learning method for security vulnerability study of XOR PUFs,” Electronics, vol. 9, no. 10, pp. 1715, 2020. [Google Scholar]

34. J. Shi, Y. Lu and J. Zhang, “Approximation attacks on strong PUFs,” IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 39, no. 10, pp. 2138–2151, 2019. [Google Scholar]

35. Y. Cui, C. Gu, Q. Ma, Y. Fang, C. Wang et al., “Lightweight modeling attack-resistant multiplexer-based multi-PUF (MMPUF) design on FPGA,” Electronics, vol. 9, no. 5, pp. 815, 2020. [Google Scholar]

36. S. S. Fard, M. Kaveh, M. R. Mosavi and S. B. Ko, “An efficient modeling attack for breaking the security of XOR-Arbiter PUFs by Using the fully connected and long-short term memory,” Microprocessors and Microsystems, vol. 94, no. 6, pp. 104667, 2022. [Google Scholar]

37. H. Mirhajianmoghadam, M. R. Akbarzadeh-T and E. Lotfi, “A harmonic emotional neural network for non-linear system identification,” in Proc. of the 2016 IEEE 24th ICEE Conf. on Electrical Engineering (ICEE), Shiraz, Iran, pp. 1260–1265, 2016. [Google Scholar]

38. F. Sadeghi, A. Larijani, O. Rostami, D. Martín and P. Hajirahimi, “A novel multi-objective binary chimp optimization algorithm for optimal feature selection: Application of deep-learning-based approaches for SAR image classification,” Sensors, vol. 23, no. 3, pp. 1180, 2023. [Google Scholar] [PubMed]

39. M. Kaveh and M. S. Mesgari, “Hospital site selection using hybrid PSO algorithm-case study: District 2 of Tehran,” Scientific-Research Quarterly of Geographical Data (SEPEHR), vol. 28, no. 111, pp. 7–22, 2019. [Google Scholar]

40. D. Lim, J. W. Lee, B. Gassend, G. E. Suh, M. van Dijk et al., “Extracting secret keys from integrated circuits,” IEEE Transactions on Very Large-Scale Integration (VLSI) Systems, vol. 13, no. 10, pp. 1200–1205, 2005. [Google Scholar]

41. W. H. Bangyal, R. Qasim, N. U. Rehman, Z. Ahmad, H. Dar et al., “Detection of fake news text classification on COVID-19 using deep learning approaches,” Computational and Mathematical Methods in Medicine, vol. 2021, no. 12, pp. 1–14, 2021. [Google Scholar]

42. R. Qasim, W. H. Bangyal, M. A. Alqarni and A. Ali Almazroi, “A fine-tuned BERT-based transfer learning approach for text classification,” Journal of Healthcare Engineering, vol. 2022, no. 2, pp. 1–17, 2022. [Google Scholar]

43. L. Rukhsar, W. H. Bangyal, M. S. Ali Khan, A. A. Ag Ibrahim, K. Nisar et al., “Analyzing RNA-seq gene expression data using deep learning approaches for cancer classification,” Applied Sciences, vol. 12, no. 4, pp. 1850, 2022. [Google Scholar]

44. M. Kaveh and M. S. Mesgari, “Application of meta-heuristic algorithms for training neural networks and deep learning architectures: A comprehensive review,” Neural Processing Letters, vol. 2022, no. 3, pp. 1–104, 2022. [Google Scholar]

45. M. Kaveh, M. S. Mesgari, D. Martín and M. Kaveh, “TDMBBO: A novel three-dimensional migration model of biogeography-based optimization (case study: Facility planning and benchmark problems),” The Journal of Supercomputing, vol. 2023, no. 9, pp. 1–56, 2023. [Google Scholar]

46. M. Kaveh, M. S. Mesgari and B. Saeidian, “Orchard algorithm (OAA new meta-heuristic algorithm for solving discrete and continuous optimization problems,” Mathematics and Computers in Simulation, vol. 208, no. 3, pp. 95–135, 2023. [Google Scholar]

47. W. Wang, Y. Yang, J. Li, Y. Hu, Y. Luo et al., “Woodland labeling in Chenzhou, China, via deep learning approach,” International Journal of Computational Intelligence Systems, vol. 13, no. 1, pp. 1393–1403, 2020. [Google Scholar]

48. H. Fan, L. Zheng, C. Yan and Y. Yang, “Unsupervised person re-identification: Clustering and fine-tuning,” ACM Transactions on Multimedia Computing, Communications, and Applications, vol. 14, no. 4, pp. 1–18, 2018. [Google Scholar]

49. Y. Sun, B. Xue, M. Zhang, G. G. Yen and J. Lv, “Automatically designing CNN architectures using the genetic algorithm for image classification,” IEEE Transactions on Cybernetics, vol. 50, no. 9, pp. 3840–3854, 2020. [Google Scholar] [PubMed]

50. F. Sadeghi, O. Rostami, M. K. Yi and S. Hwang, “A deep learning approach for detecting COVID-19 using the chest X-ray images,” Computers, Materials & Continua, vol. 74, no. 1, pp. 751–768, 2023. [Google Scholar]