Binary Archimedes Optimization Algorithm for Computing Dominant Metric Dimension Problem

1  Introduction

The primary metric dimension of graphs was just recently introduced in [1]. Based on domination theory and graph resolvability theory, the dominating metric dimension. Let G = (V, E) be a connected graph and d(u,v) be the shortest path between two vertices u,v ∈ V(G). A resolving set of G is an ordered vertex set B = {x1,x2,…,xk} ⊆ V(G) if the representation

r(v|B)=(d(v,x1),d(v,x2),…,d(v,xk))

is different for each v ∈ V(G). A resolving set B is a dominating set of G if every vertex ofV\B has at least one neighbor that belongs to B. The metric dimension of G, abbreviated dim (G), is the cardinality number of the smallest resolving set. The dominating metric dimension of G, abbreviated Ddim(G), is the cardinality number of the smallest dominating resolving set.

Example 1. The star graph S7 is given in Fig. 1. The set B = {v2,v3,v4,v5,v6} is a minimal resolving set but not a dominating set of S7 since v7 is not adjacent to vertices in B. The set B¯ = {v1,v2,v3,v4,v5,v6} is a minimal dominant resolving set of S7. Thus, dim(S7) = 5 and Ddim(S7) = 6.

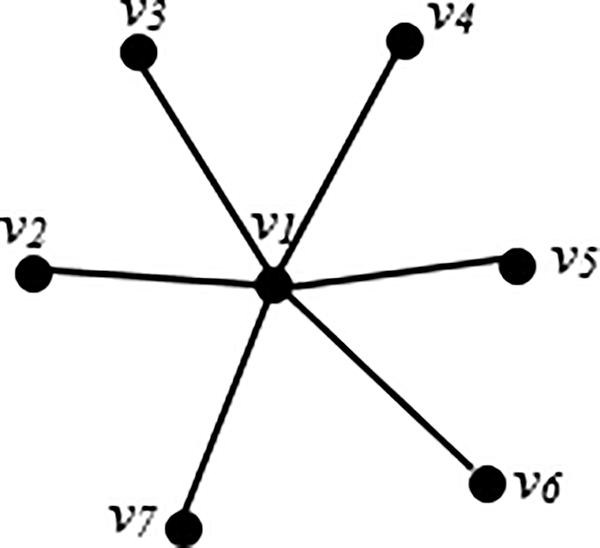
Figure 1: Star graph S7

Both the metric dimension problem and the problem with the dominant set are NP-complete problems [2,3]. As a result, finding whether Ddim(G) ≤ K for a given graph G and input K is a typical NP-complete problem for the dominating metric dimension of G. Wireless communication networks, electrical networks, commercial networks, and chemical structures are all examples of networks that apply the dominance theory [4,5]. In order to overcome the problem of uniquely locating an intruder in a network, a minimal resolving set of a graph has been introduced in [6,7]. The concept of the smallest resolving set of a graph serving as the metric basis and its cardinality number serving as the metric dimension were independently introduced by the authors in [3].

The metric dimension is determined theoretically for several graphs in the literature [8–20]. On the other hand, a few algorithms have been proposed in the literature to compute heuristically the metric dimension. These are genetic algorithm [21], particle swarm optimization [22], and variable neighborhood search [23].

The dominant metric dimension is studied in [1,24]. In [1], the dominant metric dimension of path graph Pn, cycle graph Cn, star graph Sn, complete graph Kn, and complete bipartite graph Km,n are theoretically determined. It has been shown that Ddim(Pn), n = 1, 2 is 1, Ddim(Pn), n > 4 is ⌈n3⌉, Ddim(Cn), n ≥ 7 is ⌈n3⌉, Ddim(Sn), n ≥ 2 is n−1, Ddim(Kn), n ≥ 2 is n−1, and Ddim (Km,n), m, n ≥ 2 is m + n − 2. In [24], the dominant metric dimension of the corona product graph of G and H is investigated whenever H is a path graph Pn, cycle graph Cn, complete bipartite graph Km,n, complete graph Kn and star graph Sn. Also see more details in the literature [25–30].

The smallest dominating resolving set of graphs is being calculated heuristically for the first time in this study. To resolve the problem, we modify the operations of a binary version of the Archimedes optimization algorithm (BAOA). The theoretically generated graph results are used to test the proposed BAOA. On various graphs and theoretically generated graphs, the proposed algorithm is compared with competing algorithms.

The paper is organized as follows: Section 2 gives an overview of Archimedes optimization algorithm (AOA). Section 3 gives the BAOA for computing the dominant metric dimension. Section 4 reports computational results. Finally, the conclusion is stated in Section 5.

2  Archimedes Optimization Algorithm (AOA)

AOA is a physics-inspired algorithm, specifically Archimedes’ law. This algorithm, which is a member of the meta-heuristics class, was developed by Hashim et al. [31]. The uniqueness of this algorithm is found in the way the solution is encoded, which includes three auditory signals for the basic agents: volume (V), density (D) and acceleration (Γ). As a result, a random number generator creates the initial group of agents in Dim dimensions. As additive data, random values of V, D, and are shown. After that, each item is evaluated to determine which is the best (Obest).

During the AOA process, updates to density and volume change the acceleration based on the collision notion between objects. The general AOA steps are as follows:

The first step—Initialization: Initialize the positions of all objects using (1):

Oi=lbi+rand×(ubi−lbi); i=1,2,…,N(1)

where Oi represents the ith object among N total objects. The terms lbi and ubi, respectively, stand for the lower and upper bounds of the search space.

Use (2) to specify the volume (vol) and density (den) for each ith object:

deni=rand

voli=rand(2)

The acceleration (acc) of the ith object is then initialized using the Eq. (3), where rand is a D-dimensional vector that creates a random number between 0 and 1.

acci=lbi+rand×(ubi−lbi)(3)

In this stage, evaluate the starting population and select the object with the best fitness value. xbest, denbest, volbest, and accbest should be assigned.

The second step—Update densities and volumes: The density and volume of object i for the iteration t + 1 are modified by (4):

denit+1=denit+rand×(denbest−denit)

volit+1=volit+rand×(volbest−volit)(4)

where rand stands for a random number with a uniform distribution, and volbest and denbest represent the volume and density associated with the best item discovered so far.

The third stage is the density scalar and transfer coefficient: In this phase, objects collide with one another until equilibrium is achieved. Switching from exploration to exploitation mode is the primary goal of the transfer function (Tc), according to Eq. (5):

Tc=exp⁡(t−TT)(5)

The maximum number of iterations is T, and Tc grows exponentially over time until it reaches 1. t stands for the current iteration. Additionally, the reduction in density scalar ds in AOA enables the use of Eq. (6) to find the best solution:

dst+1=exp⁡(t−TT)−(tT)(6)

The fourth step-Exploration phase: uses a random selection of material (Mr) to bring agents into contact with one another. In cases when the transfer function value is less than or equal to 0.5, acceleration objects are updated using Eq. (7).

Γit+1=DMr+VMr×ΓMrDit+1×Vit+1(7)

The fifth step-Phase of exploitation: This phase does not result in an agent collision. Eq. (8) is used to update acceleration objects when the transfer coefficient value is greater than 0.5.

Γit+1=DBest+VBest×ΓBestDit+1×Vit+1(8)

where ΓBest denotes the acceleration of the optimal object OBest.

The sixth phase-Normalization of acceleration: In this stage, normalize the acceleration in order to determine the rate of change using Eq. (9):

Γi−normt+1=α×Γit+1−ΓMinΓMax−ΓMin+β(9)

where α and β are constants of 0.9 and 0.1, respectively. The Γi−normt+1 defines the percentage of steps that each agent will change. The higher value of acceleration means that the object realizes the operation of exploration; or else, the exploitation mode is active.

The seventh step—Update process: In the exploration phase (Tc ≤ 0.5), Eq. (10) updates the position of the ith object in iteration t + 1, whereas in the exploitation phase (Tc > 0.5), Eq. (11) updates the position of the object.

Oit+1=Oit+c1×r5×Γi−normt+1×ds×(Orand−Oit)(10)

where c1 equals 2.

Oit+1=OBestt+F×c2×r6×Γi−normt+1×ds×(δ×OBest−Oit)(11)

where c2 is equal to 6.

The parameter δ is positively correlated with time and this parameter is proportionally linked to the transfer coefficient Tc, i.e., δ = 2 × Tc. The main role of this parameter is to maintain a proper balance between exploration and exploitation operations. The margin between the best object and the other object is higher during the first iterations, resulting in a high random walk. However, in the final iterations, the margin will be decreased and provide a low random walk.

F is used for flagging, while Eq. (12) is utilized to determine the direction of the search:

F={+1if P≤0.5−1if P≥0.5(12)

where P = 2 × rand − C4.

The eighth step is evaluation, where we utilize the score index Sc to assess the new population and other data such as DBest, VBest, and ΓBest to identify the best objects.

3  Binary Archimedes Optimization Algorithm for Dominant Metric Dimension

Because it maintains a population of solutions and examines a vast area to find the best global solution, the Archimedes optimization algorithm can solve difficult optimization problems with numerous locally optimal solutions. This benefit enables the binary version of the algorithm to be applied to the dominant metric dimension problem. Using position vectors in the continuous real domain, objects can navigate the search space in the continuous version of AOA. By using an S-shaped transfer function to change the continuous variable AOA into a binary one, we may convert it into binary values. Position changes in discrete binary search space necessitate flipping between 0 and 1.

The following equation is used in the initialization step:

Obinaryij={1rand()>0.50,else(13)

where a rand is a random number between 0 and 1.

A transfer function is used to be able to map continuous values to binary ones. In this study, the sigmoid function (S) is used as follows:

S=11+e−10xd(14)

where xd indicates the continuous-valued position at dimension d and S is the function output. The following equation is used to generate a binary value.

Obinaryij={1rand()<S0,otherwise(15)

The proposed algorithm deals with the dominant resolving set problem as an optimization problem where it searches for the best solution, so each object can be represented as a one-dimensional vector Obinaryij = (Oi1, Oi2, …, Oij), Obinaryij is a binary-valued position vector if the j-th element of the vector has a value of 1, it means that vertex j belongs to B. If every v ∈ V (G) has a distinct representation r(v|B), then B is a dominant resolving set. The value of a binary-valued position vector is produced by computing the value of the S-shaped transfer function. In the BAOA algorithm, when an object is not feasible as a dominant resolving set, that object is repaired by adding a vertex from V\B. This repair is applied until that object becomes a dominant resolving set.

Each solution in the population is represented by the algorithm as a string of binary values, where 1 indicates that the dominant resolving set will be chosen, in which case the corresponding value will be “1,” and 0 indicates that the dominant resolving set will not be chosen, in which case the corresponding value will be “0”.

Thus, the flowchart of the proposed BAOA algorithm is displayed in Fig. 2 and the pseudocode in Algorithm 1, respectively.

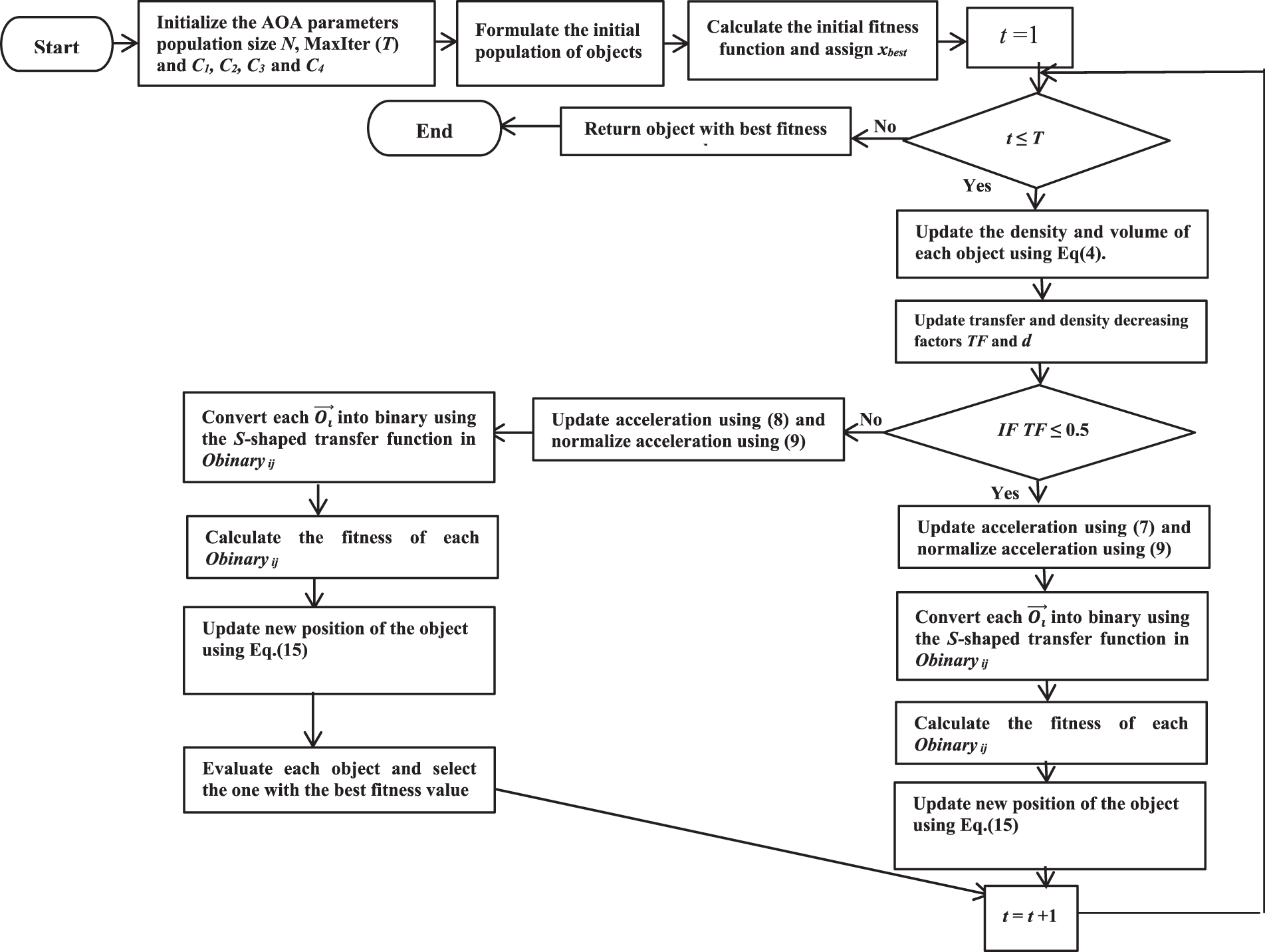
Figure 2: The flowchart of BAOA

4  Experimental Results

In this section, the proposed BAOA is tested using graph results that are computed theoretically. The proposed BAOA is compared to the BWOA and BPSO on a complete graph, a star graph, a path graph, an alternate triangular snake with pendant edge graph, and an alternate quadrilateral snake graph.

The algorithm tests and comparisons were performed on a Windows 10 Ultimate 64-bit operating system; the processor was an Intel Core i7 running at 16 GB of RAM, the hard drive was 1TBHDD+1TBSSD, and the code was implemented in MATLAB 2021b. The parameter setting values are presented in Table 1.

The BAOA, BWOA and BPSO have been run 20 times for each instance, and the results are summarized in Tables 2–5. The tables are organized as follows:

–    The first three columns contain the test instance name, the number of nodes and edges, respectively.

–    The fourth column contains the BAOA best solution (named BAOA best) obtained in 20 runs;

–    The average execution time (t) used to reach the final BAOA solution for the first time is given in the fifth column.

–    The sixth column contains the average number of generations for finishing BAOA best.

–    The seven and the eighth column variance and standard deviation contain information on the average solution quality.

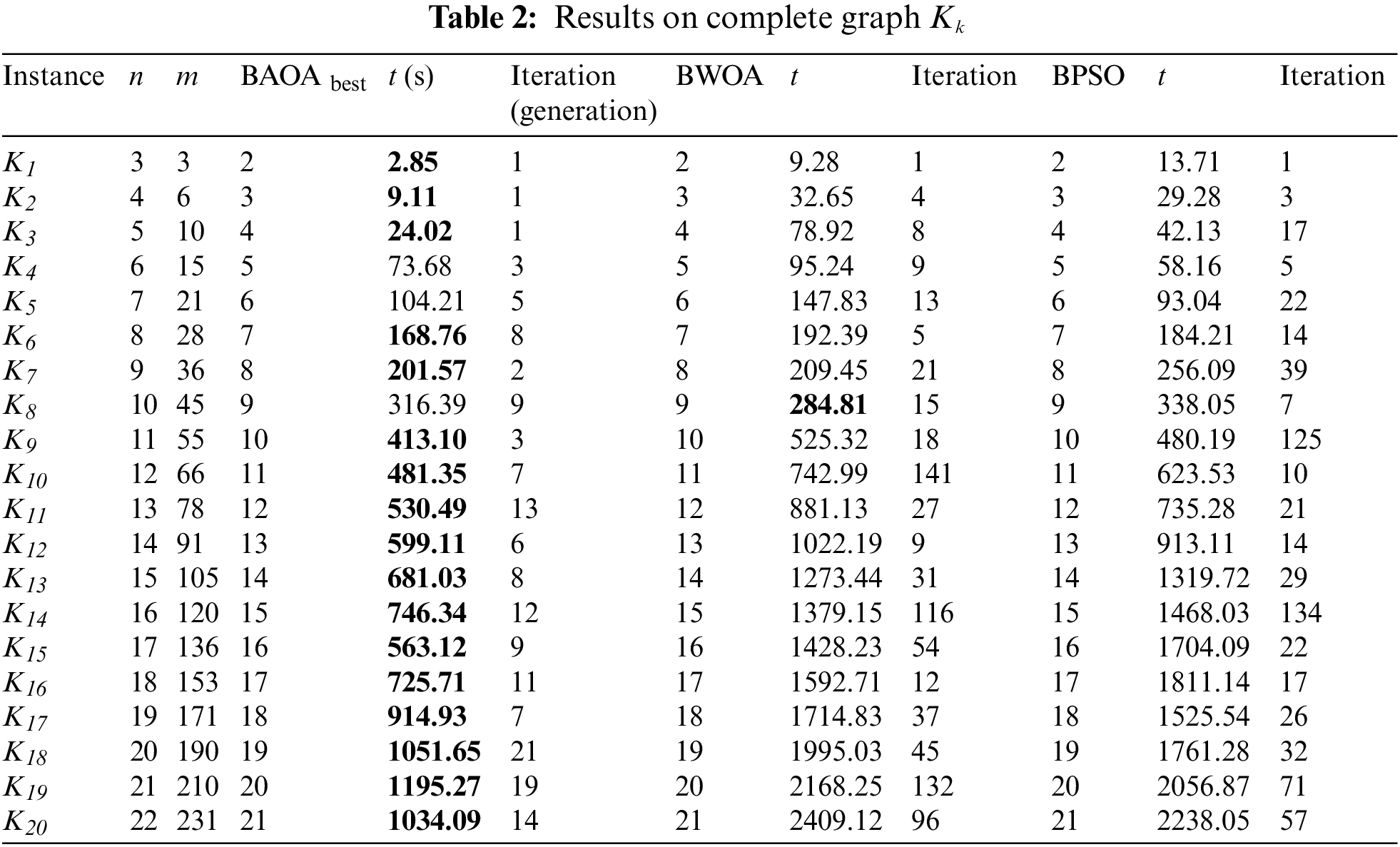
Our stopping criterion is the cardinality of the dominant resolving set that reaches the known dominant metric dimension of the complete graph. BAOA takes 168.76 s on K6, and it takes 8 iterations to complete BAOA to achieve the best solution.

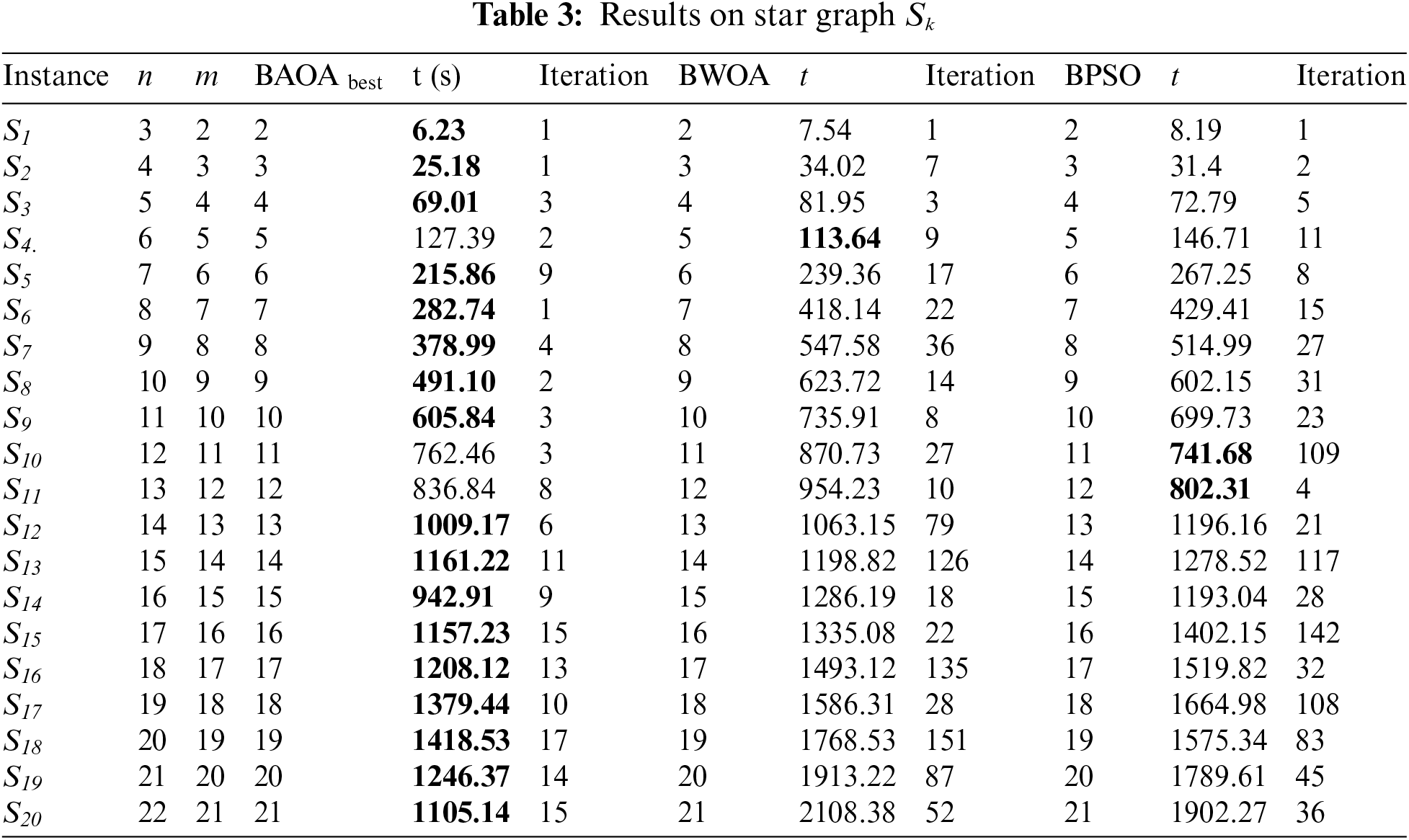
Regarding BAOA results, Table 3 shows that for the star graph Sk,1 ≤ k ≤ 20, BAOA has reached an optimal solution. For example, in S3, the time needed for BAOA is 69.01 s and reaches the best solution after 3 iteration. In [1], the dominant metric dimension for a path graph, a complete graph, and a star graph is theoretically determined.

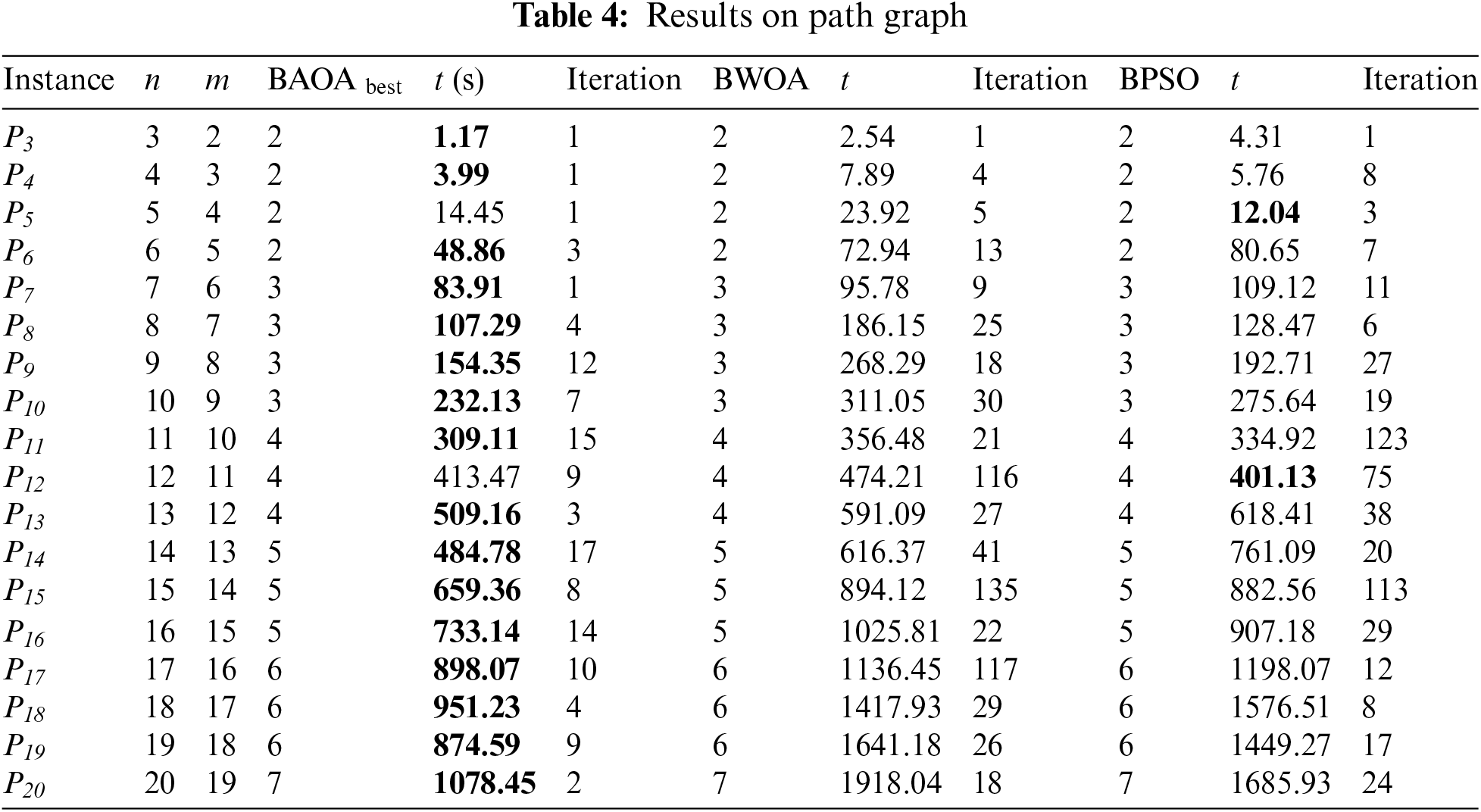
Regarding BAOA results, Table 4 shows that for path graph Pn, 3 ≤ n ≤ 20, BAOA has reached an optimal solution. For example, in P6, the time required for BAOA is 48.86 s, with 3 iterations required to achieve the best solution.

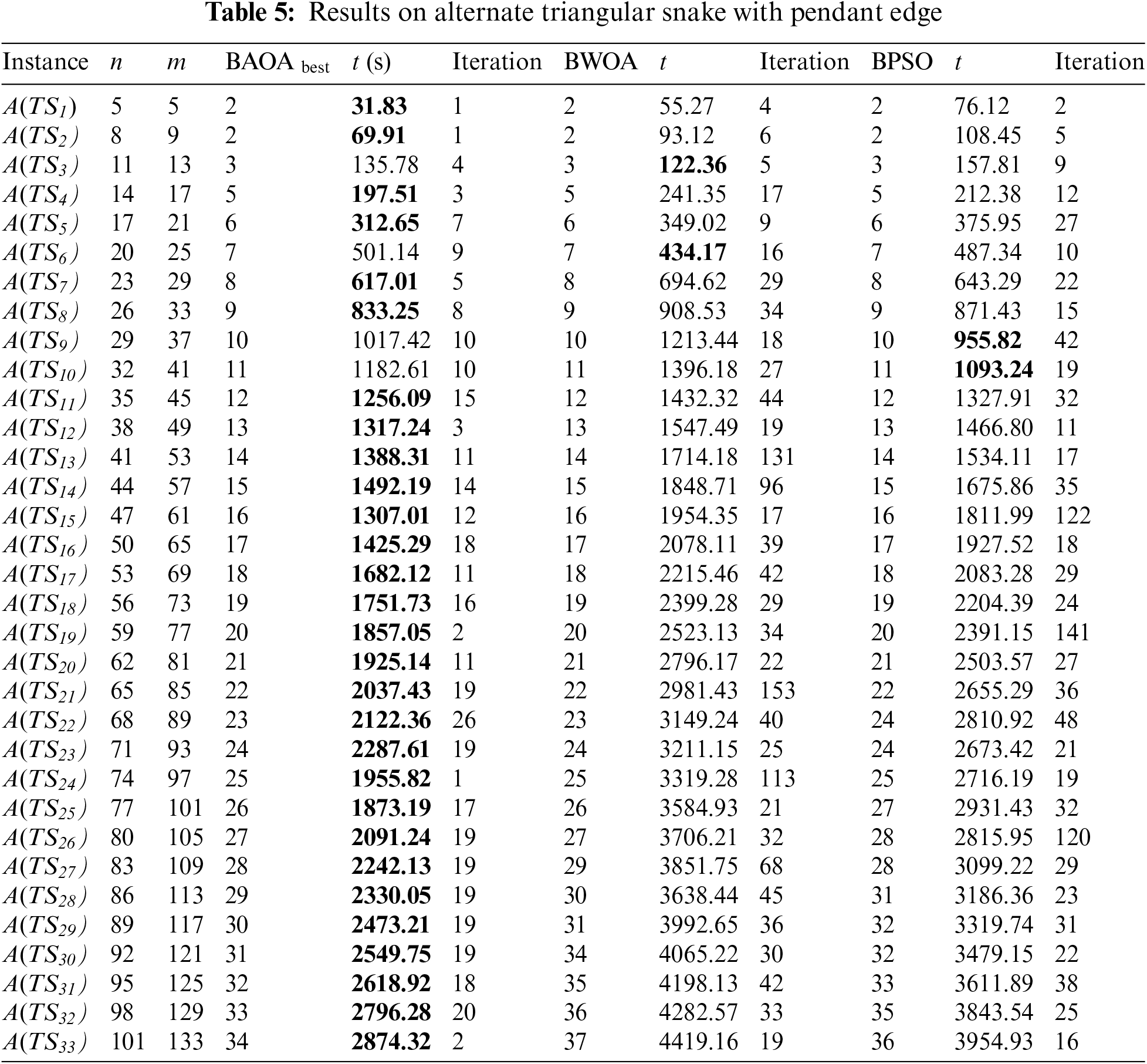
BAOA found an optimal solution for the alternate triangular snake with pendant edge A(TSk), 1 ≤ k ≤ 33, as shown in Table 5. For example, in A(TS4), the time required for BAOA is 197.51 s, with 3 iterations required to achieve the best solution.

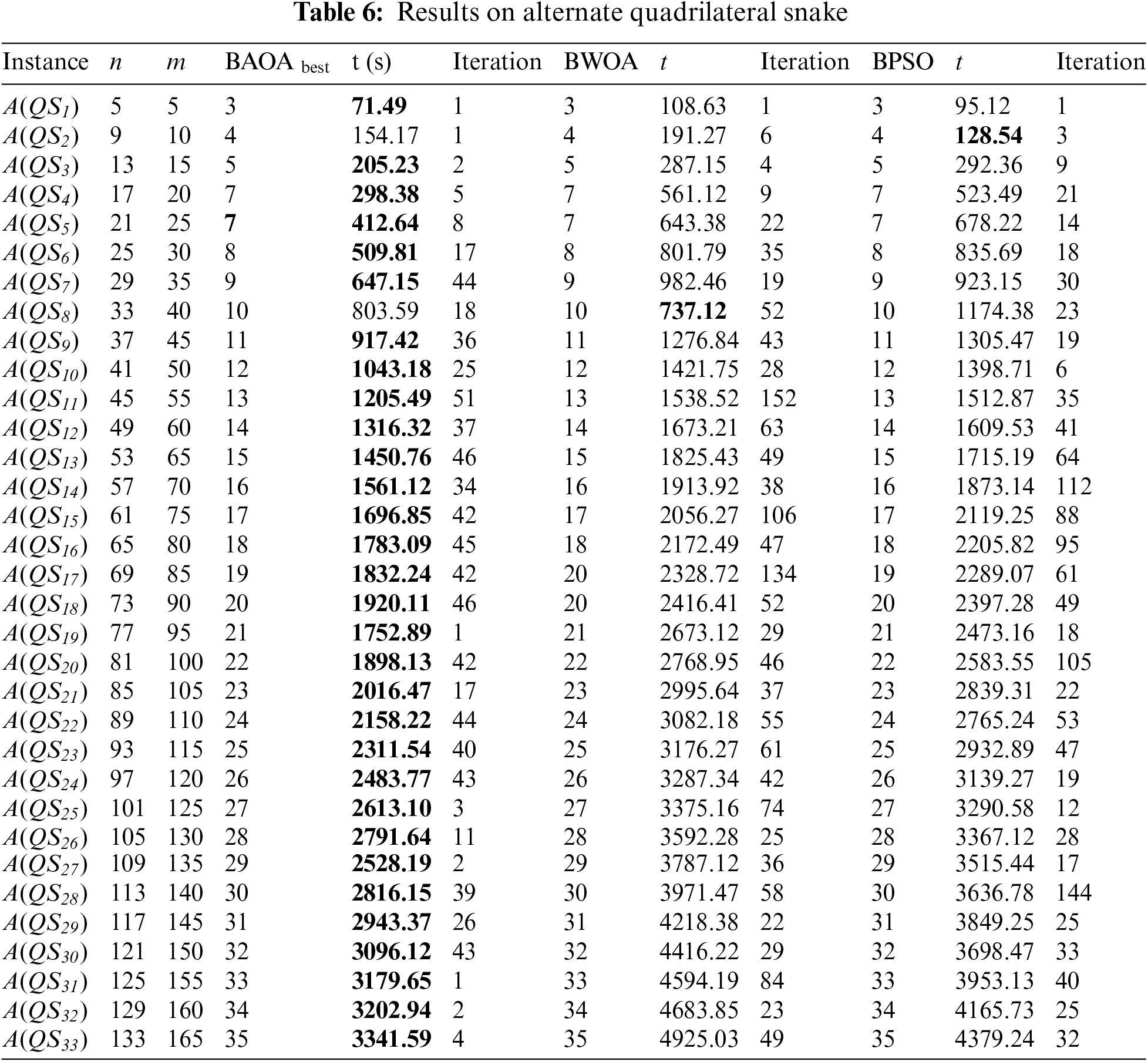
Regarding BAOA results, Table 6 shows that alternate quadrilateral snake A(QSk), 1 ≤ k ≤ 33, BAOA has reached an optimal solution. For example, A(QS3), the time needed for BAOA is 205.23 s and reaches the best solution after 2 iterations.

Tables 2–6 display the results for various graphs, which show that the proposed BAOA can achieve the best optimal solution (known dominant metric dimension) in a reasonable amount of time, especially for the path graph, complete graph and star graph. It proves the correctness and superiority of the proposed BAOA.

Experiments in this paper are performed on a subset of complete graph instances with n ≤ 22 and m ≤ 231 in Table 2, star graph instances with n ≤ 22 and m ≤ 21 in Table 3, path graph instances with n ≤ 20 and m ≤ 19 in Table 4, alternate triangular snake with pendant edge graph instances with n ≤ 101 and m ≤ 133 in Table 5, and alternate quadrilateral snake graph instances with n ≤ 133 and m ≤ 165 in Table 6.

Figs. 3–7 show the superiority of the proposed BAOA according to the dominant metric dimension. For example, the dominant metric dimension by BAOA for K2 is 3 and reaches 9.11 s. P7 is 3 and reaches 83.91 s. All figures show the superiority of the proposed BAOA.

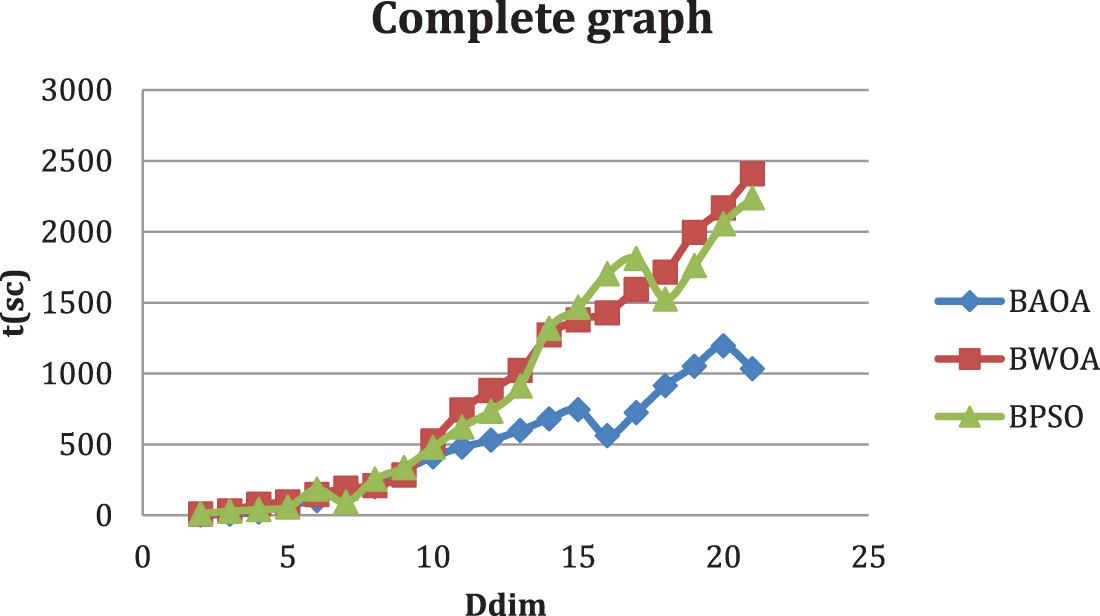
Figure 3: Comparison between BAOA best and t (s) for computing the dominant metric dimension of a complete graph

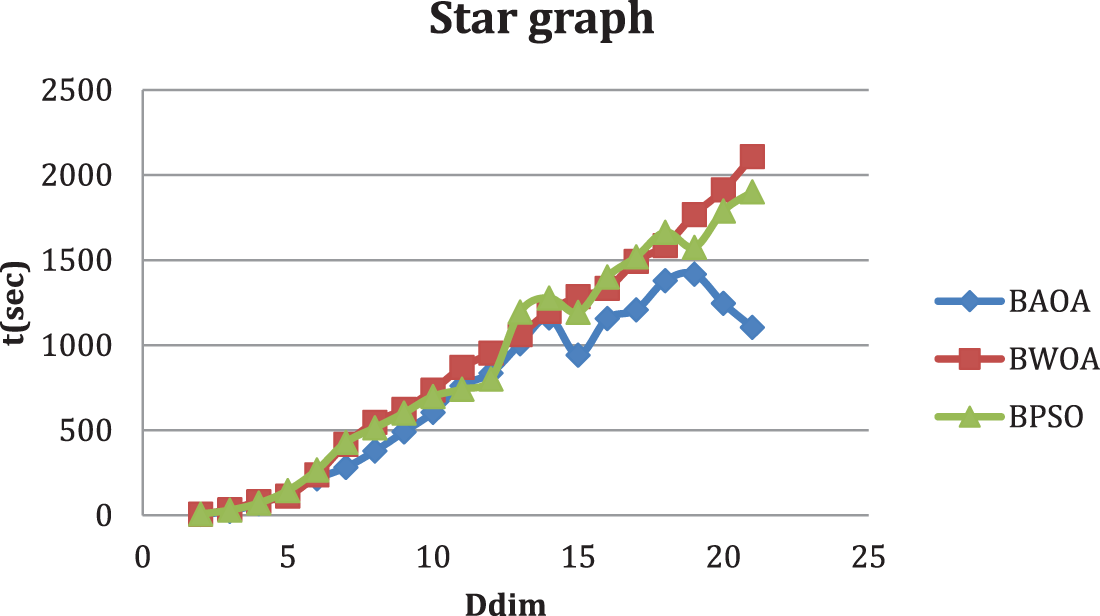
Figure 4: Comparison between BAOA best and t (s) for computing the dominant metric dimension of a star graph

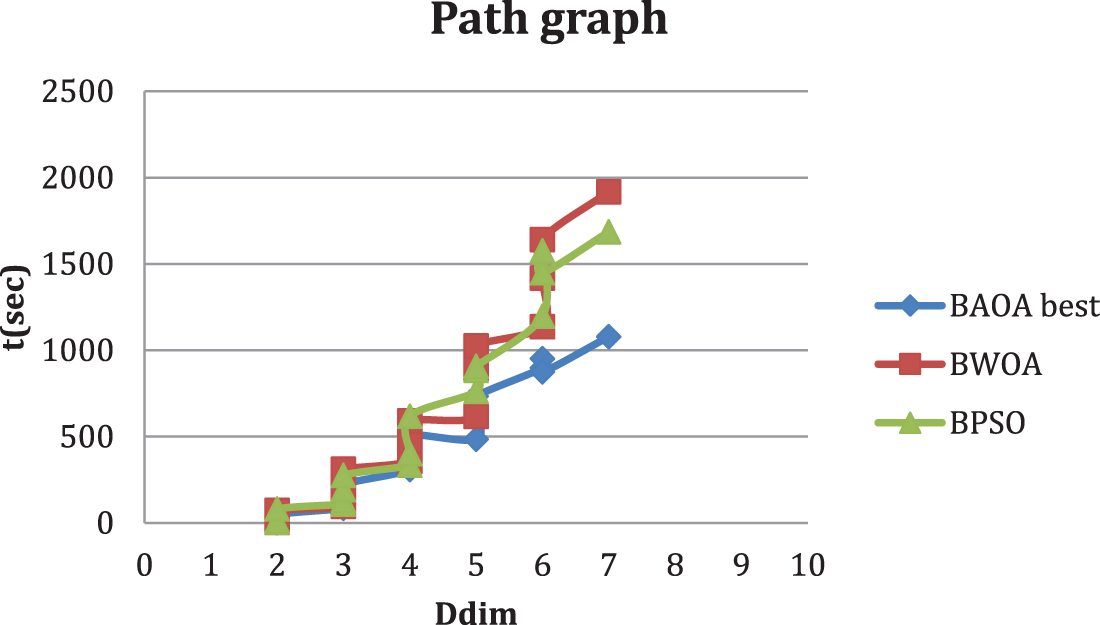
Figure 5: Comparison between BAOA best and t (s) for computing the dominant metric dimension of a path graph

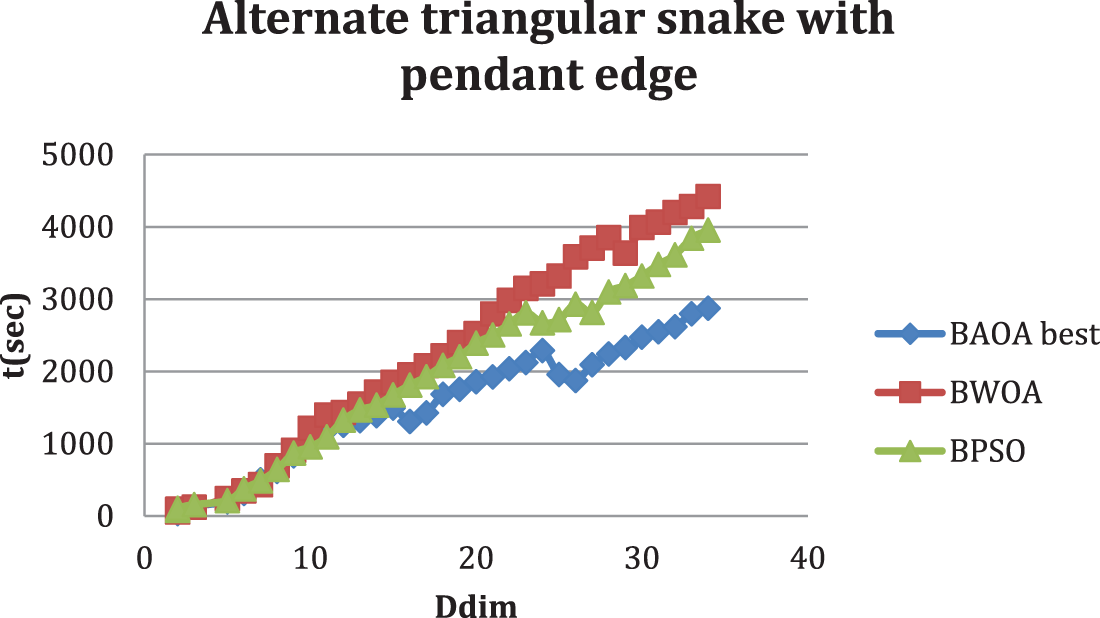
Figure 6: Comparison between BAOA best and t (s) for computing the dominant metric dimension of an alternate triangular snake with pendant edge graph

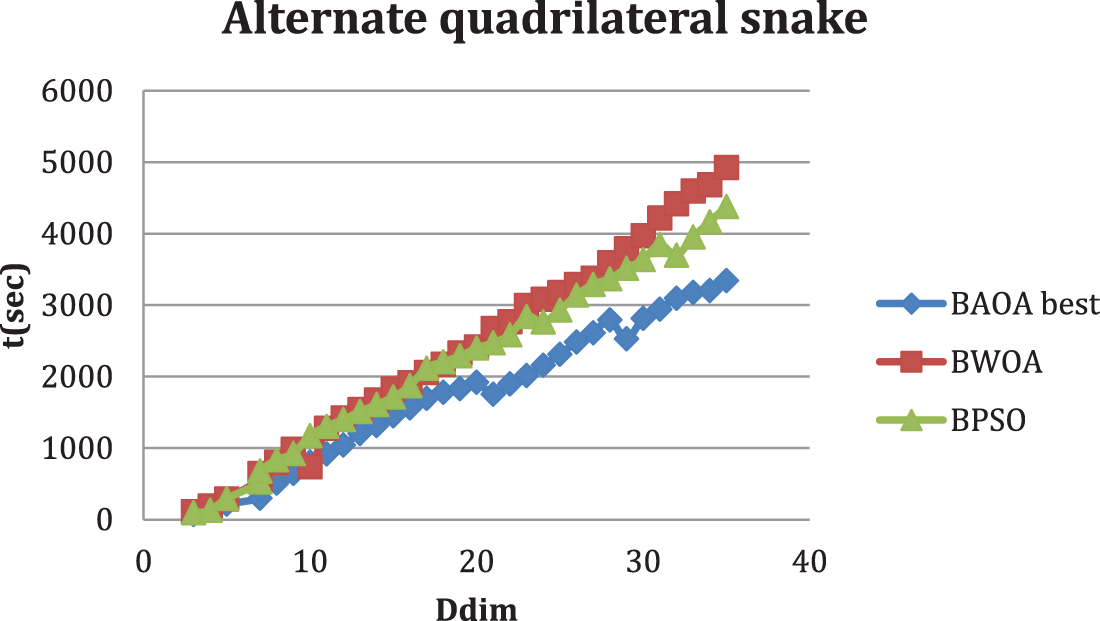
Figure 7: Comparison between BAOA best and t (s) for computing the dominant metric dimension of an alternate quadrilateral snake graph

5  Conclusion

In this paper, the operations of a binary version of the Archimedes optimization algorithm BAOA are adapted to solve the dominant metric dimension problem. The proposed BAOA is tested using graph results that are computed theoretically. The proposed algorithm is compared to competitive algorithms on graphs that are computed theoretically and other graphs. The performance of the proposed BAOA outperforms that of the BWOA and BPSO.

An Open Problem. Other efficient metaheuristic algorithms for determining any variant of metric dimension that does not compute the previous heuristically for any regular graph or planar graph, as well as comparing them to competitive algorithms.

Acknowledgement: This work was not supported by any funding.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Conceptualization, methodology, writing review and formal analysis, Basma Mohamed; investigation, resources, Linda Mohaisen; writing–original draught preparation, validation, editing and visualization, Mohammed Amin. All authors have read and agreed to the published version of the manuscript.

Availability of Data and Materials: The data underlying the results presented in the study are available within the manuscript.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. L. Susilowati, I. Sa'adah, R. Z. Fauziyyah and A. Erfanian, “The dominant metric dimension of graphs,” Heliyon, vol. 6, no. 3, pp. e03633, 2020. [Google Scholar] [PubMed]

2. M. R. Garey, “A guide to the theory of NP-completeness,” in Computers and Intractability, 1979. [Google Scholar]

3. F. Harary and R. A. Melter, “On the metric dimension of a graph,” ARS Combinatoria, vol. 2, pp. 191–195, 1976. [Google Scholar]

4. J. L. Hurink and T. Nieberg, “Approximating minimum independent dominating sets in wireless networks,” Information Processing Letters, vol. 109, no. 2, pp. 155–160, 2008. [Google Scholar]

5. A. H. Karbasi and R. E. Atani, “Application of dominating sets in wireless sensor networks,” International Journal of Security and its Applications, vol. 7, no. 4, pp. 185–202, 2013. [Google Scholar]

6. D. Vukičević and A. Klobučar, “K-dominating sets on linear benzenoids and on the infinite hexagonal grid,” Croatica Chemica Acta, vol. 80, no. 2, pp. 187–191, 2007. [Google Scholar]

7. P. J. Slater, “Leaves of trees,” Congressus Numerantium, vol. 14, pp. 549–559, 1975. [Google Scholar]

8. S. Akhter and R. Farooq, “Metric dimension of fullerene graphs,” Electron, Journal of Graph Theory and Applications, vol. 7, no. 1, pp. 91–103, 2019. [Google Scholar]

9. T. Vetrík, “On the metric dimension of directed and undirected circulant graphs,” Discussiones Mathematicae: Graph Theory, vol. 40, no. 1, pp. 67–76, 2020. [Google Scholar]

10. S. Nawaz, M. Ali, M. A. Khan and S. Khan, “Computing metric dimension of power of total graph,” IEEE Access, vol. 9, pp. 74550–74561, 2021. [Google Scholar]

11. S. Nazeer, M. Hussain, F. A. Alrawajeh and S. Almotairi, “Metric dimension on path-related graphs,” Mathematical Problems in Engineering, vol. 2021, pp. 1–12, 2021. [Google Scholar]

12. M. Mulyono and W. Wulandari, “The metric dimension of friendship graph Fn, lollipop graph Lm,n and petersen graph Pn,m,” Bulletin of Mathematics, vol. 8, no. 2, pp. 117–124, 2016. [Google Scholar]

13. M. F. Nadeem, S. Qu, A. Ahmad and M. Azeem, “Metric dimension of some generalized families of toeplitz graphs,” Mathematical Problems in Engineering, vol. 2022, pp. 1–10, 2022. [Google Scholar]

14. A. N. Koam, A. Ahmad, M. S. Alatawi, M. F. Nadeem and M. Azeem, “Computation of metric-based resolvability of quartz without pendant nodes,” IEEE Access, vol. 9, pp. 151834–151840, 2021. [Google Scholar]

15. H. Fernau, P. Heggernes, P. van’t Hof, D. Meister and R. Saei, “Computing the metric dimension for chain graphs,” Information Processing Letters, vol. 115, no. 9, pp. 671–676, 2015. [Google Scholar]

16. I. Tomescu and M. Imran, “R-sets and metric dimension of necklace graphs,” Applied Mathematics and Information Sciences, vol. 9, no. 1, pp. 63–67, 2015. [Google Scholar]

17. I. J. L. Garces and J. B. Rosario, “Computing the metric dimension of truncated wheels,” Applied Mathematical Sciences, vol. 9, no. 56, pp. 2761–2767, 2015. [Google Scholar]

18. M. Imran, F. Bashir, A. Q. Baig, A. U. H. Bokhary, A. Riasat et al., “On metric dimension of flower graphs and convex polytopes,” Utilitas Mathematica, vol. 92, pp. 389–409, 2013. [Google Scholar]

19. H. Iswadi, E. T. Baskoro and R. Simanjuntak, “On the metric dimension of corona product of graphs,” Far East Journal of Mathematical Sciences, vol. 52, no. 2, pp. 155–170, 2011. [Google Scholar]

20. A. T. Shahida and M. S. Sunitha, “On the metric dimension of joins of two graphs,” Global Journal of Pure and Applied Mathematics, vol. 5, no. 9, pp. 33–38, 2014. [Google Scholar]

21. J. Kratica, V. Kovačević-Vujčić and M. Čangalović, “Computing the metric dimension of graphs by genetic algorithms,” Computational Optimization and Applications, vol. 44, no. 2, pp. 343–361, 2009. [Google Scholar]

22. D. T. Murdiansyah, “Computing the metric dimension of hypercube graphs by particle swarm optimization algorithms,” in Int. Conf. on Soft Computing and Data Mining, Cham, Springer, pp. 171–178, 2016. [Google Scholar]

23. N. Mladenović, J. Kratica, V. Kovačević-Vujčić and M. Čangalović, “Variable neighborhood search for metric dimension and minimal doubly resolving set problems,” European Journal of Operational Research, vol. 220, no. 2, pp. 328–337, 2012. [Google Scholar]

24. R. P. Adirasari, H. Suprajitno and L. Susilowati, “The dominant metric dimension of corona product graphs,” Baghdad Science Journal, vol. 18, no. 2, pp. 0349, 2021. [Google Scholar]

25. B. Mohamed and M. Amin, “The metric dimension of subdivisions of lilly graph, tadpole graph and special trees,” Applied and Computational Mathematics, vol. 12, no. 1, pp. 9–14, 2023. [Google Scholar]

26. B. Mohamed, L. Mohaisen and M. Amin, “Computing connected resolvability of graphs using binary enhanced harris hawks optimization,” Intelligent Automation & Soft Computing, vol. 36, no. 2, pp. 2349–2361, 2023. [Google Scholar]

27. B. Mohamed, L. Mohaisen and M. Amin, “Binary equilibrium optimization algorithm for computing connected domination metric dimension problem,” Scientific Programming, vol. 2022, pp. 1–15, 2022. [Google Scholar]

28. B. Mohamed and M. Amin, “Domination number and secure resolving sets in cyclic networks,” Applied and Computational Mathematics, vol. 12, no. 2, pp. 42–45, 2023. [Google Scholar]

29. B. Mohamed, “Metric dimension of graphs and its application to robotic navigation,” International Journal of Computer Applications, vol. 184, no. 15, pp. 1–3, 2022. [Google Scholar]

30. B. Mohamed and M. Amin, “A hybrid optimization algorithms for solving metric dimension problem,” International Journal on Applications of Graph Theory in Wireless Ad hoc Networks and Sensor Networks, vol. 15, no. 1, pp. 1–10, 2023. [Google Scholar]

31. F. A. Hashim, K. Hussain, E. H. Houssein, M. S. Mabrouk and W. Al-Atabany, “Archimedes optimization algorithm: A new metaheuristic algorithm for solving optimization problems,” Applied Intelligence, vol. 51, no. 3, pp. 1531–1551, 2021. [Google Scholar]