A Network Traffic Prediction Algorithm Based on Prophet-EALSTM-GPR

1  Introduction

In recent years, with the rapid development and wide application of communication technology, the growth of smart terminals over the past ten years has accelerated network traffic creation and explosion. On the one hand, smartphones and tablet computers have become highly popular. Traditional voice communication and cell phone data communication have been used in people’s lives. On the other hand, Internet of Things (IoT) applications such as bike-sharing and take-away rider positioning have become available, bringing great convenience to people’s lives.

However, it also means that the scale and complexity of the network will increase significantly, and more traffic data will be generated in the network [1,2]. Huge networks and rising network traffic will require more spectrum, electricity, and other resources [3,4]. Moreover, network traffic is not constant, and it changes in real-time. To maintain users’ experience during peak traffic periods, lots of manpower and resources are required. However, guaranteeing the users’ experience requires few resources during valley traffic periods.

Therefore, accurate and timely network traffic prediction plays an important role in efficient and automated planning and deployment of ultra-dense base stations, multi-dimensional resource management [5] and switching base station in future networks. For example, traffic prediction can facilitate multi-access edge computing deployments and resource management. It can increase computing and storage capacity effectively at the network edge, reduce delays in the delivery of content and services, and further improve the quality of experience for users. Secondly, the ability to estimate traffic accurately also supports the rational allocation and effective use of network resources by operators. Operators dispatch some UAVs (unmanned aerial vehicles) flexibly as mobile access points (APs) to address network congestion during peak hours or certain special events (sporting events, rallies, etc.) by predicting network traffic for specific areas in advance. Conversely, operators can also turn off some idle base stations at night to reduce energy consumption. In addition, traffic prediction provides timely warnings of network congestion and guarantees the network’s operation, which is essential for improving the quality of service of the network. High traffic loads can lead to problems such as wireless channel conflicts and bandwidth resource usage. By predicting traffic, we can allocate network resources in advance and respond to network congestion on time.

Network traffic is influenced by outside influences and tends to exhibit non-smoothness in the long term. In addition to this, network traffic is characterized by suddenness, nonlinearity, periodicity, and long correlation, which makes it difficult for general models to predict wireless network traffic accurately. Based on the above background, this paper studies the prediction of network traffic by building a model adapted to the characteristics of current network traffic data and fitting it to the historical data of network traffic to enhance the shortcomings of existing algorithms in terms of the accuracy of network traffic prediction. Considering the facts above, this paper combines a Prophet model, LSTM network, attention mechanism, and GPR in machine learning to construct a network traffic prediction model. The main contributions of this paper are shown below.

•   In this paper, we propose a combined traffic prediction model based on a Prophet model, EALSTM network and GPR according to the characteristics of network traffic.

•   To extract the multifractal features of network traffic, the input traffic data are decomposed into periodic and non-periodic terms by using the decomposability of the Prophet model. Then the Prophet model is established for periodic term to predict different granularities periodic term. Then, the EALSTM model is established for the non-periodic term. It can extract features in traffic sequences and learn their long-term correlation. Meanwhile, the long-term dependency problem caused by long step length is avoided effectively. As a machine learning regression method, GPR is used to predict the residual term, which increases predictability even further.

•   Finally, the performance of the proposed Prophet-EALSTM-GPR outperforms some other baseline algorithm, including Prophet, ARIMA, LSTM and EALSTM models with respect to accuracy in network traffic data prediction.

The remainder of the paper is organized as follows. Section 2 provides an overview of relevant research on network traffic prediction. The problem modelling for this paper is briefly described in Section 3. Section 4 describes the proposed algorithm. Section 5 explain the experimental setup and describes and discusses the results in detail. Conclusion is given in Section 6.

2  Related Work

Network traffic prediction methods can be divided into two methods: linear model prediction and nonlinear model prediction. Traditional traffic prediction frequently employs linear models for prediction, such as Autoregressive Moving Average (ARMA), Autoregressive Integrated Moving Average (ARIMA) and its variant. Acun et al. [6] combined the time series prediction method ARIMA with a clustering method. Segments of the traffic network were classified based on traffic data using the K-Means clustering algorithm, and a prediction model was generated for the most representative segment in each cluster. These models were used to predict for each network segment in the network. Liu et al. [7] proposed a novel multivariate multi-order Markov transformation for multi-modal accurate network traffic prediction. ChikkaKrishna et al. [8] developed a short-term traffic prediction (STTP) model using Fb-PROPHET and Neural-PROPHET to predict traffic volumes. Although these traditional time series prediction techniques have strong predictive power, they are better suited for predicting relatively stable network traffic sequences and have difficulty capturing long-term correlations in traffic when predicting more complex network traffic.

However, with the growing development of networks, network traffic usually exhibits nonlinear characteristics such as time dependence and long correlation. Along with the development of artificial intelligence technology, many nonlinear prediction models [9] based on machine learning have emerged, such as random forest (RF), GPR, feed-forward neural networks (FFNNs), CNNs, recurrent neural networks (RNNs) and its variants. These methods have significant advantages in learning traffic nonlinear features. In [10], the method of wavelet transform is proposed to decompose the original traffic into an approximate sequence and several detail sequences for the burst and nonlinear characteristics of network traffic. Based on this, traffic’s trend is learned by the LSTM network and the burst information is extracted at multiple scales to predict future traffic. Chen [11] proposed a multi-task time series graph network (MTG-Net) framework. This framework uses a temporal convolutional network (TCN) to capture temporal relationships and a graph attention network (GAT) to establish associations between regions dynamically. In [12], a privacy-preserving machine learning technique called joint learning (FL) is introduced for trade-off privacy-accurate traffic prediction. An FL-based gated recurrent unit neural network algorithm (FedGRU) is proposed for traffic flow prediction (TFP). In [13–16], spatio-temporal correlated traffic prediction was studied. These nonlinear predictive mode models have stronger adaptive ability, higher computational power, and show better fitting ability than other algorithms in predicting nonlinear time series data. However, there are some limitations, such as high computational cost and failure to accurately reflect the trend of the overall data.

Many studies use hybrid prediction models of linear and nonlinear methods. Li et al. [17] developed a model combining ARIMA and radial basis function artificial neural network (RBF-ANN) for predicting traffic volumes. Du et al. [18] proposed a data reconstruction prediction model based on empirical mode decomposition (EMD) and gated recursive unit (GRU) neural networks to address the lack of more accurate and comprehensive characterization of network traffic in existing studies. Bayati et al. [19] designed an efficient prediction model considering different traffic characteristics, including periodic, nonlinear, and non-stationary. An ensemble of learners is proposed in which each learner is optimized by finding the optimal accuracy diversity balance in the feature space. This divide-and-conquer approach avoids complex objective functions with many local optima. In [20], a model is constructed by combining LSTM and GPR to achieve accurate cellular traffic prediction by extracting the dominant periodic components of the cellular data and then feeding the smaller components into the LSTM network. However, the existing research on traffic prediction fail to capture non-smooth, sudden, periodic, and long correlation characteristics of network traffic nowadays. Based on the above studies, combining the advantages of each method, variant methods are adapted to different tasks, a prediction algorithm based on Prophet-EALSTM-GPR is proposed in this paper to obtain better performances.

3  Statement of Problem

We formulate the network traffic data prediction as a time series prediction model and divide the time series using a constant time interval. In this paper, the entire sequence of traffic is given as X={X1(t),X2(t),…,Xn(t)}, where Xi(t) is expressed as the network traffic data collected at time t of the i-th cell, n denotes the number of cells, t denotes the length of past observations. Then the traffic prediction problem can be formulated as X~i(t+l), i.e., predicting the traffic value at the (t+l)-th moment of the i-th cell, where l denotes the predicted time range and is a positive integer.

In the following, we use the characteristics of different models combined to predict network traffic, which is beneficial for analyzing the periodicity of traffic data, improving the long correlation between traffic series and prediction accuracy. For easy understanding, we omit the subscript i, and use X(t) to denote the traffic at time t. The model formulation that we provide is as follows.

1)   Firstly, using the Prophet model’s decomposability characteristic, the network traffic is decomposed into periodic and non-periodic terms. The periodic term represents the sum of two different granularity periods, i.e., s(t)=weeklyt+dailyt, where weeklyt, dailyt denote weekly and daily period term, respectively. The non-periodic term represents the sum of trend term and residual term, i.e., A(t)=g(t)+ε(t), where g(t), ε(t) denote the trend term and error term, respectively. The Holiday term is not considered in this paper.

2)   We use the Prophet model to predict the periodic terms and obtain the predicted values s~i(t+l) in time t+l.

3)   The non-periodic terms are fed into the trained EALSTM model to obtain the predicted values A~i(t+l). The EALSTM model helps to capture long-term dependencies in the time series and enables the correct resolution of local feature relationships within time steps based on the attention mechanism.

4)   The residual term is obtained by subtracting the prediction results of the EALSTM model from the non-periodic term. The residual terms are fed into the trained Gaussian process regression model to obtain the predicted values r~i(t+l).

5)   The predictions in 2), 3), and 4) are summed to obtain the final network traffic prediction, i.e.,

X~i(t+l)=s~i(t+l)+A~i(t+l)+r~i(t+l)(1)

4  The Proposed Method

In this section, we will present the proposed prediction scheme. Specifically, the Prophet model decomposes network traffic data into periodic and non-periodic terms. The periodic term is predicted by the Prophet model for different granularity periods. The non-periodic term is fed to the EALSTM network to extract the features in the sequences and learn their long correlation. The GPR model is built to further improve the traffic prediction accuracy, to predict the residual term. Finally, the predicted values are obtained by summing the results. Fig. 1 shows the overall framework of the prediction model proposed in this paper.

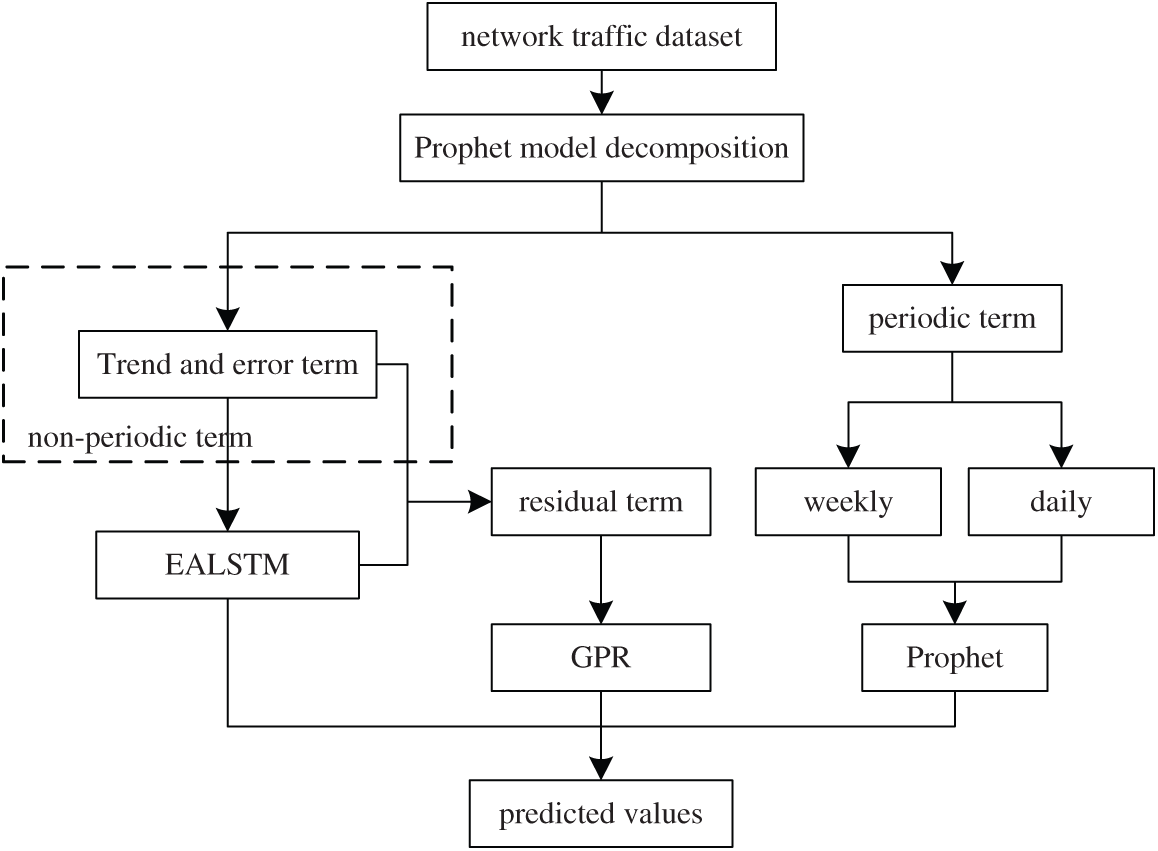
Figure 1: Prediction framework based on Prophet-EALSTM-GPR

4.1 Prophet Model Decomposition and Prediction of Periodic Term

Various time domain series and frequency domain analysis methods have been proposed to decompose complex time series to improve the prediction performance. This naturally motivates us to adopt a similar approach to deal with complex real network traffic. The Prophet model is based on the time domain analysis method in time series analysis and machine learning fitting, which treats the time series as a function of t and uses a fitted function curve to make predictions. Meanwhile, traditional network traffic prediction models cannot extract network traffic’s multifractal characteristics effectively. It is more efficient to separate the traffic components with different characteristics from the network data and predict them respectively. The Prophet model is a decomposable time series model consisting of three main model components: a trend term, a period term, and a holiday term, as shown in the following equation. The equation is defined as follows:

y(t)=g(t)+s(t)+h(t)+εt(2)

where the trend term g(t) represents the non-periodic trend of the time series; periodic term s(t) indicates the periodic variation of the time series; holiday term h(t) indicates the impact of an occasional day or days; εt denotes the error term, representing the inability of the model to accommodate any particular variation. We assume that the holiday term is noise, which is not considered in this paper.

As the most complex core component of the entire Prophet model, the trend term has two different functions. One is a nonlinear, saturated growth term, i.e., a modified logistic growth model. The saturation value changes dynamically with time and is suitable for business scenarios where data values tend to saturate. The other is a linear trend term with change points. It is suitable for business scenarios with a steady increase or decrease. According to the nature of the traffic data, a linear trend function with change points is used in this paper. The equation is defined as follows:

g(t)=(k+a(t)Tδ)t+(m+a(t)Tγ)(3)

where k+a(t)Tδ denotes the growth rate, m+a(t)Tγ denotes the corresponding offset parameter, and δ denotes the change in growth rate at the turning point.

Regarding the periodic term, the Prophet model constructs a flexible periodic model based on the Fourier series, which can customize with seasonal factors for different granularity of periodic term extraction. The equation of the model is

s(t)=∑n=1N(ancos⁡(2πntP)+bnsin⁡(2πntP))(4)

where, P denotes the period length of the time series, n denotes the number of periods, an and bn denotes the parameters to be estimated. In this paper, we focus on two different periodic granularities, i.e., daily, and weekly. By extracting two different granularity periods to observe the characteristics of traffic data, we can analyze and summarize their period variation rules.

After determining the corresponding functions of trend and periodic terms, the historical network traffic data are decomposed into periodic and non-periodic terms by the Prophet model. And then the predicted value s~(t+l) of the periodic term at the time t+l predicted by the Prophet model, i.e., dailyt+l+weeklyt+l, which is used for further prediction subsequently.

4.2 EALSTM Prediction of Non-Periodic Term

Time series prediction of features is usually performed using sliding time windows. However, the ability of LSTM to focus on each feature in a sub-window over multiple time steps is limited. Therefore, EALSTM model [21] is used for prediction of non-periodic term. In EALSTM, an attention mechanism is introduced to assign weights to the features within each specific time step in the network traffic sequence. Then the input data with different weights are sent to the LSTM network for training. To achieve better prediction results, the attention layer feature weights are solved using a competing random search (CRS) algorithm based on the idea of evolutionary computation. It replaces the original gradient-based method to avoid falling into local optima or premature convergence. The overall structure of EALSTM is shown in Fig. 2. The left part represents the competitive random search process. The right part is the evolutionary attention-based LSTM.

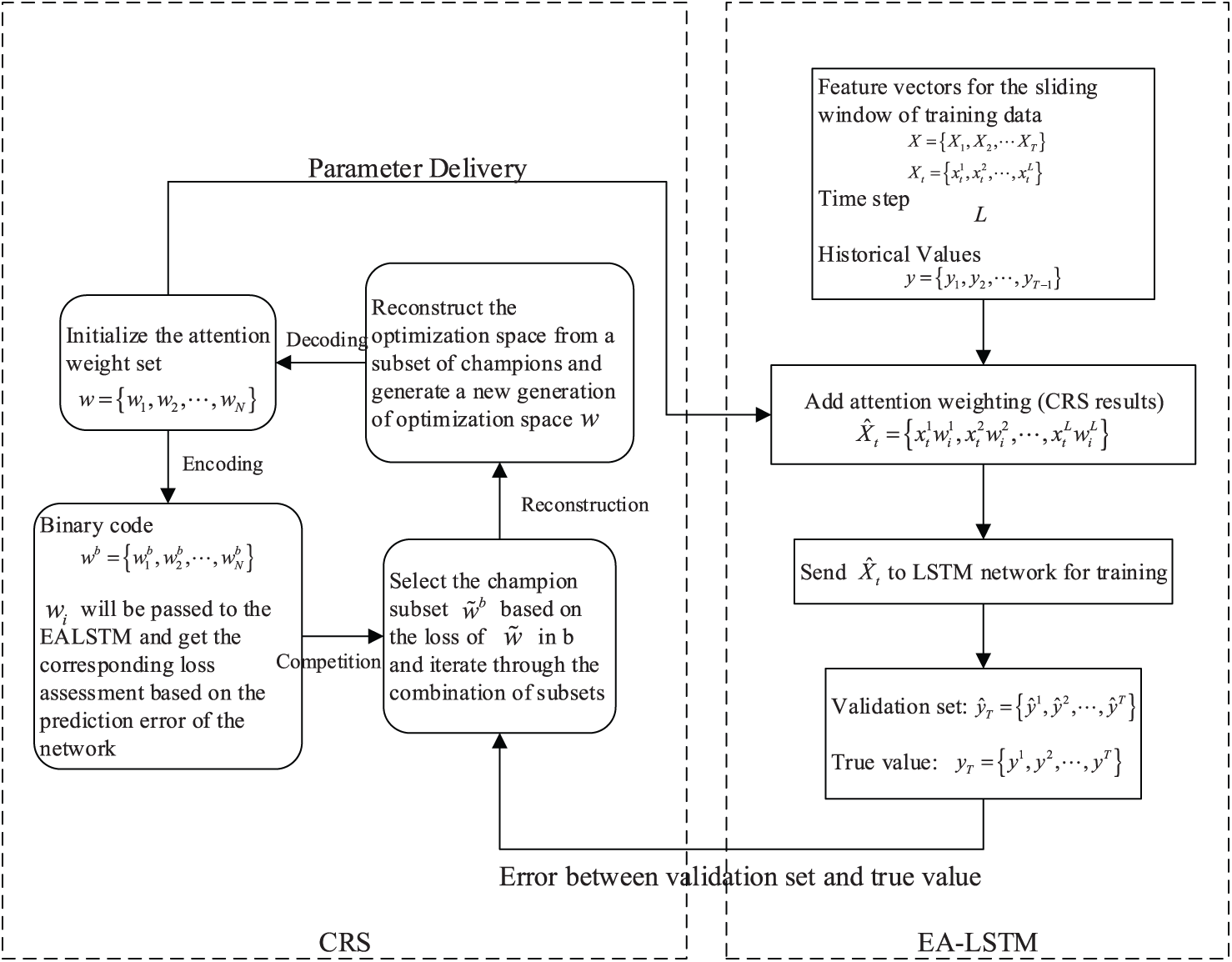
Figure 2: The overall structure of EALSTM

The EALSTM and CRS use a co-training mechanism where the two components share parameter and loss feedback. The attention weights generated by CRS will be used to determine the input attention layer before the LSTM starts training. In addition, the prediction error of the LSTM network on the validation set will be used for individual ranking meritocracy of the parameters in the competitive random search.

In the evolutionary attention-based LSTM model, the data is first preprocessed, i.e., data normalized. Normalizing the data can accelerate the convergence of the model and effectively prevent the gradient disappearance and explosion of the model. The non-periodic term data is linearly transformed so that its values are mapped between 0 and 1. After normalizing the data, the different features within the sliding window are assigned weights and fed into the LSTM model for training. In this paper, we use the Keras framework to build a two-layer LSTM network model. The optimization algorithm used in the neural network training is Adam, and the loss function uses the mean square error. After adding the attention layer, the computational process of the whole model is

it=σ(wxiX^t+whiht−1+wcict−1+bi)

ft=σ(wxfX^t+whfht−1+wcfct−1+bf)

ct=ftct−1+ittan⁡h(wxcX^t+whcht−1+bc)

ot=σ(wxoX^t+whoht−1+wcoct−1+bo)

ht=ottan⁡h(ct)(5)

where σ(⋅) denotes the sigmoid activation function and the matrix w with double subscripts denotes the connection weights between the two cells. In addition, it, ft, ct, ot and ht denote the input gate, forget gate, computational unit, output gate, and the intermediate state of the hidden layer at the current time step, respectively. The final output value is

y^T={y^1,y^2,…,y^T}(6)

where y^t=ht−1.The important point of the competitive stochastic search is the introduction of the prediction error in the EALSTM model, whose solution process can be defined as

min L(y^T(Φ(M,w)),yT)(7)

where M is the entire set of parameters in the LSTM and Φ(⋅) is the parameter space required to obtain the predicted value y^T. The process of CRS in this paper can be referred to the left part in Fig. 2 and is no longer described in detail.

4.3 GPR Prediction of Residual Term

The remaining part is called the residual term by subtracting the EALSTM prediction results from the non-periodic term. We use GPR to predict the residual term to further improve the accuracy of the traffic and learn the noise from the training data efficiently.

According to the central limit theorem, the residual term is mostly random fluctuations and obeys Gaussian distribution with high probability. GPR is a nonparametric probabilistic model based on a Bayesian approach. The purpose of regression is to learn samples that have been trained to obtain a mapping relationship f(X) between input and output. The test set Xtest can be used to predict the corresponding value Ytest. In the GPR model, the regression function f(X) is a Gaussian process uniquely described by its mean function μ(X) and covariance function k(X,X′). It can be expressed by f(X)∼GP(η(X),k(X,X′)).

In this paper, for computational simplicity, the mean function is usually taken to be 0. We input the training set X={x1,x2,…,xt} into the model for training, and then obtain the prior distribution of the output value Y, i.e., Y∼N(μY,KYY).

From the definition of the Gaussian process, joint distribution of any finite number of random variables in the Gaussian process obeys Gaussian distribution. Then for the test set of Xtest, its corresponding function value Ytest and the joint distribution of the output value Y also obey Gaussian distribution, then we can get

[YYtest]∼N(0,[KYYKYYtestKYYtestTKYtestYtest])(8)

where KYY is the covariance matrix of the training set, KYYtest, KYYtestT is the covariance matrix between the test set and the training set, and KYtestYtest is the covariance matrix of the test set. Based on the nature of the multi-dimensional Gaussian distribution, then the posterior distribution of Ytest can be obtained as

Ytest∼N(KYYtestTKYY−1Y,KYY−KYYtestTKYY−1KYYtest)(9)

From the above equation, the Gaussian process is determined only by the covariance function, i.e., the kernel function. The kernel function is the core of a Gaussian process and determines its properties. In this paper, the squared exponential function is chosen for the kernel function. Once the model is trained, the residual term prediction r~(t+l) for time t+l can be calculated.

The final prediction results are obtained by adding the results of different granularity cycles of Prophet prediction, EALSTM prediction results and Gaussian process regression results.

5  Experiments

5.1 Data Selection and Processing

In this paper, the Milan traffic dataset [22] is used for network traffic prediction. This dataset, collected by Telecom Italia, records call detail record (CDR) data generated by the network of the city of Milan for two months between November 1, 2013, and January 1, 2014, with a 10-min interval between recordings.

There are different types of Call Detail Records (CDR). Telecom Italia mainly records the following activities: incoming SMS, outgoing SMS, incoming calls, outgoing calls, and Internet. In this paper, the main network traffic prediction is Internet data, while the other CDRs are used as multivariate input data to predict traffic when non-periodic term is predicted. Traffic volumes for specific time intervals within certain grids are lost due to data storage errors, so data preprocessing should be completed before performing service prediction. In this paper, a mean-fill approach is used, i.e., missing values are filled using their data mean values.

5.2 Experimental Settings

In the experiments, 85% and 15% of the time series traffic data were used as the training and test sets, respectively. In this paper, we set the prediction time as one day and the time interval as 10 min.

First, the Prophet model is initialized. We set the period term to weekly seasonality vs. daily seasonality to observe distribution trend with different granularity periods. The trend model flexibility is set to 0.1 to increase the model’s fit to historical data and make the trend more flexible. Then initialize the EALSTM model. The EALSTM model parameters are shown in Table 1. The batch size is the number of samples selected for one training session. The number of Epochs indicates the number of training iterations for all batches in the forward and backward propagation of the network. The number of hidden cells is the size of the hidden layers within the EALSTM cells. Adam optimizer updates neural network weights iteratively based on training data.

5.3 Experimental Results

5.3.1 Prediction Results

In this paper, the proposed model predicts the traffic in three steps, which includes Prophet model predicting the periodic term with different granularity, EALSTM model predicting the non-periodic term and GPR model predicting the residual term. The results of the three steps are summed to obtain the predicted value.

As we can observed from Fig. 3 that the proposed Prophet-EALSTM-GPR can predict traffic well. The proposed model is more sensitive to data decreasing trends compared to data increasing trends. Note that the prediction results’ accuracy is excellent for traffic values below 10. In general, the performance of the proposed model is better than most models.

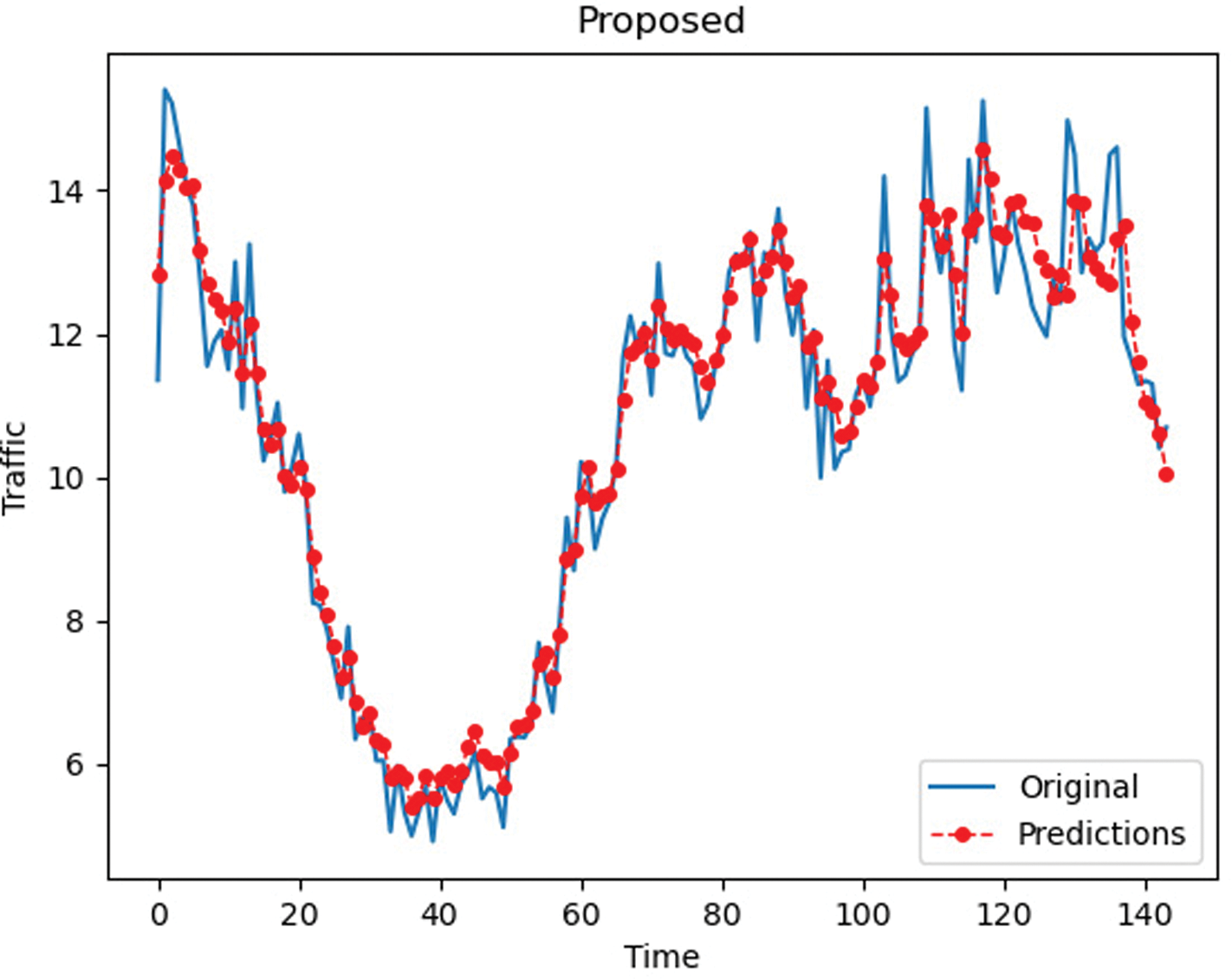
Figure 3: Prediction results of the proposed model

5.3.2 Comparison Between Different Models

In this paper, we chose four different baseline methods, i.e., Prophet, ARIMA, LSTM, and EALSTM, to evaluate the performance of the proposed model. The performance of the above baseline algorithm is shown in Fig. 4 respectively.

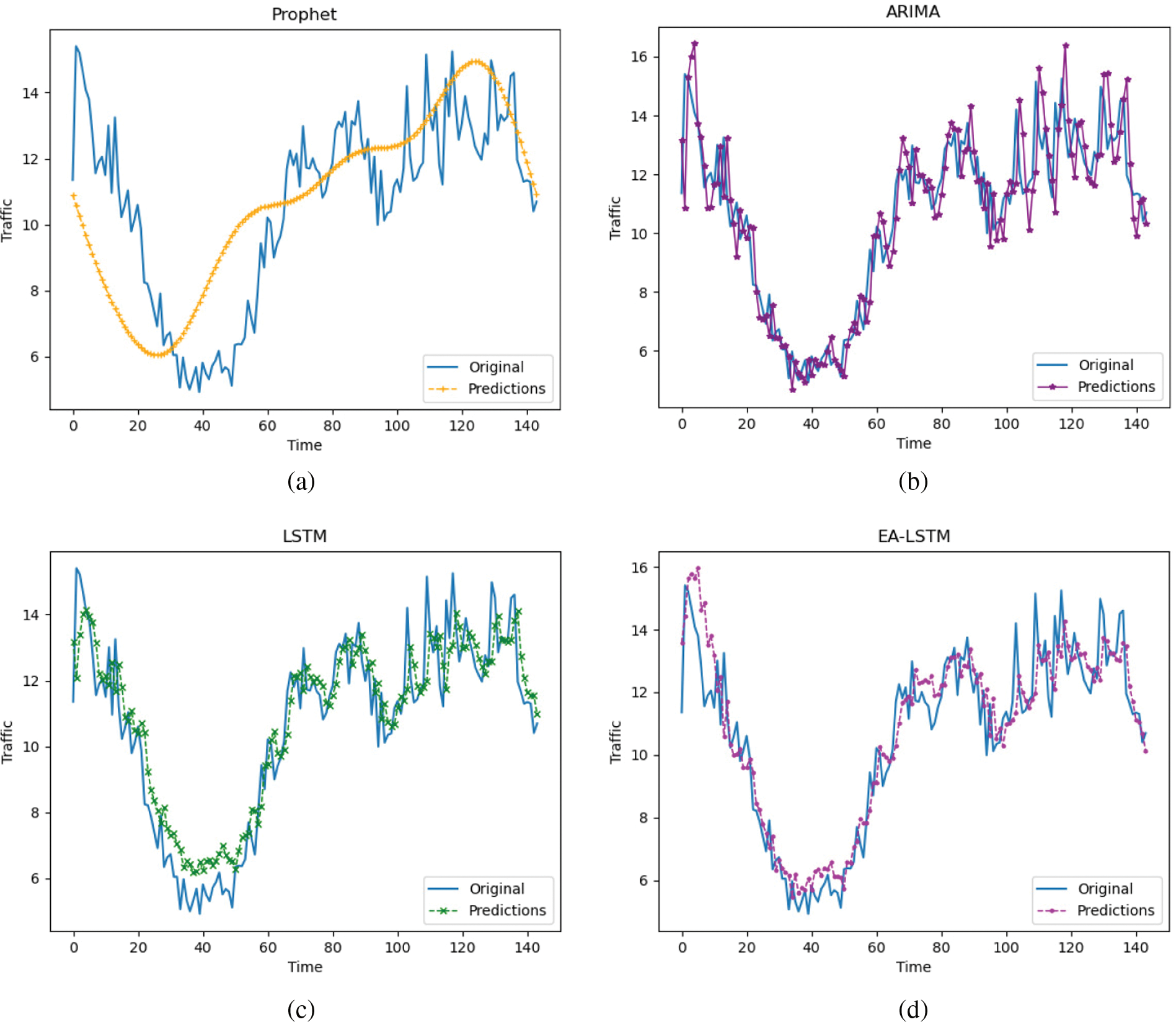
Figure 4: Prophet model, ARIMA model, LSTM model and EALSTM model prediction curves

As shown in Fig. 4a, the Prophet model predicts poorly and does not correctly reflect the frequent fluctuations of the data, resulting in some predicted values being too high or too low.

As shown in Fig. 4b, the ARIMA model predicts better than the Prophet model, which provides predictions that are consistent with the real data’s fluctuations. However, although the prediction accuracy is higher for lower traffic, the prediction accuracy is lower for more fluctuating traffic.

As shown in Fig. 4c, the LSTM model is less sensitive to the overall data trend than the linear model, and it fails to reflect the decline in traffic over time accurately. This is because the LSTM predicted values are influenced by the previous input values, i.e., the LSTM model is time dependent. In addition, the LSTM prediction results have the disadvantage of lagging due to the autocorrelation in the time series.

As shown in Fig. 4d, the EALSTM model prediction results are somewhat optimized for the lagging disadvantage compared with the LSTM, but there is still a non-trivial error. Therefore, in this paper, the proposed model uses the GPR model to overcome this problem further. Generally, the performance of a single algorithm can’t predict traffic accurately.

Table 2 demonstrates the evaluation metrics of the proposed model compared with the four baseline models.

As shown in Table 2, several other models have a significant advantage in prediction compared to the Prophet model. This is because that the Prophet model is simple, easy to underfit, and has much less prediction accuracy for nonlinear characteristic of network traffic nowadays. By comparing RSME, MAE and R2, the proposed Prophet-EALSTM-GPR outperforms other baseline algorithms. The reasons are as follows. First, the Prophet model is suitable for dealing with periodic data with outliers and trend changes, and it has the multifractal property of extracting traffic data. Second, using EALSTM to predict non-periodic terms can help capture long-term dependence on the one hand; and assign more weights to important features on the other hand. Third, GPR can recover the residual components to further accurate prediction results.

Overall, the proposed model can predict network traffic values more accurately when compared with the four baseline methods.

6  Conclusion

In this paper, we propose a traffic prediction scheme based on Prophet-EALSTM-GPR to predict network traffic and improve traffic prediction accuracy. We first decompose the traffic data into periodic and non-periodic terms using the Prophet model. The non-periodic term is fed into an EALSTM-based network to extract the features in the sequences and learn their long correlations. To further improve the prediction accuracy, GPR is used to predict the residual terms. Experiments are conducted on the Milan public dataset to verify the effectiveness of the proposed scheme, and the results show that the scheme can significantly improve prediction accuracy.

In this paper, only the temporal correlation of network traffic data is considered, and its spatial correlation is not considered. In the future, it is more practical to consider the temporal correlation in combination with the spatial correlation, which is more beneficial to predict the traffic data. In addition, future research can analyze the factors affecting network traffic to better understand the time-series traffic data.

Funding Statement: This work was supported by the National Natural Science Foundation of China under Grant Number No. 62271264 and 61972207, and the Project through the Priority Academic Program Development (PAPD) of Jiangsu Higher Education Institution.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. Y. He, Y. Yang, B. Zhao, Z. Gao and L. Rui, “Network traffic prediction method based on multi-channel spatial-temporal graph convolutional networks,” in IEEE 14th Int. Conf. on Advanced Infocomm Technology (ICAIT), Chongqing, China, pp. 25–30, 2022. [Google Scholar]

    2. C. Zhang, H. Zhang, D. Yuan and M. Zhang, “Citywide cellular traffic prediction based on densely connected convolutional neural networks,” IEEE Communications Letters, vol. 22, no. 8, pp. 1656–1659, 2018. [Google Scholar]

    3. Y. Xu, F. Yin, W. Xu, J. Lin and S. Cui, “Wireless traffic prediction with scalable Gaussian process: Framework, algorithms, and verification,” IEEE Journal on Selected Areas in Communications, vol. 37, no. 6, pp. 1291–1306, 2019. [Google Scholar]

    4. J. Zhou, T. Han, F. Xiao, G. Gui, B. Adebisi et al., “Multi-scale network traffic prediction method based on deep echo state network for internet of things,” IEEE Internet of Things Journal, vol. 9, pp. 21862–21874, 2022. [Google Scholar]

    5. F. Tang, Z. M. Fadlullah, B. Mao and N. Kato, “An intelligent traffic load prediction-based adaptive channel assignment algorithm in SDN-IoT: A deep learning approach,” IEEE Internet of Things Journal, vol. 5, no. 6, pp. 5141–5154, 2018. [Google Scholar]

    6. F. Acun and E. A. Gol, “Traffic prediction on large scale traffic networks using ARIMA and K-means,” in 29th Signal Processing and Communications Applications Conf. (SIU), Istanbul, Turkey, pp. 1–4, 2021. [Google Scholar]

    7. H. Liu, L. T. Yang, J. Chen, M. Ye, J. Ding et al., “Multivariate multi-order markov multi-modal prediction with its applications in network traffic management,” IEEE Transactions on Network and Service Management, vol. 16, no. 3, pp. 828–841, 2019. [Google Scholar]

    8. N. K. ChikkaKrishna, P. Rachakonda and T. Tallam, “Short-term traffic prediction using Fb-PROPHET and neural-PROPHET,” in IEEE Delhi Section Conf. (DELCON), New Delhi, India, pp. 1–4, 2022. [Google Scholar]

    9. W. Jiang, “Cellular traffic prediction with machine learning: A survey,” Expert Systems with Applications, vol. 201, pp. 117–163, 2022. [Google Scholar]

  10. H. Lu and F. Yang, “A network traffic prediction model based on wavelet transformation and LSTM network,” in IEEE 9th Int. Conf. on Software Engineering and Service Science (ICSESS), Beijing, China, pp. 1–4, 2018. [Google Scholar]

  11. L. Chen, “The multi-task time-series graph network for traffic congestion prediction,” in MLMI ’20: The 3rd Int. Conf. on Machine Learning and Machine Intelligence, New York, NY, USA, pp. 19–23, 2020. [Google Scholar]

  12. Y. Liu, J. J. Q. Yu, J. Kang, D. Niyato and S. Zhang, “Privacy-preserving traffic flow prediction: A federated learning approach,” IEEE Internet of Things Journal, vol. 7, no. 8, pp. 7751–7763, 2020. [Google Scholar]

  13. S. Guo, Y. Lin, N. Feng, C. Song, and H. Wan, “Attention based spatial-temporal graph convolutional networks for traffic flow forecasting,” Proceedings of the AAAI Conference on Artificial Intelligence, vol. 33, no. 1, pp. 922–929, 2019. [Google Scholar]

  14. Z. He, C. -Y. Chow and J. -D. Zhang, “STNN: A spatio-temporal neural network for traffic predictions,” IEEE Transactions on Intelligent Transportation Systems, vol. 22, no. 12, pp. 7642–7651, 2021. [Google Scholar]

  15. Y. Wang, J. Zheng, Y. Du, C. Huang and P. Li, “Traffic-GGNN: Predicting traffic flow via attentional spatial-temporal gated graph neural networks,” IEEE Transactions on Intelligent Transportation Systems, vol. 23, pp. 1–10, 2022. [Google Scholar]

  16. J. Zhang, Y. Zheng, J. Sun and D. Qi, “Flow prediction in spatio-temporal networks based on multitask deep learning,” IEEE Transactions on Knowledge and Data Engineering, vol. 32, no. 3, pp. 468–478, 2020. [Google Scholar]

  17. K. L. Li, C. J. Zhai and J. M. Xu, “Short-term traffic flow prediction using a methodology based on ARIMA and RBF-ANN,” in Chinese Automation Congress (CAC), Jinan, China, pp. 2804–2807, 2017. [Google Scholar]

  18. S. Du, Z. Xu and J. Lv, “An EMD- and GRU-based hybrid network traffic prediction model with data reconstruction,” in IEEE Int. Conf. on Communications Workshops (ICC Workshops), Montreal, QC, Canada, pp. 1–7, 2021. [Google Scholar]

  19. A. Bayati, K. -K. Nguyen and M. Cheriet, “Gaussian process regression ensemble model for network traffic prediction,” IEEE Access, vol. 8, pp. 176540–176554, 2020. [Google Scholar]

  20. W. Wang, C. Zhou, H. He, W. Wu, W. Zhuang et al., “Cellular traffic load prediction with LSTM and Gaussian process regression,” in IEEE Int. Conf. on Communications (ICC), Dublin, Ireland, pp. 1–6, 2020. [Google Scholar]

  21. Y. Li, Z. Zhu, D. Kong, H. Han and Y. Zhao, “EA-LSTM: Evolutionary attention-based LSTM for time series prediction knowledge based systems,” Knowledge-Based Systems, vol. 181, pp. 104785, 2019. [Google Scholar]

  22. G. Barlacchi, M. De Nadai and R. Larcher, “A multi-source dataset of urban life in the city of milan and the province of trentino,” Scientific Data, vol. 2, pp. 150055, 2015. [Google Scholar]