Analysis of Innovative Quantum Optimization Solutions for Shor’s Period Finding Algorithm Applied to the Computation of

1  Introduction

In the rapidly evolving field of quantum computing, Shor’s algorithm has emerged as a groundbreaking solution for efficient integer factorization, profoundly impacting cryptographic security. However, the algorithm’s efficacy hinges on the computationally demanding step of period finding, which presents significant challenges. This article explores quantum optimization solutions designed to enhance the efficiency of Shor’s period-finding algorithm, focusing particularly on the quantum development environments Qiskit and Cirq.

The investigation focuses on three prominent tools: Qiskit Transpiler, BQSKit, and Mitiq. Key performance metrics include execution time, precision, resource utilization, quantum gate count, circuit synthesis optimization, error mitigation, and qubit fidelity. Through rigorous case studies, we highlight the unique strengths and limitations of each tool, providing valuable insights into their potential impact on integer factorization and cybersecurity. Beyond emphasizing the crucial role of quantum optimization, our findings lay the foundation for future developments in enhancing quantum algorithms, especially within the Qiskit and Cirq quantum development environments.

2  Main Contributions

This study makes several significant contributions to the optimization of Shor’s algorithm, taking into account the constraints of current quantum computers (Noisy Intermediate-Scale Quantum). Contributions can be enumerated as follows:

1. Comparative analysis of quantum optimization tools

An in-depth analysis of three key tools to optimize quantum circuits was conducted. Qiskit Transpiler, BQSKit, and Mitiq. The evaluation of these tools was performed according to several criteria, including circuit depth reduction, quantum gate minimization, error mitigation, and hardware compatibility. This comparative analysis offers a practical guide for selecting the most suitable techniques for future implementations of the Shor’s algorithm.

2. Interoperable adaptation between quantum environments

We demonstrated the possibility of adapting an algorithm designed in Cirq to be executed in Qiskit, taking advantage of the strengths of both environments. This interoperable adaptation exemplifies a pragmatic approach to leveraging the collective capabilities of multiple optimization tools.

3. Circuit depth reduction through optimization

The employment of optimization levels in Qiskit Transpiler has yielded a substantial decrease in the circuit depth required for Shor’s algorithm. This optimization enhances the robustness of the algorithm on noisy quantum computers and reduces the effects of decoherence.

4. Noise mitigation using mitiq

To address the limitations of contemporary quantum computers, the Zero Noise Extrapolation (ZNE) technique, available in Mitiq, was applied to mitigate errors in the algorithm’s results. The analysis demonstrates a substantial enhancement in the fidelity of the computations, underscoring the efficacy of this approach in optimizing precision on Noisy Intermediate-Scale Quantum (NISQ) devices.

5. Exploration of tool limitations

We identified specific limitations of BQSKit, including the absence of support for “reset” gates and intermediate measurements. We then proceeded to analyze the impact of these limitations on the optimization of Shor’s algorithm. To address these limitations, we have proposed workarounds, including the modification of circuits to adapt to these constraints.

6. Experimental validation on real quantum hardware

In contrast to purely theoretical approaches, our implementations were tested on a real quantum computer, the IBM “Ibm_kyoto.” This practical validation enables the assessment of the actual performance of the proposed optimization techniques, providing the community with useful empirical data.

Impact of these contributions

These contributions serve to enhance comprehension and efficacy of optimization methodologies for Shor’s algorithm, while simultaneously providing pragmatic solutions to the challenges presented by contemporary quantum platforms. The present study establishes the foundation for future advancements in the practical application of Shor’s algorithm and quantum algorithms in general by employing systematic analysis, a range of tools, and experimental validations.

A fundamental review of Shor’s algorithm is imperative to comprehend the underlying principles and the challenges associated with its optimization in the context of contemporary quantum computers.

3  Fundamentals of Shor’s Algorithm

In this section, we will explore the foundational principles of Shor’s algorithm, offering a comprehensive overview of its operational mechanisms and revisiting the fundamental concepts that underpin it, including period finding.

3.1 General Overview of Shor’s Algorithm

Shor’s algorithm, developed by the American mathematician Shor in 1994 [1], is a quantum algorithm that has been identified as a significant breakthrough in the field. This algorithm was designed to efficiently solve the integer factorization problem on a quantum computer in polynomial time. This achievement is significant because integer factorization is recognized as a challenging problem for classical computers. Furthermore, it forms the basis for many cryptographic protocols, such as RSA encryption. Shor’s algorithm consists of two main components:

•      Reduction the factorization problem to an order-finding problem, which can be performed on a classical computer.

•      A quantum algorithm that solves the order-finding problem.

As demonstrated by the algorithm, the order-finding component requires the use of a quantum computer, while all other components can be efficiently executed on a classical computer [1,2].

Having established the general framework of Shor’s algorithm, we proceed to present the detailed process that reformulates the integer factorization problem into a period-finding problem, as described below Algorithm 1.

Having demonstrated how the factorization problem can be reduced to a period-finding problem, the following investigation explores the application of quantum mechanics to efficiently solve this critical step using the period-finding algorithm.

3.2 Period Finding

The term “order” of an integer a modulo N is defined as the smallest positive integer r such that ar≡1(modN) [1]. Mathematically, this is expressed as:

r=mink>0,such that,ak≡1(modN)(1)

The order r of integer a modulo N represents the smallest period of the function k→fak(modN). Building on this concept, we now examine how quantum computing enables the efficient determination of this order [2,3].

•      Initialization: Choose an integer a that is relatively prime to N and a quantum register of n qubits in the state |0⟩⊗n.

•      Superposition: Apply the quantum Fourier transform 𝒬ℱ𝒯 to create a superposition of states |y⟩=1N∑k=0N−1e2πiky/N|k⟩ on the quantum register, where y is a superposition variable.

•      Controlled operation: Use the controlled operation Ua to implement the quantum operation |y⟩→|aymodN⟩.

•      Inverse quantum Fourier transform: Apply the inverse of the quantum Fourier transform 𝒬ℱ𝒯−1 to the quantum register to obtain |f(y)⟩=1N∑k=0N−1e−2πik(aymodN)/N|k⟩.

•      Measurement: Measure the quantum register to obtain the result k. The measurement result estimates the period r of the function f(y).

•      Period calculation: Use the estimated value of k to calculate an estimate of the period.

The period-finding step is a critical component that distinguishes Shor’s algorithm from its counterparts. When executed efficiently, it can result in significant advancements in integer factorization and cybersecurity. This section outlines the fundamental principles necessary to understand how the quantum optimization solutions discussed later can enhance this pivotal step of the algorithm.

Following the foundational discussion of Shor’s algorithm, it is essential to explore the quantum development environments used for its implementation. This exploration aims to provide a deeper understanding of the tools and platforms that enable its optimization.

4  Quantum Development Environments

The implementation of Shor’s period-finding algorithm was conducted using two Python-based quantum programming frameworks: Qiskit and Cirq. These libraries provide a comprehensive suite of advanced tools for programming quantum algorithms, enabling efficient and flexible implementation of quantum circuits.

4.1 Overview of the Qiskit Library as a Quantum Programming Language

Qiskit is an open-source library developed by IBM Quantum, designed for creating, simulating, and executing quantum circuits. In this study, Qiskit was utilized for two primary purposes: first, to design the quantum circuit for Shor’s period-finding algorithm, and second, to optimize its implementation. The primary Qiskit classes utilized in this implementation include [4]:

•      QuantumCircuit, QuantumRegister, ClassicalRegister: These classes facilitate the construction and manipulation of quantum circuits.

•      qasm_simulator: The qasm_simulator is one of the simulators provided by Qiskit, allowing for the simulation of quantum circuit execution on classical computer. It is widely used to evaluate quantum circuit performance, facilitating rapid testing and optimization of algorithms before deployment on actual quantum hardware.

•      IBMProvider: This class is used to interact with IBM Quantum’s real quantum computers.

This combination of Qiskit classes and tools, ranging from simulators to access to real quantum hardware, creates a robust and comprehensive environment for the development and evaluation of quantum algorithms.

4.2 Preparation of the Cirq

Cirq is an open-source Python library developed by Google Quantum, designed to facilitate the creation, manipulation, and optimization of quantum circuits, as well as their execution on quantum computers and simulators. In this study, Cirq is used alongside Qiskit to investigate specific quantum optimizations tailored to Shor’s period-finding algorithm. Cirq provides powerful abstractions for addressing the challenges posed by noisy intermediate-scale quantum (NISQ) devices, where hardware specifications play a critical role in achieving state-of-the-art results [5].

4.3 Real Quantum Computer

To evaluate the performance of Shor’s period-finding algorithm, the researchers executed their implementation on a real quantum computer. For this study, the 127-qubit IBM Quantum computer, named “Ibm_kyoto”, was selected. This quantum computer is part of the IBM Quantum Experience network and utilizes superconducting qubits for quantum operations. Access to the system is provided through the IBM Quantum API and the IBMProvider class in Qiskit. The key characteristics of this quantum computer are as follows [4]:

•      128 Quantum Volume (QV): Quantum Volume is a performance metric for quantum computers, independent of their underlying technology.

•      5K CLOPS (Circuit Layer Operations Per Second): This metric quantifies the number of circuit layers a Quantum Processing Unit (QPU) can execute per second, reflecting its computational throughput.

•      3.6 EPLG (Error Per Layered Gate for a 100-Qubit Chain): This measures the fidelity or precision of each quantum gate operation, indicating how closely the implemented gate approximates an ideal quantum gate.

•      Processor Eagle r3: Quantum processors represent information in quantum form using qubits. The Eagle r3 is a 127-qubit processor and one of IBM Quantum’s most advanced and efficient processors.

4.4 Shor’s Algorithm in Qiskit

In this study, the quantum implementation of Shor’s algorithm was meticulously adapted for the factorization of a specific number (15, as specified by Qiskit). The code used in this investigation is accessible via the following link: https://github.com/qiskit-community/qiskit-community-tutorials/blob/master/algorithms/shor_algorithm.ipynb (accessed on 11 March 2025).

The provided code implements a dynamic quantum circuit [6] for Shor’s algorithm, specifically designed to factorize the number 15 using Qiskit. The algorithm utilizes the QuantumCircuit, QuantumRegister, and ClassicalRegister classes from Qiskit. In the circuit_amod15 function, controlled-swap gates (cswap) and controlled-X gates (CX) are applied based on the selected value of ‘a’ (2, 7, 8, 11, or 13). These operations simulate the computation of ax mod 15 as part of Shor’s algorithm. The circuit_aperiod15 function initializes a qubit to the state |1⟩ and applies a series of quantum operations to simulate Shor’s algorithm. It utilizes the circuit_amod15 function for the modular computation part. Operations include Hadamard gates, controlled-X gates (CX), controlled phase gates (P), and conditional measurements. Finally, the quantum circuit is visualized using the shor.draw(output=‘mpl’) command (Fig. 1) [7].

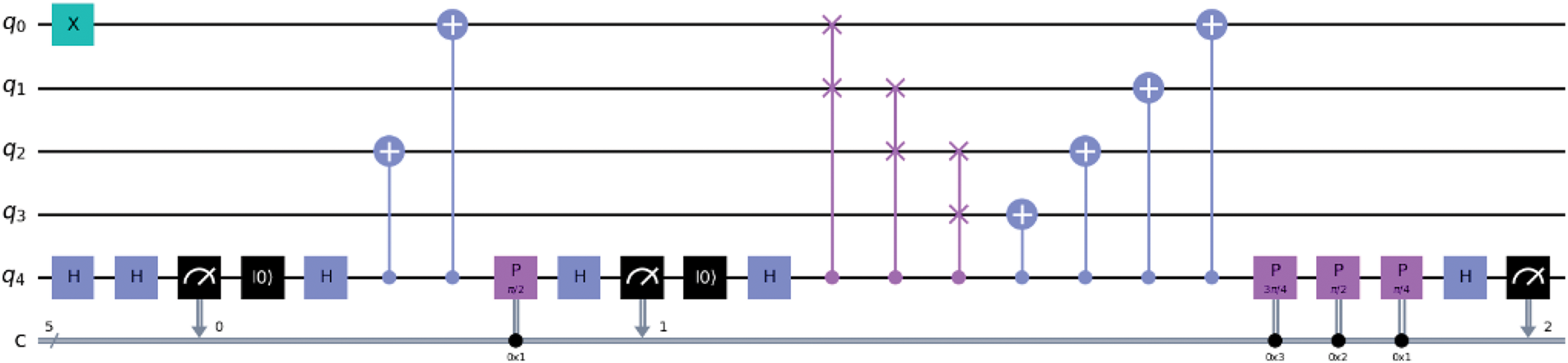
Figure 1: Illustration of a quantum circuit resulting from the execution of Shor’s quantum algorithm with 15 as the number to factor and 7 an integer coprime with 15 (7x mod 15)

The following discussion focuses on optimization techniques for this circuit. A detailed exploration of various optimization approaches will provide deeper insights into maximizing the utilization of available quantum resources. This, in turn, will contribute to the development of more robust and efficient solutions in the field of quantum computing [8].

Before presenting the optimization techniques applied to Shor’s algorithm in this study, a review of prior work in this domain is provided.

5  Previous Work on Quantum Optimization of Shor’s Algorithm

Shor’s algorithm, introduced by Peter Shor in 1994, revolutionized the field of cryptography by providing an efficient quantum approach for factoring large integers. Since its inception, subsequent research has focused on improving the algorithm’s practicality for implementation on modern quantum computers.

Reduction of quantum resources

A primary challenge in implementing Shor’s algorithm is the requirement of substantial resources, especially in terms of qubits and circuit depth. To address this challenge, researchers have proposed hybrid approaches that integrate quantum and classical resources. One such approach is the distributed hybrid quantum-classical algorithm, which aims to reduce the number of qubits required by distributing the computations between multiple quantum and classical processors. This approach also employs classical programs to correct potential errors [9].

Optimization of classical simulations

Given the current limitations of quantum hardware, classical simulations of Shor’s algorithm continue to play a critical role in evaluating and refining its implementations. In this context, techniques such as matrix product states (MPS) have been explored to improve the efficiency of these simulations. This approach has demonstrated the ability to effectively manage quantum entanglement, significantly reducing the computational resources required to simulate the algorithm for systems with a large number of qubits [10].

Improving the precision of continued fractions

A critical step in Shor’s algorithm involves the use of continued fractions to determine the periods required for factorization. Recent research has proposed methods to improve the precision of this step by refining the results obtained. Enhancements to the continued fraction algorithm have demonstrated increased efficacy, even when initial estimates are imperfect [11].

Quantum circuit optimization

The complexity of quantum circuits used in Shor’s algorithm can impede its practical implementation. Efforts have been made to optimize these circuits, notably by reducing the number of quantum gates and the circuit depth. These optimizations are designed to adapt the algorithm to the capabilities of contemporary quantum computers, thereby improving its efficiency and feasibility [12].

A review of the extant literature reveals a persistent dedication among researchers to surmounting the obstacles inherent in the implementation of Shor’s algorithm. Hybrid approaches, improvements in classical simulations, refinement of continued fraction methods, and quantum circuit optimization are promising avenues for making Shor’s algorithm more accessible and efficient on current and future quantum platforms.

6  Optimization Techniques for Quantum Circuits

6.1 Qiskit_Transpiler Library

Transpilation is the process of rewriting a given input circuit to match the topology of a specific quantum device and/or to optimize the circuit for execution on current noisy quantum systems [13].

In order to achieve compatibility with a given target device and optimize them to mitigate the effects of noise on the obtained results, most circuits must undergo a series of transformations. The process of rewriting quantum circuits to align with hardware constraints and enhance performance optimization can be a complex undertaking. The logic flow in the rewriting toolchain is not required to be linear; it can often involve iterative sub-loops, conditional branches, and other complex behaviors. The ensuing discourse will present the outcomes of empirical investigations, underscoring the quantifiable enhancements that can be realized in the implementation of Shor’s algorithm through a triad of systematic steps.

6.1.1 Distribution Step

Quantum circuits are abstract constructs where qubits serve as “virtual” representations of the physical qubits used in computations. A crucial step in implementing these circuits is the ability to uniquely map these virtual qubits onto the “physical” qubits of an actual quantum device. This process relies on predefined pass managers, which employ various methodologies to identify the optimal mapping. Typically, this involves two steps: first, searching for a “perfect” mapping, one that requires no swap operations, and second, applying a heuristic pass to determine the best possible mapping if a perfect one cannot be achieved.

The subsequent discussion will focus on the layouts automatically selected at different levels of optimization. The returned circuits are annotated with this initial layout information, which can be visually displayed to illustrate the layout selection process.

As illustrated in Fig. 2, the layout was obtained using optimization level 0. The configuration suggests that the initial five qubits were employed for the mapping of the circuit. However, it is important to note that this layout may not be optimal, as optimization level 0 does not involve any specific mapping selection process.

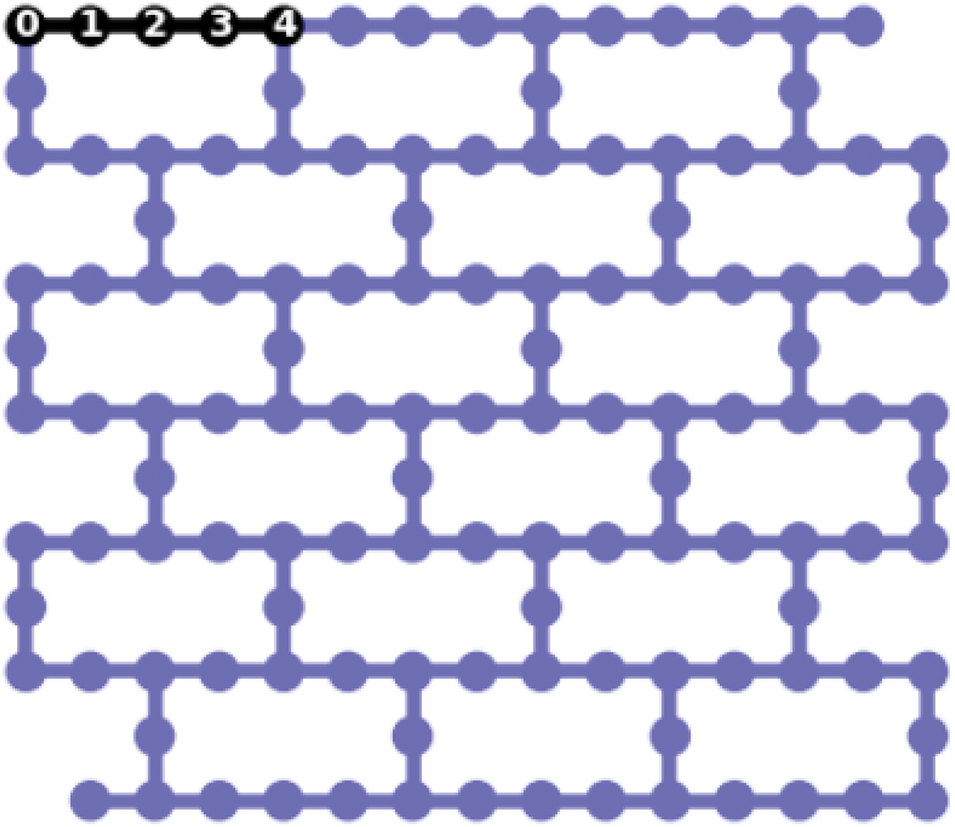
Figure 2: Layout using optimization level 0

To determine the optimal layout, it is necessary to compare the output circuit depth results for the three optimization levels (Figs. 3–5).

Figure 3: Layout using optimization level 1

Figure 4: Layout using optimization level 2

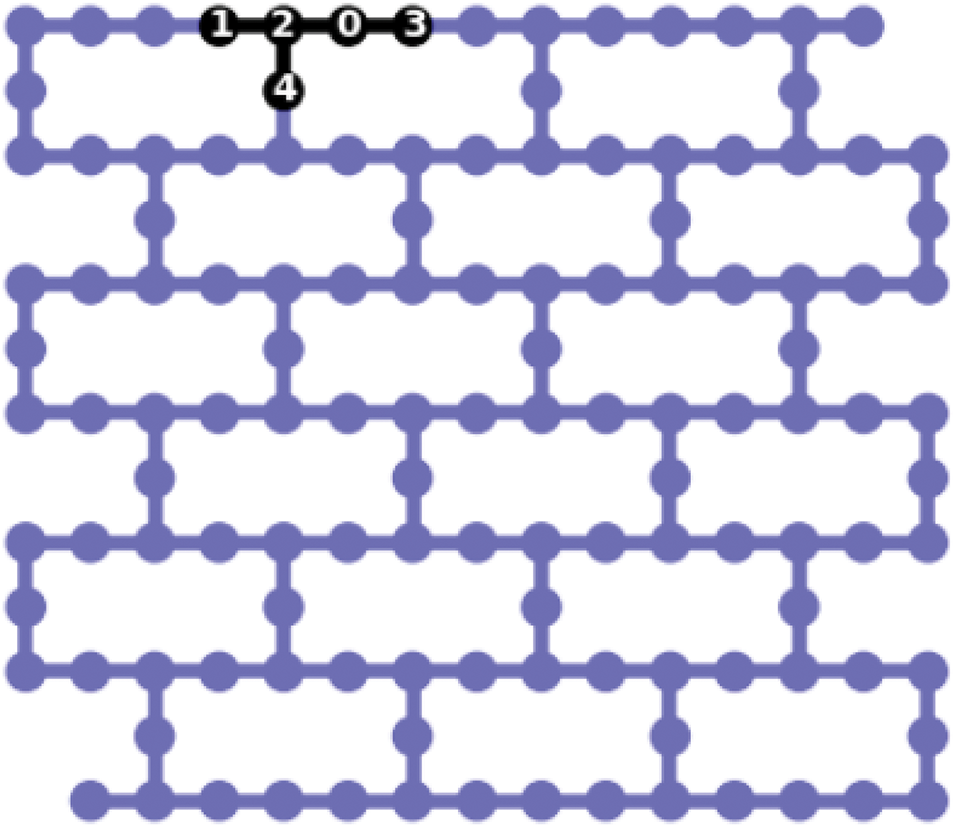
Figure 5: Layout using optimization level 3

6.1.2 Routing Step

It is evident that most circuits will exhibit a depth distribution, though typically not as extensive as the one observed in this study. This variability stems from the stochastic nature of the default swap mapper. Clearly, the goal is to achieve the most optimal circuit, especially in cases where depth is a critical factor in determining success or failure (Fig. 6).

Figure 6: Graph illustrating the distribution of the depth of our circuit

6.1.3 Optimization Step

The decomposition of quantum circuits into the target device’s set of basic gates [14], along with the addition of necessary swap gates to conform to the hardware topology, often results in increased circuit depth and gate count. Fortunately, numerous optimization routines have been developed to combine or eliminate gates, sometimes reducing the depth of the output circuit below that of the input. However, the effectiveness of these methods can vary, and executing quantum circuits on noisy devices remains a significant challenge. The activation of specific gate optimizations depends on the selected optimization level, which can take on different values. The following section will demonstrate the advantages of using a high optimization level.

The optimization of the quantum circuit for Shor’s algorithm using Qiskit Transpiler has yielded significant results (Fig. 7). The reduction in circuit depth at the output, the decrease in the number of non-local gates, and the overall reduction in circuit operations observed at optimization level 2 are promising indicators of a more efficient use of quantum resources. These improvements have the potential to accelerate execution and mitigate errors caused by decoherence. Notably, the results indicate that optimization level 2 provides the optimal mapping layout (Fig. 4).

Figure 7: Graph showing the optimization results on Qiskit Transpiler

6.2 BQSKit Library

BQSKit (Berkeley Quantum Synthesis Toolkit) is a powerful and portable quantum compiler framework developed by a U.S. Department of Energy national laboratory managed by the University of California. BQSKit provides an end-to-end compilation solution by integrating state-of-the-art partitioning, synthesis, and instantiation algorithms. Designed for accessibility and extensibility, the framework allows users to tailor workflows to their specific needs [15,16].

We employ BQSKit as a unique strategy that combines circuit partitioning and synthesis to enhance circuit performance beyond the capabilities of conventional optimization compilers. However, it is important to note that certain techniques, such as “reset” gates and measurements (whether mid-circuit or not), are not directly supported by BQSKit. These limitations required adaptations to our circuit design and optimization approach. Specifically, we removed “reset” gates and measurements to leverage BQSKit’s optimization capabilities and demonstrate its effectiveness on other quantum operations. Additionally, since BQSKit is implemented in Cirq, algorithms written in Qiskit cannot be directly executed. As a result, we re-implemented our algorithm in Cirq (Fig. 8) before converting it back to Qiskit (Fig. 9) to ensure compatibility with quantum gates.

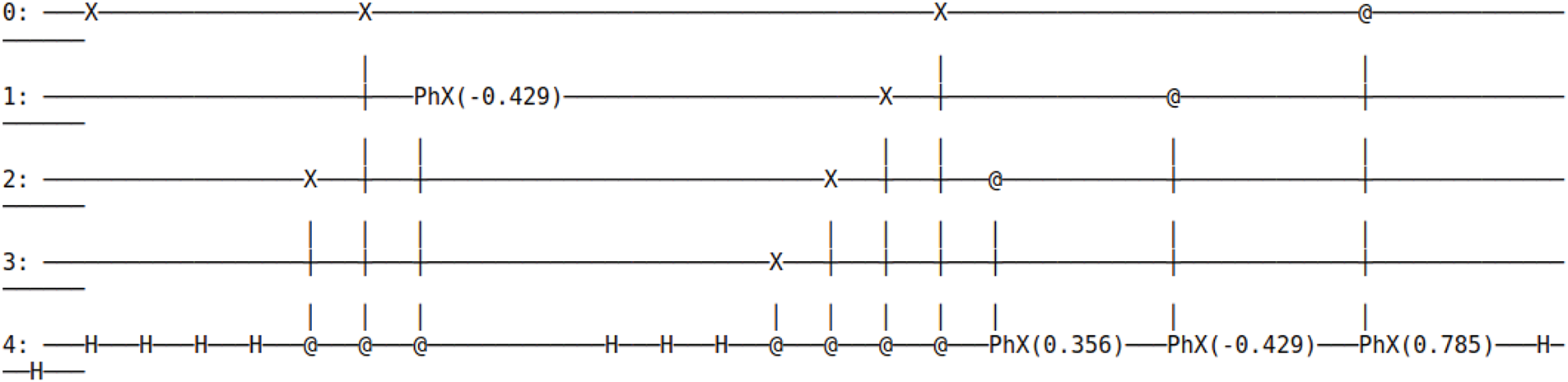
Figure 8: Circuit resulting from the execution of Shor’s algorithm, rewritten in Cirq

Figure 9: Circuit resulting from the conversion of Shor’s algorithm to Qiskit. It is observed that the conditioned gates P are replaced by U3 gates and also by S gates

Before the compilation of the circuit (Fig. 9), the statistics indicate a diversity of quantum gates, including 14 CNOT gates, 1 X gate, 9 H gates, 4 S gates, and 12 U3 gates. The logical connectivity of the initial circuit is represented by a coupling graph involving the connected qubit pairs: (2, 4), (0, 4), (3, 4), and (1, 4). After compilation, the circuit undergoes a significant transformation, simplifying to include only CNOT gates and U3 gates. The following graphical representations illustrate the circuit’s evolution across different optimization levels post-compilation [17].

Analysis of the histogram (Fig. 10) highlights a clear trend in favor of optimization level 3. At this level, a significant reduction in the total number of U3 gates is observed while keeping the number of CNOT gates constant. This observation suggests that optimization level 3 achieves greater efficiency in representing the circuit after compilation.

Figure 10: Impact of optimization levels on gate counts in compiled quantum circuit using BQSKit

6.3 Mitiq Library

We introduce Mitiq, a Python library specifically designed for error mitigation on noisy quantum computers. The objective of error mitigation techniques is to mitigate the impact of noise on near-term quantum computers while maintaining minimal overhead in quantum resources. This is achieved through a combination of quantum sampling and classical post-processing techniques [18].

In our study, we examined several error mitigation techniques offered by Mitiq (Fig. 11), including Probabilistic Error Cancellation (PEC) and Clifford Data Regression (CDR), before deciding to use Zero Noise Extrapolation (ZNE).

•      Probabilistic Error Cancellation (PEC) is an advanced technique that models and mitigates the effects of noise by reconstructing ideal operations from a weighted combination of noisy circuits. Despite its efficacy, PEC demands substantial computational resources due to the large number of circuit executions needed, making it impractical for near-term quantum computers [18].

•      Clifford Data Regression (CDR) estimates and corrects errors by comparing the results of real quantum circuits to those of noiseless (or near-ideal) Clifford circuits [18]. While effective for specific types of circuits, this method is not universally applicable, especially for more complex quantum operations.

Figure 11: The structure of Mitiq modules. Different error mitigation techniques are organized in different modules, including zero noise extrapolation (ZNE), probabilistic error cancellation (PEC), and Clifford data regression (CDR). Other modules are dedicated to auxiliary tasks such as interfacing with different quantum software libraries (interface) and bench-marking error mitigation strategies (benchmarks)

After a thorough evaluation of the available options, we selected Zero Noise Extrapolation (ZNE) due to its advantageous features and practicality in the context of NISQ systems. ZNE offers several benefits, including its simplicity and minimal requirement for additional qubits or circuit executions, as demonstrated in [18]. The ZNE methodology involves running the same circuit at different noise levels and extrapolating the results to estimate a noiseless outcome. This approach is notable for its reduced complexity compared to other methods, while maintaining a high accuracy in quantum computations. These characteristics make ZNE the optimal choice for our study, where balancing accuracy and resource efficiency is critical.

ZNE Calibration with Qiskit

The Mitiq calibration module helps to select an optimized error mitigation strategy. We will:

•      use the quantum circuit implemented for BQSKit because they share practically the same technical constraints;

•      use the Qiskit noisy simulator FakeJakarta as the backend;

•      perform the calibration with specific parameters, including benchmark settings (RB Settings), while recording the results.

We define a function that executes the quantum circuits and returns the expectation value, which is then processed by Mitiq’s execute_with_zne. In this example, the expectation value represents the probability of measuring the ground state, consistent with the expected outcome of an ideal randomized benchmarking circuit.

Based on the obtained results (Fig. 12), the implementation of the error mitigation technique has significantly improved the performance of the quantum circuit. While the mitigated value does not yet perfectly match the ideal value, it represents a substantial improvement over the non-mitigated performance. These findings suggest that the error mitigation strategy has a positive impact on the fidelity of the quantum circuit.

Figure 12: Results obtained from the use of zero noise extrapolation technique

Currently mitiq.calibration supports ZNE as a calibration technique, allowing the tuning of scale factors, extrapolation methods (Fig. 13), and circuit scaling methods [19]. To demonstrate this, we ran the calibration using custom randomized benchmarking (RB) settings while logging the results for comparison.

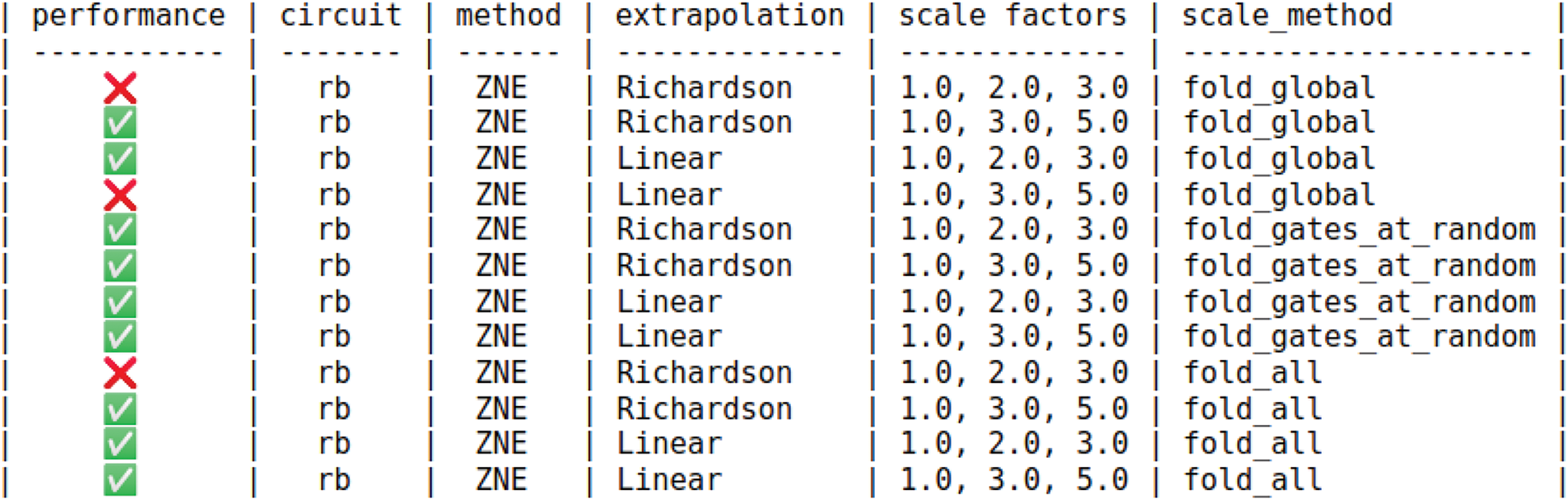
Figure 13: High-performing extrapolation strategies for noise attenuation

The results (Fig. 14) indicate an improvement in both the attenuated and calibrated-attenuated values compared to the non-attenuated value. Notably, the calibrated value shows a more significant improvement, achieving the goal of the calibration process. Among the two extrapolation methods, the Richardson method yields more favorable results in this study.

Figure 14: Histogram comparing linear and Richardson extrapolation methods

Having thoroughly examined the performance of our period-finding algorithm using various optimization techniques, such as Qiskit Transpiler, BQSKit, and Mitiq, we now draw conclusions regarding the effectiveness and relevance of these approaches in achieving our objectives.

7  Discussions

7.1 Generalizing Shor’s Algorithm for Larger Problem Sizes

The scalability of Shor’s algorithm, particularly its application beyond factoring small numbers like 15, is a crucial area of research for quantum computing. Shor’s algorithm has demonstrated significant theoretical potential, yet as the integer size increases, the quantum resources necessary also increase considerably, particularly in the domains of modular exponentiation and the Quantum Fourier Transform (QFT), both of which are fundamental components of the algorithm.

Research on scaling Shor’s algorithm involves efforts to optimize quantum circuits for larger inputs. For instance, the implementation of modular exponentiation and reducing circuit depth becomes more critical as the number to be factored increases. Studies that employ classical and hybrid techniques, such as GPU-based simulations, demonstrate the potential to factor larger semi-primes, up to 549 billion in one instance, through the enhancement of quantum circuit designs [20]. These findings underscore the necessity for continued advancements in hardware and algorithm optimization to fully leverage Shor’s algorithm in practical applications, particularly in the field of cryptography.

Subsequent studies concentrate on error mitigation techniques, which are imperative for larger problem sizes, as well as enhancements to QFT. The objective of these efforts is to make Shor’s algorithm scalable and more practical on contemporary noisy intermediate-scale quantum (NISQ) devices [21]. This research underscores the present limitations and offers a framework for the ongoing development of quantum systems with the capacity to address substantial factorization problems.

These examples underscore the fact that, while the proof of concept for factoring 15 is valuable, significant work remains to fully realize Shor’s algorithm’s potential for larger numbers. To this end, the optimization of quantum circuits and the mitigation of noise are imperative for the extension of the algorithm’s applicability to larger integer factorization challenges.

7.2 Optimization of Quantum Algorithms on Different Platforms

The optimization of quantum algorithms is imperative for maximizing computational efficiency and minimizing errors. Each quantum platform has developed its own set of optimization tools and techniques, tailored to the specific characteristics of its hardware and objectives.

•      Rigetti computing: The system utilizes its Forest suite [22], which includes tools such as the QPU Scheduler and compilation techniques to order and optimize quantum operations. These optimizations are imperative for maximizing the potential of the architecture, which features native gates like the Controlled-Z Gate (CZ) and XY Interaction Gate (XY).

•      IonQ: The company employs techniques such as Dynamical Decoupling and error correction to improve the fidelity of results on its trapped-ion quantum computers [23]. A key focus of IonQ’s approach is managing decoherence, a major challenge in quantum computing.

•      Microsoft Azure Quantum: The Quantum Development Kit (QDK) provides a comprehensive set of tools for optimizing quantum circuits at the code level. It includes the Q# Compiler, which translates circuit designs into executable code, and the Azure Quantum Optimizer, which leverages Azure’s cloud infrastructure to improve circuit performance [24].

•      Google Quantum AI: The platform focuses on minimizing circuit depth using Cirq, combined with advanced noise mitigation techniques. These efforts are designed to ensure the accuracy and reliability of quantum computations [25].

•      D-Wave Systems: The software under consideration adopts a distinct approach with its Ocean software, which integrates quantum annealing and hybrid solvers that combine classical and quantum techniques to effectively solve combinatorial optimization problems [26].

In summary, each platform has developed optimization tools and techniques tailored to its specific hardware capabilities. While this list highlights some of the most advanced systems currently available, it is not exhaustive. Future research could focus on developing more universal optimization solutions that adapt to the diverse constraints and capabilities of various quantum platforms. Such advancements could significantly enhance algorithm performance across systems and address the inherent challenges of quantum computing.

7.3 Limitations of BQSKit in Supporting “Reset” Gates and Mid-Circuit Measurements: Impact on Optimization

The dearth of support for “reset” gates and mid-circuit measurements in BQSKit imposes substantial constraints on the implementation and optimization of quantum algorithms, such as Shor’s algorithm. These features, which are present in many advanced quantum computing platforms, are critical for enhancing resource efficiency and enabling error correction during computation. The absence of these features necessitates the utilization of additional qubits, consequently leading to more complex circuits that are more susceptible to errors and decoherence.

“Reset” gates and their importance

“Reset” gates enable the reinitialization of qubits during computation, freeing up valuable quantum resources. This capability is critical for many practical quantum algorithms, particularly in scenarios where qubit resources are limited. Reusing qubits can significantly reduce circuit depth and the number of qubits required. A notable example is IBM’s Qiskit, which supports reset operations, enabling more efficient use of quantum hardware and improving the overall performance of quantum algorithms [27].

Conversely, the absence of reset gates in BQSKit requires the use of additional qubits, even for basic operations. This limitation increases hardware requirements and introduces more errors due to extended runtime, as each additional qubit adds complexity and potential for decoherence. The lack of reset gates in BQSKit compromises the overall fidelity of computations, particularly in noisy environments [15,28].

Mid-circuit measurements

Mid-circuit measurements are a critical feature absent in BQSKit but supported in more advanced frameworks like Google Cirq. These measurements facilitate the extraction of qubit states during computation, enabling error correction and adaptive operations. In this regard, the outcome of a measurement serves as a key input to guide subsequent algorithmic steps, as highlighted in [29].

The absence of mid-circuit measurements in BQSKit not only limits flexibility but also hinders the optimization of algorithms like Shor’s, which rely on real-time state feedback for efficient execution. In algorithms involving conditional operations based on intermediate results, mid-circuit measurements are imperative for achieving optimal performance. This limitation impedes the adaptability of the algorithm and affects its scalability to larger problem sizes, where error correction becomes increasingly crucial.

Impact on Shor’s algorithm

In the context of Shor’s algorithm, the inability to use reset gates and mid-circuit measurements compel developers to employ alternative strategies. These strategies often lead to increased circuit complexity and depth, which degrade performance, especially on noisy quantum devices where circuit depth is a critical factor. Moreover, the lack of these features limits the algorithm’s adaptability to different quantum hardware architectures, reducing the generalizability of optimization results across platforms.

In contrast, frameworks such as IBM’s Qiskit and Google’s Cirq enable more efficient implementations of Shor’s algorithm by supporting advanced features like reset gates and mid-circuit measurements. These capabilities reduce error rates and enhance the reliability of quantum computations. This highlights the need for BQSKit to evolve and incorporate such features in future versions to remain competitive.

Given these limitations, it is essential to evaluate their impact on the optimization of Shor’s algorithm and explore potential strategies for mitigating their effects.

7.4 Impact of BQSKit Limitations and Workarounds

The lack of support for reset gates and intermediate measurements in BQSKit presents significant challenges for optimizing Shor’s algorithm. These features are typically used to reduce the number of qubits required and to enable dynamic adaptation of the execution process. Without them, the depth of the circuit increases, leading to a high likelihood of errors due to decoherence.

Workaround strategies

•   Avoiding the use of reset gates

•   According to Christof Zalka’s work (2006), it is possible to perform the modular additions required by Shor’s algorithm using superpositions of arithmetic states. This method allows for the parallelization of certain operations and reduces the total number of qubits needed, without relying on reset operations [30].

•   An optimized qubit allocation from the start can compensate for the lack of reset operations.

•   Eliminating intermediate measurements

•   A fully quantum execution, where all operations remain coherent until the final measurement, avoids the need for intermediate measurements.

•   Restructuring the circuit to group all measurements at the end reduces the impact of intermediate dependencies.

•   Optimization via transpilation

•   Designing the circuit first in Qiskit, which supports these features, and then transpiling it into a BQSKit-compatible format can help bypass some limitations while maintaining circuit efficiency.

The implementation of these strategies would facilitate the adaptation of Shor’s algorithm to the constraints imposed by BQSKit without compromising its efficiency. Consequently, this approach would ensure enhanced compatibility with current quantum architectures.

7.5 Analysis of the Deployed Optimization Techniques

In order to develop a more nuanched understanding of the specific outcomes resulting from each optimization method that was implemented, a detailed analysis of the advantages and limitations of each approach is warranted.

7.5.1 Qiskit_Transpiler Library

•   Advantages

•   Adaptation to hardware platform: The Qiskit Transpiler is a tool designed to optimize quantum circuits based on the specific characteristics of the target hardware platform, allowing maximum performance in real quantum devices.

•   Handling hardware constraints: Qiskit Transpiler is a software that takes into account hardware constraints, including the available gates, qubit connections, and coherence times. This ensures that the generated circuits are compatible with the platform.

•   Limitations

•   Circuit complexity: In certain instances, Qiskit Transpiler may generate circuits that are more complex than anticipated due to adjustments made to accommodate hardware constraints, leading to increased latency and overhead.

•   Platform dependency: Qiskit Transpiler has been optimized for IBM quantum devices; therefore, it should be noted that certain platform-specific optimizations may not be as effective on other hardware platforms.

7.5.2 BQSKit Library

•   Advantages

•   End-to-end compilation: BQSKit provides a comprehensive quantum compilation solution that integrates partitioning, synthesis, and instantiation. This comprehensive approach enables the optimization of all circuit elements, thereby enhancing its overall performance.

•   Advanced optimization: Utilizing advanced algorithms, BQSKit achieves optimizations that surpass the capabilities of conventional compilers, a feat particularly pertinent for intricate quantum circuits.

•   Limitations

•   Limitation of “reset” gates and mid-circuit measurements: BQSKit does not support “reset” gates or mid-circuit measurements, which can constrain circuit design options and require adjustments in code structure. The parameterization aspect is addressed as follows: While customization is an advantage, it can also become a limitation if optimization parameters are not properly adjusted. Improper tuning may result in suboptimal outcomes.

7.5.3 Mitiq Library

•   Advantages

•   Enhancement of quantum fidelity: The results demonstrated a significant improvement in the fidelity of the quantum circuit when applying the ZNE technique. This indicates that Mitiq can effectively contribute to the mitigation of quantum errors and the enhancement of result quality.

•   Optimal selection of extrapolation methods: The analysis facilitated the selection of the most suitable extrapolation methods, such as linear and Richardson extrapolation. This highlights Mitiq’s capacity to adapt its techniques in accordance with the specific context.

•   Limitations

•   Deviation from ideal values: While quantum error mitigation was observed, the attenuated results do not always perfectly align with ideal values. This indicates that Mitiq’s ability to achieve complete error correction is inherently limited.

•   Dependency on extrapolation methods: Mitiq’s effectiveness depends on the careful selection of extrapolation methods. Poor choices can reduce the effectiveness of error mitigation, emphasizing the need to understand and select these methods judiciously.

7.6 Application of Error Mitigation Techniques in Gate-Model Quantum Computers

In the context of gate-model quantum computers, algorithm optimization poses a considerable challenge due to errors arising from decoherence and imperfections in quantum gates. A variety of techniques have been proposed to address these issues, and their integration into modern quantum computing architectures shows considerable promise for improving algorithmic efficiency.

The articles [31] and [32] explore two critical aspects of optimizing quantum circuits: reducing circuit depth and scaling gate-model quantum computers.

Circuit depth reduction

The reduction of circuit depth is essential to minimize the execution time of the algorithm and limit the accumulation of errors caused by decoherence. The article [32] proposes several strategies to achieve this, enabling more precise computations on current quantum systems. By minimizing circuit complexity, it becomes possible to better utilize error mitigation techniques such as Zero Noise Extrapolation (ZNE). The efficacy of ZNE is particularly pronounced in scenarios where errors are proportional to circuit depth; consequently, the reduction in circuit depth enhances the performance of this mitigation method.

Scalability of quantum computers

The article [31] discusses a distributed approach to execute complex quantum algorithms at scale. Scalability is a critical concern, as larger quantum systems are more susceptible to cumulative errors. Combining circuit depth reduction with a distributed architecture has been shown to improve both the accuracy and the feasibility of executing algorithms on larger scales.

Complementarity with error mitigation techniques

In this study, Zero Noise Extrapolation (ZNE) was selected as the error mitigation strategy. ZNE operates by executing a circuit at multiple noise levels and extrapolating the results to estimate the outcome in a noiseless scenario. This approach has been demonstrated to be particularly effective in low-depth quantum environments, as highlighted in the referenced articles. However, in high-noise environments, alternative techniques, such as Probabilistic Error Cancellation (PEC) or Clifford Data Regression (CDR), also available in the Mitiq library, can provide additional benefits by improving the robustness of results, even under significant noise conditions.

7.7 Quantum Circuit Optimization: Ideas for a More Robust Ecosystem

To strengthen the quantum computing ecosystem, it is essential to promote both interface standardization and industrial collaboration. Developing common standards and interfaces across diverse quantum platforms simplifies algorithm conversion and enhances interoperability. At the same time, fostering collaboration among quantum-focused companies encourages the sharing of best practices, the alignment of optimization strategies, and the creation of mutually compatible solutions. By combining efforts to establish standardized interfaces with collaborative initiatives, the quantum community can build a more cohesive and universally accessible quantum computing landscape. This approach ensures that advancements are not only technically robust, but also broadly applicable, driving the overall progress of quantum computing.

8  Conclusion

The exploration of quantum development environments and the implementation of Shor’s period-finding algorithm have highlighted the strengths and limitations of various optimization techniques. Qiskit Transpiler excels in adapting to hardware platforms, while BQSKit demonstrates proficiency in end-to-end compilation using advanced optimization algorithms. Mitiq stands out for its error mitigation capabilities, particularly through Zero Noise Extrapolation (ZNE). However, the effectiveness of these techniques depends on careful selection and collaborative efforts. By promoting interface standardization and fostering collaboration within the quantum community, the quantum computing ecosystem can evolve into a more robust and cohesive framework that is better equipped to address future challenges.

Acknowledgement: We would like to express our gratitude to IBM Quantum for granting us access to their 127-qubit quantum computer, “ibm_kyoto,” which significantly contributed to our practical observations. Special thanks go to Ed Younis for his valuable support with BQSKit, and to the Unitary Fund team for their collaborative efforts on Mitiq. We also extend our appreciation to CEA-SMIA (Center of Excellence in Africa-Mathematical Sciences, Computer Science, and Applications) for their valuable collaboration.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Kaleb Dias Antoine KODO designed the structure of the article, conducted the research, wrote the manuscript, and analyzed the results. Eugène C. EZIN supervised the work, provided methodological and scientific guidance, and reviewed the manuscript to ensure its rigor and coherence. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data and source code supporting the findings of this study are openly available on GitHub. The implementations of Shor’s period-finding algorithm using different quantum compilation and optimization techniques can be accessed through the following links:

1. Qiskit Transpiler Library: The implementation of Shor’s algorithm using Qiskit Transpiler, exploring quantum circuit adaptations for hardware platforms and optimization techniques, is available at: https://github.com/kaleb-rgb/Quantum-optimization/blob/main/Shor15Qiskit_Transpiler.ipynb (accessed on 11 March 2025).

2. BQSKit Library: The optimized version of Shor’s algorithm using BQSKit, which provides advanced compilation algorithms, can be found at: https://github.com/kaleb-rgb/Quantum-optimization/blob/main/Shor15bqskit.ipynb (accessed on 11 March 2025).

3. Mitiq Library: The implementation of Shor’s algorithm enhanced with Mitiq’s error mitigation techniques, including Zero Noise Extrapolation, is available at: https://github.com/kaleb-rgb/Quantum-optimization/blob/main/Shor15mitiq.ipynb (accessed on 11 March 2025).

These repositories provide detailed implementations and insights into quantum circuit optimizations applied in this study.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Shor PW. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM J Comput. 1997;26(5):1484–509. doi:10.1137/S0097539795293172. [Google Scholar] [CrossRef]

2. Nielsen MA, Chuang IL. Quantum computation and quantum information. 10th ed. Cambridge, UK: Cambridge University Press; 2010. p. 174–231. doi:10.1017/CBO9780511976667. [Google Scholar] [CrossRef]

3. Cleve R, Ekert A, Macchiavello C, Mosca M. Quantum algorithms revisited. Proc R Soc Lond A. 1998;454(1969):339–54. doi:10.1098/rspa.1998.0164. [Google Scholar] [CrossRef]

4. Quantum IBM. IBM quantum. quantum computing overview [Internet]. [cited 2023 Dec 20]. Available from: https://www.ibm.com/topics/quantum-computing. [Google Scholar]

5. Google Cirq. Quantum AI [Internet]. [cited 2023 Jun 26]. Available from: https://quantumai.google/cirq. [Google Scholar]

6. Córcoles AD, Takita M, Inoue K, Lekuch S, Minev ZK, Chow JM, et al. Exploiting dynamic quantum circuits in a quantum algorithm with superconducting qubits. Phys Rev Lett. 2021;127(10):100501. doi:10.1103/PhysRevLett.127.100501. [Google Scholar] [PubMed] [CrossRef]

7. Quantum Circuit. Qiskit documentation [Internet]. [cited 2023 May 18]. Available from: https://qiskit.org/documentation/apidoc/circuit.html. [Google Scholar]

8. Park B, Ahn D. T-count optimization of approximate quantum Fourier transform. arXiv:2203.07739. 1987. [Google Scholar]

9. Xiao L, Qiu D, Luo L, Mateus P. Distributed phase estimation algorithm and distributed Shor’s algorithm. arXiv:2304.12100. 2016. [Google Scholar]

10. Dang A, Hill CD, Hollenberg LCL. Optimising matrix product state simulations of Shor’s algorithm. Quantum. 2019;3:116. doi:10.22331/q-2019-01-25-116. [Google Scholar] [CrossRef]

11. Fernández-Alegre P, de Pedro L, de Vergara Méndez JEL. Optimizing Shor’s algorithm through approximate fractions for quantum factorization. Res Sq. 2024;2–11. doi:10.21203/rs.3.rs-5031635/v1. [Google Scholar] [CrossRef]

12. Shamikh Iqbal S, Zafar A. Enhanced Shor’s algorithm with quantum circuit optimization. Int J Inf Technol. 2024;16(4):2725–31. doi:10.1007/s41870-024-01741-0. [Google Scholar] [CrossRef]

13. IBM Quantum. Qiskit transpiler [Internet]. [cited 2023 Jun 18]. Available from: https://qiskit.org/documentation/apidoc/transpiler.html. [Google Scholar]

14. Barenco A, Bennett CH, Cleve R, DiVincenzo DP, Margolus N, Shor P, et al. Elementary gates for quantum computation. Phys Rev A. 1995;52(5):3457–67. doi:10.1103/PhysRevA.52.3457. [Google Scholar] [PubMed] [CrossRef]

15. Younis E, Iancu C. Quantum circuit optimization and transpilation via parameterized circuit instantiation. In: 2022 IEEE International Conference on Quantum Computing and Engineering (QCE); 2022 Sep 18–23; Broomfield, CO, USA: IEEE; 2022. p. 465–75. doi:10.1109/QCE53715.2022.00068. [Google Scholar] [CrossRef]

16. BQSKit [Internet]. Berkeley, CA: Lawrence Berkeley National Laboratory. [cited 2023 Dec 30]. Available from: https://bqskit.lbl.gov/. [Google Scholar]

17. BQSKit GitHub. BQSKit tutorial [Internet]. [cited 2023 Jul 4]. Available from: https://github.com/BQSKit/bqskit-tutorial/blob/main/1_comping_with_bqskit.ipynb. [Google Scholar]

18. LaRose R, Mari A, Kaiser S, Karalekas PJ, Alves AA, Czarnik P, et al. Mitiq: a software package for error mitigation on noisy quantum computers. Quantum. 2022;6:774. doi:10.22331/q-2022-08-11-774. [Google Scholar] [CrossRef]

19. Mitiq Calibration. Using calibration to improve results [Internet]. [cited 2023 Dec 24]. Available from: https://mitiq.readthedocs.io/en/stable/examples/calibration-tutorial.html#using-calibration-to-improve-the-results. [Google Scholar]

20. Willsch D, Willsch M, Jin F, De Raedt H, Michielsen K. Large-scale simulation of shor’s quantum factoring algorithm. Mathematics. 2023;11(19):4222. doi:10.3390/math11194222. [Google Scholar] [CrossRef]

21. Singleton RL. Shor’s factoring algorithm and modular exponentiation operators. Quanta. 2023;12(1):41–130. doi:10.12743/quanta.v12i1.235. [Google Scholar] [CrossRef]

22. Rigetti Computing. Forest 1.3: upgraded developer tools, improved stability, and faster execution [Internet]. [cited 2024 Oct 17]. Available from: https://www.rigetti.com/search?query=forest+. [Google Scholar]

23. Agarwal S, Abou Jaoude G, Leider A, Tappert CC. Comparing quantum computing platforms. In: Advances in information and communication. Cham: Springer International Publishing; 2022. p. 423–41. doi:10.1007/978-3-030-98012-2_32. [Google Scholar] [CrossRef]

24. Microsoft Azure Quantum. Q# [Internet]. [cited 2024 Oct 16]. Available from: https://learn.microsoft.com/en-us/azure/quantum/qsharp-ways-to-work?source=recommendations. [Google Scholar]

25. Google Quantum AI. Circuit optimization: cirq [Internet]. Mountain View, CA: Google. [cited 2024 Oct 16]. Available from: https://quantumai.google/cirq/tutorials/google/spin_echoes. [Google Scholar]

26. D-Wave Systems. Ocean Software [Internet]. Burnaby, BC: D-Wave Systems. [cited 2024 Oct 16]. Available from: https://www.dwavesys.com/solutions-and-products/ocean/. [Google Scholar]

27. IBM Quantum. Qiskit reset gate support [Internet]. [cited 2024 Oct 18]. Available from: https://docs.quantum.ibm.com/guides. [Google Scholar]

28. Chen L, Fors SP, Yan Z, Ali A, Abad T, Osman A, et al. Fast unconditional reset and leakage reduction in fixed-frequency transmon qubits. arXiv:2409.16748. 2024. [Google Scholar]

29. Botelho L, Glos A, Kundu A, Miszczak JA, Salehi Ö, Zimborás Z, et al. Error mitigation for variational quantum algorithms through mid-circuit measurements. Phys Rev A. 2022;105(2):022441. doi:10.1103/PhysRevA.105.022441. [Google Scholar] [CrossRef]

30. Zalka C. Shor’s algorithm with fewer (pure) qubits. arXiv:quant-ph/0601097. 2004. [Google Scholar]

31. Gyongyosi L, Imre S. Scalable distributed gate-model quantum computers. Sci Rep. 2021;11(1):5172. doi:10.1038/s41598-020-76728-5. [Google Scholar] [PubMed] [CrossRef]

32. Gyongyosi L, Imre S. Circuit depth reduction for gate-model quantum computers. Sci Rep. 2020;10(1):11229. doi:10.1038/s41598-020-67014-5. [Google Scholar] [PubMed] [CrossRef]