Computational Study of Anastomosis Angle of Arteriovenous Fistula for Hemodialysis

1  Introduction

The main function of the kidney is to purify the blood by removing the toxic elements like urea, creatine, and amino acids from it and excreted it out as urine. In end-stage renal disease, when the kidney stops working or is working below 10%, hemodialysis is the treatment required for the patient in which the function of the kidney is carried out by an external machine called a dialyzer. For the hemodialysis, the blood is extracted from the human blood vessels and supplied to the dialyzer and returned to the body after filtration. This transportation of blood requires vascular access needs to be surgically created in the patient’s body. In this surgery, the abnormal connection of artery and vein takes place and this connection is called an arteriovenous fistula (AVF). An arteriovenous fistula has been a widely accepted vascular access for hemodialysis over the last 50 years [1,2]. Now scientific community globally has accepted that AVF is the better choice of vascular access for achieving hemodialysis process [3]. After the formation of AVF, there is a drastic increment in the flow of blood into the venous part of AVF. In the best-case scenario, the vein bulge up to 6 mm or more than that with the remodeling of the vessel wall. As per the nephrologist, after an interval of six to twelve-week, the vein should get dilated and be matured enough for the penetration of two large needles frequently in a week [4]. Arteriovenous fistula maturation failure is a prime cause of morbidity and death rate in hemodynamic patients [5] and about 60% of the newly formed AVF fails to mature for the hemodialysis and will not be useful further [6]. Now consider this, there is a need to develop an approach to improve the maturation of AVF. The internal pressure of the artery will modulate the wall thickness by its effect on wall tension and blood flow controls arterial lumen diameter by adjusting the wall shear stress [7]. The higher range of WSS is seen in the vasculature, especially in the region with a geometry providing turbulent flow or increased flow velocity like at anastomosis [8]. WSS and oscillating WSS will increase the thickness of the vessels. An increment in the wall thickness called IH (Intimal Hyperplasia) of vessels decreases the lumen space of the vessel and further leads to stenosis. Table 1 shows the comparison of WSS values and their methods in different studies. Numerical modeling of WSS has previously been used to study porcine AVF model [9,10] and recently in human AVF [11,12] and taking the needful inputs from non-contrast MRI, computed tomography scans, or three-dimensional ultrasound imaging protocols for numerical modeling.

Nikam et al. [18] conducted first pilot study of AVF placement using the novel Optiflow device on a total of 41 subjects, concluding that the device appears to be safe and effective in the placement of AVFs, with high maturation rates. The present study aims to investigate the high wall shear stress values in the AVF geometry especially at the different anastomosis angles. In this study, four angles 45°, 60°, 75° and 90° of anastomosis are used to analyze and discover the optimal angle of anastomosis for AVF. The end-to-side connection of AVF is used for the numerical model. WSS, outflow rate, and pressure drop across the anastomosis are studied using numerical analysis. Non-dimensional Strouhal number takes into consideration to represent the frequency of oscillation of the disturbed flow at the anastomosis zone.

2  Methods

2.1 Idealized Geometry

In the process of surgery seen by the author’s, it is observed that, the cephalic vein end joins to the radial artery side directly at 90° by the surgeon, placed at the wrist of the patient. The end-to-side connection is as shown in Fig. 1. To replicate the AVF, idealized three-dimensional geometries are prepared for four different anastomotic angles. The four geometries are undergone for numerical simulation in AVF of end-to-side connection at different anastomotic angles. It is not possible to obtain information for each patient every time; however, performing a Doppler or MRI or CT-scan to search for 30°, 45°, 60°, 75°, and 90° angles of AVF is a time-consuming process. Hence, ideal geometry is used in this work. In total four geometries were considered for the present study. Specifically, each of the four configurations of the radial artery and a cephalic vein as shown in Fig. 2 is studied with a fixed arterial diameter DA of 4 mm and inflamed venous diameter DV of 6 mm. This combination of diameters is fixed with each other at various angles of anastomosis 45°, 60°, 75° and 90° for making an AVF.

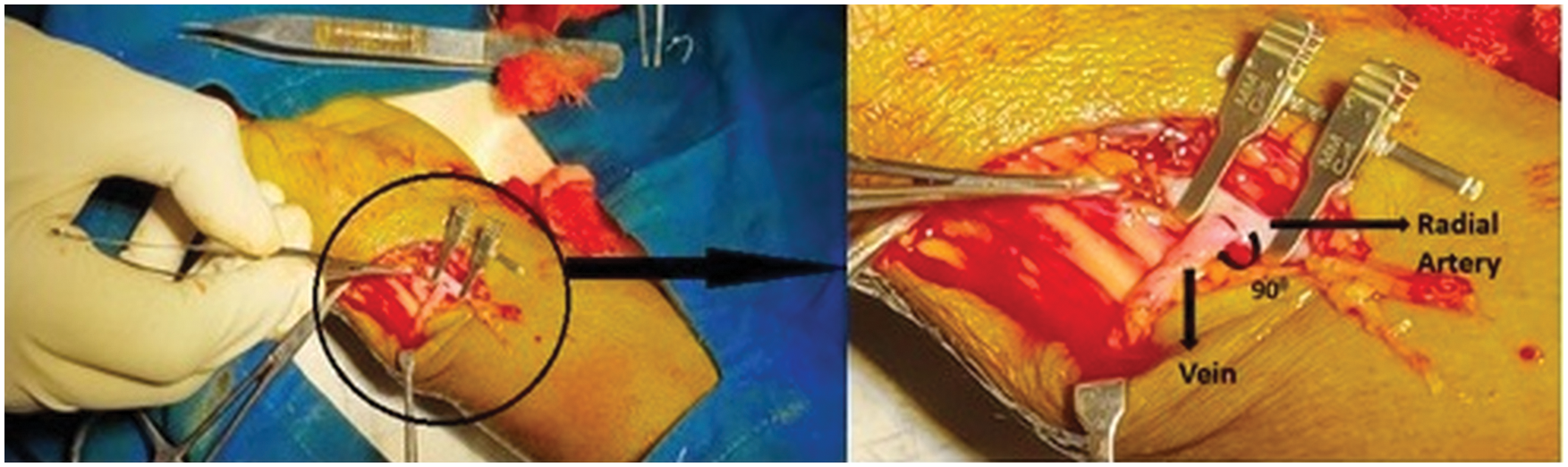
Figure 1: Creation of AVF of the radial artery side and the cephalic vein end at 90° of anastomosis

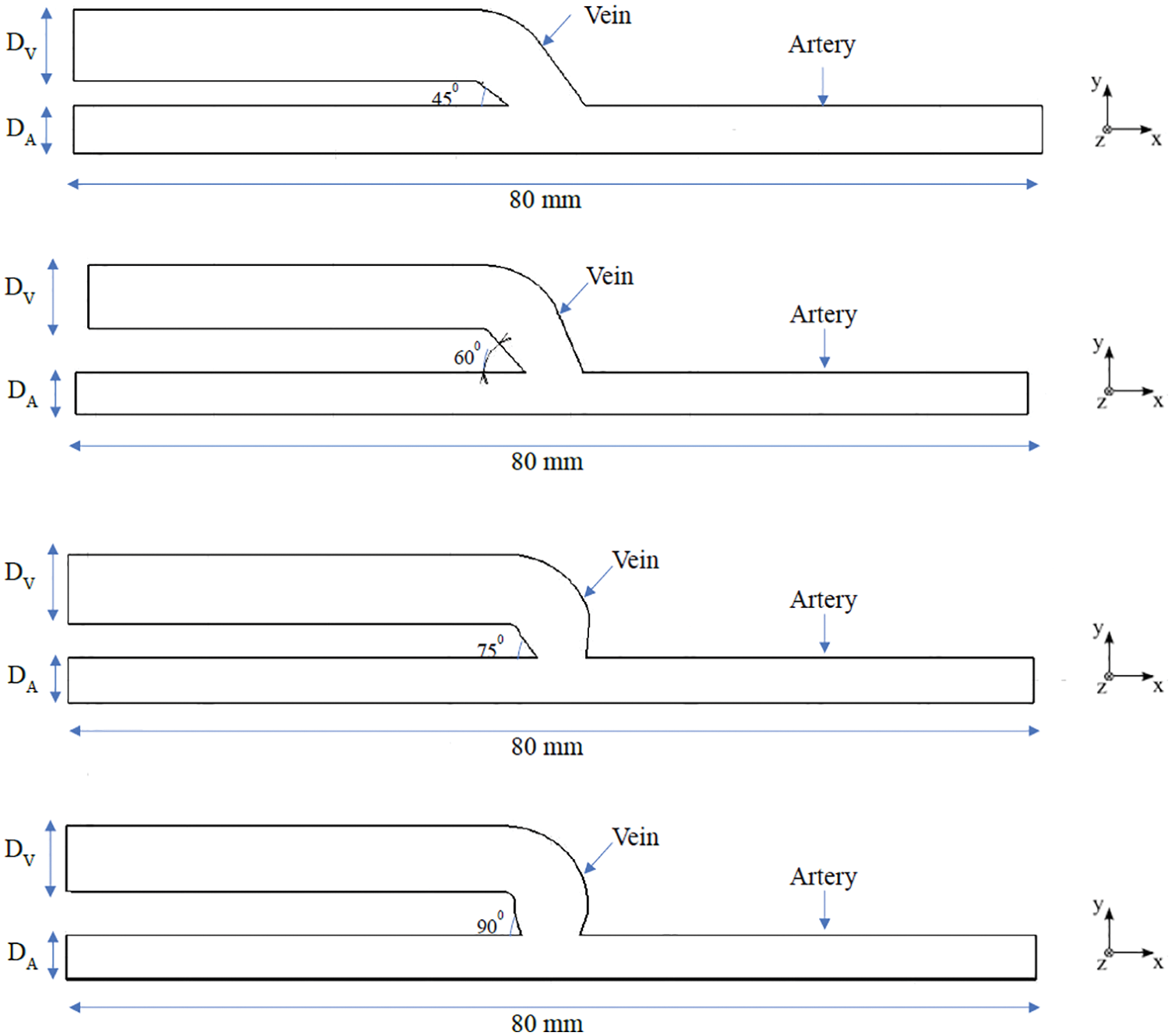
Figure 2: Schematic representation of the idealized geometries of AVF at angles of 45°, 60°, 75° and 90°

2.2 Governing Equations

In the present study the blood is treated as an incompressible Newtonian fluid [4,11,13]. The blood flow is modeled by using the incompressible continuity and Navier-Stokes equations for a constant velocity fluid, which can be represented as seen in Eqs. (1) and (2), respectively.

∇.u=0 (1)

ρ∂u∂t+ρ(u.∇)u=−∇p+μ∇2u. (2)

where p, ρ, u and μ is the pressure field, density, velocity and dynamic viscosity of the human blood within the idealized AVF geometry, respectively. Values of μ = 3.5 × 10−3 Pa s and ρ = 1060 kg/m−3 are used in this study [13–15]. In the present study gravity is not considered. Finite volume method (FVM) was used for solving the mass and momentum equation with the aid of a commercially out there CFD package, ANSYS Fluent 16. SIMPLE algorithm is chosen for the pressure velocity coupling. The second-order upwind scheme is adopted for the momentum equation discretization. The under relaxation factors are set as 0.3 for pressure, 1 for density, 1 for body forces, 0.7 for momentum and 1 for viscosity.

2.3 Boundary Conditions

Constant flow rate condition is applied at the inlet of the artery in positive x-direction keeping the outlet of artery and vein at a fixed pressure. In this study, the walls of all vessels are assumed to be rigid and non-deformable [1,4,8,19]. At the vessel wall, a no-slip boundary condition is applied. Three values of blood flow rate are used for simulation 350, 500, and 900 ml/min as per the discussion with the nephrologist. However, the range of the inflow rate used falls within the range used by the various literature [13,16,17,20].

3  Results and Discussion

3.1 Wall Shear Stress on AVF Geometry

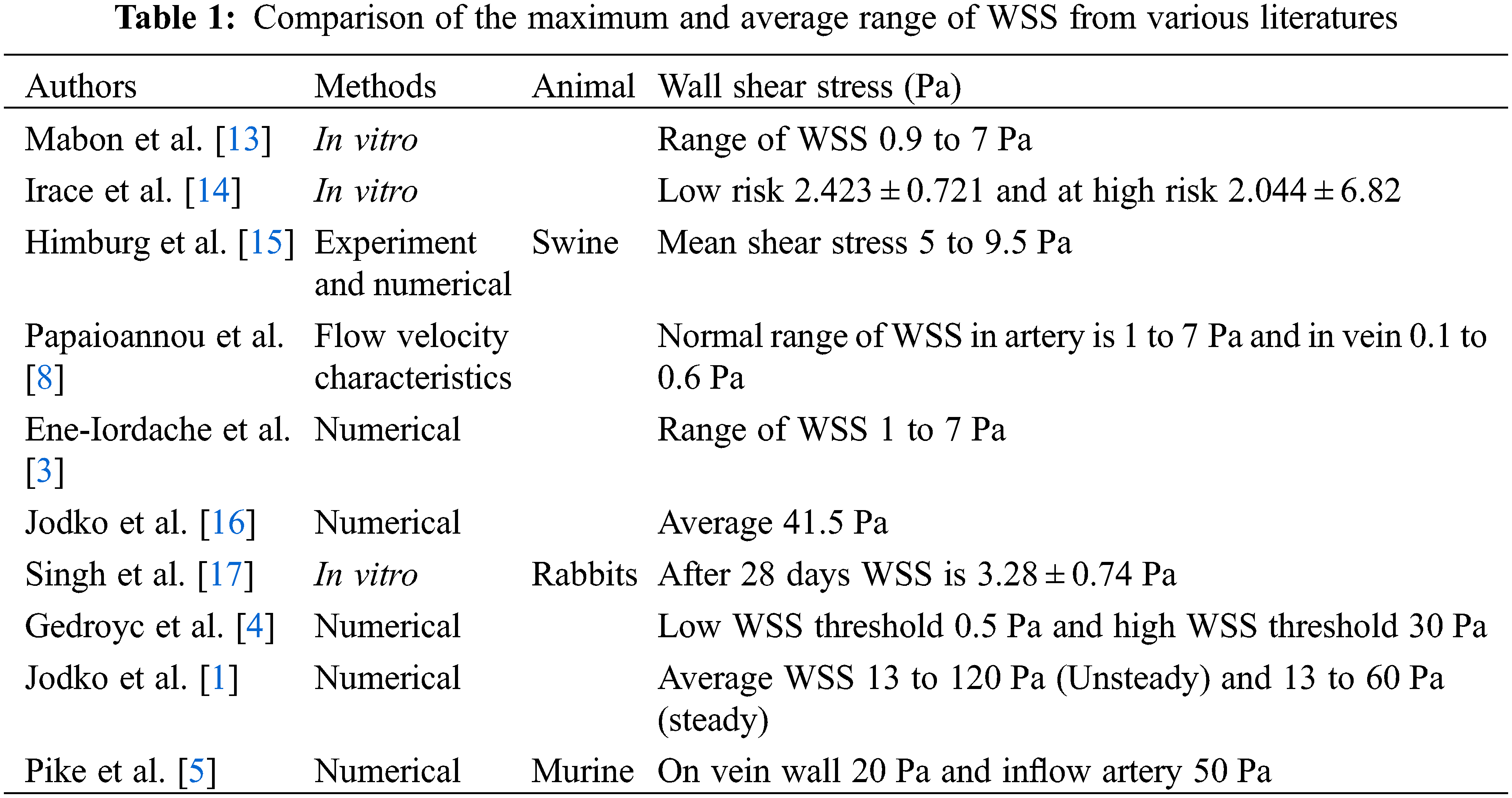
Literature has mentioned the average, upper, and lower bound values of WSS which can be seen in Table 1. The higher value of WSS are obtained by using numerical study for the three different inflow rate condition and it is shown below in Fig. 3. It is observed that in general WSS obtained for each inflow rate condition is higher for an angle of 75° compared to other angles. It is also observed that WSS for each inflow rate condition is lower at 60°. At angles 45° and 90° the values are almost similar for each inflow condition. The values acquire from the numerical analysis are within the range of literature data. The scale has been grated to shown abnormal levels of WSS, where abnormally high regions appear at the outer side of the vein just after the anastomosis as shown with black circle in Fig. 5. The high region is denoted as red on the contour and the low region is denoted by solid dark blue as shown in Fig. 4 for each case. High WSS sometimes injured the walls of the vessels [21,22]. The endothelial cells discharge provocative arbiters that permit the accumulation of platelets, fibrin testimony, and enlistment of leukocytes to the injured area [23,24]. These cells’ growth decreases the lumen space of the vessel and promotes the blood flow through the intima. This thickening of the vessel wall resulting in the formation of neo-intimal Hyperplasia (IH). Uniform and high WSS should give the least intimal hyperplasia [25]. Intimal hyperplasia further leads to stenosis which is the prime cause of the AVF failure. Also, some studies concluded that and support the hypothesis that the low wall shear stress is prone to develop intimal hyperplasia [26].

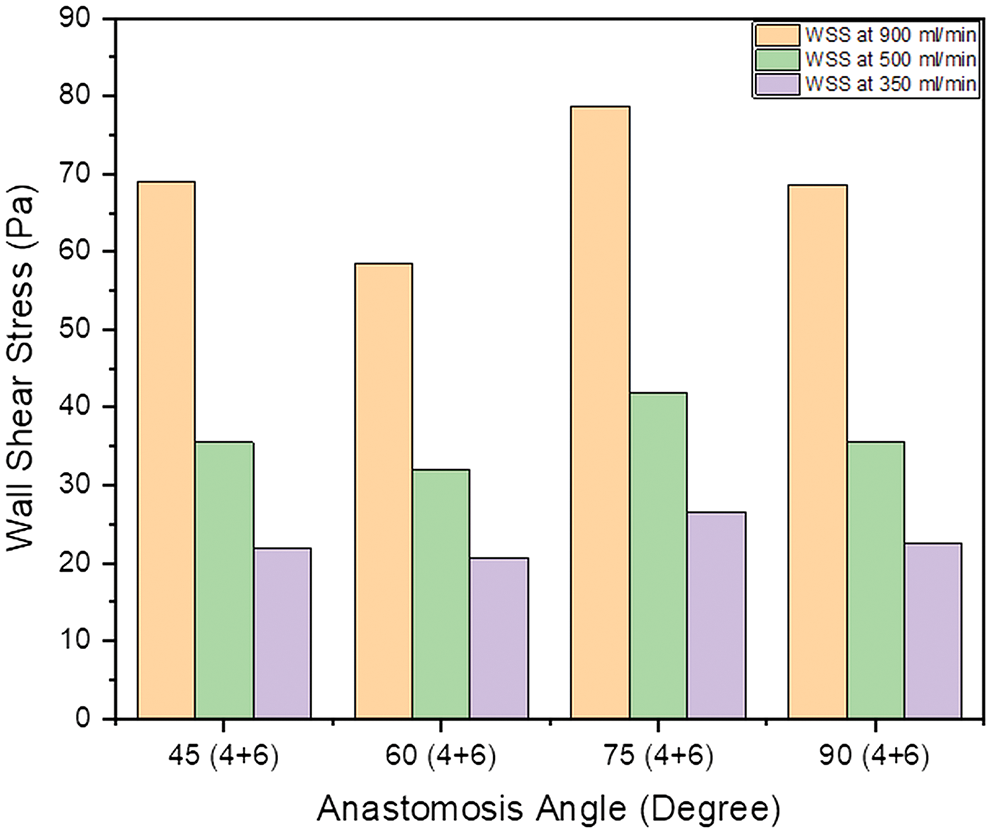
Figure 3: Bar chart showing the value of maximum WSS within the AVF geometry at a different angle of anastomosis for (4 + 6) combination

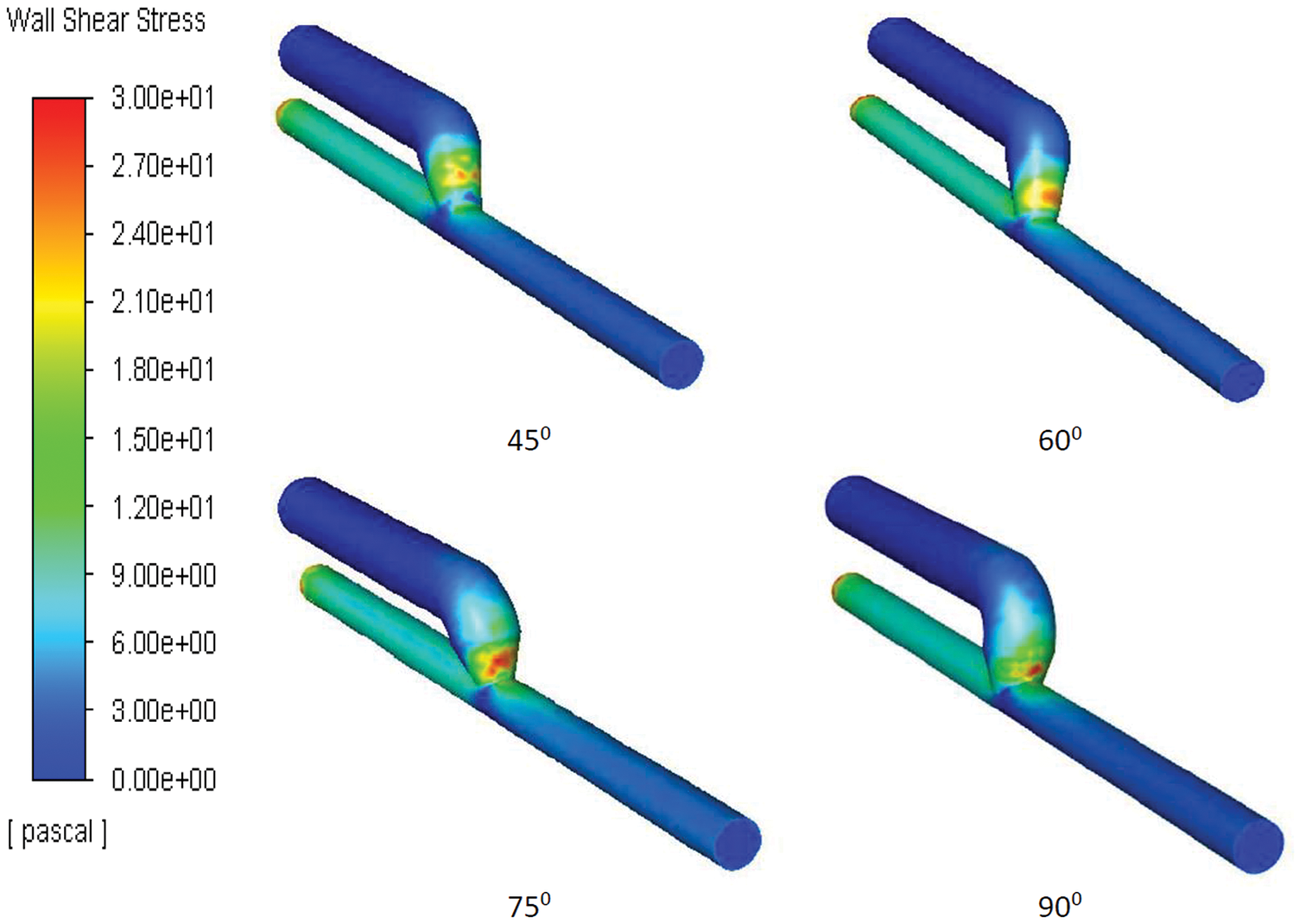
Figure 4: Snapshots of the WSS appears at angle 45°, 60°, 75° and 90°

Figure 5: Outer side of the anastomosis showing the higher WSS area

3.2 Venous Outflow Rate of Blood for the Hemodialysis

The application of a numerical model is capable for evaluating hemodynamic impact of anastomosis angle on the outflow rate of AVF. The outflow rate in ml/min is calculated at the face of a distal vein and intends to generate a reference plot that provides the values of the outflow rate for each input condition as depicted in Fig. 6. For the average value of inflow rate of 500 ml/min in hemodialysis, the angle of 45° gives the highest outflow rate of 344.85 ml/min at the distal vein. At other inflow rate conditions (350 and 900 ml/min) there is not much increment in the flow rate. For 500 and 350 ml/min, the maximum outflow rate showing at 45°. For all inlet conditions, the outflow rate at the distal vein is less at 75° than the other angles. The venous outflow is increasing with the increase in arterial inflow condition at all anastomosis angles except 45°, for 45° the outflow rate at distal end of vein is higher for 500 ml/min inflow compare to other inflow rates.

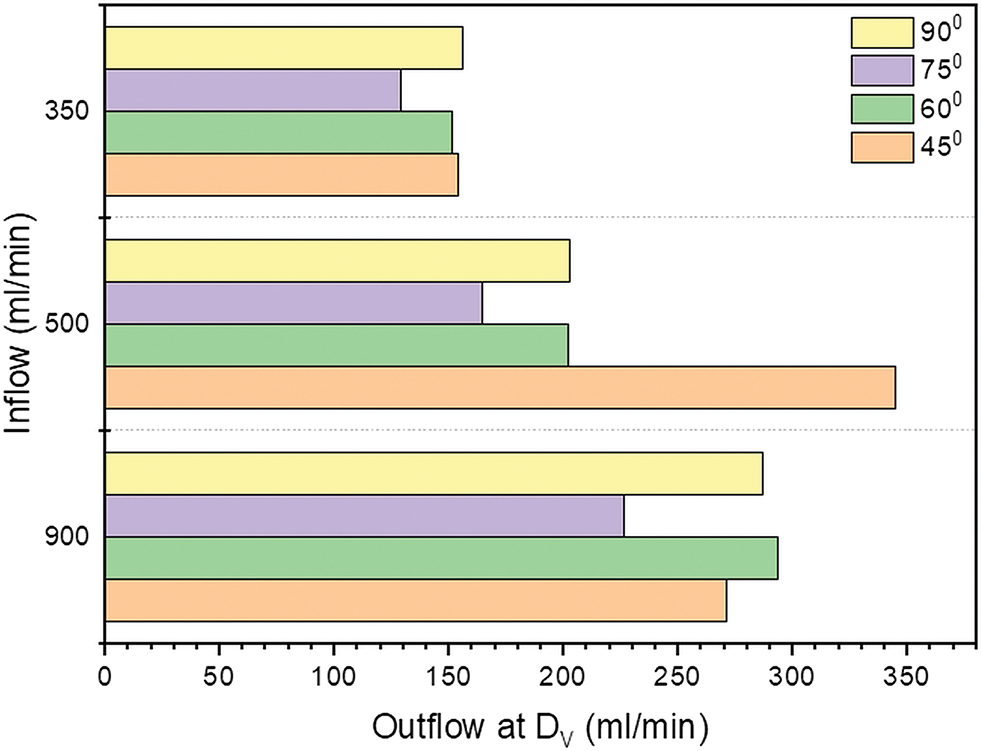
Figure 6: Outflow rate (ml/min) at outlet of vein for inflow 350, 500 and 900 ml/min

After the AVF creation, the blood flows at a high speed in the vein and the vein gets dilated. However, blood flow is disturbed and flow separation occurs just downstream of the anastomosis in the vein. The separation and the recirculation zone that occurs in the venous side of the AVF just downstream of the anastomosis can be represented by the streamlines and it is shown in Fig. 7. From the streamline behavior, it can be observed that the intensity of disturbed flow is high at 75° angle of anastomosis and it is less at 90°. The frequency of the disturbed flow can be represented in the form of the non-dimensional term called Strouhal number.

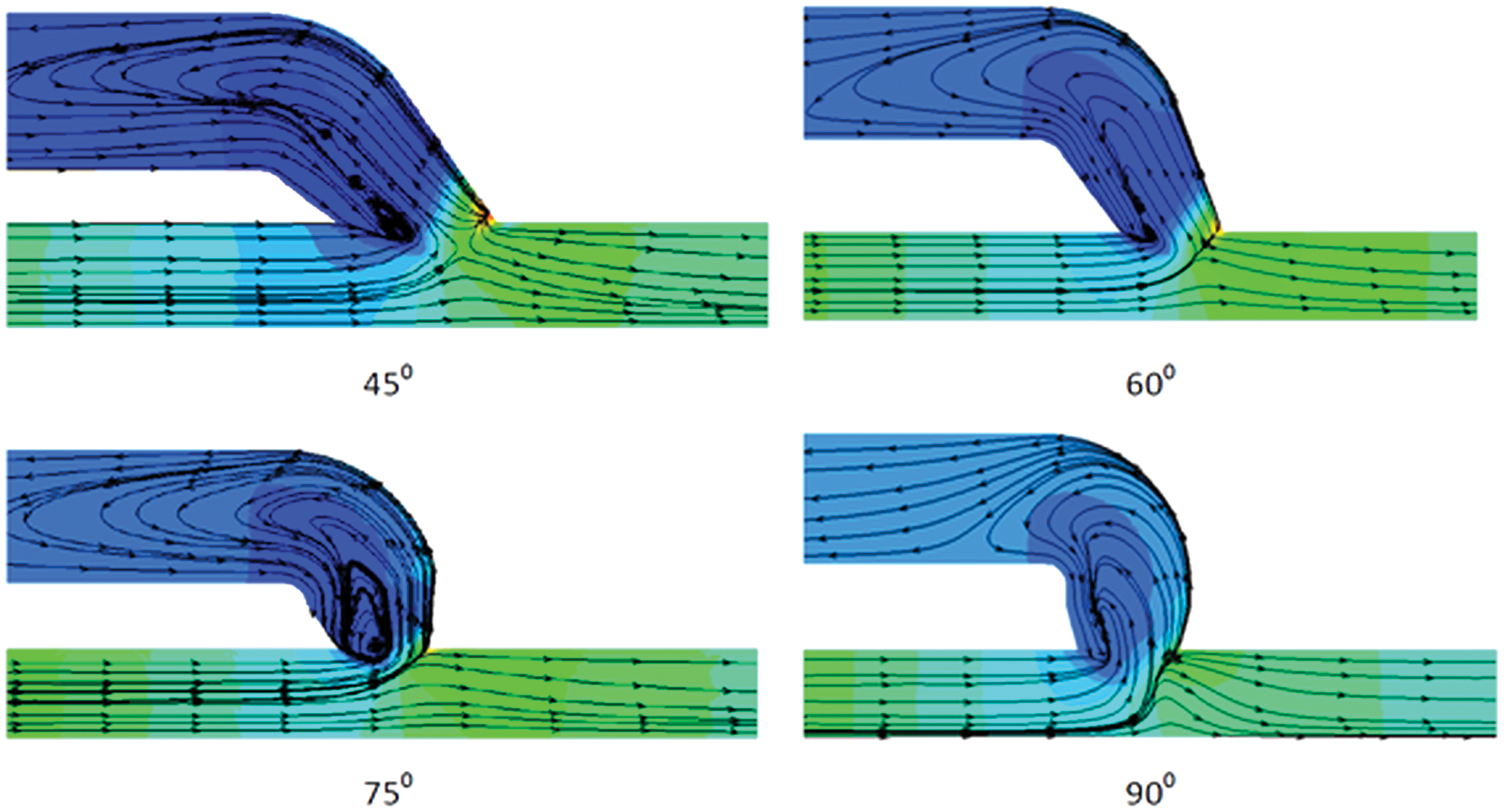
Figure 7: Streamline pattern showing the recirculation of blood flow through the AVF geometry at anastomosis angle of 45°, 60°, 75° and 90° for the inflow rate of 900 ml/min

3.3 Strouhal Number

The above-described simulation is in the form of dimensional form, also sometimes it is good practice to identify the non-dimensional quantities related to the simulation. The Strouhal number is the non-dimensional number describing the oscillation flow mechanism. The Strouhal number is often given as seen in Eq. (3)

St=ωLU (3)

where ω is the frequency of oscillation, L is the characteristic length and U is the flow velocity. The Strouhal number in the various AVF geometry is showing in Fig. 8.

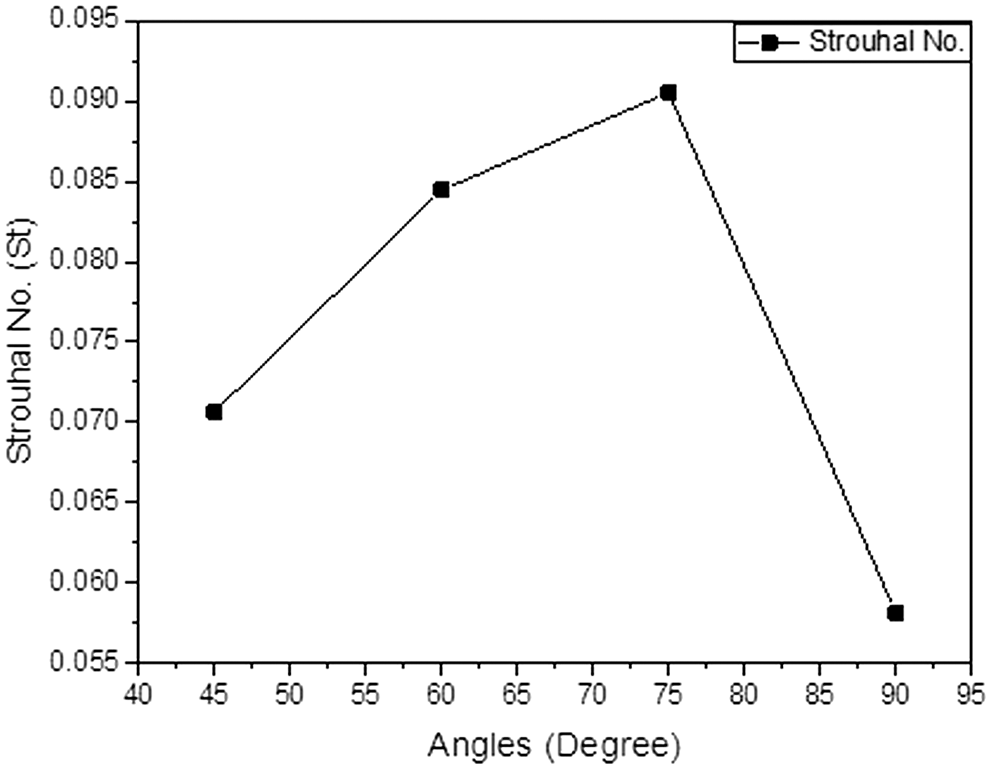
Figure 8: Strouhal number (St) at a different angle of anastomosis for the inflow rate of 900 ml/min

By observing the above graph one can easily make the hypothesis that the oscillation at the angle of 75° is much higher than the other angles of the anastomosis. The lowest oscillation was observed at an angle of 90°.

3.4 Pressure Drop

Pressure drop is the loss in the AVF geometry vessels because of the frictional resistance in this case the wall shear stress. By knowing the pressure drop across the anastomosis of AVF geometry, one can guess how much pressure is needed to get the optimum blood flow rate required for the hemodialysis. The typical pressure drop across the AVF geometry for the various angle of the anastomosis is shown in Fig. 9. The higher the pressure drop of the system the higher will be the blood flowing through the AVF. In the figure, it is seen that the pressure drop across the anastomosis is high at 45°.

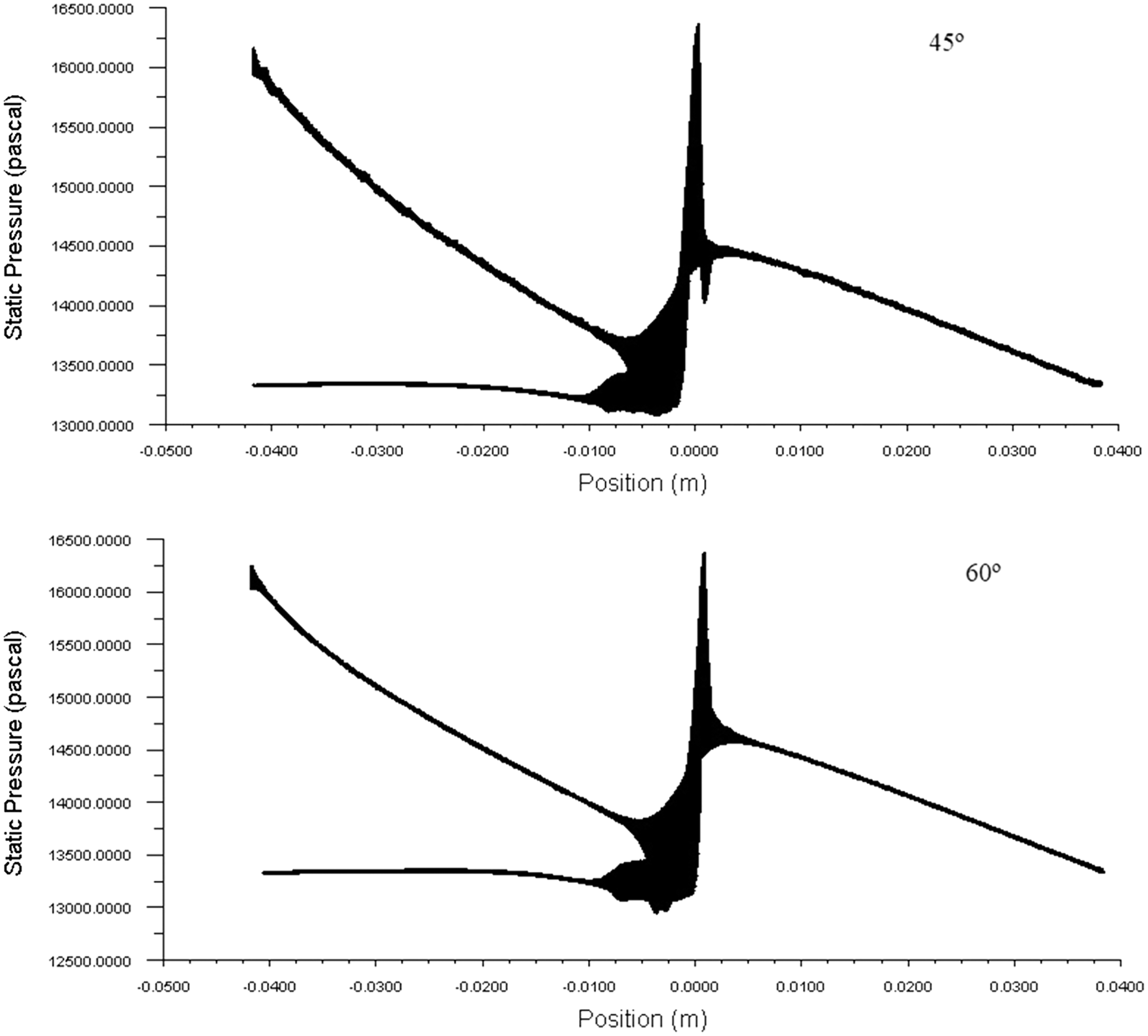
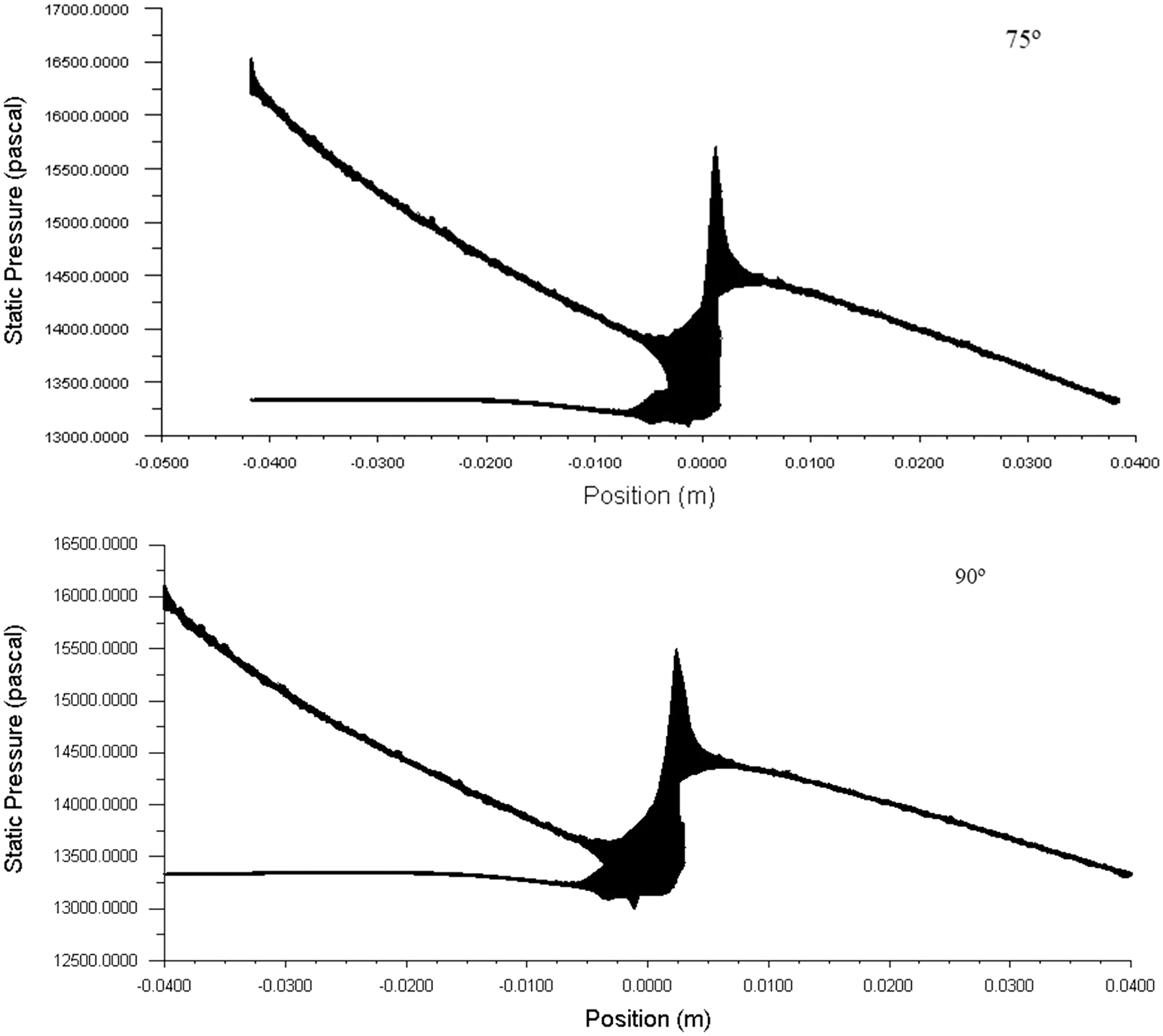
Figure 9: The behavior of pressure within the AVF geometries and pressure drop across the anastomosis area at 900 ml/min

4  Discussion and Conclusion

Simulation of the blood flow is undergone in AVF geometries at different angles of anastomosis. The objective of this research work was to identify at what angle of anastomosis the blood flow rate in the distal vein of AVF is maximum and WSS is minimum, with a focus on how the angle of anastomosis affects the blood flow and leads to intimal hyperplasia. At the time of surgery, the surgeon joins the end of the vein to the side of the artery at 90° as shown in Fig. 1. But, it is observed that (a) It is observed that, for all inflow rates the highest WSS appears at 75° and lowest at 60°. At 45° and 90° the WSS are moderate for all inflow rates, however when compare between the two, 45° has low WSS values. As a result, the 45° angle is the best anastomosis angle because it provides moderately high WSS, which is beneficial for vein inflammation. (b) Now, considering the Strouhal number in the Fig. 8, it is seen that high Strouhal number obtained at 75° and 60°, while it is low at 90°. The Strouhal number is at its moderate value for angle 45°. (c) In the hemodialysis process blood is extracted from the mature AVF, that is from bulged vein. From Fig. 6, the maximum venous outflow rate 344.85 ml/min is seen at 45° for inflow rate of 500 ml/min, except this, the venous outflow rate is increases as the inflow rate is increased. (d) The pressure drop across the anastomosis of the AVF is higher at an angle of 45° compared to 60°, 75°, and 90°.

So one can say that comparing between two angles, i.e., 45° and 60°, the WSS is greater in 45° than the 60° and the Strouhal number is greater in 60° than the 45°. The outflow rate at the vein outlet is much higher in 45° than the 60°. However for the maturation of AVF, initially quite high WSS is required for the inflammation of the vein. From the above discussion, it can be concluded that 45° angle is the best choice for the anastomosis of AVF.

Disclaimer about ethical issues: This research work is based purely on the numerical study of effect of various angle of anastomosis on AVF and its flow pattern including pressure and shear stress distribution. No clinical trials or case studies are involved. Thus no ethical approval has been sought for this study.

Acknowledgement: The authors are thankful to Ashwini Kidney & Dialysis Center Pvt., Ltd., AKDC, Nagpur, Maharashtra for the understanding of the medical terms. The authors also thankful to Mayflower Clinic, Nagpur, Maharashtra for showing the surgical technique used.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Jodko, D., Obidowski, D., Reorowicz, P., Jóźwik, K. (2017). Blood flows in end-to-end arteriovenous fistulas: Unsteady and steady state numerical investigations of three patient-specific cases. Biocybernetics and Biomedical Engineering, 37(3), 528–539. DOI 10.1016/j.bbe.2017.05.006. [Google Scholar] [CrossRef]

 2.  Canneyt, K. V., Pourchez, T., Eloot, S., Guillame, C., Bonnet, A. et al. (2010). Hemodynamic impact of anastomosis size and angle in side-to-end arteriovenous fistulae: A computer analysis. Journal of Vascular Access, 11(1), 52–58. DOI 10.1177/112972981001100111. [Google Scholar] [CrossRef]

 3.  Ene-Iordache, B., Remuzzi, A. (2012). Disturbed flow in radial-cephalic arteriovenous fistulae for haemodialysis: Low and oscillating shear stress locates the sites of stenosis. Nephrology Dialysis Transplantation, 27(1), 358–368. DOI 10.1093/ndt/gfr342. [Google Scholar] [CrossRef]

 4.  Grechy, L., Iori, F., Corbett, R. W., Gedroyc, W., Duncan, N. et al. (2017). The effect of arterial curvature on blood flow in arterio-venous fistulae: Realistic geometries and pulsatile flow. Cardiovascular Engineering Technology, 8(3), 313–329. DOI 10.1007/s13239-017-0321-2. [Google Scholar] [CrossRef]

 5.  Pike, D., Shiu, Y. T., Somarathana, M., Guo, L., Isayeva, T. et al. (2017). High resolution hemodynamic profiling of murine arteriovenous fistula using magnetic resonance imaging and computational fluid dynamics. Theoretical Biology and Medical Modelling, 14(1), 5, 1–17. DOI 10.1186/s12976-017-0053-x. [Google Scholar] [CrossRef]

 6.  Dember, L. M. (2008). Effect of clopidogrel on early failure of arteriovenous fistulas for hemodialysis. A randomized controlled trial. JAMA, 299(18), 2164–2171. DOI 10.1001/jama.299.18.2164. [Google Scholar] [CrossRef]

 7.  Sho, E., Nanjo, H., Sho, M., Kobayashi, M., Komatsu, M. et al. (2004). Arterial enlargement, tortuosity, and intimal thickening in response to sequential exposure to high and low wall shear stress. Journal of Vascular Surgery, 39(3), 601–612. DOI 10.1016/j.jvs.2003.10.058. [Google Scholar] [CrossRef]

 8.  Papaioannou, T. G., Stefanadis, C. (2005). Vascular wall shear stress: Basic principles and methods. Hellenic Journal of Cardiology, 46(1), 9–15. [Google Scholar]

 9.  Krishnamoorthy, M. K., Banerjee, R. K., Wang, Y., Zhang, J., Roy, A. S. et al. (2008). Hemodynamic wall shear stress profiles influence the magnitude and pattern of stenosis in a pig AV fistula. Kidney International, 74(11), 1410–1419. DOI 10.1038/ki.2008.379. [Google Scholar] [CrossRef]

10. Rajabi-jagahrgh, E., Banerjee, R. K., Wang, Y., Roy-Chaudhury, P., Al-Rjoub, M. et al. (2014). New techniques for determining the longitudinal effects of local hemodynamics on the intima-media thickness in arteriovenous fistulae in an animal model. Seminars in Dialysis, 27(4), 424–435. DOI 10.1111/sdi.12162. [Google Scholar] [CrossRef]

11. He, Y., Terry, C. M., Nguyen, C., Berceli, S. A., Shiu, Y. E. et al. (2013). Serial analysis of lumen geometry and hemodynamics in human arteriovenous fistula for hemodialysis using magnetic resonance imaging and computational fluid dynamics. Journal of Biomechanics, 46(1), 165–169. DOI 10.1016/j.jbiomech.2012.09.005. [Google Scholar] [CrossRef]

12. Patrick, M., Leotta, D. F., Beach, K. W., Zierler, R. E., Aliseda, A. (2013). Incomplete restoration of homeostatic shear stress within arteriovenous fistulae. Journal of Biomechanical Engineering, 135(1), 1–10. [Google Scholar]

13. Bharadvaj, B. K., Mabon, R. F., Giddens, D. P. (1982). Steady flow in a model of the human carotid bifurcation. Part I-flow visualization. Journal of Biomechanics, 15(5), 349–362. DOI 10.1016/0021-9290(82)90057-4. [Google Scholar] [CrossRef]

14. Irace, C., Cortese, C., Fiaschi, E., Carallo, C., Farinaro, E. et al. (2004). Wall shear stress is associated with intima-media thickness and carotid atherosclerosis in subjects at low coronary heart disease risk. Stroke, 35(2), 464–468. DOI 10.1161/01.STR.0000111597.34179.47. [Google Scholar] [CrossRef]

15. Himburg, H. A., Grzybowski, D. M., Hazel, A. L., Lamack, J. A., Li, X. et al. (2004). Spatial comparison between wall shear stress measures and porcine arterial endothelial permeability. American Journal of Physiology. Heart and Cardiac Physiology, 286(5), 1916–1922. DOI 10.1152/ajpheart.00897.2003. [Google Scholar] [CrossRef]

16. Jodko, D., Obidowski, D., Reorowicz, P., Jóźwik, K. (2014). Simulations of the blood flow in the arterio-venous fistula for haemodialysis. Acta of Bioengineering and Biomechanics, 16(1), 69–74. [Google Scholar]

17. Singh, T. M., Xu, C., Zarins, C. K., Masuda, H. et al. (2015). Blood flow decrease induces apoptosis of endothelial cells in previously dilated arteries resulting from chronic high blood flow. Arterioscler, Thrombosis, and Vascular Biology, 21(7), 1139–1145. DOI 10.1161/hq0701.092118. [Google Scholar] [CrossRef]

18. Nikam, M., Chemla, E. S., Evans, J., Summers, A., Brenchley, P. et al. (2015). Prospective controlled pilot study of arteriovenous fistula placement using the novel optiflow device. Journal of Vascular Surgery, 61(4), 1020–1025. DOI 10.1016/j.jvs.2014.11.082. [Google Scholar] [CrossRef]

19. Niemann, A. K., Thrysoe, S., Nygaard, J. V., Hasenkam, J. M., Petersen, S. E. (2012). Computational fluid dynamics simulation of a-v fistulas: From MRI and ultrasound scans to numeric evaluation of hemodynamics. Journal of Vascular Access, 13(1), 36–44. DOI 10.5301/JVA.2011.8440. [Google Scholar] [CrossRef]

20. Gedroyc, W., Duncan, N., Caro, C. G., Vincent, P. E., Iori, F. et al. (2015). The effect of in-plane arterial curvature on blood flow and oxygen transport in arterio-venous fistulae. Physics of Fluids, 27(3), 031903. DOI 10.1063/1.4913754. [Google Scholar] [CrossRef]

21. Sigovan, M., Rayz, V., Gasper, W., Alley, H. F., Owens, C. D. et al. (2013). Vascular remodeling in autogenous arterio-venous fistulas by MRI and CFD. Annals of Biomedical Engineering, 41(4), 657–668. DOI 10.1007/s10439-012-0703-4. [Google Scholar] [CrossRef]

22. Lowe, G. D., Fowkes, F. G., Dawes, J., Donnan, P. T., Lennie, S. E. et al. (1993). Blood viscosity, fibrinogen, and activation of coagulation and leukocytes in peripheral arterial disease and the normal population in the Edinburgh artery study. Circulation, 87(6), 1915–1920. DOI 10.1161/01.CIR.87.6.1915. [Google Scholar] [CrossRef]

23. Fry, D. L. (1969). Certain chemorheologic considerations regarding the blood vascular interface with particular reference to coronary artery disease. Circulation, 40, IV-38–IV–57. DOI 10.1161/01.CIR.40.5S4.IV-38. [Google Scholar] [CrossRef]

24. Caro, C. G., Schroter, R. C., Fitz-Gerald, J. M. (1971). Atheroma and arterial wall shear observation, correlation and proposal of a shear dependent mass transfer mechanism for atherogenesis. Proceedings of the Royal Society B, 177(1046), 109–159. [Google Scholar]

25. Hull, J. E., Balakin, B. V., Kellerman, B. M., Wrolstad, D. K. (2013). Computational fluid dynamic evaluation of the side-to-side anastomosis for arteriovenous fistula. Journal of Vascular Surgery, 58(1), 187–194. DOI 10.1016/j.jvs.2012.10.070. [Google Scholar] [CrossRef]

26. Lwin, N., Wahab, M., Carroll, J., Barber, T. (2014). Experimental and computational analysis of a typical arterio-venous fistula. Proceedings 19th Australasian Fluid Mechanics Conference, pp. 8–11, Melbourne, Australia, AFMC. [Google Scholar]