Safety Evaluation of Bridge under Moving Abnormal Indivisible Load Based on Fusing Bridge Inspection Data and Load Test Data

1  Introduction

Road transportation of oversized and/or overweight cargo, for example, agricultural machinery, production lines, and equipment for construction, mining, or other special purposes, is important for industrial development and economic growth. This special transportation and the corresponding transportation vehicle are called the Large-Cargo Transportation (LCT) and LCT vehicle, respectively. From the civil infrastructure point of view, the LCT vehicle is a Moving Abnormal Indivisible Load (MAIL). Especially, the MAIL will significantly affect the safety of highway bridges, so it is crucial to conduct a safety evaluation of bridges under MAILs. From the governing authority’s point of view, there are two categories of oversized and/or overweight vehicles: permit vehicles and illegal vehicles. An LCT vehicle is a permitted vehicle operating legally under permissions granted by the authority. It is suggested in [1] that it needs greater caution by the authority when permits for oversized and/or overweight vehicles are issued, since the possibility of inducing limit states overcoming events is considerably higher than for ordinary vehicles. Intelligent transportation system-based real-time traffic management strategies can be used to protect the bridge from overloading, and a brief discussion of this approach can be found in [1,2].

The European Commission regulated the weight and speed of the LCT vehicle, and the Danish Road Directorate encoded an informatics program to assist in the approval of permits [3]. To protect highways, the Federal Highway Administration of the United States provided an oversized/overweight load permit for each State [4]. Australia set provisions on the mass limit of single axles of agricultural vehicles [5]. China established an approval standard for LCT, including “pre-transport safety evaluation and in-transport health monitoring of civil infrastructures”. In 2023, the Ministry of Transport of the People’s Republic of China issued the “Technical Specifications for Highway Transport Safety Audit of Abnormal Indivisible Load” (hereinafter called Specifications of Abnormal Indivisible Load (JTG/T 2013-2023) [6]) as a recommended standard. According to these specifications, the technical condition (or health condition) grade of a bridge should be determined based on the “Specifications for Maintenance of Highway Bridges and Culverts” (hereinafter called Specifications for Maintenance (JTG 5120-2021) [7]) and the “Specification for Inspection and Evaluation of Load-bearing Capacity of Highway Bridges” (hereinafter called Specification for Load-bearing Capacity (JTG/T J21-2011) [8]). Bridges with technical condition grades 4 and 5 are not permitted for the pass of LCT vehicles; and bridges with grades one, two, or three must undergo a structural passability evaluation based on the safety evaluation of bridges. There are two approaches for bridge safety evaluation under MAILs: vehicle Load Effect (LE) comparison approaches and vehicle LE checking approaches. The principles, applicable scope, and calculation processes of these two methods are different, and the following will provide a detailed discussion.

Vehicle LE comparison approaches compare the LE value of the LCT Vehicle with the design vehicle LE value. According to the Specifications of Abnormal Indivisible Load (JTG/T 2013-2023) [6], when the technical condition of the bridge is classified as grade 1 or 2, and the total weight LE of the vehicle and cargo is less than the design vehicle LE , vehicle LE comparison approaches can be used. Note that vehicle LE comparison approaches only consider changes in LEs without accounting for resistance degradation. This is because these approaches implicitly assume that the technical condition of the bridge stays at a good level of grade 1 or 2, and neglect resistance degradation. In other words, the LE will not exceed the design resistance as long as the LE caused by the MAIL does not exceed the design value of the load. In this case, the LCT vehicle is allowed to pass through the bridge. However, the LE caused by a MAIL often exceeds the design value [9–11], and the bridge’s resistance normally degrades after being in service [12–14]. In conclusion, the safety evaluation process of vehicle LE comparison approaches is relatively simple, but it is only applicable to cases when the LE of the vehicle does not exceed the design value and the resistance degradation of the bridge is negligible.

Vehicle LE checking approaches compare the LE of the MAIL with the resistance of the structural component. According to the Specifications of Abnormal Indivisible Load (JTG/T 2013-2023) [6], the LE value of the MAIL must be compared with both the ultimate limit state of load-bearing capacity and the serviceability limit state under permanent conditions, as specified in the “General Specifications for Design of Highway Bridges and Culverts” (JTG D60-2015) [15] and “Unified standard for reliability design of highway engineering structures” hereinafter called Standard for Reliability Design (JTG 2120-2020) [16]. The safety evaluation can be conducted based on the Specification for Load-bearing Capacity (JTG/T J21-2011) [8]. The Specifications of Abnormal Indivisible Load (JTG/T 2013-2023) [6] states the range of application of these approaches: 1) when the technical condition of the bridge is at grade one or two, and the total weight LE of the vehicle and cargo is greater than or equal to the design vehicle LE , or 2) when the technical condition is at grade three. Zhang et al. [17] updated the Finite Element Model (FEM) by modifying physical parameters such as bending stiffness based on quasi-static load tests, and used the updated deflection calibration coefficient to approximate the actual load-bearing capacity of the bridge. Cui et al. [18], by considering partial factors under accidental combinations and transverse distribution coefficients, calculated the bending moment LE of slab beams induced by the MAIL and compared it with the structural bending moment load-bearing capacity. Xing [19], based on load test data, updated the FEM by adjusting the reinforcement ratio and compared the calculated span-to-deflection ratio with the limit value for safety evaluation. Chen et al. [20] focused on sections of the LE ratio being greater than one, and after adjusting the axle load allocation of the MAIL, performed calculations of the LEs such as bending moment, shear force, axial force, and flange stress, comparing them with the corresponding resistances. In conclusion, the safety evaluation process of vehicle LE checking approaches is relatively complex, but the approaches consider the changes in both LEs and resistances, making it suitable for the safety evaluation of bridges under MAILs in all situations.

Vehicle LE checking approaches are more suitable than vehicle LE comparison approaches for the safety evaluation of bridges under MAILs, but there still exists a critical but unsolved issue for vehicle LE checking approaches. That is, updating the safety evaluation of a bridge by fusing its inspection data and load test data. The safety evaluation depends on the LE and resistance, and the latter two factors depend on the basic quantities of interest (QoI), such as the material and geometry parameters of structural components. However, most of the existing research performed safety evaluation of bridges under MAILs based on bridge design data only without considering any updating [18]. There are two fundamental difficulties in updating. First, the inspection data contains both the structured data (e.g., sample test data of material strength and unstructured data) and the unstructured data (e.g., qualitative description of weathering, carbonization, physical and chemical damage of components). The structured data can be directly utilized to update the corresponding QoI while the unstructured data cannot. The first difficulty is to develop an updating scheme to utilize the unstructured inspection data. Second, the load test is the follow-up action of the inspection, so the successively updating using the load test data should be conducted based on the updating results of the inspection data. Most of the existing research performed safety evaluation without conducting this successively updating, e.g., updating based on load test data only [17,19] or based on bridge maintenance data only [18,20] but ignoring bridge inspection data. The second difficulty is to develop a successive updating scheme using load test data based on the previous updating results of the inspection data.

In order to tackle these two fundamental difficulties of updating, this paper proposed a framework for the safety evaluation of bridges under MAILs based on fusing bridge inspection and load test data. The framework consists of three modules. Module one is the updating of FEM and resistance of the bridge based on fusing bridge inspection data and load test data. The first difficulty in utilizing the unstructured inspection data is tackled by introducing the updating guidelines using the unstructured inspection data (recommended by Specification for Load-bearing Capacity (JTG/T J21-2011) [8]). The updating guidelines are a series of empirical equations, obtained from previous experiment studies of the unstructured inspection data and Delphi method [8]. Correspondingly, the basic QoIs are selected compatible with [8]. The above key technique is fused into the design data and structured inspection data, so updating can be performed on the Probability Density Functions (PDFs) of basic Random Variables (RVs), the FEM, and the PDF of the resistance. The second difficulty in conducting a successively updating scheme using load test data based on previous updating results is tackled by Bayesian updating. The stiffness substructural parameters are the re-parameterization of the stiffness matrix of the inspection stage. Prediction-error including measurement and modeling uncertainties are considered. The posterior PDF of the parameters is obtained based on the load test data and the prior PDF reflecting the previous updating results of the inspection data. Module two is the simulation of a bridge under a MAIL, updating of the PDFs of LEs of critical sections of critical components based on the updated FEM and the given MAIL. Module three is the safety evaluation of the bridge based on load-bearing capacity index [8] and reliability index, updating indices based on the updated resistance and LE. The focus of module three is not to develop a novel algorithm to evaluate the reliability integral, but to successively update load-bearing capacity index and reliability index for the safety assessment of an existing bridge based on the initial dataset (design data), first round updating dataset (initial dataset plus inspection data), and second round updating dataset (first round updating data plus load test data). The illustrative examples consist of a simulated example and an engineering example, demonstrating the effectiveness of the proposed framework.

2  Framework

Fig. 1 shows the framework of safety evaluation of the bridge under MAIL based on fusing bridge design, inspection, and load test data. Note that , , , and denote data, FEM, resistance, and LE, respectively. There are three modules: module one (the bold-dash part ‘3.1’), module two (the dash part ‘3.2’), and module three (the dotted part ‘3.3’). There are three kinds of data: design and as-built stages data (), inspection data (), and load test data (). Denote , , . Following this notation convention, the superscript 0, ′, ″ denote the variable/quantity to be inferred is at the initial round based on , first round updating based on , and second round updating based on . For example, is the resistance based on , i.e., the resistance fusing bridge design, inspection, and load test data.

Figure 1: Framework of safety evaluation of bridge under MAIL based on fusing bridge design, inspection and load test data

Table 1 shows the outline of module one, two, and three, as well as the initial round, first round updating, and second round updating, of the proposed framework. The table has ten rows, namely, R1 to R10, and three columns, namely, C1 to C3. Based on the row and column numbers of each cell in Table 1, one can quickly identify the location of the cell. For example, cell (R6, C2) is for the PDF of resistance of first round updating.

Modules one, two, and three correspond to cell (R1:R6, C1:C3), cell (R7:R8, C1:C3), and cell (R9:R10, C1:C3), respectively. The initial round, first round updating, and second round updating correspond to cell (R1:R10, C1), cell (R1:R10, C2), and cell (R1:R10, C3), respectively. Module one is the updating of FEM and resistance of the bridge based on fusing bridge inspection data and load test data. In order to utilize the unstructured inspection data, the updating guidelines using the unstructured inspection data recommended by Specification for Load-bearing Capacity (JTG/T J21-2011) [8] is introduced. These guidelines are a series of empirical equations, obtained from previous experiment studies of the unstructured inspection data and Delphi method. Correspondingly, the basic QoIs are selected compatible with the code [8]. The above key technique is fused into the design data and structured inspection data, so updating can be performed on the Probability Density Functions (PDFs) of basic RVs, the FEM, and the PDF of the resistance. A successively updating scheme using load test data based on previous updating results is tackled by Bayesian updating. The stiffness substructural parameters are the re-parameterization of the stiffness matrix of the inspection stage. Prediction-error including measurement and modeling uncertainties are considered. The posterior PDF of the parameters is obtained based on the load test data and the prior PDF reflecting the previous updating results of the inspection data. Module two is the simulation of a bridge under a MAIL, updating the expectations and PDFs of LEs of critical sections of critical components based on the updated FEM and the given MAIL. Module three is the safety evaluation of the bridge based on load-bearing capacity index [8] and reliability index, updating indices based on the updated resistance and LE. The focus of module three is not to develop a novel algorithm to evaluate the reliability integral, but to successively update load-bearing capacity index and reliability index for the safety assessment of an existing bridge based on the initial dataset (design data), first round updating dataset (initial dataset plus inspection data), and second round updating dataset (first round updating data plus load test data). Details of Table 1 will be presented in Section 3.

3  Modules

3.1 Module One: Updating of FEM and Resistance of Bridge Based on Fusing Bridge Inspection Data and Load Test Data

3.1.1 Module Description

Module one, shown in the bold-dash part ‘3.1’ of Fig. 1 and cell (R1:R6, C1:C3) of Table 1, is the updating of FEM and resistance of bridge based on fusing bridge inspection data and load test data. According to the QoI (Quantity of Interest), module one focuses on totally six QoI. Cell (R1, C1:C3), cell (R2, C1:C3), and cell (R3, C1:C3) of Table 1 are the basic QoI (Quantity of Interest), the inference/updating method of basic QoI, and the PDF of basic QoI, respectively, of three rounds. Note that the basic QoIs are for those quantities for which observational data are available or can be obtained. Cell (R4, C1:C3) is the FEM of three rounds. Cell (R5, C1:C3) and cell (R6, C1:C3) are the design/Code-Com resistance and the PDF of resistance, respectively. According to the utilized data for inference/updating, i.e., , , or , module one can be further divided into three submodules: submodule one (cell (R1:R6, C1)), submodule two (cell (R1:R6, C2)), and submodule three (cell (R1:R6, C3)). Details of each submodule will be presented in the following subsections.

3.1.2 Initial FEM (FEM0) and Resistance (R0) Based on Bridge Design Data (Ddesign)

The initial round is outlined in cell (R1:R6, C1) of Table 1. Although many quantities can be considered, this study selected the same basic QoI as the code (Specification for Load-bearing Capacity (JTG/T J21-2011) [8]). Thus, is called the Code-Com basic QoI, where is the material strength, is the geometric parameter of concrete, and is the geometric parameter of reinforcement. Correspondingly, the PDFs of the Basic RVs are given in cell (R3, C1), where , , and are the PDFs obtained from , respectively. For example, based on , the compressive strength of C40 concrete follows the log-normal PDF with mean as 48.0 MPa and COV (Coefficient Of Variation) as 0.15.

The initial FEM () as well as initial resistance () can be obtained directly from . Resistance generally refers to the capacity of a structure or its components to withstand these effects, including load-bearing capacity, stiffness, and crack resistance [21]. For most of common bridge structures, can be calculated according to the “Specifications for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts” (JTG 3362-2018) [22]. The PDF of resistance is obtained from the transformations of RV:

(1)

where is the function mapping from to the resistance. Note that can be obtained using the analytical way or using the Dist-Fit (probability Distribution fitting) based on the MCS (Monte Carlo Simulation) samples of for special or general cases, respectively.

3.1.3 First Round Updating of FEM (FEM’) and Resistance (R’) Based on Bridge Inspection Data (Dinspection)

The first round updating is outlined in cell (R1:R6, C2) of Table 1. Before the first round updating based on , it is required to check the bridge’s technical conditions. “The Regulations for the Management of Over-limit Transport Vehicles on Highways” [23] and the Specifications of Abnormal Indivisible Load (JTG/T 2013-2023) [6] state that over-limit transport vehicles are not allowed to pass over bridges with a technical condition grade of three or below. Table 2 shows assessment of bridge technical conditions, which can be found on page seventeen of Specification for Load-bearing Capacity (JTG/T J21-2011) [8]. According to the specification, it relies on both field inspection and engineering judgment. Field inspection is divided into two aspects: visual inspection and non-destructive testing. Visual inspection mainly records external structural issues such as cracks and defects on the bridge. Non-destructive testing includes assessing the compressive strength of concrete components and the corrosion of reinforcement. In conclusion, the first round updating is conducted only when the bridge is with a technical condition grade of three or below.

Table 3 shows first round updating of basic QoI based on according to the code [8]. Compared to the initial round, in addition to , three extra basic QoI are introduced: , . The inspection dataset contains both structured and unstructured data. The structured data, such as sample test data of material strength (), can be directly utilized to update the corresponding QoI. The unstructured data, such as the qualitative description of weathering, carbonization, and physical and chemical damage of components, cannot be directly utilized for updating. To fuse the unstructured data of inspection for updating, the expert experience method [8] is introduced that the basic QoI is updated according to a series of empirical equations by experts based on the unstructured data of inspection.

According to the second row of Table 3, the code [8] only gives guidelines about how to achieve , but it does not give updating guidelines and method. Here, we introduce Bayesian updating for based on . Let denote the prescribed PDF of the i-th measured data point conditional on uncertainty parameter vector . Note that the PDFs of and are the same but is to be inferred while is known. According to Bayes’ theorem, the posterior PDF of can be expressed as the product of the likelihood function , i.e., the probability of observing , and the prescribed prior PDF , reflecting the prior information about based on :

(2)

where the likelihood function adopts the widely accepted assumption on statistical independent between and , and the third equation is exact for the flat prior PDF or asymptotically valid as the number of observations increases. Then, the updated PDF of is:

(3)

where is evaluated at the MAP (Maximum A Posteriori) value.

Based on the third and fourth rows of Table 3, and are updated as:

(4)

(5)

where and can be updated according to Sections 7.7.5 and 7.7.6 of [8], respectively. Note that these two section-reduction coefficients are to reduce the resistance due to the loss of the effective areas of sections of a structure or its components, by taking into account the weathering, carbonization, and physical and chemical damage. According to the transformation of RVs, the updated PDF of and are:

(6)

(7)

Based on the fifth and sixth rows of Table 3, is updated as:

(8)

where is the inspection-based modification coefficient of bridge load-capacity, to comprehensively modify the resistance of a bridge structure or its components, by taking into account the inspection data , including the apparent defect of the bridge structure or component, the material strength and the natural frequency of the bridge structure; is the deterioration coefficient of load-bearing capacity, to reduce the resistance due to deterioration of a bridge structure and its components, by taking into account the defects of the structure or components, corrosion potential of the steel bars, the thickness of the protective layer, and the strength, resistivity, chloride ion content, and carbonization status of the concrete.

The updated can be obtained according to the updated PDF of . Note that if only deterministic analysis is considered, the updated can be obtained based on the expatiation of the physical parameters where , , and are the expatiations of the corresponding updated PDFs. Note that in the FEM software, can be directly modified according to .

The Code-Com resistance is:

(9)

The PDF of resistance is obtained from the transformations of RV:

(10)

Similar to cell (R6, C1), can be obtained using the analytical way or using the Dist-Fit.

One may be concerned about the issue of the completeness of an inspection report. The framework is still applicable to any inspection report without prescribing the complement of the inspection report. This is because the proposed framework fuses the updating guidelines of Specification for Load-bearing Capacity (JTG/T J21-2011) [8], and this specification allows the inspection data to be incomplete.

3.1.4 Second Round Updating of FEM (FEM”) and Resistance (R”) Based on Bridge Load Test Data (Dtest)

The second round updating is outlined in cell (R1:R6, C3) of Table 1. The purpose of the load test is to verify whether the bridge structure fulfills the design load or special load requirements. The MAIL belongs to the special load. In the basis of and , is integrated to update the FEM from to .

Consider the bridge under the load test is monitored by a sensor network with observations at each time step. Let , related to , denote the model output at the -th time step, parameterized the unknown structural parameter vector . There are two parameterization ways for the . The can be expressed in either the forms of physical parameters (similar to the parameters utilized in the initial round and first round updating) or substructural parameters.

When using the physical parameter-based updating, one or more material properties are used as parameters, and the updated material parameters and their distributions are identified based on . For example, the material parameters are the elastic modulus [24–27], density [26,27], Poisson’s ratio [27]; the geometry parameters are moment of inertia [26,28], neutral axis height [17], flexural stiffness [17,19].

When using the substructural parameter-based updating, the concept of substructures and substructure scaling parameters are introduced. First, the total stiffness matrix in the round one updating, , is obtained. Then, is divide into substructure stiffness matrices, and each substructure matrix associates an unknown substructure scaling parameter, . Finally, the parametrization of substructural parameter-based updating can be obtained:

(11)

where is the -th parameter to be identified, is the stiffness matrix of the -th substructure, and is the total number of substructures. This paper adopts the substructure updating way because it has been successfully applied to many civil engineering structures [29]. Since in many cases, major structural damage typically occurs in very few localized areas [29–31], converting the analysis of the entire structure into the analysis of independent substructures using compatibility conditions can enhance efficiency. Substructures can be selected according to component types or their locations. It is important to note that the selection of parameters as well as substructures should take into account the model’s identifiability, which is related to the parameter space, the governing equations, and the measured data. In the case of static load test, is:

(12)

where is the observation matrix related to the sensor location of the load test.

The measured noisy output at the -th time step :

(13)

(14)

where is the uncertain prediction-error at the -th time step, parameterized by the unknown error parameter vector ; and are measurement error and modelling error, respectively. There are several facts about the above error model. First, given the PDF and , the PDF of can be conducted using the convolution of probability distribution. Second, if mean and variance are specific of or , the corresponding maximum entropy probability distribution follows the normal distributions. Third, if both error follows normal distributions, also follows the normal distribution. Here, we follow the same assumption of [32] that, without further information about error, the prediction-error can be assumed to be normal distribution with zero-mean, as uncertain bias can be added to model output as another uncertain parameter, and unknown variance (denoted as “”). If one is interested in more general cases of prediction-error model, one can refer to [33].

By collecting load test data up to sampling time steps, the measured noisy output matrix is , the model output matrix is , and the uncertain measurement error matrix is . Based on spatial and temporal uncorrelated model for , the likelihood function, conditional on unknown parameter vector , can be expressed as:

(15)

According to Bayes’ theorem, we proposed the posterior PDF fusing design data, inspection data, and load test data:

(16)

where is the prior PDF, reflecting uncertainty introduced by modeling error at the parameter level based on the prior information given by the first round updating. It is assumed to be a flat PDF, this prior will be absorbed into the normalizing constant [34–36]. In this case, the posterior PDF is dominated by . Denote . In the globally identifiable case [37], the posterior PDF can be well approximated by the multivariate normal distribution with:

(17)

(18)

where is called the hessian Matrix, related to the local curvature of at . The optimization on is nonlinear, so gradient-based algorithms, random search, or heuristic algorithms can be used to solve for .

Through this model updating process, the is a well representation of the true mechanical status of the bridge. The updated can be obtained according to the updated PDF of . Note that is adopted for deterministic analysis.

According to Section 8 of [8], if the bridge load test is passed, the Code-Com resistance can be updated as:

(19)

(20)

where is called the load test-based modification coefficient of bridge load-capacity, to comprehensively modify the resistance of a bridge structure or its components, by taking into account the load test data . The PDF of resistance is obtained as:

(21)

where is obtained from the transformations of RV: , with the support reflecting the bridge load test is passed. Note that is the maximum LE corresponding to the load test, obtained by applying the load to the updated . The reason of truncating the PDF is explained as follows [38,39]: when the bridge passes the load test, it is considered that the resistance has at least reached the level of the LE corresponding to the test load. At this point, the PDF of the resistance is updated to a truncated distribution with as the lower bound.

3.2 Module Two: Simulation of Bridge under MAIL

3.2.1 Module Description

Module two, shown in the dash part ‘3.2’ of Fig. 1 and cell (R7:R8, C1:C3) of Table 1 is the simulation of a bridge under a MAIL. In Table 1, cell (R7, C1:C3) is the expectation of LE, and cell (R8, C1:C3) is the PDF of LE. The simulation analysis involves obtaining the LEs (denoted as ) and their distributions for three FEMs. For the distribution of LEs that can be explicitly calculated, the and their distributions for a specific section of a specific component can be calculated based on the principles of structural reliability analysis. For the distribution of LEs that cannot be explicitly calculated, the load of the LCT Vehicle can be added to three FEMs and the MCS method can be applied. After computation, the for a specific section of a specific component is concerned and its probability distribution is obtained through statistical analysis. The simulation analysis aims to solve the forward problem of uncertainty propagation for .

Fig. 2 shows a simulation of bridge under MAIL for the three FEMs mentioned above, the stiffness matrices are extracted, and the probability distributions of their elements are analyzed. By adding the load model of MAIL, the LEs on the bridge under MAIL conditions can be obtained. Based on the safety evaluation requirements, critical components are selected for evaluation, and critical sections are identified according to specifications or calculation results. The LEs at these critical sections, including internal forces and deflections, can be examined in the finite element analysis software. Additionally, the distribution of the LEs can be further determined using statistical data and design information. The simulation results obtained from the different models will be used for the next stage of safety evaluation.

Figure 2: Simulation of bridge under MAIL

3.2.2 Load Model of MAIL

For the safety evaluation of bridges under MAIL, only one specific LCT vehicle is considered, and its total weight and axle weights are fixed and given. Common types of trailers used in LCT include semi-trailers, full trailers, and specialized trailers for transporting specific cargo [40]. A semi-trailer has its axles located behind the center of gravity of the vehicle and transmits horizontal or vertical forces to the towing vehicle through its coupling device. The features of semi-trailers include high load capacity, faster speed compared to full trailers, the ability to carry larger and taller cargo, and a shorter, more maneuverable body compared to full trailers. Common types of semi-trailers mainly include heavy-duty low-bed trailers, box semi-trailers, and gooseneck flat semi-trailers.

A full trailer, on the other hand, has no power of its own, is independently load-bearing, and is connected to the towing vehicle via a hitch. The towing vehicle does not bear any load, providing only the power needed to overcome road friction, while the load is entirely supported by the full trailer. Compared to semi-trailers, full trailers can carry larger and heavier abnormal loads, but they are slower and less maneuverable. The most common full-trailer combinations in highway abnormal indivisible load transportation are of three types: flatbed trailers, recessed flatbed trailers, and long cargo trailers.

LCT vehicles commonly adopt multi-axle multi-wheel hydraulic flatbed trailers [41]. Compared to standard vehicles, hydraulic flatbed trailers have a larger load-bearing surface area, longer vehicle length, and a broader longitudinal load impact range, which exerts a greater influence on bridges. The reason for selecting multi-axle hydraulic flatbed trailers in LCT is that, not only these trailers distribute the axle load evenly and ensure uniform stress on the bridge structure when the vehicle crosses, but also they can reduce axle load by increasing the number of axles, allowing them to comply with the axle load limits specified in regulations. The axle spacing of hydraulic flatbed trailers generally ranges from to , with being the most common. Therefore, the axle spacing for hydraulic flatbed trailers is set to .

Fig. 3 shows a demonstration of axle load configuration of an LCT vehicle. According to Specifications of Abnormal Indivisible Load (JTG/T 2013-2023) [6], the axle load configuration of the specific LCT vehicle is given before bridge safety evaluation. Thus, the proposed framework can adopt any LCT vehicle and the corresponding MAIL. As the MAIL of an LCT vehicle is a moving load, it consists of two parts: the position of the axles and the axle load . The process of applying loads to the bridge mainly includes self-weight, secondary loads (such as pavement, sidewalks, guardrails, etc.), temperature loads (uniform temperature rise/drop and gradient temperature rise/drop), MAIL, the shape and load of prestressed tendons, and the addition of ordinary reinforcement. Self-weight, secondary loads, temperature loads, and prestressed loads all are considered static loads and need to be defined according to the actual conditions of the bridge. The input of MAIL involves three steps: first, defining lanes (for beam elements) or lane surfaces (for plate elements) by placing them on the structural model based on factors such as the LCT vehicle path, the number of design lanes, and lane width; second, inputting ; and finally, inputting the moving path of MAIL, .

Figure 3: Demonstration of axle load configuration of an LCT vehicle

3.2.3 LEs of Critical Sections of Critical Components

In structural engineering, LEs refer to the response of a structure under the applied loads, such as internal forces (e.g., axial force, shear force, bending moment), deflections, and cracks [42]. Because there are many components of a bridge, the first issue is to select or identify critical sections of critical components. It can be done based on the guidelines [8], expert judgment (e.g., structural components with poor operational conditions indicated in the bridge inspection report), or other reanalysis methods (e.g., the most unfavorable section for moving loading in bridge engineering [43,44]), or sensitivity analysis of structural responses with respect to MAIL and/or the basic QoI. Let denote the selected/identified critical sections of critical components of the bridge, and denote the function maps the MAIL to structural response. For three rounds, i.e., , the LE of is expressed as:

(22)

Note that as MAIL is a moving load, maximum LE has to be considered. It is worth noting that because the current study focuses on the safety evaluation of a bridge under an LTC vehicle in the situation that the bridge is temporarily closed to public traffic during the LTC vehicle passes through the bridge, the vehicle LE can be obtained from module two without considering other vehicles. Another issue is about choosing static analysis or dynamic analysis. Different from traditional vehicles, the speed of an LTC vehicle should be limited to a very low range. According to Specifications of Abnormal Indivisible Load (JTG/T 2013-2023) [6], the speed of a vehicle is limited at the range from 0 to 20 km/h: when the speed is less than or equal to 5 km/h, static analysis is conducted; when the speed is at the range from 5 to 20 km/h, static analysis combined with empirical dynamic impact coefficient, which is also related to the fundamental frequency of the bridge, is conducted. It is worth noting that the difficulty is not conducting dynamic analysis but achieving dynamic properties of the LCT vehicle. However, these dynamic properties are not provided in most engineering problems. Practically, due to the distinctiveness of LCT, the speed is less than 5km/h unless otherwise specified, so choosing static analysis is suitable.

The simulation of a bridge under a MAIL can be treated as static moving load problem. This problem can be solved using the influence line, which is a functional used to describe the variation of the LE at a given section under a unit moving load. Let denote the LE of the cross section at position induced by a unit load at position , where is the span length of the bridge, conditional on . Then, the response function is:

(23)

where is the Dirac delta function.

Referred to cell (R7, C1:C3) of Table 1, the expectation of the LE of three rounds can be evaluated at the optimal value of the basic QoI:

(24)

Referred to cell (R7, C1:C3) of Table 1, the PDFs of the LE of three rounds is:

(25)

where is the PDF of basic QoI shown in cell (R3, C1:C3) of Table 1. Similar to cell (R6, C1), can be obtained using the analytical way or using the Dist-Fit. Note that although the above only considers uncertainties in the bridge structure, it can be extended to consider uncertainties in both the structure and the moving load [37,45].

3.3 Module Three: Safety Evaluation of Bridge Based on Load-Bearing Capacity and Reliability

3.3.1 Module Description

Melchers et al. (2018) [46] discussed the hierarchy of structural reliability measures (see Section 2.6 and Table 2.11 of [46]): Level 1: the partial factor approach. It is a non-probabilistic generalized version of the traditional safety factor and load factor formats. It is the format most commonly used for limit state design codes and thus for applied engineering design work at the present time. Level 2 (Second moment methods): nominal probabilities based on the use of the normal distribution and some simple mathematical forms for the limit state function. Level 3 (Exact methods): the best estimate of the probability of failure, using accurate probability models as well as the use of human error and intervention data if available. Structural system effects and the influence of time may be of importance. Level 4 (Decision Methods): minimum cost or maximum benefit, i.e., any of level 1 to 3 plus economic data. Note that although Melchers et al. (2018) [46] called level 1 a “code level method”, in the newly developed code of level 1, the partial factors are calibrated using level 2 (Second moment methods) or level 3 (Exact methods). Nowak (2012) [47] discussed about the code levels. A design code intends to provide a minimum safety level. Current codes use deterministic formulas, but the optimum design will require the consideration of structural reliability as an acceptance criterion. The acceptance criterion is defined in terms of the closeness of the actual reliability index to the optimum reliability level (or probability of failure). Depending on the approach to reliability, the codes are classified into four levels (see Section 8.3 of [47]): Level I codes: These codes use deterministic design formulas. The safety margin is introduced through central safety factors (ratio of design resistance to design load) or partial safety factors (load and resistance factors). Level II codes: These codes define the acceptance criterion in terms of the “closeness” of the actual reliability index for a design to the target reliability index or other safety-related parameters. Level III codes: These codes require a full reliability analysis to quantify the probability of failure of the structure under various loading scenarios. The acceptance criterion is defined in terms of the closeness of the actual reliability index to the optimum reliability level (or probability of failure). Level IV codes: These codes use the total expected cost of the design as the optimization criterion. The acceptable design maximizes the utility function that describes the difference between the benefits and costs associated with a particular design. Note that Standard for Reliability Design (JTG 2120-2020) [16], AASHTO LRFD bridge design specifications [48], Specification for Load-bearing Capacity (JTG/T J21-2011) [8], and Manual for Bridge Evaluation (MBE) [49] belongs to level II codes.

Module three, shown in the dotted part ‘3.3’ of Fig. 1 and cell (R9:R10, C1:C3) of Table 1, is the safety evaluation of the bridge based on load-bearing capacity and reliability. In Table 1, cell (R9, C1:C3) is the Load-bearing capacity index and cell (R10, C1:C3) is the reliability index. In addition to the above two common indices, there are some other indices, e.g., a new risk index combining the probability/frequency and consequences/severity of bridge failure or overloading event [2]. When the load-bearing capacity index is used, the expectation of the LE () and design/Code-Com resistance () are compared for evaluation. When the reliability index is used, the failure probabilities of the structure are evaluated, and the reliability index () are then compared with the reliability threshold value (). The remaining parts will be devoted to the safety evaluation of different rounds shown in Fig. 4.

Figure 4: Safety evaluations of different rounds

3.3.2 Load-Bearing Capacity Index

In load-bearing capacity assessment, the partial safety factors of load and resistance are derived based on limit state design, i.e., the corresponding reliability reaches a minimum required reliability index (target reliability index). This paper adopts load-bearing capacity index of the specification [8], which is similar to the rating factor in Load and Resistance Factor Rating (LRFR) [49]. The resistance () and LE of three rounds can be obtained from modules one and two, respectively. The safety evaluations of three rounds are conducted as follows:

(1)   Initial round

(26.1)

(26.2)

(26.3)

where is the coefficient for importance of a structure and because the MAIL of a LCT vehicle is a temporarily load [8]. The fact is also applied to first and second round updating.

(2)   First round updating

(27.1)

(27.2)

(27.3)

(27.4)

(3)   Second round updating

(28.1)

(28.2)

(28.3)

(28.4)

Finally, if the above inequality holds, the structure is considered safe; otherwise, it is unsafe. It is worth noting that in contrast to the specification [8] not considering the updating of FEM, the proposed framework gives a better estimation on the LE because of incorporating the first and second rounds updated FEM.

3.3.3 Reliability Index

The structural reliability theory accounts for all factors influencing the reliability of a structure as random variables. Utilizing extensive field measurement and testing data, statistical methods are employed to identify the statistical distributions of each random variable and to assess the failure probability (or reliability index ) of the structure. It has been applied to the evaluation of the probability of failure of bridge and the estimation of the risk [50,51]. Structural reliability problems involve two opposing quantities: a capacity (or, resistance, supply, strength, etc.) and a demand (or LE, load, stress, etc.). Here, for our research problem, the capacity and demand are bridge component resistance () and LE under MAIL (), respectively. The probability of failure is:

(29)

where is the joint PDF of and . The complement of the failure probability, , is called the reliability. Because and are functions of basic RVs , the limit-state function is defined as [52]. Note that when the and are separable, where is called safety margin. The probability of failure is the N-dimensional integral of the joint PDF of the basic RVs, , over the failure domain, [53,54].

(30)

Define the indicator function

(31)

The failure probability integral can be formulated as [55]:

(32)

(33)

where is the indicator function, is the Monte-Carlo Simulation (MCS)-based estimate on , is number of simulated samples, and means is randomly simulated according to its joint PDF. From the strong law of large numbers, converges to with probability 1 as . Based on the above, the safety evaluations of three rounds are conducted as follows:

(1)   Initial round

Both and are the functions of the initial round basic RVs , so the failure probability can be evaluated as:

(34)

(35)

where can be sampled according to its PDF .

(2)   First round updating

Both and are the functions of the first round basic RVs , so the failure probability can be evaluated as:

(36)

(37)

where can be sampled according to its PDF .

(3)   Second round updating

If the bridge load test is passed, the resistance following the PDF (see cell (R6, C3) of Table 1, and Section 3.1.4), and the LE following the PDF (see Section 3.2.3). Rigorously, the term , the maximum LE corresponding to the load test, of is the functions of second round basic RVs . There are two ways of evaluating the failure probability of second round. The first is the exact way based on the MCS, and the failure probability is evaluated the same as the first or second round:

(38)

(39)

The second is the approximated way by neglecting the dependency between and [38,39], so the failure probability is evaluated as:

(40)

According to Chapter 3 of the that Standard for Reliability Design (JTG 2120-2020) [16], the reliability index must not be less than the target reliability index :

(41)

(42)

where representing a concerned round.

When performing a reliability index evaluation, a target reliability index should also be selected. Since MAIL represents a temporary load, the target reliability index does not follow the values stipulated by current codes. A well-accepted fact is that structural deterioration increases the probability of failure over time, and thus decreases the reliability index over time [56]. The ISO (International Standard Organization) provides a framework for determining reliability indices by including several factors such as risk type and loss [57,58]. Accordingly, the target reliability index is suggested to be a fixed value, such as due to considering the loss of human life [59], or for one-year reference period [60]. Target reliability index is also suggested as a function of the age of the bridge and its remaining lifetime [61,62], for instance, and for a bridge of 90 years with a remaining lifetime of 2 years and a bridge of 10 years with a remaining lifetime of 90 years, respectively. The U.S. Federal Highway Administration (FHWA) suggests the target reliability index for overload permit vehicles as and for the reference period is one year or two to five years [63,64], respectively, where the reference period is defined as the time until the next bridge evaluation. In particular, Gao et al. [65] considered the impact of normal design loads and the average annual permitted passage frequency of LCT vehicles on specific routes, and suggests . The term represents the number of LCT vehicles within one year. The term is the annual reliability index under design loads. The term is the target reliability index for the operational phase over the year. Based on the ALAPR (As Low As Reasonably Possible/Practicable) format by the ISO [57,58], Gao et al. [65] treated the LTC as the activity that it is tolerable only if further reduction of risk is impracticable or its cost is grossly disproportionate to the improvement gained, so the failure probability in the operation stage can be an order of magnitude higher than that in the design stage, leading to that [66]. This paper adopted , which is the same as [59,63,64]. If the reliability index is greater than or equal to the target reliability index, the result is considered safe; otherwise, it is considered unsafe.

3.3.4 Additional Note: Influence of Measured Data on Updating Process and Safety Evaluation

Recall Fig. 1 and Table 1, the proposed framework, based on conducting inference of three rounds (i.e., initial round, first round updating, and second round updating), performs safety evaluation of the bridge under MAIL based on fusing bridge design, inspection, and load test data.

One may be concerned about whether the proposed framework is still applicable to the situation with load test data but without inspection data. From an engineering point of view, this situation violates the current specification because a bridge technical inspection should be always performed before a bridge load test [8]. Therefore, it is rare for the situation with load test data but without inspection data. From a theoretical point of view, this situation can still be tackled by the proposed framework. This can be simply done by setting the results of first round updating as that of the initial round and then performing second round updating based on the ‘duplicated’ first round updating.

Another concerned question may be the influence of measured data on the updating process and safety evaluation. Qualitatively, for a bridge without any damage and with very good technical grade, the FEM models and safety evaluation results of three rounds are similar; for a bridge with minor damage, the results of the first and second round updating are more reliable compared to the initial model due to changes in the structure; for a bridge with significant damage or those that have been in service for a long time, the evaluation results of the second round updating model are the most reliable, as inspection reports often cannot fully infer or describe internal structural changes. Quantitatively, the above influence can be studied using sensitivity analysis. The input is the updated PDF of the basic RVs while the output can be resistance, LE related to FEM, or failure probability. For resistance and LE, many tools can be adopted. For example, Taylor importance factors (see Eq. (2.6) of [67]), derived from a Taylor expansion, are defined to rank the sensitivity of the output (resistance or LE) to the inputs (basic RVs) for central dispersion analysis. For failure probability, the sensitivity analysis of analytical cases, which is rare practically, is solvable, but that of general cases, relying on the MCS, becomes subtle. Naively, one may think that, if the effect of changing one or more basic RVs on the failure probability is required to be evaluated, two MCS assessments, with and without the change and comparing them, can be applicable. However, the uncertainty of the above approaches may be too large to make a meaningful conclusion. This is because the change is obtained by subtracting the outputs, while the variance for the change is obtained by adding the two variances. One way to alleviate the uncertainty between two outputs is to employ the same set of random numbers for both probability estimates (see Section 3.4.6 of [46]). Another insight thought about the sensitivity of failure probability with respect to uncertain basic RVs is made (see Eq. (6.7) of [55]). According to Bayes’ theorem, the relation between conditional failure probability, i.e., after changing , and the unconditional failure probability, i.e., before changing, is:

(43)

The above equation indicates that the influence on failure probability can be studied through , where is related to the statistics of the samples of changed basic RVs conditional on failure event, and is related to the statistics of the samples of original basic RVs. Subset simulation and direct MCS can be performed to obtain samples of and , respectively.

A final note is that decision making for both updating and safety evaluation should always attempt to fuse as much data as possible. If all data (design, inspection, and load test data) are available, the results of second round updating are the most reliable while the results of the initial and first round can be served for reference.

4  Illustrative Examples: Simulation and Engineering Application

4.1 Simulated Example: Safety Evaluation of Bridge under MAIL

For a simply supported beam with a total length of and a rectangular cross-section of , the concrete strength is C40, and tensile reinforcement uses HRB400 with 3ϕ25 bars. It is divided into 13 nodes, connected sequentially to form 12 elements, each element with a length of 1 m. The structural diagram is shown in Fig. 5.

Figure 5: Critical position of LCT vehicle

An LCT Vehicle passes over the bridge, consisting of a three-axle vehicle with axle loads of , , and , respectively, with axle distances of and . The theoretical displacements of nodes 2 through 12 are extracted, and noise is added to simulate measurement data.

According to Specification for Load-bearing Capacity (JTG/T J21-2011) [8], it is stipulated that for concrete simply supported girder bridges, the bending moment of the mid-span section of the beam, the most unfavorable shear force near the support, and the most unfavorable bending and shear combination effect near the 1/4 section of the span should be calculated. Therefore, to check whether the simply supported beam meets the requirements of the ultimate limit state of the bearing capacity, it is required to conduct a safety evaluation of the above effects and locations. Here, safety evaluation of the bending moment at the most unfavorable section and deflection at the mid-span section are conducted, and safety evaluation of other effects can follow similar procedures.

4.1.1 Safety Evaluation of Initial Round

To determine the critical section for the load moment effect, an equivalent axle load can be introduced into the calculation. The vehicle’s equivalent axle load , and the distance from the first axle is calculated as m. When the LCT vehicle is at the critical position shown in Fig. 5, the corresponding moment is:

(44)

The LE of bending moment follows a normal distribution with a coefficient of variation of 0.10. The corresponding resistance is the section’s flexural capacity, which can be calculated by the following formula:

(45)

where is the area of the reinforcing steel, is the yield strength of the steel, is the compressive strength of the concrete, is the width of the section, and is the height of the section. Among these, , and are RVs following normal distributions. The mean values and coefficients of variation of these variables are shown in Table 4, while and are deterministic values.

According to the design data, the initial flexural capacity of the section is , and the initial vehicle LE is . The initial load-bearing capacity index is . The limit-state function is , so the failure probability is:

(46)

The initial reliability index is . In conclusion, the flexural capacity is satisfied.

4.1.2 Safety Evaluation of First Round Updating

Based on the inspection data, it is known that the concrete at the critical section has spalled by , resulting in a change in the cross-sectional dimensions. The first round updated flexural capacity is updated to . The first round updated vehicle LE , because the moment of the simply supported beam is irrelevant to the material properties. The first round updated load-bearing capacity index is . The first round updated reliability index is . In conclusion, the flexural capacity is satisfied.

4.1.3 Safety Evaluation of Second Round Updating

Based on the load test data, the stiffness of the FEM is updated using the substructure method. Two adjacent elements are taken as one substructure, resulting in a total of six substructures, as shown in Fig. 6. During the load test, a test load of is applied at nodes 4 and 6. Displacement sensors are installed at nodes 2 through 12, totaling eleven sensors. The stiffness of the 11th element is damaged, with its elastic modulus degraded to 0.9 of its original value. The measured displacement results from the load test are 0, −2.7, −5.2, −7.26, −8.71, −9.47, −9.51, −8.91, −7.77, −6.21, −4.33, −2.22, and 0 mm. The parameters to be updated are the coefficients of each substructure, with the initial values of 1.0 for all substructures before updating. After updating, the substructural parameters are: 0.9998, 1.0001, 0.9998, 1.0005, 0.9980, and 0.9186, indicating that the sixth substructure has damage around 10%, which is identical to the true situation.

Figure 6: Structure diagram of simulated example

The maximum deflections at mid-span before and after updating are 3.24 and respectively. The limit stage function is that the maximum deflection should be less than , and this threshold can be satisfied after updating. Therefore, the maximum deflection criterion is satisfied.

The above demonstrates safety evaluation based on fusing bridge design, inspection, and load test data. If all safety evaluation criteria are satisfied, the LCT Vehicle is permitted to pass the bridge. It is worth noting that in some special cases, the updating of structural parameters may not cause changes to some LEs. For example, in the linear elastic stage, updating the stiffness of a simply supported beam does not affect the bending moment. However, in general, the updating of structural parameters will lead to changes in LEs and further changes in load-bearing capacity indicators and reliability indices. Therefore, the method proposed in this paper is essential in the sense that it integrates bridge inspection and load test data to update all QoIs related to the safety evaluation of bridge under MAILs.

4.2 Engineering Example: Safety Evaluation of Anning River Bridge of Yazhong-Jiangxi UHVDC MAIL Project

The Anning River Bridge is located on National Highway 348 in the Xichang section. The total length of the bridge is , with a total deck width of . The single span of the bridge is . The width of the driving lane is , and there are no sidewalks. The bridge deck layout is as follows: (crash barrier) + (bridge floor width) + (crash barrier). The Anning River Bridge was originally an simply supported T-beam bridge, with a bridge width of (car lane) + (sidewalks) + (railing), consisting of six T-beams. The original design load for the bridge was Vehicle-20, Trailer-100, and a pedestrian load of . The bridge was constructed and opened to traffic in 1989. In 2008, due to the need to transport large-scale equipment for the Guandi Hydropower Station, the bridge underwent reinforcement and renovation. The main contents of the reinforcement included replacing the T-beams, encapsulating the cap beams with additional concrete below the cap beam, applying carbon fiber sheets to the sides of the cap beams, reconstructing the continuous deck, repaving the bridge deck, reconstructing the sidewalks, railings, and drainage pipes, and replacing the bearings and expansion joints. After the renovation, the bridge span and width remained unchanged.

4.2.1 Safety Evaluation of Initial Round

The design load is Highway-Class I. The beams were constructed using C40 concrete, the cap beams were reinforced with C30 concrete, and the deck pavement was made of C40 steel-fiber waterproof concrete. Material parameters follow normal distributions, with the mean value and coefficient of variation listed in Table 5. The plan, elevation, and cross-sectional schematic diagrams of the bridge are shown in Fig. 7.

Figure 7: Drawing of anning river bridge: (a) Plan drawing; (b) Elevation drawing; (c) Section drawing

Fig. 8 shows the FEM in this example is established during the bridge design and is part of the bridge design data, so the finite element model in this example can accurately reflect the specific structural form, geometric characteristics, and material types of the actual bridge. The finite element model consists of six prefabricated prestressed T-beams, which are connected by diaphragms at the two fulcrums and in the middle of the span. The finite element model divides each beam into twelve elements with a total of thirteen nodes, and the elements near the supports are in the form of variable cross-sections, and the element length is smaller than that of constant cross-section. The beam body is made of C40 concrete and HRB400 steel bars, the prestressed tendons are made of steel strands, and two prestressed tendons are arranged for each beam, and the prestressed tendons are tensioned by the post-tensioning method.

Figure 8: FEM of the anning river bridge

Fig. 9 shows the axle load configuration of the LCT vehicle. The total vehicle length is , with 14 rear axles and axle spacing. The actual total vehicle and cargo weight is (including the trailer portion), with each portion weight as: = (tractor weight) + (trailer weight) + (converter transformer cargo weight). The LE of bridge under MAIL can be calculated. Table 6 provides safety evaluation of initial round. Therefore, the initial load-bearing capacity index is , and the initial reliability index is . In conclusion, the bending moment load-bearing capacity is satisfied.

Figure 9: Axle load configuration of the LCT vehicle

4.2.2 Safety Evaluation of First Round Updating

According to the inspection data, the bridge’s T-beams showed four cases of weathering, four defect areas with honeycombing and rough surfaces, three cases of exposed reinforcement, five defect areas of concrete damage, two cases of net cracking, and one longitudinal crack. The wet joints and diaphragms did not have significant damage. The estimated compressive strength of the extracted T-beams exceeded . The ratio of the average carbonization depth of the extracted components to the measured average protective layer thickness was less than 0.5, with a rating scale value of 1, indicating that the carbonization depth had a minimal impact on steel reinforcement corrosion. Six measurement points on the longitudinal reinforcement of the T-beams showed protective layer thicknesses between and . The measured profiles of the bridge deck on both the upstream and downstream sides appeared smooth, with no significant deflection. Based on the “Standards for Technical Condition Evaluation of Highway Bridges” (JTG/T H21-2011) [68], the technical condition score of the Anning River Bridge was 80.89, and the technical condition rating was classified as grade 2. The was obtained by updating the basic RVs, including the dimensions of the damaged sections, the thickness of the protective layer, the reduction factor, and etc. Note that the influence of maintenance was considered. The maintenance area was converted into an equivalent concrete area. By adding the equivalent area to the maintenance position, the equivalent cross-section was obtained. The equivalent cross-section’s elastic modulus was , the equivalent cross-section’s stiffness was , and the equivalent cross−section's area was . The LE can be calculated. Table 7 shows safety evaluation of first round updating. The first round updated load-bearing capacity index is , and the first round updated reliability index is . Thus, the bending moment load-bearing capacity is satisfied.

4.2.3 Safety Evaluation of Second Round Updating

Based on the load test data, the stiffness of the FEM is updated using the substructure method. The bridge was divided into 21 nodes with node-to-node distance being 1 m intervals. Two successive elements were treated as one substructure, so there are 10 substructures. Displacement sensors were placed from nodes 2 to 19. A test load of was applied at nodes 4 and 6, and 1% Gaussian noise was added to the theoretical displacements to simulate the measured values. The measured displacements at each point are shown in Table 8.

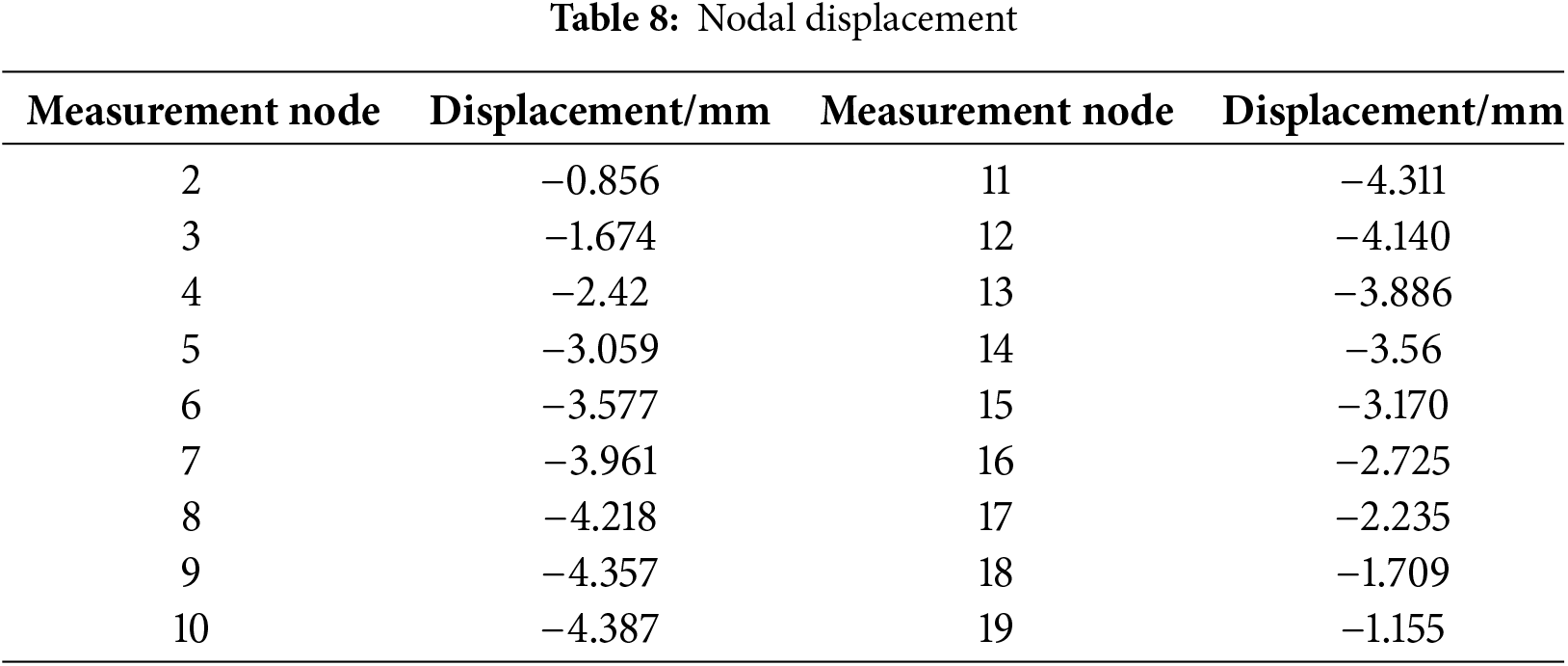
The substructural parameters were updated to be 1.0035, 1.0411, 0.9946, 0.9993, 0.9508, 0.9836, 1.0064, 1.0038, 0.9774, and 1.0000, respectively. It can be seen that the fifth substructural was subjected to about 5% degradation. In order to present how the predicted output changed with respect to the FEM updating, Fig. 10 shows comparisons of measured displacements and predicted displacements of , , and . In this figure, the circle-line, asterisk-line, square-line, and triangular-line are for measured displacements, predicted displacements of , , and , respectively. Before FEM updating, the predicted and measured outputs were significantly different. In contrast, after FEM updating, the predicted output can capture the measured output. Moreover, the prediction performances are significantly improved from the initial, first, to second rounds of updating. Thus, it can be concluded that the updated FEM accurately reflects the bridge’s real behavior, as well as being a basis for providing a more reliable bridge safety evaluation. It is worth noting that the above results also provide comparisons between the proposed framework with the existing research. Recall that the utilized data for are design data only without considering any updating [18], and the utilized data for are load test data [17,19] with additionally fusing bridge inspection data. Obviously, the safety evaluation of the proposed framework is more comprehensive than the existing research as it is capable of fusing all data, including data of design, inspection, and load test. The LCT Vehicle model, with a total axle load of , and with axle distances of 1 and 2 m in an alternative manner, was applied to the FEM. The mid-span deflection was , which is less than its limit . Therefore, the maximum deflection criterion is satisfied. Other safety evaluation criteria can be examined based on the proposed framework. If all safety evaluation criteria are satisfied, the LCT Vehicle is permitted to pass the bridge.

Figure 10: Comparisons of measured displacements and predicted displacements of , and

5  Conclusion

LCT vehicles are vehicles with oversized and/or overweight, so ignoring available inspection and/or load test data in the safety evaluation of the bridge under MAIL will possibly lead to a disorder in the safety evaluation results and furthermore cause overweight disaster to the bridge. On the one hand, most of the existing research performed safety evaluation of bridges under MAILs based on bridge design data only without considering any updating, or based on load test data only but still ignoring bridge inspection data. On the other hand, the proposed framework is capable of fusing bridge design, inspection, and load test data, to update safety evaluation. From utilizing data for updating point of view, the existing research is a special case of module one or two of the proposed framework.

In addition, there are three main conclusions related to updating safety evaluation:

(1) The first difficulty of updating is to develop an updating scheme to utilize the unstructured inspection data. This is tackled by introducing the updating guidelines using the unstructured inspection data recommended by the code. The updating guidelines are a series of empirical equations, obtained from previous experiment studies of the unstructured inspection data and Delphi method.

(2) The second difficulty of updating is to develop a successive updating scheme using load test data based on the previous updating results of the inspection data. This is tackled by Bayesian updating. The stiffness substructural parameters are the re-parameterization of the stiffness matrix of the inspection stage. Prediction errors including measurement and modeling uncertainties are considered. The posterior PDF of the parameters is obtained based on the load test data and the prior PDF reflects the previous updating results of the inspection data. It shows that the prediction performances are significantly improved from the initial, first, to second rounds of updating.

(3) To enhance the comprehensiveness of bridge safety evaluation, it is recommended to consider both the load-bearing capacity index and the reliability index, as well as compare and analyze the changing of the safety valuation results based on data of initial, first, and second round.

The current study focuses on the safety evaluation of a bridge under the LTC vehicle to be permitted in the situation that the bridge is temporarily closed to public traffic during the LTC vehicle passes through the bridge. Although closing to public traffic can increase bridge reliability, it decreases the efficiency of public traffic. As public traffic is a stochastic loading, future developments may incorporate this stochastic component into the proposed safety evaluation framework. The result of the safety evaluation can be utilized as a decision support for the governing authorities on traffic control during the LTC vehicle passes through the bridge.

Acknowledgement: The authors express their sincere gratitude for the help provided by Beijing Construction Engineering Quality Third Test Institute Co., Ltd. in providing data of engineering example of safety evaluation of the Anning River Bridge of the Yazhong-Jiangxi UHVDC moving abnormal indivisible load project.

Funding Statement: This research was funded by the Science and Technology Development Fund (SKL-IOTSC(UM)-2021-2023), the State Key Laboratory of Internet of Things for Smart City (University of Macau) (SKL-IoTSC(UM)-2024-2026/ORP/GA07/2023), and Guangdong Provincial Key Laboratory of Modern Civil Engineering Technology (2021B1212040003).

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Methodology, Data curation, Analysis and interpretation of results, Writing—original draft preparation: He Zhang; Conceptualization, Methodology, Supervision, Funding acquisition, Writing—original draft preparation, Writing—review and editing: He-Qing Mu; Data collection and curation, Resources: Xiao Zhang; Conceptualization, Methodology, Data curation, Analysis and interpretation of results, Writing—original draft preparation: He Zhang; Data curation, Analysis and interpretation of results: Yuedong Yang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Ventura R, Barabino B, Maternini G. Estimating the frequency of traffic overloading on road bridges. J Traffic Transp Eng (Eng Ed). 2024;11(4):776–96. doi:10.1016/j.jtte.2023.11.005. [Google Scholar] [CrossRef]

2. Ventura R, Maternini G, Barabino B. Traffic hazards on main road’s bridges: real-time estimating and managing the overload risk. IEEE Trans Intell Transp Syst. 2024;25(9):12239–55. doi:10.1109/TITS.2024.3371265. [Google Scholar] [CrossRef]

3. Infrastructure Technical Specifications for Interoperability (TSI). European best practice guidelines for abnormal road transports. European Commission: Directorate-General for Energy and Transport; 2021. [Google Scholar]

4. U.S. Department of Transportation Federal Highway Administration (FHWA). Oversize/overweight load permits. [cited 2024 Jan 5]. Available from: https://ops.fhwa.dot.gov/freight/sw/permit_report/index.htm#obt. [Google Scholar]

5. Department of Transport, Energy and Infrastructure (DTEI). Code of practice for oversize or overmass agricultural vehicles. South Australia: Government of South Australia; 2008. [Google Scholar]

6. Ministry of Transport of the People’s Republic of China. JTG/T 2213-2023: technical specifications for highway transport safety audit of abnormal indivisible load. Beijing: China Communications Press; 2023. [Google Scholar]

7. Ministry of Transport of the People’s Republic of China. JTG 5120-2021: specifications for maintenance of highway bridges and culverts. Beijing: China Communications Press; 2021. [Google Scholar]

8. Ministry of Transport of the People’s Republic of China. JTG/T J21-2011: specifications for inspection and evaluation of load-bearing capacity of highway bridge. Beijing: China Communications Press; 2011. [Google Scholar]

9. Huang PM, Wang JF, Han WS, Yuan YG. Study on impact factors of small-and medium-span bridges under the special-purpose vehicle load. Structures. 2022;43(4):606–20. doi:10.1016/j.istruc.2022.06.077. [Google Scholar] [CrossRef]

10. Yuan YG, Han WS, Xu X, Wang JF, Sun JP. Permit checking of overloaded customized transport vehicle based on serviceability limit state reliability of concrete bridges. Adv Struct Eng. 2021;24(5):884–96. doi:10.1177/1369433220972451. [Google Scholar] [CrossRef]

11. Ma DH, Wu WQ, Li Y, Zhao L, Cai YC, Guo P, et al. Numerical simulation-based analysis of the impact of overloading on segmentally assembled bridges. Struct Durab Health Monit. 2024;18(5):663–81. doi:10.32604/sdhm.2024.052677. [Google Scholar] [CrossRef]

12. Zheng X, Yi TH, Yang DH, Li HN, Zhou Y. Bridge evaluation based on identified influence lines and influence surfaces: multiple-scenario application. Int J Struct Stab Dyn. 2023;23:1640023. doi:10.1142/S0219455423400266. [Google Scholar] [CrossRef]

13. Feng K, González A, Casero M. A kNN algorithm for locating and quantifying stiffness loss in a bridge from the forced vibration due to a truck crossing at low speed. Mech Syst Signal Process. 2021;154(1):107599. doi:10.1016/j.ymssp.2020.107599. [Google Scholar] [CrossRef]

14. Zhu X, Cao M, Ostachowicz W, Xu W. Damage identification in bridges by processing dynamic responses to moving loads: features and evaluation. Sensors. 2019;19(3):463. doi:10.3390/s19030463. [Google Scholar] [PubMed] [CrossRef]

15. Ministry of Transport of the People’s Republic of China. JTG D60-2015: general specifications for design of highway bridges and culverts. Beijing: China Communications Press; 2015. [Google Scholar]

16. Ministry of Transport of the People’s Republic of China. JTG 2120-2020: unified standard for reliability design of highway engineering structures. Beijing: China Communications Press; 2020. [Google Scholar]

17. Zhang YF, Duan HJ, Ma ZG. Fast appraisal for girder bridge condition based on quasi stationary load test. Modern Transp Technol. 2009;6:21–4 (In Chinese). [Google Scholar]

18. Cui X, Chen Y, Hu N, Pan LW. Research on evaluation and monitoring methods of large-sized transport vehicles for non-closed traffic hollow slab beam bridges. Highway. 2020;65:124–9. (In Chinese). [Google Scholar]

19. Xing WB. Research on rapid assessment methods for bridge under abnormal indivisible load transportation. J China Foreign Highway. 2011;31:217–20 (In Chinese). [Google Scholar]

20. Chen YY, Mao JP, Yang QH. Research on bearing capacity and process monitoring analysis of large transport bridge. Western China Commun Sci Technol. 2021;5:101–5 (In Chinese). [Google Scholar]

21. Ministry of Housing and Urban-Rural Development of the People’s Republic of China. GB/T 50283-1999: unified standard for reliability design of highway engineering structures. Beijing: China Architecture & Building Press; 1999. [Google Scholar]

22. Ministry of Transport of the People’s Republic of China. JTG 3362-2018: specifications for design of highway reinforced concrete and prestressed concrete bridges and culverts. Beijing: China Communications Press; 2018. [Google Scholar]

23. Ministry of Transport of the People’s Republic of China. Decision on amending the ‘Highway management regulations for over-limit transport vehicles’. [cited 2024 Jan 5]. Available from: https://www.gov.cn/zhengce/zhengceku/2021-08/26/content_5633469.htm. [Google Scholar]

24. Schlune H, Plos M, Gylltoft K. Improved bridge evaluation through finite element model updating using static and dynamic measurements. Eng Struct. 2009;31(7):1477–85. doi:10.1016/j.engstruct.2009.02.011. [Google Scholar] [CrossRef]

25. Lam HF, Peng HY, Au SK. Development of a practical algorithm for Bayesian model updating of a coupled slab system utilizing field test data. Eng Struct. 2014;79(27):182–94. doi:10.1016/j.engstruct.2014.08.014. [Google Scholar] [CrossRef]

26. Mao JX, Wang H, Li J. Bayesian finite element model updating of a long-span suspension bridge utilizing hybrid Monte Carlo simulation and Kriging predictor. KSCE J Civ Eng. 2020;24(2):569–79. doi:10.1007/s12205-020-0983-4. [Google Scholar] [CrossRef]

27. Yin T, Zhu HP. An efficient algorithm for architecture design of Bayesian neural network in structural model updating. Comput Aided Civ Infrastruct Eng. 2020;35(4):354–72. doi:10.1111/mice.12492. [Google Scholar] [CrossRef]

28. Nguyen D, Salamak M, Katunin A, Gerges M. Finite element model updating of RC bridge structure with static load testing: a case study of Vietnamese ThiThac Bridge in coastal and marine environment. Sensors. 2022;22(22):8884. doi:10.3390/s22228884. [Google Scholar] [PubMed] [CrossRef]

29. Weng S, Zhu HP, Xia Y. Substructuring method for civil structural health monitoring. Singapore: Springer; 2023. [Google Scholar]

30. Yuen KV, Mu HQ. Real-time system identification: an algorithm for simultaneous model class selection and parametric identification. Comput Aided Civ Infrastruct Eng. 2015;30(10):785–801. doi:10.1111/mice.12146. [Google Scholar] [CrossRef]

31. Weng S, Zhu HP, Xia Y, Li JJ, Tian W. A review on dynamic substructuring methods for model updating and damage detection of large-scale structures. Adv Struct Eng. 2020;23(3):584–600. doi:10.1177/1369433219872429. [Google Scholar] [CrossRef]

32. Beck JL. Bayesian system identification based on probability logic. Struct Control Health Monit. 2010;17(7):825–47. doi:10.1002/stc.424. [Google Scholar] [CrossRef]

33. Mu HQ, Liang XX, Shen JH, Zhang FL. Analysis of structural health monitoring data with correlated measurement error by Bayesian system identification: theory and application. Sensors. 2022;22(20):7981. doi:10.3390/s22207981. [Google Scholar] [PubMed] [CrossRef]

34. Mu HQ, Zhao ZT, Yuen KV. Characterizing multivariate, asymmetric, and multimodal distributions of geotechnical data with dual-stage missing values: BASIC-H. Georisk: Assess Manag Risk Eng Syst Geohazards. 2024;18(1):85–106. doi:10.1080/17499518.2024.2313482. [Google Scholar] [CrossRef]

35. Zhao ZT, Mu HQ, Yuen KV. Probability density function modelling and credible region construction for multivariate, asymmetric, and multimodal distributions of geotechnical data. Struct Saf. 2024;107:102429. doi:10.1016/j.strusafe.2023.102429. [Google Scholar] [CrossRef]

36. Mu HQ, Shen JH, Zhao ZT, Liu HT, Yuen KV. A novel generative approach for modal frequency probabilistic prediction under varying environmental condition using incomplete information. Eng Struct. 2022;252(10):113571. doi:10.1016/j.engstruct.2021.113571. [Google Scholar] [CrossRef]

37. Mu HQ, Hu Q, Guo HZ, Zhang TY, Su C. Uncertainty quantification of load effects under stochastic traffic flows. Int J Struct Stab Dyn. 2019;19(1):1940009. doi:10.1142/S0219455419400091. [Google Scholar] [CrossRef]

38. Frangopol D, Yang D, Lantsoght E, Steenbergen R. Reliability-based analysis and life-cycle management of load tests. In: Lantsoght E, editor. Load testing of bridges. 1st ed. Florida: CRC Press; 2019. p. 265–96. [Google Scholar]

39. Alampalli S, Frangopol DM, Grimson J, Halling MW, Kosnik DE, Lantsoght EOL, et al. Bridge load testing: state-of-the-practice. J Bridge Eng. 2021;26(3):03120002. doi:10.1061/(ASCE)BE.1943-5592.0001678. [Google Scholar] [CrossRef]

40. Sun P. Study on the road curve outline passing ability of large-cargo transport vehicles [master’s thesis]. China: Jilin University; 2014. [Google Scholar]

41. Wang WT. Research on the rapid assessment method of traffic safety for large transport vehicles on highway and bridges [master’s thesis]. China: Ningxia University; 2022. [Google Scholar]

42. Ministry of Housing and Urban-Rural Development of the People’s Republic of China. GB50009-2012: load code for the design of building structures. Beijing: China Architecture & Building Press; 2012. [Google Scholar]

43. Zheng X, Yang DH, Yi TH, Li HN. Development of bridge influence line identification methods based on direct measurement data: a comprehensive review and comparison. Eng Struct. 2019;198(3):109539. doi:10.1016/j.engstruct.2019.109539. [Google Scholar] [CrossRef]

44. Zheng X, Yi TH, Zhong JW, Yang DH. Rapid evaluation of load-carrying capacity of long-span bridges using limited testing vehicles. J Bridge Eng. 2022;27(4):04022008. doi:10.1061/(ASCE)BE.1943-5592.0001838. [Google Scholar] [CrossRef]

45. Yuen KV, Guo HZ, Mu HQ. Bayesian vehicle load estimation, vehicle position tracking, and structural identification for bridges with strain measurement. Struct Control Health Monit. 2023;2023(1):4752776. doi:10.1155/2023/4752776. [Google Scholar] [CrossRef]

46. Melchers RE, Beck AT. Structural reliability analysis and prediction. 3rd ed. Hoboken: John Wiley & Sons; 2018. [Google Scholar]

47. Nowak AS, Collins KR. Reliability of structures. New York: CRC Press; 2012. [Google Scholar]

48. AASHTO LRFDBDS-2020. AASHTO LRFD bridge design specifications. 9th ed. Washington, DC, USA: AASHTO; 2020. [Google Scholar]

49. AASHTO MBE-3-I2-2020. The manual for bridge evaluation with 2020 interim revisions. 3rd ed. Washington, DC, USA: AASHTO; 2020. [Google Scholar]

50. Gusella F. Expected damage assessment of RC half-joints under traffic load. Probab Eng Mech. 2024;77(1):103656. doi:10.1016/j.probengmech.2024.103656. [Google Scholar] [CrossRef]

51. Sassu M, Puppio ML, Doveri F, Ferrini M, Mistretta F. A time and cost-effective strengthening of RC half joint bridges exposed to brittle failure: application to a case study. Struct Infrastruct Eng. 2023;1–16. doi:10.1080/15732479.2023.2275689. [Google Scholar] [CrossRef]

52. Zhang M. Structural reliability analysis: methods and procedures. Beijing, China: Science Press; 2009. [Google Scholar]

53. Li J. Fundamental of structural reliability analysis. Beijing, China: Science Press; 2021. [Google Scholar]

54. Der Kiureghian A. Structural and system reliability. New York: Cambridge University Press; 2022. [Google Scholar]

55. Au SK, Wang Y. Engineering risk assessment with subset simulation. Hoboken: John Wiley & Sons; 2014. [Google Scholar]

56. de Vries R, Lantsoght EO, Steenbergen RD, Fennis SA. Time-dependent reliability assessment of existing concrete bridges with varying knowledge levels by proof load testing. Struct Infrastruct Eng. 2024 Aug 2;20(7–8):1053–67. doi:10.1080/15732479.2023.2280712. [Google Scholar] [CrossRef]

57. ISO 2394:2015. General principles on reliability for structures. 4th ed. Geneva: International Organization for Standardization (ISO); 2015. [Google Scholar]

58. ISO 13822:2010. Bases for design of structures—assessment of existing structures. 2nd ed. Geneva: International Organization for Standardization (ISO); 2010. [Google Scholar]

59. Steenbergen R, Vrouwenvelder A. Safety philosophy for existing structures and partial factors for traffic loads on bridges. Heron. 2010;55(2):123–39. [Google Scholar]

60. Stewart MG, Rosowsky DV, Val DV. Reliability-based bridge assessment using risk-ranking decision analysis. Struct Saf. 2001;23(4):397–405. doi:10.1016/S0167-4730(02)00010-3. [Google Scholar] [CrossRef]

61. Koteš P, Vičan J. Recommended reliability levels for the evaluation of existing bridges according to Eurocodes. Struct Eng Int. 2013;23(4):411–7. doi:10.2749/101686613X13627351081678. [Google Scholar] [CrossRef]

62. Liao W. A study on key issues of bearing capacity evaluation for bridge structures based on health monitoring systems [Ph.D. thesis]. China: South China University of Technology; 2016. [Google Scholar]

63. Alampalli S, Frangopol DM, Grimson J, Kosnik D, Halling MW, Lantsoght EOL, et al. Primer on bridge load testing. In: Transportation research circular E-C257. Washington: Transportation Research Board; 2019. [Google Scholar]

64. Sivakumar B. LRFR limit states, reliability indices and load factors. In: Load and resistance factor rating of highway bridges. Washington: FHWA LRFR Seminar; 2008. [Google Scholar]

65. Gao WB, Yuan YG, Huang PM, Xu X, Wang JF, Han WS. Safety assessment of steel strand stay cable under customized transport vehicle load considering strength degradation. China J Highway Transp. 2020;33(8):169–81 (In Chinese). [Google Scholar]

66. Hou TY, Li WJ, Zhao JL, Feng M, Gong JX. Research on target reliability indexes for safety evaluation of existing concrete bridges. Highway. 2017;62(3):66–72 (In Chinese). [Google Scholar]

67. Da Veiga S, Gamboa F, Iooss B, Prieur C. Basics and trends in sensitivity analysis: theory and practice in R. Philadelphia: Society for Industrial and Applied Mathematics; 2021. [Google Scholar]

68. Ministry of Transport of the People’s Republic of China. JTG/T H21-2011: standards for technical condition evaluation of highway bridges. Beijing: China Communications Press; 2011. [Google Scholar]