1 Introduction
MCGDM is deliberated as the most suitable method for a verdict on the adequate alternative from all possible choices, following criteria or attributes. Most decisions are taken when the intentions and confines are usually unspecified or unclear in real-life circumstances. Zadeh offered the idea of the fuzzy set (FS) [1] to overcome such vague and indeterminate facts. It is a fundamental tool to handle the insignificances and hesitations in decision-making (DM). The existing FS cannot deal with the scenarios when the experts consider a membership degree (MD) in intervals form during the DM procedure. Turksen [2] presented the interval-valued FS (IVFS) with fundamental operations. The prevailing FS and IVFS cannot deliver the information about any alternative’s non-membership degree (NMD). Atanassov [3] overcame the mentioned above limitations and developed the intuitionistic fuzzy set (IFS). Wang et al. [4] introduced several operations such as Einstein product, Einstein sum, etc., and AOs for IFS. Atanassov [5] prolonged the IFS to an interval-valued intuitionistic fuzzy set (IVIFS) with some basic operations and their properties. Garg et al. [6] protracted the idea of IFS and settled the cubic intuitionistic fuzzy set (CIFS).
The models mentioned above have been well-recognized by the specialists. Still, the existing IFS cannot handle the inappropriate and vague data because it envisions the linear inequality among the MD and NMD. For example, if decision-makers choose MD and NMD 0.6 and 0.7, respectively, then the IFS, as mentioned earlier, cannot deal with it because 0.6 + 0.7 ≥ 1. Yager [7] offered the Pythagorean fuzzy set (PFS) to resolve the inadequacy mentioned above by modifying the elementary state κ+δ≤1 to κ2+δ2≤1. He also established the score and accuracy functions to compute the ranking. Rahman et al. [8] planned Einstein weighted geometric operator for PFS and showed a multi-attribute group decision-making (MAGDM) technique using their planned operator. Zhang et al. [9] developed some basic operational laws and prolonged the approach for order of preference by similarity to ideal solution (TOPSIS) to resolve multi-criteria decision-making (MCDM) problems for PFS. Wei et al. [10] offered the Pythagorean fuzzy power AOs and discussed their important features. Using their presented operators, they also established a DM technique to resolve multi-attribute decision-making (MADM). Wang et al. [11] demonstrated the interaction operational laws for Pythagorean fuzzy numbers (PFNs) and settled power Bonferroni mean operators. IIbahar et al. [12] offered the Pythagorean fuzzy proportional risk assessment technique to assess the professional health risk. Zhang [13] proposed a novel DM approach based on similarity measures to resolve MCGDM problems for the PFS. Peng et al. [14] offered the AOs for interval-valued PFS (IVPFS) and established a DM technique using their planned methodology. Rahman et al. [15] prolonged the weighted geometric aggregation operator for IVPFS and offered a DM technique based on their developed operator.
All of the above techniques have broad applications, but these theories have some limitations on parametric chemistry due to their ineffectiveness. Molodtsov [16] introduced the soft sets (SS) theory and defined some basic operations with their features to handle the misperception and haziness. Maji et al. [17] extended the theory of SS and developed many basic and binary operations for SS. Maji et al. [18] developed the fuzzy soft set with some desirable properties by merging two existing notions, FS and SS. Maji et al. [19] protracted the intuitionistic fuzzy soft set (IFSS) and some important operations with their essential properties. Arora et al. [20] presented the AOs for IFSS and planned a DM technique based on their developed operators. Jiang et al. [21] introduced the interval-valued IFSS (IVIFSS) and discussed its basic properties. Zulqarnain et al. [22] planned the TOPSIS technique based on the correlation coefficient (CC) for IVIFSS to resolve MADM problems. Peng et al. [23] anticipated the Pythagorean fuzzy soft sets (PFSS) by merging two prevailing theories, PFS and SS. Zulqarnain et al. [24] presented some operational laws for PFSS and prolonged the AOs and interaction AOs for PFSS. Zulqarnain et al. [25] developed the operational interaction laws for PFSS and protracted the interaction AOs based on established operational laws. They also established the DM methodologies using their developed AOs and interaction AOs with their application in green supplier chain management. Zulqarnain et al. [26] prolonged the Einstein-ordered operational laws for PFSS and introduced the Einstein-ordered weighted ordered geometric AO for PFSS. They also established a MAGDM technique to solve complex real-life problems. Zulqarnain et al. [27] protracted the Einstein-ordered weighted ordered average AO for PFSS and offered a DM technique based on their developed operator. Zulqarnain et al. [28] settled the TOPSIS method for PFSS using correlation coefficient and developed the MADM approach to resolve DM obstacles. Zulqarnain et al. [29] prolonged the AOs for IVPFSS and presented a MAGDM approach to solving real-life difficulties.
Samarandche [30] proposed the idea of hypersoft set (HSS), which penetrates multiple sub-attributes in the parameter function f, which is a characteristic of the cartesian product with the n attribute. Samarandche HSS is the most suitable theory compared to SS and other existing concepts because it handles the multiple sub-attributes of the considered parameters. Several HSS extensions and their DM methods have been proposed. Rahman et al. [31] developed the DM techniques based on similarity measures for the possibility IFHSS. Zulqarnain et al. [32] extended the notion of IFHSS to PFHSS with fundamental operations and their properties. Rahman et al. [33] established a DM methodology for neutrosophic HSS. Saeed et al. [34] utilized the neutrosophic hypersoft mapping to diagnose the brain tumor. Zulqarnain et al. [35] extended the TOPSIS method based on the correlation coefficient for IFHSS and used it to resolve MADM complications. Zulqarnain et al. [36] expanded the AOs under the IFHSS environment and developed a DM approach based on their presented AOs. Zulqarnain et al. [37] developed the correlation-based TOPSIS approach for PFHSS and utilized their established technique to select the most appropriate face mask. PFHSS is a hybrid intellectual structure of PFSS. An enhanced sorting process fascinates investigators to crack baffling and inadequate information. Rendering to the investigation outcomes, PFHSS plays a vital role in decision-making by collecting numerous sources into a single value. The existing AOs for PFHSS cannot cope with the situation when the information of any multi-sub attribute is given in the form of intervals. To overcome the shortcomings mentioned above, we merged the IVPFS and hypersoft set (HSS) and introduced IVPFHSS, a novel hybrid structure to cope with uncertain problems. Therefore, to inspire the current research of IVPFHSS, we will state AOs based on rough data. The core objectives of the present study are given as follows:
• The IVPFHSS capably contracts the multifaceted concerns seeing the multi sub-attributes of the deliberated parameters in the DM procedure. To preserve this benefit in concentration, we prolong the PFHSS to IVPFHSS and establish the AOs for IVPFHSS.
• The AOs for IVPFHSS are well-known attractive estimate AOs. It has been observed that the prevalent AOs aspect is unresponsive to scratch the precise finding over the DM process in some situations. To overcome these specific complications, these AOs necessary to be revised. We determine innovative operational laws for interval-valued Pythagorean fuzzy hypersoft numbers (IVPFHSNs).
• Interval-valued Pythagorean fuzzy hypersoft weighted average and geometric operators have been introduced with their necessary properties using developed operational laws.
• A novel algorithm based on the planned operators to resolve the DM problem is established to resolve MCGDM issues under the IVPFHSS scenario.
• Material selection is an imperative feature of manufacturing as it realizes the concrete conditions for all ingredients. MS is an arduous but significant step in professional development. The manufacturer’s efficiency, productivity, and eccentric will suffer due to the absence of material selections.
• A comparative analysis of advanced MCGDM technique and current methods has been presented to consider utility and superiority.
The organization of this paper is assumed as follows: the second section of this paper involves some basic notions that support us in developing the structure of the subsequent study. In Section 3, some novel operational laws for IVPFHSN have been projected. Also, in the same section, IVPFHSWA and IVPFHSWG operators have been introduced based on our developed operators’ basic properties. In Section 4, an MCGDM approach has been constructed based on the proposed AOs. In the same section, a numerical example has been discussed to confirm the pragmatism of the established technique for material selection in the manufacturing industry. Furthermore, a brief comparative analysis has been delivered to confirm the competency of the developed approach in Section 5.
2 Preliminaries
This section contains some basic definitions that will structure the following work.
Definition 2.1. [16] Let U and N be the universe of discourse and set of attributes, respectively. Let P(U) be the power set of U and A⊆N. A pair (Ω,A) is called a SS over U, and its mapping is expressed as follows:
Ω:A→P(U)
Also, it can be defined as follows:
(Ω,A)={Ω(t)∈P(U):t∈N,Ω(t)=∅ if t∉A}
Definition 2.2. [30] Let U be a universe of discourse and P(U) be a power set of U and t = {t1, t2, t3,…,tn}, (n ≥ 1) and Ti represented the set of attributes and their corresponding sub-attributes, such as Ti ∩ Tj = φ, where ???? ≠ ???? for each ???? ≥ 1 and ????, ???? ???? {1, 2, 3 … ????}. Assume T1 × T2 × T3× … × Tn = A⃛ = {d1h×d2k×⋯×dnl} is a collection of sub-attributes, where 1 ≤ h ≤ α, 1 ≤ k ≤ β, and 1 ≤ l ≤ γ, and α, β, γ ∈ N. Then the pair (F, T1 × T2 × T3 × … × Tn = (Ω, A⃛) is known as HSS and defined as follows:
Ω:T1×T2×T3×…;×Tn=A⃛→P(U).
It is also defined as
(Ω,A⃛)={dˇ,ΩA⃛(dˇ):dˇ∈A⃛,ΩA⃛(dˇ)∈P(U)}.
Definition 2.3. [14] U be a universe of discourse, and A be any subset of U. Then, the interval-valued Pythagorean fuzzy set (IVPFS) A over U is defined as
A={(x,([κAl(t),κAu(t)],[δAl(t),δAu(t)]))|t∈U}
where, [κAl(t),κAu(t)] and [δAl(t),δAu(t)] represent the MD and NMD intervals, respectively. Also, κAl(t),κAu(t), δAl(t),δAu(t) ∈[0,1]. and satisfied the subsequent condition 0≤(κAu(t))2+(δAu(t))2≤1.
Definition 2.4 [29] U be a universe of discourse and N be a set of attributes. Then a pair (Ω,N) is called an interval-valued Pythagorean fuzzy soft set (IVPFSS) over U. Its mapping can be expressed as
Ω:N→℘KU
where ℘KU represents the collection of interval-valued Pythagorean fuzzy subsets of the universe of discourse U.
(Ω,N)={x,([κAl(t),κAu(t)],[δAl(t),δAu(t)])|t∈A}
where, [κAl(t),κAu(t)],[δAl(t),δAu(t)] represent the MD and NMD intervals, respectively. Also, κAl(t),κAu(t), δAl(t),δAu(t) ∈[0,1]. And satisfied the subsequent condition 0≤(κAu(t))2+(δAu(t))2≤1 and A⊂N.
Definition 2.5. [30] Let U be a universe of discourse and P(U) be a power set of U and t = {t1, t2, t3,…,tn},(n ≥ 1) and Ti represented the set of attributes and their corresponding sub-attributes, such as Ti ∩ Tj = φ, where ???? ≠ ???? for each ???? ≥ 1 and ????, ???? ???? {1,2,3 … ????}. Assume T1 × T2 × T3 × … × Tn = A⃛ = {d1h×d2k×⋯×dnl} is a collection of sub-attributes, where 1 ≤ h ≤ α, 1 ≤ k ≤ β, and 1 ≤ l ≤ γ, and α, β, γ ∈ N. Then the pair (F, T1 × T2 × T3 × … × Tn = (Ω, A⃛) is known as IFHSS and defined as follows:
Ω:T1×T2×T3×…;×Tn=A⃛→IFSU.
It is also defined as
(Ω, A⃛) = {(dˇ,ΩA⃛(dˇ)):dˇ∈A⃛,ΩA⃛(dˇ)∈IFSU∈[0,1]}, where ΩA⃛(dˇ) = {⟨ζ,κΩ(dˇ)(ζ),δΩ(dˇ)(ζ)⟩:ζ∈U}, where κΩ(dˇ)(ζ) and δΩ(dˇ)(ζ) represents the membership and non-membership values, respectively, such as κΩ(dˇ)(ζ), δΩ(dˇ)(ζ) ∈[0,1], and 0 ≤ κΩ(dˇ)(ζ) + δΩ(dˇ)(ζ) ≤ 1.
Definition 2.6 [32] Let U be a universe of discourse and P(U) be a power set of U and t = {t1, t2, t3,…,tn},(n ≥ 1) and Ti represented the set of attributes and their corresponding sub-attributes, such as Ti ∩ Tj = φ, where ???? ≠ ???? for each ???? ≥ 1 and ????, ???? ???? {1,2,3 … ????}. Assume T1 × T2 × T3× … × Tn = A⃛ = {d1h×d2k×⋯×dnl} is a collection of sub-attributes, where 1 ≤ h ≤ α, 1 ≤ k ≤ β, and 1 ≤ l ≤ γ, and α, β, γ ∈ N. Then the pair (F, T1 × T2 × T3× … × Tn = (Ω, A⃛) is known as PFHSS and defined as follows:
Ω:T1×T2×T3×…×Tn=A⃛→PFSU.
It is also defined as
(Ω, A⃛) = {(dˇ,ΩA⃛(dˇ)):dˇ∈A⃛,ΩA⃛(dˇ)∈PFSU∈[0,1]}, where ΩA⃛(dˇ) = {⟨ζ,κΩ(dˇ)(ζ),δΩ(dˇ)(ζ)⟩:ζ∈U}, where κΩ(dˇ)(ζ) and δΩ(dˇ)(ζ) represents the MD and NMD, respectively, such as κΩ(dˇ)(ζ), δΩ(dˇ)(ζ) ∈[0,1], and 0 ≤ (κΩ(dˇ)(ζ))2 + (δΩ(dˇ)(ζ))2 ≤ 1.
The PFHSN is stated as F = {(κΩ(dˇ)(ζ),δΩ(dˇ)(ζ))}.
3 Aggregation Operators for Interval Valued Pythagorean Fuzzy Hypersoft Sets
In this section, we will extend the idea of IVPFSS to interval-valued Pythagorean fuzzy hypersoft sets (IVPFHSS) with some fundamental notions and introduce the operational laws for IVPFHSNs. We propose interval-valued Pythagorean fuzzy hypersoft weighted average (IVPFHSWA) and interval-valued Pythagorean fuzzy hypersoft geometric (IVPFHSWG) operators using the developed operational laws.
Definition 3.1. Let U be a universe of discourse and P(U) be a power set of U and t = {t1, t2, t3,…,tn},(n ≥ 1) and Ti represented the set of attributes and their corresponding sub-attributes, such as Ti ∩ Tj = φ, where ???? ≠ ???? for each ???? ≥ 1 and ????, ???? ???? {1,2,3 … ????}. Assume T1 × T2 × T3× … × Tn = A⃛ = {d1h×d2k×⋯×dnl} is a collection of sub-attributes, where 1 ≤ h ≤ α, 1 ≤ k ≤ β, and 1 ≤ l ≤ γ, and α, β, γ ∈ N. Then the pair (F, T1 × T2 × T3× … × Tn = (Ω, A⃛) is known as IVPFHSS and defined as follows:
Ω:T1×T2×T3×…×Tn=A⃛→IVPFHSU.
It is also defined as
(Ω, A⃛) = {(dˇ,ΩA⃛(dˇ)):dˇ∈A⃛,ΩA⃛(dˇ)∈IVPFSU∈[0,1]}, where ΩA⃛(dˇ) = {⟨ζ,κΩ(dˇ)(ζ),δΩ(dˇ)(ζ)⟩:ζ∈U}, and κΩ(dˇ)(ζ) = [κΩ(dˇ)l(ζ),κΩ(dˇ)u(ζ)], δΩ(dˇ)(ζ) = [δΩ(dˇ)l(ζ),δΩ(dˇ)u(ζ)], where κΩ(dˇ)(ζ) and δΩ(dˇ)(ζ) represents the membership and non-membership intervals, respectively, such as κΩ(dˇ)l(ζ),κΩ(dˇ)u(ζ), δΩ(dˇ)l(ζ),δΩ(dˇ)u(ζ) ∈[0,1], and 0 ≤ (κΩ(dˇ)u(ζ))2 + (δΩ(dˇ)u(ζ))2 ≤ 1.
The IVPFHSN can be stated as F = ([κΩ(dˇ)l(ζ),κΩ(dˇ)u(ζ)],[δΩ(dˇ)l(ζ),δΩ(dˇ)u(ζ)]).
The score and accuracy functions have been presented to compute the alternative ranking for IVPFHSS can be stated as, if F = ([κΩ(dˇ)l(ζ),κΩ(dˇ)u(ζ)],[δΩ(dˇ)l(ζ),δΩ(dˇ)u(ζ)]) be an IVPFHSN. Then
S(F)=(κΩ(dˇ)l(ζ))2+(κΩ(dˇ)u(ζ))2−(δΩ(dˇ)l(ζ))2−(δΩ(dˇ)u(ζ))22
And
A(F)=(κΩ(dˇ)l(ζ))2+(κΩ(dˇ)u(ζ))2+(δΩ(dˇ)l(ζ))2+(δΩ(dˇ)u(ζ))22
Definition 3.2. Let Fdˇk=([κdˇkl,κdˇku],[δdˇkl,δdˇku]), Fdˇ11=([κdˇ11l,κdˇ11u],[δdˇ11l,δdˇ11u]), and
Fdˇ12=([κdˇ12l,κdˇ12u],[δdˇ12l,δdˇ12u]) be three IVPFHSNs and β be a positive real number, and by algebraic norms, we have
1. Fdˇ11⊕Fdˇ12=([κdˇ11l2+κdˇ12l2−κdˇ11l2 κdˇ12l2,κdˇ11u2+κdˇ12u2−κdˇ11u2 κdˇ12u2],[δdˇ11lδdˇ12l,δdˇ11uδdˇ12u])
2. Fdˇ11⊗Fdˇ12=([κdˇ11lκdˇ12l,κdˇ11uκdˇ12u],[δdˇ11l2+δdˇ12l2−δdˇ11l2 δdˇ12l2,δdˇ11u2+δdˇ12u2−δdˇ11u2 δdˇ12u2])
3. βFdˇk= ([1−(1−κdˇkl2)β,1−(1−κdˇku2)β],[δdˇklβ,δdˇkuβ])=(1−(1−[κdˇkl,κdˇku]2)β,[δdˇklβ,δdˇkuβ])
4. Fdˇkβ= ([κdˇklβ,κdˇkuβ],[1−(1−δdˇkl2)β,1−(1−δdˇku2)β])=([κdˇklβ,κdˇkuβ],1−(1−[δdˇkl,δdˇku]2)β).
Definition 3.3. Let Fdˇk=([κdˇkl,κdˇku],[δdˇkl,δdˇku]) be a collection of IVPFHSNs, and ωi and νj are the weight vector for experts and multi sub-parameters, respectively, with given conditions ωi>0,∑i=1nωi=1;νj>0,∑j=1mνj=1. Then, the IVPFHSWA operator is defined as IVPFHSWA: Ψn⟶Ψ
IVPFHSWA(Fdˇ11,Fdˇ12,…,Fdˇnm)=⊕j=1mνj(⊕i=1nωiFdˇij)
Theorem 3.1. Let Fdˇij=([κdˇijl,κdˇiju],[δdˇijl,δdˇiju]) be a collection of IVPFHSNs, where (i=1,2,3…,n and j=1,2,3,…,m), and the aggregated value is also an IVPFHSN, such as
IVPFHSWA(Fdˇ11,Fdˇ12,…,Fdˇnm)
=(1−∏j=1m(∏i=1n(1−[κdˇijl,κdˇiju]2)ωi)νj,∏j=1m(∏i=1n([δdˇijl,δdˇiju])ωi)νj)
ωi and νj show the expert’s and multi sub-attributes weights, respectively, such as ωi>0, ∑i=1nωi=1, νj>0,∑j=1mνj=1.
Proof. The above presented IVPFHSWA operator can be proved by using the principle of mathematical induction:
For n=1, we get ω1=1. Then, we have
IVPFHSWA(Fdˇ11,Fdˇ12,…,Fdˇnm)=⊕j=1mνjFdˇ1j
IVPFHSWA(Fdˇ11,Fdˇ12,…,Fdˇnm)=(1−∏j=1m(1−[κdˇ1jl,κdˇ1ju]2)νj,∏j=1m([δdˇ1jl,δdˇ1ju])νj)
=(1−∏j=1m(∏i=11(1−[κdˇijl,κdˇiju]2)ωi)νj,∏j=1m(∏i=11([δdˇijl,δdˇiju])ωi)νj).
For m=1, we get ν1=1. Then, we have
IVPFHSWA(Fdˇ11,Fdˇ12,…,Fdˇnm)=⊕i=1nωiFdˇi1
=(1−∏i=1n(1−[κdˇi1l,κdˇi1u]2)ωi,∏i=1n([δdˇi1l,δdˇi1u])ωi)
=(1−∏j=11(∏i=1n(1−[κdˇijl,κdˇiju]2)ωi)νj,∏j=11(∏i=1n([δdˇijl,δdˇiju])ωi)νj)
So, the above theorem is proved for n=1 and m=1.
Assume that for m=α1+1,n=α2 and m=α1,n=α2+1, the above theorem holds. Such as
⊕j=1α1+1νj(⊕i=1α2ωiFdˇij)=(1−∏j=1α1+1(∏i=1α2(1−[κdˇijl,κdˇiju]2)ωi)νj,∏j=1α1+1(∏i=1α2([δdˇijl,δdˇiju])ωi)νj)
⊕j=1α1νj(⊕i=1α2+1ωiFdˇij)=(1−∏j=1α1(∏i=1α2+1(1−[κdˇijl,κdˇiju]2)ωi)νj,∏j=1α1(∏i=1α2+1([δdˇijl,δdˇiju])ωi)νj)
For m=α1+1 and n=α2+1, we have
⊕j=1α1+1νj(⊕i=1α2+1ωiFdˇij)=⊕j=1α1+1νj(⊕i=1α2ωiFdˇij⊕ωα2+1Fdˇ(α2+1)j)
=⊕j=1α1+1⊕i=1α2νjωiFdˇij⊕j=1α1+1νjωα2+1Fdˇ(α2+1)j
=(1−∏j=1α1+1(∏i=1α2(1−[κdˇijl,κdˇiju]2)ωi)νj⊕1−∏j=1α1+1((1−[κdˇ(α2+1)jl,κdˇ(α2+1)ju]2)ωα2+1)νj,
∏j=1α1+1(∏i=1α2([δdˇijl,δdˇiju])ωi)νj⊕∏j=1α1+1(([δdˇ(α2+1)jl,δdˇ(α2+1)ju])ω(α2+1))νj)
=(1−∏j=1α1+1(∏i=1α2+1(1−[κdˇijl,κdˇiju]2)ωi)νj,∏j=1α1+1(∏i=1α2+1([δdˇijl,δdˇiju])ωi)νj)
Hence, it holds for m=α1+1 and n=α2+1. So, we can say that Theorem 3.1 holds for all values of m and n.
Example. 3.1
Let R={R1,R2,R3} be a set of experts with the given weight vector ωi=(0.38,0.45,0.17)T. The group of experts describes the beauty of a house under-considered attributes Å={e1=lawn,e2=security system} with their corresponding sub-attributes Lawn = e1 = {e11=with grass,e12=withoutgrass}, security system = e2 = {e21=guards,e22=cameras}. Let Å = e1 × e2 be a set of sub-attributes
Å=e1×e2={e11,e12}×{e21,e22}={(e11,e21),(e11,e22),(e12,e21),(e12,e22)}
Å={dˇ1,dˇ2,dˇ3,dˇ4} be a set of multi sub-attributes with weights νj=(0.2,0.2,0.2,0.4)T. The rating values for each alternative in the form of IVPFHSN (F,Å)=([κdˇijl,κdˇiju],[δdˇijl,δdˇiju])3×4 given as:
(F,Å)=[([0.3,0.8],[0.4,0.5])([0.4,0.6],[0.3,0.7])([0.5,0.8],[0.5,0.6])([0.4,0.9],[0.3,0.7])([0.1,0.5],[0.2,0.3])([0.3,0.8],[0.5,0.7])([0.2,0.4],[0.2,0.3])([0.3,0.8],[0.6,0.7])([0.2,0.9],[0.2,0.3])([0.5,0.7],[0.2,0.6])([0.2,0.4],[0.2,0.8])([0.3,0.8],[0.5,0.8])]
IVPFHSWA(Fdˇ11,Fdˇ12,…,Fdˇ34)=(1−∏j=14(∏i=13(1−[κdˇijl,κdˇiju]2)ωi)νj,∏j=14(∏i=13([δdˇijl,δdˇiju])ωi)νj)
=(1−({[0.36,0.91]0.38[0.75,0.84]0.45[0.19,0.96]0.17}0.2{[0.64,0.84]0.38[0.36,0.91]0.45[0.51,0.75]0.17}0.2{[0.36,0.75]0.38[0.84,0.96]0.45[0.84,0.96]0.17}0.2{[0.19,0.84]0.38[0.36,0.91]0.45[0.36,0.91]0.17}0.4),({[0.4,0.5]0.38[0.2,0.3]0.45[0.2,0.3]0.17}0.2{[0.3,0.7]0.38[0.5,0.7]0.45[0.2,0.6]0.17}0.2{[0.5,0.6]0.38[0.2,0.3]0.45[0.2,0.8]0.17}0.2{[0.3,0.7]0.38[0.6,0.7]0.45[0.5,0.8]0.17}0.4))
=(1−({[0.36,0.91]0.38[0.75,0.84]0.45[0.19,0.96]0.17}0.2{[0.64,0.84]0.38[0.36,0.91]0.45[0.51,0.75]0.17}0.2{[0.36,0.75]0.38[0.84,0.96]0.45[0.84,0.96]0.17}0.2{[0.19,0.84]0.38[0.36,0.91]0.45[0.36,0.91]0.17}0.4),({[0.4,0.5]0.38[0.2,0.3]0.45[0.2,0.3]0.17}0.2{[0.3,0.7]0.38[0.5,0.7]0.45[0.2,0.6]0.17}0.2{[0.5,0.6]0.38[0.2,0.3]0.45[0.2,0.8]0.17}0.2{[0.3,0.7]0.38[0.6,0.7]0.45[0.5,0.8]0.17}0.4))
=(1−({[0.96,0.68][0.92,0.88][0.99,0.75]}0.2{[0.93,0.84][0.95,0.63][0.95,0.89]}0.2{[0.89,0.68][0.98,0.92][0.99,0.9]}0.2{[0.93,0.53][0.95,0.63][0.98,0.84]}0.4),({[0.77,0.70][0.58,0.48][0.81,0.76]}0.2{[0.87,0.63][0.85,0.73][0.92,0.76]}0.2{[0.82,0.76][0.58,0.48][0.96,0.76]}0.2{[0.87,0.63][0.85,0.79][0.96,0.76]}0.4))
=(1−([0.87,0.45]0.2[0.84,0.4]0.2[0.86,0.61]0.2[0.86,0.28]0.4),([0.36,0.25]0.2[0.68,0.34]0.2[0.46,0.28]0.2[0.71,0.38]0.4))
=(1−([0.8524,0.9725][0.8325,0.9657][0.9059,0.9703][0.6009,0.9414]),([0.7579,0.8152][0.8059,0.9258][0.7752,0.8561][0.6791,0.8719]))
=(1−[0.3863,0.8579],[0.3215,0.5634])
=([0.6137,0.1421],[0.3215,0.5634])
=[0.3769,0.7833],[0.3215,0.5634].
3.1 Properties of IVPFHSWA Operator
3.1.1 Idempotency
If Fdˇij=Fdˇk=([κdˇijl,κdˇiju],[δdˇijl,δdˇiju])∀i,j. Then
IVPFHSWA(Fdˇ11,Fdˇ12,…,Fdˇnm)=Fdˇk
Proof. As we know that all Fdˇij=Fdˇk=([κdˇijl,κdˇiju],[δdˇijl,δdˇiju]), then, we have
IVPFHSWA(Fdˇ11,Fdˇ12,…,Fdˇnm)
=(1−∏j=1m(∏i=1n(1−[κdˇijl,κdˇiju]2)ωi)νj,∏j=1m(∏i=1n([δdˇijl,δdˇiju])ωi)νj)
=(1−((1−[κdˇijl,κdˇiju]2)∑i=1nωi)∑j=1mνj,(([δdˇijl,δdˇiju])∑i=1nωi)∑j=1mνj)
As ∑j=1mνj=1 and ∑i=1nωi=1, then we have
=(1−(1−[κdˇijl,κdˇiju]2),[δdˇijl,δdˇiju])
=([κdˇijl,κdˇiju],[δdˇijl,δdˇiju])
=Fdˇk.
3.1.2 Boundedness
Let Fdˇij = ([κdˇijl,κdˇiju],[δdˇijl,δdˇiju]) be a collection of IVPFHSNs where Fdˇij−= (minj mini{[κdˇijl,κdˇiju]},maxjmaxi{[δdˇijl,δdˇiju]}) and Fdˇij+=(maxjmaxi{[κdˇijl,κdˇiju]},minj mini {[δdˇijl,δdˇiju]}), then
Fdˇij−≤IVPFHSWA(Fdˇ11,Fdˇ12,…,Fdˇnm)≤Fdˇij+
Proof. As we know that Fdˇij = ([κdˇijl,κdˇiju],[δdˇijl,δdˇiju]) be an IVPFHSN, then
minj mini {[κdˇijl,κdˇiju]2}≤[κdˇijl,κdˇiju]2≤maxjmaxi{[κdˇijl,κdˇiju]2}
⇒1−maxjmaxi{[κdˇijl,κdˇiju]2}≤1−[κdˇijl,κdˇiju]2≤1−minj mini{[κdˇijl,κdˇiju]2}
⇔(1−maxjmaxi{[κdˇijl,κdˇiju]2})ωi≤(1−[κdˇijl,κdˇiju]2)ωi≤(1−minjmini{[κdˇijl,κdˇiju]2})ωi
⇔(1−maxjmaxi{[κdˇijl,κdˇiju]2})∑i=1nωi≤∏i=1n(1−[κdˇijl,κdˇiju]2)ωi≤(1−minjmini{[κdˇijl,κdˇiju]2})∑i=1nωi
⇔(1−maxjmaxi{[κdˇijl,κdˇiju]2})∑j=1nνj≤∏j=1m(∏i=1n(1−[κdˇijl,κdˇiju]2)ωi)νj≤(1−minjmini{[κdˇijl,κdˇiju]2})∑j=1nνj
⇔1−maxjmaxi{[κdˇijl,κdˇiju]2}≤∏j=1m(∏i=1n(1−[κdˇijl,κdˇiju]2)ωi)νj≤1−minjmini{[κdˇijl,κdˇiju]2}
⇔minjmini{[κdˇijl,κdˇiju]2}≤1−∏j=1m(∏i=1n(1−[κdˇijl,κdˇiju]2)ωi)νj≤maxjmaxi{[κdˇijl,κdˇiju]2}
⇔minjmini{[κdˇijl,κdˇiju]}≤1−∏j=1m(∏i=1n(1−[κdˇijl,κdˇiju]2)ωi)νj≤maxjmaxi{[κdˇijl,κdˇiju]}(a)
Similarly,
minjmini{[δdˇijl,δdˇiju]}≤∏j=1m(∏i=1n([δdˇijl,δdˇiju])ωi)νj≤maxjmaxi{[δdˇijl,δdˇiju]}(b)
Let IVPFHSWA(Fdˇ11,Fdˇ12,…,Fdˇnm)=([κdˇijl,κdˇiju],[δdˇijl,δdˇiju])=Fdˇij. So, (a) and (b) can be transferred into the form:
minjmini{[κdˇijl,κdˇiju]}≤Fdˇk≤maxjmaxi{[κdˇijl,κdˇiju]} and minjmini{[δdˇijl,δdˇiju]}≤Fdˇk≤maxjmaxi {[δdˇijl,δdˇiju]}, respectively.
Using the score function, we have
S(Fdˇk)=(κdˇkl)2+(κdˇku)2−(δdˇkl)2−(δdˇku)22≤maxjmaxi{[κdˇijl,κdˇiju]}−minjmini{[δdˇijl,δdˇiju]}=S(Fdˇk−)
S(Fdˇk)=(κdˇkl)2+(κdˇku)2−(δdˇkl)2−(δdˇku)22≥minjmini{[κdˇijl,κdˇiju]}−maxjmaxi{[δdˇijl,δdˇiju]}=S(Fdˇk+)
By order relation between two IVPFHSNs, we have
Fdˇk−≤IVPFHSWA(Fdˇ11,Fdˇ12,…,Fdˇnm)≤Fdˇk+.
3.1.3 Shift Invariance
Let Fdˇk = ([κdˇkl,κdˇku],[δdˇkl,δdˇku]) be an IVPFHSN. Then
IVPFHSWA(Fdˇ11⊕Fdˇk,Fdˇ12⊕Fdˇk,…,Fdˇnm⊕Fdˇk)=IVPFHSWA(Fdˇ11,Fdˇ12,…,Fdˇnm)⊕Fdˇk
Proof. As Fdˇk = ([κdˇkl,κdˇku],[δdˇkl,δdˇku]) and Fdˇij = ([κdˇijl,κdˇiju],[δdˇijl,δdˇiju]) be two IVPFHSNs. Then, using Definition 3.2 (1)
Fdˇk⊕Fdˇij=([κdˇkl,κdˇku]+[κdˇijl,κdˇiju]2−[κdˇkl,κdˇku][κdˇijl,κdˇiju]2,[δdˇkl,δdˇku][δdˇijl,δdˇiju]),
So,
IVPFHSWA(Fdˇ11⊕Fdˇk,Fdˇ12⊕Fdˇk,…,Fdˇnm⊕Fdˇk)==⊕j=1mνj(⊕i=1nωi(Fdˇij⊕Fdˇk))
=(1−∏j=1m(∏i=1n(1−[κdˇijl,κdˇiju]2)ωi(1−[κdˇkl,κdˇku]2)ωi)νj,∏j=1m(∏i=1n([δdˇijl,δdˇiju])ωi([δdˇkl,δdˇku])ωi)νj)
=(1−(1−[κdˇkl,κdˇku]2)∏j=1m(∏i=1n(1−[κdˇijl,κdˇiju]2)ωi)νj,[δdˇkl,δdˇku]∏j=1m(∏i=1n([δdˇijl,δdˇiju])ωi)νj)
=((1−∏j=1m(∏i=1n(1−[κdˇijl,κdˇiju]2)ωi)νj,∏j=1m(∏i=1n([δdˇijl,δdˇiju])ωi)νj)⊕([κdˇkl,κdˇku],[δdˇkl,δdˇku]))
=IVPFHSWA(Fdˇ11,Fdˇ12,…,Fdˇnm)⊕Fdˇk.
3.1.4 Homogeneity
Prove that IVPFHSWA (βFdˇ11,βFdˇ12,…,βFdˇnm)=βIVPFHSWA (Fdˇ11,Fdˇ12,…,Fdˇnm) for any positive real number β.
Proof. Let Fdˇij = ([κdˇijl,κdˇiju],[δdˇijl,δdˇiju]) be an IVPFHSN and β>0. Then using Definition 3.2, we have
βFdˇij=(1−(1−[κdˇijl,κdˇiju]2)β,[δdˇijl,δdˇiju]β)
So,
(βFdˇ11,βFdˇ12,…,βFdˇnm)
=(1−∏j=1m(∏i=1n(1−[κdˇijl,κdˇiju]2)βωi)νj,∏j=1m(∏i=1n([δdˇijl,δdˇiju])βωi)νj)
=(1−(∏j=1m(∏i=1n(1−[κdˇijl,κdˇiju]2)ωi)νj)β,(∏j=1m(∏i=1n([δdˇijl,δdˇiju])ωi)νj)β)
=βIVPFHSWA (Fdˇ11,Fdˇ12,…,Fdˇnm).
Definition 3.4. Let Fdˇk=([κdˇkl,κdˇku],[δdˇkl,δdˇku]) be a collection of IVPFHSNs, and ωi and νj are the weight vector for experts and multi sub-parameters, respectively, with given conditions ωi>0,∑i=1nωi=1;νj>0,∑j=1mνj=1. Then, the IVPFHSWG operator is defined as IVPFHSWG: Ψn⟶Ψ
IVPFHSWG(Fdˇ11,Fdˇ12,…,Fdˇnm)=⊗j=1mνj(⊗i=1nωiFdˇij)
Theorem 3.2. Let Fdˇij=([κdˇijl,κdˇiju],[δdˇijl,δdˇiju]) be a collection of IVPFHSNs, where (i=1,2,3……,n and j=1,2,3,…,m), and the aggregated value is also an IVPFHSN, such as
IVPFHSWG(Fdˇ11,Fdˇ12,…,Fdˇnm)
=(∏j=1m(∏i=1n([κdˇijl,κdˇiju])ωi)νj,1−∏j=1m(∏i=1n(1−[δdˇijl,δdˇiju]2)ωi)νj)
ωi and νj represents the expert’s and multi sub-attributes weights, respectively, such as ωi>0, ∑i=1nωi=1, νj>0,∑j=1mνj=1.
Proof. Using mathematical induction, we can prove the IVPFHSWG operator as follows:
For n=1, we get ω1=1. Then, we have
IVPFHSWG(Fdˇ11,Fdˇ12,…,Fdˇnm)=⊗j=1mFdˇ1jνj
IVPFHSWG(Fdˇ11,Fdˇ12,…,Fdˇnm)
=(∏j=1m([κdˇ1jl,κdˇ1ju])νj,1−∏j=1m(1−[δdˇ1jl,δdˇ1ju]2)νj)
=(∏j=1m(∏i=11([κdˇijl,κdˇiju])ωi)νj,1−∏j=1m(∏i=11(1−[δdˇijl,δdˇiju]2)ωi)νj).
For m=1, we get ν1=1. Then, we have
IVPFHSWG(Fdˇ11,Fdˇ21,…,Fdˇn1)=⊗i=1n(Fdˇn1)ωi
=(∏i=1n([κdˇi1l,κdˇi1u])ωi,1−∏i=1n(1−[δdˇi1l,δdˇi1u]2)ωi)
=(∏j=11(∏i=1n([κdˇijl,κdˇiju])ωi)νj,1−∏j=11(∏i=1n(1−[δdˇijl,δdˇiju]2)ωi)νj)
So, for n=1 and m=1 the IVPFHSWG operators holds.
Now, for m=α1+1,n=α2 and m=α1,n=α2+1, such as
⊗j=1α1+1(⊗i=1α2(Fdˇij)ωi)νj
=(∏j=1α1+1(∏i=1α2([κdˇijl,κdˇiju])ωi,1−∏j=1α1+1(∏i=1α2(1−[δdˇijl,δdˇiju]2)ωi)νj))
⊗j=1α1(⊗i=1α2+1(Fdˇij)ωi)νj
=(∏j=1α1(∏i=1α2+1([κdˇijl,κdˇiju])ωi)νj,1−∏j=1α1(∏i=1α2+1(1−[δdˇijl,δdˇiju]2)ωi)νj)
For m=α1+1 and n=α2+1, we have
⊗j=1α1+1(⊗i=1α2+1(Fdˇij)ωi)νj=⊗j=1α1+1(⊗i=1α2(Fdˇij)ωi⊗(Fdˇ(α2+1)j)ωα2+1)νj
=⊗j=1α1+1⊗i=1α2((Fdˇij)ωi)νj⊗j=1α1+1((Fdˇ(α2+1)j)ωα2+1)νj
=(∏j=1α1+1(∏i=1α2([κdˇijl,κdˇiju])ωi)νj⊗∏j=1α1+1(([κdˇ(α2+1)jl,κdˇ(α2+1)ju])ω(α2+1))νj,
1−∏j=1α1+1(∏i=1α2(1−[δdˇijl,δdˇiju]2)ωi)νj⊗1−∏j=1α1+1((1−[δdˇ(α2+1)jl,δdˇ(α2+1)ju]2)ωα2+1)νj)
=(∏j=1α1+1(∏i=1α2+1([κdˇijl,κdˇiju])ωi)νj,1−∏j=1α1+1(∏i=1α2+1(1−[δdˇijl,δdˇiju]2)ωi)νj)
So, it is proved the for m=α1+1 and n=α2+1 holds. So, the IVPFHSWG operator holds for all values of m and n.
Example 3.2. Let R={R1,R2,R3} be a set of experts with the given weight vector ωi=(0.38,0.45,0.17)T. The group of experts describes the beauty of a house under-considered attributes Å={e1=lawn,e2=security system} with their corresponding sub-attributes Lawn = e1 = {e11=with grass,e12=without grass}, security system = e2 = {e21=guards,e22=cameras}. Let Å = e1 × e2 be a set of sub-attributes
Å = e1 × e2 = {e11,e12} × {e21,e22} = {(e11,e21),(e11,e22),(e12,e21),(e12,e22)}
Å = {dˇ1,dˇ2,dˇ3,dˇ4} be a set of multi sub-attributes with weights νj=(0.2,0.2,0.2,0.4)T. The rating values for each alternative in the form of IVPFHSN (F,Å)=([κdˇijl,κdˇiju],[δdˇijl,δdˇiju])3×4 given as:
(F,Å)=[([0.3,0.8],[0.4,0.5])([0.4,0.6],[0.3,0.7])([0.5,0.8],[0.5,0.6])([0.4,0.9],[0.3,0.7])([0.1,0.5],[0.2,0.3])([0.3,0.8],[0.5,0.7])([0.2,0.4],[0.2,0.3])([0.3,0.8],[0.6,0.7])([0.2,0.9],[0.2,0.3])([0.5,0.7],[0.2,0.6])([0.2,0.4],[0.2,0.8])([0.3,0.8],[0.5,0.8])]
By using the above theorem, we have
IVPFHSWG(Fdˇ11,Fdˇ12,…,Fdˇ34)
=(∏j=14(∏i=13([κdˇijl,κdˇiju])ωi)νj,1−∏j=13(∏i=14(1−[δdˇijl,δdˇiju]2)ωi)νj)
=(({[0.3,0.8]0.38[0.1,0.5]0.45[0.2,0.9]0.17}0.2{[0.4,0.6]0.38[0.3,0.8]0.45[0.5,0.7]0.17}0.2{[0.5,0.8]0.38[0.2,0.4]0.45[0.2,0.4]0.17}0.2{[0.4,0.9]0.38[0.3,0.8]0.45[0.3,0.8]0.17}0.4),1−({[0.75,0.84]0.38[0.91,0.96]0.45[0.91,0.96]0.17}0.2{[0.51,0.91]0.38[0.51,0.75]0.45[0.64,0.96]0.17}0.2{[0.64,0.75]0.38[0.91,0.96]0.45[0.36,0.96]0.17}0.2{[0.51,0.91]0.38[0.51,0.64]0.45[0.36,0.75]0.17}0.4))
=(({[0.92,0.63]0.38[0.73,0.35]0.45[0.98,0.76]0.17}0.2{[0.82,0.70]0.38[0.90,0.38]0.45[0.94,0.89]0.17}0.2{[0.92,0.77]0.38[0.66,0.48]0.45[0.85,0.76]0.17}0.2{[0.96,0.70]0.38[0.90,0.58]0.45[0.96,0.81]0.17}0.4),1−({[0.75,0.84]0.38[0.91,0.96]0.45[0.91,0.96]0.17}0.2{[0.51,0.91]0.38[0.51,0.75]0.45[0.64,0.96]0.17}0.2{[0.64,0.75]0.38[0.91,0.96]0.45[0.36,0.96]0.17}0.2{[0.51,0.91]0.38[0.51,0.64]0.45[0.36,0.75]0.17}0.4))
=(([0.66,0.17]0.2[0.69,0.24]0.2[0.52,0.28]0.2[0.83,0.33]0.4),1−({[0.93,0.89][0.98,0.96][0.99,0.98]}0.2{[0.96,0.77][0.88,0.74][0.99,0.93]}0.2{[0.89,0.84][0.98,0.96][0.99,0.84]}0.2{[0.96,0.77][0.81,0.74][0.95,0.84]}0.4))
=((0.7016,0.9202][0.7516,0.9284][0.7752,0.8774][0.6418,0.9282])1−([0.9023,0.8373]0.2[0.8363,0.5299]0.2[0.8634,0.6773]0.2[0.7387,0.4786]0.4))
=([0.2623,0.6957],1−([0.9651,0.9796][0.8807,0.9649][0.9250,0.9710][0.7447,0.8859]))
=[0.2623,0.6957],1−[0.5855,0.8131]
=[0.2623,0.6957],[0.4146,0.1869]
=[0.2623,0.6957],[0.4323,0.6438].
3.2 Properties of IVPFSWG
3.2.1 Idempotency
If Fdˇij=Fdˇk=([κdˇijl,κdˇiju],[δdˇijl,δdˇiju])∀i,j. Then
IVPFHSWG (Fdˇ11,Fdˇ12,…,Fdˇnm)=Fdˇk.
Proof. As we know that all Fdˇij=Fdˇk=([κdˇijl,κdˇiju],[δdˇijl,δdˇiju]), then, we have
IVPFHSWG(Fdˇ11,Fdˇ12,…,Fdˇnm)
=(∏j=1m(∏i=1n([κdˇijl,κdˇiju])ωi)νj,1−∏j=1m(∏i=1n(1−[δdˇijl,δdˇiju]2)ωi)νj)
=((([κdˇijl,κdˇiju])∑i=1nωi)∑j=1mνj,1−((1−[δdˇijl,δdˇiju]2)∑i=1nωi)∑j=1mνj)
As ∑j=1mνj=1 and ∑i=1nωi=1, then we have
=([κdˇijl,κdˇiju],1−(1−[δdˇijl,δdˇiju]2))
=([κdˇijl,κdˇiju],[δdˇijl,δdˇiju])
=Fdˇk.
3.2.2 Boundedness
Let Fdˇij be a collection of IVPFHSNs, where Fdˇij−=(minjmini{[κdˇijl,κdˇiju]},maxjmaxi{[δdˇijl,δdˇiju]}) and Fdˇij+=(maxjmaxi{[κdˇijl,κdˇiju]},minjmini{[δdˇijl,δdˇiju]}), then
Fdˇij−≤IVPFHSWG(Fdˇ11,Fdˇ12,…,Fdˇnm)≤Fdˇij+
Proof. As we know that Fdˇij=([κdˇijl,κdˇiju],[δdˇijl,δdˇiju]) be an IVPFHSN, then
minjmini{[δdˇijl,δdˇiju]2}≤[δdˇijl,δdˇiju]2≤maxjmaxi{[δdˇijl,δdˇiju]2}
⇒1−maxjmaxi{[δdˇijl,δdˇiju]2}≤1−[δdˇijl,δdˇiju]2≤1−minjmini{[δdˇijl,δdˇiju]2}
⇔(1−maxjmaxi{[δdˇijl,δdˇiju]2})ωi≤(1−[δdˇijl,δdˇiju]2)ωi≤(1−minjmini{[δdˇijl,δdˇiju]2})ωi
⇔(1−maxjmaxi{[δdˇijl,δdˇiju]2})∑i=1nωi≤∏i=1n(1−[δdˇijl,δdˇiju]2)ωi≤(1−minjmini{[δdˇijl,δdˇiju]2})∑i=1nωi
⇔(1−maxjmaxi{[δdˇijl,δdˇiju]2})∑j=1nνj≤∏j=1m(∏i=1n(1−[δdˇijl,δdˇiju]2)ωi)νj≤(1−minjmini{[δdˇijl,δdˇiju]2})∑j=1nνj
⇔1−maxjmaxi{[δdˇijl,δdˇiju]2}≤∏j=1m(∏i=1n(1−[δdˇijl,δdˇiju]2)ωi)νj≤1−minjmini{[δdˇijl,δdˇiju]2}
⇔minjmini{[δdˇijl,δdˇiju]2}≤1−∏j=1m(∏i=1n(1−[δdˇijl,δdˇiju]2)ωi)νj≤maxjmaxi{[δdˇijl,δdˇiju]2}
⇔minjmini{[δdˇijl,δdˇiju]}≤1−∏j=1m(∏i=1n(1−[δdˇijl,δdˇiju]2)ωi)νj≤maxjmaxi{[δdˇijl,δdˇiju]}(C)
Similarly,
minjmini{[κdˇijl,κdˇiju]}≤∏j=1m(∏i=1n([κdˇijl,κdˇiju])ωi)νj≤maxjmaxi{[κdˇijl,κdˇiju]}(D)
If IVPFHSWG(Fdˇ11,Fdˇ12,…,Fdˇnm)=([κdˇijl,κdˇiju],[δdˇijl,δdˇiju])=Fdˇk, then inequalities (C) and (D) can be transferred into the form.
minj mini{[κdˇijl,κdˇiju]}≤Mσ≤maxjmaxi{[κdˇijl,κdˇiju]} and minjmini{[δdˇijl,δdˇiju]}≤Fdˇk≤maxjmaxi{[δdˇijl,δdˇiju]}, respectively.
Using the score function,
S(Fdˇk)=(κdˇkl)2+(κdˇku)2−(δdˇkl)2−(δdˇku)22≤maxjmaxi{[κdˇijl,κdˇiju]}−minjmini{[δdˇijl,δdˇiju]}=S(Fdˇij−)
S(Fdˇk)=(κdˇkl)2+(κdˇku)2−(δdˇkl)2−(δdˇku)22≥minjmini{[κdˇijl,κdˇiju]}−maxjmaxi{[δdˇijl,δdˇiju]}=S(Fdˇij+)
By order relation between two IVPFHSNs, we have
Fdˇk−≤IVPFHSWG (Fdˇ11,Fdˇ12,…,Fdˇnm)≤Fdˇk+.
3.2.3 Shift Invariance
Let Fdˇk = ([κdˇkl,κdˇku],[δdˇkl,δdˇku]) be an IVPFHSN. Then
IVPFHSWG(Fdˇ11⊗Fdˇk,Fdˇ12⊗Fdˇk,…,Fdˇnm⊗Fdˇk)=IVPFHSWG(Fdˇ11,Fdˇ12,…,Fdˇnm) ⊗Fdˇk
Proof. As Fdˇk= ([κdˇkl,κdˇku],[δdˇkl,δdˇku]) and Fdˇij= ([κdˇijl,κdˇiju],[δdˇijl,δdˇiju]) be two IVPFHSNs. Then, using Definition 3.2 (2)
Fdˇk⊗Fdˇij=([κdˇklκdˇijl,κdˇkuκdˇiju],[δdˇkl2+δdˇijl2−δdˇkl2δdˇijl2,δdˇku2+δdˇiju2−δdˇku2δdˇiju2])
So,
IVPFHSWG(Fdˇ11⊗Fdˇk,Fdˇ12⊗Fdˇk,…,Fdˇnm⊗Fdˇk)
=⊗j=1mνj(⊗i=1nωi(Fdˇij⊗Fdˇk))
=(∏j=1m(∏i=1n([κdˇijl,κdˇiju])ωi([κdˇkl,κdˇku])ωi)νj,1−∏j=1m(∏i=1n(1−[δdˇijl,δdˇiju]2)ωi(1−[δdˇkl,δdˇku]2)ωi)νj)
=([κdˇkl,κdˇku]∏j=1m(∏i=1n([κdˇijl,κdˇiju])ωi)νj,1−(1−[δdˇkl,δdˇku]2)∏j=1m(∏i=1n(1−[δdˇijl,δdˇiju]2)ωi)νj)
=((∏j=1m(∏i=1n([κdˇijl,κdˇiju])ωi)νj,1−∏j=1m(∏i=1n(1−[δdˇijl,δdˇiju]2)ωi)νj)⊗([κdˇkl,κdˇku],[δdˇkl,δdˇku]))
IVPFHSWG(Fdˇ11,Fdˇ12,…,Fdˇnm)⊗Fdˇk.
3.2.4 Homogeneity
Prove that IVPFHSWG (βFdˇ11,βFdˇ12,…,βFdˇnm)=βIVPFHSWG (Fdˇ11,Fdˇ12,…,Fdˇnm) for any positive real number β.
Proof. Let Fdˇij = ([κdˇijl,κdˇiju],[δdˇijl,δdˇiju]) be an IVPFHSN and β>0. Then using Definition 3.2, we have
Fdˇkβ=([κdˇklβ,κdˇkuβ],1−(1−[δdˇkl,δdˇku]2)β)
So,
IVPFHSWG (βFdˇ11,βFdˇ12,…,βFdˇnm)
=(∏j=1m(∏i=1n([κdˇijlβ,κdˇijuβ])ωi)νj,1−∏j=1m(∏i=1n((1−[δdˇijl,δdˇiju]2)ωi)β)νj)
=((∏j=1m(∏i=1n([κdˇijl,κdˇiju])βωi)νj),1−(∏j=1m(∏i=1n(1−[δdˇijl,δdˇiju]2)ωi)νj)β)
=((∏j=1m(∏i=1n([κdˇijl,κdˇiju])ωi)νj)β,1−(∏j=1m(∏i=1n(1−[δdˇijl,δdˇiju]2)ωi)νj)β)
=βIVPFHSWG (Fdˇ11,Fdˇ12,…,Fdˇnm).
4 Multi-Criteria Group Decision-Making Approach Based on Proposed Operators
A decision-making method has been present to resolve the MCGDM obstacles to authenticate the implication of the planned AOs. Also, a statistical illustration has been offered to confirm the pragmatism of the developed methodology.
4.1 Proposed MCGDM Approach
Consider I={I1,I2,I3,…,Is} be the set of s alternatives, U={U1,U2,U3,…,Ur} be the set of r decision-makers. The weights of experts are given as ωi=(ω1,ω2,ω3,…,ωn)T such that ωi>0, ∑i=1nωi=1. Suppose Let L = {e1,e2,e3,…,em} be the set of attributes with their corresponding multi sub-attributes such as L′ = {(e1ρ×e2ρ×…×emρ)for all ρ∈{1,2,…,t}} with weights ν=(ν1,ν2,ν3,…,νn)T such that νi>0, ∑i=1nνi=1. and can be stated as L′ = {dˇ∂:∂∈{1,2,…,m}}. The group of experts {κi: i = 1, 2,…, n} assess the alternatives {H(z): z = 1, 2, …, s} under the chosen sub-attributes {dˇ∂: ∂ = 1, 2, …, k} in the form of IVPFHSNs such as (Idˇik(z))n×m= ([κdˇikl,κdˇiku],[δdˇikl,δdˇiku])n∗m. Where 0 ≤ κdˇikl,κdˇiku,δdˇikl,δdˇiku ≤ 1 and 0 ≤ (κdˇiku)2 + (δdˇiku)2 ≤ 1 for all i, k. The decision-makers give their judgment in the form of IVPFHSNs Θk for each alternative. The stepwise algorithm is based on established operators given such as follows:
Step-1: Obtain a decision matrix in IVPFHSNs for each alternative according to the expert’s opinion.
(Idˇik(z))n×m=([κdˇikl,κdˇiku],[δdˇikl,δdˇiku])n∗m
=[([κdˇ11l,κdˇ11u],[δdˇ11l,δdˇ11u])([κdˇ21l,κdˇ21u],[δdˇ21l,δdˇ21u])([κdˇ12l,κdˇ12u],[δdˇ12l,δdˇ12u])([κdˇ22l,κdˇ22u],[δdˇ22l,δdˇ22u])⋯([κdˇ1ml,κdˇ1mu],[δdˇ1ml,δdˇ1mu])([κdˇ2nl,κdˇ2nu],[δdˇ2ml,δdˇ2mu])⋮⋱⋮([κdˇn1l,κdˇn1u],[δdˇn1l,δdˇn1u])([κdˇn2l,κdˇn2u],[δdˇn2l,δdˇn2u])⋯([κdˇnml,κdˇnmu],[δdˇnml,δdˇnmu])]
Step-2: Convert the cost type attributes to benefit type using the normalization rule and establish the normalized decision matrices.
Fdˇik={Fdˇijc=([δdˇikl,δdˇiku],[κdˇikl,κdˇiku])n×mcosttypeparameterFdˇij=([κdˇikl,κdˇiku],[δdˇikl,δdˇiku])n×mbenefittypeparameter
Step-3: Calculate the aggregated values for each alternative using developed IVPFHSWA and IVPFHSWG.
Step-4: Calculate the score values for each alternative.
Step-5: Examine the ranking of the alternatives.
4.2 Numerical Example
It is an intelligent transformation of fossil waste energy, such as natural gas first converted into hydrogen. In inference, despite the overdevelopment of fossil fuels and the potential for global warming, the most important renewable energy sources will originate from the description of financial or environmental reasons. The recently formed hydrogen fuel is different in weight and volume from the commonly used hydrogen fuel in power performance. This hydrogen, irrelevant to its energy capacity, is the most prominent feature. The energy content per kilogram of hydrogen is 120 MJ. The advantage of methanol is an extraordinary six times [38]. Hydrogen has a bit of volumetric energy compactness associated with its particular gravimetric density. The compactness of hydrogen is determined by its accumulation state. A stable thickness of up to 700 bar is not a large enough property for hydrocarbons like gasoline and diesel. Only liquid hydrogen can affect a reasonable amount, still less than a quarter of the amount of gasoline. Therefore, hydrogen containers for motor tenders will conquer more than previously used fluid hydrocarbon containers [39]. Cryogenic storage containers are also considered cryogenic storage containers. The dewar is a double-walled super-insulated container. Its vehicles fluid oxygen, nitrogen, hydrogen, helium, and argon, temperatures <110 K/163°C.
The most significant features (parameters) to deliberate when electing a materiality dashboard DM. The assortment method initiates with a preliminary screening of the material used for the dashboard and is captivated by the validation configuration in-built into the application. Throughout the airing progression, potentially proper materials are acknowledged. Defining the ingredients that can be used by the preliminary MS of the dashboard fashioning is serious. Then select from four material assessment abilities: I1 = Ti–6Al–4V, I2 = SS301–FH, I3 = 70Cu–30Zn, and I4 = Inconel 718. The aspect of material assortment is specified as follows: L={d1=Specific gravity=attaining data around the meditation of resolutions of numerous materials,d2=Toughness index,d3=Yield stress,d4=Easily accessible}. The corresponding subattributes of the considered parameters, Specific gravity = attaining data around the meditation of resolutions of numerous materials = d1 ={d11=assess corporal variations,d12=govern the degree of regularity among tasters}, Toughness index = d2 = {d21=CharpyV−Notch Impact Energy,d22=Plane Strain Fracture Toughness}, Yield stress = d3 = {d31=Yield stress}, Easily accessible = d4 = {d41=Easily accessible}. Let L′ = d1 × d2 × d3× d4 be a set of sub-attributes
L′=d1×d2×d3×d4={d11,d12}×{d21,d22}×{d31}×{d41}
={(d11,d21,d31d41),(d11,d22,d31,d41),(d12,d21,d31,d41),(d12,d22,d31,d41)}, L′={dˇ1,dˇ2,dˇ3,dˇ4} be a set of all sub-attributes with weights (0.3,0.1,0.2,0.4)T. Let {u1,u2,u3,u4} be a set of four experts with weights (0.1,0.2,0.4,0.3)T. To judge the optimal alternative, experts deliver their preferences in IVPFHSNs.
4.2.1 By IVPFHSWA Operator
Step-1: Decision-maker’s opinion on IVPFHSNs is given in Tables 1–4.




Step-2: There is no need to normalize because all parameters are the same type.
Step-3: Compute the aggregated values employing the developed IVPFHSWA operator for each alternative.
Θ1=(1−∏j=14(∏i=14(1−[κdˇijl,κdˇiju]2)ωi)νj,∏j=14(∏i=14([δdˇijl,δdˇiju])ωi)νj)
Θ1=(1−({[0.98,0.97][0.99,0.87][0.96,0.89][0.95,0.87]}0.3{[0.93,0.90][0.99,0.91][0.93,0.84][0.95,0.92]}0.1{[0.98,0.96][0.99,0.98][0.93,0.76][0.97,0.95]}0.2{[0.99,0.98][0.99,0.94][0.89,0.76][0.97,0.87]}0.4),({[0.93,0.85][0.90,0.72][0.69,0.39][0.89,0.69]}0.3{[0.95,0.93][0.87,0.83][0.87,0.52][0.89,0.69]}0.1{[0.93,0.85][0.96,0.83][0.87,0.62][0.81,0.69]}0.2{[0.95,0.85][0.93,0.83][0.69,0.52][0.81,0.69]}0.4))
Θ1=(1−([0.88,0.65]0.3[0.81,0.63]0.1[0.87,0.68]0.2[0.85,0.61]0.4),([0.51,0.16]0.3[0.64,0.28]0.1[0.63,0.30]0.2[0.49,0.25]0.4))
Θ1=(1−([0.8788,0.9624][0.9548,0.9791][0.9258,0.9725][0.8206,0.9371]),([0.5771,0.8171][0.8805,0.9563][0.7860,0.9117][0.5743,0.7517]))
Θ1=(1−[0.6374,0.8587],[0.2294,0.5355])
Θ1=([0.3626,0.1413],[0.2294,0.5355])
Θ1=[0.3759,0.6022],[0.2294,0.5355].
Θ2=(1−∏j=14(∏i=14(1−[κdˇijl,κdˇiju]2)ωi)νj,∏j=14(∏i=14([δdˇijl,δdˇiju])ωi)νj)
Θ2=(1−({[0.64,0.91]0.1[0.71,0.91]0.2[0.64,0.96]0.4[0.91,0.96]0.3}0.3{[0.51,0.96]0.1[0.84,0.99]0.2[0.96,0.99]0.4[0.75,0.91]0.3}0.1{[0.51,0.96]0.1[0.75,0.99]0.2[0.51,0.84]0.4[0.51,0.91]0.3}0.2{[0.51,0.64]0.1[0.75,0.84]0.2[0.36,0.75]0.4[0.51,0.99]0.3}0.4),({[0.5,0.6]0.1[0.5,0.8]0.2[0.1,0.4]0.4[0.3,0.8]0.3}0.3{[0.5,0.7]0.1[0.4,0.5]0.2[0.2,0.9]0.4[0.2,0.8]0.3}0.1{[0.4,0.5]0.1[0.3,0.7]0.2[0.3,0.8]0.4[0.2,0.6]0.3}0.2{[0.5,0.8]0.1[0.3,0.6]0.2[0.2,0.6]0.4[0.3,0.6]0.3}0.4))
Θ2=(1−({[0.99,0.96][0.98,0.93][0.98,0.84][0.95,0.87]}0.3{[0.93,0.90][0.99,0.91][0.93,0.84][0.95,0.92]}0.1{[0.98,0.96][0.99,0.98][0.93,0.76][0.97,0.87]}0.2{[0.99,0.98][0.99,0.94][0.89,0.76][0.97,0.87]}0.4),({[0.93,0.85][0.90,0.72][0.69,0.39][0.89,0.69]}0.3{[0.95,0.93][0.87,0.83][0.87,0.52][0.89,0.69]}0.1{[0.93,0.85][0.96,0.83][0.87,0.62][0.81,0.69]}0.2{[0.95,0.85][0.93,0.83][0.69,0.52][0.81,0.69]}0.4))
Θ2=(1−([0.90,0.65]0.3[0.81,0.63]0.1[0.87,0.68]0.2[0.85,0.61]0.4),([0.51,0.16]0.3[0.64,0.28]0.1[0.63,0.30]0.2[0.49,0.25]0.4))
Θ2=(1−([0.8788,0.9689][0.9548,0.9791][0.9258,0.9725][0.8206,0.9371]),([0.5771,0.8171][0.8805,0.9563][0.7860,0.9117][0.5743,0.7517]))
Θ2=(1−[0.6374,0.8645],(0.2294,0.5355))
Θ2=([0.3626,0.1355],[0.2294,0.5355])
Θ2=[0.3681,0.6022],[0.2294,0.5355].
Θ3=(1−∏j=14(∏i=14(1−[κdˇijl,κdˇiju]2)ωi)νj,∏j=14(∏i=14([δdˇijl,δdˇiju])ωi)νj)
Θ3=(1−({[0.84,0.91]0.1[0.64,0.84]0.2[0.84,0.96]0.4[0.51,0.91]0.3}0.3{[0.84,0.91]0.1[0.75,0.91]0.2[0.75,0.91]0.4[0.75,0.91]0.3}0.1{[0.64,0.75]0.1[0.75,0.91]0.2[0.51,0.91]0.4[0.75,0.96]0.3}0.2{[0.84,0.91]0.1[0.64,0.96]0.2[0.91,0.99]0.4[0.84,0.91]0.3}0.4),({[0.2,0.7]0.1[0.3,0.7]0.2[0.3,0.4]0.4[0.3,0.7]0.3}0.3{[0.4,0.6]0.1[0.2,0.3]0.2[0.3,0.7]0.4[0.2,0.4]0.3}0.1{[0.4,0.5]0.1[0.5,0.8]0.2[0.3,0.8]0.4[0.3,0.6]0.3}0.2{[0.3,0.6]0.1[0.2,0.4]0.2[0.5,0.6]0.4[0.3,0.7]0.3}0.4))
Θ3=(1−({[0.99,0.98][0.96,0.91][0.98,0.93][0.97,0.82]}0.3{[0.99,0.98][0.98,0.94][0.96,0.89][0.97,0.92]}0.1{[0.97,0.96][0.98,0.94][0.96,0.76][0.99,0.92]}0.2{[0.99,0.98][0.99,0.91][0.99,0.96][0.97,0.95]}0.4),({[0.96,0.85][0.93,0.79][0.69,0.62][0.89,0.69]}0.3{[0.95,0.91]0.79,0.72][0.86,0.62][0.76,0.62]}0.1{[0.93,0.91][0.96,0.87][0.91,0.62][0.86,0.69]}0.2{[0.95,0.88][0.83,0.72][0.81,0.76][0.89,0.69]}0.4))
Θ3=(1−([0.90,0.68]0.3[0.90,0.75]0.1[0.90,0.63]0.2[0.94,0.81]0.4),([0.55,0.29]0.3[0.49,0.25]0.1[0.69,0.34]0.2[0.57,0.33]0.4))
Θ3=(1−([0.8907,0.9689][0.9716,0.9895][0.9117,0.9791][0.9192,0.9755]),([0.6898,0.8358][0.8705,0.9311][0.8059,0.9285][0.6418,0.7986]))
Θ3=(1−[0.7252,0.9157],(0.3183,0.4637))
Θ3=([0.7252,0.9157],(0.3183,0.4637))
Θ3=[0.2903,0.5242],[0.3183,0.4637].
Θ4=(1−∏j=14(∏i=14(1−[κdˇijl,κdˇiju]2)ωi)νj,∏j=14(∏i=14([δdˇijl,δdˇiju])ωi)νj)
Θ4=(1−({[0.75,0.91]0.1[0.51,0.84]0.2[0.75,0.96]0.4[0.51,0.75]0.3}0.3{[0.51,0.96]0.1[0.51,0.84]0.2[0.51,0.75]0.4[0.75,0.96]0.3}0.1{[0.75,0.96]0.1[0.75,0.99]0.2[0.84,0.96]0.4[0.75,0.91]0.3}0.2{[0.84,0.96]0.1[0.36,0.75]0.2[0.51,0.96]0.4[0.75,0.96]0.3}0.4),({[0.2,0.6]0.1[0.2,0.6]0.2[0.3,0.6]0.4[0.6,0.8]0.3}0.3{[0.3,0.8]0.1[0.1,0.5]0.2[0.4,0.5]0.4[0.3,0.4]0.3}0.1{[0.1,0.6]0.1[0.2,0.5]0.2[0.2,0.7]0.4[0.1,0.5]0.3}0.2{[0.5,0.8]0.1[0.2,0.5]0.2[0.3,0.6]0.4[0.4,0.5]0.3}0.4))
Θ4=(1−({[0.99,0.97][0.96,0.87][0.98,0.89][0.92,0.82]}0.3{[0.99,0.93][0.96,0.87][0.89,0.76][0.99,0.92]}0.1{[0.99,0.97][0.99,0.94][0.98,0.93][0.97,0.92]}0.2{[0.99,0.98][0.94,0.81][0.98,0.76][0.99,0.92]}0.4),({[0.95,0.85][0.90,0.72][0.81,0.62][0.93,0.86]}0.3{[0.98,0.89][0.87,0.63][0.76,0.69][0.76,0.69]}0.1{[0.95,0.79][0.87,0.72][0.87,0.52][0.81,0.50]}0.2{[0.98,0.93][0.87,0.72][0.81,0.62][0.81,0.76]}0.4))
Θ4=(1−([0.86,0.61]0.3[0.84,0.56]0.1[0.93,0.78]0.2[0.90,0.55]0.4),([0.64,0.33]0.3[0.49,0.27]0.1[0.58,0.15]0.2[0.56,0.31]0.4))
Θ4=(1−([0.8622,0.9558][0.9437,0.9827][0.9515,0.9856][0.7873,0.9587]),([0.7170,0.8747][0.8773,0.9311][0.6842,0.8968][0.6259,0.7930]))
Θ4=(1−[0.6095,0.8875],[0.2694,0.5792])
Θ4=([0.3905,0.1125],[0.2694,0.5792])
Θ4=[0.3354,0.6249],[0.2694,0.5792].
Step-4: Using score function S=(κdˇijl)2+(κdˇiju)2−(δdˇijl)2−(δdˇiju)22 for the IVPFSSS to calculate the score values for all alternatives. S(Θ1)=0.0599, S(Θ2)=0.0578, S(Θ3)=0.0266, and S(Θ4)=−0.0382.
Step-5: From the above calculation, we get S(Θ1)>S(Θ2)>S(Θ3)>S(Θ4), which shows that I1 is the best alternative. So, I1>I2>I3>I4.
4.2.2 By IVPFHSWG Operator
Step-1 and Step-2 are similar to Section 4.2.1.
Step-3: Compute the aggregated values employing the developed IVPFHSWG operator for each alternative.
Θ1=(∏j=14(∏i=14([κdˇijl,κdˇiju])ωi)νj,1−∏j=14(∏i=14(1−[δdˇijl,δdˇiju]2)ωi)νj)
Θ1=(({[0.4,0.5]0.1[0.2,0.7]0.2[0.3,0.5]0.4[0.4,0.6]0.3}0.3{[0.7,0.8]0.1[0.1,0.6]0.2[0.4,0.6]0.4[0.4,0.5]0.3}0.1{[0.4,0.6]0.1[0.2,0.3]0.2[0.4,0.7]0.4[0.3,0.6]0.3}0.2{[0.2,0.4]0.1[0.2,0.5]0.2[0.5,0.7]0.4[0.3,0.6]0.3}0.4),1−({[0.75,0.84]0.1[0.64,0.96]0.2[0.84,0.99]0.4[0.51,0.91]0.3}0.3{[0.64,0.75]0.1[0.75,0.84]0.2[0.51,0.96]0.4[0.51,0.91]0.3}0.1{[0.75,0.96]0.1[0.36,0.84]0.2[0.51,0.91]0.4[0.75,0.91]0.3}0.2{[0.64,0.96]0.1[0.51,0.84]0.2[0.84,0.91]0.4[0.75,0.91]0.3}0.4))
Θ1=(({[0.93,0.91][0.93,0.72][0.76,0.62][0.86,0.76]}0.3{[0.98,0.96][0.90,0.63][0.81,0.69][0.81,0.76]}0.1{[0.95,0.91][0.79,0.72][0.87,0.69][0.86,0.69]}0.2{[0.91,0.85][0.87,0.72][0.87,0.76][0.86,0.69]}0.4),1−({[0.98,0.97][0.99,0.91][0.98,0.76][0.97,0.82]}0.3{[0.97,0.96][0.97,0.94][0.81,0.69][0.81,0.76]}0.1{[0.99,0.97][0.96,0.81][0.96,0.76][0.97,0.92]}0.2{[0.99,0.96][0.96,0.87][0.96,0.93][0.97,0.89]}0.4))
Θ1=(([0.56,0.31]0.3[0.58,0.32]0.1[0.56,0.31]0.2[0.59,0.32]0.4),1−([0.92,0.55]0.3[0.62,0.47]0.1[0.88,0.55]0.2[0.88,0.69]0.4))
Θ1=(([0.7037,0.8403][0.8923,0.9469][0.7911,0.9747][0.6339,0.8097]),1−([0.8358,0.9753][0.9273,0.9533][0.8873,0.9747][0.8620,0.9501]))
Θ1=[0.3149,0.6279],1−[0.5928,0.8610]
Θ1=[0.3149,0.6279],[0.4072,0.139]
Θ1=[0.3149,0.6279],[0.3728,0.6381].
Θ2=(∏j=14(∏i=14([κdˇijl,κdˇiju])ωi)νj,1−∏j=14(∏i=14(1−[δdˇijl,δdˇiju]2)ωi)νj)
Θ2=(({[0.2,0.5]0.1[0.7,0.8]0.2[0.2,0.5]0.4[0.2,0.6]0.3}0.3{[0.2,0.6]0.1[0.1,0.6]0.2[0.4,0.8]0.4[0.4,0.7]0.3}0.1{[0.1,0.4]0.1[0.4,0.6]0.2[0.3,0.7]0.4[0.2,0.4]0.3}0.2{[0.3,0.7]0.1[0.4,0.5]0.2[0.3,0.5]0.4[0.3,0.5]0.3}0.4),1−({[0.75,0.84]0.1[0.64,0.75]0.2[0.64,0.84]0.4[0.84,0.96]0.3}0.3{[0.51,0.96]0.1[0.75,0.84]0.2[0.91,0.96]0.4[0.75,0.96]0.3}0.1{[0.75,0.91]0.1[0.51,0.96]0.2[0.51,0.84]0.4[0.75,0.91]0.3}0.2{[0.64,0.84]0.1[0.51,0.91]0.2[0.64,0.91]0.4[0.64,0.91]0.3}0.4))
Θ2=(({[0.93,0.85][0.96,0.93][0.76,0.52][0.86,0.62]}0.3{[0.95,0.85][0.90,0.63][0.91,0.69][0.89,0.76]}0.1{[0.91,0.79][0.90,0.83][0.87,0.62][0.76,0.62]}0.2{[0.96,0.89][0.87,0.83][0.76,0.62][0.81,0.69]}0.4),1−({[0.98,0.97][0.94,0.91][0.93,0.84][0.79,0.95]}0.3{[0.99,0.93][0.96,0.94][0.98,0.96][0.99,0.92]}0.1{[0.99,0.97][0.99,0.87][0.93,0.51][0.97,0.92]}0.2{[0.98,0.96][0.98,0.87][0.96,0.84][0.97,0.87]}0.4))
Θ2=(([0.58,0.25]0.3[0.69,0.28]0.1[0.54,0.25]0.2[0.51,0.32]0.4),1−([0.68,0.70]0.3[0.92,0.77]0.1[0.88,0.39]0.2[0.89,0.61]0.4))
Θ2=(([0.6597,0.8492][0.8804,0.9635][0.7578,0.8840][0.6339,0.7639]),1−([0.8985,0.8907][0.9742,0.9917][0.8283,0.9747][0.8206,0.9544]))
Θ2=[0.2409,0.5525],1−[0.5949,0.8217]
Θ2=[0.2409,0.5525],[0.4051,0.1783]
Θ2=[0.2409,0.5525],[0.4222,0.6365].
Θ3=(∏j=14(∏i=14([κdˇijl,κdˇiju])ωi)νj,1−∏j=14(∏i=14(1−[δdˇijl,δdˇiju]2)ωi)νj)
Θ3=(({[0.3,0.4]0.1[0.4,0.6]0.2[0.2,0.4]0.4[0.3,0.7]0.3}0.3{[0.3,0.4]0.1[0.3,0.5]0.2[0.3,0.5]0.4[0.3,0.5]0.3}0.1{[0.5,0.6]0.1[0.3,0.5]0.2[0.3,0.7]0.4[0.2,0.5]0.3}0.2{[0.3,0.4]0.1[0.2,0.6]0.2[0.1,0.3]0.4[0.3,0.4]0.3}0.4),1−({[0.51,0.96]0.1[0.51,0.91]0.2[0.84,0.91]0.4[0.51,0.91]0.3}0.3{[0.64,0.91]0.1[0.91,0.96]0.2[0.51,0.91]0.4[0.84,0.96]0.3}0.1{[0.75,0.84]0.1[0.36,0.75]0.2[0.36,0.91]0.4[0.64,0.91]0.3}0.2{[0.64,0.91]0.1[0.84,0.96]0.2[0.64,0.75]0.4[0.51,0.91]0.3}0.4))
Θ3=(({[0.91,0.89][0.90,0.83][0.69,0.52][0.89,0.69]}0.3{[0.91,0.89][0.87,0.79][0.76,0.62][0.81,0.69]}0.1{[0.95,0.93][0.87,0.79][0.87,0.62][0.81,0.62]}0.2{[0.91,0.89][0.90,0.72][0.62,0.39][0.76,0.69]}0.4),1−({[0.99,0.93][0.98,0.87][0.96,0.93][0.97,0.82]}0.3{[0.99,0.96][0.99,0.98][0.96,0.76][0.99,0.95]}0.1{[0.98,0.97][0.94,0.81][0.96,0.66][0.97,0.87]}0.2{[0.99,0.96][0.99,0.96][0.89,0.84][0.97,0.82]}0.4))
Θ3=(([0.50,0.26]0.3[0.49,0.30]0.1[0.58,0.28]0.2[0.38,0.17]0.4),1−([0.90,0.62]0.3[0.93,0.68]0.1[0.86,0.45]0.2[0.85,0.63]0.4))
Θ3=(([0.6676,0.8122][0.8866,0.9311][0.7752,0.8968][0.4922,0.6791]),1−([0.8663,0.9689][0.9622,0.9928][0.8524,0.9703][0.8312,0.9371]))
Θ3=[0.2258,0.4605],[0.3541,0.6398].
Θ4=(∏j=14(∏i=14([κijl,κiju])ωi)νj,1−∏j=14(∏i=14(1−[δijl,δiju]2)ωi)νj)
Θ4=(({[0.3,0.5]0.1[0.2,0.7]0.2[0.2,0.5]0.4[0.2,0.4]0.3}0.3{[0.2,0.6]0.1[0.1,0.5]0.2[0.2,0.5]0.4[0.2,0.5]0.3}0.1{[0.2,0.5]0.1[0.5,0.7]0.2[0.2,0.4]0.4[0.2,0.7]0.3}0.2{[0.5,0.7]0.1[0.2,0.5]0.2[0.3,0.5]0.4[0.2,0.5]0.3}0.4),1−({[0.64,0.96]0.1[0.36,0.91]0.2[0.64,0.99]0.4[0.36,0.75]0.3}0.3{[0.51,0.84]0.1[0.51,0.84]0.2[0.75,0.99]0.4[0.36,0.75]0.3}0.1{[0.84,0.91]0.1[0.75,0.84]0.2[0.51,0.96]0.4[0.64,0.91]0.3}0.2{[0.36,0.64]0.1[0.84,0.91]0.2[0.75,0.99]0.4[0.75,0.84]0.3}0.4))
Θ4=(({[0.93,0.88][0.93,0.72][0.76,0.52][0.76,0.62]}0.3{[0.95,0.85][0.87,0.63][0.76,0.52][0.81,0.62]}0.1{[0.93,0.85][0.93,0.87][0.69,0.52][0.89,0.62]}0.2{[0.96,0.93][0.87,0.72][0.76,0.62][0.81,0.62]}0.4),1−({[0.99,0.93][0.98,0.87][0.96,0.93][0.97,0.82]}0.3{[0.99,0.96][0.99,0.98][0.96,0.76][0.99,0.95]}0.1{[0.98,0.97][0.94,0.81][0.96,0.66][0.97,0.87]}0.2{[0.99,0.96][0.99,0.96][0.89,0.84][0.97,0.82]}0.4))
Θ4=(([0.49,0.20]0.3[0.51,0.17]0.1[0.53,0.24]0.2[0.51,0.26]0.4),1−([0.74,0.62]0.3[0.93,0.68]0.1[0.86,0.45]0.2[0.85,0.63]0.4))
Θ4=(([0.6170,0.8073][0.8376,0.9348][0.7517,0.8807][0.5834,0.7639]),1−([0.8663,0.9136][0.9625,0.9928][0.8523,0.9702][0.8312,0.9371]))
Θ4=[0.2266,0.5077],1−[0.5907,0.8546]
Θ4=[0.2266,0.5077],[0.4093,0.1454]
Θ4=[0.2266,0.5077],[0.3813,0.6398].
Step-4: Use the score function S=(κl)2+(κu)2−(δl)2−(δu)22 interval-valued for the Pythagorean fuzzy soft set to calculate the score values for all alternatives such as S(Θ1)=0.0752, S(Θ2)=0.0654, S(Θ3)=0.0241, and S(Θ4)=0.0114.
Step-5: From the above calculation, we get the ranking of alternatives S(Θ1)>S(Θ2)>S(Θ3)>S(Θ4). Which shows that I1 is the best alternative. So, I1>I2>I3>I4 .
Subsequently, the material assessment wonders at the theoretical level through the depiction phase of the strategy; there is more possibility to the extent of the correctness of the specific materials. Face-centered cube materials are typically used at minor temperatures −163°C and I1 = Ti–6Al–4V ratings first. This is steadfast in employing initial investigations and real-world maneuvers. Austenitic steels are still classically used in melted nitrogen or hydrogen storing vessels [40].
5 Comparative Studies
A comparison among the projected model and prevalent approaches is planned to validate the efficacy of the offered technique in the subsequent section.
5.1 Supremacy of the Planned Technique
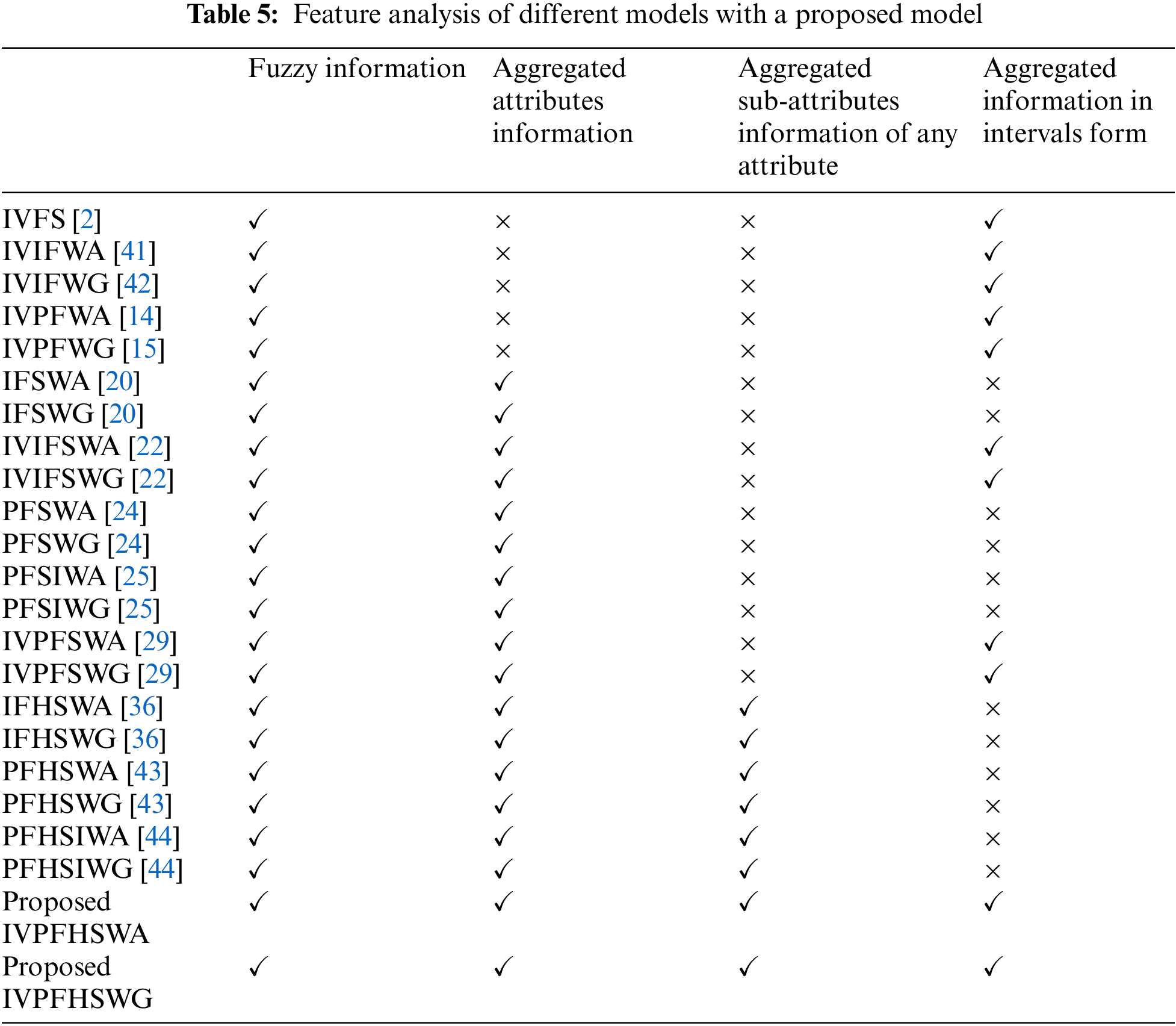
The intended method is proficient and realistic; in the IVPFHSS setting, we construct an inventive MCGDM model on the IVPFHSWA and PFHSEWG operators. Our planned model is more talented than prevalent techniques and can produce the most subtle implications in MCGDM difficulties. The cooperative model is multipurpose and conversant, adjusting to evolving instability, commitment, and output. Different models have particular ranking processes, so there is a straight modification among the rankings of the anticipated methods conferring to their expectations. This systematic study and assessment determined that the outcomes attained from prevailing procedures are irregularly equated to hybrid structures. Also, due to some favorable situations, many mixed IVFS, IVIFS, IVPFS, IVIFSS, and IVPFSS grow into special in IVPFHSS. It is easy to syndicate insufficient and ambiguous data in DM procedures. Imprecise and anxious facts are mixed in the DM procedure. Hence, our scheduled method will be more proficient, crucial, superior, and better than numerous mixed FS structures. Table 5 below presents the projected technique and the characteristic analysis of some existing models.

5.2 Comparative Analysis
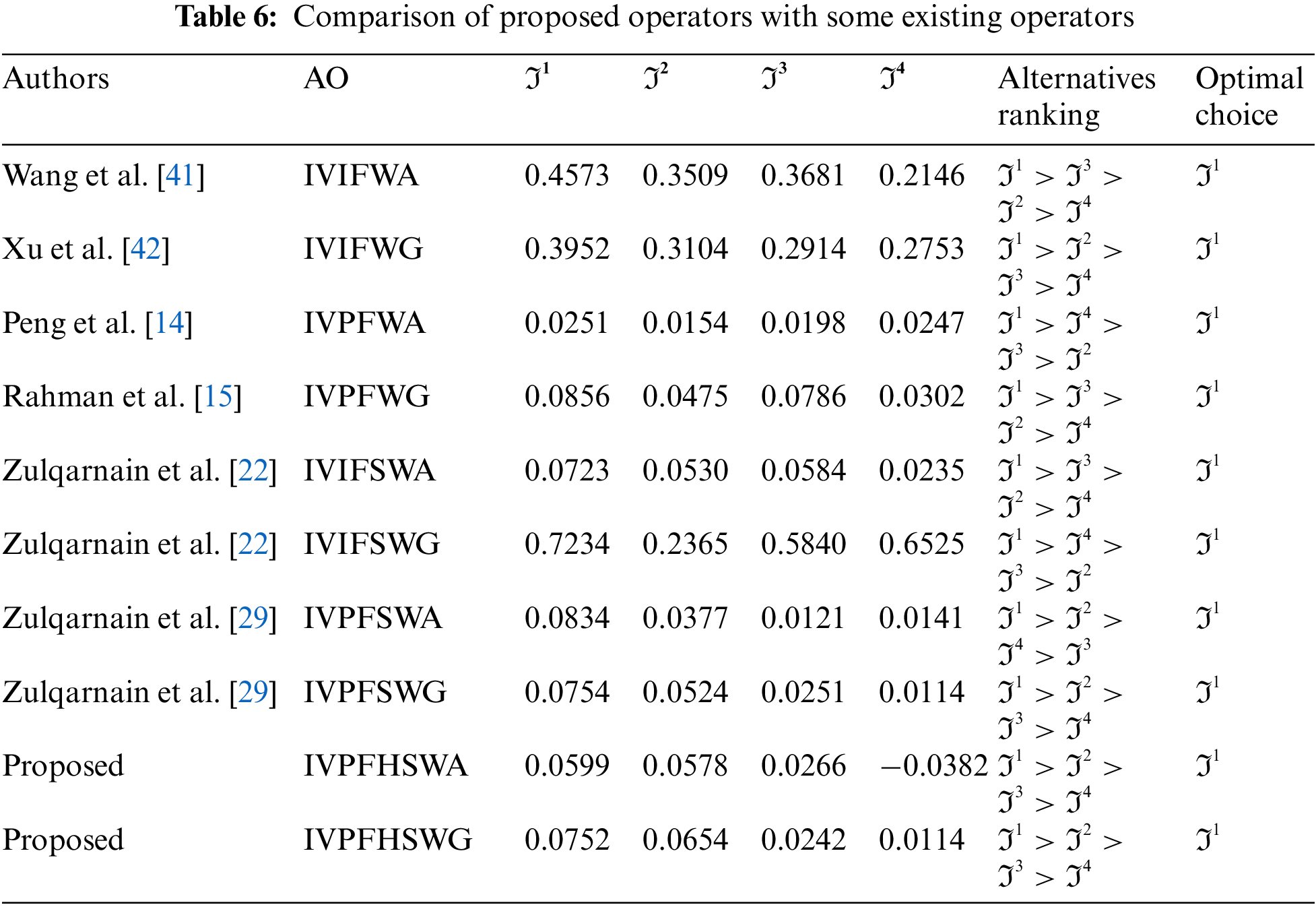
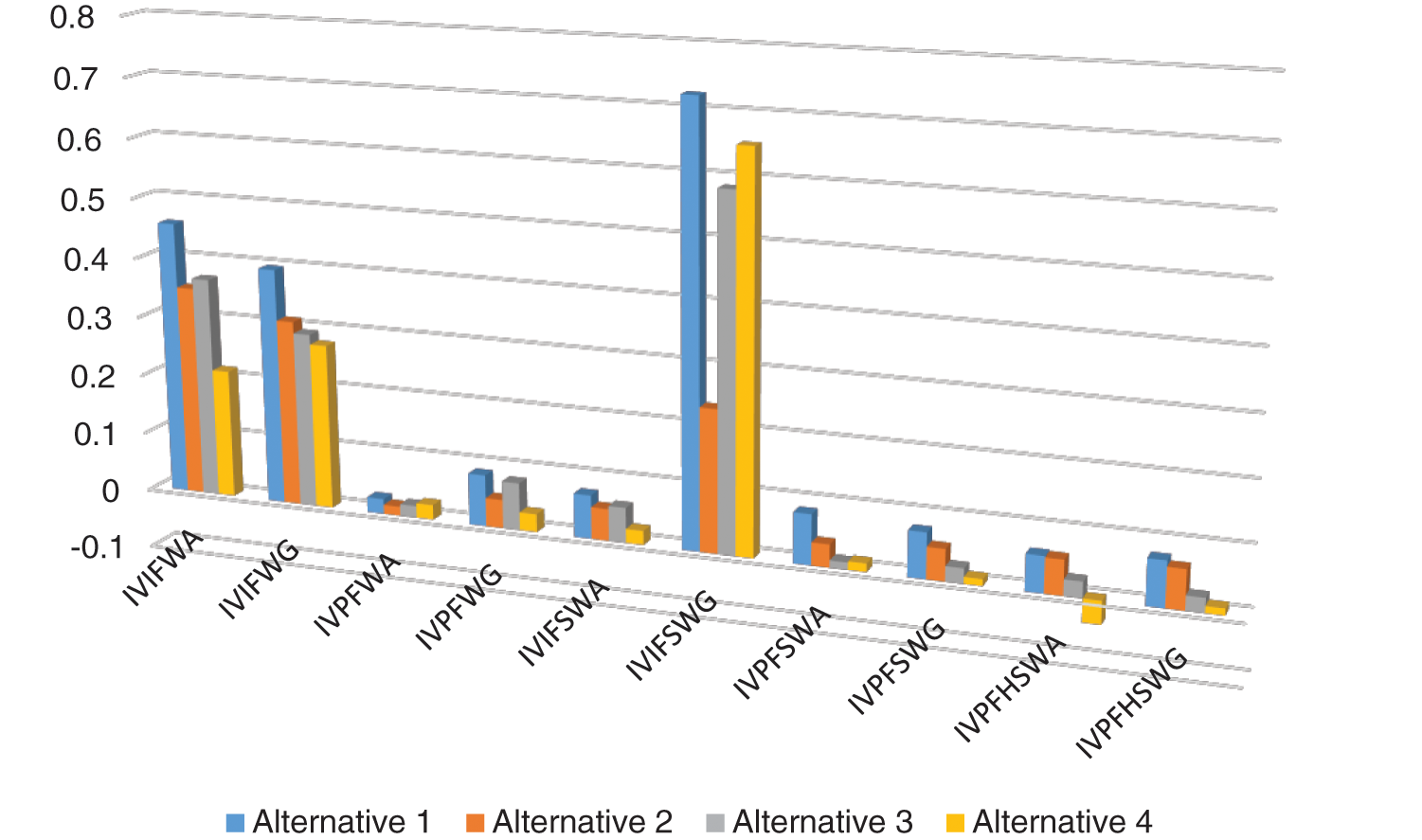
To prove the usefulness of the planned technique, we equate the attained consequences with some prevailing approaches under the setting of IVPFS, IVIFSS, and IVPFSS. A summary of outcomes is specified in Table 6. Wang et al. [41] developed IVIFWA, and Xu et al. [42] presented that IVIFWG operators cannot compute the parametrized values of the alternatives. Furthermore, if any expert considers the MD and NMD whose sum exceeds 1, the AOs mentioned above fail to accommodate the scenario. Zulqarnain et al. [22] established AOs for IVIFSS that cannot accommodate the decision-maker’s selection when the sum of upper MD and NMD of the parameters surpasses one. Peng et al.’s [14] interval-valued Pythagorean fuzzy weighted average operator and Rahman et al. [15] interval-valued Pythagorean fuzzy weighted geometric operator cannot handle the parametrized values of the alternatives. Zulqarnain et al. [29] established the interval-valued Pythagorean fuzzy soft weighted average and interval-valued Pythagorean fuzzy soft weighted geometric operators to deal with the parameterized values of alternatives. But, these AOs fail to handle the scenario if any parameter contains a different sub-parameter. Furthermore, if any parameter has any other sub-parameter, the IVPFHSS reduces to the interval-valued Pythagorean fuzzy soft set. Suppose the sum of upper values of MD and NMD is less or equal to 1. Then, IVPFHSS is reduced to IVIFHSS. Thus, IVPFHSS is the most generalized form of interval-valued Pythagorean fuzzy set and IVPFSS. Hence, based on the details mentioned above, the anticipated operators in this paper are more influential, consistent, and prosperous.

The graphical demonstration of Table 6 is given in the following Fig. 1.
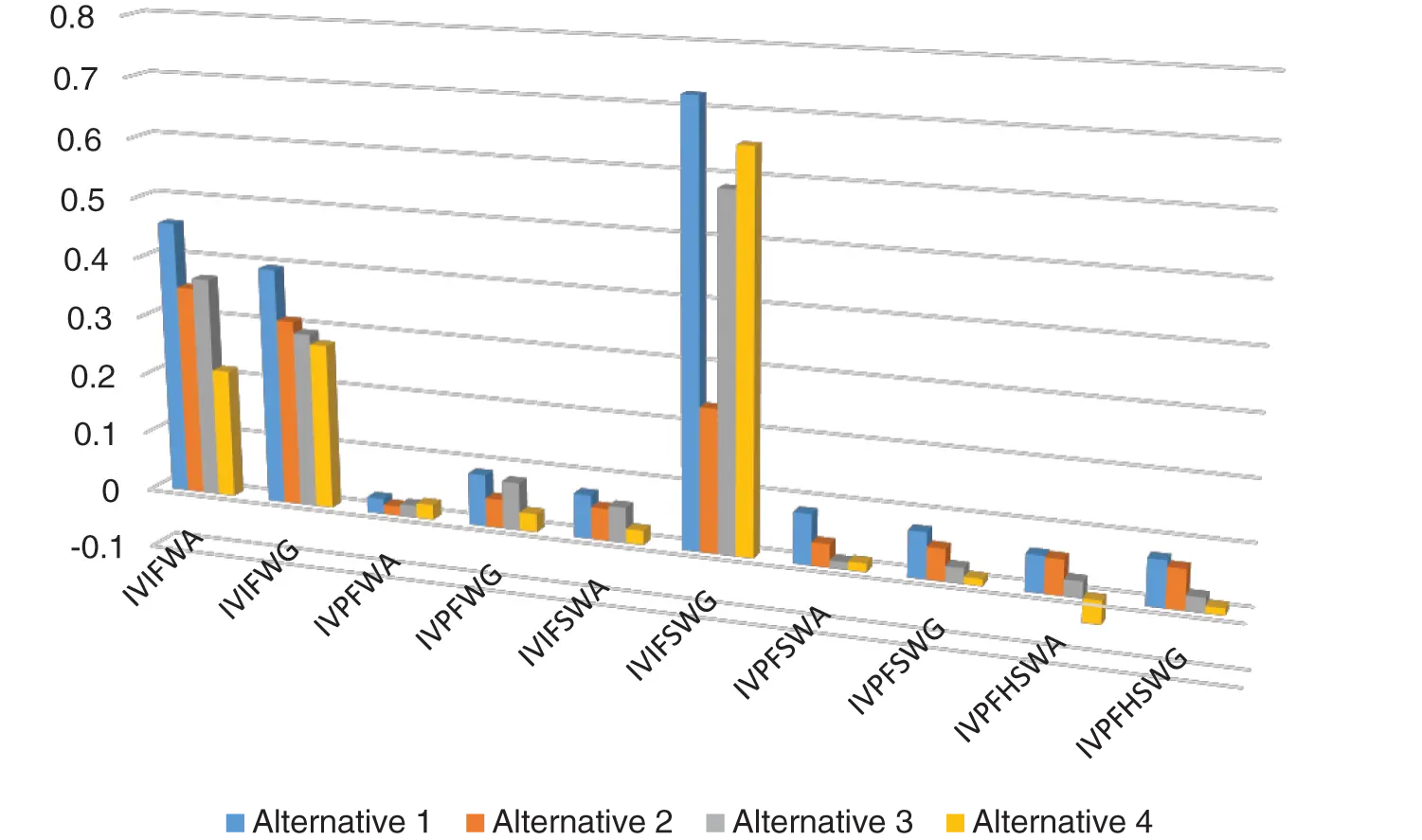
Figure 1: Comparative analysis of the proposed approach with existing models
6 Conclusion
In manufacturing, the refined solidity of manipulation is neutral; authentic materials and fabrication encompass wide-ranging materials. Mathematical demonstration in industrial inventiveness formations exploits all assets while merging design intentions under financial, superior, and safety limitations. Inquiries must be restricted for best judgment, consulting to decision requirements. In genuine DM, the valuation of alternative facts conveyed by the professional is consistently inaccurate, irregular, and impulsive, so IVPFHSNs can be used to comport this uncertain data. The principal objective of this work is to prolong the Pythagorean fuzzy hypersoft sets to interval-valued Pythagorean fuzzy hypersoft sets. Firstly, we introduce the operational laws for the interval-valued Pythagorean fuzzy hypersoft setting. Considering the developed operational laws, we presented the IVPFHSWA and IVPFHSWG operators for IVPFHSS with their desired properties. Also, a DM method has been planned to address MCGDM complications based on the validated operators. To state the stoutness of the developed methodology, we deliver a comprehensive mathematical illustration for MS in manufacturing engineering. A comprehensive analysis of some existing procedures is described to ensure the practicality of the developed approach. Lastly, based on the consequences achieved, it is determined that the method proposed in this study is the most practical and operative way to explain the problem of MCGDM.
Funding Statement:The authors extend their appreciation to Deanship of Scientific Research at King Khalid University for funding this work through General Research Project under Grant No. R.G.P. 327/43.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8(3), 338–353. DOI 10.1016/S0019-9958(65)90241-X. [Google Scholar] [CrossRef]
2. Turksen, I. B. (1986). Interval valued fuzzy sets based on normal forms. Fuzzy Sets and Systems, 20(2), 191–210. DOI 10.1016/0165-0114(86)90077-1. [Google Scholar] [CrossRef]
3. Atanassov, K. (1986). Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20(1), 87–96. [Google Scholar]
4. Wang, W., Liu, X. (2011). Intuitionistic fuzzy geometric aggregation operators based on Einstein operations. International Journal of Intelligent Systems, 26(11), 1049–1075. DOI 10.1002/int.20498. [Google Scholar] [CrossRef]
5. Atanassov, K. T. (1999). Interval-valued intuitionistic fuzzy sets. In: Intuitionistic fuzzy sets, pp. 139–177. Heidelberg: Physica. [Google Scholar]
6. Garg, H., Kaur, G. (2019). Cubic intuitionistic fuzzy sets and its fundamental properties. Journal of Multiple-Valued Logic & Soft Computing, 33(6), 507–537. [Google Scholar]
7. Yager, R. R. (2013). Pythagorean membership grades in multi-criteria decision making. IEEE Transactions on Fuzzy Systems, 22(4), 958–965. DOI 10.1109/TFUZZ.2013.2278989. [Google Scholar] [CrossRef]
8. Rahman, K., Abdullah, S., Ahmed, R., Ullah, M. (2017). Pythagorean fuzzy Einstein weighted geometric aggregation operator and their application to multiple attribute group decision making. Journal of Intelligent & Fuzzy Systems, 33(1), 635–647. DOI 10.3233/JIFS-16797. [Google Scholar] [CrossRef]
9. Zhang, X., Xu, Z. (2014). Extension of TOPSIS to multiple criteria decision making with Pythagorean fuzzy sets. International Journal of Intelligent Systems, 29(12), 1061–1078. DOI 10.1002/int.21676. [Google Scholar] [CrossRef]
10. Wei, G., Lu, M. (2018). Pythagorean fuzzy power aggregation operators in multiple attribute decision making. International Journal of Intelligent Systems, 33(1), 169–186. DOI 10.1002/int.21946. [Google Scholar] [CrossRef]
11. Wang, L., Li, N. (2020). Pythagorean fuzzy interaction power Bonferroni means aggregation operators in multiple attribute decision making. International Journal of Intelligent Systems, 35(1), 150–183. DOI 10.1002/int.22204. [Google Scholar] [CrossRef]
12. Ilbahar, E., Karaşan, A., Cebi, S., Kahraman, C. (2018). A novel approach to risk assessment for occupational health and safety using Pythagorean fuzzy AHP & fuzzy inference system. Safety Science, 103(9), 124–136. DOI 10.1016/j.ssci.2017.10.025. [Google Scholar] [CrossRef]
13. Zhang, X. (2016). A novel approach based on similarity measure for Pythagorean fuzzy multiple criteria group decision making. International Journal of Intelligent Systems, 31(6), 593–611. DOI 10.1002/int.21796. [Google Scholar] [CrossRef]
14. Peng, X., Yang, Y. (2016). Fundamental properties of interval-valued Pythagorean fuzzy aggregation operators. International Journal of Intelligent Systems, 31(5), 444–487. DOI 10.1002/int.21790. [Google Scholar] [CrossRef]
15. Rahman, K., Abdullah, S., Shakeel, M., Ali Khan, M. S., Ullah, M. (2017). Interval-valued Pythagorean fuzzy geometric aggregation operators and their application to group decision making problem. Cogent Mathematics, 4(1), 1338638. DOI 10.1080/23311835.2017.1338638. [Google Scholar] [CrossRef]
16. Molodtsov, D. (1999). Soft set theory—First results. Computers & Mathematics with Applications, 37(4–5), 19–31. DOI 10.1016/S0898-1221(99)00056-5. [Google Scholar] [CrossRef]
17. Maji, P. K., Biswas, R., Roy, A. R. (2003). Soft set theory. Computers & Mathematics with Applications, 45(4–5), 555–562. DOI 10.1016/S0898-1221(03)00016-6. [Google Scholar] [CrossRef]
18. Maji, P. K., Biswas, R., Roy, A. R. (2001). Fuzzy soft sets. Journal of Fuzzy Mathematics, 9, 589–602. [Google Scholar]
19. Maji, P. K., Biswas, R., Roy, A. R. (2001). Intuitionistic fuzzy soft sets. Journal of Fuzzy Mathematics, 9, 677–692. [Google Scholar]
20. Arora, R., Garg, H. (2018). A robust aggregation operators for multi-criteria decision-making with intuitionistic fuzzy soft set environment. Scientia Iranica, 25(2), 931–942. [Google Scholar]
21. Jiang, Y., Tang, Y., Chen, Q., Liu, H., Tang, J. (2010). Interval-valued intuitionistic fuzzy soft sets and their properties. Computers & Mathematics with Applications, 60(3), 906–918. DOI 10.1016/j.camwa.2010.05.036. [Google Scholar] [CrossRef]
22. Zulqarnain, R. M., Xin, X. L., Saqlain, M., Khan, W. A. (2021). TOPSIS method based on the correlation coefficient of interval-valued intuitionistic fuzzy soft sets and aggregation operators with their application in decision-making. Journal of Mathematics, 2021(10), 1–16. DOI 10.1155/2021/6656858. [Google Scholar] [CrossRef]
23. Peng, X. D., Yang, Y., Song, J., Jiang, Y. (2015). Pythagorean fuzzy soft set and its application. Computer Engineering, 41(7), 224–229. [Google Scholar]
24. Zulqarnain, R. M., Xin, X. L., Garg, H., Khan, W. A. (2021). Aggregation operators of pythagorean fuzzy soft sets with their application for green supplier chain management. Journal of Intelligent and Fuzzy Systems, 40(3), 5545–5563. DOI 10.3233/JIFS-202781. [Google Scholar] [CrossRef]
25. Zulqarnain, R. M., Xin, X. L., Garg, H., Ali, R. (2021). Interaction aggregation operators to solve multi criteria decision making problem under pythagorean fuzzy soft environment. Journal of Intelligent & Fuzzy Systems, 41(1), 1151–1171. DOI 10.3233/JIFS-210098. [Google Scholar] [CrossRef]
26. Zulqarnain, R. M., Siddique, I., EI-Morsy, S. (2022). Einstein-ordered weighted geometric operator for pythagorean fuzzy soft set with its application to solve MAGDM problem. Mathematical Problems in Engineering, 2022(4), 5199427. DOI 10.1155/2022/5199427. [Google Scholar] [CrossRef]
27. Zulqarnain, R. M., Siddique, I., Ahmad, S., Iampan, A., Jovanov, G. et al. (2021). Pythagorean fuzzy soft Einstein ordered weighted average operator in sustainable supplier selection problem. Mathematical Problems in Engineering, 2021(4), 2559979. DOI 10.1155/2021/2559979. [Google Scholar] [CrossRef]
28. Zulqarnain, R. M., Xin, X. L., Siddique, I., Khan, W. A., Yousif, M. A. (2021). TOPSIS method based on correlation coefficient under pythagorean fuzzy soft environment and its application towards green supply chain management. Sustainability, 13(4), 1642. DOI 10.3390/su13041642. [Google Scholar] [CrossRef]
29. Zulqarnain, R. M., Siddique, I., Iampan, A., Baleanu, D. (2022). Aggregation operators for Interval-valued Pythagorean fuzzy soft set with their application to solve Multi-attribute group decision making problem. Computer Modeling in Engineering & Sciences, 131(3), 1717–1750. DOI 10.32604/cmes.2022.019408. [Google Scholar] [CrossRef]
30. Smarandache, F. (2018). Extension of soft set to hypersoft set, and then to plithogenic hypersoft set. Neutrosophic Sets and Systems, 22, 168–170. [Google Scholar]
31. Rahman, A. U., Saeed, M., Khalifa, H. A. E. W., Afifi, W. A. (2022). Decision making algorithmic techniques based on aggregation operations and similarity measures of possibility intuitionistic fuzzy hypersoft sets. AIMS Mathematics, 7(3), 3866–3895. DOI 10.3934/math.2022214. [Google Scholar] [CrossRef]
32. Zulqarnain, R. M., Xin, X. L., Saeed, M. (2021). A development of pythagorean fuzzy hypersoft set with basic operations and decision-making approach based on the correlation coefficient. In: Theory and application of hypersoft set, vol. 2021, pp. 85–106. Pons Publishing House Brussels. [Google Scholar]
33. Rahman, A. U., Saeed, M., Alodhaibi, S. S., Abd, H. (2021). Decision making algorithmic approaches based on parameterization of neutrosophic set under hypersoft set environment with fuzzy, intuitionistic fuzzy and neutrosophic settings. Computer Modeling in Engineering & Sciences, 128(2), 743–777. DOI 10.32604/cmes.2021.016736. [Google Scholar] [CrossRef]
34. Saeed, M., Ahsan, M., Ur Rahman, A., Saeed, M. H., Mehmood, A. (2021). An application of neutrosophic hypersoft mapping to diagnose brain tumor and propose appropriate treatment. Journal of Intelligent & Fuzzy Systems, 41(1), 1677–1699. DOI 10.3233/JIFS-210482. [Google Scholar] [CrossRef]
35. Zulqarnain, R. M., Xin, X. L., Saeed, M. (2020). Extension of TOPSIS method under intuitionistic fuzzy hypersoft environment based on correlation coefficient and aggregation operators to solve decision making problem. AIMS Mathematics, 6(3), 2732–2755. DOI 10.3934/math.2021167. [Google Scholar] [CrossRef]
36. Zulqarnain, R. M., Siddique, I., Ali, R., Pamucar, D., Marinkovic, D. et al. (2021). Robust aggregation operators for intuitionistic fuzzy hypersoft set with their application to solve MCDM problem. Entropy, 23(6), 688. DOI 10.3390/e23060688. [Google Scholar] [CrossRef]
37. Zulqarnain, R. M., Siddique, I., Jarad, F., Ali, R., Abdeljawad, T. (2021). Development of topsis technique under pythagorean fuzzy hypersoft environment based on correlation coefficient and its application towards the selection of antivirus mask in COVID-19 pandemic. Complexity, 2021(2), 1–27. DOI 10.1155/2021/6634991. [Google Scholar] [CrossRef]
38. Choudhury, R., Wurster, R., Weber, T., Schindler, J., Weindorf, W. et al. (2002). GM Well-to-wheel analysis of energy use and greenhouse gas emissions of advanced fuel/vehicle systems--A European study. Ottobrunn, September. [Google Scholar]
39. Edwards, R., Larivé, J., Beziat, J. (2011). Well-to-wheels analysis of future automotive fuels and powertrains in the European context--Report, Version 3c. EUR 24952 EN. Luxembourg (LuxembourgPublications Office of the European Union. JRC65998. [Google Scholar]
40. Godula-Jopek, A., Jehle, W., Wellnitz, J. (2012). Hydrogen storage technologies: New materials, transport, and infrastructure. John Wiley & Sons. DOI 10.1002/9783527649921. [Google Scholar] [CrossRef]
41. Wang, W., Liu, X., Qin, Y. (2012). Interval-valued intuitionistic fuzzy aggregation operators. Journal of Systems Engineering and Electronics, 23(4), 574–580. DOI 10.1109/JSEE.2012.00071. [Google Scholar] [CrossRef]
42. Xu, Z., Chen, J. (2007). On geometric aggregation over interval-valued intuitionistic fuzzy information. Fourth International Conference on Fuzzy Systems And Knowledge Discovery (FSKD 2007), vol. 2, pp. 466–471. DOI 10.1109/FSKD.2007.427. [Google Scholar] [CrossRef]
43. Siddique, I., Zulqarnain, R. M., Ali, R., Jarad, F., Iampan, A. (2021). Multicriteria decision-making approach for aggregation operators of pythagorean fuzzy hypersoft sets. Computational Intelligence and Neuroscience, 2021, vol. 2, pp. 2036506. DOI 10.1155/2021/2036506. [Google Scholar] [CrossRef]
44. Zulqarnain, R. M., Siddique, I., Ali, R., Jarad, F., Iampan, A. (2021). Multicriteria decision-making approach for pythagorean fuzzy hypersoft sets’ interaction aggregation operators. Mathematical Problems in Engineering, 2021, 9964492. DOI 10.1155/2021/9964492. [Google Scholar] [CrossRef]
 Open Access
Open Access




 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.

 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools