A New Kind of Generalized Pythagorean Fuzzy Soft Set and Its Application in Decision-Making

1  Introduction

In 1965, Zadeh [1] proposed the concept of a fuzzy set (FS) to depict uncertain information in decision-making problems. Atanassov [2] also presented the notion of an intuitionistic fuzzy set (IFS) (i.e., in which the elements of an IFS satisfy the following condition: 0≤a+b≤1, where a is a membership degree and b is a non-membership degree). But there are shortcomings in intuitionistic fuzzy decision-making. For example, if a DM expresses that his/her support for membership of x is 0.9 and the support against membership of x is 0.7, then it can be found that the sum of membership and non-membership is bigger than 1. Hence, the ordered pair (0.9, 0.7) is not allowable for an IFS. To remedy this shortcoming, Yager [3] proposed the notion of a Pythagorean fuzzy set (PFS) (i.e., in which the elements of a PFS satisfy the following condition: 0≤a2+b2≤1, where a∈[0,1] is a membership degree and b∈[0,1] is a non-membership degree). Therefore, a PFS has been widely applied to many fields, for example, multi-attribute decision-making [4] and multi-attribute group decision-making [5].

In 1999, Molodtsov [6] presented the concept of a soft set (SS) to deal with uncertainties. Many researchers are developing new methods for SS. For example, Maji et al. [7,8] presented several concepts, operations, and examples of SS and gave an application to solve soft decision-making. Maji et al. [9] proposed the notion of the fuzzy soft set, followed by studies on Pythagorean fuzzy soft sets [10], generalized Pythagorean fuzzy soft set [11], the possibility Pythagorean fuzzy soft set [12], and the possibility Pythagorean bipolar fuzzy soft sets [13]. In addition, several expansion models of PFSS are very quickly developed, for example, the decision-making method related to PFSS with infectious diseases application [14], the novel entropy measure of PFSS [15], the parameter-reduction of PFSS and corresponding algorithms [16], the Q-PFS expert set and its application in the multi-criteria decision-making process [17], and the aggregation operators of PFSS with their application for green supplier chain management [18].

There are some shortcomings in the methods used to solve the decision-making problem by using the possibility fuzzy soft set [19] and the PFSS [10]. We will present the concept of generalized Pythagorean fuzzy soft sets (GPFSSs) as a combination of the two above-mentioned models. Furthermore, we study the properties and operations of GPFSSs. We also explore a MADM application under the GPFSS framework. In the end, we provide a comparative analysis between the developed hybrid model and some existing approaches.

This paper is structured as follows: In Section 2, we give several notions of Pythagorean fuzzy sets, soft sets, fuzzy soft sets, and Pythagorean fuzzy soft sets. In Section 3, we present the novel notion of GPFSSs and discuss their properties. In Section 4, we introduce an application of GPFSSs to solve fuzzy soft decision-making. In Section 5, we give a comparison between the proposed approach and some existing approaches. Finally, in Section 6, the conclusion is given.

2  Preliminaries

We will present a short survey of five needed definitions in this paper as indicated below.

2.1 Pythagorean Fuzzy Sets, Soft Sets, and Fuzzy Soft Sets

Definition 2.1. (Cf. [3]). Suppose that 𝒰 be the set. The Pythagorean fuzzy set (PFS) is represented as

ψ={<u,αψ(u),βψ(u)>∣u∈𝒰},

such that αψ∈[0,1] (i.e., the degree of membership) and βψ∈[0,1] (i.e., the degree of non-membership) satisfy the following condition

0≤(αψ)2+(βψ)2≤1,

∀u∈𝒰. The set of all Pythagorean fuzzy sets over 𝒰 is denoted by PF𝒰.

Definition 2.2. (Cf. [3]). Let

ψ={<u,αψ(u),βψ(u)>∣u∈𝒰}∈PF𝒰,

and

χ={<u,αχ(u),βχ(u)>∣u∈𝒰}∈ PF𝒰.

Then, the subset, equal, union, intersection, and complement, are defined, respectively, as follows:

(1)   ψ⊆χ if for all u∈𝒰,αψ(u)≤αχ(u) and βψ(u)≥βχ(u).

(2)   ψ=χ if ψ⊆χ and χ⊆ψ.

(3)   ψ∪χ={u,max{αψ(u),αχ(u)},min{βψ(u),βχ(u)}∣u∈𝒰}.

(4)   ψ∩χ={u,min{αψ(u),αχ(u)},max{βψ(u),βχ(u)}∣u∈𝒰}.

(5)   ψc={<u,βψ(u),αψ(u)>∣u∈𝒰}.

Definition 2.3. (Cf. [6,7,9]). Suppose that 𝒰 (i.e., be the set) and ℰ (i.e., be the set of parameters). For 𝒜⊆ℰ, then

(1) ℱ:𝒜⟶𝒫(𝒰) (i.e., 𝒫(𝒰) is the power set of 𝒰) is called soft set (SS) over 𝒰.

(2) ℱ:𝒜⟶FS𝒰 (i.e., FS𝒰 is the collection of all fuzzy subsets of 𝒰) is called fuzzy soft set (FSS) over 𝒰.

2.2 Pythagorean Fuzzy Soft Sets

Definition 2.4. (Cf. [10]). Suppose that 𝒰 (i.e., be the set) and ℰ (i.e., be the set of parameters). For 𝒜⊆ℰ, then ℱ:𝒜⟶PF𝒰 is called Pythagorean fuzzy soft set (PFSS or (PF)S𝒰) over 𝒰 (or (ℱ,𝒜)) and we can write

ℱ(e)={<u,αℱ(e)(u),βℱ(e)(u)>∣u∈𝒰},

for each e∈𝒜, αℱ(e)(u)∈[0,1] (i.e., the degree of membership) and βℱ(e)(u)∈[0,1] (i.e., the degree of non-membership) satisfies the condition 0≤(αℱ(e)(u))2+(βℱ(e)(u))2≤1.

Definition 2.5. (Cf. [10]). Let (ℱ,𝒜),(𝒢,ℬ)∈(PF)S𝒰 and 𝒜,ℬ⊆ℰ. Then,

(1) (ℱ,𝒜) is a soft subset of (𝒢,ℬ), denoted as (ℱ,𝒜)⊆~(𝒢,ℬ) if 𝒜⊆ℬ and ∀e∈𝒜,ℱ(e) is a Pythagorean fuzzy subset of 𝒢(e).

(2) (ℱ,𝒜) is a soft equal of (𝒢,ℬ), denoted as (ℱ,𝒜)=(𝒢,ℬ) if (ℱ,𝒜)⊆~(𝒢,ℬ) and (𝒢,ℬ)⊆(ℱ,𝒜).

(3) The intersection of (ℱ,𝒜) and (𝒢,ℬ) represented as (ℱ,𝒜)∩~(𝒢,ℬ) is a PFSS (ℋ,𝒞) where 𝒞=𝒜∩ℬ≠∅ and ℋ(e)=ℱ(e)∩𝒢(e) for all e∈𝒞.

(4) The union of (ℱ,𝒜) and (𝒢,ℬ) represented as (ℱ,𝒜)∪~(𝒢,ℬ) is a PFSS (ℋ,𝒞) where 𝒞=𝒜∪ℬ

ℋ(e)={ℱ(e),ife∈𝒜∖ℬ𝒢(e),ife∈ℬ∖𝒜ℱ(e)∪𝒢(e),ife∈𝒜∩ℬ

for all e∈𝒞.

(5) The complement of (ℱ,𝒜) is denoted by (ℱc,𝒜), where ℱc:𝒜→FF𝒰 is a mapping given by ℱc(e)=(ℱ(e))c for all e∈𝒜.

(6) A PFSS (ℱ,ℰ) over 𝒰 is known as a null PFSS represented as ℱ∅ if for all e∈ℰ,ℱ∅(e)=0~ where 0~ denote the null PFS, ℱ∅(e)={u(0,1)∣u∈𝒰}.

(7) A PFSS (ℱ,ℰ) over 𝒰 is known as an absolute PFSS represented as ℱ𝒰 if for all e∈ℰ,ℱ∅(e)=1~ where 1~ denote the absolute PFS, ℱ𝒰(e)={u(1,0)∣u∈𝒰}.

3  Generalized Pythagorean Fuzzy Soft Sets

In this section, we define the notion of generalized Pythagorean fuzzy soft sets as indicated below:

Definition 3.1. Suppose that 𝒰 (i.e., be the set) and ℰ (i.e., be the set of parameters). For an arbitrary ℬ⊆ℰ, then 𝒢μ:ℬ⟶(PF)S𝒰×FS𝒰 (i.e., 𝒢:ℰ⟶(PF)S𝒰 and μ:ℰ⟶FS𝒰) is called generalized Pythagorean fuzzy soft set (for short, GPFSS or (GPF)S𝒰) over the soft universe (𝒰,ℰ), and we can write

𝒢μ(e)={(u𝒢(e)(u),μ(e)(u))∣u∈𝒰},

for all e∈ℬ and μ(e)(u)∈[0,1].

Example 3.2. Let 𝒰={u1,u2,u3} be three of elements and ℰ={e1,e2,e3,e4} be four of parameters. The GPFSS (𝒢μ,ℬ), where ℬ={e1,e2,e3}⊆ℰ are defined as

𝒢μ(e1)={(u1(0.2,0.9),0.4),(u2(0.3,0.8),0.5),(u3(0.4,0.81),0.4)},

𝒢μ(e2)={(u1(0.8,0.25),0.1),(u2(0.4,0.9),0.3),(u3(0.5,0.7),0.5)},

𝒢μ(e3)={(u1(0.7,0.2),0.4),(u2(0.5,0.7),0.4),(u3(0.3,0.5),0.7)}.

Definition 3.3. Let (𝒢μ,ℬ),(ℋν,𝒞)∈ (GPF)S𝒰, where ℬ,𝒞⊆ℰ. Then, (𝒢μ,ℬ) is called GPFSS subset of (ℋν,𝒞), is denote by (𝒢μ,ℬ)⊆^(ℋν,𝒞) if ℬ⊆𝒞 and ∀e∈ℬ, μ(e) is fuzzy subset of ν(e) and 𝒢(e) is PFS subset of ℋ(e).

Example 3.4. (Continued from Example 3.2). The GPFSS (ℋν,𝒞), where 𝒞={e1,e2,e3}⊆ℰ are defined in the following:

ℋν(e1)={(u1(0.3,0.8),0.6),(u2(0.4,0.8),0.7),(u3(0.5,0.7),0.5)},

ℋν(e2)={(u1(0.8,0.25),0.1),(u2(0.4,0.8),0.5),(u3(0.5,0.6),0.6)},

ℋν(e3)={(u1(0.7,0.2),0.5),(u2(0.6,0.6),0.6),(u3(0.5,0.5),0.8)}.

Thus, (𝒢μ,ℬ)⊆(ℋν,𝒞).

Definition 3.5. Let (𝒢μ,ℬ),(ℋν,𝒞)∈ (GPF)S𝒰, where ℬ,𝒞⊆ℰ. Then, (𝒢μ,ℬ) is called GPFSS equal of (ℋν,𝒞), is denote by (𝒢μ,ℬ)=(ℋν,𝒞) if (𝒢μ,ℬ)⊆(ℋν,𝒞) and (ℋν,𝒞)⊆(𝒢μ,ℬ).

The complement of a GPFSS is elaborated in the Definition 3.6.

Definition 3.6. Let (𝒢μ,ℬ)∈ (GPF)S𝒰. The complement (𝒢μ,ℬ)c of (𝒢μ,ℬ) is defined as

𝒢μc(e)={(u𝒢c(e)(u),1−μ(e)(u))∣u∈𝒰},

where 𝒢c(e),∀e∈ℬ is defined in Definition 2.5 (4) and 1−μ(e)(u)∈[0,1].

Example 3.7. (Continued from Example 3.2). The complement (𝒢μ,ℬ)c of (𝒢μ,ℬ) is computed as

𝒢μc(e1)={(u1(0.9,0.2),0.6),(u2(0.8,0.3),0.5),(u3(0.81,0.4),0.6)},

𝒢μc(e2)={(u1(0.25,0.8),0.9),(u2(0.9,0.4),0.7),(u3(0.7,0.5),0.5)},

𝒢μc(e3)={(u1(0.2,0.7),0.6),(u2(0.7,0.5,0.6),(u3(0.5,0.3),0.3)}.

Definition 3.8. (1) A null GPFSS over (𝒰,ℰ), denoted by (∅¯0,ℰ) is a GPFSS, is defined as

∅¯0(e)={(u(0,1),0)∣u∈𝒰}.

(2) An absolute GPFSS over (𝒰,ℰ), denoted by (𝒰¯1,ℰ) is a GPFSS, is defined as

𝒰¯1(e)={(u(1,0),1)∣u∈𝒰}.

Example 3.9. (Continued from Example 3.2). The null and absolute of GPFSSs are computed, respectively, as follows:

∅¯0(e1)={(u1(0,1),0),(u2(0,1),0),(u3(0,1),0)},

∅¯0(e2)={(u1(0,1),0),(u2(0,1),0),(u3(0,1),0)},

∅¯0(e3)={(u1(0,1),0),(u2(0,1),0),(u3(0,1),0)}

and

𝒰¯1(e1)={(u1(1,0),1),(u2(1,0),1),(u3(1,0),1)},

𝒰¯1(e2)={(u1(1,0),1),(u2(1,0),1),(u3(1,0),1)},

𝒰¯1(e3)={(u1(1,0),1),(u2(1,0),1),(u3(1,0),1)}.

Proposition 3.10. Let (∅¯0,ℰ) and (𝒰¯1,ℰ) be the null and absolute of GPFSSs over (𝒰,ℰ), respectively. Then

(1) ((∅¯0,ℰ)c)c=(∅¯0,ℰ).

(2) (∅¯0,ℰ)c=(𝒰¯1,ℰ).

(3) (𝒰¯1,ℰ)c=(∅¯0,ℰ).

Proof. Follows from Definitions 3.6 and 3.8.

Definition 3.11. Let (𝒢μ,𝒜),(ℋν,ℬ)∈ (GPF)S𝒰 over (𝒰,ℰ). For 𝒞=𝒜∩ℬ≠∅, then

(1) The restricted union, denoted by (𝒦τ,𝒞)=(𝒢μ,𝒜)∪^(ℋν,ℬ) is defined by

𝒦τ(e)=𝒢μ(e)∪ℋν(e)={(u(max{α𝒢(e)(u),αℋ(e)(u)},min{β𝒢(e)(u),βℋ(e)(u)}),τ(e))∣ u∈𝒰},

where τ(e)=max(μ(e),ν(e)).

(2) The extended intersection, denoted by (ℒλ,𝒞)=(𝒢μ,𝒜)∪^(ℋν,ℬ) is defined by

ℒλ(e)=𝒢μ(e)∩ℋν(e)={(u(min{α𝒢(e)(u),αℋ(e)(u)},max{β𝒢(e)(u),βℋ(e)(u)}),λ(e))∣ u∈𝒰},

where λ(e)=min(μ(e),ν(e)).

Example 3.12. (Continued from Examples 3.2 and 3.4). By Definition 3.11, the restricted union and extended intersection are computed as

𝒦τ(e1)={(u1(0.3,0.8),0.6),(u2(0.4,0.8),0.7),(u3(0.5,0.7),0.5)},

𝒦τ(e2)={(u1(0.8,0.25),0.1),(u2(0.4,0.8),0.5),(u3(0.5,0.6),0.6)},

𝒦τ(e3)={(u1(0.7,0.2),0.5),(u2(0.6,0.6),0.6),(u3(0.5,0.5),0.8)}

and

ℒλ(e1)={(u1(0.2,0.9),0.4),(u2(0.3,0.8),0.5),(u3(0.4,0.81),0.4)},

ℒλ(e2)={(u1(0.8,0.25),0.1),(u2(0.4,0.9),0.3),(u3(0.5,0.7),0.5)},

ℒλ(e3)={(u1(0.7,0.2),0.4),(u2(0.5,0.7),0.4),(u3(0.3,0.5),0.7)}.

Proposition 3.13. Let (𝒢μ,𝒜),(ℋν,ℬ),(𝒦τ,𝒞)∈ (GPF)S𝒰 over (𝒰,ℰ). Then the following four properties hold:

(1) (𝒢μ,𝒜)∪^(ℋν,ℬ)=(ℋν,ℬ)∪^(𝒢μ,𝒜)

(2) (𝒢μ,𝒜)∩^(ℋν,ℬ)=(ℋν,ℬ)∩^(𝒢μ,𝒜)

(3) (𝒢μ,𝒜)∪^((ℋν,ℬ)∪^(𝒦τ,𝒞))=((𝒢μ,𝒜)∪^(ℋν,ℬ))∪^(𝒦τ,𝒞)

(4) (𝒢μ,𝒜)∩^((ℋν,ℬ)∩^(𝒦τ,𝒞))=((𝒢μ,𝒜)∩^(ℋν,ℬ))∩^(𝒦τ,𝒞).

Proof. Follows from Definition 3.11.

Proposition 3.14. Let (𝒢μ,𝒜),(ℋν,ℬ),(𝒦τ,𝒞)∈ (GPF)S𝒰 over (𝒰,ℰ). Then the following two properties hold:

(1) (𝒢μ,𝒜)∪^((ℋν,ℬ)∩^(𝒦τ,𝒞))=((𝒢μ,𝒜)∪^(ℋν,ℬ))∩^((𝒢μ,𝒜)∪^(𝒦τ,𝒞))

(2) (𝒢μ,𝒜)∩^((ℋν,ℬ)∪^(𝒦τ,𝒞))=((𝒢μ,𝒜)∩^(ℋν,ℬ))∪^((𝒢μ,𝒜)∩^(𝒦τ,𝒞))

Proof. Follows from Definition 3.11.

4  An Application of GPFSSs to Solve Fuzzy Soft Decision-Making Problems

Based on the notion of GPFSSs and using the comparison tables [20] and the algorithm proposed by Dinda et al. [21], we will give an application of GPFSSs to solve fuzzy soft decision-making problems as indicated below.

Example 4.1. Assume that there are three different universities in universe 𝒰={u1,u2,u3} and the parameter set ℰ={e1,e2,e3,e4,e5,e6}, where e1 stands for “modern”, e2 stands for “international”, e3 stands for “big”, e4 stands for “beautiful”, e5 stands for “full day”, and e5 stands for “high efficiency”. Suppose Mr. Z wants to choose a good university for his daughter on the basis of his wishing parameters between those listed above. Our aim is to find out the most suitable university for his daughter. Consider the GPFSSs defined as follows:

𝒢μ(e1)={(u1(0.3,0.9),0.5),(u2(0.4,0.85),0.6),(u3(0.5,0.85),0.6)}

𝒢μ(e2)={(u1(0.9,0.25),0.1),(u2(0.3,0.9),0.3),(u3(0.6,0.75),0.5)}

𝒢μ(e3)={(u1(0.7,0.7),0.25),(u2(0.5,0.7),0.35),(u3(0.3,0.4),0.35)}

𝒢μ(e4)={(u1(0.3,0.9),0.5),(u2(0.4,0.85),0.6),(u3(0.5,0.85),0.6)}

𝒢μ(e5)={(u1(0.9,0.25),0.1),(ρ2(0.3,0.9),0.3),(u3(0.6,0.75),0.5)}

𝒢μ(e6)={(u1(0.35,0.65),0.25),(u2(0.65,0.73),0.39),(u3(0.32,0.51),0.49)}.

Then, we define the following new GPFSSs (i.e., reduced the GPFSSs):

𝒢μ′(e)={(u𝒢(e)(u)×μ(e)(u))∣u∈𝒰},

for all e∈ℬ and μ(e)(u)∈[0,1]. Therefore, we get the new GPFSSs as

𝒢μ′(e1)={u1(0.15,0.45),u2(0.24,0.51),u3(0.3,0.51)}

𝒢μ′(e2)={u1(0.09,0.02),u2(0.09,0.27),u3(0.3,0.37)}

𝒢μ′(e3)={u1(0.20,0.19),u2(0.17,0.25),u3(0.11,0.14)}

𝒢μ′(e4)={u1(0.21,0.47),u2(0.24,0.51),u3(0.18,0.48)}

𝒢μ′(e5)={u1(0.09,0.02),u2(0.24,0.28),u3(0.28,0.3)}

𝒢μ′(e6)={u1(0.09,0.16),u2(0.25,0.28),u3(0.16,0.25)}.

After then, we compute the following in Table 1 (i.e, the reduced membership), Table 4 (i.e., the reduced non-membership), Tables 2 and 5 (i.e., the comparison tables), Tables 3 and 6 (i.e., the comparison scores C+ and C−), and Table 7 (i.e., the final decision scores) as

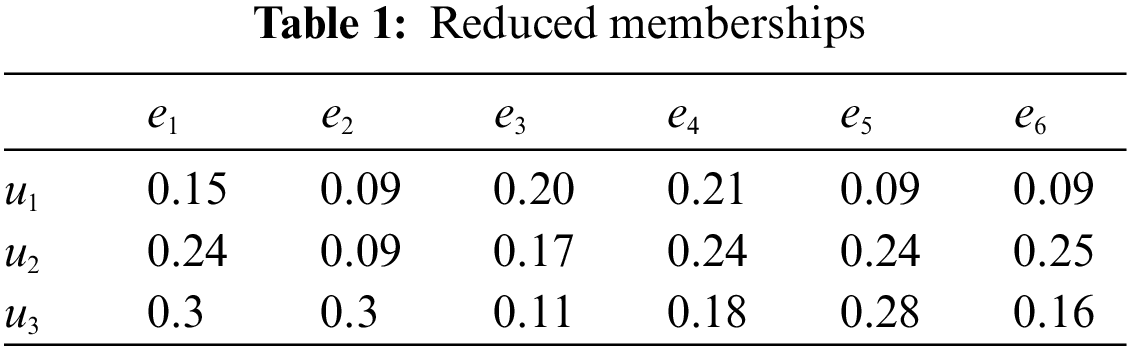
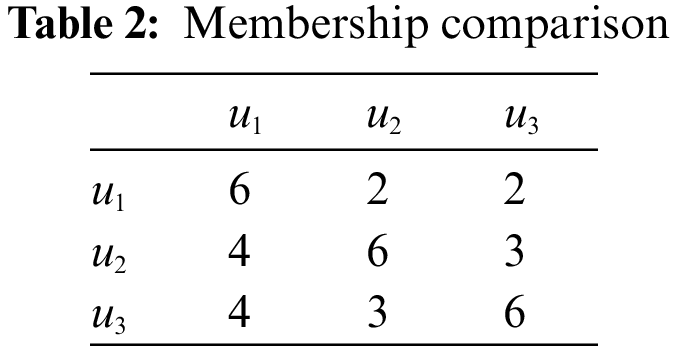
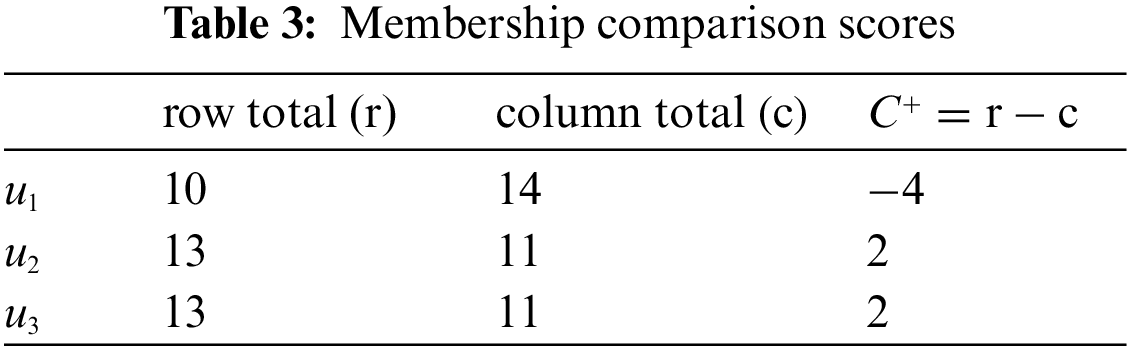
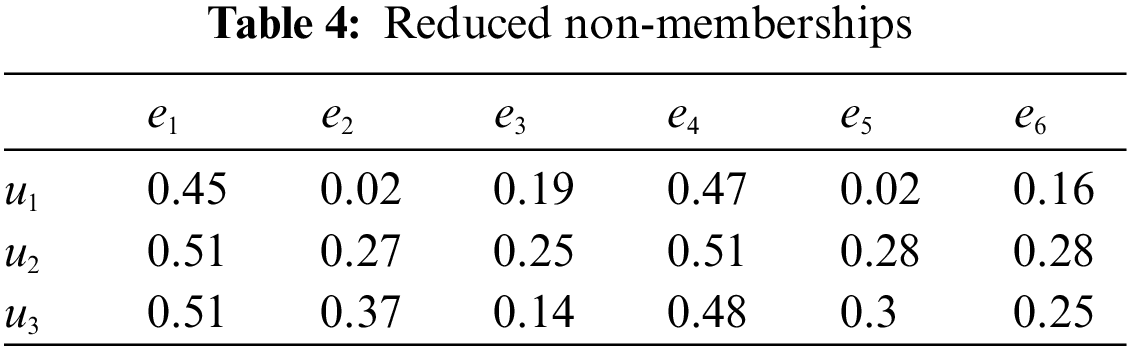
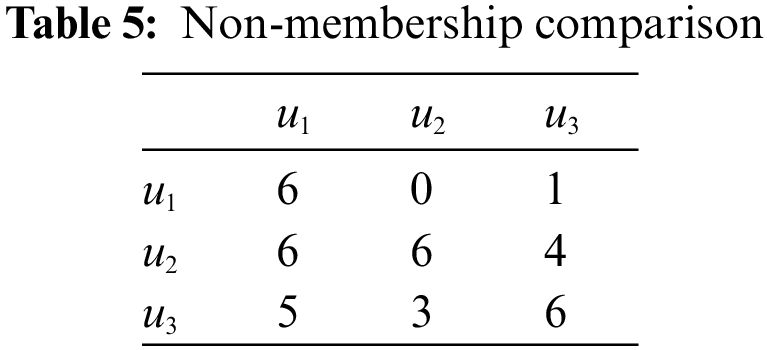
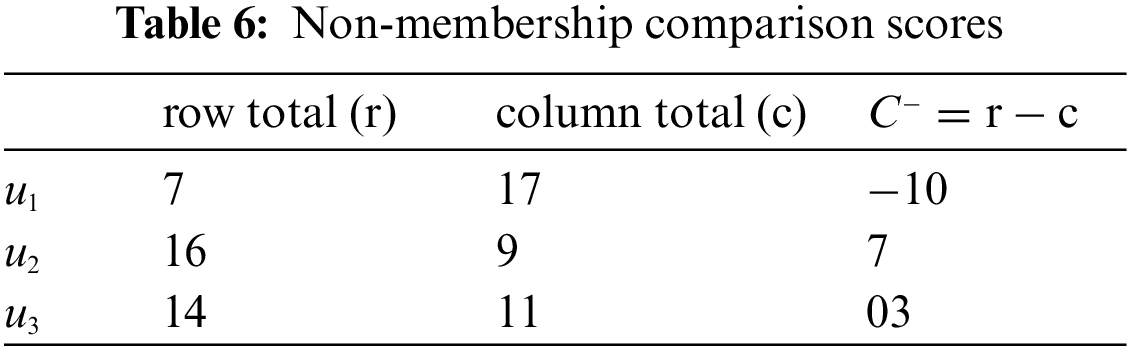
Mr. Z will choose the university u1, where the score of u1 has a high value from Table 7.

5  Comparison

In this section, we provide a comparison between (PF)S𝒰 [10], the possibility fuzzy soft sets (PFS)𝒰 [19], and the (GPF)S𝒰 by using Example 4.1. Therefore, we obtain the following Table 8:

From Table 8, we can see that the final results between (PF)S𝒰 [10], (PFS)𝒰 [19], and our approach (i.e., (GPF)S𝒰) are different. According to the ranking results of three alternatives in (GPF)S𝒰, u1 is the most accurate and finable. This is due to (PF)S𝒰 [10] dealing with the (PF)S𝒰 [10] without fuzzy set. But our method (GPF)S𝒰 depends on the (PF)S𝒰 [10] with the fuzzy set. (PFS)𝒰 [19] is the combination between a fuzzy set and fuzzy set, with fuzzy set and (GPF)S𝒰 is more general than (PFS)𝒰 [19], which makes our presented method more reasonable and effective as shown in Fig. 1.

Figure 1: Comparison among the initiated (GPF)SU model (i.e., the green line), and existing (PFS)U[19] (i.e., the red line) and (PF)SU[10] (i.e., the blue line) models

6  Conclusions

We have given the novel model of generalized Pythagorean fuzzy soft sets. We have presented their operations and properties. We have presented an application of GPFSSs in fuzzy soft decision-making. In the future, we will provide a real application with a real data set for lung cancer disease [22] and coronary artery disease [23]. Finally, we will discuss more future studies on the GPFSS information to deal with decision-making problems (for example, [4,5,24,25]).

Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Zadeh, L. A. (1965). Fuzzy sets. Information and Control, 8(3), 338–353. https://doi.org/10.1016/S0019-9958(65)90241-X [Google Scholar] [CrossRef]

2. Atanassov, K. T. (1986). Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20(1), 87–96. https://doi.org/10.1016/S0165-0114(86)80034-3 [Google Scholar] [CrossRef]

3. Yager, R. R. (2013). Pythagorean fuzzy subsets. IFSA World Congress and NAFIPS Annual Meeting 2013 Joint, pp. 57–61. Edmonton, Canada, IEEE. [Google Scholar]

4. Wan, S. P., Li, S. Q., Dong, J. Y. (2018). A three-phase method for Pythagorean fuzzy multi-attribute group decision making and application to haze management. Computers & Industrial Engineering, 123(1), 348–363. https://doi.org/10.1016/j.cie.2018.07.005 [Google Scholar] [CrossRef]

5. Wan, S. P., Jin, Z., Dong, J. Y. (2020). A new order relation for Pythagorean fuzzy numbers and application to multi-attribute group decision making. Knowledge and Information Systems, 62(2), 751–785. https://doi.org/10.1007/s10115-019-01369-8 [Google Scholar] [CrossRef]

6. Molodtsov, D. (1999). Soft set theory-first results. Computers & Mathematics with Applications, 37(4–5), 19–31. https://doi.org/10.1016/S0898-1221(99)00056-5 [Google Scholar] [CrossRef]

7. Maji, P. K., Biswas, R., Roy, A. R. (2003). Soft set theory. Computers and Mathematics with Applications, 45(4–5), 555–562. https://doi.org/10.1016/S0898-1221(03)00016-6 [Google Scholar] [CrossRef]

8. Maji, P. K., Roy, A. R., Biswas, R. (2002). An application of soft sets in a decision making problem. Computers and Mathematics with Applications, 44(8–9), 1077–1083. https://doi.org/10.1016/S0898-1221(02)00216-X [Google Scholar] [CrossRef]

9. Maji, P. K., Biswas, R., Roy, A. R. (2001). Fuzzy soft sets. The Journal of Fuzzy Mathematics, 9(3), 589–602. [Google Scholar]

10. Peng, X., Yang, Y., Song, J. (2015). Pythagorean fuzzy soft set and its application. Computer Engineering, 41(7), 224–229. [Google Scholar]

11. Kirişci, M., Demir, I., Şimşek, N., Topaç, N., Bardak, M. (2022). The novel VIKOR methods for generalized Pythagorean fuzzy soft sets and its application to children of early childhood in COVID-19 quarantine. Neural Computing and Applications, 34(3), 1877–1903. https://doi.org/10.1007/s00521-021-06427-3 [Google Scholar] [PubMed] [CrossRef]

12. Hu, D. J., Zhang, H., Heb, Y. (2019). Possibility Pythagorean fuzzy soft set and its application. Journal of Intelligent & Fuzzy Systems, 36(1), 413–421. https://doi.org/10.3233/JIFS-181649 [Google Scholar] [CrossRef]

13. Palanikumar, M., Arulmozhi, K. (2021). Possibility Pythagorean bipolar fuzzy soft sets and its application. Open Journal of Discrete Applied Mathematics, 4(2), 17–29. https://doi.org/10.30538/psrp-odam2021.0056 [Google Scholar] [CrossRef]

14. Kirişci, M., Şimşek, N. (2022). Decision making method related to Pythagorean fuzzy soft Sets with infectious diseases application. Journal of King Saud University-Computer and Information Sciences, 34(8), 5968–5978. https://doi.org/10.1016/j.jksuci.2021.08.010 [Google Scholar] [CrossRef]

15. Athira, T. M., John, S. J., Garg, H. (2020). A novel entropy measure of Pythagorean fuzzy soft sets. AIMS Mathematics, 5(2), 1050–1061. https://doi.org/10.3934/math.2020073 [Google Scholar] [CrossRef]

16. Athira, T. M., John, S. J. (2021). Parameter-reduction of Pythagorean fuzzy soft sets and corresponding algorithms. AIP Conference Proceedings, 2336(1), 040017. https://doi.org/10.1063/5.0045746 [Google Scholar] [CrossRef]

17. Chinnadurai, V., Arulselvam, A. (2021). Q-Pythagorean fuzzy soft expert set and its application in multi-criteria decision making process. Journal of Physics: Conference Series, 1850(1), 012114. https://doi.org/10.1088/1742-6596/1850/1/012114 [Google Scholar] [CrossRef]

18. Zulqarnain, R. M., Xin, X. L., Garg, H., Khan, W. A. (2021). Aggregation operators of Pythagorean fuzzy soft sets with their application for green supplier chain management. Journal of Intelligent & Fuzzy Systems, 40(3), 5545–5563. https://doi.org/10.3233/JIFS-202781 [Google Scholar] [CrossRef]

19. Alkhazaleh, S., Salleh, A. R., Hassan, N. (2011). Possibility fuzzy soft set. Advances in Decision Sciences, 2011(3), 479756. https://doi.org/10.1155/2011/479756 [Google Scholar] [CrossRef]

20. Maji, P. K., Roy, A. R. (2007). A fuzzy soft set theoretic approach to decision making problems. Journal of Computational and Applied Mathematics, 203(2), 412–418. https://doi.org/10.1016/j.cam.2006.04.008 [Google Scholar] [CrossRef]

21. Dinda, B., Bera, T., Samanta, T. K. Generalised intuitionistic fuzzy soft sets and its application in decision making (in Press). http://arxiv.org/abs/1010.2468 [Google Scholar]

22. Khalil, A. M., Li, S. G., Lin, Y., Li, H. X., Ma, S. (2020). A new expert system in prediction of lung cancer disease based on fuzzy soft sets. Soft Computing, 24(18), 14179–14207. https://doi.org/10.1007/s00500-020-04787-x [Google Scholar] [CrossRef]

23. Hassan, N., Sayed, O. R., Khalil, A. M., Ghany, M. A. (2017). Fuzzy soft expert system in prediction of coronary artery disease. International Journal of Fuzzy Systems, 19(5), 1546–1559. https://doi.org/10.1007/s40815-016-0255-0 [Google Scholar] [CrossRef]

24. Yue, Q. (2022). Bilateral matching decision-making for knowledge innovation management considering matching willingness in an interval intuitionistic fuzzy set environment. Journal of Innovation & Knowledge, 7(3), 100209. https://doi.org/10.1016/j.jik.2022.100209 [Google Scholar] [CrossRef]

25. Zulqarnain, R. M., Siddique, I., Iampan, A., Baleanu, D. (2022). Aggregation operators for interval-valued Pythagorean fuzzy so set with their application to solve multi-attribute group decision making problem. Computer Modeling in Engineering & Sciences, 131(3), 1717–1750. https://doi.org/10.32604/cmes.2022.019408 [Google Scholar] [CrossRef]