Secrecy Efficiency Maximization in Intelligent Reflective Surfaces Assisted UAV Communications

1  Introduction

In recent years, the increase of wireless devices and the requirements of intelligent terminals for quality of service have promoted the development of 5G network technology [1,2]. Now there are some emerging technologies that are committed to solving the shortage of spectrum resources in 5G [3,4], such as millimeter wave and large-scale MIMO technologies. In addition, an emerging technology that feeds back the communication demand by engineering characteristics has attracted extensive attention from industry and academia, namely UAV communication [5–7]. As a kind of high mobility, strong security and small terrain limitation, UAV has become an indispensable part of the 5G network [8–11].

UAV can be used as air relay and air base station, and has good performance in military and commercial fields [12,13]. Especially in remote areas that cannot be covered by base stations, UAVs can take advantage of their small size to lay limited communication resources on users who need more services [14,15].

As a new technology, UAV communication also has its inherent shortcomings, first of all, the energy problem of UAV [16,17]. As a mobile device, the UAV cannot carry too many energy storage devices to ensure its mobility [18,19], which means that the power control of the UAV needs to be more accurate; On the other hand, most channels in UAV communication are air to ground channels or air to air channels, which means that channels are vulnerable to potential eavesdroppers [20,21].

In recent years, the intelligent reflector (IRS) has attracted extensive attention in the field of wireless communication. Its ability to reset the transmission characteristics of signals can improve system performance in a low-power mode. In [22], the author jointly designed the discrete phase of IRS and user beamforming, which reduced the overall energy consumption of the system; In addition, in [23], the author discussed the joint design of the sender in active components and passive components, which improved the user’s receiving power. This power can be fed back to the overhead of the IRS [24].

Specifically, the intelligent reflector can rectify and retransmit the signals transmitted from the UAV to the ground or from the ground to the UAV, and improve the power of the signals received by users through interaction with the environmental channel [25]; On the other hand, the intelligent reflector can also improve the flexibility of UAV flight path. In the traditional UAV trajectory design, the UAV needs to take into account the energy limitation and the limitation of communication resource utilization. When the intelligent reflector is applied, the UAV can put more weight in the energy limitation. For example, the author of [26] realized the maximization of average speed by jointly designing UAV trajectory and IRS.

In the multi-user system, another widely concerned technology is orthogonal multiple access [27]. Multi users can realize simultaneous transmission on the same frequency. It is generally assumed that the considered NOMA system has three different scenarios: (1) downlink NOMA: S directly transmits signals to users; (2) Cooperative NOMA without direct connection has no direct connection with users, and communicates with users through DF trunk. Cooperative NOMA and direct connection: S sends signals to users through DF relay and direct connection, and users combine the received signals in two phases. NOMA is an important technology for dealing with multiple users in the communication area [28].

In UAV communication, we can also use NOMA technology to improve transmission efficiency. To the author’s knowledge, there are only a few studies on safety based energy efficiency [29]. Reference [30] considered a SWIPT based decoding and forwarding (DF) relay network, in which the relay node uses a time switching scheme to simultaneously receive information and collect energy, and then uses the collected energy to help the source forward the data to the destination. There are also exits for eavesdroppers on the network. Based on this model, the safety based energy efficiency maximization problem is expressed as an optimization problem, and a practical nonlinear energy collection model is considered. Reference [31] studied the resource allocation problem of secure communication in full duplex (FD) radio D2D networks to maximize the overall security energy efficiency (SEE). Under power constraints and security capacity requirements, resource allocation involves cluster head selection and subcarrier power allocation.

Consider a more realistic scenario. Since different users are trusted communication nodes, that is, the channel between users and IRS can be acquired in advance through pilot signals or other means. However, users are usually unable to obtain potential eavesdropper information. UAV estimates the air to ground channel by observing the position of the eavesdropper. However, due to the greater impact of the environment on the ground channel, it is impossible to obtain accurate channel state information through distance alone. Therefore, it is generally assumed that the channel for untrusted users is imperfect.

In recent years, the research on imperfect channel has also made some progress. Continuous interference canceller (SIC), imperfect channel estimation (ICSI) and hardware damage of transceiver (HWI) are considered [32]. We derive the BER expression in the CNOMA scheme, regardless of whether there is a direct link between the source and the user; Consider using Kronecker model and Poisson point process (PPP) to characterize the estimation error and spatial randomness of the base station, respectively [33].

In this paper, we would like to maximize the security transmission rate in the uplink network. Our concern is that in a communication area, there are multiple users who need to transmit information to the UAV. Due to the complexity of the geographical environment and potential eavesdroppers, the uplink network uses an IRS for assistance. We jointly optimize the trajectory of UAV, the phase shift matrix of IRS, and the beam design of multiple users to maximize the safety rate. The proposed optimization variables are highly coupled. We propose an iterative algorithm based on the block coordinate descent method. The simulation results show that the proposed scheme has higher security transmission rate than the traditional schemes.

2  System Model and Problem Formulation

As shown in Fig. 1, we consider an uplink communication system consisting of M users, UAV receivers, IRS and potential eavesdroppers. M users are all multi antenna. The eavesdropping channel is shown in red, and the reflection link is shown in blue.

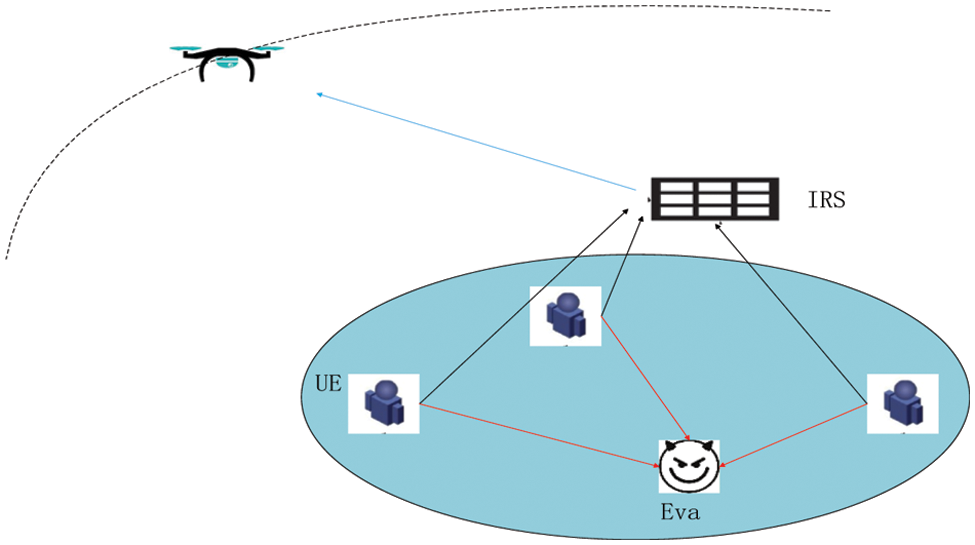
Figure 1: System model

It is assumed that the UAV flies at a fixed altitude H, where H is the safe altitude to ensure that the UAV will not collide with ground buildings and other UAVs. We assume that the flight cycle of the UAV is T, and the starting and ending points of the UAV are fixed. The UAV needs to fly back to the starting point during the flight cycle. In order to solve this issue, we divide T into N time slots, and the time length of each time slot is T/N, which means that the UAV is in a fixed position within one time slot.

q[0]=(xinit,yinit,H),(1)

in which H represents a fixed height to protect the UAV from the collision with ground buildings and other accidents.

The starting point and ending point constraints of UAV are expressed as follows:

‖q[n]−q[n−1]‖2≤D,n=1,2,...,N,(2)

where D is introduced for the minimum momentum that cannot hover for a long time due to the characteristics of UAV.

Since the energy carried by UAV is limited, the power constraint of UAV includes two parts: the power constraint in each time slot and the power constraint in the whole flight cycle.

1N∑n=1Np(n)≤Peva,p(n)≤Pmax,n=1,2,...,N.(3)

The air to ground channel can be approximately represented by the distance from the reference point to the corresponding node. However, the composition of the ground channel is usually more complex than air to ground channel. We assume that different users, users and potential eavesdroppers, and channels from users to the IRS all follow the free space path loss model. Specifically, we believe that all channels are the product of large-scale fading and small-scale fading. Therefore, hk, hE and hR can be modeled as

hk=LLOSdk−αLKk1+Kkhk,LOS+LNLOSdk−αN1+Kkhk,NLOShE=LLOSdE−αLKE1+KEhE,LOS+LNLOSdE−αN1+KEhE,NLOShR=LLOSdR−αLKR1+KRhR,LOS+LNLOSdR−αN1+KRhR,NLOS(4)

The transmission rate of k-th user could be expressed as

Rk[n]=Blog2(1+pk[n]gk[n]pj[n]gj[n]+σ2).(5)

In the scenario considered in this paper, the eavesdropper is silent. The eavesdropper can passively obtain user information rather than actively attack users. The eavesdropping rate of the potential eavesdropper is thus defined as

Re[n]=Blog2(1+pe[n]ge[n]pj[n]gj[n]+σ2).(6)

Due to its structure and weight limitations, the UAV cannot carry a large number of energy equipment, so its maximum power will be strictly limited. Therefore, it is necessary to comprehensively consider the demand for safe communication and the minimization of power. We consider safety energy efficiency in this paper, which is defined as follows:

Rsec=∑nRsec,n[n],(7)

where Rsec,n[n] is the security rate in n-th slot, which is defined as

Rsec,n[n]={Rk[n]Rk[n]>Re[n]0else(8)

According to above discussing, we formulate the original problem as

maxp[n],θl,q[n] Rsec∑n=1Np(n)s.t.1N∑n=1Np(n)≤Peva,p(n)≤Pmax,n=1,2,...,N‖q[n]−q[n−1]‖2≤D,n=1,2,...,N0≤θl≤2π,q[0]=(xinit,yinit,H)(9)

3  Proposed Solution

In this section, we first decompose the original problem, and propose an approximate problem to relax the original problem. Then, we designed the beam vector, UAV trajectory and IRS reflection phase, respectively. Finally, we propose a joint optimization algorithm and analyze its complexity.

3.1 Conversion of Equivalence Problem

Note that the original problem is highly nonconvex, especially in its goal. Maximizing the safe rate is obviously contrary to minimizing the power. In order to seek an equilibrium effect, we introduce the power into a constant to express it, and propose the following lemma:

Lemma 1: We transform the original problem (9) into the following form:

maxp[n],θl,q[n] Rsecs.t.∑n=1Np(n)≤Pnow1N∑n=1Np(n)≤Peva,p(n)≤Pmax,n=1,2,...,N‖q[n]−q[n−1]‖2≤D,n=1,2,...,Nq[0]=(xinit,yinit,H)(10)

The optimal solution of (19) is equal to that of (9).

Proof. We first define the optimal solution of (19) and (9) as {q2[n]},w2,Pnow and {q1[n]},w1. It is obvious that the optimal solution of (19) is equal to that of (9) is and only if ∑n=1Np(n)≤Pnow.

We then assume that the optimal solution of (19) satisfies that ∑n=1Np(n)<Pnow. There exists another solution of (19) satisfying w3=ηw2, where η=Pnow/‖∑p(n)‖. The proof is thus completed.

According to Lemma 1, we obtain an equivalence problem of the original problem. In the following subsections, we would propose the solution of (19).

3.2 Trajectory Design

Because of the non convexity of the objective function and the coupling of the optimization variables, it is challenging to solve P0. The block coordinate descent method is used to decompose the problem into three subproblems, which can effectively solve the problem. This leads us to propose an algorithm based on alternating optimization (AO), which solves the sub optimization problem by iterating one of the optimizations, and fixes the other two optimizations in each iteration until convergence is achieved.

maxp[n],θl,q[n] Rsecs.t.‖q[n]−q[n−1]‖2≤D,n=1,2,...,Nq[0]=(xinit,yinit,H)(11)

We use the following combination to represent the current state of UAV trajectory:

pk[n]=[gu[n],dEk−1[n]gEkH[n]Θ[n]],(12)

where gu refers to the channel from the eavesdropper to UAV, and dEk is the distance between k-th user and UAV.

By substituting (12) int the objective of (11), we obtain the following problem:

max log2⁡(1+∑kpkhR+pkhR+pkhR∑kpkhR+pkhR+pkhR+σ02[n])s.t.‖q[n]−q[n−1]‖2≤D,n=1,2,...,Nq[0]=(xinit,yinit,H)(13)

Note that problem (13) is still non-convex, we then introduce the complex variable L={L[n]} and I ={I[n]} and rewrite problem (13) as

maxQ,L,I,ηηs.t.1N∑n∈Nlog2(1+1L[n]I[n])≥η,p[n]hq,kH[n]hq,kH[n]≥L−1[n],∀n,p[n]hm,kH[n]hm,kH[n]≥L−1[n],‖q[n]−q[n−1]‖2≤D,n=1,2,...,Nq[0]=(xinit,yinit,H)(14)

It is obvious that the optimal solution of (13) is equal to that of (14) is and only if the following constrains are satisfied.

R(L[n],I[n])=∑n∈Nlog2(1+1L[n]I[n])+W[n](L[n]−I[n]),(15)

where W[n] refers to the SCA constraints defined as

W[n]=−log2(I[n]+L[n]I[n]L[n]+L[n]I[n])(16)

Based on the above discussion, we transform the trajectory optimization problem (11) as

maxQ,L,I,ηηs.t.R(L[n],I[n])≥η,p[n]hq,kH[n]hq,kH[n]≥L−1[n],∀n,p[n]hm,kH[n]hm,kH[n]≥L−1[n],‖q[n]−q[n−1]‖2≤D,n=1,2,...,Nq[0]=(xinit,yinit,H)(17)

Problem (17) is a convex problem. It can be obtained from the constraints of (17) that the UAV trajectory is not a closed-form expression here, but is optimized according to the current trajectory state until it reaches the convergence condition. The specific convergence performance is reflected in the simulation part.

3.3 Beamforming Matrixs Design

In this section, we show the beamforming design of (19).

maxp[n],θl,q[n] Rsecs.t.∑n=1Np(n)≤Pnow1N∑n=1Np(n)≤Peva,p(n)≤Pmax,n=1,2,...,N‖q[n]−q[n−1]‖2≤D,n=1,2,...,Nq[0]=(xinit,yinit,H)(18)

It should be noted that the optimal target value of (18) only serves the upper bound of (11). Because SDR is applied, it cannot be guaranteed that w[n] obtained in each slot is rank 1. Specifically, when w[n] obtained is rank 1, it can be written as W[n]=w[n]Hw[n] through eigenvalue decomposition, and w[n] obtained is the optimal solution of (18). Otherwise, Gaussian randomization is required to restore w[n] close to [19].

3.4 Phase-Shift Matrix Design

In this subsection, we would show the phase-shift matrix design for the original problem with fixed trajectory and beamforming. First, we reformulate the original problem as

maxp[n],θl,q[n] Rsecs.t.∑n=1Np(n)≤Pnow1N∑n=1Np(n)≤Peva,p(n)≤Pmax,n=1,2,...,N‖q[n]−q[n−1]‖2≤D,n=1,2,...,Nq[0]=(xinit,yinit,H)(19)

Then we take the trajectory and beamforming as fixed ones. The optimization of phase-shift matrix is simplified as

maxΓ⁡∑n∈Nlog2(1+p[n]g0[n]pm[n]gm[n]+σ2)s.t.0≤θi[n]<2π,i∈{1,2,...,L},∀n,(20)

which is still non-convex and difficult to solve.

We then introduce the vector variable v=[ejθ1[n],ejθ2[n],...,ejθL[n]], and the extern of v as v^=ejτ[v,1]. As a result, the non-convex problem (20) is rewritten as

maxv⁡minwm⁡vH[n]wg[n]wgH[n]v[n]vH[n]wm[n]wmH[n]v[n]+σ2s.t.0≤θi[n]<2π,i∈{1,2,...,L},∀n,(21)

where wm and wg are respectively defined as

wm[n]=diag{h0[n]}hm[n](22)

wg[n]=diag{h0[n]}hg[n](23)

To solve (21), we apply SCA method and let

V[n]=v[n]v[n]H,(24)

Wm[n]=wm[n]wm[n]H,(25)

Wg[n]=wg[n]wg[n]H,(26)

which transform (21) into

maxVtr(Wg[n]V[n])s.t.Vl,l[n]=k[n],l=1,2,...,L+1,∀n,Vl,l[n]⪰0,∀n,tr(Wm[n]V[n])+k[n]σ2=1,∀n,k[n]≥0,∀n,rank(V)=1.(27)

It is worth noting that (27) is convex if we ignore the rank-1 constraint. Thus we first solve the convex problem as follows:

maxVtr(Wg[n]V[n])s.t.Vl,l[n]=k[n],l=1,2,...,L+1,∀n,Vl,l[n]⪰0,∀n,tr(Wm[n]V[n])+k[n]σ2=1,∀n,k[n]≥0,∀n,(28)

which can be solved by CVX. If the optimal solution of (28) satisfies the rank1 constraint, then it is considered that the optimal solution of (28) is also the optimal solution of (27) [34]. Of course, this is usually not true. If the optimal solution of (28) does not satisfy the rank1 constraint, the Gaussian random method is used to find the closest optimal vector.

3.5 Alternate Optimization Algorithm Design

In this section, we consider combining the above alternative optimization algorithms to obtain a general algorithm for the joint design of all optimization variables. In addition, we discuss the complexity of the proposed algorithm.

3.6 Complexity Analysis

We first focus on the complexity in each iteration. Each iteration of Algorithm 1 involves the following computations:

Wk(n+1)–recall that Consequently, the number of operations needed to compute g(k) is 𝒪(P). The updating of Mi involves a single addition and the identification of the smallest entry in g(k). This complexity order of such an operation does not surpass 𝒪(P). Thus the complexity in each iteration is of the order of 𝒪(P). Then, we obtain the maximum number of iterations of Algorithm 1 is M, and thus the whole complexity order of Algorithm 1 is 𝒪(MP). Accordingly, if we reduce the number of quantizers from P to P∗, the reduction in the complexity order would be 𝒪(M(P−P∗)).

4  Robust Scheme Design

In the above algorithm, we have made a strong assumption that the channel state information of the eavesdropper is perfectly obtained, which is actually difficult to achieve. When the eavesdropping channel is different from our assumption, the performance of the proposed algorithm will also be affected. In order to improve the robustness of the proposed algorithm, we have improved the algorithm in this chapter, that is, to consider imperfect channel state information.

4.1 Imperfect CSI Assumption

In the actual communication environment, it is very difficult to obtain a perfect eavesdropping channel due to the lack of specific link information of potential eavesdroppers. On the other hand, we assume that imperfect CSI can be obtained through the vision advantage of UAV, that is, the eavesdropping channel can be approximately estimated by the location of the eavesdropper. Further, we assume that the approximate eavesdropping channel is an imperfect CSI, which satisfies the following conditions:

Hi(e)=Hi(e)¯+ΔHi(e),(29)

ei={ΔHi(e)∈CN×N,Tr(ΔHi(e)HΔHi(e))≤ζp2},(30)

where ζp2 denotes the uncertainty boundary of Hi. Similarly, the estimated channel state information could be defined as

Hi(m)=Hi(e)¯+ΔHi(m),(31)

mi={ΔHi(e)∈CN×N,Tr(ΔHi(e)HΔHi(m))≤ζe2}.(32)

4.2 S-Procedure Based Scheme

We first record the S-procedure. For a function fi(x), i∈{1,2}, x∈CN, which is defined as

fi(x)=xHBx+2Re{biHx}.(33)

It can be obtained that the condition f1(x)≥0 could obtain f2(x)≥0 if and only if the following constraints are satisfied:

[B2b2b2Hb2]−ϖ[B1b1b1Hb1]⪰0,(34)

where ϖ is a parameter satisfying ϖ>0.

Conversely, f2(x)≤0 could be obtained from f1(x)≤0 is and only if

[B1b1b1Hb1]−ϖ[B2b2b2Hb2]⪰0,(35)

where ϖ is a parameter satisfying ϖ>0.

By introducing S-procedure to equivalently transform (P3), we thus rewrite (P3) and obtain the following equivalent expression:

Δe(α1,W,L,β)=[ α1I−(W−(β−1)L)−(W−(β−1)L)He(e)¯−(W−(β−1)L)He(e)¯HΔ, ],(36)

where Δ=(β−1)σe2−He(e)¯H(W−(β−1)L)He(Φ)¯−α1ξe2.

Δe(α2,W,L)=[α2I−(W+L)−(W+L)He(e)¯−(W+L)He(E)¯HPm−He(Φ)¯H(W+L)He(Φ)¯−α2ξp2.](37)

It can be observed that (37) is convex and the robust algorithm is thus obtained.

4.3 Proposed Robust Based Scheme

According to the above discussion, we could replace the non-convex constraints in the original problem, i.e., the constraints about the imperfect CSI as following:

max Rs.t.∑n=1Np(n)≤Pnow1N∑n=1Np(n)≤Peva,p(n)≤Pmax,n=1,2,...,N‖ q[ n ]−q[ n−1 ] ‖2≤D,n=1,2,...,Nq[ 0 ]=(xinit,yinit,H),Δe(α1,W,L,β)=[ α1I−(W−(β−1)L)−(W−(β−1)L)He(e)¯−(W−(β−1)L)He(e)¯HΔ, ],Δe(α2,W,L)=[ α2I−(W+L)−(W+L)He(e)¯−(W+L)He(E)¯HPm−He(Φ)¯H(W+L)He(Φ)¯−α2ξp2. ](38)

Note that (38) is convex, which can be solved by CVX [35]. The robust scheme for imperfect CSI is thus obtained.

5  Discussion

In this paper, we pay attention to the UAV-NOMA system supported by IRS for the first time, and jointly design the trajectory of UAV and the phase shift matrix of IRS. Different from the goal of maximizing the communication rate or minimizing the power consumption in previous studies, we balance them to flexibly meet the needs of different scenarios.

We design the known perfect CSI and imperfect CSI at the same time. For the perfect CSI, we use the classical alternating optimization algorithm and analyze its complexity; For the case of imperfect CSI, we use S-lemma to transform and solve the original problem.

Some unfinished work is left for future work, such as 3-D trajectory design of UAV. At present, the flight design of UAV at fixed altitude is mainly for the safety consideration of collision prevention. However, extending the UAV trajectory to the 3-D range will undoubtedly increase the design difficulty, but it will also bring higher design freedom. And the introduction of UAV group will be our follow-up work.

6  Numerical Results

First, we simulate the simulation environment proposed in the paper. As shown in Fig. 2, the UAV flies along the preset trajectory with a fixed altitude; Multiple users are randomly distributed in the communication area. We take the center point of the communication area as the origin of Cartesian coordinates. The radius of the communication area is 1000 m. The flight height of the UAV is 100 m. The IRS and potential eavesdroppers are located on both sides of the communication area.

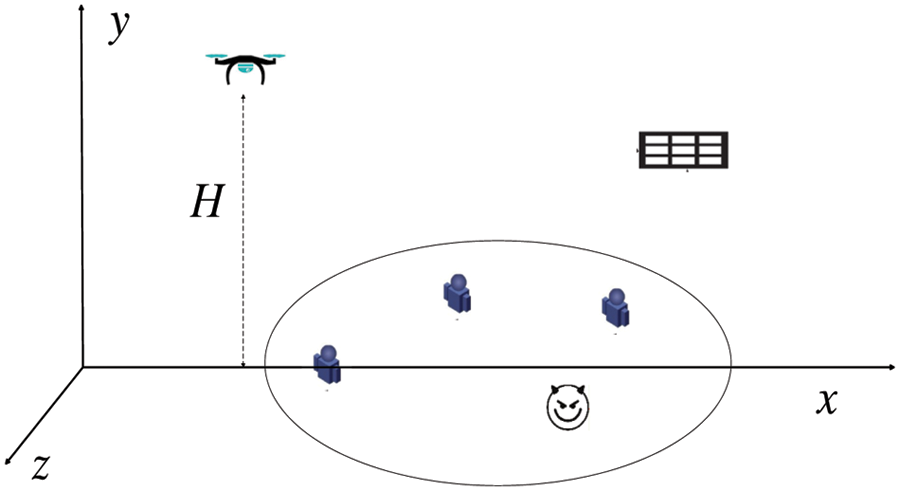
Figure 2: Simulation area

6.1 Simulation for Perfect CSI

In the fourth chapter, we propose a method based on alternating optimization, and analyze the complexity of the algorithm. From the analysis of algorithm complexity, it can be concluded that the time consumption of alternative optimization is linear with the number of iteration convergence. Therefore, we verified the number of iterations of the algorithm and compared it with other existing algorithms. The results are as follows:

It can be seen from Fig. 3 that the proposed algorithm can converge within 10 times compared with other alternative optimization algorithms. This shows that our algorithm can run efficiently. On the other hand, when we try to set the initial point at different positions, the final convergence effect is the same, and different initial points will not improve the convergence times.

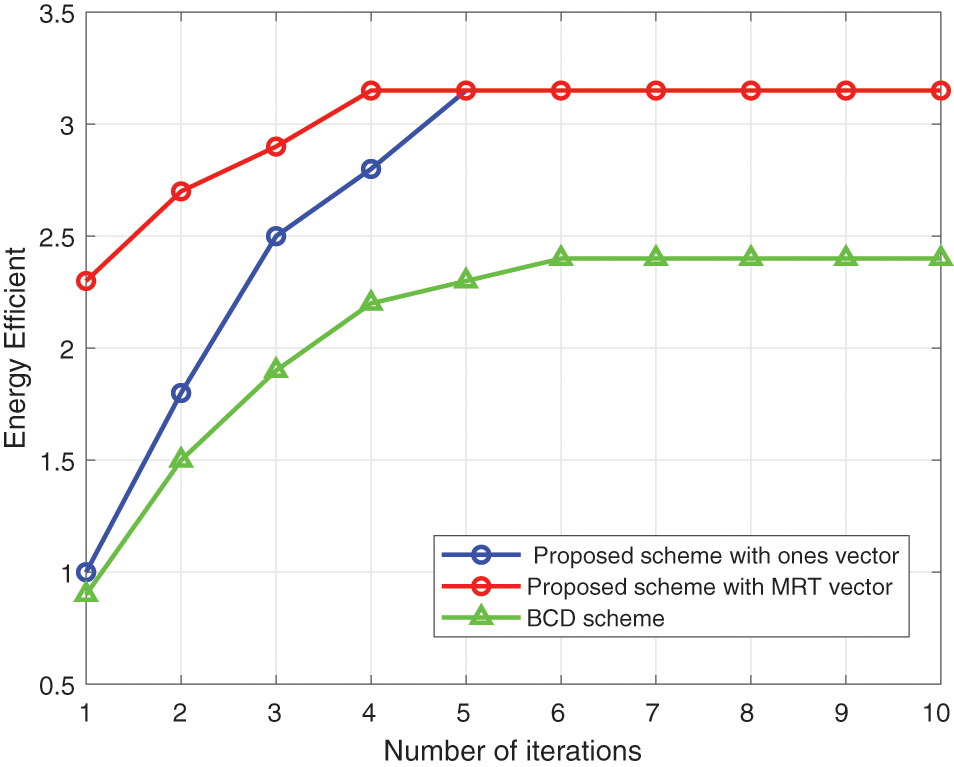
Figure 3: Convergence of the proposed algorithm

In Fig. 4, we show the flight path of UAV under the proposed algorithm. The following characteristics can be found: the flight speed of the UAV will not fluctuate greatly, because the UAV is limited by the speed and power in each time slot, as well as the overall flight power. Once the UAV moves too far in a time slot, it will not meet the power constraints; On the other hand, the trajectory of the UAV will slightly deviate from the potential eavesdropper, because it can better improve the security rate to stay away from the eavesdropper.

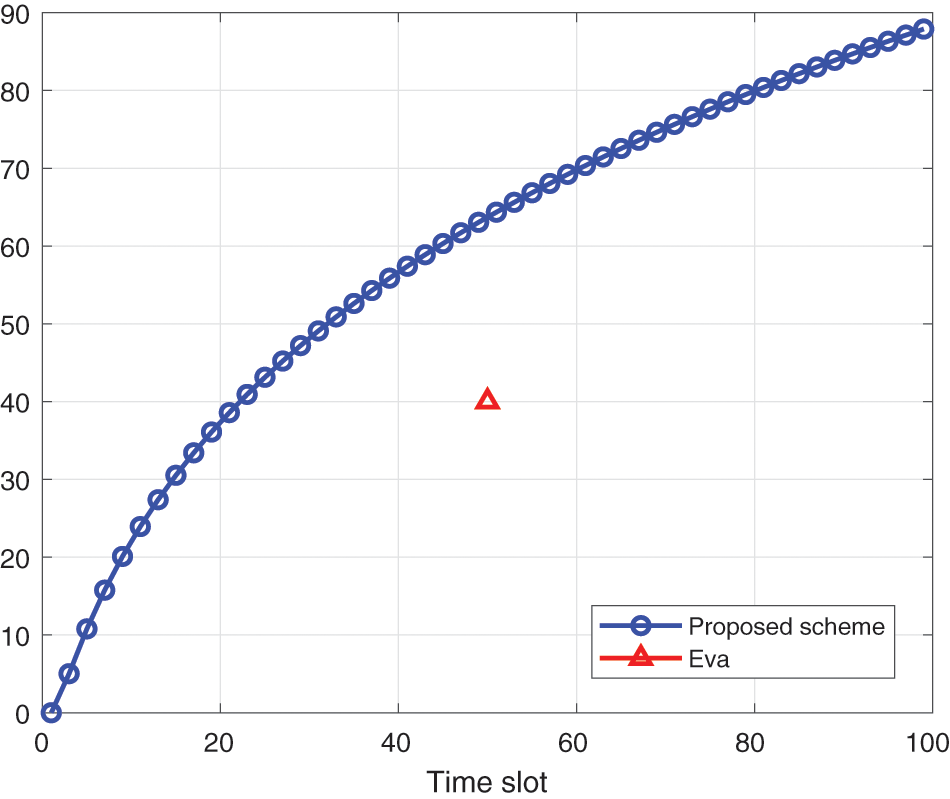
Figure 4: Trajectory of UAV

We show the curve of energy efficiency vs. noise power of the proposed algorithm in Fig. 5. Noise power is a kind of interference factor that can not be ignored. When the noise power is high, both the uplink communication and the eavesdropper’s eavesdropping link will be greatly affected. The algorithm proposed by us has better performance because it makes full use of the trajectory of UAV and the phase design of IRS, and can avoid the influence of noise.

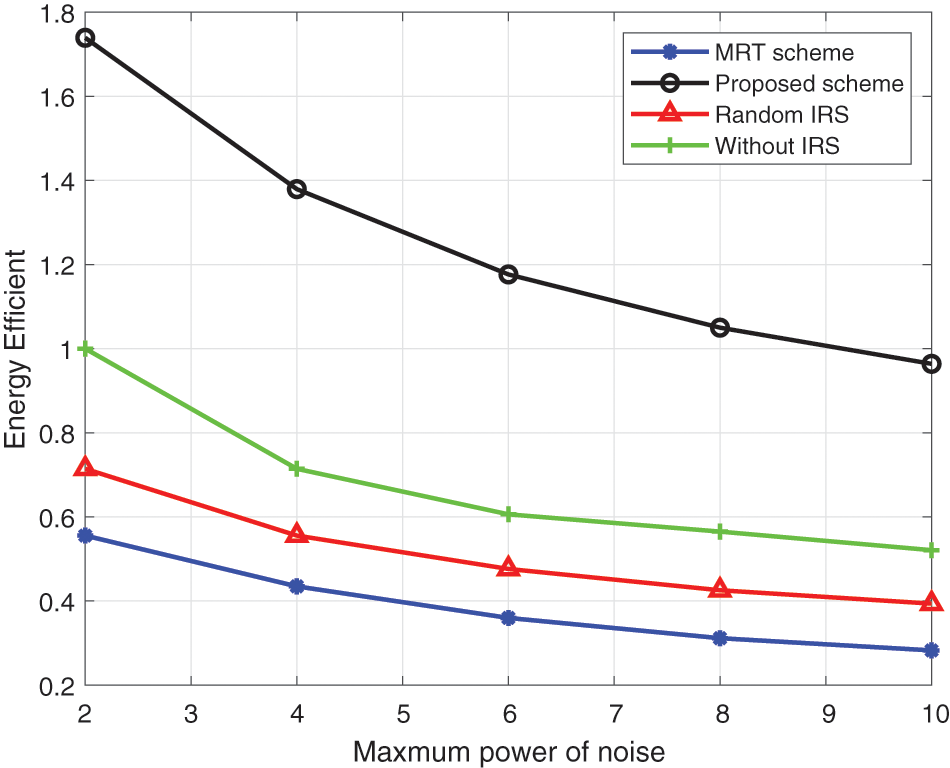
Figure 5: Energy efficiency vs. power of noise

In Fig. 6, we show the relationship between energy efficiency and user power. It is worth noting that for simplicity, we assume that all users have the same maximum power; On the other hand, the user’s actual transmission power is not necessarily the same as its maximum power, that is, the abscissa is marked. This is because when each user transmits at the maximum power, the interference and the rate of eavesdroppers will also be increased. Therefore, the proposed scheme will comprehensively consider the trajectory of UAV and the phase impact of IRS, and bring about performance improvement.

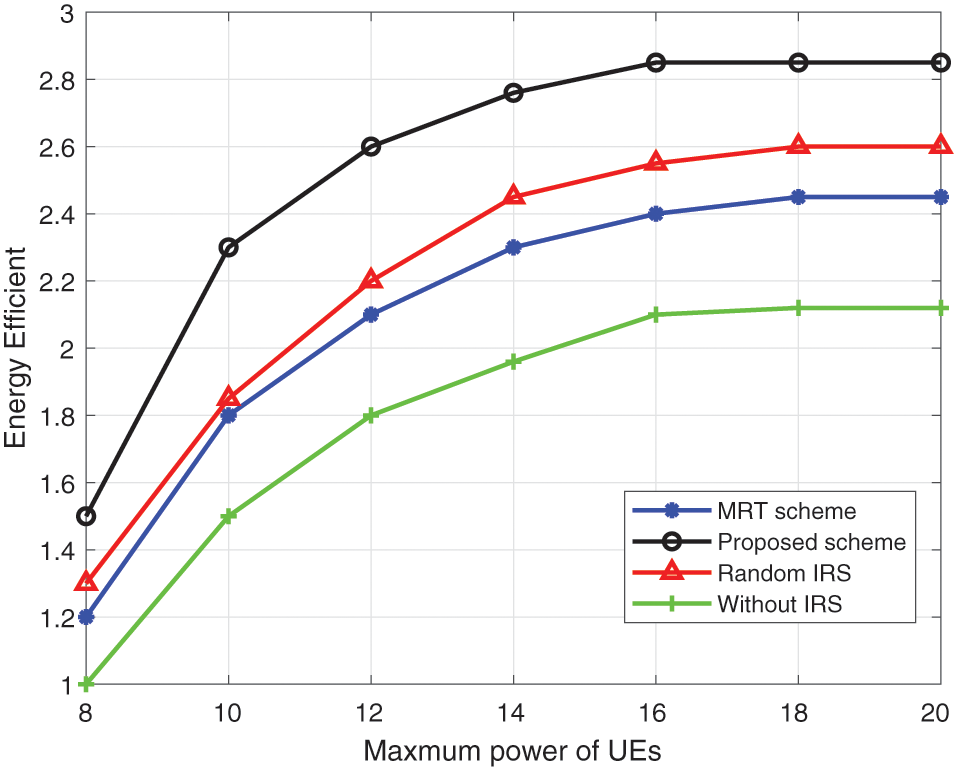
Figure 6: Energy efficiency vs. power of users

In Fig. 7, we consider the effect of the number of IRS elements on energy efficiency. It is worth noting that when the IRS is not used for auxiliary communication, the number of IRS elements will not have any impact on energy efficiency. When the random IRS distribution is adopted, increasing the number of elements can slightly increase the energy efficiency but will not produce more effects. Only MRT and the proposed scheme can better apply the IRS auxiliary function. By comparison, the scheme proposed by us has better efficiency.

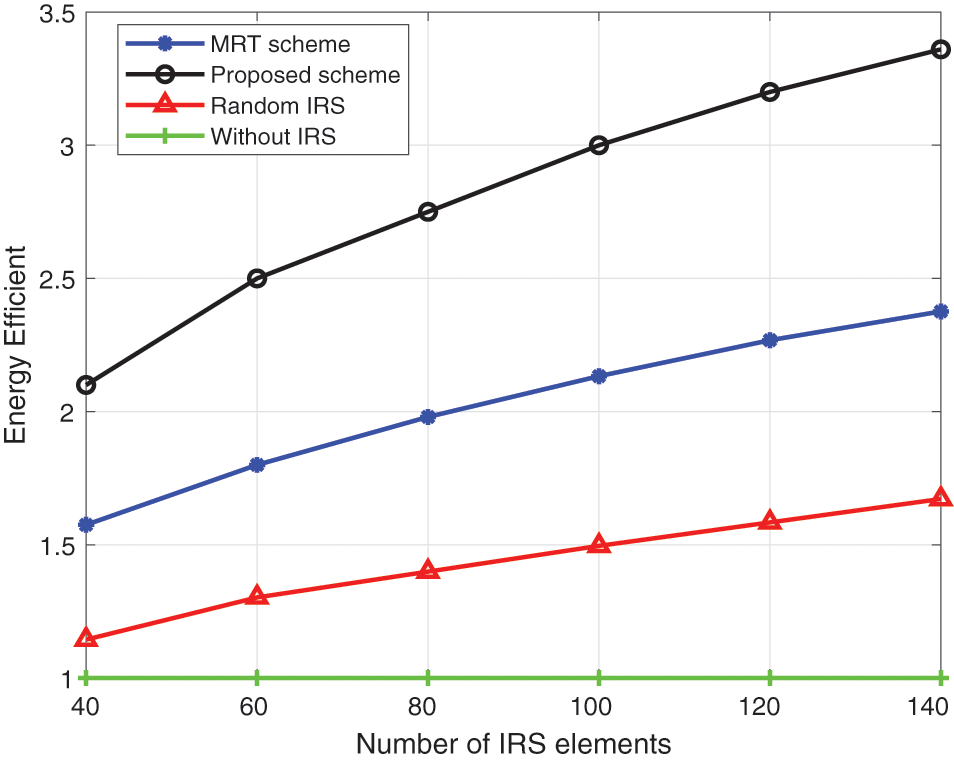
Figure 7: Energy efficiency vs. number of IRS elements

It can be seen from Figs. 8 and 9 that when we adopt a robust scheme, we can improve the energy efficiency of the system in a statistical sense. For simplicity, we only simulated the curve of energy efficiency changing with the maximum power of the user. However, it can be found from the curve that the proposed scheme has better performance under the condition of imperfect CSI.

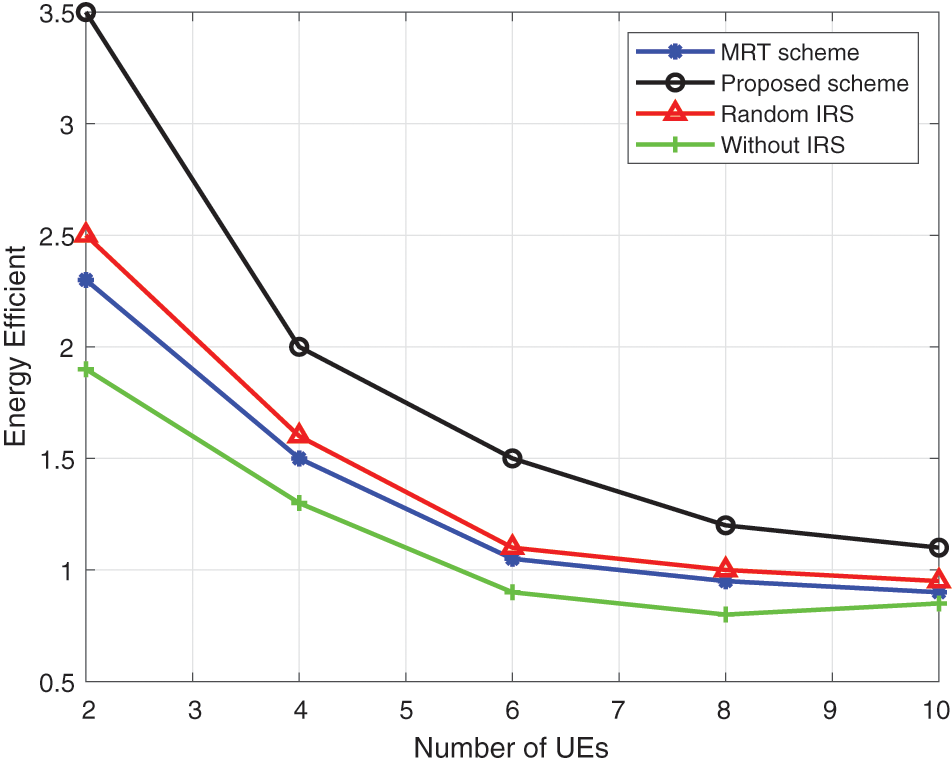
Figure 8: Energy efficiency vs. number of UEs

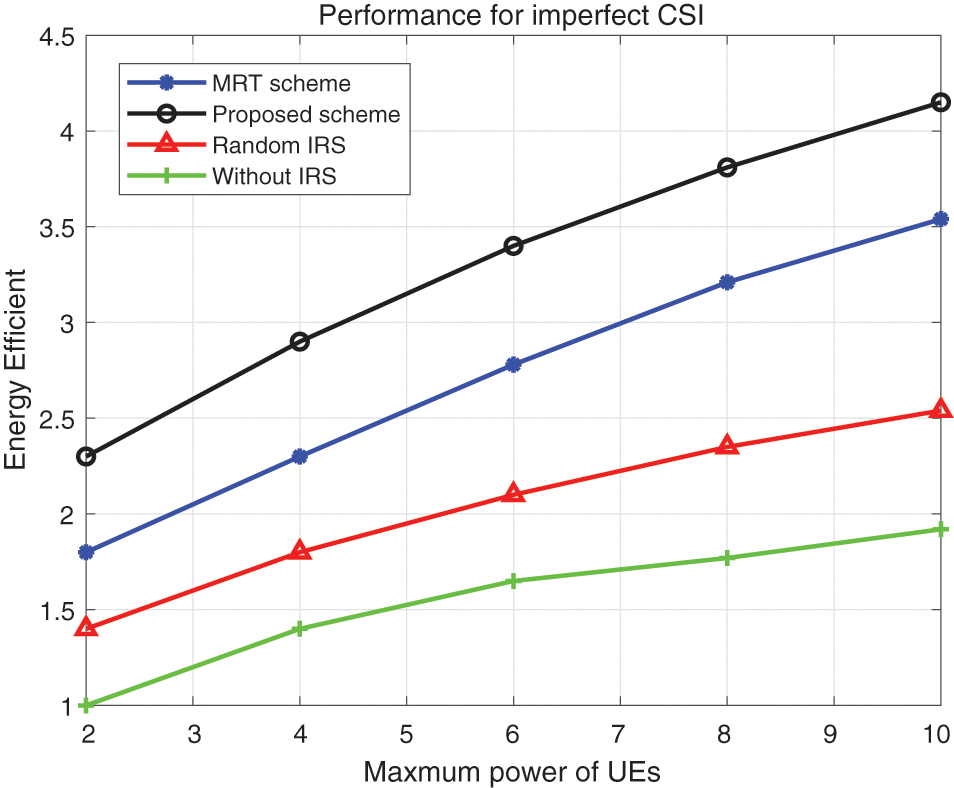
Figure 9: Energy efficiency vs. maximum power of UEs

6.2 Simulation for Imperfect CSI

In this section, we simulate the proposed scheme of imperfect CSI. To facilitate comparison, we still choose other existing schemes as comparison schemes.

For the completeness of the experimental results, we obtain that the results of perfect CSI are compared with the results of imperfect CSI. As the number of users increases, the energy efficiency inevitably decreases. The robust algorithm we proposed can well reduce the performance loss caused by imperfect CSI. As shown in Fig. 10, the scheme that does not use the IRS has the worst effect, because it cannot reconstruct the channel through the IRS.

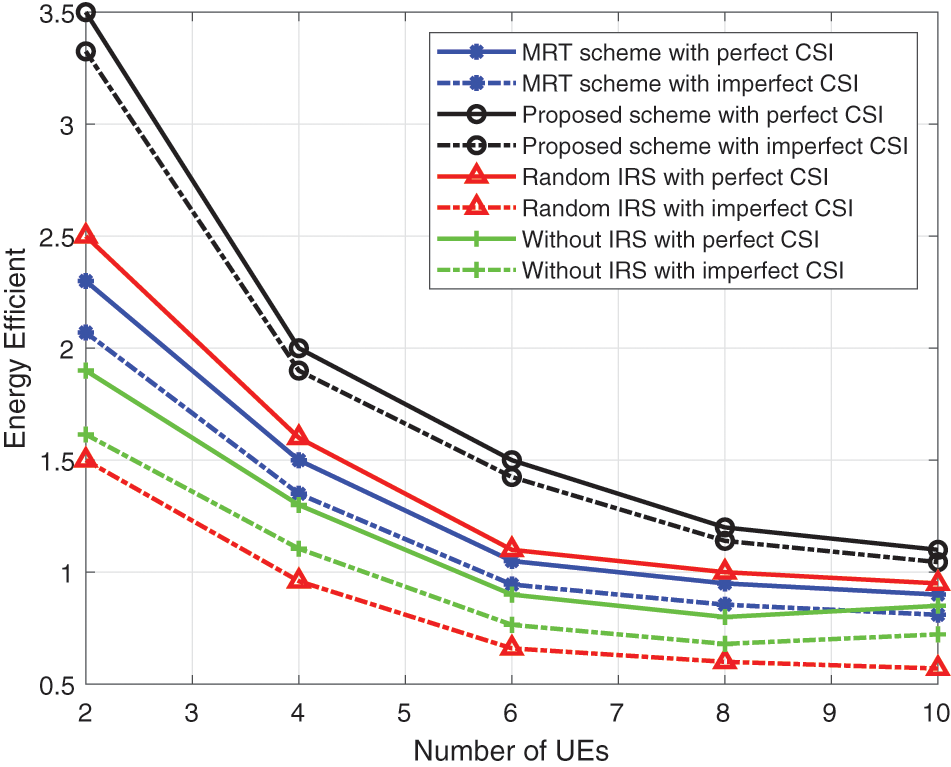
Figure 10: Energy efficiency vs. number of UEs for imperfect CSI

Finally, we also simulated the influence of noise in Fig. 11. It can be found that the robust iterative optimization algorithm proposed by us can still maintain better performance under large noise, and the gap between the energy efficiency for imperfect CSI and that of known perfect CSI is very small, which comes from the design for the worst channel estimation situation and maximizing the energy efficiency in this situation.

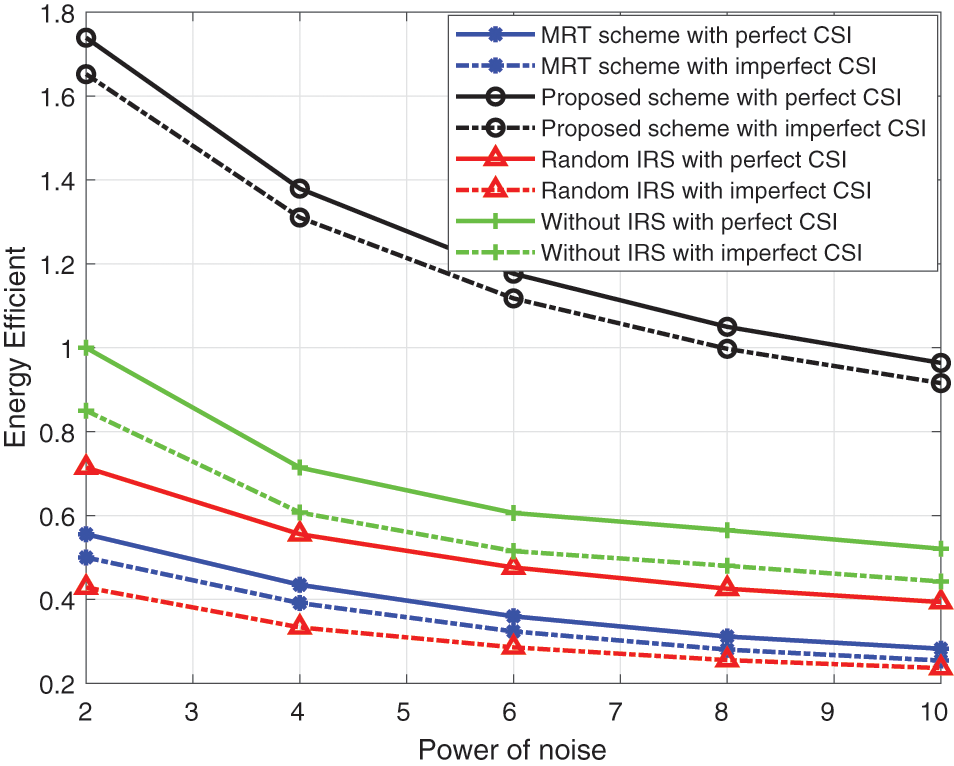
Figure 11: Energy efficiency vs. power of noise for imperfect CSI

7  Conclusion

In this paper, we focus on the issue of maximizing energy efficiency based on security in UAV communication network. We assume that there is a potential eavesdropper trying to obtain the information sent by the user to the UAV. On the other hand, multiple users are in the NOMA working mode, and there is an IRS to help improve secure communication. By designing the user’s transmission beam and the IRS reflection phase matrix, we can maximize the energy efficiency on the premise of ensuring a certain security rate. Compared with the existing algorithms, the proposed scheme can better utilize energy. In addition, we also consider a wider range of imperfect known CSIs, and propose an optimization scheme for this case, which shows the robustness of the scheme.

Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.

Funding Statement: This work was supported in part by the Key Scientific and Technological Project of Henan Province (Grant Nos. 212102210558, 222102210212), Doctoral Research Start Project of Henan Institute of Technology (Grant No. KQ1852).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Palattella, M. R., Dohler, M., Grieco, A., Rizzo, G., Torsner, J. et al. (2016). Internet of Things in the 5G era: Enablers, architecture and business models. IEEE Journal on Selected Areas in Communications, 34(3), 510–527. https://doi.org/10.1109/JSAC.2016.2525418 [Google Scholar] [CrossRef]

2. Di, B., Zhang, H., Song, L., Li, Y., Han, Z. et al. (2020). Hybrid beamforming for reconfigurable intelligent surface based multi-user communications: Achievable rates with limited discrete phase shifts. IEEE Journal on Selected Areas in Communications, 38(8), 1809–1822. https://doi.org/10.1109/JSAC.2020.3000813 [Google Scholar] [CrossRef]

3. Barbarossa, S., Sardellitti, S., Lorenzo, P. D. (2014). Communicating while computing: Distributed mobile cloud computing over 5G heterogeneous networks. IEEE Signal Processing Magazine, 31(6), 45–55. https://doi.org/10.1109/MSP.2014.2334709 [Google Scholar] [CrossRef]

4. Liu, Y., Zhao, J., Xiong, Z., Niyato, D., Chau, Y. et al. (2020). Intelligent reflecting surface meets mobile edge computing: Enhancing wireless communications for computation offloading. https://doi.org/10.48550/arXiv.2001.07449 [Google Scholar] [CrossRef]

5. Li, X., Zheng, Y., Zeng, M., Liu, Y., Dobre, O. A. (2022). Enhancing secrecy performance for STAR-RIS NOMA networks. IEEE Transactions on Vehicular Technology, 72(2), 2684–2688. https://doi.org/10.1109/TVT.2022.3213334 [Google Scholar] [CrossRef]

6. Ju, H., Lim, S., Kim, D., Poor, H. V., Hong, D. (2012). Full duplexity in beamforming-based multi-hop relay networks. IEEE Journal on Selected Areas in Communications, 30(8), 1554–1565. https://doi.org/10.1109/JSAC.2012.120922 [Google Scholar] [CrossRef]

7. Wu, X., Ma, J., Xing, Z., Gu, C., Xue, X. et al. (2022). Secure and energy efficient transmission for irs-assisted cognitive radio networks. IEEE Transactions on Cognitive Communications and Networking, 8(1), 170–185. https://doi.org/10.1109/TCCN.2021.3114176 [Google Scholar] [CrossRef]

8. Haykin, S. (2005). Cognitive radio: Brain-empowered wireless communications. IEEE Journal on Selected Areas in Communications, 23(2), 201–220. https://doi.org/10.1109/JSAC.2004.839380 [Google Scholar] [CrossRef]

9. Yu, X., Xu, D., Schober, R. (2019). Miso wireless communication systems via intelligent reflecting surfaces. 2019 IEEE/CIC International Conference on Communications in China (ICCC), Changchun, China. [Google Scholar]

10. Ma, Y., Lv, T., Liu, H., Li, T., Zeng, J. et al. (2022). Secrecy outage analysis of cr-swipt networks with artificial noise and spatially random secondary terminals. IEEE Transactions on Cognitive Communications and Networking, 8(2), 931–945. https://doi.org/10.1109/TCCN.2021.3130968 [Google Scholar] [CrossRef]

11. Mishra, D., Johansson, H. (2019). Channel estimation and low-complexity beamforming design for passive intelligent surface assisted miso wireless energy transfer. ICASSP 2019-2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK. [Google Scholar]

12. Guan, X., Wu, Q., Zhang, R. (2020). Intelligent reflecting surface assisted secrecy communication: Is artificial noise helpful or not? IEEE Wireless Communications Letters, 9(6), 778–782. https://doi.org/10.1109/LWC.2020.2969629 [Google Scholar] [CrossRef]

13. Huang, C., Zappone, A., Debbah, M., Yuen, C. (2018). Achievable rate maximization by passive intelligent mirrors. ICASSP 2018-2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada. [Google Scholar]

14. Shi, L., Ye, Y., Chu, X., Lu, G. (2021). Computation energy efficiency maximization for a noma based WPT-MEC network. IEEE Internet of Things Journal, 8(13), 10731–10744. https://doi.org/10.1109/JIOT.2020.3048937 [Google Scholar] [CrossRef]

15. Wu, Q., Zhang, R. (2019). Intelligent reflecting surface enhanced wireless network via joint active and passive beamforming. IEEE Transactions on Wireless Communications, 18(1), 5394–5409. https://doi.org/10.1109/TWC.2019.2936025 [Google Scholar] [CrossRef]

16. Liu, Y., Zhao, J., Xiong, Z., Niyato, D., Chau, Y. et al. (2020). Intelligent reflecting surface meets mobile edge computing: Enhancing wireless communications for computation offloading. https://doi.org/10.48550/arXiv.2001.07449 [Google Scholar] [CrossRef]

17. Rangan, S. (2011). Generalized approximate message passing for estimation with random linear mixing. 2011 IEEE International Symposium on Information Theory Proceedings, St. Petersburg, Russia. [Google Scholar]

18. Liu, H., Li, G., Li, X., Liu, Y., Huang, G. et al. (2022). Effective capacity analysis of star-ris-assisted noma networks. IEEE Wireless Communications Letters, 11(9), 1930–1934. https://doi.org/10.1109/LWC.2022.3188443 [Google Scholar] [CrossRef]

19. Shi, Q., Razaviyayn, M., Luo, Z. Q., He, C. (2011). An iteratively weighted mmse approach to distributed sum-utility maximization for a mimo interfering broadcast channel. IEEE Transactions on Signal Processing, 59(9), 4331–4340. https://doi.org/10.1109/TSP.2011.2147784 [Google Scholar] [CrossRef]

20. Wu, Q., Zhang, R. (2020). Beamforming optimization for wireless network aided by intelligent reflecting surface with discrete phase shifts. IEEE Transactions on Communications, 68(3), 1838–1851. https://doi.org/10.1109/TCOMM.2019.2958916 [Google Scholar] [CrossRef]

21. Griffin, J. D., Durgin, G. D. (2009). Complete link budgets for backscatter-radio and RFID systems. IEEE Antennas and Propagation Magazine, 51(2), 11–25. https://doi.org/10.1109/MAP.2009.5162013 [Google Scholar] [CrossRef]

22. Wu, Q., Zhang, R. (2019). Towards smart and reconfigurable environment: Intelligent reflecting surface aided wireless network. IEEE Communications Magazine, 58(1), 106–112. [Google Scholar]

23. Liu, B., Liu, X., Mu, X., Hou, T., Al-Dhahir, N. (2021). Reconfigurable intelligent surfaces: Principles and opportunities. IEEE Communications Surveys and Tutorials, 23(3), 1546–1577. https://doi.org/10.1109/COMST.2021.3077737 [Google Scholar] [CrossRef]

24. Zargari, S., Khalili, A., Zhang, R. (2021). Energy efficiency maximization via joint active and passive beamforming design for multiuser MISO IRS-aided SWIPT. IEEE Wireless Communications Letters, 10(3), 557–561. https://doi.org/10.1109/LWC.2020.3037750 [Google Scholar] [CrossRef]

25. Bai, T., Pan, C., Deng, Y., Elkashlan, M., Nallanathan, A. et al. (2020). Latency minimization for intelligent reflecting surface aided mobile edge computing. IEEE Journal on Selected Areas in Communications, 38(11), 2666–2682. https://doi.org/10.1109/JSAC.2020.3007035 [Google Scholar] [CrossRef]

26. Yan, W., Yuan, X., Kuai, X. (2020). Passive beamforming and information transfer via large intelligent surface. IEEE Wireless Communications Letters, 9(4), 533–537. https://doi.org/10.1109/LWC.2019.2961670 [Google Scholar] [CrossRef]

27. Li, X., Xie, Z., Chu, Z., Menon, V. G., Mumtaz, S. et al. (2022). Exploiting benefits of irs in wireless powered noma networks. IEEE Transactions on Green Communications and Networking, 6(1), 175–186. https://doi.org/10.1109/TGCN.2022.3144744 [Google Scholar] [CrossRef]

28. Yu, Y. (2016). Mobile edge computing towards 5G: Vision, recent progress, and open challenges. China Communications, 13(S), 89–99. https://doi.org/10.1109/CC.2016.7405725 [Google Scholar] [CrossRef]

29. Tao, Q., Su, G., Chen, B., Dai, M., Lin, X. et al. (2021). Secrecy energy efficiency maximization for UAV enabled communication systems. 2021 30th Wireless and Optical Communications Conference (WOCC), pp. 240–244. Taipei, Taiwan. https://doi.org/10.1109/WOCC53213.2021.9603100 [Google Scholar] [CrossRef]

30. Shen, Y., Luo, W., Wang, S. (2018). Maximization of security based energy-efficiency in multicarrier relay networks with SWIPT. 2018 IEEE 9th International Conference on Software Engineering and Service Science (ICSESS), pp. 936–940. Beijing, China. https://doi.org/10.1109/ICSESS.2018.8663863 [Google Scholar] [CrossRef]

31. Wei, C., Zhang, T., Wang, J., Wang, L., Cui, J. et al. (2021). Secure energy efficiency resource allocation for D2D communication with full-duplex radio. 2021 13th International Conference on Wireless Communications and Signal Processing (WCSP), pp. 1–6. Changsha, China. https://doi.org/10.1109/WCSP52459.2021.9613163 [Google Scholar] [CrossRef]

32. Ning, Z., Dong, P., Kong, X., Xia, F. (2019). A cooperative partial computation offloading scheme for mobile edge computing enabled Internet of Things. IEEE Internet of Things Journal, 6(3), 4804–4814. https://doi.org/10.1109/JIOT.2018.2868616 [Google Scholar] [CrossRef]

33. Hum, S. V., Perruisseau-Carrier, J. (2014). Reconfigurable reflectarrays and array lenses for dynamic antenna beam control: A review. IEEE Transactions on Antennas and Propagation, 62(1), 183–198. https://doi.org/10.1109/TAP.2013.2287296 [Google Scholar] [CrossRef]

34. Li, Z., Chen, W., Wu, Q., Wang, K., Li, J. (2022). Joint beamforming design and power splitting optimization in IRS-assisted SWIPT NOMA networks. IEEE Transactions on Wireless Communications, 21(3), 2019–2033. https://doi.org/10.1109/TWC.2021.3108901 [Google Scholar] [CrossRef]

35. Grant, M., Boyd, S. P. (2014). CVX: Matlab software for disciplined convex programming. http://cvxr.com/cvx/ [Google Scholar]