 Open Access
Open Access
ARTICLE
Radiative Blood-Based Hybrid Copper-Graphene Nanoliquid Flows along a Source-Heated Leaning Cylinder
1 Institute of Mathematical Sciences, Faculty of Science, Universiti Malaya, Kuala Lumpur, 50603, Malaysia
2 Center for Data Analytics Consultancy & Services (UM-CDACS), Faculty of Science, Universiti Malaya, Kuala Lumpur, 50603, Malaysia
* Corresponding Author: Noor Fadiya Mohd Noor. Email:
(This article belongs to the Special Issue: Numerical Modeling and Simulations on Non-Newtonian Flow Problems)
Computer Modeling in Engineering & Sciences 2024, 139(1), 1017-1037. https://doi.org/10.32604/cmes.2023.031372
Received 07 June 2023; Accepted 13 September 2023; Issue published 30 December 2023
Abstract
Variant graphene, graphene oxides (GO), and graphene nanoplatelets (GNP) dispersed in blood-based copper (Cu) nanoliquids over a leaning permeable cylinder are the focus of this study. These forms of graphene are highly beneficial in the biological and medical fields for cancer therapy, anti-infection measures, and drug delivery. The non-Newtonian Sutterby (blood-based) hybrid nanoliquid flows are generalized within the context of the Tiwari-Das model to simulate the effects of radiation and heating sources. The governing partial differential equations are reformulated into a nonlinear set of ordinary differential equations using similar transformational expressions. These equations are then transformed into boundary value problems through a shooting technique, followed by the implementation of the bvp4c tool in MATLAB. The influences of various parameters on the model’s non-dimensional velocity and temperature profiles, reduced skin friction, and reduced Nusselt number are presented for detailed discussions. The results indicated that Cu-GNP/blood and Cu-GO/blood hybrid nanofluids exhibit the lowest and highest velocity distributions, respectively, for increased nanoparticles volume fraction, curvature parameter, Sutterby fluid parameter, Hartmann number, and wall permeability parameter. Conversely, opposite trends are observed for the temperature distribution for all considered parameters, except the mixed convection parameter. Increases in the reduced skin friction magnitude and the reduced Nusselt number with higher values of graphene/GO/GNP nanoparticle volume fraction are also reported. Finally, GNP is identified as the superior heat conductor, with an average increase of approximately 5% and a peak of 7.8% in the reduced Nusselt number compared to graphene and GO nanoparticles in the Cu/blood nanofluids.Keywords
Nomenclature
| External magnetic field (T) | |
| Specific heat capacity (J/kgK) | |
| Uniform surface mass flux (kg/(m2s)) | |
| Reference length (m) | |
| Flow component index (–) | |
| Nanoparticle shape factor (–) | |
| Source of heating (J) | |
| Flux of heat (W/m2) | |
| Reynolds number (–) | |
| Temperature (K) | |
| Velocity associated components (m/s) | |
| Velocity of free stream (m/s) | |
| Greek Symbols | |
| Coefficient for thermal expansion (1/K) | |
| Electrical conductivity (S/m) | |
| Shear stress (Pa) | |
| Nanoparticles volume fraction for Cu (–) | |
| Nanoparticles volume fraction for graphene/GO/GNP (–) | |
| Subscripts | |
| Based fluid | |
| Mono/single nanofluids | |
| Duo/hybrid nanofluids | |
| Cu solid nanoparticles | |
| Graphene/GO/GNP solid nanoparticles | |
| Wall surface of a cylinder | |
| Initial or reference | |
| Ambient | |
The boundary layer is a fundamental concept in understanding fluid transportation over a surface from theoretical fluid mechanics perspectives, pioneered by Prandtl in 1904 [1]. Conventional liquids, such as oil, ethylene glycol (EG), and water, used in various mechanical and technical operations, typically exhibit poor thermal conductivity, limiting the heat transfer efficiency for specific engineering processes. In 1993, Choi et al. [2] introduced a nanotechnology-based fluid aimed at enhancing energy efficiency and heat transfer capacity. As a result, nanofluids became prominent in heat transfer applications, including the biomedical and pharmaceutical sectors, microelectronics, magma solidification, cooling and heating exchangers, drug delivery, and food manufacturing. A mono nanofluid is defined as a single type of solid nanoparticle homogeneously dispersed in an ordinary liquid. Recent attention has shifted toward the introduction of multiple different nanoparticles suspended in that ordinary liquid, referred to as hybrid, ternary, or composite nanofluids. These advanced nanofluids integrate the chemical and physical properties of the suspended nanoparticles within a single phase, yielding diverse effects from the combined elements [3]. Babu et al. [4] found that hybrid nanomaterials display distinct physicochemical characteristics absent in general fluids or mono nanofluids. This discovery spurred further research on various hybrid nanofluids, examining their preparation, synthesis, and characterization stages. It was reported that thermal conductivity in hybrid nanofluids surpassed that of mono nanofluids [5]. In addition, hybrid nanofluids achieved higher heat flux than mono nanofluids in a study of Copper-Alumina/water (Cu-Al2O3/H2O) by Nadeem et al. [6]. Salah et al. [7] reported that using the Al-Mg-TiO2/water-ethylene glycol ternary hybrid nanofluid substantially increases the heat transfer coefficient for swirl flow within a rotating cone.
Blood is considered an incompressible flow consisting of the boundary layer flow and the potential flow within arteries. Analyzing blood flow over cylindrical surfaces has crucial applications in diagnosing and treating conditions related to plaque deposition and aneurysms in cardiovascular diseases, minimizing post-operative complications, and reducing healthcare costs. This analysis also applies to tumor treatments, blood clot removals, brain aneurysms, and infections. However, selecting appropriate models and approaches to depict blood flow challenges is vital to ensure realistic and effective solutions. According to Akhtar et al. [8], many researchers preferred non-Newtonian boundary layer models to study arterial blood flows, as these models provide a more accurate representation of hemodynamics. Recent studies have also reported on blood nanofluid boundary layer flows. Akhtar et al. [8] simulated blood flow within a symmetrically stenosed artery using the non-Newtonian Casson model, suggesting that their findings are crucial for surgical considerations, including assessing stenosis shape, location, and formation. McCash et al. [9] numerically explored the entropy analysis of the peristaltic flow of a Cu-Ag/water hybrid nanofluid within an elliptical duct with sinusoidal progressing boundaries. Tripathi et al. [10] presented a theoretical and numerical evaluation of unsteady blood flow in a diseased artery featuring irregular stenosis, focusing on drug delivery applications for blood vessels using an Ag-gold/blood hybrid nanofluid boundary layer model. Sharma et al. [11] examined the impact of the Au-Al2O3/blood hybrid nanoliquid on the hemodynamic properties of unsteady blood flow in a curved artery with stenosis and aneurysm. They concluded that the chosen hybrid nanomaterials can modulate blood velocity and temperature, enabling surgeons to adjust them as required.
Sutterby liquid is crucial in the polymer industry, making it one of the most frequently discussed non-Newtonian fluids due to its rheological features [12]. This non-Newtonian fluid model characterizes the behavior of pseudoplastic substances. To date, researchers have presented their findings using both analytical and numerical methods across various geometries to evaluate the heat energy efficiency of non-Newtonian Sutterby hybrid nanofluid flows. Waqas et al. [13] studied SiO2-SWCNT/EG and MoS2-MWCNT/EG hybrid nanofluid boundary layer flows in the three-dimensional Sutterby model over a stretchy surface affected by thermal convection, radiation, and heat melting. They observed that the temperature and velocity profiles decrease when larger melting parameter values are applied. Al-Mughanam et al. [14] numerically examined the characteristics of mono, duo, and tri-nanoparticles suspended in the Sutterby fluid model using the Finite Element Method (FEM). They noted moderate values of thermal memory effects in the hybrid nanofluid compared to other types of nanofluids under consideration. Bouslimi et al. [15] discussed the heat transport efficiency of Sutterby mono and hybrid nanofluid flows past a slippery hot surface, while Jamshed et al. [16] found in their study that Sutterby nanofluids using hybrid Copper-Sodium-Alginate (Cu-SA) and Gold-Sodium-Alginate (Au-SA) nanoparticles enhance the rate of heat transfer in the Parabolic Trough Solar Collector (PSTC). These studies highlight that non-Newtonian Sutterby fluids have found use in various applications, including lubrication and drilling operations.
The importance of nanoliquids by focusing on the solid nanoparticles’ volume fraction, where the thermophysical properties of both the base fluid and nanoparticles are heterogeneously correlated, was initially examined by Tiwari et al. [17]. Numerous studies on the Tiwari and Das hybrid nanofluid models are now available in the literature. Dinarvand et al. [18] analytically explored the Cu-Ag/water hybrid nanoliquid model developed based on the Tiwari–Das framework near a vertically permeable circular channel. A subsequent study by Dinarvand et al. [19] found that the Tiwari-Das Falkner-Skan model for TiO2-CuO/water hybrid nanofluids outperforms mono-nanofluids regarding heat flux. Additionally, Ramzan et al. [20] utilized the Tiwari-Das model for SiO2-TiO2/water hybrid nanofluid flows through a rotary channel influenced by the Hall current. They indicated that the hybrid nanofluid flow is superior to the performance of mono-nanofluid systems in solar thermal applications. Alwawi et al. [21] developed the Tiwari-Das mathematical model to simulate the behavior of Williamson hybrid nanoliquid flows over a cylinder. They reported that silver-aluminum oxide nanoparticles demonstrate superiority in enhancing the velocity and energy transfer of the base fluid. Furthermore, Saranya et al. [22] examined the thermal behavior of the Blasius-Sakiadis Tiwari-Das flow for water-based ternary hybrid nanofluids, considering the effect of nanoparticle shape.
The attention focused on selecting various types of graphene-based solid nanoparticles for producing single and hybrid nanoliquids offers significant advantages for technological and scientific approaches. Graphene-based nanoparticles provide excellent thermal conductivity and stability and serve as flexible transporters with minimal corrosion and erosion [23]. Moreover, because graphene-based materials exhibit superior electrical conductivity, high chemical stability, and exceptional mechanical behavior, they are efficiently utilized in supercapacitors and other energy storage devices [24]. Graphene-based materials have also demonstrated vast applicability in the medical field for applications such as cancer therapy and diagnosis, sensing and imaging, tissue regeneration, and drug delivery [25]. Mehrali et al. [26] reported that graphene-magnetite hybrid nanoparticles increase the fluid thermal conductivity by approximately 11%. In contrast, Sadeghinezhad et al. [27] observed that graphene nanoparticles offer higher stability and a surface area thousands of times greater than other nanoparticles. Additionally, Purbia et al. [28] reported that the heat flux increases by about 32% at a 0.1% concentration of graphene nanomaterials, attributed to the enhanced thermal conductivity and Reynolds number of the conducting solid nanomaterials. Bouslimi et al. [15] also found that the thermal transmission rate of the Sutterby hybrid Cu-GO/engine oil nanoliquid surpasses that of the mono Cu/engine oil nanoliquid.
Limited studies on the Sutterby liquid model over a cylinder inspired the current research to further investigate the heat flux efficiency of selected hybrid nanofluids. The examination of graphene, graphene oxides (GO), and graphene nanoplatelets (GNP) as potential nanomaterials in fluid mechanics remains infrequent despite their exceptional combination of mechanical and electrical properties. This research is the first to analyze graphene, GO, and GNP nanoparticles dispersed in the radiative Cu/blood mono nanofluid to form various hybrid mixtures around a slanted permeable cylinder in the existing literature. The impacts of thermal radiation and the heat source are also considered in this study. MATLAB’s bvp4c code is utilized to address the transformed boundary value problems derived from the primary set of partial differential equations (PDEs). Comprehensive results are validated and compared, and the effects of specific parameters on the hybrid Sutterby non-Newtonian nanofluids in terms of non-dimensional velocity and temperature distributions, reduced skin friction value, and reduced Nusselt number are thoroughly investigated. The findings are then presented in tables and graphs in the final section of this research.
Accordingly, the contributions of this research are outlined as follows:
1. This study represents the first exploration of the non-Newtonian Sutterby Tiwari-Das model using blood as the base fluid with hybrid nanoparticles, while previous research focused on other conventional base fluids [15,16].
2. The dispersion of various graphene, GO, and GNP nanoparticles in the radiative Cu/blood mixture is theoretically conducted for the first time to formulate hybrid nanofluid models.
3. Thermal radiation and the effects of the heat source are incorporated into this expanded model alongside a slanted permeable cylinder.
In the current research, a non-Newtonian Sutterby fluid model over a leaning permeable cylinder is given due consideration. The stress tensor is specified as [15]:
where I and p express identity-tensor and pressure, respectively, while S implies an additional stress-tensor, which is defined as follows:
The viscosity of blood varies with shear rate and is determined by several factors, such as the viscosity of plasma, blood cell distribution, and the mechanical properties of the blood cells. Due to their high concentration and distinct mechanical properties, most non-Newtonian effects originate from red blood cells. As blood exhibits non-Newtonian properties of shear-thinning and viscoelasticity, the present research uses the Sutterby model to represent a steady, incompressible, laminar, non-Newtonian blood fluid flow.
The base blood fluid is initially mixed with copper nanoparticles to form Cu/blood mono nanofluids using the Tiwari-Das hybrid nanofluid model. Subsequently, hybrid nanofluids are fabricated by dispersing three types of selected nanoparticles (graphene, GO, and GNP). Table 1 presents the existing models of mono and hybrid nanofluids’ thermophysical properties [18]. Similarly, quantities from references [12,18,29,30] for the base fluid and selected nanoparticles for this study are provided in Table 2. The velocity of the mainstream flow over the cylindrical coordinates

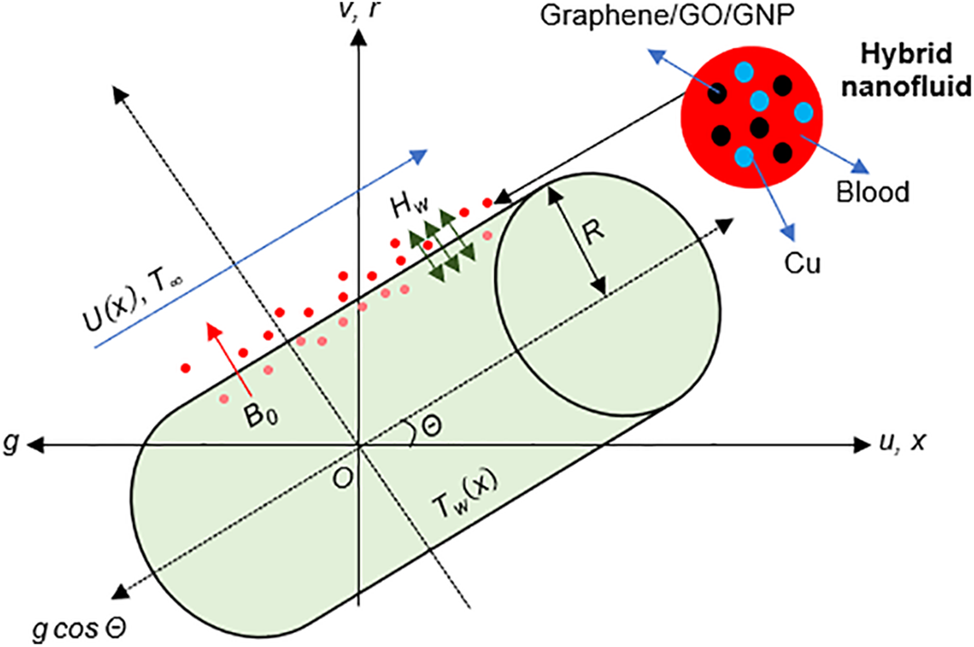
Figure 1: Schematic diagram of the flow with geometrical coordinates
The governed PDEs of continuity, momentum, and energy, as referenced in [15,18,29] with the corresponding boundary conditions (BCs), are given as:
For these, two cases of suction
with
By substituting Eq. (9) into Eqs. (6) and (7), a dimensionless system of nonlinear ODEs is derived as below:
These equations depend on the BCs:
The selected parameters used in this problem are defined mathematically as follows:
The skin friction,
where
When Eq. (9) is substituted into Eq. (14), the resulting reduced skin friction and reduced Nusselt number are obtained:
In order to address the mathematical model for this problem, a robust solution technique is needed to ensure the accuracy and reliability of the outcomes of the controlling PDEs. Therefore, the numerical procedure for this non-Newtonian Sutterby hybrid nanoliquid flow of Cu-blood with chosen graphene, GO, or GNP over a slanted permeable cylinder is conducted using the bvp4c package in MATLAB. The bvp4c tool, derived from the finite difference technique, uses the collocation process in the Lobatto IIIa [32] formula. Additionally, the package implements a derivative scheme in the form of
Given the variables:
a shooting approach is employed to reformulate the nonlinear Eqs. (10) and (11) with the BCs (13). The equations are decreased into the first-order DEs as follows:
Thus, the boundary conditions are defined as follows:
The range of selected nanoparticles’ volume fraction for
For the purpose of validation, the current results of the bvp4c code for Cu-water mono nanofluid are compared with the outcomes of previous work [18]. The comparison in Table 4 supports the conclusions drawn from the present study.
4.2 Velocity and Temperature Disseminations
In this section, the velocity and temperature distributions are thoroughly analyzed. Fig. 2 illustrates the effects of
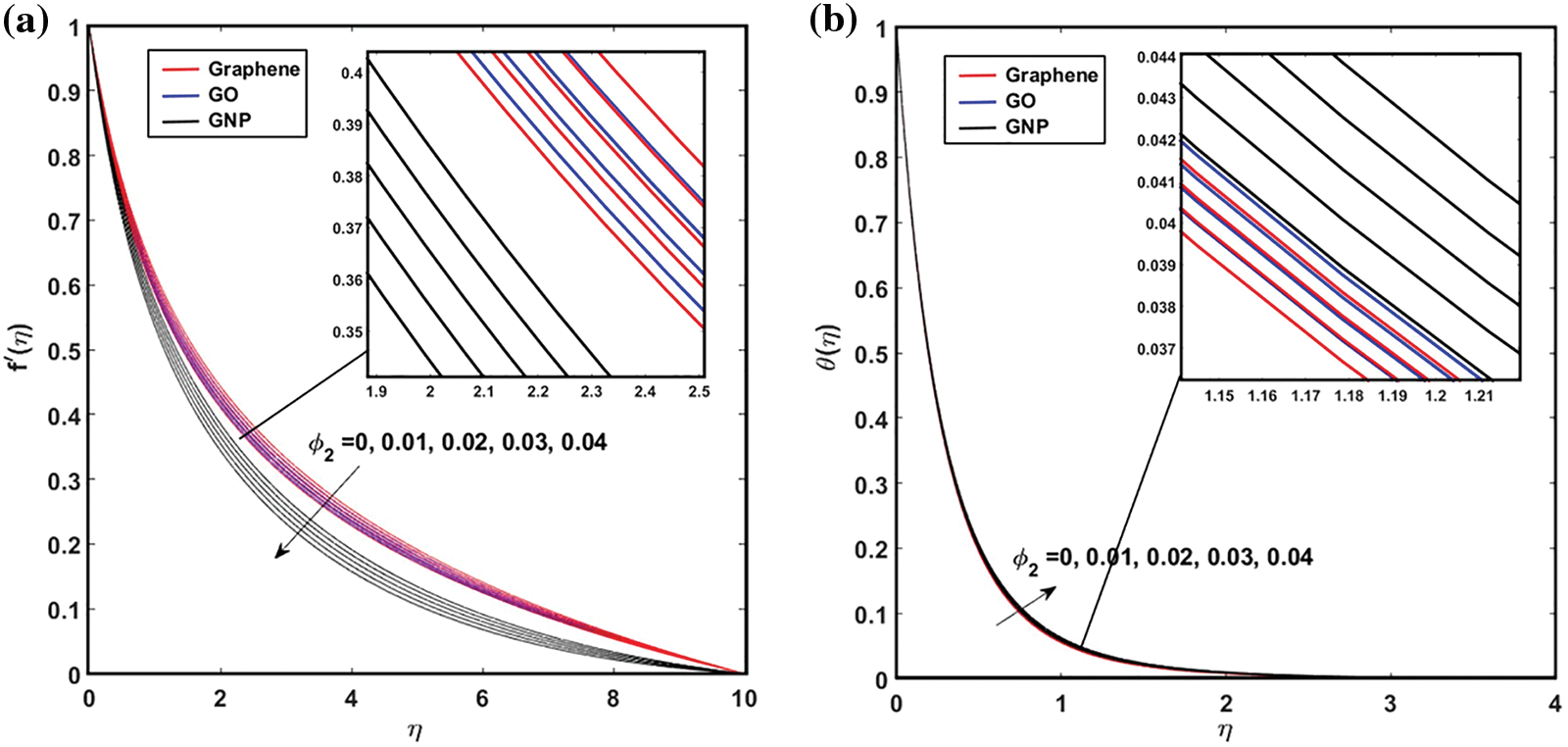
Figure 2: The repercussion of
Fig. 3 elucidates the effects of
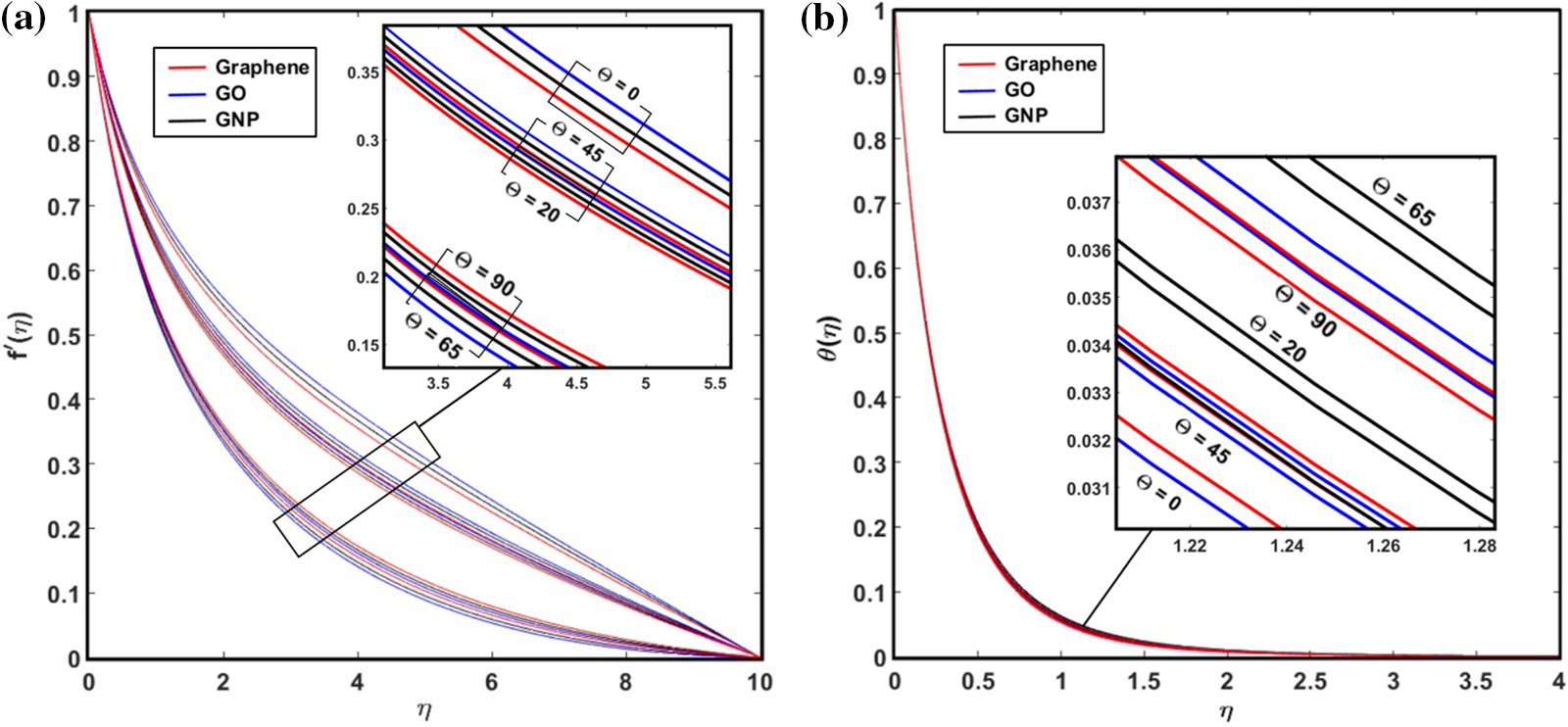
Figure 3: The repercussion of
Fig. 4 illustrates the influences of
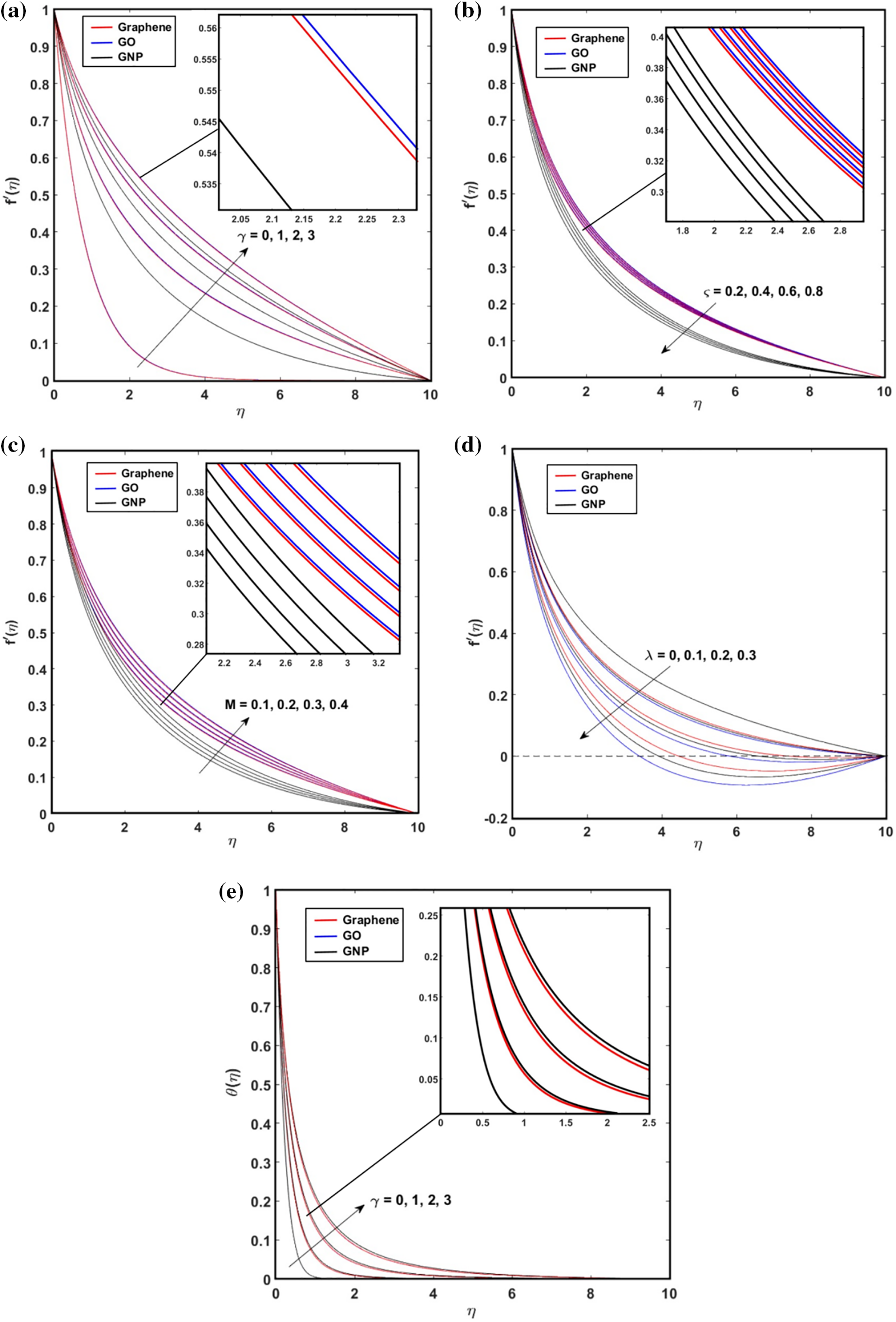
Figure 4: The repercussions of (a)
Alternatively, Figs. 4d and 4e demonstrate that the velocity distributions decline as the values of the mixed convection parameter,
The influences of
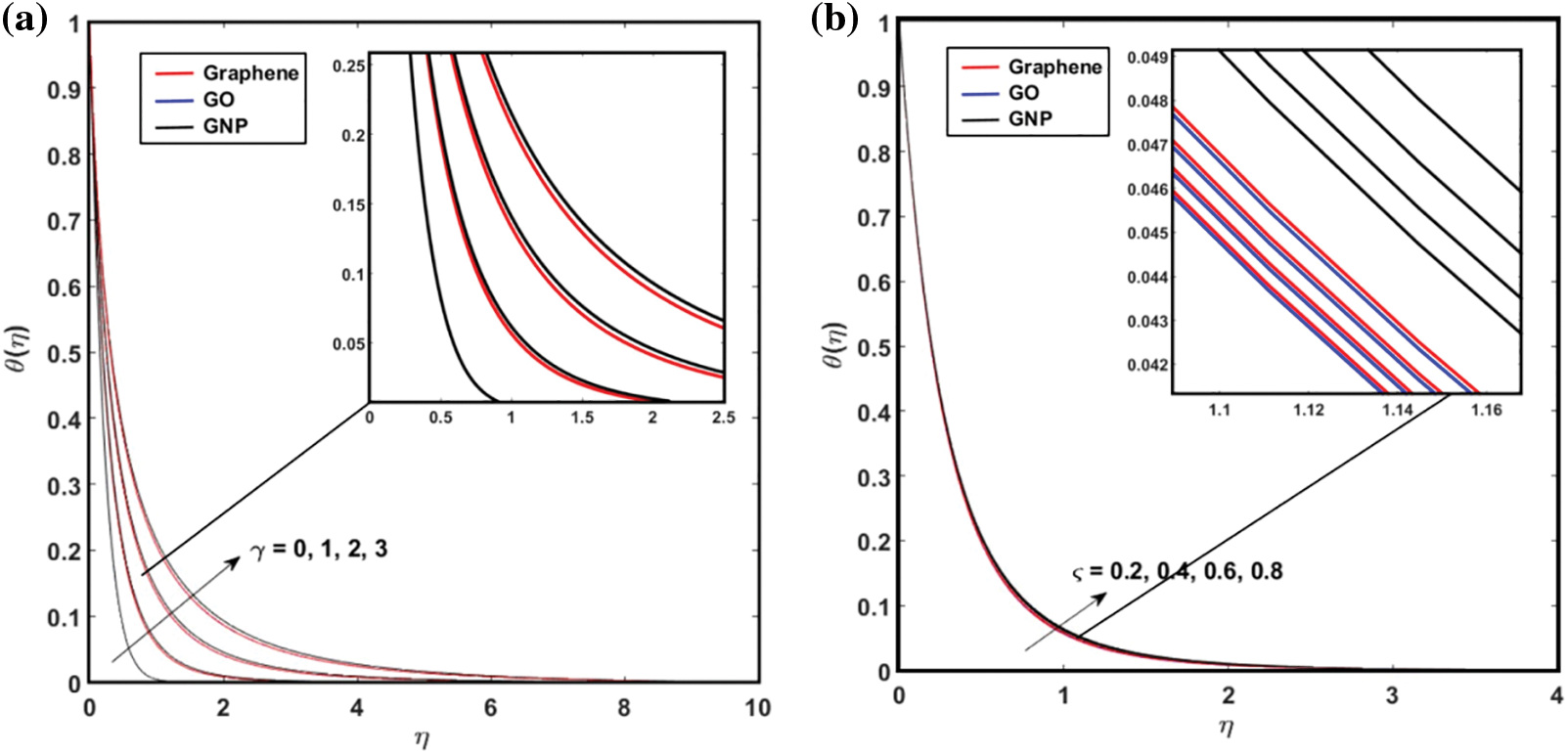
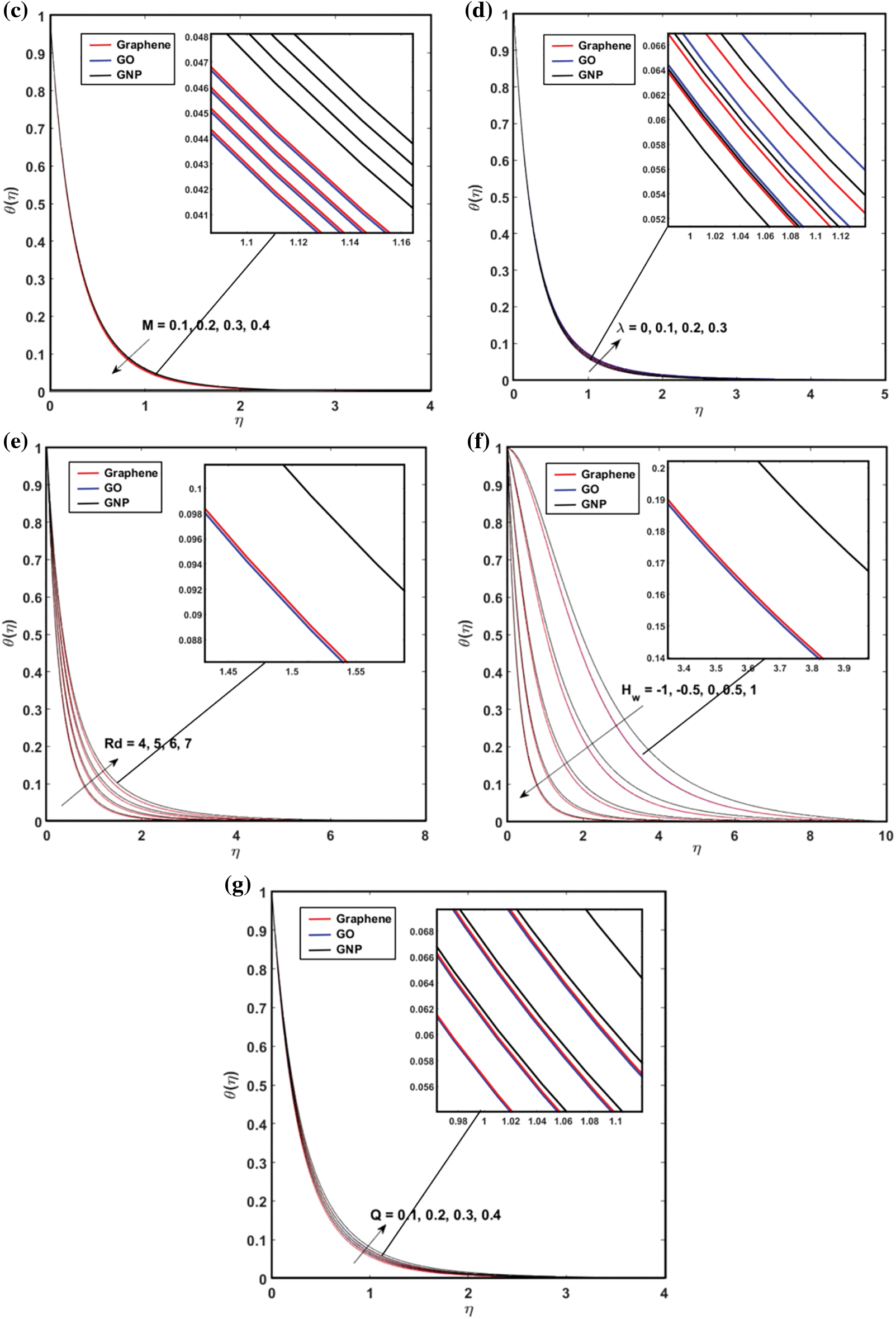
Figure 5: The repercussion of (a)
4.3 Reduced Skin Friction Value and Reduced Nusselt Number
This section particularly interprets and explains the outcomes of reduced skin friction value and reduced Nusselt number. It is important to note that negative signs for the values of reduced skin friction generated from this present study represent the magnitude in which it shows the friction is opposite to the direction of the flow. The impacts of
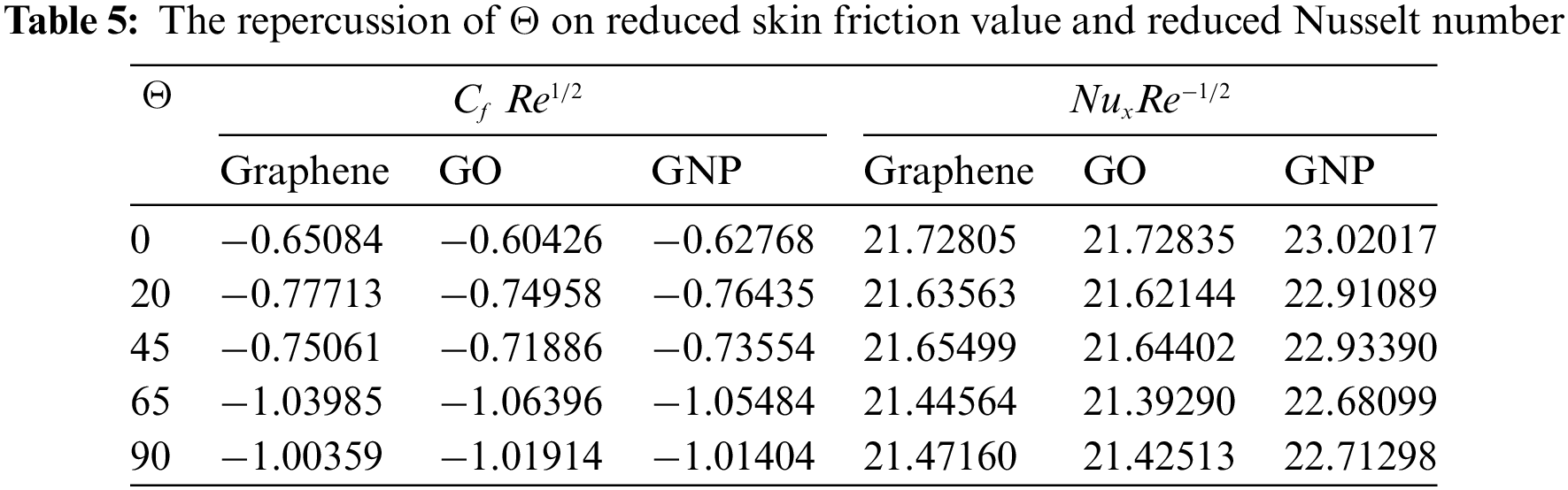
The impact of value variations of
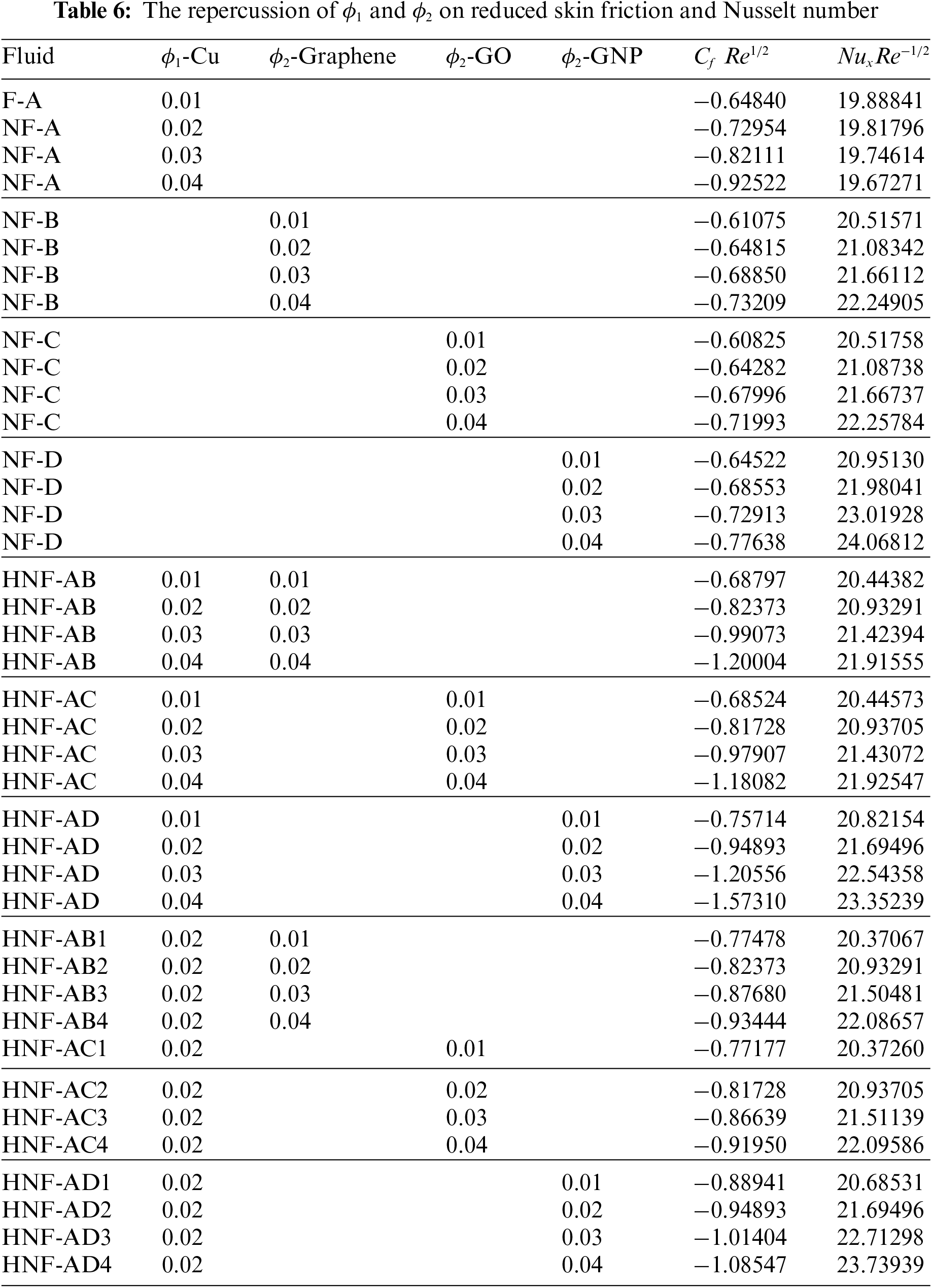
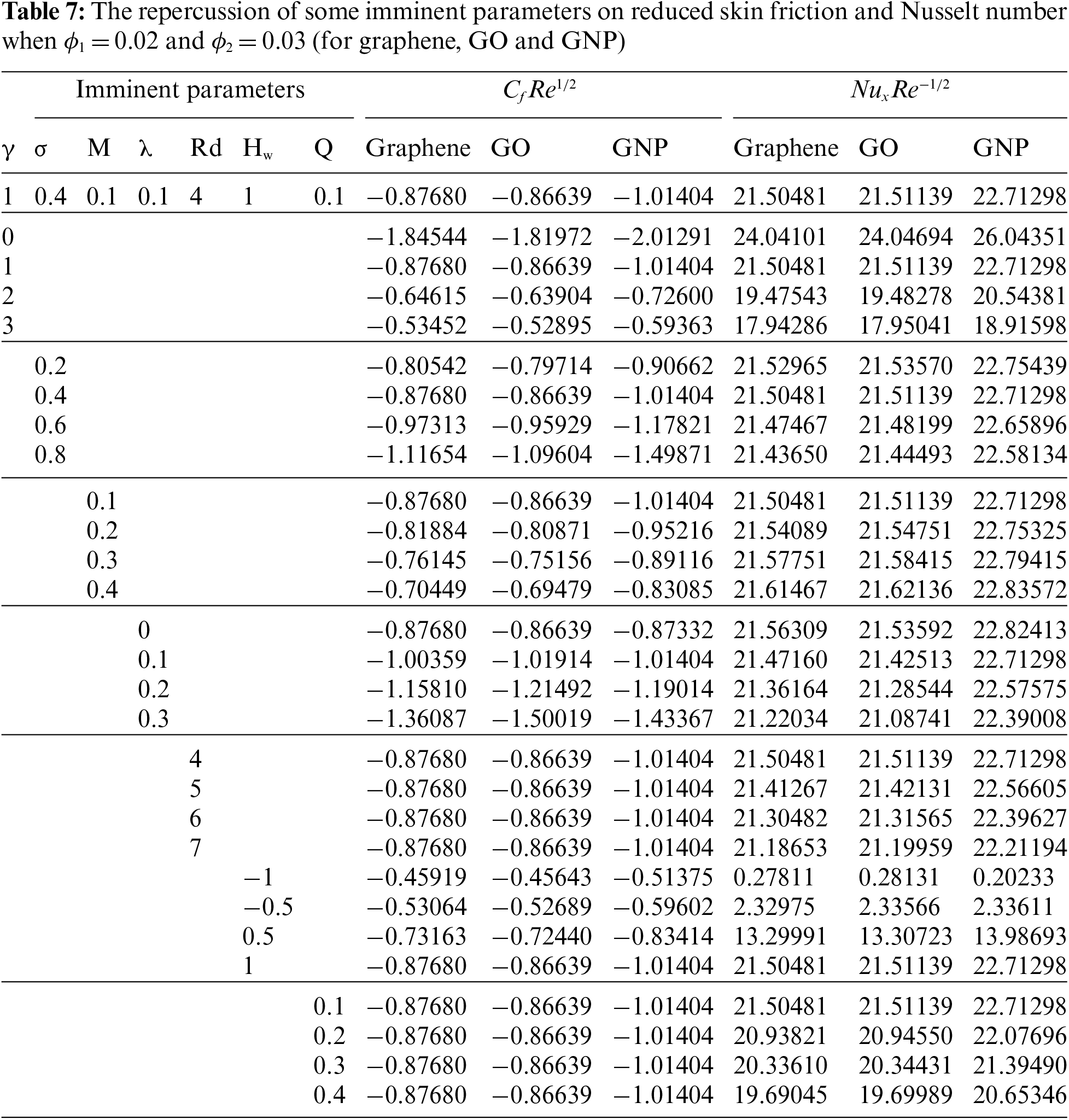
Table 7 displays the impacts of the parameters of
This study examines the effects of thermal radiation and heating sources on non-Newtonian Sutterby hybrid nanofluids consisting of various types of graphene, GO, and GNP with Cu-blood over a slanted permeable cylinder. Initially, the governing PDEs of the fluid model are transformed into nonlinear ordinary DEs using analogous transformational terms. Subsequently, they are addressed with the bvp4c scheme in MATLAB to obtain numerical solutions. The effects of other pertinent parameters on the Sutterby non-Newtonian blood nanofluids are also assessed and presented in figures and tables. The results are as follows:
• The velocity distributions increase with increasing values of
• The temperature distributions rise for greater values of
• Cu-graphene/blood hybrid nanofluids exhibit the highest velocity but the lowest temperature distribution, while Cu-GNP/blood hybrid nanofluids show the lowest velocity and the highest temperature distributions for all values of
• Cu-GO/blood hybrid nanofluids have the greatest velocity distributions, followed by Cu-graphene/blood hybrid nanofluids, while Cu-GNP/blood hybrid nanofluids display the lowest velocity distribution for all values of
• Cu-GNP/blood hybrid nanofluids possess the maximum temperature distribution, followed by Cu-graphene/blood and Cu-GO/blood hybrid nanofluids for
• The magnitude of the reduced skin friction values is at its minimum and maximum when
• Both magnitude quantities of reduced skin friction and reduced Nusselt number increase for greater values of
• HNF-AD4 (Cu-GNP/blood hybrid nanofluid with
• Thus, GNPs (with the nanoplatelet shape factor
• The reduced skin friction value rises with higher values of
• The reduced Nusselt number increases for increasing values of M and
Several potential applications arise from these research findings. For example, guidance for evaluating occupational and public health risks related to radiation and electromagnetic field exposure can be based on blood studies in rats. Moreover, the nanoparticles selected for this study can be particularly effective in medical treatments such as cancer therapy, anti-infection measures, and drug delivery. Hence, they promise to enhance medical systems, equipment, and devices. Nevertheless, further research in this domain must address the study’s limitations and comprehensively meet industrial objectives and practical requirements.
Acknowledgement: Authors highly appreciate the contributions made by reviewers towards the final improvement of this manuscript.
Funding Statement: This research is funded by the Ministry of Higher Education, Malaysia, through the Research Fund of Fundamental Research Grant Scheme (FRGS/1/2020/STG06/UM/02/1: FP009-2020).
Author Contributions: Conceptualization, N.F.M.N.; methodology, S.N.A.G.; validation, S.N.A.G.; formal analysis, S.N.A.G.; investigation, S.N.A.G. and N.F.M.N.; data curation, S.N.A.G.; writing—original draft preparation, S.N.A.G.; writing—review and editing, N.F.M.N.; visualization, S.N.A.G.; supervision, N.F.M.N.; project administration, N.F.M.N.; funding acquisition, N.F.M.N. All authors have read and consented the finalized version of the manuscript.
Availability of Data and Materials: The present study utilizes data simulation with the numerical results as presently calculated.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Yamaguchi, H. (2008). Engineering fluid mechanics, vol. 85. Dordrecht, Netherlands: Springer Science & Business Media. [Google Scholar]
2. Choi, S. U., Eastman, J. A. (1995). Enhancing Thermal Conductivity of Fluids with Nanoparticles. Argonne National Lab (ANLArgonne, IL, USA. [Google Scholar]
3. Sarkar, J., Ghosh, P., Adil, A. (2015). A review on hybrid nanofluids: Recent research, development and applications. Renewable and Sustainable Energy Reviews, 43, 164–177. [Google Scholar]
4. Babu, J. R., Kumar, K. K., Rao, S. S. (2017). State-of-art review on hybrid nanofluids. Renewable and Sustainable Energy Reviews, 77, 551–565. [Google Scholar]
5. Manjunatha, S., Kuttan, B. A., Jayanthi, S., Chamkha, A., Gireesha, B. J. (2019). Heat transfer enhancement in the boundary layer flow of hybrid nanofluids due to variable viscosity and natural convection. Heliyon, 5(4), e01469. [Google Scholar] [PubMed]
6. Nadeem, S., Abbas, N., Malik, M. Y. (2020). Inspection of hybrid based nanofluid flow over a curved surface. Computer Methods and Programs in Biomedicine, 189, 105193. [Google Scholar] [PubMed]
7. Salah, Y., Al Mukbel, O., Sabsabi, Y., Saranya, S., Al-Mdallal, Q. M. et al. (2023). Influence of PST and PHF heating conditions on the swirl flow of Al+Mg+TiO2 ternary hybrid water-ethylene glycol based nanofluid with a rotating cone. International Journal of Thermofluids, 19, 100371. [Google Scholar]
8. Akhtar, S., Hussain, Z., Nadeem, S., Najjar, I. R., Sadoun, A. M. (2023). CFD analysis on blood flow inside a symmetric stenosed artery: Physiology of a coronary artery disease. Science Progress, 106(2). [Google Scholar]
9. McCash, L. B., Akhtar, S., Nadeem, S., Saleem, S. (2021). Entropy analysis of the peristaltic flow of hybrid nanofluid inside an elliptic duct with sinusoidally advancing boundaries. Entropy, 23(6), 732. [Google Scholar] [PubMed]
10. Tripathi, J., Vasu, B., Bég, O. A. (2021). Computational simulations of hybrid mediated nano-hemodynamics (Ag-Au/Blood) through an irregular symmetric stenosis. Computers in Biology and Medicine, 130, 104213. [Google Scholar] [PubMed]
11. Sharma, B. K., Kumawat, C., Vafai, K. (2022). Computational biomedical simulations of hybrid nanoparticles (Au-Al2O3/blood-mediated) transport in a stenosed and aneurysmal curved artery with heat and mass transfer: Hematocrit dependent viscosity approach. Chemical Physics Letters, 800, 139666. [Google Scholar]
12. Akram, J., Akbar, N. S., Tripathi, D. (2020). Blood-based graphene oxide nanofluid flow through capillary in the presence of electromagnetic fields: A sutterby fluid model. Microvascular Research, 132, 104062. [Google Scholar] [PubMed]
13. Waqas, H., Farooq, U., Alghamdi, M., Muhammad, T. (2022). Significance of melting process in magnetized transport of hybrid nanofluids: A three-dimensional model. Alexandria Engineering Journal, 61(5), 3949–3957. [Google Scholar]
14. Al-Mughanam, T., Almaneea, A. (2022). Numerical study on thermal efficiencies in mono, hybrid and tri-nano sutterby fluids. International Communications in Heat and Mass Transfer, 138, 106348. [Google Scholar]
15. Bouslimi, J., Alkathiri, A. A., Alharbi, A. N., Jamshed, W., Eid, M. R. et al. (2022). Dynamics of convective slippery constraints on hybrid radiative sutterby nanofluid flow by galerkin finite element simulation. Nanotechnology Reviews, 11(1), 1219–1236. [Google Scholar]
16. Jamshed, W., Safdar, R., Rehman, Z., Lashin, M. M., Ehab, M. et al. (2022). Computational technique of thermal comparative examination of Cu and Au nanoparticles suspended in sodium alginate as Sutterby nanofluid via extending PTSC surface. Journal of Applied Biomaterials & Functional Materials, 20. [Google Scholar]
17. Tiwari, R. K., Das, M. K. (2007). Heat transfer augmentation in a two-sided lid-driven differentially heated square cavity utilizing nanofluids. International Journal of Heat and Mass Transfer, 50(9–10), 2002–2018. [Google Scholar]
18. Dinarvand, S., Rostami, M. N. (2019). Mixed convection of a Cu-Ag/water hybrid nanofluid along a vertical porous cylinder via modified Tiwari-Das model. Journal of Theoretical and Applied Mechanics, 49(2), 149–169. [Google Scholar]
19. Dinarvand, S., Rostami, M. N., Pop, I. (2019). A novel hybridity model for TiO2-CuO/water hybrid nanofluid flow over a static/moving wedge or corner. Scientific Reports, 9(1), 16290. [Google Scholar] [PubMed]
20. Ramzan, M., Shahmir, N., Ghazwani, H. A. S. (2022). Hybrid nanofluid flow comprising spherical shapedparticles with hall current and irreversibility analysis: An application of solar radiation. Waves in Random and Complex Media. https://doi.org/10.1080/17455030.2022.2123571 [Google Scholar] [CrossRef]
21. Alwawi, F. A., Al Faqih, F. M., Swalmeh, M. Z., Ibrahim, M. A. H. (2022). Combined convective energy transmission performance of Williamson hybrid nanofluid over a cylindrical shape with magnetic and radiation impressions. Mathematics, 10(17), 3191. [Google Scholar]
22. Saranya, S., Duraihem, F. Z., Isaac Lare, A. L., Al-Mdallal, Q. M. (2023). Quartic autocatalysis on horizontal surfaces with an asymmetric concentration: Water-based ternary-hybrid nanofluid carrying titania, copper, and alumina nanoparticles. Physica Scripta, 98(7), 075214. [Google Scholar]
23. Arshad, A., Jabbal, M., Yan, Y., Reay, D. (2019). A review on graphene based nanofluids: Preparation, characterization and applications. Journal of Molecular Liquids, 279, 444–484. [Google Scholar]
24. Smaisim, G. F., Abed, A. M., Al-Madhhachi, H., Hadrawi, S. K., Al-Khateeb, H. M. M. et al. (2023). Graphene-based important carbon structures and nanomaterials for energy storage applications as chemical capacitors and supercapacitor electrodes: A review. BioNanoScience, 13(1), 219–248. [Google Scholar]
25. Shafiee, A., Iravani, S., Varma, R. S. (2022). Graphene and graphene oxide with anticancer applications: Challenges and future perspectives. MedComm, 3(1), e118. [Google Scholar] [PubMed]
26. Mehrali, M., Sadeghinezhad, E., Akhiani, A. R., Latibari, S. T., Metselaar, H. S. C. et al. (2017). Heat transfer and entropy generation analysis of hybrid graphene/Fe3O4 ferro-nanofluid flow under the influence of a magnetic field. Powder Technology, 308, 149–157. [Google Scholar]
27. Sadeghinezhad, E., Mehrali, M., Saidur, R., Mehrali, M., Latibari, S. T. et al. (2016). A comprehensive review on graphene nanofluids: Recent research, development and applications. Energy Conversion and Management, 111, 466–487. [Google Scholar]
28. Purbia, D., Khandelwal, A., Kumar, A., Sharma, A. K. (2019). Graphene-water nanofluid in heat exchanger: Mathematical modelling, simulation and economic evaluation. International Communications in Heat and Mass Transfer, 108, 104327. [Google Scholar]
29. Ghani, S. N. A., Yarmand, H., Noor, N. F. M. (2023). Assorted graphene-based nanofluid flows near a reversed stagnation point over an inclined permeable cylinder. Proceedings of the National Academy of Sciences, India Section A: Physical Sciences, 93(1), 43–55. [Google Scholar]
30. Xiao, W., Zhai, X., Ma, P., Fan, T., Li, X. (2018). Numerical study on the thermal behavior of graphene nanoplatelets/epoxy composites. Results in Physics, 9, 673–679. [Google Scholar]
31. Massoudi, M. D., Ben Hamida, M. B., Almeshaal, M. A. (2021). Free convection and thermal radiation of nanofluid inside nonagon inclined cavity containing a porous medium influenced by magnetic field with variable direction in the presence of uniform heat generation/absorption. International Journal of Numerical Methods for Heat & Fluid Flow, 31(3), 933–958. [Google Scholar]
32. Kierzenka, J., Shampine, L. F. (2001). A BVP solver based on residual control and the maltab PSE. ACM Transactions on Mathematical Software, 27(3), 299–316. [Google Scholar]
33. Shampine, L. F., Kierzenka, J., Reichelt, M. W. (2000). Solving boundary value problems for ordinary differential equations in MATLAB with bvp4c. Tutorial Notes, 2000, 1–27. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF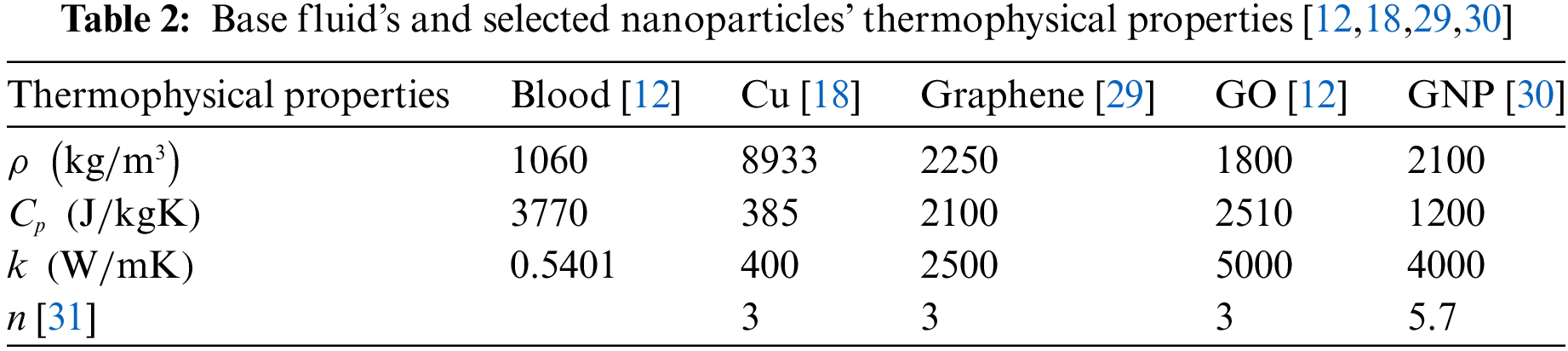
 Downloads
Downloads
 Citation Tools
Citation Tools