Topology Optimization of Metamaterial Microstructures for Negative Poisson’s Ratio under Large Deformation Using a Gradient-Free Method

1  Introduction

Metamaterials [1,2] are artificial materials with unique and unusual properties not commonly found in natural materials. These unusual properties mainly arise from their microstructure geometry. Negative Poisson’s ratio (NPR) or auxetic materials [3–5] belong to the class of metamaterials with a distinct mechanical property that allows them to expand laterally when stretched, unlike most other materials that contract laterally under similar conditions. NPR metamaterials possess mechanical properties that are suitable for various applications, such as deformation control [6,7], vibration and noise reduction [8,9], energy absorption [10–12], etc.

With the rapid development of additive manufacturing and other advanced techniques, fabricating metamaterials, such as NPR materials [13–15], has become more convenient and accessible. Additive manufacturing enables precise and customizable fabrication of complex geometries [16], which is essential for the design and production of metamaterials. This increased design freedom allows for the development of new attainable metamaterials that are tailored to specific applications.

Topology optimization [17,18] is a powerful design technique that can optimize material distribution and structural performance while considering multiple constraints. This field has seen rapid development over the past three decades since Bendsøe and Kikuchi’s seminal work [19] on structural topology optimization using homogenization. Today, various methods are widely adopted in the topology optimization community, such as the Solid Isotropic Material with Penalization (SIMP) method [20,21], the level set method [22,23], and the evolutionary structural optimization (ESO) method [24,25]. Over time, topology optimization has expanded its focus from developing basic methods for structural mechanical design [26] problems to addressing other challenging design problems in different fields, including the metamaterial design problem. In the case of designing metamaterials, optimization is employed to determine the optimized topology of the periodic unit cell microstructure. Currently, research on metamaterial design covers a wide range of material properties, such as elasticity [27,28], viscoelasticity [29], extreme thermal expansion [30], photonic bandgap [31], thermal exchange [32], phononic bandgap [33–35], and negative permeability [36], etc. Also, several methods [37–41] are developed to design and distribute metamaterial microstructures in multiscale structures.

In recent years, there has been growing interest in the design of NPR materials using topology optimization. Different methods and formulations have been developed to achieve NPR microstructures, showing typical geometrical features such as re-entrance or chirality. For example, Andreassen et al. [13] used the SIMP method to investigate the design of 3D isotropic elastic microstructures with NPR, incorporating a robustness formulation to ensure a minimum size constraint. Wang et al. [42] employed the parametric level set method to design the material microstructures that attain a negative Poisson’s ratio as prescribed by an effective stress-strain matrix. Zheng et al. [43] developed optimization strategies using the bi-directional evolutionary structural optimization method to obtain orthogonal materials with auxetic properties. By combining the independent point-wise density interpolation (iPDI) model [44] with a bi-material interpolation scheme, Zhang et al. [45] studied the design of chiral auxetic metamaterials. Utilizing isogeometric analysis, Gao et al. [46] investigated the design of multi-material NPR microstructures in both 2D and 3D settings. De Lima et al. [47] achieved auxetic microstructures through compliant mechanisms topological design at the microscale using polygonal finite element meshes. Wu et al. [48] explored robust topological design of NPR metamaterial designs under hybrid uncertainties. Besides the NPR behavior itself, studies [49] have also been carried out to optimize the energy absorption of NPR metamaterials.

As pointed out in [50], when metamaterials designed under the assumption of infinitesimal strain are subjected to large stretches, their NPR may rapidly attenuate or even become positive. Clausen and colleagues [50] designed 2D material microstructure topologies with analytical sensitivities to attain programmable negative Poisson’s ratios in the context of finite strain design. Their design strategy also includes a parameter optimization procedure for fabricating microstructures with uniform width members using 3D printing. Wang [51] extended this method by considering the hyperelastic constitutive behavior of the base material, resulting in designs for three-dimensional programmable negative Poisson’s ratio microstructures under finite strain. Based on nonlinear homogenization, Zhang et al. [52] proposed a computational framework for designing auxetic metamaterials composed of single- or multi-phase hyperelastic constituents at finite deformations using topology optimization. The above studies rely on sensitivity analysis and gradient-based algorithms to update the design. However, it may be challenging for engineers to derive the sensitivities when considering geometry or other nonlinearities. With prescribed and fixed auxetic microstructure topology configurations, researchers [53,54] have also explored genetic algorithms to study shape or size designs of the microstructures.

The present paper introduces a gradient-free topology optimization strategy for generating mechanical metamaterial microstructures. These materials are designed to achieve the desired NPR when subjected to up to 20% strain in a uniaxial loading case. The current method utilizes the finite element method to model and design a periodic representative unit cell. It considers geometric nonlinearity and incorporates periodic boundary conditions. The metamaterial microstructure topology is described with the material-field series expansion (MFSE) method [55], which can greatly reduce the number of required design variables by assuming a spatial correlation in the material distribution. This enables the adoption of a series of Kriging surrogate models to approximately solve the original optimization problem [56]. To address the large deformation NPR metamaterial design problem with this method, a two-step optimization strategy is suggested. Firstly, the homogenization method is employed to generate preliminary NPR metamaterial designs under the small deformation assumption. In the second step, these preliminary designs will undergo further optimization in order to achieve the desired negative Poisson’s ratio when subjected to large deformations. The focus of the second optimization stage is on minimizing deviations of the design’s Poisson’s ratio from a targeted value. With this two-stage optimization strategy and the Kriging surrogate model-based solution technique, we have successfully obtained a group of metamaterials that can maintain different targeted NPRs within the range of [−0.8, −0.1] under 20% strain in uniaxial tension. Furthermore, several optimized microstructures were fabricated and their effective Poisson’s ratio was measured through experiments. The experimental results show good consistency with our numerical results.

The present paper is organized as follows: Section 2 introduces the geometry nonlinear finite element analysis of the metamaterial unit cell. Section 3 presents the MFSE method, the suggested two-step optimization strategy, and the optimization problems’ solution techniques. In Section 4, numerical examples are given. The conducted uniaxial tensile experiment is introduced in Section 5. Finally, conclusions are drawn.

2  The Finite Element Analysis of the NPR Metamaterial Unit Cell with Geometry Nonlinearity under Large Deformation

Our study focuses on the design of metamaterials with periodic microstructures that exhibit 1/4 geometry symmetries. Specifically, we design the metamaterial’s effective Poisson’s ratio μ12E under large deformation, which is determined as the negative ratio of the unit cell’s y-directional engineering strain to its applied x-directional engineering strain.

To evaluate this effective Poisson’s ratio, we employ finite element analysis on the square unit cell’s microstructure, taking into account periodic boundary conditions and uniaxial stretching. Considering the symmetries of the unit cell, these boundary conditions ensure that during deformation, the unit cell’s right edge remains vertical and the top edge remains horizontal. The specific applied boundary conditions are as follows: the displacement in the x-axis (i.e., u) on the left edge of the unit cell is set to zero, displacement in the y-axis (i.e., v) on the bottom edge is also set to zero, v on all the top edge nodes are constrained to one unknown value to be solved for, and a prescribed u¯ is applied on all the nodes on the right edge. These boundary conditions are illustrated in Fig. 1. Denoting the edge length of the square unit cell by L, and the metamaterial’s effective Poisson’s ratio μ12E is expressed as

μ12E=−ε2ε1=−(vtop/L)(u¯right/L)=−vtopu¯right.(1)

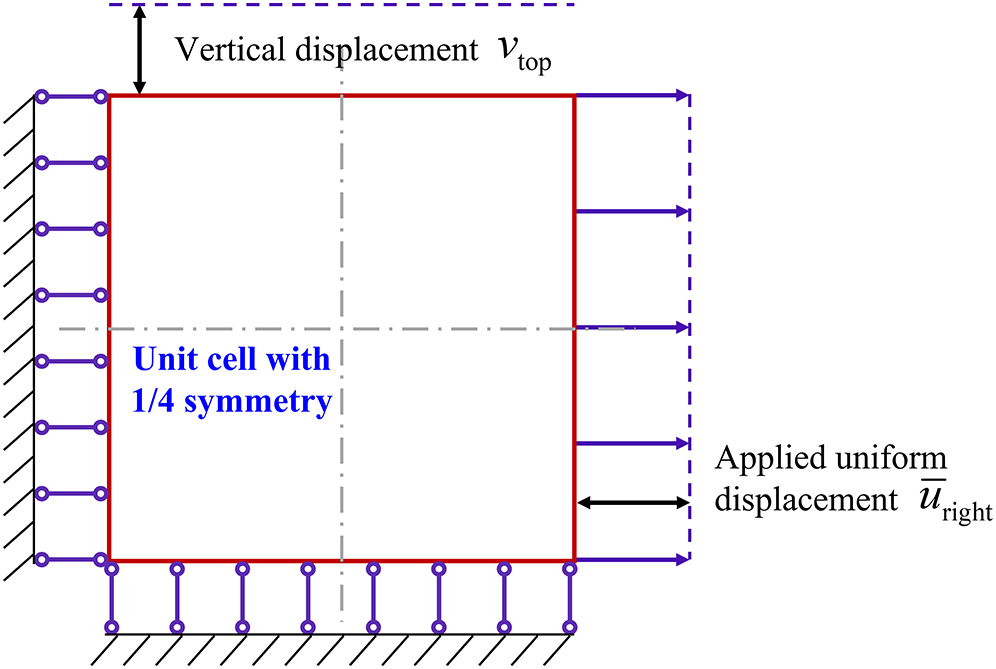
Figure 1: Schematic illustration of the studied unit cell’s boundary conditions

The finite element analysis takes into account the geometry nonlinearity due to significant deformation. Once the quantities from time 0 to time t have been calculated, the virtual work principal can be built on the deformed configuration at time t+Δt as

∫t+ΔtVτijt+Δtδt+Δteijt+ΔtdV=∫t+ΔtVfit+Δt δ uit+Δt dV+∫t+ΔtStit+Δtδuit+ΔtdS,(2)

where the superscript t+Δt refers to quantities at this time, the subscript t+Δt denotes the configuration at which time is referenced, τijt+Δt is the Cauchy stress, ui is the incremental displacement defined as ui=uit+Δt−uit , δui stands for the virtual displacement and δt+Δteij represents the virtual infinitesimally small strain computed from δui, fit+Δt and tit+Δt are the applied body force and surface traction, respectively.

To account for the unknown configuration at time t+Δt, we utilize the total Lagrange formulation [57]. This involves transforming Eq. (2) into expressions that reference the configuration at time 0. By using linearization and finite element discretization, the following typical Newton-Raphson iterative formulations can be derived as

K0tΔU(k)=F0t+Δtext−F0t+Δtintk−1,(3)

in which K0trepresents the tangent stiffness matrix, ΔU(k) is the incremental structural displacement in iteration k from time t to time t+Δt so that the nodal displacement can be expressed as Ukt+Δt = Uk−1t+Δt+ΔU(k)(U0t+Δt=Ut), F0t+Δtext is the external nodal force, and F0t+Δtintk−1 is the internal nodal force computed with U k−1t+Δt. The iterative solution procedure in Eq. (3) is repeated until internal and external nodal forces are equivalent, at this point, the displacement Ut+Δt is obtained.

3  The Design Methodology of the Metamaterial Microstructures with Desired NPR under Large Deformation

This section introduces the unit cell’s microstructural topology description method and the interpolation model for material properties, both of which are based on the material-field series-expansion (MFSE) method [55]. The suggested optimization formulation and two-stage solution strategy are discussed in detail thereafter.

3.1 The Metamaterial Unit Cell Microstructural Topology Description with the Material-Field Series- Expansion Method

Our study utilizes the MFSE method for topology optimization, which can efficiently describe the microstructural topologies using only a few design variables. A brief introduction to this method is given here for completeness.

The MFSE method uses a bounded material field function φ(x) whose value is between [0,1] to describe the base material’s distribution within the unit cell. The definition of the microstructural topology is as follows:

x∈{Ωsolid,if  0≤φ(x)≤1,Ωvoid,if  −1≤φ(x)<0,(4)

where x is a spatial point within the design domain, Ωsolid and Ωvoid respectively denote the solid and void phase.

This method assumes a correlation between the material field values at any two points within the design domain by specifying a correlation length lc. The exponential form correlation formulation adopted in this study reads.

c(φ(xa), φ(xb))=exp⁡(−||xa−xb||2lc2),(5)

where xa and xb are two spatial points, and the operator ||⋅|| computes the Euclidean distance between these two points. Eq. (5) indicates that the correlation between material field functions on two points depends on their distance from each other. When the distance is zero, the correlation equals one; as it approaches infinity, the correlation approaches zero. Based on Eq. (5), the MFSE method further distributes a certain number of material-field points x1, x2, ⋯, xNpt within the design domain and builds the correlation matrix C whose expression reads

C=[c(φ(x1), φ(x1))c(φ(x1), φ(x2))⋯c(φ(x1), φ(xNpt))c(φ(x2), φ(x1))c(φ(x2), φ(x2))⋯c(φ(x2), φ(xNpt))⋮⋮⋱⋮c(φ(xNpt), φ(x1))c(φ(xNpt), φ(x2))⋯c(φ(xNpt), φ(xNpt))].(6)

It should be noted that when designing periodic unit cell microstructures, Eq. (5) should also consider the periodic arrangement of neighboring unit cells to compute the minimum distance between the material-field points, as illustrated in Fig. 2.

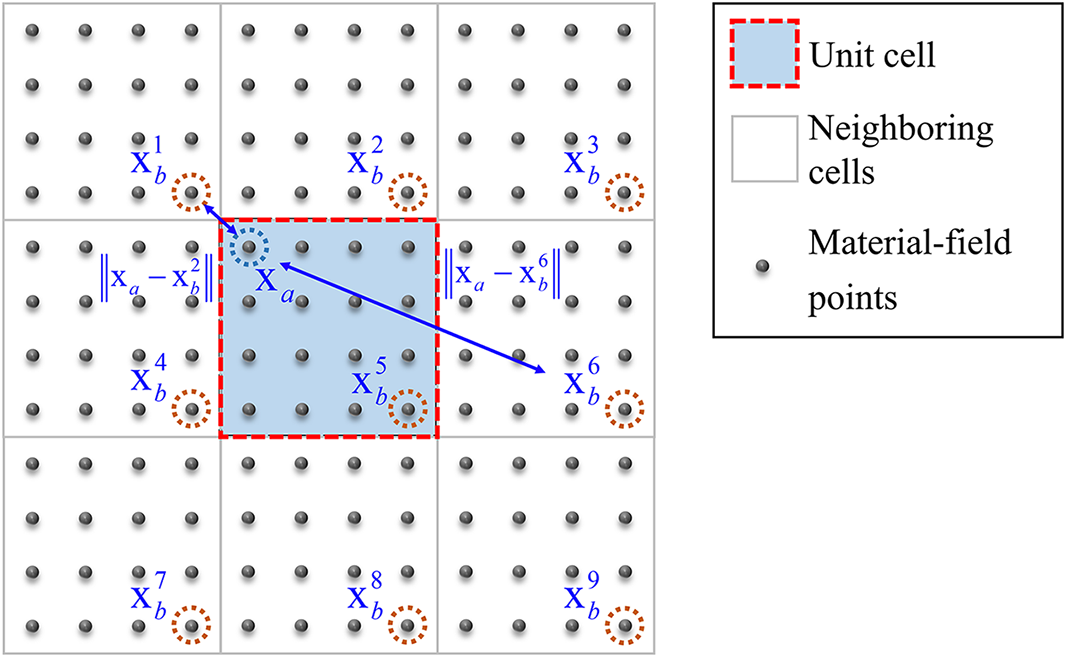
Figure 2: The computation of correlation matrix entries for periodic unit cells based on the material-field points

Then, by employing the series expansion technique for bounded fields with correlation [55], a material field function φ(x) with correlation length lc can be expressed with the eigenvalues λk and eigenvectors ψk of the correlation matrix C as

φ(x)=∑k=1Npt(ηk1λkψkTCd(x)),(7)

in which Npt is the number of the material-field points, and Cd(x) is a vector defined as

Cd(x)=[c(φ(x), φ(x1)), c(φ(x), φ(x2)), ⋯, c(φ(x), φ(xNpt))]T,(8)

whose entries are the correlation (Eq. (5)) between the point x and all the material field points. It should also be noted that the eigenvalue analysis of the matrix C is only required once during the optimization process.

Eq. can be rearranged in descending order of eigenvalues and truncated accordingly to reduce the number of parameters needed to describe the field function. This process neglects the contribution corresponding to small eigenvalues by keeping the first M largest eigenvalues to fulfill a criterion with given error ε, i.e., (∑m=1Mλm)/(∑k=1Nptλk)≥1−ε. Once truncated, the material field function can be expressed as

φ(x)≈∑k=1M(ηk1λkψkTCd(x)).(9)

The MFSE method utilizes the expansion coefficients ηk in Eq. (9) as design variables. Fig. 3 illustrates the composition of eigenvectors of a correlation matrix to describe a typical microstructure topology. The expression in Eq. (9) greatly reduces the number of design variables while keeping the capability to describe relatively complex structural topologies. Reducing the number of design variables is vital for adopting gradient-free optimization solution methods adopted in this study.

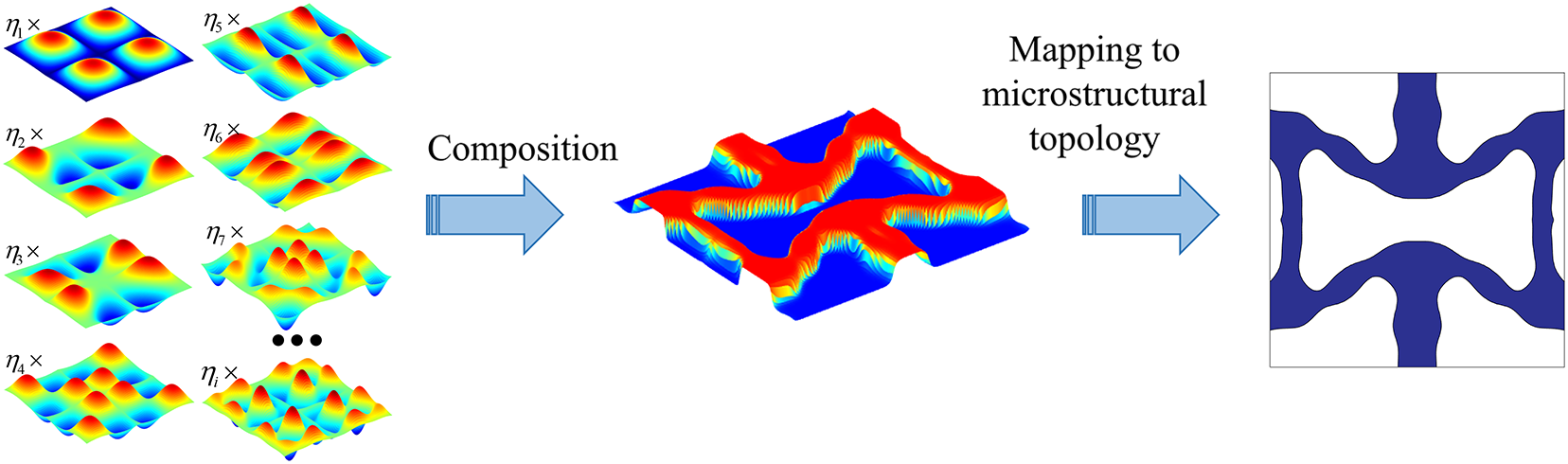
Figure 3: Schematic illustration of the topological description of a unit cell microstructure using the MFSE method

Although the MFSE method provides a clear boundary description, it differs from the level set method in several ways. The most obvious difference is that the MFSE method considers material distribution correlation and uses basis function coefficients as design variables, while the level set method relies on boundary evolution.

3.2 The Two-Stage Topology Optimization Strategy for Metamaterials with Desired NPR under Large Deformation

Describing the unit cell microstructural topologies using the MFSE method, the material properties interpolation scheme within the microstructure reads.

Ee=Emin+(1+φ~(xe)2)p(E0−Emin),   e=1,…,ne,(10)

where Emin is a small positive value to avoid singularity in the finite element analysis, E0 and Ee represent Young’s modulus of the base material and that of element e respectively, p is the penalty parameter (p=3 in this study), xe denotes the center of element e, and φ~(xe) is the projected material field function used to reduce the amount of non-solid/non-void material. The adopted projection formulation [58] reads

φ~(x)={φ(x)e−β+1−e−βφ(x),if  φ(x)≥0,φ(x)e−β−1+eβφ(x),if  φ(x)<0,(11)

in which the parameter β controls the steepness of the projection function.

To obtain metamaterials with a desired NPR under large deformation, a two-stage gradient-free topology optimization strategy is proposed. This optimization strategy builds upon Latin super-cubic sampling and the series Kriging surrogate model optimization solution techniques [56].

As the optimized NPR microstructure is unknown, we typically start our search with initial configurations that have a positive effective Poisson’s ratio. For example, microstructures with uniform base material distribution. However, we observed that directly minimizing the value of effective Poisson’s ratio through sampling and surrogate models often results in local minima with discontinuous base material distribution and near-zero Poisson’s ratio values. To overcome this, we suggest a two-stage optimization framework. In Stage-I, we adopt an objective function of deviation from a prescribed stress-strain matrix to induce a preliminary NPR design. Then in Stage-II, this preliminary design is elaborately designed while considering the objective function of effective Poisson’s ratio under large deformation.

Optimization Stage I: this stage aims to search the design space for a preliminary NPR microstructural design under infinitesimal strain. In this stage, topology optimization is achieved by minimizing the deviation of the homogenized stress-strain matrix from a given one expressed with a specific negative Poisson’s ratio. This initial design then serves as a starting point for optimizing the metamaterial microstructure under large deformation in optimization Stage II. The optimization formulation for this stage can be expressed using the MFSE method as

minηf1(DijH(φ~(η), χq))=(D11H−D11ref)2+(D12H−D12ref)2+(D21H−D21ref)2+(D22H−D22ref)2s.t.Kχq=Fq,  q=1,2,3, vol(φ~(η))=∑e=1ne(1+φ~(xe,η)2Ve)VD−V¯frac1≤0,−1≤φ(xj, η)≤1,  j=1,2, ⋯, Npt,(12)

where the design variable vector, consisting of the expansion coefficients in Eq. (9), is denoted by η. The first group of constraints represents the equilibrium equations corresponding to the three load cases applied in the numerical homogenization method, followed by the microstructural volume constraint and upper/lower bound constraints on the material field points. It should be noted that only the first 2×2 entries in the homogenized stress-strain matrix are considered in objective function f1, since they sufficiently describe the NPR under small deformation for the considered orthogonal metamaterial.

Optimization Stage II: This stage builds upon the preliminary designs obtained in optimization Stage I. It specifically considers large deformation and aims to achieve a desired NPR. The optimization formulation for this stage is as follows:

minη  f2( tiμ12E(φ˜(η), tiU))=∑ti∈Tctiw( tiμ12E−μ12ref)2s.t.    tiR=F0ti ext−F0ti in(φ˜(η), tiU)=0,         g(DijH(φ˜(η)))=D¯lower−min(D11H, D22H)≤0,         vol(φ˜(η))=∑e=1ne(1+φ˜(xe, η)2Ve)VD−V¯frac2≤0,         −1≤φ(xj, η)≤1, j=1, 2, ⋯, Npt.(13)

In Eq. (13), Tc represents a set of selected time steps corresponding to different applied uniaxial strains. The objective function f2 aims to minimize the deviation between the design’s effective Poisson’s ratio (calculated with Eq. (1)) and a desired value μ12ref, based on displacements evaluated on deformed configurations in set Tc with weights wti. The first group of constraints denotes the equilibrium equations at different time steps. As will be shown in numerical Example 4.1 that the minimum member size in the microstructure affects the achievable NPR. Thus, the second constraint indirectly controls the minimum member size in the metamaterial microstructure by setting a lower limit on diagonal elements of the homogenized stress-strain matrix. It is important to note that we do not mean to measure or constrain the stiffness of the metamaterial; rather, this constraint merely serves as a means to impose a size control using the MFSE method. To minimize the occurrence of nonconvergence in the nonlinear finite element analysis due to mesh distortion, elements with material field values of −1 (i.e., void phase) are deleted from the finite element model during optimization process.

The solution of both topology optimization stages involves transforming the optimization formulations Eqs. (12) and (13) into unconstrained optimization formulations using the penalty method, i.e., minηf(η)+∑i=1mλimax(gi(η),0), where f(η) denotes the objective function, gi(η) represent the inequality constraints, λi are the penalty parameters. Then, the unconstrained optimization problem is solved by constructing and solving a series of Kriging surrogate models within sub-domains of the design space [56]. To begin this process, the first sub-optimization problem is to solve the Kriging model constructed within the sub-domain centered at the initial design η0 using sampling and the EI criterion. This yields an updated design η1. The second subdomain is then chosen to be centered at η1, and the constructed sub-optimization therein further yields an updated design η2. This procedure continues until reaching a maximum number of allowed sub-optimizations as shown in Fig. 4.

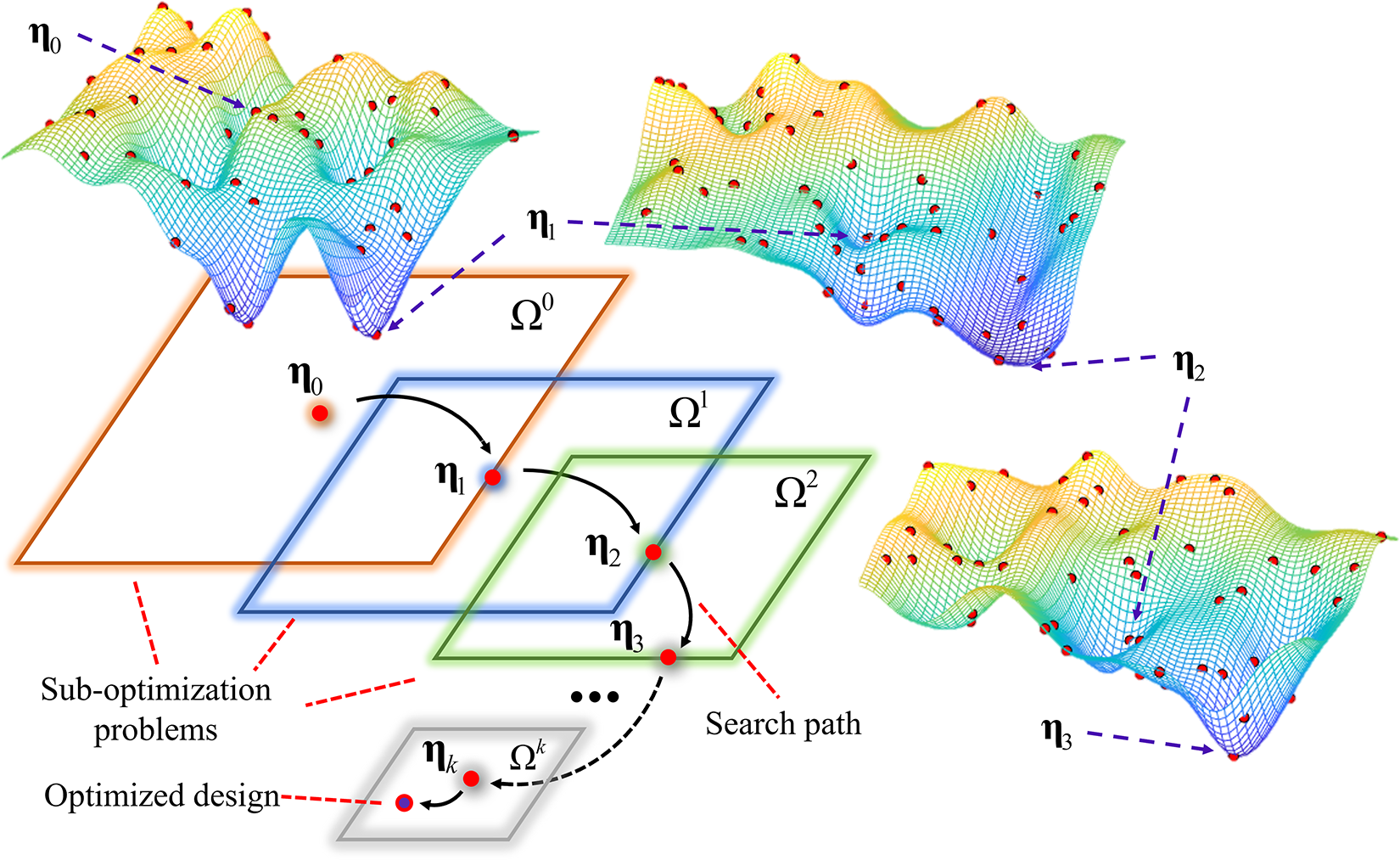
Figure 4: Schematic illustration of the Kriging-based optimization solution technique

The two-stage metamaterial microstructural topology optimization flowchart for achieving a targeted negative Poisson’s ratio under large deformation is depicted in Fig. 5.

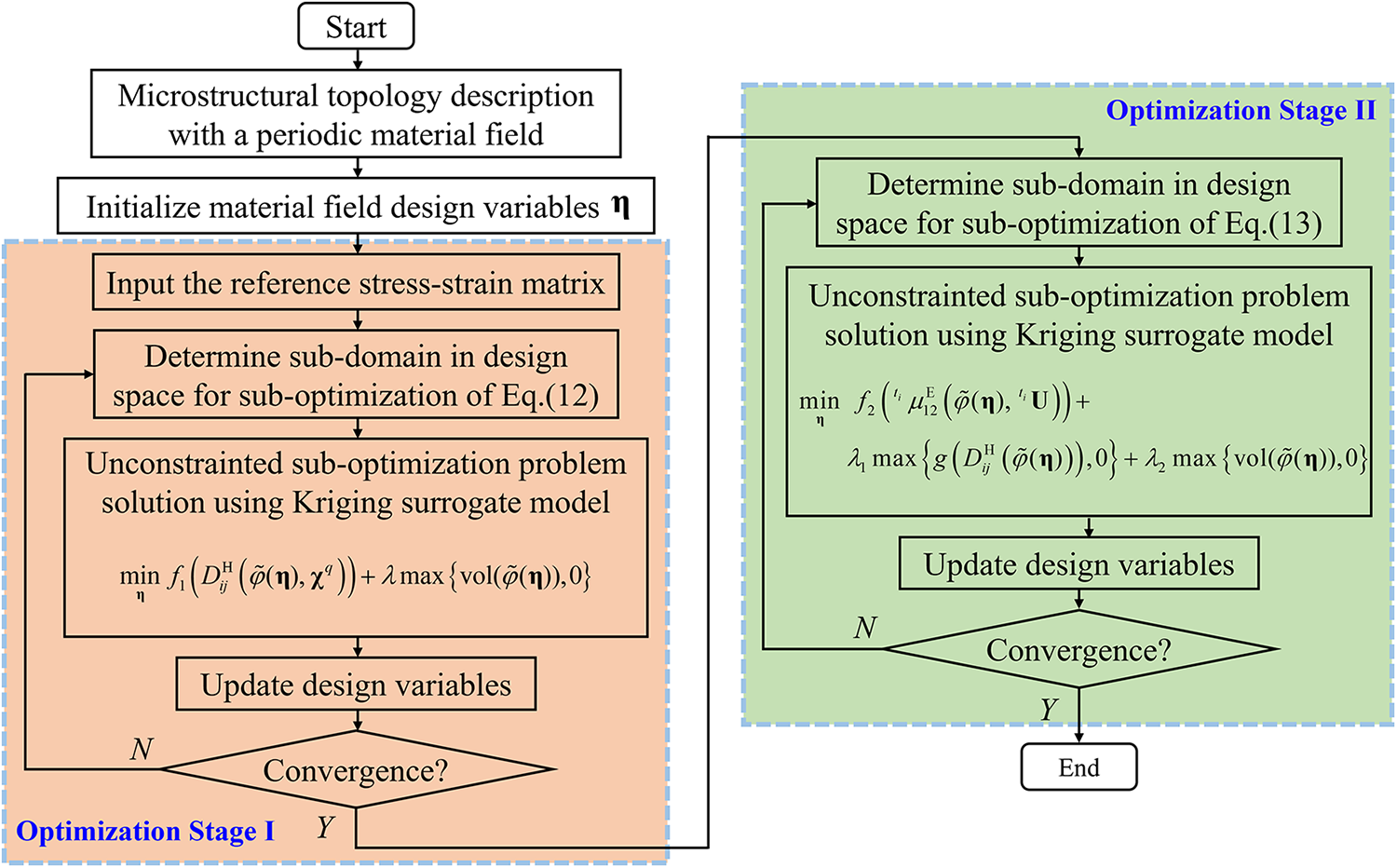
Figure 5: The flowchart of the two-stage NPR metamaterial topology optimization strategy

The two-stage optimization method in this paper is based on Kriging surrogate models with sampling. In Stage I, a linear finite element procedure is needed for each sample, while in Stage II, a non-linear finite element procedure that takes into account geometry nonlinearity is required for each sample. The efficiency of the two-stage method depends on the number of sub-optimization problems in the series Kriging model and the number of samples in each sub-problem.

Although a number of samples are needed in the present method, it does not require the sensitivity information which may be non-trivial to derive for the considered non-linear design problem. In addition, the optimization efficiency can be improved by sampling in a parallel manner.

4  Numerical Examples

This section presents numerical examples, with the focus on the mechanism of geometry nonlinearity and the design of metamaterial with 1/4 geometry symmetrical microstructure. During the design process, we adopt a linear elastic material constitutive model and assume a Young’s modulus of 1 and a Poisson’s ratio of 0.3 for the base material composing these microstructures. For nonlinear finite element analysis, an entire unit cell with an edge length of 70 is modeled. It is noted that when considering only geometry nonlinearity, the edge length does not affect the optimization process. The unit cell is discretized using 140 by 140 plane stress elements. Due to the symmetry, only one-fourth of the unit cell’s microstructure is described using MFSE method, by uniformly distributing 35 by 35 material-field points therein. According to [55], we set the correlation length as 0.3 times the unit cell length. The material field function expansion is truncated at the first 60 terms, resulting in a total number of design variables being equal to 60 in both optimization stages. The projection parameter β is gradually increased from 0 up to a maximum value of 40 by increasing it by 1.5 for each Kriging model used in the series surrogate model solution technique. In optimization Stages I and II, the maximum number optimization sub-problem is set to 16 and 24, respectively. The number of samples is set to 210 for each sub-problem. Among them, 180 samples are used to construct the Kriging surrogate model, and 30 samples are added according to the EI criterion to further improve the accuracy of the surrogate model. The initial design in Stage I is chosen as uniform material distribution correspond to the specified volume fraction. The weights in the objective function f2 for optimization Stage II in Eq. (13) are all set to 1.

4.1 Designing Metamaterials to Achieve NPRs of −0.6 and −0.8 with 20% Applied Uniaxial Strain

4.1.1 The First Topology Optimization Stage for Metamaterial Design with Targeted NPRs of −0.6 and −0.8

This numerical example explores the design of metamaterial microstructures to achieve NPRs of −0.6 and −0.8. These metamaterials are designed to withstand a maximum applied uniaxial strain of 20%.

During the first optimization stage for NPR metamaterials, effective reference stress-strain matrixes that achieve targeted NPRs under infinitesimal strain are first provided. For the design scenarios with Poisson’s ratio of −0.6 and −0.8, these matrices are given as follows:

D−0.6ref=(0.080−0.0480.000−0.0480.0800.0000.0000.0000.050),(14)

D−0.8ref=(0.080−0.0640.000−0.0640.0800.0000.0000.0000.050).(15)

The matrixes presented in Eqs. (14) and (15) represent the properties of orthogonal materials, with Poisson’s ratios of −0.6 and −0.8, respectively. By using the formulation described in Eq. (12) with a volume fraction constraint of 0.4, two optimized microstructures are obtained with the Kriging model-based solution technique. The optimized designs are listed in Table 1. The volume fractions for the −0.6 and −0.8 Poisson’s ratio designs are 0.3995 and 0.3873, respectively. It is seen from Table 1 that although the topologies of both designs are similar, their member sizes differ to achieve different homogenized Poisson’s ratios under infinitesimal strain assumption. Also, it is seen that the boundary description of the microstructures using the MFSE method is clear and smooth. The first 2 by 2 entries in the homogenized stress-strain matrixes D−0.6H and D−0.8H closely match those in the corresponding reference constitutive matrices, while also achieving homogenized Poisson’s ratios close to their targeted values (−0.6 and −0.8). This illustrates the effectiveness of the first stage optimization formulation used here.

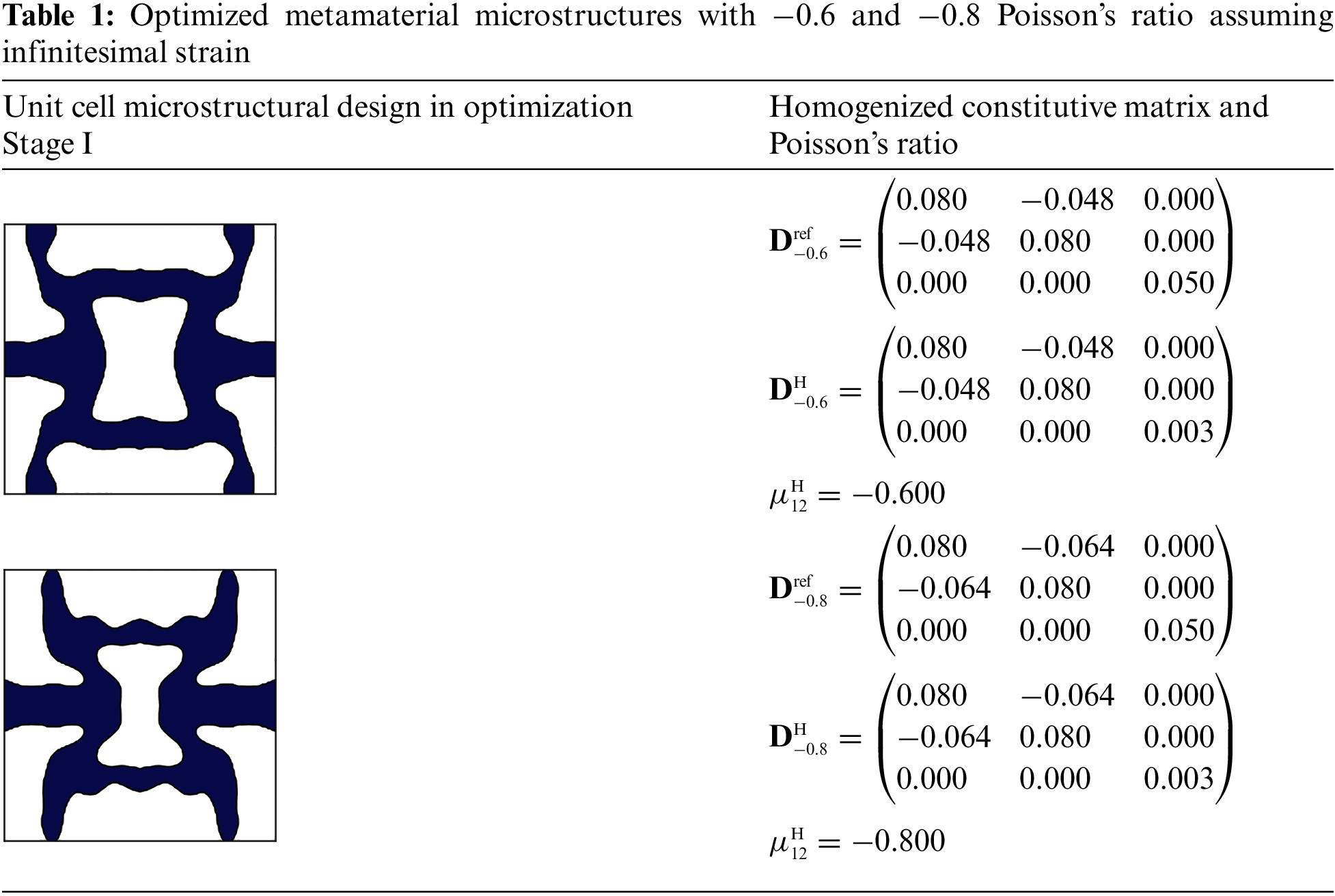
Note that the reference matrixes in Eqs. (14) and (15) are used to specify a desired NPR value, which helps in finding a feasible NPR design with the surrogate model under small deformation. That is, only the ratio of Dref(1,2)/Dref(1,1) is important. As the first optimization stage aims to provide a preliminary NPR design, the diagonal entries Dref(1,1) and Dref(2, 2) can be specified according to the designer. However, it should be noted that excessively large values for these diagonal entries may not achieve the desired NPR value.

Further, we assess the effective NPR (Eq. (1)) values for small strain designs listed in Table 1 under large deformation. To perform this evaluation, we applied periodic boundary conditions as explained in Section 2 and subjected these optimized microstructures to up to 20% uniaxial strain. The results are presented in Figs. 6 and 7, which show that the NPR value varies rapidly with increasing applied strain.

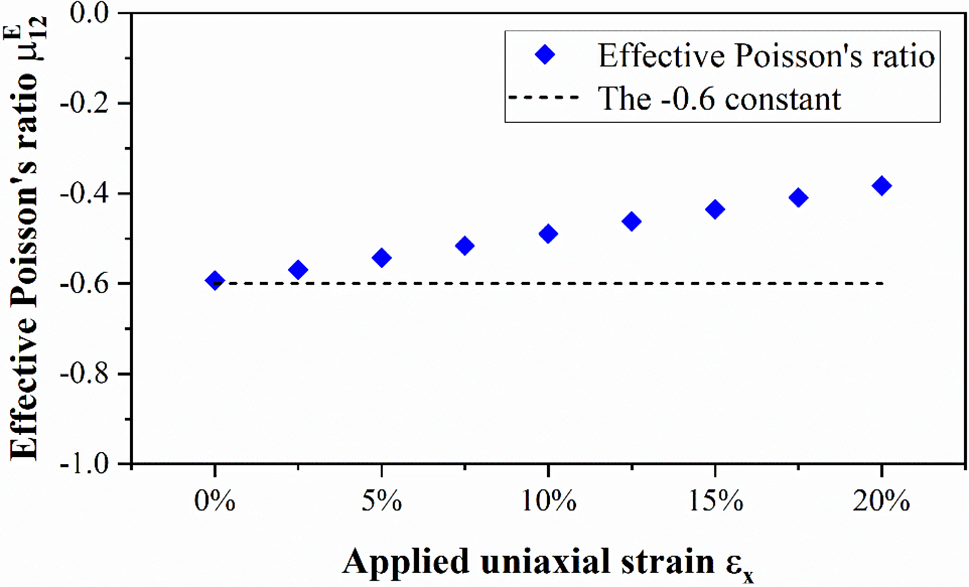
Figure 6: The effective NPR values of the −0.6 Poisson’s ratio design assuming infinitesimal strain under 20% uniaxial stretching

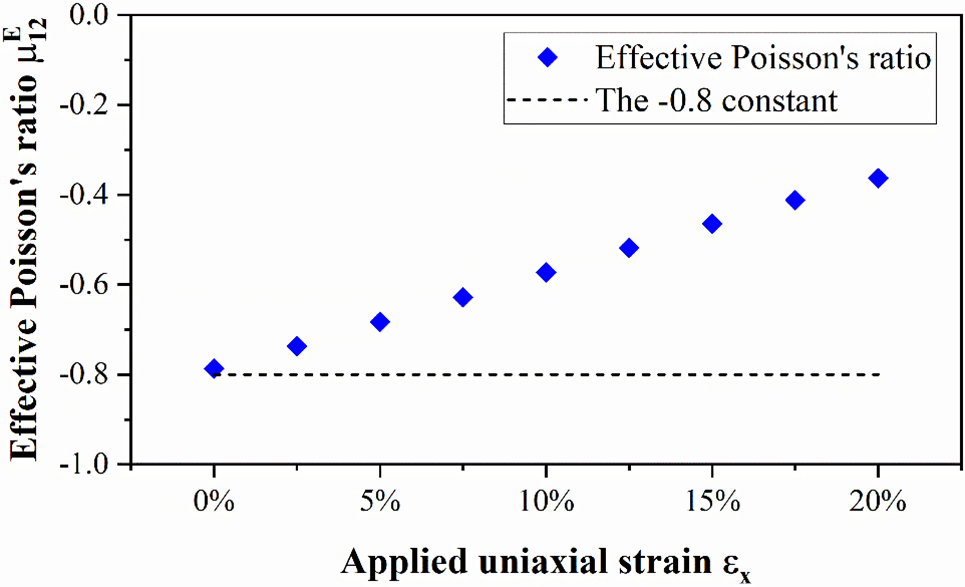
Figure 7: The effective NPR values of the −0.8 Poisson’s ratio design assuming infinitesimal strain under 20% uniaxial stretching

To quantify the deviation between the effective NPR of the optimized design and its targeted value, we suggest a mean deviation expression as

E=∑ti∈TE( tiμ12E−μ12ref)2n,(16)

where TE is a set of time steps during the loading process. For instance, for the design case with a maximum applied strain of 20%, TE includes time steps corresponding to 0.1%, 2.5%, 5%, 7.5%, 10%, 12.5%, 15%, 17.5%, and 20% applied strains. Based on this expression, we found the mean NPR deviation for the −0.6 and −0.8 Poisson’s ratio metamaterial designs assuming infinitesimal strain are respectively equal to 0.1306 and 0.2652 under applied uniaxial strain up to 20%. These deviations are quite large compared with the targeted NPR value.

4.1.2 The Second Topology Optimization Stage for Metamaterial Design with Targeted NPRs of −0.6 and −0.8

In this optimization stage, the small deformation designs obtained in Section 4.1.1 are chosen as the initial designs considering a maximum applied uniaxial strain of 20%. Specifically, the optimized design variable values (i.e., the expansion coefficients in Eq. (9)) from Stage I are used as the design variable initial values for this optimization stage. The projection parameter β in the continuation scheme is reset to a value of 8 to begin with. The volume fraction constraint is set to 0.4. The parameter D¯lower in Eq. (13) is set to 0.03, which indirectly controls the minimum member size in the optimized microstructures.

To optimize the design, we employed a specific search approach. First, we searched for NPR designs with applied uniaxial strain ranging from 0% to 15%. Then, we continue to search for designs with applied strain in the range from 0% to 20%. Our numerical experience suggests that this approach yielded better results compared to directly searching for designs within the entire range of [0%, 20%]. This is because the first search procedure allows for an easier identification of feasible designs before moving on to a wider applied strain range.

Using the second stage optimization formulation (Eq. (13)), we obtained optimized designs with Poisson’s ratios of −0.6 and −0.8 under large deformation. Table 2 presents the initial design, intermediate optimized design with applied strain in range of [0%, 15%], and the optimized designs with applied strain in range of [0%, 20%]. The volume fractions of these optimized designs are 0.3789 and 0.3904. It can be observed that as the applied strain increases, certain locations in the optimized microstructures exhibit thinner and curved local member sizes. These features enhance their deformation capability for large stretches, as demonstrated by the finite element analysis on a reconstructed metamaterial microstructure with −0.8 Poisson’s ratio using conformal mesh considering geometry nonlinearity (see Fig. 8). Here the colormap represents the principal strain. As can be seen in Fig. 8, as the applied strain increases, the curved members rotate to provide capability to achieve NPR under large deformation.

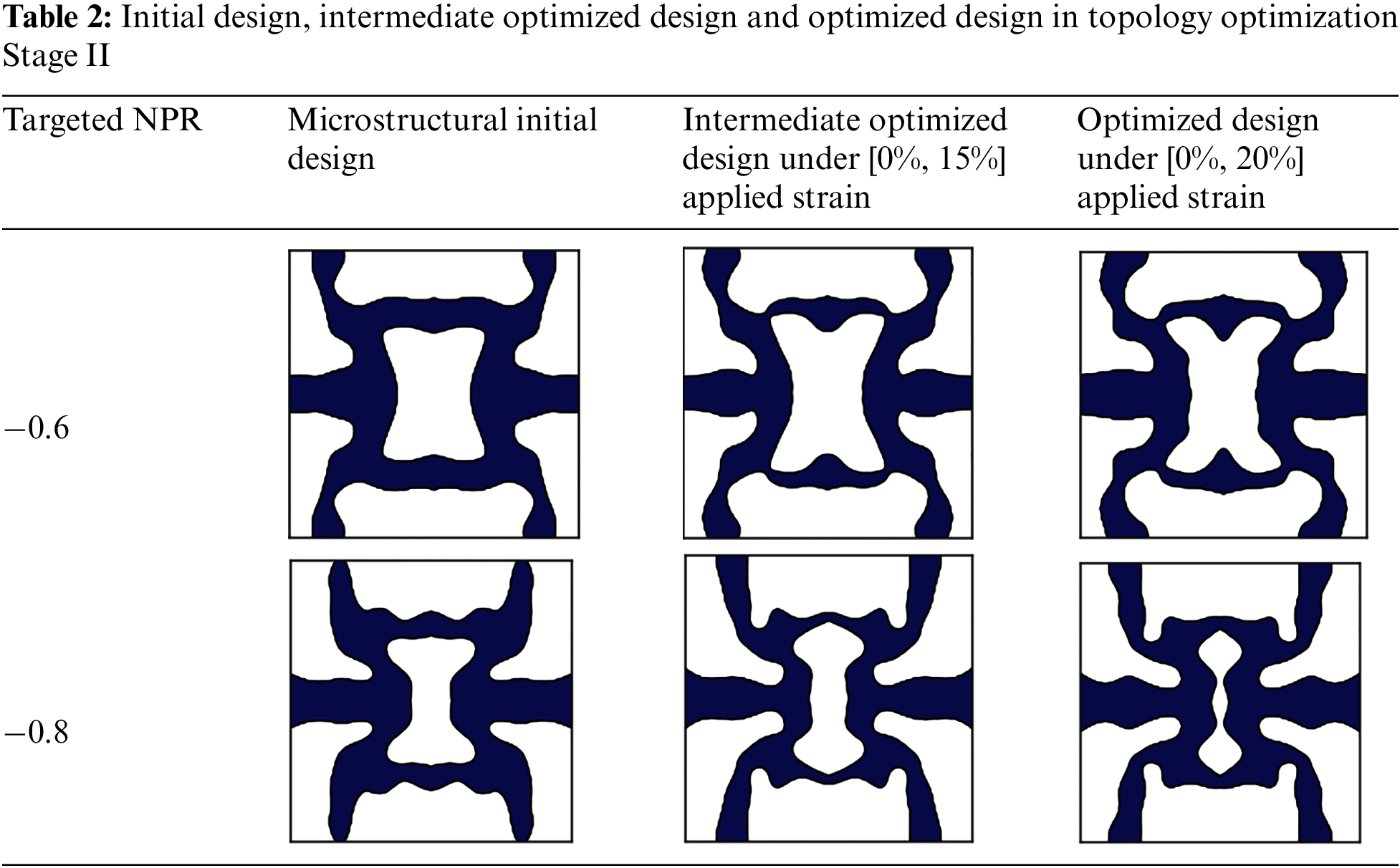
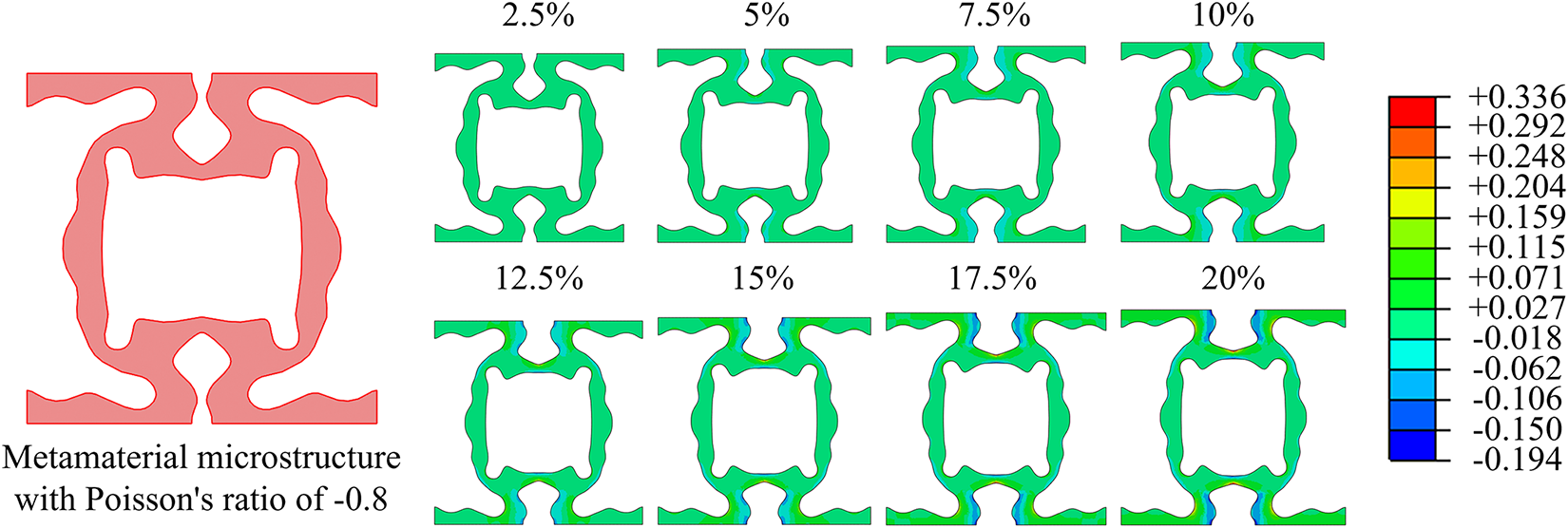
Figure 8: The finite element analysis of the reconstructed metamaterial microstructure with −0.8 Poisson’s ratio using conformal mesh

To evaluate the effective NPR of the designed metamaterials without the gray elements, we manually project the optimized designs to “0–1” designs. This is done by applying a threshold of 0 material field value for projection. This threshold is equivalent to an elemental density of 0.5, and we remove the elements located in the void region. We then re-conduct non-linear finite element analysis on these manually projected designs and depict their effective NPR values computed with Eq. (1) in Figs. 9 and 10. As can be seen from these figures, both optimized designs can sustain the targeted NPR well for an applied uniaxial strain from 0% to 20%. This is also illustrated by the mean deviation computed with Eq. (16), where TE involves time steps correspond to 9 equally distributed applied strain values ranging from 0.1% to 20%. Compared to designs assuming infinitesimal strain, our second-stage optimization formulation and search approach effectively reduces mean NPR deviation under large deformation. Specifically, for the −0.8 Poisson’s ratio design, we observed a decrease in mean NPR deviation from 0.2652 to 0.0318, while for the −0.6 design, there was a decrease from 0.1306 to 0.0198.

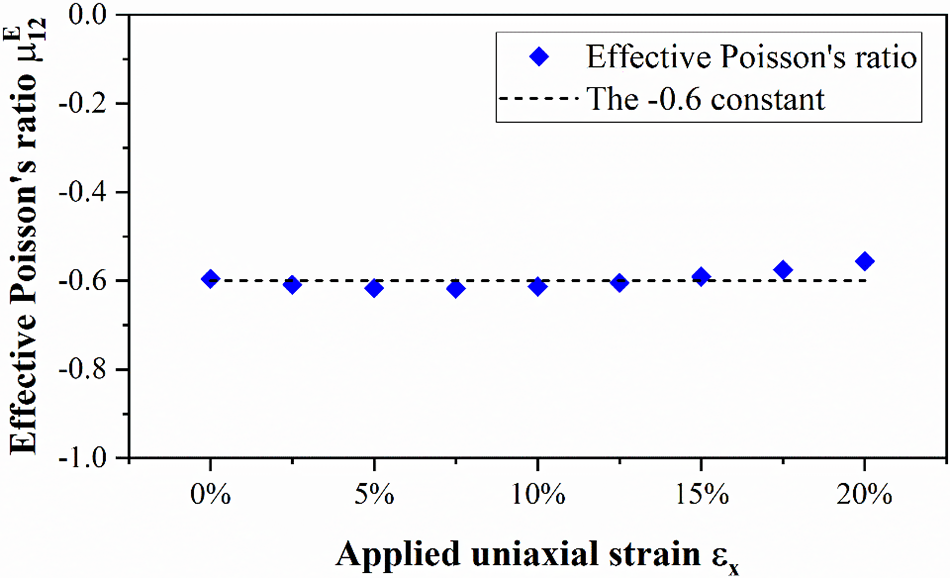
Figure 9: The effective NPR values of the optimized metamaterial microstructure with targeted NPR of −0.6 under 20% uniaxial stretching

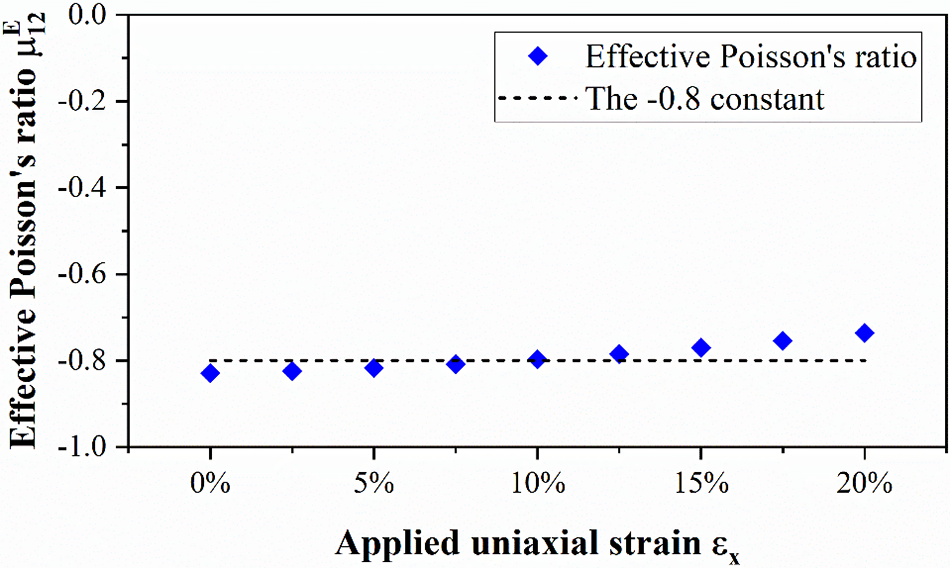
Figure 10: The effective NPR values of the optimized metamaterial microstructure with targeted NPR of −0.8 under 20% uniaxial stretching

At the end of this sub-section, we check the impact of the parameter D¯lower in Eq. (13) on the large deformation microstructural design in the second optimization stage by setting its value to 0.05 and 0.01 and re-run the design process for the −0.8 Poisson’s ratio design case. The optimized designs with these parameters are depicted in Fig. 11. By comparing these designs with those D¯lower=0.03 shown in Table 2, it is seen that as the value of D¯lower decreases, the minimum member size in the optimized design becomes thinner. Again, we analyze and illustrate the effective NPR values of manually projected optimized designs under a maximum 20% uniaxial strain in Fig. 12. It can be observed that as the value of D¯lower decreases from 0.05 to 0.01, the deviation of the effective NPR values from the targeted value becomes smaller and smaller. This observation can also be verified by the mean NPR deviation computed with Eq. (16), which yields 0.0625, 0.0318, 0.0253 for D¯lower values of 0.05, 0.03 and 0.01, respectively. It is noted that though a low minimum member size can match the desired NPR value more closely under large deformation, it also makes manufacturing these designs more challenging and may lead to lower stiffness. Therefore, for all subsequent numerical examples presented hereafter, the value of D¯lower is set to be 0.03 as a compromise between the manufacturability and NPR performances.

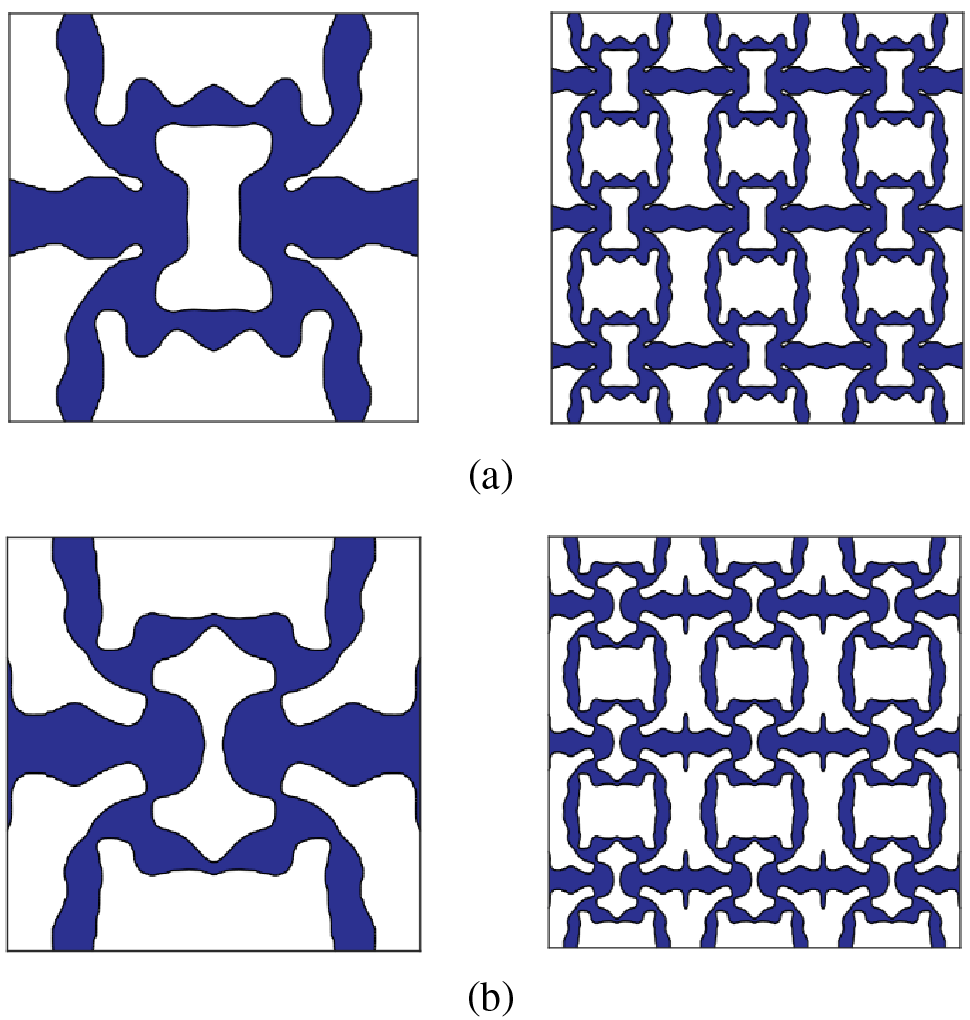
Figure 11: Optimized −0.8 Poisson’s ratio metamaterial microstructure (left) and its 3 by 3 array (right) using parameter setting (a) D¯lower=0.05 and (b) D¯lower=0.01

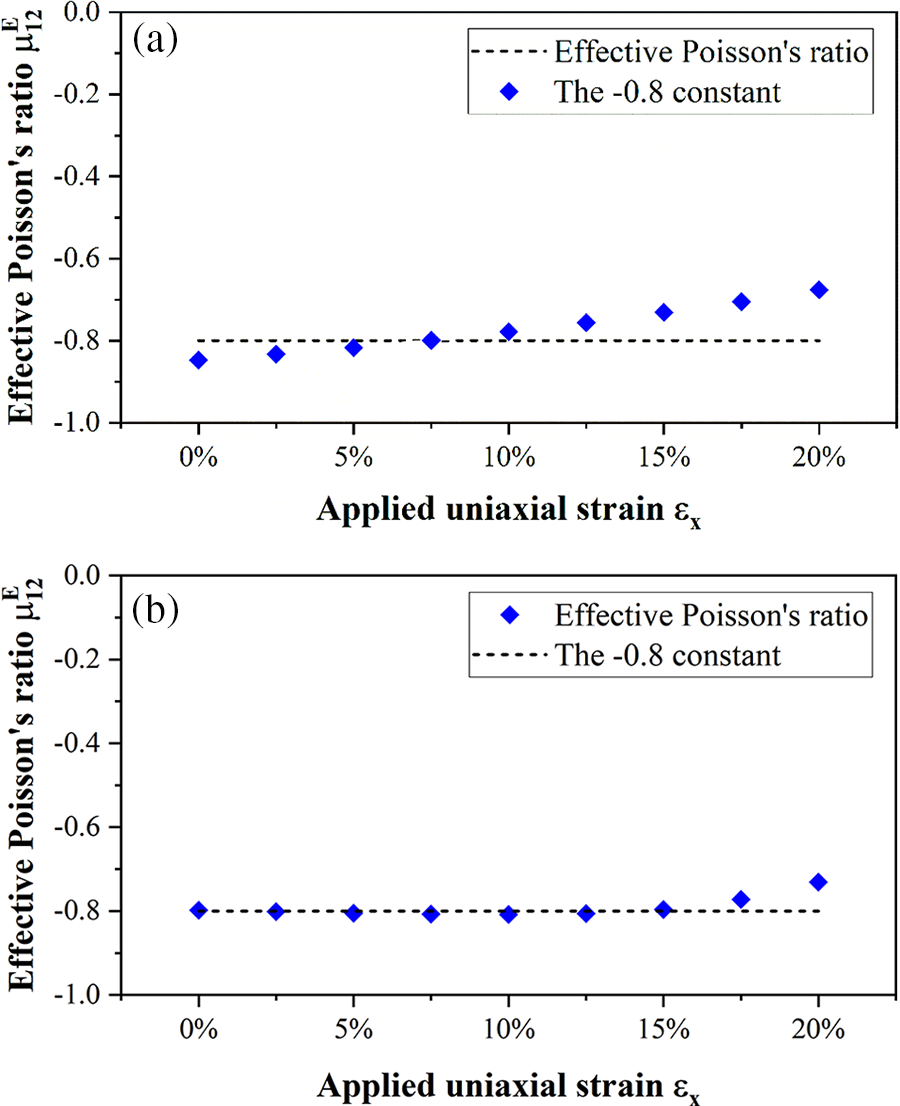
Figure 12: The effective NPR values of the optimized −0.8 Poisson’s ratio metamaterial using parameter setting (a) D¯lower=0.05 and (b) D¯lower=0.01

4.2 Design of a Group of Metamaterials with Targeted NPRs in Range of [−0.8, −0.1] with 20% Uniaxial Applied Strain

This example investigates the design of a group of metamaterials with targeted NPRs in range of [−0.8, −0.1], under applied uniaxial strain between 0% and 20%.

As is known, designing large deformation NPR metamaterials is a highly non-linear process, which may result in multiple local minima with comparable NPR values. In numerical Example 4.1, we observed that optimized designs with −0.6 and −0.8 Poisson’s ratio had similar microstructural topologies. This suggests that similar topologies with differences in member shape and size can lead to different desired NPRs under large deformation. Based on these findings, our focus in this example is to design a group of metamaterials with similar microstructural topologies but different NPRs. To achieve this, we start by choosing the optimized microstructure with a −0.8 Poisson’s ratio (from Section 4.1) as an initial design for optimization Stage II, aiming to generate an optimized design with a −0.7 Poisson’s ratio. Then, the resulting −0.7 NPR design serves as the initial design for obtaining a metamaterial with an NPR of −0.6. This process continues until we obtain the optimized design with an NPR of −0.1.

Table 3 presents the optimized metamaterial microstructures. We also re-analyze the manually projected “0–1” designs without the void phase to examine their NPR behaviors, as depicted in Fig. 13. From both Table 3 and Fig. 13, it is seen that by adjusting the curvature and local size of microstructural members, the present method successfully generates a group of metamaterial microstructures that closely match the targeted NPR values in the range of [−0.8, −0.1]. Moreover, as the value of the targeted NPR value increases, a general decrease in deviations computed using Eq. (16) is observed, indicating that higher NPR value designs are relatively easier to achieve with the present topology optimization approach. Notably, the maximum mean NPR deviation for all these group of designs occurs at the −0.8 Poisson’s ratio design case, which yields a mean NPR deviation of 0.0318. This mean deviation is relatively small from the targeted NPR value of −0.8, illustrating the effectiveness of the present method.

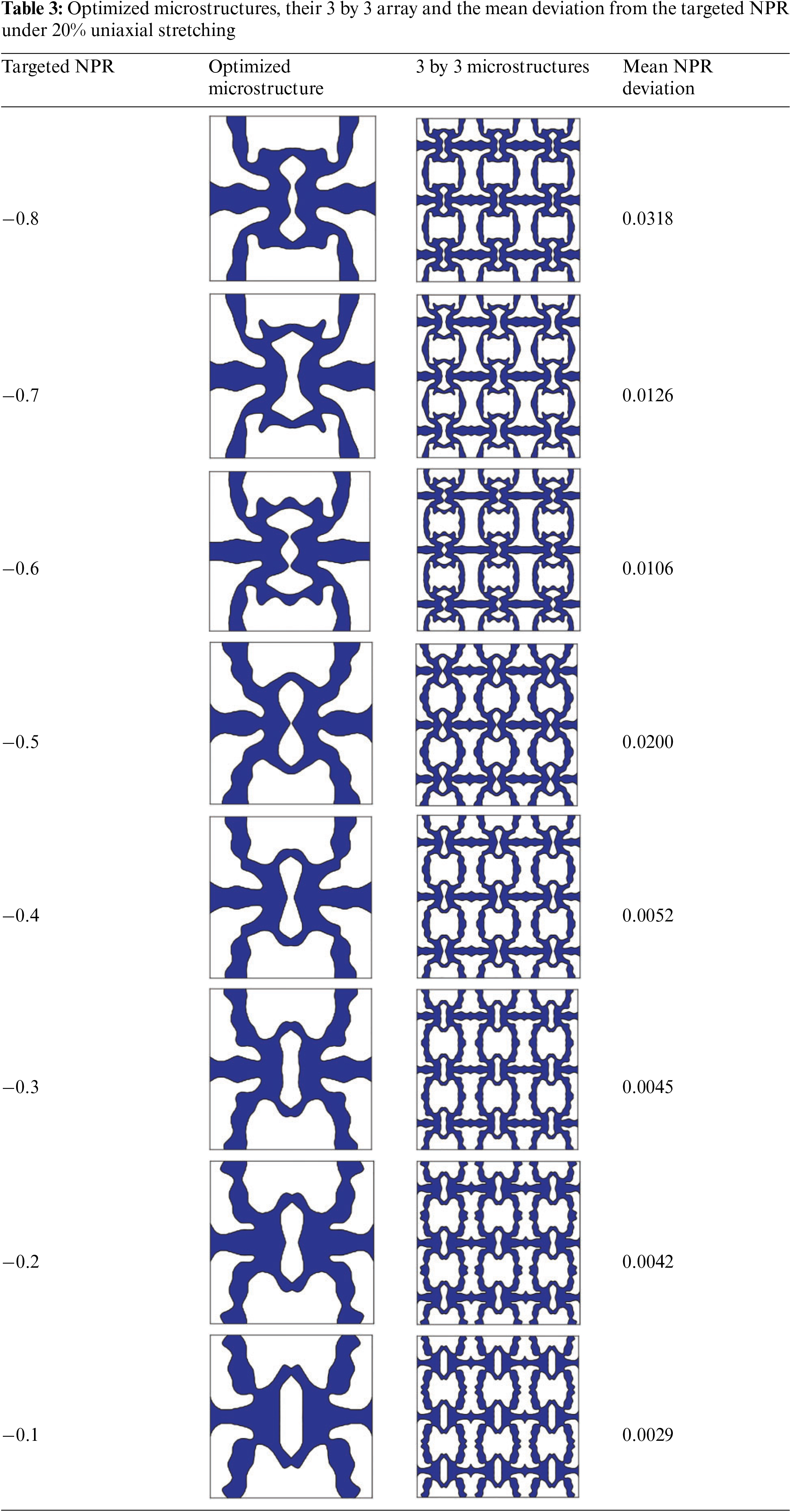
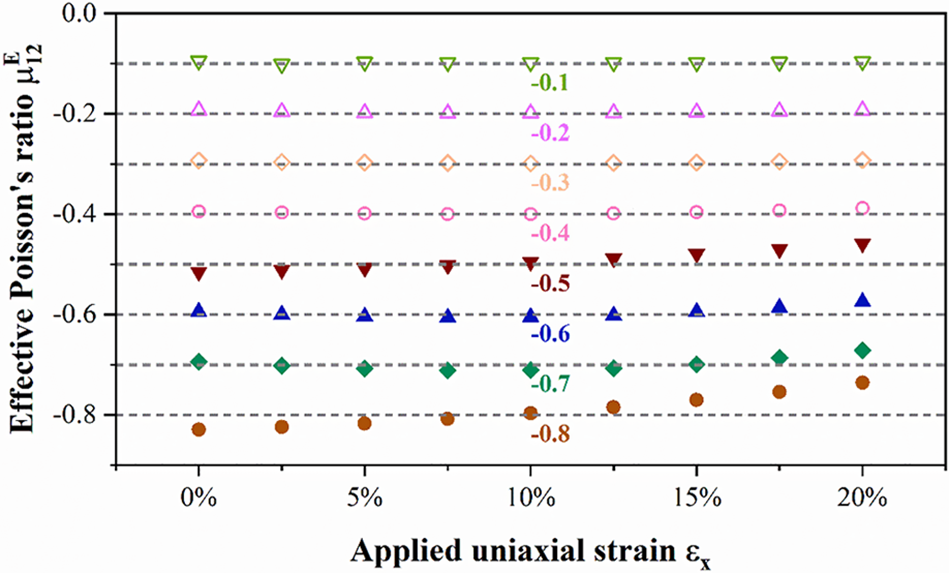
Figure 13: The effective NPR values of the optimized metamaterial microstructures under 20% uniaxial stretching

Regarding the large deformation metamaterial design with −0.6 Poisson’s ratio, the optimized microstructure in this example is obtained by using the large deformation metamaterial design with −0.7 Poisson’s ratio as an initial design. An optimized design is also successfully obtained using a homogenized NPR initial design in Example 4.1. Both of these optimized microstructures are local minima for the current design problem. In this specific case, the former has a slightly lower mean NPR deviation compared to the latter (i.e., 0.0106 vs. 0.0198).

5  The Experimental Tests on the Fabricated NPR Optimized Designs

To examine the NPR values of the optimized metamaterial microstructures, we fabricate the optimized designs with targeted NPRs of −0.8, −0.6, and −0.4 using the Thermoplastic Polyurethane (TPU) material. The manufacturing process involves 3D printing an array of the optimized microstructures, immersing the printed object in the silicone liquid to solidify and get a silicone mold, and then injecting TPU material into the mold to fabricate the TPU metamaterial microstructural array.

To determine the material properties of TPU, we conducted uniaxial tensile tests on standard dog-bone-shaped specimens. The dimensions of these specimens are depicted in Fig. 14. Three specimens were fabricated and then tested using the Instron 34TM-10 testing machine with an applied tensile displacement of 180 mm and a loading rate of 3.6 mm/min. The resulting engineering stress-strain curve is shown in Fig. 15.

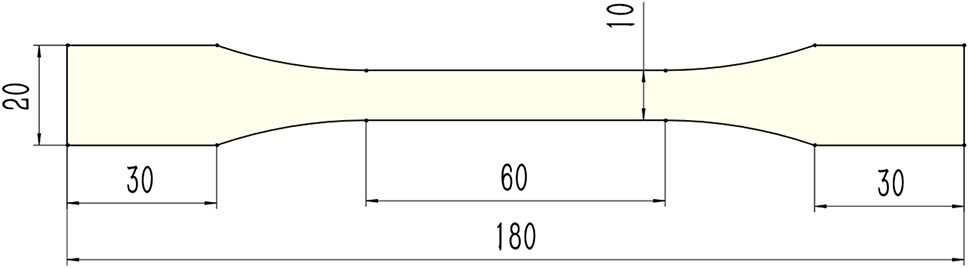
Figure 14: The dimension of the dog-bone-shaped TPU specimens

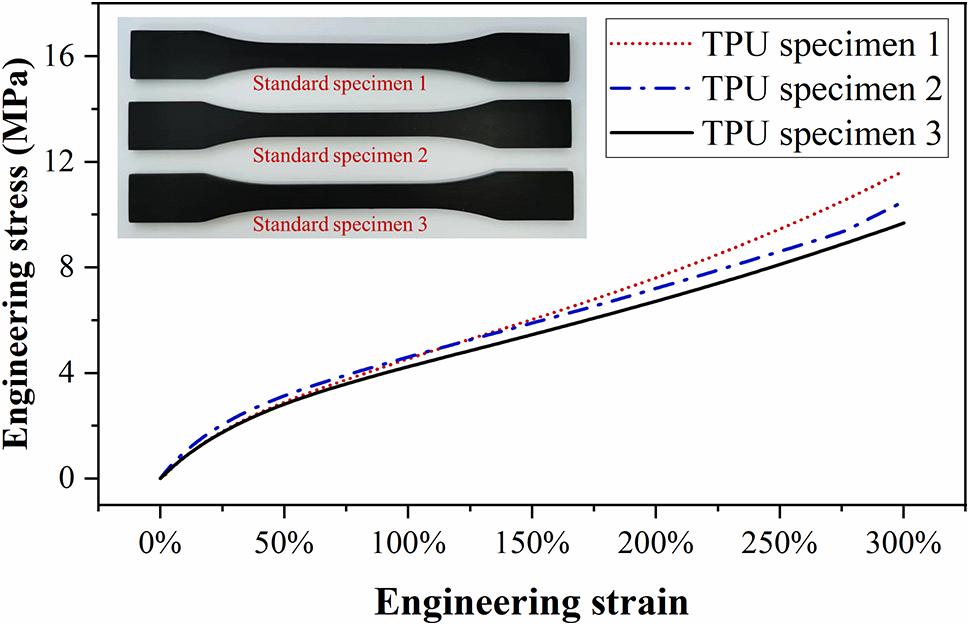
Figure 15: The engineering stress-strain curves of three TPU specimens

For tests on the metamaterial microstructure specimens, they are clamped at both ends using fixtures during experiments. To accommodate deformation perpendicular to the tension direction, a fixture with vertical displacement fixation and lateral sliding is used. The length of this fixture is 300 mm. An 8 by 4 microstructure array specimen is fabricated due to manufacturing capability. Each cell has dimensions of 42 mm by 42 mm with a thickness of 5 mm. The overall size of the test specimen is 383 mm by 183 mm as shown in Fig. 16. Several tabs are placed at both the upper and lower boundaries of the metamaterial specimen and connected to sliding fixtures through bolt connections as shown in Fig. 16.

Figure 16: Schematic illustration of the tensile test setting

During testing, a maximum tensile displacement corresponding to 20% unit cell strain is applied to the upper boundary at a rate of 3.6 mm/min. The lower boundary is clamped to fix its vertical displacement. To facilitate measurement of longitudinal and lateral displacements for each individual cell, circular through-holes with a diameter of 1.5 mm are positioned at the four corners of each unit cell for marking purposes. Due to the limited number of microstructures in the fabricated metamaterial specimen, the free edges may not maintain a perfectly straight-line shape. To reduce the impacts of boundary effects, we measured the horizontal displacements of the two middle column microstructures in Fig. 16 using a vernier caliper. These measurements were then averaged to determine the horizontal displacement of the metamaterial microstructure. The displacements were recorded at deformed configurations corresponding to eight evenly distributed applied tensile strains, ranging from 2.5% to 20%.

The metamaterial specimens with targeted NPRs of −0.8, −0.6, and −0.4 were fabricated and tested. Fig. 17 shows the tensile experiment conduced on the specimen with the −0.8 Poisson’s ratio microstructural design. The experimental measured Poisson’s ratios for all these three specimens are shown in Fig. 18, along with the effective NPR values from finite element analysis for comparison purposes. As can be seen in Fig. 18, the experimental measured NPRs show good consistency with the numerical results. This verifies the effectiveness of the present method. Also, from Figs. 15 and 17, it is seen that material nonlinearity has a relative low impact on this optimized design for this particular material, as the maximum strain occurs at localized positions and this maximum local strain does not lead to significant changes in material stiffness. The slight deviation shown in Fig. 18 could also potentially be attributed to manufacturing geometry errors and the limited number of fabricated microstructures.

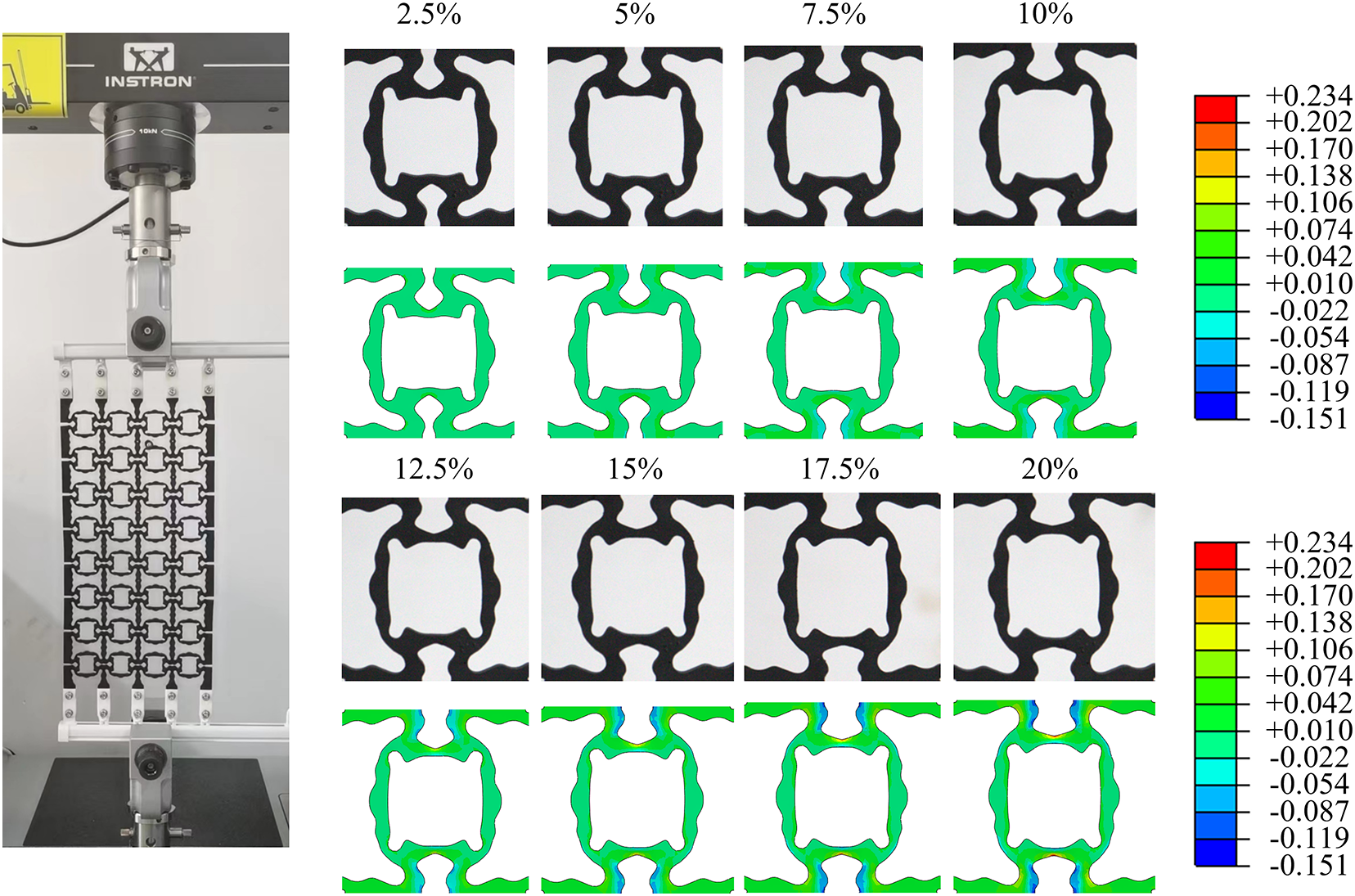
Figure 17: Experimental measured unit cell deformations and the corresponding simulation results under different applied strains

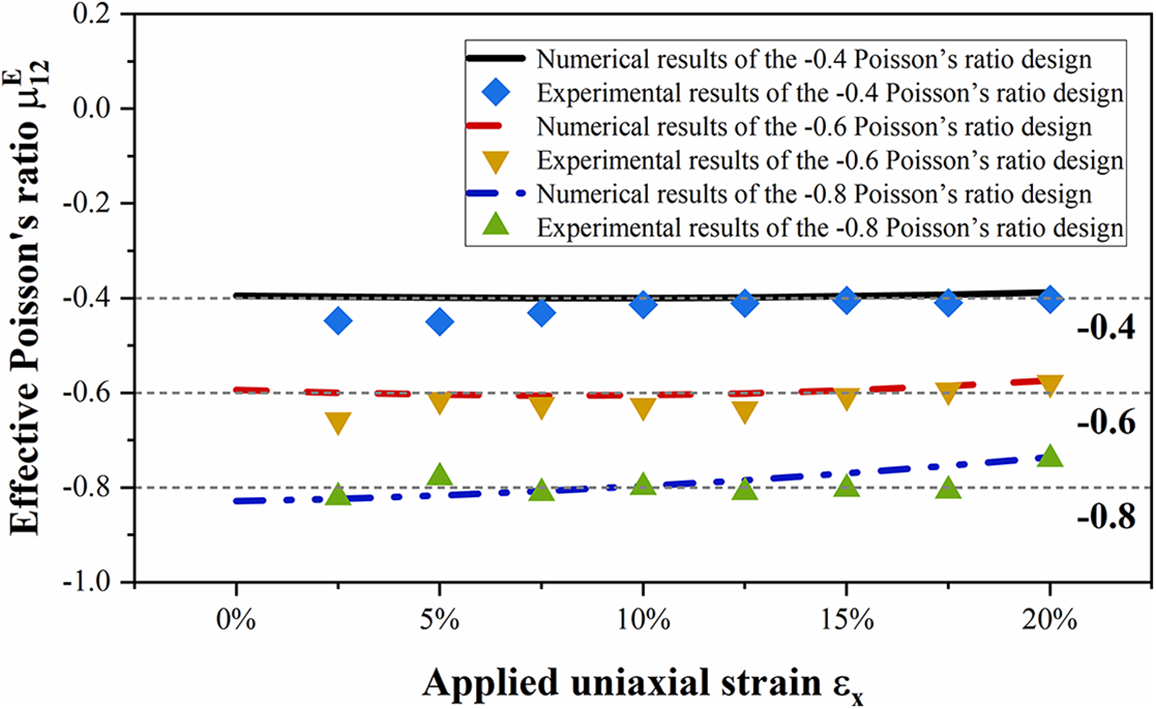
Figure 18: The experimental measured Poisson’s ratios of three metamaterial array specimens and their corresponding finite element analysis results under a 20% uniaxial applied strain

6  Conclusions

This paper investigates the topological design of NPR metamaterial microstructures under up to 20% uniaxial tension strain, with a focus on using a gradient-free method. The unit cell microstructural topology is described using the MFSE method, which greatly reduces the number of required design variables. To achieve targeted NPR under large deformation, a two-stage metamaterial topology optimization strategy is proposed. In the first design stage, the homogenization method is used to search for a preliminary NPR design assuming infinitesimal strain. In the second stage, the design is continuously updated by minimizing deviation from the desired NPR value considering large deformation. Due to dimension reduction in the design space with the MFSE method, the design in each optimization stage is obtained by solving a series of sub-optimization problems through sampling and Kriging surrogate models.

With the present NPR metamaterial optimization strategy, we have obtained a group of optimized metamaterial microstructures. These microstructure designs share similar topology but differ in local member size and curvature, achieving targeted NPR values ranging from −0.8 to −0.1 when subjected to up to 20% uniaxial strain. We have also fabricated and tested some of these optimized designs through experiments, which yielded results consistent with our numerical analysis, demonstrating the effectiveness of this method. Our study focuses on utilizing the geometry nonlinearity mechanism in achieving targeted NPR under large deformation, while other nonlinearities, such as material nonlinearity and contact nonlinearity can be explored in further studies concerning metamaterial design, to fully take advantage of the gradient-free feature of this approach.

Acknowledgement: The authors acknowledge the support of the National Science Foundation of China, the Liaoning Revitalization Talents Program and Fundamental Research Funds for the Central Universities. The authors would like to give thanks to the Dalian University of Technology, China for promoting this research and providing the laboratory facility and support.

Funding Statement: The authors acknowledge the support of the National Science Foundation of China (12372120, 12172075), the Liaoning Revitalization Talents Program (XLYC2007027) and Fundamental Research Funds for the Central Universities (DUT21RC(3)067).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Pai Liu, Yiqiang Wang; data collection: Weida Wu, Zhonghao Gao; analysis and interpretation of results: Weida Wu, Pai Liu; draft manuscript preparation: Pai Liu, Weida Wu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: None.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Cui, T. J., Smith, D. R., Liu, R. (2010). Metamaterials (prevajalec, Trans.). New York: Springer. [Google Scholar]

2. Engheta, N., Ziolkowski, R. W. (2006). Metamaterials: Physics and engineering explorations (prevajalec, Trans.). New York: Wiley-IEEE Press. [Google Scholar]

3. Saxena, K. K., Das, R., Calius, E. P. (2016). Three decades of auxetics research−materials with negative Poisson’s ratio: A review. Advanced Engineering Materials, 18(11), 1847–1870. [Google Scholar]

4. Luo, C., Han, C. Z., Zhang, X. Y., Zhang, X. G., Ren, X. et al. (2021). Design, manufacturing and applications of auxetic tubular structures: A review. Thin-Walled Structures, 163, 107682. [Google Scholar]

5. Lakes, R. (1987). Foam structures with a negative Poisson’s ratio. Science, 235(4792), 1038–1040. [Google Scholar] [PubMed]

6. Airoldi, A., Crespi, M., Quaranti, G., Sala, G. (2012). Design of a morphing airfoil with composite chiral structure. Journal of Aircraft, 49(4), 1008–1019. [Google Scholar]

7. Dale, A. S., Cooper, J. E., Mosquera, A. (2014). Topology optimization & experimental validation of 0-υ honeycomb for adaptive morphing wing. 22nd AIAA/ASME/AHS Adaptive Structures Conference, National Harbor, Maryland. [Google Scholar]

8. Wang, Y. C., Lakes, R. (2002). Analytical parametric analysis of the contact problem of human buttocks and negative Poisson’s ratio foam cushions. International Journal of Solids and Structures, 39(18), 4825–4838. [Google Scholar]

9. Ma, Y., Scarpa, F., Zhang, D., Zhu, B., Chen, L. et al. (2013). A nonlinear auxetic structural vibration damper with metal rubber particles. Smart Materials and Structures, 22(8), 084012. [Google Scholar]

10. Qi, C., Jiang, F., Yang, S., Remennikov, A. (2021). Multiscale characterization of novel re-entrant circular auxetic honeycombs under quasi-static crushing. Thin-Walled Structures, 169, 108314. [Google Scholar]

11. Wang, T., An, J., He, H., Wen, X., Xi, X. (2021). A novel 3D impact energy absorption structure with negative Poisson’s ratio and its application in aircraft crashworthiness. Composite Structures, 262, 113663. [Google Scholar]

12. Ma, N., Han, Q., Han, S., Li, C. (2023). Hierarchical re-entrant honeycomb metamaterial for energy absorption and vibration insulation. International Journal of Mechanical Sciences, 250, 108307. [Google Scholar]

13. Andreassen, E., Lazarov, B. S., Sigmund, O. (2014). Design of manufacturable 3D extremal elastic microstructure. Mechanics of Materials, 69(1), 1–10. [Google Scholar]

14. Zhou, Y., Gao, L., Li, H. (2023a). A Ready-to-manufacture optimization design of 3D chiral auxetics for additive manufacturing. Engineering with Computers, 1–22. [Google Scholar]

15. Han, S., Han, Q., Ma, N., Li, C. (2023). Design and reinforcement-learning optimization of re-entrant cellular metamaterials. Thin-Walled Structures, 191, 111071. [Google Scholar]

16. Liu, J., Gaynor, A. T., Chen, S., Kang, Z., Suresh, K. et al. (2018). Current and future trends in topology optimization for additive manufacturing. Structural and Multidisciplinary Optimization, 57(6), 2457–2483. [Google Scholar]

17. Bendsoe, M. P., Sigmund, O. (2003). Topology optimization: Theory, methods, and applications (prevajalec, Trans.). New York: Springer Science & Business Media. [Google Scholar]

18. Rozvany, G. I. (2009). A critical review of established methods of structural topology optimization. Structural and Multidisciplinary Optimization, 37, 217–237. [Google Scholar]

19. Suzuki, K., Kikuchi, N. (1991). A homogenization method for shape and topology optimization. Computer Methods in Applied Mechanics and Engineering, 93(3), 291–318. [Google Scholar]

20. Rozvany, G. I., Zhou, M., Birker, T. (1992). Generalized shape optimization without homogenization. Structural Optimization, 4, 250–252. [Google Scholar]

21. Bendsøe, M. P., Sigmund, O. (1999). Material interpolation schemes in topology optimization. Archive of Applied Mechanics, 69, 635–654. [Google Scholar]

22. Wang, M. Y., Wang, X., Guo, D. (2003). A level set method for structural topology optimization. Computer Methods in Applied Mechanics and Engineering, 192(1–2), 227–246. [Google Scholar]

23. Allaire, G., Jouve, F., Toader, A. M. (2004). Structural optimization using sensitivity analysis and a level-set method. Journal of Computational Physics, 194(1), 363–393. [Google Scholar]

24. Xie, Y. M., Steven, G. P. (1993). A simple evolutionary procedure for structural optimization. Computers & Structures, 49(5), 885–896. [Google Scholar]

25. Huang, X., Xie, Y. (2007). Convergent and mesh-independent solutions for the bi-directional evolutionary structural optimization method. Finite Elements in Analysis and Design, 43(14), 1039–1049. [Google Scholar]

26. Luo, Y., Wang, M. Y., Kang, Z. (2015). Topology optimization of geometrically nonlinear structures based on an additive hyperelasticity technique. Computer Methods in Applied Mechanics and Engineering, 286, 422–441. [Google Scholar]

27. Sigmund, O. (1995). Tailoring materials with prescribed elastic properties. Mechanics of Materials, 20(4), 351–368. [Google Scholar]

28. Zhou, Y., Gao, L., Li, H. (2023b). Topology optimization design of graded infills for 3D curved volume by a conformal sweeping method. Computer Methods in Applied Mechanics and Engineering, 412, 116009. [Google Scholar]

29. Huang, X., Zhou, S., Sun, G., Li, G., Xie, Y. M. (2015). Topology optimization for microstructures of viscoelastic composite materials. Computer Methods in Applied Mechanics and Engineering, 283, 503–516. [Google Scholar]

30. Sigmund, O., Torquato, S. (1997). Design of materials with extreme thermal expansion using a three-phase topology optimization method. Journal of the Mechanics and Physics of Solids, 45(6), 1037–1067. [Google Scholar]

31. Sigmund, O., Søndergaard Jensen, J. (2003). Systematic design of phononic band–gap materials and structures by topology optimization. Philosophical Transactions of the Royal Society A, 361(1806), 1001–1019. [Google Scholar]

32. Takezawa, A., Zhang, X., Kato, M., Kitamura, M. (2019). Method to optimize an additively-manufactured functionally-graded lattice structure for effective liquid cooling. Additive Manufacturing, 28, 285–298. [Google Scholar]

33. Yi, G., Youn, B. D. (2016). A comprehensive survey on topology optimization of phononic crystals. Structural and Multidisciplinary Optimization, 54, 1315–1344. [Google Scholar]

34. Han, S., Han, Q., Li, C. (2022). Deep-learning-based inverse design of phononic crystals for anticipated wave attenuation. Journal of Applied Physics, 132(15), 154901. [Google Scholar]

35. Han, S., Han, Q., Jiang, T., Li, C. (2023). Inverse design of phononic crystals for anticipated wave propagation by integrating deep learning and semi-analytical approach. Acta Mechanica, 234(10), 4879–4897. [Google Scholar]

36. Diaz, A. R., Sigmund, O. (2010). A topology optimization method for design of negative permeability metamaterials. Structural and Multidisciplinary Optimization, 41, 163–177. [Google Scholar]

37. Li, H., Luo, Z., Gao, L., Qin, Q. (2018). Topology optimization for concurrent design of structures with multi-patch microstructures by level sets. Computer Methods in Applied Mechanics and Engineering, 331, 536–561. [Google Scholar]

38. Xia, L., Breitkopf, P. (2014). Concurrent topology optimization design of material and structure within FE2 nonlinear multiscale analysis framework. Computer Methods in Applied Mechanics and Engineering, 278, 524–542. [Google Scholar]

39. Xu, L., Cheng, G. (2018). Two-scale concurrent topology optimization with multiple micro materials based on principal stress orientation. Structural and Multidisciplinary Optimization, 57, 2093–2107. [Google Scholar]

40. Wang, Y., Kang, Z. (2019). Concurrent two-scale topological design of multiple unit cells and structure using combined velocity field level set and density model. Computer Methods in Applied Mechanics and Engineering, 347, 340–364. [Google Scholar]

41. Xu, B., Xie, Y. M. (2015). Concurrent design of composite macrostructure and cellular microstructure under random excitations. Composite Structures, 123, 65–77. [Google Scholar]

42. Wang, Y., Luo, Z., Zhang, N., Kang, Z. (2014). Topological shape optimization of microstructural metamaterials using a level set method. Computational Materials Science, 87, 178–186. [Google Scholar]

43. Zheng, Y., Wang, Y., Lu, X., Liao, Z., Qu, J. (2020). Evolutionary topology optimization for mechanical metamaterials with auxetic property. International Journal of Mechanical Sciences, 179, 105638. [Google Scholar]

44. Kang, Z., Wang, Y. (2011). Structural topology optimization based on non-local Shepard interpolation of density field. Computer Methods in Applied Mechanics and Engineering, 200(49–52), 3515–3525. [Google Scholar]

45. Zhang, H., Luo, Y., Kang, Z. (2018). Bi-material microstructural design of chiral auxetic metamaterials using topology optimization. Composite Structures, 195, 232–248. [Google Scholar]

46. Gao, J., Xiao, M., Gao, L., Yan, J., Yan, W. (2020). Isogeometric topology optimization for computational design of re-entrant and chiral auxetic composites. Computer Methods in Applied Mechanics and Engineering, 362, 112876. [Google Scholar]

47. de Lima, C. R., Paulino, G. H. (2019). Auxetic structure design using compliant mechanisms: A topology optimization approach with polygonal finite elements. Advances in Engineering Software, 129, 69–80. [Google Scholar]

48. Wu, J., Luo, Z., Li, H., Zhang, N. (2017). Level-set topology optimization for mechanical metamaterials under hybrid uncertainties. Computer Methods in Applied Mechanics and Engineering, 319, 414–441. [Google Scholar]

49. Liu, J. Y., Liu, H. T. (2022). Energy absorption characteristics and stability of novel bionic negative Poisson’s ratio honeycomb under oblique compression. Engineering Structures, 267, 114682. [Google Scholar]

50. Clausen, A., Wang, F., Jensen, J. S., Sigmund, O., Lewis, J. A. (2015). Topology optimized architectures with programmable Poisson’s ratio over large deformations. Advanced Materials, 27(37), 5523–5527. [Google Scholar] [PubMed]

51. Wang, F. (2018). Systematic design of 3D auxetic lattice materials with programmable Poisson’s ratio for finite strains. Journal of the Mechanics and Physics of Solids, 114, 303–318. [Google Scholar]

52. Zhang, G., Khandelwal, K. (2019). Computational design of finite strain auxetic metamaterials via topology optimization and nonlinear homogenization. Computer Methods in Applied Mechanics and Engineering, 356, 490–527. [Google Scholar]

53. Kepeng, Q., Ruoyao, W., Jihong, Z., Zhang, W. (2020). Optimization design of chiral hexagonal honeycombs with prescribed elastic properties under large deformation. Chinese Journal of Aeronautics, 33(3), 902–909. [Google Scholar]

54. Pokkalla, D. K., Poh, L. H., Quek, S. T. (2021). Isogeometric shape optimization of missing rib auxetics with prescribed negative Poisson’s ratio over large strains using genetic algorithm. International Journal of Mechanical Sciences, 193, 106169. [Google Scholar]

55. Luo, Y., Bao, J. (2019). A Material-field series-expansion method for topology optimization of continuum structures. Computers & Structures, 225, 106122. [Google Scholar]

56. Luo, Y., Xing, J., Kang, Z. (2020). Topology optimization using material-field series expansion and Kriging-based algorithm: An effective non-gradient method. Computer Methods in Applied Mechanics and Engineering, 364, 112966. [Google Scholar]

57. de Borst, R., Crisfield, M. A., Remmers, J. J., Verhoosel, C. V. (2012). Nonlinear finite element analysis of solids and structures (prevajalec, Trans.). New York: Wiley. [Google Scholar]

58. Guest, J. K., Prévost, J. H., Belytschko, T. (2004). Achieving minimum length scale in topology optimization using nodal design variables and projection functions. International Journal for Numerical Methods in Engineering, 61(2), 238–254. [Google Scholar]