Review of Collocation Methods and Applications in Solving Science and Engineering Problems

1  Introduction

In engineering, simulation and solving complex mathematical models is a critical task. However, as the complexity of problems increases, traditional analytical methods often seem inadequate, which makes researchers and engineers turn to numerical methods [1,2] to obtain accurate and feasible solutions to practical problems. For the solution to a numerical model can be summarized as the function approximation. Generally, interpolation and summation of the basis function are two commonly used ways. Based on these two thoughts, a large number of numerical methods have emerged, such as finite element method (FEM) [3], finite volume method (FVM) [4], and boundary element method (BEM) [5,6]. Among these methods, the collocation method has attracted widespread attention due to its distinct advantages (shown in Fig. 1). Specific advantages include natural treatment of boundaries, high computational efficiency, applicability to a wide range of physical fields, and so on. By selecting appropriate collocation points or discrete points within the problem domain, the collocation method can transform engineering problems into a series of algebraic equations, so that the numerical solution of the problem can be implemented. For a given differential problem, a collocation scheme frequently results in some of the most effective practical numerical results. Furthermore, the method is so versatile and intuitive that it is unsurprising that these methods have been extensively used for numerous decades. In addition, the collocation method, as a numerical technique, has achieved great success in solving various engineering problems attributed to its flexibility and adaptability.

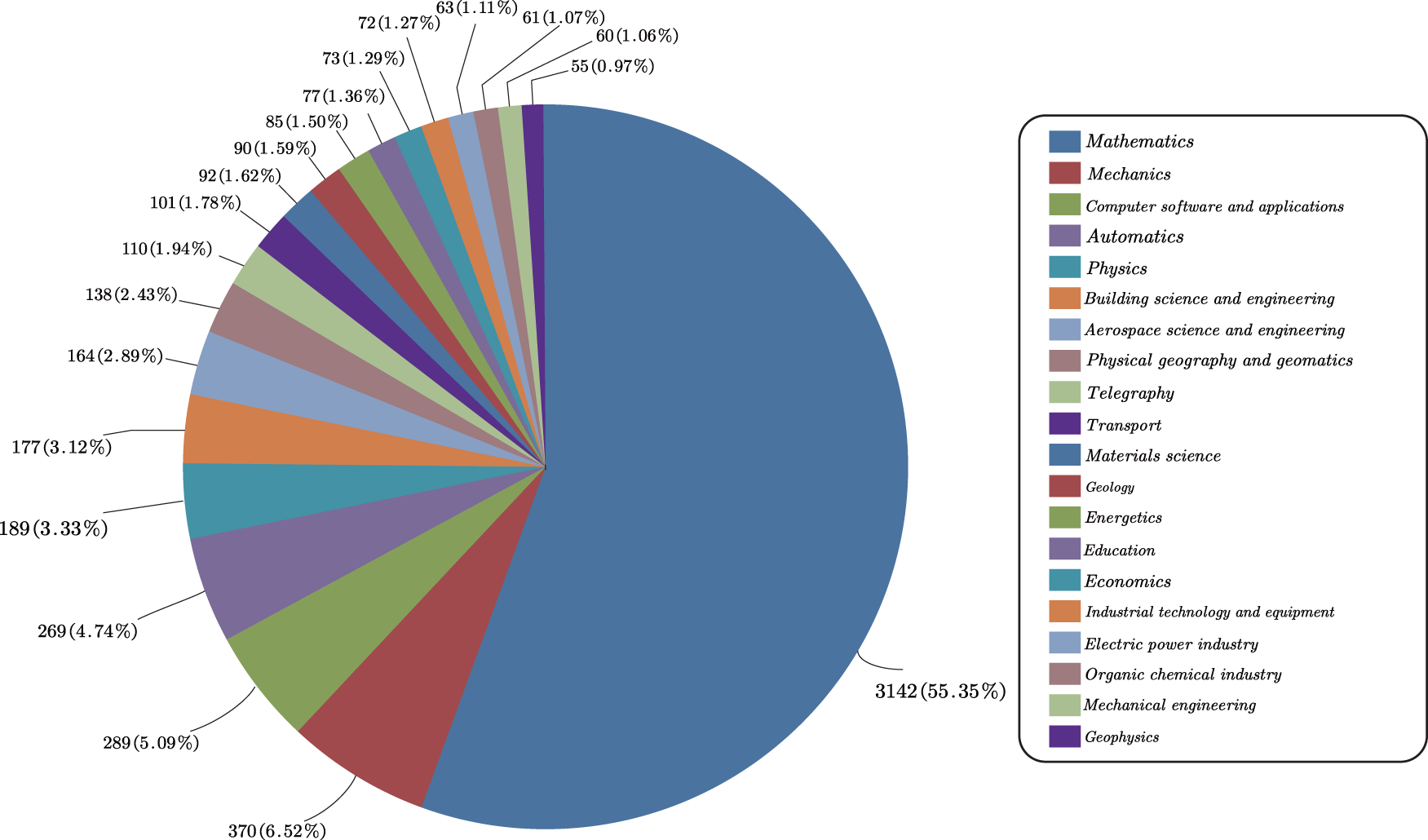
Figure 1: The main application disciplines of the collocation method

The collocation method has some key milestones and early applications including early works on numerical analysis [7], application in fluid dynamics and structural mechanics [8], and advancements in radial basis functions [9]. Certainly, the collocation method, as a node-based method, is naturally combined with the meshless method. With the deepening research into meshless methods, collocation techniques have also seen further developments. Factually, the development of meshless methods has a long history, with early representative methods tracing back to the generalized finite difference method (GFDM) [10–13] and smoothed particle hydrodynamics (SPH) [14–17]. Subsequently, Onate et al. [18,19] proposed the finite point method (FPM) by combining the moving least squares approximation with collocation discretization techniques. Building upon the FPM, Breitkopf et al. [20] presented a double-grid diffuse collocation method using a sequence of two first-order numerical derivations. Duarte and Oden proposed the h-p cloud method [21,22] to solve boundary-value problems. Lee et al. [23] introduced the meshfree point collocation method (MPCM) and applied it to elastic crack problems. Aluru developed the point collocation method with reproducing kernel approximations [24] to overcome the problems of nodal volumes and the implementation in boundary conditions. The moving least-square reproducing kernel approximations technique [25] does not require the derivative calculation and has been successfully used to solve the Poisson and Stokes equations. However, the relevant researches indicate that the direct collocation method is not inferior in accuracy and stability [26,27] to the Galerkin-type meshless methods in solving simple problems, but its accuracy and stability significantly decrease when dealing with complex problems [28].

To mitigate the instability issues in traditional collocation methods, some methods based on the least-squares discretization technique have emerged. Zhang et al. [29] came up with the least-squares collocation meshless method, which possesses high accuracy with low computational effort. Park et al. [30–32] suggested the least-squares meshfree method (LSMM) to eliminate problems caused by integration operations and employed it to perform the metal forming analysis. Zhang et al. [33] extended their study to the weighted least-square method. Liu et al. [34] proposed a least-squares radial point collocation method (LS-RPCM) to perform adaptive analysis stably. The nonlinear integral differential equation with multiple kernel terms was calculated in two steps by a localized meshless collocation method [35], which has the characteristic of unconditional stability. The fractional Rayleigh-Stokes problem was solved by Avazzadeh et al. [36] using a localized hybrid kernel meshless technique, which makes the method obtain stable results after overcoming the ill-conditioning issue. Kee et al. [37] proposed the regularized least-squares radial point collocation method (RLS-RPCM1), where the regularization technique has successfully stabilized the solution of RPCM for the forward problems.

Moreover, in order to eliminate the computational instability of the collocation method, Yang et al. [38] conducted a meshless intervention point method (MIP) with h-p-d adaptability by using the local interpoint approximation technique and extended their research [39] to a meshless global dielectric method (MGIP) derived from the generalized variational principle.

Aiming to cure some defects of a single discrete approach, or to improve computational stability, or to facilitate the application of boundary conditions, a class of coupled discrete methods have also been proposed. Through combining collocation method and meshless local petrov-galerkin (MLPG), Liu et al. [40] put forth a meshfree weak-strong (MWS) form method. On the basis of collocation method and Galerkin method, Pan et al. [41] developed the Galerkin lest-squares method (MGLS). The coupling of SPH [42–45] and finite element method (FEM), outlined by Vuyst et al. [46], showcased benefits in extreme deformations problems. Merging the merits of MLPG and MIP, Yang et al. [47] illustrated the meshless local strong-weak (MLSW), which can easily implement boundary conditions while ensuring accuracy.

The following sections of this paper aim to provide a comprehensive perspective review on the applicability of the collocation method to solve engineering problems. Firstly, in Section 2, the principles of the collocation method are presented, along with the common approximation schemes used within this method. Next, successful applications of the collocation method to address problems in solid mechanics, beam-plate-shell structures, fracture problems, multi-field coupling problems, as well as heat conduction and fluid flow problems are thoroughly illustrated. To present the performance of the collocation method in real engineering scenarios, a numerical example is provided in Section 6, showcasing the application of a subdomain-free element method developed by our research group to a corrugated sandwich structure within a thermal protection system. Finally, the future trends and developments with respect to the collocation method are outlined in Section 7.

2  The Principle of Collocation Method

From the perspective of interpolation, the collocation method can be introduced as follows. Let us first consider function interpolation methods. Subsequently, a function u(x) can be approximated by a simpler function u~(x) that fulfills the interpolation conditions

u~(xi)=u(xi),i=1,2,…,n(1)

where n is the number of interpolation points distributed in the domain Ω. Generally, the interpolation function is a part of a n-dimensional linear space V. Thus, it can be shown as

u~(x)=∑i=1nβiYi(x)(2)

where Y1(x),…,Yn(x) are basis functions which span V. Note that the coefficients βi can be determined according to the interpolation conditions, viz. Eq. (1) after a linear system of n algebraic equations are solved.

Subsequently, the following differential equation needs to be solved approximately

Lu(x)=Q(x)(3)

where L is an invertible differential operator, and q(x) is a source function. Similar to the interpolation implement, the collocation method aims to find an approximating function u~(x)∈V that satisfies

Lu~(xi)=Q(xi),i=1,2,…,n(4)

Substituting Eqs. (2) into (4), the collocation method can be presented in a matrix form:

[LY1(x1)LY2(x1)…LYn(x1)LY1(x2)LY2(x2)…LYn(x2)⋮⋮⋱⋮LY1(xn)LY2(xn)…LYn(xn)][β1β2⋮βn]=[Q(x1)Q(x2)⋮Q(xn)](5)

From the perspective of numerical computation, collocation method can be regarded as a special type of weighted residual method (WRM) [48]. Its basic theory is described as follows. For a given engineering problem governed by partial differential equations (PDEs), it has the following definition:

F(u)−f=0,inΩ(6)

G(u)−g=0,on∂Ω(7)

When substituting the trial function u~=∑i=1nβiYi into Eqs. (6) and (7), generally, residuals appear, which can be expressed as

RI=F(u~)−f≠0(8)

RB=F(u~)−g≠0(9)

The collocation method is defined as treating the weighted function that plays a role in eliminating residual as Dirac δ function, which can be mathematically written as

∫ΩwiRIdΩ=∫Ωδ(x−xi)RIdΩ=RI=0(10)

∫ΓwiRBdΓ=∫Γδ(x−xi)RBdΓ=RB=0(11)

in which

δ(x−xi)={∞,x=xi0,x≠xi(12a)

∫−∞∞δ(x−xi)dx=1(12b)

∫xi−cxi+cδ(x−xi)dx=1(c>0,c→0)(12c)

Observing Eqs. (10) and (11), in a word, the collocation method is a numerical method that enforces the residual generated by each collocation point in the governing equation to be zero. Therefore, the advantages of the collocation method lie in its simplicity, implement convenience, and high efficiency. However, its drawbacks are primarily manifested in computational instability, lower solution accuracy, and slow convergence speed.

2.1 Approximation Scheme

There are many ways to construct approximation functions according to collocation information, and the choice and definition of these functions will directly affect the stability, accuracy, and applicability of the method. The following content will briefly introduce some commonly used approximation schemes.

2.1.1 Moving Least Square (MLS) Approximation

Moving least square method was initially used for curve fitting [49], and was then further developed by Wixom et al. [50], Lancaster et al. [51]. As shown in Fig. 2, MLS approximation functions generally employ a linear combination of polynomial basis functions and for the nodeIin the support domain ΩS (Generally with circular Fig. 3 and rectangular shape Fig. 4), the approximation function can be written as

uI(x)≈u~I(x)=∑i=1mpi(x)ai(x)=pIT(x)a(x),x∈ΩS(13)

which p(x)=[p1(x),p2(x),…,pm(x)]T is polynomial basis functions, m is the number of terms in the complete polynomial basis functions, a(x)=[a1(x),a2(x),…,am(x)]T is the coefficient vector.

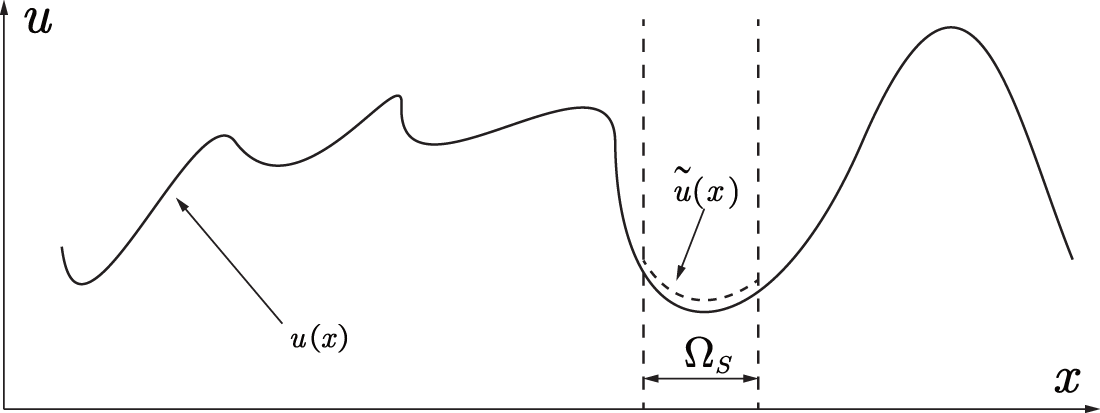
Figure 2: MLS approximation for the 1D problem

Figure 3: Support domain with circular shape

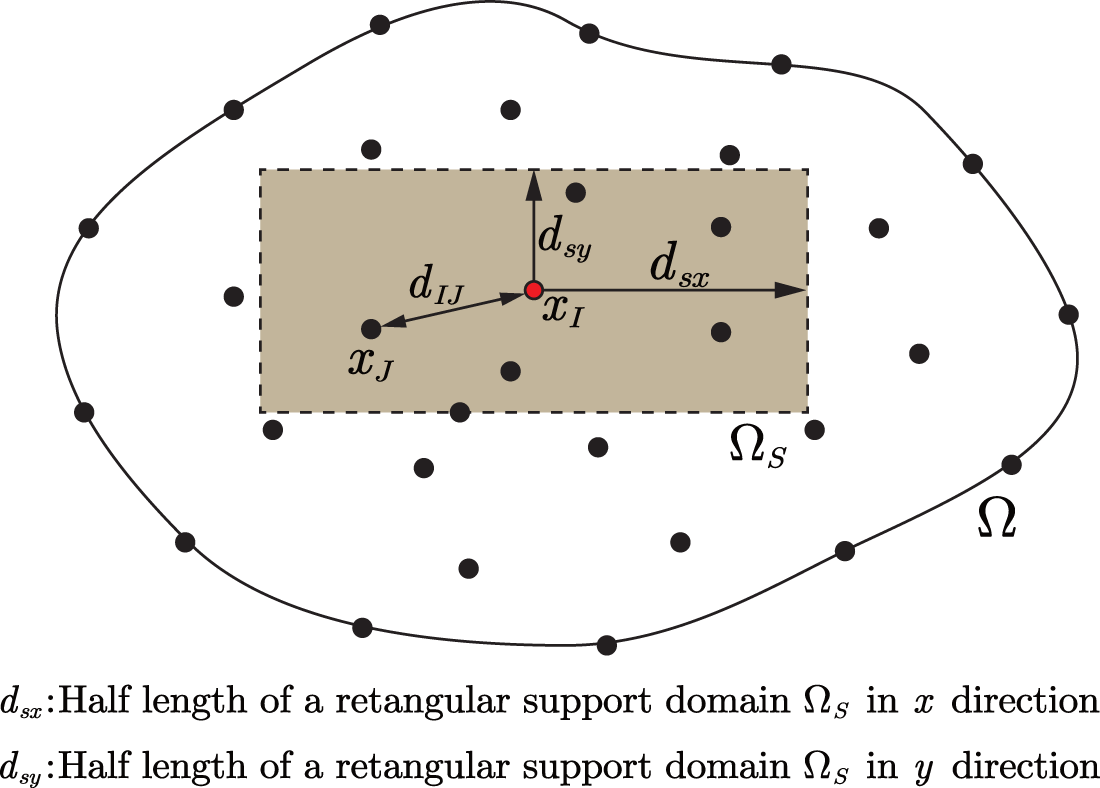
Figure 4: Support domain with rectangular shape

Aiming to determine the coefficient vector a(x), a weighted discrete L2-norm is constructed in the support domain ΩS:

J(a)=∑J=1NwJ(x)[pJT(x)a(x)−u^(xJ)]2(14)

where N is the total number of nodes in the domain ΩS, wJ(x) is the weight function at node J.

To find the stationary value of the functional J(a) with respect to a(x), viz. ∂J/∂a=0, it yields

a(x)=A−1(x)B(x)u^(15)

in which

A(x)=∑J=1NwJ(x)pJ(x)pJT(x)(16)

B(x)=[w1(x)p1(x),w2(x)p2(x),…,wN(x)pN(x)](17)

u^=[u^1,u^2,…,u^N]T(18)

Substituting Eqs. (15) into (13) leads to

u~I(x)=pIT(x)A−1(x)B(x)u^=∑J=1NϕJ(x)u^J=Φ(x)u^(19)

in which

ϕJ(x)=pIT(x)[A−1(x)BJ(x)](20)

For the calculation of the derivative of the shape function ϕJ(x), two ways have been proposed by Nayroles et al. [52] and Belytschko et al. [53]. In addition, to improve the efficiency of constructing the MLS approximation scheme, Cheng et al. [54] proposed the complex variable meshless method (CVMLS). In this method, the unknown coefficients are smaller in number than the MLS approximation, which means that there are fewer nodes used to discretize the model.

2.1.2 Kernel Approximation

Smoothed particle hydrodynamics (SPH) [55–57] has been widely employed in various fields, such as fluid, impact, and explosion mechanics, and it offers distinct advantages for problems that involve density as a field variable.

For the function u(x), Kernel approximation can be presented as

uI(x)≈u~I(x)=∫ΩuJ(x)wJ(x−xI,h)dΩS(21)

where h is the radius of the smooth domain. wJ(x−xI,h) is the kernel function, which can also be called the weight function. And the kernel generally has the following properties:

∫ΩwJ(x−xI,h)dΩS=1(22)

limh→0wJ(x−xI,h)=δ(x−xI)(23)

wJ(x−xI,h)>0,∀x∈ΩS(xI)(24)

wJ(x−xI,h)>0,∀x∉ΩS(xI)(25)

In general, the weight function in Eq. (21) is selected as the Gaussian and spline functions. And Eq. (21) can be calculated as

u~I=∑J=1NuJ(x)wJ(x−xI,h)VJ(26)

where VJ represents the spatial measure corresponding to the J-numbered particle xJ, that is, the three-dimensional problem represents the volume and has

VJ=mJ/ρJ(27)

where mJ and ρJ are the mass and density at node xJ, respectively.

Hence, substituting Eqs. (27) into (26), it yields

u~I=∑J=1NϕJ(x)uJ(28)

in which

ϕJ(x)=mJρJwJ(x−xI,h)(29)

2.1.3 Polynomial Basis Approximation

For the approximation function, polynomial basis approximation uses a linear combination of polynomial basis functions:

u~(x)=∑i=1pi(x)ai=pT(x)a(30)

where p(x)=[p1(x),p2(x),…,pm(x)]T, a=[a1,a2,…,am]T is the coefficients vector, which can be obtained by constructing a functional expression,

J=∑J=1N[pJT(x)a−u^J](31)

Let J=0 at each collocation node, it yields

a=P−1u^(32)

where

P=[pJT(x)]J=1N=[p1(x1)p2(x1)…pm(x1)p1(x2)p1(x2)…p1(x2)⋮⋮⋱⋮p1(xN)p2(xN)…pm(xN)](33)

Hence, for the computation node xI, the approximation scheme can be written as

u~I(x)=pIT(x)a=pIT(x)P−1u^=∑J=1NϕJ(x)u^J=Φ(x)u^(34)

where Φ(x) is the shape function:

Φ(x)=[ϕ1(x),ϕ2(x),…,ϕN(x)]=pIT(x)P−1(35)

in which its derivative can be calculated as

Φ,i(x)=pI,iT(x)P−1(36a)

Φ,ij(x)=pI,ijT(x)P−1(36b)

Note that the shape functions belonging to the point interpolation have Kronecker δ property. Hence, the Dirichlet boundary conditions can be directly imposed. However, point interpolation approximate requires that the number of support points N must be strictly equal to the number of terms m of the basis function vector, which is a very strict condition, and the arbitrary distribution of support points can easily lead to the singularity of the P(x) or the deterioration of the condition number. Therefore, the compatibility of the construction method of this approximation function is poor.

2.1.4 Generalized Finite Difference Approximate

The generalized finite difference approximation is proposed to adapt to arbitrary irregular grids, which belongs to a nodal approximation technique in essence. However, this approximation scheme is not aimed at approximating the field function, but rather at approximating the differential variables of the field function. On the supporting domain ΩS of a node xI, the approximate function of the field variable u(x) can be expressed by Taylor expansion:

u(x)≈u~(x)=uI+h∂uI∂x+k∂uI∂y+h22∂2uI∂x2+k22∂2uI∂y2+kh∂2uI∂x∂y+O(Δ3)(37)

in which

uI=u(xI,yI)(38a)

h=x−xI(38b)

k=y−yI(38c)

Δ=h2+k2(38d)

By applying Eq. (37) to calculate the local support point set xJJ=1N of point xI, a set of linear equations can be obtained

a⋅d=f(39)

Note that the node xI are not in the set xJJ=1N, and

a=[h1k1h12/2k12/2h1k1h2k2h22/2k22/2h2k2⋮⋮⋮⋮⋮hJkJhJ2/2kJ2/2hJkJ⋮⋮⋮⋮⋮hNkNhN2/2kN2/2hNkN](40)

d=[∂uI∂x,∂uI∂y,∂2uI∂x2,∂2uI∂y2,∂2uI∂x∂y]T(41)

f=[(u1−uI),(u2−uI),…,(uN−uI)]T(42)

Then, the five unknown derivative variables of the node xI can be expressed as

d=a−1f(43)

In order to ensure the consistency of the approximations and avoid the singularity of a, it is necessary to increase the number of supporting points, namely, N>5, and construct the following functional expression on this set of points

Π=∑J=1N1ΔJ3(aJd−fJ)2,N>5(44)

in which

aJ=[hJkJhJ22kJ22hJkJ](45)

fJ=uJ−uI(46)

Taking the stationary value of a functional, viz. ∂Π/∂d=0, it yields,

d=A−1Bf(47)

in which

A=∑J=1N1ΔJ3aJTaJ(48a)

B=[a1TΔ13a2TΔ23…aJTΔJ3…aNTΔN3](48b)

Obviously, the generalized finite difference approximation results in a differential expression for the field variable computed at point xI

di=∑J=1N(A−1BJ)i⋅(uJ−uI)(49)

In the process of calculation, only the field variable uI and its differential approximation di are brought into the governing equation and its boundary conditions, then the discrete equation can be constructed and solved.

3  Collocation Methods in Solid Mechanics

In order to study the behavior mechanism of solid mechanics, collocation methods have been paid considerable attention. Known for their meshless characteristics, collocation methods have been widely used to simulate elasticity, plasticity, fracture mechanics, and multi-filed coupling problems. This section will provide an overview of research achievements in collocation methods in the solid mechanics field, at the same time, the perspective of future research to further advance the development of this field is explored.

3.1 Elasticity and Plasticity

Elastic and plastic mechanics have consistently represented fundamental challenges in the engineering field, encompassing various aspects from the elastic behavior of materials to plastic deformation and failure. Collocation methods, as a highly promising numerical approach, have demonstrated remarkable potential in addressing problems related to elastic and plastic solid mechanics. Collocation methods discretize structures through distributed points, also known as nodes or collocation nodes, providing flexibility in handling complex geometries and material heterogeneity. Consequently, these characteristics become a powerful tool for studying material elasticity and plasticity. This subsection will focus on the application of the collocation methods in problems related to elastic and plastic solid mechanics problems, and focus on the advantages of the collocation methods in dealing with complex geometries, large deformations, and large strains. Through an extensive literature review, the aim is to provide a comprehensive perspective to better understand and apply the collocation method to solve complex engineering problems involving material behavior.

A meshless stable collocation method [58] using reconstructed kernel approximation as an approximation function is presented. Through performing high-order accurate integration in regular subdomains, it has the characteristics of high efficiency, high accuracy, and good stability, and the superiority of the method is verified by elasticity examples. The variable collocation method [59] combines the efficiency of the collocation method with the accuracy of the Galerkin method, and the potential of the method is demonstrated in examples of linear and nonlinear elasticity. Incorporating isogeometric techniques and boundary scaling techniques, the 2D solid problem can be solved by a surface-oriented formulation called the Non uniform rational B-spline (NURBS)-based hybrid collocation-Galerkin method [60], which allows modeling with an arbitrary number of boundaries. Then through using NURBS based collocation method to solve ordinary differential equations, Chen et al. [61] extended their research to three-dimensional solid problems, which can also be nonlinear problems. Using the meshless point grafting method, an effective shear modulus approach [62] was presented to analyze the elastoplastic analysis for two-dimensional solids and plates, and this method has the advantages of its simplicity and easy implementation for material properties. For the transient elastodynamic cracked solid with anisotropy material properties, the time-domain boundary element method [63] was presented with spatial discretization by the Galerkin method and temporal discretization by the collocation method. The contribution of this method is to convert the arising hypersingular integrals to weakly singular integrals and this method was further applied to transient 2D piezoelectric cracked solids [64]. Isogeometric (IGA) collocation formulation [65] was developed to solve steady-state statics and dynamics problems. It has stable results, robust, high-order accuracy, and higher computational efficiency than the finite element method. Afterward, this method was extended to solve large deformation problems and hyperelastic material behavior [66]. Subsequently, for linear and plastic materials, the mixed stress-displacement isogeometric collocation method [67] was proposed. It not only has higher computational efficiency than the conventional IGA method but also overcomes existing issues such as volume self-locking and instability. Stevens et al. [68] proposed a meshless local radial basis function (RBF) collocation method with high convergence rates and applied it to solve linear elasticity problems. Based on the moving least squares approximation, the local meshless formulations [69] were established for the elastic field, which can ensure the accuracy of the results and reduce the calculation cost. Based on the T-spline IGA technique, the hybrid variational-collocation immersed method [70] was proposed to solve the fluid-structure coupling problem, and its results agree well with the exact solution. The gradient-reproducing kernel collocation method [71] was developed to solve elastic problems. The main highlight of this method is that it simplifies the calculation process of the reproducing kernel collocation method (RKCM) method while ensuring optimal convergence. Afterward, this method [72] was employed to solve high-order PDEs, and the results show that its computational efficiency is much higher than the traditional RKCM. In addition, using the least square approximation, the weighted reproducing kernel collocation method [73] was introduced to the inverse elasticity problem. The meshless singular boundary method [74] combines the dimensionality reduction of the BEM method and maintains the merits of meshless and integration-free attributes of the fundamental solution method. Besides, it performs well for elastic problems with complex geometries. By introducing the fixed, moving, and multiple fixed kernel techniques, the efficiency and accuracy of the finite cloud method [75] surpass those of the point collocation method. Computational outputs show that as a truly meshless method, this method has a good prospect in engineering applications. The radial point interpolation collocation method [76] was adopted in dealing with nonlinear Poisson equations. In this method, for imposing Neumann boundary conditions, Hermite interpolation was chosen to improve the numerical stability. Next, the radial point collocation method was evolved to a regularized least-square radial point collocation method [37] through introducing a regularization technique, which can ensure the stability and accuracy of the results. Moreover, as a pure meshless method, this method can avoid the mesh reconstruction progress. A weighted strong-form collocation framework [77] was constructed to numerically analyze incompressible linear elastic structures. And this method does not exist the volume locking problem and has good convergence. The advantage of the modified equilibrium on line method (ELM) [78] was that in elastodynamics problems, the natural boundary conditions are automatically satisfied through a weak formulation, and the two forms of shape function construction including moving least square approximation and radial basis point interpolation approximation, are discussed. The results show that the method was more stable and accurate than the direct collocation method. Compared with the DRK approximation based-collocation method, the differential reproducing kernel (DRK) interpolation-based collocation method [79] has the advantage that the shape function of the DRK interpolation function has the delta property, which can achieve the purpose of reducing the computational cost.

3.2 Beams, Plates, and Shells

The analysis and design of beam, plate, and shell structures have always been crucial tasks in engineering problems. They are widely used in aerospace, bridges, vessels, and various mechanical systems. Comprehensive understanding and optimizing the behavior of these structures are paramount to ensuring their performance, safety, and sustainability. And various corresponding theories have been developed, including the first-order shear deformation theory and higher-order shear deformation theory. Collocation methods, as a powerful numerical tool, have played a pivotal role in addressing engineering problems related to beam, plate, and shell structures. Unlike traditional finite element methods, collocation methods do not require mesh, offering greater flexibility in handling complex geometries and boundary conditions. This makes them an ideal choice for exploring deformation, heat conduction, vibration, and other issues in these structural elements. In this subsection, a series of relevant literature on the application of meshless methods in beam, plate, and shell structures is reviewed to showcase the latest research advancements and engineering practices in this field. By gaining an in-depth understanding of the strengths and limitations of these methods, a better understanding of their potential and applicability in the analysis of beam, plate, and shell structures can be obtained.

The isogeometric analysis (IGA) method [80] has gained wide attention from scholars. Reali and Gomez first introduced the isogeometric collocation approach [81] to thin structures including Euler beams and Kirchhoff plates, and numerical results show that this approach has strong adaptability for complex geometric models and has good convergence. Marino applied the isogeometric collocation method [82] to calculate the nonlinear beam, and the selected rotation parameterization technique made the approach accurate and efficient. The displacement-based and mixed IGA formulations [83] allow to analyze beams with arbitrary bending curvature, and it can adapt to complex geometric models without the self-locking problem. Pavan et al. [84] extended the isogeometric collocation (IGA) method to solve laminated composite beams. Like in most strong-form methods, the governing equations are discretized directly, which makes the computation more efficient, and a variety of shear deformation theories are considered in numerical examples to verify the method’s accuracy. In order to overcome the problem appearing in the Serret–Frenet (SF) local frame and on the Darboux vector, an IGA-C method [85] relying on Bishop frames was presented. The nonlinear dynamic state of the piezoelectric energy harvester was analyzed by a nonlocal couple stress-based meshless collocation scheme [86], in which the coalesce basis function can effectively eliminate the singularity. The Chebyshev collocation method [87] computed the dynamic behavior of nonlinear beams without integral operation, and the eigenvalue analysis was accurately given. A collocation meshless method [88] is proposed to study 3D functionally graded beams, in which the non-classical effects can be dealt with directly. For the Bernoulli-Euler beams and Kirchhoff-Love plates, Chen et al. [89] developed a Hermite DRK interpolation-based collocation method to solve them with a variety of boundary conditions. Absorbing the advantages of the IGA method and boundary element method, the collocation-based isogeometric boundary element method [90] can calculate the shell structure at a lower computational cost. The nanocomposite cylindrical shells were analyzed by a Chebyshev collocation-based semi-analytical approach [91], and its results can help to improve the stability of the shell structures. Based on the higher-order shear formula, the free vibration behavior of functionally graded shells is carried out by the collocation method [92] using the radial basis function. The spectral collocation method with orthogonal polynomials [93] was used to analyze the free vibration of laminated shell structures. The advantage of this method relied on that it allows shell structures with arbitrary boundary conditions. For the steady-state or transient nonlinear behavior of circular plates, the interior global orthogonal point collocation method was developed by Nath et al. [94]. According to the first-order shear theory, the displacement and rotation of a shell with conical geometry were expressed by Chebyshev and Fourier polynomials [95], respectively. The highlight of this method was its simplicity owing to no need for any numerical integration or differentiation in the computing process. Combining the radial basis functions and collocation method, Wang et al. [96] proposed radial basis collocation method (RBCM) to adopt the thin functionally graded shells with heterogeneous materials. Afterward, Wang et al. [97] proposed the Hermitian collocation method and showed that the introduced gradient reproducing kernel approximations technique can avoid the high order differential operation to improve the computational efficiency. Moreover, this method has higher precision than the direct collocation method at the boundary. Considering the thermal environment, the buckling analysis of the nanocomposite plates was studied by a 2D Chebyshev collocation method [98], and the factors affecting the stability and critical angular velocity were investigated. The Chebyshev collocation method [99] was used to discretize the dynamic equations of large deformation displacement of sandwich plates in the post-buckling state, and many factors affecting the natural frequency were discussed in detail. The meshless collocation method [100] using the spline radial basis function was performed to research the hyperelastic behavior of silicone plates under uniformly distributed loading, and the effectiveness of the method was verified by experiments. Three kinds of formulations were listed to solve the bending problem of laminated composite plates, and then the isogeometric collocation method [101] was used to discretize the equations, the effect of which can reduce the shear locking issue of plates under a clamped state. For laminated plates composed of thin plates and thick plates, Ferreira et al. [102] suggested a solution method that brings the radial basis function collocation technique into Carrera’s Unified formula to predict the steady-state and transient behaviors. By using the meshless collocation technique to deal with the boundary and using the weak formula to deal with the differentiation calculation, Wu et al. [103] proposed the Reissner mixed variational theorem (RMVT)-based meshless collocation (MC) and element-free Galerkin (EFG) methods for functionally graded plates, and this method had good convergence. For the bending problem of Kirchhoff plates [104], the governing equation was discretized by the radial basis approximation scheme, and the singularity and symmetry belonging to the system of equations were handled by the Hermitian collocation method.

3.3 Fracture Analysis

In materials science, the issue of fracture behavior has always been a vital study area, impacting structural reliability and safety. Collocation methods with meshless nature allow for less effort handling in complex geometric shapes and crack propagation processes. Moreover, it eliminates the complexities associated with mesh generation and remeshing, thus offering remarkable flexibility and precision in predicting crack propagation, crack tip behavior, and stress intensity factors. Subsequently, the research achievements of collocation methods in the fracture mechanics field will be presented in this subsection.

Nguyen-Thanh et al. [105] established a scheme for the crack propagation in fiber-reinforced composites on a microscopic scale by means of the isogeometric meshfree collocation method. In addition, this method has the strength of adaptive analysis. Schillinger et al. [106] advocated a hybrid isogeometric method with higher computational efficiency than the Galerkin method. The combination of the collocation method and the Galerkin formula can deal not only with the second boundary conditions and interface constraints but also with the integral terms. Combining with the boundary element and boundary collocation technique [107], crack propagation and coalescence phenomena were accurately predicted. The enriched meshfree collocation method [108] was presented to build a framework for fracture problems. The advantage of this method was that the calculation of the derivative for the weight function or moment matrix could be avoided by an approximation technique. Problems with non-convex geometry and local characteristics were dealt with by the subdomain radial basis collocation method [109], which improves the adaptability of the traditional RBCM. The crack problem for functionally graded piezoelectric/piezomagnetic materials was performed in a finite domain by the boundary collocation method [110] with the semi-inverse technique, and the factors affecting the crack behavior were discussed.

3.4 Coupled Multi-Physics Problems

Multi-field coupling problems involve interactions between multiple physical fields including elastic, thermal, electric, magnetic fields, and so on. Collocation methods, with their high suitability for addressing multifield problems, can effectively simulate the behavior of multi-physical fields. In this subsection, the relevant literature on the application of collocation methods to predict multi-field coupling problems will be reviewed.

For the 2D flexoelectric structures, the collocation mixed finite element method [111] with C0 continuous approximation can reduce the number of degrees of freedom compared with the traditional Lagrangian method, and the obtained results were helpful to the structural safety analysis. Later, they continued their research [112] to explore the effect of flexoelectricity properties on the crack tip. The virtual boundary element-integral collocation method [113] was proposed to address the magneto-electro-elastic coupling problem. The key innovation of this method lies in the use of a virtual boundary to circumvent singularity issues at the physical boundary. Considering the elasto-visco-plastic problem for 3D beams, a mixed isogeometric collocation method [114] directly discretized nonlinear differential equations like most strong-form approaches. In this method, the physical variables including displacement, orientations, and stress were discretized by B-splines or NURBS, and the time term was discretized by an implicit return-mapping scheme. The relationship between the nonlinear dynamic behavior and the size of the energy harvester involving the electro-elastic coupling field was studied by the meshless collocation method [115], and the accuracy of this method was guaranteed by the strain gradient technique. Wu et al. [116] extended the meshless collocation method to shell structures under thermo-electro-elastic multi-coupled fields. The method’s highlights rely on that the differential of the shape functions could be obtained by differential reproducing conditions, and the delta property owing to the shape functions made it easy to impose Dirichlet boundary conditions. In our previous work, the zonal free element method [117], initially proposed by Gao et al. [118], discretized the governing equations for the electro-elastic coupling field in a strong form, and its highlight lay in overcoming the corner problem in the meshless method through the zonal technique. Then, our research was extended to treat the transient thermo-electro-mechanical multi-field coupling problem [119], whose accuracy and stability are guaranteed by the Galerkin scheme. Due to the wide applicability of the magnetoelectric coupling effect, the multi-physics zonal Galerkin free element method [120] was proposed to analyze the dynamic responses of the functionally graded magneto-electro-elastic structures.

4  Collocation Methods in Heat Conduction and Fluid Flow

Heat conduction and fluid dynamics are pivotal and inescapable engineering problems. For heat transfer problems, the collocation method can effectively simulate intricate heat transfer phenomena such as heat conduction, convection, and radiation by employing numerical discretization and approximation techniques. For fluid flow problems, by modeling them into differential equations and applying suitable numerical techniques, the collocation method efficiently addresses various crucial aspects including flow velocities, pressure distributions, and fluid characteristics, which play a pivotal role in enhancing the design and optimizing the performance of engineering systems. This section embarks on an exploration of a series of literature studies to showcase the significant advancements and successful cases of the collocation method in solving heat conduction and fluid flow problems.

4.1 Heat Conduction Problems

Accompanied by randomly distributed collocation points and radial basis functions approximation, a meshless collocation framework [121] was brought up to solve heat conduction problems. However, two significant issues urgently required resolution. One is that the solution matrix is not sparse. The other is that with an increase in the number of collocation points, the ill-conditioning of the solution matrix and computational cost also increased. The Legendre wavelet collocation method [122] was employed to simulate the behavior of porouselastic structures in a thermal environment. Utilizing the Kirchhoff mapping technique, the solution of the non-linear term caused by variable thermal conductivity was achieved. A standout feature of this method was its ability to provide high-accuracy results even with a low number of collocation points. The heat transfer problem about an infinitely long cylindrical structure was computed by the spectral collocation method [123]. Both the Eulerian scheme and spectral collocation scheme discretize the time, spatial, and derivative terms, resulting in computational results with high accuracy. In a similar vein, Chen et al. [124] utilized the spectral collocation method to analyze two physical models for natural convection in a square cavity, and they investigated several factors that influence the dimensionless stream function and temperature distribution. The temperature distribution for the radiative heat-conductive porous fin [125] was approximated using Lagrange interpolation polynomials in the spectral collocation method. Besides, the method’s effectiveness was validated by comparing the results with previously reported literature. In heat conduction problems with functionally graded materials properties, the time-fractional derivative terms were handled by a localized collocation approach [126] with fundamental solutions. A hybrid method [127] that combined collocation methods with the Galerkin method was capable of efficiently computing the convective heat transfer problems generated by incompressible flow outside a cylinder. The contribution of this method was that under the assumption that the heat flux has no influence on the velocity field, the uncertainty of inflow velocity and the wall heat flux were solved. The meshless collocation method using the B-spline function approximation technique, named the meshless local B-spline collocation method [128], provided a new idea for addressing transient heat conduction problems with heterogeneous material properties. As a purely meshless technique, its advantage lay in that it could directly deal with the discontinuity of the material interface.

4.2 Fluid Flow Problems

Karageorghis et al. [129] obtained the answer to the two-point boundary value problems using the spectral collocation method, and the standout feature of the method was that the performance of the trial function was not affected by nonlinear terms. In the Lagrangian framework, the weighted meshless collocation method [130] excelled not only in its ability to easily capture moving boundaries or interfaces but also in its avoidance of the introduction of coefficients to handle incompressible terms. Besides, numerical results obtained by this method were better than traditional finite difference method (FDM) or SPHs. Aronson et al. [131] introduced the residual-based stability technique into the isogeometric collocation method. The method not only inherits excellent convergence and accuracy but also can address the issue of spurious oscillations in scalar transport and incompressible fluid problems. Aiming to treat the fluid-structure coupling problem, the research objects within the Eulerian mesh were discretized by Lagrangian particles. In addition, this method [132] ensured high-order continuity between nodes and particles and offered greater efficiency in calculating shape functions compared to SPH methods. Then, they applied this method to simulate the water wave problem [133]. Aronson et al. proposed two schemes, the velocity-pressure scheme and the vorticity-velocity-pressure scheme, for analyzing incompressible flow problems [134], and the results indicated that the latter approach exhibited a faster convergence rate compared to the former one. Furthermore, this method combined high-order accuracy while inheriting the advantages of computational efficiency associated with the collocation method. The fluid flow phenomena in the thermal environment were studied through the local radial basis function collocation method [135] in which the numerical solution’s efficiency was ensured by the artificial compressibility method. The groundwater flow with unconfined conditions was predicted by the meshless point collocation method [136] using radial basis functions, which had the simplicity of directly discretizing the governing equation. The challenge of the 2D stream-vorticity problem has been resolved using the meshless point collocation method [137]. The contribution of this approach lies in its ability to obtain derivatives of arbitrary functions through shape functions constructed by the moving least squares approximation, offering a novel way for imposing vorticity boundary conditions. For biomedical issues, a localized collocation meshless method [138] has been employed to investigate the hemodynamics problem with incompressible flow properties. Numerical oscillations had been suppressed by a high-order upwind scheme, leading to third-order accuracy in the obtained results. The meshless collocation method using Hermitian radial basis approximation calculated the transient responses of the convective-diffusion problem [139]. It is worth noting that accurate calculation results could still be obtained even under conditions of a strong velocity field and a long time. A spectral collocation method [140] numerically computed the 2D axisymmetric boundary layer equations with the compressible properties. In addition, the preconditioning operation for the governing equations accelerated computational efficiency, and the results indicated that the influence of transverse curvature on stability should be paid attention. Later, they continued their study [141] to three-dimensional incompressible flow problems. The real compressible flow problem was explored by the finite point method [142], at the same time, the h-adaptive technique was also proposed. The numerical results including the wings were satisfactory, which proved the ability of the method to solve practical problems. Through the singularity subtraction technique and asymptotic expansion, Botella and Peyret also applied the Chebyshev collocation method [143] to address singularity issues arising from boundary discontinuities or changes in boundary condition types. Still utilizing the Chebyshev collocation method, the boundary layer flow problem of magnetohydrodynamic, as a non-Newtonian fluid, was numerically investigated [144]. Note that in this approach, the governing equations could be transformed into ordinary differential equations.

5  Recent Advances in Collocation Methods

With the development of numerical methods, several novel collocation methods have emerged in recent years. Based on smoothed gradients technique, Wang et al. [145] proposed a superconvergent gradient smoothing meshfree collocation method. This method not only overcomes the basis degree discrepancy issue but also realizes the second accuracy by linear basis function. Subsequently, they extended their research to laminated composite plates [146] and completed work on accuracy analysis [147] of meshless collocation methods. By introducing fractional Lagrange interpolants obeying the spectral theory, fractional spectral collocation method with exponential convergence was proposed by Zayernouri et al. [148] to deal with fractional partial differential equations. Fu et al. [149] first introduced the localized collocation schemes and summarized several complicated problems successfully solved by these methods. Trigonometric Fourier collocation method with arbitrary order was proposed by Wang et al. [150] to solve multi-frequency oscillatory problems. Combining collocation method and deep learning method, the bending problem of the Kirchhoff plate was computed by the deep collocation method proposed by Guo et al. [151]. Through the recursive gradient formulation, Wang et al. [152] established a superconvergent isogeometric collocation method, which processes higher computational efficiency than the standard isogeometric collocation method while ensuring the superconvergence property. Recently, our research group has also done a lot of work on the collocation methods. The three main methods to be described here are the element differential method [153], free element method [154], and finite line method [155]. Yan et al. [156–158] used updated Lagrangian particle hydrodynamics (ULPH) method to simulate the multiphase flows problem and solid object water entry problem. Yu et al. [159] established nonlocal differential operators in a unified way. Jingwen Ren et al. [160] gave a new idea for the IGA problems. Taking heat conduction as the background, the introduction to these three methods is briefly given below. First, in heat conduction, the governing equation and boundary conditions are presented as follows:

∂∂xi(λij(x)∂T(x)∂xj)+Q(x)=0,x∈Ω(50)

T(x)=T~(x),x∈Γ1(51)

q(x)=−λij∂T(x)∂xjni=q~(x),x∈Γ2(52)

q(x)=−λij∂T(x)∂xjni=h(T(x)−T∞),x∈Γ3(53)

where λij is second-order thermal conductivity tensor, T the temperature, T∞ the environmental temperature, Q the heat-generation rate, q the heat flux, and Γ1, Γ2, and Γ3 are the boundaries with respect to the given T~, q~ and T∞. ∂Ω=Γ1∪Γ2∪Γ3.

5.1 Element Differential Method (EDM)

As shown in Fig. 5, the isoparametric collocation elements are used to discretize the computational model. It is worth noting that in the 2D 9-node collocation element, the governing equation and flux equilibrium equation are satisfied at the internal node, interface nodes, and boundary nodes, respectively. The main innovation in EDM is to give the analytic expression (Eqs. (54) and (55)) of the derivative of shape functions in the second-order isoparametric element, which can directly discretize the governing equation without any other operation [153].

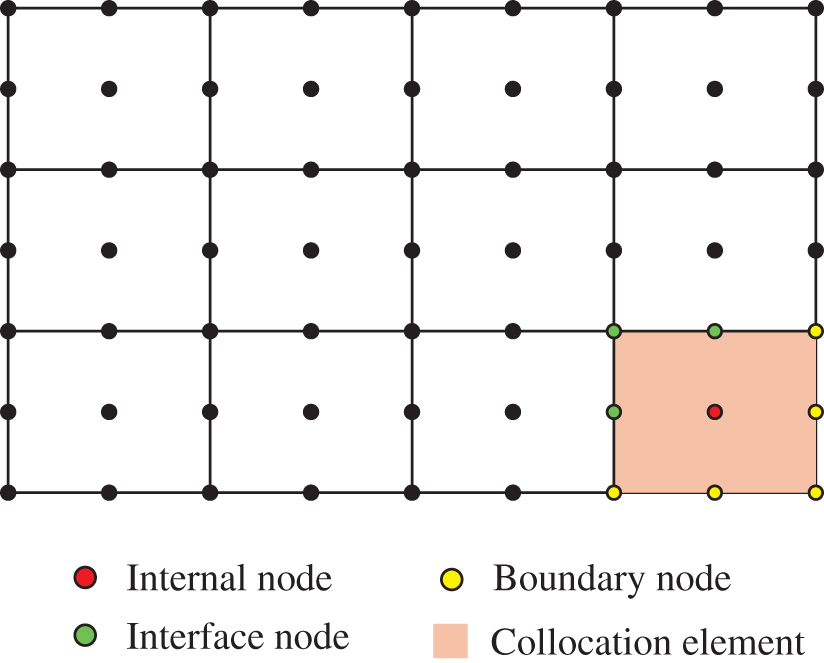
Figure 5: Collocation element in EDM

∂Nα∂xi=∂Nα∂ξk∂ξk∂xi=Jik−1∂Nα∂ξk(54)

∂2Nα∂xi∂xj=[[J]ik−1∂2Nα∂ξk∂ξl+∂[J]ik−1∂ξl∂Nα∂ξk]∂ξl∂xj(55)

where Nα is the shape function at node α. Jik is the Jacobi matrix. ξ and x are the coordinates in the global and local coordinates system, respectively.

Hence, the discretized equations for internal, interface, and boundary nodes are given as follows [153,161]:

[∂λij(ξ)∂xi∂Nα(ξ)∂xj+λij(ξ)∂2Nα(ξ)∂xi∂xj]Tα=−Q(ξ),ξ∈Ω(56a)

∑f=1M−λij(ξI)∂Nα(ξI)∂xjnif(ξI)Tα=0,ξ∈ΓI(56b)

∑f=1K−λij(ξb)∂Nα(ξb)∂xjnif(ξb)Tα=q(ξb),ξ∈Γb(56c)

where λij is the thermal conductivity. ξ,ξI,ξb are the local coordinates of internal, interface, and boundary nodes, respectively. M and K are the number of element surfaces related to the interface node and boundary node, respectively. nif is the unit normal with respect to surface f. q is known heat flux.

In summary, the element differential method is an element collocation method with high precision and high computational efficiency.

5.2 Free Element Collocation Method (FrEM)

The free element collocation element method retains the merits in using the analytic expression to directly discretize the governing equation and boundary conditions, and it has the distinct feature of freely forming the collocation element at each point and the element is connection-free with neighbor nodes’ elements [154]. Like in meshfree methods, a series of nodes are discretized in the computational domain in FrEM. At each collocation node, an independent local element, called as the free element, can be formed with the surrounding nodes, as shown in Fig. 6. Contrasting to EDM, no element interfaces exist in FrEM and therefore FrEM is suitable for both solid mechanics [118] and fluid mechanics [162].

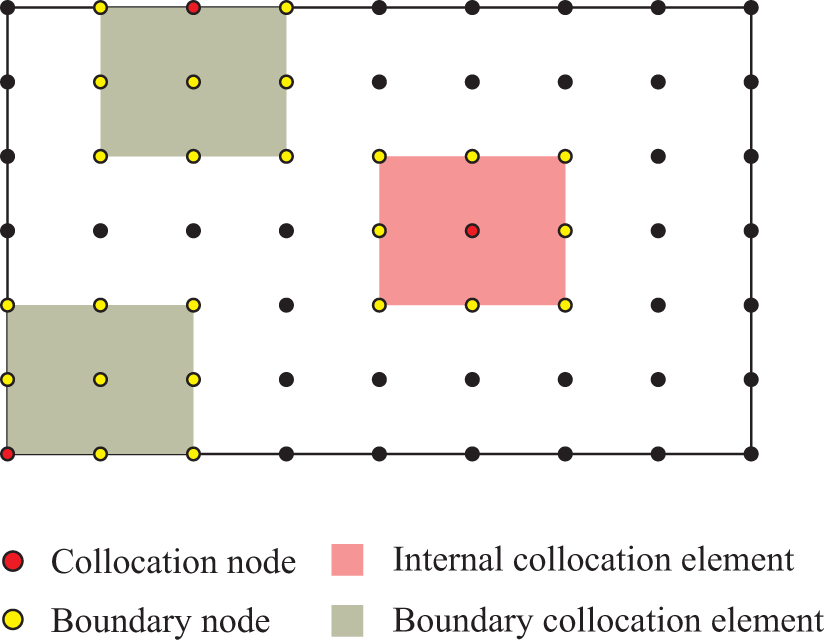
Figure 6: Collocation nodes and their 9-node free elements in FrEM

Taking the heat conduction problem as an example, the discretized equations in FrEM can be obtained from Eqs. (50) and (51) as [154]

[∂λij(ξc)∂xi∂Nα(ξc)∂xj+λij(ξ)∂2Nα(ξc)∂xi∂xj]Tα=−Q(ξc),ξ∈Ω(57a)

−λij(ξb)∂Nα(ξb)∂xjni(ξb)Tα=q(ξb),ξ∈Γb(57b)

where ξc and ξb are the local coordinates of internal and boundary nodes, respectively. ni is the unit normal. q is known heat flux.

In FrEM, the use of isoparametric elements can ensure its stability. Moreover, the distinct feature of freely forming an element at each point avoids the appearance of interfaces between elements, making it very adaptable for dealing with fluid problems using an upwind scheme [163]. FrEM has strong-form and weak-form schemes [164,165], and a lot of examples have been used to examine their stability and flexibility [154,162–165].

5.3 Zonal Galerkin Free Element Method (ZGFREM)

By absorbing the idea of the finite block method, ZGFREM is proposed by introducing the zone technique into FrEM. As shown in Fig. 7, the computational model is first divided into five zones, then each zone is discretized by a group of collocation nodes. Compared with FrEM, a new type of collocation node, the interface collocation node appears. It will form a collocation element for zone I and zone IV, respectively.

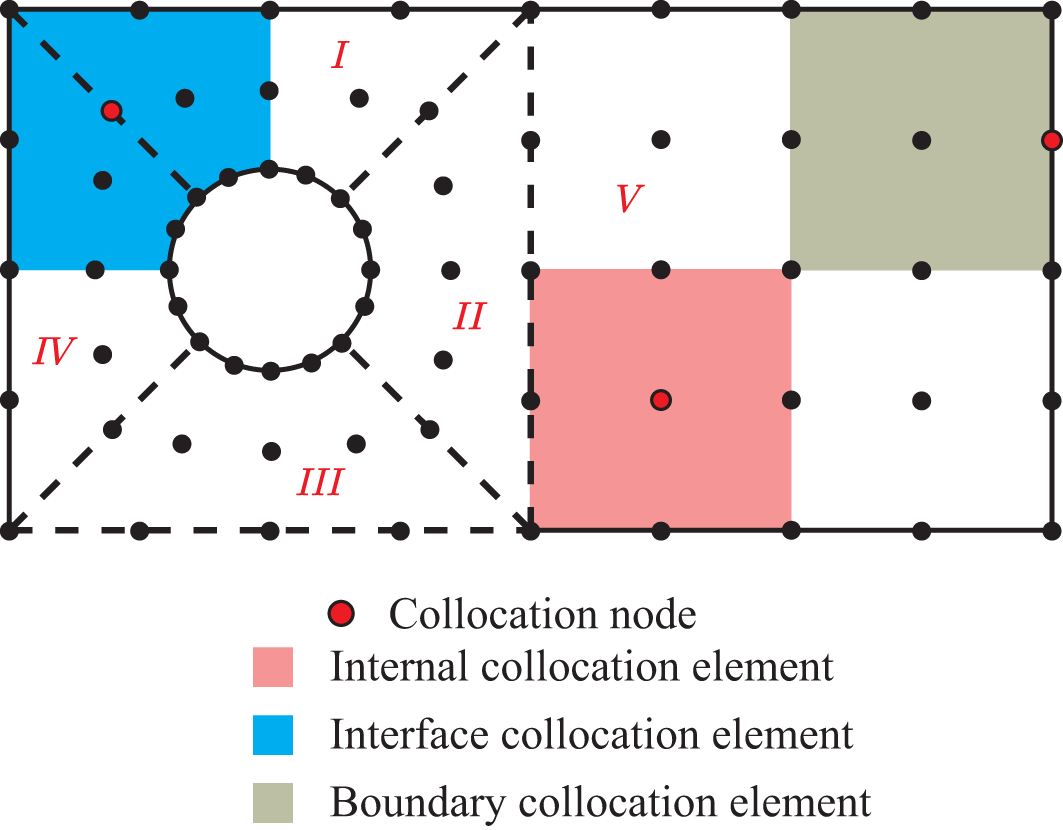
Figure 7: Collocation nodes and their 9-node collocation elements in ZGFREM

Besides, the relevant equations of the zonal Galerkin free element method for thermal-mechanical problem are as follows:

∂∂xj(Dijmn(x)∂um(x)∂xn−βij(x)T(x))+fi(x)=0,x∈Ω(58a)

um(x)=u~m(x),x∈Γu(58b)

σij(x)nj=(Dijmn(x)∂um(x)∂xn−βij(x)T(x))nj=t~i(x),x∈Γσ(58c)

where βij is the temperature-stress coefficient. Dijmn is the stress-strain tensor. u is mechanical displacement. T is temperature. fi is body force. Γu and Γσ are the boundaries to the specific displacements and tensions. Through the generalized format of the Galerkin method and taking the shape function as the weighted function Nc=w, the governing equation for thermal-mechanical coupling problems is changed into

∫ΩDijmn∂um∂xn∂Nc∂xjdΩ=∫ΩNcfidΩ+∫ΓσNct~idΓ+∫ΩβijT∂Nc∂xjdΩ(59)

which can be further written as

∫ΩDijmn∂Nα∂xn∂Nc∂xjumαdΩ=∫ΩNcfidΩ+∫ΓσNct~idΓ+∫ΩβijT∂Nc∂xjdΩ(60)

5.4 Finite Line Method (FLM)

Finite line method (FLM) is a new concept numerical method [155], which sets up the solution scheme based on a finite number of lines crossing the collocation node. As in the free element method [154], the solution domain in FLM is still discretized into a series of collocation nodes and a line-set consisting of 2 or 3 lines is defined for each collocation node in 2D or 3D problems, respectively. Fig. 8 shows three 2D line-sets defined at three different positions for the 2D case. The first-order and high-order partial derivatives of physical variables with respect to the global coordinates can be derived by the arclength derivative over each line [166]. For example, the first-order partial derivative of the physical variable u can be derived and expressed as follows:

∂u(xc)∂xi=dicαuα,dicαuα=Ni′α(xc)(61)

where uα is the α-th nodal value of u over the line-set defined for the collocation node xc, and

dicα=∑I=1d[J]iI−1∂LIα(l)∂l|l=l(xc)(62)

in which, d=2 or 3 for 2D or 3D problems, LIα is the Lagrange interpolation function of node α defined over the I-th line measured by the arclength l, and [J] is the Jacobian matrix from l to global coordinates xi [166]. High-order spatial derivatives can be obtained by recursively using Eq. (61).

Figure 8: 2D line system in FLM

It is very simple to use Eq. (61) to set up a discretized system for PDEs. For example, the governing Eq. (50) with boundary conditions (51) and (52) can be discretized as

dicβλijβdjβαTα=−Q(xc),xc∈Ω(63)

T(xc)=T~(xc),xc∈Γ1(64a)

−λij(xc)ni(xc)djcαTα=q(xc),xc∈Γ2(64b)

FLM not only can get rid of constructing high-dimensional elements for 2D or 3D problems but also can compute high-order partial differential problems with geometrically complex models by means of flexible line sets. It is also noted that FLM only has the strong-form scheme, without weak-form formulation, and experience shows that FLM is the most stable one in the strong-form numerical methods.

6  A Demonstration Example

6.1 Heat Conduction Analysis for a 2D Plate

A 2D plate with homogeneous material is considered and its geometry and boundary conditions are shown in Fig. 9. The analytical solution of the temperature at any point in this problem is

T(x,y)=(2π∑n=1∞(−1)n+1+1nsin⁡nπxL∗sinh⁡(nπy/L)sinh⁡(nπW/L))∗(T2−T1)+T1(65)

where T1=300K,T2=500K.

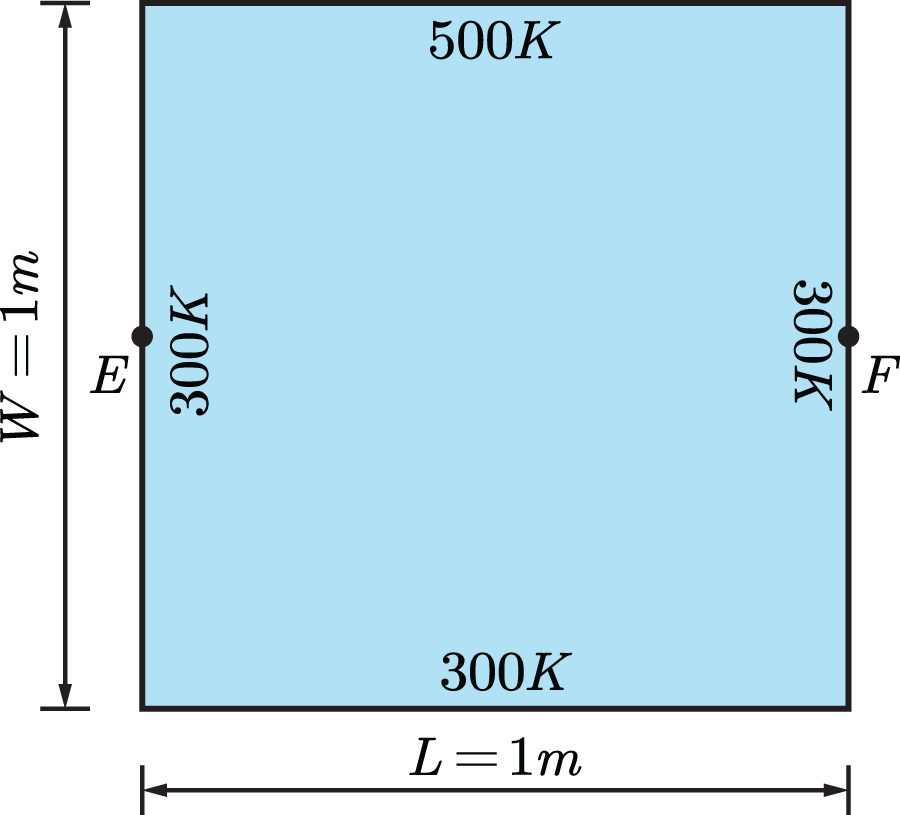
Figure 9: Model for the 2D plate

EDM, FrEM, and ZGFREM these three methods are all used to calculate this problem. The contour plot and the temperature along the path EF (E (0, 0.5), F (1, 0.5)) are plotted in Figs. 10 and 11, respectively. In addition, in order to test the global convergence, the three methods are performed to calculate using the number of 121, 441, and 1681 nodes. The relationship between the L2 norm and the number of nodes is shown in Fig. 12.

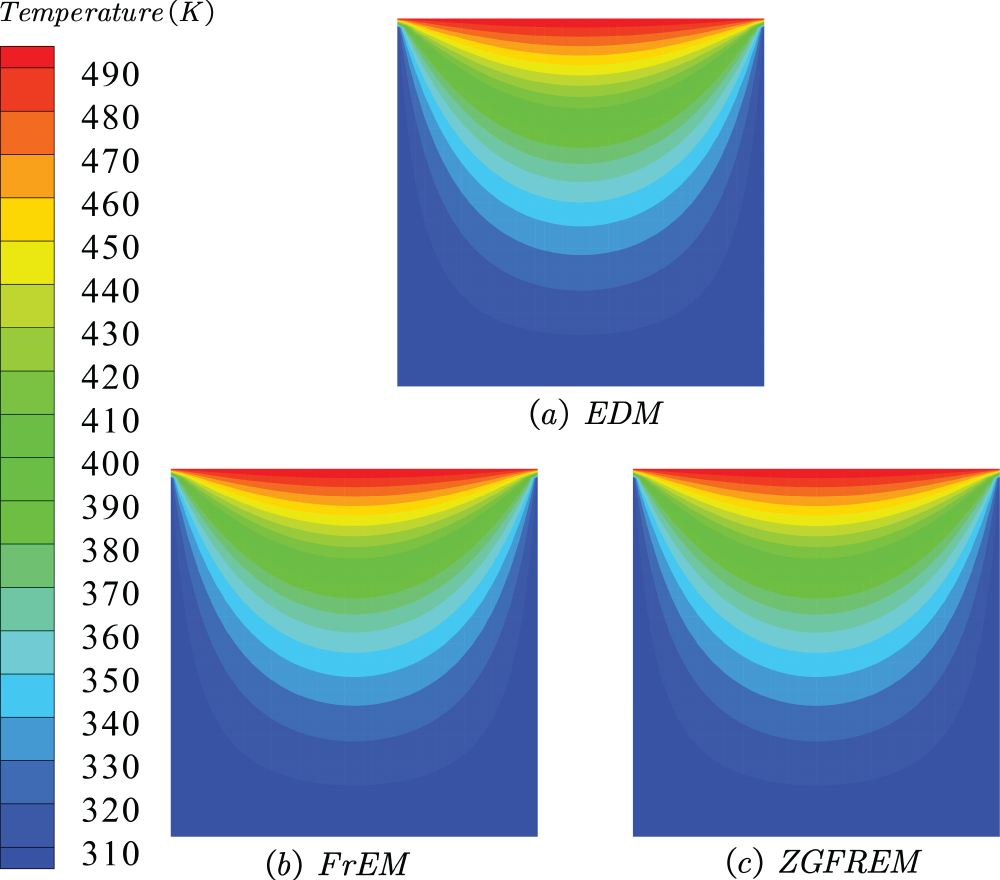
Figure 10: Contour plots for the temperature of the 2D plate obtained by different collocation methods

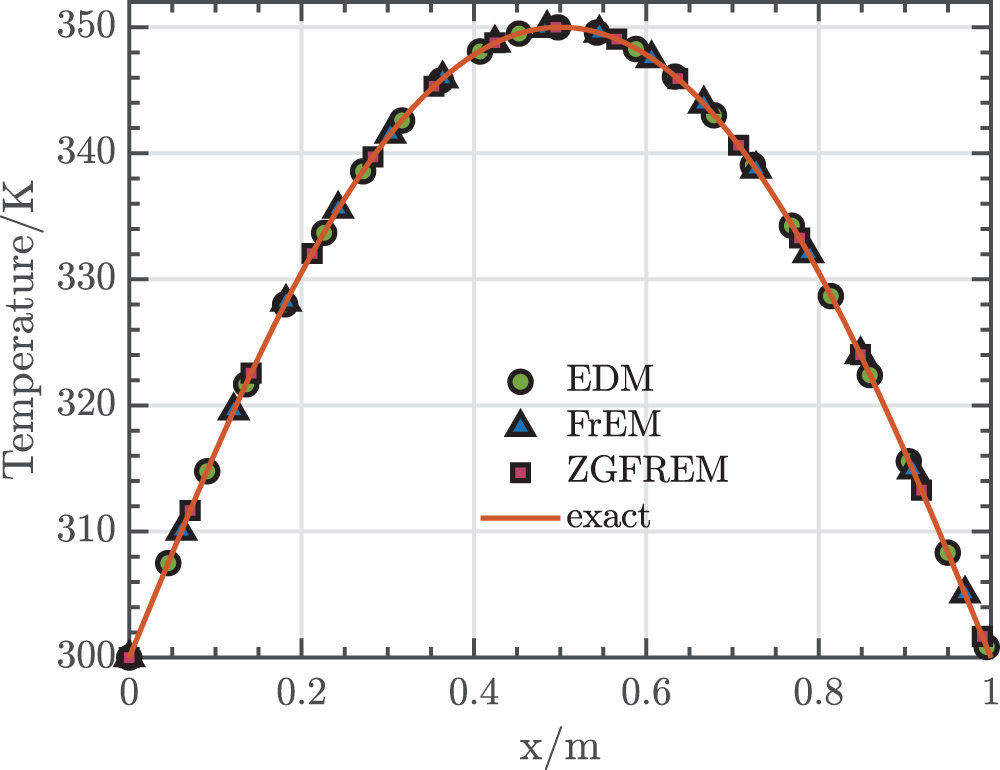
Figure 11: The temperature along path EF obtained by different collocation methods

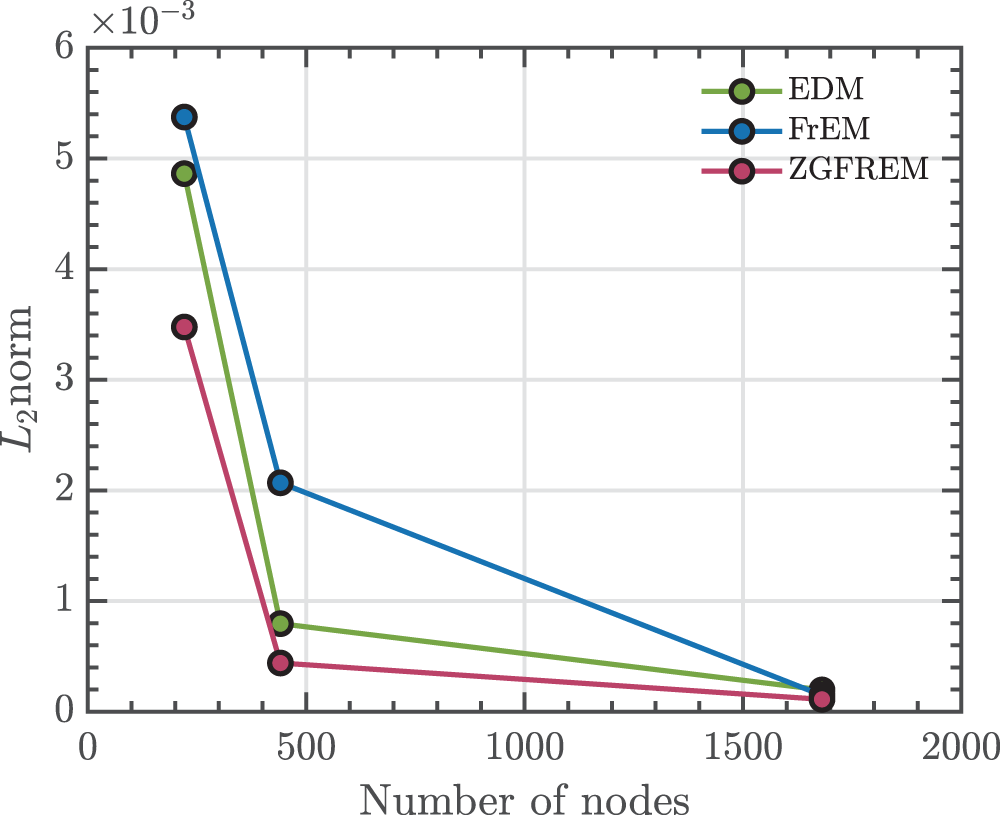
Figure 12: The curve of L2 norm vs. the number of nodes obtained by different collocation methods

6.2 Corrugated Sandwich Structure

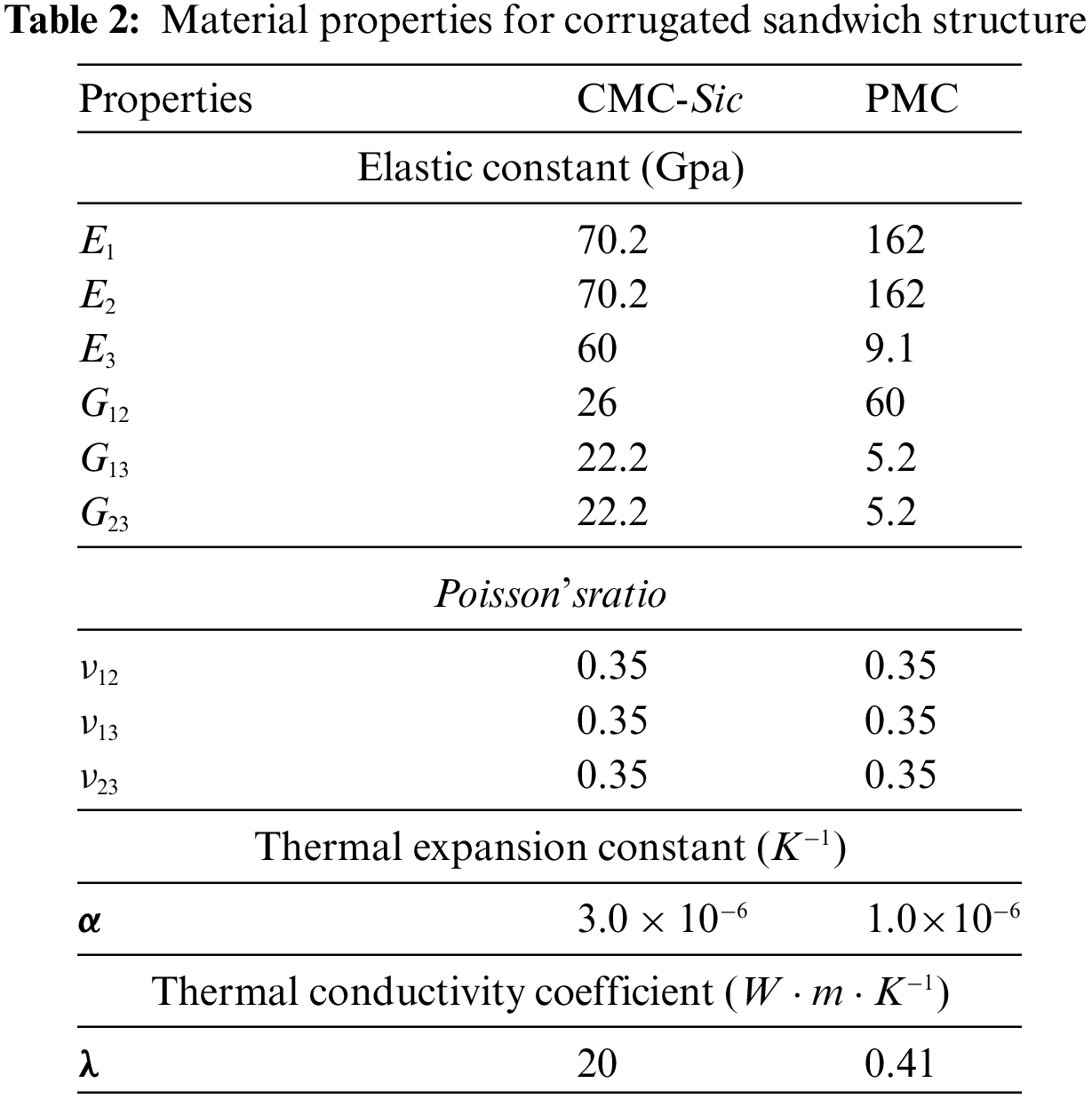
To better demonstrate the performance of the collocation method, a numerical example for predicting the responses of corrugated sandwich structures by the zonal Galerkin free element method proposed by our research group is given. This problem encompasses heat transfer, solid mechanics, and thermal-mechanical coupling aspects. The zone distribution used in this example is illustrated in Fig. 13. Geometric details of the model and material properties can be found in Fig. 14, Tables 1 and 2. Under the premise that the displacement of the bottom surface is fixed in all directions, the upper and lower surfaces of the structure are subjected to temperature boundary conditions of 317 and 573K, respectively, while the remaining surfaces are imposed as free boundary conditions.

Figure 13: Schematic diagram of zone distribution of the corrugated sandwich structure

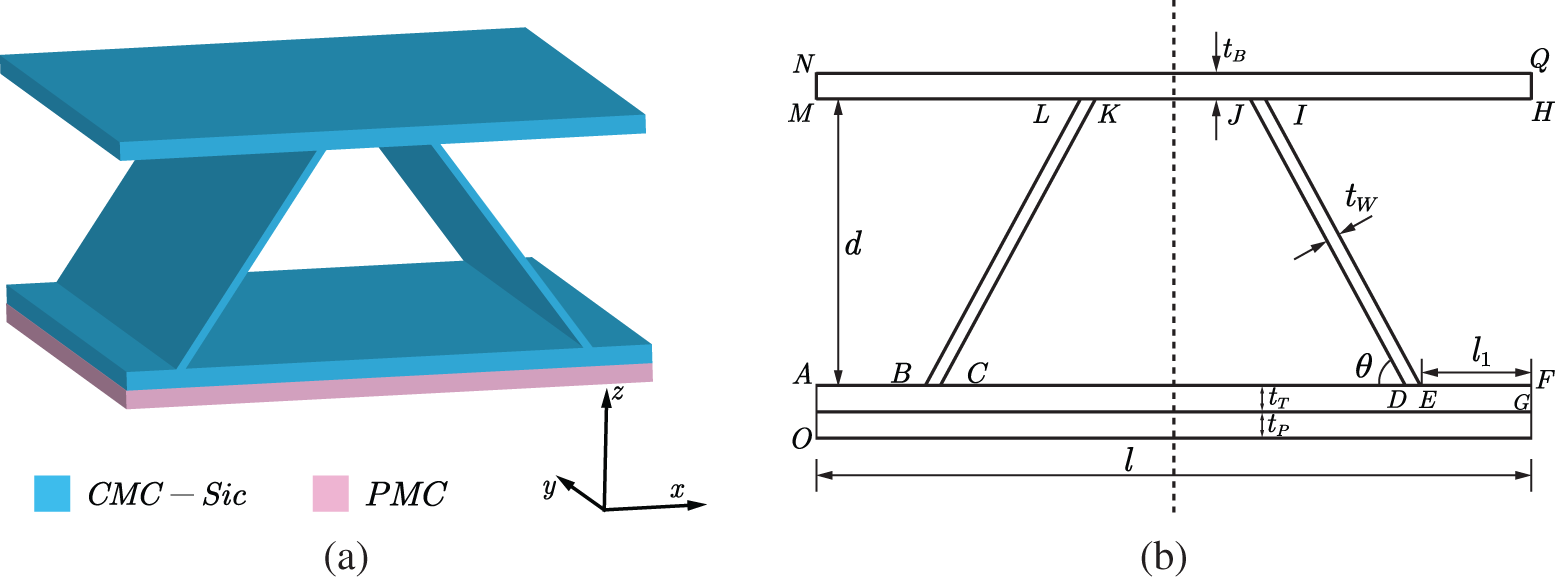
Figure 14: Model of corrugated sandwich structure (a) geometry (b) front view (plane y = 0)

For comparative purposes, finite element analysis (ABAQUS) is also performed using a similar number of nodes. Fig. 15 presents the computed temperature distribution and structural deformation. It is evident that the temperature propagates downward along the sternum. Fig. 16 presents the total heat flux and mises stress. In Fig. 17, the temperature along line CD and the displacements along line PQ are given, with lines formed by coordinates (0.0526,0.16,0.059), (0.0185,0.16,0), (0, 0.16, 0.006), (0.16, 0.16, 0.006) at points C, D, P, and Q. Notably, substantial displacements are observed on both sides of the bottom plate, a region of particular interest. Furthermore, in Fig. 17b, the maximum relative error between the two methods is 1.35%, which validates the accuracy of the zonal Galerkin free element method.

Figure 15: Contour plots over the corrugated sandwich structure in the thermal environment (a) temperature (b) total displacement

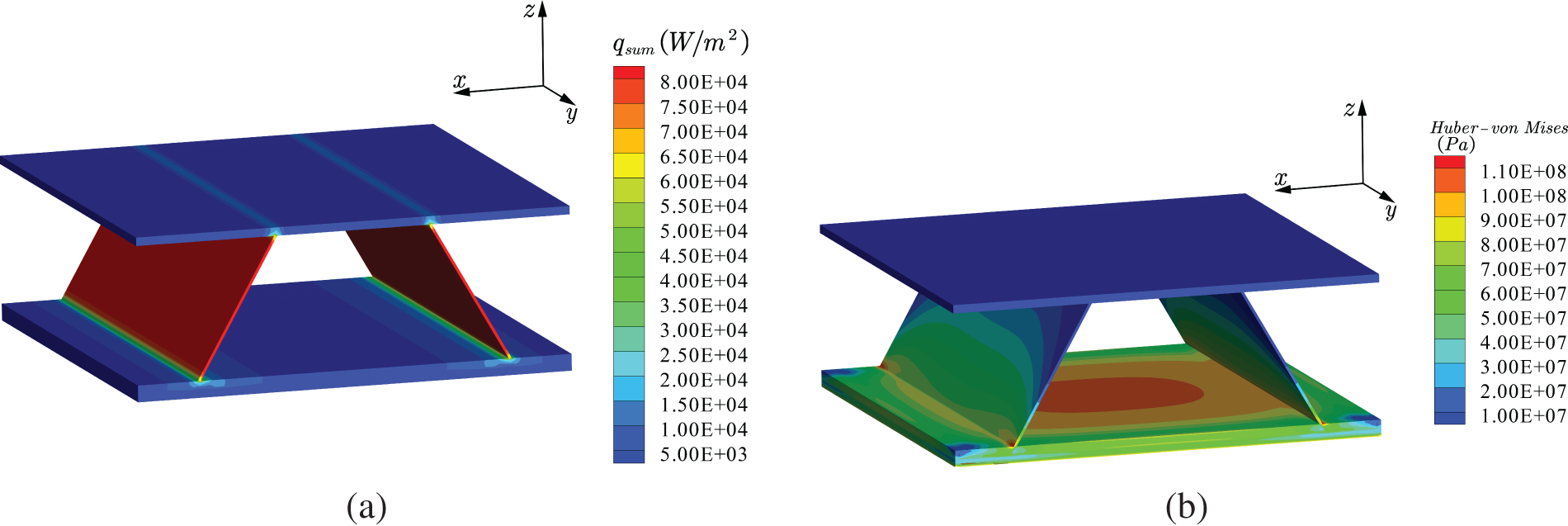
Figure 16: Contour plots over the corrugated sandwich structure in the thermal environment (a) total heat flux (b) Huber-von mises

Figure 17: Structural responses obtained by two different methods (a) temperature along line CD (b) displacement along line PQ

7  Conclusion and Further Research Perspectives

In this paper, an overview of the origin, development, and application of the collocation method is presented. The principle and some common approximation techniques in the collocation method are briefly introduced. Compared with the numerical methods with integral operation, the collocation method has a more direct processing way, and owing to its node-based characteristic, the collocation method becomes a powerful tool in dealing with problems such as large deformation, stamping process, and explosion problems. Some techniques for improving the stability of the collocation method are also summarized. Moreover, the collocation method with different approximation techniques can be combined with some high-precision methods, so as to play their respective advantages. From this review, it can be seen that the collocation method has a wide range of practical engineering application problems including solid mechanics (beam, plate, shell, fracture, etc.), heat conduction and fluid flow problems, as well as multi-field coupling problems.

To date, there are still some challenging works needing to be done on the collocation method, and some suggestions for future research directions can be summarized as follows:

(a)   The collocation method, attributing to its distinct node-by-node feature, offers a pathway to performing parallel high-performance computing. Exploring parallel computing techniques and optimizing algorithms for distributed computing can significantly enhance the collocation method’s applicability to solving large-scale problems in various engineering and scientific areas.

(b)   Leveraging the advantages of isogeometric collocation methods in computer-aided design (CAD) modeling, there is potential for relevant work in biomechanical research, particularly in the study of biological tissues like skeletal structures. The interdisciplinary approach can offer valuable insights into the behavior of complex biological systems under mechanical loads.

(c)   Combining the collocation method with other high-precision numerical techniques can harness the strengths of each method, ensuring both high accuracy and efficiency. By integrating complementary methods, it can improve the overall performance of numerical simulations, especially in scenarios where extreme precision is required.

(d)   Coupling the collocation method with artificial intelligence techniques, such as machine learning, can present an interesting research topic. This integration can enhance the collocation method’s adaptability, enabling it to self-optimize and adapt to evolving problem domains. The application of AI methods in guiding adaptive mesh refinement or optimization of collocation point distributions may be a promising research direction.

(e)   Developing commercial software packages centered around the collocation method can promote its wider adoption in engineering and scientific communities. These softwares can provide user-friendly interfaces, efficient solvers, and support for a wide range of engineering applications, making the collocation method more accessible to practitioners.

These suggested research directions aim to further expand the capabilities and applications of the collocation method, making it a versatile and powerful tool in various scientific and engineering disciplines. The reviewed collocation method is only a part of numerical methods. More comprehensive investigations on various numerical methods, especially classified by operation dimensions, can be found in the reference [167].

Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.

Funding Statement: The author gratefully acknowledges the National Natural Science Foundation of China for financial support to this work under Grant NSFC No. 12072064.

Author Contributions: Study conception and design: Xiaowei Gao, Weiwu Jiang; data collection: Weiwu Jiang; analysis and interpretation of results: Weiwu Jiang; draft manuscript preparation: Weiwu Jiang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data can be obtained from the literature cited in this paper. More detailed data will be shared on reasonable request to the corresponding authors.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Mysovskih, I. P. (1969). Lectures on numerical methods. Springer Science & Business Media. [Google Scholar]

2. Meinardus, G. (1967). Approximation of functions: Theory and numerical methods. Springer Science & Business Media. [Google Scholar]

3. Clough, R. W. (1960). The finite element method in plane stress analysis. 2nd Conference on Electronic Computation, pp. 345–378. [Google Scholar]

4. Roache, P. J. (1976). A generalized finite difference formulation for differential expressions using colocated variables. International Journal for Numerical Methods in Engineering, 8, 48–56. [Google Scholar]

5. Rizzo, Frank, J. (1967). An integral equation approach to boundary value problems of classical elastostatics. Quarterly of Applied Mathematics, 25(1), 83. [Google Scholar]

6. Cruse, T., Rizzo, F. (1968). A direct formulation and numerical solution of the general transient elastodynamic problem. Journal of Mathematical Analysis and Applications, 22(1), 244–259. [Google Scholar]

7. Mayers, E. S. D. F. (2003). An introduction to numerical analysis. Cambridge University Press. [Google Scholar]

8. Atluri, S. N., Zhu, T. (1998). A new meshless local petrov-galerkin (MLPG) approach in computational mechanics. Computational Mechanics, 22(2), 117–127. [Google Scholar]

9. Hardy, R. L. (1971). Multiquadric equations of topography and other irregular surfaces. Journal of Geophysical Resarch, 76(8), 1905–1915. [Google Scholar]

10. Perrone, N., Kao, R. (1975). A general finite difference method for arbitrary meshes. Computers Structures, 5(1), 45–57. [Google Scholar]

11. Liszka, T., Orkisz, J. (1977). Finite difference method at arbitrary irregular meshes in non-linear problems of applied mechanics. International Conference on Structural Mechanics in Reactor Technology, San Francisco, USA. [Google Scholar]

12. Liszka, T., Orkisz, J. (1980). The finite difference method at arbitrary irregular grids and its application in applied mechanics. Computers Structures, 11(1), 83–95. [Google Scholar]

13. Liszka, T. (1984). An interpolation method for an irregular net of nodes. International Journal for Numerical Methods in Engineering, 20(9), 1599–1612. [Google Scholar]

14. Gingold, R. A., Monaghan, J. J. (1977). Smoothed particle hydrodynamics: Theory and application to non-spherical stars. Monthly Notices of the Royal Astronomical Society, 181(3), 375–389. [Google Scholar]

15. Monaghan, J. J. (1992). Smoothed particle hydrodynamics. Annual Review of Astronomy Astrophysics, 30, 543–574. [Google Scholar]

16. Lucy, L. B. (1977). A numerical approach to the testing of the fission hypothesis. The Astrophysical Journal, 8(12), 1013–1024. [Google Scholar]

17. Colagrossi, A., Landrini, M. (2003). Numerical simulation of interfacial flows by smoothed particle hydrodynamics. Journal of Computational Physics, 191(2), 448–475. [Google Scholar]

18. Onate, E., Idelsohn, S., Zienkiewicz, O. C., Taylor, R. L. (1996). A finite point method in computational mechanics. Application to convective transport and fulid flow. International Journal for Numerical Methods in Engineering, 39(22), 3839–3866. [Google Scholar]

19. Onate, E., Idelsohn, S., Zienkiewicz, O. C., Taylor, R. L., Sacco, C. (1996). A stabilized finite point method for analysis of fulid mechanics problems. Computer Methods in Applied Mechanics and Engineering, 139(1–4), 315–346. [Google Scholar]

20. Breitkopf, P., Touzot, G., Villon, P. (2000). Double grid diffuse collocation method. Computational Mechanics, 25(2), 199–206. [Google Scholar]

21. Duarte, C. A., Oden, J. T. (1996). An h-p adaptive method using clouds. Computer Methods in Applied Mechanics and Engineering, 139(1), 237–262. [Google Scholar]

22. Duarte, C. A., Oden, J. T. (1996). H-p clouds-an h-p meshless method. Numerical Methods for Partial Differential Equations, 12(6), 673–705. [Google Scholar]

23. Lee, S. H., Yoon, Y. C. (2004). Meshfree point collocation method for elasticity and crack problems. International Journal for Numerical Methods in Engineering, 61(1), 22–48. [Google Scholar]

24. Aluru, N. R. (2000). A point collocation method based on reproducing kernel approximations. International Journal for Numerical Methods in Engineering, 47(6), 1083–1121. [Google Scholar]

25. Kim, D. W., Kim, Y. (2003). Point collocation methods using the fast moving least-square reproducing kernel approximation. International Journal for Numerical Methods in Engineering, 56(10), 1445–1464. [Google Scholar]

26. Li, J., Cheng, A. H. D., Chen, C. S. (2003). A comparison of efficiency and error convergence of multiquadric collocation method and finite element method. Engineering Analysis with Boundary Elements, 27(3), 251–257. [Google Scholar]

27. Hillman, M., Chen, J. S. (2018). Performance comparison of nodally integrated galerkin meshfree methods and nodally collocated strong form meshfree methods. Springer International Publishing. [Google Scholar]

28. Hu, H. Y., Chen, J. S., Hu, W. (2007). Weighted radial basis collocation method for boundary value problems. International Journal for Numerical Methods in Engineering, 69(13), 2736–2757. [Google Scholar]

29. Zhang, X., Liu, X. H., Song, K. Z., Lu, M. W. (2001). Least-squares collocation meshless method. International Journal for Numerical Methods in Engineering, 51(9), 1089–1100. [Google Scholar]

30. Park, S. H., Youn, S. K. (2001). The least-squares meshfree method. International Journal for Numerical Methods in Engineering, 52(9), 997–1012. [Google Scholar]

31. Park, S. H., Kwon, K. C., Youn, S. K. (2003). A study on the convergence of least-squares meshfree method under inaccurate integration. International Journal for Numerical Methods in Engineering, 56(10), 1397–1419. [Google Scholar]

32. Kwon, K. C., Park, S. H., Youn, S. K. (2005). The least-squares meshfree method for elasto-plasticity and its application to metal forming analysis. International Journal for Numerical Methods in Engineering, 64(6), 751–788. [Google Scholar]

33. Zhang, X., Hu, W., Pan, X. F., Lu, M. W. (2003). Meshless weighted least-square method. Chinese Journal of Theoretical and Applied Mechanics, 35, 1089–1100. [Google Scholar]

34. Liu, G. R., Kee, B. B. T., Chun, L. (2006). A stabilized least-squares radial point collocation method (LS-RPCM) for adaptive analysis. Computer Methods in Applied Mechanics and Engineering, 195(37),4843–4861. [Google Scholar]

35. Cao, Y., Nikan, O., Avazzadeh, Z. (2023). A localized meshless technique for solving 2D nonlinear integro-differential equation with multi-term kernels. Applied Numerical Mathematics, 183, 140–156. [Google Scholar]

36. Avazzadeh, Z., Nikan, O., Nguyen, A. T., Nguyen, V. T. (2023). A localized hybrid kernel meshless technique for solving the fractional Rayleigh-Stokes problem for an edge in a viscoelastic fluid. Engineering Analysis with Boundary Elements, 146, 695–705. [Google Scholar]

37. Kee, B. B. T., Liu, G. R., Lu, C. (2007). A regularized least-squares radial point collocation method (RLS-RPCM) for adaptive analysis. Computational Mechanics, 40(5), 837–853. [Google Scholar]

38. Yang, J., Zheng, J. (2013). Intervention-point principle of meshless method. Chinese Science Bulletin, 58(4), 478–485. [Google Scholar]

39. Yang, J., Zheng, J. (2017). Meshless global intervention point method. Chinese Journal of Applied Mechanics, 5, 956–962 (In Chinese). [Google Scholar]

40. Liu, G. R., Gu, Y. T. (2003). A meshfree method: Meshfree weak-strong (MWS) form method, for 2-D solids. Computational Mechanics, 33(1), 2–14. [Google Scholar]

41. Pan, X. F., Zhang, X., Lu, M. W. (2005). Meshless Galerkin least-squares method. Computational Mechanics, 35(3), 182–189. [Google Scholar]

42. Morris, J. P., Fox, P. J., Zhu, Y. (1997). Modeling low reynolds number incompressible flows using SPH. Journal of Computational Physics, 136(1), 214–226. [Google Scholar]

43. Randles, P. W., Libersky, L. D. (1996). Smoothed particle hydrodynamics: Some recent improvements and applications. Computer Methods in Applied Mechanics and Engineering, 139(1), 375–408. [Google Scholar]

44. Liu, M. B., Liu, G. R. (2010). Smoothed particle hydrodynamics (SPHAn overview and recent developments. Archives of Computational Methods in Engineering, 17(1), 25–76. [Google Scholar]

45. Liu, G. R., Liu, M. B. (2003). Smoothed particle hydrodynamics: A meshfree particle method. Singapore: World Scientific. [Google Scholar]

46. De Vuyst, T., Vignjevic, R., Campbell, J. C. (2005). Coupling between meshless and finite element methods. International Journal of Impact Engineering, 31(8), 1054–1064. [Google Scholar]

47. Yang, J., Zheng, J. (2017). Meshless local strong-weak(MLSW) method for irregular domain problems. Chinese Journal of Theoretical and Applied Mechanics, 49, 659–666. [Google Scholar]

48. Bird, R. B. (1954). Application of the method of weighted residuals to the equation of transport phenomena. Journal of Applied Mechanics. [Google Scholar]

49. Mclain, D. H. (1974). Drawing contours from arbitrary data points. Computer Journal, 17(4), 318–324. [Google Scholar]

50. Wixom, J. A., Gordon, W. J. (1978). Shepard’s method of “metric interpolation” to bivariate and multivariate interpolation. Mathematics of Computation, 32(141), 253–264. [Google Scholar]

51. Lancaster, P., Salkauskas, K. (1981). Surface generated by moving least square methods. Mathematics of Computation, 37(155), 141. [Google Scholar]

52. Nayroles, B., Touzot, G., Villon, P. (1992). Generalizing the finite element method: Diffuse approximation and diffuse elements. Computational Mechanics, 10(5), 307–318. [Google Scholar]

53. Belytschko, T., Lu, Y. Y., Gu, L. (1994). Element-free Galerkin methods. International Journal for Numerical Methods in Engineering, 37(2), 229–256. [Google Scholar]

54. Cheng, Y., Li, J. (2006). A complex variable meshless method for fracture problems. Science in China Series G, 49(1), 46–59. [Google Scholar]

55. Wong, S., Wong, Y. (2008). Large deformation analysis with Galerkin based smoothed particle hydrodynamics. Computer Modeling in Engineering & Sciences, 36(2), 97–118. [Google Scholar]

56. Monaghan, J. J. (1992). Smoothed particle hydrodynamics. Annual Review of Astronomy and Astrophysics, 30(1). [Google Scholar]

57. Liu, M. B., Liu, G. R., Zong, Z., Lam, K. Y. (2003). Computer simulation of high explosive explosion using smoothed particle hydrodynamics methodology. Computers & Fluids, 32(3), 305–322. [Google Scholar]

58. Wang, L., Liu, Y., Zhihao Qian, W. Z. (2021). Meshfree stabilized collocation method in elasticity. Chinese Journal of Computational Mechanics, 38, 305–312. [Google Scholar]

59. Gomez, H., de Lorenzis, L. (2016). The variational collocation method. Computer Methods in Applied Mechanics and Engineering, 309, 152–181. [Google Scholar]

60. Klinkel, S., Chen, L., Dornisch, W. (2015). A NURBS based hybrid collocation-Galerkin method for the analysis of boundary represented solids. Computer Methods in Applied Mechanics and Engineering, 284, 689–711. [Google Scholar]

61. Chen, L., Dornisch, W., Klinkel, S. (2015). Hybrid collocation-Galerkin approach for the analysis of surfacerepresented 3D-solids employing SB-FEM. Computer Methods in Applied Mechanics and Engineering, 295, 268–289. [Google Scholar]

62. Tu, W., Gu, Y. T., Wen, P. H. (2012). Effective shear modulus approach for two dimensional solids and plate bending problems by meshless point collocation method. Engineering Analysis with Boundary Elements, 36(5), 675–684. [Google Scholar]

63. Wunsche, M., Garcia-Sanchez, F., Saez, A., Zhang, C. (2010). A 2D time-domain collocation-Galerkin BEM for dynamic crack analysis in piezoelectric solids. Engineering Analysis with Boundary Elements, 34(4), 377–387. [Google Scholar]

64. Tan, A., Hirose, S., Zhang, C. (2005). A time-domain collocation-Galerkin BEM for transient dynamic crack analysis in anisotropic solids. Engineering Analysis with Boundary Elements, 29(11), 1025–1038. [Google Scholar]

65. Auricchio, F., Beirao da Veiga, L., Hughes, T. J. R., Reali, A., Sangalli, G. (2012). Isogeometric collocation for elastostatics and explicit dynamics. Computer Methods in Applied Mechanics and Engineering, 249–252, 2–14. [Google Scholar]

66. Kruse, R., Nguyen-Thanh, N., de Lorenzis, L., Hughes, T. J. R. (2015). Isogeometric collocation for large deformation elasticity and frictional contact problems. Computer Methods in Applied Mechanics and Engineering, 296, 73–112. [Google Scholar]

67. Fahrendorf, F., Morganti, S., Reali, A., Hughes, T. J. R., Lorenzis, L. D. (2020). Mixed stress-displacement isogeometric collocation for nearly incompressible elasticity and elastoplasticity. Computer Methods in Applied Mechanics and Engineering, 369, 113112. [Google Scholar]

68. Stevens, D., Power, H., Cliffe, K. A. (2014). A meshless local RBF collocation method using integral operators for linear elasticity. International Journal of Mechanical Sciences, 88, 246–258. [Google Scholar]

69. Oliveira, T., Portela, A. (2016). Weak-form collocation—A local meshless method in linear elasticity. Engineering Analysis with Boundary Elements, 73, 144–160. [Google Scholar]

70. Casquero, H., Liu, L., Bona-Casas, C., Zhang, Y., Gomez, H. (2016). A hybrid variational-collocation immersed method for fluid-structure interaction using unstructured T-splines. International Journal for Numerical Methods in Engineering, 105(11), 855–880. [Google Scholar]

71. Chi, S. W., Chen, J. S., Hu, H. Y., Yang, J. P. (2013). A gradient reproducing kernel collocation method for boundary value problems. International Journal for Numerical Methods in Engineering, 93(13), 1381–1402. [Google Scholar]

72. Mahdavi, A., Chi, S. W., Zhu, H. (2019). A gradient reproducing kernel collocation method for high order differential equations. Computational Mechanics, 64(5), 1421–1454. [Google Scholar]

73. Yang, J. P., Hsin, W. C. (2019). Weighted reproducing kernel collocation method based on error analysis for solving inverse elasticity problems. Acta Mechanica, 230(10), 3477–3497. [Google Scholar]

74. Gu, Y., Chen, W., Gao, H., Zhang, C. (2016). A meshless singular boundary method for three-dimensional elasticity problems. International Journal for Numerical Methods in Engineering, 107(2), 109–126. [Google Scholar]

75. Aluru, N. R., Li, G. (2001). Finite cloud method: A true meshless technique based on a fixed reproducing kernel approximation. International Journal for Numerical Methods in Engineering, 50(10), 2373–2410. [Google Scholar]

76. Liu, X., Liu, G. R., Tai, K., Lam, K. Y. (2005). Radial point interpolation collocation method (RPICM) for the solution of nonlinear poisson problems. Computational Mechanics, 36(4), 298–306. [Google Scholar]

77. Chi, S. W., Chen, J. S., Hu, H. Y. (2014). A weighted collocation on the strong form with mixed radial basis approximations for incompressible linear elasticity. Computational Mechanics, 53(2), 309–324. [Google Scholar]

78. Sadeghirad, A., Mahmoudzadeh Kani, I., Rahimian, M., Vaziri Astaneh, A. (2009). A numerical approach based on the meshless collocation method in elastodynamics. Acta Mechanica Sinica, 25(6), 857–870. [Google Scholar]

79. Wang, Y. M., Chen, S. M., Wu, C. P. (2010). A meshless collocation method based on the differential reproducing kernel interpolation. Computational Mechanics, 45(6), 585–606. [Google Scholar]

80. Hughes, T. J. R., Cottrell, J. A., Bazilevs, Y. (2005). Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Computer Methods in Applied Mechanics and Engineering, 194(39), 4135–4195. [Google Scholar]

81. Reali, A., Gomez, H. (2015). An isogeometric collocation approach for Bernoulli-Euler beams and Kirchhoff plates. Computer Methods in Applied Mechanics and Engineering, 284, 623–636. [Google Scholar]

82. Marino, E. (2016). Isogeometric collocation for three-dimensional geometrically exact shear-deformable beams. Computer Methods in Applied Mechanics and Engineering, 307, 383–410. [Google Scholar]

83. Marino, E. (2017). Locking-free isogeometric collocation formulation for three-dimensional geometrically exact shear-deformable beams with arbitrary initial curvature. Computer Methods in Applied Mechanics and Engineering, 324, 546–572. [Google Scholar]

84. Pavan, G. S., Muppidi, H., Dixit, J. (2022). Static, free vibrational and buckling analysis of laminated composite beams using isogeometric collocation method. European Journal of Mechanics—A/Solids, 96, 104758. [Google Scholar]

85. Ignesti, D., Ferri, G., Auricchio, F., Reali, A., Marino, E. (2023). An improved isogeometric collocation formulation for spatial multi-patch shear-deformable beams with arbitrary initial curvature. Computer Methods in Applied Mechanics and Engineering, 403, 115722. [Google Scholar]

86. Atif Shahzad, M., Sahmani, S., Safaei, B. (2023). Nonlocal couple stress-based meshless collocation model for nonlinear dynamic performance of microbeam-type piezoelectric energy harvesters. European Journal of Mechanics—A/Solids, 101, 105059. [Google Scholar]

87. Khaneh Masjedi, P., Maheri, A. (2017). Chebyshev collocation method for the free vibration analysis of geometrically exact beams with fully intrinsic formulation. European Journal of Mechanics—A/Solids, 66, 329–340. [Google Scholar]

88. Giunta, G., Belouettar, S., Ferreira, A. J. M. (2016). A static analysis of three-dimensional functionally graded beams by hierarchical modelling and a collocation meshless solution method. Acta Mechanica, 227(4), 969–991. [Google Scholar]

89. Chen, S. M., Wu, C. P., Wang, Y. M. (2011). A hermite DRK interpolation-based collocation method for the analyses of Bernoulli-Euler beams and Kirchhoff-Love plates. Computational Mechanics, 47(4), 425–453. [Google Scholar]

90. Yang, H., Dong, C., Wu, Y., Dai, R. (2021). Mixed dimensional isogeometric FE-BE coupling analysis for solid-shell structures. Computer Methods in Applied Mechanics and Engineering, 382, 113841. [Google Scholar]

91. Dai, Z., Kiani, Y. (2023). Stability of higher-order lattice composite cylindrical shell reinforced with graphene platelets by means of a Chebyshev collocation-based semi-analytical approach. Engineering Structures, 296, 116952. [Google Scholar]

92. Neves, A. M. A., Ferreira, A. J. M., Carrera, E., Cinefra, M., Roque, C. M. C. et al. (2013). Free vibration analysis of functionally graded shells by a higher-order shear deformation theory and radial basis functions collocation, accounting for through-the-thickness deformations. European Journal of Mechanics—A/Solids, 37, 24–34. [Google Scholar]

93. Xie, X., Zheng, H., Jin, G. (2015). Integrated orthogonal polynomials based spectral collocation method for vibration analysis of coupled laminated shell structures. International Journal of Mechanical Sciences, 98, 132–143. [Google Scholar]

94. Nath, Y., Dumir, P. C., Bhatiaf, R. S. (1985). Nonlinear static and dynamic analysis of circular plates and shallow spherical shells using the collocation method. International Journal for Numerical Methods in Engineering, 21(3), 565–578. [Google Scholar]

95. Lee, J. (2018). Free vibration analysis of joined conical-cylindrical shells by matched Fourier-Chebyshev collocation method. Journal of Mechanical Science and Technology, 32(10), 4601–4612. [Google Scholar]

96. Wang, L., Liu, Y., Zhou, Y., Yang, F. (2021). Static and dynamic analysis of thin functionally graded shell with in-plane material inhomogeneity. International Journal of Mechanical Sciences, 193, 106165. [Google Scholar]

97. Wang, L., Liu, Y., Liao, Z., Zhou, Y., Yang, F. (2023). Gradient reproducing kernel based Hermite collocation method (GHCM) for eigenvalue analysis of functionally graded thin plates with in-plane material. Engineering Analysis with Boundary Elements, 148, 73–89. [Google Scholar]

98. Huang, Y., Peng, S., Habibi, M., Moradi, Z. (2023). Buckling simulation of eccentrically rotating nanocomposite sector plates in thermal environment using the 2D Chebyshev collocation method. Thin-Walled Structures, 193, 111203. [Google Scholar]

99. Chu, C., Al-Furjan, M. S. H., Kolahchi, R., Farrokhian, A. (2023). A nonlinear Chebyshev-based collocation technique to frequency analysis of thermally pre/post-buckled third-order circular sandwich plates. Communications in Nonlinear Science and Numerical Simulation, 118, 107056. [Google Scholar]

100. Hosseini, S., Rahimi, G. (2023). Experimental and numerical analysis of hyperelastic plates using Mooney-Rivlin strain energy function and meshless collocation method. Engineering Analysis with Boundary Elements, 150, 199–218. [Google Scholar]

101. Pavan, G. S., Nanjunda Rao, K. S. (2017). Bending analysis of laminated composite plates using isogeometric collocation method. Composite Structures, 176, 715–728. [Google Scholar]

102. Ferreira, A. J. M., Carrera, E., Cinefra, M., Roque, C. M. C. (2013). Radial basis functions collocation for the bending and free vibration analysis of laminated plates using the Reissner-mixed variational theorem. European Journal of Mechanics—A/Solids, 39, 104–112. [Google Scholar]

103. Wu, C. P., Chiu, K. H., Wang, Y. M. (2011). RMVT-based meshless collocation and element-free Galerkin methods for the quasi-3D analysis of multilayered composite and FGM plates. Composite Structures, 93(2), 923–943. [Google Scholar]

104. Leitao, V. M. A. (2001). A meshless method for Kirchhoff plate bending problems. International Journal for Numerical Methods in Engineering, 52(10), 1107–1130. [Google Scholar]

105. Nguyen-Thanh, N., Li, W., Huang, J., Zhou, K. (2022). Multi phase-field modeling of anisotropic crack propagation in 3D fiber-reinforced composites based on an adaptive isogeometric meshfree collocation method. Computer Methods in Applied Mechanics and Engineering, 393, 114794. [Google Scholar]

106. Schillinger, D., Borden, M. J., Stolarski, H. K. (2015). Isogeometric collocation for phase-field fracture models. Computer Methods in Applied Mechanics and Engineering, 284, 583–610. [Google Scholar]

107. Fatehi Marji, M., Dehghani, I. (2010). Kinked crack analysis by a hybridized boundary element/boundary collocation method. International Journal of Solids and Structures, 47(7), 922–933. [Google Scholar]

108. Yoon, Y. C., Lee, S. H., Belytschko, T. (2006). Enriched meshfree collocation method with diffuse derivatives for elastic fracture. Computers and Mathematics with Applications, 51(8), 1349–1366. [Google Scholar]

109. Wang, L., Chen, J. S., Hu, H. Y. (2010). Subdomain radial basis collocation method for fracture mechanics. International Journal for Numerical Methods in Engineering, 83(7), 851–876. [Google Scholar]

110. Cheng, J., Sun, B., Wang, M., Li, Z. (2019). Analysis of III crack in a finite plate of functionally graded piezoelectric/piezomagnetic materials using boundary collocation method. Archive of Applied Mechanics, 89(2), 231–243. [Google Scholar]

111. Tian, X., Sladek, J., Sladek, V., Deng, Q., Li, Q. (2021). A collocation mixed finite element method for the analysis of flexoelectric solids. International Journal of Solids and Structures, 217–218, 27–39. [Google Scholar]

112. Tian, X., Xu, M., Zhou, H., Deng, Q., Sladek, J. et al. (2023). Modeling the flexoelectric effect around the tip of nano-cracks using a collocation MFEM. Engineering Fracture Mechanics, 289, 109452. [Google Scholar]

113. Li, X. C., Yao, W. A. (2006). Virtual boundary element-integral collocation method for the plane magnetoelectroelastic solids. Engineering Analysis with Boundary Elements, 30(8), 709–717. [Google Scholar]

114. Weeger, O., Schillinger, D., Muller, R. (2022). Mixed isogeometric collocation for geometrically exact 3D beams with elasto-visco-plastic material behavior and softening effects. Computer Methods in Applied Mechanics and Engineering, 399, 115456. [Google Scholar]

115. Alshenawy, R., Sahmani, S., Safaei, B., Elmoghazy, Y., Al-Alwan, A. et al. (2023). Nonlinear dynamical performance of microsize piezoelectric bridge-type energy harvesters based upon strain gradient-based meshless collocation approach. Engineering Analysis with Boundary Elements, 151, 199–215. [Google Scholar]

116. Wu, C. P., Chiu, K. H., Jiang, R. Y. (2012). A meshless collocation method for the coupled analysis of functionally graded piezo-thermo-elastic shells and plates under thermal loads. International Journal of Engineering Science, 56, 29–48. [Google Scholar]

117. Jiang, W. W., Gao, X. W., Xu, B. B., Lv, J. (2021). Analysis of piezoelectric problems using zonal free element method. Engineering Analysis with Boundary Elements, 127, 40–52. [Google Scholar]

118. Gao, X. W., Liu, H. Y., Ruan, B. (2021). Discontinuous zone free element method with variable condensation and applications in thermal-stress analysis of functionally graded material structures with cracks. Computers and Structures, 243, 106411. [Google Scholar]

119. Jiang, W. W., Gao, X. W. (2023). Analysis of thermo-electro-mechanical dynamic behavior of piezoelectric structures based on zonal Galerkin free element method. European Journal of Mechanics—A/Solids, 99, 104939. [Google Scholar]

120. Jiang, W. W., Gao, X. W., Liu, H. Y. (2023). Multi-physics zonal Galerkin free element method for static and dynamic responses of functionally graded magneto-electro-elastic structures. Composite Structures, 321, 117217. [Google Scholar]

121. Zerroukat, M., Power, H., Chen, C. S. (1998). A numerical method for heat transfer problems using collocation and radial basis functions. International Journal for Numerical Methods in Engineering, 42(7), 1263–1278. [Google Scholar]

122. Jangid, K., Mukhopadhyay, S. (2023). Application of legendre wavelet collocation method to the analysis of poro-thermoelastic coupling with variable thermal conductivity. Computers and Mathematics with Applications, 146, 1–11. [Google Scholar]

123. Sun, Y., Li, X., Zhao, J., Hu, Y., Jing, X. et al. (2022). Investigation of transient coupled conduction and radiation heat transfer in the linearly anisotropic scattering cylindrical medium by spectral collocation method. International Journal of Thermal Sciences, 172, 107308. [Google Scholar]

124. Chen, Y. Y., Li, B. W., Zhang, J. K. (2016). Spectral collocation method for natural convection in a square porous cavity with local thermal equilibrium and non-equilibrium models. International Journal of Heat and Mass Transfer, 96, 84–96. [Google Scholar]

125. Ma, J., Sun, Y., Li, B., Chen, H. (2016). Spectral collocation method for radiative-conductive porous fin with temperature dependent properties. Energy Conversion and Management, 111, 279–288. [Google Scholar]

126. Xi, Q., Fu, Z., Rabczuk, T., Yin, D. (2021). A localized collocation scheme with fundamental solutions for long-time anomalous heat conduction analysis in functionally graded materials. International Journal of Heat and Mass Transfer, 180, 121778. [Google Scholar]

127. Constantine, P. G., Doostan, A., Iaccarino, G. (2009). A hybrid collocation/Galerkin scheme for convective heat transfer problems with stochastic boundary conditions. International Journal for Numerical Methods in Engineering, 80(6–7), 868–880. [Google Scholar]

128. Hidayat, M. I. P. (2019). Meshless local B-spline collocation method for heterogeneous heat conduction problems. Engineering Analysis with Boundary Elements, 101, 76–88. [Google Scholar]

129. Karageorghis, A., Phillips, T. N., Davies, A. R. (1988). Spectral collocation methods for the primary two-point boundary value problem in modelling viscoelastic flows. International Journal for Numerical Methods in Engineering, 26(4), 805–813. [Google Scholar]

130. Wang, L., Qian, Z., Zhou, Y., Peng, Y. (2020). A weighted meshfree collocation method for incompressible flows using radial basis functions. Journal of Computational Physics, 401, 108964. [Google Scholar]

131. Aronson, R. M., Wetterer-Nelson, C., Evans, J. A. (2023). Stabilized isogeometric collocation methods for scalar transport and incompressible fluid flow. Computer Methods in Applied Mechanics and Engineering, 417, 116283. [Google Scholar]

132. Qian, Z., Wang, L., Zhang, C., Chen, Q. (2022). A highly efficient and accurate Lagrangian-Eulerian stabilized collocation method (LESCM) for the fluid-rigid body interaction problems with free surface flow. Computer Methods in Applied Mechanics and Engineering, 398, 115238. [Google Scholar]

133. Qian, Z., Wang, L., Zhang, C., Liu, Q., Chen, Q. et al. (2023). Numerical modeling of water waves with the highly efficient and accurate Lagrangian-Eulerian stabilized collocation method (LESCM). Applied Ocean Research, 138, 103672. [Google Scholar]

134. Aronson, R. M., Evans, J. A. (2023). Divergence-conforming isogeometric collocation methods for the incompressible Navier-Stokes equations. Computer Methods in Applied Mechanics and Engineering, 410, 115990. [Google Scholar]

135. Hon, Y. C., Šarler, B., Yun, D. (2015). Local radial basis function collocation method for solving thermo-driven fluid-flow problems with free surface. Engineering Analysis with Boundary Elements, 57, 2–8. [Google Scholar]

136. Meenal, M., Eldho, T. I. (2012). Two-dimensional contaminant transport modeling using meshfree point collocation method (PCM). Engineering Analysis with Boundary Elements, 36(4), 551–561. [Google Scholar]

137. Kim, Y., Kim, D. W., Jun, S., Lee, J. H. (2007). Meshfree point collocation method for the stream-vorticity formulation of 2D incompressible Navier-stokes equations. Computer Methods in Applied Mechanics and Engineering, 196(33), 3095–3109. [Google Scholar]

138. Zahab, Z. E., Divo, E., Kassab, A. J. (2009). A localized collocation meshless method (LCMM) for incompressible flows CFD modeling with applications to transient hemodynamics. Engineering Analysis with Boundary Elements, 33(8), 1045–1061. [Google Scholar]

139. La Rocca, A., Hernandez Rosales, A., Power, H. (2005). Radial basis function hermite collocation approach for the solution of time dependent convection-diffusion problems. Engineering Analysis with Boundary Elements, 29(4), 359–370. [Google Scholar]

140. Pruett, C. D., Streett, C. L. (1991). A spectral collocation method for compressible, non-similar boundary layers. International Journal for Numerical Methods in Fluids, 13(6), 713–737. [Google Scholar]

141. Subich, C. J., Lamb, K. G., Stastna, M. (2013). Simulation of the Navier-stokes equations in three dimensions with a spectral collocation method. International Journal for Numerical Methods in Fluids, 73(2), 103–129. [Google Scholar]

142. Ortega, E., Onate, E., Idelsohn, S. (2009). A finite point method for adaptive three-dimensional compressible flow calculations. International Journal for Numerical Methods in Fluids, 60(9), 937–971. [Google Scholar]

143. Botella, O., Peyret, R. (2001). Computing singular solutions of the Navier-stokes equations with the Chebyshev-collocation method. International Journal for Numerical Methods in Fluids, 36(2), 125–163. [Google Scholar]

144. Kudenatti, R. B., Sandhya, L., Bujurke, N. M. (2022). Numerical study on magnetohydrodynamic boundary layer flow of the Carreau fluid in a porous medium: The Chebyshev collocation method. Engineering with Computers, 38(3), 2633–2654. [Google Scholar]

145. Wang, D., Wang, J., Wu, J. (2018). Superconvergent gradient smoothing meshfree collocation method. Computer Methods in Applied Mechanics and Engineering, 340, 728–766. [Google Scholar]

146. Deng, L., Wang, D., Xu, X., Lin, Z., Fu, S. (2023). A superconvergent meshfree collocation formulation for laminated composite plates with particular focus on convergence analysis. Composite Structures, 321, 117248. [Google Scholar]

147. Deng, L., Wang, D. (2023). An accuracy analysis framework for meshfree collocation methods with particular emphasis on boundary effects. Computer Methods in Applied Mechanics and Engineering, 404, 115782. [Google Scholar]

148. Zayernouri, M., Karniadakis, G. (2014). Fractional spectral collocation method. SIAM Journal on Scientific Computing, 36, A40–A62. [Google Scholar]

149. Fu, Z. J., Tang, Z., Liu, Q., Gu, Y., Wang, F. (2022). Localized collocation schemes and their applications. Acta Mechanica Sinica, 38. [Google Scholar]

150. Wang, B., Iserles, A., Wu, X. (2016). Arbitrary-order trigonometric fourier collocation methods for multi-frequency oscillatory systems. Foundations of Computational Mathematics, 16(1), 151–181. [Google Scholar]

151. Guo, H., Zhuang, X., Rabczuk, T. (2019). A deep collocation method for the bending analysis of Kirchhoff plate. Computers, Materials & Continua, 59(2), 433–456. https://doi.org/10.32604/cmc.2019.06660 [Google Scholar] [PubMed] [CrossRef]

152. Wang, D., Qi, D., Li, X. (2021). Superconvergent isogeometric collocation method with Greville points. Computer Methods in Applied Mechanics and Engineering, 377, 113689. [Google Scholar]

153. Gao, X. W., Huang, S. Z., Cui, M., Ruan, B., Zhu, Q. H. et al. (2017). Element differential method for solving general heat conduction problems. International Journal of Heat and Mass Transfer, 115, 882–894. [Google Scholar]

154. Gao, X. W., Gao, L. F., Zhang, Y., Cui, M., Lv, J. (2019). Free element collocation method: A new method combining advantages of finite element and mesh free methods. Computers and Structures, 215, 10–26. [Google Scholar]

155. Gao, X. W., Ding, J. X., Liu, H. Y. (2022). Finite line method and its application in coupled heat transfer between fluid-solid domains. Acta Physica Sinica, 71(19). [Google Scholar]

156. Yan, J., fan Li, S., Zhang, A., yu Kan, X., Sun, P. N. (2019). Updated Lagrangian particle hydrodynamics (ULPH) modeling and simulation of multiphase flows. Journal of Computational Physics, 393, 406–437. [Google Scholar]

157. Yan, J., Li, S., Kan, X., Zhang, A., Lai, X. (2020). Higher-order nonlocal theory of updated Lagrangian particle hydrodynamics (ULPH) and simulations of multiphase flows. Computer Methods in Applied Mechanics and Engineering, 368, 113176. [Google Scholar]

158. Yan, J., Li, S., Kan, X., Zhang, A., Liu, L. (2021). Updated Lagrangian particle hydrodynamics (ULPH) modeling of solid object water entry problems. Computational Mechanics, 67(6), 1685–1703. [Google Scholar]

159. Yu, H., Li, S. (2021). On approximation theory of nonlocal differential operators. International Journal for Numerical Methods in Engineering, 122(23), 6984–7012. [Google Scholar]

160. Jingwen Ren, H. L. (2023). New perspective to isogeometric analysis: Solving isogeometric analysis problem by fitting load function. Computer Modeling in Engineering & Sciences, 136(3), 2957–2984. https://doi.org/10.32604/cmes.2023.025983 [Google Scholar] [PubMed] [CrossRef]

161. Jiang, W. W., Gao, X. W., Xu, B. B., Lv, J. (2023). Static and forced vibration analysis of layered piezoelectric functionally graded structures based on element differential method. Applied Mathematics and Computation, 437, 127548. [Google Scholar]

162. Gao, X. W., Liu, H., Cui, M., Yang, K., Peng, H. (2019). Free element method and its application in CFD. Engineering Computations, 36(8), 2747–2765. [Google Scholar]

163. Liu, H. Y., Gao, X. W., Xu, B. B. (2019). An implicit free element method for simulation of compressible flow. Computers & Fluids, 192, 104276. [Google Scholar]

164. Gao, X. W., Xu, B. B., Lv, J., Peng, H. F. (2019). Free element method and its application in structural analysis. Chinese Journal of Theoretical and Applied Mechanics, 51(3), 703–713. [Google Scholar]

165. Xu, B. B., Gao, X. (2023). Petrov-Galerkin zonal free element method for 2D and 3D mechanical problems. International Journal for Numerical Methods in Engineering, 124, 5047–5068. [Google Scholar]

166. Gao, X. W., Zhu, Y. M., Pan, T. (2022). Finite line method for solving high-order partial differential equations in science and engineering. Partial Differential Equations in Applied Mathematics, 7, 100477. [Google Scholar]

167. Gao, X. W., Jiang, W. W., Xu, X. B., Liu, H. Y., Yang, K. et al. (2023). Overview of advanced numerical methods classified by operation dimensions. Aerospace Research Communications, 1. [Google Scholar]