Adaptive Fusion Neural Networks for Sparse-Angle X-Ray 3D Reconstruction

1  Introduction

Feature-based 3D reconstruction and tracking technology has found extensive application in the medical field [1–3]. Combined with feature matching methods based on convolutional neural networks [4–6], 3D reconstruction of medical images can learn from 3D reconstruction algorithms for natural images [7–10]. There are a large number of open-source datasets for natural image processing [11–13]. These datasets include millions of labeled images for scholars to train and debug various models. However, there are many differences between medical images and natural images [14–16], therefore, research on medical image processing has gradually become a popular subject. Medical image labeling requires professional labeling, and the labeling cost is much higher than that of natural images. Due to the privacy property of medical images, a large amount of data cannot be disclosed or can only be disclosed after desensitization. The difficulty of obtaining and the amount of available data is very limited, which greatly limits the development of artificial intelligence in the direction of medical images. A small dataset can easily lead to overfitting of the neural network. Compared with natural images, the information in medical images is more complex, and the requirements for accuracy are also higher. Theoretically, it is necessary to design networks with more complex parameters, which makes the network easy to understand. In the case of limited data, scholars need to balance the scale of the network to better transfer the 3D reconstruction network of natural images to medical image reconstruction.

Different from natural images, X-ray images not only include external information, but also have internal structure [17–20]. Currently, most research efforts are focused on addressing the predictability of three-dimensional space from two-dimensional space.

Wu et al. [21] proposed an end-to-end model, MarrNet, to complete 3D reconstruction from 2.5D sketches. Compared to 3D images, 2.5D sketches are not only easier to extract from 2D images but also remain consistent despite variations in object appearance. Most importantly, this framework does not require labeled images, which greatly solves the problem of insufficient labeled image data in the field of 3D reconstruction. Tulsiani et al. [22] proposed a differentiable formula based on the consistency between a 3D shape and a 2D observed image to compute the gradient of a 3D shape observed from any angle. And then they put this formula into the learning framework for training and realize 3D reconstruction from any angle. Sun et al. [23] proposed Pix3D to realize the reconstruction from a single image to a 3D image at the pixel level.

In the earlier works, there were variations in the number and types of layers in the network architecture. For example, Yan et al. [24] used three convolutional layers with channel numbers 64, 128, and 256, and fully connected layers with node numbers 1024, 1024, and 512. In their work, the 3D reconstruction process is framed as an interaction between 3D and 2D representations. They propose an encoder-decoder network that incorporates projection loss into the model. Han et al. [25] incorporated a pooling operation into their approach to achieve 3D reconstruction of general objects from single or multiple RGB images. The aforementioned works represented three-dimensional objects using voxel-based discrete representations, encoding inputs from different angles into feature vectors. However, this encoding method has certain limitations as the feature vectors from different angles may not necessarily generate an effective three-dimensional object. The three-dimensional image reconstruction network based on single-angle X-ray is suitable for parts with a single structure. For most parts of the human body, its structure is complex and diverse, and single-angle X-rays cannot reconstruct understandable three-dimensional images.

To address the issue of inconsistent mapping of X-rays from various angles in 3D space, this paper builds a 3D reconstruction neural network based on orthogonal angle X-rays using the fundamental autoencoder neural network model [26–28]. It does this by referring to the adaptive fusion module in multi-angle 3D reconstruction of natural images. In the training stage, this module is used to reduce the distance between X-ray maps at different angles in 3D space. On the one hand, this module minimizes the distance between two maps to achieve solution stability. On the other hand, it reduces the distance between the solution and the real sample and improves the accuracy of the solution. In the inference phase, this module can evaluate the reconstruction results and assign scores. Then, these scores are used as the weights of the initial reconstruction results from different angles to achieve the adaptive fusion of multi-angle reconstruction results. This module organically combines the parts of each initial reconstruction that exhibit better quality to further improve the overall reconstruction quality.

In medical imaging analysis, training deep networks to reconstruct three-dimensional structures from X-ray images typically requires strict pairings of X-rays and corresponding 3D “ground truth.” However, real clinical X-ray images usually lack matched 3D volumetric data or cannot ensure identical imaging conditions, making it difficult to establish sufficient paired training samples. To address this, we employ an open lung CT dataset (LIDC-IDRI) and apply digitally reconstructed radiography (DRR) to project each 3D volume into simulated X-ray images from multiple angles, thereby constructing paired data of “frontal/lateral DRR projections–3D CT volumes.” In this way, the CT scans not only serve as the three-dimensional reference for supervised training and performance evaluation but also generate sparse-angle simulated X-ray images from different views, compensating for the scarcity and alignment challenges often encountered in real clinical data. Finally, this paper conducts comparative experiments with various fusion schemes on the LIDC-IDRI dataset. The results show that the adaptive fusion module can evaluate the quality of reconstruction results from different perspectives during the inference process. During training, this evaluation facilitates the reconstruction network to produce higher-quality 3D voxels. The adaptive weight fusion scheme uses a set of network parameters to reconstruct two inputs, gradually guiding different 2D inputs to converge to the true value in 3D space and achieve consistency. Therefore, the adaptive fusion module proposed in this paper partially addresses the problem of inconsistent mapping of multi-angle reconstruction results in 3D space, improves the reconstruction quality, and realizes interpretable 3D images based on sparse-angle X-ray reconstruction.

2  Method

2.1 Reconstruction Network Framework Based on Adaptive Weight Fusion

This study mainly proposes a 3D reconstruction network based on adaptive weight fusion, which is based on the basic self-encoder neural network model. Before introducing the details of each module in detail, this section will introduce the framework of the whole network and the direct connection mode of each module.

In the fields of image super-resolution reconstruction and restoration, the auto-encoder (AE) is the basic structure of various generation networks [29]. AE is a neural network that reconstructs the data itself through training. As shown in Fig. 1, its main body is composed of encoder F and decoder G. Encoder F maps the original data X to hidden layer h, and the function of the decoder is the opposite. The decoder G takes the hidden layer has the input to generate the reconstruction of the data X^. The training goal of AE is to make X^ as close to X as possible. Therefore, AE belongs to the unsupervised neural network model. The encoder F reduces the dimension of input features, and its function is similar to the principal component analysis method. It extracts the most representative information from input X and reduces the amount of information. This learning process is simple. The function of the decoder is not to generate the reconstruction of data X but to map h to other learning objectives. By changing the structure and learning objectives of the decoder, AE is suitable for all kinds of generation tasks.

Figure 1: Structure of AE

The three-dimensional reconstruction network infrastructure in this section is similar to AE, which consists of an encoder and decoder. The key difference lies in the dimensionality of the decoder, which differs from that of the encoder. The decoder will map the two-dimensional output of the encoder to three-dimensional space, and the learning goal is to output the three-dimensional image corresponding to the two-dimensional image. The function of the encoder is to extract two-dimensional features. Through dimensional transformation, the decoder samples the low-resolution features into high-resolution features, which is the forward propagation process of a single input network. The input for this paper is two orthogonal-angle X-rays. Therefore, how to design a multi-input code is one of the key problems in reconstructing the network. For the reconstruction problem, we hope that the reconstruction resolution is as high as possible, so that it is possible to reconstruct more detailed texture features. However, the higher the resolution corresponds to the more complex network parameters, the more difficult the training is, and the higher the requirements for the data set. If a separate codec network is trained for each input image, the network volume may be too large, and it is easy to overfit the network in the case of less training data. Without reducing the reconstruction quality, let two inputs share the codec network, which will greatly reduce the complexity of the network. Therefore, the 3D reconstruction network in this section shares a codec weight for two X-rays, and the two X-rays are input into the codec in turn to infer the initial reconstruction result.

Feature dimension transformation is key to 3D reconstruction based on 2D images, as it relates is to the starting point of 3D mapping. A low-resolution 3D feature containing a certain spatial structure relationship undoubtedly provides a good origin for upsampling 3D reconstruction. Two-dimensional features, whether advanced abstract features or primary simple features such as edges and corners are obtained under a certain two-dimensional spatial arrangement that reflects the corresponding three-dimensional spatial distribution to a certain extent, which is one of the reasons why a three-dimensional reconstruction based on a two-dimensional image is feasible. It is simply transformed into three-dimensional features by changing the arrangement order of two-dimensional features. Therefore, this paper uses the feature dimension transformation method based on a full connection network to retain some spatial information through full connection mapping.

To better integrate the reconstruction results from two perspectives and fully leverage the complementary strengths and weaknesses of the reconstruction results from different angles, inspired by the multi-angle fusion natural images in [30], this section proposes a weight fusion module. In [30], the parameters of the weight generation network corresponding to the input images from different angles are not shared. The weight fusion module in this section can be regarded as a reconstruction result scoring network. By scoring each voxel of the initial results to evaluate the quality of the voxel reconstruction and using the scores as weights for the fusion of the two results, adaptive fusion of the reconstruction outcomes is achieved.

To sum up, the reconstruction network framework based on adaptive weight fusion proposed in this study is shown in Fig. 2.

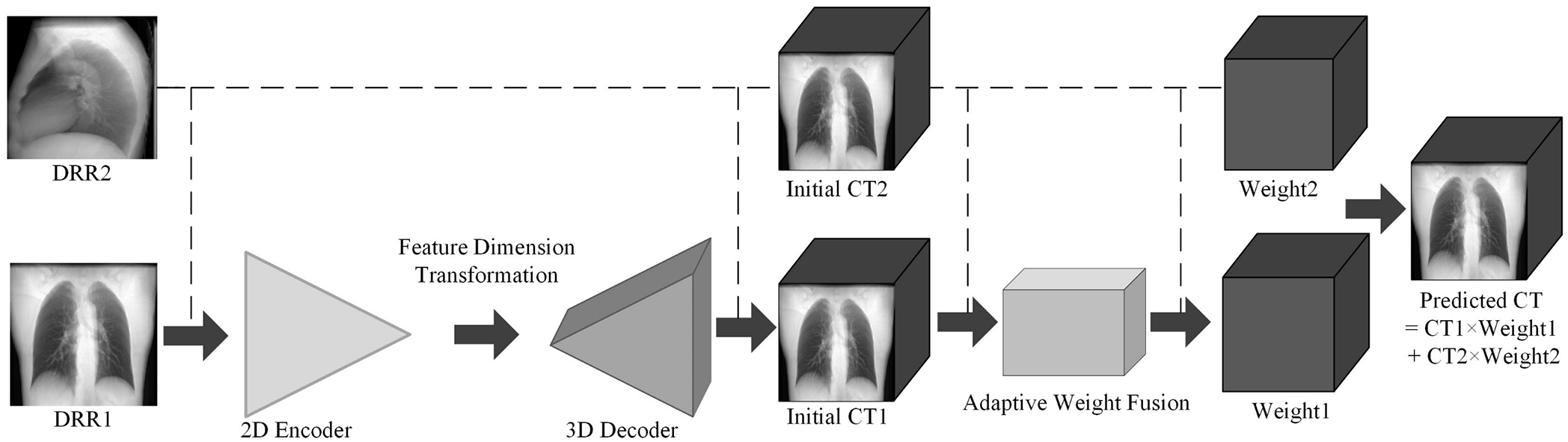
Figure 2: Schematic diagram of reconstruction network framework based on adaptive weight fusion.

2.2 3D Reconstruction Network Design

2.2.1 2D Convolutional Layer

The core of the convolutional neural network is the convolutional layer, whose main function is to extract the input image, also known as the feature extraction layer. Its characteristics are weight sharing and local connection, which realize most of the calculations in the forward propagation and backpropagation of the model. The parameters of each convolutional layer are optimized by the backpropagation algorithm. Generally, when referring to the convolution operation, not only the convolution operation but also the bias and activation functions are included. The complete calculation process is shown in Eq. (1):

Z(l+1)=Wlχl+bl(1)

χl=f(Z(l+1))

Among them, χl represents the input of the current convolutional layer, as well as the output of the previous convolutional layer. Wl represents the convolution kernel weight, represents the bias value, and bl represents the activation function. The convolution layer extracts feature by convolving the input with the convolution kernel. The original image, or intermediate layer features, are inputs to the convolution kernel of a certain layer. The function of the convolution kernel is a feature extractor, and the calculation result is a feature. The convolution kernel can filter out the local features in the picture, and the visualization of the feature map can clearly identify the image features observed by human vision. The first few layers of convolution generally extract some relatively low-level features, such as edges, corners, and lines, and multi-layer convolution operations can iterate more complex and abstract features from low-level features. Specifically, the convolution kernel slides the input matrix from left to right and from top to bottom to perform the convolution operation with a certain step size. In each coverage area, it is multiplied and summed with the corresponding value to obtain the output feature matrix eigenvalue. Taking the convolution of two 3 × 3 matrices as an example, the convolution operation is shown in Eq. (2):

(f∗g)(1,1)=∑k=02∑h=02f(h,k)g(1−h,1−k)(2)

where, f represents the feature matrix, g represents the convolution kernel matrix, while h and k respectively represent the horizontal and vertical coordinates of the matrix. A convolution kernel has only one feature map output, regardless of single-channel input or multi-channel input. When the input has multiple channels, the convolution kernel simultaneously performs convolution on each of those channels and sums the resulting values to form a single feature in the output feature map.

In the actual operation, to make each point on the feature map participate in the convolution operation as a convolution center, zeros are filled around the feature map, which is called padding. In the convolution operation, the sliding interval of the convolution kernel is also different, which influences the dimensions of the output feature map. For a convolution operation, the size relationship between the input and output feature maps is shown in Eq. (3):

o=(i−2p−k)s+1(3)

Here, i represents the input feature size, o represents the output feature size, p refers to the number of rows or columns of zero padding, k to the convolution kernel size and s to the sliding step size

The two-dimensional convolutional layer is the core structure of the encoder. It forms a convolutional block with the batch normalization layer and the activation function layer. As the number of convolutional network layers increases, the image features extracted by the convolutional block become more and more abstract. Fig. 3 shows the first 16-channel 2D feature maps extracted from the front-side DRR image (simulated X-ray images, explanation will be provided in following section) by the first-layer convolutional block of the encoder in this paper.

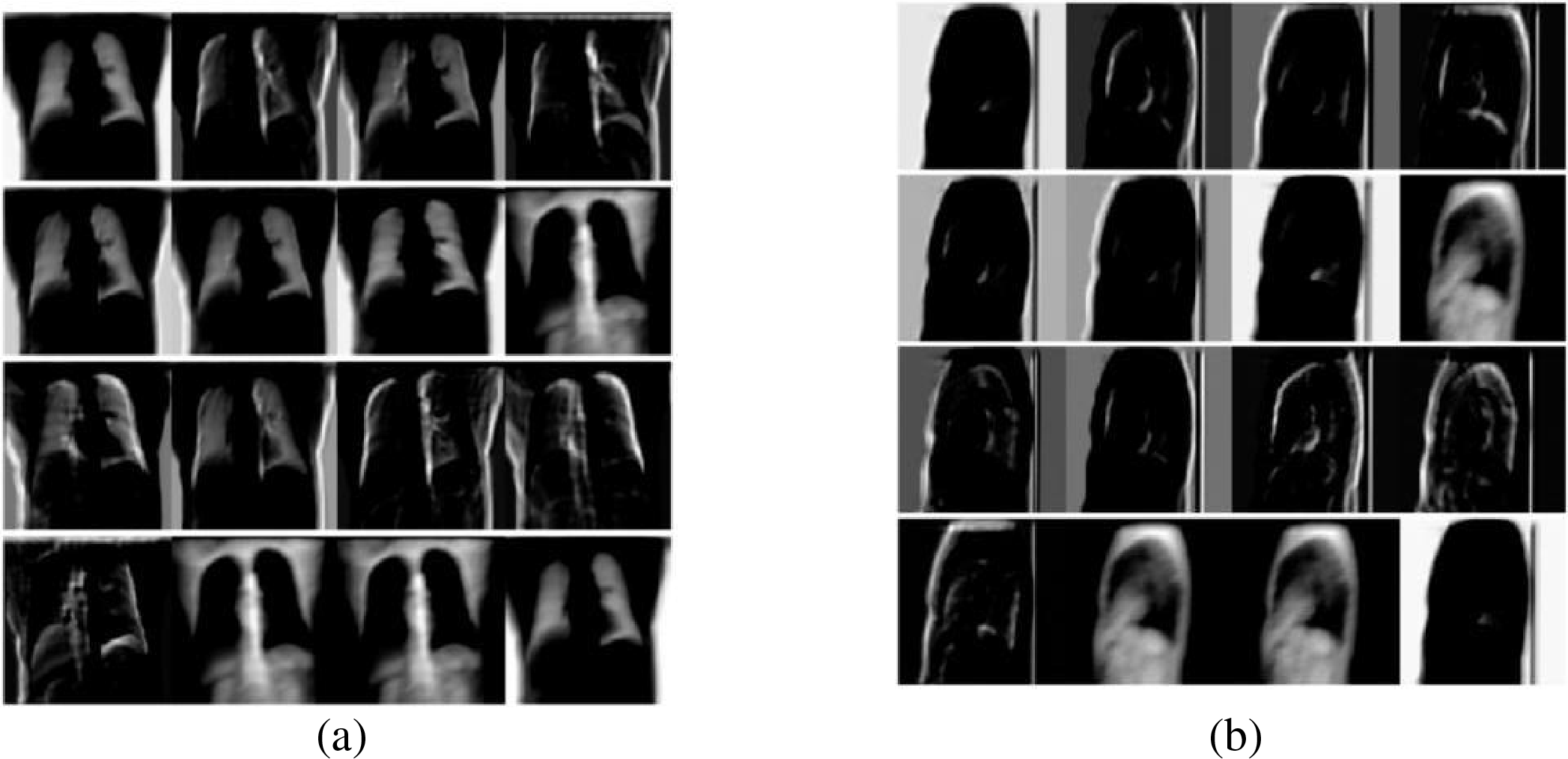
Figure 3: Schematic diagram of feature map extracted by convolution block (a) front view; (b) lateral view

Fig. 3 illustrates the feature extraction results of a simple convolution layer: (a) shows the features extracted from the front X-ray, and (b) displays the features extracted from the lateral view. The single-layer convolution block in Fig. 3 mainly extracts low-level semantic information such as edges and contours, which is particularly evident for side-view images where only the chest cavity and background can be identified. Despite the strong feature extraction capability of convolution blocks, fully leveraging their potential for multi-level feature extraction requires careful alignment with specific task objectives, dataset constraints, loss functions, and available hardware resources.

2.2.2 2D Encoder

The function of the two-dimensional encoder is to extract multi-level features from the input 2D image, which the decoder then uses to upsample and reconstruct the 3D image [31]. Extracting sufficiently rich features from 2D images is an important part and cornerstone of the entire reconstruction work. Any decoder structure or multi-angle fusion network cannot reconstruct the details of 3D images without sufficient features, and it is impossible to perform well.

The role of the designed fusion network is to fully extract the features of the input image. The basic structure of the 2D encoder adopts DenseBlock [32]. A DenseBlock consists of several layers of convolution. The multiplexing method for multi-layer features in DenseBlock is the splicing of multiple channels. The forward propagation method of DenseBlock is shown in Fig. 4, while Fig. 5 shows the 2D encoder structure with DenseBlock as the basic.

Figure 4: Structure diagram of dense block

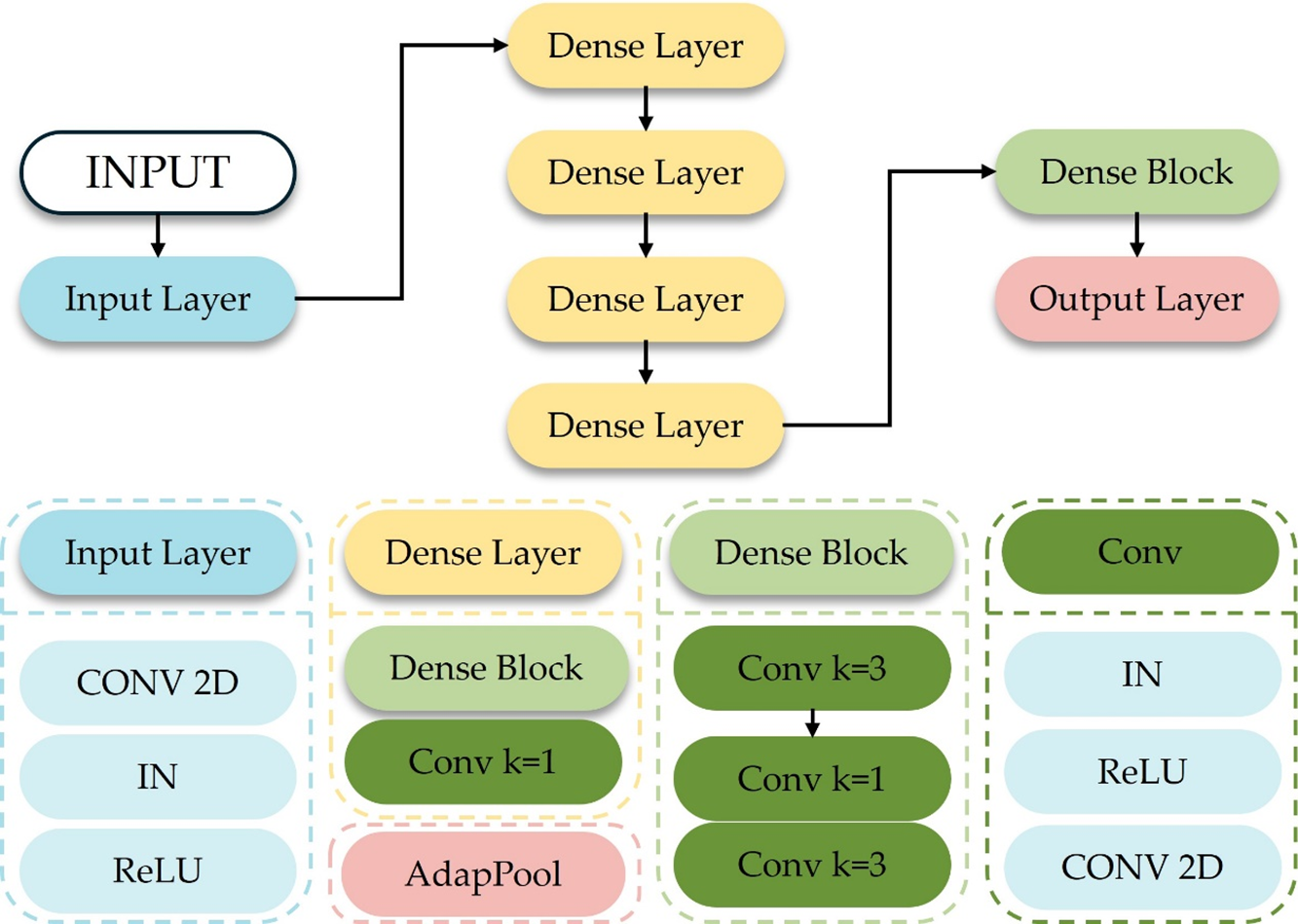
Figure 5: Schematic diagram of the structure of the two-dimensional encoder

In Fig. 5, IN (Instance Norm) represents instance normalization. When the amount of data in each batch in batch normalization is one, batch normalization is equivalent to instance normalization, and the normalization is performed on a per-channel basis. The size of the convolution kernel, the length, and the width are both k. The following is a detailed description of the structure in Fig. 5.

1) Input Layer

The encoder begins with a single convolutional block composed of a 7×7 convolution (64 output channels), followed by ReLU activation and an Instance-Normalization layer.

2) Dense Layer

As illustrated in Fig. 5, the encoder contains four Dense Layers. Each Dense Layer consists of a Dense Block immediately followed by a 1×1 Transition Layer. A Dense Block adopts the standard ordering IN→ReLU→3×3Conv and is densely connected: if the block contains n+1 convolutional layers, the first layer comprises only a single k=3 convolution with 64 channels, whereas every subsequent layer contains two convolutions with kernel sizes k=1 and k=3, respectively, and outputs 32 feature channels. Consequently, after each additional layer the composite feature tensor grows by 32 channels.

To permit deeper feature reuse while preventing uncontrolled channel inflation, a 1×1 Transition Layer is inserted after every Dense Block to reduce the channel count such that the net increase across each Dense Layer is 64 channels. The number of composite layers inside successive Dense Blocks first increases and then decreases with network depth (as 6,12,24,16,6) thereby achieving a wide receptive field in the middle of the network without sacrificing either shallow- or deep-level detail.

3) Output Layer

The final stage of the encoder is an Adaptive Average Pooling layer (AdapPool). Unlike fixed-size max or average pooling, adaptive pooling automatically adjusts its kernel size so that the output spatial dimensions are reduced to 1 × 1 regardless of the preceding feature-map size. This property renders the network robust to moderate variations in input resolution and produces a compact 704-channel descriptor that feeds the subsequent three-dimensional reconstruction module.

2.2.3 Feature Dimension Transformation

Fig. 6 shows the process of the feature dimension transformation. Mapping two-dimensional features to three-dimensional space requires appropriate dimension expansion. Within the domain of deep learning, it can be directly transformed into three-dimensional features by rearrangement of features, or the two-dimensional features of several channels can be regarded as a three-dimensional feature. In this paper, the input size of the fully connected network is 1 × 704, the output size is 1 × 16,384, and the output features are rearranged to obtain 3D features of size 1 × 256 × 4 × 4 × 4, which are used as the input of the 3D decoder.

Figure 6: Schematic diagram of feature dimension transformation process

2.2.4 3D Encoder

To further enhance the quality of image upsampling, this section uses the structure of 3D convolution and then deconvolution as the basic structure of the upsampling module. The structure of the 3D decoder is shown in Fig. 7.

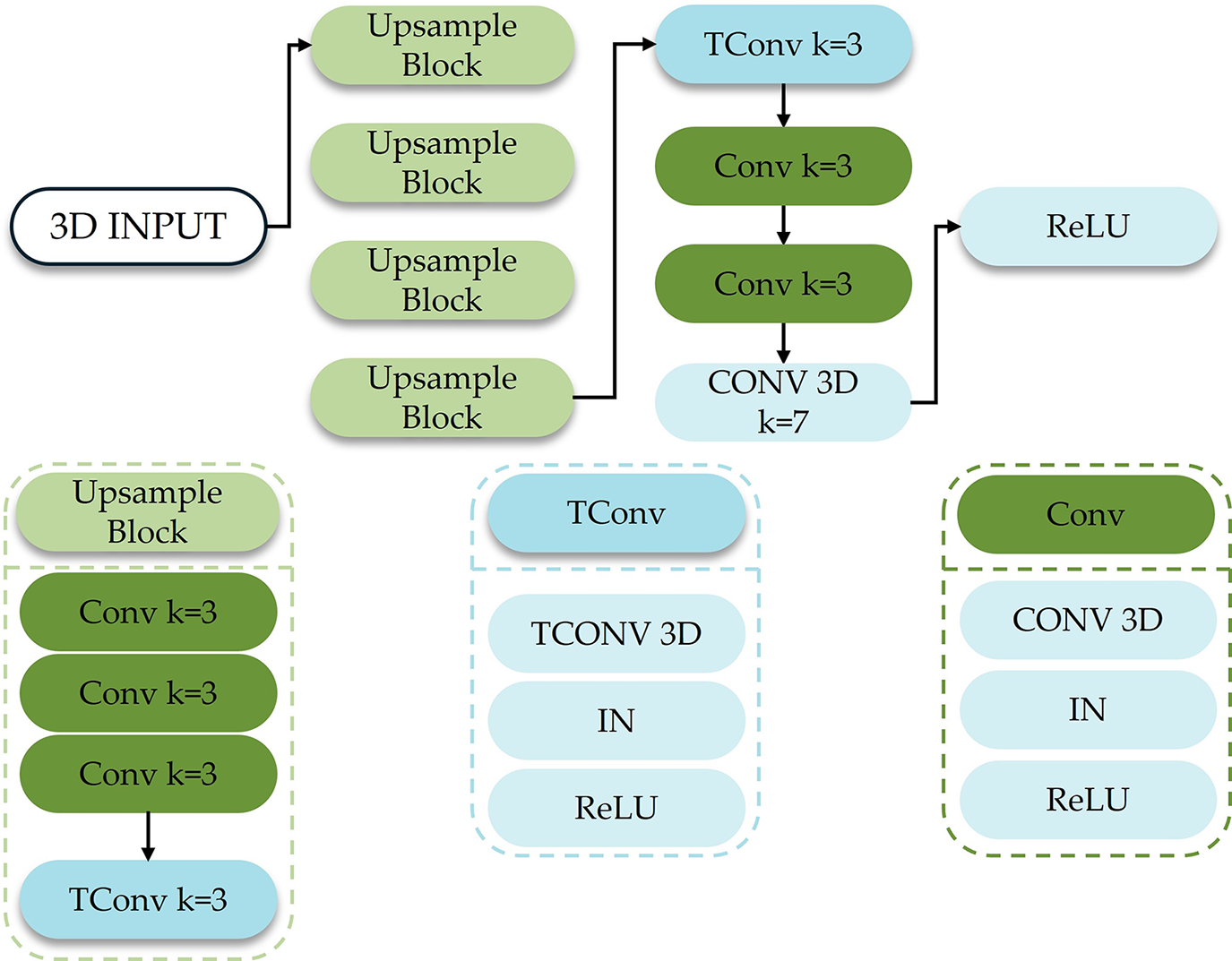
Figure 7: Schematic diagram of the structure of the 3-dimensional encoder

In Fig. 7, TConv (Transposed Convolution) represents three-dimensional deconvolution; the size of the convolution kernel, the number of padding zeros, and the step size of each TConv are 3, 1 and 2, respectively. There are 5 TConv in the figure. The size of each channel of the input 3D features is 4, and the output feature size of the 3D decoder is 128.

2.2.5 Adaptive Weight Fusion Module

The adaptive weight fusion module in this paper is shared by two angle inputs. The initial results generated by the two angles of X-rays are respectively scored and then normalized by the Softmax classifier, and the final result is obtained after weighting. The structure of the adaptive weight fusion module is shown in Fig. 8.

Figure 8: Schematic diagram of the structure of the adaptive weight fusion module

In the figure, C (Concat) represents the feature splicing in the channel direction, and AdaptWeight (Adaptive eight) represents the adaptive weight. The two initial 3D reconstruction results correspond to weights, respectively. At the same voxel point, the weighted sum is 1. As the network layers deepen, the receptive field of the feature map expands. To account for both global and local features in scoring the input, this section concatenates the output features from the first four layers of 3D convolution blocks and feeds them into the fifth convolution block. The input shown in the figure represents the output from the 3D decoder and the input features from the final convolution layer, resulting in a total of 17 channels of 3D features being used as the single input for the Adaptive Weight Module.

The adaptive weighting method, in addition to the one shown in the figure, can also be weighed by confidence value, which is called the confidence value fusion module in this article. This module has the same structure as the adaptive weight fusion module. The only difference is that it has been scored by SoftMax. The weight obtained by the generator will not be directly multiplied by the initial reconstruction result. The score is regarded as the confidence value of each voxel point. The score with a larger confidence value is set to 1 while 0 for the smaller one, as it has been scored by SoftMax. Thus, value above 0.5 is assigned as 1, value below 0.5 is assigned as 0, which is equal to 0.5 remains unchanged.

3  Dataset and Preprocessing

Since accurate three-dimensional ground truth is essential for training and evaluating 3D reconstruction networks, real clinical X-ray images typically do not come with precisely corresponding 3D volumetric data. Therefore, we utilize an open-source lung CT dataset and generate digitally reconstructed radiographs (DRR) at sparse angles to serve as the dataset for subsequent experiments. This approach provides a reliable way to pair simulated X-ray images with their true 3D references, effectively supporting training and validation in sparse-angle X-ray 3D reconstruction.

3.1 CT Image Dataset

The development of medical image analysis is in separable from the support of open-source data sets [33,34]. This study uses LIDC-IDRI set as the CT dataset for this research. which includes human thoracic CT and the labeling of corresponding pulmonary nodules [35].

The resampling of natural images directly unifies images of different sizes through downsampling or interpolation. The resampling of CT needs to consider the distance between voxels, and the distances in the slice direction are all equal, and only the axial distance needs to be unified. In this paper, the axial distance is unified to 1, and the formula for the number of slices before and after interpolation is shown in Eq. (4):

numz=numz∗spacingznew_spacing(4)

Among them, numz is the number of initial slices, spacing is the initial axial distance, and new_spacing is the desired new distance.

To standardise the axial dimension while leaving the in-plane metric unchanged, we first determined the mode of slice counts in the raw CT cohort (256 slices) and adopted it as a unified reference. CT volumes with ≥256 slices were subsampled at an integer interval; those with <256 slices were upsampled to 256 by simple linear interpolation along the z-axis only. No rescaling was applied in the x–y plane, so the original PixelSpacing (Δx,Δy) contained in the Digital Imaging and Communications in Medicine (DICOM )header remains intact.

All volumes were then embedded into a fixed cuboid and voxels outside the valid field-of-view were filled with −2000 Hounsfield Units (HU), while intensity values <−1024 HU were clipped to −1024 HU. These steps merely normalise slice count and suppress non-informative air regions; they do not alter physical dimensions: every voxel can still be mapped back to patient space by multiplying its index with (Δx,Δy,Δz). Consequently, any linear or volumetric measurement made on the reconstructed volume is identical. The comparison of CT slices before and after preprocessing is shown on Fig. 9.

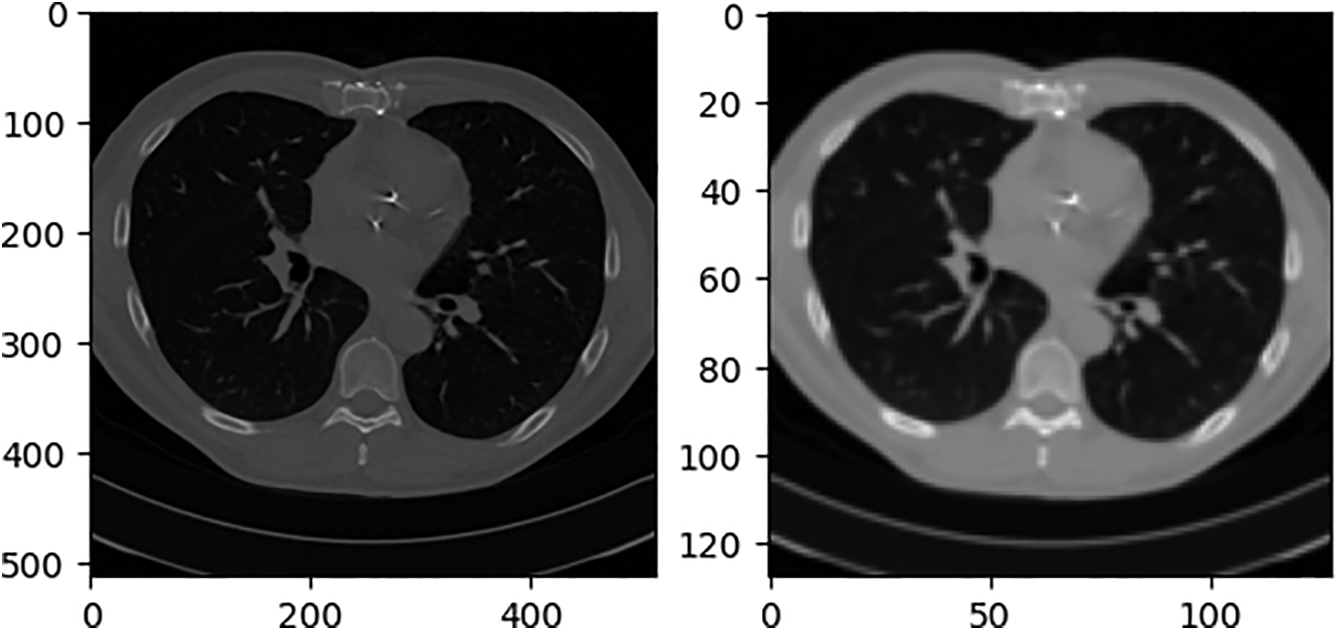
Figure 9: Schematic diagram of the structure of the adaptive weight fusion module

3.2 X-Ray Dataset

Our “virtual X-ray” images are standard DRRs generated by Siddon ray-casting directly on the CT voxel grid without any additional filtering or down-sampling. This technique is widely used in radiotherapy treatment-planning systems and has been validated against clinical radiographs in multiple studies [36,37]. Hence it is generally accepted as a surrogate for conventional projection X-ray. In this paper, we project from the front and sides of CT. During projection, if the projection resolution is too low, the projection image cannot be used and does not necessarily contain the entire CT content. If the projection resolution is too high, the content is excessive, the network input does not require a high-resolution image, and the projection calculation time is increased. After several projection experiments, the projection resolution of 180 × 200 can maximize the inclusion of the entire CT content and occupy as many pixels as possible. To distinguish real X-rays from simulated X-rays generated by the DRR algorithm, this paper refers to simulated X-rays as DRR images. The initial projection results are shown in Fig. 10.

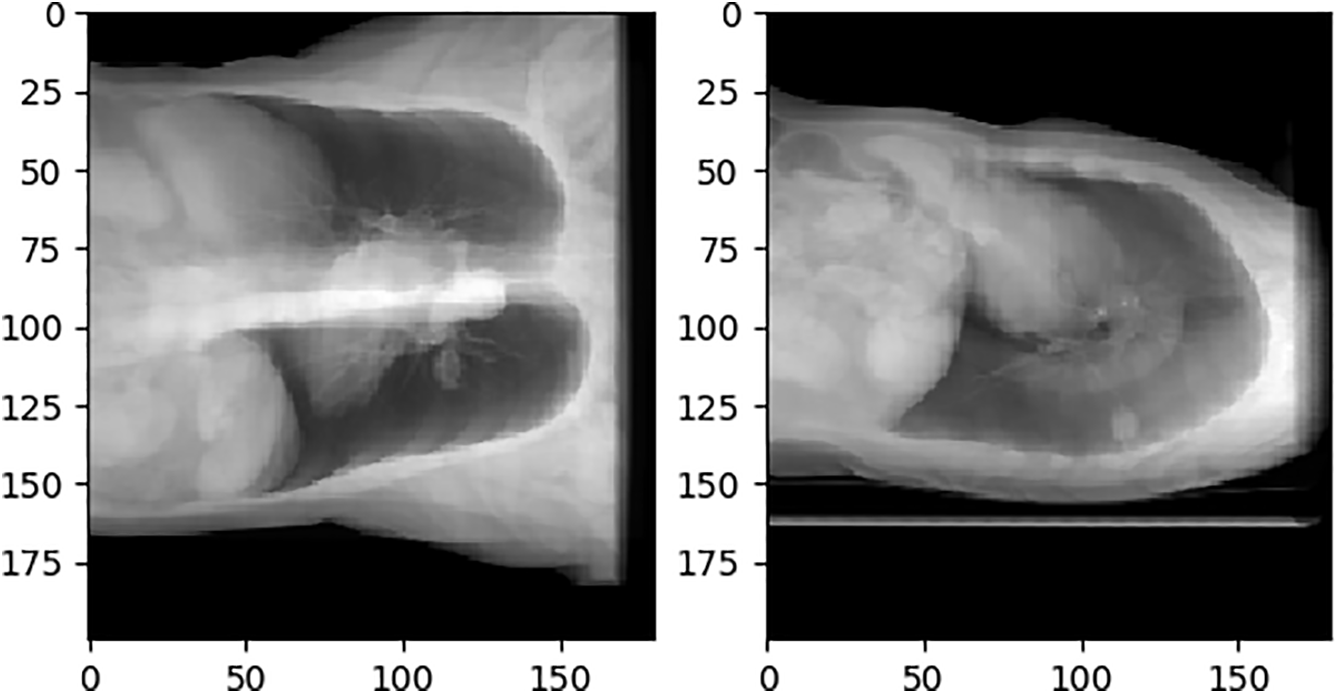
Figure 10: Initial DRR image

As the input of the network, the ideal DRR image should only contain valid information and have the same size. The front projection Cor (Coronal plane) ratio is close to 1:1, while the side projection Sag (Sagittal plane) is obviously different. If the black pixels in the sag are deleted and the ratio is adjusted to 1:1, it will seriously destroy the information ratio on the lateral side of the thorax. The adjusted DRR image is not conducive to the convergence of the network, and it also does not match the distribution of the real human thoracic cavity, which increases the difficulty of generalizing the network to real X-rays. Fig. 11 shows the sag with the black border removed and the resolution adjusted from 180 × 200 to 128 × 128 compared to just the resolution.

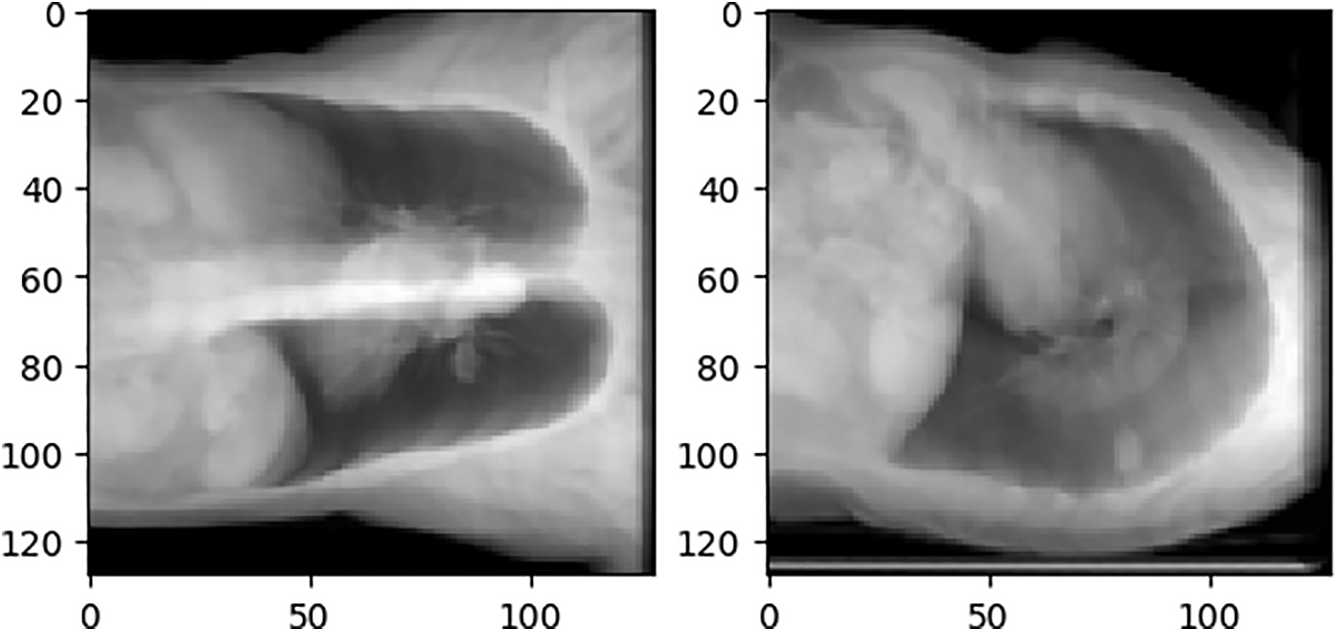
Figure 11: Comparison of different scales of sag

4  Experiment

4.1 Experimental Environment and Evaluation Metrics

The experimental environment of this study is shown in Table 1.

The experiments were designed to reconstruct coarse-resolution chest volumes from routine radiographic views while preserving all clinically relevant scale information. First, 1012 chest CT studies from the public LIDC-IDRI cohort were converted into paired postero-anterior (PA) and lateral (LAT) DRRs using a standard Siddon ray-casting pipeline. Each CT volume was normalised to 256 axial slices by interval subsampling or linear interpolation along the z-axis only, after which voxels outside the lung–mediastinum field-of-view were padded with –2000 HU and intensities <–1024 HU were clipped. The resulting DRRs were cropped to their valid region and resized to 128 × 128 pixels, yielding geometry-conserved CT–DRR pairs. The dataset was partitioned into a fixed training set of 800 pairs and a test set of 212 pairs, with no further shuffling during optimisation.

A weight-fusion three-dimensional reconstruction network was implemented in PyTorch; convolutional kernels were initialised with a zero-mean Gaussian distribution (σ=0.02). During training the network received the two 128 × 128 projections as input, processed one pair per iteration (batch = 1), and was optimised for 50 epochs with the Adam optimiser at a constant learning rate of 2×10−4(β1=0.5,β2=0.9). At inference time each DRR pair from the held-out test set was fed through the trained model to produce a 1283-voxel volume. Performance was assessed quantitatively by MAE (Mean Absolute Error),PSNR (Peak Signal-to-Noise Ratio) and SSIM (Structural Similarity) against the corresponding ground-truth CT and qualitatively by visual inspection.

The calculation methods of SSIM, PSNR and MAE are shown in Eqs. (5)–(7):

SSIM(X,Y)=(2μXμY+C1)(2σXY+C2)(μX2+μY2+C1)(σX2+σY2+C2),C1=(K1L)2,C2=(K2L)2(5)

where, symbol X and Y are predictions and ground-truth volumes, reshaped as 1-D voxel vectors. μX,μY mean voxel value of X and Y. σX2,σY2 are variance of X and Y. σXY is covariance between X and Y. Stabilizing constants with K1=0.01,K2=0.03 and dynamic range L=4095HU. SSIM ranges from –1 to +1, indicating structural agreement.

PSNR(X,Y)=10log10⁡(L21N∑i=1N(Xi−Yi)2),(6)

where N is total number of voxels. L is maximum possible voxel value. Xi and Yi are the i-th voxel in prediction and ground truth. PSNR is expressed in decibels (dB); higher values imply better fidelity.

MAE(X,Y)=1N∑i=1N|Xi−Yi|.(7)

MAE retains the physical HU unit, reporting the average absolute deviation per voxel. These three complementary metrics respectively capture structural similarity, overall signal fidelity relative to dynamic range, and average voxel-wise intensity error, providing a balanced quantitative assessment of the proposed 3-D reconstruction framework.

4.2 Preliminary Experiment

The experimental results in this study are analyzed from both quantitative and qualitative perspectives. The quantitative analysis uses three evaluation indexes, SSIM, PSNR, and MAE, to evaluate and average the test sets in the data set. The qualitative analysis uses a test sample to show reasoning results for different network structures. The test sample inputs for all qualitative analyses in this section are Cor and Sag, as shown in Fig. 12.

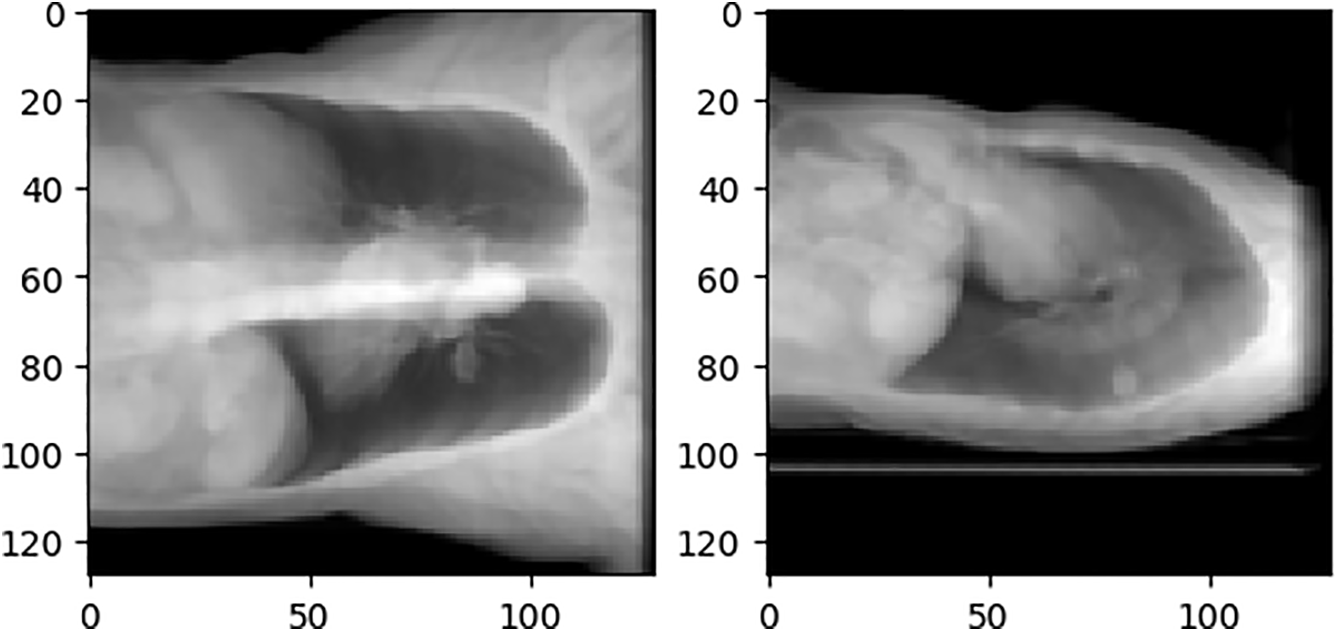
Figure 12: Qualitative analysis test samples Cor and Sag

Besides the design of the network structure, the design of the loss function is also crucial to the performance of the network. MAE loss and MSE (Mean-Square Error) loss are used in the codec network and feature dimension conversion modules introduced in this section, respectively. The test sample output of the network is shown in Fig. 13. The two figures are the sum of voxels in the same direction as Cor and Sag. It can be seen that the reconstruction results of MAE are similar to Cor and Sag, while MSE cannot recognize the clear contour, and MAE should be clearer in terms of the slice.

Figure 13: Comparison of MSE and MAE. (a) MSE result; (b) MAE result

4.3 Ablation Experiment

For the convenience of narration, the networks participating in the experiment are named before introducing the experiment. All reconstructed networks use the same encoder-decoder and feature dimension transformation module. The difference is in the number of input-DRR images and whether the adaptive fusion module is included. In this experiment, three fusion methods are selected: ConfFusionNet, AvgFusionNet, and SingleViewNet to compare with AdapFusionNet. Table 2 introduces the network names, inputs, whether the adaptive fusion module is included, and the fusion method of multi-angle output when the input is greater than 1.

This experiment uses MAE as the reconstruction loss function. The training loss curve during model training is shown in Fig. 14.

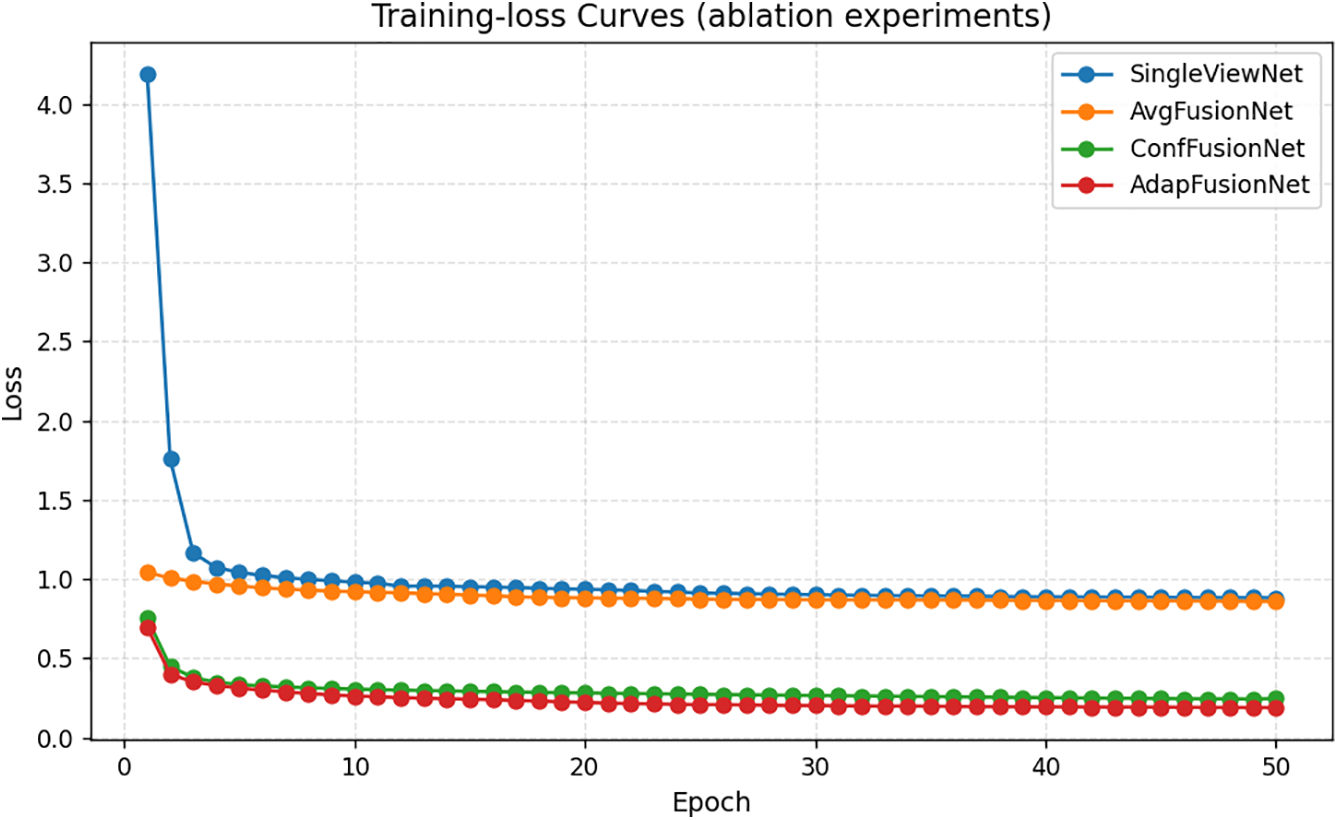
Figure 14: Model training loss curve

The encoder of AdapFusionNet can extract features from DRR images at different angles. Fig. 15 shows the feature maps of the first 16 channels of the features output by the first Dense Layer of the AdapFusionNet encoder for Cor and Sag.

Figure 15: AdapFusionNet encoder feature map diagram. (a) Cor; (b) Sag

Compared with AdapFusionNet, AvgFusionNet lacks the adaptive weight fusion module. The reconstruction results of Cor and Sag are averagely weighted to obtain the output result. Similarly, the feature map of the first Dense Layer is extracted and visualized as shown in Fig. 16.

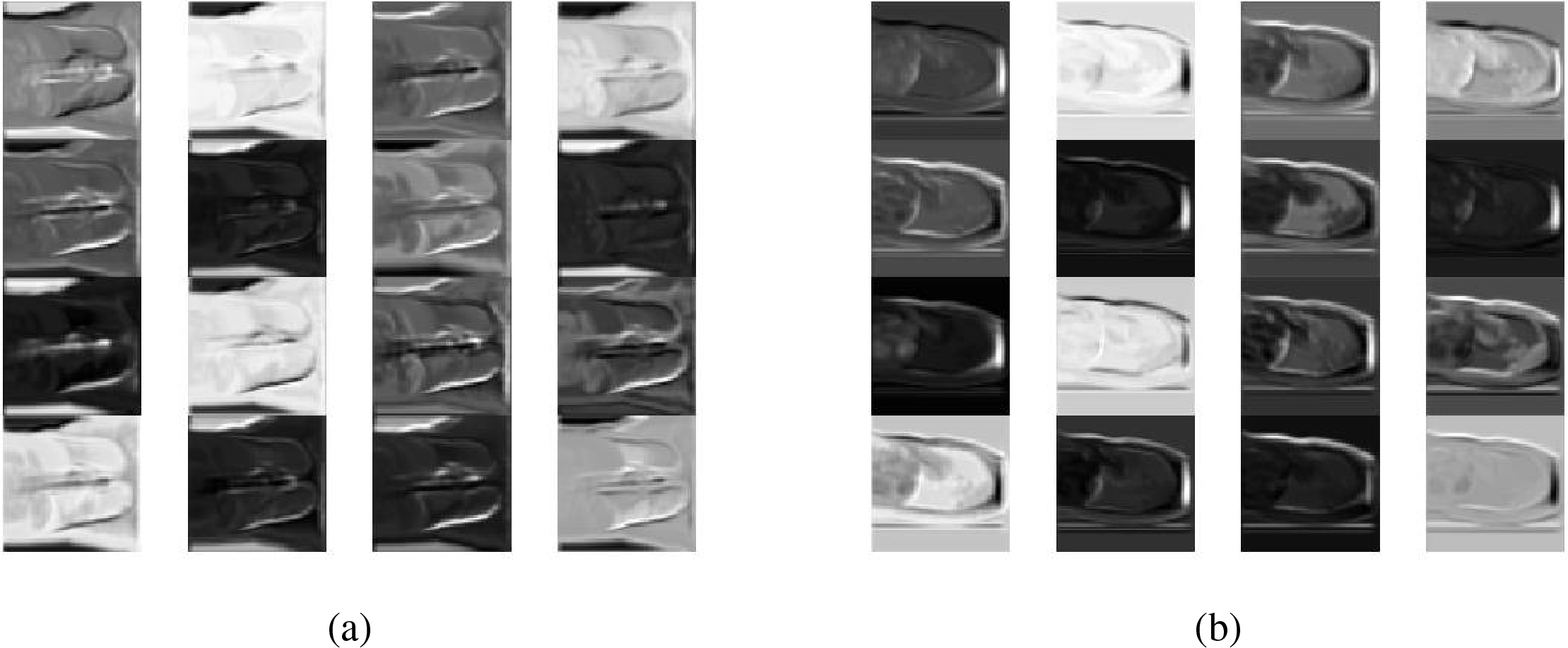
Figure 16: AvgFusionNet encoder feature map diagram. (a) Cor; (b) Sag

The average evaluation results based on the test set are shown in Table 3. AdapFusionNet has better PSNR and SSIM performance, and its MAE is slightly inferior to AvgFusionNet.

In terms of qualitative evaluation, the reasoning results of the four networks on the test samples are shown in Fig. 17. The experimental results show axial (horizontal) slices extracted from the reconstructed 3D volume at the same anatomical level as the source CT.

Figure 17: Qualitative evaluation of ablation experiments

The reconstruction result of SingleViewNet has obvious unreasonableness in the chest edge contour. Based on it, AvgFusionNet adds another sag as input, which improves the chest contour information, but there are still obvious deficiencies in the lung contour. After adding the adaptive fusion module to ConfFusionNet and AdapFusionNet, there are obvious improvements in both chest contour and lung contour reconstruction. The improvement of the reconstruction effect by the adaptive fusion module is very obvious in qualitative evaluation.

The edges of ConfFusionNet are very clear, and the grayscale is relatively consistent within the same tissue, but the noise is obvious. The contour of AdapFusionNet is relatively clear, but the grayscale distribution within the same tissue is somewhat uneven. Although the contour of this fusion method is not as clear as ConfFusionNet, it will not bring additional noise at the same time. In summary, AdapFusionNet is significantly better than SingleViewNet and AvgFusionNet in qualitative evaluation and has a slight advantage in quantitative evaluation.

In AdapFusionNet, with the aim of verifying the evaluation effect of the adaptive fusion module on the initial reconstruction results, the codec trained based on AdapFusionNet is used to experiment with different fusion methods. In AdapFusionNet and ConfFusionNet, the adaptive weight module generates the corresponding fusion weights adapweight1 and adapweight2 for the initial reconstructed voxels volumes1 and volumes2 of cor and sag and obtains the reconstructed voxels Adapvolumes based on adaptive weight fusion Adapfusion and Avgvolumes based on average fusion AvgFusionNet. Based on confidence value fusion, the reconstructed voxel Confvolumes with confidence weights confweight1 and confweight2 are fused. Multiple-slice examples are selected. The results of the experiment are shown in Fig. 18, where Adapweight and Confweight represent the weight of input volumes 1, and the sum of volumes 2 is 1, which is not displayed repeatedly.

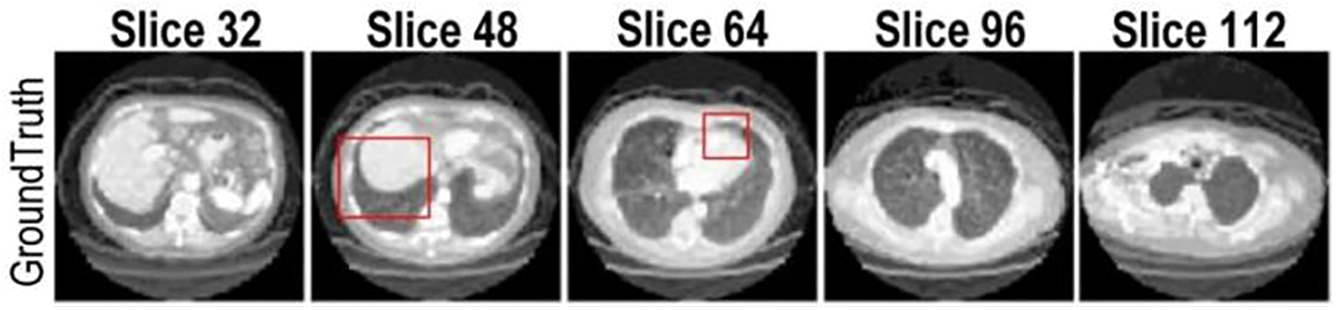
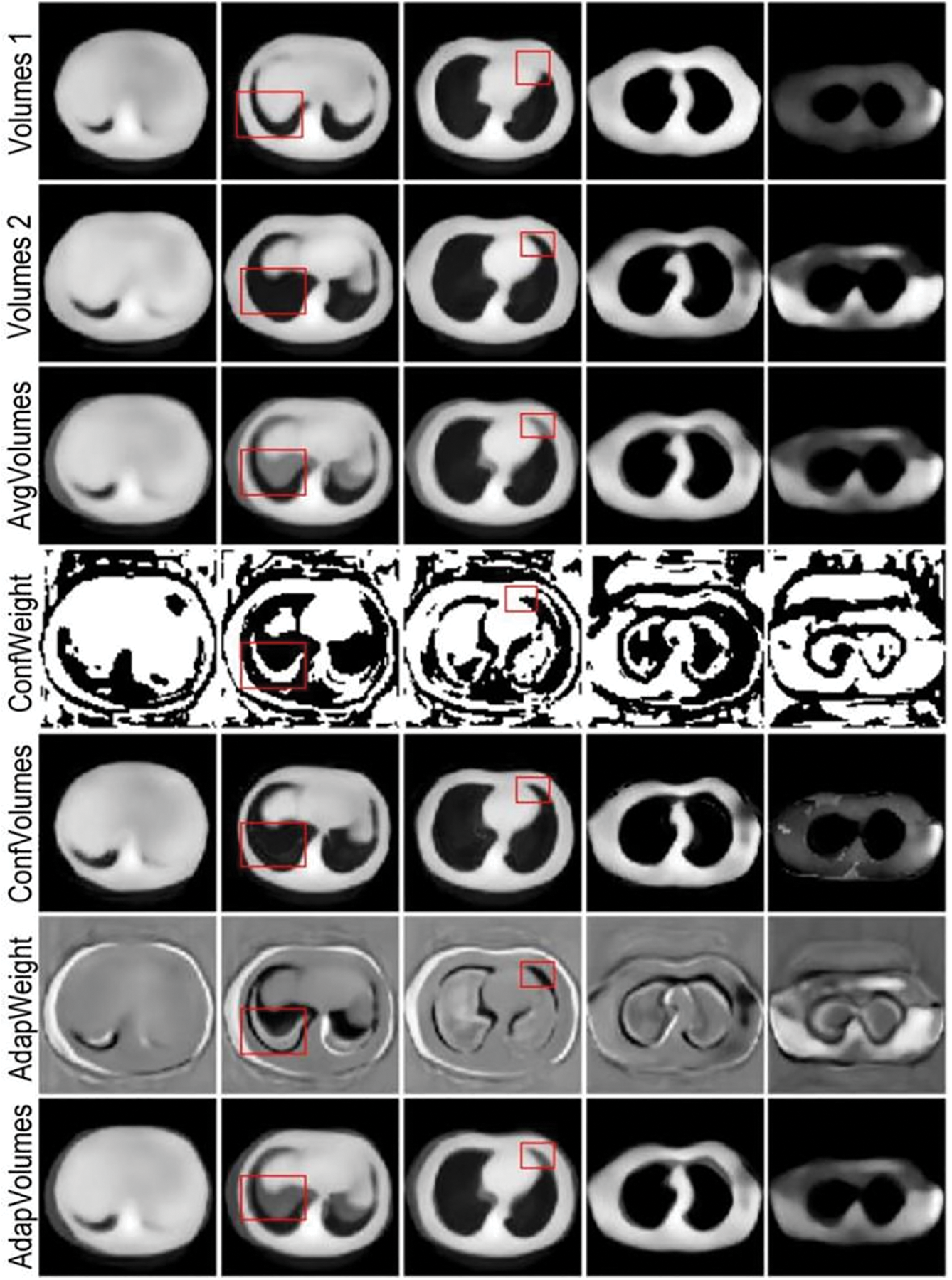
Figure 18: Comparison of experimental results of multiple fusion methods based on adaptive fusion module

5  Discussion

Reconstruction quality depended strongly on the choice of loss. Using MAE produced sharper and more coherent anatomical contours than MSE, particularly in axial and sagittal planes, so MAE was retained as the principal training objective.

Across the four tested architectures the adaptive-fusion model consistently delivered the highest SSIM and PSNR, whereas the single-view baseline performed worst on every metric. MAE values showed a smaller spread, favouring simple average fusion, yet the composite ranking still placed AdapFusionNet first and SingleViewNet last. These quantitative differences align with visual impressions: fusion-based methods recover both chest wall and lung boundaries more faithfully than the single-view approach.

Qualitatively, the adaptive-weight strategy achieves a balanced compromise between the crisp but noisy output of confidence-based fusion and the over-smoothed result of average fusion. By down-weighting mutually inconsistent voxels rather than applying a uniform blend, it preserves edge integrity while avoiding the speckle artefacts that accompany hard confidence masks.

The fusion module also acts as a form of self-supervision during training. Shared encoder parameters receive gradient signals from two orthogonal projections, encouraging depth cues extracted from each view to converge toward a coherent volumetric representation. Consequently, the initial single-view reconstructions become more anatomically plausible, and their weighted combination further boosts fidelity.

Compared to recent related works, XTransCT [38] leverages a transformer-based architecture to reconstruct volumetric data from two orthogonal X-ray projections. While it excels at capturing long-range dependencies through attention mechanisms, its fusion process is largely implicit, lacking explicit mechanisms to assess or modulate reconstruction quality from each input view. Similarly, XGenRecon [39] relies on geometry-guided multi-scale fusion, which improves performance under ultra-sparse conditions but applies static or uniform fusion strategies that do not account for local inconsistencies or noise.

In contrast, AdapFusionNet introduces an explicit weighted adaptive fusion module that evaluates the voxel-wise quality of initial reconstructions from each input view. These scores are normalized via Softmax and used to dynamically weight the final fusion. This design allows the network to retain high-quality structural details while suppressing contributions from noisier or misaligned reconstructions.

Chest radiography remains the first-line imaging modality worldwide because it is fast, inexpensive, and exposes the patient to only a fraction of the radiation dose of CT. By reconstructing a course 3-D chest volume directly from the routinely acquired postero-anterior and lateral projections, our method supplies clinicians with an immediate volumetric overview while the patient is still in the X-ray room. Such on-the-spot 3-D cues can expedite triage decisions, guide the need for further cross-sectional imaging, and ultimately reduce both diagnostic delay and patient burden.

A key limitation of the present study is the absence of truly contemporaneous X-ray/CT pairs from the same patient. Instead, the network was trained on digitally DRRs derived from CT volumes. Although DRRs are widely accepted surrogates, the domain gap between simulated and real radiographs inevitably constrains absolute accuracy and could mask failure modes related to noise, scatter, or acquisition geometry. And only two orthogonal projections (postero-anterior and lateral) were investigated, reflecting standard chest-film practice; extension to oblique or multi-view acquisitions warrants further study. In future work we plan to curate or prospectively collect datasets that contain temporally matched radiographs and CT scans of the same subject, enabling more rigorous validation and potential fine-tuning of the model for clinical deployment.

6  Conclusions

In this paper, we proposed a 3D reconstruction network based on adaptive weight fusion. Compared with other fusion networks, the adaptive fusion module can evaluate the quality of the reconstruction results from different perspectives during the inference process, and this evaluation can promote the reconstruction network to reconstruct better quality 3D images during the training process. AdapFusionNet uses a single network parameter to reconstruct both inputs, so that the mapping of different 2D inputs in 3D space gradually moves toward the truth value. Therefore, the adaptive fusion module proposed in this paper addresses the issue of inconsistent mapping of multi-angle reconstruction results in 3D space to some extent, improves the reconstruction quality, and preliminarily realizes 3D reconstruction based on sparse Angle X-rays.

Although the proposed model achieves good results, and the codec initially realizes 3D mapping of sparse Angle X-rays, the complex structure and large number of parameters require high-end hardware equipment for training, which is time-consuming. Therefore, in the future, we can further study how to simplify the network structure without degrading or even improving the quality of the reconstruction results. In addition, dataset scarcity is one of the key issues in deep learning-based 3D reconstruction of medical images. The rich data sets can undoubtedly help more scholars to devote themselves to the research of medical images, thus promoting the vigorous development of this field.

Acknowledgement: Not applicable.

Funding Statement: Supported by Sichuan Science and Technology Program (2023YFSY0026, 2023YFH0004).

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Jiawei Tian and Minyi Tang; methodology, Yan Chen; software, Shaoyong Hong; validation, Bo Yang, Jiawei Tian and Shan Liu; formal analysis, Hao Quan; investigation, Shaoyong Hong; resources, Yan Chen; data curation, Shan Liu; writing—original draft preparation, Shaoyong Hong; writing—review and editing, Jiawei Tian; visualization, Hao Quan; supervision, Minyi Tang; project administration, Shan Liu; funding acquisition, Bo Yang, Shan Liu and Hao Quan. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are openly available in The Lung Image Database Consortium (LIDC) and Image Database Resource Initiative (IDRI): A completed reference database of lung nodules on CT scans at https://www.cancerimagingarchive.net/collection/lidc-idri/ (accessed on 1 March 2025).

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Tian J, Zhou Y, Chen X, AlQahtani SA, Chen H, Yang B, et al. A novel self-supervised learning network for binocular disparity estimation. Comput Model Eng Sci. 2024;142(1):209–29. doi:10.32604/cmes.2024.057032. [Google Scholar] [CrossRef]

2. Ahishakiye E, Gijzen MBV, Tumwiine J, Wario R, Obungoloch J. A survey on deep learning in medical image reconstruction. Intell Med. 2021;1(3):118–27. doi:10.1016/j.imed.2021.03.003. [Google Scholar] [CrossRef]

3. Li X, Sui J, Wang Y. Three-dimensional reconstruction of fuzzy medical images using quantum algorithm. IEEE Access. 2020;8:218279–88. doi:10.1109/access.2020.3039540. [Google Scholar] [CrossRef]

4. Zhu F, Xu J, Yao C. Local information fusion network for 3D shape classification and retrieval. Image Vis Comput. 2022;121(8):104405. doi:10.1016/j.imavis.2022.104405. [Google Scholar] [CrossRef]

5. Lu S, Liu S, Hou P, Yang B, Liu M, Yin L, et al. Soft tissue feature tracking based on deep matching network. Comput Model Eng Sci. 2023;136(1):363–79. doi:10.32604/cmes.2023.025217. [Google Scholar] [CrossRef]

6. Tian J, Ma B, Lu S, Yang B, Liu S, Yin Z. Three-dimensional point cloud reconstruction method of cardiac soft tissue based on binocular endoscopic images. Electronics. 2023;12(18):3799. doi:10.3390/electronics12183799. [Google Scholar] [CrossRef]

7. Ghous M, Khan A. Efficient image enhancement using improved RIQMC based ROHIM model. Multimed Tools Appl. 2022;81(20):28823–47. doi:10.1007/s11042-022-12721-6. [Google Scholar] [CrossRef]

8. Puttagunta M, Ravi S. Medical image analysis based on deep learning approach. Multimed Tools Appl. 2021;80(16):24365–98. doi:10.1007/s11042-021-10707-4. [Google Scholar] [PubMed] [CrossRef]

9. Lu S, Yang B, Xiao Y, Liu S, Liu M, Yin L, et al. Iterative reconstruction of low-dose CT based on differential sparse. Biomed Signal Process Control. 2023;79(5):104204. doi:10.1016/j.bspc.2022.104204. [Google Scholar] [CrossRef]

10. Hou W, Liu H, Zheng T, Shen W, Xiao F. Hierarchical MPS-based three-dimensional geological structure reconstruction with two-dimensional image(s). J Earth Sci. 2021;32(2):455–67. doi:10.1007/s12583-021-1443-x. [Google Scholar] [CrossRef]

11. Shrestha R, Hu S, Gou M, Liu Z, Tan P. A real world dataset for multi-view 3D reconstruction. In: Computer Vision—ECCV 2022. Cham: Springer Nature Switzerland; 2022. [Google Scholar]

12. Wu T, Zhang J, Fu X, Wang Y, Ren J, Pan L, et al. OmniObject3D: large-vocabulary 3D object dataset for realistic perception, reconstruction and generation. In: 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR); 2023 June 17–24; Vancouver, BC, Canada. [Google Scholar]

13. Reizenstein J, Shapovalov R, Henzler P, Sbordone L, Labatut P, Novotny D. Common objects in 3D: large-scale learning and evaluation of real-life 3D category reconstruction. In: 2021 IEEE/CVF International Conference on Computer Vision (ICCV). Montreal, QC, Canada; 2021 Oct 10–17. [Google Scholar]

14. Asgari Taghanaki S, Abhishek K, Cohen JP, Cohen-Adad J, Hamarneh G. Deep semantic segmentation of natural and medical images: a review. Artif Intell Rev. 2021;54(1):137–78. doi:10.1007/s10462-020-09854-1. [Google Scholar] [CrossRef]

15. Ma J, He Y, Li F, Han L, You C, Wang B. Segment anything in medical images. Nat Commun. 2024;15(1):654. [Google Scholar] [PubMed]

16. Nguyen KM, Nguyen HC, Huy Nguyen H, Nguyen T-B, Nguyen P-T, Tran V, et al. Enhanced medical image generation through advanced latent space diffusion. Mater Emerg Tech Sustain. 2025;1(1):2550003. doi:10.1142/s3060932125500037. [Google Scholar] [CrossRef]

17. Maken P, Gupta A. 2D-to-3D: a review for computational 3D image reconstruction from X-ray images. Arch Comput Methods Eng. 2023;30(1):85–114. doi:10.1007/s11831-022-09790-z. [Google Scholar] [CrossRef]

18. Ha H-G, Lee J, Jung G-H, Hong J, Lee H. 2D-3D reconstruction of a femur by single X-ray image based on deep transfer learning network. IRBM. 2024;45(1):100822. doi:10.1016/j.irbm.2024.100822. [Google Scholar] [CrossRef]

19. Van Houtte J, Audenaert E, Zheng G, Sijbers J. Deep learning-based 2D/3D registration of an atlas to biplanar X-ray images. Int J Comput Assist Radiol Surg. 2022;17(7):1333–42. doi:10.1007/s11548-022-02586-3. [Google Scholar] [PubMed] [CrossRef]

20. Su H, Zhao D, Yu F, Heidari AA, Zhang Y, Chen H, et al. Horizontal and vertical search artificial bee colony for image segmentation of COVID-19 X-ray images. Comput Biol Med. 2022;142:105181. doi:10.1016/j.compbiomed.2021.105181. [Google Scholar] [PubMed] [CrossRef]

21. Wu J, Wang Y, Xue T, Sun X, Freeman B, Tenenbaum J. MarrNet: 3D shape reconstruction via 2.5D sketches. In: Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach, CA, USA: Curran Associates Inc.; 2017 Dec 4–9. p. 540–50. [Google Scholar]

22. Tulsiani S, Zhou T, Efros AA, Malik J. Multi-view supervision for single-view reconstruction via differentiable ray consistency. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition; 2017 July 21–26; Honolulu, HI, USA. [Google Scholar]

23. Sun X, Wu J, Zhang X, Zhang Z, Zhang C, Xue T, et al, editors. Pix3d: dataset and methods for single-image 3d shape modeling. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Salt Lake City, UT, USA; 2018 Jun 18–23. [Google Scholar]

24. Yan X, Yang J, Yumer E, Guo Y, Lee H, editors. Perspective transformer nets: learning single-view 3D object reconstruction without 3D supervision. In: Advances in Neural Information Processing Systems. Barcelona, Spain; 2016 Dec 5–10. [Google Scholar]

25. Han XF, Laga H, Bennamoun M. Image-based 3D object reconstruction: state-of-the-art and trends in the deep learning era. IEEE Trans Pattern Anal Mach Intell. 2021;43(5):1578–604. doi:10.1109/tpami.2019.2954885. [Google Scholar] [PubMed] [CrossRef]

26. Zheng Y, Li Q, Wang C, Wang X, Hu L. Multi-source adaptive selection and fusion for pedestrian dead reckoning. IEEE/CAA J Autom Sin. 2022;9(12):2174–85. doi:10.1109/jas.2021.1004144. [Google Scholar] [CrossRef]

27. Guangbin Z, Lifeng H, Jiqiang P, Xiao Z, Bin Y, Yuyan C, et al. An improved dehazing algorithm using multi-scale weighted transmission fusion and self-adaptive gamma correction. In: ProcSPIE. Xi’an, China; 2021 Nov 13–15. [Google Scholar]

28. Sun Z, Hu Z-P, Chiong R, Wang M, Zhao S. An adaptive weighted fusion model with two subspaces for facial expression recognition. Signal Image Video Process. 2018;12(5):835–43. doi:10.1007/s11760-017-1226-0. [Google Scholar] [CrossRef]

29. Li P, Pei Y, Li J. A comprehensive survey on design and application of autoencoder in deep learning. Appl Soft Comput. 2023;138(7553):110176. doi:10.1016/j.asoc.2023.110176. [Google Scholar] [CrossRef]

30. Johnston A, Garg R, Carneiro G, Reid I, van den Hengel A. Scaling CNNs for high resolution volumetric reconstruction from a single image. In: Proceedings of the IEEE International Conference on Computer Vision Workshops. Venice, Italy; 2017 Oct 22–29. [Google Scholar]

31. Wu P, Yang Z, Wang X, Zhang Z. Two-dimensional encoder with independent in-plane and out-of-plane detection for nanometric measurement. Opt Lett. 2020;45(15):4200–3. doi:10.1364/ol.397858. [Google Scholar] [PubMed] [CrossRef]

32. Huang G, Liu Z, Van Der Maaten L, Weinberger KQ, editors. Densely connected convolutional networks. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. Honolulu, HI, USA; 2017 Jul 21–26. [Google Scholar]

33. Marias K. The constantly evolving role of medical image processing in oncology: from traditional medical image processing to imaging biomarkers and radiomics. J Imaging. 2021;7(8):124. doi:10.3390/jimaging7080124. [Google Scholar] [PubMed] [CrossRef]

34. Guan H, Liu M. Domain adaptation for medical image analysis: a survey. IEEE Trans Biomed Eng. 2022;69(3):1173–85. doi:10.1109/tbme.2021.3117407. [Google Scholar] [PubMed] [CrossRef]

35. Armato SGIII, McLennan G, Bidaut L, McNitt-Gray MF, Meyer CR, Reeves AP, et al. The lung image database consortium (LIDC) and image database resource initiative (IDRIa completed reference database of lung nodules on CT scans. Med Phys. 2011;38(2):915–31. doi:10.1118/1.3469350. [Google Scholar] [CrossRef]

36. Shu L, Li M, Guo X, Chen Y, Pu X, Lin C. Isocentric fixed angle irradiation-based DRR: a novel approach to enhance x-ray and CT image registration. Phys Med Biol. 2024;69(11):115032. doi:10.1088/1361-6560/ad450a. [Google Scholar] [PubMed] [CrossRef]

37. Aubert B, Cresson T, Guise JAD, Vazquez C. X-ray to DRR images translation for efficient multiple objects similarity measures in deformable model 3D/2D registration. IEEE Trans Med Imaging. 2023;42(4):897–909. doi:10.1109/tmi.2022.3218568. [Google Scholar] [PubMed] [CrossRef]

38. Zhang C, Liu L, Dai J, Liu X, He W, Chan Y, et al. XTransCT: ultra-fast volumetric CT reconstruction using two orthogonal x-ray projections for image-guided radiation therapy via a transformer network. Phys Med Biol. 2024;69(8):085010. doi:10.1088/1361-6560/ad3320. [Google Scholar] [PubMed] [CrossRef]

39. Zhang C, Xie Y, Liang X. XGenRecon: a new perspective in ultrasparse volumetric CBCT reconstruction through geometry-controlled X-ray projection generation. IEEE Trans Radiat Plasma Med Sci. 2025;9(1):95–106. doi:10.1109/trpms.2024.3420742. [Google Scholar] [CrossRef]