 Open Access
Open Access
ARTICLE
A Computationally Efficient Density-Aware Adversarial Resampling Framework Using Wasserstein GANs for Imbalance and Overlapping Data Classification
1 School of Mathematical Sciences, Dalian University of Technology, Dalian, 116024, China
2 Key Laboratory for Computational Mathematics and Data Intelligence of Liaoning Province, Dalian, 116024, China
3 School of Mathematics and Statistics, Central South University, Changsha, 410083, China
4 Department of Statistics and Operations Research, College of Science, King Saud University, P.O. Box 2455, Riyadh, 11451, Saudi Arabia
* Corresponding Author: Jie Yang. Email:
Computer Modeling in Engineering & Sciences 2025, 144(1), 511-534. https://doi.org/10.32604/cmes.2025.066514
Received 10 April 2025; Accepted 08 July 2025; Issue published 31 July 2025
Abstract
Effectively handling imbalanced datasets remains a fundamental challenge in computational modeling and machine learning, particularly when class overlap significantly deteriorates classification performance. Traditional oversampling methods often generate synthetic samples without considering density variations, leading to redundant or misleading instances that exacerbate class overlap in high-density regions. To address these limitations, we propose Wasserstein Generative Adversarial Network Variational Density Estimation WGAN-VDE, a computationally efficient density-aware adversarial resampling framework that enhances minority class representation while strategically reducing class overlap. The originality of WGAN-VDE lies in its density-aware sample refinement, ensuring that synthetic samples are positioned in underrepresented regions, thereby improving class distinctiveness. By applying structured feature representation, targeted sample generation, and density-based selection mechanisms strategies, the proposed framework ensures the generation of well-separated and diverse synthetic samples, improving class separability and reducing redundancy. The experimental evaluation on 20 benchmark datasets demonstrates that this approach outperforms 11 state-of-the-art rebalancing techniques, achieving superior results in F1-score, Accuracy, G-Mean, and AUC metrics. These results establish the proposed method as an effective and robust computational approach, suitable for diverse engineering and scientific applications involving imbalanced data classification and computational modeling.Keywords
Machine learning applications have expanded dramatically across various domains such as medical diagnosis [1], finance and risk management [2], fault diagnosis [3], cybersecurity, and anomaly detection [4]. However, one recurring computational modelling challenge in these applications is handling imbalanced datasets, where the minority class contains significantly less data than the majority class. This distortion affects the performance of classifiers, mostly recognizing the minority class patterns, and degrading the overall system accuracy [5,6]. This challenge is especially important in situations where predicting such examples is crucial, like fraud, rare diseases, and intrusion detection [7]. Since real-world datasets often exhibit varying degrees of imbalance, addressing this issue has become a fundamental concern in classification tasks [8].
To address these issues, many data-level and algorithm-level methods have been introduced in the literature. Some examples of conventional methods are undersampling and oversampling. While undersampling reduces the size of the majority class to balance the dataset, it risks discarding valuable information. Oversampling, on the other hand, increases the minority class by generating synthetic samples, often using methods like the Synthetic Minority Oversampling Technique (SMOTE) [9–11]. Although SMOTE and similar methods improve class balance, they often generate redundant samples or exacerbate the problem of overfitting by placing synthetic points in high-density regions, leading to overlapping between classes, which further reduces model generalization and increases classification errors.
Recent advancements in deep learning have introduced Generative Adversarial Networks (GANs) [12] as a promising alternative for synthetic data generation. Unlike traditional resampling methods, GANs employ an adversarial framework where the generator learns to create realistic synthetic samples that resemble the real data distribution. While GANs provide a more data-driven approach to resampling, they also suffer from training instability, mode collapse, and a lack of control over sample placement in feature space. The introduction of Wasserstein GAN (WGAN) and its many variants [13,14] helped to address some of these issues by improving training stability and diversity [15], but existing GAN-based approaches still lack a mechanism to control where synthetic samples are placed in feature space, which often results in class overlap and sample redundancy, similar to traditional resampling methods.
To overcome these computational modelling challenges, we introduce a novel generative resampling framework, WGAN-VDE (Wasserstein Generative Adversarial Network with Variational Density Estimation), that strategically refines synthetic sample placement to enhance class separability while preserving minority class diversity. Contrary to existing GAN-based resampling techniques, WGAN-VDE does not generate synthetic samples indiscriminately. Instead, it incorporates structured representation learning, density-aware adversarial training, and statistical refinement mechanisms to ensure that synthetic samples contribute meaningfully to the classification task.
The first key innovation in this framework is structured minority class representation learning using Variational Autoencoders (VAE). Conventional GAN-based oversampling methods generate synthetic data from random noise, often failing to maintain the intrinsic feature distribution of the minority class. In contrast, VAE encodes minority class instances into a structured latent space, ensuring that synthetic samples retain key statistical properties of real samples, leading to more diverse and representative synthetic data.
The second innovation is density-aware synthetic sample generation using a modified Wasserstein GAN (WGAN). Traditional GANs often suffer from mode collapse, where the generator produces a limited set of synthetic variations, reducing diversity. While WGAN improves stability, it lacks an explicit mechanism to optimize sample placement in feature space. To address this, a density-constrained Wasserstein loss is introduced, ensuring that synthetic samples are generated in underrepresented feature space regions rather than high-density areas dominated by the majority class. This controlled placement of synthetic instances reduces class overlap and enhances class separability, making it more effective than conventional GAN-based resampling.
The final innovation is post-generation sample refinement using Kernel Density Estimation (KDE). Unlike conventional oversampling methods that assume all generated samples are useful, this framework evaluates and selectively filters synthetic instances before they are added to the dataset. KDE is applied to measure the density distribution of synthetic samples relative to real minority class instances, ensuring that redundant samples in already well-represented areas are removed, while informative samples in sparse regions are retained. Unlike static threshold-based filtering, a dynamic KDE thresholding mechanism is used, where only synthetic samples with densities lower than 80% of real minority class samples are retained, thereby ensuring optimal sample placement and preventing class overlap.
By introducing density constraints into the generative process and incorporating a structured sample selection mechanism, this generative resampling framework overcomes key limitations in both traditional oversampling and GAN-based methods. While SMOTE and similar techniques introduce synthetic points without considering density distributions, and GAN-based resampling lacks explicit sample placement control, this framework ensures that each generated sample enhances class separability rather than contributing to redundancy. Unlike conventional hybrid approaches that combine oversampling with undersampling, this method does not rely on majority class reduction but instead optimizes synthetic sample distribution to improve classifier performance.
Extensive experimental evaluations on 20 benchmark datasets demonstrate that this generative resampling framework outperforms 11 state-of-the-art resampling techniques, including traditional oversampling, hybrid sampling, and GAN-based methods. Results show consistent improvements in F1-score, Accuracy, G-Mean, and AUC metrics, highlighting the effectiveness of structured representation learning, density-aware adversarial training, and KDE-based refinement in improving class separability and classifier generalization. The ability to strategically refine synthetic samples rather than blindly generating data represents a significant advancement in imbalanced learning, making this framework particularly well-suited for real-world high-stakes classification tasks.
In this section, we present a brief overview of GANs and their variants, including WGANs and their usage in dealing with class imbalance. Furthermore, we discuss their efficacy and also highlight the shortcomings of these methods, particularly in dealing with class overlap and poor sample diversity in class imbalance that led to the groundwork of our proposed method WGAN-VDE (Wasserstein GAN with Variational Density Estimation).
The Generative Adversarial Networks (GANs), proposed by Goodfellow et al. [12], train two neural networks, a generator and a discriminator, in an adversarial setting. The generator learns to produce synthetic samples that the discriminator attempts to distinguish from real data. While effective for various generative tasks, GANs and their variants encounter multiple challenges while working with datasets with imbalanced distributions. A crucial problem with GANs is mode collapse, which results in the generator creating few sample variations while missing out on the complete diversity of the minority class. GANs usually experience unpredictable training instabilities, making convergence hard to achieve when operating in complex data distributions with severe class imbalances. These limitations reduce the reliability of GAN-based oversampling strategies in addressing class imbalance issues.
To address these instabilities and mode collapse limitations in Traditional GANs, Arjovsky et al. [15] proposed Wasserstein Generative Adversarial Networks (WGANs), which address GAN instabilities by replacing the original loss function with the Wasserstein distance, offering smoother gradients and improved convergence. Enhanced versions, such as the gradient penalty [16], incorporate gradient penalties to better enforce the Lipschitz constraint. However, even with these improvements, WGANs lack mechanisms to control sample density or prevent class overlap, making them insufficient for nuanced oversampling in imbalanced settings. As shown in Fig. 1, the WGAN architecture uses the Wasserstein distance to guide adversarial training between the generator and critic.
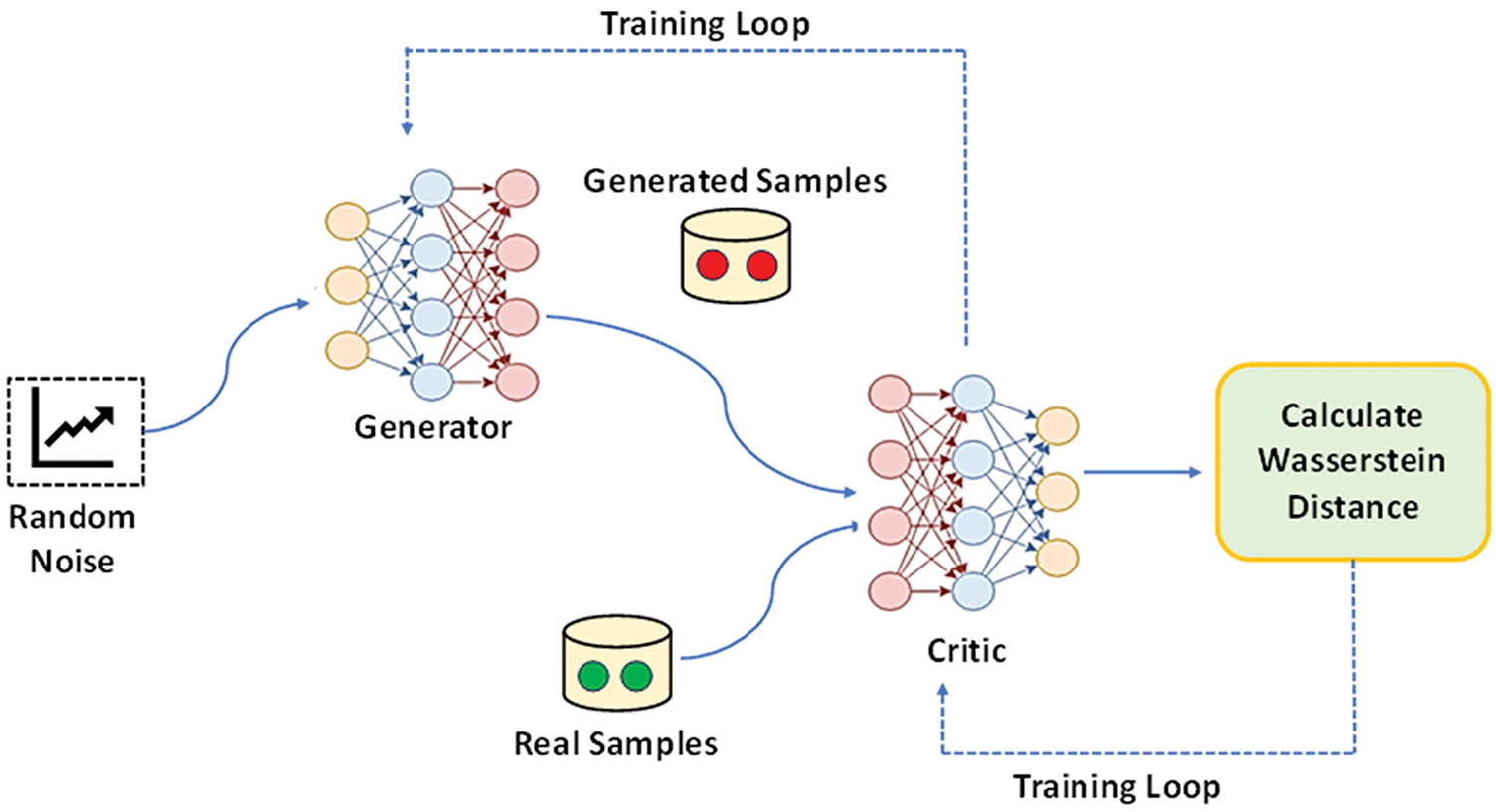
Figure 1: A framework of the WGAN model
However, beyond this, the main focus of WGAN-based hybrid oversampling methods lies in the creation of synthetic samples. Still, these methods do not handle the density and overlapping issues that occur in tabular datasets.
2.3 Recent Advancements and Challenges
In recent years, several advancements have emerged in the application of GANs and WGANs for imbalanced classification, with a focus on enhancing sample diversity and addressing the limitations of traditional oversampling techniques [17]. Several architectures have incorporated domain-specific enhancements to guide the generation of synthetic data more effectively. For instance, Conditional Wasserstein GANs (CWGAN and CWGAN-GP) [18–20] utilize conditional learning strategies, enabling the generator to focus on class-specific characteristics, thereby improving the relevance of generated samples. Similarly, GNP-WGAN [21] enhances distribution matching by incorporating global non-local priors, enabling the model to capture more generalized data structures.
Building upon these concepts, AWGAN [22] adopts adaptive weighting mechanisms to better model minority class variability, while OWGAN-GP [23] introduces a meta-learning framework combined with Wasserstein optimization to improve the placement of synthetic samples, ultimately seeking better class separability. Although these innovations contribute to improved performance over basic GAN-based oversampling, they continue to suffer from a fundamental limitation, namely the lack of explicit density-aware control during the generative process. Most of these methods generate synthetic instances based on global distribution patterns, often leading to sample redundancy in high-density regions or overlapping with majority class boundaries, which deteriorates classifier performance.
To address this issue, recent research has also introduced density estimation methods into oversampling pipelines [24–26]. Techniques such as GADE [27] employ Kernel Density Estimation (KDE) to align the distribution of synthetic samples more closely with that of the real minority class. Others use KDE-driven filtering to detect and remove overlapping or uninformative sample problems [28–30]. However, these approaches typically apply KDE as a global, static post-processing step, failing to account for local variations in feature space density. As a result, their ability to reduce class overlap and improve sample utility remains limited in complex imbalanced scenarios.
In contrast, our proposed WGAN-VDE framework introduces a novel approach by embedding KDE directly within the generative process. This dynamic, density-aware filtering mechanism ensures that synthetic samples are generated and retained only if they reside in low-density, underrepresented regions of the minority class, thereby minimizing class overlap and increasing class separability. Moreover, WGAN-VDE leverages a structured encoding of the minority class into a latent space, effectively preserving key statistical characteristics and enhancing the quality and diversity of the generated synthetic samples. By combining this structured representation with density-aware adversarial resampling, the framework directly addresses the dual challenge of poor sample diversity and uncontrolled spatial distribution that plagues earlier methods.
Ultimately, while prior GAN and WGAN variants have advanced the field of generative oversampling, they fall short of optimizing sample placement in the feature space. WGAN-VDE transcends these limitations by integrating structured feature learning, localized density estimation, and adaptive refinement, resulting in a scalable and robust solution for imbalanced learning challenges across diverse, real-world applications.
In this paper, we design a generative resampling framework, WGAN-VDE (Wasserstein Generative Adversarial Network with Variational Density Estimation), to address the challenges of class imbalance and overlapping distributions in imbalanced datasets. In contrast to the traditional resampling technique, where samples are generated in areas of high-density regions, WGAN-VDE employs a structured, density-aware approach to strategically place generated minority class samples in low-density regions, ensuring enhanced class separability and reduced misclassification risks. The proposed method consists of the following key steps, and the detailed framework is depicted in Fig. 2.
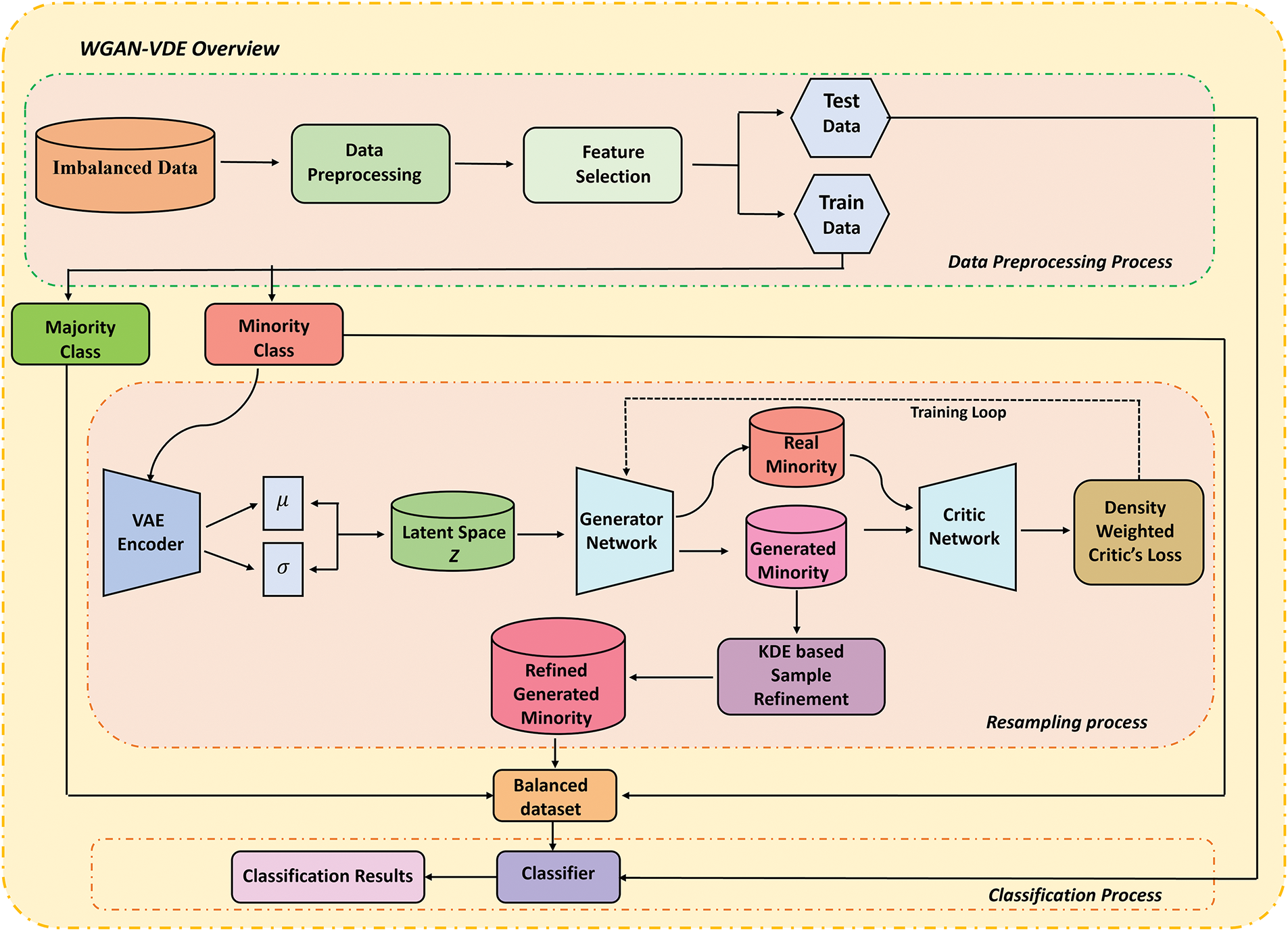
Figure 2: Overview of WGAN-VDE framework
First of all, in order to ensure optimal model performance, the dataset undergoes preprocessing, which includes feature normalization, class labeling, and data partitioning. First, all numerical features are normalized using z-score standardization to bring them to a common scale. This transformation is computed as:
where
After normalization, the class labelling process is applied, which separates the majority instances (y = 0) from the minority ones (y = 1). Special attention has been paid to maintaining the original class distribution within the imbalanced dataset before generating synthetic samples.
The dataset is divided into separate training and testing sections at the final stage. During the training phase, both synthetic sample generation and classification models use the training set, but the test set stays hidden to prevent bias in model evaluation. The proposed method undergoes testing to evaluate its generalization capability when applied to fresh data that was not present for training purposes.
3.2 Structured Feature Representation for Minority Class
After data preprocessing, the next critical step in WGAN-VDE is constructing a structured feature representation for the minority class. Traditional oversampling techniques generate synthetic data either by random perturbations or interpolations between existing samples, which often fail to capture the underlying feature distribution of the minority class. This results in synthetic instances that are either too similar to real data (redundant) or poorly representative (outliers), ultimately increasing class overlap. To enhance the diversity along with the realistic outcome of minority class samples, we apply a Variational Autoencoder (VAE) to discover structured latent minority class distributions. VAE differs from deterministic autoencoders because it uses a probabilistic approach to encode data while achieving better minority class variation representation in the latent space. During encoding, the minority class instances get transformed into a lower-dimensional latent representation that includes
The model incorporates two components where
During optimization, the VAE applies both reconstruction loss to measure decoder reconstruction accuracy and Kullback-Leibler (KL) divergence loss to maintain a structured distribution in the latent space.
where
3.3 Density-Aware Generative Resampling
The resulting latent variables processing becomes input to the Wasserstein Generative Adversarial Network (WGAN) for producing credible minority class samples. As the main components of the WGAN framework, the generator generates new data samples while the Critic checks sample quality to teach the generator how to produce more realistic outcomes. The generator within the WGAN system uses the latent Z variables obtained from the VAE to create synthetic feature vectors that match minority class samples. The generator functions will generate
After this, these generated samples move to the Critic for authenticity assessment through comparison against authentic minority-class samples. Unlike conventional GANs, WGAN does not use a binary classifier as a discriminator. Instead, it uses a Critic function that assigns each sample a real-valued authenticity score while measuring the Wasserstein distance between the real and generated data distributions. The Critic receives optimization through a density-weighted Wasserstein loss function that integrates density estimation to reduce majority-class to minority-class misalignments.
where
where
This encourages the generator to create such synthetic samples to which Critic assigns high authenticity scores, rendering them indistinguishable from real minority class samples. This step uses density-based weighting in Critic’s loss function to position synthetic samples optimally throughout minority class regions, which results in reduced class overlap and preserves data diversity.
3.4 Density-Based Sample Refinement
Following the creation of synthetic minority samples using density-aware WGAN, we apply density-based methods for refining these samples to optimize overlap reduction and preserve diversity. Traditional resampling techniques often produce more redundant synthetic data in dense areas, causing overlap with the majority class rather than improving class separability. To address this issue, a density estimation technique is used to evaluate the location of each synthetic sample and filter those that cause extreme overlap.
To address this, we employ Kernel Density Estimation (KDE) to evaluate how “crowded” or “sparse” a region is around each synthetic sample, based on the distribution of real minority class data. KDE allows us to statistically estimate the probability density function of the minority class distribution in a non-parametric way, using a smooth kernel (typically Gaussian). Let
where
Substituting Eq. (8) in Eq. (7) gives the simplified expression for density estimation:
This score reflects the local density of the synthetic sample x relative to real minority samples. Higher values indicate that x lies in a dense (potentially overlapping) region, while lower values suggest it is located in a sparse area, which is desirable for improving coverage.
To reduce class overlap, we apply a threshold-based density strategy. A KDE model is first fitted using only the real minority class samples. Then, the KDE score of each synthetic sample is evaluated using Eq. (10). We retain only those synthetic samples whose density scores are lower than a threshold
In our implementation, the selection threshold
To quantitatively compare how different methods address class overlap, we compute the average KDE score of their synthetic samples as:
Lower values of
After density-based sample refinement, the selected synthetic samples are integrated with the original dataset to create a balanced and well-separated dataset. The refined dataset contains:
• All original majority class samples for preserving real-world information.
• Original minority class samples to maintain true minority class characteristics.
• Filtered synthetic minority class samples generated by WGAN and refined via density estimation.
The balanced dataset is then used to train classifiers, evaluating the effectiveness of WGAN-VDE against traditional resampling methods. By integrating density-based refinement with dataset balancing, WGAN-VDE ensures superior class separability and improved classifier performance on imbalanced datasets.
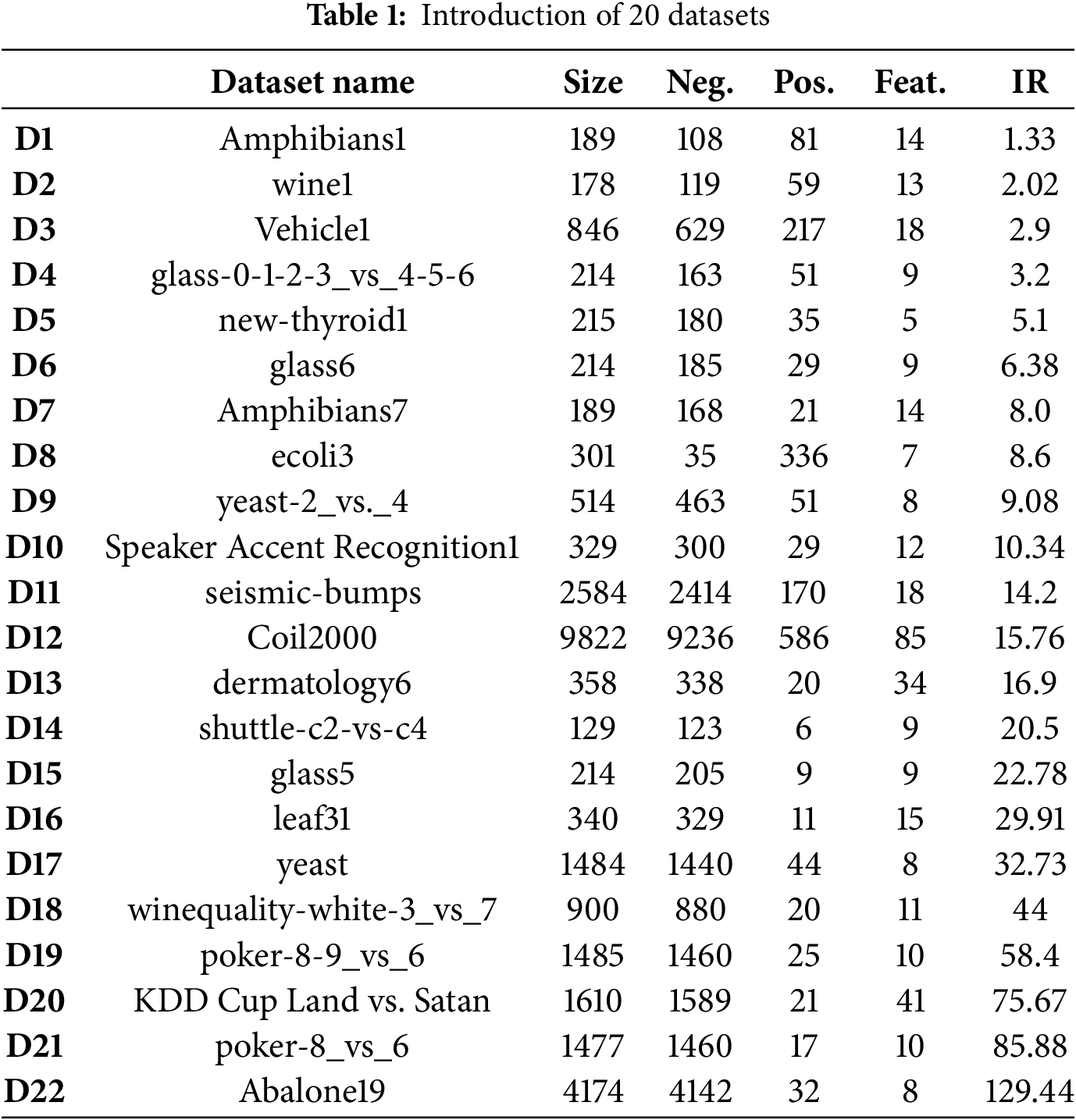
To evaluate the effectiveness of the proposed E-WGAN model, we conduct the following experiments using 20 binary imbalanced datasets. Among these, nine datasets are obtained from the UCI Machine Learning Repository (http://archive.ics.uci.edu) (accessed on 7 July 2025), while the rest of the 13 datasets are publicly available at the KEEL repository (http://www.keel.es) (accessed on 7 July 2025). Table 1 presents an overview of the dataset characteristics, regarding dataset size, imbalance ratio (IR), the counts of minority samples (P), the counts of majority samples (N), and the counts of features (Feat.). The datasets exhibit diverse characteristics, with IR values ranging from 1.33 to 129.44, the number of features extending from 5 to 85, and dataset sizes ranging from 129 to 9822 samples.
When dealing with imbalanced classification models, these measures must be taken into account accurately to note the results of the models. Common metrics include:
i. Precision
ii. Recall
iii. F1-Score
iv. G-Mean
where sensitivity and specificity evaluate the quality of minority and majority classes, respectively [31,32].
In this research, we examine the effectiveness of our proposed method, WGAN-VDE, by performing a baseline comparison with 12 other existing resampling approaches. It divides into five major groups, including Undersampling, Oversampling, Hybrid Sampling, Advanced Oversampling, and Deep Learning-based approaches. Table 2 provides full explanations regarding the procedures used for these methods.
In case of undersampling, we perform baseline comparison with Tomek Links (TL) as it eliminates nearby majority class samples that reduce boundary separation. The oversampling category includes SMOTE and Borderline-SMOTE (BS) for creating artificial minority samples to stabilize class distributions. In the hybrid sampling methods, we analyze SMOTEENN (SME) and SMOTETomek (SMT) as they enhance class distributions by minimizing noise through undersampling and oversampling approaches. In addition, we also use two advanced oversampling techniques for comparison, like Gaussian_SMOTE (GSM) and SMOTEWB (SMOTE with Boosting Procedure), which bring new mechanisms for improving class imbalance and synthetic sample quality.
In the deep learning category, we compare WGAN-VDE with four state-of-the-art GAN-based resampling methods, including WGAN-GP, RVGAN-TL, GNP-WGAN, and VAE-WACGAN. These methods use generative models to generate synthetic data that is consistent with the underlying data distribution, improving the classifier’s performance in imbalanced learning circumstances.
We implement all methods on the same 20 imbalanced datasets (Given in Table 1) as WGAN-VDE for better comparability of the outcomes. This assessment enables us to analyze the capability of our proposed method, reducing overlap and improving the quality of synthetic samples compared to the existing 11 resampling techniques.
In this study, to perform a fair baseline comparison across 12 resampling techniques, we use an Extreme Gradient Boosting (XG-Boost) classifier [41] with the scale_pos_weight parameter set to 1, which is then trained on the refined dataset acquired after synthetic sample generation and density-based filtering. Thus, 5-fold cross-validation is used to provide a more stable and impartial assessment across all the datasets. Another advantage of this approach is that the performance of the classifier is checked on a different split of the training and validation set, so that the variability of datasets does not influence it.
The WGAN-VDE framework is configured with carefully tuned hyperparameters to optimize synthetic data generation while minimizing class overlap. The training process involves 100 epochs, with the Critic and Generator trained iteratively to achieve stable convergence. The learning rate for both the Generator and Critic is set to 0.0002, while the gradient penalty coefficient (η) is fixed at 10 to enforce the 1-Lipschitz constraint, ensuring stable training.
The VAE component is trained on a latent space, resulting in a diversified and well-structured representation of the minority class. Batch Normalization is used to stabilize learning, while LeakyReLU activation functions introduce non-linearity, allowing the model to capture complex feature interactions. The output layer of the Generator uses a Tanh activation function, ensuring that generated samples align with the original feature distribution. The Critic network consists of fully connected layers with Batch Normalization and LeakyReLU activation, which gradually reduce the dimensionality of input samples before mapping them to a scalar output, representing the Wasserstein distance between real and generated samples. Importantly, Batch Normalization is not applied in the final layer of the Critic to ensure the preservation of Wasserstein distance and allow for a stable Wasserstein loss computation.
Table 3 contains all necessary hyperparameter configurations for WGAN-VDE alongside Table 4 depicting the architectural information for both the Generator and Critic networks.


Using Batch Normalization and LeakyReLU activation, the Generator transforms latent vectors to high dimensions through steadily growing fully connected layers, which provides training stability. The Critic network performs input compression by using smaller dense layers that guarantee proper Wasserstein distance approximation. Gradient Penalty (GP) finalizes the stability of the network design while maintaining true synthetic sample output and stopping mode collapse issues.
As for the KDE filtering stage, a percentile-based threshold is used to identify synthetic samples that lie within low-density regions of the minority class distribution. To empirically justify the choice of the 20th percentile, we conducted an ablation study on benchmark datasets D5 and D17, evaluating performance at thresholds ranging from 10% to 50%. As illustrated in Fig. 3, the 20% threshold consistently offered the best trade-off across G-Mean, F1-Score, and AUC. Lower thresholds (e.g., 10%) were overly restrictive, discarding potentially useful samples, while higher thresholds (e.g., 30% to 50%) introduced redundancy and increased the likelihood of class overlap. These results validate the 20th percentile as an optimal setting that balances performance with overlap minimization.

Figure 3: Sensitivity of WGAN-VDE to KDE threshold
To analyze the efficacy of our method, we perform a baseline comparison of the WGAN-VDE with 11 other resampling and deep learning techniques as mentioned in Table 2. The evaluation process is carried out on 22 benchmark imbalanced datasets by using four important performance metrics: G-Mean, F1-Score, Accuracy, and AUC. A detailed numerical comparison of G-Mean is present in Table 5, while F1-Score, Accuracy, and AUC metrics are visualized using figures to improve interpretability.
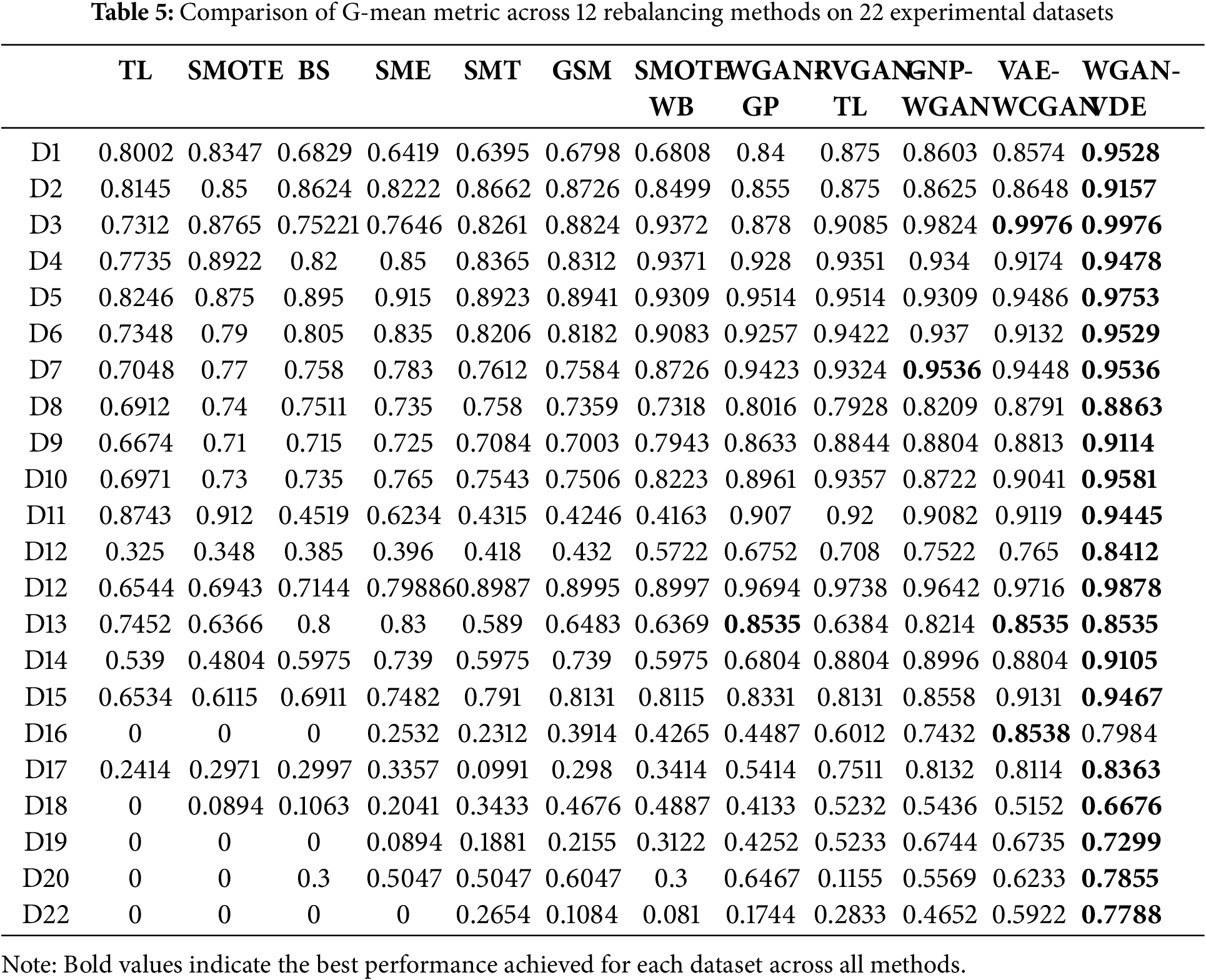
Table 5 presents the G-Mean values for WGAN-VDE and the compared methods across all datasets. G-Mean is a crucial metric in imbalanced classification as it captures the balance between sensitivity and specificity. The results indicate that WGAN-VDE consistently outperforms traditional oversampling techniques (such as SMOTE, BS, SME, GSM, and SMOTEWB) and also surpasses advanced generative models (such as WGAN-GP, RVGAN-TL, GNP-WGAN, and VAE-WCGAN) in most cases. The highest G-Mean value for each dataset is bolded, and it is evident that WGAN-VDE achieves the best performance in the majority of datasets. Notably, WGAN-VDE shows similar performance on D3, D7, and D14, but its improvement is particularly significant in datasets with a high imbalance ratio (e.g., D18, D19, D20, D21), highlighting the effectiveness of our method in handling extreme class imbalance. This improvement can be attributed to density-based sample refinement, which reduces class overlap while maintaining diversity in the generated minority samples. Two large sizes of imbalanced datasets, D12 and D22, also demonstrate the scalability of our proposed WGAN-VDE method, especially on D22, where traditional resampling methods failed due to the extreme imbalance ratio. This underscores the robustness of WGAN-VDE in large-scale, highly Imbalanced datasets.
The F1-Score results are presented in Fig. 4, which shows the relative performance of different methods across 22 imbalanced datasets. The F1-score is particularly useful in assessing the trade-off between precision and recall for the minority class. From Fig. 3, it is evident that the red bold line of our proposed method, WGAN-VDE, achieves consistently high F1-Scores across all datasets, outperforming conventional oversampling techniques and even advanced GAN-based methods. The improvement is especially pronounced in datasets where the minority class is highly underrepresented. The ability of WGAN-VDE to refine synthetic samples based on density estimation plays a crucial role in preventing redundant sample generation and enhancing classification robustness. Moreover, WGAN-VDE maintains competitive F1-score performance even on challenging large-scale datasets like D12 and extremely imbalanced datasets such as D22, where traditional methods often fail to produce meaningful predictions.
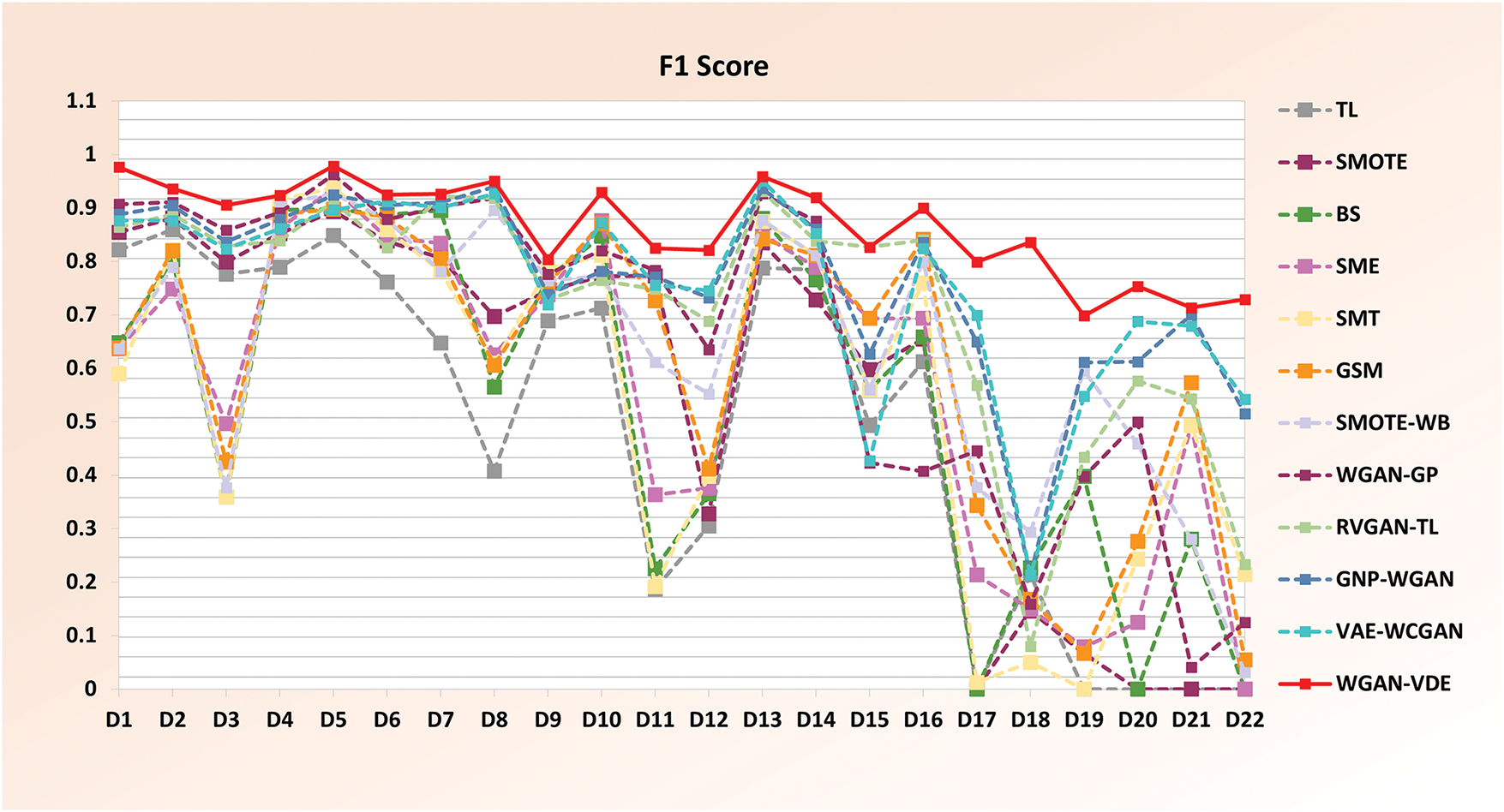
Figure 4: Line chart comparing F1-score performance of 12 rebalancing methods on 22 experimental datasets
The column chart in Fig. 5 illustrates the Accuracy performance of all 12 resampling methods across 22 experimental datasets with varying imbalance ratios. While Accuracy is often not the best metric for imbalanced classification, it still provides insights into the overall performance of a classifier. The results show that WGAN-VDE achieves the highest accuracy in most datasets, reinforcing its ability to generate high-quality synthetic samples that improve classification. A key takeaway from Fig. 4 is that accuracy differences become more noticeable in datasets with extreme class imbalance. Traditional oversampling methods, such as SMOTE, tend to overfit to the minority class, resulting in only marginal improvements, whereas WGAN-VDE is better at generalizing due to its density-based refinement step.

Figure 5: Column chart comparing the accuracy performance of 12 rebalancing methods on 22 experimental datasets
The AUC (Area Under the ROC Curve) values for all 12 resampling methods across 22 datasets are shown in Fig. 6. AUC evaluates the classifier’s ability to distinguish between classes, making it a robust metric for imbalanced learning. The figure demonstrates that WGAN-VDE appears in the red solid line, which covers all other lines, and achieves the highest AUC values in most datasets, further confirming its superiority. Other GAN-based deep learning resampling methods, such as WGAN-GP and VAE-WCGAN, also show strong performance, but with some variations across datasets. Traditional methods like SMOTE and TL exhibit fluctuations in performance, indicating their limited adaptability to certain imbalance levels. The strong AUC performance of WGAN-VDE highlights that our approach not only improves recall but also ensures that false positive rates remain low, leading to a well-calibrated classifier.

Figure 6: Radar chart comparing AUC performance of 12 rebalancing methods on 22 experimental datasets
To further evaluate the generalizability of WGAN-VDE, we conducted a classifier sensitivity analysis under cost-sensitive settings. While our original experiments used XG-Boost with scale_pos_weight = 1, this analysis explores how WGAN-VDE performs across three classifiers: Support Vector Machine (SVM), Random Forest (RF), and XG-Boost, each now configured with cost-sensitive adjustments. Specifically, we applied class_weight = ‘balanced’ for SVM and RF, and used an updated scale_pos_weight value for XG-Boost based on the ratio of majority to minority class instances. As illustrated in Fig. 7, WGAN-VDE maintains strong performance across all classifiers across 22 datasets, with RF and XG-Boost achieving the highest scores in G-Mean, AUC, Accuracy, and F1-Score. SVM also shows notable improvement, demonstrating that WGAN-VDE is not only effective across diverse classification architectures but also compatible with cost-sensitive configurations.

Figure 7: Performance of WGAN-VDE across cost-sensitive classifiers across 22 datasets
To provide quantitative insight into the overlap control ability of different resampling methods, we conducted a KDE-based analysis of the synthetic samples generated by each method. Table 6 presents the average kernel density estimation (KDE) scores for synthetic minority samples across 22 benchmark datasets and 12 resampling techniques. These scores measure the likelihood that generated samples lie within high-density regions of the minority distribution, a proxy for potential class overlap. KDE scores were computed using a Gaussian kernel with fixed bandwidth, applied over the real minority class samples as the reference distribution. Lower KDE scores imply that the synthetic samples are generated in sparser regions of the feature space, away from already dense clusters, hence reducing the risk of class overlap and enhancing class separability.
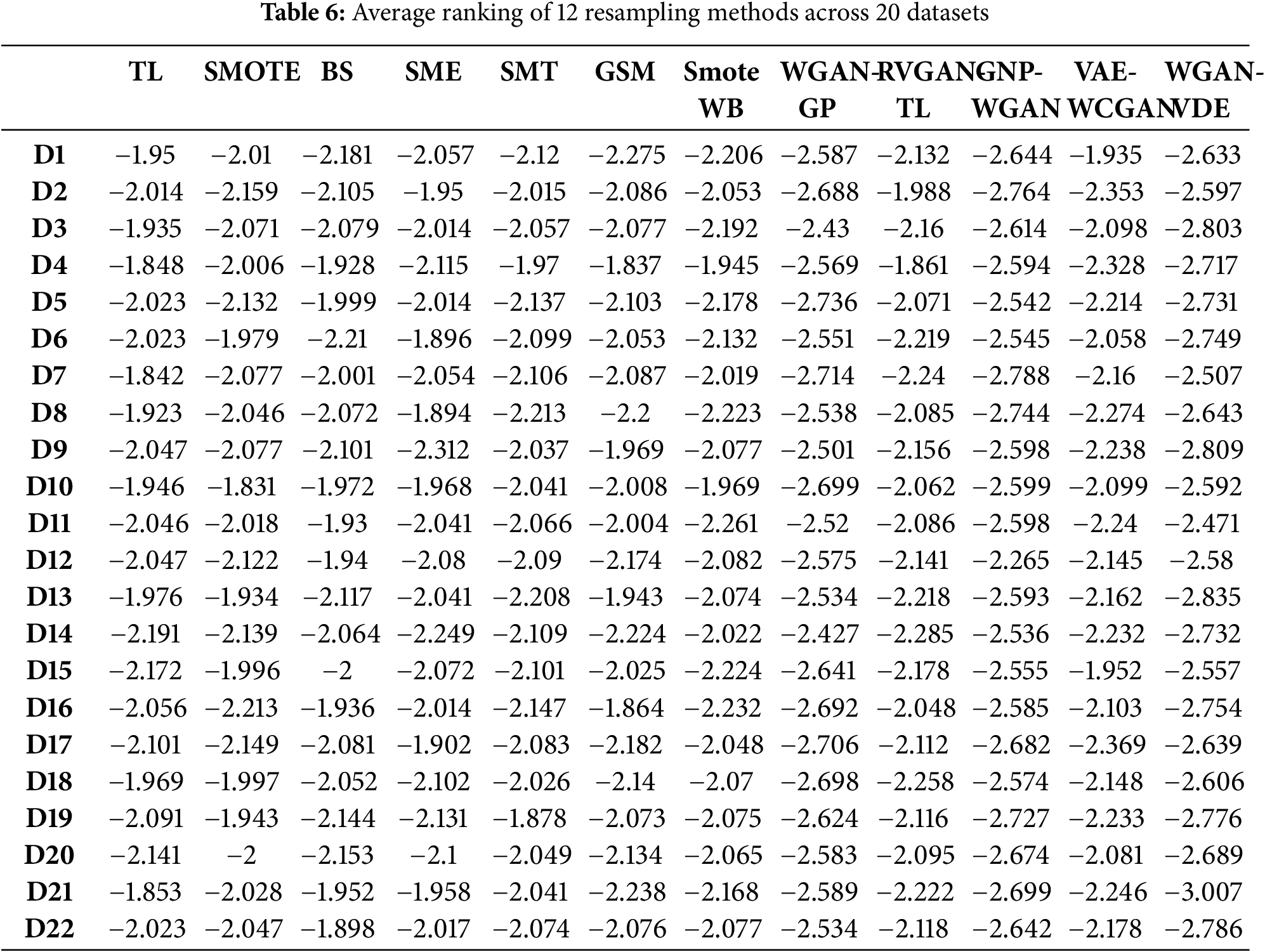
From the results, it is clear that WGAN-VDE consistently achieves the lowest KDE scores across almost all datasets, including highly imbalanced and high-dimensional ones such as Coil2000 and Abalone19. This indicates that our method is highly effective in placing synthetic samples in low-density, non-overlapping regions, thus addressing one of the core challenges in imbalanced classification, class overlap. Traditional techniques like SMOTE or ADASYN produce higher KDE scores, suggesting greater overlap and redundancy in synthetic data. This KDE-based overlap analysis complements our primary evaluation metrics (F1, G-Mean, AUC, Accuracy) and provides an additional layer of interpretability and evidence for the effectiveness of the proposed WGAN-VDE framework.
To show the rigorous and unbiased performance of WGAN-VDE, we also conduct a statistical analysis test, i.e., the Friedman test [42] to validate ranking performances. The Friedman test operates as a non-parametric statistical method to evaluate the importance of differences among multiple groups of means. Using the XG-Boost classifier, we compute average ranking calculations for 12 resampling techniques across 22 datasets to evaluate their performance based on four metrics, as shown in Table 7.
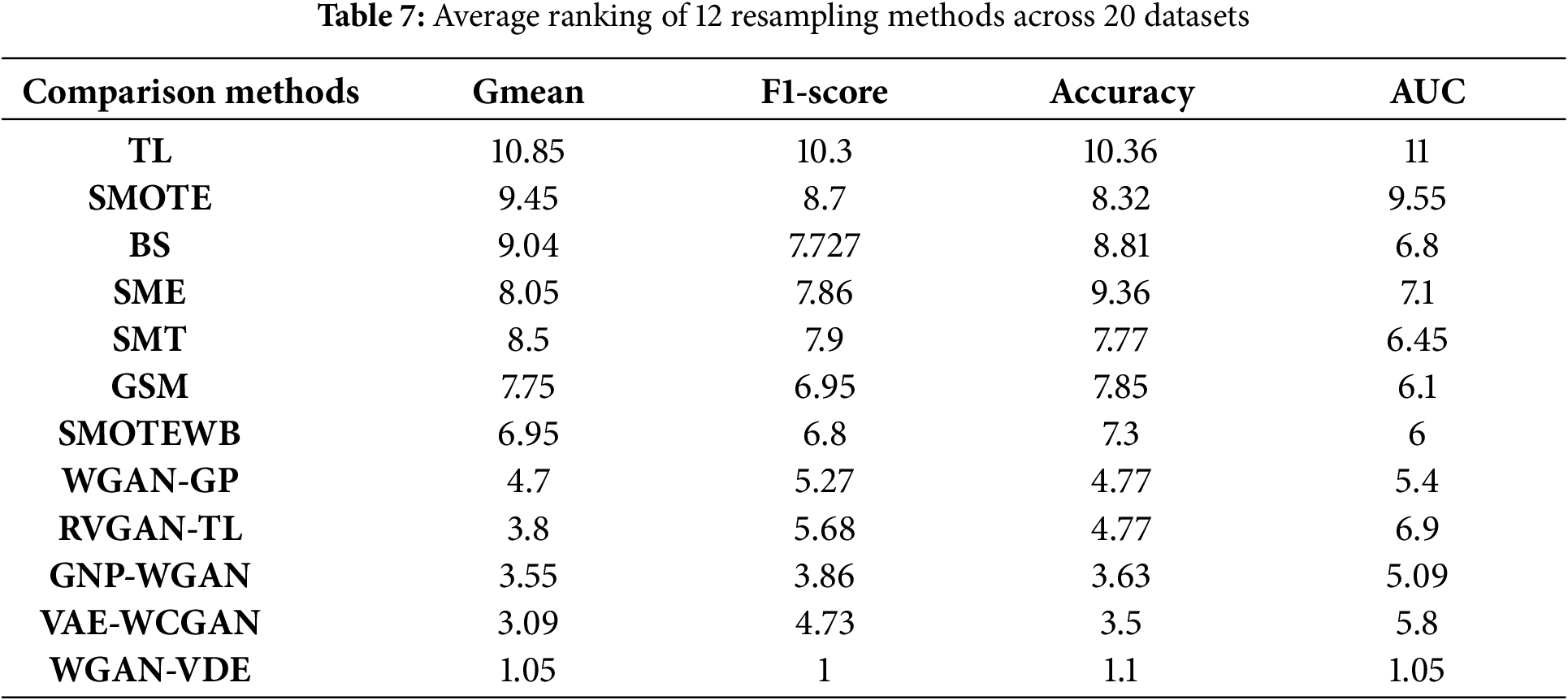
To determine the statistical significance, we compute the critical value by utilizing the null hypothesis
The Friedman statistic is calculated as:
And the F-distribution-based test statistic is calculated as:
Here, N = 22 denotes the number of datasets used for evaluation, and K = 12 represents the total number of methods used for comparison. Based on the computed statistics, the
In order to study these differences in more detail, we also conducted a Nemenyi post hoc test [43] in the context of comparing the resampling methods by calculating the critical difference (CD) at a significance level of 0.5. Fig. 8 shows that if the solid black ranking line of one method aligns with the red dashed line of another method, then they are essentially similar. However, Fig. 8 shows that the WGAN-VDE performs better in terms of ranking across various datasets, showing that it is more useful for improving class balance, increasing separability, and increasing classification accuracy when used on imbalanced datasets.
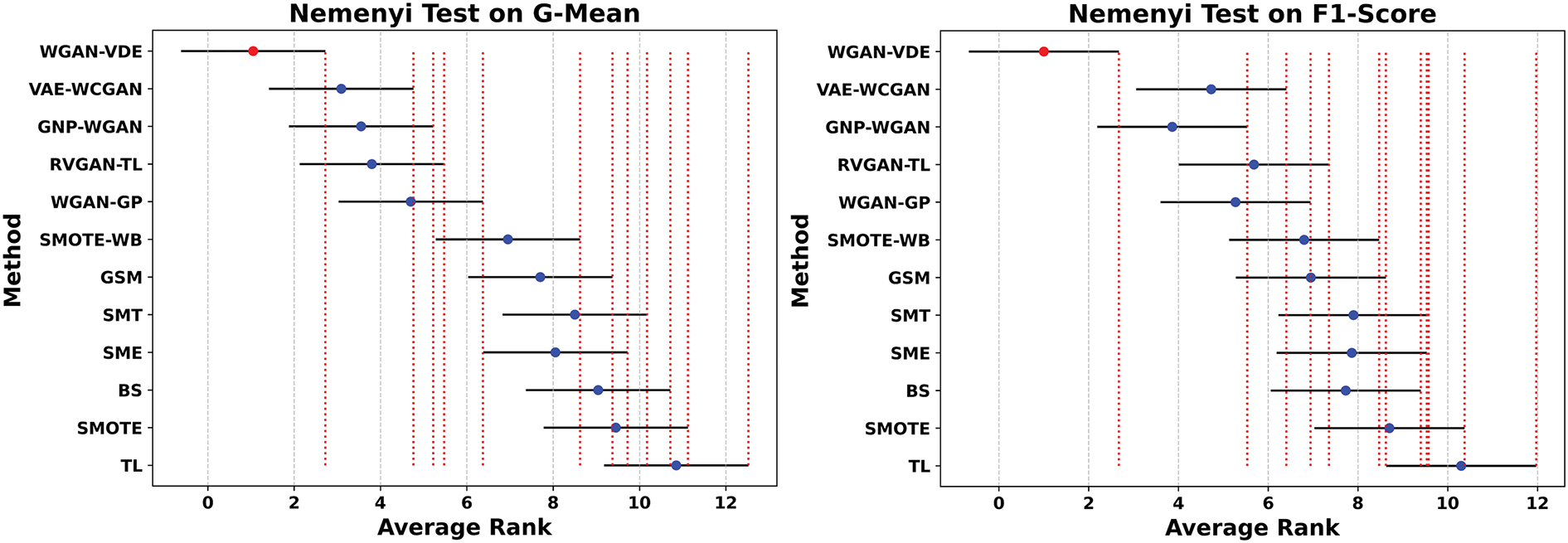

Figure 8: Ranking comparison results of Nemenyi post-hoc tests of 12 rebalancing methods across 22 imbalanced datasets
A rebalanced method with excellent performance should not only excel in predictive metrics but also demonstrate efficient training behavior. Fig. 9 presents the average training time per sample across several advanced GAN-based oversampling methods, evaluated on dataset D11 over 100 epochs. Among these, WGAN-VDE achieves the lowest runtime at 0.8426 s per sample, outperforming WGAN-GP (1.3952 s), RVGAN-TL (1.105 s), GNP-WGAN (1.245 s), and VAE-WACGAN (0.998 s). This superior efficiency is attributed to the lightweight VAE encoder and the density-aware KDE filtering, which selectively generates only informative synthetic samples and avoids redundancy. Despite its three-stage architecture, WGAN-VDE offers competitive computational efficiency compared to other deep learning resampling methods. However, it still carries higher overall computational complexity than conventional techniques like SMOTE, due to its adversarial and variational components. Nevertheless, the performance gains and scalable design make it a practical solution for large-scale imbalanced learning tasks.

Figure 9: Average training time per sample for WGAN-VDE and four deep learning methods on D11
As demonstrated by the study results in Sections 5.1 and 5.2, WGAN-VDE achieves superior performance than both conventional as well as deep learning-based oversampling practices throughout various evaluated datasets. The proposed approach effectively enhances data diversity and minimizes the risk of synthetic-majority class overlap by learning structured feature representations, generating high-quality synthetic samples, and refining their placement based on density distributions. This ensures that synthetic instances are well-separated and strategically positioned in underrepresented regions, preventing redundancy and improving overall class balance. The experiments revealed that established oversampling approaches, SMOTE, Borderline-SMOTE (BS), and Gaussian-SMOTE (GSM) consistently produce inferior results when dealing with severe class imbalance. The approach of creating new minority class instances through these methods often produces artificial data points in dense areas that make interpretation and generalization less effective. This problem is noticeable in datasets with high imbalance ratios (e.g., D16, D18, D19, and D20), where standard approaches fail to enhance classification performance. On the other hand, the GAN-based techniques WGAN-GP, GNP-WGAN, and VAE-WCGAN demonstrate superiority over traditional oversampling methods by achieving more accurate learning of the underlying data distribution, but these methods are suppressed by WGAN-VDE. Mode collapse represents a widespread problem in these techniques because the generator produces similar unintelligible minority class samples, which fail to show diversity effectively. WGAN-VDE solves the mode collapse issue by implementing density-based sample refinement that removes repetitive synthetic examples without eliminating minority class diversity. Similarly, WGAN-VDE also shows superior outcome performance than RVGAN-TL and VAE-WCGAN on all metrics according to the obtained G-Mean, F1-Score, Accuracy, and AUC results. KDE integration allows the WGAN-VDE to generate meaningful samples because it focuses on underrepresented minority class regions.
The key feature of WGAN-VDE lies in its ability to intentionally place synthetic samples in less-density areas where the minority class is underrepresented. The placement evaluation through Kernel Density Estimation (KDE) eliminates unbeneficial samples, thereby generating a well-balanced synthetic dataset that enhances class separability. This refinement process becomes essential in high-dimensional datasets since it reduces class overlap, which causes major degradation of classifier performance. WGAN-VDE exhibits strong performance, which indicates that it would work effectively in real-world applications involving rare event identification, such as fraud detection in financial transactions, medical diagnosis for rare diseases, intrusion detection in cybersecurity, and manufacturing defect detection.
Despite its strong performance, WGAN-VDE presents certain areas for improvement. While our runtime analysis (Fig. 7) shows that WGAN-VDE is more efficient than other deep GAN-based oversampling methods, it remains computationally more intensive than traditional resampling approaches such as SMOTE or Random Oversampling. This added complexity arises from the integration of VAE encoding, adversarial training, and KDE-based filtering. Furthermore, WGAN-VDE’s performance is sensitive to several hyperparameters, including the number of training epochs, learning rates, and KDE threshold settings. To further enhance efficiency and generalization, future work will focus on automated hyperparameter tuning strategies such as Bayesian Optimization, as well as potential architecture simplifications to reduce overhead without compromising sample quality. In addition, possible strategies to reduce training time include applying early stopping based on validation loss, batch-wise KDE approximation to speed up refinement, and exploring parameter sharing between the VAE encoder and GAN generator. Lightweight model variants with fewer hidden layers or reduced dimensionality could also help balance performance and computational cost.
In this research, we present WGAN-VDE, a computationally efficient adversarial resampling designed to tackle the dual challenge of class imbalance and overlap issues in tabular datasets. The originality of WGAN-VDE lies in its density-aware synthetic sample refinement, which strategically reduces class overlap while preserving minority class diversity. Unlike conventional oversampling techniques that generate synthetic samples without structural considerations, WGAN-VDE strategically refines the placement of synthetic instances to enhance class separability. By employing structured feature encoding, targeted sample generation, and density-based refinement, the proposed framework mitigates the risk of redundant or misleading synthetic samples. Experimental evaluations across 20 datasets show that WGAN-VDE surpasses all other 11 traditional resampling and advanced GAN-based methods in terms of metrics G-Mean, F1-Score, Accuracy, and AUC. These findings establish WGAN-VDE as a robust and scalable solution for real-world applications where imbalanced learning and rare event detection remain critical challenges.
While this work focuses on binary classification tasks, future research should explore extending WGAN-VDE to multi-class and multi-label settings. This will involve adapting class-conditional generation mechanisms, performing density-aware refinement in a class-specific manner, and incorporating appropriate loss functions to handle label dependencies. Addressing these challenges will broaden the usability of WGAN-VDE in complex classification scenarios.
Acknowledgement: The study was supported by Ongoing Research Funding Program (ORF-2025-488), King Saud University, Riyadh, Saudi Arabia.
Funding Statement: The study was supported by Ongoing Research Funding Program (ORF-2025-488), King Saud University, Riyadh, Saudi Arabia.
Author Contributions: Conceptualization, Sidra Jubair; methodology, Sidra Jubair and Jie Yang; software, Sidra Jubair; validation, Bilal Ali, Walid Emam and Yusra Tashkandy; formal analysis, Yusra Tashkandy; investigation, Sidra Jubair and Jie yang; resources, Jie Yang; data curation, Sidra Jubair and Jie yang; writing—original draft preparation, Sidra Jubair; writing—review and editing, Jie Yang and Bilal Ali; visualization, Sidra Jubair and Bilal Ali; supervision, Jie Yang; project administration, Sidra Jubair and Jie Yang; funding acquisition, Walid Emam. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data collection includes 9 imbalanced datasets sourced from the Machine Learning Repository UCI, which can be accessed at http://archive.ics.uci.edu, and an additional 13 imbalanced datasets that are publicly accessible on KEEL, found at http://www.keel.es. The data presented in this study are available on request from the corresponding author.
Ethics Approval: Not applicable
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Ahmad GN, Fatima H, Ullah S, Saidi AS. Efficient medical diagnosis of human heart diseases using machine learning techniques with and without GridSearchCV. IEEE Access. 2022;10(4):80151–73. doi:10.1109/access.2022.3165792. [Google Scholar] [CrossRef]
2. Sousa MR, Gama J, Brandão E. A new dynamic modeling framework for credit risk assessment. Expert Syst Appl. 2016;45(2-3):341–51. doi:10.1016/j.eswa.2015.09.055. [Google Scholar] [CrossRef]
3. Wu Z, Zhang H, Guo J, Ji Y, Pecht M. Imbalanced bearing fault diagnosis under variant working conditions using cost-sensitive deep domain adaptation network. Expert Syst Appl. 2022;193(1):116459. doi:10.1016/j.eswa.2021.116459. [Google Scholar] [CrossRef]
4. Kong J, Kowalczyk W, Menzel S, Bäck T, editors. Improving imbalanced classification by anomaly detection. In: International Conference on Parallel Problem Solving from Nature. Cham: Springer; 2020. [Google Scholar]
5. Gu X, Angelov PP, Soares EA. A self-adaptive synthetic over-sampling technique for imbalanced classification. Int J Intell Syst. 2020;35(6):923–43. doi:10.1002/int.22230. [Google Scholar] [CrossRef]
6. Khan SH, Hayat M, Bennamoun M, Sohel FA, Togneri R. Cost-sensitive learning of deep feature representations from imbalanced data. IEEE Trans Neural Netw Learn Syst. 2017;29(8):3573–87. doi:10.1109/tnnls.2017.2732482. [Google Scholar] [PubMed] [CrossRef]
7. Shi L, Ma X, Xi L, Duan Q, Zhao J. Rough set and ensemble learning based semi-supervised algorithm for text classification. Expert Syst Appl. 2011;38(5):6300–6. doi:10.1016/j.eswa.2010.11.069. [Google Scholar] [CrossRef]
8. Latif MA, Mushtaq Z, Rahman S, Arif S, Mursal SNF, Irfan M, et al. Oversampling-enhanced feature fusion-based hybrid ViT-1DCNN model for ransomware cyber attack detection. Comput Model Eng Sci. 2025;142(2):1667–95. doi:10.32604/cmes.2024.056850. [Google Scholar] [CrossRef]
9. Douzas G, Bacao F, Last F. Improving imbalanced learning through a heuristic oversampling method based on k-means and SMOTE. Inf Sci. 2018;465(1):1–20. doi:10.1016/j.ins.2018.06.056. [Google Scholar] [CrossRef]
10. Ng WW, Hu J, Yeung DS, Yin S, Roli F. Diversified sensitivity-based undersampling for imbalance classification problems. IEEE Trans Cybern. 2014;45(11):2402–12. doi:10.1109/tcyb.2014.2372060. [Google Scholar] [PubMed] [CrossRef]
11. Hassan MM, Eesa AS, Mohammed AJ, Arabo WK. Oversampling method based on Gaussian distribution and K-Means clustering. Comput Mater Contin. 2021;69(1):451–69. doi:10.32604/cmc.2021.018280. [Google Scholar] [CrossRef]
12. Goodfellow I, Pouget-Abadie J, Mirza M, Xu B, Warde-Farley D, Ozair S, et al. Generative adversarial networks. Commun ACM. 2020;63(11):139–44. doi:10.1145/3422622. [Google Scholar] [CrossRef]
13. Douzas G, Bacao F. Self-organizing map oversampling (SOMO) for imbalanced data set learning. Expert Syst Appl. 2017;82(2):40–52. doi:10.1016/j.eswa.2017.03.073. [Google Scholar] [CrossRef]
14. Tian W, Shen Y, Guo N, Yuan J, Yang Y. VAE-WACGAN: an improved data augmentation method based on VAEGAN for intrusion detection. Sensors. 2024;24(18):60–76. doi:10.3390/s24186035. [Google Scholar] [PubMed] [CrossRef]
15. Arjovsky M, Chintala S, Bottou L. Wasserstein generative adversarial networks. In: International Conference on Machine Learning; 2017 Jul 17. p. 214–23. [Google Scholar]
16. Gulrajani I, Ahmed F, Arjovsky M, Dumoulin V, Courville A. Improved training of wasserstein gans. Adv Neural Inf Process Syst. 2017;30:576–98. [Google Scholar]
17. Jiang Z, Zhao L, Lu Y, Zhan Y, Mao Q. A semi-supervised resampling method for class-imbalanced learning. Expert Syst Appl. 2023;221(185):119733. doi:10.1016/j.eswa.2023.119733. [Google Scholar] [CrossRef]
18. Zheng M, Li T, Zhu R, Tang Y, Tang M, Lin L, et al. Conditional Wasserstein generative adversarial network-gradient penalty-based approach to alleviating imbalanced data classification. Inf Sci. 2020;512:1009–23. doi:10.1016/j.ins.2019.10.014. [Google Scholar] [CrossRef]
19. Yu Y, Tang B, Lin R, Han S, Tang T, Chen M. CWGAN: conditional wasserstein generative adversarial nets for fault data generation. In: 2019 IEEE International Conference on Robotics and Biomimetics (ROBIO). Dali, China: IEEE; 2019. p. 2713–8. [Google Scholar]
20. Zhai J, Lin P, Cui Y, Xu L, Liu M. GraphCWGAN-GP: a novel data augmenting approach for imbalanced encrypted traffic classification. Comput Model Eng Sci. 2023;136(2):2069–92. doi:10.32604/cmes.2023.023764. [Google Scholar] [CrossRef]
21. Yao R, Li K, Dou Y, Xu Z, Wang M. GNP-WGAN: generative non-local a priori augmented wasserstein generative adversarial networks for seismic data reconstruction. IEEE Trans Geosci Remote Sens. 2024;62(1):5921112. doi:10.1109/tgrs.2024.3431243. [Google Scholar] [CrossRef]
22. Guan S, Zhao X, Xue Y, Pan H. AWGAN: an adaptive weighting GAN approach for oversampling imbalanced datasets. Inf Sci. 2024;663:120311. doi:10.1016/j.ins.2024.120311. [Google Scholar] [CrossRef]
23. Doan QH, Keshtegar B, Kim S-E, Thai D-K. Generative adversarial networks for overlapped and imbalanced problems in impact damage classification. Inf Sci. 2024;675:120752. doi:10.1016/j.ins.2024.120752. [Google Scholar] [CrossRef]
24. Wang S, Wang J, Chung F. Kernel density estimation, kernel methods, and fast learning in large data sets. IEEE Trans Cybern. 2013;44(1):1–20. doi:10.1109/tsmcb.2012.2236828. [Google Scholar] [PubMed] [CrossRef]
25. Moreo A, González P, delCoz J. Kernel density estimation for multiclass quantification. Mach Learn. 2025;114(4):92–112. [Google Scholar]
26. Jiang Z, Lu Y, Zhao L, Zhan Y, Mao Q. A post-processing framework for class-imbalanced learning in a transductive setting. Expert Syst Appl. 2024;249(2002):123832. doi:10.1016/j.eswa.2024.123832. [Google Scholar] [CrossRef]
27. Abbasnejad ME, Shi J, van den Hengel A, Liu L. Gade: a generative adversarial approach to density estimation and its applications. Int J Comput Vis. 2020;128(10–11):2731–43. doi:10.1007/s11263-020-01360-9. [Google Scholar] [CrossRef]
28. Zhang R, Lu S, Yan B, Yu P, Tang X. A density-based oversampling approach for class imbalance and data overlap. Comput Ind Eng. 2023;186:109–35. [Google Scholar]
29. Lee D, Kim H. Adaptive oversampling via density estimation for online imbalanced classification. Information. 2025;16(1):23–48. doi:10.3390/info16010023. [Google Scholar] [CrossRef]
30. Sun Z, Ying W, Zhang W, Gong S. Undersampling method based on minority class density for imbalanced data. Expert Syst Appl. 2024;249(5):123–48. doi:10.1016/j.eswa.2024.123328. [Google Scholar] [CrossRef]
31. Zhou Z, Zhang B, Lv Y, Shi T, Chang F, editors. Data augment in imbalanced learning based on generative adversarial networks. In: International Conference on Neural Information Processing. Cham: Springer; 2019. [Google Scholar]
32. Xie Y, Peng L, Chen Z, Yang B, Zhang H, Zhang H. Generative learning for imbalanced data using the Gaussian mixed model. Appl Soft Comput. 2019;79(2–3):439–51. doi:10.1016/j.asoc.2019.03.056. [Google Scholar] [CrossRef]
33. Tomek I. Two modifications of CNN. IEEE Trans Systems, Man, Cyber. 1976;6:769–72. [Google Scholar]
34. Chawla N, Bowyer K, Hall LO, Kegelmeyer W. SMOTE: synthetic minority over-sampling technique. J Artif Intell Res. 2002;16:321–57. doi:10.1613/jair.953. [Google Scholar] [CrossRef]
35. Han H, Wang WY, Mao BH. Borderline-SMOTE: a new over-sampling method in imbalanced data sets learning. In: International Conference on Intelligent Computing. Berlin/Heidelberg: Springer; 2005 Aug 23. p. 878–87. [Google Scholar]
36. Batista G, Bazzan A, Monard M. Balancing training data for automated annotation of keywords: a case study. Wob. 2003;3:10–8. [Google Scholar]
37. Batista G, Prati R, Monard M. A study of the behavior of several methods for balancing machine learning training data. ACM SIGKDD Explor Newsl. 2004;6(1):20–9. doi:10.1145/1007730.1007735. [Google Scholar] [CrossRef]
38. Lee H, Kim J, Kim S. Gaussian-based SMOTE algorithm for solving skewed class distributions. Int J Fuzzy Logic and Intell Syst. 2017;17(4):229–34. doi:10.5391/ijfis.2017.17.4.229. [Google Scholar] [CrossRef]
39. Sağlam F, Cengiz M. A novel SMOTE-based resampling technique trough noise detection and the boosting procedure. Expert Syst Appl. 2022;200(2–3):117–33. doi:10.1016/j.eswa.2022.117023. [Google Scholar] [CrossRef]
40. Ding H, Sun Y, Huang N, Shen Z, Wang Z, Iftekhar A, et al. RVGAN-TL: a generative adversarial networks and transfer learning-based hybrid approach for imbalanced data classification. Inf Sci. 2023;629(6):184–203. doi:10.1016/j.ins.2023.01.147. [Google Scholar] [CrossRef]
41. Chen T, He T, Benesty M, Khotilovich V, Tang Y, Cho H, et al. XGBoost: extreme gradient boosting. R package version 04-2. 2015;1(4):1–4. [Google Scholar]
42. Barbado R, Araque O, Iglesias CA. A framework for fake review detection in online consumer electronics retailers. Inf Process Manag. 2019;56(4):1234–44. doi:10.1016/j.ipm.2019.03.002. [Google Scholar] [CrossRef]
43. Demsar J. Statistical comparisons of classifiers over multiple data sets. J Mach Learn Res. 2006;7:1–30. [Google Scholar]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF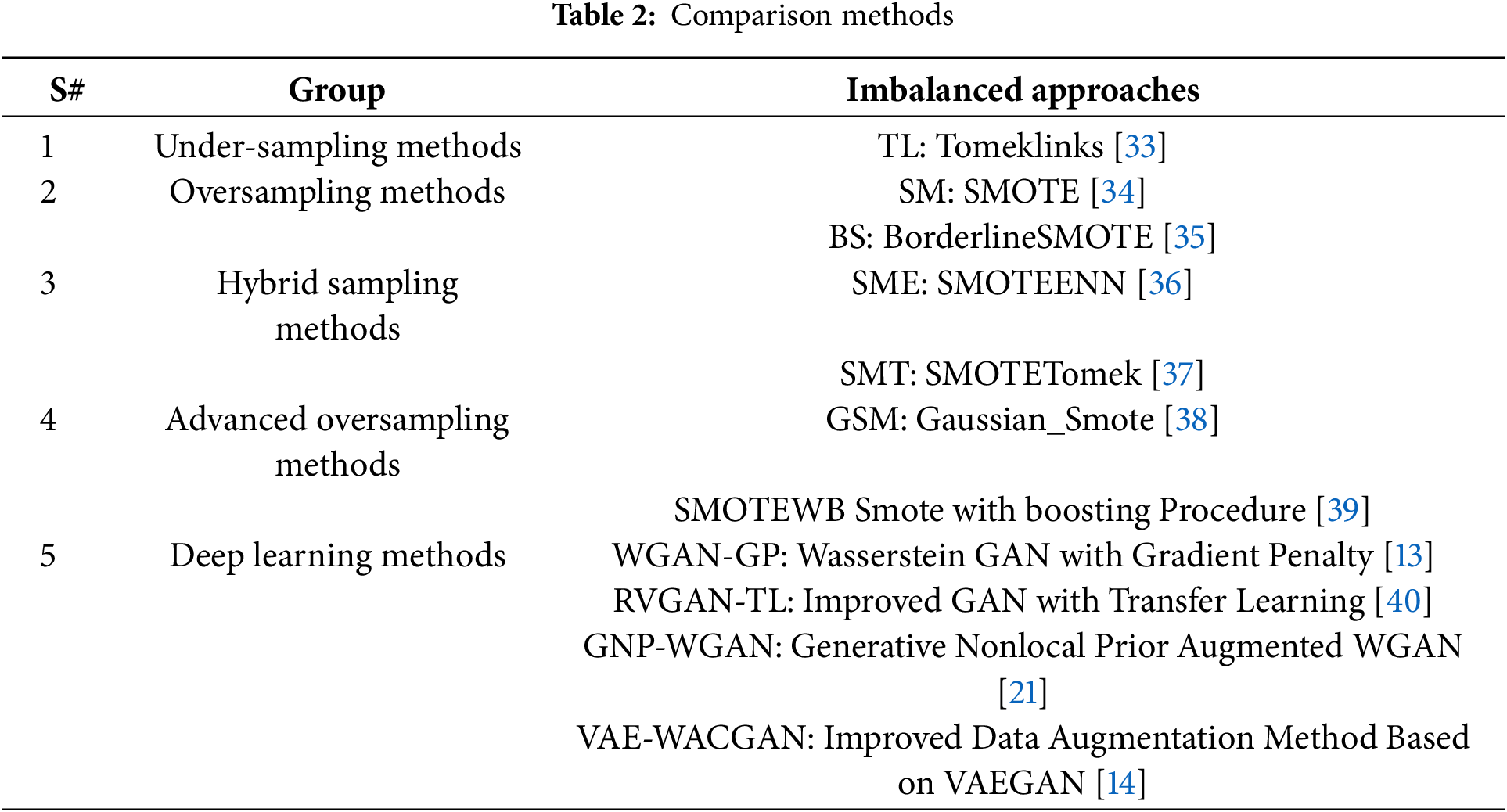
 Downloads
Downloads
 Citation Tools
Citation Tools