Novel Analysis of SiO₂ + ZnO + MWCNT-Ternary Hybrid Nanofluid Flow in Electromagnetic Squeezing Systems

1  Introduction

Energy usage has been identified as the demanding problem confronting humans, particularly over the next 50–70 years, particularly the global warming and monitoring carbon emissions [1]. Most wealthy countries now prioritise the security of renewable energy. Primarily, energy conversion and transmission occur at the atomic level; nanotechnology is anticipated to play a key role in invigorating current energy industries and boosting emerging renewable sectors. More than 80% of the energy we use today is generated or consumed in the form of heating. Several manufacturing procedures require the movement of heat to either input or remove energy from the system. Given the enormous increase in global energy consumption, improving heat transfer and reducing energy loss caused by inefficient use have become essential priorities [2]. Heat extraction and regulation are challenging tasks in many high-heat-flux networks, including microchemical processes, nuclear fission, fusion, and process intensification.

Nanofluids are a revolutionary form of nanotechnology-based heat transfer fluid generated by dispersing and stabilizing nanoparticles with typical lengths ranging from 1 to 5 nm in standard heat transfer fluids. Over the past few decades, scientists have discovered that adding modest amounts of guest nanoparticles may significantly improve the thermal characteristics of base fluids. A nonlinear relationship between concentration and thermal conductivity, strong size-dependent thermal conductivity, anomalously low nanoparticle concentrations despite high thermal conductivity, and an upsurge in critical heat flux at a small particle concentration of roughly 10 ppm are just a few examples of the superior thermal traits of certain nanofluids [3]. Sidik et al. [4] reviewed and compiled on the production of hybrid nanoparticles, hybrid nanofluids, and hybrid nanofluid thermophysical characteristics. The problems and future advancements in the use of hybrid nanofluids in heat transfer applications were investigated. Sajid and Ali [5] provided a critical study of nanofluid applications in heat transfer devices. Raja et al. [6] assessed several factors that influence the properties of nanofluids, their ability to transport heat, and their implications in engineering. An initiative that commenced more than 140 years ago, when J. P. Joule (1861) presented the first approach to improving the heat transfer rate in condensing steam in his renowned research [7]. Household, commercial, and industrial uses comprise a heat-transfer process for power transformation, exploitation, and restoration [8]. Heat transfer improvements are commonly used in the following applications: ventilation and air conditioning of viscous instruments in heat processing of materials [9]; refrigerator evaporation [10]; gas flow warming in infrastructure and waste rehabilitation [11]; pharmaceutical and agricultural products [12]. It is well acknowledged that the thermal conductivity of nanofluids may be significantly increased by mixing nanoparticles with a base fluid. This results in the flow of hybrid nanofluids across various geometries to improve thermal conductivity.

A hybrid substance is a material that integrates the physicochemical characteristics of many substances at the same time and delivers these properties in a cohesive aspect. The physical and chemical characteristics of fabricated hybrid nanostructures are extraordinary since they do not exist in separate components [13]. Muneeshwaran et al. [14] presented hybrid nanofluids in a diversity of heat transport applications. The characteristics, preparation, and stability of hybrid nanofluids were scrutinized by Eshgarf et al. [15]. Additionally, a few correlations and models for forecasting the features of hybrid nanofluids were provided. Sharma et al. [16] inspected how a unique Ag/ZnO hybrid nanofluid at different concentrations improves thermal characteristics and the heat transfer coefficient. Using the Arrhenius activation energy and a non-Newtonian flow model, Ref. [17] investigated heat and mass exchange in the chemically reactive, unstable boundary layer flow of an ethylene glycol (EG) hybrid nanofluid in a hydromagnetic environment. The ZnO−MWCNTs/EG hybrid nanofluid achieved the greatest increase in heat transfer rate, according to experimental data. Ekiciler [18] studied the two-phase (60:40)%  of  SiO2−MWCNT/water flow in a square duct with Reynolds numbers ranging from 3000−10,000 using first- and second-law analyses. The greatest substantial increase in PEC were observed in hybrid nanofluids with PC and PP forms, at 2.27 and 3.24%, respectively. When PS−,PC−, and PP−shaped nanomaterials were used, the exergy demolition of the hybrid fluid with the second nanoparticle forms carbon and phosphorus is 43.9% and 58.7% higher than that of sulfur, respectively.

Ternary nanofluids have been shown to significantly improve heat transport properties of base fluids when compared to conventional fluids, nanomaterials-induced fluids, and hybrid materials-based fluids. As predicted, these are useful in energy control, cooling, and further applications requiring efficient heat transmission. Mahabaleshwar et al. [19] focused on ternary nanofluid flow with heat transfer over the Riga plates, taking into account the Newtonian heating effect. The current framework discovered that in the presence of a Newtonian heating effect, the temperature profile performs better thermally than in the absence of the heating effect. Farooq et al. [20] studied the mixed convection at the stagnation point of ternary hybrid nanofluids approaching an upright Riga plate. Further, note that Silicon dioxide (SiO2), Aluminum trioxide (Al2O3), and Titanium dioxide (TiO2) were considered nanomaterials, using water (H2O) as the basic fluid. Additionally, when the convection (mixed) parameter is used to oppose the flow model, the noticeable temperature profile decreased while the flow transport profile increased. Abbas et al. [21] analysed the transport of ternary nanofluids (Thnf) across a Riga plate while taking into account the heating impact of the Prandtl fluid. Hybrid ternary nanomaterials made of aluminium alloys AA7072 & AA7075 and Titanium dioxide (TiO2) were suspended in engine oil. The velocity profile grew as the Prandtl fluid parameters increased. The rise of heat in the ternary nanofluid (Tnf) was due to rising thermal heat generation/absorption factors. Furthermore, the prominent temperature of the ternary nanofluid raised significantly when the variables, particularly nanoparticle’s size and shape altered. Ramzan et al. [22] studied the properties of transient, electro-viscous, ternary hybrid nanofluid flow via squeezing parallel infinite plates. The ternary hybrid nanofluid is made by dissolving titanium dioxide, aluminum oxide, and silicon dioxide nanoparticles in glycol/water, the carrier fluid. The goal of the current study is to maximize the rate of mass and energy transfer for engineering and industrial applications. In addition to the impacts of activation energy, magnetic field, heat generation and absorption, and chemical reaction, the phenomenon of fluid flow is explored. Gangadhar et al. [23] observed the impact of electromagnetic initiation through the Riga plate under specific circumstances on the electrical magnetic field. Using copper, silver, and copper oxide nanoparticles, and blood as a base fluid were dispersed to generate the ternary hybrid nanofluid. Additionally, the effects of the slip state, uniform heat source, convective energy, and thermal radiation were taken into account when designing this ternary hybrid nanofluid flow. Karthikeyan et al. [24] looked at the effect of Maxwell fluid and entropy production on the mobility of ternary hybrid nanoparticles (Thn) as they pass through a Riga plate under convection boundary constraints. Higher Maxwell fluid parameter values had been demonstrated to enhance the velocity curve. Additionally, the results showed that the tri hybrid nano liquid’s thermal layer strengthened in response to rising Biot number (Bi) and thermal radiation (Rd). Sharif et al. [25] investigated the momentum, and thermal properties of MHD Ellis ternary nanomaterials implanted with dust particles using a flexible Riga plate, taking into account the dust material volume concentration. The findings showed that tri hybrid nano phase heat transfer outperformed the dusty phase. Furthermore, the noticing temperature profile improved for the rotational and volume fraction of dust particle parameters. The heat transfer properties of Al2O3−Cu−Ni/H2O tri hybrid nanofluid were inspected by Thakur and Sood [26] using a convectively heated stretched Riga plate with varying thickness. Rammoorthi and Mohanavel [27] investigated the MHD flow of a compressed ternary nanofluid between two horizontally parallel Riga plates. The primary findings showed that although variations in viscous dissipation and thermal conductivity altered the temperature distribution, the Riga plate actuator greatly increased fluid velocity.

Table 1 discusses the applications and reference works of various nanofluids.

2  Flow Model

2.1 Physical Layout of the Model

This study examines the unsteady convective squeezing flow of a viscous, tri-hybrid nanomaterial fluid through two perforated Riga plates. This flow regime occurs between the compressed infinitely parallel Riga plates and is influenced by thermal radiation, varying thermal conductivity, magnetic fields, and viscous dissipation. The top plate moves with velocity toward the lower plate, generating a squeezing motion.

The symbol h¯(t) represents the height of the channel or the separation between the horizontal plates. The range of variation in the separation variable is 0 to h¯, where h¯ is much higher than the thickness of the wall’s border layer. While the upper surface can make a movement vertically toward the bottom plate for a suitable compression, the upper plate remains immovable. The vertical displacement of the proposed channel may be expressed using the following criterion, per the findings of Khaled and Vafai [34]. The following equations, where h0 is a constant, which expresses the function h¯(t) in two distinct contexts.

h¯(t)={h0(s+at)−1a,ifa>0,h0exp⁡(−st),ifa=0.}(1)

The proposed model is structured utilizing the x−y plane, with the x−axis show to be the actual direction of flow. The physical depiction of the problem at hand is exposed in Fig. 1.

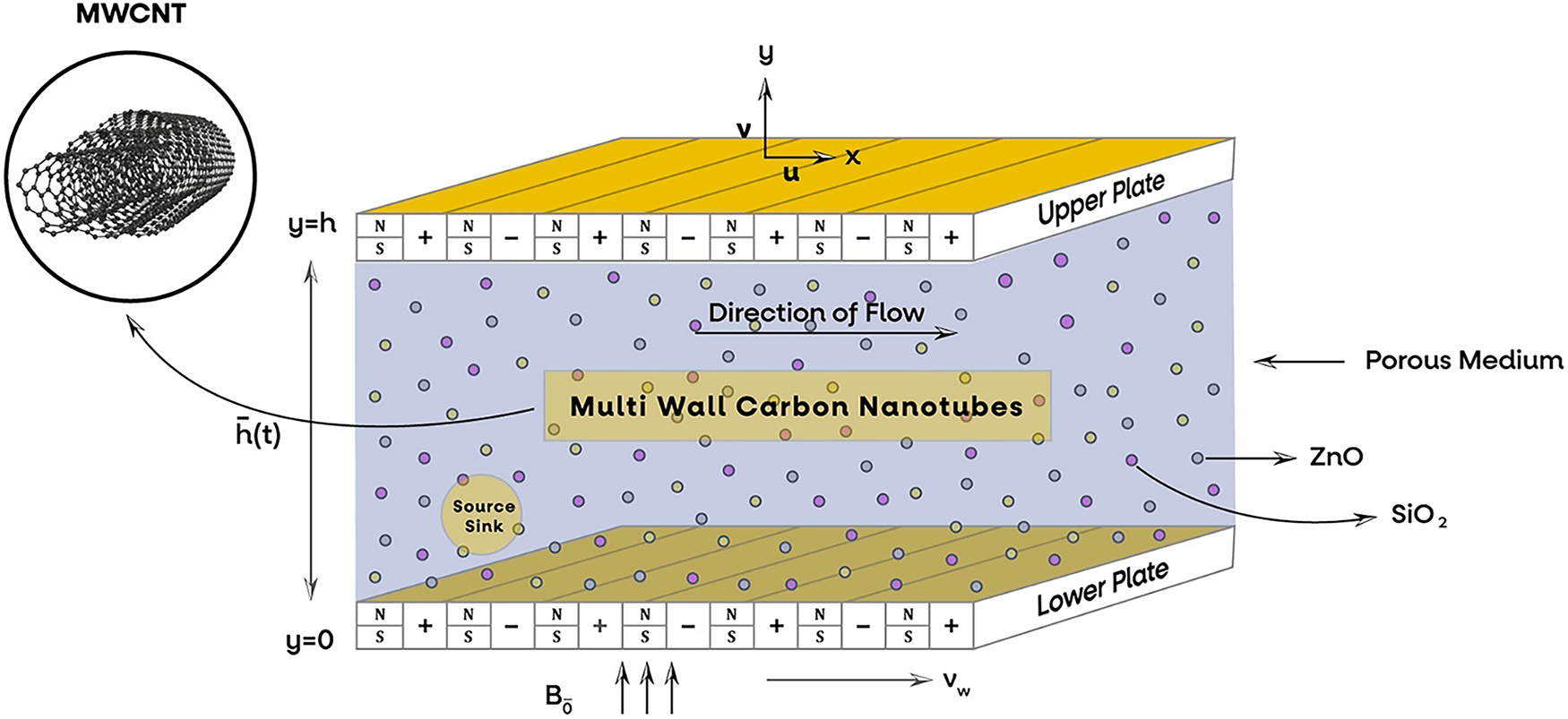
Figure 1: Physical arrangement of the flow model

The following are the governing continuity equation (principle of conservation of mass), Navier-Stokes equation (principle of conservation of momentum), and temperature equation (principle of conservation of energy). Based on the literature [34–36].

2.2 Mathematical Modeling of the Problem

Continuity Equation:

ux+vy=0,(2)

Momentum Equation:

ut+uux+vuy=u¯t+u¯u¯x+μThnfρThnfuyy−1KμThnfρThnf(u¯−u)−Bx¯2σThnfρThnf(u¯−u)+1ρThnfπJ0M08e−πly,(3)

Energy Equation:

Tt+uTx+vTy=kThnf(T)(ρCp)ThnfTyy−16σ∗∗T¯∞33k∗∗1(ρCp)ThnfTyy−μThnf(ρCp)Thnf(uy)2+Q0(ρcp)Thnf(T−T∞),(4)

where the Rosseland approximation yields a radiative unidirectional heat flux (qr∗), as follows by [36], this means that heat transport is largely in one direction. This approximation is commonly utilized when the medium is thought to be in radiative equilibrium.

qr∗=−4σ∗∗3k∗∗(T¯4)y(5)

It is anticipated that the fluid temperature corresponds to T closely be similar to T∞ by expanding the Taylor series expansion T¯4 near to T∞. By leaving out all the higher-order terms starting from the second order, T¯4 is stated as:

T¯4≅4T¯∞3−3T¯∞4.(6)

The current model considers the following boundary conditions (BCs):

Atlowerplate(y=0):u(y)=0;v(y)=vw(t);−κThnf(Ty(y))=hf(Tw−T∞),ForfreestreamCondition(y→∞):u(y)=u¯;T(y)=T∞.}(7)

In Eq. (7), when y=0, the Riga plates are supposed to be immobile. This means that the flow in x−axis is zero. Along y direction, the velocity of the fluid equals the vw(t), i.e., wall permeable velocity and the heat flux on the wall qw(x) is the same as the temperature gradient. As y approaches to infinity, the velocity and temperature distributions in the x−direction approach that of the unconstrained stream.

Role and Modelling of Porosity and Permeability

In the current study, the porous medium is modelled using Darcy’s law, which introduces a resistance force proportional to the fluid velocity. This is captured in the momentum equation through the term:

−1KμThnfρThnf(u−u¯)

Here, K denotes the permeability of the porous medium, which quantifies how easily fluid can flow through it. A lower K implies higher flow resistance, simulating denser or more compact porous materials.

While permeability directly enters the governing equations, porosity is inherently embedded in the effective thermophysical properties of the ternary hybrid nanofluid. It influences how heat and momentum are transported through the medium by altering the apparent density, heat capacity, and viscosity. These effects are considered in the definitions of ρThnf,μThnf, and (ρcp)Thnf which vary based on the solid–fluid volume fractions and porosity-dependent mixing rules.

The combined effect of porosity and permeability controls the extent of momentum suppression and heat dispersion within the porous region, which is crucial for realistic modelling of nanofluid behaviour in engineered materials and biological tissues.

Similarity Variables:

Suitable similarity variables are proposed to solve the gained nonlinear coupled boundary value problem numerically. The stated equations are converted into a nondimensional form employing the dimensionless similarity variables. They were added in order to make the equations simpler and facilitate analysis. Eq. (8), which represents these dimensionless variables, is based on a related work by Muhammad et al. [36]. Using these scaling modifications, a nonlinear ordinary differential model is created using the 2D, unstable TNF flow Eqs. (2)–(4) and the boundary conditions given by Eq. (7).

u¯=bx;vw(t)=v0b;Bx¯(t)=Bo¯b;qw(x)=qo¯x;kThnf(T)=[1+ε{(T−T∞)kfqo¯xbνf}],θ(ζ)=(T−T∞)kfqo¯xbνf;b=(s+at)−1;u=bxf′(ζ);v=−bνff(ζ).}(8)

when Eq. (8) is applied to Eqs. (2)–(4) and (7), they are modified as follows.

γ1⁢f′′′+f⁡f′′+a⁢ζ2⁢f′′−(f′)2+a⁢(f′−1)+γ1⁢λ⁢(1−f′)+γ2⁢M⁢(1−f′)+γ3⁢Z⁢exp⁡(−S∗⁢ζ)+1=0,(9)

1Pr{γ4(1+εθ)+4γ53Rd}θ′′+(f+aζ2)θ′−(f′+a2)θ+γ6Ec(f′′)2−Qθ=0.(10)

Furthermore, Eq. (11) incorporates the boundary constraints from Eq. (7):

Atζ=0,f′(ζ)=0,f(ζ)=−S,γ4θ′(0)=−Bi(1−θ(ζ)),Asζ→∞,f′(ζ)=1,θ′(ζ)=0.}(11)

where,

γ1=(μThnfμf)γ3;γ2=(σThnfσf)γ3;γ3=ρfρThnf;γ4=(kThnfkf)γ5;γ5=(ρCρ)f(ρCρ)Thnf;γ6=μThnfμfγ5,λ=νfxu¯K;M=σfBo¯ρf;Rd=4σ∗∗T¯∞33k∗∗kf;Pr=(ρCρ)fkf;Z=πJ0M8ρfu¯b;Ec=(u¯)2kf(Cρ)fqo¯xbνf;S=ν0νf.](12)

Based on the similarity transformation, the parameters shown in Eq. (12) are taken into consideration. Using TNF correlation, Table 2 lists the values for γi where i=1–6. Here, M the magnetic, λ represents a porous medium, Rd the thermal radiation, Z the Hartmann number, Ec the Eckert number, Pr the Prandtl number, and f0 the surface permeability velocity.

when examining the behavior of fluid flow and heat transfer at boundaries, Eq. (14) is important. It provides the information required to assess and predict the thermal and momentum characteristics of a system. Where the local Reynolds number is defined as Rex=ux¯νf.

Thermophysical Characteristics:

As thermophysical characteristics are extremely important since they allow us to more accurately calculate efficiency. According to the literature, heat transfer characteristics are dependent on the formulation, whereas viscosity is temperature-dependent and thermal conductivity is concentration-dependent.

Density

ρThnf=(1−ϕ1){(1−ϕ2)[(1−ϕ3)ρf+ϕ3ρ3]+ϕ2ρ2}+ϕ1ρ1

Viscosity

μThnf=μf(1−ϕ1)2.5(1−ϕ2)2.5(1−ϕ3)2.5

Thermal conductivity

kThnfkhnf=k1+khnf(n−1)−(n−1)(khnf−k1)ϕ1k1+(n−1)khnf+ϕ1(khnf−k1)

where,

khnfknf=k2+(n−1)knf−ϕ2(n−1)(knf−k2)k2+knf(n−1)+(knf−k2)ϕ2, knfkf=k3+(n−1)kf−(kf−k3)(n−1)ϕ3k3+kf(n−1)+(kf−k3)ϕ3

Thermal expansion coefficient

(ρβ)Thnf=(1−ϕ1){(1−ϕ2)[(1−ϕ3)(ρβ)f+ϕ3(ρβ)2]+ϕ2(ρβ)2}+ϕ1(ρβ)1

3  Numerical Analysis

The system of coupled ordinary differential equations ODEs that forms the boundary value problem (BVP) is defined by using a MATLAB solver. After that, functions are developed for the ODEs along with the boundary conditions, and the boundary constraints are given for the interval’s ends. The numerical solver has an option called collocation that uses these functions in addition to an initial guess for the answer. The behavior of the system may be further analyzed and visualised by extracting the solution from the returning structure. Convergence requires adjusting the tolerance and iteration settings, which also offers a reliable method for resolving BVPs via collocation with the solver. A system of nonlinear, differential equations, Eqs. (9) and (10), with matching boundary constraints, Eq. (11), is solved using this approach. The following is how equations are converted into first-order ODEs:

Let

f⁡(ζ)=d⁡(1),f′⁡(ζ)=d⁡(2),f′′⁡(ζ)=d⁡(3),θ⁡(ζ)=d⁡(4),θ′=d⁡(5).

d′(1)=d(2),

d′(2)=d(3),

d′(3)=1γ1[(d(2))2−d(1)d(3)−aζ2d(3)−ad(2)+a−γ1ζ+γ1ζd(2)−γ2M+γ2Md(2)−γ3Z(exp(−S∗ζ))−1]

d′(4)=d(5),

d′(5)=Pr(γ4+γ4εθ+4γ53R)−1d(2)+a2d(4)−{d(1)+aλ2−γ6Ec(d(3))2}−d(4)Q,

The system is defined by the initial conditions listed below:

Atζ=0:d1=−S;d2=0,d5γ4=−Bi(1−d4),Asζ→∞:d2=1,d4=0.}

We tackled the boundary value problem using MATLAB’s BVP4C solver, which utilizes a collocation method that keeps an eye on errors based on the residuals of the differential equations. Instead of directly managing the error of the true solution, this solver focuses on making sure the norm of the residual stays within certain limits, dictated by both relative and absolute tolerances. By default, these tolerances are set to RelTol=10−3 and AbsTol=10−6, which helps keep the residual error below a threshold proportional to AbsTol+RelTol×|f(x,y)|. This method strikes a nice balance between achieving numerical accuracy and maintaining computational efficiency. Furthermore, details about the chosen numerical scheme are discussed in Fig. 2.

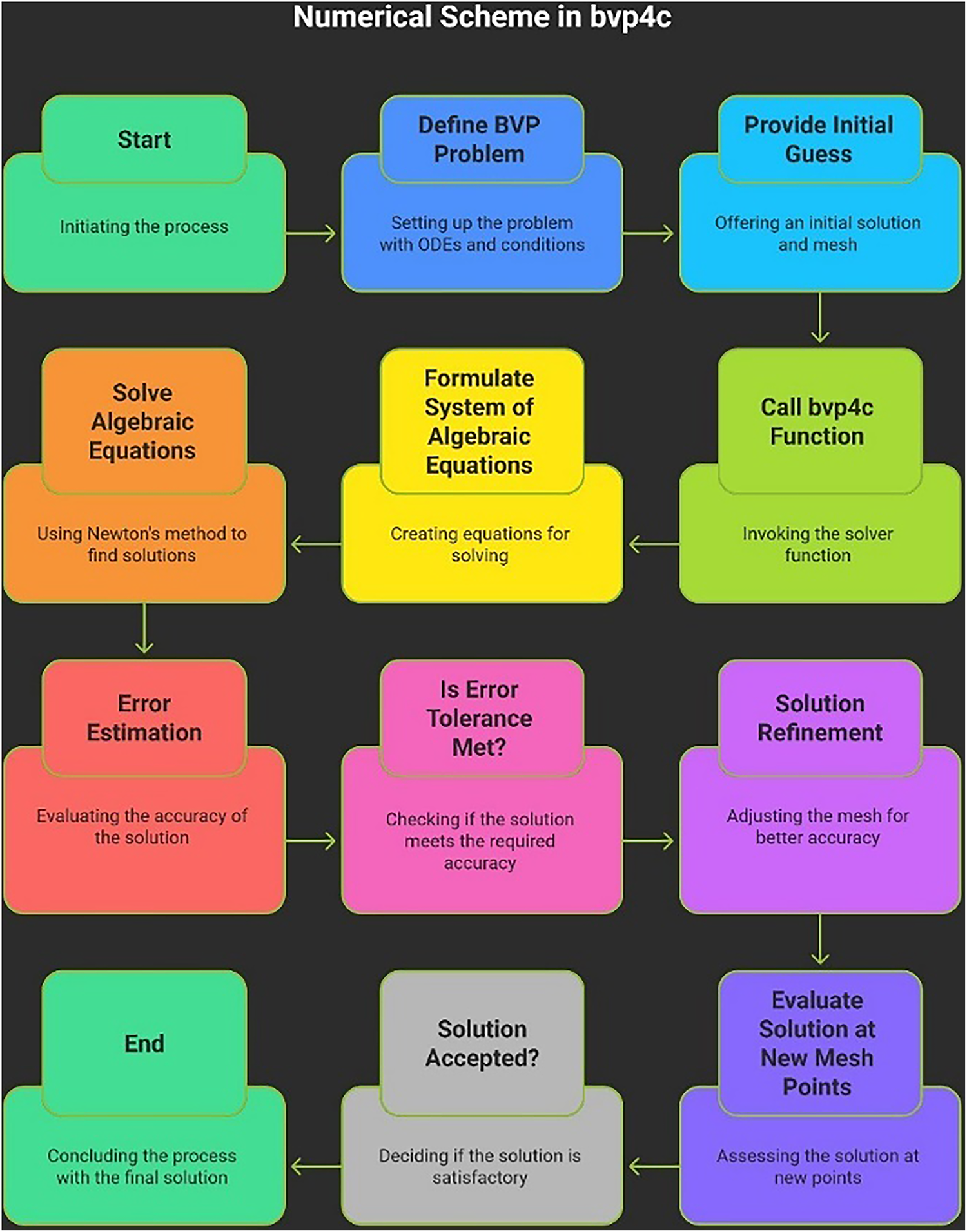
Figure 2: Flow chart of numerical scheme

4  Results and Discussion

The fluid behaviour in this study is illustrated by the graphical illustrations of temperature and momentum profiles for the tri-hybrid nanofluid (SiO2+ZnO+MWCNT/Water−EthylGlycol,(60:40)) flows between two parallel Riga plates. Using similarity variables, the physical model is first transformed into ODEs to produce these profiles. Following conversion, the equations are put into practice with MATLAB, a program that offers a means of resolving intricate mathematical issues and displaying the outcomes. The temperature and velocity profiles at various locations inside the flow domain are shown in Figs. 3–14. Through analysing these profiles, one may learn more about the fluid’s behaviour and how the relevant factors impact these profiles [38–41].

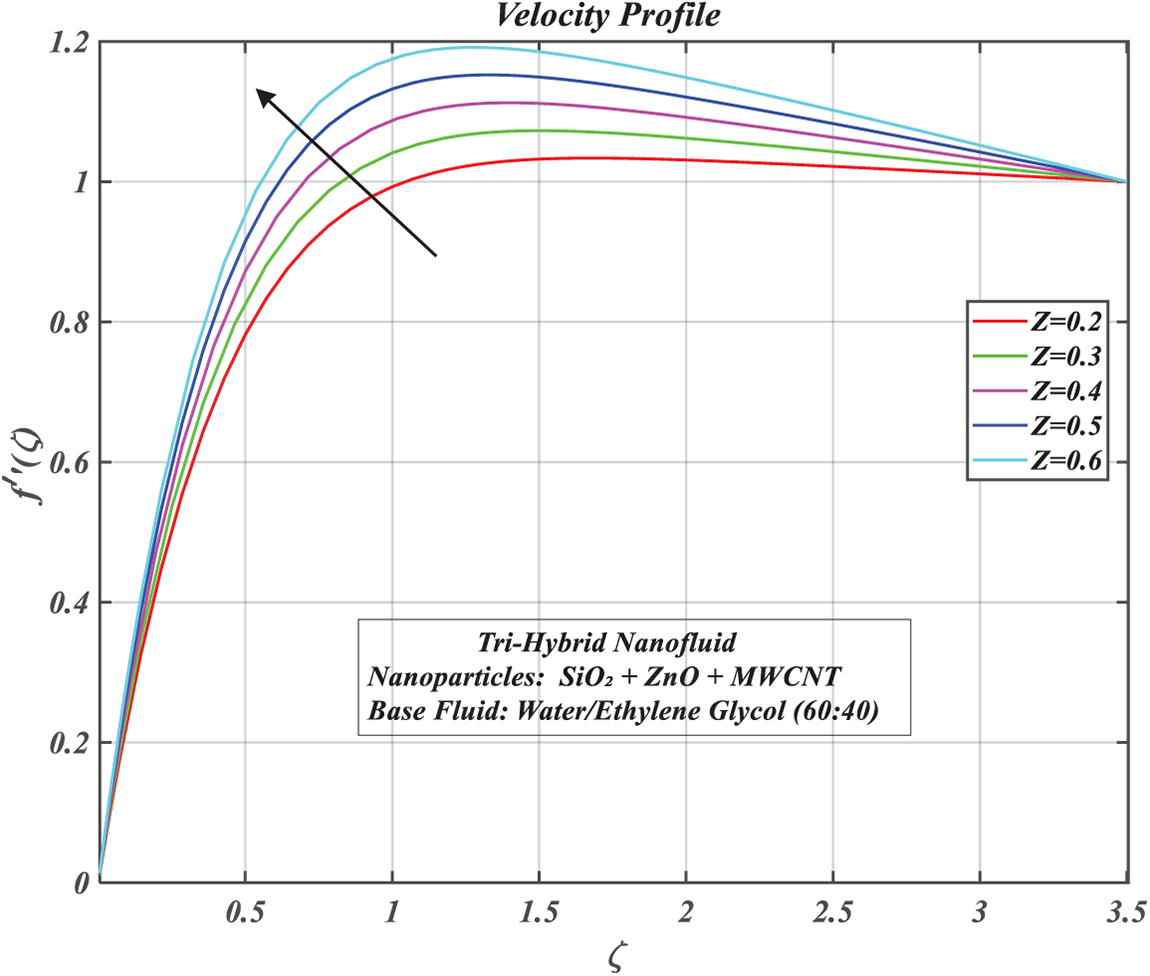
Figure 3: Consequences of hertman number on f′(ζ)

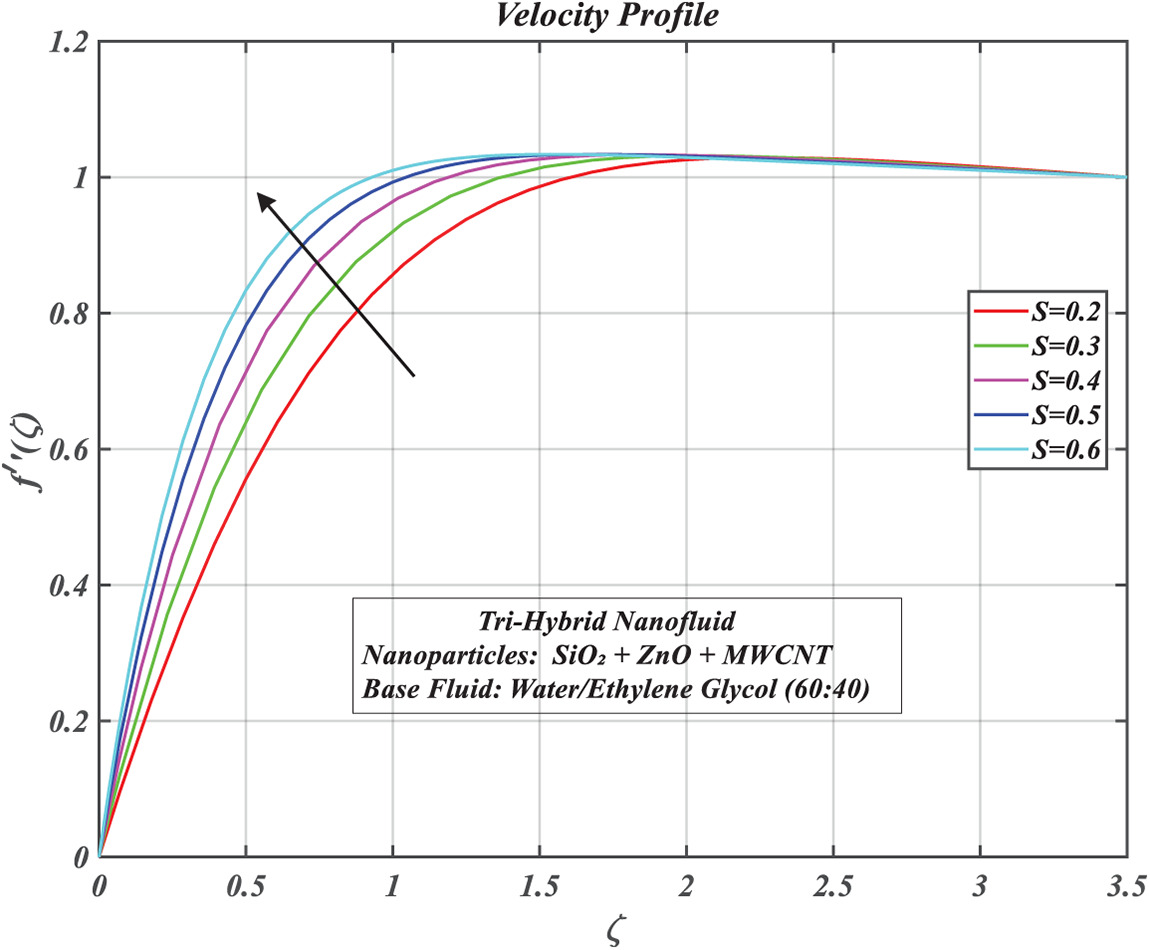
Figure 4: Consequences of suction on f′(ζ)

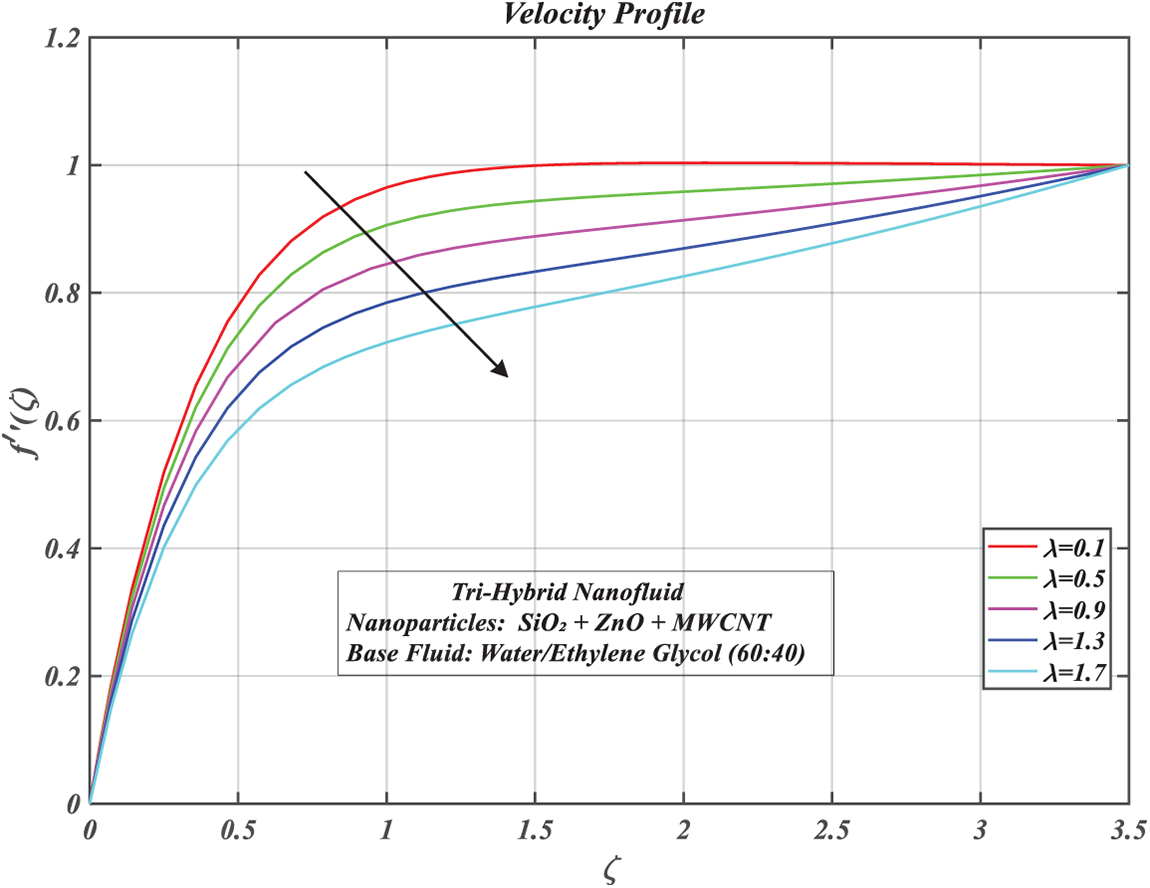
Figure 5: Consequences of porous parameter on f′(ζ)

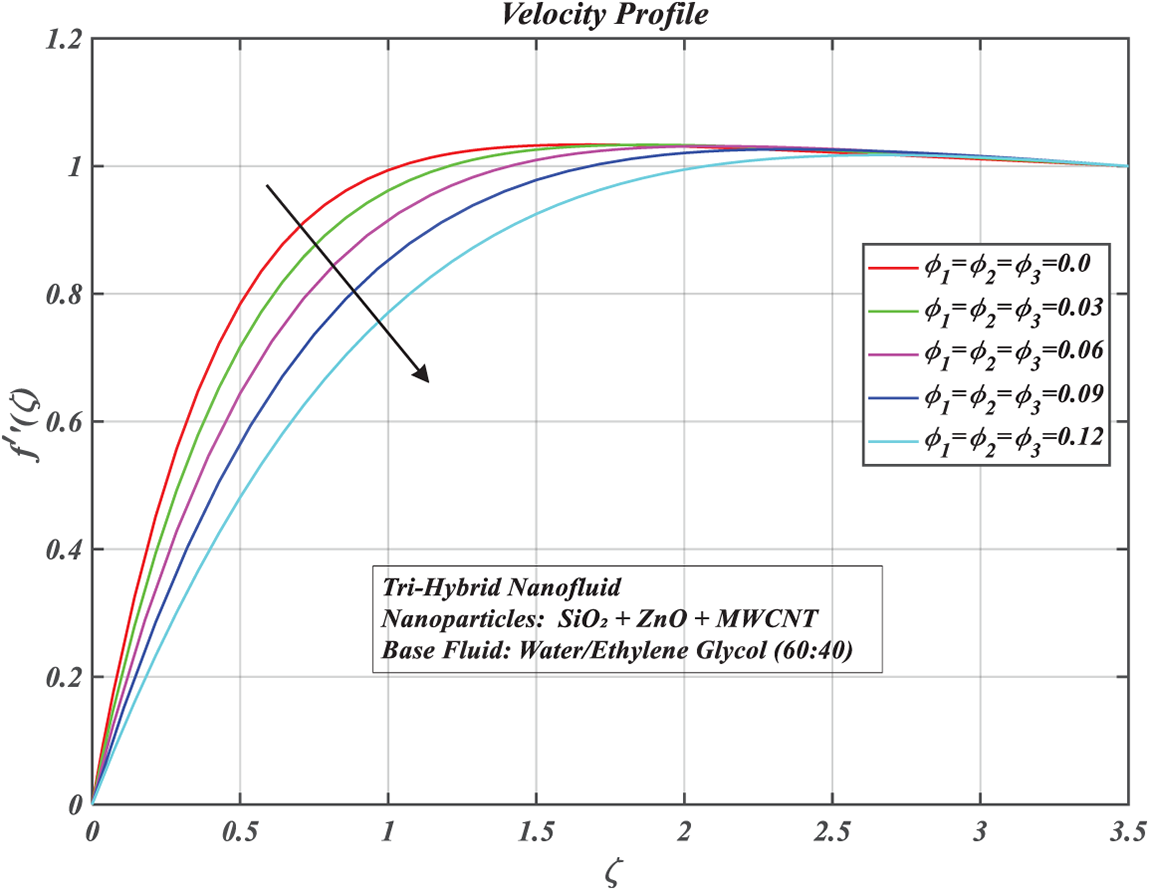
Figure 6: Consequences of volume fractions of nanoparticles on f′(ζ)

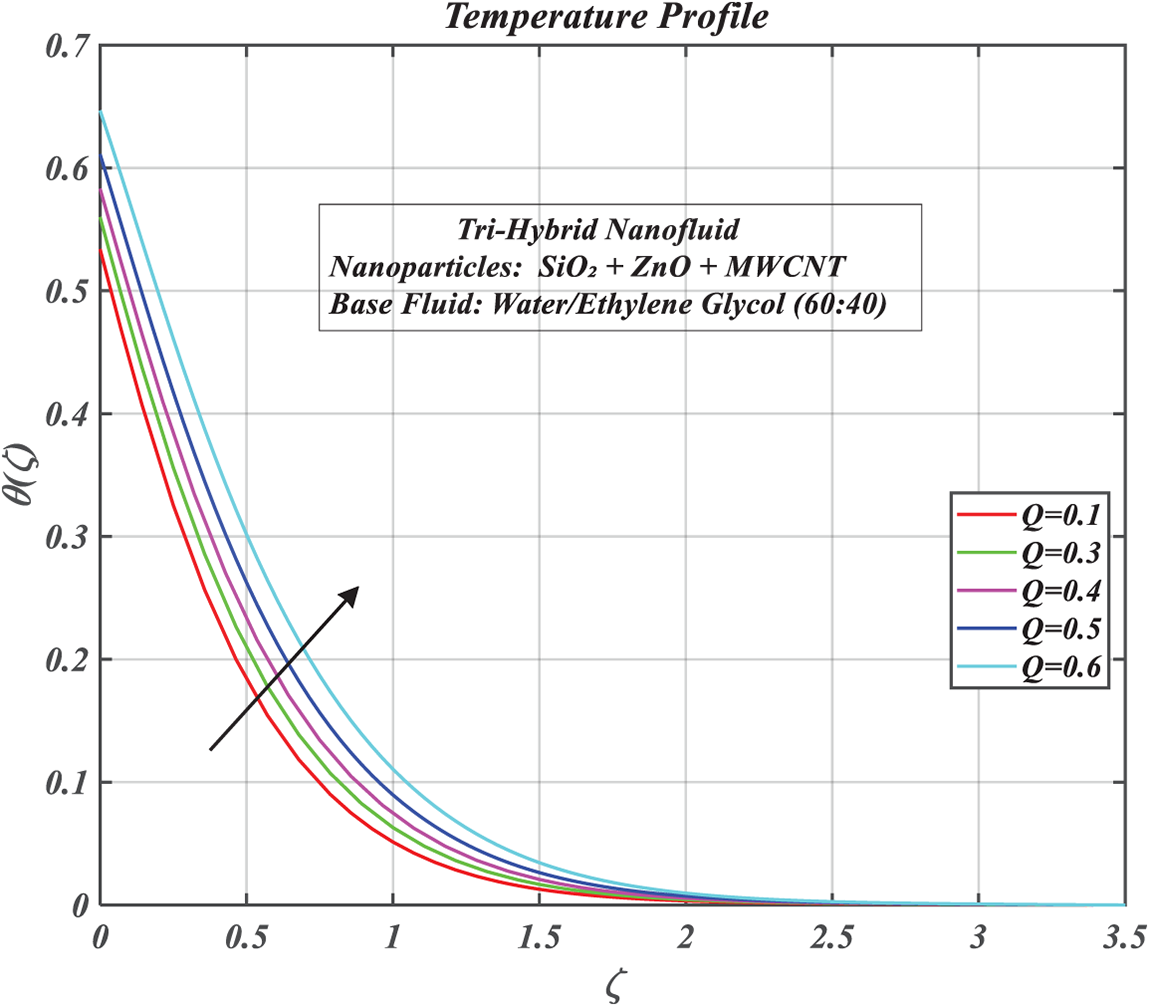
Figure 7: Consequences of suction parameter on θ(ζ)

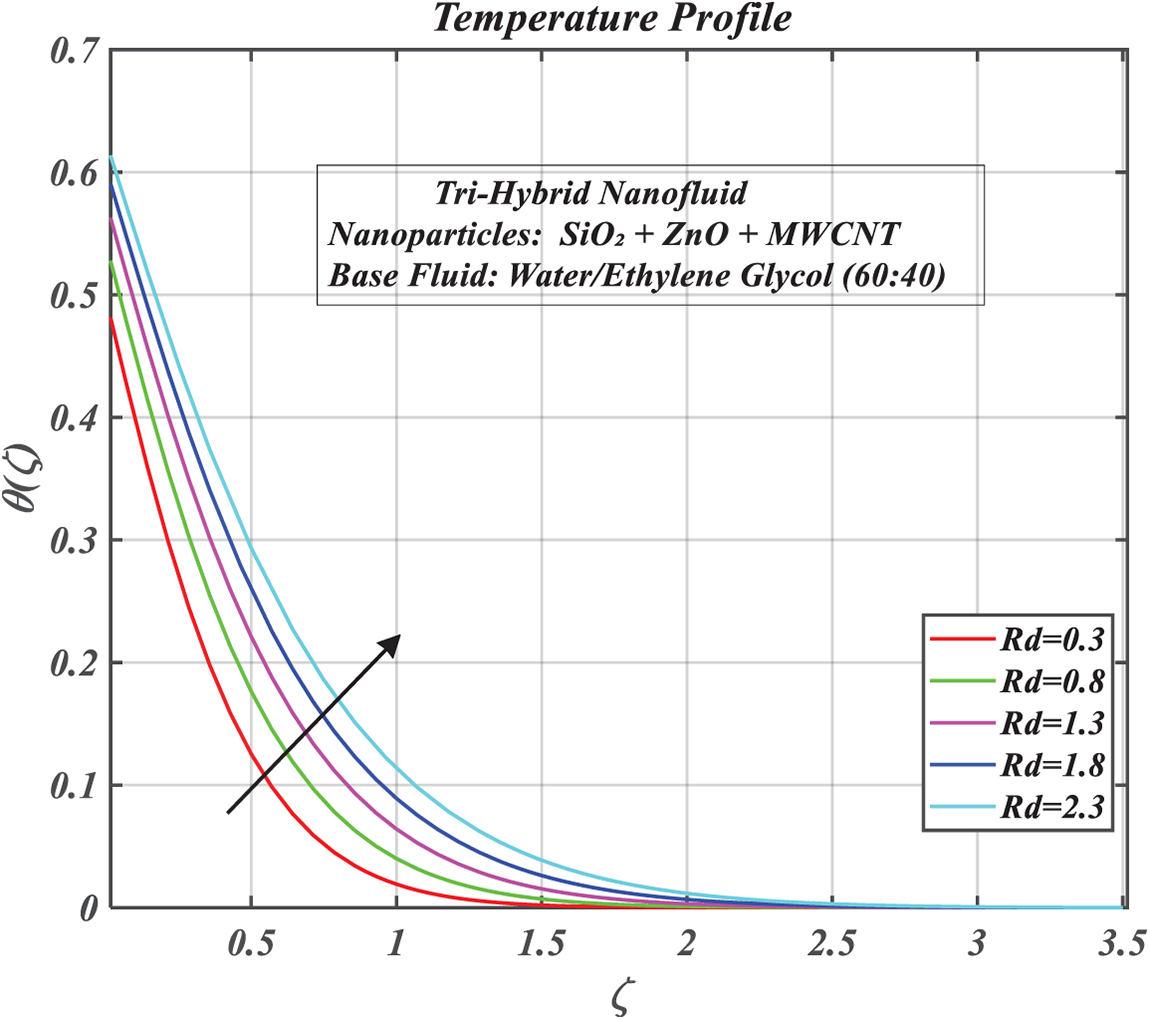
Figure 8: Consequences of thermal radiation on θ(ζ)

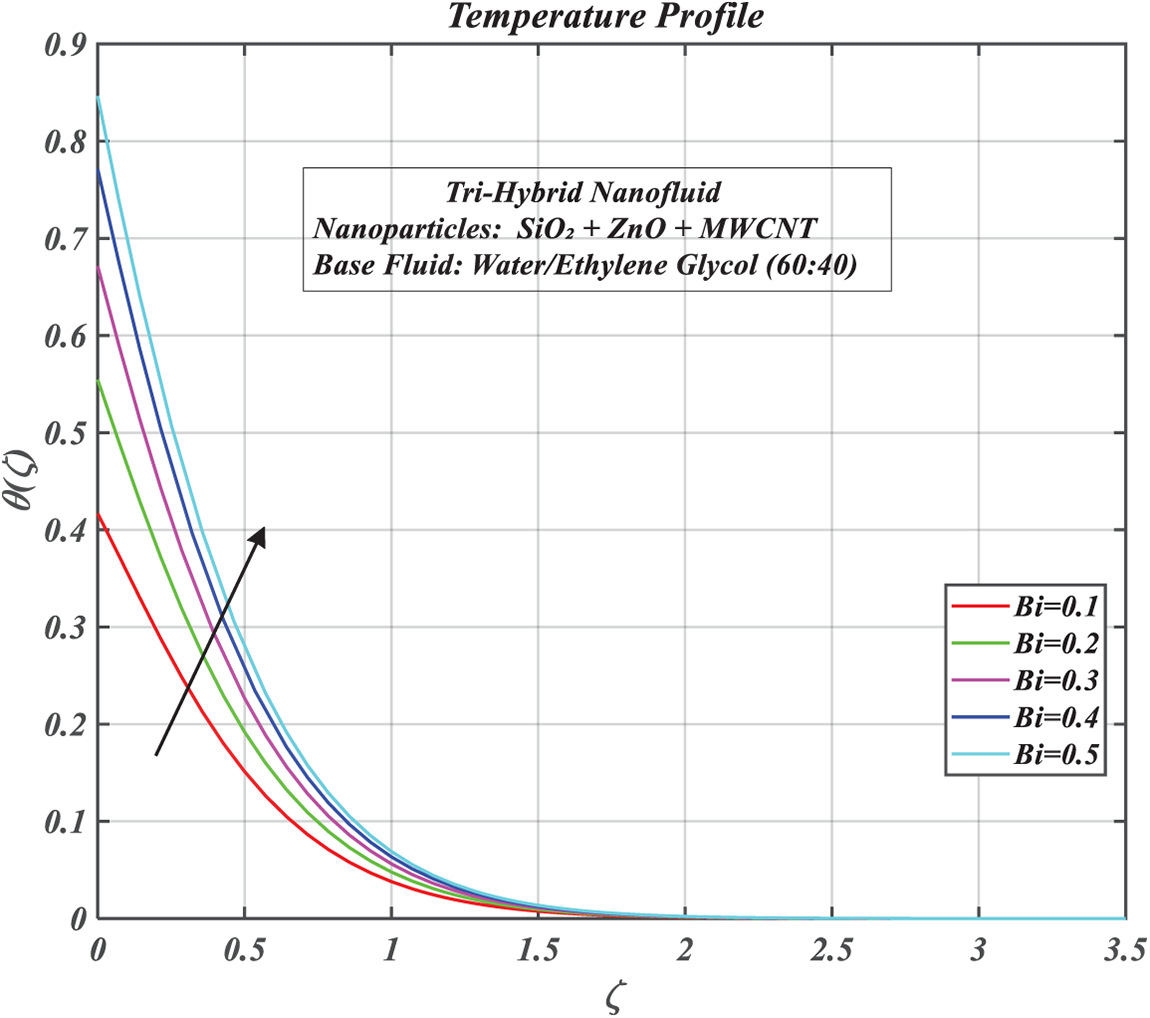
Figure 9: Consequences of Biot number on θ(ζ)

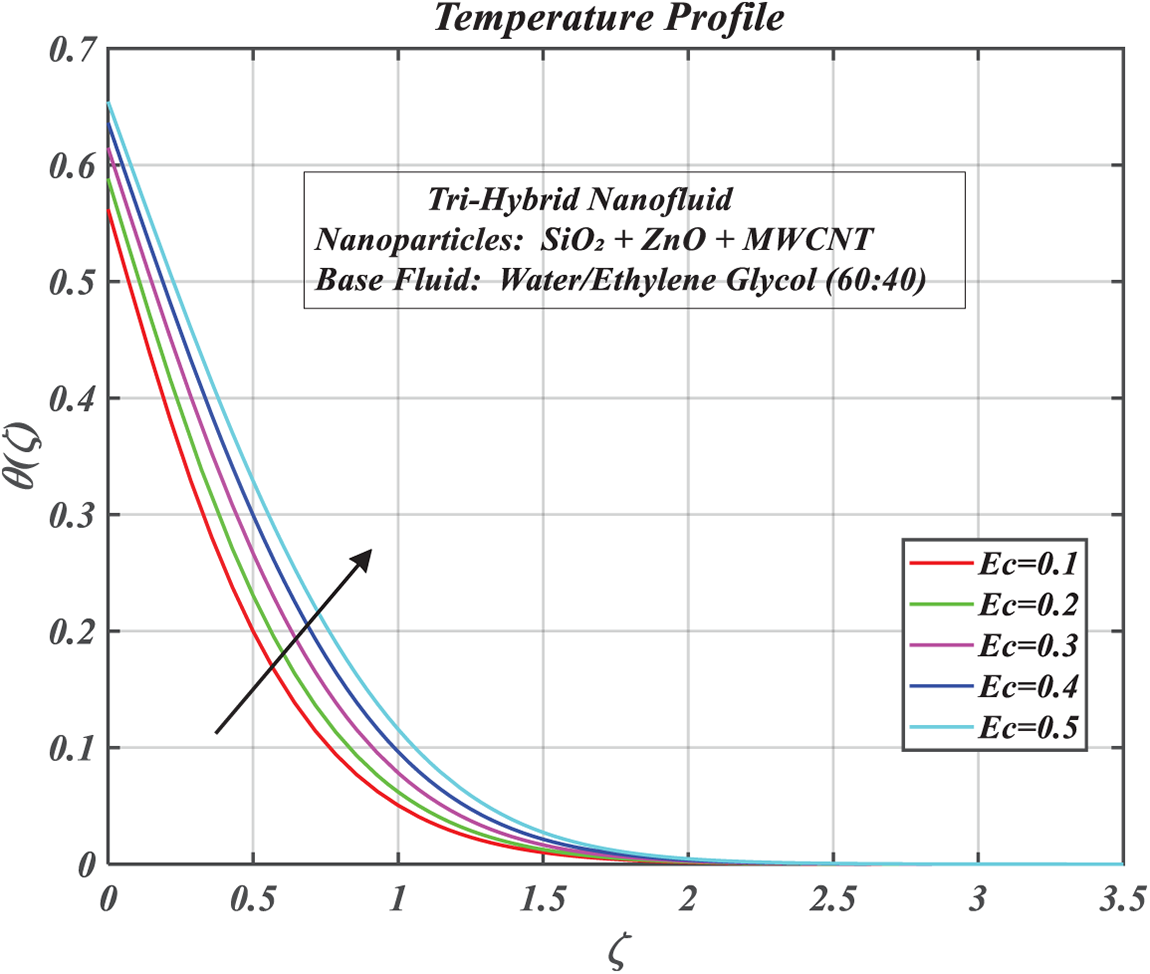
Figure 10: Consequences of Eckert number on θ(ζ)

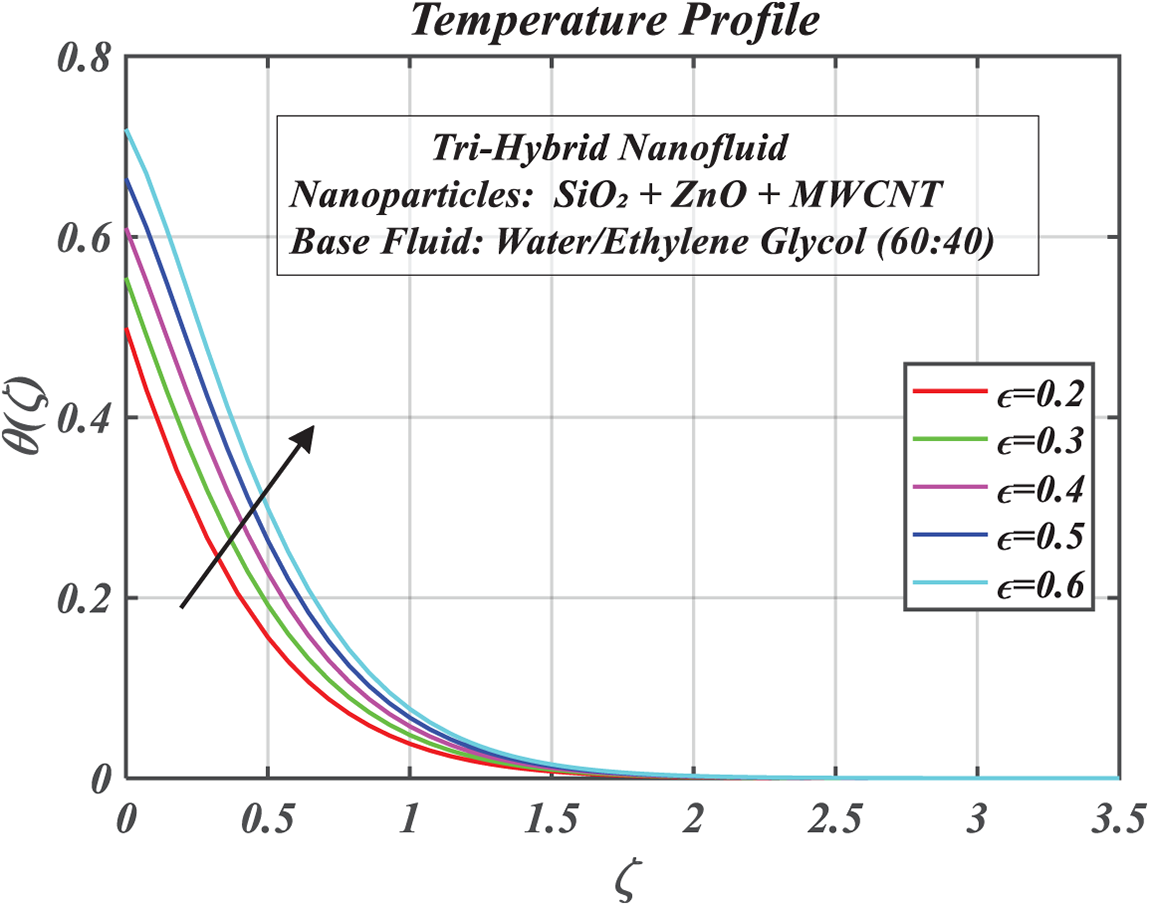
Figure 11: Consequences of thermal conductivity on θ(ζ)

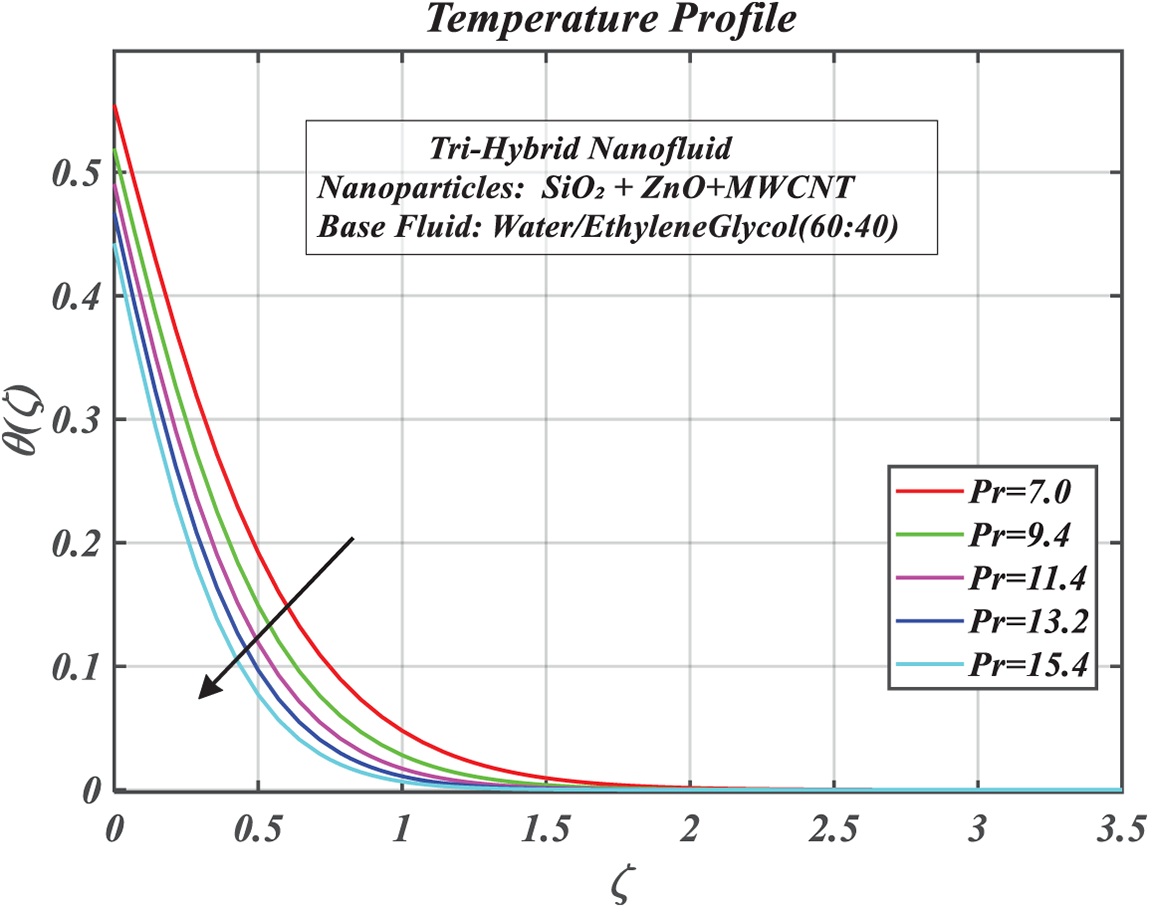
Figure 12: Consequences of Prandtl number on θ(ζ)

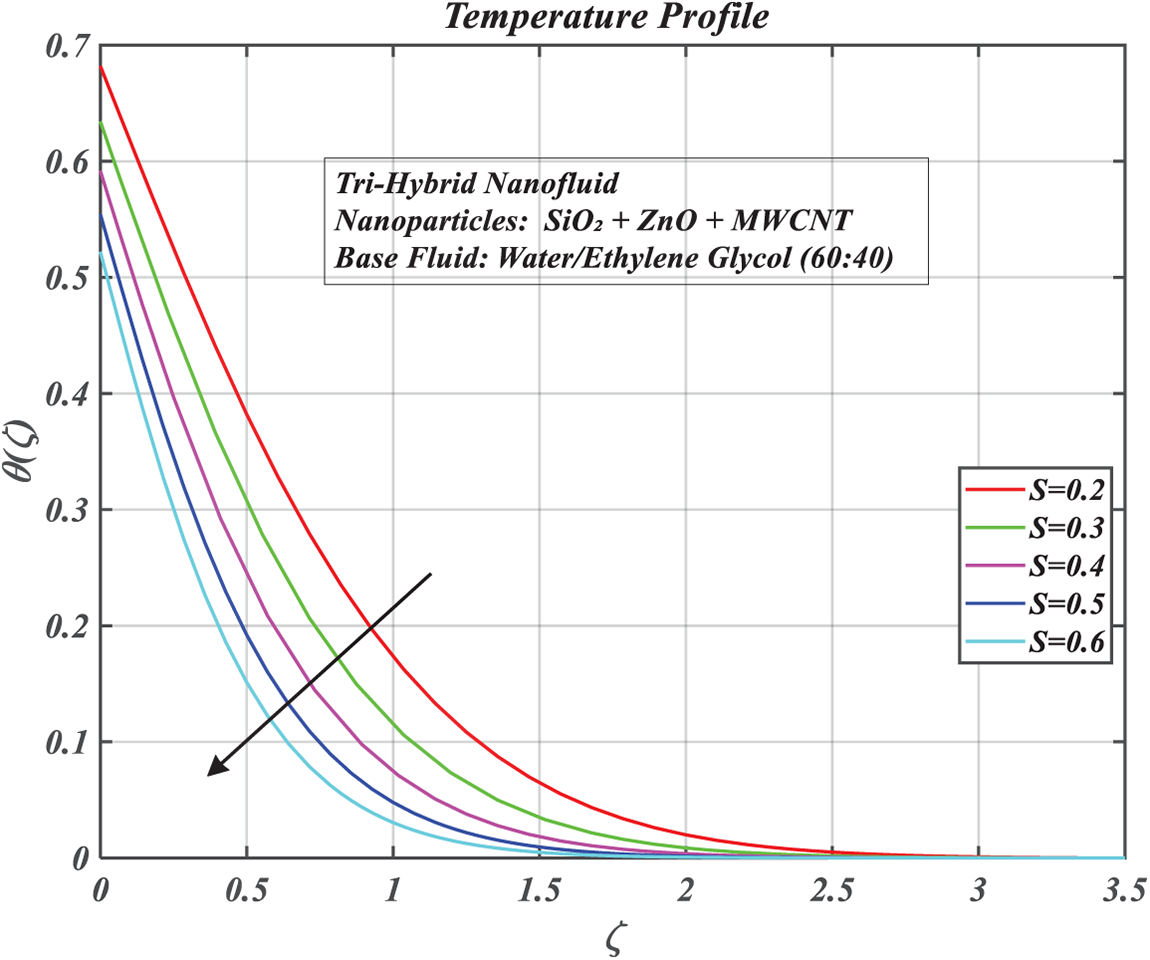
Figure 13: Consequences of the sSuction parameter on θ(ζ)

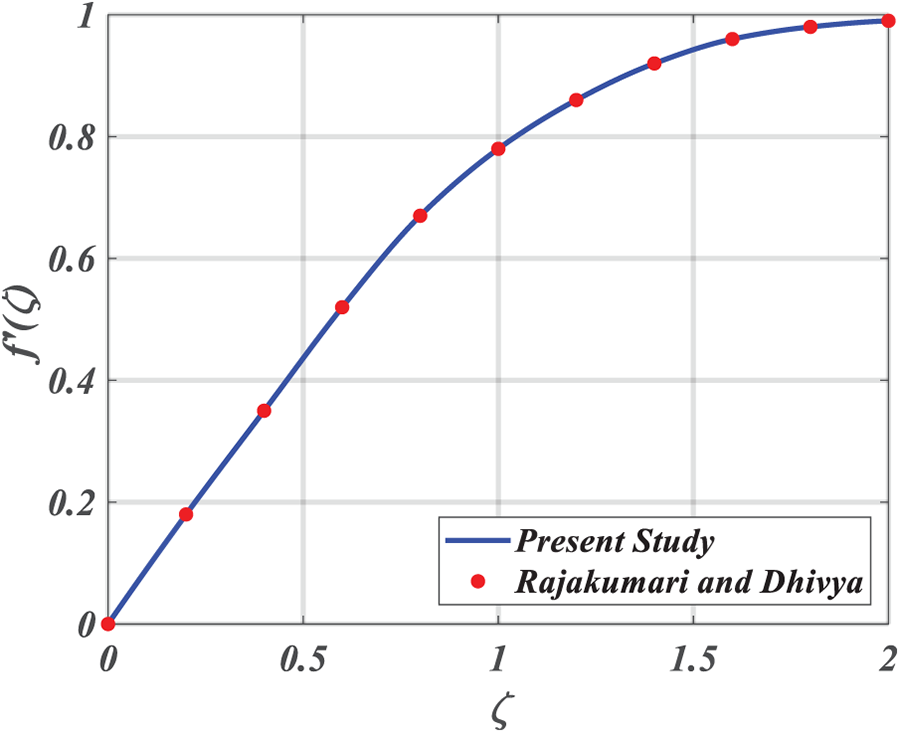
Figure 14: Velocity profile comparison between the present study and the benchmark results by Rammoorthi and Mohanavel

4.1 Influence of Various Parameters on the Velocity Profile

The impact of (0.2≤Z≤0.6) on the velocity distribution f′(ζ) is depicted in Fig. 3. The magnetic field between the plates is strengthened as Z is increased. The stronger magnetic effect between the plates drives the fluid flow. The performance of Riga plates will resemble that of a regular channel when Z goes back to zero. The Hartmann number greatly influences the velocity profile in the presence of a magnetic field. The interaction between electromagnetic and viscous forces, whose relative intensity is measured by the Hartmann number, is where the physical relevance is found. Therefore, it may be possible to effectively use the increased magnetism between the plates to speed up the flow in the squeezing phase. As a result, if Z disappears, velocities are reduced, and the Riga plates become normal plates.

The effect of the suction parameter (0.2≤S≤0.6) can be seen in Fig. 4, one can notice that as the suction rises, the overall fluid velocity upsurges. The act of sucking a fluid in, or suction, has a large influence on flow behaviour and velocity profiles. Faster fluid flow close to the surface is usually the result of decreasing the thickness of the boundary layer (BL) and increasing the velocity gradient at the surface of the plate. The boundary layer is thinned by suction, which removes fluid close to the surface. Because of the suction, the velocity profile steepens at the surface, indicating that the fluid is travelling more quickly toward the wall than it would in a suction-free situation. Even if the velocity increases close to the wall, if the suction is high, the total velocity profile may be lower farther from the wall.

The impact of a porous parameter (0.1≤λ≤1.7) on a velocity profile is seen in Fig. 5. The porosity characteristic reduces fluid velocity in the velocity profile. Generally speaking, a higher porosity parameter (which signifies greater permeability of the porous material) results in higher drag force, which lowers velocity.

The volume fraction (0.00≤ϕ1,ϕ2,ϕ3≤0.12) of SiO2, ZnO, and MWCNT nanoparticles dominate the velocity field as seen in Fig. 6. As volume fractions grow, disturbances like eddies and flow separations seen to be more noticeable. The volume percentage of nanoparticles in a fluid usually reduces the velocity profile, owing to the higher viscosity and friction induced by the nanoparticles. Essentially, the nanoparticles thicken the fluid and increase its resistance to flow, slowing it down.

4.2 Influence of Various Parameters on the Temperature Profile

The effect of the heat source parameter on the thermal field θ(ζ) is portrayed in Fig. 7. The thermal boundary layer expands as the fluid temperature increases as a result of a heat source. Temperature intensifies the thermal energy added due to heat sources. Thermal energy is introduced into a system via a heat source, such as a resistor that dissipates electrical power. This energy raises the molecules’ kinetic energy, which raises the thermal effect and causes the thermal boundary layer to grow.

The effect of the thermal radiation parameter, (0.3≤Rd≤2.3), on the thermal distribution, θ(ζ), across the gap is shown in Fig. 8. The dimensionless heat equation Eq. (10) in the increased thermal diffusion term includes the parameter Rd. It specifies how much heat transport from thermal radiation and thermal conduction contributes to each other. The contribution of heat radiation disappears with Rd=0. Thermal radiation becomes more and more dominant over thermal conduction when Rd>1. In traditional boundary layer flows, this would result in increased flow energy and temperature, but in the existing model, raising the radiation parameter has the reverse effect. The decreasing temperatures linked to a larger radiation heat flow impact are caused by the squeezing effect, which suppresses thermal diffusion. The decline of temperature between the two Riga plates is almost linear when unidirectional radiative flux is not present. However, the connection gets increasingly nonlinear as the radiative influence increases, especially toward the downside Riga plate.

The impact of thermal Biot number, (0.1≤Bi≤0.5), on temperature profiles, θ(ζ), is seen in Fig. 9. This quantity, which is a variation of the traditional thermal Biot number, appears in the boundary conditions at the bottom Riga plate. Physically speaking, when this value is less than 0.2, it indicates that temperature gradients are minimal within the lower Riga plate and that heat conduction there is substantially quicker than heat convection outside of it. This is in line with the “thermally thin” situation. The “thermally thick” situation occurs when Bi>0.2, meaning that thermal conduction within the downside Riga plate proceeds at a significantly slower rate than thermal convection far from its plate into the pierced flow regime. The temperature across the gap significantly rises as Boit number increases. Increased thermal convection warms the flow, resulting in higher convection from the downside Riga plate to the squeezing regime.

Fig. 10 demonstrates the impact of the Eckert number (0.1≤Ec≤0.5), i.e., energy dissipation parameter effects on thermal profiles θ(ζ). The relative contribution of kinetic energy dissipated to the boundary layer (BL) enthalpy difference is represented by the Eckert number. Viscous dissipation is assumed to be zero for Ec≈0. A higher temperature is the outcome of a gradually larger conversion of kinetic energy to heat as Ec rises. This conversion mostly occurs through viscous dissipation, in which the flow’s mechanical energy is converted to heat, raising the temperature due to frictional forces between the walls and the fluid.

The transport of heat to the fluid is influenced by varied thermal conductivity (0.2≤ε≤0.6), as seen in Fig. 11. Higher thermal conductivity areas of the fluid will heat faster and subsequently radiate heat to the fluid’s cooler areas. It also lessens the fluid’s internal temperature gradients. This is because the fluid’s parts with higher thermal conductivity act as temperature sinks, taking up heat from the hotter segments and transferring it to the colder ones.

The inspiration of the Prandtl number (7.0≤Pr≤15.4) on θ(ζ) is demonstrated in Fig. 12. The fluid’s momentum diffusivity and thermal diffusivity are related by the Prandtl number Pr. Thus, the fluid flow with a greater Pr has low thermal diffusivity, which causes the temperature gradient to steepen and decrease. Designing thermal systems i.e., heat exchangers, requires particular nanofluids with variable Pr values to ensure optimal thermal performance.

The inspection of suction parameter, (0.2≤S≤0.6), on the thermal distribution θ(ζ) can be noticed in Fig. 13. The Temperature often fall when a fluid is drawn into a porous media by suction. In particular, raising the suction parameter lowers the temperature and may also lower the local skin friction coefficient and heat flow. In a physical sense, suction cools the system by removing heat.

4.3 Validation

The present analysis is benchmarked against the study by Rammoorthi and Mohanavel [27] by employing parameter values consistent with their work. The reliability of the results is validated through the graphical comparisons presented in Figs. 14 and 15. As shown in Table 2, the skin friction coefficient and Nusselt number exhibit sensitivity to various dimensionless parameters. Specifically, both (Rex)1/2Cf and (Rex)−1/2Nux increase with higher values of Z,λ,ϕ1,ϕ2,ϕ3, and M while they decline with increasing b. Conversely, parameters such as Ec,Rd, and ε exert a negligible effect on skin friction. The Nusselt number increases with Rd and decreases with both Ec and ε. These observed patterns offer critical insights into the influence of physical parameters on thermal transport behaviour.

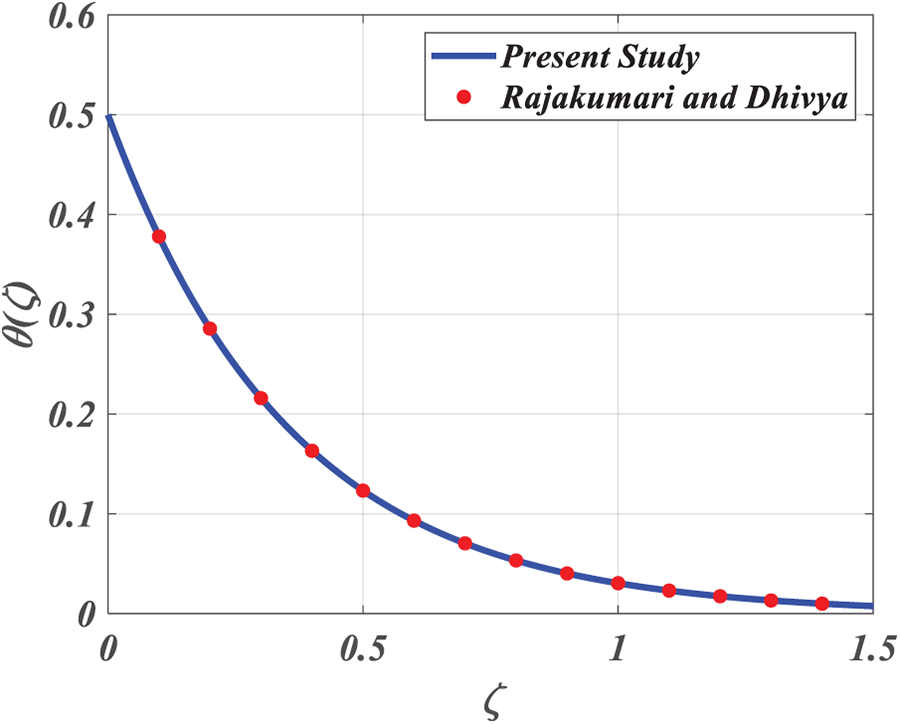
Figure 15: Temperature profile comparison between the present study and the benchmark results by Rammoorthi and Mohanavel

4.4 Streamlines

In this section, 3D surface plots against various flow factors are illustrated in Figs. 16 and 17. The following 3D surface plots show how in a magnetohydrodynamic tri-hybrid nanofluid flow system, the local Nusselt number (Nu) as well as the local Skin Friction Coefficient (Cf) are affected by M and ϕ that are magnetic parameter and nanoparticle volume fraction, respectively. Nu grows linearly with the growth of M and the nanoparticle volume fraction ϕ. Nu increases from around 2.7 to 5.3 at M=0.5 when ϕ is increased from 0 to 0.1. Nu rises from approximately 2.7 to 5.2 when M is increased from 0.5 to 2.5 at ϕ=0. Thermal conductivity is improved by a higher nanoparticle concentration. Increasing M improves flow stability, which raises the effectiveness of heat transfer. Cf grows with magnetic parameter M and volume fraction ϕ, although at a smaller gradient than Nu. At M=0.5, Cf rises from approximately 1.5 to 2.3 as ϕ goes from 0 to 0.1. For constant ϕ=0, Cf rises from approximately 1.5 to 2.2 as M rises from 0.5 to 2.5. The generation of Lorentz force due to the magnetic field increases flow hinderance, resulting in increased skin friction. Nanoparticles thicken the boundary layer, resulting in more viscous effects.

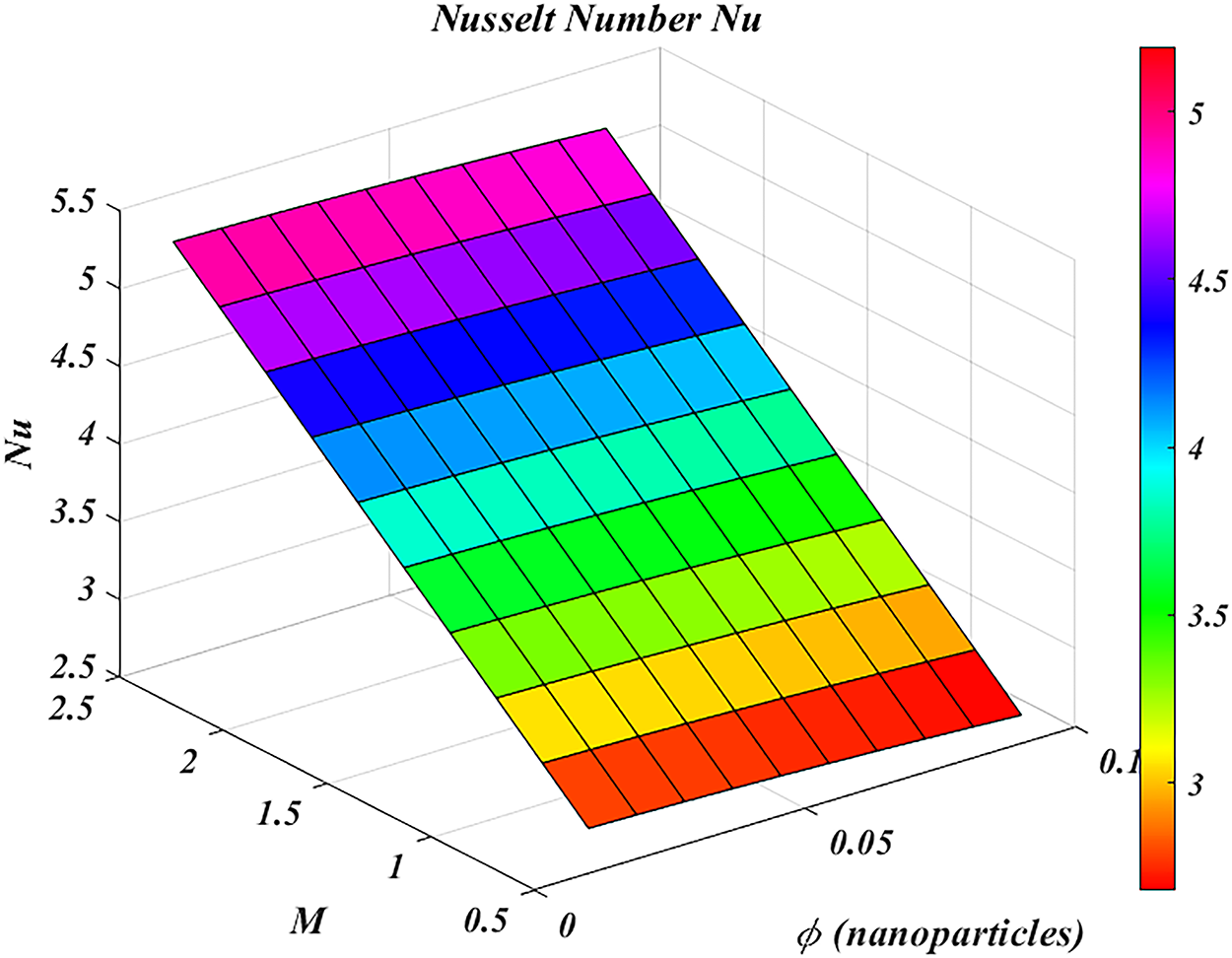
Figure 16: 3D surface plots of M and ϕ against Nusselt number

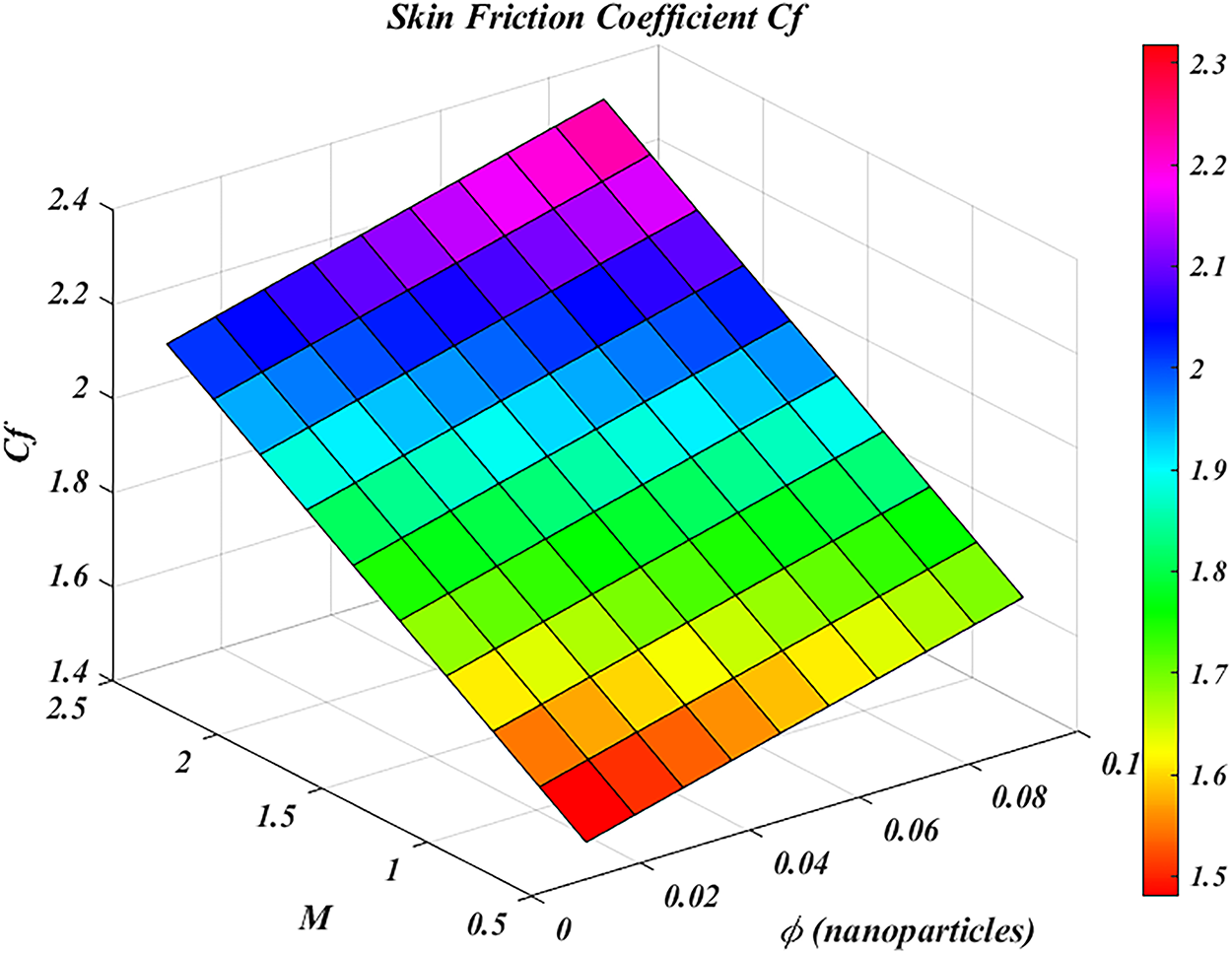
Figure 17: 3D surface plots of M and ϕ against skin friction coefficient

5  Conclusion

The fluid transport and thermal properties of nanofluids between horizontal, parallel Riga plates are examined in this work, when magnetic fields and radiative impacts are present. A scrutiny of a time-dependent(unsteady), squeezing flow of tri-hybrid nanofluid (SiO2+ZnO+MWCNT/Water−EthylGlycol,(60:40)) between two parallel plates is presented in this article. The study considers the impacts of thermal radiation, the suction effect, viscosity dissipation, and the heat source. Using the similarity transformation approach, the leading system of connected nonlinear partial differential equations PDEs was transformed into a system of ODEs. These equations were then numerically solved using the shooting technique together with the Bvp4c approach. The following is a list of the investigation’s noteworthy findings.

•   The enrichment of Hartmann number (Z) results in increased fluid flow, indicating the significant impact of magnetohydrodynamics on fluid flow.

•   Raising the suction parameter enhances the flow field but reduces the temperature profile of the used tri-hybrid nanofluid.

•   Water-Ethyl Glycol (60:40) based nanofluids containing Silicon dioxide (SiO2), zinc oxide (SiO2), and multiwall carbon nanotubes (MWCNTs) nanoparticles improve heat transport efficiency and also the reliability of the system.

•   Higher values of Rd and ε make an increase in the thermal profile. They pointedly enhance the thermal distribution and the thermal effect within the system.

•   A combined investigation through streamline plots reveals quantifiable changes in Nu and Cf due to ϕ and M. The streamlined behaviour shows that raising ϕ improves thermal mixing and heat transmission, whereas increasing M causes Lorentz forces that reduce flow velocity. Higher ϕ increases the Nusselt number, while higher M decreases it and increases skin friction.

This work offers a new numerical investigation of ternary hybrid nanofluid flow in a Riga plate-based squeezing system, although it has certain drawbacks. Only two-dimensional, laminar, and incompressible flow with simplified boundary conditions is included in the study; turbulence, surface roughness, and geometric imperfections are not taken into account. The impacts of temperature variations, nanoparticle clumping, and interparticle forces are also ignored, as it is assumed that the thermophysical characteristics of the nanofluid stay constant. Furthermore, a streamlined Riga plate configuration with homogeneous fields is used to model the electromagnetic effects, which may not fully represent actual situations.

Furthermore, the lack of experimental validation means that the findings remain speculative. These simplifications, while required for tractability, limit the findings’ direct application to complicated practical systems. Future research could address these constraints by expanding the model to include three-dimensional geometries, experimental benchmarks, and non-ideal effects like slip conditions, temperature-dependent characteristics, and turbulence modelling.

Acknowledgement: The authors are grateful to King Saud University, Riyadh, Saudi Arabia, for funding this work through the Ongoing Research Funding program—Research Chairs (ORF-RC-2025-0127). Furthermore, this study is supported via Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R443), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Funding Statement: This research was funded by King Saud University, Riyadh, Saudi Arabia, through the Ongoing Research Funding program—Research Chairs (ORF-RC-2025-0127). Furthermore, this research was funded via Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R443).

Author Contributions: Conceptualization, Muhammad Hamzah and Muhammad Ramzan; methodology, Muhammad Ramzan; software, Muhammad Hamzah; validation, Muhammad Hamzah, Muhammad Ramzan, Abdulrahman A. Almehizia, and Ibrahim Mahariq; formal analysis, Laila A. AL-Essa; investigation, Ahmed S. Hassan; resources, Abdulrahman A. Almehizia and Ahmed S. Hassan; data curation, Ibrahim Mahariq and Laila A. AL-Essa; writing—original draft preparation, Muhammad Hamzah and Muhammad Ramzan; writing—review and editing, Muhammad Hamzah and Muhammad Ramzan; visualization, Laila A. AL-Essa; supervision, Ahmed S. Hassan. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author upon reasonable request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

1. Smalley RE. Future global energy prosperity: the terawatt challenge. Mrs Bull. 2005;30(6):412–7. doi:10.1557/mrs2005.124. [Google Scholar] [CrossRef]

2. Wen D, Lin G, Vafaei S, Zhang K. Review of nanofluids for heat transfer applications. Particuology. 2009;7(2):141–50. doi:10.1016/j.partic.2009.01.007. [Google Scholar] [CrossRef]

3. Huminic G, Huminic A. Hybrid nanofluids for heat transfer applications-a state-of-the-art review. Int J Heat Mass Transf. 2018;125:82–103. doi:10.1016/j.ijheatmasstransfer.2018.04.059. [Google Scholar] [CrossRef]

4. Sidik NAC, Adamu IM, Jamil MM, Kefayati GHR, Mamat R, Najafi G. Recent progress on hybrid nanofluids in heat transfer applications: a comprehensive review. Int Commun Heat Mass Transf. 2016;78(1):68–79. doi:10.1016/j.icheatmasstransfer.2016.08.019. [Google Scholar] [CrossRef]

5. Sajid MU, Ali HM. Thermal conductivity of hybrid nanofluids: a critical review. Int J Heat Mass Transf. 2018;126:211–34. doi:10.1016/j.ijheatmasstransfer.2018.05.021. [Google Scholar] [CrossRef]

6. Raja M, Vijayan R, Dineshkumar P, Venkatesan M. Review on nanofluids characterization, heat transfer characteristics and applications. Renew Sustain Energy Rev. 2016;64(6):163–73. doi:10.1016/j.rser.2016.05.079. [Google Scholar] [CrossRef]

7. Jensen MK, Bergles AE, Shome B. The literature on enhancement of convective heat and mass transfer. J Enhanc Heat Transf. 1997;4(1):1–6. doi:10.1615/jenhheattransf.v4.i1.10. [Google Scholar] [CrossRef]

8. Manglik RM. Heat transfer enhancement. In: Heat transfer handbook. Hoboken, NJ, USA: Wiley, Inc.; 2003. p. 1029–130. [Google Scholar]

9. Alam T, Kim MH. A comprehensive review on single phase heat transfer enhancement techniques in heat exchanger applications. Renew Sustain Energy Rev. 2018;81:813–39. doi:10.1016/j.rser.2017.08.060. [Google Scholar] [CrossRef]

10. Xuan Y, Li Q. Heat transfer enhancement of nanofluids. Int J Heat Fluid Flow. 2000;21(1):58–64. doi:10.1016/s0142-727x(99)00067-3. [Google Scholar] [CrossRef]

11. Guo ZY, Li DY, Wang BX. A novel concept for convective heat transfer enhancement. Int J Heat Mass Transf. 1998;41(14):2221–5. doi:10.1016/s0017-9310(97)00272-x. [Google Scholar] [CrossRef]

12. Kakaç S, Bergles AE, Mayinger F, Yüncü H, editors. Heat transfer enhancement of heat exchangers. Vol. 355. New York, NY, USA: Springer Science & Business Media; 2013. [Google Scholar]

13. Sundar LS, Sharma KV, Singh MK, Sousa ACM. Hybrid nanofluids preparation, thermal properties, heat transfer and friction factor—a review. Renew Sustain Energy Rev. 2017;68(3):185–98. doi:10.1016/j.rser.2016.09.108. [Google Scholar] [CrossRef]

14. Muneeshwaran M, Srinivasan G, Muthukumar P, Wang CC. Role of hybrid-nanofluid in heat transfer enhancement-a review. Int Commun Heat Mass Transf. 2021;125(8):105341. doi:10.1016/j.icheatmasstransfer.2021.105341. [Google Scholar] [CrossRef]

15. Eshgarf H, Kalbasi R, Maleki A, Shadloo MS. A review on the properties, preparation, models and stability of hybrid nanofluids to optimize energy consumption. J Therm Anal Calorim. 2021;144(5):1959–83. doi:10.1007/s10973-020-09998-w. [Google Scholar] [CrossRef]

16. Sharma PO, Barewar SD, Chougule SS. Experimental investigation of heat transfer enhancement in pool boiling using novel Ag/ZnO hybrid nanofluids. J Therm Anal Calorim. 2021;143(2):1051–61. doi:10.1007/s10973-020-09922-2. [Google Scholar] [CrossRef]

17. Prashar P, Ojjela O. Numerical investigation of ZnO-MWCNTs/ethylene glycol hybrid nanofluid flow with activation energy. Indian J Phys. 2022;96(7):2079–92. doi:10.1007/s12648-021-02132-y. [Google Scholar] [CrossRef]

18. Ekiciler R. Performing SiO2-MWCNT/water hybrid nanofluid with differently shaped nanoparticles to enhance first-and second-law features of flow by considering a two-phase approach. J Therm Anal Calorim. 2024;149(4):1725–44. doi:10.1007/s10973-024-12885-3. [Google Scholar] [CrossRef]

19. Mahabaleshwar US, Nihaal KM, Pérez LM, Oztop HF. An analysis of heat and mass transfer of ternary nanofluid flow over a Riga plate: newtonian heating. Numer Heat Transf Part B Fundam. 2025;86(2):310–25. doi:10.1080/10407790.2023.2282165. [Google Scholar] [CrossRef]

20. Farooq U, Bibi A, Abbasi JN, Jan A, Hussain M. Nonsimilar mixed convection analysis of ternary hybrid nanofluid flow near stagnation point over vertical Riga plate. Multidiscip Model Mater Struct. 2024;20(2):261–78. doi:10.1108/mmms-09-2023-0301. [Google Scholar] [CrossRef]

21. Abbas Z, Mahmood I, Batool S, Shah SAA, Ragab AE. Evaluation of thermal radiation and flow dynamics mechanisms in the Prandtl ternary nanofluid flow over a Riga plate using artificial neural networks: a modified Buongiorno model approach. Chaos Soliton Fract. 2025;193(2):116083. doi:10.1016/j.chaos.2025.116083. [Google Scholar] [CrossRef]

22. Ramzan M, Ali F, Akkurt N, Saeed A, Kumam P, Galal AM. Computational assesment of Carreau ternary hybrid nanofluid influenced by MHD flow for entropy generation. J Magn Magn Mater. 2023;567(1):170353. doi:10.1016/j.jmmm.2023.170353. [Google Scholar] [CrossRef]

23. Gangadhar K, Sangeetha Rani M, Wakif A. Improved slip mechanism and convective heat impact for ternary nanofluidic flowing past a riga surface. Int J Mod PhysB. 2025;39(8):2550064. doi:10.1142/s021797922550064x. [Google Scholar] [CrossRef]

24. Karthikeyan S, Ali F, Loganathan K, Thamaraikannan N. An implication of entropy generation in Maxwell fluid containing engine oil based ternary hybrid nanofluid over a riga plate. J Taibah Univ Sci. 2024;18(1):2387925. doi:10.1080/16583655.2024.2387925. [Google Scholar] [CrossRef]

25. Sharif H, Ali B, Siddique I, Saman I, Jaradat MM, Sallah M. Numerical investigation of dusty tri-hybrid Ellis rotating nanofluid flow and thermal transportation over a stretchable Riga plate. Sci Rep. 2023;13(1):14272. doi:10.1038/s41598-023-41141-1. [Google Scholar] [PubMed] [CrossRef]

26. Thakur A, Sood S. Tri-hybrid nanofluid flow towards convectively heated stretching Riga plate with variable thickness. J Nanofluids. 2023;12(4):1129–40. doi:10.1166/jon.2023.1990. [Google Scholar] [CrossRef]

27. Rammoorthi R, Mohanavel D. Numerical investigation and sensitivity analysis of MHD ternary nanofluid flow between perforated squeezed Riga plates under the surveillance of microcantilever sensor. AIP Adv. 2024;14(9):95020. doi:10.1063/5.0218608. [Google Scholar] [CrossRef]

28. Algehyne EA, Alduais FS, Saeed A, Dawar A, Ramzan M, Kumam P. Framing the hydrothermal significance of water-based hybrid nanofluid flow over a revolving disk. Int J Nonlinear Sci Numer Simul. 2024;24(8):3133–48. doi:10.1515/ijnsns-2022-0137. [Google Scholar] [CrossRef]

29. Chung SY, Brinza DE, Minton TK, Liang RH. BMDO materials testing in the EOIM-3 experiment. In: NASA Conference Publication. Washington, DC, USA: NASA; 1993. [Google Scholar]

30. Rana S, Zahid H, Kumar R, Bharj RS, Rathore PKS, Ali HM. Lithium-ion battery thermal management system using MWCNT-based nanofluid flowing through parallel distributed channels: an experimental investigation. J Energy Storage. 2024;81(2023):110372. doi:10.1016/j.est.2023.110372. [Google Scholar] [CrossRef]

31. Sreekumar S. Performance enhancement of photovoltaic/thermal system using hybrid nanofluid [dissertation]. Northern Ireland, UK: Ulster University; 2023. [Google Scholar]

32. Moita A, Moreira A, Pereira J. Nanofluids for the next generation thermal management of electronics: a review. Symmetry. 2021;13(8):1362. doi:10.3390/sym13081362. [Google Scholar] [CrossRef]

33. Wciślik S. The influence of nusselt correlation on exergy efficiency of a plate heat exchanger operating with TiO2: SiO2/EG:DI hybrid nanofluid. Inventions. 2024;9(1):11. doi:10.3390/inventions9010011. [Google Scholar] [CrossRef]

34. Khaled AR, Vafai K. Hydromagnetic squeezed flow and heat transfer over a sensor surface. Int J Eng Sci. 2004;42(5–6):509–19. doi:10.1016/j.ijengsci.2003.08.005. [Google Scholar] [CrossRef]

35. Elsebaee FAA, Bilal M, Mahmoud SR, Balubaid M, Shuaib M, Asamoah JKK, et al. Motile micro-organism based trihybrid nanofluid flow with an application of magnetic effect across a slender stretching sheet: numerical approach. AIP Adv. 2023;13(3):35237. doi:10.1063/5.0144191/2881329. [Google Scholar] [CrossRef]

36. Muhammed RK, Basha H, Reddy GJ, Shankar U, Bég OA. Influence of variable thermal conductivity and dissipation on magnetic Carreau fluid flow along a micro-cantilever sensor in a squeezing regime. In: Waves in random and complex media. London, UK: Taylor & Francis; 2022. p. 1–30 doi:10.1080/17455030.2022.2139013. [Google Scholar] [CrossRef]

37. Venkateswarlu B, Chavan S, Woo Joo S, Kim SC. Entropy analysis in squeezing flow of CoFe2O4+TiO2+MgO/H2O trihybrid nanofluid between parallel plates with viscous dissipation and chemical reaction: a numerical approach. In: Numerical heat transfer, part A: applications. London, UK: Taylor & Francis; 2024. p. 1–30 doi:10.1080/10407782.2024.2375634. [Google Scholar] [CrossRef]

38. Loganathan K, Thamaraikannan N, Eswaramoorthi S, Jain R. Entropy framework of the bioconvective Williamson nanofluid flow over a Riga plate with radiation, triple stratification and swimming microorganisms. Int J Thermofluids. 2025;25(5):101000. doi:10.1016/j.ijft.2024.101000. [Google Scholar] [CrossRef]

39. Eswaramoorthi S, Loganathan K, Choudhary P, Senthilvadivu K, Ahlawat A, Sivakumar M. Computational analysis of sutterby nanofluid with heat and mass convective conditions: a comparative study of Riga plate and stationary plate. Discov Appl Sci. 2025;7(3):1–24. doi:10.1007/s42452-025-06508-1. [Google Scholar] [CrossRef]

40. Akindele AO, Ogunsola AW, Zhiri AB, Ohaegbue AD, Obalalu AM, Salawu SO. Significance of Solar radiation and Cattaneo-Chistov heat flux on Maxwall tri-component hybrid nanofluid flow with heat generation and entropy analysis: application in drone technology. Hybrid Adv. 2025;11(6):100524. doi:10.1016/j.hybadv.2025.100524. [Google Scholar] [CrossRef]

41. Adebisi O, Ajala OA, Akindele AO, Okunade IO, Ohaegbue AD, Yahaya AA. Investigation of heat transfer in a radiative Casson triple particle nanofluid flow with Riga plate and variable thermo-physical characteristics. Nano-Struct Nano-Objects. 2025;42(8):101486. doi:10.1016/j.nanoso.2025.101486. [Google Scholar] [CrossRef]