Fractional Order Nonlinear Bone Remodeling Dynamics Using the Supervised Neural Network

1  Introduction

Remodeling is a procedure where the bone is constantly renewed across the skeleton. The bone formation methodology is sparsely heterogeneous using the common and sync cycles that can occur in various locations by using 5% to 25% based on the bone surface [1]. As a result, each skeleton part undergoes regular remodeling over time. Various aspects of bone renovation have been studied by using mathematical models. Michaelis-Menten investigated the dynamics based on the modelling of the OC activity (system through which OC break the bone) [2] along with the physiological stress that persuades the bone growth [3–6]. Many studies of bone metabolism based on the signal transduction models have been presented using the OC and osteoblasts (OB) [7]. The behavior of OC and OB in a cellular environment is recognized as a basic multicellular unit [8–12].

In this study, the numerical simulations of the myeloma bone disease have been discussed. Myeloma is one of the forms of hematological cancer, distinguished by the growth and division of the cancerous plasma cells. The evolution of the dangerous disease based on the osteolytic, bone pain, psychopathology breaks, osteoporosis, hyperglycemia, and spinal stenosis, is among the most common clinical symptoms of myeloma. Furthermore, the connection between the melanoma cells and the bone marrow systemic immune cells has been performed through the myeloma survival and growth [13,14].

The investigations of these actions are significant due to both primary bone tumors and metastatic, caused by the other types of cancer. In smooth extension procedures, prostate and breast cancers are notably recognized [15]. In tumor-induced osteolytic lesions, a process is not wholly obtained that promotes the OC bustle and changes the quantity of the OB [16,17]. However, the bone tissue attitude has been extensively studied to understand the phenomenon. Several theories about functional adaptation and many adaptive capacity models have been presented over the last few decades. The proposed models can be classified into the phenomenologist or monolithic. The mechanism is modeled by considering the initial and final states to focus on the mechanical variables, whereas deterministic models attempt to incorporate biological and biochemical processes into the model [18].

The biochemical procedures of the remodeling of bone can be emulated by using the computational and statistical systems, which are designed to allow the association with the healthy and pathophysiological bone actions. A differential system that correspond to the communication of OB and OC to simulate the consequences of paracrine and autocrine mechanisms. The dynamic response of these cell populations was calculated; as a result to determine the changes in bone during the remodeling cycles. A confined system for the tissue of healthy bone was first anticipated in [19], and it was later expanded in [20] to comprise the tumorous impact of several myeloma diseases along with the non-local approach with diffusion. Biological processes frequently exhibit anomalous spreading or viscoelasticity using fractional differential equations [21,22]. As a result, by including a fractional-order, existing models can be improved [23,24]. Numerous biological tissues have thus been sufficiently explained, e.g., the human respiratory system [25] and the movement of sap in leaves [26]. Although not trivial, it is vital to show a geometrical or physical perception of the resulting differential equations [27]. Bone remodeling demonstrates anomalous dissemination in the case under consideration. On the other hand, many underlying mechanisms, show fractional-order behavior that varies over time or space [28,29]. Instead of myeloma, the referred models have been seen to understand the osteolytic metastatic bone environment better.

The effects of cancer growth are based on bone remodeling, which indicates specifically to check the influence of tumor and paracrine signaling in bone resorption and OB cells. Autocrine signaling is the reaction from OCs and OBs that regulates their formation. The factors produced by OCs that control OB formation are referred to as paracrine signaling. The mathematical form of the bone remodeling is provided in the absence of cancer and further investigations [30–32]. In this nonlinear system with no exact space proportions, a dependent form of the variable tracks the bone mass over time. One spatial dimension is mentioned by interpreting the bone mass equation as one of the localized trabecular masses (spongy bone found within the bone marrow) beneath a point on the bone’s surface.

The fractional-order derivatives of regular and myeloma bone disease models based on the bone remodeling with tumor effects have been presented in this study by using the stochastic mathematical performances of the Levenberg-Marquardt backpropagation (LVMBP) neural networks (NN), i.e., LVMBPNN.

The paper is systematized as follows: Section 2 demonstrates the configuration of the fractional MDM mathematical form, Section 3 contains the information on the stochastic applications, Section 4 is explained the LVMBPNN method, and Section 5 contains the simulations procedures of the fractional MDM model. Finally, Section 6 is presented based on the concluding remarks.

2  Fractional Order Mathematical Bone Remodeling System

In this section, the presence of the myeloma disrupts the regular rotations of the system of normal bone. The tumor (cancer) parameters represent the usual cycles, cycles culminating, mostly damped fluctuations that combine the nontrivial stable position. The unknown form of the independent variables based on the tumor and bone remodeling model (TBRM) are C(t), B(t), and T(t) is tumor cell density. The MDM form of the mathematical system is given as [33]:

{dC(t)dt=−βCC(t)+αCB(t)gBC(1+rBCT(t)LT)C(t)gcc(1+rCCT(t)LT),C0=k1,dB(t)dt=−βBB(t)+αBC(t)(gCB1+rCBT(t)LT)B(t)(gBB−rBBT(t)LT),B0=k2,dT(t)dt=γTT(t)log⁡(LTT(t)).T0=k3.(1)

C0=k1, B0=k2, and T0=k3 are the initial conditions (ICs). Eq. (1) shows the Gompertz tumor form with growth constant γT>0 with greater tumor size LT. γT has been assumed to be independent of osteoporosis. Models, biological tests, and simulations have been applied to find the γT dependence. The tumor measures rBC, rCC, rCB, and rBB are all nonnegative in the system (1). The presence of tumor changes (1) is as follows: autocrine advancement of OCs increases (gcc(1+rCCT(t)LT)>0,sincegCC>0); paracrine suppression of OCs decreases (gCB1+rCBT(t)LT)<gCB, since gCB>0), paracrine advancement of OBs decreases (−gBC>−gBC(1+rBCT(t)LT), since gBC>0); and autocrine promotion of OBs decreases (gBB−rBBT(t)LT<gBB, since gBB>0). A major distinction between the mathematical model and the extension of term T(t)LT, which connects the tumor density and maximum length to the power laws for the OC/OB contacts (1).

The numerical studies of the fractional MBD model based on the bone remodeling with the tumor effects (1) have been provided in the current study by using the artificial intelligence (AI) together with the configuration of LVMBPNN [34–41]. Furthermore, the fractional MBD model has been designed to present the analysis of super slow evolvement and superfast progressions by substituting the ordinary integer order derivation in the set of Eq. (1) with fractional orders.

{dτC(t)dtτ=−βCC(t)+αCB(t)gBC(1+rBCT(t)LT)C(t)gcc(1+rCCT(t)LT),C0=k1,dτB(t)dtτ=−βBB(t)+αBC(t)(gCB1+rCBT(t)LT)B(t)(gBB−rBBT(t)LT),B0=k2,dτT(t)dtτ=γTT(t)log⁡(LTT(t)).T0=k3.(2)

This system, τ shows the fractional kind of derivative based on the MBD model. Tab. 1 shows the details of the parameter characterization based on the myeloma bone disease.

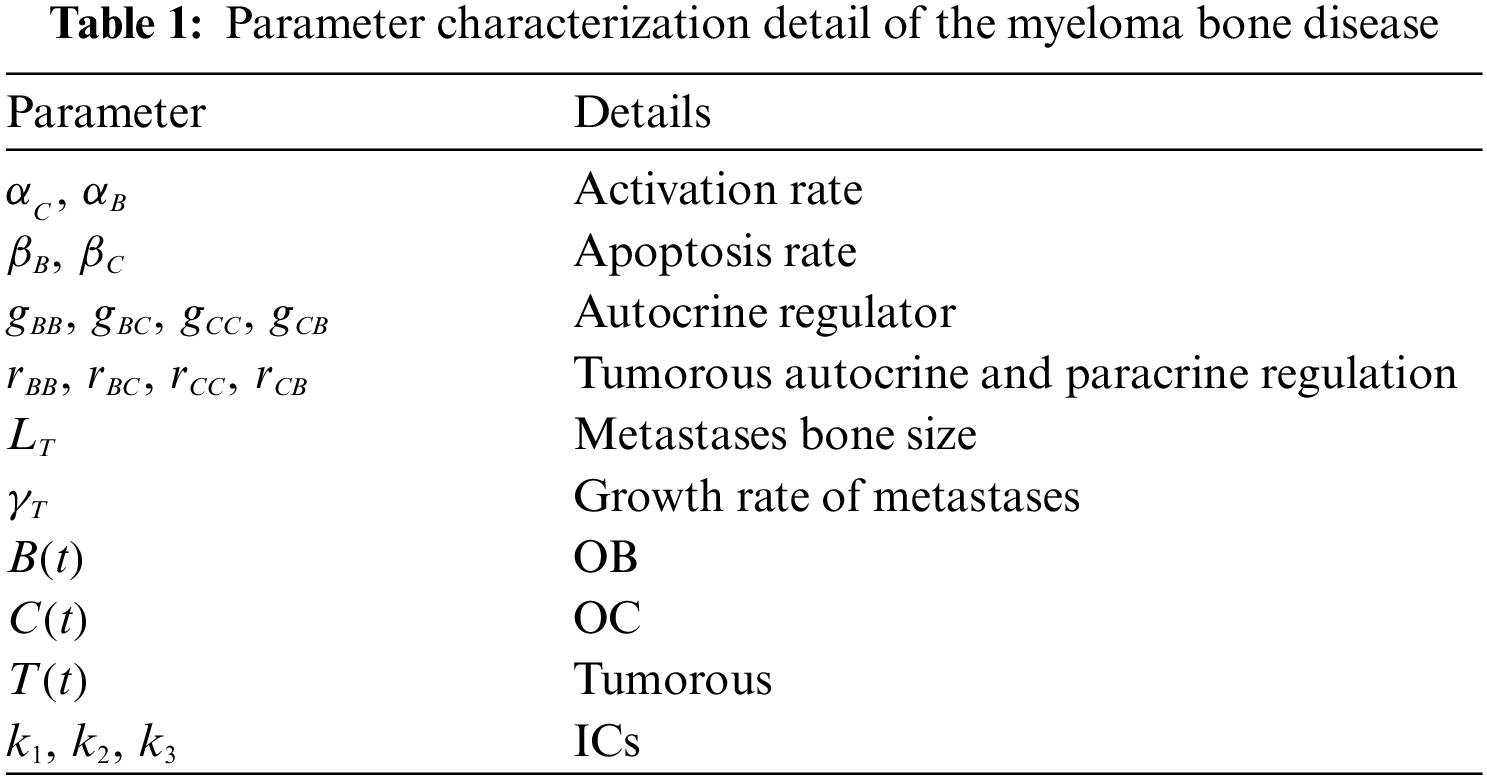
3  Novel Stochastic Solvers Features

In this section, the existing section shows the stochastic operator performances for solving the fractional order computational myeloma bone disease model with LVMBPNN. In the literature, stochastic software solvers have been investigated to solve complicated, singular, and rigid systems [42,43]. Recently, the simulation based on the food chain function [44], infection control model [45], Lane-Emden systems [46], functional order approaches [47], and nonlinear dynamic HIV systems [48–50].

This research aims to calculate the numerical performances using the stochastic LVMBPNN for the fractional MBD based on the bone remodeling and the effects of the tumor. It has been discovered that the time-fractional kinds of derivatives can be applied to define the conditions. The remembrance is represented by the derivative order form, but the memory function is represented by the derivative of fractional. Real-world applications are indicated by these fractional derivatives. Some novel characteristics of the LVMBPNN for the mathematical fractional MBD model are reported as:

•   A novel design numerical solution and fractional derivatives of the MBD model with tumor are presented.

•   Stochastic measures have never been used to solve a fractional-order MBD model based on a remodeling bone with tumor effects.

•   The numerical studies using stochastic paradigms are presented successfully utilizing fractional order MBD mathematical model,

•   To solve the nonlinear fractional-order MBD mathematical model, AI with the design of LMBS-NNs is presented.

•   Three distinct fractional-order deviations based on the MBD model were numerically solved to authorize the proposed approach’s dependability.

•   The comparison of the proposed and Adams–Bashforth–Moulton results demonstrates the excellence of the stochastic solver-based LVMBPNN.

•   The performance of the designed LVMBPNN in solving the fractional order MBD mathematical model is validated by the correlation, regression, STs, MSE, and EHs, results.

4  Proposed Procedures: ANN-LMBP Method

This section of the study describes the proposed LVMBPNN method for presenting numerical bone remodeling model solutions. The proposed LVMBPNN system is introduced in two stages: the significant performances of the ANN-LMBP method and operational plans for solving the mathematical bone remodeling model using the LVMBPNN method.

Fig. 1 depicts the designed approach for solving the nonlinear fractional differential model, based on the number of layer optimization procedures of the ANN-LMBP method. This study statics performances are 82%, 9%, and 9% for training, certification, and checking for dealing with the fractional order computer simulation based on myeloma bone disease.

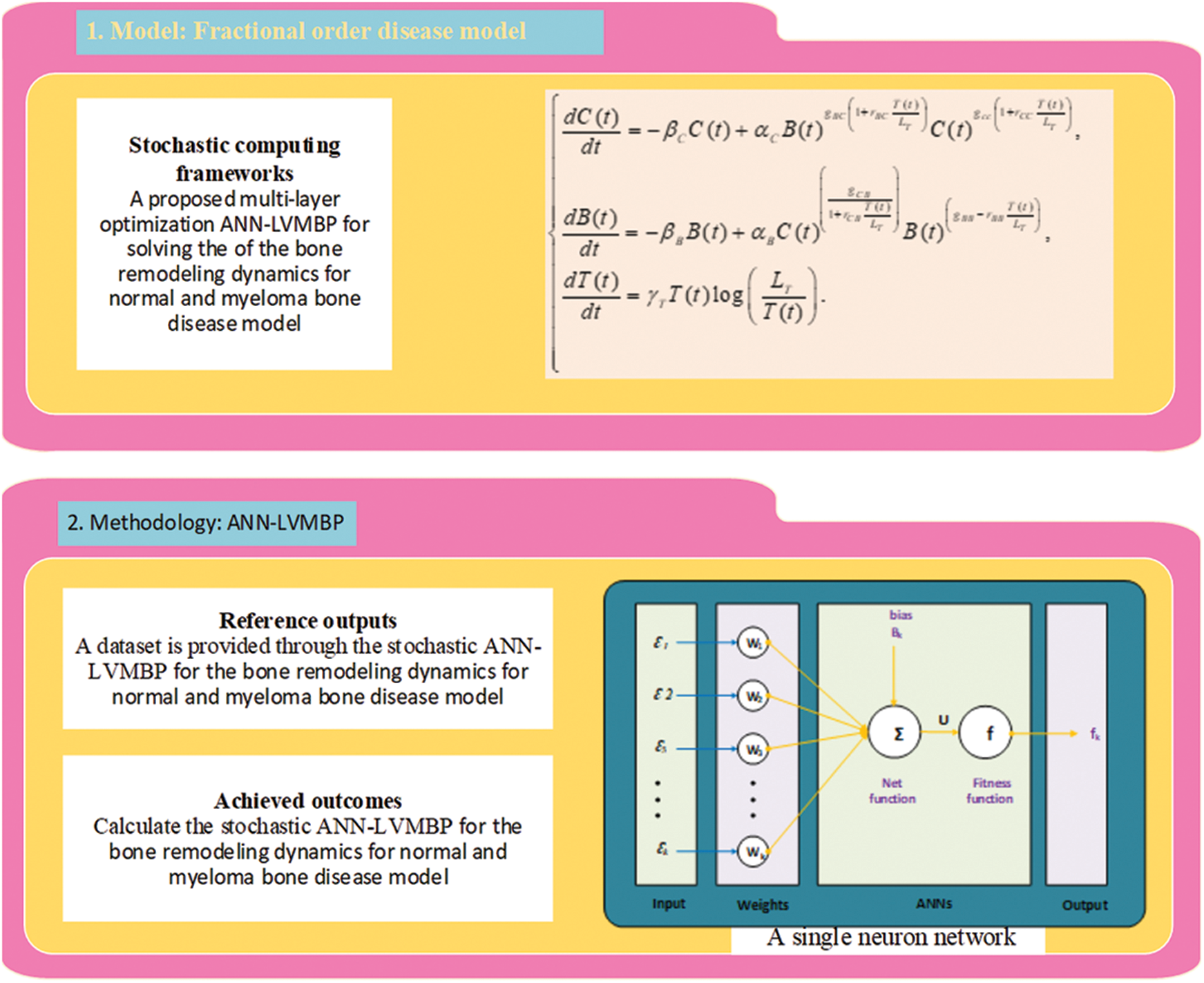
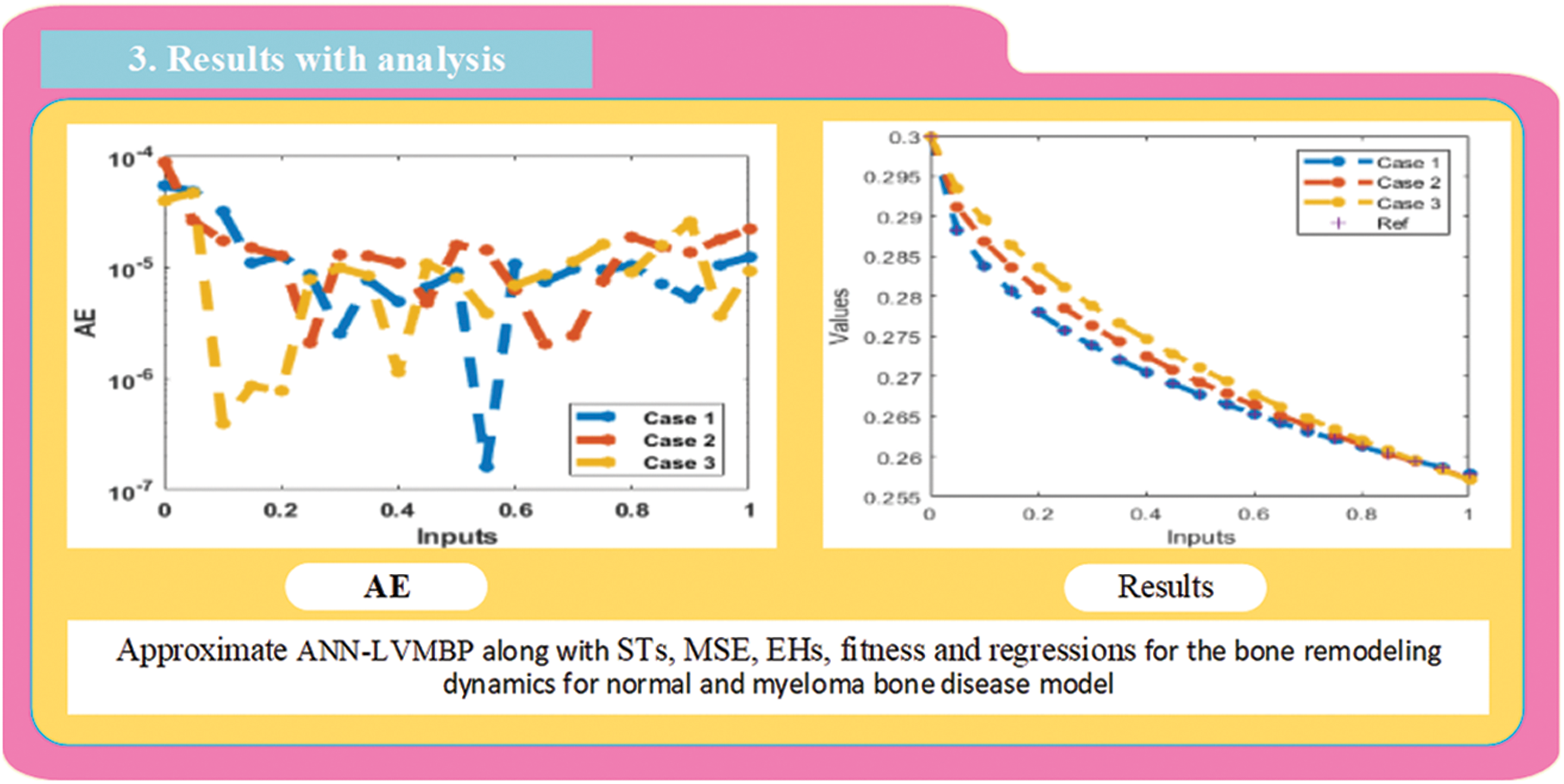
Figure 1: Workflow-based fractional myeloma bone disease model using the LVMBPNN method

5  Results and Discussions

Three distinct variabilities of fractional order differential equations of the computational myeloma bone disease model using LVMBPNN are presented in this section. The mathematical representations for each type are as follows:

Case 1: Ad opt the following fractional order (FO) bone disease related model with the suitable values τ=0.5, γT=0.22, LT=0.14, βB=0.25, βC=0.1, αB=0.22, αC=0.12, rBB=0.1, rCC=0.18, rBC=0.2, rCB=0.19, gBB=0.09, gCC=0.16, gBC=0.15, gCB=0.17, k1=0.1, k2=0.2 and k3=0.3.

{d0.5C(t)dt0.5=−0.1C(t)+0.12B(t)0.15(1+0.2T(t)LT)C(t)0.16(1+0.18T(t)LT),C0=0.1,d0.5B(t)dt0.5=−0.25B(t)+0.22C(t)(0.171+0.19T(t)LT)B(t)(0.09−0.1T(t)LT),B0=0.2,d0.5T(t)dt0.5=0.22T(t)log⁡(100T(t)).T0=0.3.(3)

Case 2: Implement the following FO bone disease related mathematical model with the suitable values τ=0.6, γT=0.22, LT=0.14, βB=0.25, βC=0.1, αB=0.22, αC=0.12, rBB=0.1, rCC=0.18, rBC=0.2, rCB=0.19, gBB=0.09, gCC=0.16, gBC=0.15, gCB=0.17, k1=0.1, k2=0.2 and k3=0.3.

{d0.6C(t)dt0.6=−0.1C(t)+0.12B(t)0.15(1+0.2T(t)LT)C(t)0.16(1+0.18T(t)LT),C0=0.1,d0.6B(t)dt0.6=−0.25B(t)+0.22C(t)(0.171+0.19T(t)LT)B(t)(0.09−0.1T(t)LT),B0=0.2,d0.6T(t)dt0.6=0.22T(t)log⁡(100T(t)).T0=0.3.(4)

Case 3: Consider a FO mathematical model based on the myeloma bone disease by using these values τ=0.7, γT=0.22, LT=0.14, βB=0.25, βC=0.1, αB=0.22, αC=0.12, rBB=0.1, rCC=0.18, rBC=0.2, rCB=0.19, gBB=0.09, gCC=0.16, gBC=0.15, gCB=0.17, k1=0.1, k2=0.2 and k3=0.3.

{d0.7C(t)dt0.7=−0.1C(t)+0.12B(t)0.15(1+0.2T(t)LT)C(t)0.16(1+0.18T(t)LT),C0=0.1,d0.7B(t)dt0.7=−0.25B(t)+0.22C(t)(0.171+0.19T(t)LT)B(t)(0.09−0.1T(t)LT),B0=0.2,d0.7T(t)dt0.7=0.22T(t)log⁡(100T(t)).T0=0.3.(5)

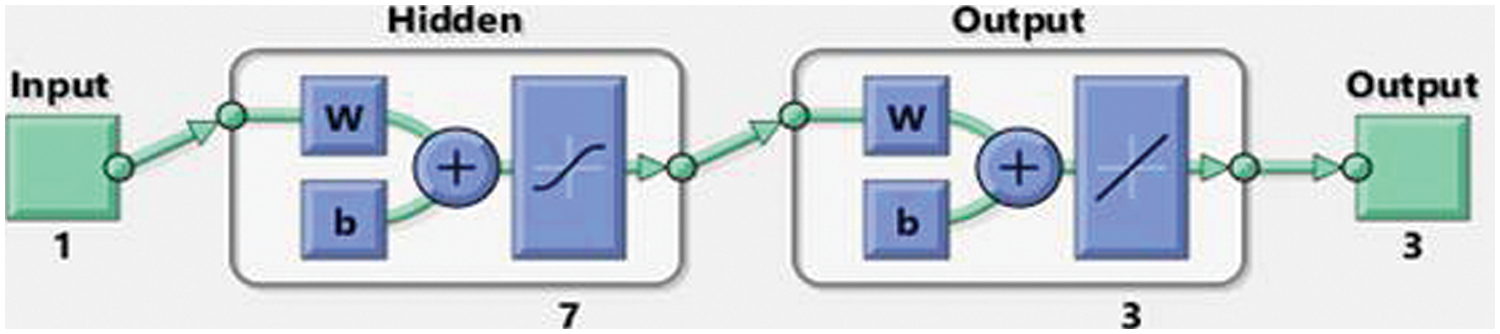
Figure 2: Designed LVMBPNN method for the myeloma bone disease

Figs. 3–5 depict the LVMBPNN-based fractional myeloma bone disease model. Figs. 3 and 4 show the perfect EHs, curves, validations, and STs for the fractional-order derivative mathematical myeloma bone model. The best fractional-order mathematical bone disease model (BDM) results were obtained at epochs 46, 32, and 36, measured as 5.7193 × 10−09, 2.4386 × 10−09, and 1.1786 × 10−09, respectively. The gradient performances for cases 1, 2, and 3 are 9.9654 × 10−08, 9.73 × 10−08, and 9.2864 × 10−08. The graphical methodologies indicate that the LVMBPNN method for solving the fractional MBD model converges. Fig. 4 depicts the numerical outcomes and EHs for the fractional-order mathematical bone disease using the LVMBPNN technique. The performances of the obtained and reference solutions have been compared to assess the correctness of the scheme. The fractional-order mathematical MBD model training, testing, and validation results are plotted. The second section of Fig. 4 discusses the EHs values, which are −2.1 × 10−05, −1.6 × 10−05, and −1.2 × 10−05 for cases 1–3. Fig. 5 depicts the correlation techniques using the LVMBPNN method. The correlation for the fractional-order MBD system is one using the LVMBPNN method. The accuracy of the LVMBPNN method for the fractional-order mathematical model has been achieved through training, testing, and validation. Tab. 2 displays the MSE for the fractional model based on the verification, complexity, training, generations, and back propagation using the LVMBPNN method.

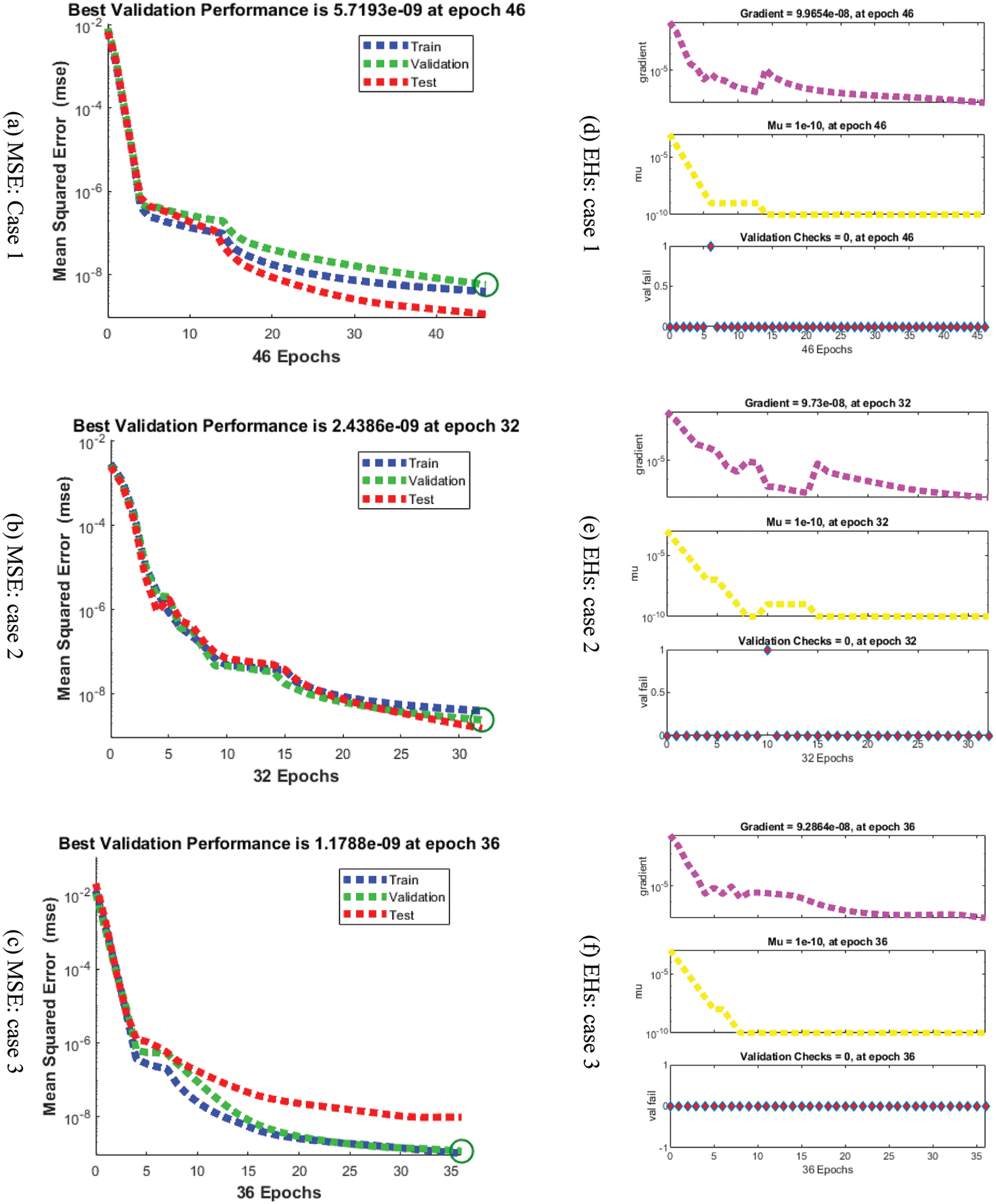
Figure 3: MSE and STs performances for the fractional order system

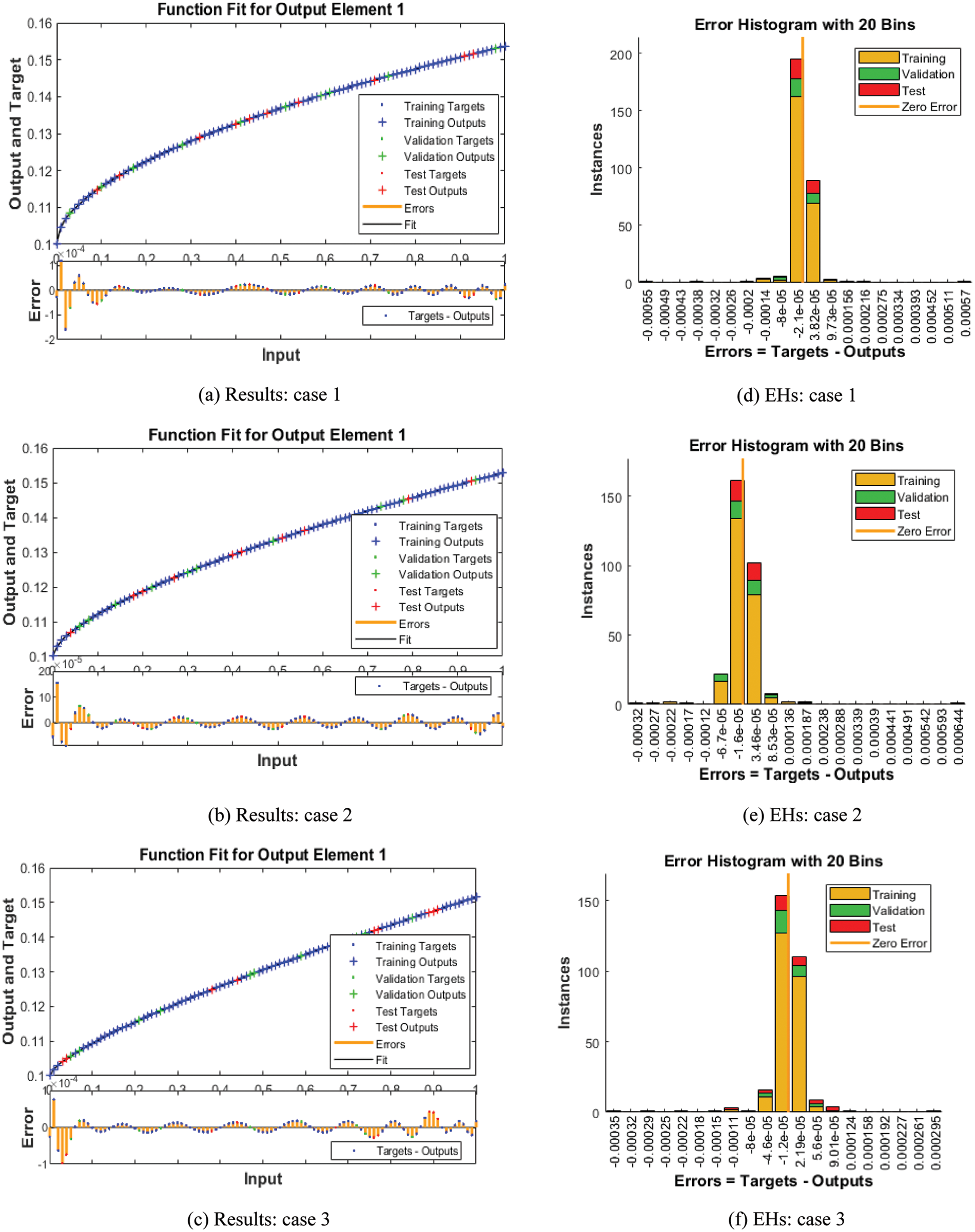
Figure 4: Results and EHs performances for the fractional order system

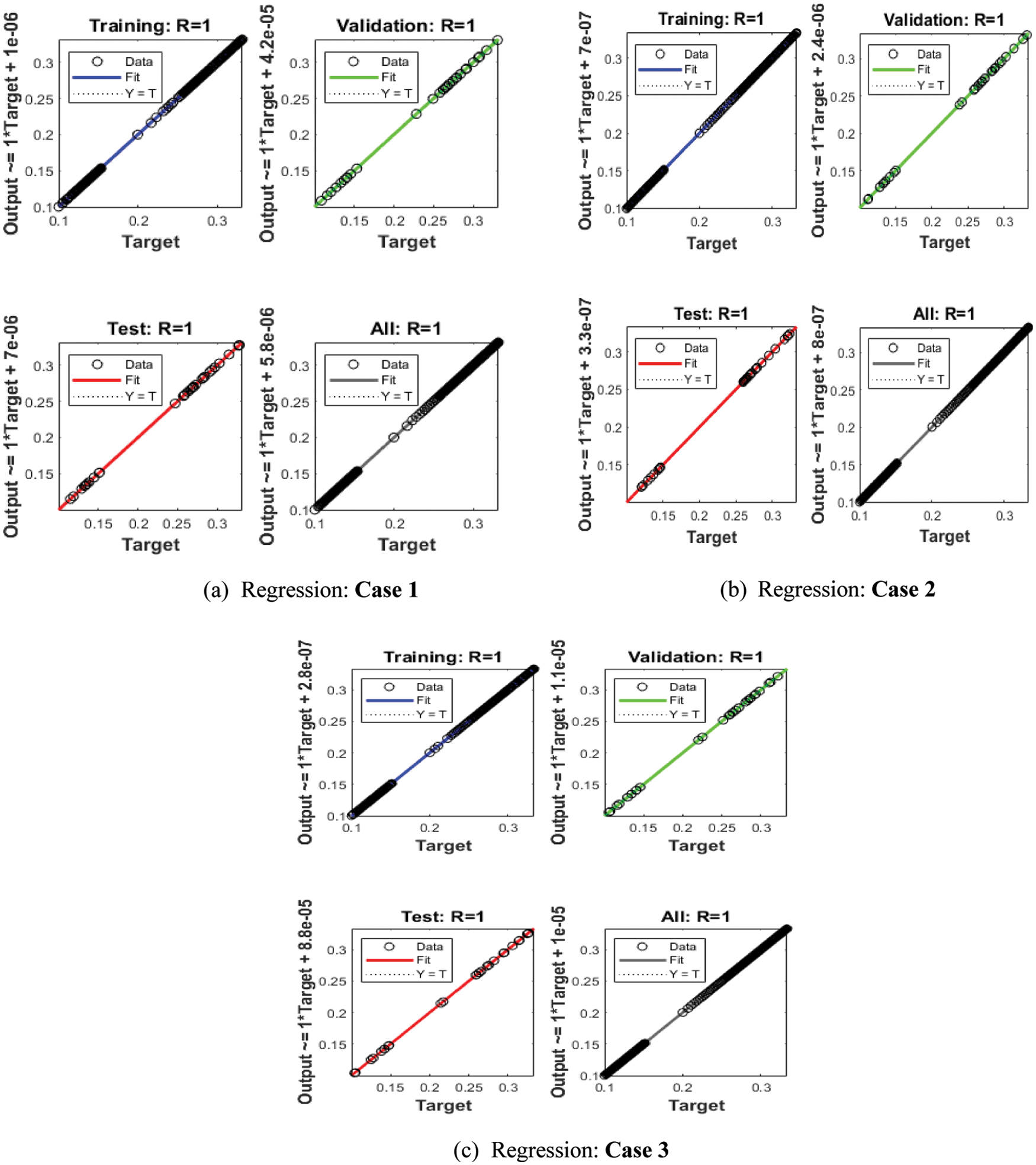
Figure 5: Regression performances for the fractional-order system

The correctness of the proposed ANN-LMBP method for the fractional-order MBD model is observed in Figs. 6 and 7 based on the comparison of the result and AE performances. The calculated form of the numerical solutions has been drawn to solve the nonlinear model using the LVMBPNN. The matching of the calculated and reference results has been illustrated in Fig. 6. These plots present the precision of the LVMBPNN for the fractional myeloma bone disease model. The performances of the AE to solve the fractional MBD model using the stochastic paradigms are plotted in Fig. 7. The AE is provided based on the OCs C(t), OBs B(t) and tumor T(t). It is observed that the cases of OCs C(t) lie around 10−04 to 10−05, 10−04 to 10−06 and 10−04 to 10−07 for cases 1, 2, and 3. The AE for the OBs B(t) lies around 10−04 to 10−06, 10−03 to 10−05 and 10−04 to 10−08 for cases 1, 2 and 3. The AE for the tumor case T(t) found 10−04 to 10−07, 10−04 to 10−06, and 10−04 to 10−07 for cases 1, 2 and 3. These best AE values represent the exactness of the proposed ANN-LMBP method for the fractional-order mathematical MBD model.

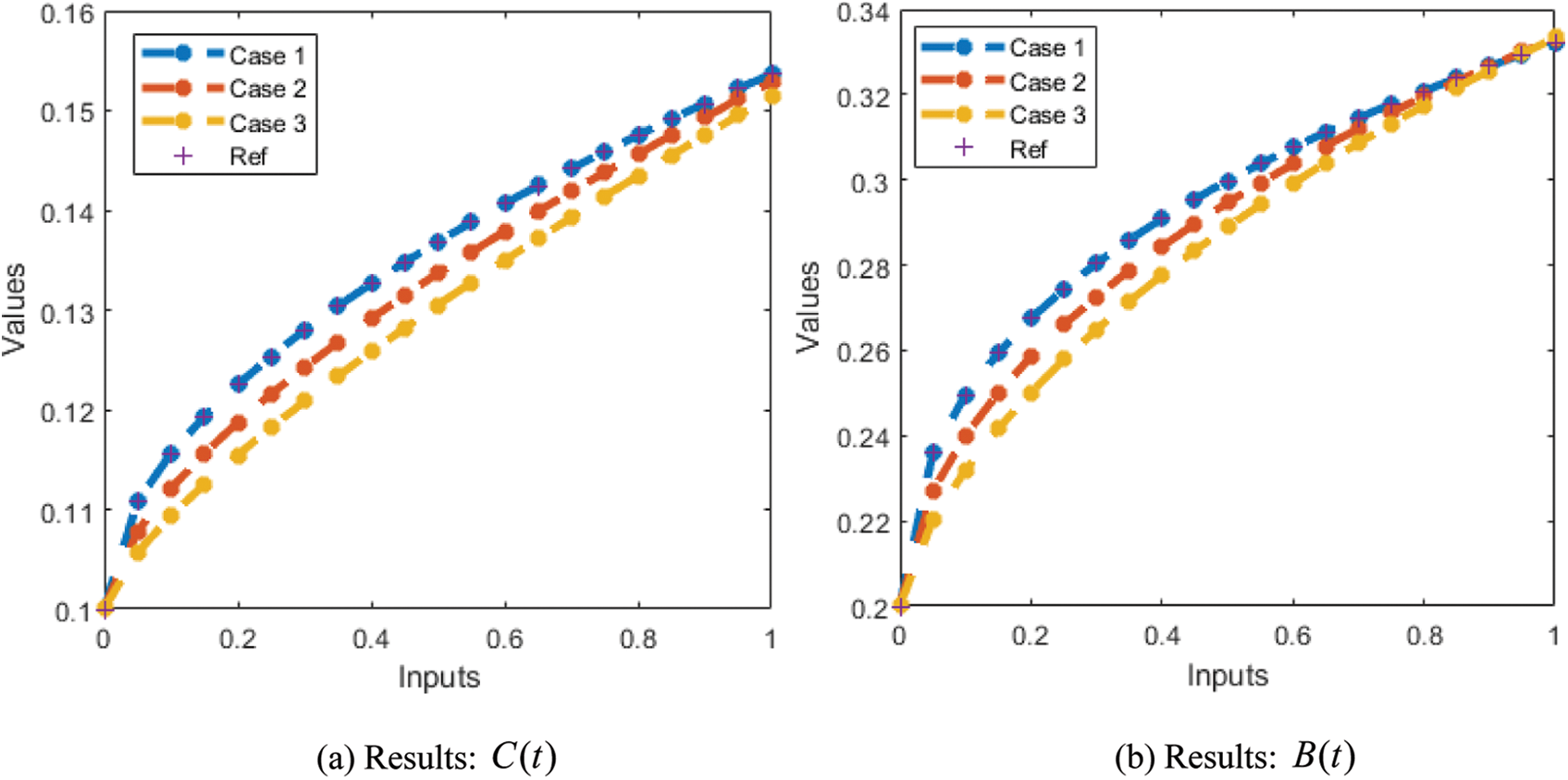
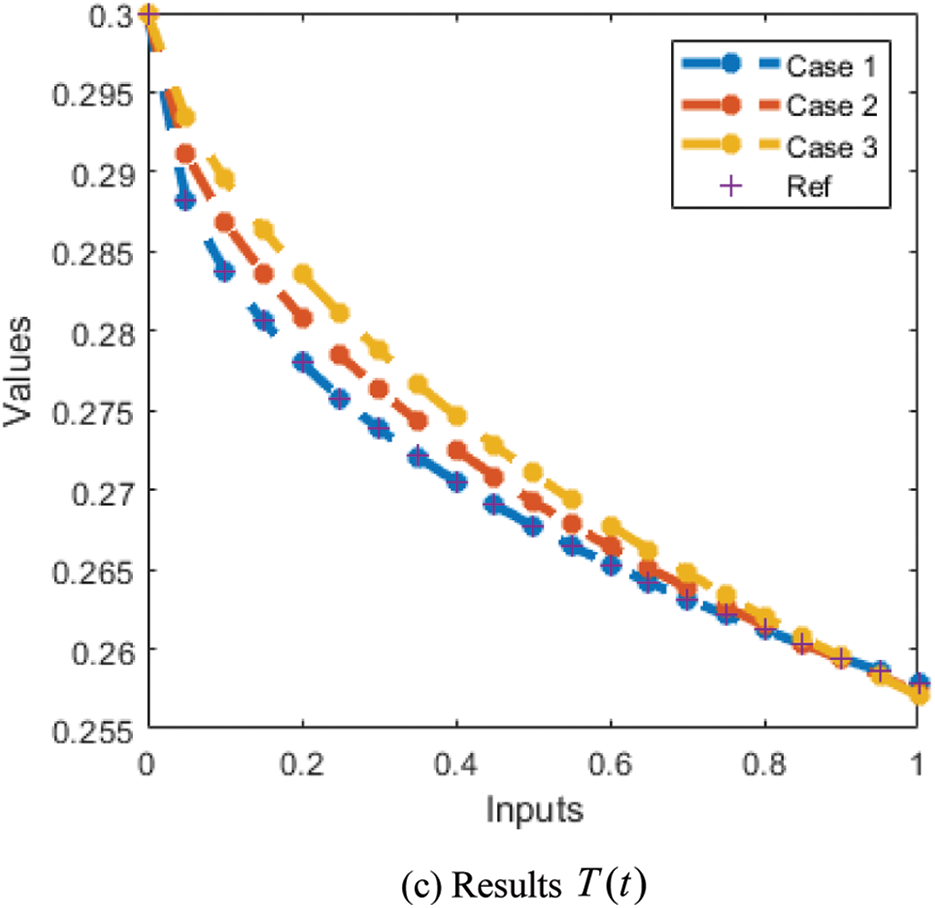
Figure 6: Result comparisons for the fractional order MBD system

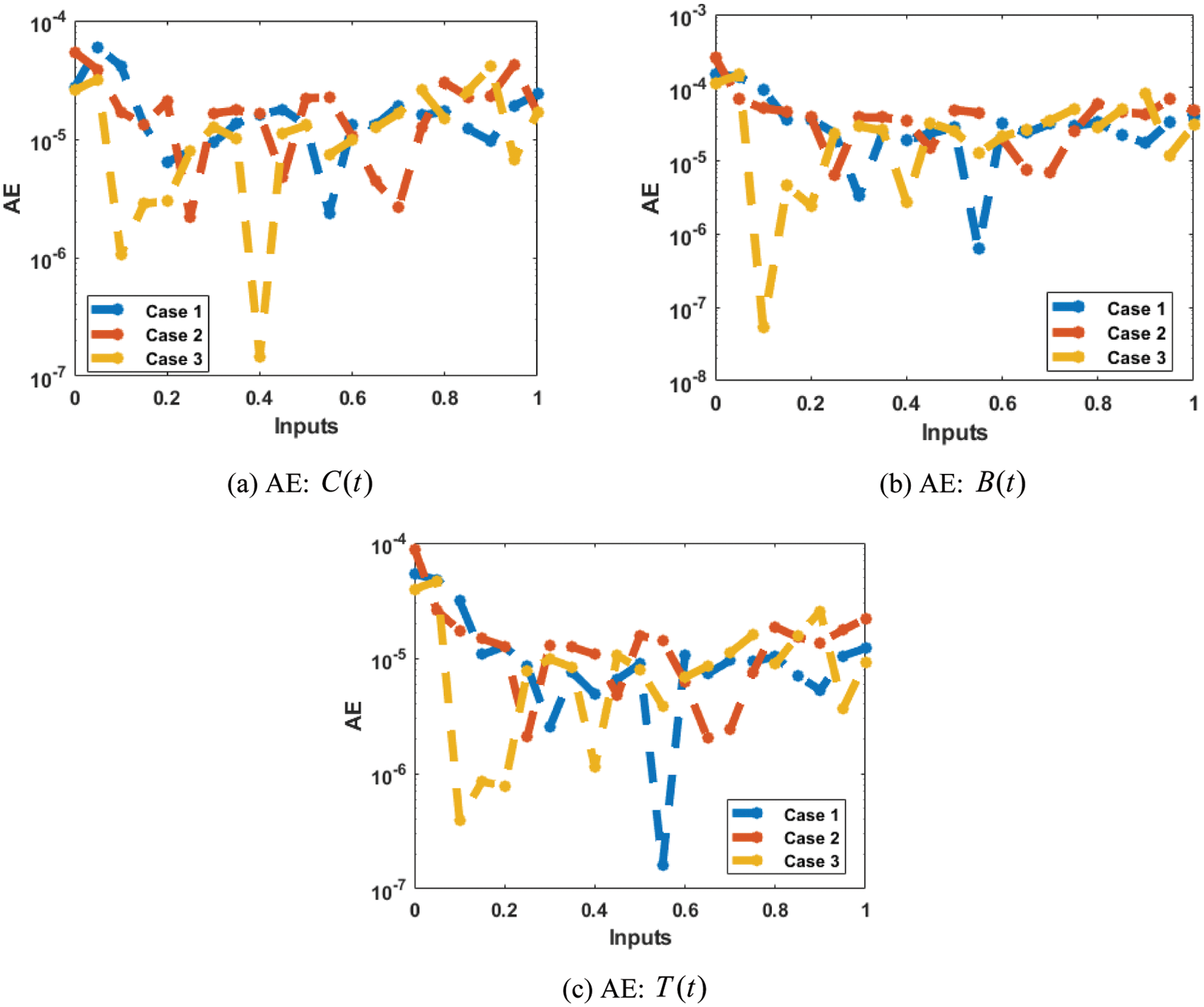
Figure 7: AE values for solving the fractional order MBD system

6  Conclusion

The numerical representations of the bone remodeling-based MBD mathematical model are presented in this work. The goal of this study is to get a fractional-order study that focuses on the dynamics of bone remodeling based MBD mathematical models in order to get more accurate system performances. This study also included an integer nonlinear mathematical MBD system with a tumor effect. Based on fractional-order bone remodeling, the MBD mathematical system is divided into three dynamics: OCs (bone resorption), OBs (bone formation), and tumors. The stochastic performances of the MBD mathematical model based on fractional-order bone remodeling have not been introduced or calculated using the stochastic paradigms based on the LVMBPNN. For the fractional order MBD mathematical system, three variants with different values of the fractional order have been provided. The data applied to show the fractional-order MDB mathematical model results were divided as 82% for training and 9% for both testing and certification. The numerical performances of the fractional MBD system were presented using seven numbers of neurons. The statistical solutions of the fractional MBD system were compared to the results of the Adams–Bashforth–Moulton. The correctness of the schemes is performed based on the AE, which is calculated as 10−04 to 10−06 for each case of the model. The obtained results were performed using the LVMBPNN to reduce the MSE. The regression, STs, correlation, MSE, and EHs, were applied to validate the competence of LVMBPNN along with the numerical representations. The reference and obtained result’s matching demonstrate the precision of the LMBS-NNs. The scheme’s presentation is authenticated using the uniformity and dependability of the proposed LVMBPNN.

The LVMBPNN can be used in future work to present numerical measures of the fractional order systems, lonngren-wave, fluid mechanics systems, omics studies, and data security models [51–62].

Funding Statement: This research project is supported by Thailand Science Research and Innovation (TSRI). Contract No. FRB650059/NMA/10. The eighth author is supported by the NSRF via the Program Management Unit for Human Resources & Institutional Development, Research and Innovation (grant number B05F640092).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. M. Parfitt, “Osteonal and hemi-osteonal remodeling: The spatial and temporal framework for signal traffic in adult human bone,” Journal of Cellular Biochemistry, vol. 55, no. 3, pp. 273–286, 1994. [Google Scholar]

 2.  M. J. Martin and J. C. Buckland-Wright, “Sensitivity analysis of a novel mathematical model identifies factors determining bone resorption rates,” Bone, vol. 35, no. 4, pp. 918–928, 2004. [Google Scholar]

 3.  T. Lekszycki, “Functional adaptation of bone as an optimal control problem,” Journal of Theoretical and Applied Mechanics, vol. 43, no. 3, pp. 555–574, 2005. [Google Scholar]

 4.  S. Maldonado, R. Findeisen and F. Allgower, “Describing force-induced bone growth and adaptation by a mathematical model,” Journal of Musculoskeletal & Neuronal Interactions, vol. 8, no. 1, pp. 15–17, 2008. [Google Scholar]

 5.  G. Martínez, J. M. G. Aznar, M. Doblaré and M. Cerrolaza, “External bone remodeling through boundary elements and damage mechanics,” Mathematics and Computers in Simulation, vol. 73, no. 1-4, pp. 183–199, 2006. [Google Scholar]

 6.  K. I. Tezuka, Y. Wada, A. Takahashi and M. Kikuchi, “Computer-simulated bone architecture in a simple bone-remodeling model based on a reaction-diffusion system,” Journal of Bone and Mineral Metabolism, vol. 23, no. 1, pp. 1–7, 2005. [Google Scholar]

 7.  V. Lemaire, F. L. Tobin, L. D. Greller, C. R. Cho and L. J. Suva, “Modeling the interactions between osteoblast and osteoclast activities in bone remodeling,” Journal of Theoretical Biology, vol. 229, no. 3, pp. 293–309, 2004. [Google Scholar]

 8.  J. M. Garcia-Aznar, T. Rüberg and M. Doblare, “A bone remodelling model coupling microdamage growth and repair by 3D BMU-activity,” Biomechanics and Modeling in Mechanobiology, vol. 4, no. 2, pp. 147–167, 2005. [Google Scholar]

 9.  A. Moroz and D. I. Wimpenny, “Allosteric control model of bone remodelling containing periodical modes,” Biophysical Chemistry, vol. 127, no. 3, pp. 194–212, 2007. [Google Scholar]

10. P. Pivonka, J. Zimak, D. W. Smith, B. S. Gardiner, C. R. Dunstan et al., “Model structure and control of bone remodeling: A theoretical study,” Bone, vol. 43, no. 2, pp. 249–263, 2008. [Google Scholar]

11. J. M. Restrepo, R. Choksi and J. M. H. Y. Jiang, “Improving the damage accumulation in a biomechanical bone remodelling model,” Computer Methods in Biomechanics and Biomedical Engineering, vol. 12, no. 3, pp. 341–352, 2009. [Google Scholar]

12. M. D. Ryser, N. Nigam and S. V. Komarova, “Mathematical modeling of Spatio-temporal dynamics of a single bone multicellular unit,” Journal of Bone and Mineral Research, vol. 24, no. 5, pp. 860–870, 2009. [Google Scholar]

13. G. R. Mundy, “Myeloma bone disease,” European Journal of Cancer, vol. 34, no. 2, pp. 246–251, 1998. [Google Scholar]

14. G. R. Mundy, L. G. Raisz, R. A. Cooper, G. P. Schechter and S. E. Salmon, “Evidence for the secretion of an osteoclast stimulating factor in myeloma,” New England Journal of Medicine, vol. 291, no. 20, pp. 1041–1046, 1974. [Google Scholar]

15. L. J. Suva, C. Washam, R. W. Nicholas and R. J. Griffin, “Bone metastasis: Mechanisms and therapeutic opportunities,” Nature Reviews Endocrinology, vol. 7, no. 4, pp. 208–218, 2011. [Google Scholar]

16. I. Holen, “Pathophysiology of bone metastases,” In: R. Coleman, P. Abrahamsson, Hadji, P. (Edsin Handbook of Cancer-Related Bone Disease, 2nd ed, vol. 1. Bristol, UK: Bioscientifica, pp. 33–52, 2012. [Google Scholar]

17. S. Casimiro, T. A. Guise and J. Chirgwin, “The critical role of the bone microenvironment in cancer metastases,” Molecular and Cellular Endocrinology, vol. 310, no. 1-2, pp. 71–81, 2009. [Google Scholar]

18. R. T. Hart, Z. M. Oden, S. W. Parrish and D. B. Burr, “Computational methods for bone mechanics studies,” The International Journal of Supercomputing Applications, vol. 6, no. 2, pp. 164–174, 1992. [Google Scholar]

19. S. V. Komarova, R. J. Smith, S. J. Dixon, S. M. Sims and L. M. Wahl, “Mathematical model predicts a critical role for osteoclast autocrine regulation in the control of bone remodeling,” Bone, vol. 33, no. 2, pp. 206–215, 2003. [Google Scholar]

20. B. P. Ayati, C. M. Edwards, G. F. Webb and J. P. Wikswo, “A mathematical model of bone remodeling dynamics for normal bone cell populations and myeloma bone disease,” Biology Direct, vol. 5, no. 1, pp. 1–17, 2010. [Google Scholar]

21. H. Zhang and G. H. Li, “Anomalous epidemic spreading in heterogeneous networks,” Physical Review E, vol. 102, no. 1, p. 012315, 2020. [Google Scholar]

22. R. Metzler and J. Klafter, “The random walk’s guide to anomalous diffusion: A fractional dynamics approach,” Physics Reports, vol. 339, no. 1, pp. 1–77, 2000. [Google Scholar]

23. D. Sierociuk, A. Dzieliński, G. Sarwas, I. Petras, I. Podlubny et al., “Modelling heat transfer in heterogeneous media using fractional calculus,” Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, vol. 371, no. 1990, pp. 1–10, 2013. [Google Scholar]

24. M. Rahimy, “Applications of fractional differential equations,” Applied Mathematical Sciences, vol. 4, no. 50, pp. 2453–2461, 2010. [Google Scholar]

25. I. Assadi, A. Charef, D. Copot, R. De Keyser, T. Bensouici et al., “Evaluation of respiratory properties by means of fractional order models,” Biomedical Signal Processing and Control, vol. 34, pp. 206–213, 2017. [Google Scholar]

26. A. M. Lopes and J. T. Machado, “Fractional order models of leaves,” Journal of Vibration and Control, vol. 20, no. 7, pp. 998–1008, 2014. [Google Scholar]

27. V. E. Tarasov, “Geometric interpretation of fractional-order derivative,” Fractional Calculus and Applied Analysis, vol. 19, no. 5, pp. 1200–1221, 2016. [Google Scholar]

28. S. Ladaci and A. Charef, “On fractional adaptive control,” Nonlinear Dynamics, vol. 43, no. 4, pp. 365–378, 2006. [Google Scholar]

29. C. F. Lorenzo and T. T. Hartley, “Variable fractional order and distributed order operators,” Nonlinear Dynamics, vol. 29, pp. 57–98, 2002. [Google Scholar]

30. T. Akchurin, T. Aissiou, N. Kemeny, E. Prosk, N. Nigam et al. “Complex dynamics of osteoclast formation and death in long-term cultures,” PloS One, vol. 3, no. 5, pp. 1–11, 2008. [Google Scholar]

31. S. V. Komarova, “Mathematical model of paracrine interactions between osteoclasts and osteoblasts predicts anabolic action of parathyroid hormone on bone,” Endocrinology, vol. 146, no. 8, pp. 3589–3595, 2005. [Google Scholar]

32. S. V. Komarova, “Bone remodeling in health and disease: Lessons from mathematical modeling,” Annals of the New York Academy of Sciences, vol. 1068, no. 1, pp. 557–559, 2006. [Google Scholar]

33. J. P. Neto, R. M. Coelho, D. Valério, S. Vinga, D. Sierociuk et al., “Simplifying biochemical tumorous bone remodeling models through variable order derivatives,” Computers & Mathematics with Applications, vol. 75, no. 9, pp. 3147–3157, 2018. [Google Scholar]

34. X. R. Zhang, X. Sun, W. Sun, T. Xu and P. P. Wang, “Deformation expression of soft tissue based on BP neural network,” Intelligent Automation & Soft Computing, vol. 32, no. 2, pp. 1041–1053, 2022. [Google Scholar]

35. W. Sun, G. C. Zhang, X. R. Zhang, X. Zhang and N. N. Ge, “Fine-grained vehicle type classification using lightweight convolutional neural network with feature optimization and joint learning strategy,” Multimedia Tools and Applications, vol. 80, no. 20, pp. 30803–30816, 2021. [Google Scholar]

36. Z. Sabir, M. Umar, M. A. Z. Raja, H. M. Baskonus and W. Gao, “Designing of morlet wavelet as a neural network for a novel prevention category in the HIV system,” International Journal of Biomathematics, vol. 15, no. 4, pp. 2250012, 2022. [Google Scholar]

37. S. Luemsai and T. Botmart, “Improved extended dissipativity results for t-s fuzzy generalized neural networks with mixed interval time-varying delays,” IEEE Access, vol. 10, pp. 2480–2496, 2022. [Google Scholar]

38. G. Rajchakit, R. Sriraman, N. Boonsatit, P. Hammachukiattikul, C. P. Lim et al., “Exponential stability in the lagrange sense for clifford-valued recurrent neural networks with time delays,” Advances in Difference Equations, vol. 2021, no. 1, pp. 1–21, 2021. [Google Scholar]

39. N. Boonsatit, G. Rajchakit, R. Sriraman, C. P. Lim and P. Agarwal, “Finite-/fixed-time synchronization of delayed clifford-valued recurrent neural networks,” Advances in Difference Equations, vol. 2021, no. 1, pp. 1–25, 2021. [Google Scholar]

40. G. Rajchakit, R. Sriraman, N. Boonsatit, P. Hammachukiattikul, C. P. Lim et al., “Global exponential stability of clifford-valued neural networks with time-varying delays and impulsive effects,” Advances in Difference Equations, vol. 2021, no. 1, pp. 1–21, 2021. [Google Scholar]

41. B. Wang, H. Jahanshahi, C. Volos, S. Bekiros, M. A. Khan et al., “A new RBF neural network-based fault-tolerant active control for fractional time-delayed systems,” Electronics, vol. 10, no. 12, pp. 1–17, 2021. [Google Scholar]

42. Z. Sabir, M. A. Z. Raja, S. R. Mahmoud, M. Balubaid and A. Algarni, “A novel design of morlet wavelet to solve the dynamics of nervous stomach nonlinear model,” International Journal of Computational Intelligence Systems, vol. 15, no. 1, pp. 1–15, 2022. [Google Scholar]

43. Z. Sabir, M. A. Z. Raja, T. Botmart and W. Weera, “A Neuro-evolution heuristic using active-set techniques to solve a novel nonlinear singular prediction differential model,” Fractal and Fractional, vol. 6, no. 1, pp. 1–14, 2022. [Google Scholar]

44. Z. Sabir, “Stochastic numerical investigations for nonlinear three-species food chain system,” International Journal of Biomathematics, vol. 15, no. 4, pp. 2250005, 2021. [Google Scholar]

45. Z. Sabir, M. A. Z. Raja and Y. G. Sánchez, “Solving an infectious disease model considering its anatomical variables with stochastic numerical procedures,” Journal of Healthcare Engineering, vol. 2022, pp. 1–12, 2022. [Google Scholar]

46. Z. Sabir, M. A. Z. Raja, M. Umar, M. Shoaib and D. Baleanu, “FMNSICS: Fractional meyer neuro-swarm intelligent computing solver for nonlinear fractional lane–Emden systems,” Neural Computing and Applications, vol. 34, no. 6, pp. 4193–4206, 2022. [Google Scholar]

47. M. A. Abdelkawy, Z. Sabir, J. L. Guirao and T. Saeed, “Numerical investigations of a new singular second-order nonlinear coupled functional lane–Emden model,” Open Physics, vol. 18, no. 1, pp. 770–778, 2020. [Google Scholar]

48. M. Umar, Z. Sabir, M. A. Z. Raja, H. M. Baskonus, S. W. Yao et al., “A novel study of morlet neural networks to solve the nonlinear HIV infection system of latently infected cells,” Results in Physics, vol. 25, pp. 1–13, 2021. [Google Scholar]

49. Y. G. Sánchez, M. Umar, Z. Sabir, J. L. Guirao and M. A. Z. Raja, “Solving a class of biological HIV infection model of latently infected cells using heuristic approach,” Discrete & Continuous Dynamical Systems-S, vol. 14, no. 10, pp. 3611, 2021. [Google Scholar]

50. M. Umar, Z. Sabir, M. A. Z. Raja, J. G. Aguilar, F. Amin et al., “Neuro-swarm intelligent computing paradigm for nonlinear HIV infection model with CD4 + T-cells,” Mathematics and Computers in Simulation, vol. 188, pp. 241–253, 2021. [Google Scholar]

51. K. Vajravelu, S. Sreenadh and R. Saravana, “Influence of velocity slip and temperature jump conditions on the peristaltic flow of a Jeffrey fluid in contact with a Newtonian fluid,” Applied Mathematics and Nonlinear Sciences, vol. 2, no. 2, pp. 429–442, 2017. [Google Scholar]

52. M. S. M. Selvi and L. Rajendran, “Application of modified wavelet and homotopy perturbation methods to nonlinear oscillation problems,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 2, pp. 351–364, 2019. [Google Scholar]

53. Z. Sabir, T. Botmart, M. A. Z. Raja and W. Weera, “An advanced computing scheme for the numerical investigations of an infection-based fractional-order nonlinear prey-predator system,” Plos One, vol. 17, no. 3, pp. 1–13, 2022. [Google Scholar]

54. M. Gürbüz and Ç. Yıldız, “Some new inequalities for convex functions via Riemann-Liouville fractional integrals,” Applied Mathematics and Nonlinear Sciences, vol. 6, no. 1, pp. 537–544, 2021. [Google Scholar]

55. N. Yotha, T. Botmart, K. Mukdasai and W. Weera, “Improved delay-dependent approach to passivity analysis for uncertain neural networks with discrete interval and distributed time-varying delays,” Vietnam Journal of Mathematics, vol. 45, no. 4, pp. 721–736, 2017. [Google Scholar]

56. A. N. Akkilic, Z. Sabir, M. A. Z. Raja and H. Bulut, “Numerical treatment on the new fractional-order SIDARTHE COVID-19 pandemic differential model via neural networks,” The European Physical Journal Plus, vol. 137, no. 3, pp. 1–14, 2022. [Google Scholar]

57. T. Botmart, Z. Sabir, M. A. Z. Raja, W. Weera, R. Sadat et al., “A numerical study of the fractional order dynamical nonlinear susceptible infected and quarantine differential model using the stochastic numerical approach,” Fractal and Fractional, vol. 6, no. 3, pp. 1–13, 2022. [Google Scholar]

58. Z. Sabir, M. Munawar, M. A. Abdelkawy, M. A. Z. Raja, C. Ünlü et al., “Numerical investigations of the fractional-order mathematical model underlying immune-chemotherapeutic treatment for breast cancer using the neural networks,” Fractal and Fractional, vol. 6, no. 4, pp. 1–16, 2022. [Google Scholar]

59. A. O. Akdemir, E. Deniz and E. Yüksel, “On some integral inequalities via conformable fractional integrals,” Applied Mathematics and Nonlinear Sciences, vol. 6, no. 1, pp. 489–498, 2021. [Google Scholar]

60. G. L. Guirao, Z. Sabir, M. A. Z. Raja and D. Baleanu, “Design of neuro-swarming computational solver for the fractional bagley–Torvik mathematical model,” The European Physical Journal Plus, vol. 137, no. 2, pp. 1–15, 2022. [Google Scholar]

61. E. İlhan and İO Kıymaz, “A generalization of truncated M-fractional derivative and applications to fractional differential equations,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 171–188, 2020. [Google Scholar]

62. A. Yokuş and S. Gülbahar, “Numerical solutions with linearization techniques of the fractional Harry Dym equation,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 1, pp. 35–42, 2019. [Google Scholar]