An Intelligence Computational Approach for the Fractional 4D Chaotic Financial Model

1  Introduction

The characteristics based on the dynamics of the system provides the interest of many scientists with its complex and important features. This behavior depends directly on the parameters, which are used to describe the physical phenomenon as well as the sensitivity of the dynamical models with slight change in the initial conditions [1]. These dynamical systems can be widened to have several applications in various branches of science, engineering, and Eco physics. This terminology has been introduced and invented by those researchers who are working in the field of simulating financial and economic systems. This branch deals with some of the physical theories and real-world applications and techniques applied to financial fields [2–4]. The memory effects in the study based on these financial models play an important role to understand these complex systems [5]. In economy, the memory effects can be represented by a fractional order term to describe the model, and hence the role of the fractional calculus has its presence in this part. The fact that integer differentiations can be considered as a local operator, cannot be used to describe these financial systems, and become more realistic through the fractional models to describe the effect of memory on these models.

The concept of fractional calculus has been first introduced by two famous scientists Riemann et al. [6–9]. Since then, many definitions based on the fractional operators have been used to simulate different phenomena, including the Caputo fractional operator, Rieman Liouville operator, and others [10]. Each of these definitions has its properties and drawbacks, which may suit some models more than others. The definition of the fractional operators in terms of Caputo and Riemann Liouville has singular kernels and stasis as some of the exceptional criteria including the index law which promote them to be one of the best definitions in fractional calculus. Nowadays, there has been another rising definition of fractional operators based on the exponential kernels and the generalized Mittag -Lefler functions [11] and also by Atangana et al. (AB) [12]. Several problems have been simulated through different definitions as described. For example, the Caputo fractional derivative has been used to describe the mosaic disease with some optimal control by Vellappandi et al. [13]. A delayed model describing the vector-borne plant epidemic has been studied by Kumar et al. [14] to better understand the behavior of such models. The AB definition can be used to describe the physical phenomenon with its property of preserving information over some time [15]. Recently, there have been many works on the definition of Mittag-Leffler with nonsingular Kernel and their possible applications with different forms. Singh [16] expanded the definition of the Mittag-Leffler law for understanding the rumor spreading through the fractional dynamical model in social networks. In biology, the application of the Mittag-Leffler laws was studied by Qureshi et al. [17] for simulating the blood ethanol concentration leading to some new insight into its dynamics. The smoking dynamic model was investigated by using some of the definitions by Uçar et al. [18]. This study aims to present a new technique for solving a fractional order optimal 4D chaotic financial model under some Mittag-Leffler laws in the following form as:

{0cDtαg1(t)=g3(t)+(g22(t)−β)g1(t),g1(0)=H10cDtαg2(t)=1−βg22(t)−g12(t),g2(0)=H20cDtαg3(t)=−g1(t)+γg2(t)g3(t)−ωg1(t),g3(0)=H30cDtαg4(t)=−ℵg22(t)−Mg12(t),g4(0)=H4,(1)

where 0CDtα is defined as the Caputo fractional derivative and α are the fractional order that is taken between 0 and 1. β,γ,ω,ℵ and M are all positive parameters in the financial model (1). The model (1) represents a more realistic form rather than the integer model, since it is known in financial models that surplus investments are some the examples of investment market contradictions. These points are of a major effect on the interest rates and control input variables. In addition, this flaw is also affected by the irregularity subsequent from the organizational adjustment of the prices. This was the main motivation for using the fractional-order model and trying to adapt some new states of the artificial neural network (ANNs).

Recently, ANNs have been considered one of the most important techniques that have been used to find the solutions to the complex problems. Due to the wide real-life applications in different areas of science and engineering, scientists have been striving for expanding the applications of these techniques along with different properties. For example, El-Mahelawi et al. [19] investigated the solution of some model classifications using the tumors. Sabir et al. [20] adapted the Morlet wavelet neural network for solving a class of nonlinear system to simulate the nervous stomach system. Also, biology has its share of the simulations done with the aid of these methods. For example, the influenza disease model is one of the models that have been solved using a novel design of the ANNs accompanied by the Levenberg-Marquardt backpropagation [21]. COVID- 19 pandemic is one of the most important models that have been solved by Umar et al. in [22]. In addition, Umar et al. [23] proposed a computational framework applying the same algorithm for solving the SIR model, which provides better understanding of dengue fever. For more details regarding the ANNs-LMB method and its applications, the reader may refer to [24–28] and references therein.

This work aims to simulate the nonlinear 4-D chaotic financial model represented in the system (1) to gain more insight into the dynamics of this important model. The ANNs-LMB technique consists of merging the regular artificial neural networks (ANNs) along with the Levenberg-Marquardt backpropagation (LMB), resulting as a new technique. The proposed algorithm is a promising one since it can deal with different complex problems. The main concept of this algorithm is based on the samples of training, testing and verification samples to get the obtained solutions by using the accurate and efficient technique. This method proves to be a valuable key player in stimulating real p = life phenomena, e.g., the simulation of the heat distribution in the human head and simulated using this technique as in [29]. Also, ANNs procedures have been used to solve the third kind of Emden–Fowler model in [30] by Sabir et al. A new solver based on the Meyer fractional neuro-evolution computing method for solving a doubly singular fractional kind of systems [31]. Few other applications of the stochastic methods can be found [32–37] in references therein.

The novelty of the proposed technique can be summarized in the following few points:

•   A model of the 4-D chaotic financial model under some Mittag-Leffler nature and have the benefit of a more realistic application.

•   The proposed technique is used to solve system (1) with the combination of the ANNs-LMB method.

•   The correction of the proposed scheme is observed through the comparison of the proposed and reference solutions.

•   The absolute error is provided in good measure, which authenticates the proposed solver is an accurate and reliable to solve the fractional form of the 4-D chaotic financial problem.

•   The combined features of the ANNs with the LMB enhance the accuracy of the obtained results in terms of error for solving the 4-D chaotic financial problem.

2  Methodology: ANNs-LMB

This section is illustrated the main steps for the proposed technique named the ANNs-LMB method. This method shall be used to solve the 4-D chaotic financial model represented by Eq. (1) along with their initial conditions. The main steps of the proposed algorithm may be summarized in the following few points as:

1-   A numerical method with stochastic features based on the ANNs-LMB technique will be used to solve the model (1).

2-   The effectiveness and robustness of the proposed algorithm will be tested for solving the 4-D chaotic model through the application of the proposed technique.

These main steps are illustrated in Fig. 1 with the action of the multilayer procedure where the method is based on the ANNs-LMB stochastic solver. Fig. 1 demonstrates the use of the ANNs-LMB method for simulating the data and compared it to the reference solution.

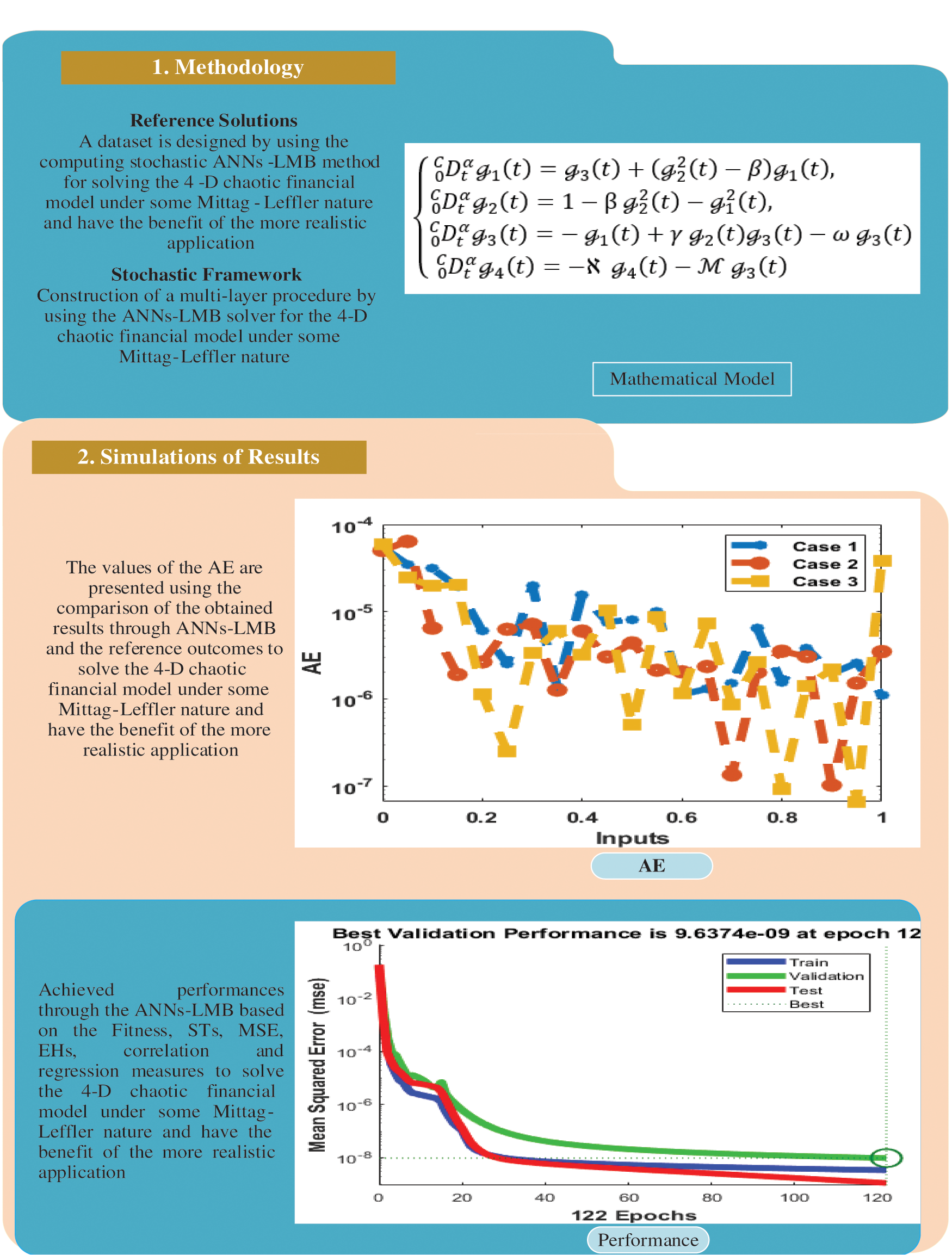
Figure 1: Workflow illustrations of the proposed method for the fractional-order chaotic financial model

3  Numerical Validation

This section is devoted to validating the performance of the proposed technique by using the numerical results. The performance of the method in solving the problem (1) is tested with three different cases of the fractional terms. The mathematical representations of the system (1) are simulated for the setup of parameters in the following form as:

{0cDtαg1(t)=g3(t)+(g22(t)−0.1)g1(t)g1(0)=0.10cDtαg2(t)=1−0.1g22(t)−g12(t),g2(0)=0.20cDtαg3(t)=−g1(t)+0.2g2(t)g3(t)−0.25g1(t),g3(0)=0.30cDtαg4(t)=−0.3g22(t)−0.4g12(t),g4(0)=0.4.(2)

Three cases are investigated for the solution of the system (2) with different values of the fractional order α=0.6,α=0.7, and 0.8, respectively. The complete results have been accomplished using the ANNs-LMB technique with a training value of 73%, testing of 15%, and certification of 12% to solve the model (2). The obtained numerical performances using 14 neurons for using the proposed technique is drawn in Fig. 2.

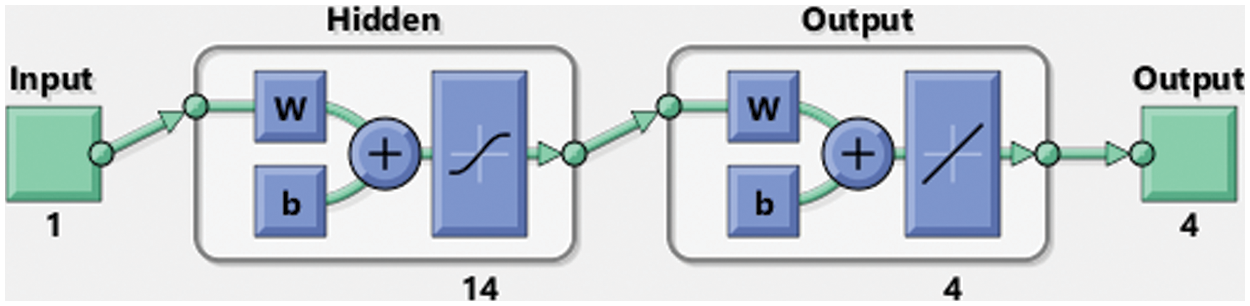
Figure 2: Schematic diagram for the proposed technique to solve the model (2)

The acquired results of the proposed 4-D chaotic system are presented in Tab. 1. The graphical representations of the obtained results for simulating the solution for model (2) are demonstrated in Figs. 3–9. In addition, the performance measures for three cases are provided in Tab. 1. Figs. 3a–3f provides the MSE measure for three cases with different values at epochs as 176 for case I, 165 for case II, and 122 for case III. It can be noticed through these Figs based on the validity and excellent performances of the ANNs-LMB technique producing results of the MSE of 3.281×10−09 for the case I, 2.44×10−10 for case II and 9.64×10−09 for case III. In addition, the gradient value for simulating model (2) for solving the 4-D chaotic financial system is found to have 3.457×10−07 for the case I, 9.86×10−08 for case II and 9.83×10−08 for case III. Figs. 4a–4f represents the exactness and convergence of the ANNs-LMB for the model (2). These fitting curves are plotted and these results are based on the comparative performance of the obtained results through the application of the proposed method. These plots are drawn based on the EH results for approximating model (2) and these values lie in 4.20×10−05 for the case I, 1.70×10−06 for case II and 2.75×10−05 for case III. The verification of the performance of the proposed ANNs-LMB technique is measured through some regression performance measures that can be seen in Figs. 5–7 for cases I, II, and III, respectively. The correlation measures indicate that the regression performance is calculated as one, which proves the perfect model. Fig. 8 provides a comparison of the results obtained for different three cases with some reference results that ensure that the provided method is effective. The AE using the comparative are drawn in Fig. 9 for the 4-D chaotic model. One can find from these data and plots that the acquired results and reference solutions are overlapping for each case of the 4-D chaotic system. The results matching signify the perfection, significance, and precision of the scheme. In addition, the value of the AE for the case I and II is around 10−05 and around 10−06 for case III.

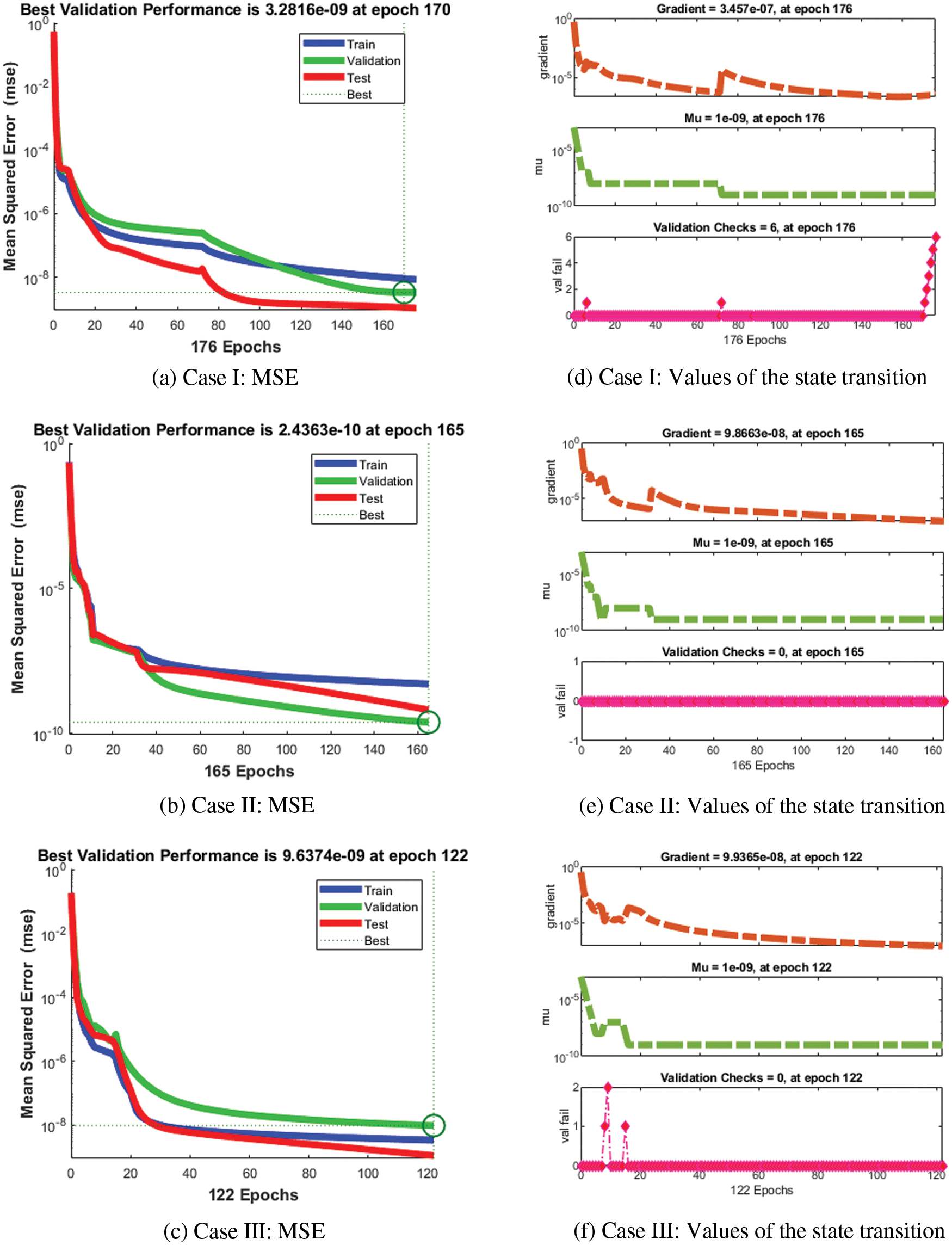
Figure 3: MSE and state transitions to solve model (2)

Figure 4: Comparisons and EHs values for solving problem (2) using ANNs-LMB

Figure 5: Regression measures for case I using the ANNs-LMB

Figure 6: Regression measures for case II using the ANNs-LMB

Figure 7: Regression measures for case III using the ANNs-LMB

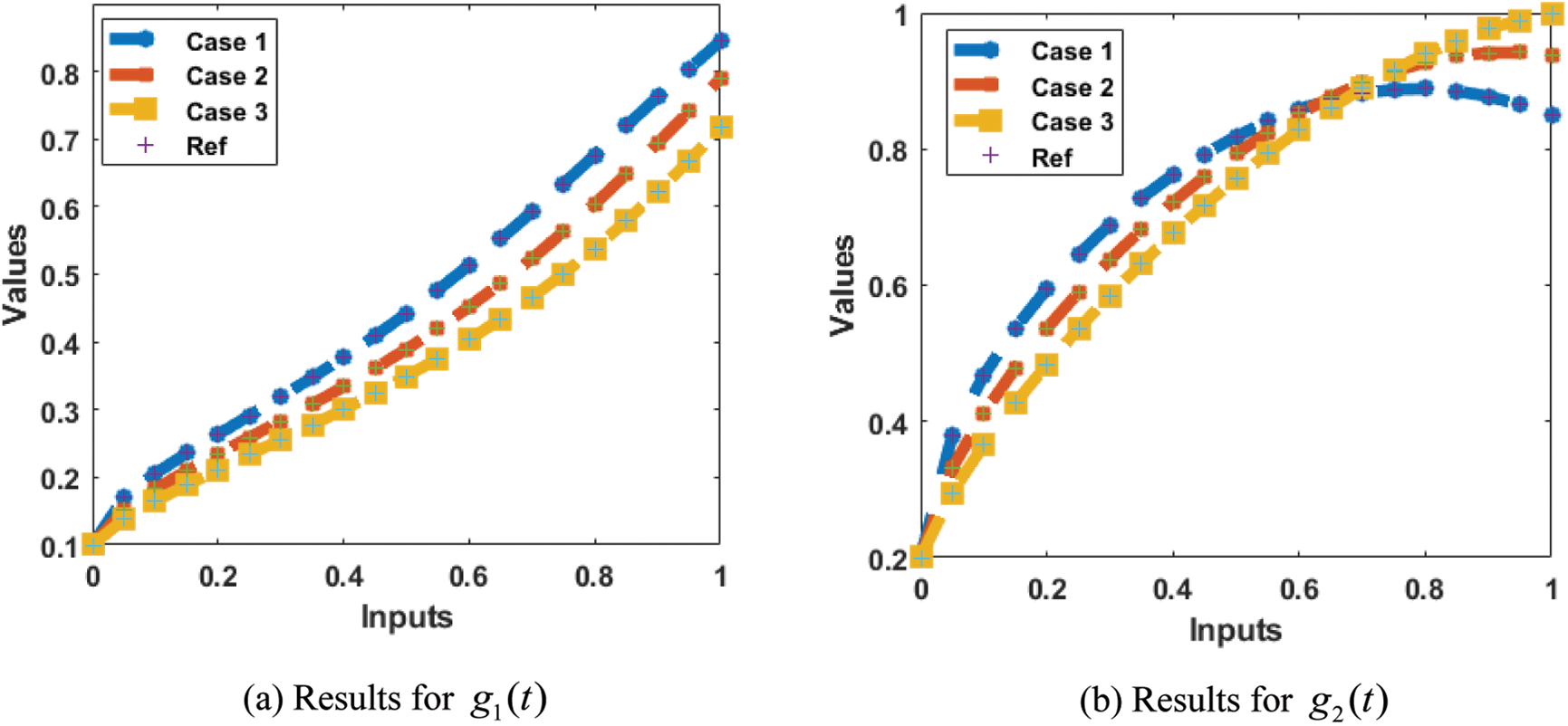
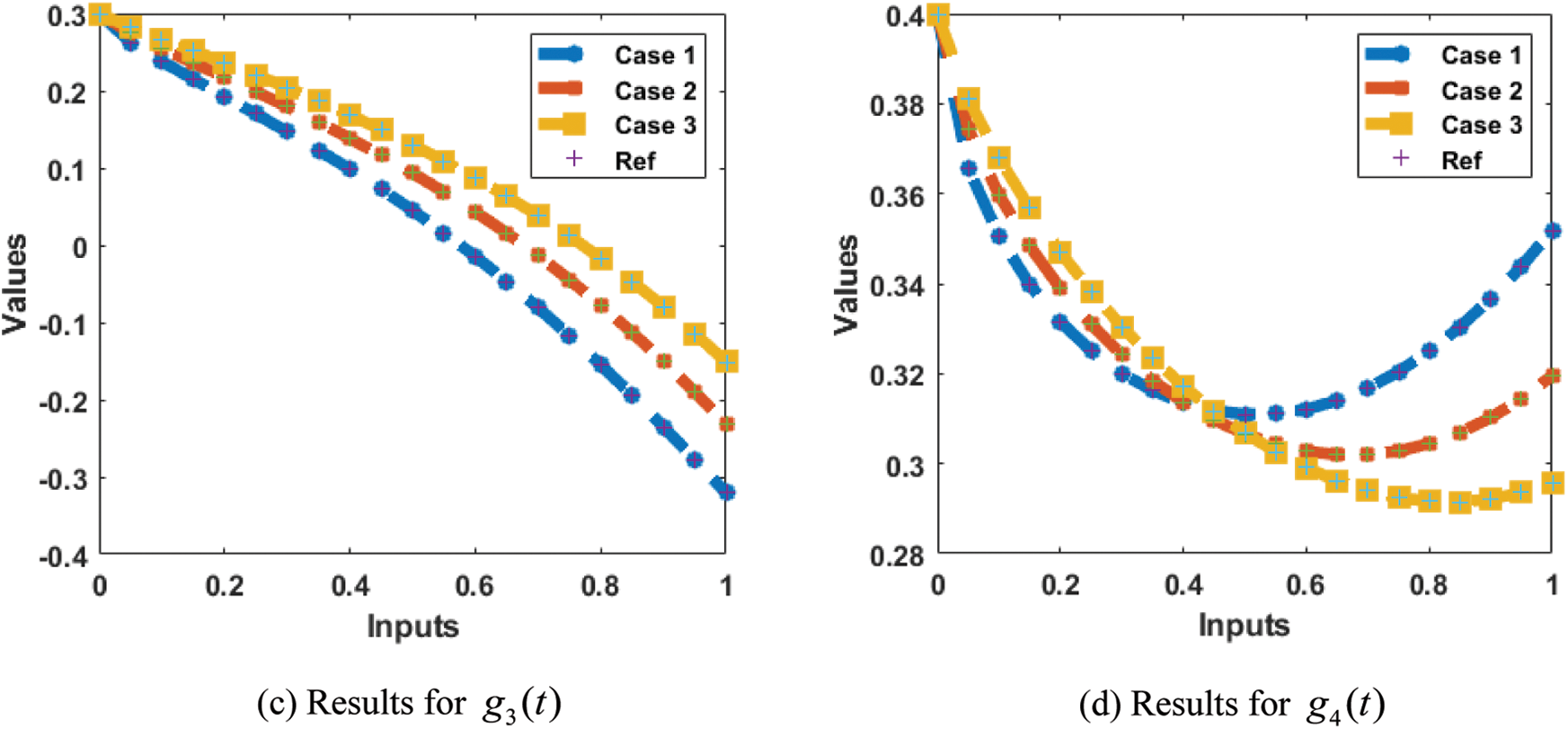
Figure 8: Comparison of the results for model (2)

Figure 9: Measure of AE for the financial system

4  Conclusion

The current study aims to investigate the numerical simulation of a 4-D chaotic financial system under some Mittag-Leffler laws using a combination of the artificial neural network and the Levenberg-Marquardt backpropagation techniques named the ANNs-LMB technique. The fractional order derivatives have been implemented to perform more realistic solutions of the 4-D chaotic financial system. The computational scheme is applied for three variations of the fractional kinds of models using different fractional values. The statics proportions have been applied as 73%, 15%, and 12% for training, testing, and certification for the 4-D chaotic model. The number of neurons used is 14 to solve the model. The numerical outcomes for the nonlinear fractional chaotic system are obtained by using the ANNs-LMB technique in order to reduce the MSE for the acquired approximate solutions. To ensure the reliability, and effectiveness of the scheme, the numerical measure is plotted and compared to a reference solution. The absolute error is provided in good ranges, which shows the competence of the proposed stochastic solver. The performance of the technique is witnessed to be ideal for the proposed model in terms of precision and accuracy.

Future Research Directions: The method can be considered a promising new solver, which can be applied to solve more complicated nonlinear problems [38–43].

Funding Statement: This project is funded by National Research Council of Thailand (NRCT) and Khon Kaen University: N42A650291.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  E. N. Lorenz, “Deterministic nonperiodic flow,” Journal of the Atmospheric Sciences, vol. 20, no. 2, pp. 130–141, 1963. [Google Scholar]

 2.  İ. O. Baycan and G. Yildirim, “Examining the dynamics of the Turkish manufacturing industry: A hidden Markov model approach,” Chinese Journal of Physics, vol. 55, no. 3, pp. 703–709, 2017. [Google Scholar]

 3.  C. W. Chen and W. J. Ma, “Toward a scenario with complementary stochastic and deterministic information in financial fluctuations,” Chinese Journal of Physics, vol. 56, no. 3, pp. 853–862, 2018. [Google Scholar]

 4.  W. T. Yu and H. Y. Chen, “Herding and zero-intelligence agents in the order book dynamics of an artificial double auction market,” Chinese Journal of Physics, vol. 56, no. 4, pp. 1405–1414, 2018. [Google Scholar]

 5.  C. Ma and X. Wang, “Hopf bifurcation and topological horseshoe of a novel finance chaotic system,” Communications in Nonlinear Science and Numerical Simulation, vol. 17, no. 2, pp. 721–730, 2012. [Google Scholar]

 6.  M. Caputo, “Linear model of dissipation whose q is almost frequency independent-II,” Geophysical Journal International, vol. 13, no. 5, pp. 529–539, 1967. [Google Scholar]

 7.  N. H. Aljahdaly, R. P. Agarwal, R. Shah and T. Botmart, “Analysis of the time fractional-order coupled Burgers equations with non-singular kernel operators,” Mathematics, vol. 9, no. 2326, pp. 1–24, 2021. [Google Scholar]

 8.  A. Atangana and A. Akgül, “On solutions of fractal fractional differential equations,” Discrete & Continuous Dynamical Systems-S, vol. 14, no. 10, pp. 3441–3457, 2021. [Google Scholar]

 9.  J. Losada and J. J. Nieto, “Properties of a new fractional derivative without singular kernel,” Progress in Fractional Differentiation and Applications, vol. 1, no. 2, pp. 87–92, 2015. [Google Scholar]

10. Z. Sabir, T. Botmart, M. A. Z. Raja and W. Weera, “An advanced computing scheme for the numerical investigations of an infection-based fractional-order nonlinear Prey-Predator system,” PLoS One, vol. 17, no. 3, pp. 1–13, 2022. [Google Scholar]

11. M. Caputo and M. Fabrizio, “A new definition of fractional derivative without singular kernel,” Progress in Fractional Differentiation and Applications, vol. 1, no. 2, pp. 1–13, 2015. [Google Scholar]

12. A. Atangana and D. Baleanu, “New fractional derivatives with nonlocal and non-singular Kernel theory and application to heat transfer model,” The Journal Thermal Science, vol. 20, no. 2, pp. 1–8, 2015. [Google Scholar]

13. M. Vellappandi, P. Kumar, V. Govindaraj and W. Albalawi, “An optimal control problem for mosaic disease via Caputo fractional derivative,” Alexandria Engineering Journal, vol. 61, no. 10, pp. 8027–8037, 2022. [Google Scholar]

14. P. Kumar, D. Baleanu, V. S. Erturk, M. Inc and V. Govindaraj, “A delayed plant disease model with Caputo fractional derivatives,” Advances in Continuous and Discrete Models, vol. 2022, no. 1, pp. 1–22, 2022. [Google Scholar]

15. J. F. Gómez-Aguilar and A. Atangana, “New insight in fractional differentiation: Power, exponential decay and Mittag-Leffler laws and applications,” European Physical Journal Plus, vol. 132, no. 1, pp. 1–21, 2017. [Google Scholar]

16. J. Singh, “A new analysis for fractional rumor spreading dynamical model in a social network with Mittag-Leffler law,” Chaos, vol. 29, no. 1, pp. 1–8, 2019. [Google Scholar]

17. S. Qureshi, A. Yusuf, A. A. Shaikh, M. Inc and D. Baleanu, “Fractional modeling of blood ethanol concentration system with real data application,” Chaos, vol. 29, no. 1, pp. 1–9, 2019. [Google Scholar]

18. S. Uçar, E. Uçar, N. Özdemir and Z. Hammouch, “Mathematical analysis and numerical simulation for a smoking model with Atangana–Baleanu derivative,” Chaos, Solitons & Fractals, vol. 118, pp. 300–306, 2019. [Google Scholar]

19. J. K. El-Mahelawi, J. U. Abu-Daqah, R. I. Abu-Latifa, B. S. Abu-Nasser and S. S. Abu-Naser, “Tumor classification using artificial neural networks,” International Journal of Academic Engineering Research, vol. 4, no. 11, pp. 1–10, 2020. [Google Scholar]

20. Z. Sabir, M. A. Z. Raja, S. R. Mahmoud, M. Balubaid, A. Algarni et al., “A novel design of morlet wavelet to solve the dynamics of nervous stomach nonlinear model,” International Journal of Computational Intelligence Systems, vol. 15, no. 1, pp. 1–15, 2022. [Google Scholar]

21. Z. Sabir, T. Botmart, M. A. Z. Raja, R. Sadat, M. R. Ali et al., “Artificial neural network scheme to solve the nonlinear influenza disease model,” Biomedical Signal Processing and Control, vol. 75, pp. 1–13, 2022. [Google Scholar]

22. M. Umar, Z. Sabir, M. A. Z. Raja, S. Javeed, H. Ahmad et al., “Numerical investigations through ANNs for solving COVID-19 model,” International Journal of Environmental Research and Public Health, vol. 18, no. 22, pp. 1–15, 2021. [Google Scholar]

23. M. Umar, Kusen, M. A. Z. Raja, Z. Sabir and Q. Al-Mdallal, “A computational framework to solve the nonlinear dengue fever SIR system,” Computer Methods in Biomechanics and Biomedical Engineering, vol. 14, pp. 1–14, 2022. [Google Scholar]

24. H. Sun and R. Grishman, “Lexicalized dependency paths based supervised learning for relation extraction,” Computer Systems Science and Engineering, vol. 43, no. 3, pp. 861–870, 2022. [Google Scholar]

25. H. Sun and R. Grishman, “Employing lexicalized dependency paths for active learning of relation extraction,” Intelligent Automation & Soft Computing, vol. 34, no. 3, pp. 1415–1423, 2022. [Google Scholar]

26. M. Kannaiyan and J. G. T. Raghuvaran, “Prediction of specific wear rate for LM25/ZrO2 composites using Levenberg–Marquardt backpropagation algorithm,” Journal of Materials Research and Technology, vol. 9, no. 1, pp. 530–538, 2020. [Google Scholar]

27. A. Manik, A. Adiwijaya and D. Q. Utama, “Classification of electrocardiogram signals using principal component analysis and Levenberg Marquardt backpropagation for detection ventricular tachyarrhythmia,” Journal of Data Science and Applications, vol. 2, no. 1, pp. 29–37, 2019. [Google Scholar]

28. J. Zhao, H. Nguyen, T. Nguyen-Thoi, P. G. Asteris and J. Zhou, “Improved Levenberg–Marquardt backpropagation neural network by particle swarm and whale optimization algorithms to predict the deflection of RC beams,” Engineering with Computers, vol. 37, pp. 1–23, 2021. [Google Scholar]

29. M. A. Z. Raja, M. Umar, Z. Sabir, J. A. Khan and D. Baleanu, “A new stochastic computing paradigm for the dynamics of nonlinear singular heat conduction model of the human head,” European Physical Journal Plus, vol. 133, no. 9, pp. 1–21, 2018. [Google Scholar]

30. Z. Sabir, M. Umar, J. L. Guirao, M. Shoaib and M. A. Z. Raja, “Integrated intelligent computing paradigm for nonlinear multi-singular third-order Emden–Fowler equation,” Neural Computing and Applications, vol. 33, no. 8, pp. 3417–3436, 2021. [Google Scholar]

31. M. A. Z. Raja, J. Mehmood, Z. Sabir, A. K. Nasab and M. A. Manzar, “Numerical solution of doubly singular nonlinear systems using neural networks-based integrated intelligent computing,” Neural Computing and Applications, vol. 31, no. 3, pp. 793–812, 2019. [Google Scholar]

32. Z. Sabir, M. A. Z. Raja, M. Shoaib and J. G. Aguilar, “FMNEICS: Fractional Meyer neuro-evolution-based intelligent computing solver for doubly singular multi-fractional order Lane–Emden system,” Computational and Applied Mathematics, vol. 39, no. 4, pp. 1–18, 2020. [Google Scholar]

33. Z. Sabir, J. L. Guirao and T. Saeed, “Solving a novel designed second order nonlinear Lane–Emden delay differential model using the heuristic techniques,” Applied Soft Computing, vol. 102, pp. 1–12, 2021. [Google Scholar]

34. Z. Sabir, D. Baleanu, M. A. Z. Raja and J. L. Guirao, “Design of neuro-swarming heuristic solver for multi-pantograph singular delay differential equation,” Fractals, vol. 29, no. 5, pp. 2140022–2140049, 2021. [Google Scholar]

35. Z. Sabir, “Stochastic numerical investigations for nonlinear three-species food chain system,” International Journal of Biomathematics, vol. 15, no. 4, pp. 1–17, 2022. [Google Scholar]

36. Z. Sabir, “Neuron analysis through the swarming procedures for the singular two-point boundary value problems arising in the theory of thermal explosion,” The European Physical Journal Plus, vol. 137, no. 5, pp. 1–19, 2022. [Google Scholar]

37. T. Saeed, Z. Sabir, M. S. Alhodaly, H. H. Alsulami and Y. G. Sánchez, “An advanced heuristic approach for a nonlinear mathematical based medical smoking model,” Results in Physics, vol. 32, pp. 1–13, 2022. [Google Scholar]

38. H. M. Baskonus, M. S. Osman, M. Ramzan, M. Tahir and S. Ashraf, “On pulse propagation of soliton wave solutions related to the perturbed Chen–Lee–Liu equation in an optical fiber,” Optical and Quantum Electronics, vol. 53, no. 10, pp. 1–17, 2021. [Google Scholar]

39. W. Adel and A. Yildirim, “Studying the thermal analysis of rectangular cross section porous fin: A numerical approach,” Computational Methods for Differential Equations, vol. 10, no. 2, pp. 338–350, 2022. [Google Scholar]

40. E. Ilhan, P. Veeresha and H. M. Baskonus, “Fractional approach for a mathematical model of atmospheric dynamics of CO2 gas with an efficient method,” Chaos, Solitons & Fractals, vol. 152, pp. 111347, 2021. [Google Scholar]

41. M. Izadi, Ş Yüzbaşı and W. Adel, “Two novel bessel matrix techniques to solve the squeezing flow problem between infinite parallel plates,” Computational Mathematics and Mathematical Physics, vol. 61, no. 12, pp. 2034–2053, 2021. [Google Scholar]

42. P. Veeresha, N. S. Malagi, D. G. Prakasha and H. M. Baskonus, “An efficient technique to analyze the fractional model of vector-borne diseases,” Physica Scripta, vol. 97, no. 5, pp. 054004, 2022. [Google Scholar]

43. Z. Sabir, H. A. Wahab, S. Javeed and H. M. Baskonus, “An efficient stochastic numerical computing framework for the nonlinear higher order singular models,” Fractal and Fractional, vol. 5, no. 4, pp. 1–14, 2021. [Google Scholar]