Submit

Login Login

Register Register

Home/ Journals/ CMC/ Vol.74, No.3, 2023/ 10.32604/cmc.2023.034362

Table of Content

iconOpen Access

ARTICLE

crossmark

A Stochastic Framework for Solving the Prey-Predator Delay Differential Model of Holling Type-III

Naret Ruttanaprommarin1, Zulqurnain Sabir2,3, Rafaél Artidoro Sandoval Núñez4, Emad Az-Zo’bi5, Wajaree Weera6, Thongchai Botmart6,*, Chantapish Zamart6

1 Department of Science and Mathematics, Faculty of Industry and Technology, Rajamangala University of Technology Isan Sakonnakhon Campus, Sakonnakhon, 47160, Thailand
2 Department of Mathematics and Statistics, Hazara University, Mansehra, Pakistan
3 Department of Mathematical Sciences, United Arab Emirates University, P. O. Box 15551, Al Ain, UAE
4 Universidad Nacional Autónoma de Chota, Cajamarca, Perú
5 Department of Mathematics and Statistics, Mutah University, Mutah-Al Karak-Jordan
6 Department of Mathematics, Faculty of Science, Khon Kaen University, Khon Kaen, 40002, Thailand

* Corresponding Author: Thongchai Botmart. Email: email

Computers, Materials & Continua 2023, 74(3), 5915-5930. https://doi.org/10.32604/cmc.2023.034362

Received 14 July 2022; Accepted 14 October 2022; Issue published 28 December 2022

Abstract

The current research aims to implement the numerical results for the Holling third kind of functional response delay differential model utilizing a stochastic framework based on Levenberg-Marquardt backpropagation neural networks (LVMBPNNs). The nonlinear model depends upon three dynamics, prey, predator, and the impact of the recent past. Three different cases based on the delay differential system with the Holling 3rd type of the functional response have been used to solve through the proposed LVMBPNNs solver. The statistic computing framework is provided by selecting 12%, 11%, and 77% for training, testing, and verification. Thirteen numbers of neurons have been used based on the input, hidden, and output layers structure for solving the delay differential model with the Holling 3rd type of functional response. The correctness of the proposed stochastic scheme is observed by using the comparison performances of the proposed and reference data-based Adam numerical results. The authentication and precision of the proposed solver are approved by analyzing the state transitions, regression performances, correlation actions, mean square error, and error histograms.

Keywords

1  Introduction

The interactions of the prey and predator present the major evolutionary force, which can be performed to consider the mechanisms impacts based on the population’s cooperation of the ecological societies. Many researchers have designed mathematical models based on the influences of the predator population on the prey along with the density-dependent conditions of the ecology. Several prey-predator systems have been used in the growth ratio of the predator species, which are directly linked to the prey density and its converse processes. The prey’s growth ratio can be directly linked to the density of the predator at the current time, and predictably, the predator’s growth ratio is dependent on the prey density in the present [1,2]. Hence, the biological impacts are more reasons to use the fading effects of the memory that can significantly alter the dynamics. Few more recent studies based on the density of past prey using the prey-predator interactions are presented in the references [3–6].

The perception of the effect presented by Allee provides a positive form of the correlation between the size of the population and specific fitness [7–12]. Most prey-predator relations are considered with the prey’s logistic growth. The Allee effect using the prey dynamics provides the population difficulties, including deficient alimentation at low densities, mate restriction, genetic drift, inbreeding depression, and predator evading of defense [13–17]. As a result, the Allee effects are considered a crucial component for biological regulators and frequently increase the loss probability [18]. These effects can perform the strong/weak relations associated with the growth ratio. The strong effects of the Allee [19–21] show the growth rate (positive) per capita, while the weak effects of the Allee suggest a growth rate (negative) per capita. The presence of Allee impacts has already been discussed in various biological creatures, like mammals (suricates) [22], insects (Glanville fritillary butterfly) [23], and marine invertebrates (gastropod) [24].

Since a few of the transitions from one to another state cannot be instantaneous, the interactions of the prey-predator models using the time delay have gained immense importance over the last few decades [25–27]. The dynamic of the natural populations presents constancy, which is related to the species response. The time delay form impacts the population’s constancy [28,29]. Consequently, the time delay conditions are used in various ordinary differential systems. In various mechanisms, the use of time delay provides the system’s destabilization using the co-occurrence state via Hopf bifurcation, along with the dynamics of the strong oscillation [30,31]. Few investigations have been presented in the literature along with the discussion of the Allee effects that make the system’s stability with time delay [32]. In the population dynamics, two biological mechanisms named as competition and cooperation have gained colossal importance using the time delay. Competition in the population commonly arises for food, while the cooperation in the population usually means evading the predator or adopting the prey.

The purpose of the present investigations is to provide the numerical results for the delay differential system using the stochastic framework based on the Levenberg-Marquardt backpropagation neural networks (LVMBPNNs). The interaction dynamics of the prey-predator, along with the delays in the prey’s cooperation/competition factors exposed to the effects of Allee with fading memory, have never been discussed before using the LVMBPNNs stochastic scheme. Stochastic computing studies have been defined to solve several singular, complex and complicated dynamical models. Few of them are food chain models [33,34], HIV dynamical models [35], the dynamics of the coronavirus systems [36], the singular form of the thermal explosion theory [37], eye surgery differential model [38,39], smoking differential model [40], and singular differential models [41]. The novel outputs of the proposed study are presented as follows:

•   A nonlinear form of the mathematical prey-predator system, including two delay factors based on the dynamics of the competition and cooperation, is provided using the prey Allee effects along with the Holling 3rd type.

•   The numerical solutions of the prey-predator with the delay factors in the Allee effects and the Holling 3rd type are presented using the LVMBPNNs stochastic framework.

•   Using the suggested LVMBPNNs stochastic method, three alternative deviations of the nonlinear dynamical delay factors in the Allee effects and the Holling third type of model have been numerically stimulated.

•   By comparing the results of the acquired and the reference solutions, one can see the brilliance of the LVMBPNNs stochastic scheme.

•   The reliability of the LVMBPNNs stochastic method is performed by using the absolute error (AE) performances for solving the prey-predator model with the delay factors in the Allee effects along with the Holling 3rd type.

•   The regression, state transitions, error histograms, mean square error, and correlation performances are provided using the LVMBPNNs stochastic scheme for the delay differential mathematical system.

The organization of the paper is provided as follows: Section 2 performs the mathematical form of the delay models. The proposed network structure is provided in Section 3, while Section 4 provides the simulations of the results. Conclusions are reported in the last Section.

2  Mathematical Model

This section provides a nonlinear form of the mathematical prey-predator system, including two delay factors based on the dynamics of the competition and cooperation, using the prey Allee effects. The predator density is dependent on both present and past prey populations. In the model, a weakening form of memory is also added. The competition form of the delay factor induces instability, while the delay factor induces the system’s stability through the Hopf bifurcation.

The prey-predator model, along with the Allee effects with two-time delay constant factors combined with the prey dynamics, is presented. The fading form of the memory factor is considered using the predator’s growth ratio. Therefore, a biological system based on the growth ratio in predator species is considered, which is dependent upon the prey density. The predator’s functional response in the interactions of the prey-predator has been categorized in four forms called Holling I–IV type. The Holling 3rd type shows the functional response to the positive predation effects correlated to the prey population. The predation effect enhances with the increment in the population of the prey. Such responses are typically considered when the predator efficiently finds an alternate source with a low prey density. There are many investigations that have been presented based on the Allee effects and Holling 3rd type using the functional response [42]. The delayed mathematical model with the Holling 3rd type using the functional response is provided as [43]:

{ dP(x)dx=ϕP(x)(1−Px1k)(Px1−h)−a(P(x))2Q(x)b+(P(x))2             P(0)=c1,[7pt]dQ(x)dx=υa(R(x))2Q(x)b+(R(x))2−ξQ(x)−S(Q(x))2                   Q(0)=c2,[7pt]dR(x)dx=1d(P(x)−R(x))                                                          R(0)=c3,(1)

where Px1=P(x−τ1) and Px2=P(x−τ2) are the time delay terms in the system (1). The parameters used in the delay differential weakening memory system are provided in Table 1.

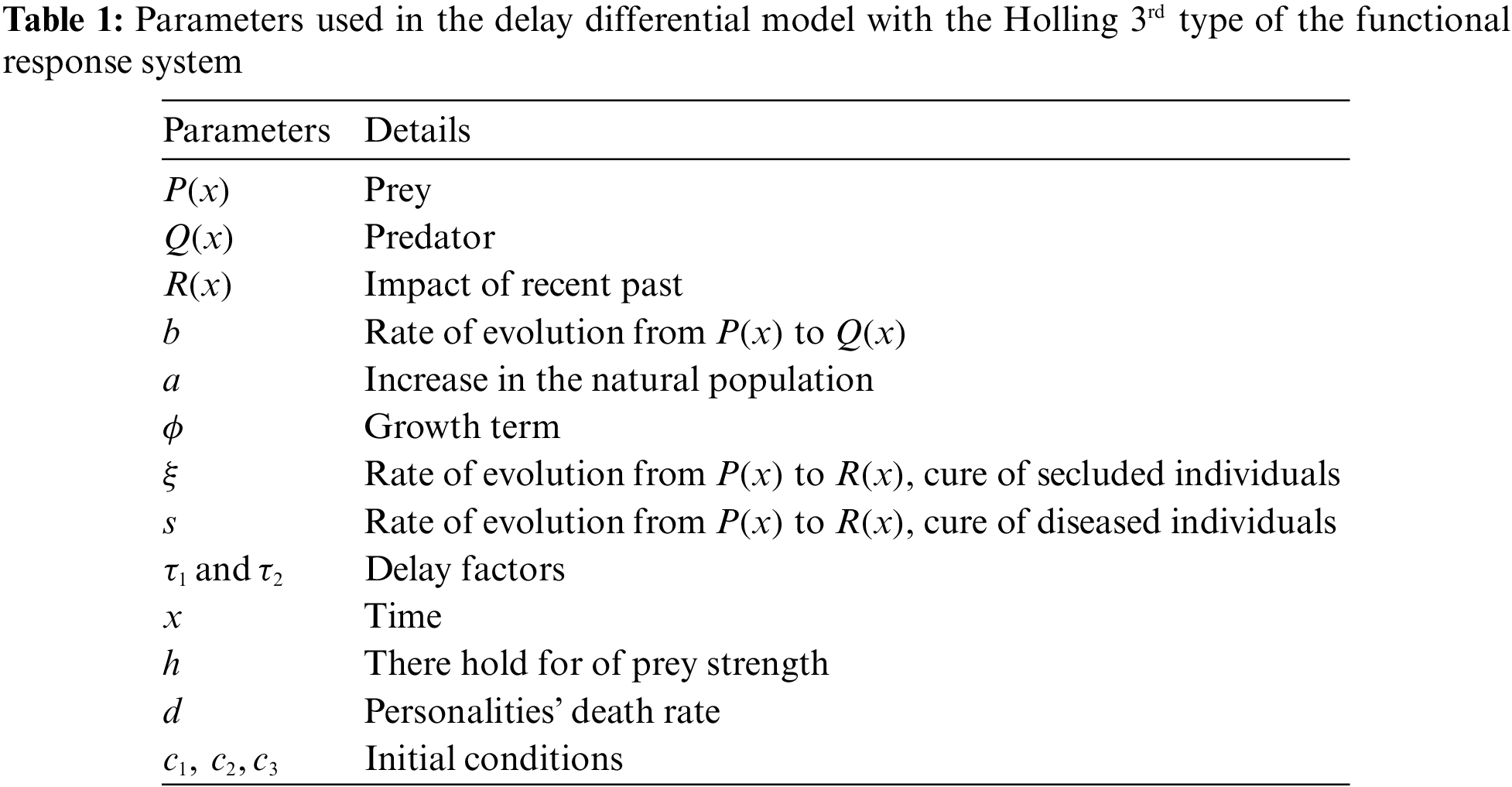
images

3  Stochastic LVMBPNNs Methodology

The current section performs the Levenberg-Marquardt backpropagation neural networks (LVMBPNNs) stochastic structure for solving the prey-predator model with the delay factors in the Allee effects along with the Holling 3rd type as:

•   The necessary operator performances by using the LVMBPNNs stochastic scheme are provided.

•   In addition, the implementation procedures based on the LVMBPNNs scheme are provided to solve the prey-predator model with the delay factors in the Allee effects along with the Holling 3rd type.

Fig. 1 presents the optimization performances using the multi-layer procedures based on the LVMBPNNs stochastic scheme. In addition, the statistic computing framework for solving the delay differential system is provided through the selection of 12%, 11% and 77% for training, testing, and verification, along with 13 neurons.

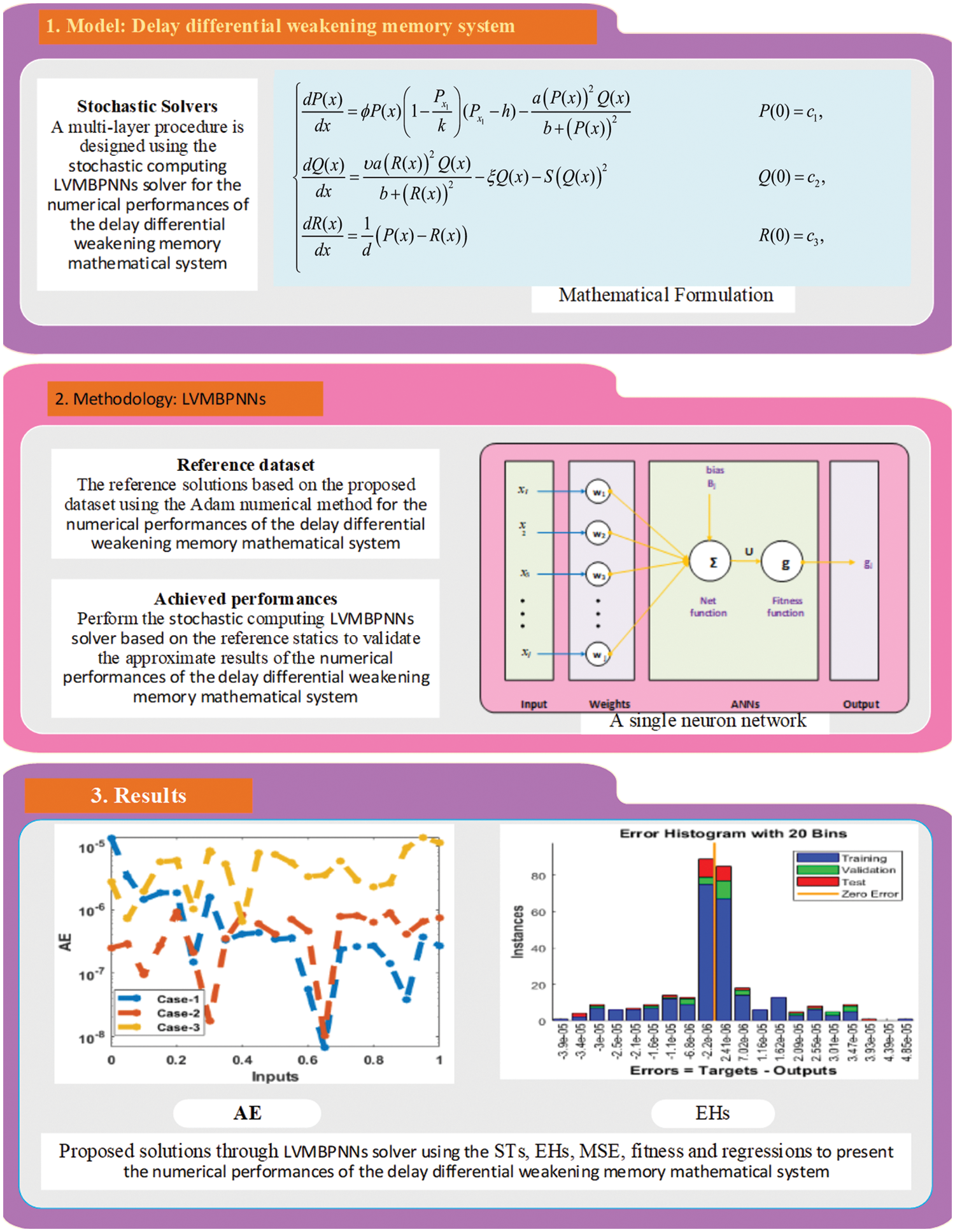
images

Figure 1: Proposed LVMBPNNs procedure for solving the delay factor based on the Holling 3rd type of the functional response

4  Numerical Simulations

This section provides numerical simulations for three different variations of the delay differential weakening memory system using the stochastic Levenberg-Marquardt backpropagation neural networks (LVMBPNNs) approach. The mathematical representation of each deviation is presented as:

Case 1: Consider the values a=0.15,b=0.5,d=0.1,τ2=0.5,τ1=0.5,v=0.4,S=0.31,h=0.1,ξ=0.4,k=0.2,ϕ=0.01,c1=0.1,c2=0.2,andc3=0.3 used in the system (1) as:

{ dP(x)dx=0.1P(x)(1−5P(x−0.5))(P(x−0.5)−0.1)−0.15(P(x))2Q(x)0.5+(P(x))2      P(0)=0.1,[6pt]dQ(x)dx=0.21(R(x))2Q(x)0.5+(R(x))2−0.4Q(x)−0.31(Q(x))2                                                    Q(0)=0.2,[6pt]dR(x)dx=10(P(x)−R(x))                                                                                                          R(0)=0.3.(2)

Case 2: Consider the values a=0.15,b=0.5,d=0.1,τ2=0.5,τ1=0.5,v=0.4,S=0.31,h=0.1,ξ=0.4,k=0.2,ϕ=0.01,c1=0.2,c2=0.3andc3=0.4 used in the system (1) as:

{ dP(x)dx=0.1P(x)(1−5P(x−0.5))(P(x−0.5)−0.1)−0.15(P(x))2Q(x)0.5+(P(x))2          P(0)=0.2,[6pt]dQ(x)dx=0.21(R(x))2Q(x)0.5+(R(x))2−0.4Q(x)−0.31(Q(x))2                                                        Q(0)=0.3,[6pt]dR(x)dx=10(P(x)−R(x))                                                                                                            R(0)=0.4.(3)

Case 3: Consider the values a=0.15,b=0.5,d=0.1,τ2=0.5,τ1=0.5,v=0.4,S=0.31,h=0.1,ξ=0.4,k=0.2,ϕ=0.01,c1=0.3,c2=0.4andc3=0.5 used in the system (1) as:

{ dP(x)dx=0.1P(x)(1−5P(x−0.5))(P(x−0.5)−0.1)−0.15(P(x))2Q(x)0.5+(P(x))2        P(0)=0.3,[6pt]dQ(x)dx=0.21(R(x))2Q(x)0.5+(R(x))2−0.4Q(x)−0.31(Q(x))2                                                       Q(0)=0.4,[6pt]dR(x)dx=10(P(x)−R(x))                                                                                                              R(0)=0.5.(4)

The delay differential weakening memory system solutions are provided through the designed LVMBPNNs for three cases. Thirteen neurons have been obtained for the delay differential model by selecting the data as 12%, 11%, and 77% for training, testing, and verification. The construction of the layers based on the hidden input and output is illustrated in Fig. 2.

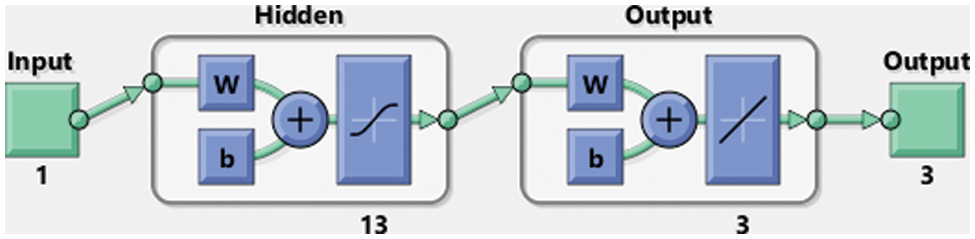
images

Figure 2: Input, hidden, and output layers structure for the delay factor in the Holling 3rd type of mathematical model

The numerical performances for three different cases of the delay factor in the Holling 3rd type of mathematical model are provided in Figs. 3 to 5. The state transitions (STs) and the best performances are provided in Figs. 3 and 4. Fig. 3 represents the STs and mean square error (MSE) depictions for best curves, training, and verification to solve three different deviations of the delay differential system. These precise measures of the delay differential form of the weakening memory system are provided by using the epochs at 45, 74, and 59, which are calculated as 5.8824 × 10−10, 2.7183 × 10−10, and 3.6402 × 10−09, respectively. The gradient operator values have been derived in Fig. 3 for the delay differential system. The performances of these gradient measures have been reported as 9.722 × 10−08, 9.7663 × 10−08, and 9.902 × 10−08 for the delay differential form of the system. These representations of the graphical plots signify the convergence of the LVMBPNNs statistical procedure. Fig. 4 authenticates the design of the fitting cure to obtain the numerical performances of the delay differential form of the weakening memory system. The graphical curve representations provide the result comparisons for each deviation of the delay differential form of the system. The error representations using the authentication, testing, and training measures have been signified to solve the delay differential form of the weakening memory system using the LVMBPNNs stochastic procedure. The EHs plots and the regression presentations are also illustrated in Fig. 4 based on the delay differential form of the system using the LVMBPNNs stochastic procedure. The performances of the EHs have been drawn as 5.60 × 10−06, 2.41 × 10−06, and 1.41 × 10−05 for each deviation of the delay differential form of the system. The plots based on the regression have been illustrated in Fig. 5 to signify the correlation performances. It is indicated that the correlation is reported as one for each deviation of the delay differential form of the system using the LVMBPNNs stochastic procedure. The validation, training, and testing performances label the correctness and exactness of the LVMBPNNs stochastic method to present the numerical solutions of the delay differential form of the system. The convergence based on the MSE through the validation, training, testing performances, generations, complexity, and backpropagation is tabulated in Table 2 for the validation, training, and testing performances based on the LVMBPNNs stochastic operator.

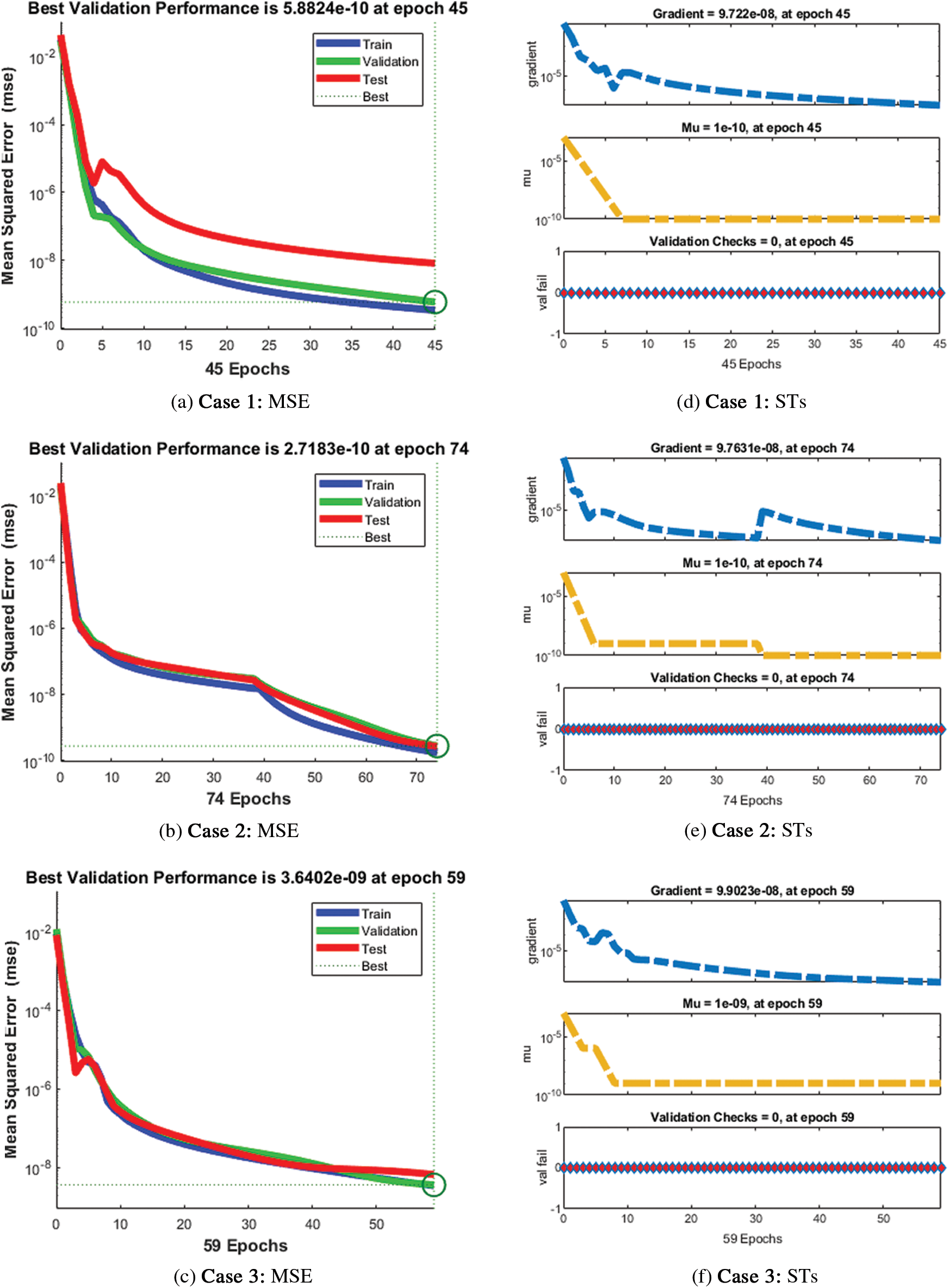
images

Figure 3: Performances of the mean square error and state transitions through the LVMBPNNs for delay factor in the Holling 3rd type of mathematical model

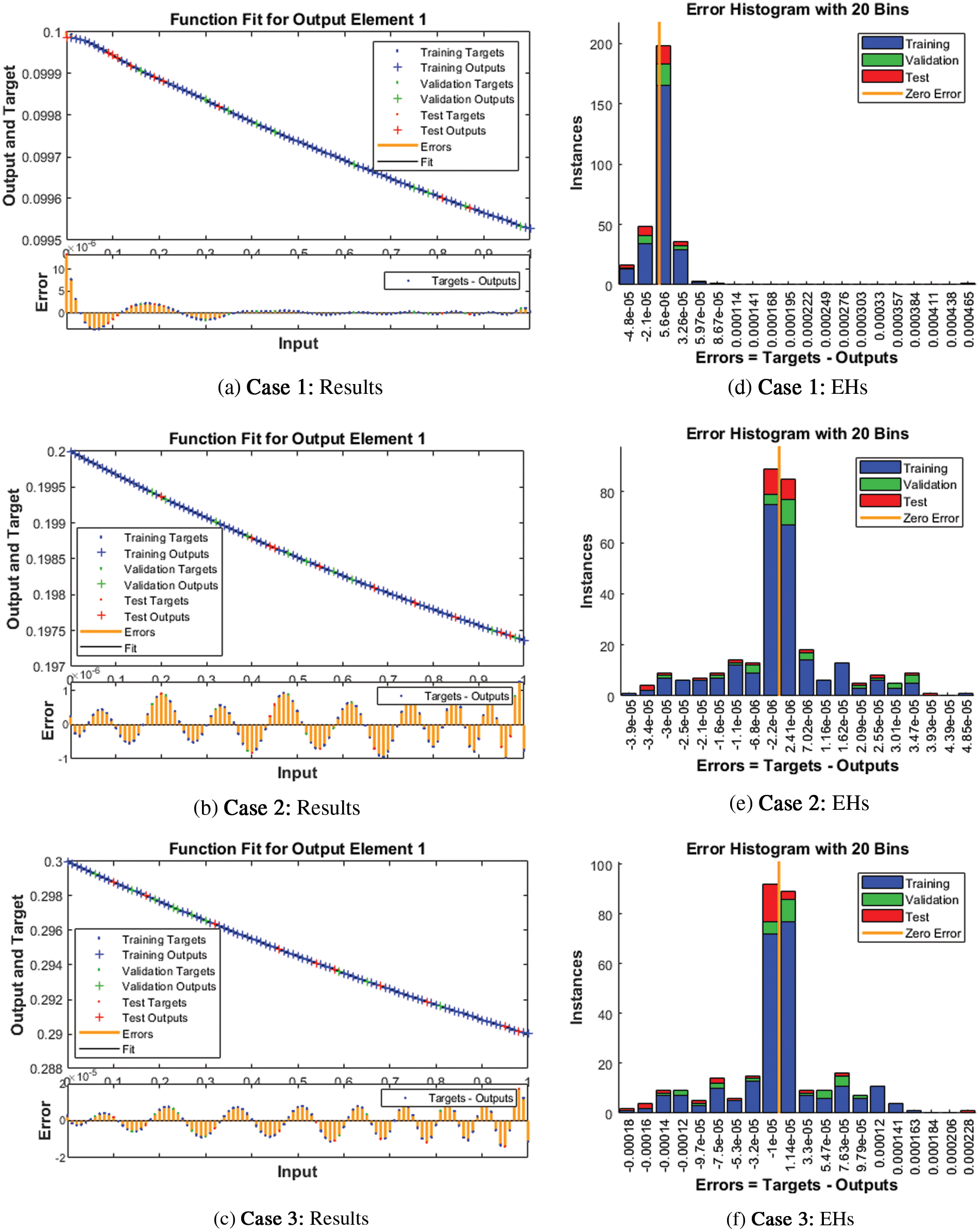
images

Figure 4: Performances of the error histograms and result simulations for the delay factor in the Holling 3rd type of mathematical model

images

Figure 5: Performances of the regression for the delay factor in the Holling 3rd type of mathematical model

images

Figs. 6 and 7 indicate the results comparison and the absolute error (AE) performances based on three different deviations of the validation, training, and testing performances by using the LVMBPNNs stochastic procedure. These plots aim to provide the exactness of the LVMBPNNs stochastic procedure for the delay factor in the Holling 3rd type of mathematical model. Fig. 6 represents the comparison measures based on the obtained and reference solutions for solving the delay factor in the Holling 3rd type of mathematical model using the LVMBPNNs stochastic procedure. The overlapping of the obtained and reference solutions provides the exactness of LVMBPNNs stochastic procedure to solve the obtained and reference solutions. The AE values for the LVMBPNNs stochastic solver based on three different deviations of the delay differential system are provided in Fig. 7. The delay factor in the Holling 3rd type of mathematical model depends upon three dynamics, prey P(x), predator Q(x), and the memory factor in the growth rate of the predator R(x). The AE for prey P(x) is calculated as 10−05 to 10−07, 10−06 to 10−07, and 10−05 to 10−08 for cases 1, 2 and 3 based on the delay differential system. The values of the AE for the predator Q(x) dynamics are found as 10−04 to 10−06, 10−03 to 10−06, and 10−04 to 10−05 for 1st, 2nd and 3rd cases based on the delay differential working memory system. The AE performances of the memory factor in the impact of the recent past R(x) are calculated as 10−05 to 10−07 for each case of the delay differential system. These precise performances enhance the correctness of the LVMBPNNs stochastic procedure for solving the delay factor in the Holling 3rd type of mathematical model.

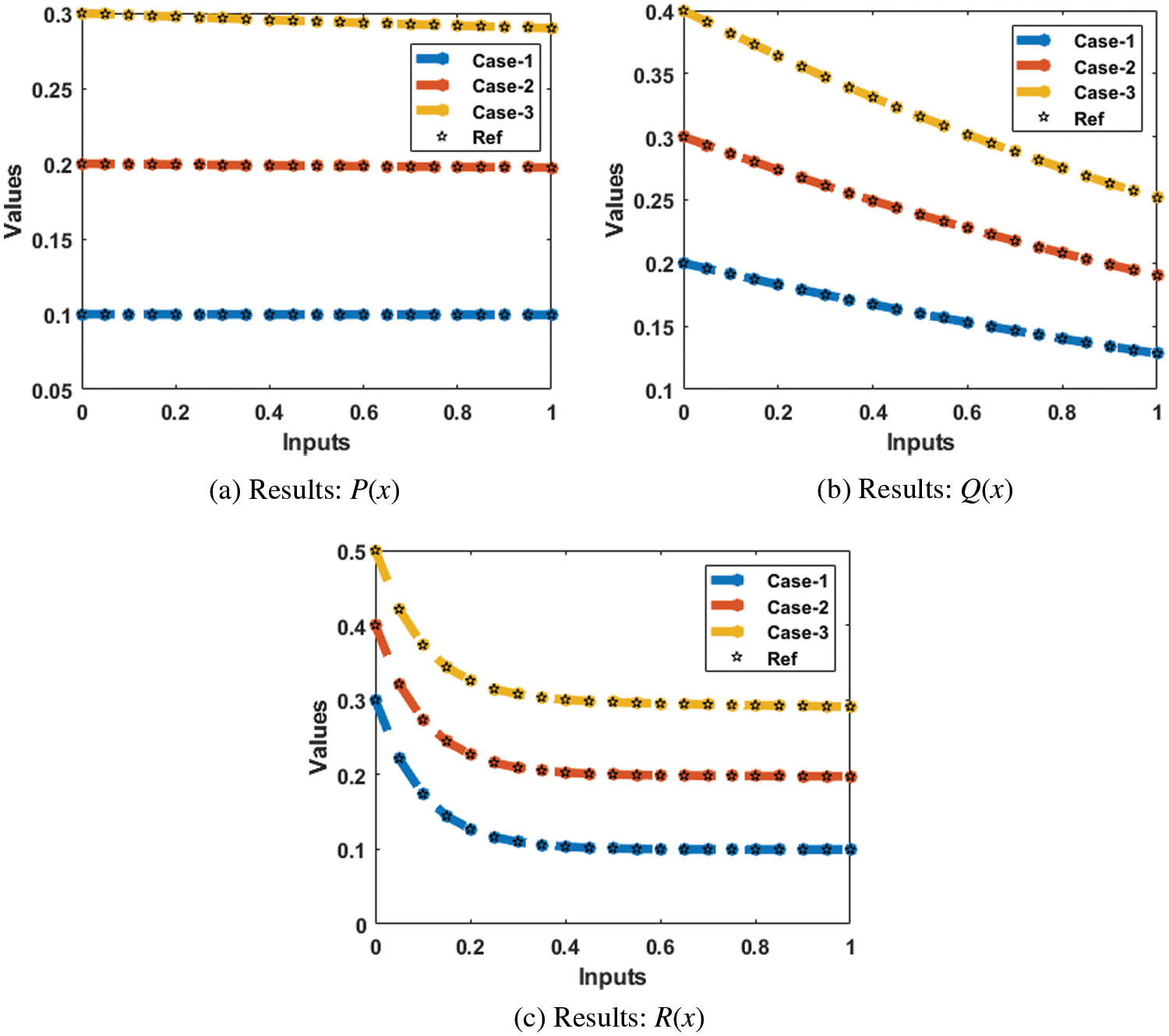
images

Figure 6: Comparison of the results for the prey-predator model based on the delay factor in the Holling 3rd type

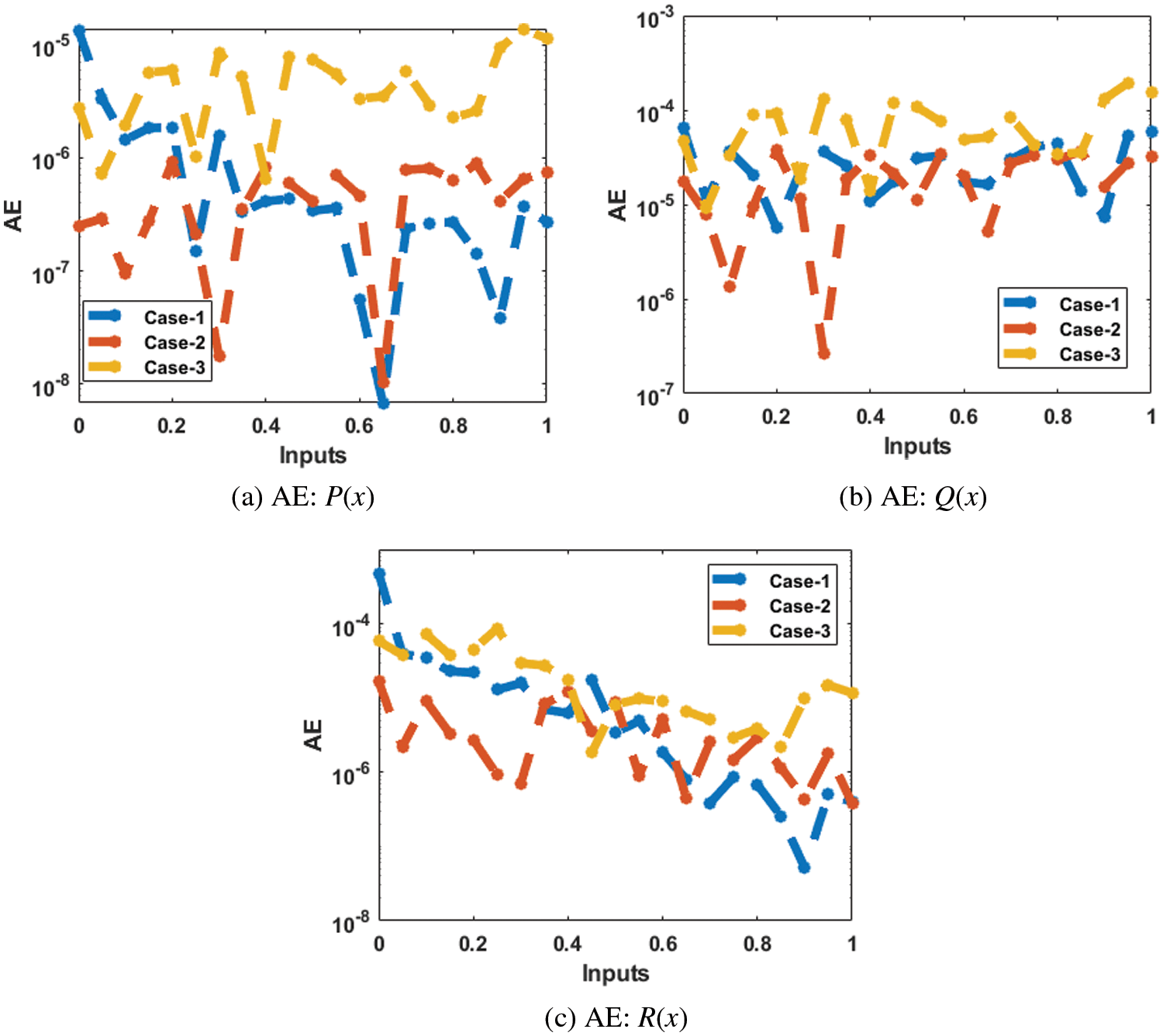
images

Figure 7: AE performances for the delay factor in the Holling 3rd type of mathematical model

5  Conclusions

The current project’s goal is to present numerical simulations of the prey-predator model based on the delay factor in the Holling 3rd type. Prey Allee effects are used to give the nonlinear mathematical prey-predator system, which includes two delay factors based on the dynamics of the competition and cooperation. The predator density is dependent on both present and past prey populations. In the model, a weakening form of memory is also added. The competition form of the delay factor induces instability, while the cooperation form of the delay factor induces the system’s stability through the Hopf bifurcation. Few concluding features of the present study are provided:

•   A nonlinear form of the mathematical prey-predator system, including two delay factors based on the dynamics of the competition and cooperation, is provided using the prey Allee effects along with the Holling 3rd type.

•   The dynamical model is complicated since delay factors are present in it; as a result, the LVMBPNNs stochastic framework is the best option for delivering the numerical results.

•   The statistic computing framework for solving the delay differential system is provided through the selection of 12%, 11%, and 77% for training, testing, and verification, along with 13 neurons.

•   Comparing the obtained and reference solutions demonstrates the accuracy of the LVMBPNNs stochastic framework.

•   The values of the AE are performed in suitable measures, which are calculated around 10−04 to 10−07 for each dynamic of the dynamical model.

Future research directions: The proposed stochastic solver can be used to solve the fractional order delayed differential models [44–51], delayed dynamical models [52–55], and nonlinear systems of differential equations [56,57].

Funding Statement: This research received funding support from the NSRF via the Program Management Unit for Human Resources & Institutional Development, Research and Innovation [Grant Number B05F650018].

Conflicts of Interest: The authors declare that they have no conflicts of intrest to report regarding the present study.

References

  1. M. Cavani and M. Farkas, “Bifurcations in a predator-prey model with memory and diffusion. I: Andronov-hopf bifurcation,” Acta Mathematica Hungarica, vol. 63, no. 3, pp. 213–229, 1994.
  2. J. D. Ferreira, C. A. T. Salazar and P. C. Tabares, “Weak Allee effect in a predator–prey model involving memory with a hump,” Nonlinear Analysis: Real World Applications, vol. 14, no. 1, pp. 536–548, 2013.
  3. M. Umar, Z. Sabir and M. A. Z. Raja, “Intelligent computing for numerical treatment of nonlinear prey–predator models,” Applied Soft Computing, vol. 80, pp. 506–524, 2019.
  4. U. Ghosh, S. Pal and M. Banerjee, “Memory effect on bazykin’s prey-predator model: Stability and bifurcation analysis,” Chaos, Solitons & Fractals, vol. 143, pp. 1–10, 2021.
  5. Z. Sabir, T. Botmart, M. A. Z. Raja and W. Weera, “An advanced computing scheme for the numerical investigations of an infection-based fractional-order nonlinear prey-predator system,” Plos One, vol. 17, no. 3, pp. 1–13, 2022.
  6. B. Sahoo and S. Poria, “Dynamics of predator–prey system with fading memory,” Applied Mathematics and Computation, vol. 347, pp. 319–333, 2019.
  7. A. Gökçe, “The influence of past in a population system involving intraspecific competition and Allee effect,” The European Physical Journal Plus, vol. 137, no. 2, pp. 1–11, 2022.
  8. L. Berec, E. Angulo and F. Courchamp, “Multiple Allee effects and population management,” Trends in Ecology & Evolution, vol. 22, no. 4, pp. 185–191, 2007.
  9. E. Angulo, G. M. Luque, S. D. Gregory, J. W. Wenzel, C. Bessa-Gomes et al., “Allee effects in social species,” Journal of Animal Ecology, vol. 87, no. 1, pp. 47–58, 2018.
  10. B. Souayeh, Z. Sabir, M. Umar and M. W. Alam, “Supervised neural network procedures for the novel fractional food supply model,” Fractal and Fractional, vol. 6, no. 6, pp. 1–15, 2022.
  11. B. Dennis, “Allee effects: Population growth, critical density, and the chance of extinction,” Natural Resource Modeling, vol. 3, no. 4, pp. 481–538, 1989.
  12. T. Perälä, J. A. Hutchings and A. Kuparinen, “Allee effects and the Allee-effect zone in northwest Atlantic cod,” Biology Letters, vol. 18, no. 2, pp. 1–6, 2022.
  13. M. Ghosh, P. Chandra, P. Sinha and J. B. Shukl, “Modelling the spread of carrier-dependent infectious diseases with environmental effect,” Applied Mathematics and Computation, vol. 152, pp. 385–402, 2004.
  14. C. Çelik, H. Merdan, O. Duman and Ö. Akın, “Allee effects on population dynamics with delay,” Chaos, Solitons & Fractals, vol. 37, no. 1, pp. 65–74, 2008.
  15. H. W. Hethcote, “Qualitative analyses of communicable disease models,” Mathematical Biosciences,vol. 28, no. 3–4, pp. 335–356, 1976.
  16. P. C. Tabares, J. D. Ferreira and V. Rao, “Weak Allee effect in a predator-prey system involving distributed delays,” Computational & Applied Mathematics, vol. 30, pp. 675–699, 2011.
  17. J. P. Tripathi, P. S. Mandal, A. Poonia and V. P. Bajiya, “A widespread interaction between generalist and specialist enemies: The role of intraguild predation and allee effect,” Applied Mathematical Modelling,vol. 89, pp. 105–135, 2021.
  18. M. JovanoviĆ and M. KrstiĆ, “Extinction in stochastic predator-prey population model with Allee effect on prey,” Discrete & Continuous Dynamical Systems-B, vol. 22, no. 7, pp. 2651–2667, 2017.
  19. P. J. Pal, T. Saha, M. Sen and M. Banerjee, “A delayed predator–prey model with strong Allee effect in prey population growth,” Nonlinear Dynamics, vol. 68, no. 1, pp. 23–42, 2012.
  20. M. Jankovic and S. Petrovskii, “Are time delays always destabilizing? Revisiting the role of time delays and the Allee effect,” Theoretical Ecology, vol. 7, no. 4, pp. 335–349, 2014.
  21. A. Surendran, M. J. Plank and M. J. Simpson, “Population dynamics with spatial structure and an Allee effect,” Proceedings of the Royal Society A, vol. 476, no. 2242, pp. 1–19, 2020.
  22. F. Courchamp, B. T. Grenfell and T. H. Clutton-Brock, “Impact of natural enemies on obligately cooperative breeders,” Oikos, vol. 91, no. 2, pp. 311–322, 2000.
  23. M. Kuussaari, I. Saccheri, M. Camara and I. Hanski, “Allee effect and population dynamics in the Glanville fritillary butterfly,” Oikos, vol. 82, pp. 384–392, 1998.
  24. A. W. Stoner and M. Ray-Culp, “Evidence for Allee effects in an over-harvested marine gastropod: Density-dependent mating and egg production,” Marine Ecology Progress Series, vol. 202, pp. 297–302, 2000.
  25. Z. Ma, “Hopf bifurcation of a generalized delay-induced predator–prey system with habitat complexity,” International Journal of Bifurcation and Chaos, vol. 30, no. 6, pp. 1–20, 2020.
  26. K. Shah, T. Abdeljawad and R. U. Din, “To study the transmission dynamic of SARS-CoV-2 using nonlinear saturated incidence rate,” Physica A: Statistical Mechanics and its Applications, vol. 604,pp. 1–16, 2022.
  27. H. Yu, M. Zhao and R. P. Agarwal, “Stability and dynamics analysis of time delayed eutrophication ecological model based upon the Zeya reservoir,” Mathematics and Computers in Simulation, vol. 97,pp. 53–67, 2014.
  28. K. Chakraborty, M. Chakraborty and T. K. Kar, “Bifurcation and control of a bioeconomic model of a prey–predator system with a time delay,” Nonlinear Analysis: Hybrid Systems, vol. 5, no. 4, pp. 613–625, 2011.
  29. A. Gökçe, “A mathematical study for chaotic dynamics of dissolved oxygen-phytoplankton interactions under environmental driving factors and time lag,” Chaos, Solitons & Fractals, vol. 151, pp. 1–13, 2021.
  30. A. Gökçe, “Numerical bifurcation analysis for a prey-predator type interactions with a time lag and habitat complexity,” Bitlis Eren Üniversitesi Fen Bilimleri Dergisi, vol. 10, no. 1, pp. 57–66, 2021.
  31. H. Zhao, X. Huang and X. Zhang, “Hopf bifurcation and harvesting control of a bioeconomic plankton model with delay and diffusion terms,” Physica A: Statistical Mechanics and its Applications, vol. 421,pp. 300–315, 2015.
  32. K. Gopalsamy and G. Ladas, “On the oscillation and asymptotic behavior of N˙(t)=N(t)[a+bN(t−τ)−cN2(t−τ)],” Quarterly of Applied Mathematics, vol. 48, pp. 433–440, 1990.
  33. Z. Sabir, “Stochastic numerical investigations for nonlinear three-species food chain system,” International Journal of Biomathematics, vol. 15, no. 4, pp. 1–17, 2022.
  34. R. Naresh, S. Pandey and A. K. Misra, “Analysis of a vaccination model for carrier dependent infectious diseases with environmental effects,” Nonlinear Analysis: Modelling and Control, vol. 13, no. 3, pp. 331–350, 2008.
  35. M. Umar, Z. Sabir, F. Amin, J. L. Guirao and M. A. Z. Raja, “Stochastic numerical technique for solving HIV infection model of CD4+ T cells,” The European Physical Journal Plus, vol. 135, no. 5, pp. 1–19, 2020.
  36. T. Botmart and P. Niamsup, “Exponential synchronization of complex dynamical network with mixed timevarying and hybrid coupling delays via intermittent control,” Advances in Difference Equations,vol. 2014, no. 116, pp. 1–33, 2014.
  37. T. Botmart, N. Yotha, P. Niamsup and W. Weera, “Hybrid adaptive pinning control for function projective synchronization of delayed neural networks with mixed uncertain couplings,” Complexity, vol. 2017,no. 4654020, pp. 1–19, 2017.
  38. M. Umar, F. Amin, H. A. Wahab and D. Baleanu, “Unsupervised constrained neural network modeling of boundary value corneal model for eye surgery,” Applied Soft Computing, vol. 85, pp. 105826, 2019.
  39. B. Wang, J. F. Gomez-Aguilar, Z. Sabir, M. A. Z. Raja, W. F. Xia et al., “Numerical computing to solve the nonlinear corneal system of eye surgery using the capability of Morlet wavelet artificial neural networks,” Fractals, vol. 30, no. 5, pp. 1–19, 2022.
  40. T. Saeed, Z. Sabir, M. S. Alhodaly, H. H. Alsulami and Y. G. Sánchez, “An advanced heuristic approach for a nonlinear mathematical based medical smoking model,” Results in Physics, vol. 32, pp. 105137, 2022.
  41. Z. Sabir and H. A. Wahab, “Evolutionary heuristic with Gudermannian neural networks for the nonlinear singular models of third kind,” Physica Scripta, vol. 96, no. 12, pp. 125261, 2021.
  42. M. R. Ali, S. Raut, S. Sarkar and U. Ghosh, “Unraveling the combined actions of a holling type III predator–prey model incorporating Allee response and memory effects,” Computational and Mathematical Methods, vol. 3, no. 2, pp. 1–18, 2021.
  43. A. Gökçe, “A dynamic interplay between Allee effect and time delay in a mathematical model with weakening memory,” Applied Mathematics and Computation, vol. 430, pp. 127306, 2022.
  44. Z. Sabir, M. A. Z. Raja, M. Shoaib and J. F. Aguilar, “FMNEICS: Fractional Meyer neuro-evolution-based intelligent computing solver for doubly singular multi-fractional order Lane–Emden system,” Computational and Applied Mathematics, vol. 39, no. 4, pp. 1–18, 2020.
  45. H. Günerhan and E. Çelik, “Analytical and approximate solutions of fractional partial differential-algebraic equations,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 109–120, 2020.
  46. K. A. Touchent, Z. Hammouch and T. Mekkaoui, “A modified invariant subspace method for solving partial differential equations with non-singular kernel fractional derivatives,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 2, pp. 35–48, 2020.
  47. Z. Sabir, M. A. Z. Raja, J. L. Guirao and T. Saeed, “Meyer wavelet neural networks to solve a novel design of fractional order pantograph Lane-Emden differential model,” Chaos, Solitons & Fractals, vol. 152,pp. 1–14, 2021.
  48. E. İlhan and İ. O Kıymaz, “A generalization of truncated M-fractional derivative and applications to fractional differential equations,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 171–188, 2020.
  49. K. Shah, M. Arfan, A. Ullah, Q. Al-Mdallal, K. J. Ansari et al., “Computational study on the dynamics of fractional order differential equations with applications,” Chaos, Solitons & Fractals, vol. 157, pp. 1–17, 2022.
  50. M. Sinan, K. Shah, P. Kumam, I. Mahariq, K. J. Ansari et al., “Fractional order mathematical modeling of typhoid fever disease,” Results in Physics, vol. 32, pp. 1–13, 2022.
  51. K. Shah, T. Abdeljawad and A. Ali, “Mathematical analysis of the Cauchy type dynamical system under piecewise equations with Caputo fractional derivative,” Chaos, Solitons & Fractals, vol. 161, pp. 1–8, 2022.
  52. P. Lakshminarayana, K. Vajravelu, G. Sucharitha and S. Sreenadh, “Peristaltic slip flow of a Bingham fluid in an inclined porous conduit with Joule heating,” Applied Mathematics and Nonlinear Sciences, vol. 3,no. 1, pp. 41–54, 2018.
  53. N. Yotha, T. Botmart, K. Mukdasai and W. Weera, “Improved delay-dependent approach to passivity analysis for uncertain neural networks with discrete interval and distributed time-varying delays,” Vietnam Journal of Mathematics, vol. 45, no. 4, pp. 721–736, 2017.
  54. R. Ahmad, A. Farooqi, J. Zhang and N. Ali, “Steady flow of a power law fluid through a tapered non-symmetric stenotic tube,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 1, pp. 255–266, 2019.
  55. T. Botmart and W. Weera, “Guaranteed cost control for exponential synchronization of cellular neural networks with mixed time-varying delays via hybrid feedback control,” Abstract and Applied Analysis,vol. 2013, no. 175796, pp. 1–13, 2013.
  56. H. M. Baskonus, H. Bulut and T. A. Sulaiman, “New complex hyperbolic structures to the lonngren-wave equation by using sine-gordon expansion method,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 1, pp. 129–138, 2019.
  57. J. B. Liu, Y. Bao, W. T. Zheng and S. Hayat, “Network coherence analysis on a family of nested weighted n-polygon networks,” Fractals, vol. 29, no. 8, pp. 1–15, 2021.

Cite This Article

N. Ruttanaprommarin, Z. Sabir, R. A. Sandoval Núñez, E. Az-Zo’bi, W. Weera et al., "A stochastic framework for solving the prey-predator delay differential model of holling type-iii," Computers, Materials & Continua, vol. 74, no.3, pp. 5915–5930, 2023. https://doi.org/10.32604/cmc.2023.034362


cc This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

  • 741

    View

  • 410

    Download

  • 0

    Like

Related articles

Copyright© 2024 Tech Science Press
© 1997-2024 TSP (Henderson, USA) unless otherwise stated

Share Link