 Open Access
Open Access
ARTICLE
Robust Image Watermarking Using LWT and Stochastic Gradient Firefly Algorithm
1 Department of CSE, Koneru Lakshmaiah Education Foundation, Guntur, Andhra Pradesh, 522302, India
2 Deparmtent of CSE, Chandigarh University, Mohali, Punjab, 140413, India
3 Chitkara University Institute of Engineering and Technology, Chitkara University, Punjab, 140401, India
4 College of Computer and Information Sciences, Princess Nourah Bint Abdulrahman University, 84428, Riyadh, 11671,
Saudi Arabia
5 Department of Computer Science, College of Computer Science and Information Systems, Najran University, Najran,
55461, Saudi Arabia
* Corresponding Author: Sachin Sharma. Email:
Computers, Materials & Continua 2023, 75(1), 393-407. https://doi.org/10.32604/cmc.2023.033536
Received 20 June 2022; Accepted 21 September 2022; Issue published 06 February 2023
Abstract
Watermarking of digital images is required in diversified applications ranging from medical imaging to commercial images used over the web. Usually, the copyright information is embossed over the image in the form of a logo at the corner or diagonal text in the background. However, this form of visible watermarking is not suitable for a large class of applications. In all such cases, a hidden watermark is embedded inside the original image as proof of ownership. A large number of techniques and algorithms are proposed by researchers for invisible watermarking. In this paper, we focus on issues that are critical for security aspects in the most common domains like digital photography copyrighting, online image stores, etc. The requirements of this class of application include robustness (resistance to attack), blindness (direct extraction without original image), high embedding capacity, high Peak Signal to Noise Ratio (PSNR), and high Structural Similarity Matrix (SSIM). Most of these requirements are conflicting, which means that an attempt to maximize one requirement harms the other. In this paper, a blind type of image watermarking scheme is proposed using Lifting Wavelet Transform (LWT) as the baseline. Using this technique, custom binary watermarks in the form of a binary string can be embedded. Hu’s Invariant moments’ coefficients are used as a key to extract the watermark. A Stochastic variant of the Firefly algorithm (FA) is used for the optimization of the technique. Under a prespecified size of embedding data, high PSNR and SSIM are obtained using the Stochastic Gradient variant of the Firefly technique. The simulation is done using Matrix Laboratory (MATLAB) tool and it is shown that the proposed technique outperforms the benchmark techniques of watermarking considering PSNR and SSIM as quality metrics.Keywords
Watermarking of digital media is one of the most common requirements in the digital world [1]. A watermark is used as proof of ownership at any stage, for some digital media. The desired features of watermarking applications depend upon the type of applications and the required level of protection. For most applications, a blind watermarking technique that is imperceptible and has sufficient robustness is desirable. The summarization of the domains, types and descriptions of watermarking is comprehensively given in Table 1.
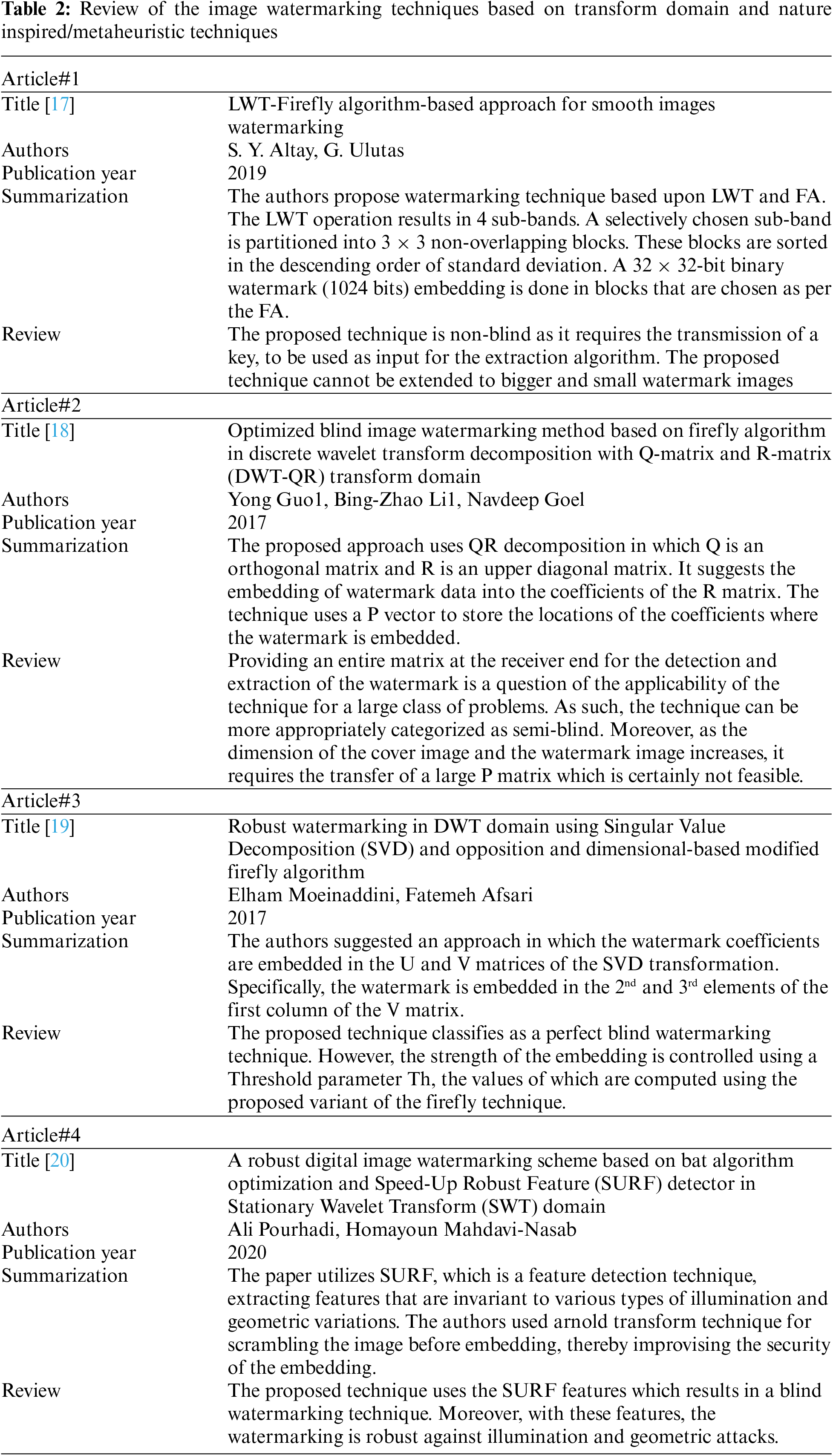
There are a large number of techniques proposed by researchers, for domain and type of watermarking requirements. Recent advancements in computational power have revolutionized the techniques for watermark embedding. This can be harnessed for optimal watermarking using metaheuristic and nature-inspired algorithms [8–10] to achieve desired characteristics as required by the application. In this paper, we focus on watermarking of color images using Lifting Wavelet Transform (LWT) [11], Hu’s Invariant Moments [12] and a proposed variant of Firefly Algorithm (FA) [13] called Stochastic Gradient Descent Firefly Algorithm (SGD-FA). Firefly technique is a nature-inspired technique while Stochastic Gradient Descent [14] is derived from simulated Annealing which belongs to a family of Local Search Artificial Intelligence (AI) techniques.
The primary motivation for using SGD-FA is that the effectiveness of FA depends upon the cost function (CF), formulated by following the desired type of watermarking. In the case of non-linear Cost Function, the algorithm occasionally gets trapped in a local-minima or a plateau or a ridge. A stochastic variant of FA will eliminate such possibilities and enables the algorithm to converge to a global minimum. We use the “local-minima” terminology as the process is gradient descent and not hill climbing. As a typical variation of the cost function, consider the formulation in which the numerator is Mean Square Error, and the denominator is the robustness parameter and embedding capacity. The said function, when plotted with the most common independent parameters like embedding positions, gives the type of plot as shown in Fig. 1.
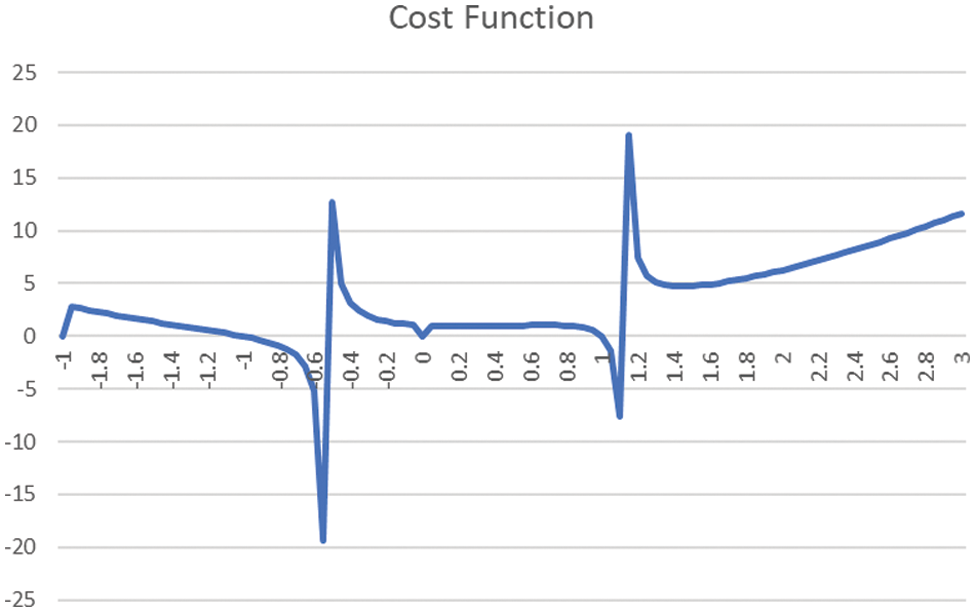
Figure 1: Cost function curve illustration for global/local maxima/minima and ridges
The above plot shows two local maxima, two local minima, a plateau and a possible ridge [15] which never reaches the maxima. All these are issues that are difficult to address without a stochastic variant of the optimization technique.
In the Section of the literature review, some of the important formulations of cost functions which are proposed by authors in metaheuristic techniques are investigated. We consider the one which is most widely accepted, consisting of a weighted sum of PSNR and SSIM indexes. The same formulation of the cost function is investigated with FA and SGD-FA. It turns out the proposed variant of FA outperforms and enables the algorithm to converge with fewer iterations to a global minimum state. Moreover, the flexibility of using different weights in the cost function gives the choice of a particular cost function that is suitable for a particular use case.
Several techniques have been proposed in the literature for Image Watermarking in the transform domain using Nature Inspired and Metaheuristic approaches [16]. Comprehensive summarization of all such techniques is presented in Table 2.
3 Watermarking Using LWT and SGD-FA Technique
Lifting Wavelet Transform [21,22] is a class of Wavelet Transform that is found as one of the most efficient techniques for frequency domain watermarking. After the application of two-dimensional LWT over the image matrix, four bands are obtained, viz Low-Low (LL), Low-High (LH), High-Low (HL) and High-High (HH). LH and HL correspond to the decomposition components across the rows and columns, whereas the HH components correspond to the diagonal component. LWT is preferred over DWT due to its faster and more efficient implementation and better results in the image denoising domain. It offers a perfect reconstruction and has better frequency localization as compared to many other transforms.
Most of the lifting transforms are recursive. This means that the output is again fed into the input for smoother computing while generating an entire sequence in iterations, thereby getting a desirable compression. The following nomenclature is adopted here. The first subscript represents the even or odd component (e or o). The second subscript is the iteration count of the looping mechanism. The symbol in brackets is the index count.
The signal decomposition using LWT requires three steps as shown below.
1. Split Signal: The samples of the signal are split into even and odd as per their position in the array or matrix (corresponding to a one or two-dimensional transform). This is represented as follows:
2. The Predict step also replaces the odd elements of the set with the difference between the odd values and the predict-function values. These values are close to Zero as in most cases, the prediction function is fairly accurate.
3. Update Signal: The update operation can be described mathematically as shown in the below equation. Here, the second subscript represents the iteration cycle. The coefficient values at even positions are updated at each iteration.
This scheme is depicted as shown in Fig. 2.
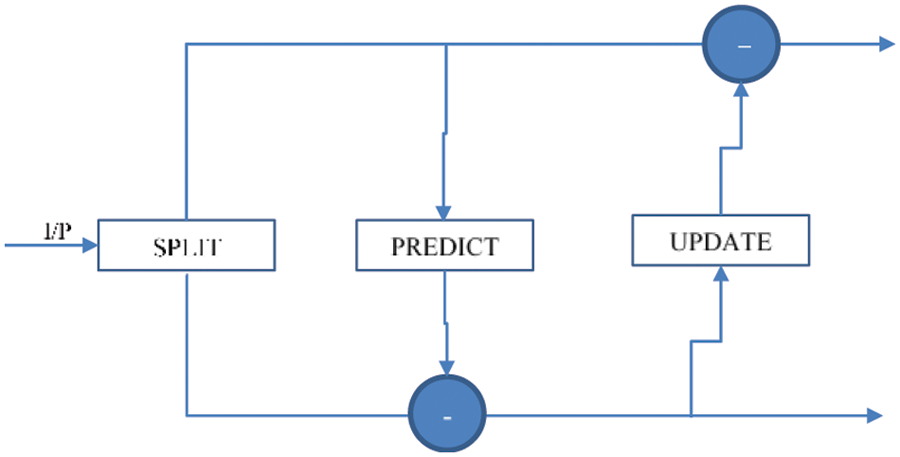
Figure 2: Illustration of lifting scheme transformation
The most commonly used lifting scheme for Haar Wavelet Transformation includes the following operations in prediction and update.
1. Predict: It is presumed that the Odd position coefficient is equal in magnitude to the previous even coefficient. Thus
The odd elements are replaced by the difference in the even and odd elements in this step.
2. Update: The Update step updates the value of the even component as the average of the even-odd pair. This is depicted as shown below:
Substituting the value of
For a given image of dimensions NxN, the dimensions of the LWT coefficients are shown in Table 3.

The components LH, HL and HH corresponds to the frequency level components. The three dimensions of the matrix correspond to each of the three color bands in the three-color plane. The Blue color plane is chosen for optimal embedding for its least perceptiveness for the human eye. We consider watermark embedding in the LL band, thereby achieving ¼ embedding capacity of the dimensions of the original image.
Invariant moments [23–26], as the name indicates are those numeric values that remain unchanged with certain operations. Hu’s invariant Moments are a set of 7 values that can be computed for an image using standard equations. These seven values remain unchanged (variate within negligible range) with rotation, scaling and translation (RST). Thus, these moments are widely used by researchers as a key to implementing blind watermarking. Authors in [20] give a detailed analysis of the variations in the moment values with RST operations as a function of image resolution. A detailed analysis of encryption and steganographic techniques is summarized by Yu et al. [27].
The firefly algorithm [13] is one of the nature-inspired techniques of optimization. The algorithm is inspired by the flashing behavior of fireflies which can be summed up as shown:
1. Fireflies are unisexual. Each firefly can be attracted to any other firefly.
2. The strength of attraction is proportional to the brightness of the firefly. More accurately, the more the difference in the brightness of the firefly, the more the attraction strength.
3. The brightness (I) of a firefly, as seen from other fireflies depends upon the distance between the fireflies.
4. The brightness of a firefly is computed as an optimized Objective Function.
The following equations hold for intensity and attraction parameters respectively.
where
The attraction rate β between fireflies can be defined as:
With each iteration, the position of the fireflies is updated as per the following equation:
where
3.5 Stochastic Gradient Descent Firefly Algorithm (SGD-FA)
SGD-FA is a variant of FA which takes a randomization parameter, by following its name. In this variant of FA, there is a set of values, from largest to a given threshold, and the probability of the firefly being attracted to another firefly is proportional to its brightness. However, there exists a probability that the Fireflies can also be attracted to a firefly of comparatively lower brightness. In this case, the position of the fireflies can be updated with each iteration as per the following equation:
Here,
The Stochastic Gradient Descent FA is based upon the randomization process for implementing a local search. It considers the MSE values and the value of the strength parameter for embedding. As indicated previously, both these are conflicting parameters. As the process is of gradient descent, we propose an objective function whose value is to be a minimum. This function is termed the Cost Function (CF).
SGD-FA will iterate through the CF values to achieve a global minimum, eventually, corresponding to the optimum values of the watermark strength parameter and MSE.
It is clear from Fig. 3 that the algorithmic iterations are required to be made selectively. The two red arrows depict the iterations. If the parameter jumps are too large, then it might be the case that the algorithm might not achieve a global minimum. However, if the parameter values are too small, it may possible that the iteration may be trapped to a local-minima after taking a long time to converge.
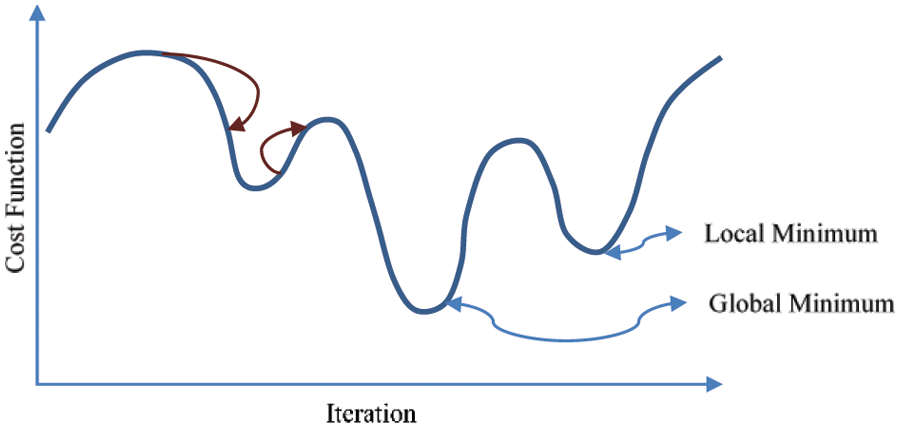
Figure 3: Iterations of the algorithm for computation of the minimum value of the cost function
3.6 Image Watermarking (Blind) Using SGD-FA
Most Metaheuristics are designed to be used for non-blind watermarking techniques where the original, unmarked image is available for watermark detection. Such a privilege is not available in Blind Techniques where the challenge is bigger and requires more complex mathematical techniques. It is due to this limitation that the non-blind techniques found limited applications in real-world use cases. However, a large mass of literature is focused on nature-inspired meta-heuristics, based on watermarking in the transform domain.
In the case of the blind technique, we need a key which is preferably some key that is extracted, in the form of some invariant feature, from the image itself, to surpass the requirement of explicitly sending the key at the detector terminal. The watermark is required to be embedded in the host coefficients as per a policy known to both the embedder and the detector. The embedding policy proposed is illustrated below:
Transform domain coefficients:
String to be Embedded:
Lifting Wavelet Transform creates positive integer coefficients in the LL band of transform.
Let the Watermark Strength Factor be λ. For embedding a 1, we suggest an addition or subtraction operation which makes the coefficient exactly divisible by λ. The bigger the value of the λ, the more robustness of the watermark and the more will be the mean square error. The algorithm for watermark embedding is described as follows:
Algorithm: Watermark Embedding
INPUT-1, Embedding Coefficients:
INPUT-2, Embedding Bits:
Consider the initial value of λ
#Iteration = k
Loop Until desired iteration count or when no update in Cost Function Value.
If Embedding Bit = 1
If
else
end
end
Compute
end
Update λ as per SGD-FA
Goto Step#1
This simple embedding scheme enriched using SGD-FA will give the optimum value of CF resulting in the best possible trade-off between robustness and imperceptibility. The extraction for the said technique is straightforward. It checks for those coefficient values which are exactly divisible by λ. However, this key is required to be provided to the receiver end for watermark extraction, failing which there is no way to extract the watermark.
Considering the legacy of benchmark images, we take the example of the (all-time) LENA image for the simulation of the proposed watermarking technique. The original colored image is shown in Fig. 4A.

Figure 4: (A) Test image Lena, (B) Copyright image
We consider an input image of dimension 512 × 512, in RGB mode, with a watermark image of 64 × 64 which is binary. The two-level LWT produces LL, LH, HL and HH sub-bands corresponding to the high and low pass filtering scheme. The image sub-band images corresponding to LL, LH, HL and HH band of the transform are shown in Figs. 5 and 6.

Figure 5: LL band plane: (A) red, (B) green and (C) blue
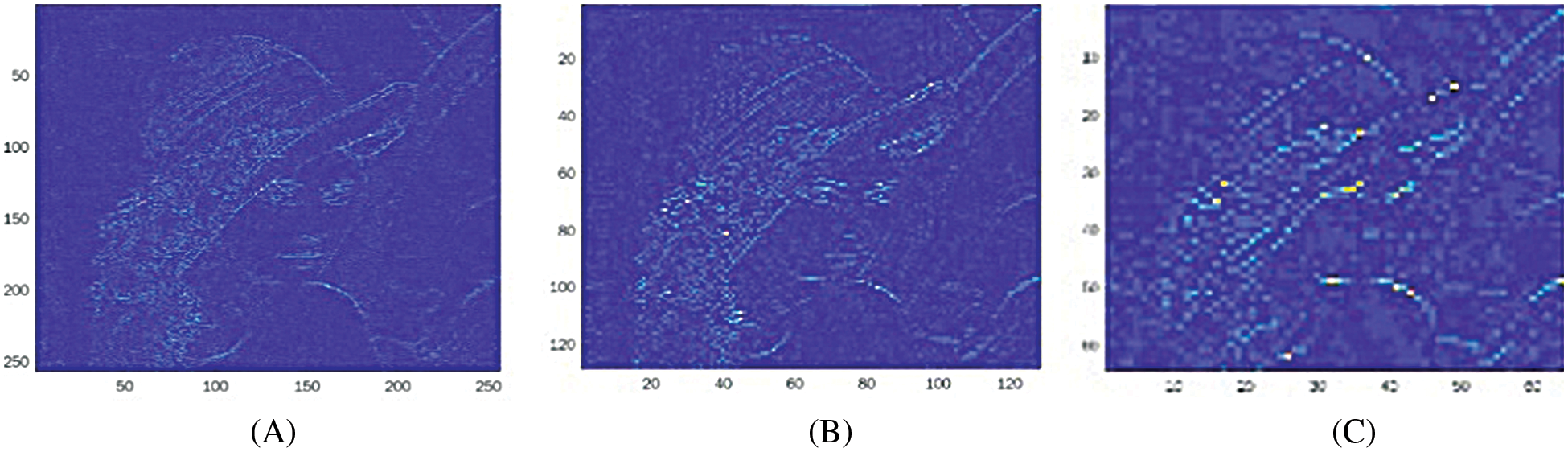
Figure 6: (A) LH{1}, (B) LH{2}, and (C) LH{3}. Dimensions 256 × 256, 128 × 128 and 64 × 64 respectively (Blue-colour plane)
The simulation results in the form of extracted watermark and SSIM map are shown in Table 4.
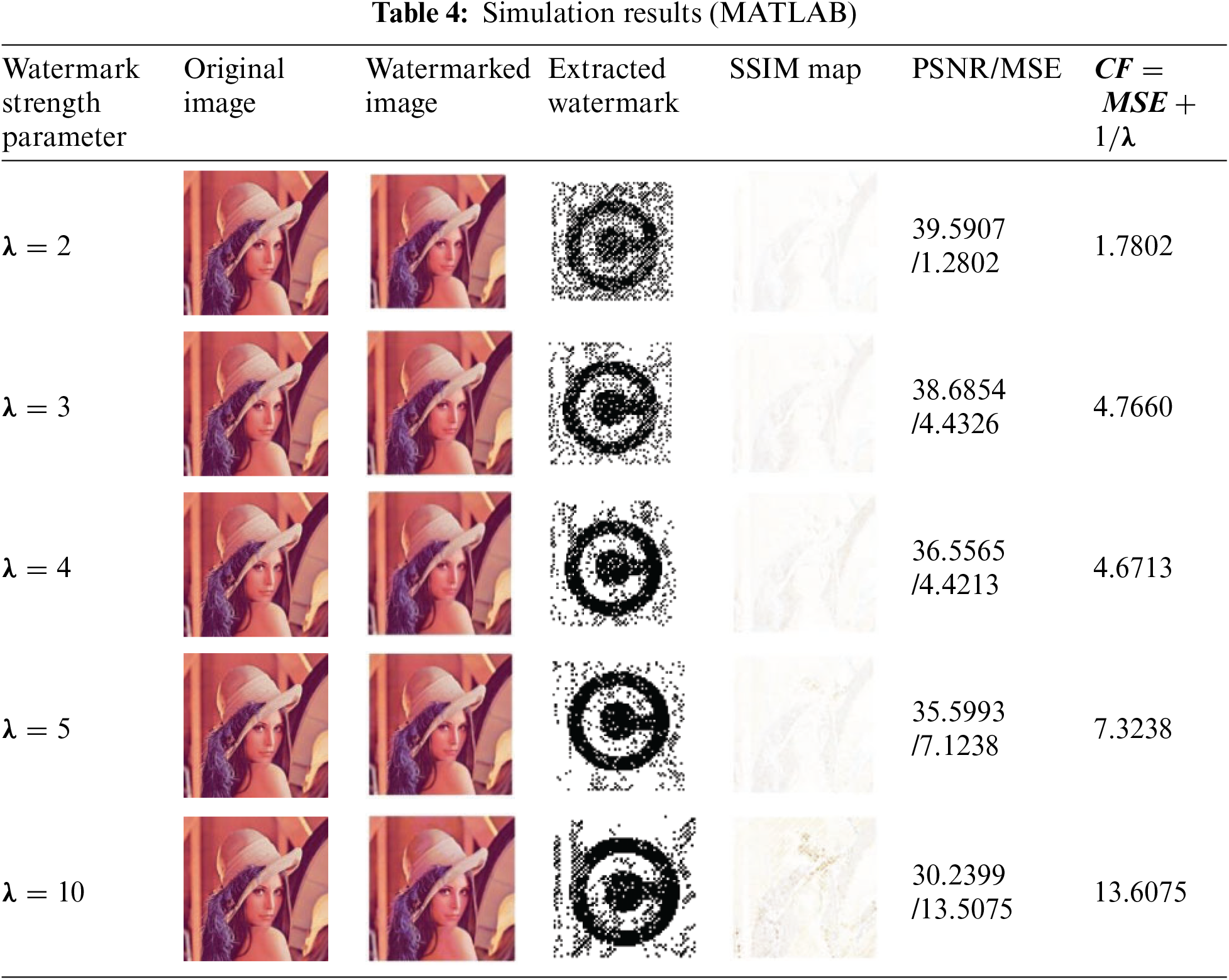
It turns out that the optimum value of CF is achieved with the 4th iteration of the process, under strengthening-factor λ = 4 and CF = 4.6713. The value of the strength factor depends upon the image and the watermark under consideration. It also depends strongly upon the formulation of the cost function as shown in Fig. 7.
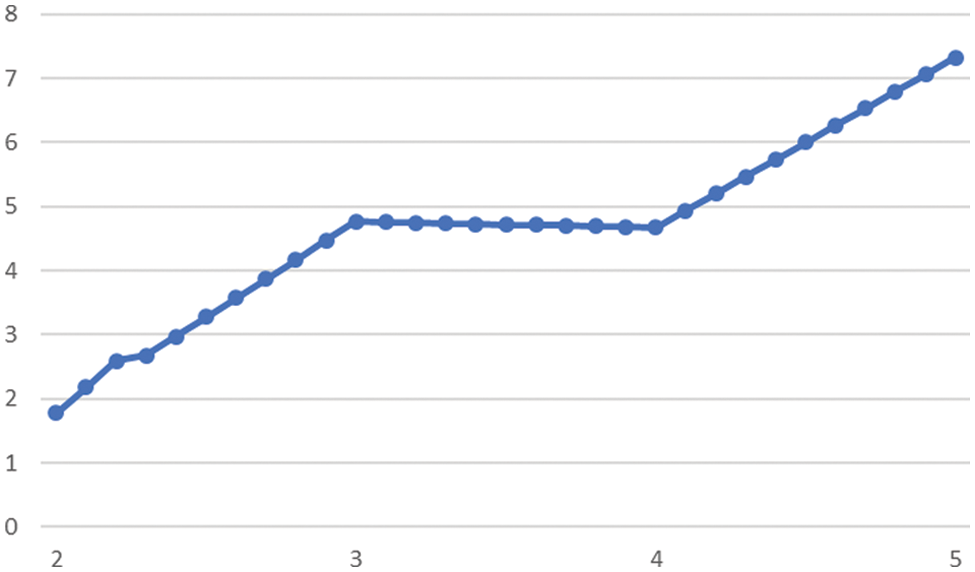
Figure 7: The minimum value of CF corresponds to strength factor λ = 4. The vertical axis shows the values of the cost function and the horizontal axis shows the value of the strength parameter (λ)
The benchmark images for watermarking comparison are shown in Fig. 8.

Figure 8: Benchmark images for computation of quality parameters
The comparison of the PSNR values of the proposed watermarking scheme with those of the benchmark LWT techniques is shown in the following Fig. 9.
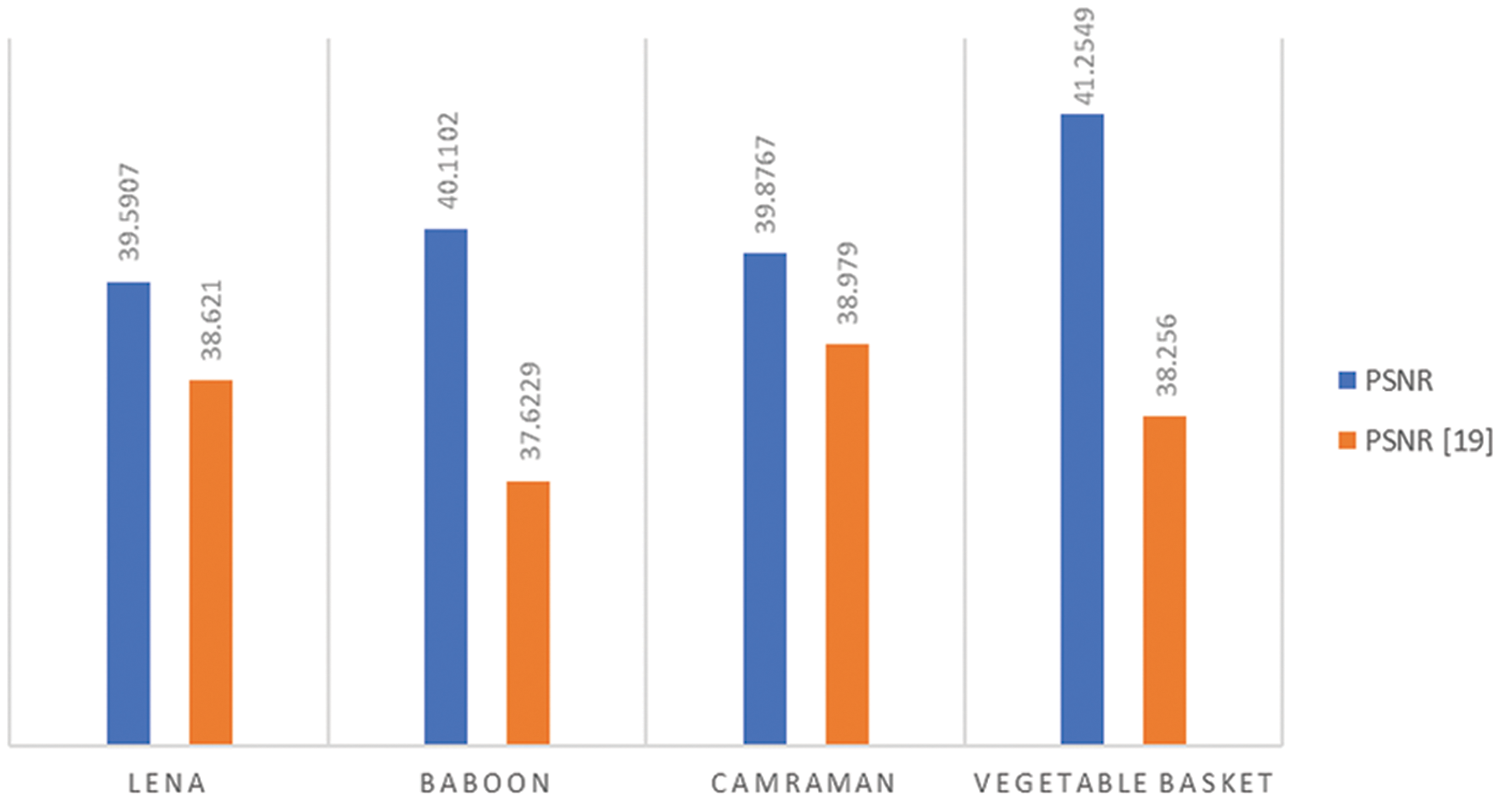
Figure 9: The comparison of values of PSNR of the benchmark images
A robust, blind image watermarking scheme is presented using LWT-DWT, Hu’s invariant moments and SGD-Firefly metaheuristic-based optimization technique. The scheme presented is semi-blind as it requires sending the watermark strength parameter as a key to be sent to the receiver for extraction. This requirement is critical as the computation of the strength factor depends upon the image under investigation and the iterations of the SGD-FA. The embedding scheme uses a strength factor which acts as a key for the embedding of the watermark. Moreover, the Invariant Moments are used as a key to enhance the security as well as to give a robust watermarking technique resistant to rotation, scaling and translation attacks. For different resolution and image sizes, the SGD-FA would converge to a global minimum value of cost function which is the sum of PSNR and the strength factor, designed in a way to achieve its minimum for optimization. Other definitions of Cost Functions can be used as per the use-case of watermarking under consideration. Future work will focus on embedding the key value in the image itself to implement a pure blind watermarking scheme.
Acknowledgement: The authors acknowledge their Organizations for the support they provided for carrying out the research work in the stipulated time.
Funding Statement: This research work is funded by Princess Nourah Bint Abdulrahman University Researchers Supporting Project Number (PNURSP2022R235), Princess Nourah Bint Abdulrahman University, Riyadh, Saudi Arabia.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. M. Begum and M. S. Uddin, “Digital image watermarking techniques: A review,” Information, vol. 11,no. 2, pp. 110, 2020. [Google Scholar]
2. N. Agarwal, A. K. Singh and P. K. Singh, “Survey of robust and imperceptible watermarking,” Multimedia Tools and Applications, vol. 78, no. 7, pp. 8603–8633, 2019. [Google Scholar]
3. S. Naidu and G. Upadhyay, “A review on blind watermarking technique for copyright protection of image-based on DCT, DWT, and SVD domain,” International Research Journal of Engineering and Technology, vol. 7, no. 1, pp. 364–366, 2020. [Google Scholar]
4. M. Arora and M. Khurana, “Secure image encryption technique based on jigsaw transform and chaotic scrambling using digital image watermarking,” Optical and Quantum Electronics, vol. 52, no. 2, pp. 1–30, 2020. [Google Scholar]
5. M. Begum, J. Ferdush and M. S. Uddin, “A Hybrid robust watermarking system based on discrete cosine transform, discrete wavelet transform, and singular value decomposition,” Journal of King Saud University-Computer and Information Sciences, vol. 34, no. 8, pp. 5856–5867, 2022. [Google Scholar]
6. U. Sara, M. Akter and M. S. Uddin, “Image quality assessment through FSIM, SSIM, MSE and PSNR—A comparative study,” Journal of Computer and Communications, vol. 7, no. 3, pp. 8–18, 2019. [Google Scholar]
7. T. Samajdar and M. Quraishi, “Analysis and evaluation of image quality metrics,” in Information Systems Design and Intelligent Applications: Advances in Intelligent Systems and Computing, Singapore: Springer, pp. 369–378, 2015. [Google Scholar]
8. P. Garg and R. R. Kishore, “Comparative analysis: Role of meta-heuristic algorithms in image watermarking optimization,” in Proc. of Second Doctoral Symp. on Computational Intelligence, Singapore, Springer, pp. 315–327, 2022. [Google Scholar]
9. H. C. Huang, F. C. Chang, Y. H. Chen and S. C. Chu, “Survey of bio-inspired computing for information hiding,” Journal of Information Hiding and Multimedia Signal Processing, vol. 6, no. 3, pp. 430–443, 2015. [Google Scholar]
10. S. Ayesha and M. Nivedita, “Digital watermarking technique in transform domain using meta-heuristic algorithm,” in Proc. of Int. Virtual Conf. on Industry 4.0, Singapore, Springer, pp. 157–168, 2021. [Google Scholar]
11. D. B. Taha, T. B. Taha and N. B. A. Dabagh, “A comparison between the performance of DWT and LWT in image watermarking,” Bulletin of Electrical Engineering and Informatics, vol. 9, no. 3, pp. 1005–1014, 2020. [Google Scholar]
12. B. Lutovac, M. Dakovic, S. Stankovic and I. Orovic, “An algorithm for robust image watermarking based on the DCT and zernike moments,” Multimedia Tools and Applications, vol. 76, no. 22, pp. 23333–23352, 2017. [Google Scholar]
13. S. L. Tilahun and J. M. T. Ngnotchouye, “Firefly algorithm for discrete optimization problems: A survey,” KSCE Journal of Civil Engineering, vol. 21, no. 2, pp. 535–545, 2017. [Google Scholar]
14. E. Cuevas, J. Galvez and O. Avalos, “Introduction to optimization and metaheuristic methods,” in Recent Metaheuristics Algorithms for Parameter Identification, Cham: Springer, pp. 1–8. 2020. [Google Scholar]
15. Y. Chen, Y. Chi, J. Fan and C. Ma, “Gradient descent with random initialization: Fast global convergence for nonconvex phase retrieval,” Mathematical Programming, vol. 176, no. 1, pp. 5–37, 2019. [Google Scholar]
16. M. Issa, “Digital image watermarking performance improvement using bio-inspired algorithms,” in Advances in Soft Computing and Machine Learning in Image Processing, Cham: Springer, pp. 683–698, 2018. [Google Scholar]
17. S. Y. Altay, S. Yucel and G. Ulutaş, “A LWT-firefly algorithm based approach for smooth images watermarking,” in Proc. of 4th Int. Conf. on Computer Science and Engineering, (UBMKSamsun, Turkey, pp. 1–6, 2019. [Google Scholar]
18. Y. Guo, B. Z. Li and N. Goel, “Optimized blind image watermarking method based on firefly algorithm in DWT-QR transform domain,” IET Image Processing, vol. 11, no. 6, pp. 406–415, 2017. [Google Scholar]
19. E. Moeinaddini and F. Afsari, “Robust watermarking in DWT domain using SVD and opposition and dimensional based modified firefly algorithm,” Multimedia Tools and Applications, vol. 77, no. 19, pp. 26083–26105, 2018. [Google Scholar]
20. A. Pourhadi and H. M. Nasab, “A robust digital image watermarking scheme based on bat algorithm optimization and SURF detector in SWT domain,” Multimedia Tools and Applications, vol. 79, no. 29, pp. 21653–21677, 2020. [Google Scholar]
21. V. S. Verma, R. K. Jha and A. Ojha, “Significant region based robust watermarking scheme in lifting wavelet transform domain,” Expert Systems with Applications, vol. 42, no. 21, pp. 8184–8197, 2015. [Google Scholar]
22. K. Loukhaoukha and J. Y. Chouinard, “Hybrid watermarking algorithm based on SVD and lifting wavelet transform for ownership verification,” in 11th Canadian Workshop on Information Theory, Ottawa, Canada: IEEE, pp. 177–182, 2009. [Google Scholar]
23. M. Alghoniemy and A. H. Tewfik, “Image watermarking by moment invariants,” in Proc. of Int. Conf. on Image Processing, (Cat. No. 00CH37101Vancouver, British Columbia, Canada: IEEE, vol. 2, pp. 73–76, 2000. [Google Scholar]
24. M. Alghoniemy and A. H. Tewfik, “Geometric invariance in image watermarking,” IEEE Transactions on Image Processing, vol. 13, no. 2, pp. 145–153, 2004. [Google Scholar]
25. G. Duan, X. Zhao, A. Chen and Y. Q. Liu, “An improved Hu moment invariants-based classification method for watermarking algorithm,” in Proc. of ICINS 2014–2014 Int. Conf. on Information and Network Security, Beijing, China, IET, pp. 205–209, 2014. [Google Scholar]
26. S. Sharma, S. Choudhary, V. K. Sharma, A. Goyal and M. M. Balihar, “Image watermarking in frequency domain using hu’s invariant moments and firefly algorithm,” International Journal of Image, Graphics and Signal Processing (IJIGSP), vol. 14, no. 2, pp. 1–15, 2022. [Google Scholar]
27. C. Yu, J. Li, X. Li., X. Ren and B. B. Gupta, “Four-image encryption scheme based on quaternion fresnel transform, chaos and computer-generated hologram,” Multimedia Tools and Applications, vol. 77, no. 4, pp. 4585–4608, 2018. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF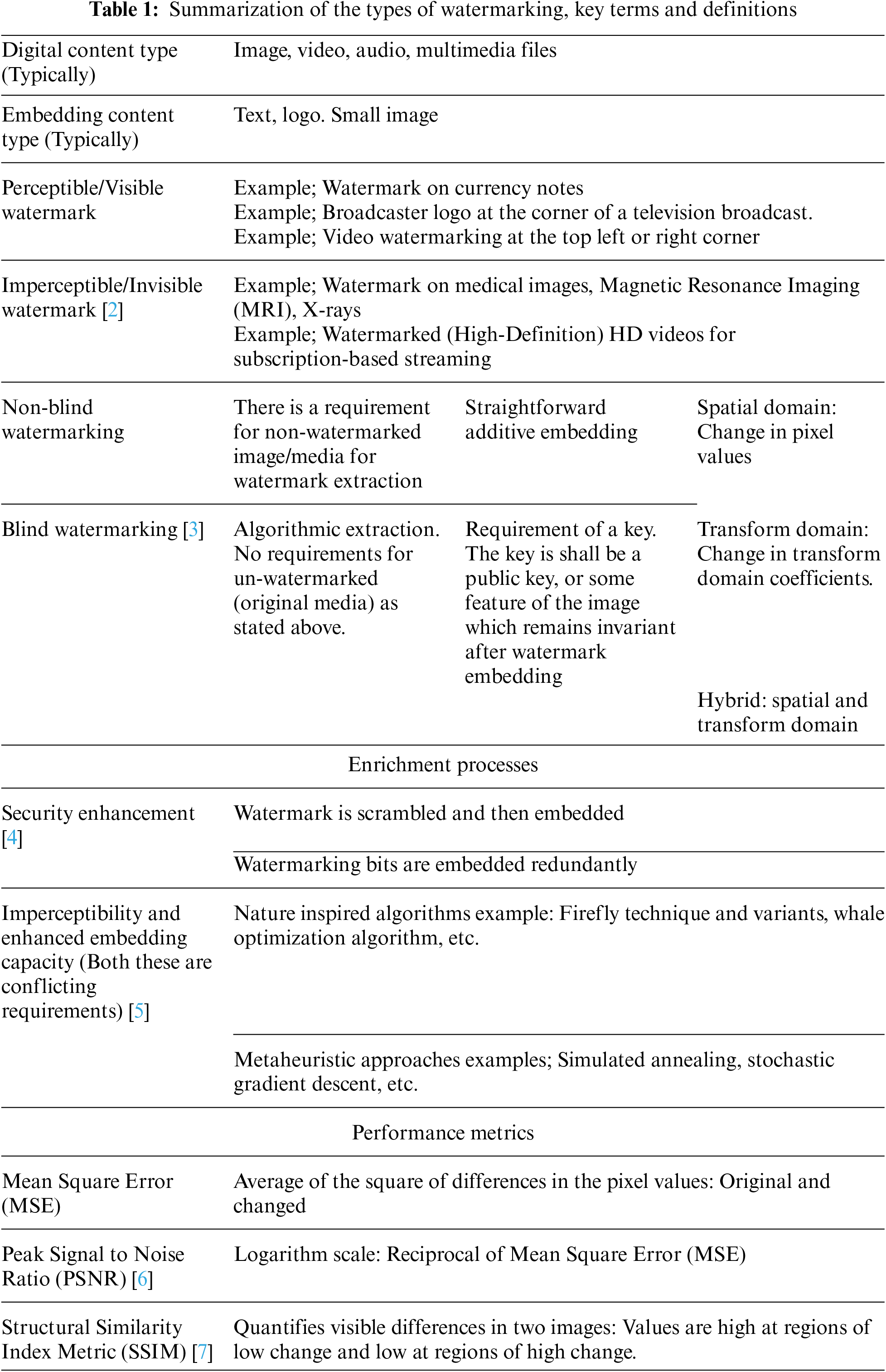
 Downloads
Downloads
 Citation Tools
Citation Tools