Dark Forest Algorithm: A Novel Metaheuristic Algorithm for Global Optimization Problems

1  Introduction

With the continuing development of modern industry, optimization strategies are becoming increasingly essential; therefore, novel optimization algorithms need to be developed. To date, numerous optimization algorithms have been proposed, with nature-inspired algorithms being some of the most successful algorithms. Compared to traditional optimization methods, such as the gradient descent and direct search methods [1,2], metaheuristic algorithms have the following advantages: 1) Simplicity: The process and the procedural implementation of metaheuristic algorithms are often relatively straightforward. 2) Flexibility: Metaheuristic algorithms can be applied to many different fields. 3) Avoiding local optima: Metaheuristic algorithms aim to search beyond the local optima for the global optima of the target solutions or to directly find global optima. 4) Free of derivatives: Derivatives are generally expensive or difficult to evaluate within complex systems, and metaheuristic algorithms usually do not employ gradients for optimization. 5) Fast Processing: Most metaheuristic algorithms perform quick searches in the sample space to obtain a suitable solution.

Metaheuristic algorithms are often inspired by observations from natural phenomena. For example, the ant colony optimization (ACO) algorithm is inspired by the foraging behavior of ants [3]; the particle swarm optimization (PSO) algorithm mimics the predatory behavior of birds [4]; the genetic algorithm (GA) models the crossover variation of DNA [5]; the simulated annealing algorithm simulates the annealing technology in materials physics [6]. Algorithm designs aim not to mimic the behavior of an individual or population but rather to derive an algorithm to solve specific problems. Thus, versatile and intelligent variants could be introduced into metaheuristic algorithms to solve various optimization problems. In fact, metaheuristic algorithms are widely used in industrial applications, including solar energy forecasting, demand and supply analysis optimization in food manufacturing industry [7–9].

Most metaheuristic algorithms are characterized by their randomness, communication, exploration, and exploitation. Randomness provides algorithms with the possibility of achieving superior optimization solutions. Communication renders information exchange between individual solutions and thereby enables their learning from each other to yield superior optimization solutions. Exploration provides algorithms with a trail of new ideas or strategies, while exploitation allows algorithms to adopt the techniques that have proven successful in the past [10].

In this study, a new algorithm called dark forest algorithm (DFA) is proposed based on the rule of superiority and inferiority among natural civilizations and the universe’s dark forest law [11]. Then, the performance of DFA is compared with that of other well-known metaheuristic algorithms according to 35 benchmark functions and five engineering projects. The 35 benchmark functions comprise single-peaked, multi-peaked, high-dimensional, and fixed-dimensional functions. The results show that DFA can obtain qualified optimization results and it outperforms the compared algorithms in terms of overall performance.

The rest of this paper is organized as follows. Section 2 introduces the literature related to the development and applications of metaheuristic algorithms. Section 3 describes the mathematical model of the proposed DFA and the workflow and pseudo-code of the algorithm. Section 4 compares the performance of DFA with six other metaheuristic algorithms on 35 benchmark functions. Section 5 illustrates three engineering design problems using DFA with discussions on their outcomes. Finally, Section 6 presents the conclusions and suggestions for future research.

2  Related Works

Many intricate and fascinating phenomena can be observed in nature that provide inspiration for solving practical problems. The known metaheuristic algorithms can be classified into five categories according to the sources of their inspiration: evolutionary algorithms, swarm intelligence algorithms, physics-based algorithms, human-based algorithms, and other algorithms (Fig. 1).

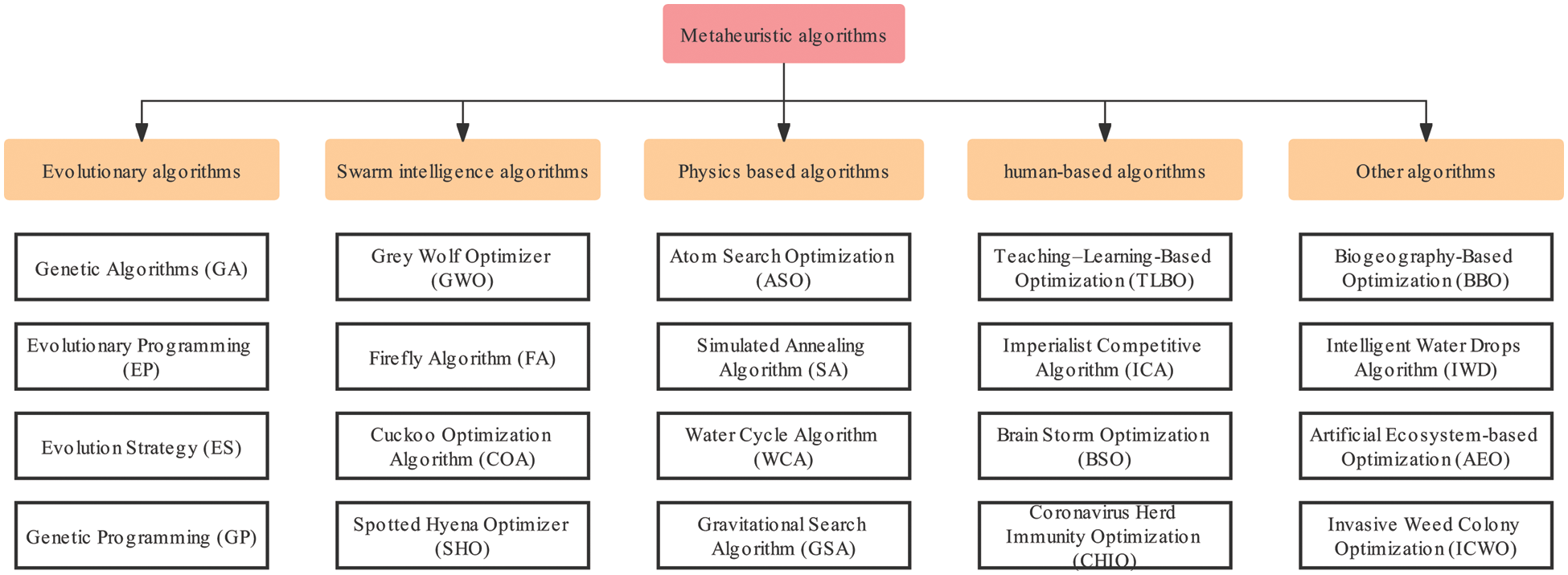
Figure 1: Classification of metaheuristic algorithms

Evolutionary algorithms are based on natural evolution and are the first metaheuristic algorithms proposed. They are the most commonly used. They are based on phenomena and developed theories within biological evolution. Typical algorithms in this category include GA, evolutionary programming [12], differential evolution algorithms [13], evolution strategy [14], flower pollination algorithm [15], and harmony search algorithm (HS) [16]. Among them, GA is the earliest, best known, and one of the most widely used evolutionary algorithms. To date, GA has solved many problems, such as carpool service problems in cloud computing [17], image enhancement and segmentation [18], and routing problems with lost sales [19].

Swarm intelligence algorithms are constructed by simulating group activities inspired by swarms in nature, such as coenosis or social animals. The so-called group intelligence includes the behaviors of simple individuals and the whole group, exhibiting a specific intelligent feature without centralized control. Typical examples include ACO algorithm, PSO algorithm, artificial bee colony algorithm (ABC) [20], artificial fish swarming algorithm [21], grey wolf optimizer (GWO) [22], firefly algorithm (FA) [23], cuckoo search algorithm [24], chimp optimization algorithm [25], grasshopper optimization algorithm (GOA) [26], slime mold algorithm [27], and whale optimization algorithm (WOA) [28].

Physics-based algorithms are inspired by the physics of matter, and they usually have a solid theoretical basis. Some popular algorithms in this category are SA, central force optimization [29], gravitational search algorithm [30], water cycle algorithm [31], atom search optimization [32], electromagnetic field optimization [33], Henry gas solubility optimization [34], and wind driven optimization [35].

Human-based algorithms are designed based on human activities in the society. For example, teaching-learning-based optimization (TLBO) is inspired by the interaction between a learner’s learning and a teacher’s teaching [36]. TLBO simulates the traditional classroom teaching process. The entire optimization process includes the teacher and learner sections. At the teacher level, each student learns from the best individuals. During the learning section, each student randomly learns from the other students. Examples of popular human-based algorithms are brain storm optimization [37], imperialist competitive algorithm [38], cultural algorithm [39], coronavirus herd immunity optimization [40], and team competition and cooperation optimization algorithm [41].

Some algorithms do not fall into any of the above categories but are inspired by other natural phenomena, such as water drops algorithm [42], artificial ecosystem-based optimization [43], and invasive weed colony optimization [44].

Although many metaheuristic algorithms already exist, new algorithms still need to be designed. According to the No Free Lunch (NFL) theorem [45], no single metaheuristic algorithm can accurately solve all optimization problems. In practice, some algorithms perform better than others in specific situations, and many researchers are trying to find ways to improve existing metaheuristic algorithms or develop new ones. This study proposes a novel algorithm, i.e., DFA. Rigorous experiments are conducted to demonstrate DFA as a feasible metaheuristic algorithm that can be readily used in engineering problems.

3  Dark Forest Algorithm

3.1 Inspiration

Civilizations in the universe survive under the dark forest law. According to the dark forest law, a civilization once discovered will inevitably be attacked by other civilizations in the universe. The universe’s evolution is endless and is always accompanied by the extinction of existing civilizations and the birth of new ones. Civilizations plunder each other and cooperate, constantly moving toward a better direction. Civilizations can be classified according to their level of development: highest, advanced, normal, and low civilizations.

Each civilization has its own exploration strategy. The highest civilizations cannot learn from others because no known civilizations are superior to them, and they usually move around during exploration. The highest civilizations sometimes plunder other civilizations for their development. If the highest civilization does not evolve, they remain unchanged. Advanced civilizations learn from the highest civilizations and plunder the normal civilizations. Normal civilizations learn from the highest and advanced civilizations, and they choose which civilizations to learn from based on the strengths and weaknesses of the other civilizations and their distance. Finally, the low civilizations are subject to elimination, at which point newly created civilizations enter the iterations.

3.2 Algorithm

This section describes the mathematical model, algorithmic workflow, and pseudo-code of DFA. The general workflow of the algorithm is as follows: 1) randomly initializing the population coordinates in the solution space; 2) classifying civilizations according to the adaptability of each civilization coordinate; 3) iteratively updating all locations according to the corresponding civilization level; and 4) separately performing a refined search for the highest civilization in the last few iterations. Fig. 2 illustrates the flowchart.

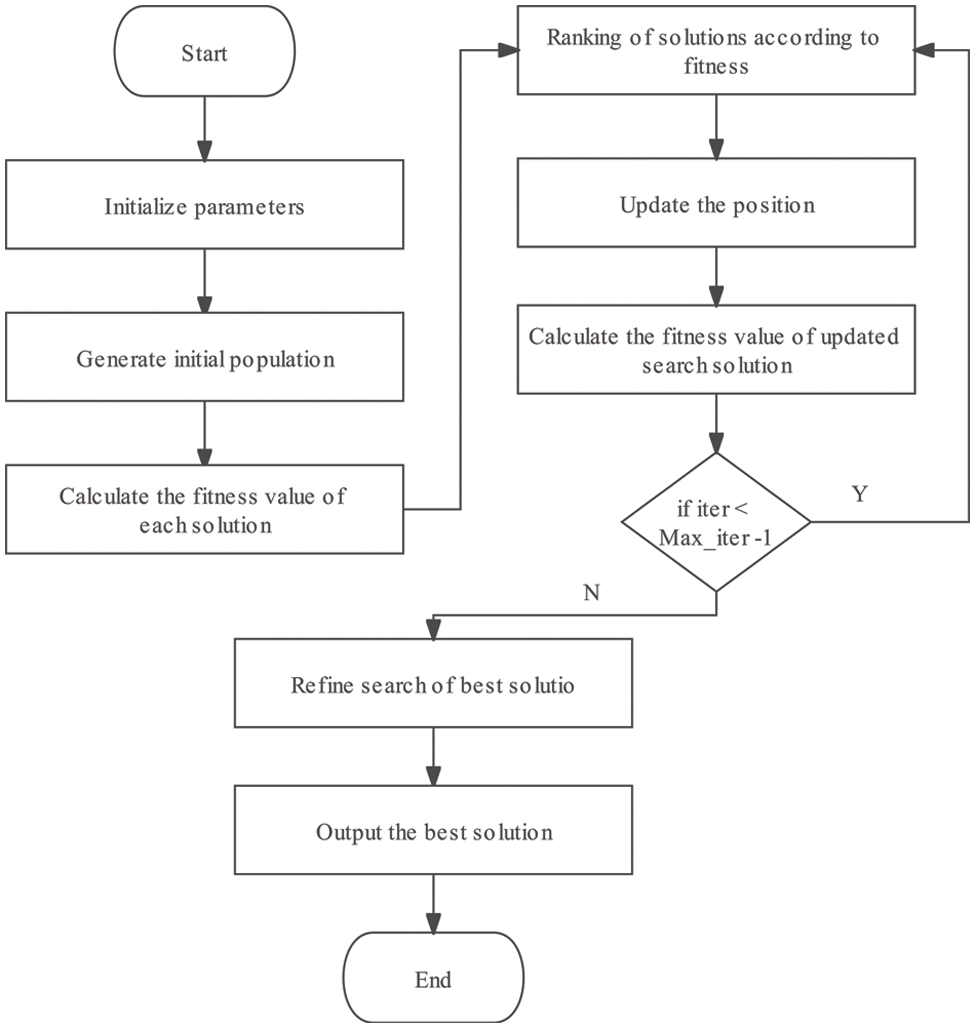
Figure 2: Flowchart of the proposed DFA

3.2.1 Population Initialization

DFA is a population-based algorithm. Similar to other population-based metaheuristic algorithms, it generates several uniformly distributed initial solutions in the search space at the beginning as follows:

xij=xi,minj+α⋅(xi,maxj−xi,minj)(1)

Xi=[xi1,xi2,…,xid](2)

where xij is the initial value of the jth component of the ith solution, xi,minj is the minimum value allowed for the jth component of the candidate solution, xi,maxj is the maximum value allowed for the j th component of the candidate solution, and α is a uniformly distributed random number in the range of [0, 1]. These components form the corresponding initial solution Xi, and d is the dimension of the solution. Xi corresponds to the degree of adaptation; f(Xi) is evaluated according to the fitness function as follows:

f(Xi)=f([xi1,xi2,…,xid])(3)

All solutions are constructed into a matrix X:

X=[X1X2⋮Xi⋮Xn]=[x11x12…x1j…x1dx21x22…x2j…x2d⋮⋮⋮⋮⋮⋮xi1xi2…xij…xid⋮⋮⋮⋮⋮⋮xn1xn2…xnj…xnd],{i=1,2,…,nj=1,2,…,d(4)

where n is the number of populations, i is an integer in the range of [1,n], and j is an integer in the range of [1,d].

3.2.2 Civilization Location Update

After the initial population is generated, the population is sorted according to the fitness values of each civilization. The top-ranked civilization is the highest civilization; the civilizations with the top 3/10 of the population, except for the highest civilization, are the advanced civilizations. The civilizations with ranking between 3/10 and 8/10 are defined as the normal civilizations, and the remaining civilizations are defined as low civilizations. Different civilization types update their coordinates in different ways.

Locations of the highest civilizations are updated as follows. The highest civilization has globally optimal fitness, and its primary purpose of movement is to find coordinates with enhanced fitness. During the iteration process, the highest civilization only changes its coordinates when it finds improved fitness. The highest civilization moves randomly in 50% of the cases and takes reference from the advanced civilization for the other 50% of the cases. The update formulas are as follows:

Xi,t+1={Xnew,f(Xnew)<f(Xi,t+1)Xi,t,otherwise(5)

Xnew={Xtry,p<0.5Xi,t+r⋅step⋅U,otherwise(6)

Xtryj={Xi,tj,p<0.5Xs,tj,otherwise(7)

step=(1−tMax_Iter)2tMax_Iter(8)

where t is the current index of iteration, and p and r are random numbers in the range of [0,1]. U is a randomly generated vector with the same dimension as Xi and elements in the range of [−1,1], and step is the step size that decreases with increasing number of iterations, allowing civilizations to have exploration capability at the beginning and a more vital exploitation ability at the end. Xs,t is a randomly selected advanced civilization, and Max_Iter is the maximum number of iterations.

Locations of the advanced civilizations are updated as follows. Advanced civilizations obtain reference from normal civilizations for 20% of the cases. Since the highest civilization has better fitness than the advanced civilization, advanced civilizations that move to the highest civilizations are more likely to obtain superior results. Hence, the probability for advanced civilizations to move to the highest civilization is set as 80%. Advanced civilizations use spiral location updates in most cases, similar to the spiral update in WOA, but with variations. Mathematically, the update formulas are as follows:

Xi,t+1={Xtry,p<0.2Xi,t+D⋅ebl⋅cos⁡(2πl),otherwise(9)

Xtryj={Xi,tjj,p<0.5Xc,tj,otherwise(10)

D=|X∗−Xi,t|(11)

where b is a logarithmic spiral shape constant, l is a random number in the range of [−1, 1], Xc,t is a randomly selected normal civilization, and X∗ is the coordinate of a highest civilization.

Locations of normal civilizations are updated as follows. Normal civilizations also employ spiral position update. The reference is a civilization coordinate obtained via linear ranking and roulette selection, which may be either the highest civilization or an advanced civilization. In the selection process, the probability of each civilization is jointly determined by its fitness and its distance from the current normal civilization, with the weight ratio of fitness to distance length of 4:1. The update formulas are

Xi,t+1=Xi,t+D⋅ebl⋅cos⁡(2πl)(12)

D=|Xm,t−Xi,t|(13)

where Xm,t is a civilization coordinate obtained by linear ranking and roulette selection.

Locations of low civilizations are updated as follows. Due to the poor adaptation of the low civilizations themselves, the coordinates of the low civilizations are reset for 50% of the cases. This is reasonable as the primary responsibility of a low civilization is to maintain the population diversity to ensure that it does not fall into a local optimum. A new coordinate is updated by mapping the coordinate centroid of mass of all the highest and advanced civilizations for 50% of the cases. The update formulas are

Xi,t+1={Xinit,p<0.5Xw+δ⋅(Xw−Xi,t)⋅step,otherwise(14)

Xw=1N∑1NXi(15)

where Xinit is a coordinate re-generated at random using Eq. (1), Xw is the generated centroid of mass of the highest and advanced civilizations, δ is the mapping factor with values in the range of [0, 1], and N is the sum of the number of highest and advanced civilizations.

After all civilization locations are updated, one refined search in the last ten iterations is performed for the highest civilizations. The refined search is performed to update each component Xi,t+1 of the coordinates of the highest civilization. At the beginning of an initial update vector β, the fitness of Xi,t+1 plus βi is calculated corresponding to Xnew. If no better fitness is obtained, this update is abandoned and the minus value of βi is taken. If a better fitness is obtained, then βi is kept unchanged. If no better result is obtained in two consecutive updates of βi, then βi is inverted and reduced by half. The refined search process only updates the highest civilizations for better optimization results. The above stated process can be represented as

Xi,t+1={Xnew,f(Xnew)<f(Xi,t+1)Xi,t,otherwise(16)

Xnewj=Xi,tj+(−1)k⋅βi⌈k2⌉(17)

k={k,f(xnew)<f(xi,t+1)(k+1)mod2,otherwise(18)

where β is the search radius typically in the range of [0, 1] and the value of k is initially 1.

3.3 Termination

The algorithm ends after a specified number of iterations is reached, with the coordinates recorded by the highest civilization at the end being the optimal solution and the corresponding fitness being the optimal fitness. The pseudo-code of DFA algorithm is presented in Table 1.

4  Results and Discussion

In this section, the results of DFA on 35 benchmark functions are shown. Table 2 presents these 35 benchmark functions, and Fig. 3 displays the 3D representations of some benchmark functions. Among them, F1–F6 are low-dimensional single-peaked functions; F7–F13 are low-dimensional multi-peaked functions; F14–F20 are high-dimensional single-peaked functions; F21–F29 are high-dimensional multi-peaked functions; and F30–F35 are fixed-dimensional functions. The performance of DFA on these functions is compared with that of six well-known algorithms: ABC, FA, GWO, HS, GOA, and WOA.

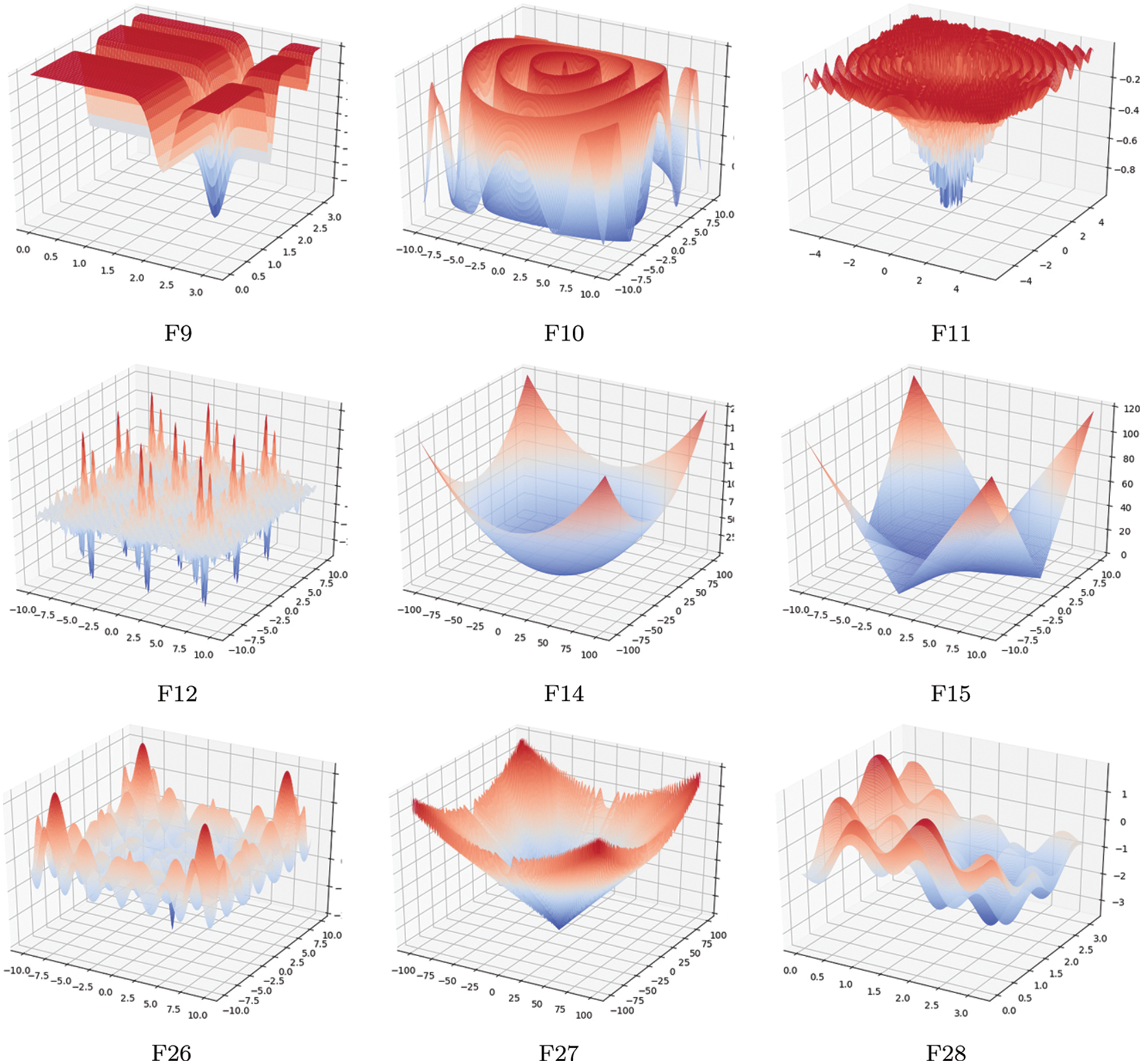
Figure 3: 3D representations of some benchmark functions

For the abovementioned metaheuristic algorithms, the same initialization process as DFA is employed. To reduce the effect of randomness on the test results, all algorithms on the benchmark function are executed in 30 independent runs with 500 iterations per run. The average values and standard deviations are obtained after the evaluation of the algorithms’ performance.

4.1 Evaluation of Exploitation Capability

Benchmark functions F1–F6 are single-peaked functions since they have only one global optimum. They are mainly used to assess the exploitation capability of metaheuristic algorithms. Table 3 shows the optimization results of DFA and other algorithms. The table shows that DFA yields better optimization results than the other algorithms, indicating that DFA has the best exploitation capability.

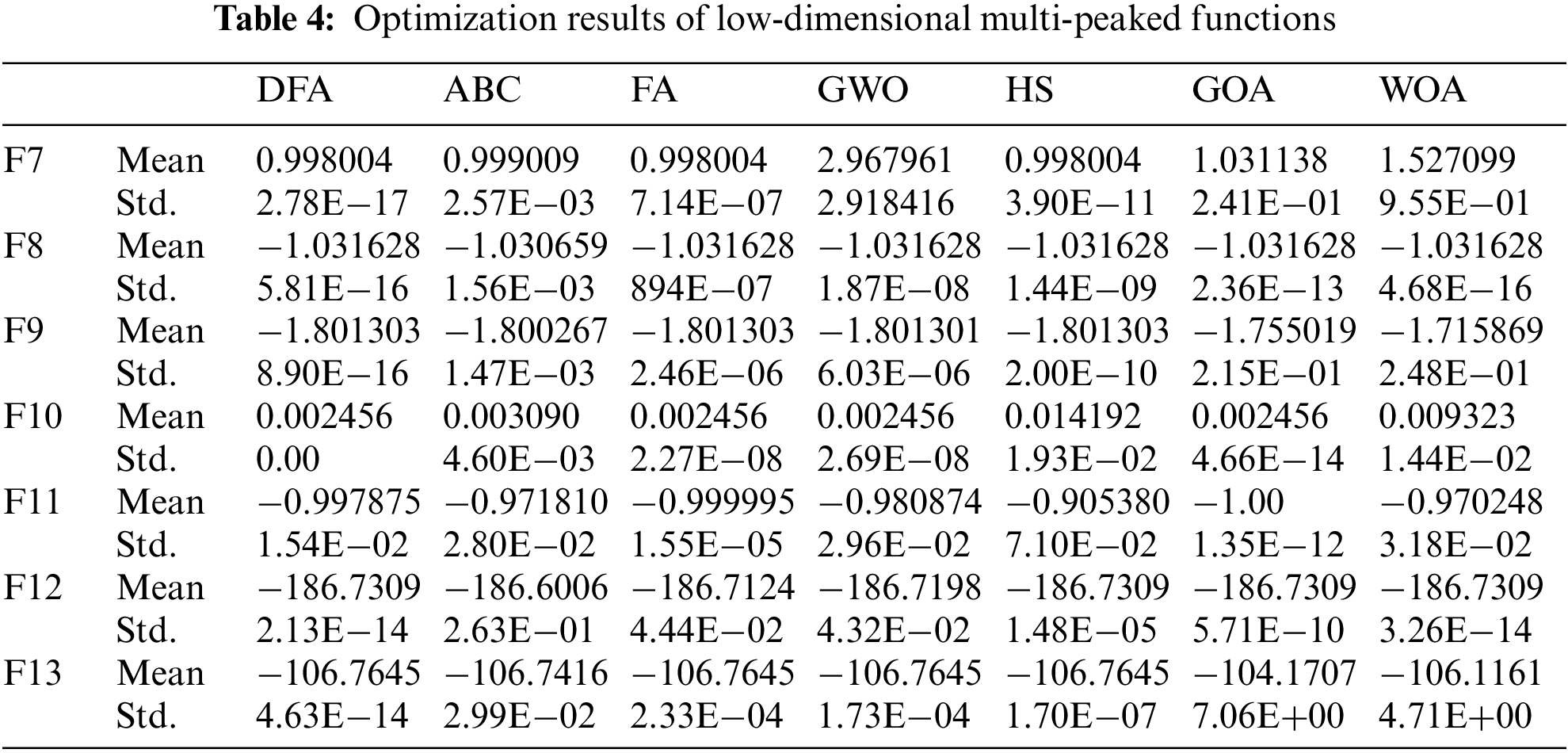
Benchmark functions F7–F13 are multi-peaked functions that have many local optima. The multimodal function can well detect the exploration ability of metaheuristic algorithms. Poor performing metaheuristic algorithms can be easily trapped in the local optimal values in the function and thus will not yield global optimization results. Table 4 shows that DFA yields optimal results for six benchmark functions, proving that it has a good exploration capability.

Compared to F1–F6, benchmark functions F14–FF20 have increased dimensionality from 2 to 30 dimensions, and thus, their difficulty of exploitation is dramatically higher. Table 5 shows that DFA is highly competitive with other metaheuristic algorithms and yields the best or second best optimization results for most of the benchmark functions.

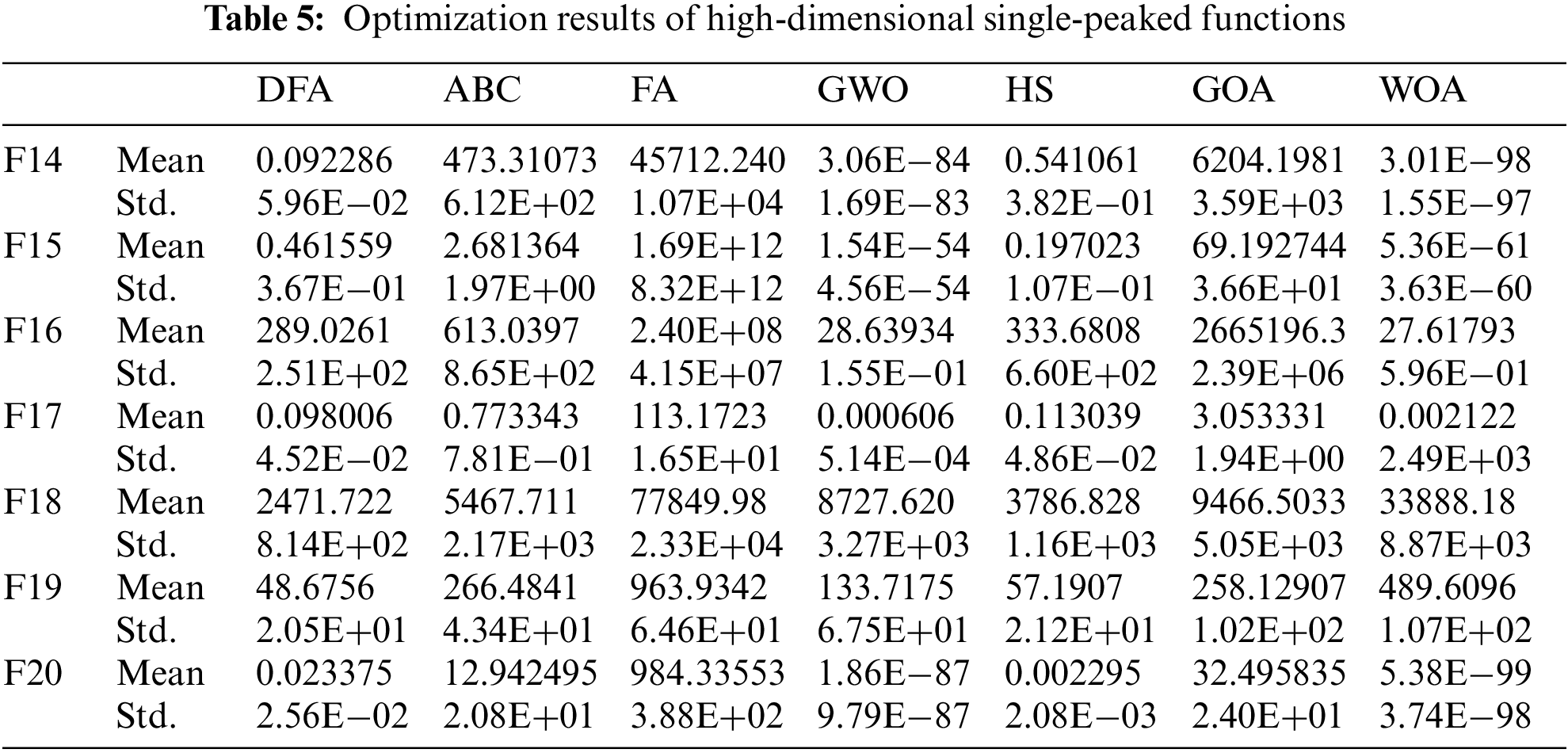
With increasing dimensions, the number of optima in the multimodal function exponentially increases. The optimization results of F21–F29 in Table 6 shows that DFA yields superior optimization results for the multimodal functions, even in the case of high dimensions. Even if the optimal result cannot be obtained, DFA yields a result close to the optimal.

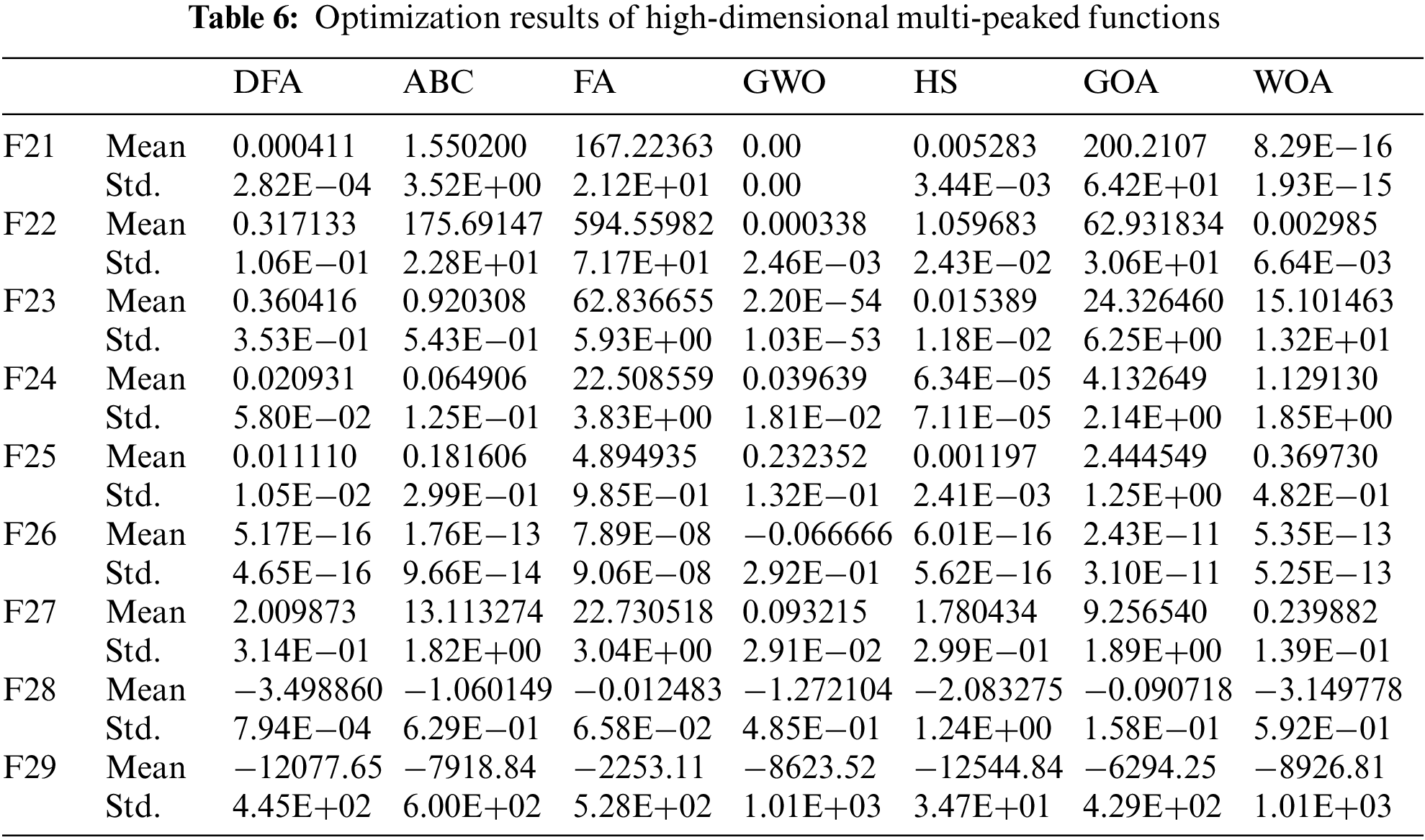
Fixed-dimensional functions usually comprise several low-dimensional functions, which greatly test the exploitation and exploration abilities of metaheuristic algorithms. Metaheuristic algorithms that balance the exploitation and exploration capabilities could obtain optimization results with better chance. Table 7 shows that DFA achieves the best overall optimization results and has balanced development and exploration capabilities.

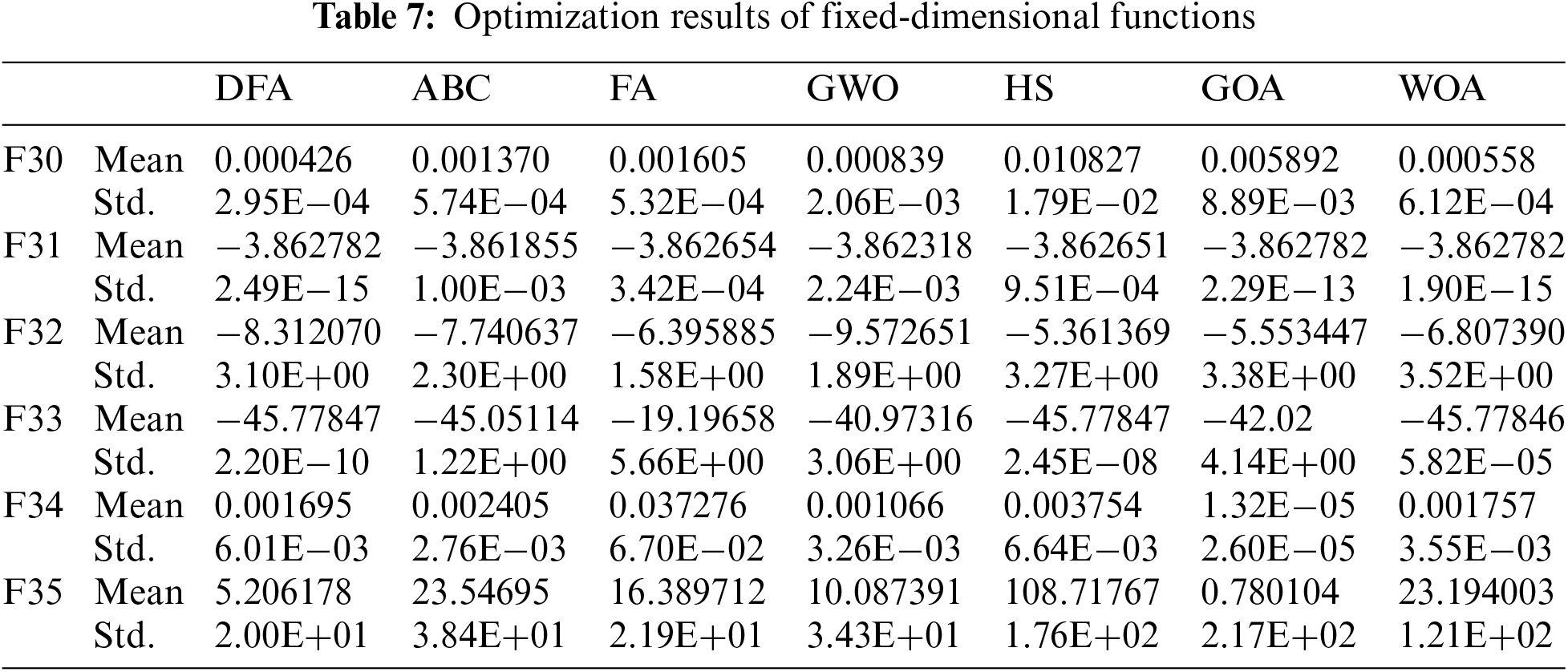
Overall, DFA shows best performance compared to other algorithms in the low-dimensional single-peaked, low-dimensional multi-peaked, and fixed-dimensional functions; and also achieves better results than most algorithms in the high-dimensional functions.

4.2 Statistical Analysis

Although the optimization results show that DFA exhibits better overall performance than other metaheuristic algorithms, the superior performance of DFA needs to be demonstrated in statistical analysis. This section uses the classic statistical analysis method, i.e., the rank-sum ratio (RSR) [46], to conduct statistical analysis. The RSR values embody information on all evaluation indicators, showing the comprehensive level of these indicators. The large RSR value indicates the merit of the algorithm. The optimization mean of the algorithm on the benchmark functions is used as an evaluation indicator. The analysis results of RSR are given in Table 8, which shows that DFA exhibits better overall performance than other metaheuristic algorithms.

4.3 Convergence Analysis

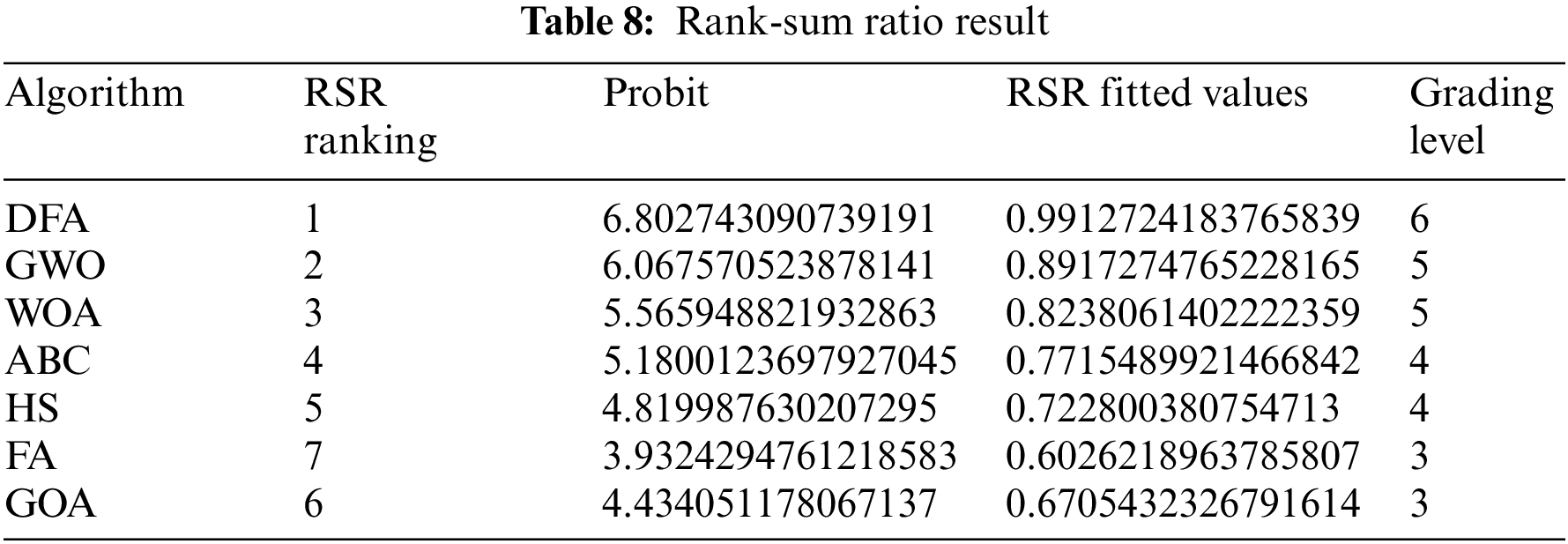
Fig. 4 shows the convergence curves of DFA along with those of other algorithms on some of the benchmark functions. The figure shows that DFA usually converges quickly at the beginning and the convergence speed starts slowing down shortly after the beginning; thus, the overall convergence rate of DFA is not fast, which is attributed to DFA’s conservative exploitation strategy. However, the continuous update of DFA during subsequent iterations enables a preferable exploration capability that prevents DFA from falling into the local optimum. In most cases, DFA converges to the optimum at 1/3 of the iterations.

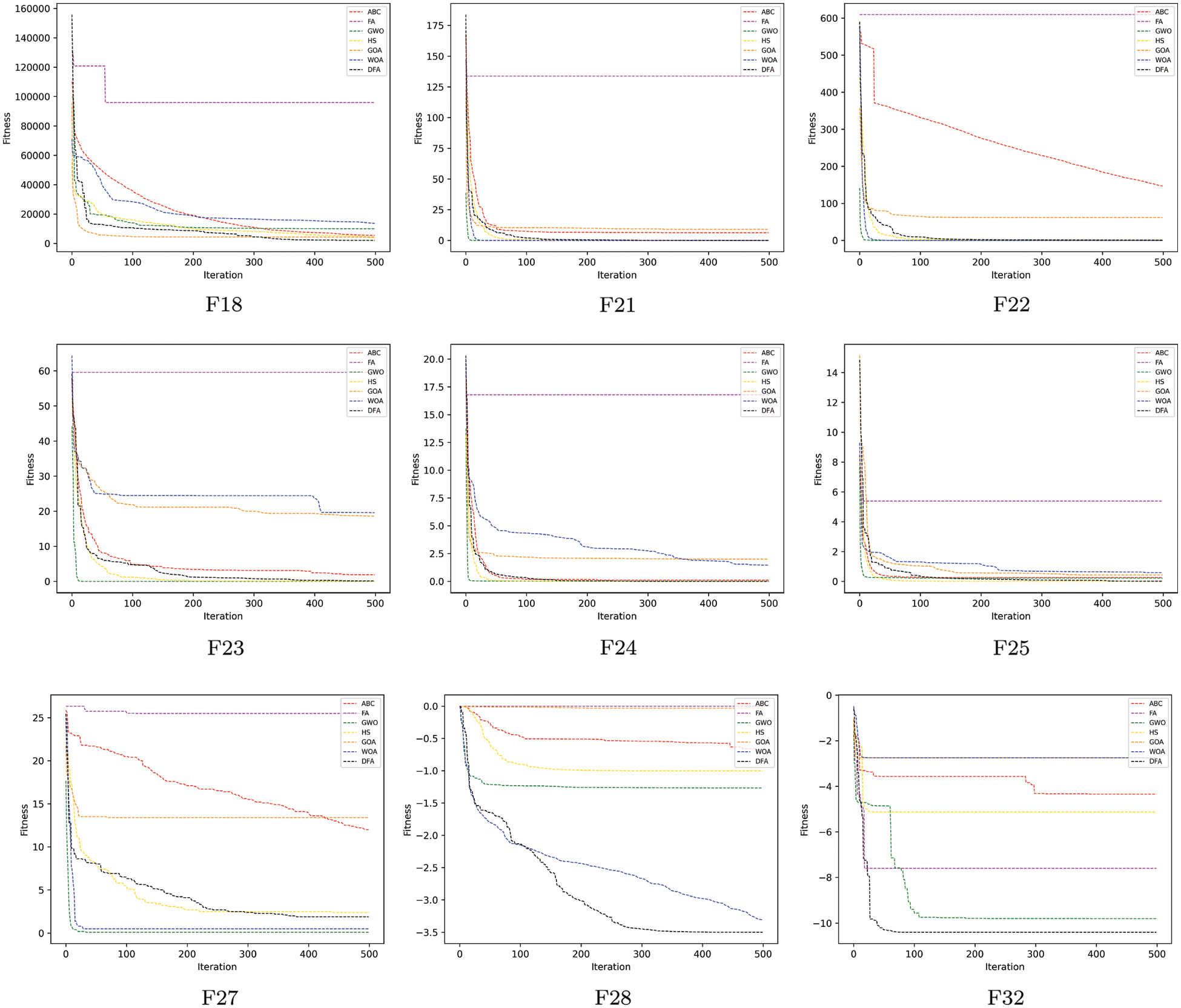
Figure 4: Convergence curves of DFA and comparison algorithms on some benchmark functions

5  DFA for Engineering Projects

In this section, DFA is applied to five constrained engineering design problems: welded beam design, pressure vessel design, three-bar truss design, compression spring design, and cantilever beam design. All the algorithms are tested for each engineering project in 30 independent runs with 500 iterations per run and the best value is taken as the final optimization result.

5.1 Welded Beam Design

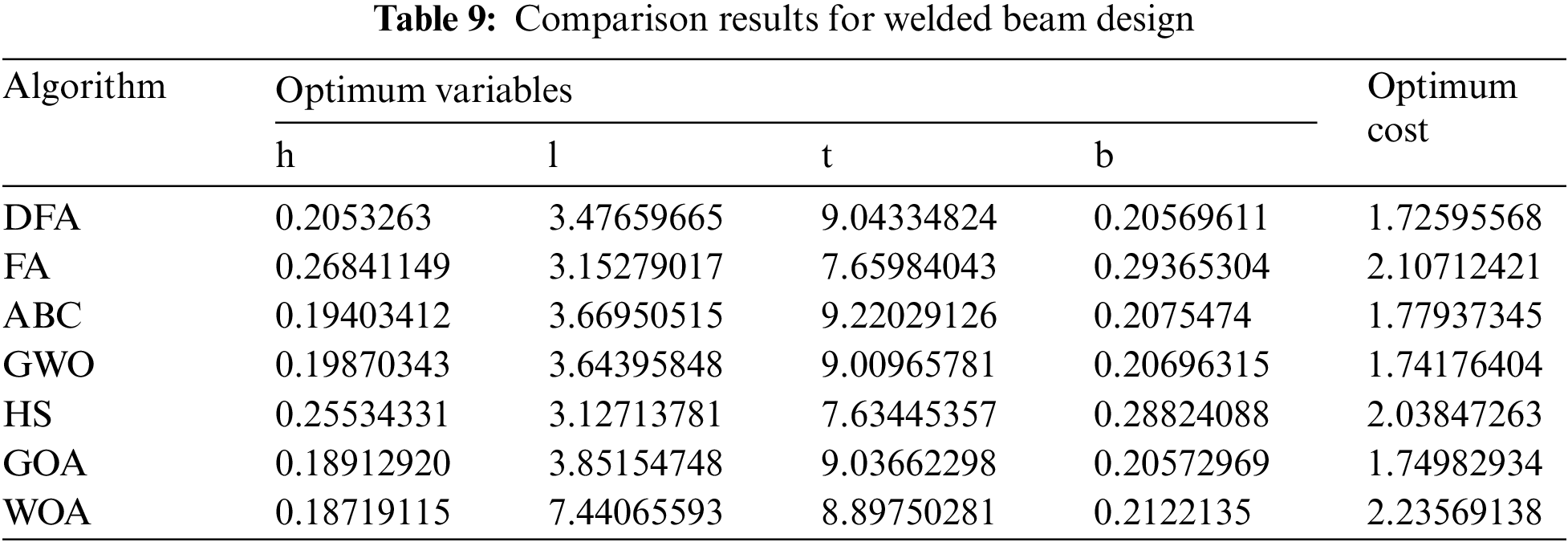
Welded beam design is a common engineering optimization problem where the objective is to find the optimum length of the clamped bar l, height of the bar t, thickness of the bar b, and weld thickness h of a beam bar to minimize the manufacturing cost of a welded beam (Fig. 5). The cost of a welded beam is formulated as

minf(x→)=1.10471x12x2+0.04811x3x4(14+x2)

x→=[x1x2x3x4]=[hltb]

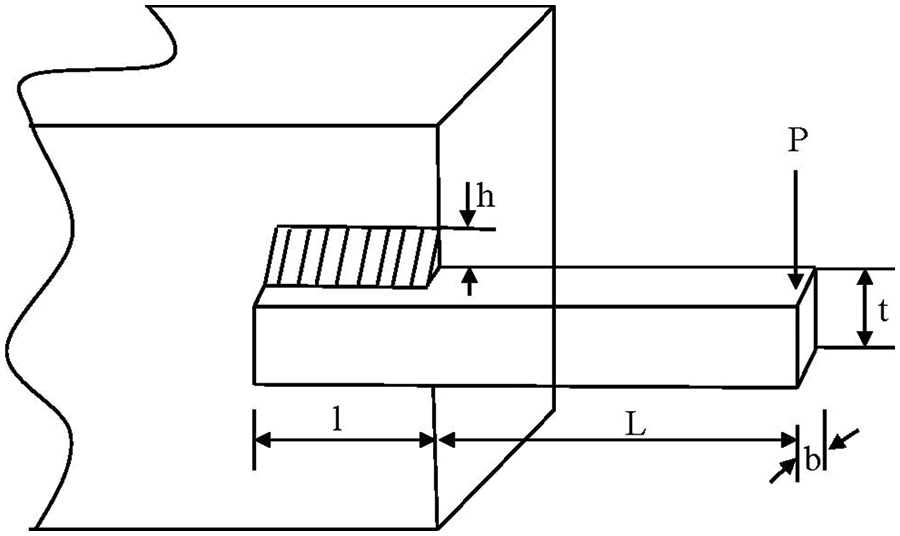
Figure 5: Diagram of welded beam design

Subject to

g1(x→)=τ(x→)−τmax≤0,

g2(x→)=σ(x→)−σmax≤0,

g3(x→)=x1−x4≤0,

g4(x→)=0.10471x12+0.04811x3x4(14+x2)−5≤0,

g5(x→)=0.125−x1≤0,

g6(x→)=δ(x→)−δmax≤0,

g7(x→)=P−Pc(x→)≤0

Variable range

0.1≤x1≤2, 0.1≤x2≤10, 0.1≤x3≤10, 0.1≤x4≤2

The constraints and their associated constants are expressed as follows:

τ(x→)=(τ′)2+2τ′τ″x22R+(τ″)2

τ′=P2x1x2,τ″=MRJ,M=P(L+x2/2)

R=x224+(x1+x3)24

J=2[2x1x2(x2212+(x1+x3)24)]

σ(x→)=6PLx4x32,

Pc(x→)=4.013Ex32x4636L2(1−x32LE4G)

P=6000lb,L=14in, E=30×106psi

G=12×106psi,τmax=13,600psi,

σmax=30,000psi,δmax=0.25in

The results of DFA are compared with those of the other algorithms, and the data in Table 9 show that DFA yields the lowest manufacturing cost, indicating that DFA has the potential to solve the welded beam design problem.

5.2 Pressure Vessel Design

DFA is employed for the pressure vessel design problem. This design aims to find the appropriate shell (Ts=x1), thickness of the head (Th=x2), inner radius (R=x3), and length of the shell (L=x4) to minimize the total material cost, incorporating four constraints: Ts and Th are integer multiples of 0.625 and R and L are continuous variables. Fig. 6 shows the dimensions of the pressure vessel structure. The cost of the pressure vessel design is formulated as

minf(x→)=0.6224x1x3x4+1.7781x2x32+3.1661x12x4+19.84x12x3

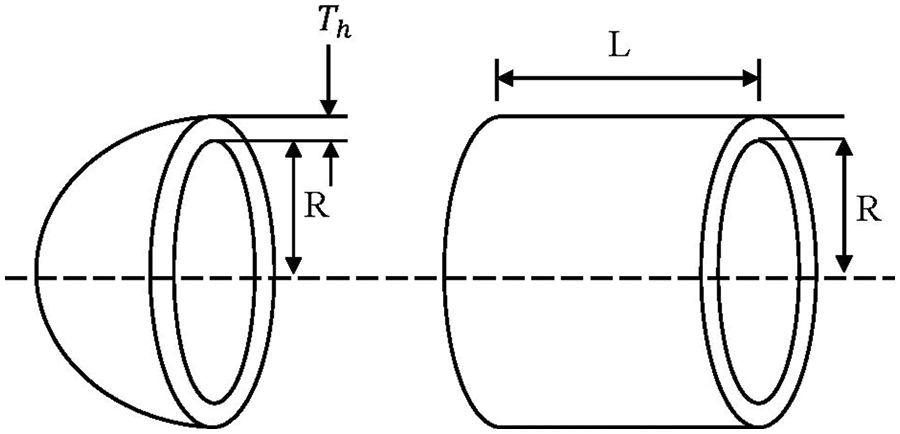
Figure 6: Diagram of pressure vessel design

Subject to

g1=−x1+0.0193x3≤0,g2=−x2+0.00954x3≤0,g3=−πx32x4−43πx33+1296000≤0,g4=x4−240≤0,

Variable range

0≤x1≤99,0≤x2≤99,

10≤x3≤200,10≤x4≤200,

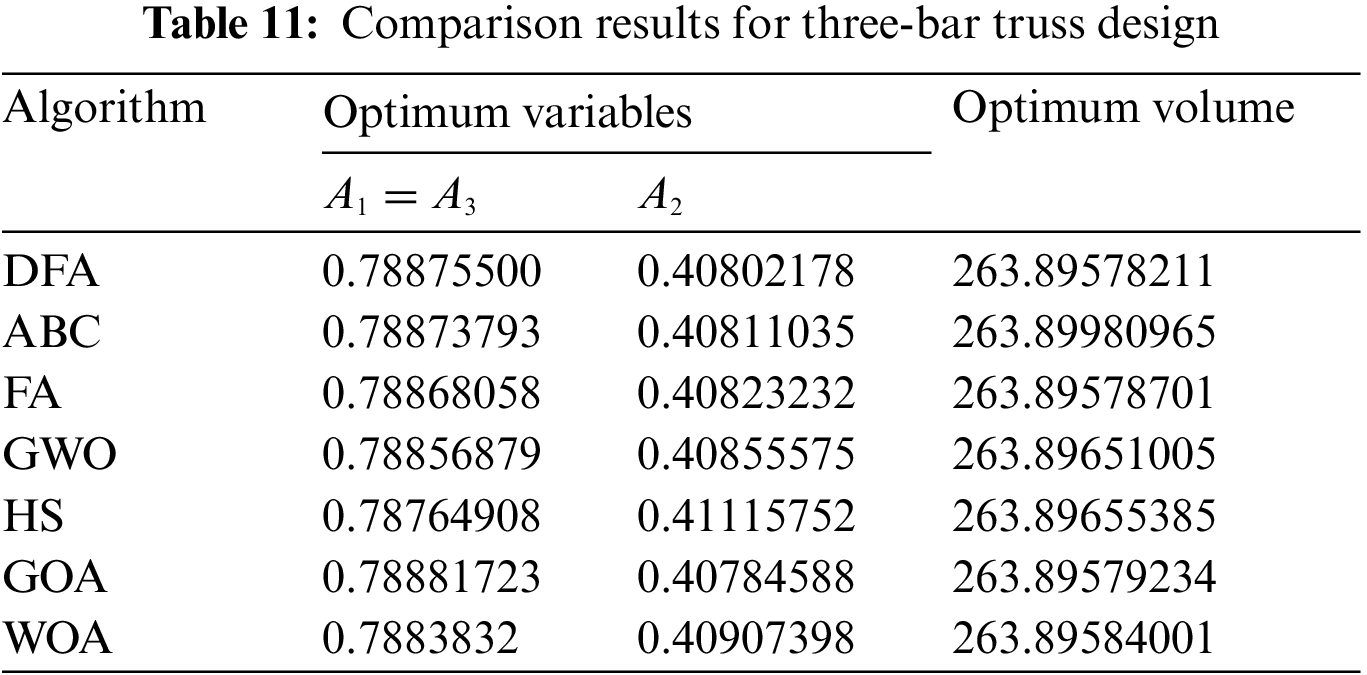
Table 10 presents the optimization results of DFA and other algorithms and shows that DFA yields the best optimization results.

5.3 Three-Bar Truss Design

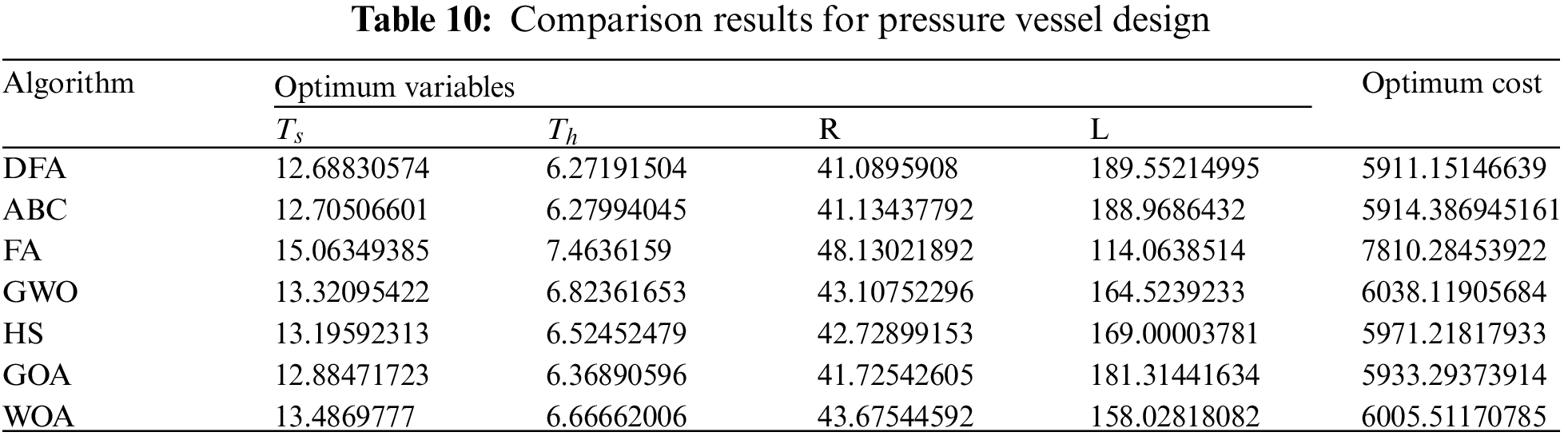
The three-bar truss design is the third case study employed. It aims to evaluate the optimum cross-sectional areas A1=A3=x1 and A2=x2 so that the volume of the static load truss structure is minimized and constrained considering the stress (σ). Fig. 7 displays the dimensions of the three-bar truss design. The volume equation of the truss structure is

minf(x→)=(22x1+x2)×H,

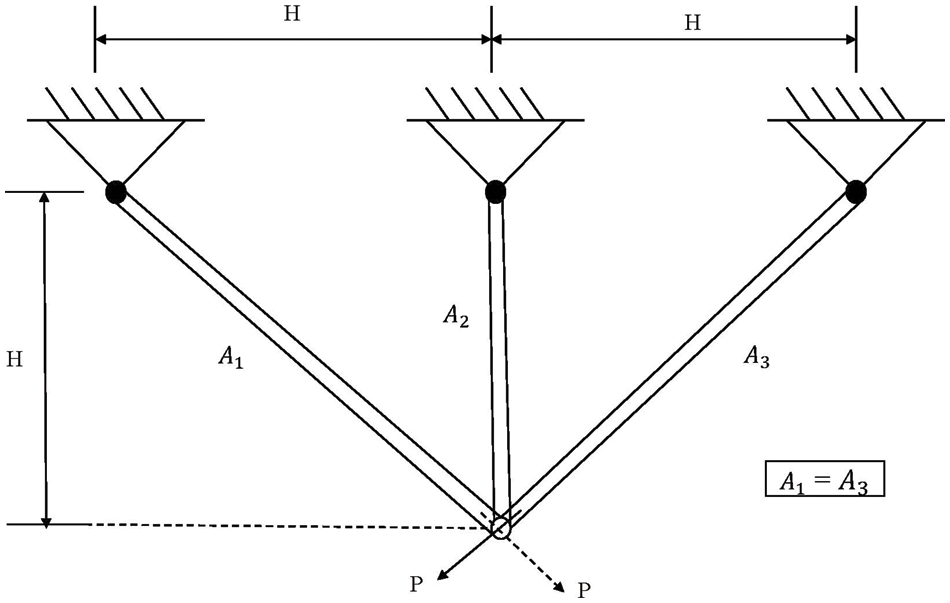
Figure 7: Diagram of pressure vessel design

Subject to

g1=2x1+x22x12+2x1x2P−σ≤0,g2=x22x12+2x1x2P−σ≤0,g3=1x1+2x2P−σ≤0,

Variable range

0≤x1≤1,0≤x2≤1,

H=100cm,P=2KN/cm2,σ=2KN/cm2

The statistical results of DFA and the other algorithms for the three-bar truss design problem are shown in Table 11, indicating that DFA yields the lowest volume compared to the other optimization algorithms.

5.4 Compression Spring Design

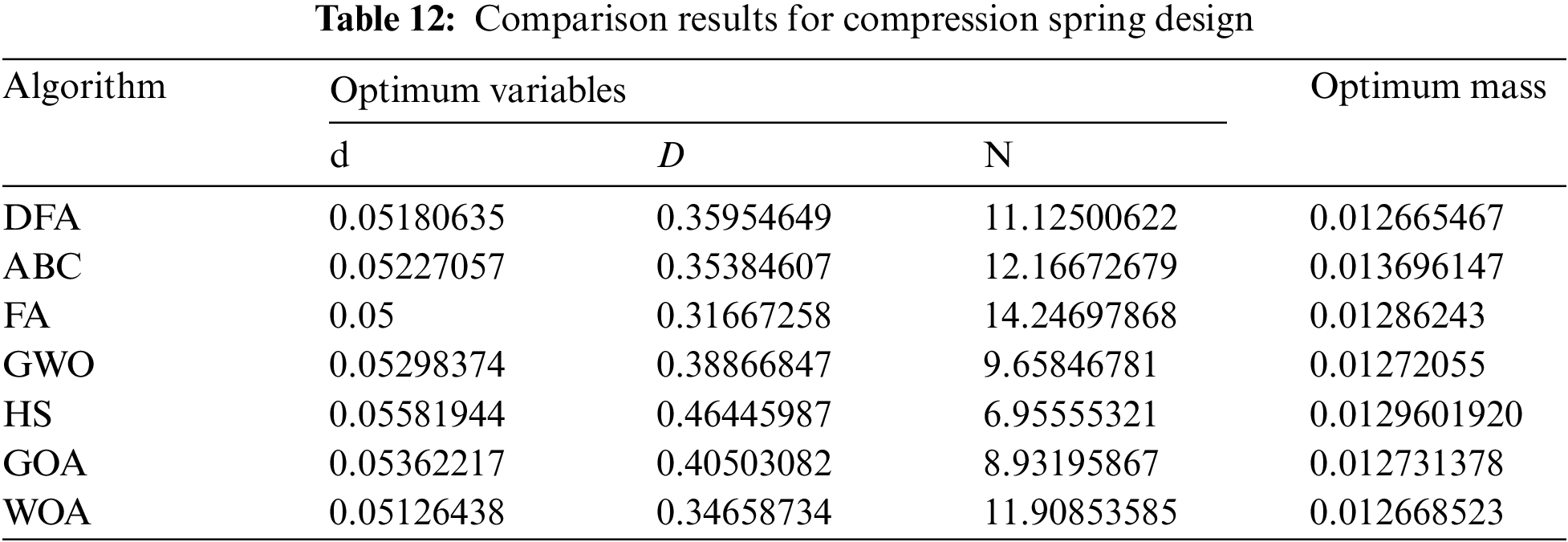
Compression spring design aims to minimize the mass f(x) under certain constraints, including four inequality constraints of minimum deflection, shear stress, surge frequency, and deflection. Three design variables are present: the mean coil diameter (D), wire diameter (d), and number of active coils (N). Fig. 8 shows the dimensions of the compression spring design. The mass equation of the compression spring is

minf(x)=(N+2)Dd2

Figure 8: Diagram of compression spring design

Subject to

g1(x)=1−D3N71785d4≤0

g2(x)=4D2−dD12566(Dd3−d4)+15108d2−1≤0

g3(x)=1−140.45dD2N≤0

g4(x)=D+d1.5−1≤0

Variable range

0.05≤d≤2, 0.25≤D≤1.3, 2≤N≤15

The statistical results of DFA and the other algorithms for the three-bar truss design problem are shown in Table 12. DFA yields the lowest mass, denoting that DFA can well solve the compression spring design problem.

5.5 Cantilever Beam Design

Cantilever beam design is a structural engineering design problem related to the weight optimization of the square section cantilever. The cantilever beam is rigidly supported at one end, and a vertical force acts on the free node of the cantilever. The beam comprises five hollow square blocks of constant thickness, the height (or width) of which is the decision variable and the thickness is fixed. Fig. 9 depicts the dimensions of the cantilever beam design. The weight equation of the cantilever beam is

f(X)=0.0624(x1+x2+x3+x4+x5)

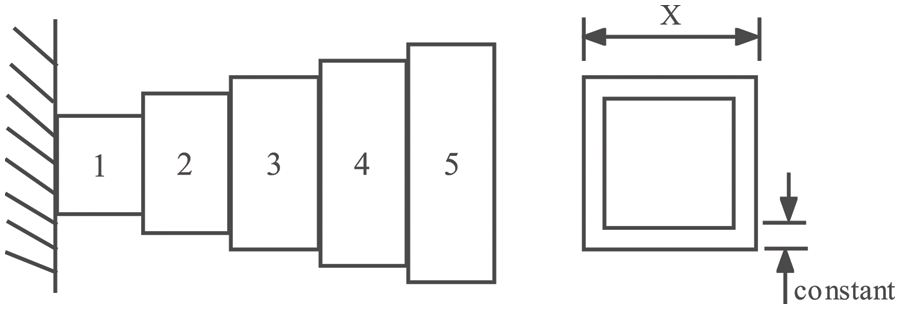
Figure 9: Diagram of cantilever beam design

Subject to

g(X)=61x13+37x23+19x33+7x43+1x53−1≤0

Variable range

0.01≤xi≤100,i=1,2⋯,5

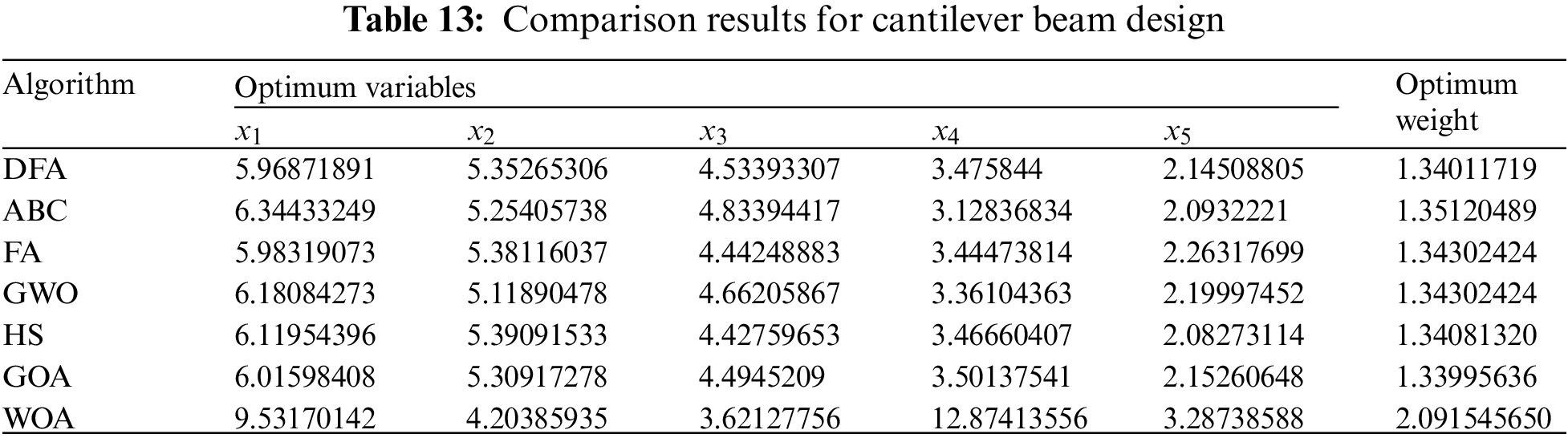
The statistical results of DFA and the other algorithms for the cantilever beam design problem are shown in Table 13. The table shows that DFA outperforms all other algorithms except GOA. Although DFA achieves suboptimal optimization results, this result is acceptable according to NFL.

6  Conclusion

This study presented a novel metaheuristic algorithm called DFA. The effectiveness of DFA was validated on 35 well-known benchmark functions and compared with that of six well-known metaheuristic algorithms. The optimization capabilities of DFA were examined in terms of exploitation capability, statistical analyses, and convergence analyses. The results indicate that DFA is a competitive metaheuristic algorithm with outstanding performance in terms of global optimization problems.

DFA was also applied to five engineering design problems for verification in practical applications (i.e., welded beam, pressure vessel, three-bar truss, compression spring, and cantilever beam design problems). DFA outperforms the other six metaheuristic algorithms in the chosen evaluation criteria. In subsequent studies, DFA will be used to improve the efficiency of machine learning potential development for Fe–Cr–Al ternary alloys.

Funding Statement: This work is performed under collaboration with College of Materials Science and Chemical Engineering, Harbin Engineering University by the support of National Key Research and Development Program of China (2019YFB1901003). The authors also acknowledge the financial support of National Natural Science Foundation of China (Grants No. 52250005, 21875271, 21707147, 11604346, 21671195, and 51872302), the Key R & D Projects of Zhejiang Province No. 2022C01236, the Zhejiang Province Key Research and Development Program (No. 2019C01060), and the project of the key technology for virtue reactors from NPIC. Entrepreneurship Program of Foshan National Hi-tech Industrial Development Zone.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. S. H. Haji and A. M. Abdulazeez, “Comparison of optimization techniques based on gradient descent algorithm: A review,” PalArch’s Journal of Archaeology of Egypt/Egyptology, vol. 18, no. 4, pp. 2715–2743, 2021. [Google Scholar]

2. A. L. Custódio and J. F. A. Madeira, “GLODS: Global and local optimization using direct search,” Journal of Global Optimization, vol. 62, no. 1, pp. 1–28, 2015. [Google Scholar]

3. M. Dorigo and T. Stützle, “Ant colony optimization: Overview and recent advances,” in Handbook of Metaheuristics, 1st edition, vol. 272. Cham, CH: Springer, Cham, pp. 311–351, 2019. [Google Scholar]

4. D. Wang, D. Tan and L. Liu, “Particle swarm optimization algorithm: An overview,” Soft Computing, vol. 22, no. 2, pp. 387–408, 2018. [Google Scholar]

5. J. H. Holland, “Genetic algorithms,” Scientific American, vol. 267, no. 1, pp. 66–73, 1992. https://www.jstor.org/stable/24939139 [Google Scholar]

6. S. Kirkpatrick, C. D. Gelatt and M. P. Vecchi, “Optimization by simulated annealing,” Science, vol. 220, no. 4598, pp. 671–680, 1983. [Google Scholar] [PubMed]

7. O. Abedinia, N. Amjady and N. Ghadimi, “Solar energy forecasting based on hybrid neural network and improved metaheuristic algorithm,” Computational Intelligence, vol. 34, no. 1, pp. 241–260, 2018. [Google Scholar]

8. O. Kramer, “Genetic algorithms,” Genetic Algorithm Essentials, vol. 679, pp. 11–19, 2017. https://doi.org/10.1007/978-3-319-52156-5_2 [Google Scholar] [CrossRef]

9. W. Ezra and W. Zhu, “A survey on metaheuristics for optimization in food manufacturing industry,” Applied Soft Computing, vol. 46, pp. 328–343, 2016. [Google Scholar]

10. S. Dan, “Optimization,” in Evolutionary Optimization Algorithms, 1st edition, vol. 1. Hoboken, New Jersey, Canada: John Wiley & Sons, pp. 11–35, 2013. [Google Scholar]

11. C. Liu, “The dark forest,” in The Three-Body Problem, 1st edition, vol. 1. Chongqing, China: Chongqing Publishing Group, pp. 441–449, 2008. [Google Scholar]

12. X. Yao, Y. Liu and G. Lin, “Evolutionary programming made faster,” IEEE Transactions on Evolutionary Computation, vol. 3, no. 2, pp. 82–102, 1999. [Google Scholar]

13. Bilal, M. Pant, H. Zaheer, L. Garcia-Hernandez and A. Abraham, “Differential evolution: A review of more than two decades of research,” Engineering Applications of Artificial Intelligence, vol. 90, pp. 103479, 2020. https://doi.org/10.1016/j.engappai.2020.103479 [Google Scholar] [CrossRef]

14. N. Hansen, D. V. Arnold and A. Auger, “Evolution strategies,” in Springer Handbook of Computational Intelligence, 1st edition. Heidelberg, BER, DE: Springer, Berlin, Heidelberg, pp. 871–898, 2015. [Google Scholar]

15. M. Abdel-Basset and L. A. Shawky, “Flower pollination algorithm: A comprehensive review,” Artificial Intelligence Review, vol. 52, no. 4, pp. 2533–2557, 2019. [Google Scholar]

16. T. Zhang and Z. W. Geem, “Review of harmony search with respect to algorithm structure,” Swarm and Evolutionary Computation, vol. 48, pp. 31–43, 2019. [Google Scholar]

17. A. Lambora, K. Gupta and K. Chopra, “Genetic algorithm-a literature review,” in 2019 Int. Conf. on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Faridabad, India, pp. 380–384, 2019. [Google Scholar]

18. M. Paulinas and A. Ušinskas, “A survey of genetic algorithms applications for image enhancement and segmentation,” Information Technology and Control, vol. 36, no. 3, pp. 278–284, 2007. [Google Scholar]

19. Y. Park, J. Yoo and H. Park, “A genetic algorithm for the vendor-managed inventory routing problem with lost sales,” Expert Systems with Applications, vol. 53, pp. 149–159, 2016. [Google Scholar]

20. E. Hancer, “Artificial bee colony: Theory, literature review, and application in image segmentation,” Recent Advances on Memetic Algorithms and its Applications in Image Processing, vol. 873, pp. 47–67, 2020. [Google Scholar]

21. F. Pourpanah, R. Wang, C. P. Lim, X. Wang and D. Yazdani, “A review of artificial fish swarm algorithms: Recent advances and applications,” Artificial Intelligence Review, pp. 1–37, 2022. https://doi.org/10.1007/s10462-022-10214-4 [Google Scholar] [CrossRef]

22. S. Mirjalili, L. Aljarah, M. Mafarja, A. A. Heidari and H. Faris, “Grey wolf optimizer: Theory, literature review, and application in computational fluid dynamics problems,” Nature-Inspired Optimizers, vol. 811, pp. 87–105, 2020. [Google Scholar]

23. V. Kumar and D. Kumar, “A systematic review on firefly algorithm: Past, present, and future,” Archives of Computational Methods in Engineering, vol. 28, no. 4, pp. 3269–3291, 2021. [Google Scholar]

24. A. S. Joshi, O. Kulkarni, G. M. Kakandikar and V. M. Nandedkar, “Cuckoo search optimization-a review,” Materials Today: Proceedings, vol. 4, no. 8, pp. 7262–7269, 2017. [Google Scholar]

25. Q. Zhang, S. Du, Y. Zhang, H. Wu, K. Duan et al., “A novel chimp optimization algorithm with refraction learning and its engineering applications,” Algorithms, vol. 15, no. 6, pp. 189, 2022. [Google Scholar]

26. L. Abualigah and A. Diabat, “A comprehensive survey of the grasshopper optimization algorithm: Results, variants, and applications,” Neural Computing and Applications, vol. 32, no. 19, pp. 15533–15556, 2022. [Google Scholar]

27. Y. Zhang, S. Du and Q. Zhang, “Improved slime mold algorithm with dynamic quantum rotation gate and opposition-based learning for global optimization and engineering design problems,” Algorithms, vol. 15, no. 9, pp. 317–341, 2022. [Google Scholar]

28. F. S. Gharehchopogh and H. Gholizadeh, “A comprehensive survey: Whale optimization algorithm and its applications,” Swarm and Evolutionary Computation, vol. 48, pp. 1–24, 2019. [Google Scholar]

29. Y. Liu, and P. Tian, “A Multi-start central force optimization for global optimization,” Applied Soft Computing, vol. 27, pp. 92–98, 2015. [Google Scholar]

30. E. Rashedi, E. Rashedi and H. Nezamabadi-Pour, “A comprehensive survey on gravitational search algorithm,” Swarm and Evolutionary Computation, vol. 41, pp. 141–158, 2018. [Google Scholar]

31. H. Eskandar, A. Sadollah, A. Bahreininejad and M. Hamdi, “Water cycle algorithm–a novel metaheuristic optimization method for solving constrained engineering optimization problems,” Computers & Structures, vol. 110, pp. 151–166, 2012. [Google Scholar]

32. W. Zhao, L. Wang and Z. Zhang, “Atom search optimization and its application to solve a hydrogeologic parameter estimation problem,” Knowledge-Based Systems, vol. 163, pp. 283–304, 2019. [Google Scholar]

33. H. Abedinpourshotorban, S. M. Shamsuddin, Z. Beheshti and D. N. A. JawawI, “Electromagnetic field optimization: A physics-inspired metaheuristic optimization algorithm,” Swarm and Evolutionary Computation, vol. 26, pp. 8–22, 2016. [Google Scholar]

34. F. A. Hashim, E. H. Houssein, M. S. Mabrouk, W. Al-Atabany and S. Mirjalili, “Henry gas solubility optimization: A novel physics-based algorithm,” Future Generation Computer Systems, vol. 101, pp. 646–667, 2019. [Google Scholar]

35. O. Abdalla, H. Rezk and E. M. Ahmed, “Wind driven optimization algorithm based global MPPT for PV system under non-uniform solar irradiance,” Solar Energy, vol. 180, pp. 429–444, 2019. [Google Scholar]

36. F. Zou, D. Chen and Q. Xu, “A survey of teaching–learning-based optimization,” Neurocomputing, vol. 335, pp. 366–383, 2019. [Google Scholar]

37. S. Cheng, Q. Qin, J. Chen and Y. Shi, “Brain storm optimization algorithm: A review,” Artificial Intelligence Review, vol. 46, no. 4, pp. 445–458, 2016. [Google Scholar]

38. A. Fathy and H. Rezk, “Parameter estimation of photovoltaic system using imperialist competitive algorithm,” Renewable Energy, vol. 111, pp. 307–320, 2017. [Google Scholar]

39. A. Maheri, S. Jalili, Y. Hosseinzadeh, R. Khani and M. Miryahyavi, “A comprehensive survey on cultural algorithms,” Swarm and Evolutionary Computation, vol. 62, pp. 100846, 2021. [Google Scholar]

40. M. A. Al-Betar, Z. A. A. Alyasseri, M. A. Awadallah and L. A. Doush, “Coronavirus herd immunity optimizer (CHIO),” Neural Computing and Applications, vol. 33, no. 10, pp. 5011–5042, 2021. [Google Scholar] [PubMed]

41. T. Wu, X. Wu, J. Chen, X. Chen and A. H. Ashrafzadeh, “A novel metaheuristic algorithm: The team competition and cooperation optimization algorithm,” CMC-Computers Materials & Continua, vol. 73, no. 2, pp. 2879–2896, 2022. [Google Scholar]

42. H. Ma, D. Simon, P. Siarry, Z. Yang and M. Fei, “Biogeography-based optimization: A 10-year review,” IEEE Transactions on Emerging Topics in Computational Intelligence, vol. 1, no. 5, pp. 391–407, 2017. [Google Scholar]

43. W. Zhao, L. Wang and Z. Zhang, “Artificial ecosystem-based optimization: A novel nature-inspired meta-heuristic algorithm,” Neural Computing and Applications, vol. 32, no. 13, pp. 9383–9425, 2020. [Google Scholar]

44. A. R. Pouya, M. Solimanpur and M. J. Rezaee, “Solving multi-objective portfolio optimization problem using invasive weed optimization,” Swarm and Evolutionary Computation, vol. 28, pp. 42–57, 2016. [Google Scholar]

45. T. Joyce and J. M. Herrmann, “A review of no free lunch theorems, and their implications for metaheuristic optimisation,” Nature-Inspired Algorithms and Applied Optimization, vol. 744, pp. 27–51, 2018. [Google Scholar]

46. Z. Wang, S. Dang, Y. Xing, Q. Li and H. Yan, “Applying rank sum ratio (RSR) to the evaluation of feeding practices behaviors, and its associations with infant health risk in Rural Lhasa, Tibet,” International Journal of Environmental Research and Public Health, vol. 12, no. 12, pp. 15173–15181, 2015. [Google Scholar] [PubMed]