Ensemble of Population-Based Metaheuristic Algorithms

1  Introduction

Multiple optimization techniques have been proposed to address the challenges of various optimization problems, which include accurate and approximate methods [1]. Accurate methods obtain an exact solution to guarantee optimality. Approximate methods can generate a high-quality solution in a reasonable time to meet the actual requirements, but they cannot ensure a globally optimal solution. As one type of approximate method, metaheuristics are general for solving optimization problems. Metaheuristics include single-solution-based and population-based by the number of solutions processed in the optimization phase [2].

Although engineers apply meta-heuristic algorithms to various optimization problems, the solution to a specific optimization problem is only sometimes satisfactory. Therefore, researchers widely use integration strategies to design general algorithms for particular problem sets. Many practical and available algorithms have been developed for single-objective optimization [3], constrained optimization [4], multi-objective optimization [5], niche [6], and others. Metaheuristic algorithms have significantly been developed and applied to solving optimization problems in many fields [7], such as scheduling [8], data mining [9], and unmanned system [10].

When engineers integrate various optimization algorithms, they have to design appropriate integration schemes to take advantage of their respective strengths. The paper proposes an ensemble of population-based metaheuristics (EPM) to solve the single-objective problem. We consider each population-based metaheuristic algorithm as a whole in the ensemble framework without understanding its characteristics and internal mechanisms. The ensemble framework puts forward the transformation between the real and virtual populations to coordinate exploration and exploitation at the population level. It also adopts an elite strategy to realize information exchanges among virtual populations to enhance the diversity of populations. The transformation between the real and virtual populations mainly solves the problem of falling into local optimum. We also apply an elite strategy to speed up the convergence. The practical issues that the ensemble framework can solve are related to the application field of its integrated meta-heuristic algorithms. If a meta-heuristic algorithm can be applied to solve a particular practical problem, then the algorithm can still solve the optimization problem in the ensemble framework.

The rest of this paper is structured as follows. Section 2 summarizes the ensemble methods of the population-based metaheuristic algorithms. Section 3 describes the design of the EPM framework and how to use it to integrate various metaheuristic algorithms. Section 4 conducts testing and analysis, where it tests the original and ensemble algorithms using two test function sets and two engineering application problems. Finally, in Section 5, the full text is summarized, pointing to future research.

2  Related Work

2.1 Population-Based Metaheuristics

Population-based metaheuristics have the same paradigm, as shown in Fig. 1. A population represents a set of solutions, and each individual represents a feasible solution. Generation strategies are designed to generate a new population, and the original individual is replaced by the newly generated individual according to selection strategies so that the population is continuously optimized until the set stop condition is met. The various population-based metaheuristic algorithms differ in how they perform the generation and selection processes.

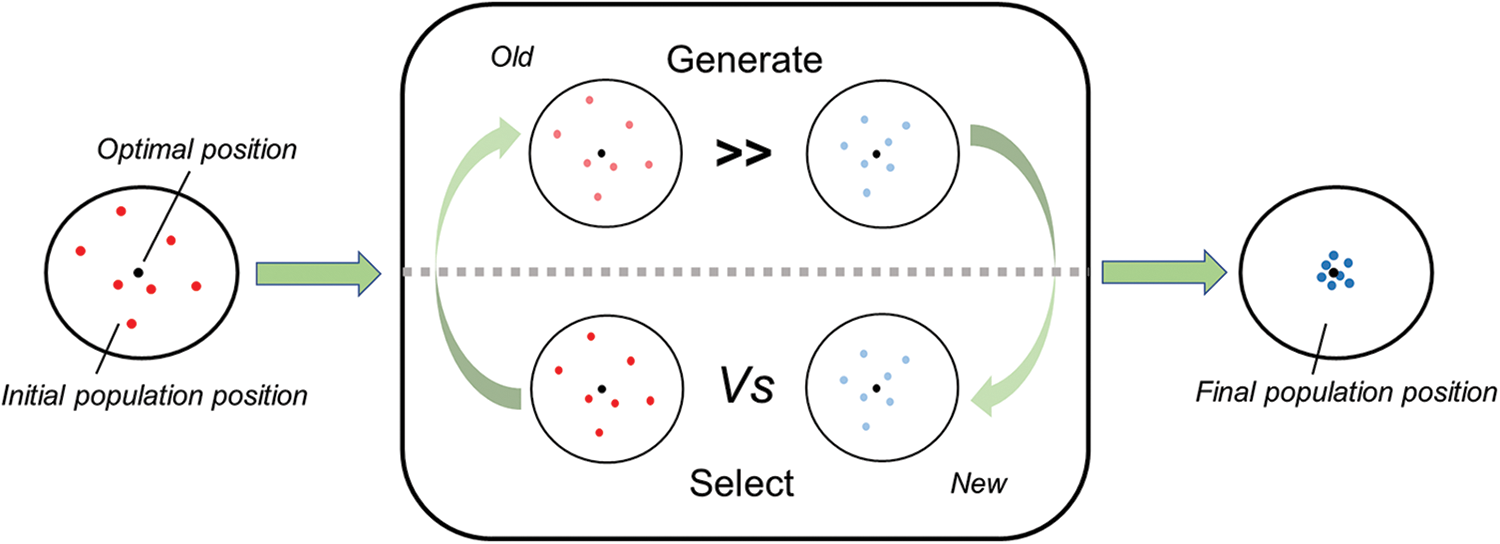
Figure 1: The typical process diagram of population-based metaheuristics

The design of population-based metaheuristics is inspired by nature and human society, including evolutionary processes, physics, biology, chemistry, mathematics, human bodies, society, and so on. Evolutionary algorithms simulate the process of biological evolution, using crossover, mutation, reproduction, and other operators to produce better solutions. Typical algorithms include differential evolution [11], genetic algorithm [12], and genetic programming [13]. Biology-based algorithms mimic the behaviors in biological groups, such as foraging, mating, and movement, including particle swarm optimization [14], artificial bee swarm optimization [15], cuckoo search [16], and sand cat swarm optimization [17]. Human-based algorithms mainly simulate human body structure, way of thinking, and social behavior, including tabu search [18], cooperation search [19], brainstorming algorithms [20], heap-based optimization [21], and war strategy optimization [22]. Physics-based algorithms draw lessons from the classical laws of physics. For example, the idea of gravity search comes from the law of gravity [23]. The big bang algorithm simulates the big bang effects and the big bang processes [24]. The electromagnetic mechanism-like algorithm simulates charged particles’ attraction and repulsion mechanisms in the electromagnetic field [25]. The algorithm based on mathematics draws lessons from mathematical formulas and mathematical theorems, such as the sine cosine algorithm based on the mathematical properties of the sine and cosine functions [26], the chaotic golden section algorithm based on chaotic motion and golden section [27] and the arithmetic optimization algorithm based on the main arithmetic operators in mathematics [28].

Engineers apply metaheuristic algorithms in many fields, such as engineering, material, robot, computer, home life, and medical treatment. Chopra et al. proposed a golden jackal optimization algorithm for the economic load dispatch problem in electrical engineering [29]. Zhang et al. designed a generalized normal distribution optimization to improve the accuracy of extracting the model parameters in the photovoltaic material industry [30]. Ibrahim et al. proposed a hybrid wind-driven-based fruit fly optimization algorithm for adjusting several model parameters in the double-diode cell material industry [31]. Tang et al. combined fuzzy C-means clustering and ant colony optimization algorithm for mission planning of unmanned aerial vehicles in emergent scenarios [32]. Tian applied a backtracking search optimization algorithm to adjust the algorithm parameters of the least square support vector machine in the computer field [33]. Jordehi designed a quadratic binary particle swarm optimization to schedule multiple interruptible and non-interruptible appliances in an intelligent home [34]. Nadimi-Shahraki et al. applied an enhanced whale optimization algorithm to detect coronavirus disease 2019 [35].

The search steps of these algorithms include exploration and exploitation phases [36]. In the exploration phase, it ensures the diversity of the population as much as possible so that the individuals in the population can fully explore each area of the feature space. If there is insufficient exploration, the solution is locally optimal. In the exploitation phase, the search should focus on areas with high-quality solutions, constantly searching the neighborhood. If underexploited, there is no way to converge to a global solution.

2.2 Ensemble Approaches of Population-Based Metaheuristics

A single algorithm cannot handle all the optimization problems [37], so the ensemble of multiple meta-heuristic algorithms can increase the effect of optimization. The ensemble technology of the meta-heuristic algorithms includes low-level and high-level ensembles depending on the objects. The low-level ensemble integrates multiple search strategies and variable parameter values of a single algorithm. The high-level ensemble integrates multiple meta-heuristic algorithms and their variants.

An algorithm may be excellent at solving one type of optimization problem and not good at solving another. The search strategy of the algorithm mainly expresses this particularity. Therefore, to enhance the effect of the algorithm on optimization problems that the algorithm is not good at, a variety of search strategies can be integrated to improve the algorithm to obtain a better solution. Qin et al. proposed a self-adaptive differential evolution algorithm that randomly assigned the experimental vector generation strategy and the control parameters to population individuals based on the characteristics of the historical solution [38]. Pan et al. designed an adaptive differential evolution algorithm based on the hybrid leapfrog strategy, which can maintain the overall diversity of the population during dynamic evolution [39]. Gong et al. applied a multi-operator search strategy based on a cheap agent model, using multiple sub-generation search operators and proxy models to select the best candidate solution [40]. Ali et al. divided the population into several subgroups, each adopting a modified mutation strategy based on differential evolution [41]. Rakhshani et al. proposed a new extension of the cuckoo algorithm, which combines the exploration capabilities of computer science with the development behavior provided by the covariance matrix adaptation evolution strategy through multiple search strategies [42]. Li et al. designed an adaptive learning framework for particle swarm optimization to select the optimal method from some strategies to deal with different search spaces [43].

When the set of optimization problems is vast, a single swarm intelligence optimization algorithm cannot handle it. So researchers ensemble multiple algorithms to solve optimization problems. Lynn et al. proposed an evolutionary particle swarm optimization algorithm that integrates different particle swarm optimization algorithms [44]. Zhang et al. proposed a multivariable coordination framework, which coordinates multiple improved differential evolution algorithms [45]. Thangavelu et al. designed an island-based dynamic data exchange algorithm mixing four classical differential evolution variants that fill each island with different dynamic data exchange variables as a possible way to implement a robust dynamic data exchange system [46]. Wu et al. proposed an algorithm based on an ensemble of multiple differential evolution variants, which divides the whole population into index and reward subpopulations and allocates the reward subpopulation dynamics to the well-performing differential evolution variant algorithm according to the performance of the index subpopulation [47]. Elsayed et al. applied a group of different particle swarm optimization variants to integrate and measure the performance of varying optimization variants according to the improvement index to adaptively determine the number of individuals allocated to the variant algorithm in each generation [48]. Vrugt et al. applied an adaptive learning strategy that integrates evolution strategy, genetic algorithm, and particle swarm optimization to dynamically adjust the influence of these three algorithms on individuals [49]. Xue et al. proposed an integrated evolutionary algorithm using an adaptive learning search technique incorporating three different algorithms [50]. Elsayed et al. designed a framework with multiple adaptive algorithms and operators, using two decisions to adaptively select the appropriate algorithm and search operator [51]. The existing ensemble frameworks are usually designed for specific algorithms and their variants, focusing on complementarity and neglecting generality.

In this paper, we design an ensemble framework based on common structural features of metaheuristic algorithms rather than a specific algorithm. The ensemble framework belongs to the high-level ensemble, which could integrate various meta-heuristic and variant algorithms. These algorithms can have multiple search strategies, including low-level ensembles.

3  Ensemble of Population-Based Metaheuristics

This section introduces the EPM framework in detail. Section 3.1 explains the idea and features of the framework. Section 3.2 shows the stages of using the EPM framework to integrate the metaheuristic algorithm. It presents the implementation procedure and pseudocode in Section 3.3.

3.1 Basic Concepts

3.1.1 Algorithm Library

After filling in multiple meta-heuristic algorithms, the ensemble framework can only solve optimization problems. These meta-heuristic algorithms are placed together in the algorithm library. It is hard to judge which population-based metaheuristic algorithm is the best for a particular optimization problem, especially when there is not enough information about the problem. While engineers can find better algorithms through trial and error, it would be time-consuming and labor-intensive. In addition, to solve some problems, a satisfactory solution cannot be obtained through a search strategy using a single algorithm. Neither the specific transition point from one algorithm to another nor which algorithms to apply is known. Each algorithm has its characteristics: local search, global search, optimization speed, and population diversity. The role of the EPM framework is to make all kinds of algorithms give full play to their respective strengths and provide a communication bridge for these algorithms. It requires that as many algorithms as possible be included in the algorithm library.

3.1.2 Real and Virtual Populations

The EPM framework proposes the setting and conversion of real and virtual populations. Virtual populations represent various virtual states of the population obtained by the evolution of the real population in different directions. All virtual populations come from the real population. Each virtual population applies a population-based metaheuristic algorithm, which updates the population by selection rules to obtain individuals with better fitness values. Each virtual population can exchange information to facilitate population optimization. When certain conditions are satisfied, it retains the optimal virtual population as the optimal population, which materializes into a real population. After that, it uses the same operation to virtualize and set up the next population that meets certain conditions, constantly optimizing the population until reaching the stop condition. The adjustment of parameters for each swarm intelligence algorithm is not considered, nor is the specific update strategy within the population. The setting of the real and virtual populations is a new idea for coordinated exploration and exploitation at the population level.

3.1.3 Elite Strategy

The exchange of information among virtual populations enables the population to obtain satisfactory solutions more quickly in the renewal process, reducing the incidences of falling into local optima. The algorithm framework designed in this study uses an elite strategy to communicate between virtual populations. To minimize the interference in the virtual population, the individual with the smallest fitness value is an elite in each virtual population. If multiple individuals have the same fitness value, it randomly selects one as the elite. It brings these elites together to form a group and selects the best elite according to their fitness. When meeting certain conditions, the best elite individual is added to each virtual population to complete the exchange of information between populations. In this way, it reduces the interference of virtual populations and realizes population optimization with the help of the optimal individual’s influence on the population.

3.2 The Framework of EPM

The EPM framework consists of three stages: the initial stage, the update stage, and the final stage. The update stage includes two sub-stages high-level generation and selection. Fig. 2 shows the entire process diagram of EPM. These three stages are described in detail below.

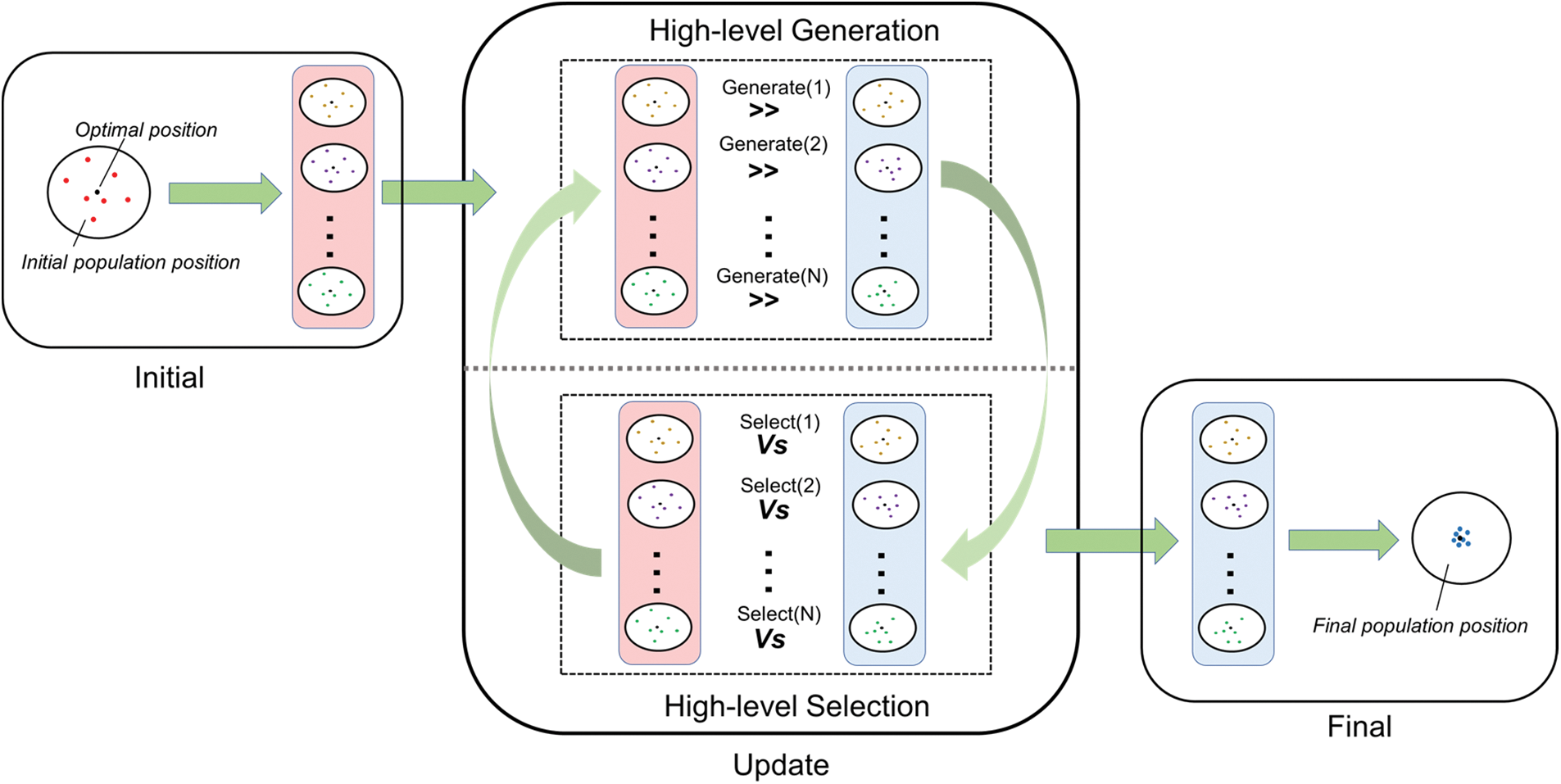
Figure 2: The entire process diagram of EPM

3.2.1 The Initial Stage

The search space dimension of the optimization problem is D. Its upper boundary U is (u1,u2,…,ud,…,uD), and its lower boundary L is (l1,l2,…,ld,…,lD). The number of individuals in the population is N, and the population set X is {X1,X2,…,Xn,…,XN}. The position of the nth individual Xn is (x1n,x2n,…,xdn,…,xDn), where xdn is calculated according to Eq. (1), r is a random number in the [0,1].

It selects the required algorithm in the algorithm library, and the number of algorithms selected is M. The set of algorithms A is {A1,A2,…Am,…,AM}. R represents the real population, and XR(t) represents the population at the tth iteration. The virtual population set V is {V1,V2,…,Vm,…,VM}. XVm(t) represents the virtual population corresponding to the mth algorithm at the tth iteration. When t=0, XR(t) and XVm(t) are obtained from Eq. (2).

xdn=ud+r(ud−ld)(1)

XVm(0)=XR(0)=X(0),m=1,2,3,…M(2)

3.2.2 The Update Stage

At the high-level generation process, each virtual population adopts the corresponding algorithm to update separately, where their internal update strategy set Rw is {Rw1,Rw2,…,Rwm,…,RwM}. Rwm represents the internal update strategy of the algorithm Am, and the update process of the virtual population position XVm is shown in Fig. 3.

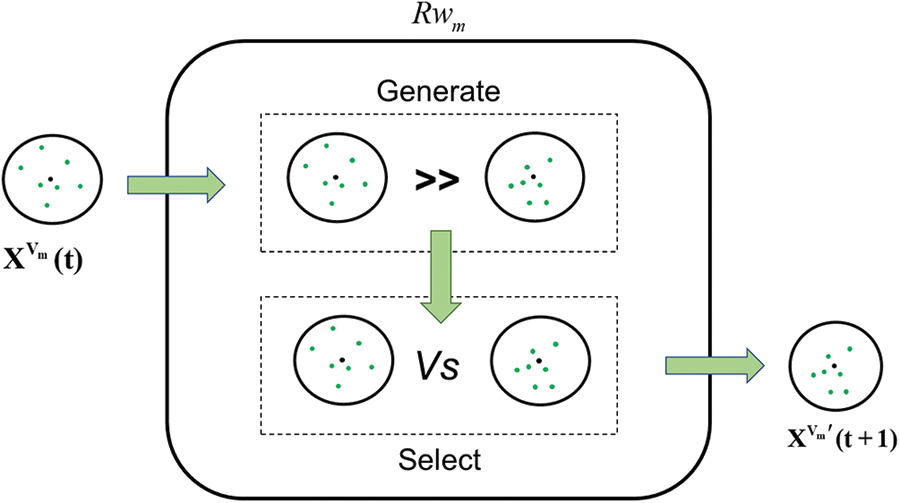
Figure 3: The updating process diagram of the virtual population position

At the (t+1)th iteration, XVm′(t+1) is obtained from XVm(t) through the generation and selection strategy within the algorithm Am, as shown in Eq. (3). However, it is not the virtual population for the next update XVm(t+1), which needs to be determined according to the high-level selection process.

XVm′(t+1)=Rwm(XVm(t))(3)

The entire high-level selection process is shown in Fig. 4. The elite swarm consists of individuals corresponding to the minimum fitness value in each virtual population. The set of these fitness values E is {E1,E2,…,Em,…,EM}, where Em represents the minimum fitness value in the mth virtual population. At the (t+1)th iteration, Em(t+1) is calculated by Eq. (4), where f() represents calculating the fitness value. B is the minimum in the set E, and B(t+1) is calculated by Eq. (5). Then, the individual with the minimum fitness value of the elite swarm B is considered as the best elite. Its corresponding virtual population is called the optimal virtual population Vb and its corresponding individual position is XeVb. If there are multiple individuals corresponding to the minimum fitness value, random selection is performed.

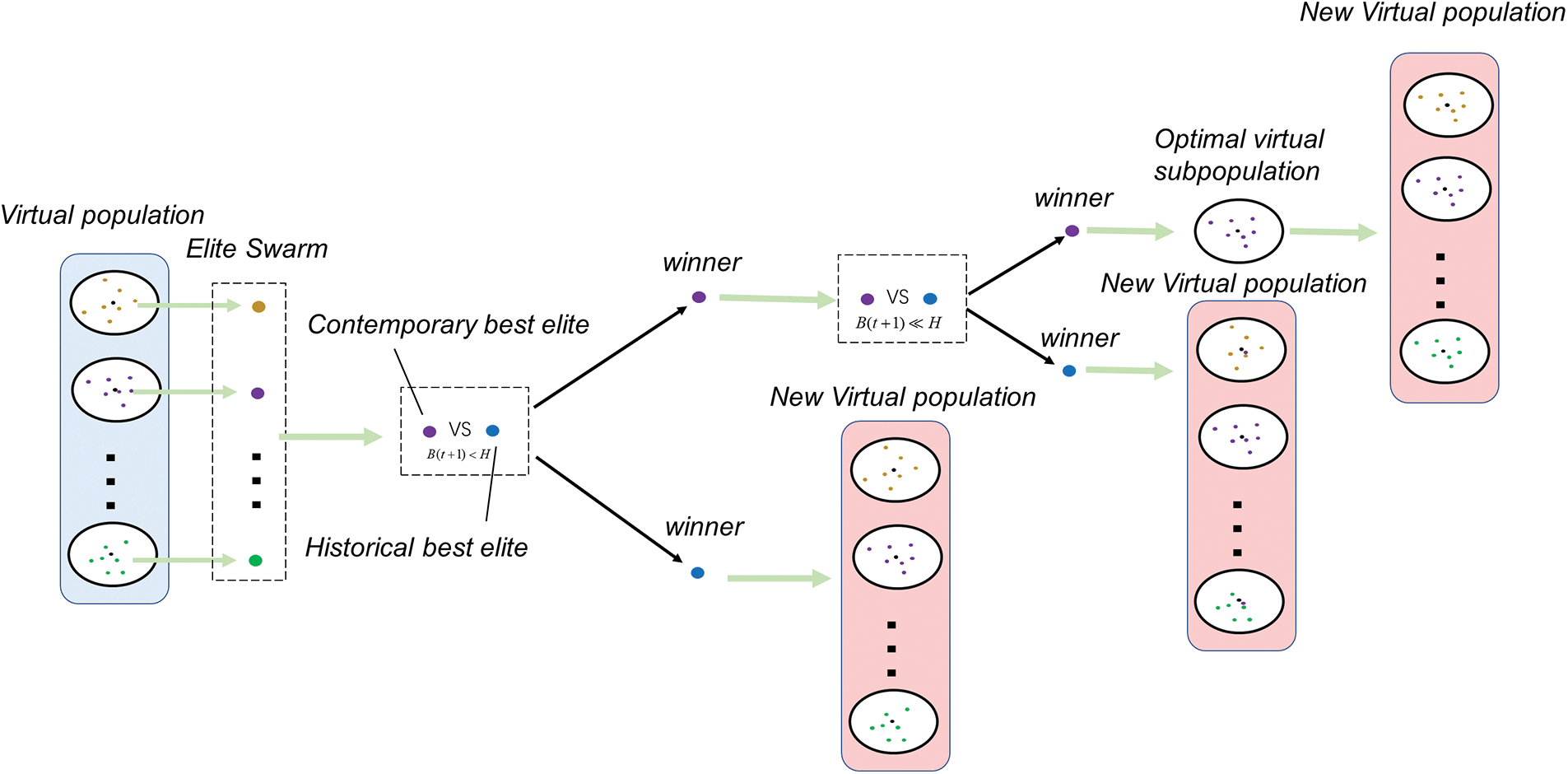
Figure 4: The process of a high-level selection

Em(t+1)=minf(XiVm′(t+1)),i=1,2,3,…,N(4)

B(t+1)=min{E1(t+1),…,Ej(t+1),…,EM(t+1)}(5)

H is the minimum fitness value of the best elite in history. When B(t+1)≥H, all virtual populations are preserved, and no information exchange is carried out among them. The virtual populations to be updated next time is shown in Eq. (6).

XVj(t+1)=XVj′(t+1),j=1,2,…M(6)

When B(t+1)<H, if B(t+1)≪H, the optimal virtual population Vb is materialized to the real population. The real population generates new virtual populations to be updated next time, as shown in Eq. (7). In this process, the parameters in the algorithms corresponding to the original virtual populations are retained. In this paper, it can be determined that the difference is large if one of the following three conditions is met: {B(t+1)×H>0,B(t+1)>0,a≤0.1}, {B(t+1)×H>0,H<0,a≥10}, {B(t+1)×H<0,eB(t+1)<eH}, where a is the ratio of B(t+1) to H, as shown in Eq. (8). If B(t+1) is not much different from H, the best elite is copied and distributed to other virtual populations and an individual in each virtual population is randomly replaced in the process. For virtual population Vm, q is a random integer in [1,N], representing a random individual which will be replaced by the best elite. The improved population will be updated in the next time as the new virtual populations, and the process is shown in Eq. (9).

XVj(t+1)=XR(t+1)=XVb′(t+1),j=1,2,…,N(7)

a=B(t+1)H,H≠0(8)

XVj(t + 1)⟵XqVj′(t+1)=XeVb(t+1)XVj′(t+1),j=1,2,…,M(9)

3.2.3 The Final Stage

The update stage repeats until reaching the maximum of iterations T, then the whole process ends. In the last iteration, the optimal virtual population Vb is materialized to obtain the real population, as shown in Eq. (10). After the last iteration, the optimal virtual population is transformed into the real population.

XR(T)=XVb(T)(10)

3.3 General Process of EPM

The ensemble range covered by the EPM framework includes all population-based metaheuristic algorithms and their modified versions. The larger the number of algorithms in the algorithm library, the better the possibility of covering many aspects of the optimization problem. First, it selects an appropriate number of algorithms from the algorithm library for the ensemble. In this process, the number of algorithms can be set without prior knowledge and then selected randomly. In the case of specific prior knowledge, it chooses the appropriate algorithm according to the previous knowledge. The pseudocode of EPM is presented below:

4  Experiment Results

It applies ensemble algorithms to two test sets, 23 standard benchmark functions [52] and the 2017 congress on evolutionary computation (CEC2017) benchmark functions [53]. Section 4.1 describes these functions in detail. Section 4.2 presents the five algorithms in the algorithm library along with a comprehensive comparison between the integrated and original algorithms, introducing the parameters of each algorithm in the experiment. Section 4.3 illustrates the experimental results of the nine algorithms. It gives the iterative curves of all algorithms on some functions in Section 4.4 to directly observe the optimization effect and convergence of the algorithms. Section 4.5 shows the evolution of the real and virtual populations in the optimization process. Section 4.6 applies the ensemble framework to solve two engineering application problems.

4.1 Benchmark Functions

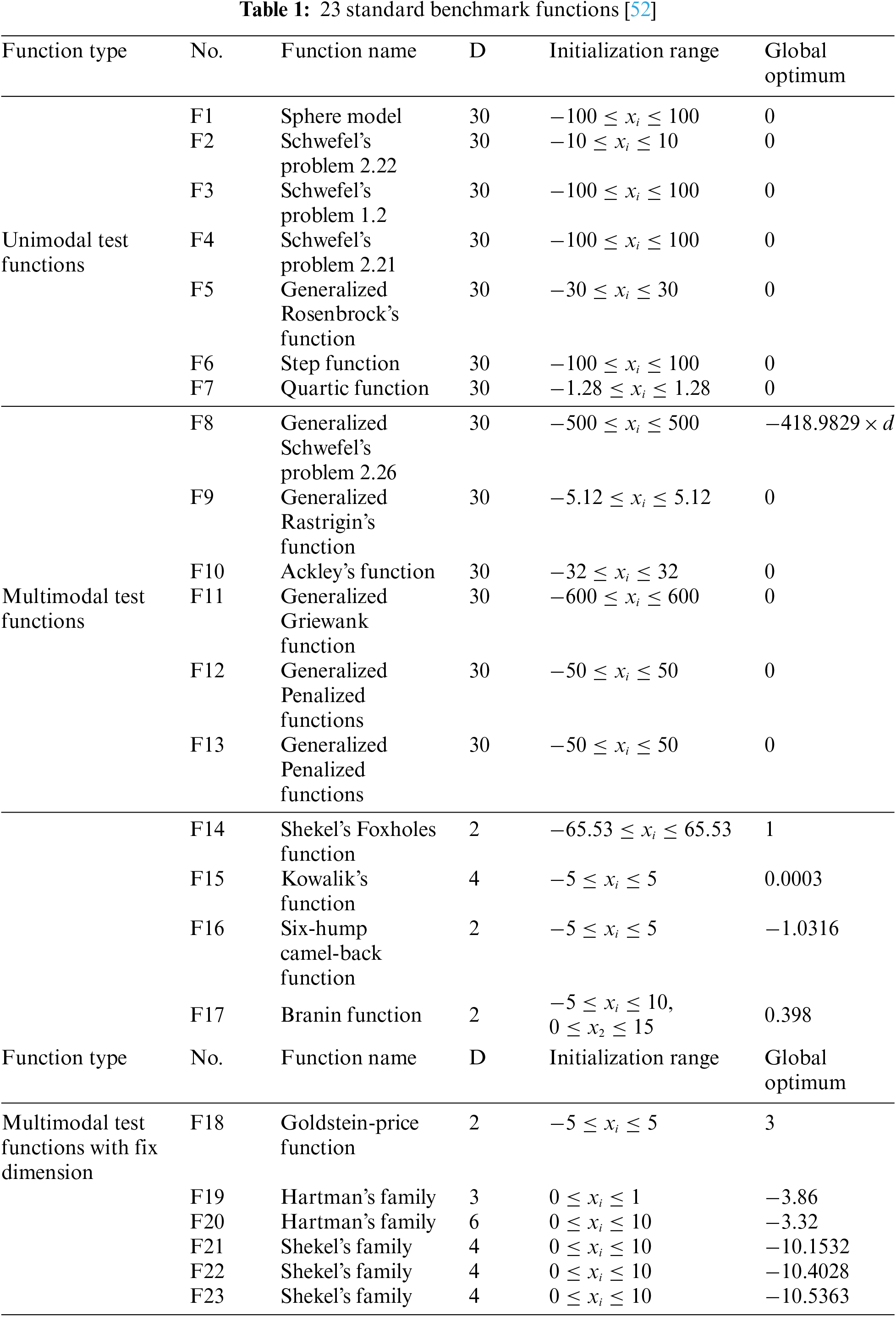
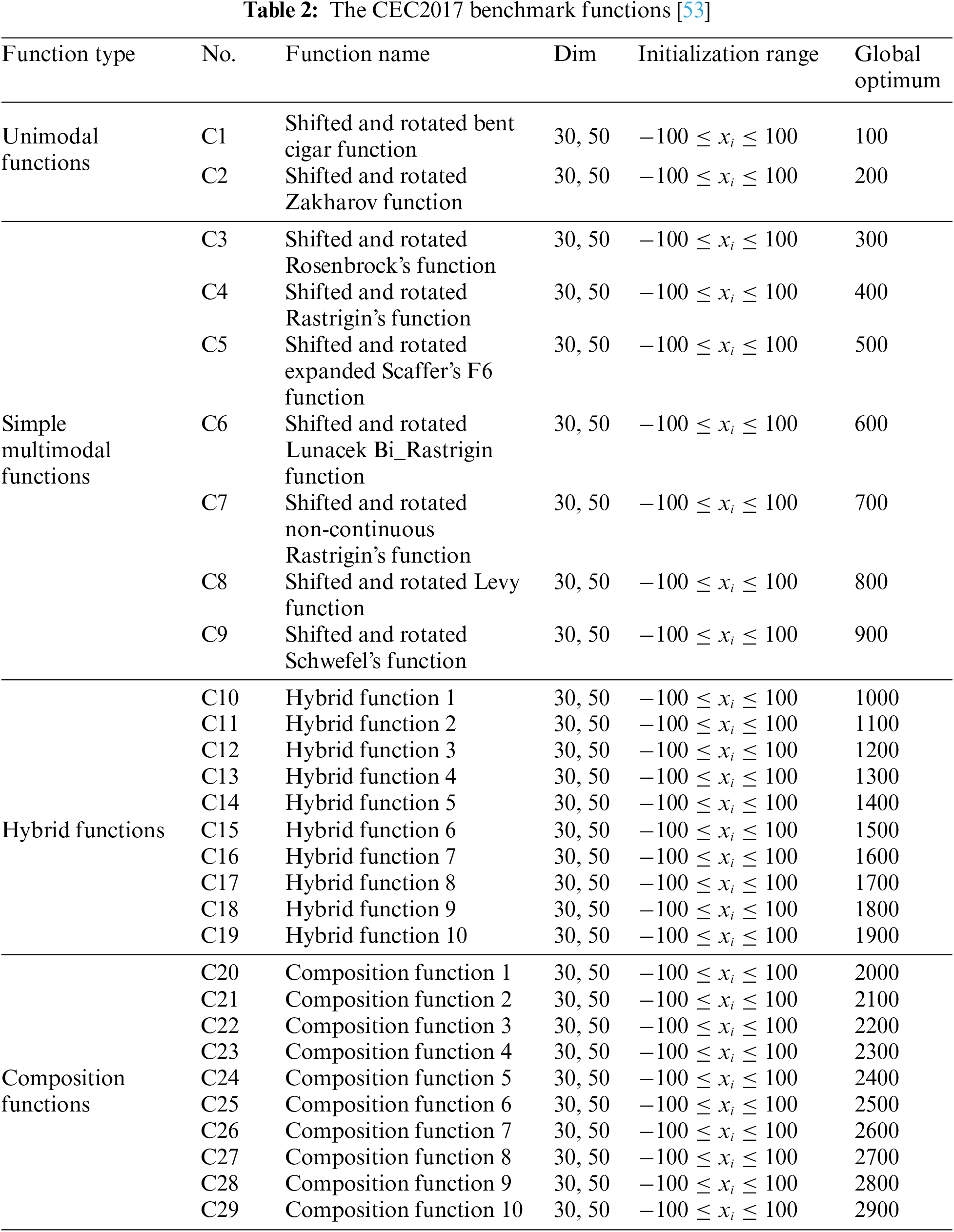
We select two sets of benchmark functions. One set consists of the 23 standard benchmark functions of the experiment, which are described in detail in Table 1, including function type, function name, and function definition. D denotes the number of independent variables in the function, and the initialization range means the range of variables. The optimal value corresponding to each function is the global optimum. In these functions, F1–F13 are high-dimensional with a dimension of 30; F1–F7 are unimodal; F8–F13 are multi-peak; F14–F23 are low-dimensional with only a few local minima. The other set is the CEC2017 benchmark functions set, as described in Table 2. Among these functions, C1–C2 are unimodal; C3–C9 are simple multi-peak; C10–C19 are mixed; C20–C29 are compound. The variable dimensions range from [−100, 100]. We set the dimensions uniformly to 30 and 50.

4.2 Original Algorithms and Ensemble Algorithms

In the experiment, we select some new representative algorithms for the ensemble, which are Harris hawks optimization (HHO) [54], seagull optimization algorithm (SOA) [55], slime mold algorithm (SMA) [56], salp swarm algorithm (SSA) [57], manta ray foraging optimization (MRFO) algorithm [58]. The EPM class algorithms represent the algorithms integrated under the EPM framework. This paper names the algorithms integrated by the EPM framework as “EPM + number”, where “number” represents the number of filled algorithms in the ensemble framework. It obtains the EPM2 algorithm by integrating HHO and SOA, the EPM3 algorithm by integrating HHO, SOA, and SMA, the EPM4 algorithm by integrating HHO, SOA, SMA, and SSA, the EPM5 algorithm by integrating HHO, SOA, SMA, SSA, and MRFO. The ensemble framework does not interfere with the updated formulas of the integrated algorithms, so researchers can adjust their parameters according to the characteristics of the original algorithms. The parameters of the original algorithms are consistent with the papers that proposed these algorithms. The parameters in integrated algorithms are the same as the original algorithms’ parameters. It lists the settings of the parameters in Table 3.

4.3 Comparison Results

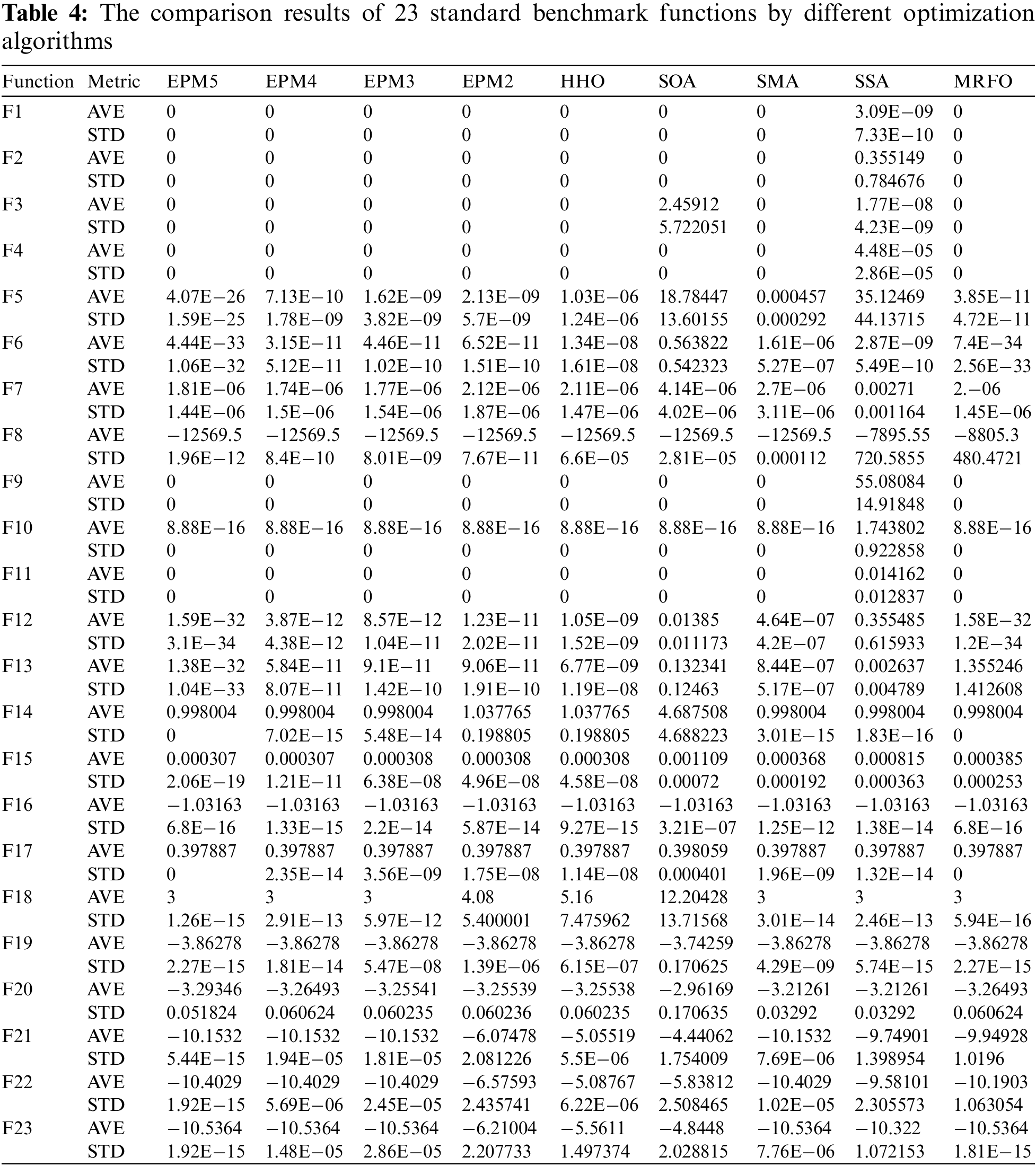
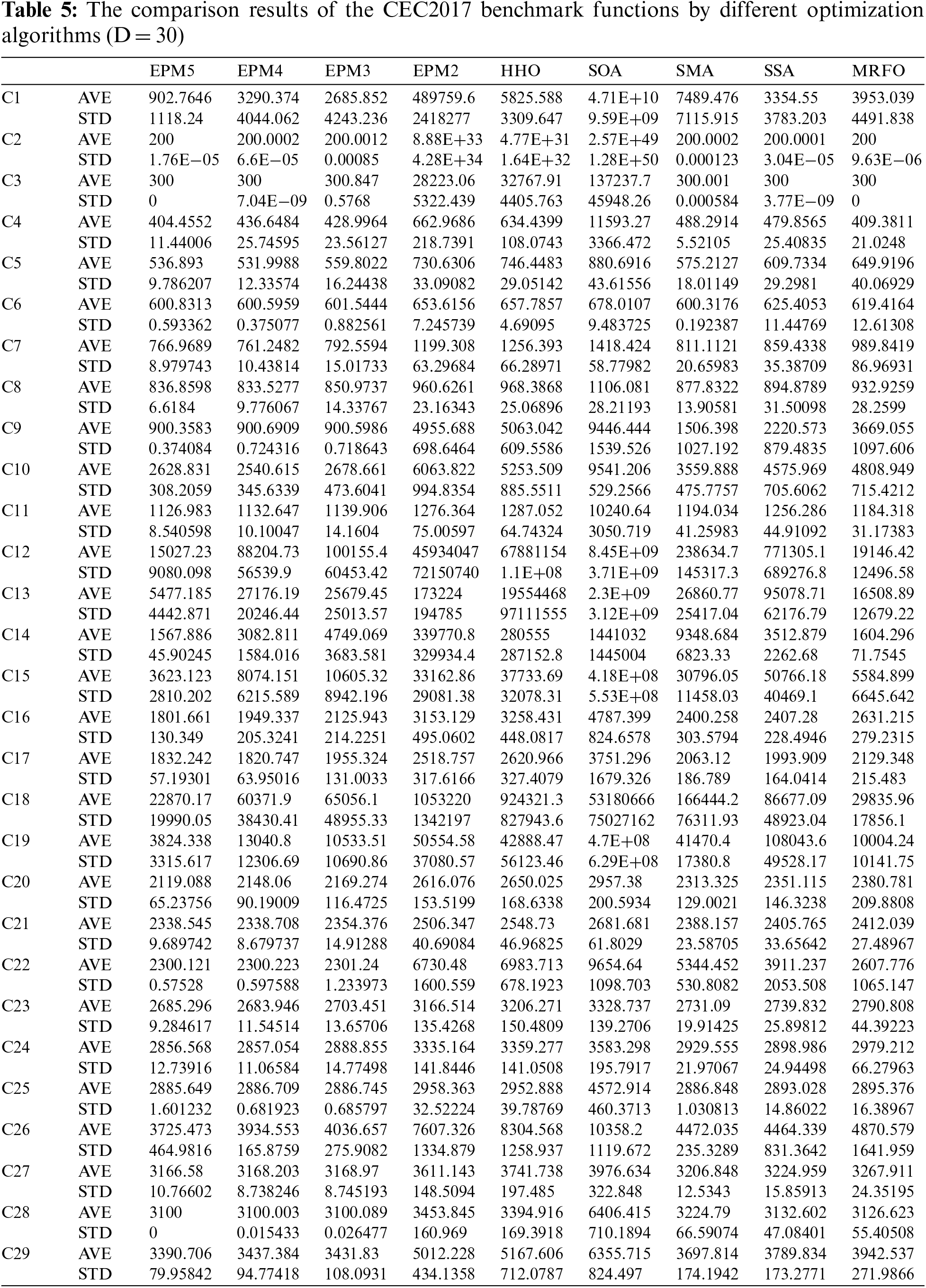
The average (AVE) and standard deviation (STD) of the best solutions obtained by all test algorithms in 25 independent runs and 500 iterations in each dimension were recorded (see Tables 4–6) and compared.

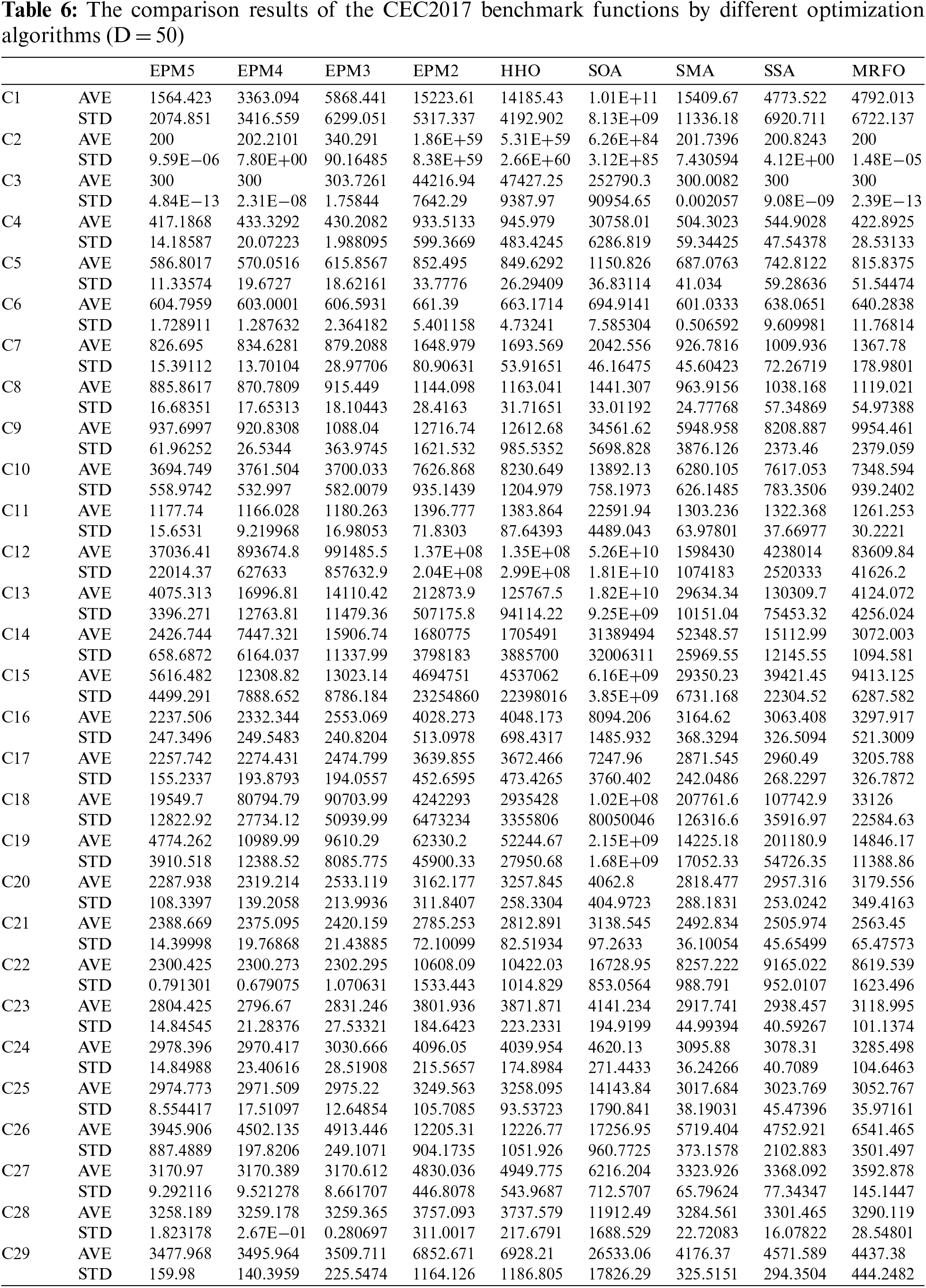
The population size is 70, and the number of iterations is 500 × D. D is the dimension of the test function. According to the characteristics of the EPM framework, the more algorithms are integrated into the framework, the more times the function will be evaluated. To compare the results of the integration algorithm and the original algorithm more fairly, we design a perfect ensemble (PE) that takes the optimal value from the effects of multiple original algorithms. In each independent run, it records the best result of several original algorithms as the result of this run, and after 25 runs, all the results are averaged. This paper names the results obtained by the PE framework as “PE + number”, where “number” represents the number of integrated results in the framework. It expresses the results obtained by averaging the optimal values of HHO and SOA as PE2, the results obtained by averaging the running results of HHO, SOA, and SMA as PE3, the results obtained by averaging the optimal values of HHO, SOA, SMA, and SSA as PE4, the results obtained by averaging the optimal values of HHO, SOA, SMA, SSA, and MRFO as PE5.

Table 7 displays the results of Friedman’s mean rank test for the benchmark functions. On the 23 standard benchmark functions, the mean rankings of EPM5, EPM3, and EPM2 are higher than those of PE5, PE3, and PE2, respectively; the mean ranking of EPM4 is lower than that of PE4. On the CEC2017 benchmark functions with 30 dimensions, the mean rankings of EPM5, EPM4, EPM3, and EPM2 are higher than that of PE5, PE4, PE3, and PE2, respectively. On the CEC2017 benchmark functions with 50 dimensions, the mean rankings of EPM5, EPM4, EPM3, and EPM2 are higher than that of PE5, PE4, PE3, and PE2, respectively. In most cases, the algorithms in the ensemble framework get a better ranking. Increasing the number of integrated metaheuristic algorithms enhances the average optimization ability of the overall ensemble framework.

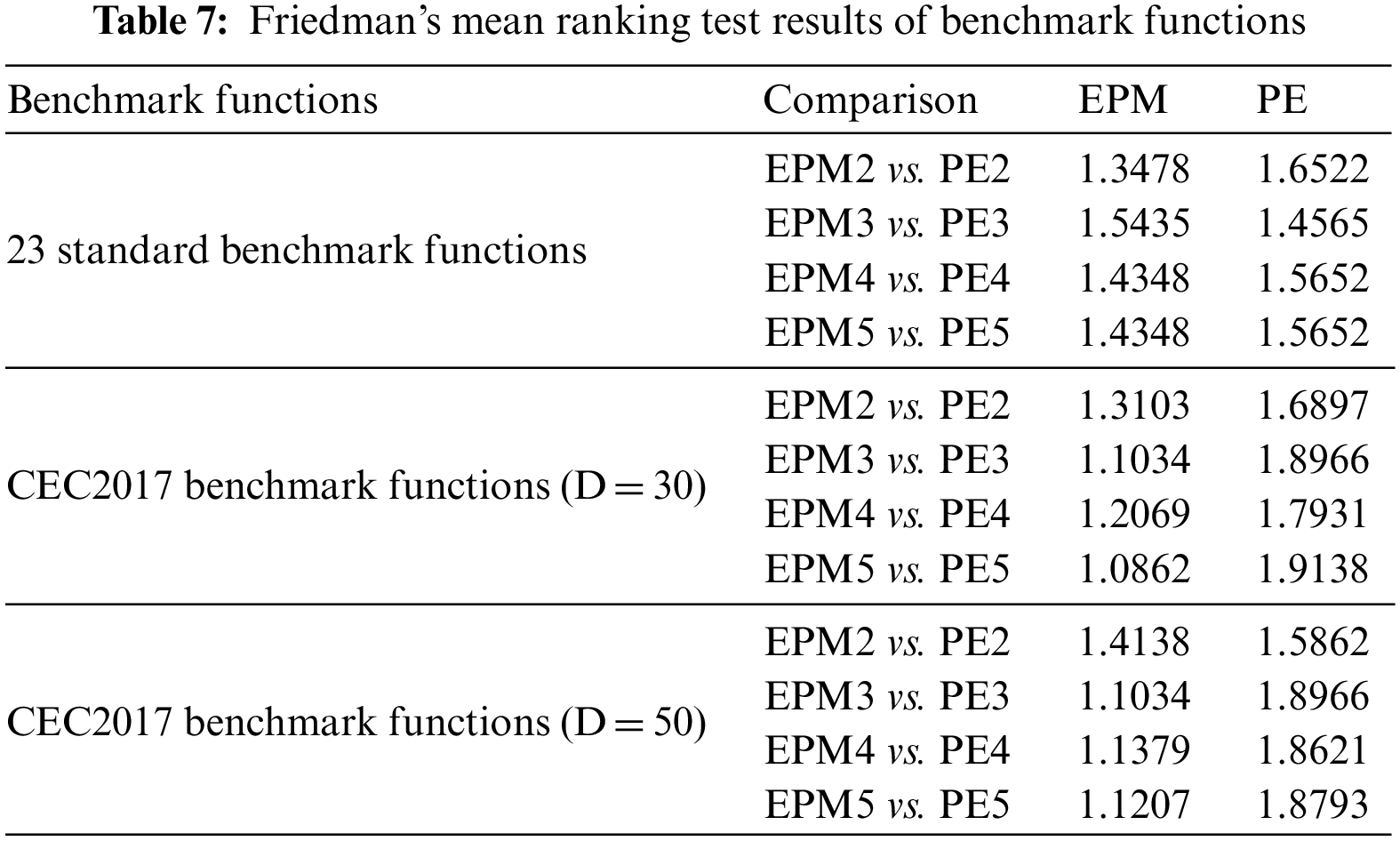
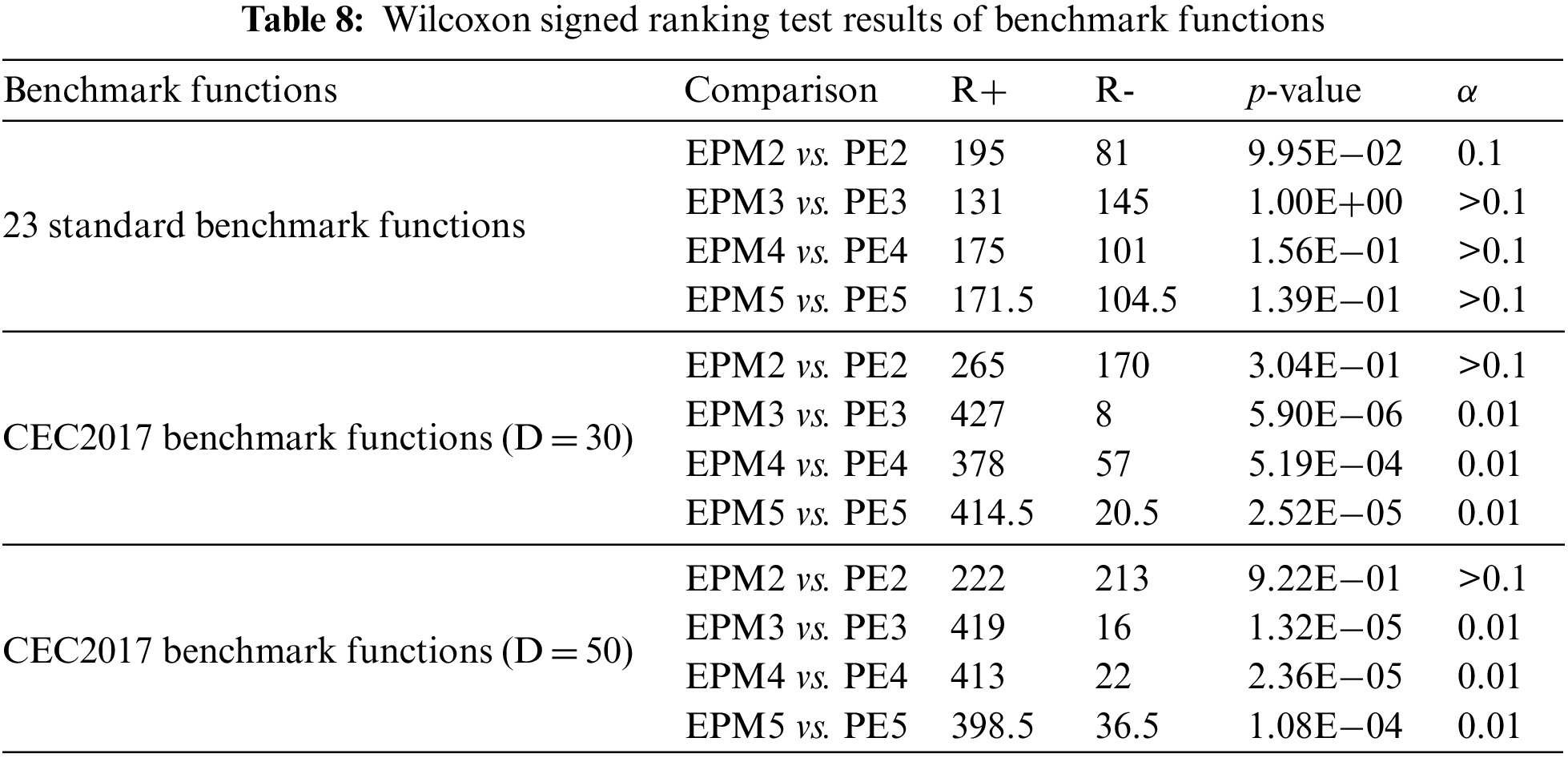
Table 8 displays the p-value test results on benchmark functions. On the 23 standard benchmark functions, the p-value resulting from the comparison between EPM2 and PE2 is less than 0.1 and more significant than 0.05, indicating that the results of the algorithms are different at the significance level of 0.1. The p-values resulting from the comparisons between EPM3 and PE3, between EPM4 and PE4, and between EPM5 and PE5 are greater than 0.1, indicating no significant difference between the results. On the CEC2017 benchmark functions with 30 dimensions, the p-value resulting from the comparison between EPM2 and PE2 is greater than 0.1, indicating no significant difference between the results. The p-values for the comparison between EPM3 and PE3, between EPM4 and PE4, and between EPM5 and PE5 are less than 0.01, indicating that the results of these algorithms are significantly different at the significance level of 0.01. On the CEC2017 benchmark functions with 50 dimensions, the p-value resulting from the comparison between EPM2 and PE2 is greater than 0.1, indicating no significant difference between the results. The p-values for the comparison between EPM3 and PE3, between EPM4 and PE4, and between EPM5 and PE5 are less than 0.01, indicating that the results of these algorithms are significantly different at the significance level of 0.01.

4.4 Iterative Curves

We select some test functions, draw the iterative curve of the experimental algorithm, and visually observe the convergence of the algorithms. The iterative curves in Fig. 5 correspond to functions F3, F15, F20, C5, C16, and C20, representing the performance of EPM5 under different types of functions. It is observed that the EPM5 algorithm has a faster iterative optimization speed and achieves better results through the iterative curves.

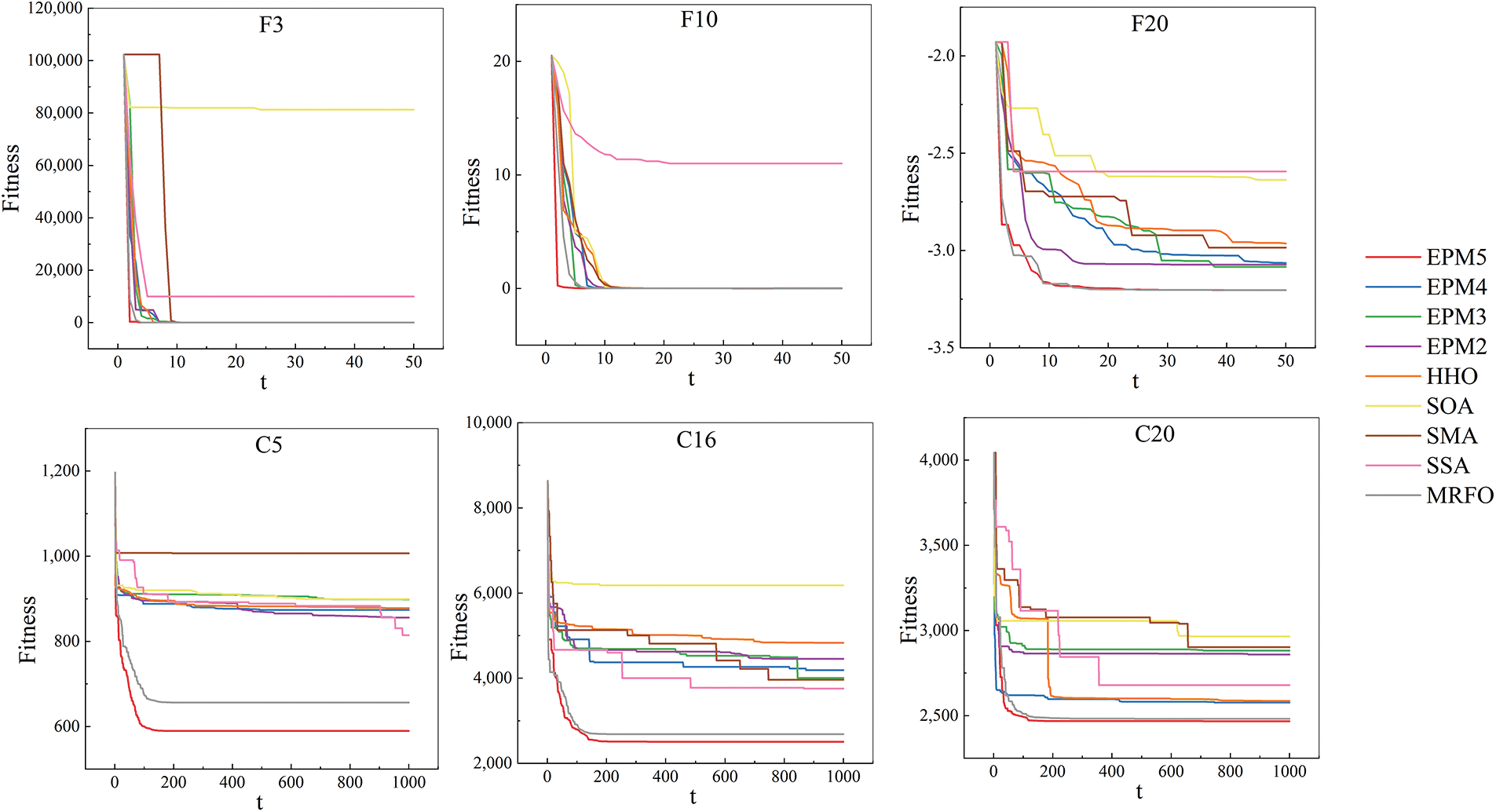
Figure 5: Iterative curves of partial test functions

4.5 Evolution Process of Real Population and Virtual Population

We analyzed the process of solving function F3 by the EPM5 algorithm to observe the relationship between the real and virtual populations and follow the evolution process more intuitively during the operation of the ensemble algorithm. Fig. 6 shows the position changes of the virtual populations in the x1 and x2 dimensions, before and after 1, 2, 5, 6, 20, 21, 100, 101, 1000, 1001, 14999, and 15000 iterations, where ‘a’ represents the population before the iteration and ‘b’ represents the population after the iteration. It lists the historical optimal solutions corresponding to the number of partial iterations in Table 9.

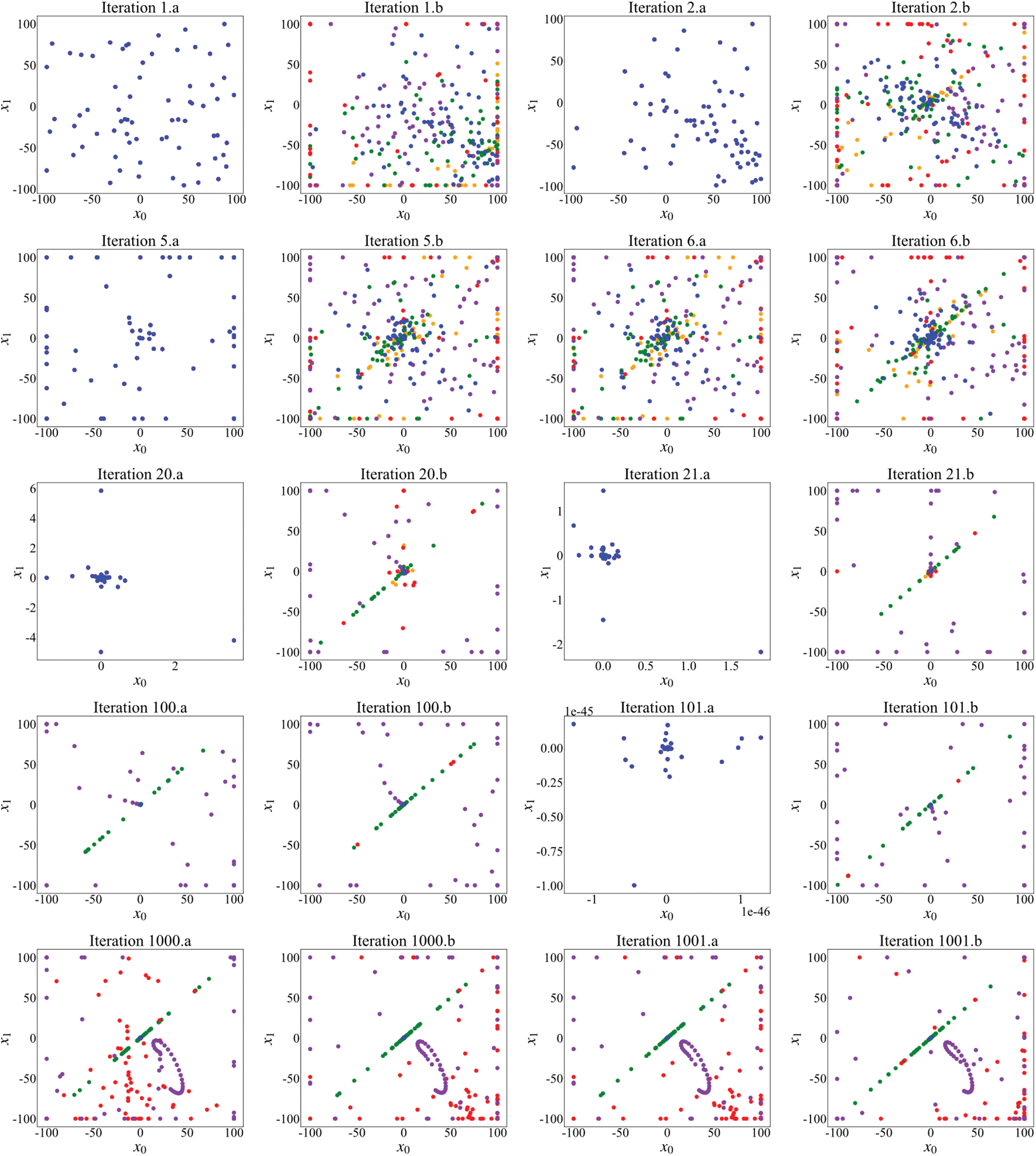
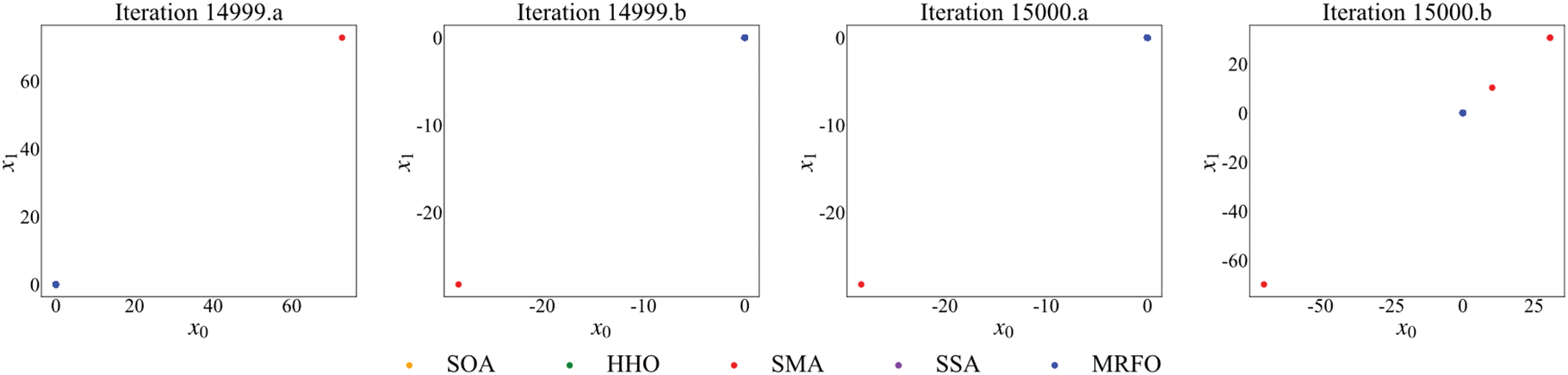
Figure 6: The virtual population distribution diagram of the EPM5 algorithm under some iterations in the process of solving the function F3

In Iteration 1.a, it is observed that the positions of the five virtual populations come from the same real population before the start of the first iteration. After the high-level generation sub-stage, the five virtual populations update their locations independently, and the positions of the populations are different, as shown in Iteration 1.b. Because the fitness value of the best elite is smaller than the historical optimum, it materializes the population where the optimal elite resides, and the population distribution after materialization is shown by Iteration 2.a. It transforms the five virtual populations into the real population. In Iteration 5.b and Iteration 6.a, the best elite of the virtual populations after the fifth iteration is not less than an order of magnitude smaller than the historically best fitness value. Thus, the virtual population continues to exist. In Iteration 20.a, the entity population has converged at this time. However, after the high-level generation sub-stage, the virtual population can still be distributed in every corner of the map, as shown in Iteration 20.b. After the high-level selection sub-stage, it obtains the population distributed in iteration 21.a, and the virtual populations are transformed into the real population again. It can be seen from this figure that the premature convergence of single or multiple populations will not lead to the convergence of all populations, and other populations still have good exploratory properties. In Iteration 100.b and Iteration 101.b, it is observed that the red population has converged. But in Iteration 1000.a, the red population is dispersed again, indicating that the converged population has a chance to reexplore. In Iteration 14999.a and Iteration 15000.b, all populations have converged. The red population has several individual sporadic distributions related to the corresponding algorithm characteristics of the population.

4.6 Engineering Application Problems

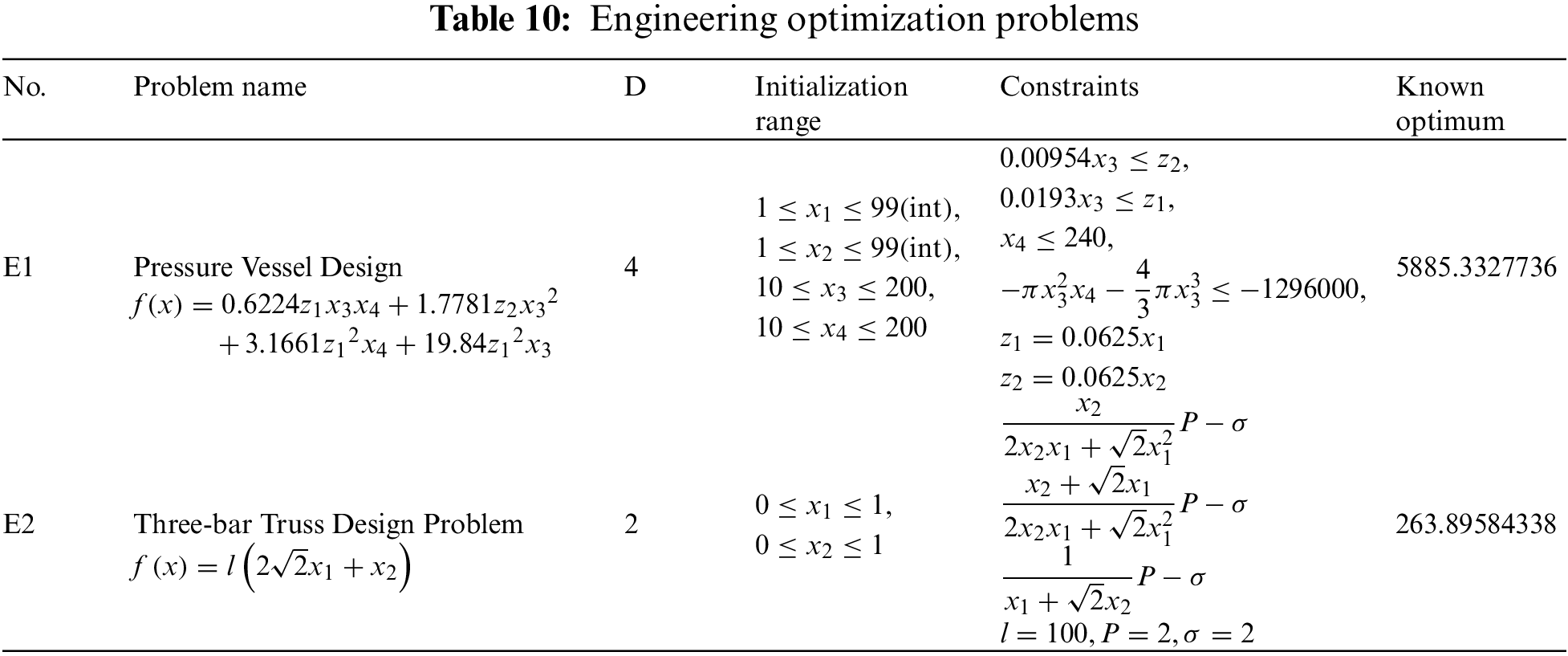
The pressure vessel design optimization problem optimizes the cost of welding, material, and forming of the pressure vessel by adjusting the shell thickness, head thickness, inner diameter, and length of the vessel under four constraints [59]. The three-bar truss design optimization problem is based on the stress constraint of each bar to optimize the total weight of the bar structures [60]. Table 10 gives the mathematical description of these problems. It abbreviates the first engineering problem as E1 and the second engineering problem as E2.

The average and standard deviation of the best solutions obtained by all test algorithms in 25 independent runs and 500 iterations in each dimension were recorded and compared (see Table 11). For the optimization results of the pressure vessel design problem, EPM3, EPM4, and EPM5 are better than their integrated original algorithms. EPM2 is better than SOA but worse than HHO. For the optimization results of the three-bar truss design problem, both EPM4 and EPM5 are better than their integrated original algorithm. EPM3 is better than HHO and SOA but worse than SMA. EPM2 is better than SOA but worse than HHO. Two practical engineering problems obtain better optimization results from the average optimization results by adopting the ensemble framework.

5  Conclusion

We propose a new population-based metaheuristic ensemble framework in this paper. The main innovation is to use the common structural characteristics of the population-based meta-heuristic algorithms to design a framework, which is a bridge for cooperative optimization of multiple algorithms through the transformation of virtual population and entity population and elite strategy. The framework leverages the differentiation and unification of real and virtual populations to coordinate exploration and exploitation at the population level. Meanwhile, an elitist strategy is adopted to communicate among virtual populations to guarantee diversity and reduce the internal influence on each metaheuristic algorithm. In the experiment, five algorithms, SOA, HHO, SMA, SSA, and MRFO, are integrated using the ensemble framework to obtain EPM algorithms. The EPM algorithms perform superior on 23 standard benchmark functions and the CEC2017 benchmark functions. According to Friedman’s average ranking, the results of algorithms integrated with the EPM framework, in most cases, outperformed the results of the same algorithms integrated with the PE framework, demonstrating the superiority of the ensemble framework. The ensemble framework also demonstrated excellent results in solving two practical engineering problems and obtained better solutions.

With the increase in the number of optimization algorithms integrated into the ensemble framework, the information exchange between various algorithms will increase, and these algorithms will be more likely to jump out of the local optimization. However, we cannot distinguish the role of each algorithm in optimization and the influence of algorithm parameters on the optimization results. Meanwhile, each additional algorithm in the ensemble framework will increase the calculation of the virtual population corresponding to the algorithm, the storage cost of the calculation results, and the cost of information exchange, reducing the optimization speed. In future research, we will study two aspects: improving the optimization ability and speed. We will analyze the contribution of a single algorithm in the integration framework and adjust the algorithm parameters to improve the optimization ability. We will study the factors that affect the optimization speed and reduce unnecessary computing and storage costs to improve the optimization speed according to the role of different algorithms in the different stages.

Acknowledgement: The authors would like to acknowledge the editor-in-chief, associate editors, and reviewers for their contributions to the improvement of this paper.

Funding Statement: This work was supported by National Natural Science Foundation of China under Grant 62073330. The auther J. T. received the grant.

Author Contributions: Study conception and design: H. Li, J. Tang, S. Lao; data collection: Q. Pan, J. Zhan; analysis and interpretation of results: H. Li, Q. Pan; draft manuscript preparation: H. Li, J. Zhan. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available on request from the authors. The data that support the findings of this study are available from the corresponding author, (J. T.), upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. E. G. Talbi, “Optimization methods,” in Metaheuristics: From Design to Implementation, vol. 1. Hoboken, NJ, USA: John Wiley & Sons, no. 3, pp. 18–33, 2009. [Google Scholar]

2. T. G. Crainic and M. Toulouse, “Meta-heuristics and parallelism,” in Handbook of Metaheuristics, vol. 17. New York, NY, USA: Springer, no. 2, pp. 498–505, 2010. [Google Scholar]

3. I. Boussaïd, J. Lepagnot and P. Siarry, “A survey on optimization metaheuristics,” Information Sciences, vol. 237, pp. 82–117, 2013. [Google Scholar]

4. D. P. Bertsekas, “Lagrangian methods–local convergence,” in Constrained Optimization and Lagrange Multiplier Methods, vol. 4. New York, NY, USA: Academic Press, no. 5, pp. 231–256, 1982. [Google Scholar]

5. K. Deb, “Two approaches to multi-objective optimization,” in Search Methodologies, vol. 15. New York, NY, USA: Springer, no. 2, pp. 407–410, 2014. [Google Scholar]

6. J. H. Vandermeer, “Niche theory,” Annual Review of Ecology and Systematics, vol. 3, no. 1, pp. 107–132, 1972. [Google Scholar]

7. J. Tang, G. Liu and Q. Pan, “A review on representative swarm intelligence algorithms for solving optimization problems: Applications and trends,” IEEE/CAA Journal of Automatica Sinica, vol. 8, no. 10, pp. 1627–1643, 2021. [Google Scholar]

8. E. Pacini, C. Mateos and C. G. Garino, “Distributed job scheduling based on swarm intelligence: A survey,” Computers & Electrical Engineering, vol. 40, no. 1, pp. 252–269, 2014. [Google Scholar]

9. B. H. Nguyen, B. Xue and M. Zhang, “A survey on swarm intelligence approaches to feature selection in data mining,” Swarm and Evolutionary Computation, vol. 54, pp. 100663, 2020. [Google Scholar]

10. J. Tang, H. Duan and S. Lao, “Swarm intelligence algorithms for multiple unmanned aerial vehicles collaboration: A comprehensive review,” Artificial Intelligence Review, vol. 56, no. 5, pp. 4295–4327, 2022. [Google Scholar]

11. K. V. Price, “Differential evolution,” in Handbook of Optimization, vol. 2. New York, NY, USA: Springer, no. 1, pp. 187–214, 2013. [Google Scholar]

12. D. Whitley, “A genetic algorithm tutorial,” Statistics and Computing, vol. 4, no. 2, pp. 65–85, 1994. [Google Scholar]

13. J. R. Koza, “Overview of genetic programming,” in Genetic Programming: On the Programming of Computers by Means of Natural Selection, vol. 5. Cambridge, MA, USA: MIT Press, no. 1, pp. 73–78, 1992. [Google Scholar]

14. J. Kennedy and R. C. Eberhart, “A discrete binary version of the particle swarm algorithm,” in 1997 IEEE Int. Conf. on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation, Orlando, FL, USA, vol. 5, pp. 4104–4108, 1997. [Google Scholar]

15. D. Karaboga and B. Basturk, “A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm,” Journal of Global Optimization, vol. 39, no. 3, pp. 459–471, 2007. [Google Scholar]

16. X. S. Yang and S. Deb, “Cuckoo search via lévy flights,” in 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, pp. 210–214, 2009. [Google Scholar]

17. A. Seyyedabbasi and F. Kiani, “Sand cat swarm optimization: A nature-inspired algorithm to solve global optimization problems,” Engineering with Computers, pp. 1–25, 2022. [Google Scholar]

18. F. Glover, “Tabu search—Part I,” ORSA Journal on Computing, vol. 1, no. 3, pp. 190–206, 1989. [Google Scholar]

19. Z. Feng, W. Niu and S. Liu, “Cooperation search algorithm: A novel metaheuristic evolutionary intelligence algorithm for numerical optimization and engineering optimization problems,” Applied Soft Computing, vol. 98, pp. 106734, 2021. [Google Scholar]

20. Y. Shi, “Brain storm optimization algorithm,” in Int. Conf. in Swarm Intelligence, Chongqing, China, pp. 303–309, 2011. [Google Scholar]

21. Q. Askari, M. Saeed and I. Younas, “Heap-based optimizer inspired by corporate rank hierarchy for global optimization,” Expert Systems with Applications, vol. 161, pp. 113702, 2020. [Google Scholar]

22. T. S. Ayyarao, N. S. Ramakrishna, R. M. Elavarasan, N. Polumahanthi, M. Rambabu et al., “War strategy optimization algorithm: A new effective metaheuristic algorithm for global optimization,” IEEE Access, vol. 10, pp. 25073–25105, 2022. [Google Scholar]

23. E. Rashedi, H. Nezamabadi-Pour and S. Saryazdi, “GSA: A gravitational search algorithm,” Information Sciences, vol. 179, no. 13, pp. 2232–2248, 2009. [Google Scholar]

24. O. K. Erol and I. Eksin, “A new optimization method: Big bang–big crunch,” Advances in Engineering Software, vol. 37, no. 2, pp. 106–111, 2006. [Google Scholar]

25. Ş. İ. Birbil and S. C. Fang, “An electromagnetism-like mechanism for global optimization,” Journal of Global Optimization, vol. 25, no. 3, pp. 263–282, 2003. [Google Scholar]

26. S. Mirjalili, “SCA: A sine cosine algorithm for solving optimization problems,” Knowledge-Based Systems, vol. 96, pp. 120–133, 2016. [Google Scholar]

27. J. A. Koupaei, S. M. M. Hosseini and F. M. Ghaini, “A new optimization algorithm based on chaotic maps and golden section search method,” Engineering Applications of Artificial Intelligence, vol. 50, pp. 201–214, 2016. [Google Scholar]

28. L. Abualigah, A. Diabat, S. Mirjalili, M. Abd Elaziz and A. H. Gandomi, “The arithmetic optimization algorithm,” Computer Methods in Applied Mechanics and Engineering, vol. 376, pp. 113609, 2021. [Google Scholar]

29. N. Chopra and M. M. Ansari, “Golden jackal optimization: A novel nature-inspired optimizer for engineering applications,” Expert Systems with Applications, vol. 198, pp. 116924, 2022. [Google Scholar]

30. Y. Zhang, Z. Jin and S. Mirjalili, “Generalized normal distribution optimization and its applications in parameter extraction of photovoltaic models,” Energy Conversion and Management, vol. 224, pp. 113301, 2020. [Google Scholar]

31. I. A. Ibrahim, M. Hossain and B. C. Duck, “A hybrid wind driven-based fruit fly optimization algorithm for identifying the parameters of a double-diode photovoltaic cell model considering degradation effects,” Sustainable Energy Technologies and Assessments, vol. 50, pp. 101685, 2022. [Google Scholar]

32. J. Tang, X. Chen, X. Zhu and F. Zhu, “Dynamic reallocation model of multiple unmanned aerial vehicle tasks in emergent adjustment scenarios,” IEEE Transactions on Aerospace and Electronic Systems, vol. 59, no. 2, pp. 1139–1155, 2023. [Google Scholar]

33. Z. Tian, “Backtracking search optimization algorithm-based least square support vector machine and its applications,” Engineering Applications of Artificial Intelligence, vol. 94, pp. 103801, 2020. [Google Scholar]

34. A. R. Jordehi, “Binary particle swarm optimisation with quadratic transfer function: A new binary optimization algorithm for optimal scheduling of appliances in smart homes,” Applied Soft Computing, vol. 78, pp. 465–480, 2019. [Google Scholar]

35. M. H. Nadimi-Shahraki, H. Zamani and S. Mirjalili, “Enhanced whale optimization algorithm for medical feature selection: A COVID-19 case study,” Computers in Biology and Medicine, vol. 148, pp. 105858, 2022. [Google Scholar] [PubMed]

36. S. Salcedo-Sanz, “Modern meta-heuristics based on nonlinear physics processes: A review of models and design procedures,” Physics Reports, vol. 655, pp. 1–70, 2016. [Google Scholar]

37. D. H. Wolpert and W. G. Macready, “No free lunch theorems for optimization,” IEEE Transactions on Evolutionary Computation, vol. 1, no. 1, pp. 67–82, 1997. [Google Scholar]

38. A. K. Qin, V. L. Huang and P. N. Suganthan, “Differential evolution algorithm with strategy adaptation for global numerical optimization,” IEEE Transactions on Evolutionary Computation, vol. 13, no. 2, pp. 398–417, 2008. [Google Scholar]

39. Q. Pan, J. Tang, H. Wang, H. Li, X. Chen et al., “SFSADE: An improved self-adaptive differential evolution algorithm with a shuffled frog-leaping strategy,” Artificial Intelligence Review, vol. 55, no. 5, pp. 3937–3978, 2021. [Google Scholar]

40. W. Gong, A. Zhou and Z. Cai, “A Multi-operator search strategy based on cheap surrogate models for evolutionary optimization,” IEEE Transactions on Evolutionary Computation, vol. 19, no. 5, pp. 746–758, 2015. [Google Scholar]

41. M. Z. Ali, N. H. Awad and P. N. Suganthan, “Multi-population differential evolution with balanced ensemble of mutation strategies for large-scale global optimization,” Applied Soft Computing, vol. 33, pp. 304–327, 2015. [Google Scholar]

42. H. Rakhshani and A. Rahati, “Intelligent multiple search strategy cuckoo algorithm for numerical and engineering optimization problems,” Arabian Journal for Science and Engineering, vol. 42, no. 2, pp. 567–593, 2017. [Google Scholar]

43. C. Li, S. Yang and T. T. Nguyen, “A self-learning particle swarm optimizer for global optimization problems,” IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), vol. 42, no. 3, pp. 627–646, 2011. [Google Scholar]

44. N. Lynn and P. N. Suganthan, “Ensemble particle swarm optimizer,” Applied Soft Computing, vol. 55, pp. 533–548, 2017. [Google Scholar]

45. S. X. Zhang, S. Y. Zheng and L. M. Zheng, “An efficient multiple variants coordination framework for differential evolution,” IEEE Transactions on Cybernetics, vol. 47, no. 9, pp. 2780–2793, 2017. [Google Scholar] [PubMed]

46. S. Thangavelu and C. S. Velayutham, “An investigation on mixing heterogeneous differential evolution variants in a distributed framework,” International Journal of Bio-Inspired Computation, vol. 7, no. 5, pp. 307–320, 2015. [Google Scholar]

47. G. Wu, X. Shen, H. Li, H. Chen, A. Lin et al., “Ensemble of differential evolution variants,” Information Sciences, vol. 423, pp. 172–186, 2018. [Google Scholar]

48. S. M. Elsayed, R. A. Sarker and E. Mezura-Montes, “Self-adaptive mix of particle swarm methodologies for constrained optimization,” Information Sciences, vol. 277, pp. 216–233, 2014. [Google Scholar]

49. J. A. Vrugt, B. A. Robinson and J. M. Hyman, “Self-adaptive multimethod search for global optimization in real-parameter spaces,” IEEE Transactions on Evolutionary Computation, vol. 13, no. 2, pp. 243–259, 2008. [Google Scholar]

50. Y. Xue, S. Zhong, Y. Zhuang and B. Xu, “An ensemble algorithm with self-adaptive learning techniques for high-dimensional numerical optimization,” Applied Mathematics and Computation, vol. 231, pp. 329–346, 2014. [Google Scholar]

51. S. M. Elsayed, R. A. Sarker and D. L. Essam, “Adaptive configuration of evolutionary algorithms for constrained optimization,” Applied Mathematics and Computation, vol. 222, pp. 680–711, 2013. [Google Scholar]

52. X. Yao, Y. Liu and G. Lin, “Evolutionary programming made faster,” IEEE Transactions on Evolutionary Computation, vol. 3, no. 2, pp. 82–102, 1999. [Google Scholar]

53. G. Wu, R. Mallipeddi and P. N. Suganthan, “Problem definitions and evaluation criteria for the CEC 2017 competition on constrained real-parameter optimization,” Technical Report, 2017. [Online]. Available: https://www.researchgate.net/publication/317228117_Problem_Definitions_and_Evaluation_Criteria_for_the_CEC_2017_Competition_and_Special_Session_on_Constrained_Single_Objective_Real-Parameter_Optimization [Google Scholar]

54. A. A. Heidari, S. Mirjalili, H. Faris, I. Aljarah, M. Mafarja et al., “Harris hawks optimization: Algorithm and applications,” Future Generation Computer Systems, vol. 97, pp. 849–872, 2019. [Google Scholar]

55. G. Dhiman and V. Kumar, “Seagull optimization algorithm: Theory and its applications for large-scale industrial engineering problems,” Knowledge-Based Systems, vol. 165, pp. 169–196, 2019. [Google Scholar]

56. S. Li, H. Chen, M. Wang, A. A. Heidari and S. Mirjalili, “Slime mold algorithm: A new method for stochastic optimization,” Future Generation Computer Systems, vol. 111, pp. 300–323, 2020. [Google Scholar]

57. S. Mirjalili, A. H. Gandomi, S. Z. Mirjalili, S. Saremi, H. Faris et al., “Salp swarm algorithm: A bio-inspired optimizer for engineering design problems,” Advances in Engineering Software, vol. 114, pp. 163–191, 2017. [Google Scholar]

58. W. Zhao, Z. Zhang and L. Wang, “Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications,” Engineering Applications of Artificial Intelligence, vol. 87, pp. 103300, 2020. [Google Scholar]

59. E. Sandgren, “Nonlinear integer and discrete programming in mechanical design,” in Int. Design Engineering Technical Conf. and Computers and Information in Engineering Conf., Kissimmee, FL, USA, vol. 26584, pp. 95–105, 1988. [Google Scholar]

60. H. Nowacki, “Optimization in pre-contract ship design,” in Int. Conf. on Computer Applications in the Automation of Shipyard Operation and Ship Design, Tokyo, Japan, pp. 1–12, 1973. [Google Scholar]