Hybrid Algorithm-Driven Smart Logistics Optimization in IoT-Based Cyber-Physical Systems

1  Introduction

The emergence of the Cyber-Physical Systems (CPS) paradigm has ignited immense interest and fascination in the research community, solidifying its position as a technological frontier with vast potential. The industry views CPS as a revolutionary innovation, leading many countries to incorporate CPS models into their frameworks [1]. The Internet of Things (IoT) has evolved continuously, capturing the attention of dedicated scholars who have expanded its capabilities, laying the foundation for CPS research. In the CPS domain, researchers often divide the system model into two core tiers: the perception tier and the utilization tier. The intermediary layer connecting them distinguishes these tiers [2]. CPS transforms human interaction with the physical world, influencing the healthcare, transportation, aerospace and agriculture sectors. The logistics industry benefits from IoT and CPS integration, leading to intelligence and sustainability enhancements.

The integration of CPS within logistics has enabled ingenious solutions, optimizing operations and promoting eco-friendliness, driving groundbreaking research [3]. Traditional logistics route planning focused on task characteristics, load management and vehicle categorization. IoT integration into logistics route planning is transformative, optimizing automated scheduling and fostering competitiveness. In one study, researchers explored the RoboCup logistics alliance, aiming to automate logistics deployment and set groundbreaking benchmarks [3]. Simultaneously, a researcher focused on production-logistics differences within processing workshops, resulting in an intelligent system that improved efficiency. However, unexplored possibilities await the integration of intelligent algorithms with CPS technology. Our research combines IoT and CPS to revolutionize logistics decision-making, uncovering optimal routes and driving efficiency.

In optimization, two key algorithms, the Firefly Algorithm (FO) and the Spotted Hyena Optimization Algorithm (SHO), offer unique strengths and limitations. FO excels in global exploration but may need more details in local search. SHO focuses on intense local search but may overlook global solutions. To address this, the Hybrid Firefly-Spotted Hyena Optimization (HFSHO) algorithm combines FO’s global search with SHO’s local search, aiming to enhance convergence and efficiency, particularly in logistics path optimization.

This research bridges critical gaps in optimization, encompassing structural design, truss optimization, aerospace innovation and logistics optimization through innovative metaheuristic algorithms. Addressing the logistics optimization research gap is essential due to several key factors:

•   Complex Logistics Data: Logistics operates in a dynamic environment with variables like transport options, delivery locations, vehicle capacities and changing demand patterns, demanding efficient management.

•   Sustainable Growth: As the backbone of global trade, logistics needs optimization to ensure sustainable and resilient growth, with distribution route optimization playing a crucial role.

•   Route Optimization Challenges: Finding efficient distribution routes that reduce cost, and delivery times and maximize resource use is challenging, involving complex computations.

•   Resource Utilization and Cost Savings: Improving resource utilization, efficiency and cost savings in logistics is paramount, but research quantifying these improvements through advanced algorithms is limited.

•   Hybrid Algorithm Innovation: Innovative approaches like the Hybrid Firefly-Spotted Hyena Optimization (HFSHO) algorithm are underexplored. HFSHO combines Firefly and Spotted Hyena algorithms to address logistics’ unique complexities.

•   Empirical Validation and Practicality: Empirical evidence is vital to convince logistics professionals of HFSHO’s advantages over existing methods. Researchers must explore the algorithm’s practical implications in real-world scenarios, highlighting its potential for resource management and cost savings—a critical assessment benchmark in the logistics industry.

The contribution of this work is in the identification of problems in current logistics systems and the analysis of the challenges they face. It recognizes issues such as inefficiencies, the absence of real-time data and suboptimal route planning within traditional logistics systems. This article’s contributions are summarized in the following concise summary:

•   Conducted an assessment and comparative analysis of the Spotted Hyena Optimization Algorithm, Firefly Algorithm and the proposed Hybrid Firefly-Spotted Hyena Optimization Algorithm (HFSHO).

•   Attained optimal values: 853 for the SHO Algorithm, 858 for the FO and an impressive 546 for the HFSHO Algorithm, demonstrating the exceptional performance of the HFSHO Algorithm in optimizing logistics path decisions.

•   Embarked on a harmonious fusion of the FO and the SHO within the HFSHO Algorithm, harnessing the best of both worlds to achieve minimal optimal distances, resulting in cost savings, heightened distribution efficiency and optimized resource allocation.

•   Contributed to advancing an intelligent system for logistics path decision-making utilizing the Internet of Things, enhancing the convergence speed and quality of solutions achieved by the HFSHO Algorithm.

•   Offered potential applications in multi-sensor management systems for urban logistics path decisions, propelling the progress in optimizing logistics path decisions and providing valuable insights for integrating industrial structures.

By highlighting the limitations of existing solutions, it emphasizes the necessity for a more intelligent and interconnected approach to logistics management. The existing methods and research work are described in the related work.

2  Related Work

This section explores optimal path-finding studies, offering an in-depth analysis of their findings and limitations. Each study addresses logistics and vehicle routing optimization problems, presenting comprehensive frameworks. However, while discussing their major themes and proposed approaches, we also critically examine their limitations.

The logistics industry has evolved significantly, demanding modern logistics management methods. Conventional approaches no longer suffice and the advent of IoT technology has been pivotal. IoT seamlessly integrates physical and digital systems, revolutionizing logistics operations. The convergence of IoT and CPS is particularly promising, allowing real-time monitoring, simulation, analysis and manipulation of interconnected systems. In [4], a logistics CPS design was proposed, emphasizing the fusion of IoT and CPS for global optimization. Building upon [5] and other research, we aim to enhance the Intelligent Physical System (IPS) logistics system within a CPS architecture, creating an advanced logistics route decision system. In [6], the Tabu Search Algorithm addressed the Vehicle Routing Problem (VRP), focusing on efficient search and avoiding local optima. However, it needs a comparative analysis with other algorithms, limiting performance assessment. The author in [7] focused on logistics distribution path optimization with an improved ACO Algorithm, emphasizing global search and local optimization but noting the risk of premature convergence.

In [8], an Optimal Logistics Distribution Path Optimization framework tackles large-scale combinatorial problems by emphasizing exploration and exploitation for shorter paths. The study acknowledges that results may only sometimes be optimal or suitable for existing paths, hinting at limitations. The authors in [9] dealt with VRP and NP-hard problems using a Hybrid GA that integrates K-means and an enhanced GA. While emphasizing autonomous adaptation and intrinsic advancement, the investigation lacks comprehensive scalability and resilience examination, implying limitations.

Several algorithms have been developed in logistics path optimization to address the challenges of finding efficient solutions. The Social Spider Optimization (SSO) Algorithm, described in the study [10], inspires spider behavior to optimize logistics paths. However, the study needs comparative analyses with other algorithms, limiting a comprehensive assessment of SSO’s performance. Similarly, the Grey Wolf Optimizer (GWO) Algorithm, discussed in [11], shows promise for logistics path optimization, but performance comparisons with existing algorithms are needed to understand its strengths and weaknesses. The JA algorithm, presented in [12], offers a simplified approach to logistics path optimization, but it requires comprehensive performance evaluations against other algorithms. The Sailfish Optimizer (SFO) Algorithm, as discussed in [13], is known for its adaptability and speed. However, further research is needed to assess its performance, scalability and robustness under diverse scenarios.

In multi-objective Vehicle Routing Problems (VRP), the Hybrid PSO Algorithm introduced in the study [14] leverages swarm intelligence for Pareto optimization. However, a deeper analysis of its convergence behavior and solution diversity is necessary. The Improved Harmony Search Algorithm (HSA) in [15] addresses Capacitated VRP but requires more investigation into scalability and efficiency. For VRP with Time Windows, the Enhanced Variable Neighborhood Search proposed in [16] lacks an in-depth exploration of convergence and stability. The Improved Bee Algorithm in [17] solves VRP with Multiple Depots but needs comprehensive evaluations across different problem sizes and complexities. In Green Logistics Optimization, the Enhanced Artificial Bee Colony (ABC) Algorithm introduced in the study [18] considers environmental factors and solution quality but requires a more thorough analysis of convergence and diversity. The Enhanced Firefly Algorithm in [19] tackles VRP with Time Constraints but has limited investigation into performance with larger problem instances. In the domain of Multi-objective VRP, the Improved Strength Pareto Evolutionary Algorithm presented in the study [20] aims for Pareto optimization and non-dominated solution generation. However, its robustness and applicability need further assessment and comparative analyses under various problem settings and real-world scenarios.

In addressing the VRP with a Heterogeneous Fleet, researchers introduce the Enhanced ICA algorithm, which considers fleet composition and solution selection for routing optimization. However, a limitation emerges as the study needs more scalability and performance assessment in large-scale scenarios. To understand its practical applicability, further investigations are essential to evaluate its performance and scalability when dealing with larger and more complex VRP instances [21]. Various enhanced algorithms have been proposed for Vehicle Routing Problems (VRP). In VRP with Dynamic Traffic Conditions [22], the Enhanced Bat Algorithm (BA) accounts for traffic conditions but requires thorough examination in diverse scenarios to assess its performance under varying traffic conditions. Similarly, the Capacitated VRP (CVRP) introduces an Enhanced ABC Algorithm. Still, a comprehensive analysis is needed to evaluate its convergence and solution diversity for a comprehensive assessment.

Innovative algorithms such as the Dragonfly Algorithm (DA) in [23], ACO [24], MOEA/D [25] and CMA-ES [26] exhibit potential in optimizing logistics routes and enhancing logistics decision-making. Similarly, in the VRP with Multiple Constraints, a proposed Hybrid GA with PSO in [27] focuses on managing various constraints and harnesses swarm intelligence, mirroring the importance of advanced security mechanisms for logistics networks. However, comprehensive evaluations are necessary to understand its performance, convergence characteristics and solution quality when addressing complex constraints.

3  Development of a Smart CPS Logistics Route Selection System

Cyber-Physical Systems (CPS) integrate advanced sensor technology, embedded systems and robust network infrastructure, enhancing devices with intelligence and sensory capabilities.

Leveraging CPS for logistics path optimization requires a thorough understanding of the logistics process and developing an intelligent logistics decision system within the CPS framework. CPS is built on three tiers: the physical tier, the connectivity tier and the operational tier. The physical tier involves sensor and execution devices interacting with the physical environment. The connectivity tier facilitates interconnection among CPS nodes, while a specialized wireless sensor network operates within CPS. This paper focuses on node interconnectivity within the physical tier and seamless data transfer in the connectivity layer, utilizing cloud infrastructures. Fig. 1 illustrates the CPS architecture.

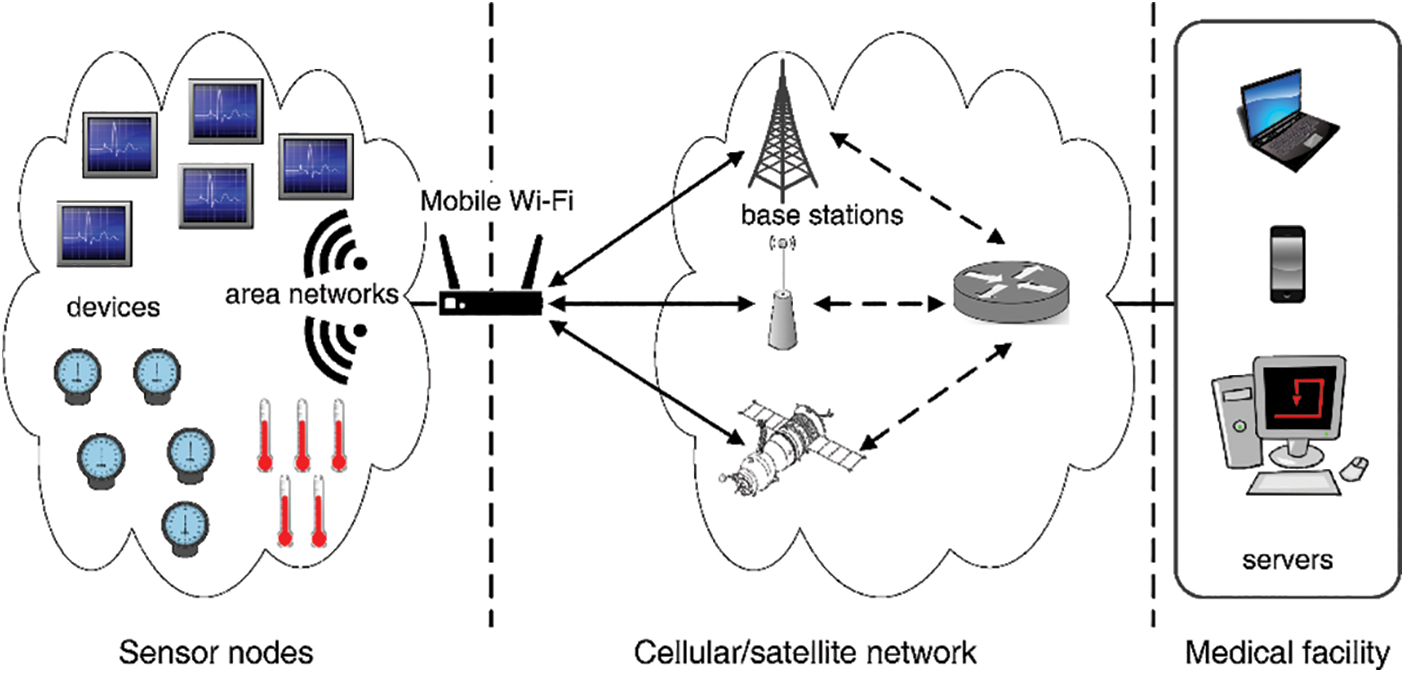
Figure 1: Architecture of CPS

3.1 Analysis of Logistics Routing Method

In the conventional urban logistics conveyance procedure, customers or senders initiate online purchases, opt for preferred products and subsequently allocate tasks via e-commerce platforms, utilizing order details [28]. Delivery staff employ portable RFID scanners to scan merchandise and execute the transportation procedure, consistently refreshing pertinent data until the goods achieve their ultimate endpoint. Fig. 2 shows the intricate urban logistics transportation process with utmost precision. Conventional transportation approaches heavily depend on a manual workforce, devoid of modernization and the integration of computer systems and intelligent algorithms for logistical and transportation decision-making. Within the scope of this study, a CPS-centered logistics path decision system harnesses the extraordinary capabilities of the HFSHO algorithm to determine the most optimal route for transportation and logistics operations. The system breaks down the journey into multiple segments, prompting delivery staff at the start of each road section to retrieve goods from locations specified by customers. To accomplish this objective, the labels attached to cargo boxes are scanned by a portable RFID reader, capturing vital data that is subsequently transmitted to the control center. The delivery personnel then takes the order to the next warehouse. The control center diligently monitors the truck’s location through GPS technology. Ensuring a seamless and efficient delivery to the designated destination. Upon arrival, a final scan of the RFID label signifies completing the entire order delivery task.

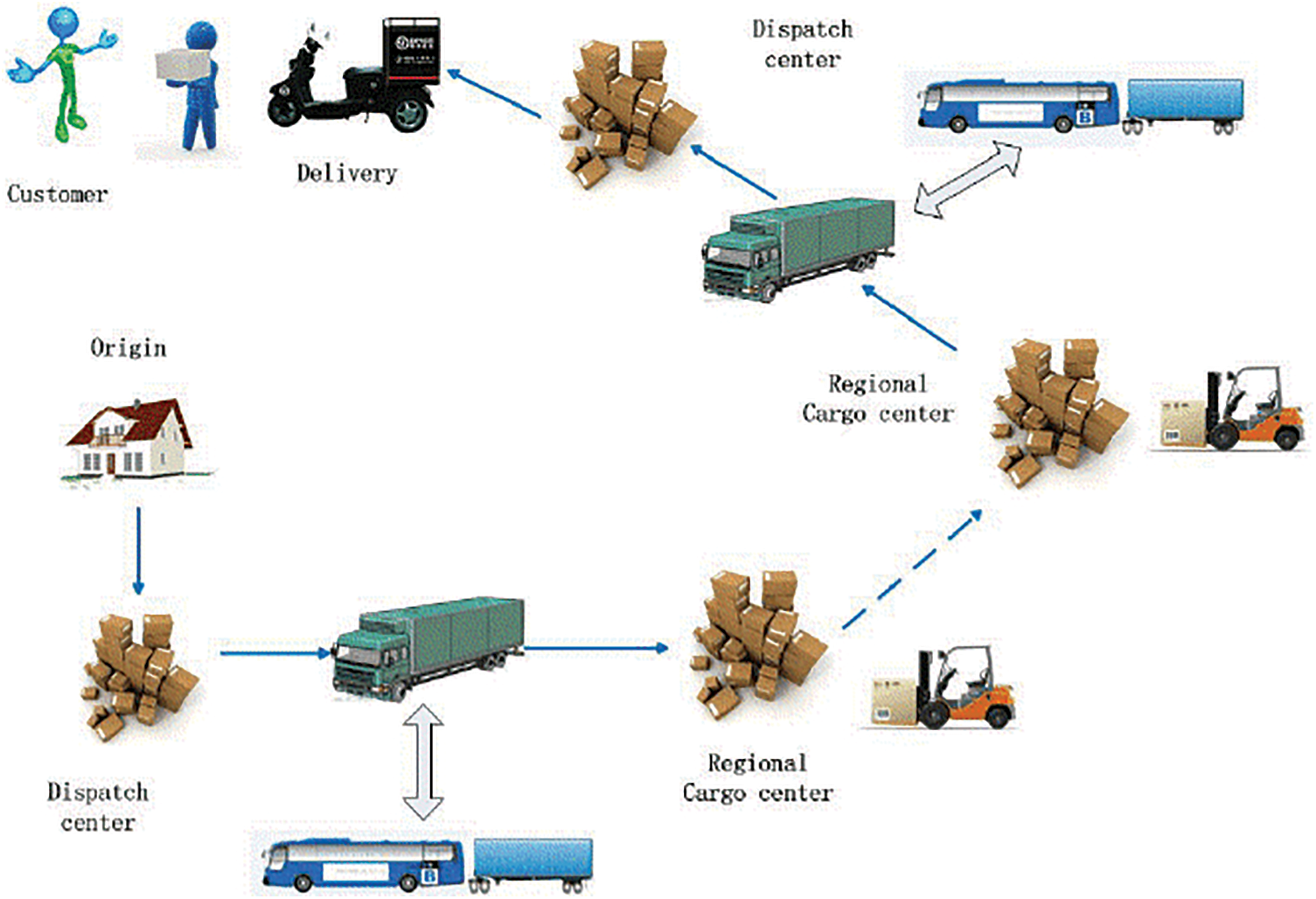
Figure 2: Logistics process of metropolitan

3.2 CPS-Based Intelligent Logistics Path Selection

Traditional cargo transportation often relies on manual methods like 2D code scanning, which is less efficient than RFID technology. In the evolving landscape of IoT technology in supply chain management, this article introduces an innovative system that combines RFID with wireless sensor networks to enhance transportation efficiency and connectivity [5]. Based on CPS, the intelligent logistics decision system comprises three interconnected layers: the Equipment Layer, the Cloud Platform and the Application Layer. These layers collectively enhance system functionality. The Equipment Layer deploys devices like sensors and RFID readers for real-time data capture and interaction with the physical environment. The Cloud Platform serves as the system’s backbone, enabling seamless connectivity and data storage, processing and analysis. The Application Layer, driven by software and algorithms, handles intelligent path decision-making, route optimization and real-time logistics monitoring. Integrating these three layers, the CPS-based intelligent logistics routing system improves transportation effectiveness, precision and dependability, offering streamlined supply chain oversight and improved customer satisfaction.

Upon observing Figs. 1 and 2, it becomes clear that the decision-making system for intelligent logistics in CPS consists primarily of three crucial entities: the equipment stratum, the cloud platform and the application stratum. Each stratum serves unique functions and encompasses the following indispensable elements:

Equipment Layer: This layer empowers intelligent operations by integrating components such as handheld readers, USB data cables, 3G and wireless modules. It enhances networking capabilities and data transmission speed. Key components include an electronic identification chip with a radio frequency receiver, analog signal processor, digital computing module and data storage facility. An integrated RFID reader unit with wireless signal processing, data computation and command execution further enhances its capabilities. It efficiently converts received RF signals into direct current to power tags and employs envelope detection techniques for RF signal analysis.

Cloud Platform: This crucial element facilitates agile data integration in the decision-making system. It leverages cloud computing’s distributed processing capabilities, enabling efficient data processing and integration. The cloud platform directly presents customer-specific data and seamlessly integrates real-time third-party information, enhancing agility and reliability. It ensures prompt feedback and data dissemination to service recipients.

Application Layer: As the conductor of smooth operations, the application layer involves users, command centers, distribution staff, storage facilities and vessels. Users interact with the system, place orders and monitor progress. They receive real-time updates on orders, including RFID codes, delivery schedules, driver details and estimated delivery times. Delivery teams are responsible for goods transportation and detailed recording, with cargo terminals uploading RFID tag data upon warehouse arrival. The central control center manages tasks like order reception, personnel deployment, warehouse coordination and task assignment. Effective coordination ensures the efficient management of the logistics system.

These layers and components optimize logistics decision-making, enhancing efficiency, precision and dependability throughout the supply chain.

4  Proposed Model System (Optimizing Logistics Path Decisions Using Intelligent Algorithms)

Effectively harnessing a wide array of sensor resources and optimizing the decision-making process for urban logistics paths is a critical challenge in smart logistics. This paper aims to address this issue with a novel hybrid algorithm, namely Hybrid Firefly and Spotted Hyena Optimizer (HFSHO) and other intelligent existing algorithms, namely JA, ACO, CSA, PSO, ICA and GA, to optimize logistics paths. A comprehensive evaluation of these algorithms’ performance in path optimization aims to identify a more efficient and effective decision-making approach.

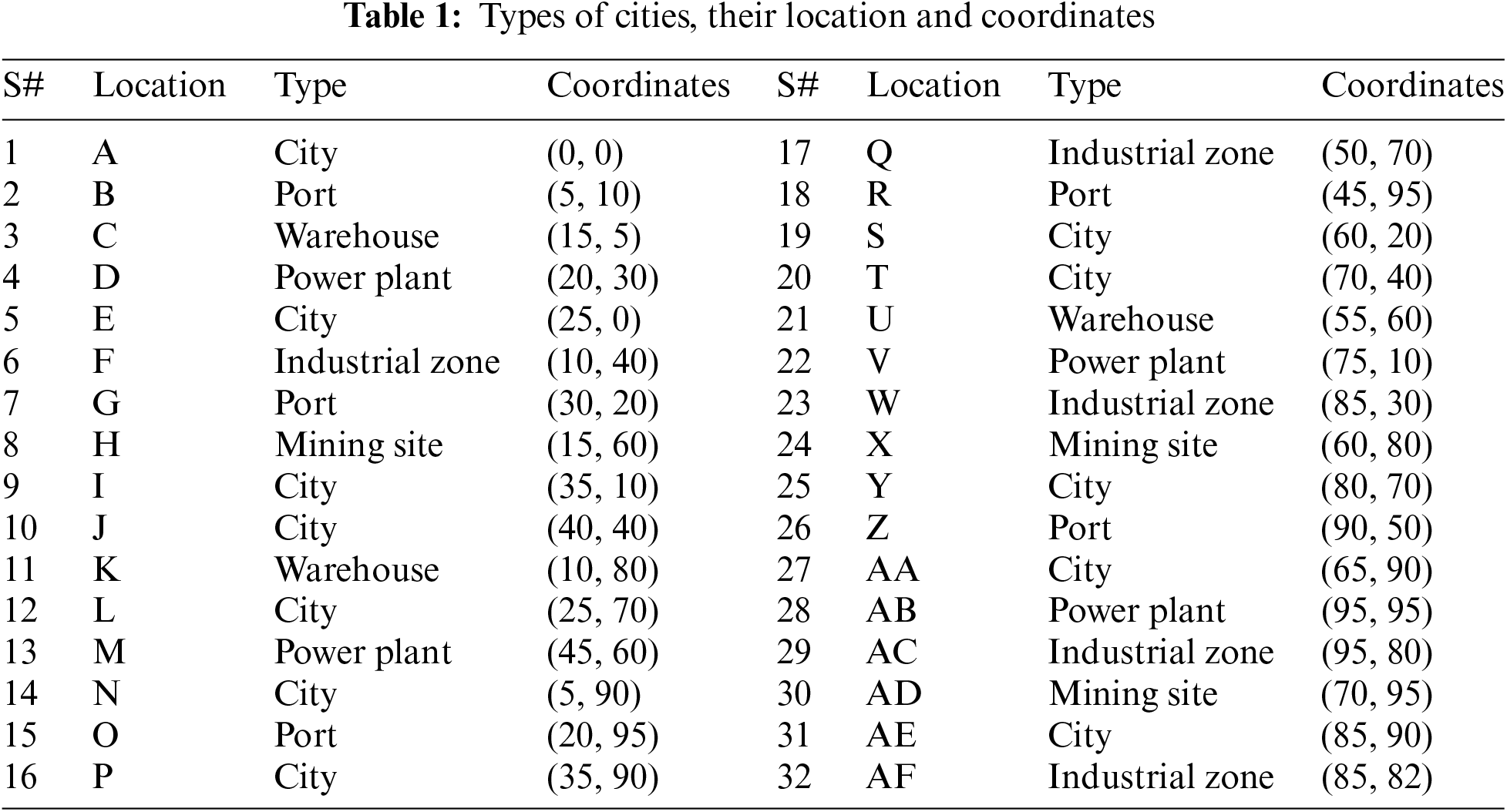
Table 1 provides a comprehensive overview of diverse locations and their coordinates, aiding in understanding their spatial arrangement. The coordinates reveal their distribution within the area, serving as a valuable reference for analyses, strategies and decision-making related to these sites. A comparative analysis of HFSHO, FO and SHO algorithms determines the most effective decision-making method for optimizing logistics paths. Each algorithm leverages unique strengths and their performance in path optimization is assessed to identify the most effective approach for smart logistics. Subsequent sections will delve into each algorithm’s evaluation.

4.1 Firefly (FO) Algorithm

The Firefly Optimization (FO) algorithm, inspired by fireflies’ behavior [20], is a robust metaheuristic for optimizing Smart Logistics Transportation System delivery routes. FO initializes a population of fireflies, each representing a potential solution. They move based on brightness, attraction and distance, promoting exploration and avoiding local optima. Brighter fireflies can absorb others, converging toward the best solution. The algorithm iteratively refines solutions until termination criteria are met. FO optimizes delivery routes, balancing factors like distance and time, enhancing operational efficiency, logistics management and customer satisfaction. Fig. 3 depicts the FO algorithm’s steps in a flowchart.

Figure 3: Steps of FO algorithm

The Firefly Optimization (FO) algorithm is ideal for logistics path selection, especially in intelligent transportation systems like the Vehicle Routing Problem (VRP). It excels at optimizing complex logistics routes, efficiently handling varying scales without relying on pheromones and ensuring stable optimization. FO employs a mathematical model considering constraints like vehicle capacity and delivery time windows, represented by Eqs. (1) and (2) [20]. It contributes to efficient logistics operations, improving cost and travel time while adhering to constraints. FO promises to enhance intelligent logistics path selection in various scenarios, benefiting logistics management and customer satisfaction. FO’s equations model firefly movement toward optimal solutions, balancing exploration and exploitation effectively.

A(i,j)=βe−γ.r2(1)

xi(t+1)=xi(t)+βe−γ.r2(xj(t)−(xi(t))+αrand()(2)

Parameters details: The optimization algorithm employs the following parameters: “num fireflies” (30), which represents the population size; “iterations” (100), indicating the number of optimization cycles; “alpha” (0.3) for introducing randomness; “beta” (3) governing attraction between fireflies; and “gamma” (1) serving for absorption during convergence. These parameters collectively guide the algorithm’s behavior in finding optimal logistics paths. FO uses attractiveness and movement equations to guide fireflies toward optimal paths, effectively considering logistics constraints and objectives.

Fig. 4 shows the trajectory of the optimal path calculated by the FO algorithm. The algorithm has determined the most efficient route among the given locations based on the defined objective, such as minimizing the total distance or travel time. The plot displays the locations as points in a 2D coordinate system. The optimal path is represented by a line connecting these points.

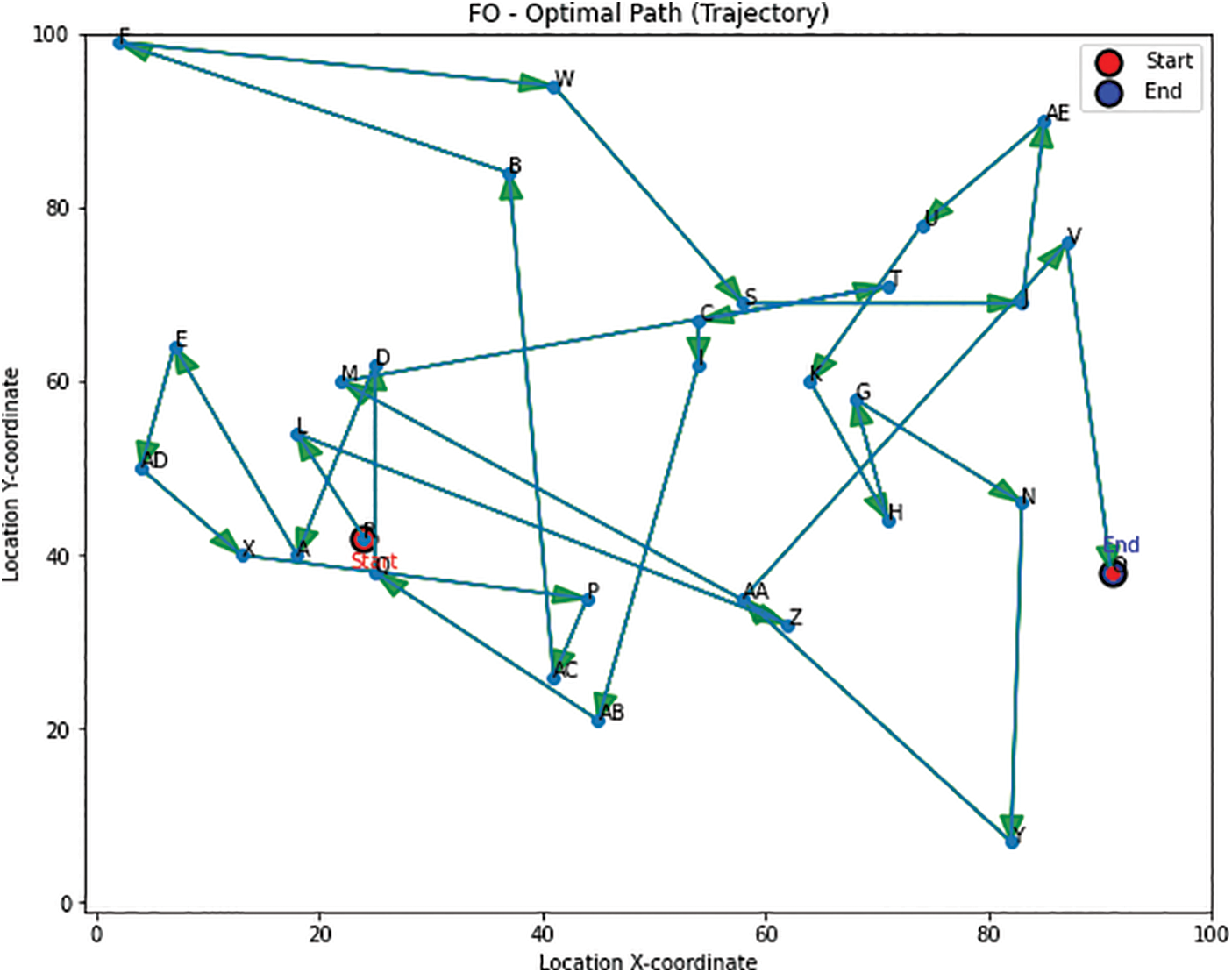
Figure 4: Optimal logistics paths achieved with FO

Each point on the path corresponds to a specific location in the logistics network. Figs. 4 to 6 offer valuable visualizations of the optimal logistics path and the distances between locations, aiding in route efficiency comprehension and logistics planning decision-making. In Fig. 5, the crimson circle marks the starting point and the cobalt circle designates the destination, with labels “Start” and “End” for clarity. Each location on the path is labeled with letters (A, B, C, etc.) for easy tracking. The FO algorithm achieves an objective value of 858, representing minimized travel distance or time. Fig. 6 displays the optimized logistics route, considering distances between coordinates and Fig. 7 shows the achieved optimal solution during the optimization process. Fig. 6 features a scatter plot of path locations connected by a line, with start and end points denoted by crimson and sapphire circles. Each location includes its name and distance from the previous point, calculated using the Euclidean distance formula. The total path distance is shown in the title, arrows indicate direction and a red dot marks the endpoint. Replacing x and y coordinates with distances enhances clarity, aiding logistics evaluation and planning.

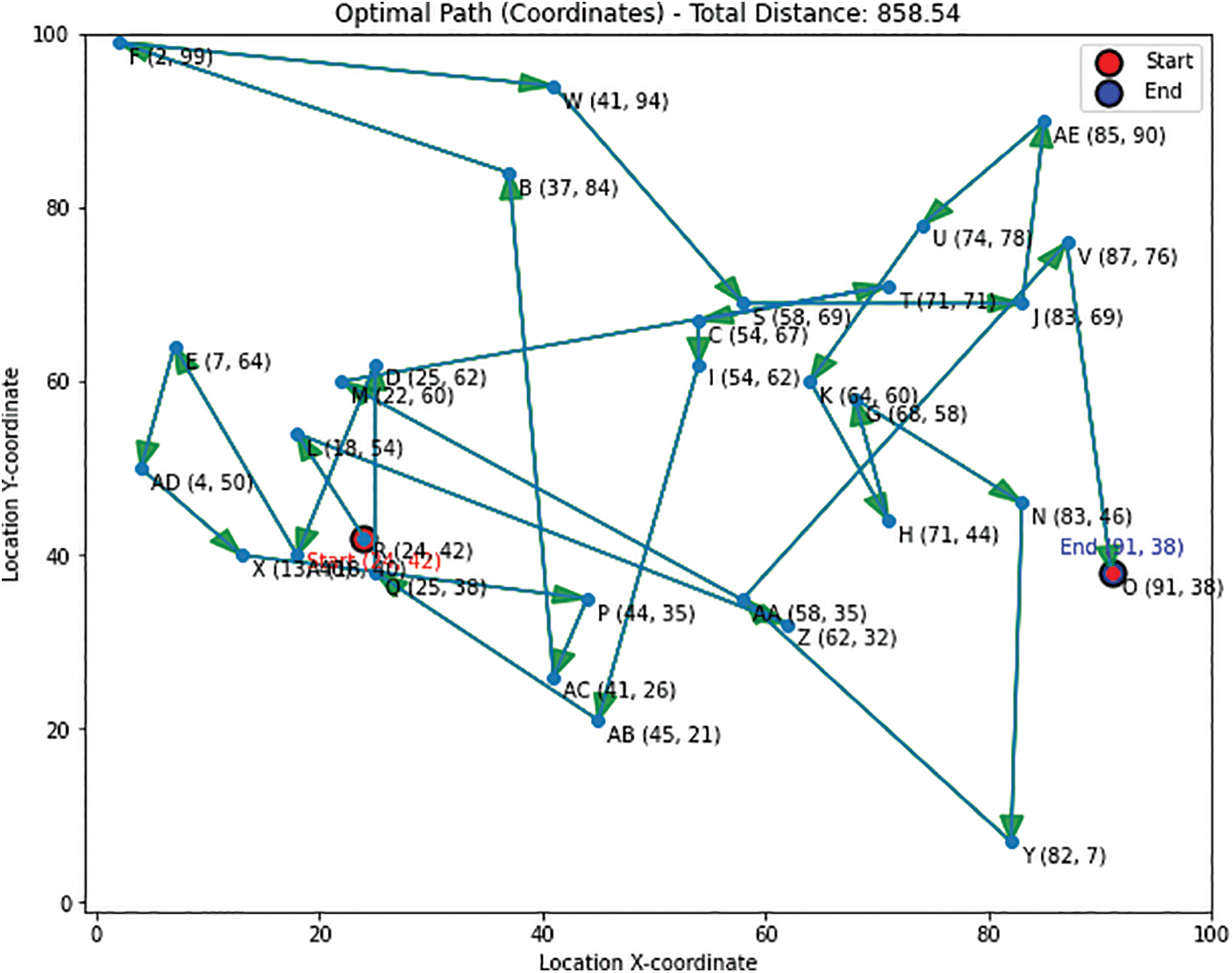
Figure 5: Optimal logistics paths with coordinates achieved with FO

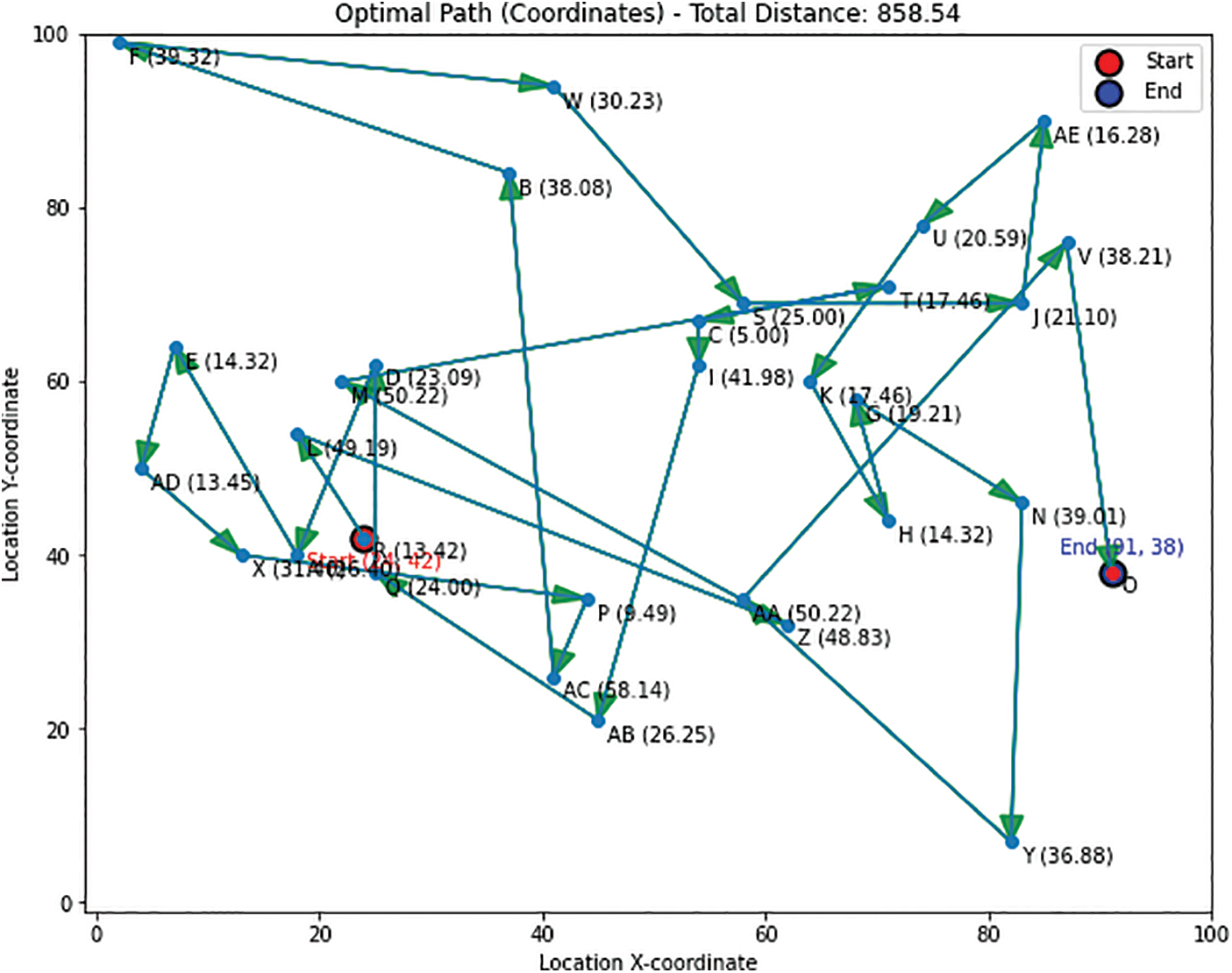
Figure 6: Optimal logistics paths with distance between two coordinates by FO algorithm

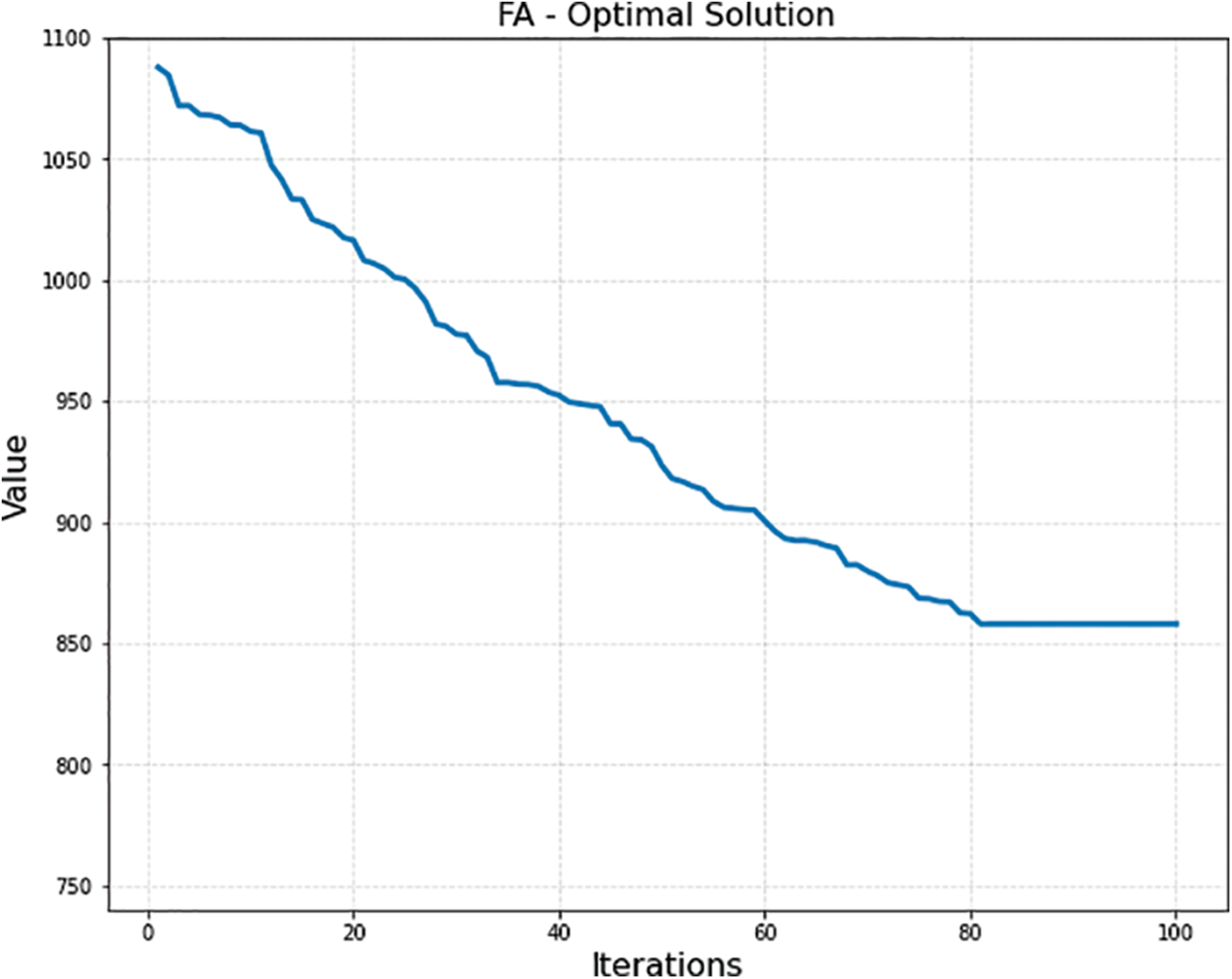
Figure 7: FO algorithm optimal solution achievement along with the iteration

4.2 Spotted Hyena Optimizer (SHO)

The Spotted Hyena Optimizer (SHO) utilizes hyenas’ cooperative hunting behavior for logistics pathfinding, balancing cost minimization with constraints like delivery windows [29]. It initializes a population of hyenas to represent potential paths, ensuring compliance with constraints. SHO combines exploration via stochastic search with exploitation through specific mechanisms [30]. Selected paths undergo further optimization using local search algorithms like 2-opt or 3-opt. This iterative process balances computational efficiency and solution quality until a predefined termination criterion is met. The best path found represents the optimal logistics route, effectively addressing pathfinding while accommodating logistical constraints and objectives.

Parameter details: The essential parameters used in the optimization process are: Population Size (30) indicates the number of hyenas in the population, while Maximum Iterations (100on optimization iterations. Exploration Rate (0.2) controls the exploration pace and Social Hierarchy Weight (0.5) signifies social interactions’ importance. Global (0.1) and Individual (0.2) Learning Rates update positions. Randomness Factor (0.3) adjusts randomness, Crossover (0.8) and Mutation (0.1). Probabilities govern genetic operations. Inertia Weight (0.9) influences velocity impact and Velocity Limit (5) caps hyenas’ speed. These parameters collectively shape hyena behavior, impacting exploration, convergence and the overall efficiency of logistics path optimization.

Fig. 8 visually portrays the optimal path achieved using the SHO algorithm, featuring directional arrows, distinct start and end points and unique alphabet labels for locations. This clear representation showcases the algorithm’s performance in identifying optimal solutions efficiently. Fig. 9 provides a detailed visualization of the optimized trajectory by SHO, highlighting path coordinates and the optimal value of 868. This figure effectively communicates critical information about the algorithm’s ability to maximize desired objectives or minimize specified criteria within the given problem.

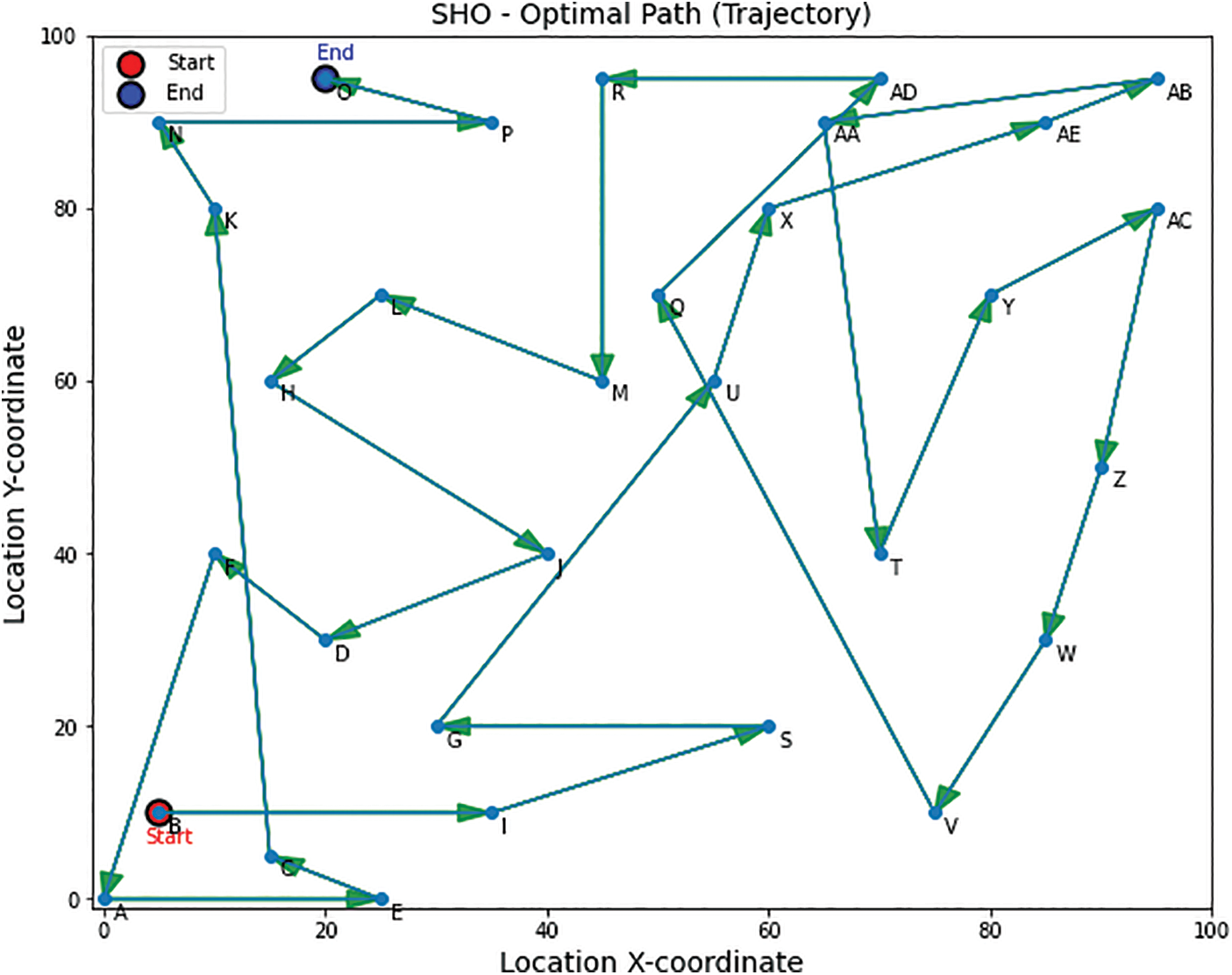
Figure 8: Optimal path generated (Trajectory) by SHO algorithm

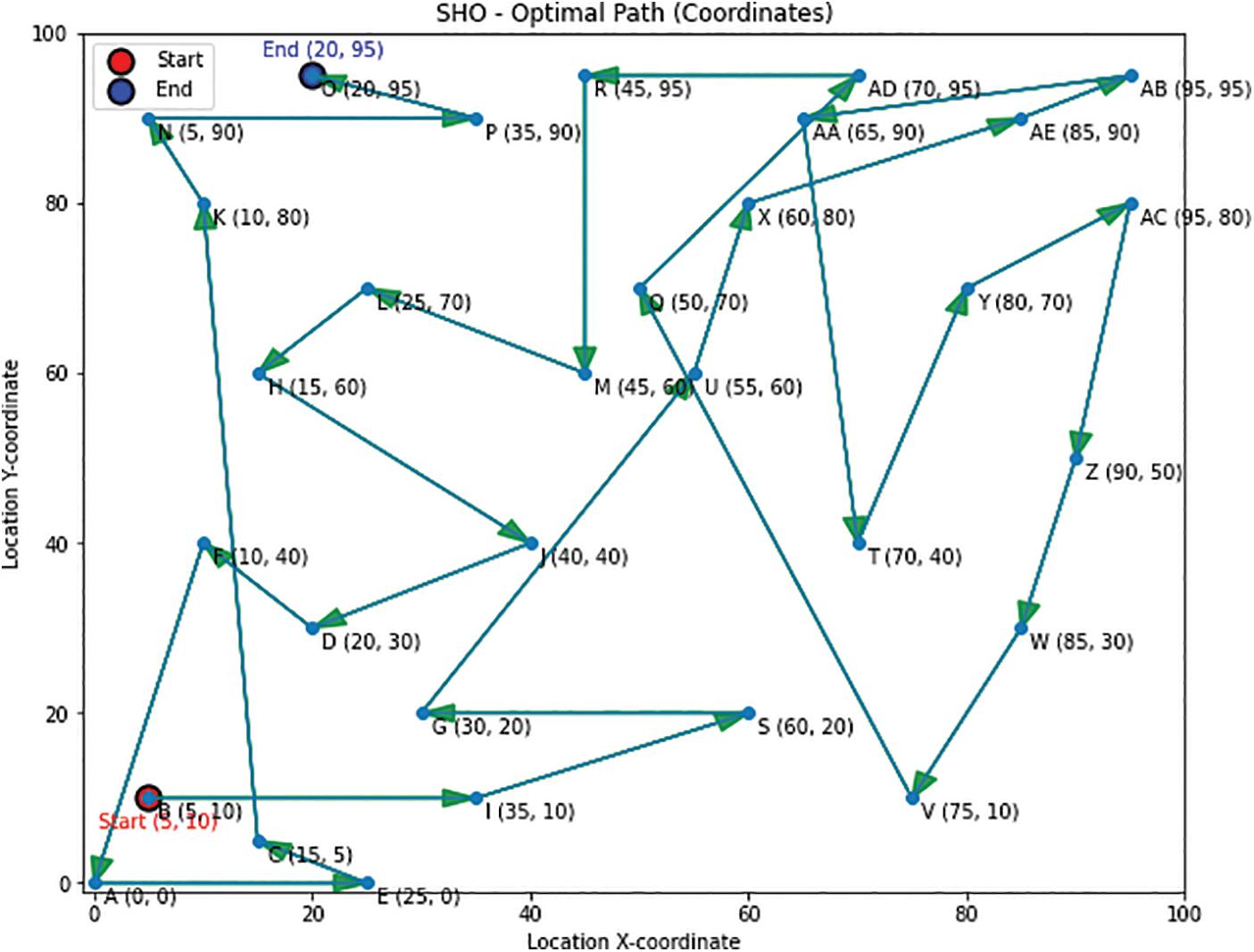
Figure 9: Optimal path calculated by SHO

Fig. 10 provides a comprehensive depiction of the optimal path generated using the SHO algorithm, going beyond visual representation to include distances between each location on the trajectory. Incorporating these distance values offers a detailed view of spatial connections and lengths within the path. This description enhances understanding of the path’s structure and the algorithm’s efficiency in minimizing overall path length or maximizing route effectiveness. Revealing distances between locations, the figure highlights the algorithm’s optimization success. Fig. 11 offers an extensive view of the SHO algorithm’s optimal path, enriching our understanding of its attributes and accomplishments within the given problem.

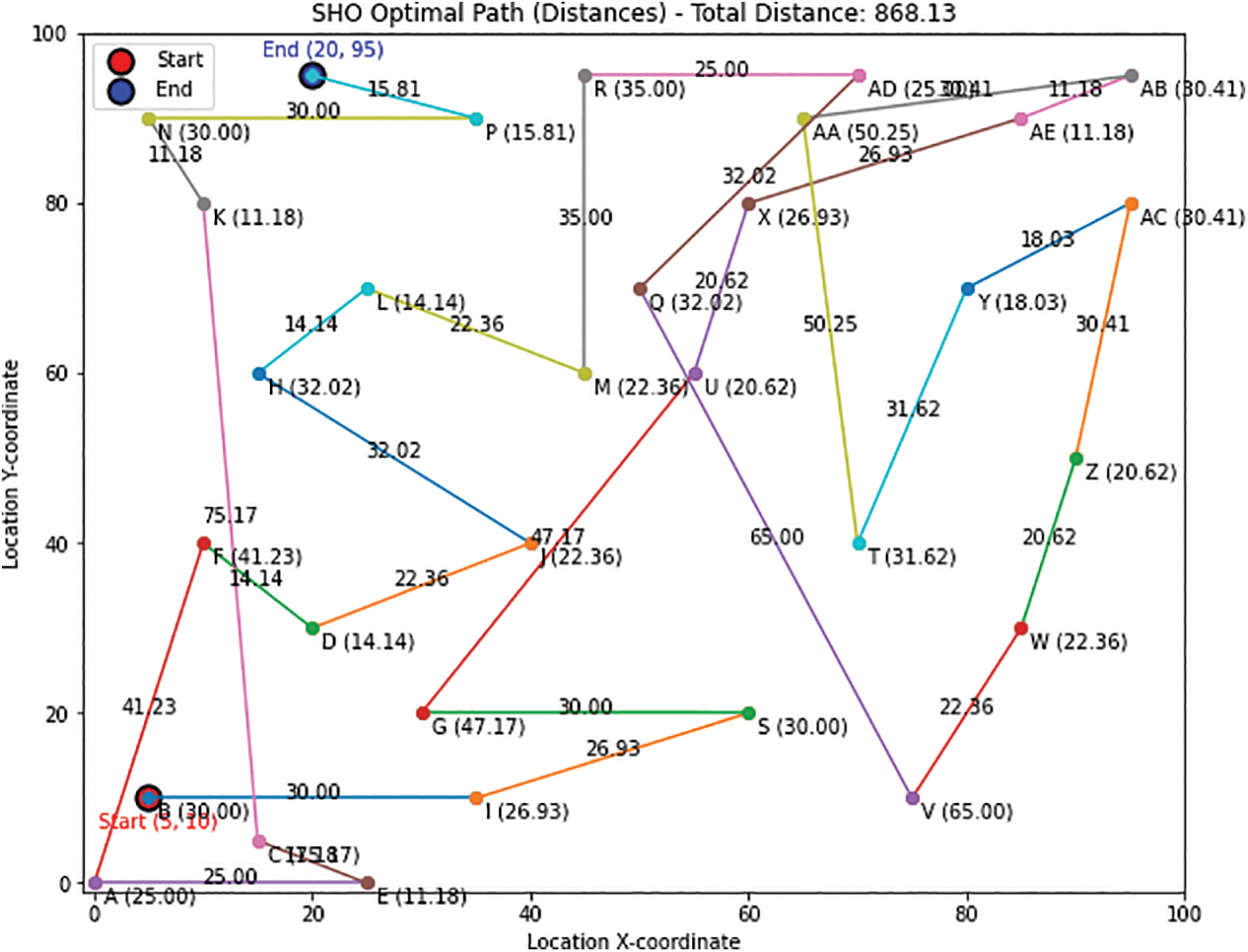
Figure 10: Optimal path calculated by SHO

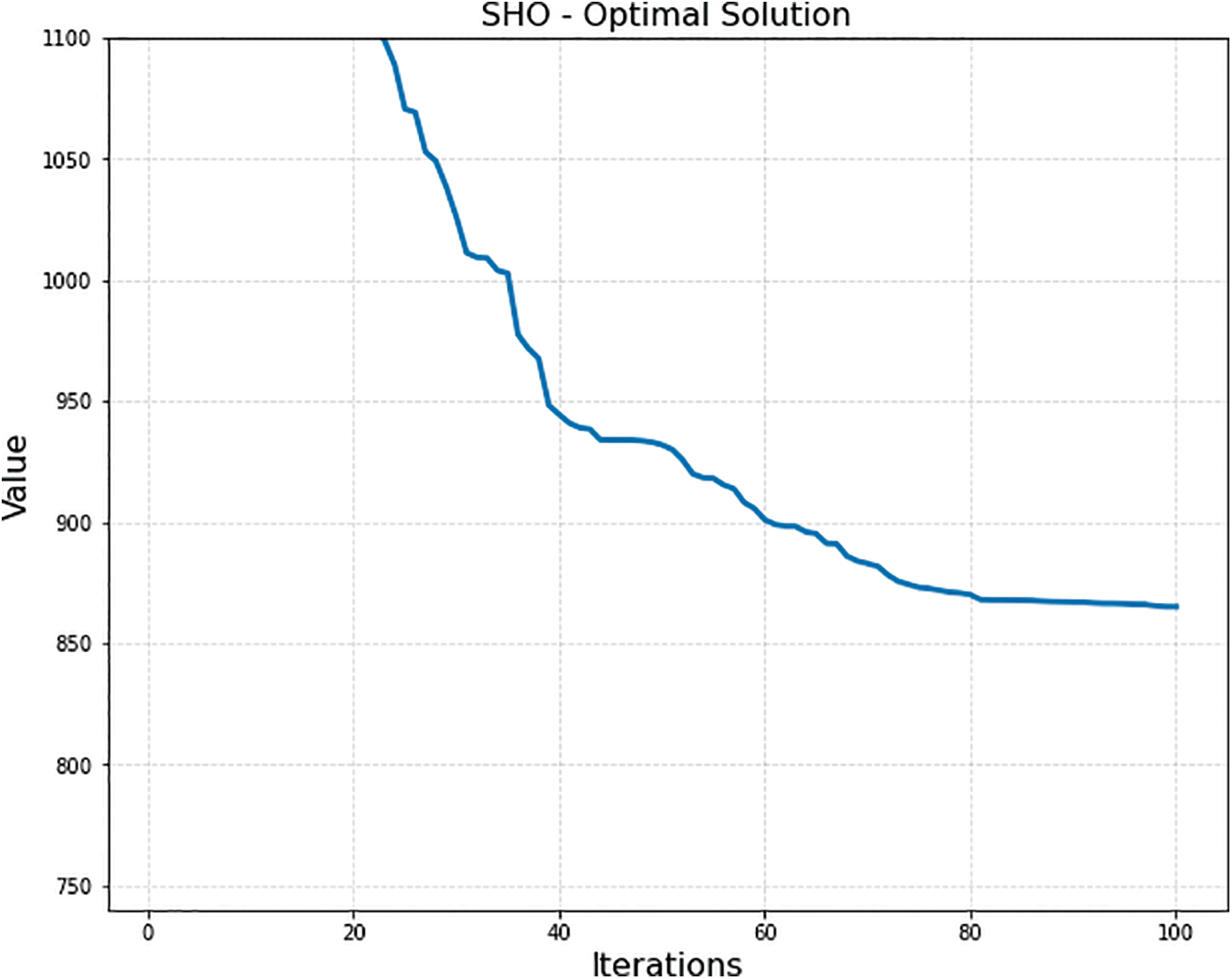
Figure 11: Optimal solution by SHO

4.3 Hybrid Firefly and Spotted Hyena Optimizer (HFSHO)

The Hybrid Firefly and Spotted Hyena Optimizer (HFSHO) is a novel metaheuristic algorithm designed to tackle logistics path-finding problems efficiently. It leverages the attributes of fireflies and spotted hyenas to optimize routes for transporting goods while considering various constraints and objectives. Fireflies communicate using bioluminescent signals, a foundation of the FO algorithm, where their brightness represents solution quality. In HFSHO, fireflies symbolize potential paths and their brightness guides optimization. The algorithm iteratively updates firefly positions based on brightness, directing them toward better solutions. HFSHO also fosters cooperation among fireflies, emulating spotted hyenas’ collaborative behavior. It dynamically adapts exploration and exploitation rates, making it versatile for diverse logistics problems, including those with time windows or capacity constraints. HFSHO excels in complex logistics scenarios, offering robust solutions that adapt to dynamic environments. HFSHO is a promising metaheuristic for logistics pathfinding, as detailed in Algorithm 1.

HFSHO, combining fireflies’ exploration with hyenas’ adaptability and cooperation, offers an efficient logistics optimization solution. Its ability to handle complex scenarios and adapt to dynamic environments makes it valuable for practitioners and researchers. Table 2 summarizes the computational complexities of FO, SHO and HFSHO. FO and SHO have O(N^2) complexity, while HFSHO introduces parallel processing with O(N * I), where ‘N’ is the population size and ‘I’ is the iteration count. HFSHO’s efficiency is evident in complex logistics and resource allocation tasks.

Mathematical Modeling: Mathematical modeling for Hybrid Firefly Optimization and Spotted Hyena Optimizer (HFSHO) in Logistics Path Optimization involves formulating equations governing fireflies and hyenas’ interactions to optimize paths while efficiently using sensor resources. Key variables and parameters include the, fireflies (F) and hyenas (H) populations, fitness functions for both and their positions in a problem space. FO algorithm updates firefly positions based on attractiveness (Ai) and distance. Ai between fireflies fi and fj is calculated using Ai = exp(−γ * dist(fi, fj)^2). Fireflies move towards attractive ones using the equation xi(t+1) = xi(t) + β * Ai * (xj(t) − xi(t)) + α * εi(t). SHO updates hyena positions based on aggressiveness (Pi). Pi between hyenas hi and hj is given by Pi = exp(−δ * fitnesshyena(hi) * dist(h1,h2)2). Hyenas move towards less aggressive ones using ρ and yj(t).

Fitness functions update during iterations to optimize logistics paths and sensor resource utilization. The best performers are selected for subsequent iterations. HFSHO combines FO and SHO, enhancing efficiency and effectiveness. Table 3 provides parameter details for HFSHO customization.

In Fig. 12, our hybrid algorithm, Trajectory, combines SHO and FO to optimize logistics paths, achieving an optimal value of 546.91. HFSHO is 33% more efficient than SHO and 34% more efficient than FO, reducing logistics costs. Fig. 13 illustrates the Optimal Path, enhancing logistics efficiency by minimizing distances, reducing resource usage, streamlining the supply chain and optimizing schedules. HFSHO provides actionable insights for logistics and transportation companies. In Fig. 14, precise coordinates of the best path are shown, enabling efficient distance calculations between logistics locations and reducing travel distance.

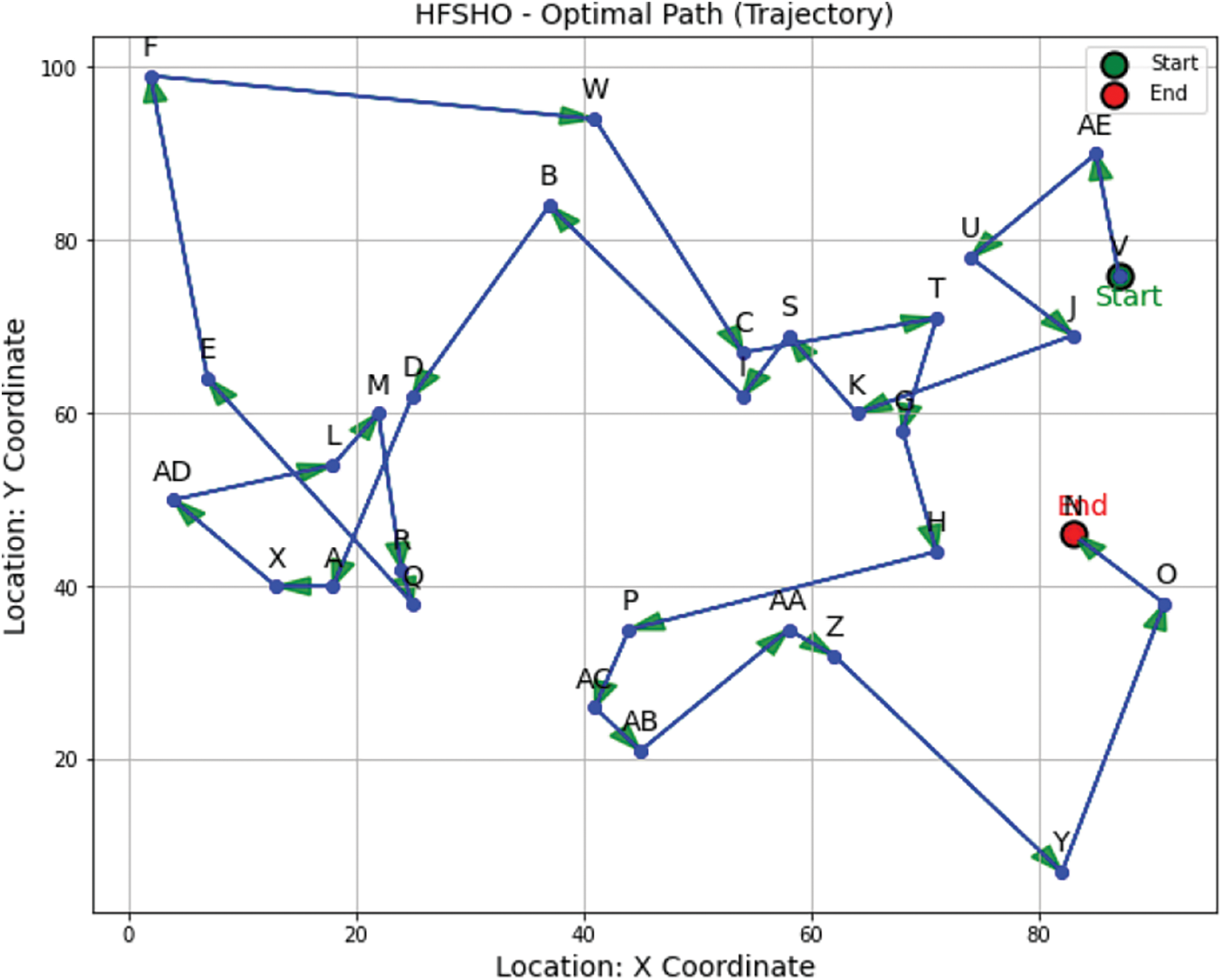
Figure 12: Proposed algorithm HFSHO-Optimal path (Trajectory)

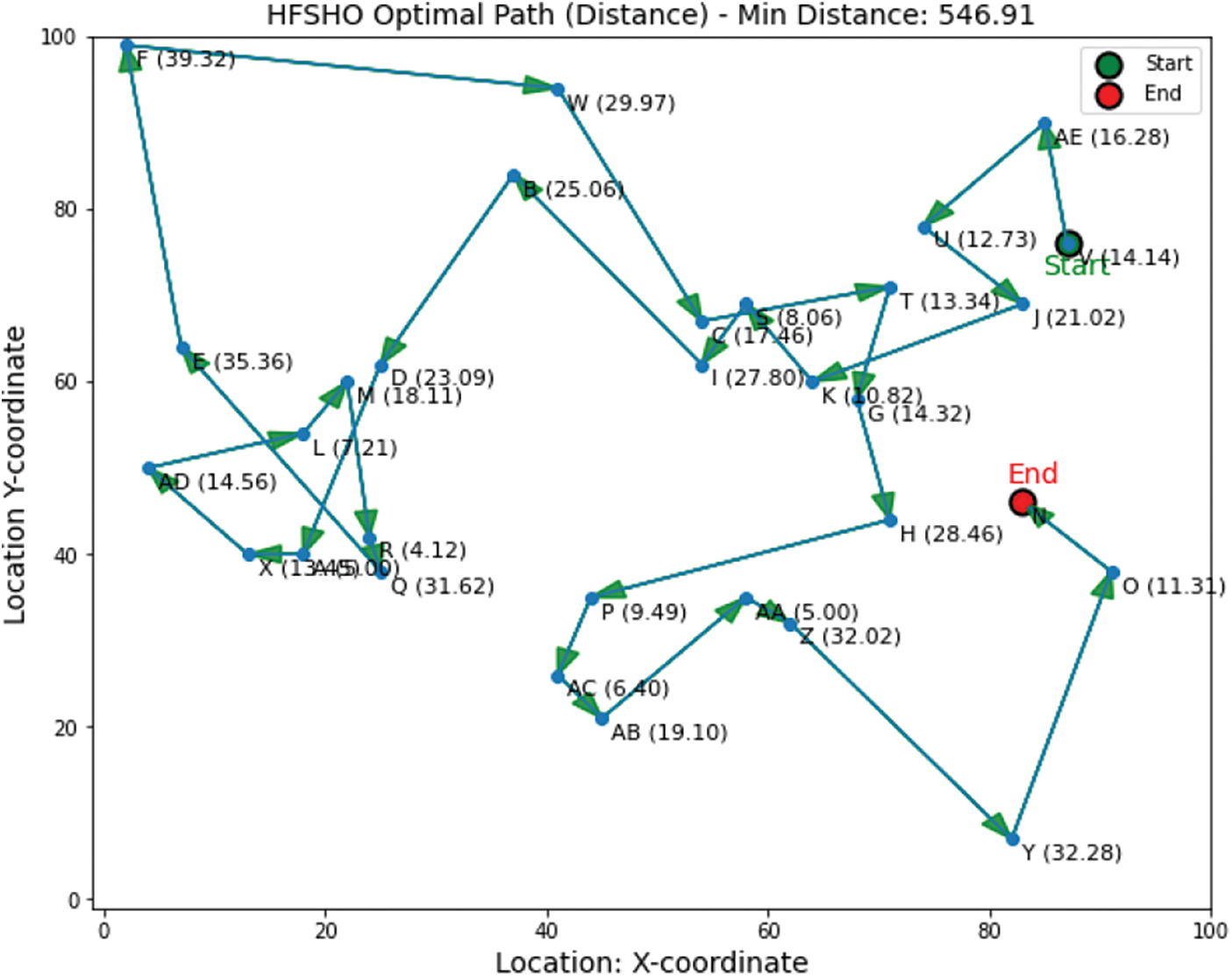
Figure 13: Distance between two coordinates along with optimal path

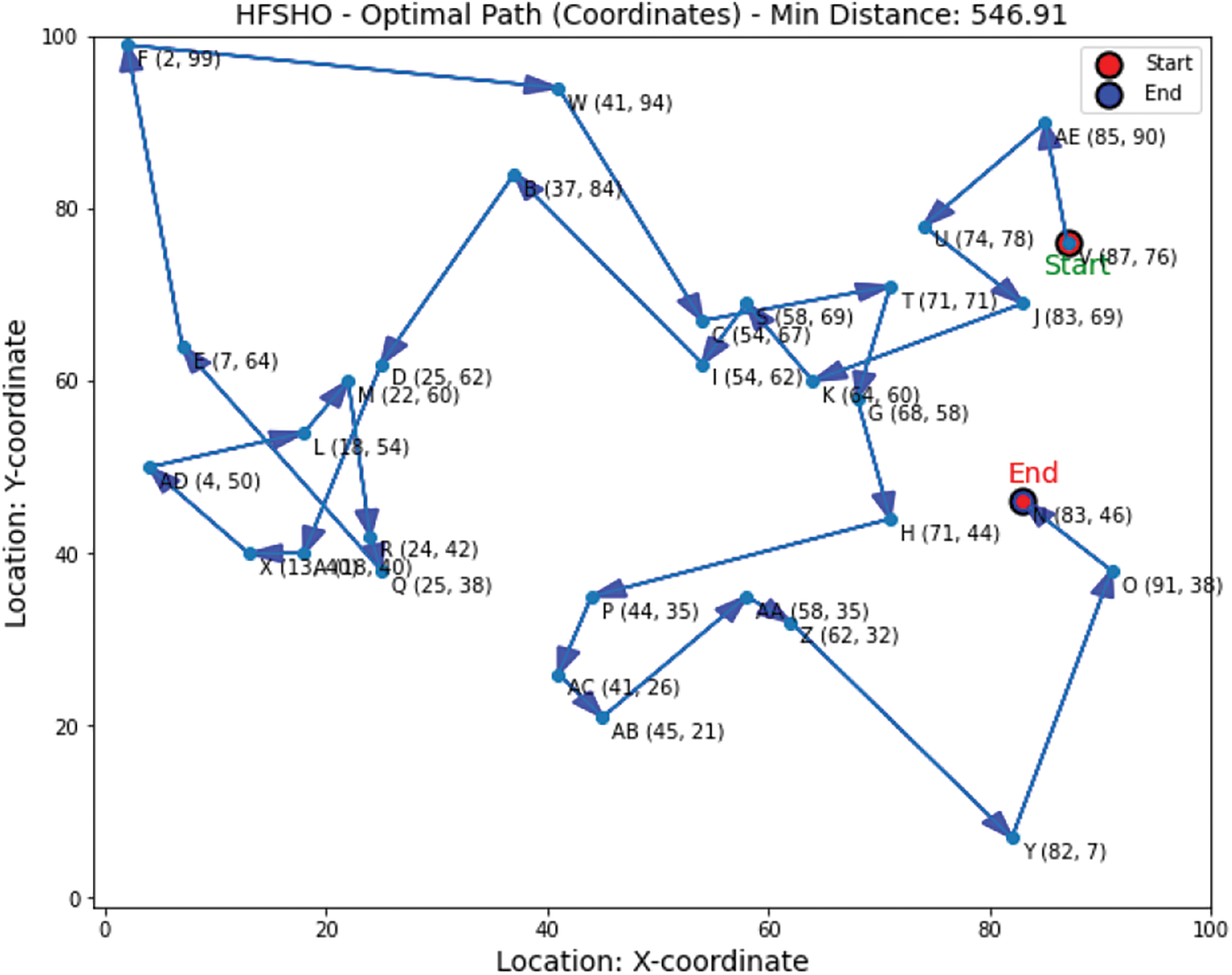
Figure 14: Optimal path distances calculated by HFSHO

In Fig. 15, our algorithm begins with an initial optimal value of 958 and steadily improves the solution through 100 iterations, achieving an outstanding optimal distance of 546.26. This surpasses other algorithms, establishing its superiority in logistics path optimization and enhancing efficiency. Fig. 16 compares minimum path distances achieved by various algorithms, with HFSHO outperforming others at 546 units. In Fig. 17, HFSHO excels with 58.43% efficacy, while other algorithms range from 26.23% to 47.12%, demonstrating varied optimization performance. These results underscore HFSHO’s exceptional logistics path optimization capacity, offering valuable insights for logistics planning, resource utilization and route optimization.

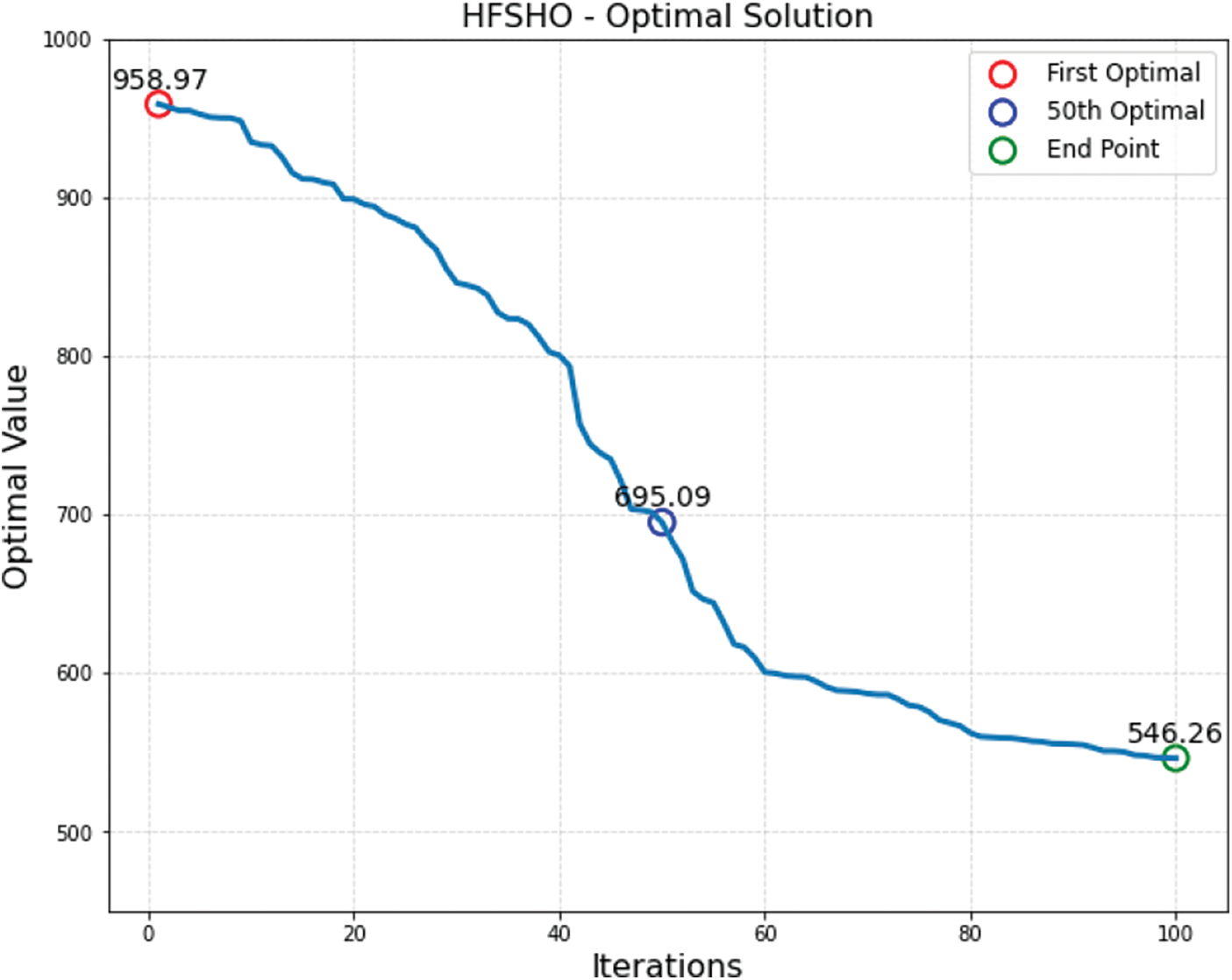
Figure 15: HFSHO process solution process vs. iterations

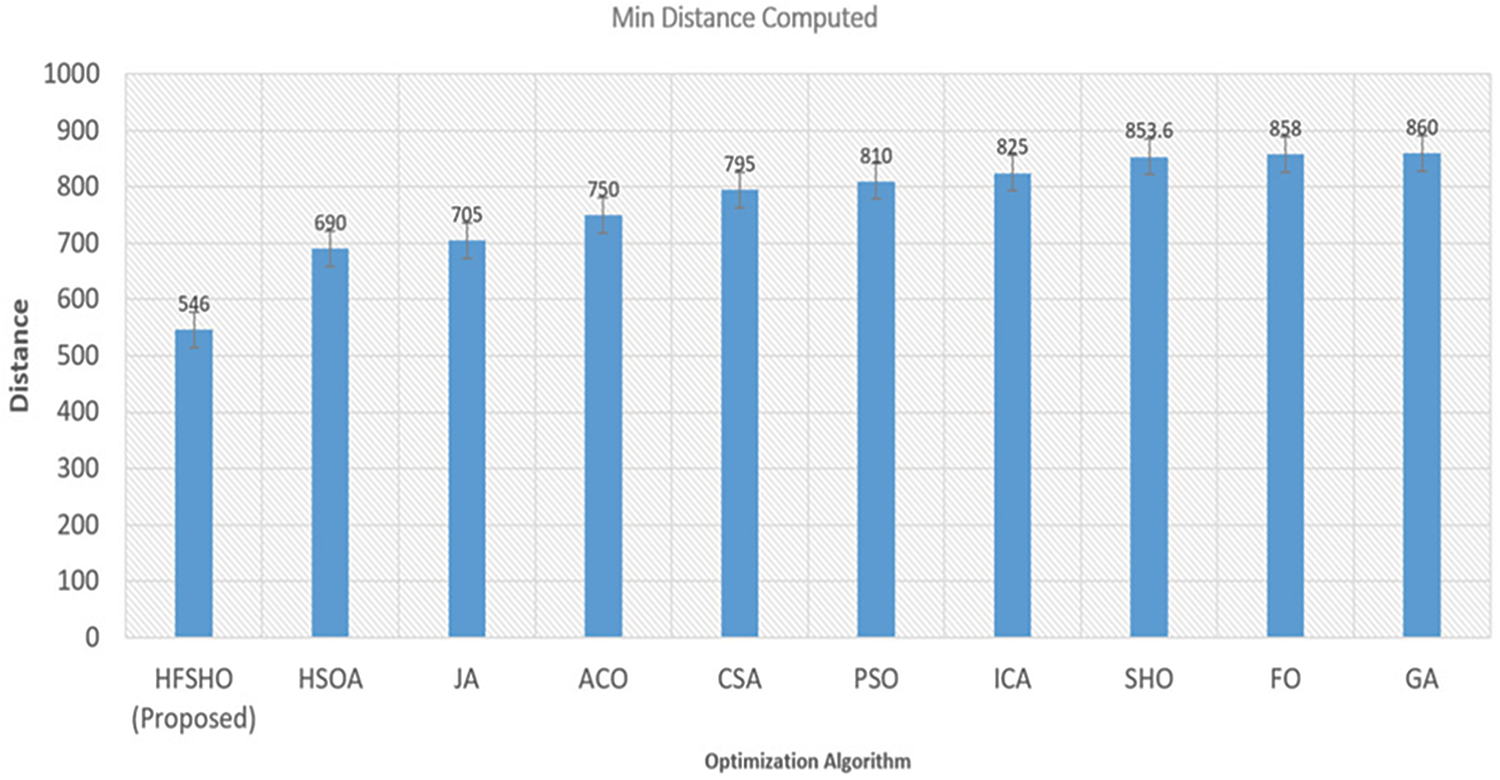
Figure 16: Proposed vs. existing algorithm minimal path calculation

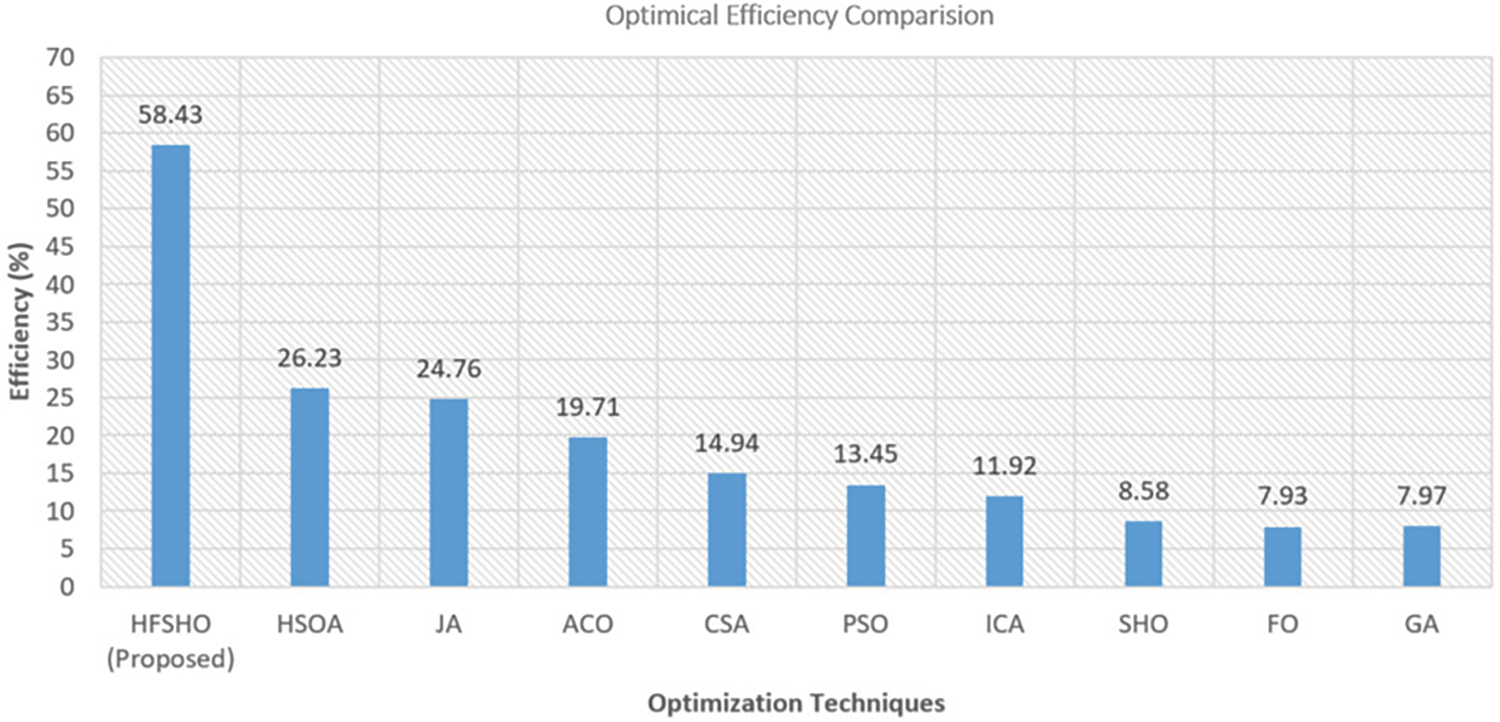
Figure 17: Efficiency of proposed vs. existing optimization algorithms

FO yielded a minimum path distance of 858, demonstrating its path optimization competence. GA achieved 860, indicating suboptimal paths. HFSHO outperforms, reducing travel distance significantly.

This enhances logistics efficiency and reduces costs, emphasizing HFSHO’s potential for optimal pathfinding. Algorithm choice in logistics pathfinding is crucial and HFSHO excels in this regard, as shown in Table 4.

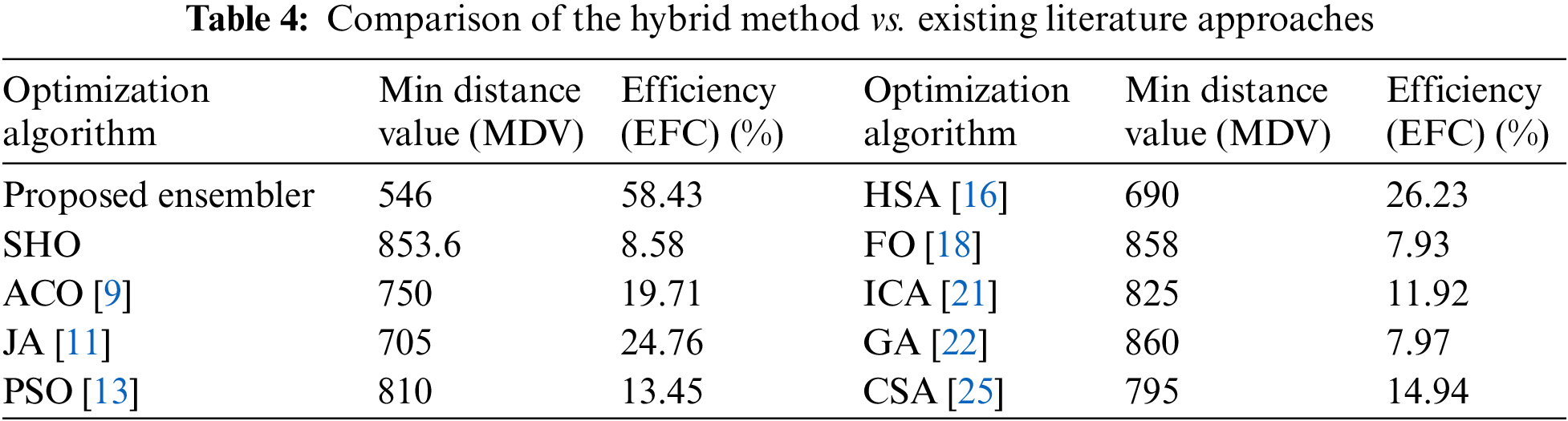
Table 5 evaluates various optimization methods across diverse objective functions, including Schwefel’s, Rastrigin’s, ZDT, DTLZ, Ackley’s and Sphere’s functions. It measures their Minimum Distance Value (MDV) and Efficiency (EFC). Smaller MDV values indicate better performance in approaching the global minimum, while EFC showcases computational efficiency as a percentage. Researchers and practitioners can use this table to select optimization methods aligned with their specific requirements and constraints, facilitating informed decision-making when tackling complex optimization problems across various domains.

5  Conclusion

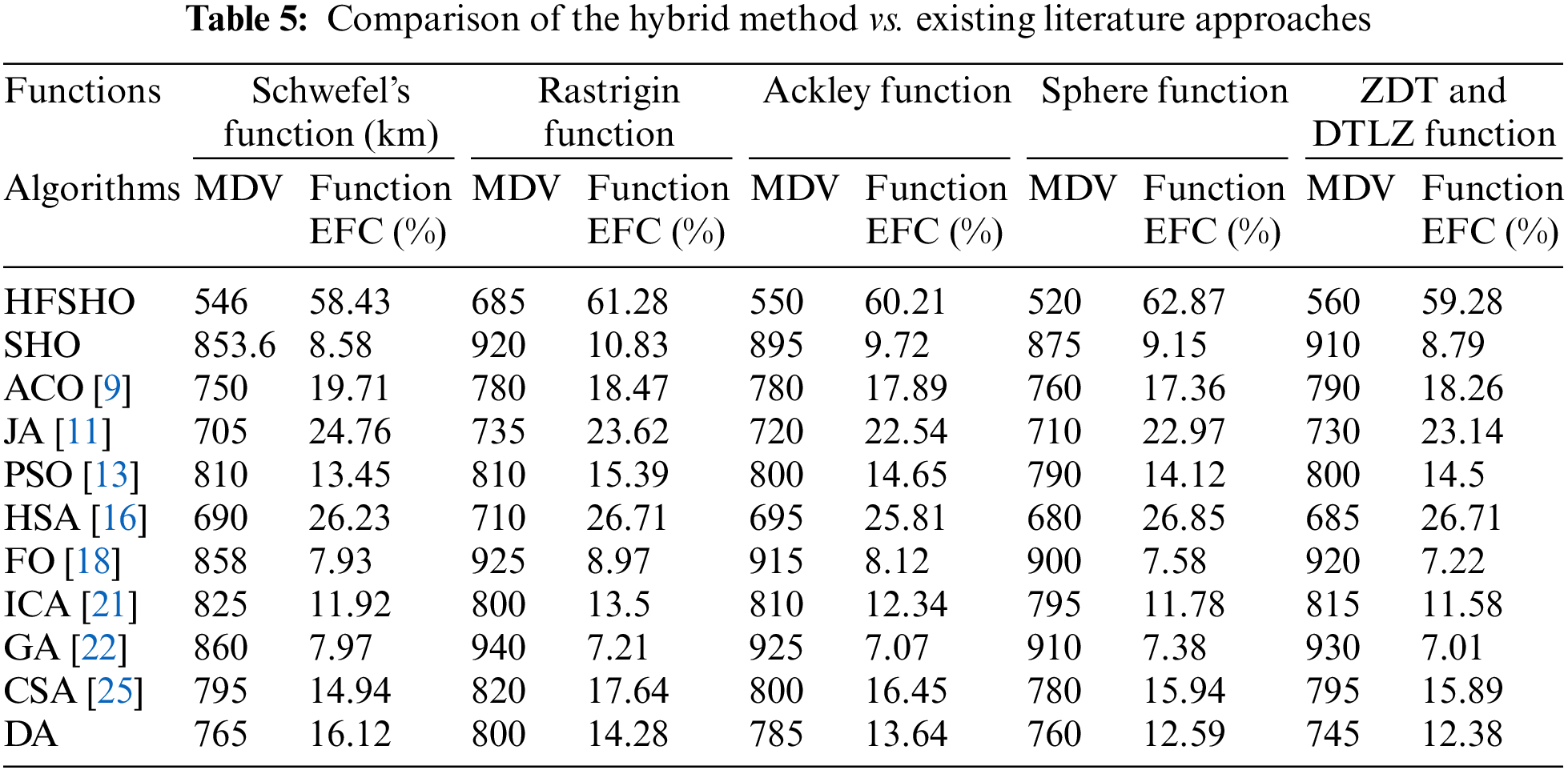
Our study provides a comprehensive exploration of logistics path optimization within the broader context of supply chain management. We evaluated three key optimization algorithms: SHO, FO and our innovative Hybrid algorithm, HFSHO, uncovering their strengths and limitations. SHO demonstrated competence with an optimal path distance of 853 units but an Efficiency Factor of 8.58%. FO was effective, achieving 858 units with an Efficiency Factor of 7.93. HFSHO outperformed, with a 546-unit path and an Efficiency Factor of 58.43, highlighting its promise in logistics path optimization, a crucial aspect of supply chain route optimization. Recognizing HFSHO’s potential, we acknowledge and aim to address its limitations, particularly related to computational efficiency and sensitivity to parameters. Future objectives include refining HFSHO, making it more practical and efficient for real-world logistics applications, a vital part of supply chain optimization. We also intend to explore multi-objective optimization to cater to logistics operations’ diverse and evolving needs, a core component of supply chain management.

Acknowledgement: This work was funded by the University of Jeddah, Jeddah, Saudi Arabia, under Grant No. (UJ-22-DR-61). The authors, therefore, acknowledge with thanks the University of Jeddah for its technical and financial support.

Funding Statement: This work was funded by the University of Jeddah, Jeddah, Saudi Arabia, under Grant No. (UJ-22-DR-61). The authors, therefore, acknowledge with thanks the University of Jeddah for its technical and financial support.

Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Ayub, N.; Methodology: Almazroi, A. A.; Formal analysis and investigation, Almazroi, A. A.; Writing-original draft preparation, Ayub, N.; Writing-review and editing, Almazro, A. A.; Funding acquisition, Almazroi, A. A.; Resources: Ayub, N.; Supervision, Almazroi, A. A. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data used in this study is publicly available at [7].

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. J. Wang, M. K. Lim, Y. Y. Zhan and X. Wang, “An intelligent logistics service system for enhancing dispatching operations in an IoT environment,” Transportation Research Part E: Logistics and Transportation Review, vol. 135, no. 1, pp. 101886, 2020. [Google Scholar]

2. M. H. Alkinani, A. A. Almazroi, M. Adhikari and V. G. Menon, “Design and analysis of logistic agent-based swarm-neural network for intelligent transportation system,” Alexandria Engineering Journal, vol. 61, no. 10, pp. 8325–8334, 2022. [Google Scholar]

3. R. M. Prabhu, G. Hema, S. Chepure and M. N. Guptha, “Logistics optimization in supply chain management using clustering algorithms,” Scalable Computing: Practice and Experience, vol. 21, no. 1, pp. 107–114, 2020. [Google Scholar]

4. A. A. Almazroi and M. A. Qureshi, “Dynamic deployment of road side units for reliable connectivity in internet of vehicles,” International Journal of Advanced Computer Science and Applications, vol. 13, no. 1, pp. 189–194, 2022. [Google Scholar]

5. S. Kumar, P. Jangir, G. G. Tejani and M. Premkumar, “A decomposition based multi-objective heat transfer search algorithm for structure optimization,” Knowledge-Based Systems, vol. 253, no. 1, pp. 109591, 2022. [Google Scholar]

6. G. Li and J. Li, “An improved tabu search algorithm for the stochastic vehicle routing problem with soft time windows,” IEEE Access, vol. 8, no. 1, pp. 158115–158124, 2020. [Google Scholar]

7. A. Fuller, Z. Fan, C. Day and C. Barlow, “Digital Twin: Enabling technologies, challenges and open research,” IEEE Access, vol. 8, no. 1, pp. 108952–108971, 2020. [Google Scholar]

8. Y. Liu, X. Tao, X. Li, A. Colombo and S. Hu, “Artificial intelligence in smart logistics cyber-physical systems: State-of-the-arts and potential applications,” IEEE Transactions on Industrial Cyber-Physical Systems, vol. 1, no. 1, pp. 1–20, 2023. [Google Scholar]

9. Y. Yilmaz and C. B. Kalayci, “Variable neighborhood search algorithms to solve the electric vehicle routing problem with simultaneous pickup and delivery,” Mathematics, vol. 10, no. 17, pp. 3108, 2022. [Google Scholar]

10. W. Deng, J. Xu and H. Zhao, “An improved ant colony optimization algorithm based on hybrid strategies for scheduling problem,” IEEE Access, vol. 7, no. 1, pp. 20281–20292, 2019. [Google Scholar]

11. T. H. Nguyen and J. J. Jung, “Swarm intelligence-based green optimization framework for sustainable transportation,” Sustainable Cities and Society, vol. 71, no. 1, pp. 102947, 2021. [Google Scholar]

12. M. A. Rahman, R. Sokkalingam, M. Othman, K. Biswas, L. Abdullah et al., “Nature-inspired metaheuristic techniques for combinatorial optimization problems: Overview and recent advances,” Mathematics, vol. 9, no. 1, pp. 2633, 2021. [Google Scholar]

13. N. Zhang, “Smart logistics path for cyber-physical systems with Internet of Things,” IEEE Access, vol. 6, no. 1, pp. 70808–70819, 2018. [Google Scholar]

14. A. H. Sadeghi, E. A. Bani, A. Fallahi and R. Handfield, “Grey wolf optimizer and whale optimization algorithm for stochastic inventory management of reusable products in a two-level supply chain,” IEEE Access, vol. 11, no. 1, pp. 1–16, 2023. [Google Scholar]

15. C. N. Vanitha, S. Malathy, R. K. Dhanaraj and A. Nayyar, “Optimized pollard route deviation and route selection using Bayesian machine learning techniques in wireless sensor networks,” Computer Networks, vol. 216, no. 1, pp. 109228, 2022. [Google Scholar]

16. S. Shadravan, H. R. Naji and V. K. Bardsiri, “The sailfish optimizer: A novel nature-inspired metaheuristic algorithm for solving constrained engineering optimization problems,” Engineering Applications of Artificial Intelligence, vol. 80, no. 1, pp. 20–34, 2019. [Google Scholar]

17. Y. Shi, Y. Zhou, T. Boudouh and O. Grunder, “A memetic algorithm for a relocation-routing problem in green production of gas considering uncertainties,” Swarm and Evolutionary Computation, vol. 74, no. 1, pp. 101129, 2022. [Google Scholar]

18. B. Moradi, “The new optimization algorithm for the vehicle routing problem with time windows using multi-objective discrete learnable evolution model,” Soft Computing, vol. 24, no. 9, pp. 6741–6769, 2020. [Google Scholar]

19. J. Cai, P. Wang, S. Sun and H. Dong, “A dynamic space reduction ant colony optimization for capacitated vehicle routing problem,” Soft Computing, vol. 26, no. 17, pp. 8745–8756, 2022. [Google Scholar]

20. Y. Li, H. Soleimani and M. Zohal, “An improved ant colony optimization algorithm for the multi-depot green vehicle routing problem with multiple objectives,” Journal of Cleaner Production, vol. 227, no. 1, pp. 1161–1172, 2019. [Google Scholar]

21. H. Rachih, F. Z. Mhada and R. Chiheb, “Meta-heuristics for reverse logistics: A literature review and perspectives,” Computers & Industrial Engineering, vol. 127, no. 1, pp. 45–62, 2019. [Google Scholar]

22. R. Yesodha and T. Amudha, “A bio-inspired approach: Firefly algorithm for multi-depot vehicle routing problem with time windows,” Computer Communications, vol. 190, no. 1, pp. 48–56, 2022. [Google Scholar]

23. J. Dutta, P. S. Barma, A. Mukherjee, S. Kar and T. De, “A hybrid multi-objective evolutionary algorithm for open vehicle routing problem through cluster primary-route secondary approach,” International Journal of Management Science and Engineering Management, vol. 17, no. 2, pp. 132–146, 2022. [Google Scholar]

24. W. Liu, “Route optimization for last-mile distribution of rural E-commerce logistics based on ant colony optimization,” IEEE Access, vol. 8, no. 1, pp. 12179–12187, 2020. [Google Scholar]

25. A. A. Almazroi and N. Ayub, “Multi-task learning for electricity price forecasting and resource management in cloud based industrial IoT systems,” IEEE Access, vol. 11, no. 1, pp. 1–20, 2023. [Google Scholar]

26. S. J. Chung, “Applications of smart technologies in logistics and transport: A review,” Transportation Research Part E: Logistics and Transportation Review, vol. 153, no. 1, pp. 102455, 2021. [Google Scholar]

27. R. Liu, P. Yang and J. Liu, “A dynamic multi-objective optimization evolutionary algorithm for complex environmental changes,” Knowledge-Based Systems, vol. 216, no. 1, pp. 106612, 2021. [Google Scholar]

28. D. Cattaruzza, N. Absi, D. Feillet and J. González-Feliu, “Vehicle routing problems for city logistics,” EURO Journal on Transportation and Logistics, vol. 6, no. 1, pp. 51–79, 2017. [Google Scholar]

29. H. C. Altunay and Z. Albayrak, “A hybrid CNN+ LSTM-based intrusion detection system for industrial IoT networks,” Engineering Science and Technology an International Journal, vol. 38, no. 1, pp. 101322, 2023. [Google Scholar]

30. G. Dhiman and V. Kumar, “Spotted hyena optimizer: A novel bio-inspired based metaheuristic technique for engineering applications,” Advances in Engineering Software, vol. 114, no. 1, pp. 48–70, 2017. [Google Scholar]