An Efficient Clustering Algorithm for Enhancing the Lifetime and Energy Efficiency of Wireless Sensor Networks

1  Introduction

Wireless Sensor Networks (WSNs) are self-organizing network systems composed of a large number of low-power micro-sensor nodes, integrating wireless communication, environmental sensing, local computing, and data storage capabilities [1]. They are characterized by flexible deployment, low cost, and high reliability. These networks demonstrate unique advantages in complex scenarios such as power grid monitoring. However, their resource-constrained nodes and dynamically changing network topology pose significant challenges to the effectiveness of traditional routing protocols. The core objective of current research is to overcome the physical limitations of node battery capacity by designing resource-aware routing protocols to maximize network lifespan, which has become the most promising research direction in this field [2–4]. The wireless sensor clustering network model is shown in Fig. 1.

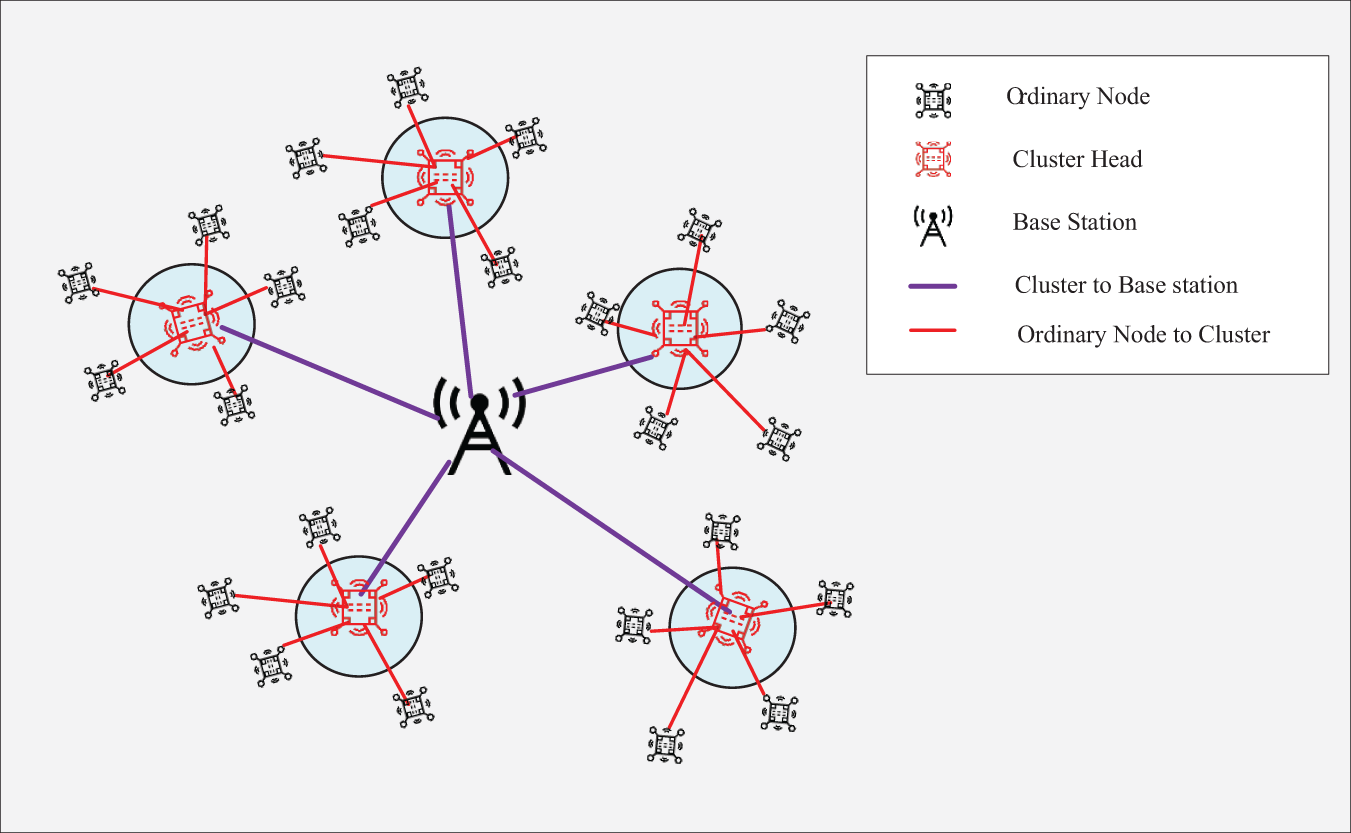
Figure 1: Wireless sensor clustering network model

At the technical implementation level, WSNs face three core contradictions: first, the conflict between the high-density deployment requirements of massive nodes and their limited energy reserves [5]; second, the conflict between limited data transmission rates and the quality-of-service requirements for real-time monitoring [6]; and third, the adaptability conflict between static predefined protocols and dynamic network environments [7]. To address these challenges, the academic community has gradually developed a solution system dominated by computational intelligence technologies [8]. Among these, clustering-based protocol architectures have gained widespread attention due to their energy efficiency advantages [9]. Such protocols achieve breakthroughs in key aspects such as cluster head selection and clustering optimization through technologies like neural network feature extraction, reinforcement learning for dynamic decision-making, and swarm intelligence for global optimization. Additionally, they address derivative needs such as network security enhancement, data aggregation efficiency improvement, and time synchronization precision control [10].

Due to the interdependent nature of nodes in WSNs and their close correlations, traditional predefined rules for cluster formation are no longer suitable [11]. Additionally, the dynamic nature of wireless sensor application environments requires algorithms to adaptively handle node energy consumption, network density changes, and environmental condition fluctuations [12]. Research has shown that swarm intelligence algorithms exhibit unique advantages in addressing the dynamic adaptability issues of WSNs [13]. Taking the ant colony algorithm as an example, it simulates the natural foraging path optimization mechanism and constructs a pheromone update model with positive feedback characteristics, effectively solving the energy balance problem in data transmission paths. Meanwhile, the particle swarm optimization algorithm, leveraging its powerful global search capability, achieves optimal cluster head selection in dynamic network topologies [14]. Its iterative process can adaptively handle real-time changes such as node energy decay and network density fluctuations. Research data indicate that swarm intelligence-optimized routing protocols can improve network lifespan by 30%–45% while reducing end-to-end transmission delays by approximately 25% [15].

To further enhance the energy efficiency and extend the lifespan of WSNs, recent research has focused on improving and optimizing existing swarm intelligence algorithms. These improvements include hybridizing multiple optimization techniques, introducing chaotic mapping to enhance the algorithm’s exploration capability, adopting multi-objective optimization methods to simultaneously consider multiple performance metrics, and developing new fitness evaluation mechanisms to more accurately reflect network states [16].

The dynamic environment and complex topology of WSNs make it difficult for traditional optimization algorithms to balance global convergence and local search capabilities. Standard optimization methods may perform well in static environments, but their adaptability often falls short when faced with issues such as topology changes, uneven energy consumption, or data transmission interference [17]. Especially in highly dynamic network scenarios, fixed optimization strategies may fail to adjust parameters in a timely manner, leading to degraded network performance. Adaptive chaotic strategies, by introducing the ergodicity and randomness of chaotic mapping, enable optimization algorithms to escape local optima traps and achieve more uniform global exploration in the search space [18,19].

The application of chaos theory in optimization problems is mainly reflected in two aspects: on the one hand, the aperiodic characteristics of chaotic sequences can enhance the algorithm’s search capability in complex environments, prevent premature convergence, and increase the probability of finding global optimal solutions [20]; on the other hand, combined with adaptive adjustment mechanisms, the search process can dynamically adjust parameters based on network states, ensuring optimization effectiveness under varying network densities, energy distributions, or traffic loads [21]. For example, in the cluster head selection process, adaptive chaotic strategies can integrate factors such as node energy, data load, and geographical location, dynamically adjusting pheromone update rules through chaotic mapping mechanisms to enhance search diversity and improve optimization efficiency [22].

Furthermore, in routing optimization, chaotic strategies can be used to adjust path exploration and data forwarding strategies, enabling the network to flexibly select optimal transmission paths based on current energy distribution and traffic demands [23]. Under low traffic conditions, the algorithm tends to stabilize energy consumption balance, while under high traffic conditions, it adaptively optimizes load distribution to ensure transmission efficiency [24]. Compared to traditional methods such as Ant Colony Optimization (ACO) or Particle Swarm Optimization (PSO), adaptive chaotic strategies can achieve better convergence speed and stability without increasing computational overhead [25].

The practical application of WSNs involves various complex environments and dynamic constraints, such as sensor deployment in smart agriculture, energy consumption optimization in industrial IoT, and efficient data transmission in disaster warning systems [26]. In these scenarios, the operating environment of the network often exhibits uncertainties, such as climate changes affecting sensor power consumption or network congestion impacting data delays. Adaptive chaotic strategies can dynamically optimize network parameters based on different application requirements and achieve a balance between global and local performance across different time scales [27].

Therefore, by introducing chaotic mapping mechanisms, adaptive chaotic strategies not only enhance the robustness and adaptability of WSNs but also improve the global search capability of algorithms, achieving superior comprehensive performance in energy consumption optimization, data transmission stability, and network lifespan extension. In the future, this strategy can be further integrated with deep reinforcement learning or distributed optimization methods to enhance its applicability in large-scale heterogeneous networks, providing more efficient solutions for the intelligent optimization of WSNs [28].

Against this background, this study proposes an innovative and efficient clustering method that combines adaptive chaotic strategies with the ACO algorithm to address the challenges of improving energy efficiency in WSNs. The main contributions of this study are as follows:

1.    Proposed an Adaptive Chaotic Cluster Head Selection Mechanism: AC-ACO introduces chaotic mapping to dynamically weight factors such as node residual energy, communication cost, network topology position, and load conditions during cluster head selection. Leveraging the randomness and ergodicity of chaotic mapping, the algorithm avoids local optima traps, prioritizes high-energy nodes as cluster heads, and prevents rapid energy depletion of nodes due to frequent cluster head roles. The dynamic nature of chaotic mapping ensures adaptability, enabling real-time weight adjustments based on network states.

2.    Designed a Chaos-Driven Intra-Cluster Data Aggregation Strategy: For intra-cluster data transmission, AC-ACO employs an adaptive data aggregation method based on chaotic event triggering. Dynamic thresholds generated through chaotic mapping adapt data fusion methods according to the temporal correlation and spatial redundancy of sensing data. This reduces redundant transmissions, optimizes data compression and aggregation, and significantly lowers communication overhead. The randomness of chaotic mapping enhances adaptability to network changes, improving data processing flexibility and efficiency.

3.    Proposed an Efficient Clustering Algorithm: AC-ACO optimizes cluster formation and data transmission in WSNs by combining the global search capability of ACO with the dynamic characteristics of chaotic mapping. It introduces an adaptive mechanism to dynamically adjust optimization strategies in response to network state changes. By mapping ant path exploration behavior to node energy consumption, AC-ACO achieves a multi-objective trade-off among energy consumption, load balancing, and network lifespan, offering a novel solution for WSN clustering optimization.

2  Related Work

In recent years, WSNs have demonstrated broad application prospects in various fields such as industrial automation, environmental monitoring, and intelligent transportation. However, issues related to energy efficiency, network lifetime, and data transmission reliability remain focal points of attention in both academia and industry [29]. To address these challenges, researchers have proposed numerous clustering protocols and optimization algorithms aimed at extending network lifetime and enhancing overall performance through efficient energy management and node scheduling strategies. Among these, bio-inspired algorithms have been widely applied in WSN clustering optimization due to their excellent global search capabilities and adaptability [30]. Nevertheless, the limitations of traditional bio-inspired algorithms in terms of convergence speed and local optima issues persist. To this end, researchers have introduced various improvement strategies, including adaptive operators, chaotic mapping techniques, and elite strategies, to further enhance algorithm performance. This paper systematically reviews recent research progress in the field of WSN clustering optimization and explores how to design more efficient clustering methods by improving swarm intelligence optimization algorithms to tackle the complex challenges faced by WSNs in practical applications [18].

Low-Energy Adaptive Clustering Hierarchy (LEACH) is a highly influential clustering protocol in WSNs, proposed by Heinzelman et al. [31], aiming to balance network energy consumption through a clustering mechanism. However, the protocol’s strategy of randomly selecting cluster heads (CHs) leads to premature energy depletion in some nodes, thereby shortening the overall network lifetime. To address this issue, Tadros et al. [32] proposed an unsupervised learning clustering algorithm based on an improved LEACH protocol and K-means data clustering, further optimizing the cluster head selection process. By integrating the K-means clustering method, this algorithm avoids the energy imbalance caused by the random selection of cluster heads in the traditional LEACH protocol, demonstrating excellent performance in applications such as environmental pollution monitoring and significantly enhancing network lifetime and monitoring efficiency.

On the other hand, Nisha et al. [33] proposed a score-based link delay-aware routing protocol (SBLDAR), which achieves collision-free data transmission by combining multi-channel MAC protocols and utilizes a fuzzy-modified sunflower optimization algorithm (FMSFO) to elect efficient cluster heads, thereby improving network lifetime and performance. Nevertheless, the application of these protocols in industrial WSNs still faces limitations, primarily due to the more stringent requirements of IWSNs for energy consumption, transmission delay, and energy balance.

Clustering methods in WSNs are inspired by bio-inspired algorithms, which can output optimal clustering solutions within a limited time. Zhou et al. [34] proposed a multi-hop routing algorithm based on semi-fixed clustering and an improved ant colony optimization (SFC-IACO) algorithm. By dividing the network into fixed regions, dynamically rotating cluster heads, and balancing inter-cluster energy consumption, the algorithm achieved network energy balance and load balancing, effectively extending the network lifetime. Stodola and Nohel [35] introduced a novel metaheuristic algorithm based on ACO, which solves the multi-depot vehicle routing problem (MDVRP) by incorporating node clustering and adaptive pheromone evaporation mechanisms. By organizing transition vertices into candidate lists and adaptively adjusting the pheromone evaporation rate based on population diversity, the algorithm effectively reduces the risk of falling into local optima and improves optimization efficiency. To enhance data transmission reliability, Yesodha et al. [36] proposed a secure routing protocol (TECC-ACO-SRP) based on trust modeling, elliptic curve encryption (ECC), and improved ACO. Through intrusion detection, node authentication, and encryption technologies, combined with fuzzy rules and clustering mechanisms, the protocol achieved energy optimization, security enhancement, and high packet delivery rates. Additionally, to optimize network energy consumption and extend network lifetime, Mishra and Yadav [37] proposed an energy-efficient clustering routing protocol based on nature-inspired algorithms. By combining the butterfly optimization algorithm (BOA) to select optimal cluster heads and utilizing PSO and ACO mechanisms to optimize cluster formation and path selection, the protocol demonstrated excellent performance in stability, active node count, and energy consumption. However, it may still fall into local optima when adjusting node residual energy, communication distance, and load, thereby affecting clustering performance.

Over time, chaotic mapping strategies have increasingly been used to enhance the global search performance of bio-inspired algorithms. For example, Sivakumar et al. [38] proposed an energy-aware clustering protocol based on the chaotic gorilla troops optimization algorithm (EACP-CGTOA), marking a new step in metaheuristic algorithms for improving energy efficiency and network lifetime in WSNs. El-Hageen et al. [39] introduced a cluster head selection method based on the chaotic zebra optimization algorithm (CZOA). By combining chaotic mapping and the zebra optimization algorithm, the method effectively avoids local optima, significantly reduces energy consumption, and extends network lifetime, while outperforming other swarm intelligence algorithms in terms of node survival rate. Elashry et al. [40] proposed a hybrid metaheuristic optimization algorithm based on the chaotic reptile search algorithm (CRSA), which effectively avoids local optima and significantly reduces energy consumption while extending network lifetime. However, the parameter settings of chaotic mapping greatly influence algorithm performance, and inappropriate parameter choices may lead to slower convergence or suboptimal results. Adaptive operator tuning can dynamically adjust parameters and strategies based on network state and node characteristics, ensuring optimization effectiveness while reducing computational overhead.

Overall, although existing literature has explored numerous clustering methods, they often fail to fully consider critical factors such as node residual energy, intra-cluster distance, and distance to the base station, all of which significantly impact the clustering performance of WSNs. To address this research gap, this paper proposes a novel clustering model for WSNs and develops a new bio-inspired clustering method incorporating adaptive chaotic strategies, aiming to achieve optimal clustering solutions. Additionally, this study focuses on improving the search efficiency and solution quality of the algorithm, thereby accelerating its convergence speed. Through these strategies, the research aims to optimize the energy efficiency of WSNs and significantly extend their operational lifespan in grid systems, providing an efficient and feasible solution for future WSN deployments. The important abbreviations in this article are summarized in Table 1.

3  Model Definition

In WSNs, sensor nodes are deployed in the monitoring area to collect environmental data and transmit it to the Base Station (BS). Since the distance between sensor nodes and the base station is usually long, direct communication would consume a significant amount of energy, thereby drastically reducing the network’s lifespan. To address this challenge, the clustering model has been introduced as an efficient network organization method, which optimizes energy consumption and extends the network lifespan by dividing the network into multiple clusters. In the clustering model, each cluster consists of a Cluster Head (CH) node and multiple ordinary nodes. The cluster head node is responsible for receiving data from nodes within the cluster, performing data aggregation, and forwarding the aggregated data to the base station, while ordinary nodes only need to communicate with the cluster head, thereby reducing the energy consumption caused by long-distance transmission.

During the clustering process, the selection of the cluster head is a critical step that directly affects the network’s energy efficiency and overall performance. To ensure the long-term stable operation of the network, cluster head selection needs to comprehensively consider multiple parameters, including the residual energy of nodes, the distance between nodes, communication delays, and network load. By optimizing the cluster head selection strategy, it is possible to prevent certain nodes from being overused and depleting their energy, while balancing the network load and reducing communication delays, thereby extending the network’s lifespan. Additionally, the clustering model further reduces energy consumption by employing data aggregation techniques to minimize redundant data transmission.

This paper proposes a new hybrid optimization algorithm that selects the optimal cluster head by comprehensively considering parameters such as delay, distance, and energy, thereby achieving efficient optimization among energy efficiency, load balancing, and network lifespan extension. To quantify energy consumption and optimize network performance, the objective optimization function in the WSN clustering model can be expressed as Eq. (1):

Em=ETx(k,d)+ERx(k)+EDA(k)(1)

This model describes the energy consumption of nodes during data transmission, reception, and aggregation. The energy consumption is calculated based on the distance between the transmitter and receiver and the amount of data transmitted. Specifically, the energy consumption ETx(k,d) for a sensor transmitting k-bit information over a distance d can be expressed as:

ETx(k,d)=ETx−dec(k)+ETx−amp(k,d)(2)

where ETx−dec(k) is the energy consumed by the circuit, and ETx−amp(k,d) is the energy consumed by the amplifier. Depending on the transmission distance, the energy consumption model is divided into the free space propagation model and the multipath fading model:

ETx(k,d)={kEelec+kεfsd2,if d<d0kEelec+kεmpd4,if d≥d0(3)

where Eelec is the circuit energy consumption coefficient, εfs and εmp are the energy loss coefficients for free space and multipath propagation, respectively, and d0 is the distance threshold, calculated as:

The distance threshold d0 is calculated as:

d0=εfsεmp(4)

The energy consumption ERx(k) for a data-receiving node to receive k-bit data is calculated as:

ERx(k)=kEelec(5)

The energy consumption EDA(k) for aggregating k-bit data is calculated as:

EDA(k)=kEagg(6)

The residual energy update formula for node j is expressed as:

Ej(k+1)=Ej(k)−Em(7)

where Eagg is the data aggregation energy coefficient, and Eelec depends on several factors such as digital encoding, modulation, filtering, and signal spreading. The amplifier energy εfsd2/εmpd4 depends on the distance between the transmitter and receiver, as well as the acceptable bit error rate. Here, d0 is the distance threshold, When the distance is less than the threshold d0, the free space propagation model is used to calculate energy consumption. When the distance reaches or exceeds d0, the multipath fading model is applied instead.

4  The AC-ACO Method for WSNs

In typical deployment scenarios of WSNs, the base station is usually located at the center of the monitoring area to efficiently receive data transmitted by sensor nodes. However, due to the long distance between some sensor nodes and the base station, direct communication results in high energy consumption. At the same time, when using a multi-hop transmission mode, nodes closer to the base station bear a heavier relay data forwarding burden, causing their energy consumption to deplete much faster than nodes farther away. This creates a “hotspot” problem, affecting the overall network lifespan and stability.

To address the inherent nature of this issue as a path optimization problem, this paper adopts the ACO algorithm as the fundamental optimization framework. Compared to other swarm intelligence algorithms, ACO demonstrates inherent advantages in path planning. Its pheromone update mechanism dynamically adapts to changes in network topology and node energy levels, offering strong global search and local refinement capabilities. Moreover, it is suitable for distributed implementation with low computational overhead, making it particularly appropriate for resource-constrained WSN environments. However, conventional ACO algorithms tend to fall into local optima in complex search spaces, limiting their ability to achieve global optimization in clustering and routing decisions. Therefore, further improvements are necessary to enhance the algorithm’s search performance and adaptability.

To improve the energy efficiency of WSNs and balance the network load, this paper proposes an Adaptive Chaotic Ant Colony Optimization (AC-ACO) algorithm to optimize cluster structures and data transmission paths. By introducing an adaptive chaotic strategy, the algorithm maintains the global search capability of ACO while leveraging the random perturbation characteristics of chaotic mapping to enhance the algorithm’s ability to escape local optima, improve the rationality of cluster head selection, and optimize data transmission paths.

Most current heuristic-based clustering and routing algorithms for WSNs are prone to falling into local optima and suffer from unbalanced energy utilization, which affects the long-term operation of the network. To address this, AC-ACO adopts a dynamic competition radius mechanism to cluster the network, forming appropriately sized data clusters in different regions to balance the energy consumption of nodes. Additionally, the algorithm combines chaotic perturbation to optimize the pheromone update strategy, enabling data flows to dynamically adjust transmission paths based on energy consumption. This reduces the energy depletion problem in high-load areas, effectively extending the network’s lifespan.

In the following sections, this paper will detail the key components of the AC-ACO algorithm, including the conventional ant colony algorithm, the improved ant colony optimization algorithm, and the optimization process of the algorithm.

4.1 Conventional Ant Colony Optimization Algorithm

ACO is a bio-inspired heuristic optimization algorithm based on the simulation of ant foraging behavior. In nature, ants release pheromones on the paths they traverse while searching for food. Other ants sense these pheromones and tend to choose paths with higher pheromone concentrations. Over time, the pheromone concentration on shorter paths gradually increases, eventually forming an optimal path. The ACO algorithm is based on this mechanism, solving combinatorial optimization problems through the collaborative behavior of artificial ant colonies.

In the cluster routing optimization problem of WSNs, the core objective of ACO is to determine the optimal cluster head nodes while optimizing intra-cluster and inter-cluster data transmission paths to extend network lifetime and improve energy efficiency. During the search process, ants select cluster heads based on pheromone concentrations and heuristic information on the paths, thereby optimizing data transmission strategies. In ACO, the probability of an ant choosing the next-hop node is determined by both pheromone concentration and heuristic information, calculated as follows:

Pij=τijα⋅ηijβ∑k∈Niτikα⋅ηikβ(8)

where Pij is the probability of an ant moving from node i to node j, τij is the pheromone concentration on the path i→j, ηij is the heuristic information, typically related to the distance dij, i.e., ηij=1dij, α and β are parameters that adjust the influence weights of pheromone and heuristic information, respectively, Ni is the set of neighboring nodes available for selection from the current node.

The path optimization in ACO primarily relies on the dynamic updating of pheromones. After each iteration, the pheromones are updated according to the following formula:

τij=(1−ρ)⋅τij+∑k=1mΔτij(k)(9)

where ρ is the pheromone evaporation coefficient (0<ρ<1), which prevents the infinite accumulation of pheromones and ensures the algorithm’s ability to explore new paths. Δτij(k) is the pheromone increment released by the k-th ant on the path i→j, typically defined as:

Δτij(k)={QLk,if ant k traverses path (i,j)0,otherwise(10)

where Q is the pheromone intensity constant, which controls the overall level of pheromone release. Lk is the path length traversed by the k-th ant. The shorter the path, the more pheromone the ant releases, thereby reinforcing high-quality paths.

Through the continuous updating of pheromones, ACO can gradually optimize path selection, guiding the entire ant colony toward the optimal solution. However, ACO still faces several issues, such as a tendency to fall into local optima, slow convergence speed, and susceptibility to random factors during the initial search phase. Therefore, based on ACO, this study introduces an Adaptive Chaos Strategy to further enhance the algorithm’s global search capability and improve its ability to escape local optima.

4.2 Adaptive Chaotic Ant Colony Optimization Algorithm

This paper proposes a novel adaptive chaotic strategy. Based on chaotic dynamics, this strategy aims to enhance the global search capability of optimization algorithms through the randomness and irregularity of chaotic sequences, thereby effectively avoiding the algorithms falling into local optimal solutions during the solving process. This paper employs the Logistic chaotic mapping to generate chaotic sequences, which possess extensive exploration capabilities in the solution space and can adaptively adjust the search behavior at different stages. The strategy demonstrates significant advantages in solving high-dimensional, multi-modal, and complex optimization problems. By introducing chaotic perturbations to alter the search trajectory of the algorithm, the adaptive chaotic strategy enhances the algorithm’s ability to locate the global optimal solution. The core of the adaptive chaotic strategy lies in utilizing the randomness and irregularity of chaotic sequences to boost the global search capability of optimization algorithms. Chaotic sequences are typically generated by the Logistic map, with the formula as follows:

xn+1=r⋅xn⋅(1−xn)(11)

When the control parameter r∈(3.57,4), the sequence exhibits fully developed chaotic behavior. These properties enable AC-ACO to traverse the solution space more extensively, which is especially beneficial in high-dimensional and dynamic environments like WSNs. Specifically, the chaotic sequence serves as a global stochastic disturbance that perturbs the pheromone update process:

τij(t+1)=(1−ρ)⋅τij(t)+Δτij+α⋅Chaos(xi)(12)

Here, τij(t) is the pheromone intensity on edge (i,j), ρ is the evaporation rate, Δτij is the pheromone deposit, α is the perturbation weight, and Chaos(xi) is the Logistic-derived chaotic term. This formulation allows the search trajectory to be influenced by global perturbations in addition to conventional local guidance (pheromone and heuristic values), thus improving the algorithm’s ability to escape local optima and discover high-quality clustering solutions.

The integration of chaotic perturbation is particularly well-suited to WSN clustering problems, where network topology and energy distribution evolve dynamically due to uneven node deployment and varying residual energy. Traditional ACO variants, such as elitist ACO, adaptive pheromone tuning, or hybrid ACO-PSO/GA models, often suffer from premature convergence, high parameter sensitivity, or computational inefficiency in such environments. In contrast, the proposed chaotic strategy provides a lightweight and self-adaptive mechanism that introduces sufficient exploration diversity without incurring significant computational overhead.

To further enhance the adaptivity and convergence efficiency of the algorithm, this study introduces a three-level optimization mechanism based on the iterative process:

1.   Dynamic Adjustment of the Basic Parameter ρ:

The pheromone evaporation coefficient ρ controls the rate at which pheromone trails decay. A linearly decreasing strategy is adopted to balance exploration in the early stage and exploitation in the later stage:

ρ(t)=ρmax−(tT)⋅(ρmax−ρmin)(13)

where t denotes the current iteration number, and T is the total number of iterations. ρmax and ρmin represent the upper and lower bounds of the evaporation coefficient, typically set to 0.9 and 0.1, respectively.

2.   Adaptive Adjustment of Heuristic Weight β:

The parameter β determines the influence of heuristic information (e.g., distance, energy efficiency) during path construction. An adaptive sigmoid-like transition function is employed to smoothly enhance its effect during the iterative process:

β(t)=βmin+(βmax−βmin)⋅(11+e−k⋅(t−T/2))(14)

This function ensures that heuristic guidance becomes more dominant as the algorithm progresses.

3.   Energy-Aware Chaotic Disturbance Adjustment Based on Total Network Energy Consumption Etotal:

The chaotic disturbance strength α is dynamically adjusted according to the total network energy consumption at iteration t:

α(t)=αmin+(αmax−αmin)⋅Etotal(t)−ElbEub−Elb(15)

where Eub and Elb denote the upper and lower bounds of energy consumption within the current iteration window. When Etotal exceeds a dynamic threshold, the chaotic disturbance is automatically intensified to explore new solution spaces.

This multi-level adjustment mechanism allows the algorithm to maintain exploratory flexibility in the early stage while gradually shifting toward heuristic-driven convergence, thus ensuring both stability and quality of the final solution.

In summary, the proposed adaptive chaotic strategy not only has a solid theoretical foundation but also demonstrates practical necessity in WSN clustering tasks. Compared to existing ACO variants, it effectively overcomes the limitations of local optima and insufficient exploration, while maintaining low computational cost, offering a promising and generalizable enhancement for clustering optimization in wireless sensor networks.

4.3 The Algorithm Flow of AC-ACO

In AC-ACO, the pheromone matrix is a core component that guides the path selection and cluster head election processes of the ants. To describe the algorithm flow more clearly, this section represents the pheromone matrix using a character function and elaborates on the algorithm flow of AC-ACO in detail. The iterative pseudocode is shown in Algorithm 1. The flowchart of AC-ACO is shown in Fig. 2.

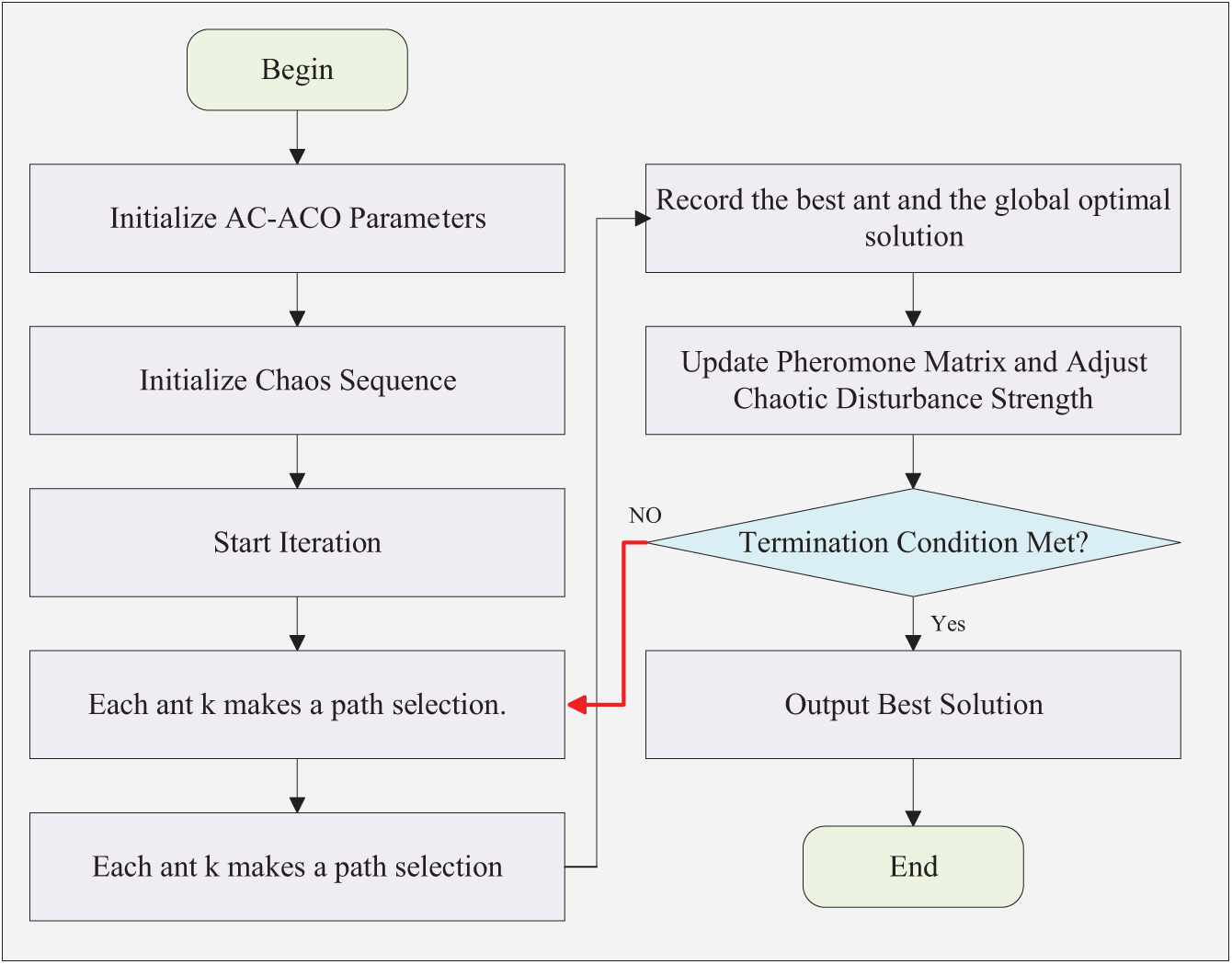
Figure 2: Flowchat of AC-ACO in WSNs

The pheromone matrix τ represents the pheromone concentration between nodes, where the element τij denotes the pheromone concentration from node i to node j. For ease of description, this paper uses the character function τ(i,j) to represent the elements of the pheromone matrix:

τ(i,j)=τij(16)

where i and j represent the indices of the nodes, i,j∈[1,s], and s is the total number of nodes in the WSNs. The specific algorithm flow can be described as the following steps:

Step 1: Initialization

Initialize the parameters of AC-ACO for WSN clustering, including the maximum number of iterations, the number of nodes, node positions, and initial energy. Initialize the pheromone concentration matrix to allow ants to randomly select paths in the early search stage, enhancing exploration capability:

τ(i,j)=τ0,     ∀i,j∈[1,s](17)

Initialize the heuristic function: Define the heuristic function η(i,j) to represent the heuristic information for node i selecting node j as the cluster head:

η(i,j)=Ejdist(i,j)(18)

where Ej is the residual energy of node j, and dist(i,j) is the distance between node i and node j. Normalization is applied to ensure the stability of heuristic information during the search process.

Chaos sequence initialization: Generate a chaotic sequence using the Logistic map:

xn+1=r⋅xn⋅(1−xn)(19)

where r is the control parameter, and the initial value is set according to optimization requirements.

Step 2: Ant Path Selection

Specifically, each ant selects the next node based on the pheromone concentration τ(i,j) and the heuristic function η(i,j). The selection probability P(i,j) is calculated using the following formula:

P(i,j)=[τ(i,j)]α⋅[η(i,j)]β⋅[1/Em(i,j)]γ∑k∈allowed[τ(i,k)]α⋅[η(i,k)]β⋅[1/Em(i,k)]γ(20)

where α, β, and γ are the weighting factors for pheromone, heuristic function, and energy consumption, respectively, and allowed represents the set of currently available candidate nodes. During the path selection process, the algorithm prioritizes nodes with higher residual energy, lower energy consumption, and shorter communication distances as the next-hop targets, thereby ensuring balanced energy consumption across the network.

To enhance the randomness and diversity of path selection, chaotic perturbation is introduced into the path selection process: P′(i,j)=P(i,j)+α⋅Chaos(xi), By adjusting the value of α, a balance between global exploration and local exploitation in path searching can be achieved.

Step 3: Pheromone Update

Global Pheromone Update: In the global pheromone update process, a chaotic disturbance term is added:

τ(i,j)=(1−ρ)⋅τ(i,j)+Δτ(i,j)+α⋅Chaos(xi).(21)

Step 4: Adaptive Adjustment Mechanism

In the AC-ACO algorithm, the adaptive adjustment mechanism is one of the key strategies to improve the search efficiency and stability of the algorithm. First, the intensity of the chaotic disturbance needs to be dynamically adjusted according to the optimization process. In the early stages of optimization, to enhance global exploration capabilities, a larger disturbance intensity is set, allowing the ants to explore the solution space more widely during path selection. As the optimization progresses and the algorithm begins to converge, the disturbance intensity should be reduced to promote more refined local search, thereby improving the quality of the final solution.

Additionally, the control parameter of the Logistic map, r, needs to be dynamically adjusted based on the iteration count and optimization objectives. By setting an adaptive function, the r value can change over time, allowing the algorithm to adapt to the search needs at different stages and improving optimization performance.

Step 5: Termination Condition and Output

The termination conditions of the AC-ACO algorithm mainly include two aspects: first, the algorithm reaches the preset maximum number of iterations; second, the optimization goal converges, meaning the change in the solution is smaller than the set error threshold, indicating that the search process has stabilized. To ensure the algorithm’s effectiveness, an error threshold can be set, and by monitoring the trend of the objective function during the optimization process, it can be determined whether to terminate the process early.

The specific process is shown in the Fig. 2. After the algorithm ends, the optimal cluster head node set and clustering results need to be output, along with an evaluation of key performance indicators such as network energy consumption, lifetime, and data transmission efficiency. Additionally, to further analyze the algorithm’s convergence trends and stability, multiple rounds of experiments can be conducted to observe the algorithm’s performance under different parameter settings and perform comparative analysis of the results.

4.4 Complexity Analysis of AC-ACO

The computational complexity of the AC-ACO algorithm primarily depends on three key components: path construction, fitness evaluation, and pheromone matrix updates. Let N denote the number of nodes in the network, M the number of ants, and Tmax the maximum number of iterations.

•   Path Construction: For each ant, constructing a path involves selecting a node based on the pheromone matrix and heuristic function. This operation has a complexity of O(N). Since there are M ants, the total complexity for path construction in each iteration is O(M⋅N).

•   Fitness Evaluation: Evaluating the fitness value of a path requires calculating the energy consumption, load balancing, and network lifespan metrics. Assuming each metric can be computed in O(N), the fitness evaluation for all ants in an iteration has a complexity of O(M⋅N).

•   Pheromone Matrix Update: Updating the pheromone matrix involves adjusting the pheromone values for all edges based on the paths of all ants. This operation has a complexity of O(M⋅N).

The complexity of LEACH-family protocols is given by:

LEACH=Tmax×N(22)

LEACH-C=Tmax×(N2)(23)

GA=Tmax×N×M(24)

PSO=Tmax×N×M(25)

Combining these components, the overall complexity of AC-ACO for Tmax iterations is O(Tmax⋅M⋅N). This demonstrates that AC-ACO maintains a polynomial-time complexity, making it computationally feasible for large-scale wireless sensor networks while achieving high optimization performance.

4.5 Convergence Analysis of AC-ACO

To establish the mathematical convergence of the AC-ACO algorithm, we employ a Markov chain framework to model the stochastic optimization process. Let 𝒮 denote the state space comprising all possible cluster configurations and pheromone distributions. The following theorem guarantees asymptotic convergence to the global optimal solution.

Theorem 1. For the AC-ACO algorithm defined in Algorithm 1, let ϕ∗ represent the pheromone matrix corresponding to the optimal cluster configuration. Under the conditions:

1.   The chaotic disturbance strength r satisfies limt→∞r(t)=0 with ∑t=1∞r(t)=∞

2.   The pheromone persistence factor ρ∈(0,1) ensures ∏t=1∞(1−ρ)t=0

then,

limt→∞P(ϕ(t)=ϕ∗)=1(26)

where P(⋅) denotes the probability measure over the Markov chain states.

Proof: Step 1: State Space Construction Define the Markov chain {ϕt}t≥0 where each state corresponds to a unique pheromone matrix configuration. The state transition incorporates both the ACO update rules and chaotic perturbations.

Step 2: Ergodicity Analysis The chaotic mapping operator Γ:Rn→Rn satisfies:

limN→∞1N∑k=1NΓk(x)=∫𝒳f(x)dμ(x)(27)

for almost all x∈𝒳, where μ is the ergodic measure. This ensures the exploration capability covers the entire solution space.

Step 3: Martingale Convergence Define the Lyapunov function V(t)=‖ϕ(t)−ϕ∗‖F2. The update rule ensures:

E[V(t+1)|Ft]≤(1−αt)V(t)+βt(28)

where ℱt is the filtration, αt=O(t−1/2), and βt represents chaotic perturbation bounded by r(t). The Robbins-Siegmund theorem guarantees limt→∞V(t)=0 almost surely.

Step 4: Absorption Probability As r(t)→0, the chaotic disturbance becomes negligible. The pheromone update rule converges to a stationary distribution concentrated on ϕ∗ due to the positive probability of selecting optimal paths through:

pijk(t)=[τij(t)]α[ηij]β∑l∈𝒩k[τil(t)]α[ηil]β(29)

where ηij incorporates energy and topology constraints. The global convergence follows from the first-visit lemma in stochastic approximation. □

Remark 1. The adaptive chaotic mechanism provides faster convergence than classical ACO by:

•   Accelerating exploration through ergodic chaotic perturbations in early iterations

•   Enhancing exploitation via diminishing chaotic noise in later phases

•   Maintaining diversity through nonlinear pheromone updates

Experimental validation in Section 5 confirms the theoretical results.

5  Experiments and Analysis

In this study, the effectiveness of the AC-ACO optimization algorithm in WSNs is comprehensively validated. To objectively assess its performance, the algorithm is compared with several classic clustering protocols, including ACO [41], PSO [28], GA [42], LEACH [43], and LEACH-C [44]. The experiments are conducted in rounds, with each round consisting of a TDMA-based data collection process and a data aggregation process completed by the cluster head nodes. The performance of the AC-ACO algorithm in terms of energy consumption, network lifetime, data transmission reliability, and communication delay is evaluated by systematically monitoring, recording, and analyzing the energy consumption balance and the failure time points of active nodes. The experiments are carried out on the MATLAB 2021a platform, with the running environment being a computer equipped with an Intel (R) Core (TM) i5-13500H CPU, 16GB of RAM, and running the Windows 11 operating system. To ensure the reliability and comparability of the experimental results, all the comparison algorithms are configured with consistent network parameters, including node density, initial energy distribution, packet size, and transmission power. Through this standardized experimental setup, the performance advantages of the AC-ACO algorithm in energy balance, network lifetime, and algorithm efficiency are accurately assessed, providing theoretical support for its deployment in practical applications. The detailed simulation parameters are given in Table 2.

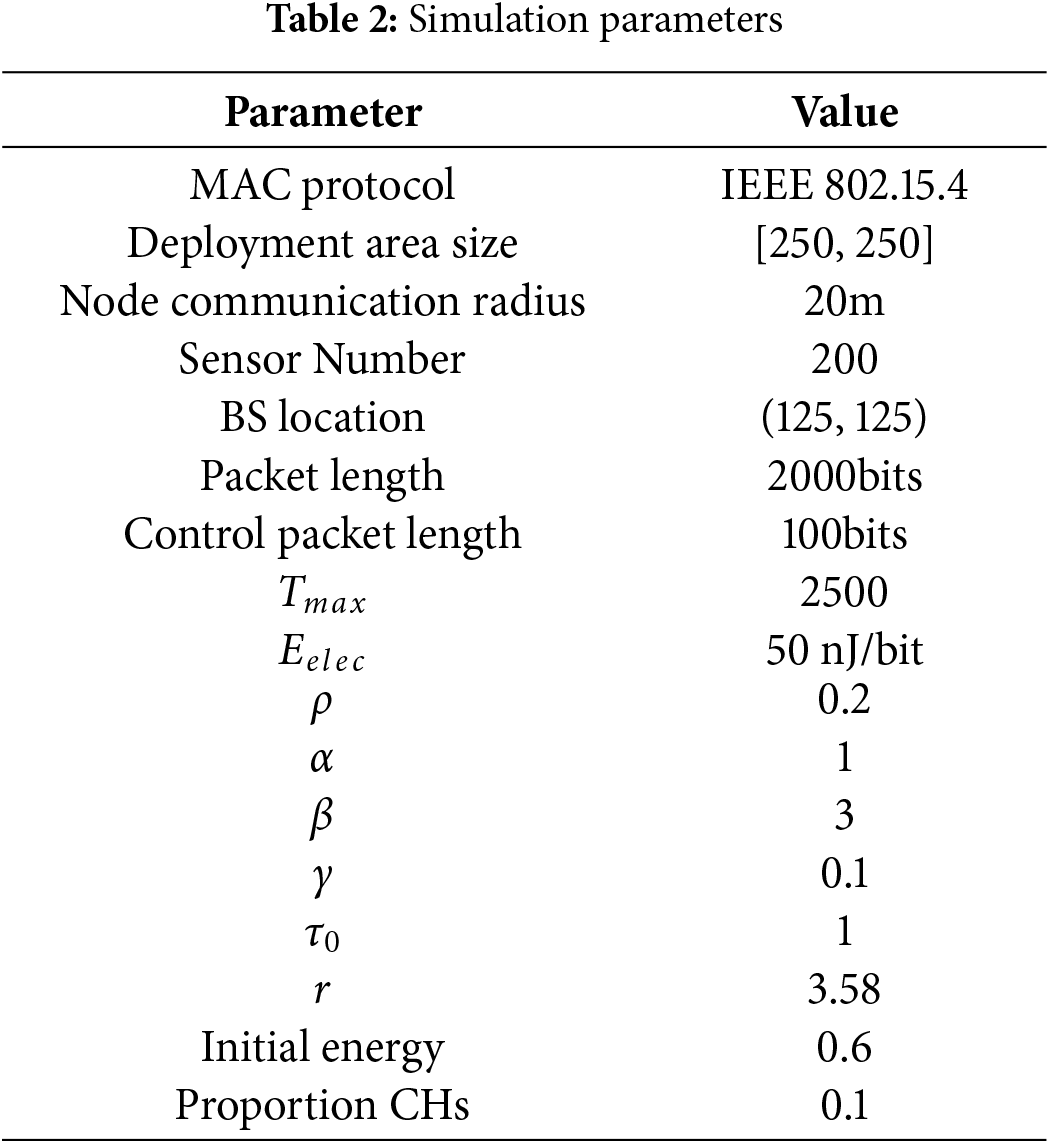
In this study, the simulation parameters are designed to replicate a realistic wireless sensor network environment and ensure the reliability and reproducibility of the experimental results. The network employs the IEEE 802.15.4 MAC protocol, with nodes deployed in a 250m×250m area and a communication radius of 50m. The total number of sensor nodes is set to 200, and the base station is located at the center of the area (125,125). The data packet length and control packet length are set to 2000bits and 100bits, respectively, to simulate real-world data transmission scenarios. For the algorithm parameters, the maximum number of iterations, Tmax, is set to 2500, and the electronic energy consumption, Eelec, is 50nJ/bit. The pheromone evaporation coefficient, ρ, is set to 0.2, while the pheromone importance factor, α, and the heuristic information factor, β, are set to 1 and 3, respectively. The chaos disturbance factor, γ, is 0.1, the initial pheromone concentration, τ0, is 1, and the chaos mapping parameter, r, is 3.58. Additionally, the initial energy of each node is set to 0.6J, and the proportion of cluster heads (Proportion CHs) is 0.1. These parameter settings are based on literature research and preliminary experimental tuning, aiming to balance the global search capability and local optimization ability of the algorithm while ensuring reasonable and efficient energy consumption distribution across the network. Through the above parameter configurations, this study comprehensively evaluates the performance of the algorithm under various network conditions.

5.1 Energy Efficiency

This study first compares and analyzes the energy consumption performance differences of the AC-ACO algorithm and several classical clustering protocols, including GA, ACO, PSO, LEACH, and LEACH-C, in WSNs. As shown in Fig. 3 and Table 3, the experimental results indicate that AC-ACO has significant advantages in data transmission path optimization and energy balancing. The algorithm can dynamically adjust the cluster head selection strategy and, by combining a chaotic disturbance mechanism, effectively reduces the overall energy consumption of the network. Through optimal path selection, AC-ACO reduces the number of unnecessary relay nodes during data forwarding while ensuring that energy-efficient nodes take on more forwarding tasks, thus significantly extending the network lifetime. In contrast, traditional optimization methods such as GA, ACO, and PSO fail to fully consider global energy balance in the path selection process, resulting in imbalanced energy consumption and rapid energy depletion of some nodes. Although LEACH and LEACH-C improve energy consumption distribution to some extent, their energy utilization rate remains low, leading to a shorter network lifetime.

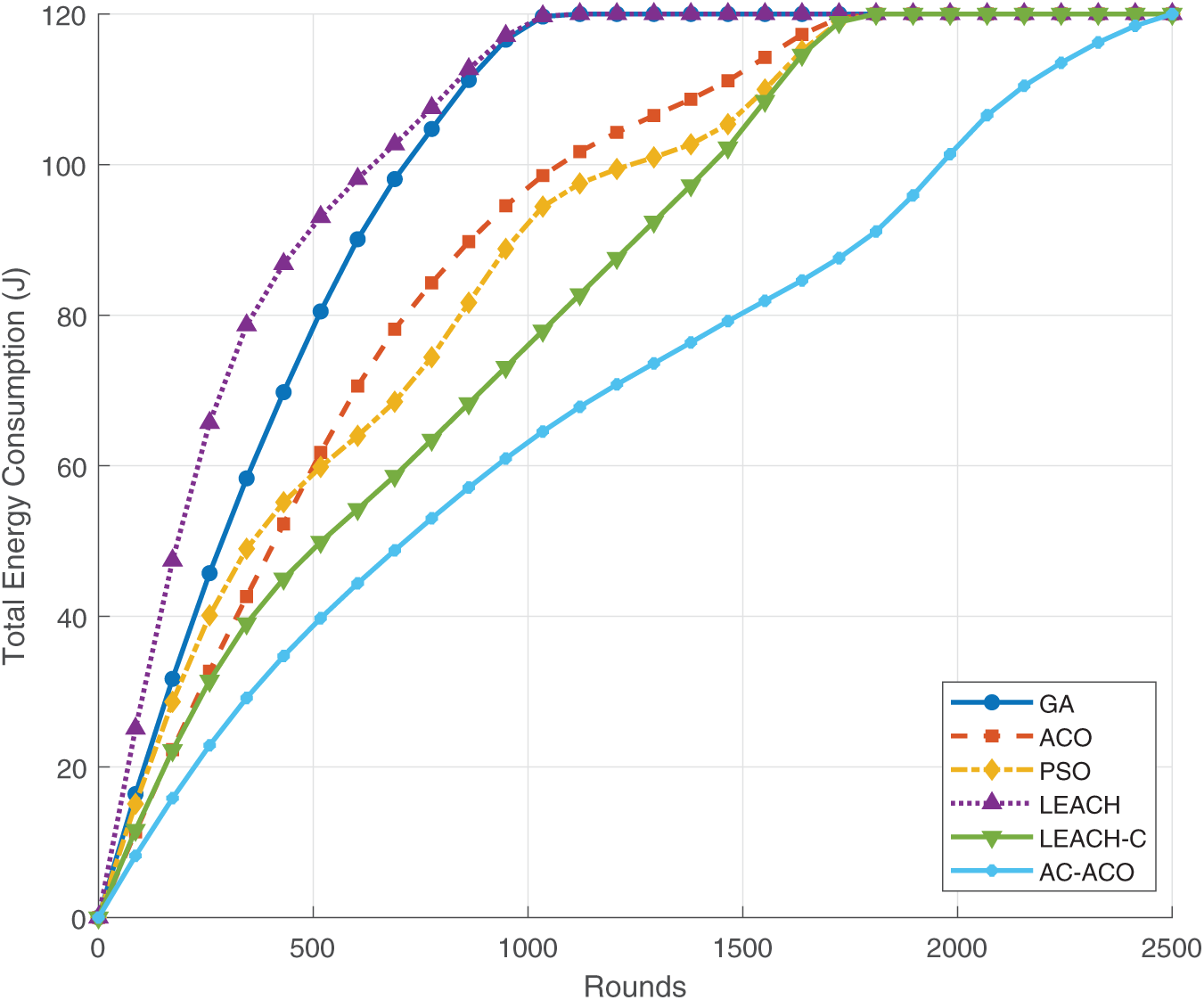
Figure 3: Total energy consumption of WSNs under different algorithms

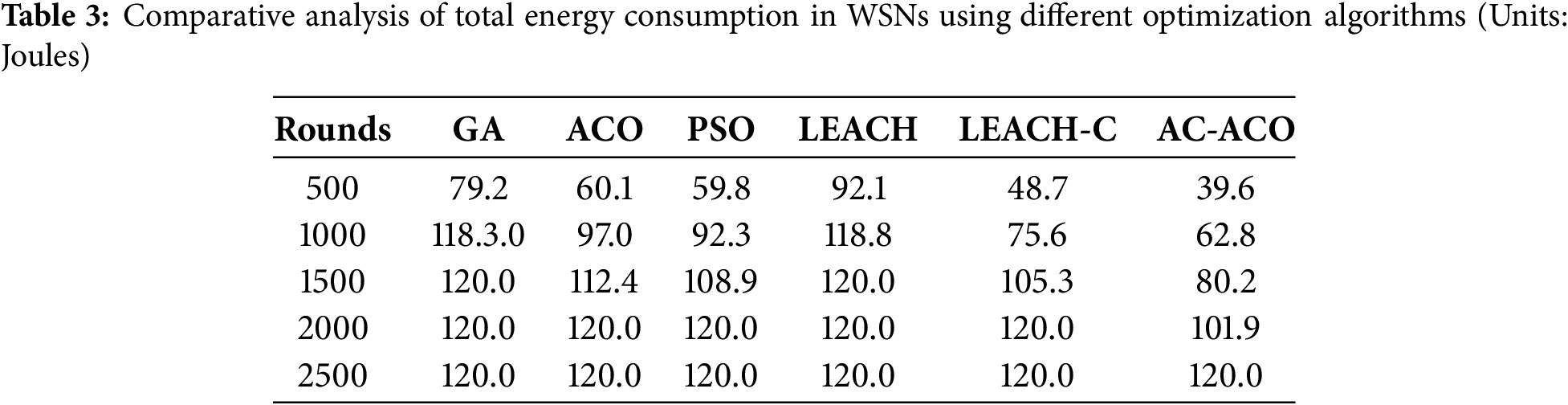
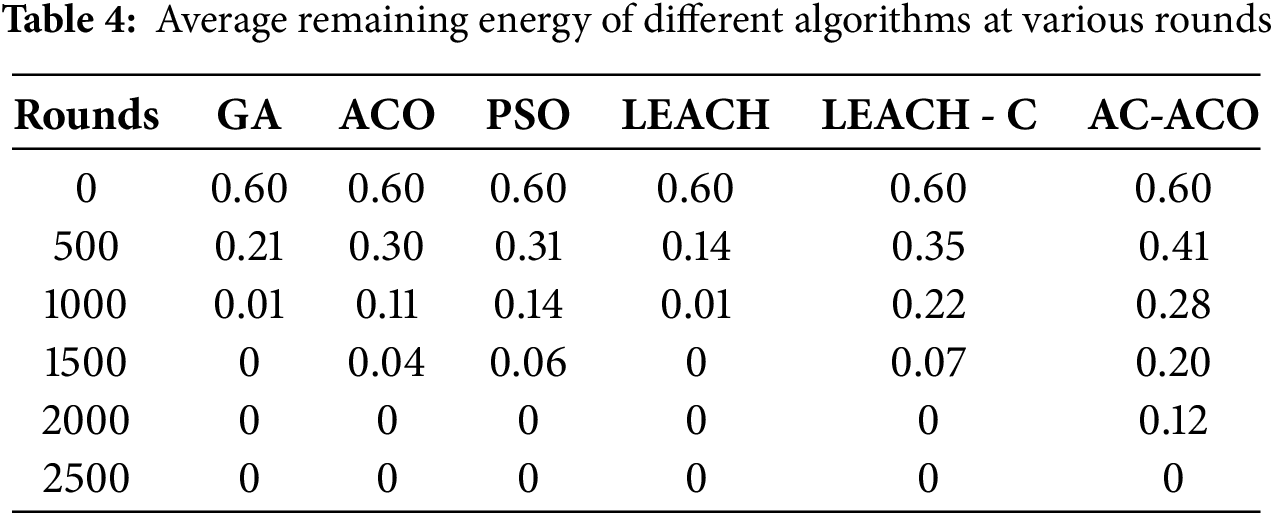
The experiments in Fig. 4 and Table 4 further confirm that as the number of network runs increases, although the average remaining energy of all algorithms shows a decreasing trend, the rate of decrease in the average remaining energy of AC-ACO is significantly lower than that of the comparative algorithms, fully reflecting its scalability and sustainability in large-scale WSN deployment.

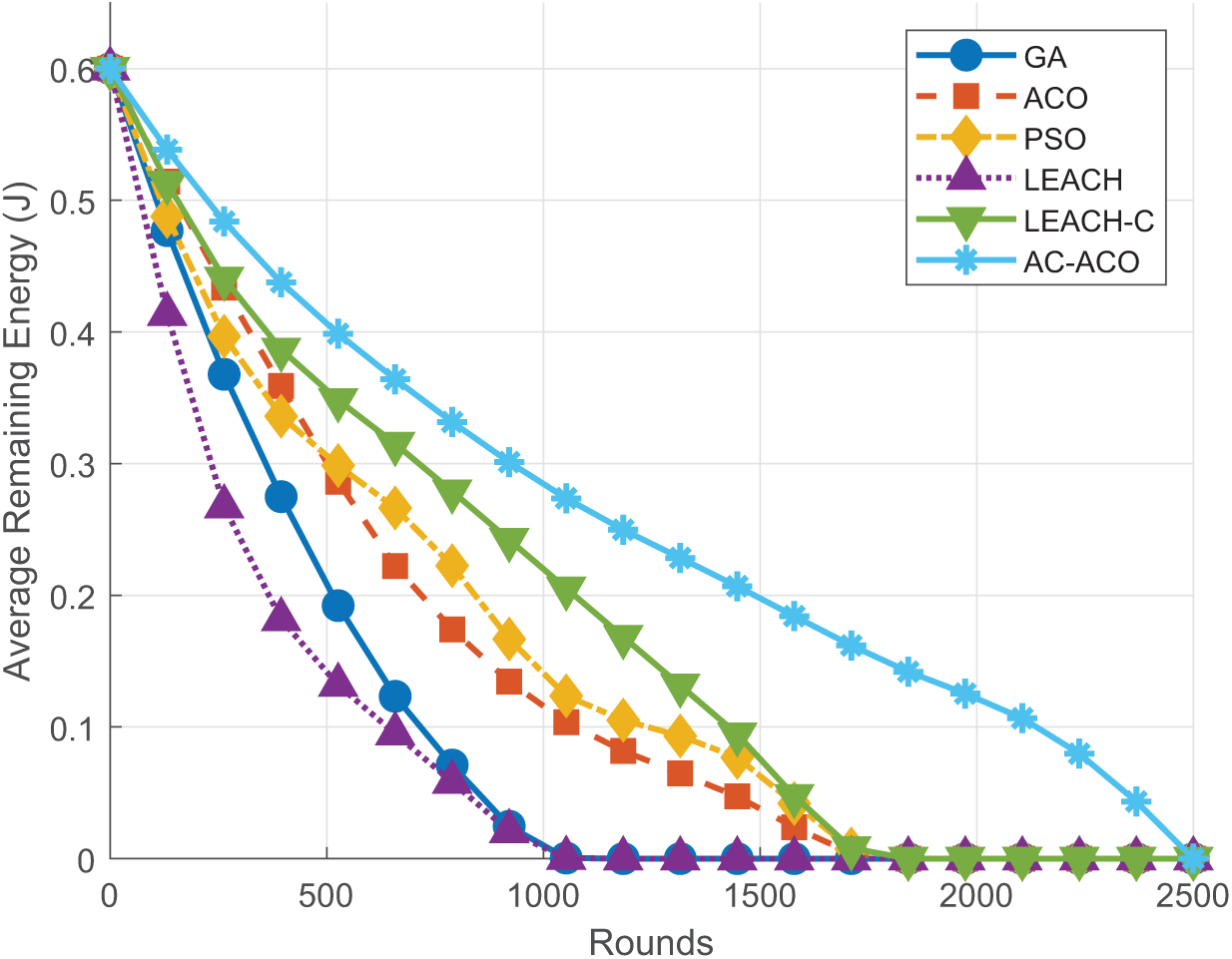
Figure 4: Average energy of WSNs nodes under different algorithms

5.2 Network Lifetime

In this experiment, we conducted a comparative analysis of the number of surviving nodes in WSNs under different clustering algorithms, as shown in Fig. 5 and Table 5. The AC-ACO algorithm performed the best, with the slowest decline in the number of surviving nodes, maintaining a high proportion even in the later iterations. This is attributed to its adaptive chaotic strategy, which dynamically adjusts parameters to enhance global search capabilities, combined with a precise node selection mechanism that activates only nodes with sufficient energy and optimal locations. This effectively balances energy consumption and extends the network lifespan. The LEACH-C algorithm performed second best, with a slower decline in the number of surviving nodes, showing stable performance during the mid-iterations. By optimizing energy distribution through centralized cluster head selection, it is suitable for medium-scale networks. However, its performance is slightly inferior to AC-ACO in large-scale networks, primarily due to its static cluster head selection mechanism, which cannot dynamically adapt to network changes.

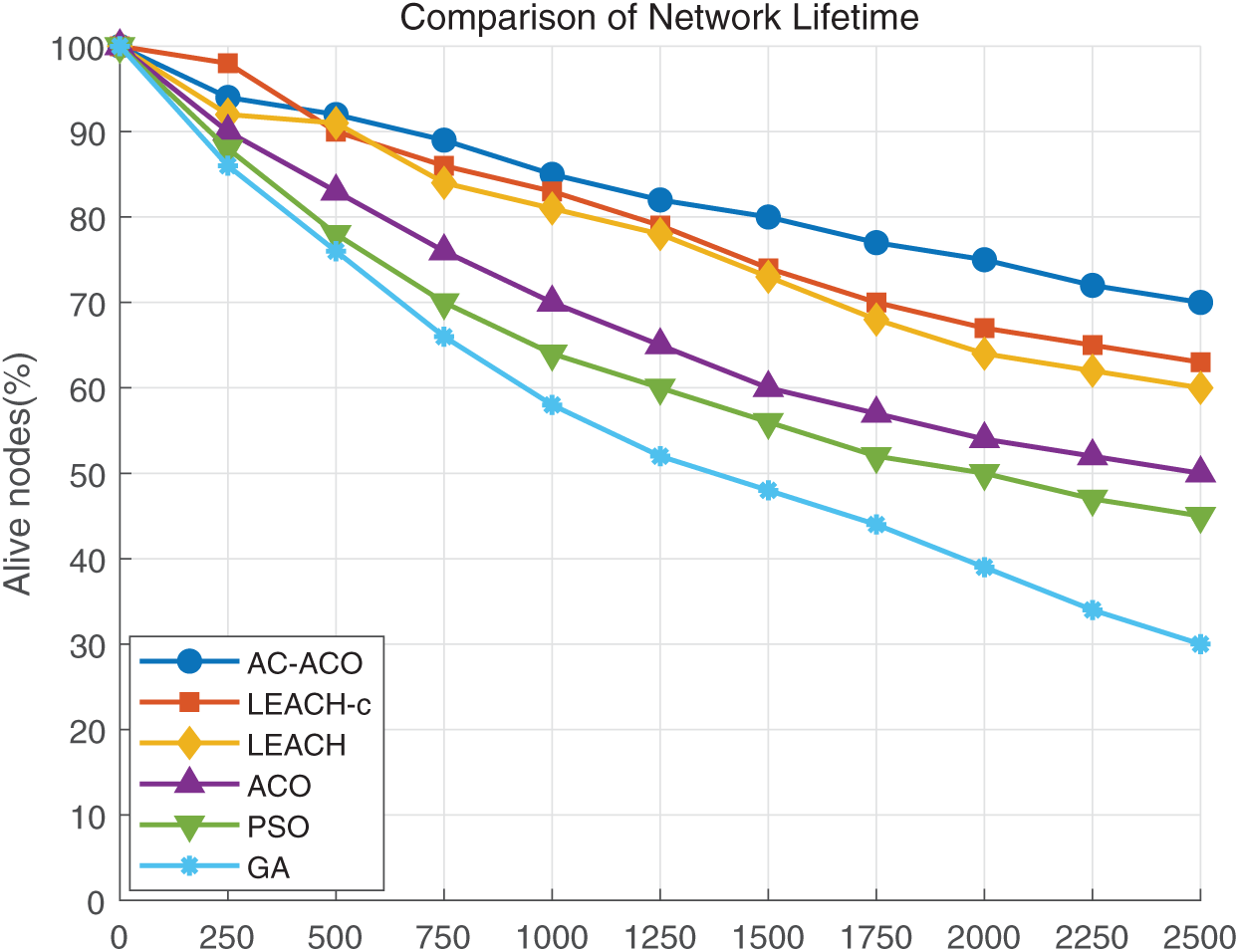
Figure 5: Comparison of surviving nodes under different algorithms

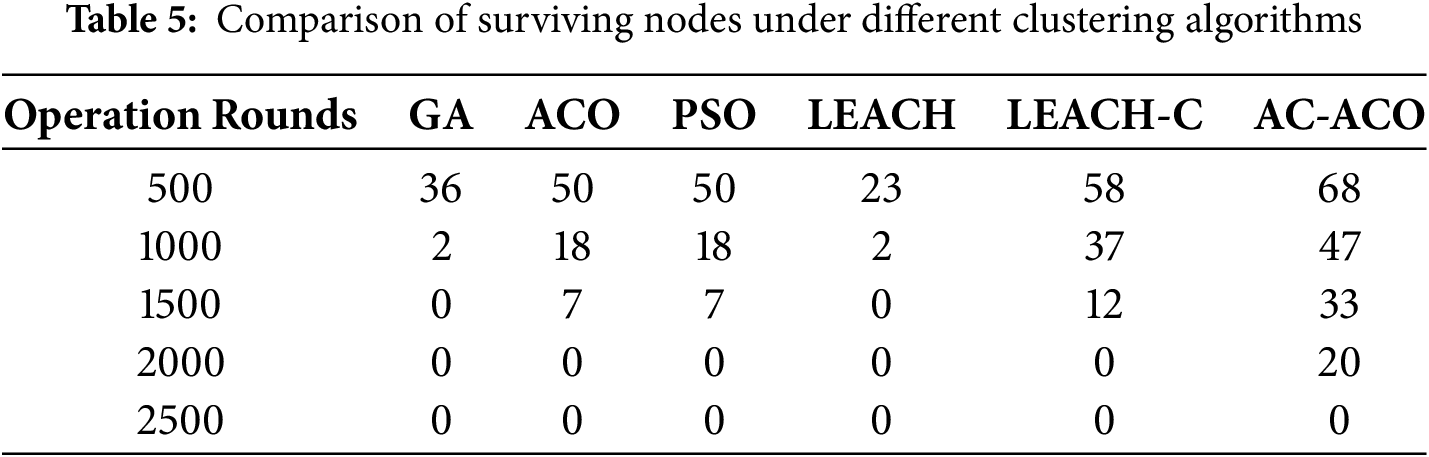
Traditional algorithms such as LEACH, ACO, PSO, and GA performed poorly. LEACH, due to its lack of global energy optimization, leads to premature failure of some nodes, resulting in a sharp decline in the number of surviving nodes in the later stages. ACO and PSO, while optimizing paths and cluster head selection, are prone to falling into local optima, causing energy consumption imbalances and a noticeable decline in the number of surviving nodes during the mid-iterations. GA performed the worst, as its high computational complexity and tendency to fall into local optima result in inefficient energy management.

5.3 Data Transmission Reliability

The AC-ACO algorithm demonstrates significant advantages in data delivery rate (DDR). The specific performance of the algorithm is shown in Fig. 6. Under ideal unidirectional communication conditions, the algorithm maximizes the successful transmission rate of data packets through its adaptive chaotic strategy and precise path optimization. Compared to LEACH, ACO, PSO, and GA, under the same node configuration, AC-ACO can deliver more data packets to the specified target, maintaining a high data delivery rate even in the later iterations. The LEACH-C algorithm performs second best, optimizing data transmission paths through centralized cluster head selection, making it suitable for medium-scale networks, though its performance is slightly inferior to AC-ACO in large-scale networks. In contrast, traditional algorithms such as LEACH, ACO, PSO, and GA exhibit lower data delivery rates, with significant declines in the later iterations, primarily due to their lack of global optimization and dynamic adaptability. Overall, the AC-ACO algorithm excels in ensuring reliable network communication, particularly in resource-constrained wireless sensor network environments, showcasing its efficient data transmission capabilities. Future research could combine the strengths of AC-ACO and LEACH-C to further optimize data transmission algorithms and enhance network performance.

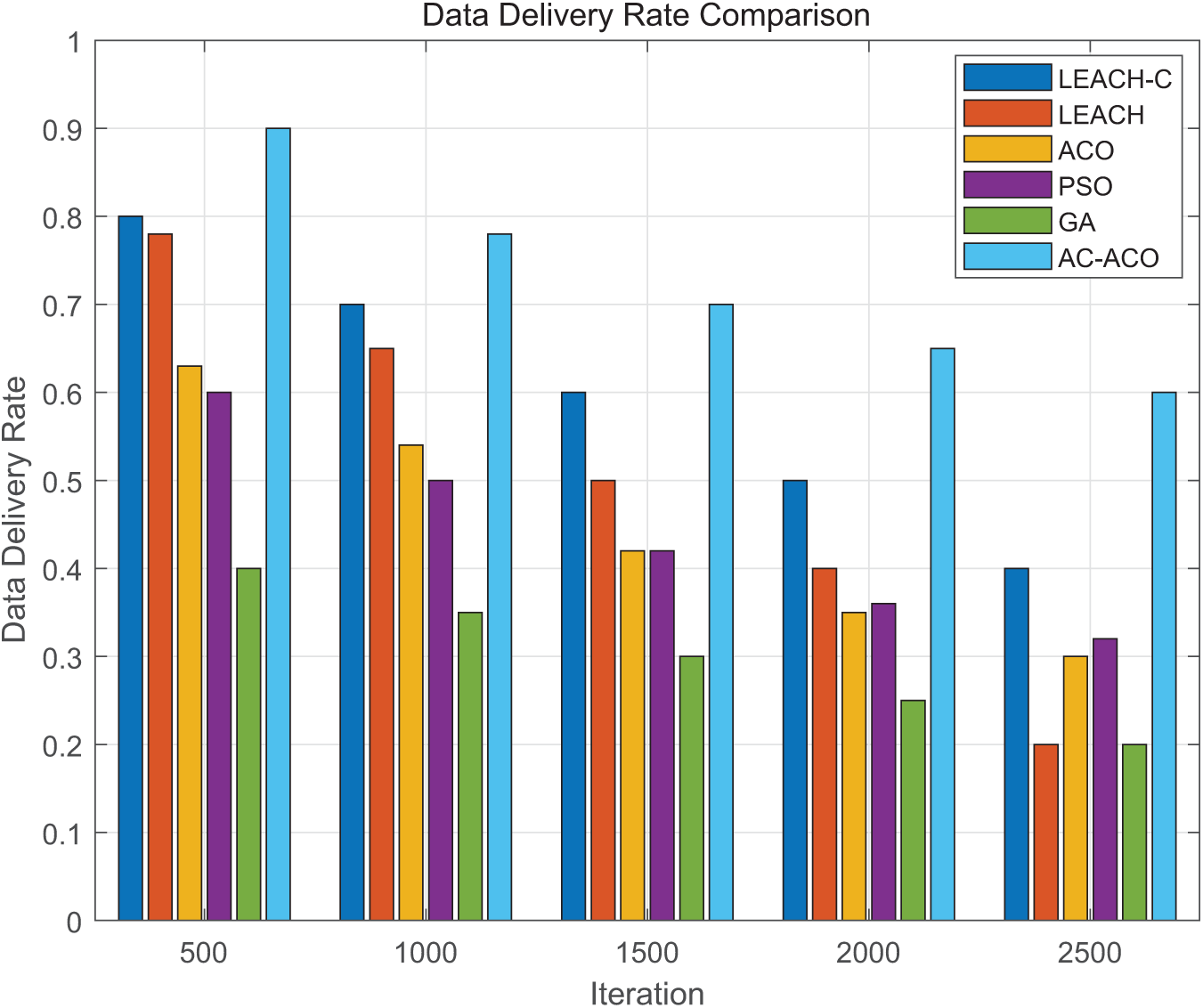
Figure 6: Comparison of data delivery rate under different algorithms

6  Conclusion

This paper proposes an efficient clustering algorithm based on Adaptive Chaotic Ant Colony Optimization (AC-ACO), aiming to address critical issues such as low energy efficiency and short network lifetime in WSNs. By integrating the global search capability of Ant Colony Optimization (ACO) with the dynamic perturbation characteristics of chaotic mapping, AC-ACO achieves significant innovations in cluster head selection, pheromone update, and path optimization. Experimental results demonstrate that, compared to classical algorithms such as LEACH, PSO, GA, and ACO, AC-ACO exhibits superior performance in key metrics including network lifetime, energy efficiency, data transmission reliability, and communication delay. Specifically, in a 250 m × 250 m monitoring area, AC-ACO extends the network lifetime while reducing end-to-end communication delay, significantly improving the energy consumption balance in large-scale WSNs.

The core contributions of this study are as follows: (1) An efficient clustering algorithm (AC-ACO) is designed, which combines chaotic perturbation to optimize the pheromone update strategy, effectively achieving a multi-objective trade-off among energy consumption, load balancing, and network lifetime. (2) An adaptive chaotic strategy based on Logistic mapping is proposed, which dynamically adjusts the perturbation intensity to balance global exploration and local exploitation capabilities. (3) A chaotic-driven intra-cluster data aggregation method is developed, reducing redundant data transmission and lowering communication overhead. These innovations provide theoretical support and technical guarantees for the application of WSNs in complex and dynamic environments.

However, the computational complexity of AC-ACO in ultra-large-scale heterogeneous networks still requires further optimization. Future research will focus on the following directions: (1) Integrating deep reinforcement learning techniques to enhance the algorithm’s real-time response capability to dynamic topologies. (2) Exploring a distributed chaotic optimization framework to reduce the resource consumption of centralized computing. (3) Extending AC-ACO to multi-objective optimization scenarios to simultaneously optimize energy consumption, security, and service quality. This study provides a new solution for the long-term stable deployment of WSNs in fields such as smart cities and industrial IoT, with significant theoretical value and engineering application prospects.

Acknowledgement: We would like to thank all the authors for their contributions to this work. We are also grateful to the corresponding author for the financial support.

Funding Statement: The research was funded by the Natural Science Foundation of Xinjiang Uygur Autonomous Region: No. 22D01B148; Bidding Topics for the Center for Integration of Education and Production and Development of New Business in 2024: No. 2024-KYJD05; Basic Scientific Research Business Fee Project of Colleges and Universities in Autonomous Region: No. XJEDU2025P126; Xinjiang College of Science & Technology School-level Scientific Research Fund Project: No. 2024-KYTD01.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Peng Zhou, Bingyu Cao; methodology and software: Peng Zhou, Wei Chen; validation, formal analysis, and investigation: Peng Zhou, Bingyu Cao; resources and project administration: Bingyu Cao; data curation and visualization: Peng Zhou; original draft preparation: Wei Chen; review and editing: Peng Zhou, Bingyu Cao. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The raw data supporting the conclusions of this article will be made available by the authors on request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Hada RPS, Srivastava A. Dynamic cluster head selection in WSN. ACM Trans Embed Comput Syst. 2024;23(4):64–27. doi:10.1145/3665867. [Google Scholar] [CrossRef]

2. Biradar M, Mathapathi B. Reliability, and trust-based security framework for clustering-based routing model in WSN. Int J Inf Secur Priv. 2023;17(1):1–18. doi:10.4018/IJISP.315817. [Google Scholar] [CrossRef]

3. Abdulzahra AMK, Al-Qurabat AKM, Abdulzahra SA. Optimizing energy consumption in WSN-based IoT using unequal clustering and sleep scheduling methods. Internet Things. 2023;22(1):100765. doi:10.1016/j.iot.2023.100765. [Google Scholar] [CrossRef]

4. Kanimozhi T, Umarani S. A comparative study of energy-efficient clustering protocols for WSN-Internet-of-Things. Int J Hydromech. 2023;6(2):177–96. doi:10.1504/IJHM.2023.130521. [Google Scholar] [CrossRef]

5. Krishnan N, Raja K, Divakaran S. Maximization of WSN Based IoT systems lifetime by minimized intra-cluster transmission distance clustering protocol. Inform Technol Control. 2023;52(1):140–54. doi:10.5755/j01.itc.52.1.32199. [Google Scholar] [CrossRef]

6. Rekha, Garg R. K-LionER: meta-heuristic approach for energy efficient cluster based routing for WSN-assisted IoT networks. Cluster Comput. 2024;27(4):4207–21. doi:10.1007/s10586-024-04280-2. [Google Scholar] [CrossRef]

7. Mertens JS, Galluccio L, Morabito G. I-WSN league: clustered distributed learning in wireless sensor networks. IEEE Internet of Things J. 2023;10(20):17920–33. doi:10.1109/JIOT.2023.3280843. [Google Scholar] [CrossRef]

8. Guo X, Ye Y, Li L, Wu R, Sun X. WSN clustering routing algorithm combining sine cosine algorithm and levy mutation. IEEE Access. 2023;11(8):22654–63. doi:10.1109/ACCESS.2023.3252027. [Google Scholar] [CrossRef]

9. Mir F, Meziane F. Unequal-radius clustering in WSN-based IoT networks: energy optimization and load balancing in UDCOPA protocol. J Supercomput. 2024;80(19):26890–921. doi:10.1007/s11227-024-06426-w. [Google Scholar] [CrossRef]

10. Prasad KHV, Sasikumar P. Energy-efficient quad tree-based clustering using edge-assisted UAV-relay to enhance network lifetime in WSN. Sci Rep. 2024;14(1):17160. doi:10.1038/s41598-024-68085-4. [Google Scholar] [PubMed] [CrossRef]

11. Kalimuthu VK, Srinivasan B. Multi-objective sand piper optimization based clustering with multihop routing technique for IoT assisted WSN. Braz Arch Biol Technol. 2023;66(8):e23220866. doi:10.1590/1678-4324-2023220866. [Google Scholar] [CrossRef]

12. Prasad KHV, Periyasamy S. Secure-energy efficient bio-inspired clustering and deep learning-based routing using blockchain for edge assisted WSN environment. IEEE Access. 2023;11:145421–40. doi:10.1109/ACCESS.2023.3345218. [Google Scholar] [CrossRef]

13. Janaki RS, Nagarajan V. Optimized scheme for cluster head selection and EAMPR routing protocol design in WSN. J Intell Fuzzy Syst. 2023;45(4):7113–27. doi:10.3233/JIFS-231342. [Google Scholar] [CrossRef]

14. Rani KP, Sreedevi P, Poornima E, Sri TS. FTOR-Mod PSO: a fault tolerance and an optimal relay node selection algorithm for wireless sensor networks using modified PSO. Knowl Based Syst. 2023;272(1):110583. doi:10.1016/j.knosys.2023.110583. [Google Scholar] [CrossRef]

15. Yoon C, Cho S, Lee Y. Extending WSN lifetime with enhanced LEACH protocol in autonomous vehicle using improved K-Means and advanced cluster configuration algorithms. Appl Sci. 2024;14(24):11720. doi:10.3390/app142411720. [Google Scholar] [CrossRef]

16. Sinha A, Aljrees T, Pandey SK, Kumar A, Banerjee P, Kumar B, et al. Semi-supervised clustering-based DANA algorithm for data gathering and disease detection in healthcare wireless sensor networks (WSN). Sensors. 2024;24(1):18. doi:10.3390/s24010018. [Google Scholar] [PubMed] [CrossRef]

17. Osamy W, Khedr AM, Elsawy AA, Raj P, Aziz A. SEACDSC: secure and energy-aware clustering based on discrete sand cat swarm optimization for IoT-enabled WSN applications. Wirel Netw. 2024;30(4):2781–800. doi:10.1007/s11276-024-03682-9. [Google Scholar] [CrossRef]

18. Kumar RP, Prabakaran MP, Arumugam D, Selvakumar J. A novel hybridization of ML algorithms for cluster head selection in WSN. Infocommun J. 2024;16(2):33–42. doi:10.36244/ICJ.2024.2.5. [Google Scholar] [CrossRef]

19. Srivastava A, Paulus R. ELR-C: a multi-objective optimization for joint energy and lifetime aware cluster based routing for WSN assisted IoT. Wireless Pers Commun. 2023;132(2):979–1006. doi:10.1007/s11277-023-10645-4. [Google Scholar] [CrossRef]

20. Selvi MS, Kumar CR, Rani SJ. A cluster-based routing in WSN for smart city applications using neural networks. J Intell Fuzzy Syst. 2023;44(6):9363–77. doi:10.3233/JIFS-222615. [Google Scholar] [CrossRef]

21. Sangeetha K, Shanthini J, Karthik S. ECAR: energy efficient cluster based adaptive routing for large scale WSN. J Intell Fuzzy Syst. 2023;45(5):7811–25. doi:10.3233/JIFS-233445. [Google Scholar] [CrossRef]

22. Anguraj DK, Mythrayee D, Shiny XSA. An enhanced lifespan of WSN using hybrid fuzzy-machine learning-based clustering process. Wireless Personal Commun. 2024;139(3):1637–57. doi:10.1007/s11277-024-11682-3. [Google Scholar] [CrossRef]

23. Juwaied A, Jackowska-Strumillo L. Improving performance of cluster heads selection in DEC protocol Using K-means algorithm for WSN. Sensors. 2024;24(19):6303. doi:10.3390/s24196303. [Google Scholar] [PubMed] [CrossRef]

24. Ahmad I, Hussain T, Shah B, Hussain A, Ali I, Ali F. Accelerated particle swarm optimization algorithm for efficient cluster head selection in WSN. Comput Mater Contin. 2024;79(3):3585–629. doi:10.32604/cmc.2024.050596. [Google Scholar] [CrossRef]

25. Shinde NK, Patil VH. Secured and energy efficient cluster based routing in WSN via hybrid optimization model. TICOA Sustain Comput-Inform Syst. 2024;44(8):101052. doi:10.1016/j.suscom.2024.101052. [Google Scholar] [CrossRef]

26. Jeevanantham S, Venkatesan C, Rebekka B. Distributed neuro-fuzzy routing for energy-efficient IoT smart city applications in WSN. Telecommun Syst. 2024;87(2):497–516. doi:10.1007/s11235-024-01195-6. [Google Scholar] [CrossRef]

27. Lekhraj, Kumar A, Kumar A. Load balanced and optimal clustering in WSNs using grey wolf optimizer. Int J Syst Assuran Eng Manage. 2024;15(7):2950–64. doi:10.1007/s13198-024-02306-x. [Google Scholar] [CrossRef]

28. Prakash V, Singh D, Pandey S, Singh S, Singh PK. Energy-optimization route and cluster head selection using M-PSO and GA in wireless sensor networks. Wirel Pers Commun. 2024;107(2):1289. doi:10.1007/s11277-024-11096-1. [Google Scholar] [CrossRef]

29. Ramalingam S, Dhanasekaran S, Sinnasamy SS, Salau AO, Alagarsamy M. Performance enhancement of efficient clustering and routing protocol for wireless sensor networks using improved elephant herd optimization algorithm. Wirel Netw. 2024;30(3):1773–89. doi:10.1007/s11276-023-03617-w. [Google Scholar] [CrossRef]

30. Rao AK, Nagwanshi KK, Shukla MK. An optimized secure cluster-based routing protocol for IoT-based WSN structures in smart agriculture with blockchain-based integrity checking. Peer Peer Netw Appl. 2024;17(5):3159–81. doi:10.1007/s12083-024-01748-1. [Google Scholar] [CrossRef]

31. Heinzelman WB, Chandrakasan AP, Balakrishnan H. An application-specific protocol architecture for wireless microsensor networks. IEEE Trans Wirel Commun. 2002;1(4):660–70. doi:10.1109/TWC.2002.804190. [Google Scholar] [CrossRef]

32. Tadros CN, Shehata N, Mokhtar B. Unsupervised learning-based WSN clustering for efficient environmental pollution monitoring. Sensors. 2023;23(12):5733. doi:10.3390/s23125733. [Google Scholar] [PubMed] [CrossRef]

33. Nisha UN, Manikandan A, Venkataramanan C, Dhanapal R. A score based link delay aware routing protocol to improve energy optimization in wireless sensor network. J Eng Res. 2023;11(4):404–13. doi:10.1016/j.jer.2023.100115. [Google Scholar] [CrossRef]

34. Zhou J, Zhang Z, Zhong Q, Li J. A semifixed clustering routing protocol based on improved ACO algorithm for WSNs. IEEE Sens J. 2024;24(21):34664–75. doi:10.1109/JSEN.2024.3416961. [Google Scholar] [CrossRef]

35. Stodola P, Nohel J. Adaptive ant colony optimization with node clustering for the multidepot vehicle routing problem. IEEE Trans Evol Comput. 2023;27(6):1866–80. doi:10.1109/TEVC.2022.3230042. [Google Scholar] [CrossRef]

36. Yesodha K, Krishnamurthy M, Thangaramya K, Kannan A. Elliptic curve encryption-based energy-efficient secured ACO routing protocol for wireless sensor networks. J Supercomput. 2024;80(13):18866–99. doi:10.1007/s11227-024-06235-1. [Google Scholar] [CrossRef]

37. Mishra R, Yadav RKK. Energy efficient cluster-based routing protocol for WSN using nature inspired algorithm. Wirel Pers Commun. 2023;130(4):2407–40. doi:10.1007/s11277-023-10385-5. [Google Scholar] [CrossRef]

38. Sivakumar D, Devi SS, Nalini T. Energy aware clustering protocol using chaotic gorilla troops optimization algorithm for Wireless Sensor Networks. Multimed Tools Appl. 2024;83(8):23853–71. doi:10.1007/s11042-023-16487-3. [Google Scholar] [CrossRef]

39. El-Hageen HM, Alfaifi YH, Albalawi H, Alzahmi A, Alatwi AM, Ali AF, et al. Chaotic zebra optimization algorithm for increasing the lifetime of wireless sensor network. J Netw Syst Manage. 2024;32(4):85. doi:10.1007/s10922-024-09860-6. [Google Scholar] [CrossRef]

40. Elashry SS, Abohamama AS, Abdul-Kader HM, Rashad MZ, Ali AF. A chaotic reptile search algorithm for energy consumption optimization in wireless sensor networks. IEEE Access. 2024;12(3):38999–9015. doi:10.1109/ACCESS.2024.3374781. [Google Scholar] [CrossRef]

41. Kumar NA, Sukhi Y, Preetha M, Sivakumar K. Ant colony optimization with levy-based unequal clustering and routing (ACO-UCR) technique for wireless sensor networks. J Circ Syst Comput. 2024;33(3):2450043. doi:10.1142/S0218126624500439. [Google Scholar] [CrossRef]

42. Zhao G, Meng X. Routing in wireless sensor networks using clustering through combining whale optimization algorithm and genetic algorithm. Int J Commun Syst. 2025;38(3):e6099. doi:10.1002/dac.6099. [Google Scholar] [CrossRef]

43. Paszkiewicz A, Cwikla C, Bolanowski M, Ganzha M, Paprzycki M, Hodon M. Multifunctional clustering based on the LEACH algorithm for edge-cloud continuum ecosystem. Bull Polish Acad Sci Tech Sci. 2023;71(6):e147919. doi:10.24425/bpasts.2023.147919. [Google Scholar] [CrossRef]

44. Navarrete CES, Soto PA, Firoozabadi AD. Maximizing nodes’ service lives in wireless sensor networks: an innovative application of the P-median optimization problem to the leach-C protocol. INGE CUC. 2024;20(1):171–83. doi:10.17981/ingecuc.20.1.2024.09. [Google Scholar] [CrossRef]