Neighbor Dual-Consistency Constrained Attribute-Graph Clustering^#

1  Introduction

Attribute-graph clustering has emerged as a critical area of research in recent years, spurred by the increasing availability of graph-structured data across diverse domains, including social networks, biological networks, and recommendation systems. The primary aim of graph clustering is to partition the nodes of a graph into distinct groups based on their inherent similarities. Recent advances in Graph Neural Networks (GNNs) [2,3] have significantly improved clustering performance in this field.

GNNs utilize both node features and graph connectivity to learn representations that capture complex relationships among samples. The foundational encoder of the current graph clustering method is typically a GNN, which is based on the homophily assumption [4]. Bo et al. [5] proposed a dual self-supervision mechanism that integrates the auto-encoder and the graph auto-encoder into a unified framework. He et al. [6] further utilized the attention-mechanism to fuse the data representations of AE and GAE. By propagating information through the graph structure, GNN-based approaches can effectively leverage local attribute information while simultaneously accounting for global structural patterns.

However, a notable limitation of these graph clustering methods is their inadequate consideration of neighbor information during the clustering process. Traditional graph clustering techniques often rely solely on node attributes or topological structures, neglecting the rich contextual information provided by neighboring nodes. This oversight can lead to suboptimal clustering results, as the relationships between nodes and their neighbors are critical for accurately identifying community structures within the graph.

The homophily assumption of the networks suggests that connected nodes often belong to the same class. Neighboring nodes often exhibit similar characteristics and structural roles, and leveraging this neighbor information allows more comprehensive graph structure information to be mined. Moreover, incorporating neighbor information can enhance the robustness and accuracy of clustering by leveraging the collective properties of neighboring nodes to reinforce cluster boundaries and improve the overall clustering coherence. Hence, it is essential to develop a novel graph clustering framework that can fully leverage neighbor information to overcome these limitations and achieve more accurate clustering results.

Motivated by this observation, we propose a graph clustering framework that emphasizes neighbor dual-consistency by leveraging information from neighboring nodes in two critical dimensions: neighbor feature consistency and neighbor distribution consistency. Specifically, we first construct a dual-branch network for feature learning to integrate sample features with the graph structure. To enhance feature consistency among nodes and their neighbors, we design a neighbor contrastive learning loss where each node and its neighboring nodes across the two branches are treated as positive samples while other non-neighboring nodes are considered negative samples. Additionally, to ensure consistent cluster assignments between nodes and their neighbors, we introduce a neighbor distribution consistency strategy that combines structural information from the graph with attribute similarity to align cluster assignments effectively. By integrating both local structural information and global attribute data, our approach captures comprehensive patterns within the graph. The experimental results verify the effectiveness of the proposed model and the ablation experiments test the importance of each component.

The main contributions of this paper can be primarily summarized in three key aspects:

•   We design a feature learning module which integrates graph structure information into node representations and alleviates the over-smoothing problem of GNN by supplementing AE information layer-by-layer.

•   We introduce a neighbor feature consistency module leveraging a contrastive loss based on a dual-branch network to enhance feature consistency among nodes and their neighbors, which helps the model better capture local feature information.

•   We introduce a neighbor distribution consistency module to ensure consistent cluster assignments between nodes and their neighbors, effectively combining local structural information and global attribute information.

The rest of this paper is structured as follows. Section 2 provides a concise review of related works in the field of graph clustering model. In Section 3, we present an elaborate description of the proposed neighbor-based graph clustering model. In Section 4, the experimental results are reported and analyzed in detail. Finally, the main contributions are concluded in Section 5.

2  Related Work

In this section, we review several related works about deep graph clustering and contrastive graph clustering.

2.1 Deep Graph Clustering

Kipf and Welling [7] pioneered the integration of variational auto-encoders into the graph domain, combining graph structure with node attributes through a graph convolutional encoder and an inner product decoder. Pan et al. [8] proposed an adversarially regularized framework based on Graph Auto-Encoders (GAE), which ensures that the latent representation aligns with a prior distribution. Wang et al. [9] introduced a graph attention auto-encoder framework designed to unify structural and attribute information in a goal-directed manner. Park et al. [10] developed a symmetric graph convolutional auto-encoder utilizing Laplacian sharpening. Zhang et al. [11] proposed an adaptive graph convolution method to capture clustering information and dynamically determine the order for different graphs.

More recently, Bo et al. [5] unified Auto-Encoders (AE) and Graph Convolutional Networks (GCN) through a delivery operator and a dual self-supervised mechanism. Tu et al. [12] introduced an information fusion module to integrate structural and attribute information, coupled with a triplet self-supervision strategy to generate target distributions. Cheng et al. [13] exploited graph neural network for multi-view attribute graph clustering to map graph embedding features and learn view-consistency information. Xia et al. [14] used the clustering labels to guide the network learning and connect clustering and representation learning seamlessly to improve clustering performance. He et al. [6] further utilized the attention-mechanism to fuse the data representations of AE and GAE. In addition, there are currently some research efforts focusing on semi-supervised graph clustering [15].

2.2 Contrastive Graph Clustering

Recent advances in contrastive learning have demonstrated its effectiveness in learning discriminative representations by maximizing agreement among similar samples while minimizing agreement among dissimilar ones. This paradigm leverages meaningful relationships between samples to derive supervisory signals, leading to more robust representations.

Several studies have applied contrastive learning to graph-structured data. Hassani and Ahmadi [16] introduced a self-supervised approach for learning node and graph-level representations by contrasting different structural views of graphs. Liu et al. [17] utilized contrastive learning to improve topological alignment through a self-enhanced learning objective, optimizing graph structures in the process. To mitigate sampling bias, Zhao et al. [18] developed a debiasing contrastive framework that jointly performs representation learning and clustering.

Further refinements have focused on sample selection strategies. Park et al. [19] proposed a multi-level framework that carefully selects positive and negative samples to capture hierarchical community structures and network homophily. Xia et al. [20] introduced a self-consistent contrastive loss based on imprecise clustering labels to enhance node representation quality. More recently, Liu et al. [21] designed a neighbor-oriented contrastive loss to strengthen the discriminative power of graph neural networks. Xu et al. [22] presented a global and local topology-aware contrastive graph clustering network for attributed graph clustering. Liu et al. [23] proposed a novel contrastive-learning-based method termed IDCRN to solve the representation collapse problem in the existing deep graph clustering methods.

Although these contrastive learning-based methods have shown promising results in graph clustering, they still have limitations in fully capturing neighbor information and integrating it with attribute and structure information for more comprehensive clustering.

3  The Proposed Model

In this section, we propose a novel neighbor dual-consistency constrained attribute-graph clustering model. The architecture flowchart is shown in Fig. 1. The proposed model comprises three principal components:

•   The Feature Learning Module (FL) considers both attribute and structural information by employing attribute auto-encoder, graph auto-encoder.

•   The Neighbor Feature Consistency Module (NF) maximizes the similarity between the target node and its neighbors so as to enhance their feature consistency.

•   The Neighbor Distribution Consistency Module (ND) maximizes the similarity of distribution between the target node and its neighbors considering both structure and attribute information to ensure consistent cluster assignment of them.

Figure 1: The framework of the proposed neighbor consistency constrained graph clustering. It contains three main modules: Feature learning module, Neighbor feature consistency module, Neighbor distribution consistency module. Among Neighbor distribution consistency module, the inconsistency matrix S measures how inconsistent a node’s clustering assignment is with respect to its neighbors. And the combined similarity matrix A⊙(Y+R) integrates the graph structure and attribute similarities

3.1 Notations and Preliminaries

Before introducing the proposed model, it is essential to define some necessary symbols. Given a set of samples X∈RN×F, the corresponding undirected graph G={V,E} is constructed, where V=∈RN×F and E respectively represent the node set and the edge set. Here, N and F mean the number of samples and the feature dimension. In the context of the undirected graph G, we build the adjacency matrix A∈RN×N, where aij=1 if there exists a connection between the i-th and j-th nodes; otherwise, aij=0. The corresponding degree matrix is D=diag(d1,d2,⋯,dN)∈RN×N, where di=∑vj∈𝒩viaij and 𝒩vi denotes the neighbors of node vi. The normalized adjacency matrix A~∈RN×N is formulated by D−12(A+I)D−12, where I∈RN×N is the identity matrix.

3.2 Feature Learning Module

To comprehensively capture both structural and attribute information, we build a dual-branch network for feature learning. This network comprises a text encoder and a graph encoder, working in tandem to mitigate the over-smoothing issue commonly associated with graph neural network by supplementing text encoder information layer-by-layer.

3.2.1 Attribute Encoder

We first exploit a full-connected auto-encoder ΦT(⋅) to extract the node attribute information hi(l) as follows,

hi(l)=ΦT(hi(l−1);θT),(1)

where the input data of the initial layer is hi(0)=xi and the network parameter is θT.

To preserve the original feature information in the latent representations as much as possible, we establish a reconstruction loss Lre as follows,

Lre=12N‖X^−X‖F2,(2)

where the corresponding reconstructed representation of the i-th sample is x^i=hi(L).

3.2.2 Graph Encoder

To effectively harness the graph structure information, we integrate the feature data hi(l−1) derived from the attribute encoder with the structural data zi(l−1) progressively layer-by-layer as follows,

fi(l)=ϵhi(l)+(1−ϵ)zi(l−1),(3)

where ϵ balances the importance between feature information and structural information. Besides, zi(0)=ΦG(xi;θG).

Then, the latent representation of the (l−1)-th graph encoder layer is,

zi(l)=ΦG(fi(l);θG),(4)

where ΦG and θG respectively denote the graph auto-encoder and the corresponding network parameters.

Similarly, a graph decoder is designed to reconstruct the graph data z^i=zi(L) to preserve the structure information as much as possible,

Lrge=12N‖A~X−Z^‖F2.(5)

In conclusion, the objective function of the feature learning module can be summarized as follows,

Lfl=Lre+αLrge,(6)

where α is a weight parameter.

3.3 Neighbor Feature Consistency Module

It is well known that the characteristics of a target node should be similar to those of its neighbors, due to the inherent homophilic nature of the graph. To take advantage of this property, we propose a neighbor contrastive learning module which aims to ensure that the feature distributions of target nodes and their neighbors remain consistent, improving the quality of node embeddings learned by the model.

Specifically, for the target node in the attribute encoder branch, we treat its neighboring nodes, the corresponding nodes, and the neighbors in the graph encoder branch as positive samples, while treating nodes that are not directly connected to the target node as negative samples. That is, the number of positive pairs should be (2|𝒩i|+1), where 𝒩i is the number of neighbors of vi. The contrastive learning framework aims to maximize the similarity between the target node and its positive samples, while simultaneously minimizing the similarity to negative samples, formulated as,

ℓ(hi)=−log⁡(eθ(hi,zi)/τ+∑vj∈𝒩i(eθ(hi,hj)/τ+eθ(hi,zj)/τ))/(2|𝒩i|+1)eθ(hi,zi)/τ+∑j≠i(eθ(hi,hj)/τ+eθ(hi,zj)/τ)(7)

where τ is a temperature parameter, and θ denotes a similarity measure, and here we use inner product.

Since two branches are symmetric, for the target node in the grapg encoder branch, the neighbor contrastive loss ℓ(zi) can be similarly defined accrding to Eq. (7). The final neighbor contrastive loss is formulated as,

Lnf=ℓ(H,Z)=12N∑i=1N[ℓ(hi)+ℓ(zi)](8)

By enforcing this contrastive learning objective, we promote feature consistency between the target node and its neighbors in both attribute and graph encoder representations. This strategy effectively leverages the graph structure to improve the robustness and quality of node embeddings, leading to better generalization in downstream tasks.

3.4 Neighbor Distribution Consistency Module

Based on the homophily assumption, which posits that connected nodes often belong to the same class, we introduce a neighbor distribution consistency module to enforce alignment between the distributions of target nodes and their neighbors. By constraining the neighbor distributions to be consistent, we effectively exploit the local structure of the data, thereby enhancing the robustness of our model against noise and ensuring that similar instances exhibit coherent behavior.

To facilitate this alignment, we first perform K-means on the compact representations h(L) learned from AE to generate initial cluster centroids {μf}f=1k and obtain an initial distribution Q. Student’s t-distribution serves as the kernel function to measure the similarity between the i-th learned data representation hi and the f-th cluster centroid μf. The probability qif that assigns the i-th sample to the f-th cluster is expressed as,

qif=(1+‖hi−μf‖2)−1∑k(1+‖hi−μk‖2)−1.(9)

Then we normalize Q to enhance numerical stability and distinguishable,

Uif=exp⁡(Qif)∑fexp⁡(Qif)(10)

After obtaining U, we would like to improve the consistency of cluster assignment between the target node and its neighbors through U,

ℒnd=minUTr(UTS)−12Tr(UT(A⊙(Y+R))U)+φ2‖U‖F2.(11)

In the first term of ℒnd, the matrix S is an n×k matrix, where n is the number of nodes in the graph and k is the number of clusters. Each element Sif of S represents the inconsistency of node vi with respect to cluster Cf based on its neighbors’ clustering assignments. Specifically, Sif is computed as,

Sif=∑j=1n∑g=1,g≠fkAijUjg,(12)

which accumulates the membership values of node vi’s neighbors to clusters other than Cf, thus quantifying the inconsistency of node vi with respect to cluster Cf. By minimizing this term, the model is encouraged to reduce the inconsistency through penalizing nodes that have inconsistent clustering assignments compared to their neighbors.

In the second term, the element-wise multiplication A⊙(Y+R) serves as a crucial component to integrate both the structural connectivity of the graph and the attribute similarities between nodes. Here, A denotes the adjacency matrix of the graph, capturing the direct connections between nodes. The matrix Y is a universal matrix, often set as the identity matrix, which provides a baseline structural importance for each node. Meanwhile, R represents the attribute similarity matrix, where each element Rij=sim(xi,xj) measures similarity between vi and vj in terms of their attribute information. By summing Y and R, we obtain a matrix that combines the inherent structural importance and attribute similarities of nodes. The element-wise multiplication with A ensures that this combined importance is only considered between nodes that are directly connected in the graph. This operation effectively highlights the significance of both structural and attribute-based relationships between neighboring nodes, making it a powerful tool for guiding the optimization process in our clustering model.

The regularization term (controlled by hyperparameter φ) prevents overfitting by constraining the Frobenius norm of U.

Collectively, these components work together to foster cohesive neighborhood distributions around target nodes considering both local structure information and global attribute information.

3.5 The Overall Objective Function

Upon finalizing the primary network architecture, we develop the self-supervised clustering loss to enhance the reliability of the guidance provided to the clustering network.

To achieve a target distribution that emphasizes data points assigned with high confidence, we square and normalize the element qij with matrix Q, thereby deriving the target distribution P as outlined below,

pij=qij2/fj∑cqic2/fc,(13)

where fj=∑iqij denotes the soft cluster frequency, which takes the sum for each column of Q.

Then, we minimize the Kullback-Leibler divergence loss between distributions Q and P, ensuring that the soft distribution Q aligns with the target distribution P,

Lpq=KL(P∥Q)=∑i=1N∑j=1Kpijlog⁡(pijqij).(14)

Similarly, we learn the final cluster assignment C from the latent representations Z(L) learned by the graph encoder, then minimizing the KL divergence between P and C as follows,

Lpc=KL(P∥C)=∑i=1N∑j=1Kpijlog⁡(pijcij).(15)

In summary, the overall loss function of the proposed module is summarized as,

L=Lfl+λ1Lnf+λ2Lnd+λ3Lpq+λ4Lpc,(16)

where λ1, λ2, λ3 and λ4 balance the importance of different modules.

The whole optimization process is summarized in Algorithm 1.

3.6 The Complexity Computation

The major time-consuming burdens of the proposed method lie in four major modules:

•   In the feature learning module, the time complexity of the attribute encoder is 𝒪(N(d1d2+d2d3+⋯+dL−1dL)), and the time complexity of the graph encoder is 𝒪(N2d1+Nd1d2+Nd2d3+⋯+dL−1dL)) due to the use of sparse matrix multiplication;

•   In the neighbor feature consistency module, the time complexity is 𝒪(N(|N|+1)dL) due to the similarity calculation, where |N| is the average number of neighbors per node;

Overall, the aggregated complexity of the proposed method is about 𝒪(N∑i=1Ldidi+1+N2d1+NdL).

4  Experiments

4.1 Experiment Setup

4.1.1 Datasets

We assess the effectiveness of the proposed model across three prominent graph datasets. The statistical details of the three datasets employed are presented in Table 1.

•   ACM1 is a paper network dataset collecting papers published in KDD, SIGMOD, SIGCOMM, MobiCOMM, which is divided into three classes: database, wireless communication and data mining. A heterogeneous graph is constructed, which comprises 3025 papers, 5835 authors and 56 subjects.

•   DBLP [24] is an author network dataset that contains 4058 authors and is divided into four classes: database, data mining, machine learning and information retrieval.

•   CITE2 is a citation network dataset that contains 3327 articles and is divided into six categories: agents, artificial intelligence, database, information retrieval, machine language and HCI.

4.1.2 Baseline Methods

Seven classic graph clustering methods are chosen as comparison method.

•   K-means [25]: A traditional clustering method directly implements the clustering task on the raw data.

•   AE [26]: An auto-encoder-based clustering method performs K-means on the latent representation learned from an AE module.

•   IDEC [27]: An auto-encoder-based clustering method combines the clustering loss with the AE loss for the better representation learning.

•   GAE [7]: An unsupervised GCN-based clustering method replaces the decoder of AE with a graph decoder to learn the data representation.

•   DAEGC [9]: A GCN-based clustering method adds a graph attention network for the data representation learning and adds a clustering loss to supervise the clustering process.

•   SDCN [5]: A hybrid clustering method transfers the data representation learned by auto-encoder layers to corresponding GCN layers, and designs a dual self-supervised mechanism to integrate two sub-networks into a unified framework.

•   CaEGCN [28]: A hybrid clustering method uses attention-mechanism to fuse the data representations of AE and GAE.

•   ICCSM [1]: A hybrid clustering method designs information correlation co-supervision loss to supervise the correlation of node representations learned by AE and GAE.

4.1.3 Implementation and Detail Settings

For the proposed model, we set the dimension of attribute encoder and graph encoder parts to F−500−500−2000−10, where F is the dimension of input data. Besides, we set the hyper-parameters λ1, λ2, λ3 and λ4 of the CITE dataset to {0.001,10,0.1,0.01}, respectively, and set other datasets to {0.001,0.001,0.1,0.01}. We train the proposed model with 300 epochs for all datasets. Finally, the learning rate is set to 10−3 for ACM and DBLP, and 10−4 for CITE. For other compared methods, we set the parameter following the setting in the original papers.

All experiments are conducted within the PyTorch 2.3.1 and CUDA 12.0 environment, utilizing a workstation equipped with an NVIDIA vGPU and an 12 vCPU Intel Xeon Platinum 8352V CPU. The code is available: https://github.com/tiantianbjut (accessed on 23 July 2025).

4.1.4 Evaluation Metrics

We evaluate the clustering performance by four commonly-used metrics: Accuracy (ACC), Normalized Mutual Information (NMI), Average Rand Index (ARI) and macro F1 score (F1). For each metric, the higher scores signify better clustering performance.

4.2 Analysis of Clustering Results

Table 2 summarizes the clustering performance results of all methods on three datasets. According to these results, we have the following analysis:

•   The proposed model significantly improves the clustering performance compared with other methods. This enhancement verifies that it is necessary to restrict the consistency of neighbor characteristics and distribution. Specifically, constraining neighbor feature consistency ensures that connected nodes are represented closely in the embedding space, thereby enhancing local feature coherence and improving the model’s ability to capture fine-grained patterns within the graph. Meanwhile, enforcing neighbor distribution consistency aligns the cluster assignments of neighboring nodes, leveraging the graph’s structural information to produce more coherent and meaningful clusterings that reflect the inherent organization of the data.

•   Both AE-based and GCN-based clustering methods demonstrate suboptimal performance compared to hybrid clustering methods. This is because these methods consider only attribute information or structure information individually, rather than integrating both.

•   Compared with other hybrid clustering methods, our proposed model takes the neighbor information into account and captures comprehensive patterns within the graph, which effectively improves the clustering performance.

4.3 Analysis of Ablation Experiment

The proposed model performance relies on two key modules, i.e., neighbor contrastive learning module and neighbor distribution consistency module. To assess the effectiveness of these modules, we conduct a set of ablation experiments to test the effectiveness of these two modules. The experimental results are presented in Table 3. These experiments help isolate the contribution of each module to the overall model performance, providing insights into their respective impacts on clustering performance.

•   In the ablation study, BL (Baseline) represents the core setup, which includes a feature learning module combined with a self-supervised clustering mechanism.

•   NF is the neighbor feature consistency module.

•   ND is the neighbor distribution consistency module.

Observing the experimental results, we note that BL+NF+ND performs higher than others, indicating the effectiveness of the proposed components. We analyze these components from the following three aspects:

•   BL+NF obtains considerable improvements compared to BL. This outcome demonstrates that the NF module effectively captures local structure of the graph, ensuring that nodes with similar features are grouped together, which is essential for accurate clustering.

•   BL+ND shows significant improvement compared to BL. By aligning the cluster assignments of neighboring nodes, the ND module effectively captures the global structure of the graph, leading to more meaningful and accurate cluster assignments.

•   BL+NF+ND reaches the highest performance on all evaluation metrics, because these modules provide a comprehensive approach to graph clustering, leveraging both local feature information and global attribute and structural information to achieve superior performance.

4.4 Analysis of Hyper-Parameters

The hyper-parameters λ1,λ2,λ3 and λ4 are designed to balance the influence of different loss components in Eq. (16). We use grid search to evaluate their effects. Specifically, we methodically adjust a single hyper-parameter within the set {0.001,0.01,0.1,1,10} on DBLP, while maintaining the remaining three hyper-parameters at their fixed values. As shown in Fig. 2, the proposed model achieves the best clustering performance when {λ1,λ2,λ3,λ4} = {0.001,0.001,0.1,0.01}.

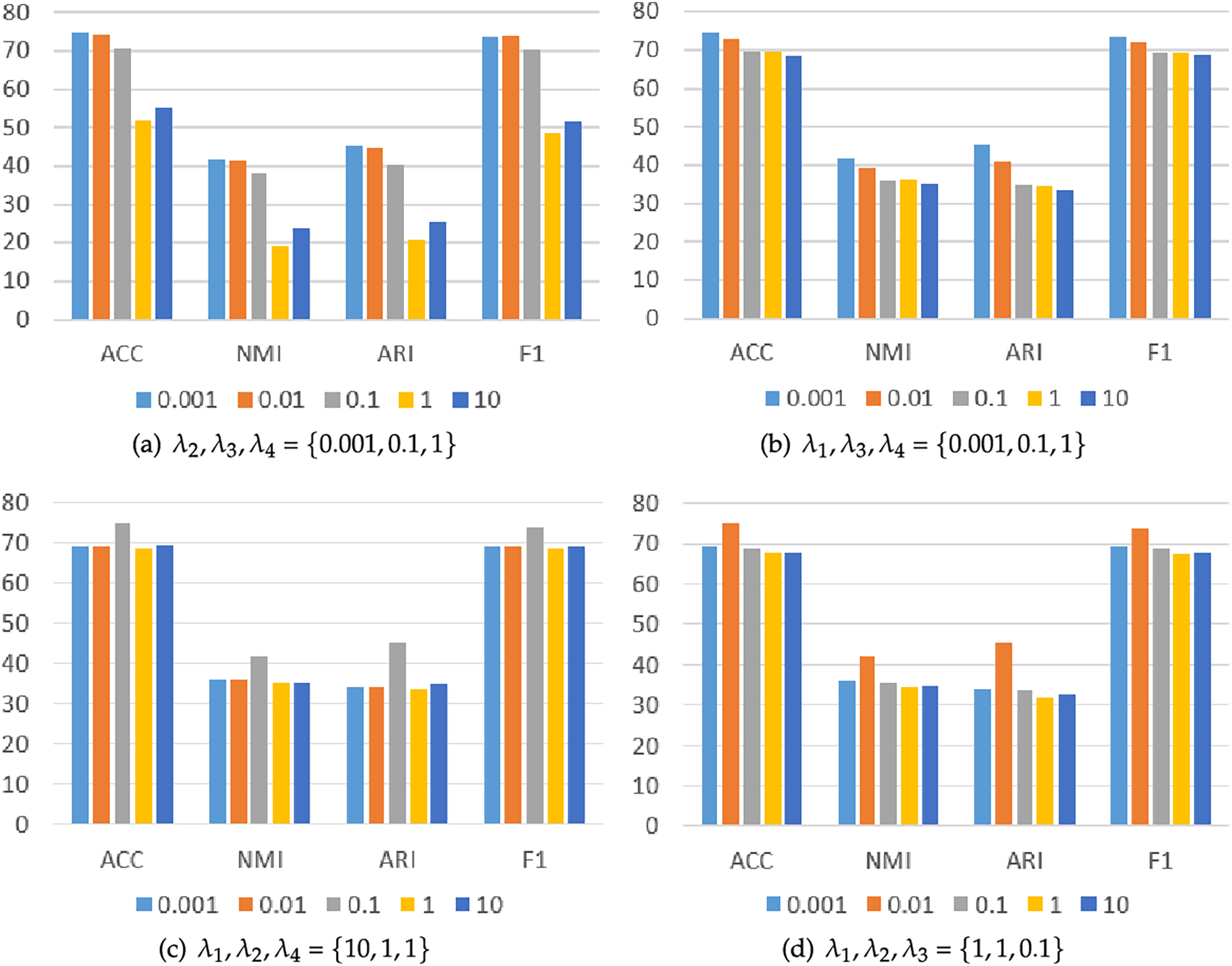
Figure 2: Clustering performance with different λ1,λ2,λ3,λ4 in the domain {0.001,0.01,0.1,1,10} on subCora, respectively

5  Conclusion

In this paper, we propose a novel neighbor dual-consistency constrained attribute-graph clustering model that consists of a feature learning module, a neighbor feature consistency module and a neighbor distribution consistency module. The feature learning module extracts the origin feature representations considering both attribute and structure information. The neighbor feature consistency module effectively leverages a contrastive loss to enhance feature consistency among nodes and their neighbors. The neighbor distribution consistency module ensures consistent cluster assignments between nodes and their neighbor. The experiment results on three public datasets verify the effectiveness of the proposed model. In addition, the ablation experiment and parameter analysis comprehensively prove the superiority of the proposed model.

Acknowledgement: Not applicable.

Funding Statement: The research project is supported by National Natural Science Foundation of China (Nos. 62272015, 62441232).

Author Contributions: The authors confirmed contribution to the paper as follows: study conception and design: Tian Tian and Boyue Wang; code and experiment: Tian Tian and Xiaxia He; draft manuscript preparation: Tian Tian, Xiaxia He, Wentong Wang, and Meng Wang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets used in this paper can be requested from the authors.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

1https://dl.acm.org/ (accessed on 23 July 2025).

2https://csxstatic.ist.psu.edu/downloads/data (accessed on 23 July 2025).

References

1. Tian T, He X, Wang B, Li X, Hu Y. Information correlation co-supervision based graph convolutional clustering model. In: 2023 42nd Chinese Control Conference (CCC); 2023 Jul 24–26; Tianjin, China. p. 7657–62. doi:10.23919/CCC58697.2023.10240220. [Google Scholar] [CrossRef]

2. Hamilton WL, Ying Z, Leskovec J. Inductive representation learning on large graphs. Adv Neural Inf Process Syst. 2017;30. [Google Scholar]

3. Kipf T, Welling M. Semi-supervised classification with graph convolutional networks. In: 2017 International Conference on Learning Representations; 2017 Apr 24–26; Toulon, France. p. 1–14. [Google Scholar]

4. Ma Y, Liu X, Shah N, Tang J. Is homophily a necessity for graph neural networks? In: International Conference on Learning Representations; 2022 Apr 25–29; Online. p. 1–28. [Google Scholar]

5. Bo D, Wang X, Shi C, Zhu M, Lu E, Cui P. Structural deep clustering network. In: WWW '20: Proceedings of the Web Conference 2020; 2020 Apr 20–24; Taipei, Taiwan. p. 1400–10. [Google Scholar]

6. He X, Wang B, Hu Y, Gao J, Sun Y, Yin B. Parallelly adaptive graph convolutional clustering model. IEEE Trans Neural Netw Learn Syst. 2024;35(4):4451–64. doi:10.1109/tnnls.2022.3176411. [Google Scholar] [PubMed] [CrossRef]

7. Kipf T, Welling M. Variational graph auto-encoders. arXiv:1611.07308. 2016. [Google Scholar]

8. Pan S, Hu R, Fung S, Long G, Jiang J, Zhang C. Learning graph embedding with adversarial training methods. IEEE Trans Cybern. 2020;50(6):2475–87. doi:10.1109/tcyb.2019.2932096. [Google Scholar] [PubMed] [CrossRef]

9. Wang C, Pan S, Hu R, Long G, Jiang J, Zhang C. Attributed graph clustering: a deep attentional embedding approach. In: IJCAI’19: Proceedings of the 28th International Joint Conference on Artificial Intelligence; 2019 Aug 10–16. Macao, China. p. 3670–6. [Google Scholar]

10. Park J, Lee M, Chang HJ, Lee K, Choi JY. Symmetric graph convolutional autoencoder for unsupervised graph representation learning. In: Proceedings of the 2019 IEEE/CVF International Conference on Computer Vision; 2019 Oct 27–Nov 2; Seoul, Republic of Korea. p. 6519–28. [Google Scholar]

11. Zhang X, Liu H, Li Q, Wu X. Attributed graph clustering via adaptive graph convolution. In: IJCAI’19: Proceedings of the 28th International Joint Conference on Artificial Intelligence; 2019 Aug 10–16; Macao, China. p. 4327–33. [Google Scholar]

12. Tu W, Zhou S, Liu X, Guo X, Cai Z, Zhu E, et al. Deep fusion clustering network. In: Proceedings of the AAAI Conference on Artificial Intelligence; 2021 Feb 2–9; Online. p. 9978–87. [Google Scholar]

13. Cheng J, Wang Q, Tao Z, Xie D, Gao Q. Multi-view attribute graph convolution networks for clustering. In: Proceedings of the Twenty-Ninth International Conference on International Joint Conferences on Artificial Intelligence; 2021 Jan 7–15; Yokohama, Japan. p. 2973–9. [Google Scholar]

14. Xia W, Wang Q, Gao Q, Zhang X, Gao X. Self-supervised graph convolutional network for multi-view clustering. IEEE Trans Multimed. 2021;24(3):3182–92. doi:10.1109/tmm.2021.3094296. [Google Scholar] [CrossRef]

15. Daneshfar F, Soleymanbaigi S, Yamini P, Amini MS. A survey on semi-supervised graph clustering. Eng Appl Artif Intell. 2024;133(B):108215. doi:10.1016/j.engappai.2024.108215. [Google Scholar] [CrossRef]

16. Hassani K, Ahmadi AHK. Contrastive multi-view representation learning on graphs. In: ICML’20: Proceedings of the 37th International Conference on Machine Learning; 2020 Jul 13–18; Online. p. 4116–26. [Google Scholar]

17. Liu Y, Zheng Y, Zhang D, Chen H, Peng H, Pan S. Towards unsupervised deep graph structure learning. In: WWW ’22: Proceedings of the ACM Web Conference 2022; 2022 Apr 25–29; Lyon, France. p. 1392–403. [Google Scholar]

18. Zhao H, Yang X, Wang Z, Yang E, Deng C. Graph debiased contrastive learning with joint representation clustering. In: Proceedings of the Thirtieth International Joint Conference on Artificial Intelligence (IJCAI-21); 2021 Aug 19–27; Montreal, QC, Canada. p. 3434–40. [Google Scholar]

19. Park N, Rossi RA, Koh E, Burhanuddin IA, Kim S, Du F, et al. CGC: contrastive graph clustering for community detection and tracking. In: Proceedings of the ACM Web Conference 2022; 2022 Apr 25–29; Lyon, France. p. 1115–26. [Google Scholar]

20. Xia W, Wang Q, Gao Q, Yang M, Gao X. Self-consistent contrastive attributed graph clustering with pseudo-label prompt. IEEE Trans Multimed. 2021;25(86):6665–77. doi:10.1109/tmm.2022.3213208. [Google Scholar] [CrossRef]

21. Liu Y, Yang X, Zhou S, Liu X, Wang S, Liang K, et al. Simple contrastive graph clustering. IEEE Trans Neural Netw Learn Syst. 2024;35(10):13789–800. doi:10.1109/tnnls.2023.3271871. [Google Scholar] [PubMed] [CrossRef]

22. Xu YK, Huang D, Wang CD, Lai JH. GLAC-GCN: global and local topology-aware contrastive graph clustering network. IEEE Trans Artif Intell. 2025;6(6):1448–59. doi:10.1109/TAI.2024.3413694. [Google Scholar] [CrossRef]

23. Liu Y, Zhou S, Yang X, Liu X, Tu W, Li L, et al. Improved dual correlation reduction network with affinity recovery. IEEE Trans Neural Netw Learn Syst. 2025;36(4):6159–73. doi:10.1109/TNNLS.2024.3406538. [Google Scholar] [PubMed] [CrossRef]

24. Ley M. DBLP–Some lessons learned. Proc VLDB Endowment. 2009;2(2):1493–150. doi:10.14778/1687553.1687577. [Google Scholar] [CrossRef]

25. MacQueen J. Some methods for classification and analysis of multivariate observations. In: The Fifth Berkeley Symposium on Mathematical Statistics and Probability. Oakland, CA, USA: University of California Press; 1967. p. 281–97. [Google Scholar]

26. Kingma DP, Welling M. Auto-encoding variational bayes. arXiv:1312.6114. 2013. [Google Scholar]

27. Guo X, Gao L, Liu X, Yin J. Improved deep embedded clustering with local structure preservation. In: IJCAI’17: Proceedings of the 26th International Joint Conference on Artificial Intelligence; 2017 Aug 19–25; Melbourne, VIC, Australia. p. 1753–9. [Google Scholar]

28. Huo G, Zhang Y, Gao J, Wang B, Hu Y, Yin B. CaEGCN: cross-attention fusion based enhanced graph convolutional network for clustering. IEEE Trans Knowl Data Eng. 2023;35(4):3471–83. doi:10.1109/TKDE.2021.3125020. [Google Scholar] [CrossRef]