Spotted Hyena-Bat Optimized Extreme Learning Machine for Solar Power Extraction

1  Introduction

The utilization of energy is dramatically expanding internationally. Energy utilization is probably going to arrive at its pinnacle, driven by rising per capita power utilization on one hand and expansion in financial advancement on the other. To repay the high use of energy, sustainable power sources are the suitable answers for covering this energy interest and turned into an essential type of energy because of their adaptability and adaptability [1].

The Solar power framework is considered as one of the most encouraging sustainable energy sources because of its cost-effectiveness, high efficiency, and high abundance compared with other conventional energy source such as oil, biogases and natural gases [2]. Despite of its advantages, output active power P from solar varies according to the solar irradiance and an environmental temperature T, especially under dynamic Partial Shading Conditions (PSC) due to the non-linear characteristic of PV cells [3]. The unsatisfactory power extraction is yielded due to the characteristics mentioned above and remains on the darker side of the research. To alleviate this problem, Maximum Power Point Tracking (MPPT) [4] has become the shining research to track the maximum peak and ensure the system operates only in the peaks.

Several MPPT techniques such as Hill-Climbing [5], Perturb and Observe [6], and incremental conductance [7] are used nowadays, which are used to track the uniform peak power without the influence of PSC. However, the output power from the solar power system generates multiple peaks under PSC, including one Global Maximum Power Point (GMPP) and several local peaks. Many reformed meta-heuristic algorithms [8–16] have been used on the conventional MPPT techniques to track the global peak power. However, it’s resulted in infrastructure complexity and also an increase in time of complexity.

Recently, the integration of Artificial Intelligence in MPPT techniques is aimed to resolve and rectify the problem mentioned above. Artificial Intelligence (AI) based MPPT techniques such as HERBS-MPPT [17], Artificial Neural Networks (ANN) Based MPPT [18], Genetic Algorithm (GA)-ANN based MPPT [19], Fuzzy ANN based MPPT [20] are extensively used for tracking the maximum peak power in which the HERBS-MPPT has proven its superiority over the other MPPT algorithms. Unfortunately, HERBS-MPPT suffers from trapping problems at local MPPT under maximum PSC or sudden irradiance change due to MPPT failure.

Motivated by this drawback in HERBS-MPPT, this paper proposes Spotted Hyena Enabled Reliable BAT (SHERB) learning models, SHERB-MPPT, the new hybrid optimization technique which works on the principle of Spotted Hyena over BAT algorithms with high-speed Extreme Learning Machine (ELM) to detect the GMPP effectively with high speed convergence, high performance, and zero trapping problems. This proposed method can be represented as reliable, which means consistently well in performances. The paper tells the following information, A novel hybrid integration of the spotted hyena with bat algorithm has been proposed with ELM has been proposed to achieve better tracking efficiency and high speed, which is designed using MATLAB based solar test beds have been designed to collect the different data based on the environmental temperature and solar irradiations. These datasets are used to train the proposed model, which is then used for better analysis.

The rest of the paper is organized as follows: Section-2 discusses the works proposed by more than one author. The working mechanism of the proposed framework is presented in Section-3. The experimental setup and findings with comparative analysis are detailed in section-4. Finally, the paper is concluded with future enhancement in Section-5.

2  Related Works

The fundamental MPPT procedures for Photo Voltaic (PV) frameworks are investigated and summed up and isolated into three gatherings as indicated by their control hypothetical and streamlining standards [21]. The principle benefit of these systems is that it covers the wise calculations on MPPT. In any case, this study needs an expansion to manage complex conditions like PSCs. It should utilize the current control techniques to give full play to their separate potential benefits, creating qualities and staying away from shortcomings. The arrangement of the most applied MPPT calculations. It additionally has tended to a few characterizations of the MPPT strategies [22]. MPPT technique raking dependent on broad terms like following velocity, proficiency, cost, and intricacy is given. This paper is a yield of a total composing study which can be a valuable mechanical assembly and extraordinary reference for the experts working PV system region. This study needs an update to manage more MPPT examinations dependent on the constant climate.

A counterfeit neural organization-based MPPT regulator for sunlight-based PV framework [23]. As per reproduction results, the ANN-based MPPT calculation predicts the most significant force in various irradiance and temperature more precisely than that of MPPT calculation without ANN. For better execution, the versatile neuro-fluffy-based regulator can be utilized instead of the ANN-based regulator for MPPT. A quick hybrid strategy is introduced, which joins the Particle Swarm Optimization (PSO) technique with the ANN technique [24]. In this crossbreed strategy, the ANN empowers the current PSO technique to follow MPP rapidly by giving more exact starting molecule places of the PSO calculation. Notwithstanding this, the following pace and productivity of the proposed mixture technique lead to the conviction that this strategy may give a few commitments to advancing of sun-oriented energy.

The improved MPPT strategy using the state assessment by the consecutive Monte Carlo (SMC) sifting is helped by the expectation of MPP using an ANN [25]. Recreation results show that the proposed improved MPPT technique accomplishes high proficiency and is strong to quick irradiance change under various clamor levels. Notwithstanding, this technique has the deadly weakness that its continuous presentation is inferior, as it can’t change the functioning mark of the PV exhibit rapidly enough as the outside climate changes. An arbitrary timberland Random Forest (RF) model to further develop MPPT execution is described in [26]. The RF model breezes through the Bland–Altman appraisal within the abundance of 95% sufficiency. The proposed procedure responds quickly to fast-changing biological conditions; subsequently, the strategy can be embraced for continuous MPPT. At any rate, the power following speed is low.

A computation for an ANN-based MPPT controller for wind energy structure and mutt PV/wind is discussed in [27]. The fundamental mark of this investigation is to show the Total Harmonic Distortion (THD) potential gains of PV, wind, and scattered lattice voltage and current profiles, all of which show redesigns in power quality when the micro grid is joined to harmless to the ecosystem power sources. The saw THD potential gains of the proposed system are under 5% as per standard (IEEE 1547). But, it is excessively costly for a little force framework. Moreover, a nitty-gritty correlation of mainstream AI-based MPPT strategies is for the sun-oriented force framework [3]. They are intended to follow GMPP rather than nearby MPP in reducing the impacts of PSC. In any case, the majority of the strategies are expensive and complex to assemble and require more datasets contrasted and ordinary MPPT methods. This survey is required to give a definite knowledge of the most recent headway of AI-based MPPT strategies for the application in the sun-oriented force framework.

A profound learning-based model DPLSTM utilizing LSTM and crossover enhancement is described in [28] to resolve such issues in the “12306 tagging framework”. This structure used a mean fundamental percentage error, mean absolute error, and a root means square error to assess the proposed model’s exhibition utilizing genuine information. An examination with the standard time series anticipating calculations showed the prevalence of the proposed model. Notwithstanding, mistake investigation/lingering arrangement examination showed that the proposed model could be streamlined. Then a novel GMPPT technique depends on using an AI calculation [29]. The mathematical outcomes introduced in the paper show that the time needed for distinguishing the worldwide MPP, when obscure halfway concealing examples are applied, is decreased by 80.5%–98.3% by executing the proposed Q-learning-based GMPPT calculation. However, the exchanging gadget will influence the dynamic and consistent state qualities of the framework following.

3  Proposed Framework

The proposed framework is implemented through the PV system with SHERB-MPPT algorithm.

3.1 PV Modeling

It is critical to construct a numerical model for PV cells to have high power tracking. Fig. 1 shows the typically used single diode equivalent circuit that enables the PV cells with its characteristics. It is a PN junction that works on the principle of photovoltaic effects to get electricity. The diode is parallel to the current source, which changes with temperature and irradiance. SHERB-MPPT, the new hybrid optimization technique, works on the principle of Spotted Hyena over BAT algorithms with high-speed ELM to detect the GMPP effectively with high speed convergence, high performance, and zero trapping problems.

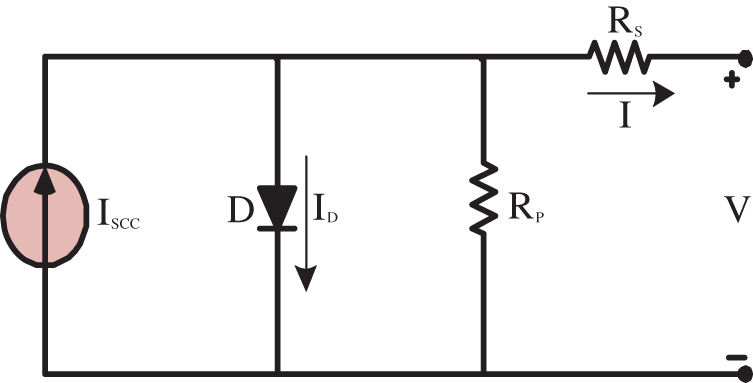
Figure 1: Single diode model

The following equation provides the current ‘I’ or ‘IL’, neglecting shunt resistance.

I = ISCC− ID (1)

As per Eq. (1), the value of current in the PV cell is denoted by excluding the shunt resistance effect.

ID=Io,ref[exp⁡(q(v+IRSKAT)−1] (2)

The short circuit current,

Iscc=GGref[Iscc,ref+Kj(T−Tref)] (3)

where, T=cell temperature in K, Gref=1000W/m2 , q = electron charge is 1.6 × 10−19 C, A = ideality factor is 1.5 and K = Boltzmann constant is 1.38 × 10-23 J/K. ISCC denotes the short circuit current at the reference condition, G denotes the irradiance in W/m2, the reference temperature is denoted by Tref in K, KJ denotes the temperature coefficient at ISCC,ref and RS denotes the series resistance in Ω . Both RS and RP are important to identify the system losses. Based on Fig. 1, by taking the shunt resistance into account, the load current expression is defined in Eq. (5).

ISCC−ID−VDRP−1=0 (4)

Thus, based on Eq. (4), the load current is modified in Eq. (5).

I(or)IL=ISCC−ID−VDRP (5)

Tab. 1 exhibits the parameter values of the P1310X990 module on the basis of which the current paper is developed. These data values are also to be used in simulation work.

Assuming NS and NP denote the number of cells connected in series and parallel and then the current equation of the PV cell is as follows:

I=NPISCC−NsIrs1{exp(q(V+IRsNsAKT−1)} (6)

where, Irs1 denotes the cell reverse saturation current which is given as

Irs1=Io1[(TTref)3eqBgAK1Tref−1T]] (7)

where Bg is energy gap usually taken as 1.107 eV and RP is shunt resistance in Ω . The conduct of the PV model, which changes with the sun-powered irradiance and temperature, is given in Fig. 2.

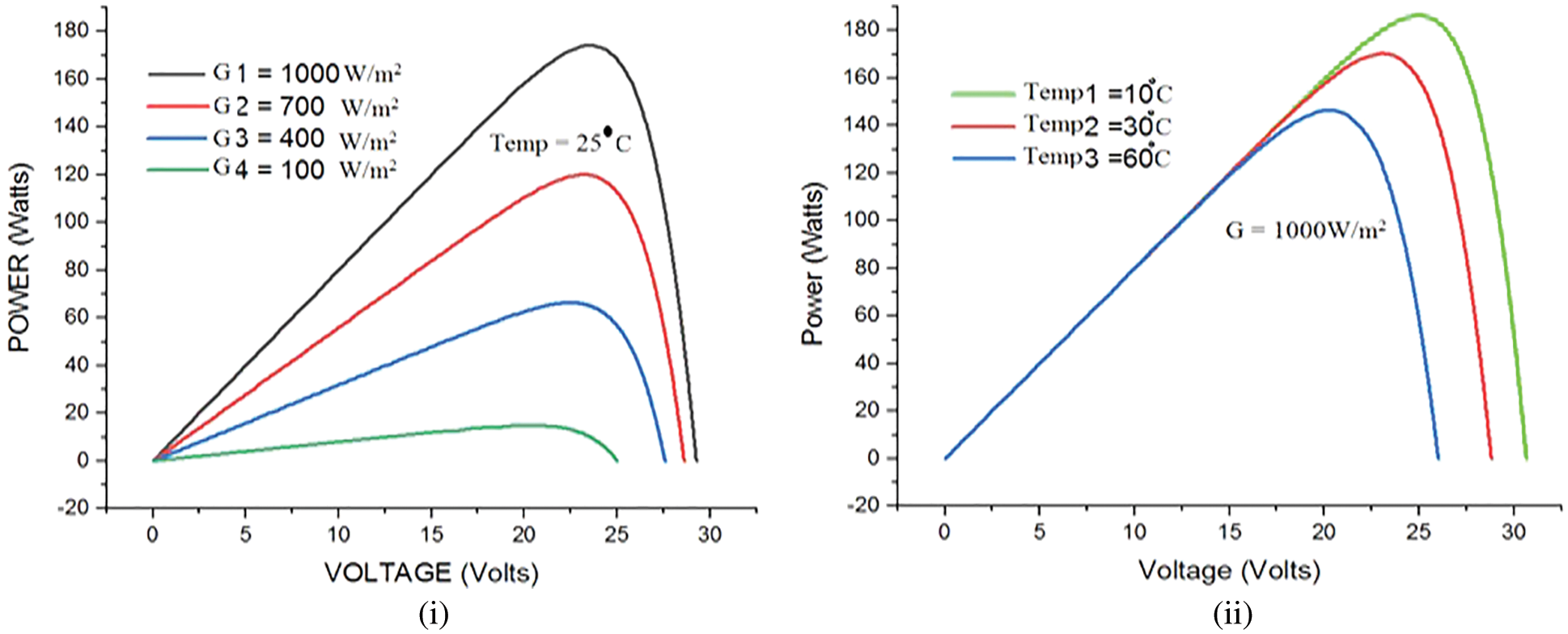
Figure 2: Power voltage graph for solar module (i) change in solar irradiance (ii) Change in temperature

3.2 SHERB-MPPT Algorithms

Fig. 3 illustrates the functioning instrument of the proposed engineering. The proposed design comprises two significant stages, example, ELM [30–32] preparing stage and the Hybrid enhancement stages. The incremental conductance and various local peaks by the solar irradiance and temperature are used for ELM training which results in the reduced local peaks. The first phase of ELM training reduces the number of peaks from the above conditions. In the second phase, a spotted hyena [33,34] based bat algorithm is used to optimize the peaks to produce the best global power point peak. Finally, optimized maximum output power is given to the grid application using Direct Current (DC)-DC convertor.

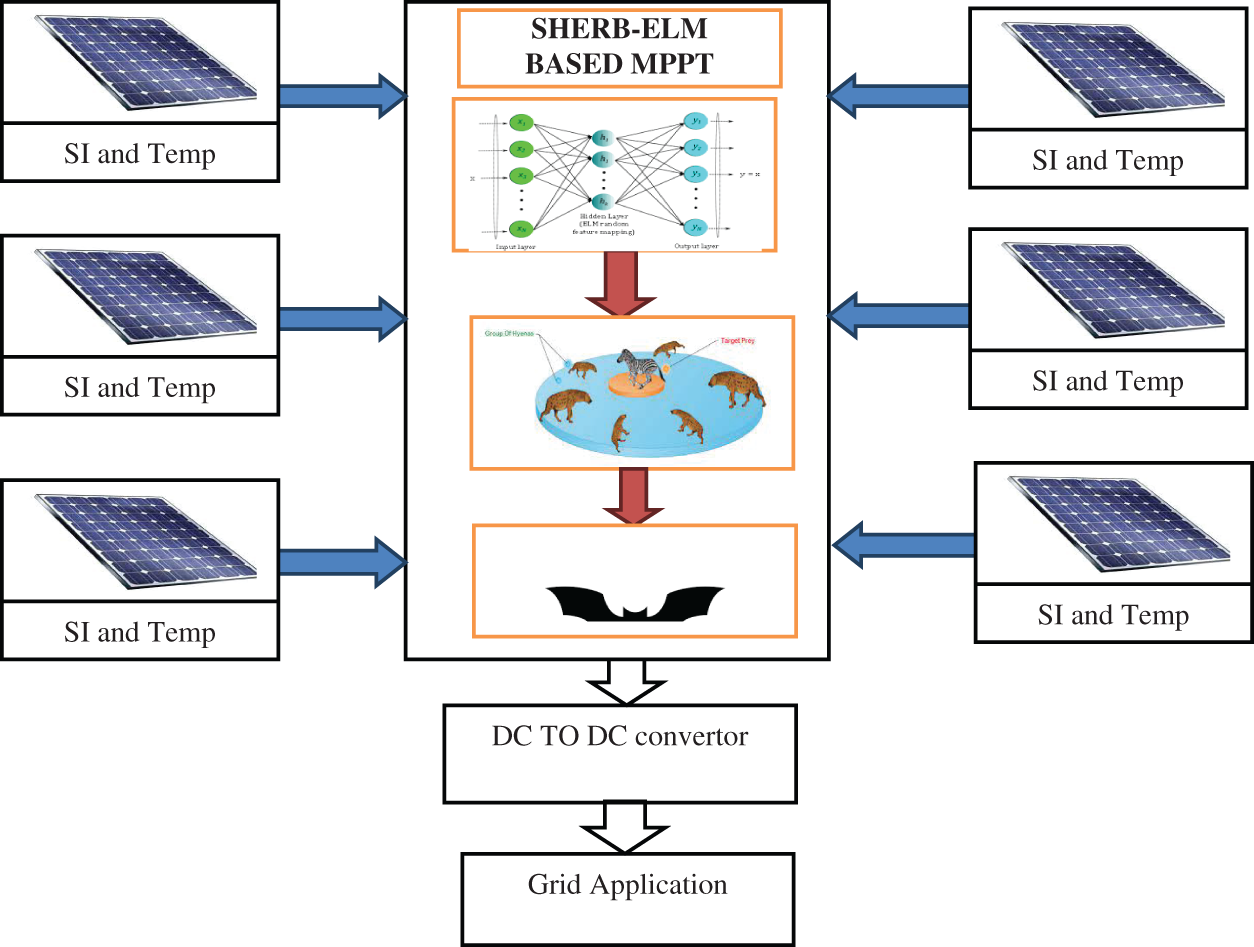
Figure 3: Proposed framework for the SHERB-ELM MPPT algorithm

As discussed in [35], though the BAT algorithm a exhibits high convergence rate at early stage, it slowly degrades in the later stage. This leads to the false detection of peaks and results in the high false alarm rates. To overcome this problem, this research proposed the hybrid combination of spotted hyena-based bat algorithm to detect optimal GMPP for any number of data. The method’s dependability is evaluated under various partial shading situations [36], and the simulated results are shown to demonstrate the usefulness of the suggested Golden Section Search (GSS) based GMPPT algorithm. Further presents a new approach 12-parameter model [37] with the inherent capacity to forecast the two-diode model parameters for any meteorological data without trial runs.

The SHERB uses the hunting procedure of spotted hyena for the BAT algorithm to find the best optimal values. At the initial stage, the echolocation principle is used with the minimum loudness, frequency, and velocity.

For every iteration in the process of identifying the prey, loudness, position, frequency and velocity of bats are updated by the hyena‘s procedure of hunting using the following mathematical Eqs. (8)–(10).

F→=2f→.rd→2−f→ (8)

f→=5(cycle∗5maxcycle) (9)

where F→ is vector coefficient as the population is dynamic in nature, cycle=1,2,3…maxcycle. In the cycle of updating the best hyena, the f→ value linearly reduces from 5 to 0. rd→1,rd→2 are the random vectors residing in the limit [0, 1]. The position of the target prey is updated from the calculated values of E→ and F→ vector. The behavior of the spotted hyena is observed and located mathematically, leading to the best solution of determining the optimum solution space.

D→sh=|E→.P→f−P→k| (10)

P→k=P→j−F→..D→sh (11)

C→f=P→k+P→k+1+…+P→k+N (12)

E→ is vector coefficient as the population is dynamic, P→f be the position of the best spotted hyena

P→k be the position of other hyenas in search space, N is the No. of hyena in the overall population.

N=CountVal(P→f,P→f+1,…P→f+M) (13)

M is a vector with a value distributed from [0.5, 1] manually. CountVal is the candidate solution count

C→f is the cluster of solutions reaching close to the optimal solution. For attacking the target, The vector f→ can be reduced to reach 0 until the target prey is attacked. When |F|<1 , the cluster of spotted hyena catches the prey. This is mathematically expressed as

P→(x+1)=C→fN (14)

where the position of the vector P→(x+1) updates for each search space till the best solution is attained.

The pseudo code for the proposed algorithm is given in Algorithm-1

The significant advantage of SHERB has overcome the local convergence of the BAT algorithm, which can detect the best optimal value with a low convergence speed.

For the detection of optimal GMPP value, incremental conductance and various power peaks in accordance with the solar irradiance and temperature are used for ELM training which results in the local peak points. These multiple peak points, along with Short circuit current (Isc), are used as the input for the proposed hybrid SHERB, which determines the global best fitness function. The fitness function of the proposed algorithm is given in Eq. (15).

FitnessFunction=Maximum(PeakValues) (15)

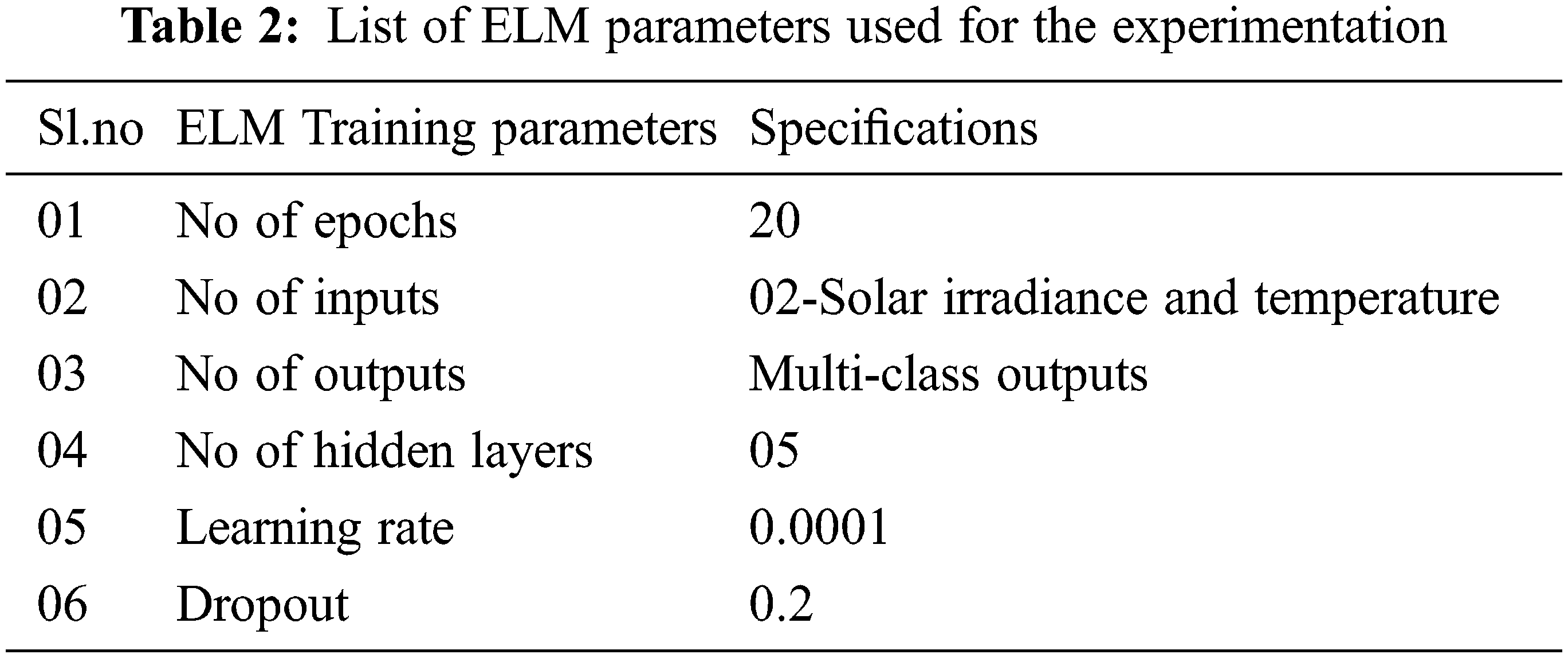
The parameters used for the ELM training is given in Tab. 2.

The working mechanism of the proposed SHERB-MPPT is depicted in Algorithm-2

4  Results and Discussions

The performance of the proposed architecture has been evaluated in four different scenarios. The first scenario, three solar arrays are subjected to solar irradiance at 1000W/m2, and non-uniform irradiance is applied to the other three solar cells. In the second scenario, uniform solar irradiance is exposed to two solar cells, with the remaining cells subjected to PSC. All the algorithms run on the same system. The faster the CPU works the more processes it can perform at once. A CPU with a 3 GHz clock speed, for example, may do 3 thousand million cycles per second. The cache of the CPU is the onboard memory that is used to store the information so that the processor can access it rapidly.

4.1 Experimental Datasets

To prove and validate the efficiency, the proposed algorithm’s datasets which consist of different variants of temperature and irradiance, are collected using the model developed using MATLAB and Simulink. The proposed architecture uses six solar cells for 200 watts as inputs, and four varieties of partial shading trial patterns were taken into account. Fig. 4 shows the Simulink model created for one PV cell, and nearly 40,000 pattern traces were collected to evaluate the proposed architecture. Fig. 5 shows the Maximum Peak Power Detected by the Proposed Algorithm at a Solar irradiance of 300 m/W. Fig. 6 shows the simulation outputs obtained from the different scenarios of solar irradiance and temperature at 1000 m/W.

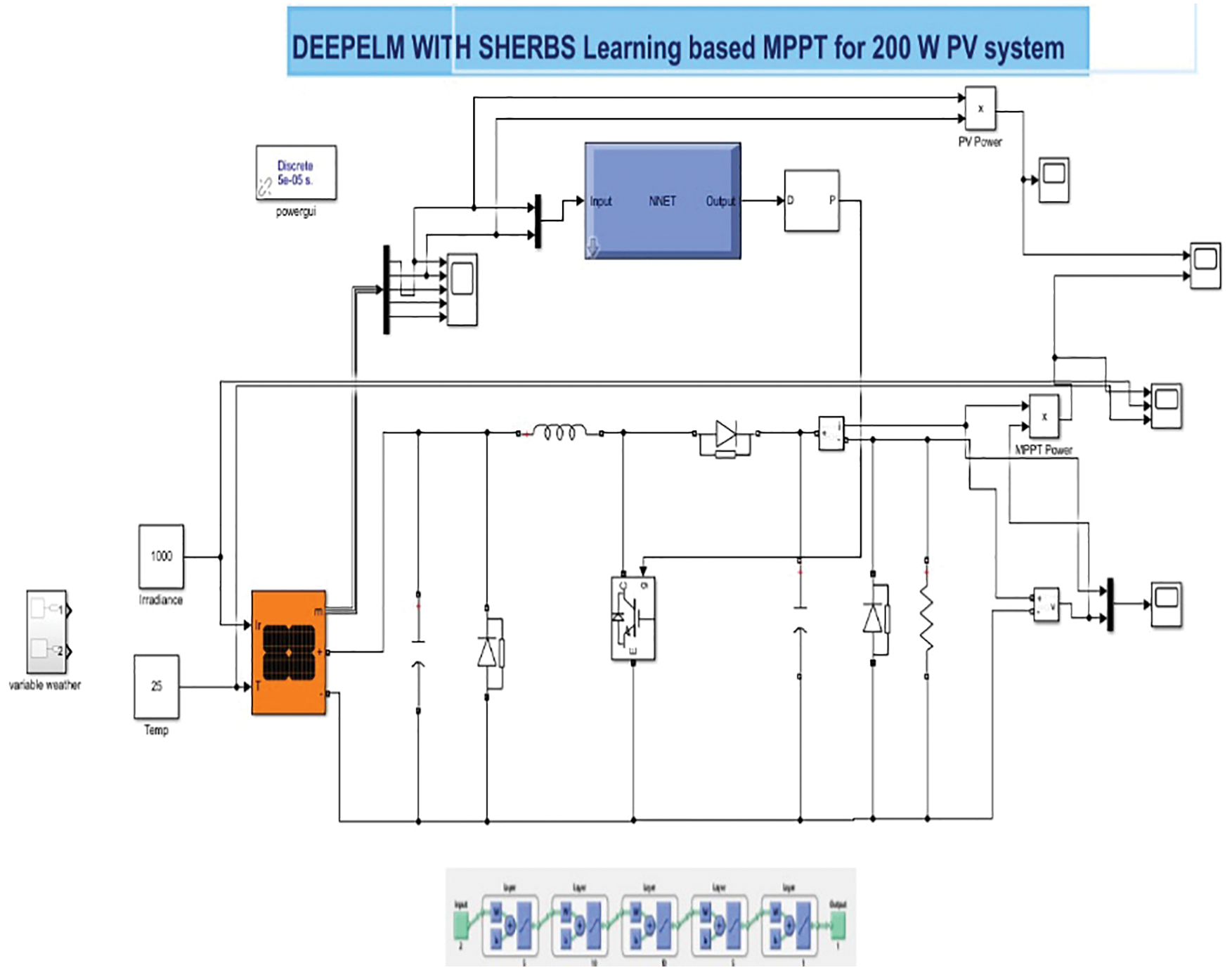
Figure 4: Proposed model developed using one PV cell for experimentation

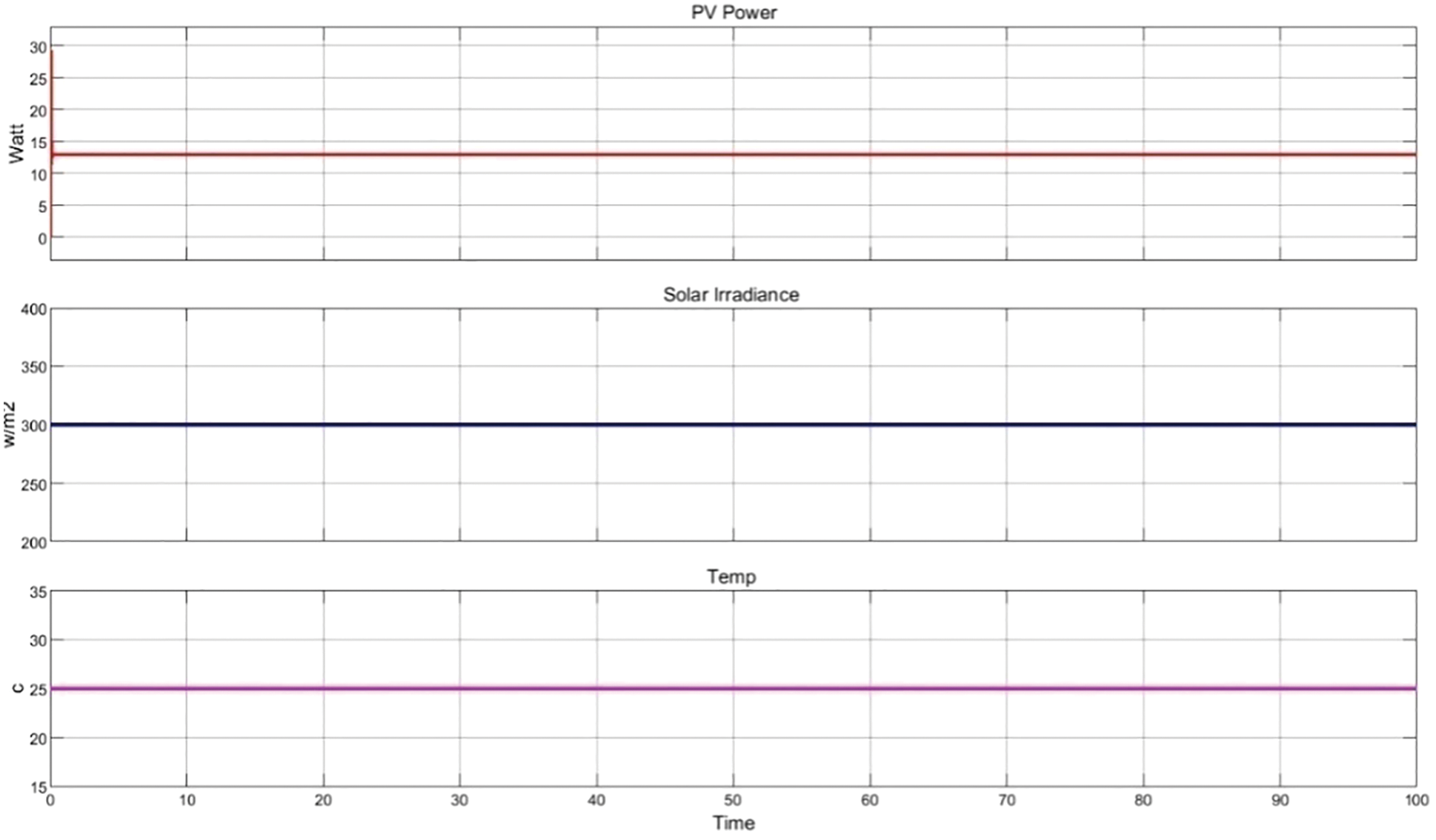
Figure 5: Maximum peak power detection at solar irradiance 300 m/W

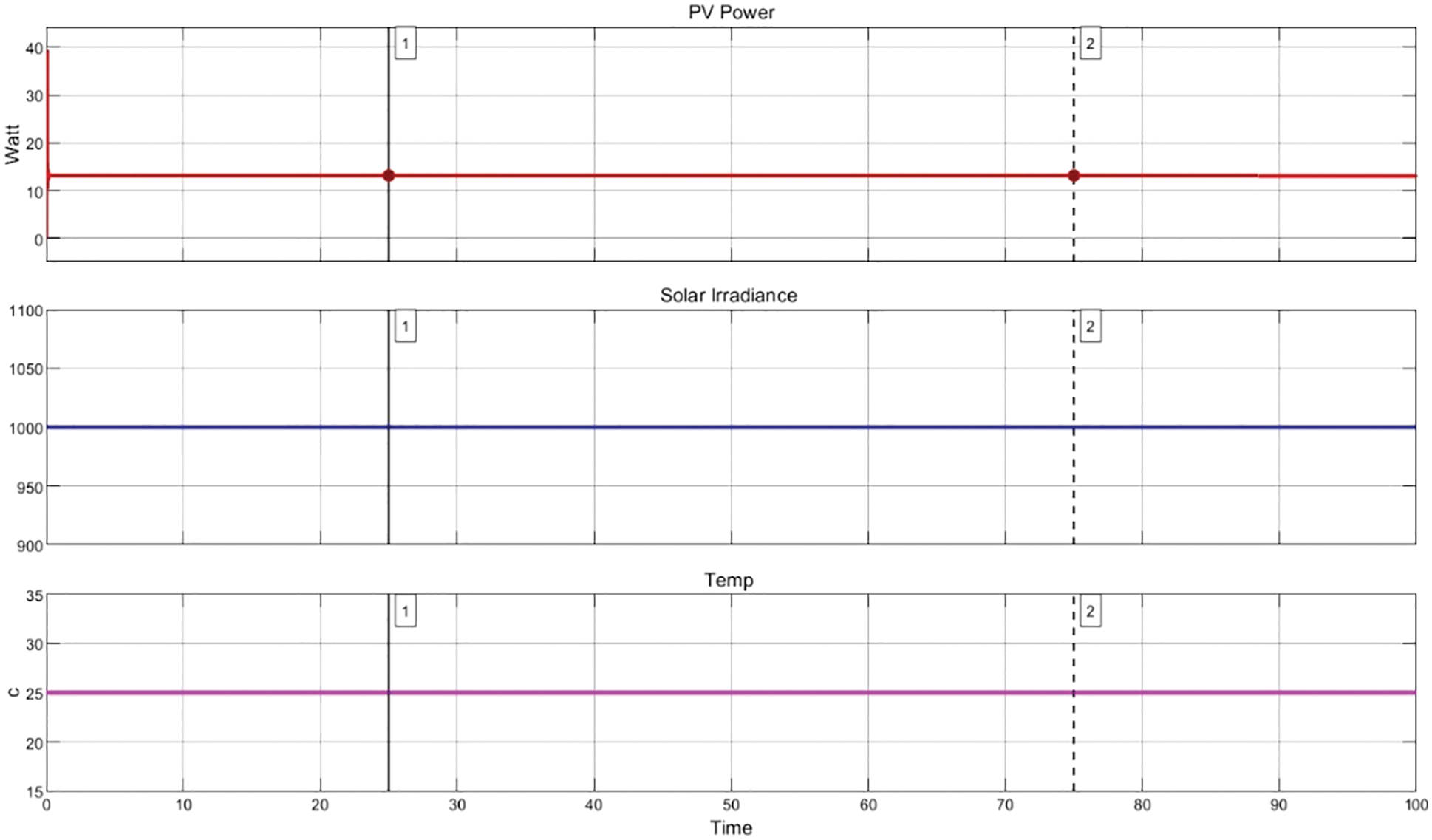
Figure 6: Simulation outputs obtained from the different scenario of solar irradiance and temperature at 1000 m/W

4.2 Tracking Efficiency

The performance of the proposed algorithm is evaluated by the metrics called tracking efficiency, which is given by the mathematical expression (16).

TrackingEfficiency:PMPPTPMAX∗100% (16)

where PMPPT is the power achieved at the time of MPPT with SHERB-MPPT algorithm, PMAX is actual/maximum power obtained. In the third scenario, five cells are subjected to non-uniformity conditions, and finally, all cells were exposed to non-uniform solar irradiance. The tracking performance of the proposed architecture is depicted in Tabs. 3–6.

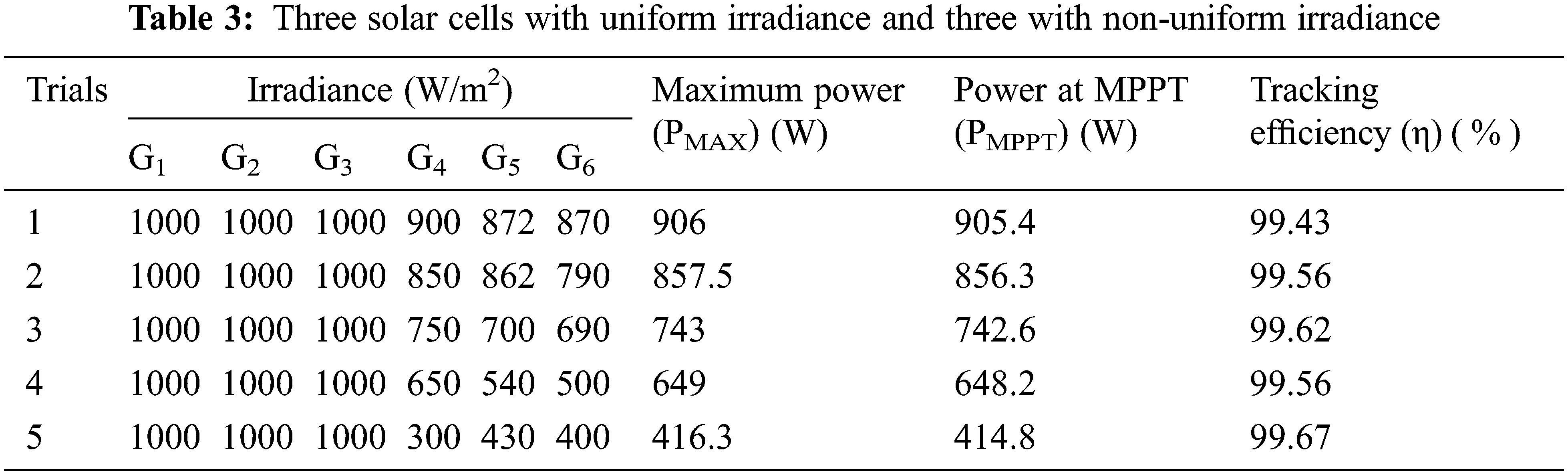
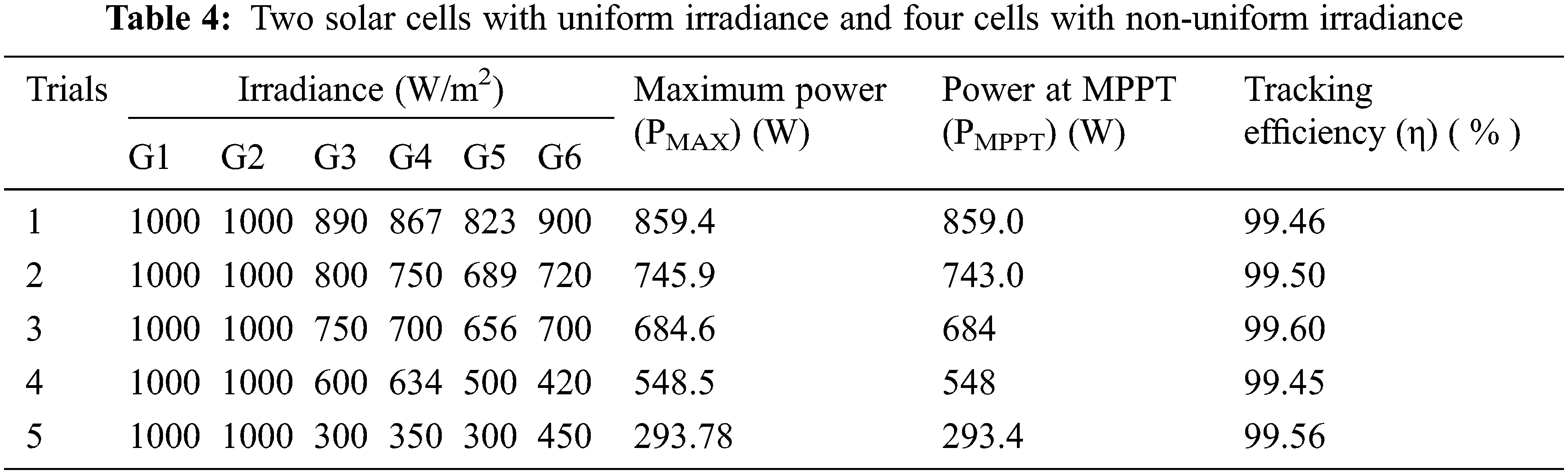
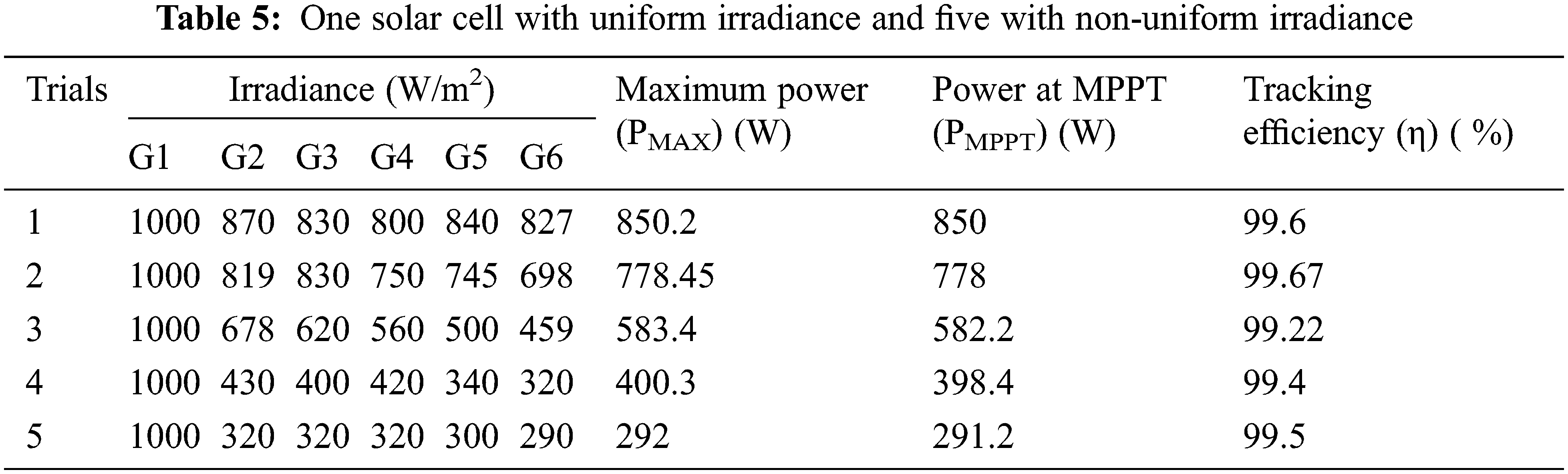
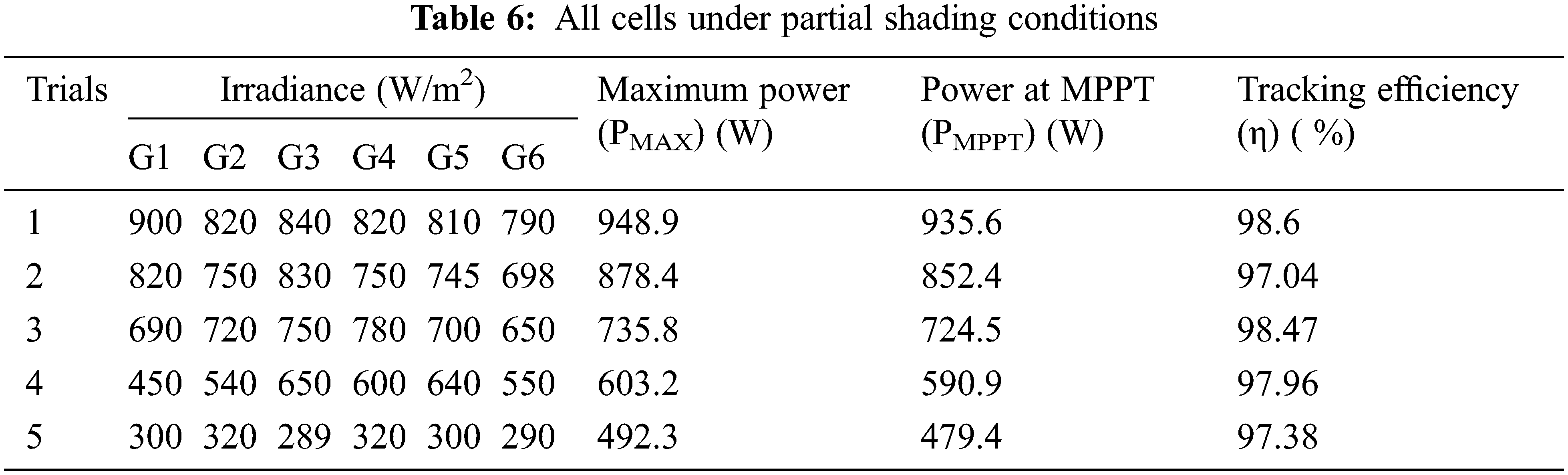
From Tabs. 3–6, it is clear that the proposed framework SHERB-MPPT has produced 99.5% for the first scenario, 99.46% for the second scenario, 99.6% for the third scenario, and 99.6% for the fourth scenario. Even though the PSC increases, SHERB-MPPT has detected a GMPP with high tracking efficiency of 99.6%. This is due to the integration of the Spotted-Hyena with the BAT algorithm and ELM training. To demonstrate the predominance of the proposed calculation, we have contrasted the proposed calculation and the current calculation, for example, PSO-ANN [18], GA-ANN [19], BAT-ANN [20, and HERBS-MPPT [17]. The techniques are compared with GA-ANN and PSO-ANN, HERBS, BAT-ANN. Also, this system is compared with proposed algorithm of HERBS. This is one of the BAT-based hybrid systems. Also, the comparative examination of MPPT techniques bio-inspired by the Bat-based optimization approach can achieve more promising results than GMPP [38]. This BAT-MPPT techniques has achieved the traction efficiency is 92.45%, which is less than our proposed algorithm is 99.6%. It shows a similar examination of the various calculations in identifying the worldwide greatest powepoint. Tab. 7 shows the maximum tracking power of second scenario.

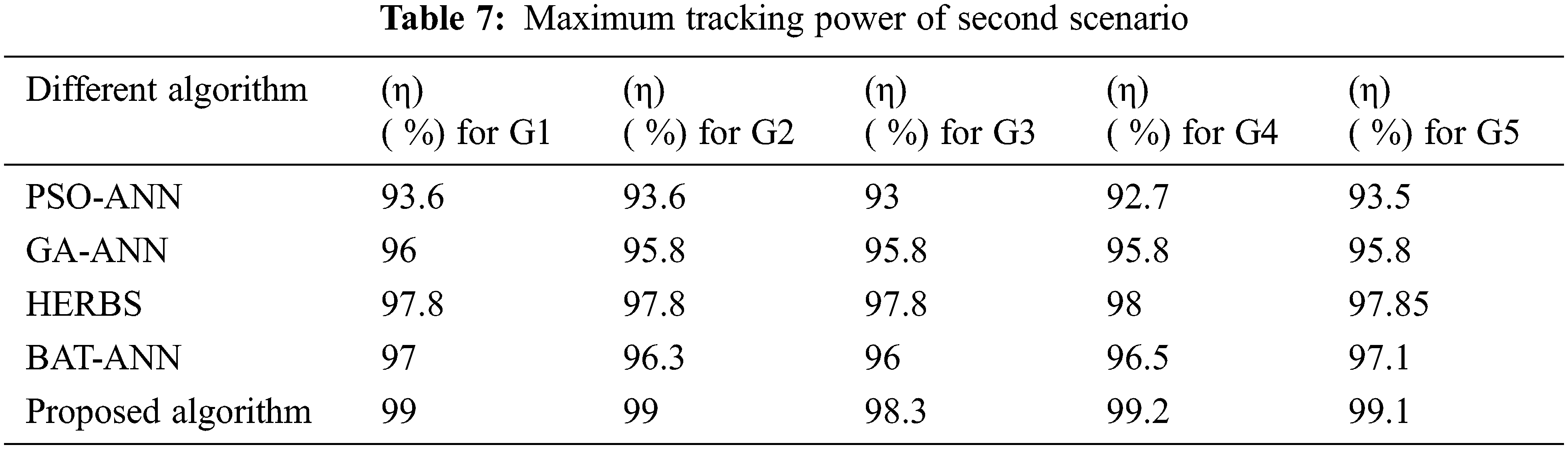
From the Tabs. 3–6, it is clear that the proposed framework SHERB-MPPT achieves better tracked power efficiency.

From Figs. 7–10, it is found that the tracking efficiency of HERBS is 98%, whereas the proposed architecture achieves 99.6%. From the figures, it is clear that the proposed architecture has outperformed the other existing algorithms when the PSC is exposed to four cells and five cells respectively, Fig. 9 shows the comparative analysis of tracking efficiency between the different algorithms for the third testing scenario. The tracking efficiency of the performance matrices of PSO-ANN, GA-ANN, HERBS, BAT-ANN and the proposed algorithm are compared as well as the proposed algorithm has high tracking efficiency, which has achieved a better tracking efficiency of 99.5%, In contrast , the other existing algorithms have seen adrop in tracking when the PSC is extended to all solar cells, as shown in Fig. It is evident that the proposed architecture has shown better and uniform tracking efficiency than the other existing algorithms under the different scenarios of partial shading conditions. Fig. 11 shows the computational time of tracking between the different hybrid learning models. From the figure, it is clear that the proposed algorithm needs less tracking time for GMPP detection.

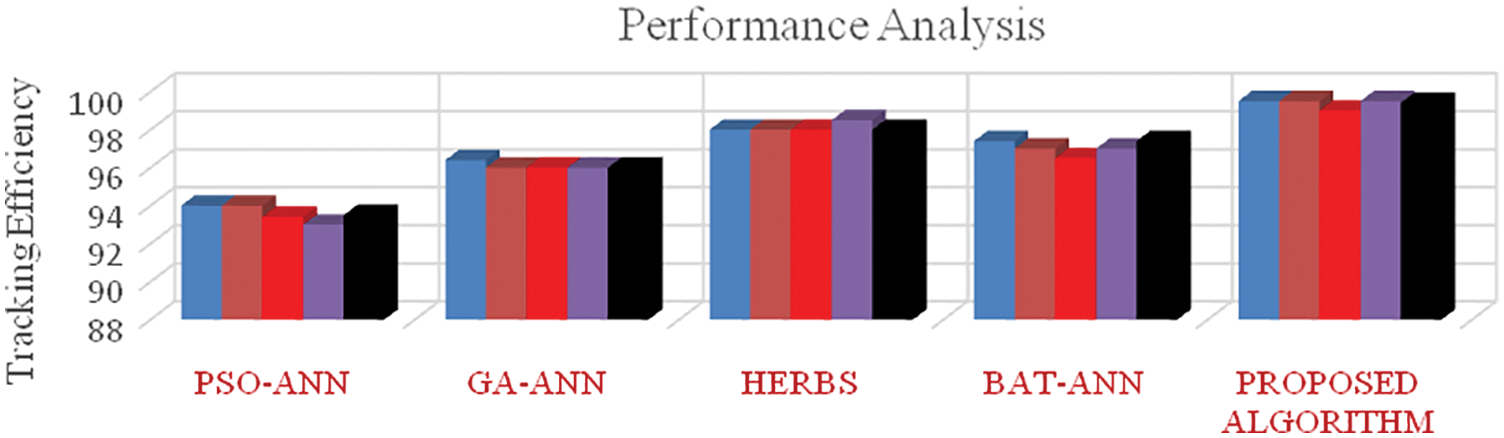
Figure 7: Comparative analysis of tracking efficiency for the 1st scenario of testing

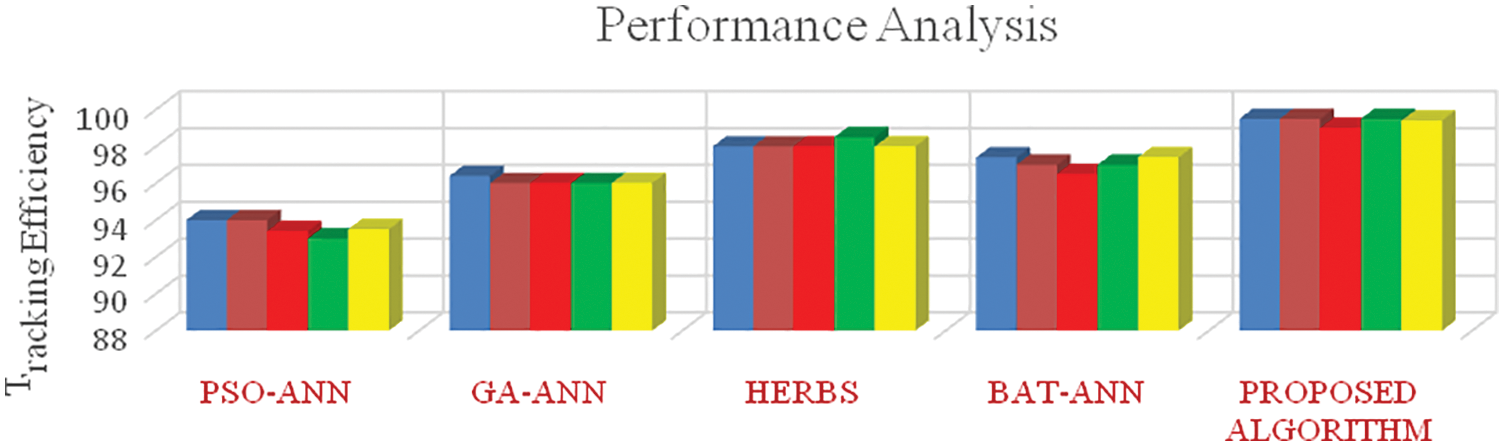
Figure 8: Comparative analysis of tracking efficiency for the 2nd scenario of testing

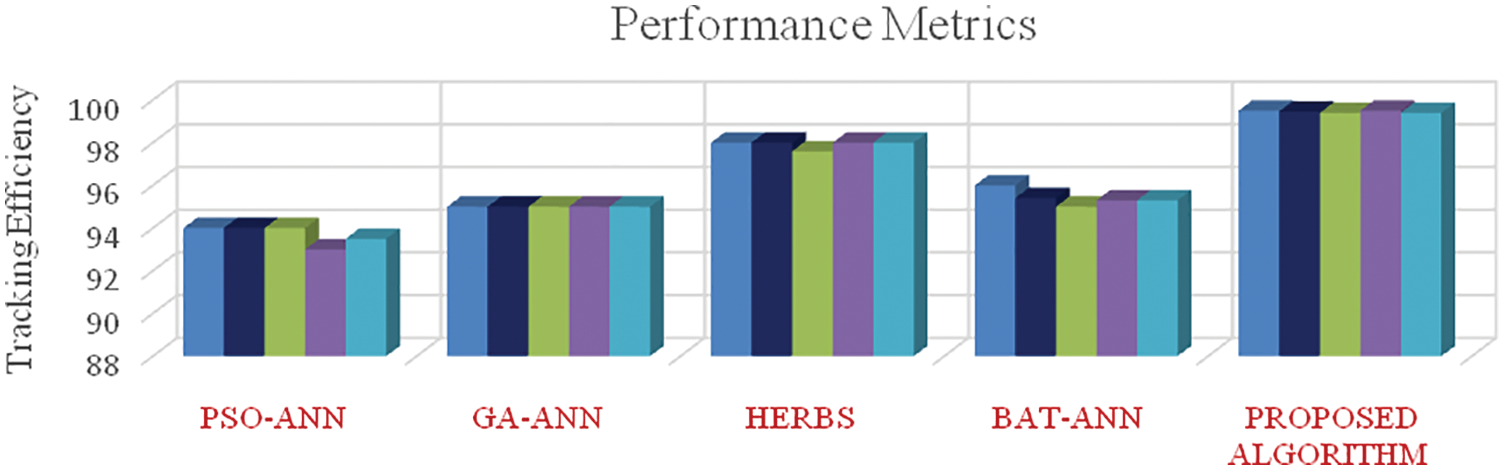
Figure 9: Comparative analysis of tracking efficiency between the different algorithms for the third scenario of testing

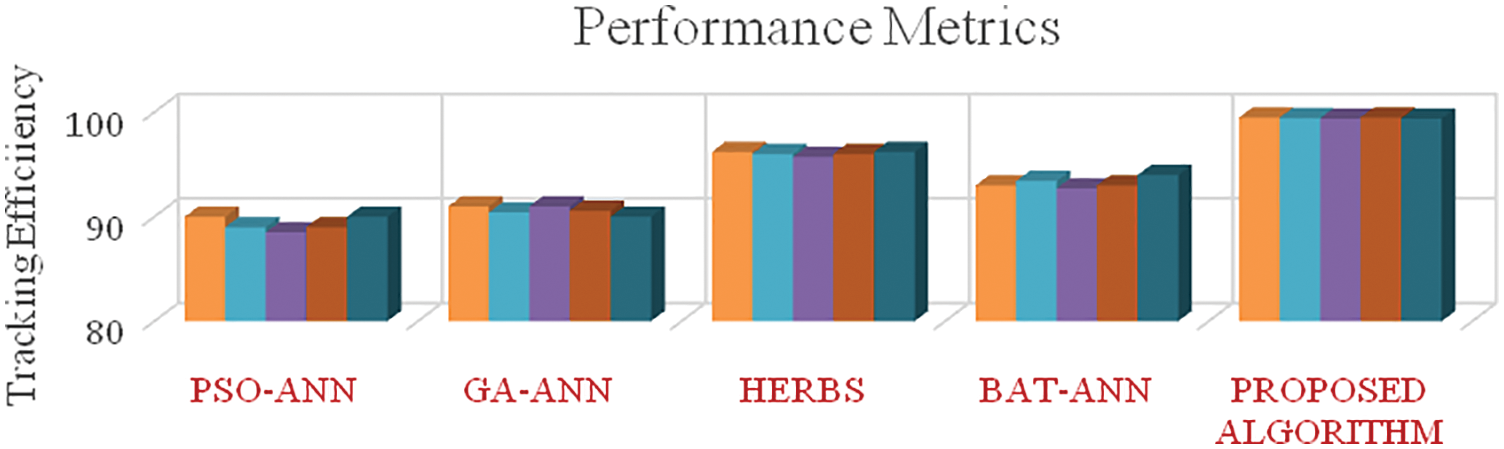
Figure 10: Comparative analysis of tracking efficiency between the different algorithms for the final scenario of testing

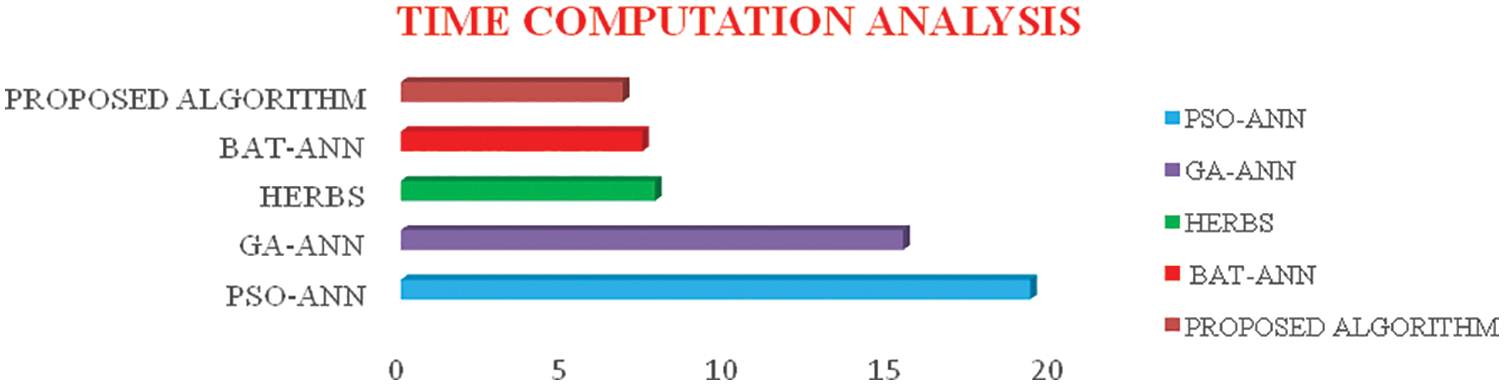
Figure 11: Time computation analysis for the different algorithm in detecting the maximum peaks

5  Conclusion

In this paper, an original crossover SHERB-MPPT approach for the most extreme power extraction in PV frameworks. The spotted hyena and BAT calculation has been utilized alongside ELMs to work on the exhibition of the PV cells during the incomplete concealing conditions. The SHERB uses the hunting procedure of spotted hyena for the BAT algorithm to find the best optimal values. At the initial stage, the echolocation principle is used with the minimum loudness, frequency, and velocity. The experimentation is carried out using six solar cells implemented using the MATLAB-SIMULINK under different operating scenarios of partial shading conditions. Simulation results show that the proposed SHERB-MPPT algorithm has outperformed other existing hybrid frameworks such as PSO-ANN, GA-ANN, HERBS-MPPT, and BAT-ANN. Extensive testing with 50000 data combinations collected in partial shade and typical circumstances. Based on simulation results, the suggested technique provides 99.7% tracking efficiency with a slower convergence speed. The tracking efficiency is as high as 99.6% in all partial shading conditions with high convergence speed. However, the proposed algorithm needs the limelight of improvisation for real-time implementation. In future, the meta-heuristic optimization algorithm should be improved to achieve a more tracking efficiency with a low speed of convergence.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  H. Elaissaoui, M. Zerouali, A. El Ougli and B. Tidhaf, “MPPT algorithm based on fuzzy logic and artificial neural network (ANN) for a hybrid solar/wind power generation system,” in Fourth Int. Conf. on Intelligent Computing in Data Sciences, Fez, Morocco, pp. 1–6, 2020. [Google Scholar]

 2.  J. Jurasz and J. Mikulik, “Economic and environmental analysis of a hybrid solar, wind and pumped storage hydroelectric energy source: A polish perspective,” Bulletin of the Polish Academy of Sciences: Technical Sciences, vol. 65, no. 6, pp. 859–869, 2017. [Google Scholar]

 3.  K. Y. Yap, C. R. Sarimuthu and J. M. Lim, “Artificial intelligence based MPPT techniques for solar power system: A review,” Journal of Modern Power Systems and Clean Energy, vol. 8, no. 6, pp. 1043–1059, 2020. [Google Scholar]

 4.  Y. Yang and H. Wen, “Adaptive perturb and observe maximum power point tracking with current predictive and decoupled power control for grid-connected photovoltaic inverters,” Journal of Modern Power Systems and Clean Energy, vol. 7, no. 2, pp. 422–432, 2019. [Google Scholar]

 5.  K. Y. Yap, H. Chua, M. J. K. Bashir, F. Y. Albert and S. Govinda, “Central composite design (CCD) for parameters optimization of maximum power point tracking (MPPT) by response surface methodology (RSM),” Journal of Mechanics of Continua and Mathematical Sciences, vol. 1, no. 1, pp. 259–270, 2019. [Google Scholar]

 6.  A. Ibrahim, S. Obukhov and R. Aboelsaud, “Determination of global maximum power point tracking of PV under partial shading using cuckoo search algorithm,” Applied Solar Energy, vol. 55, pp. 367–375, 2020. [Google Scholar]

 7.  C. Correa-Betanzo, H. Calleja, C. Aguilar, A. R. Lopez-Nunez and E. Rodriguez, “Photovoltaic-based DC microgrid with partial shading and fault tolerance,” Journal of Modern Power Systems and Clean Energy, vol. 7, no. 2, pp. 340–349, 2019. [Google Scholar]

 8.  E. Lodhi, R. N. Shafqat, K. D. Kerrouche and Z. Lodhi, “Application of particle swarm optimization for extracting global maximum power point in PV system under partial shadow conditions,” International Journal of Electronics and Electrical Engineering, vol. 5, no. 3, pp. 223–229, 2017. [Google Scholar]

 9.  S. Rajendran and H. Srinivasan, “Simplified accelerated particle swarm optimisation algorithm for efficient maximum power point tracking in partially shaded photovoltaic systems,” IET Renewable Power Generation, vol. 10, no. 9, pp. 1340–1347, 2016. [Google Scholar]

10. P. S. Gavhane, S. Krishnamurthy, R. Dixit, J. P. Ram and N. Rajasekar, “EL-PSO based MPPT for solar PV under partial shaded condition. Energy Procedia, vol. 117, pp. 1047–1053, 2017. [Google Scholar]

11. M. Mao, Q. Duan, P. Duan and B. Hu, “Comprehensive improvement of artificial fish swarm algorithm for global MPPT in PV system under partial shading conditions,” Transactions of the Institute of Measurement and Control, vol. 40, no. 7, pp. 2178–2199, 2018. [Google Scholar]

12. S. Titri, C. Larbes, K. Y. Toumi and K. Benatchba, “A new MPPT controller based on the ant colony optimization algorithm for photovoltaic systems under partial shading conditions,” Applied Soft Computing, vol. 58, pp. 465–479, 2017. [Google Scholar]

13. D. F. Teshome, C. H. Lee, Y. W. Lin and K. L. Lian, “A modified firefly algorithm for photovoltaic maximum power point tracking control under partial shading,” IEEE Journal of Emerging and Selected Topics in Power Electronics, vol. 5, no. 2, pp. 661–671, 2016. [Google Scholar]

14. K. Aygül, M. Cikan, T. Demirdelen and M. Tumay, “Butterfly optimization algorithm based maximum power point tracking of photovoltaic systems under partial shading condition,” Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, pp. 1–9, 2019. [Google Scholar]

15. J. P. Ram and N. Rajasekar, “A new global maximum power point tracking technique for solar photovoltaic (PV) system under partial shading conditions (PSC),” Energy, vol. 118, pp. 512–525, 2017. [Google Scholar]

16. F. Belhachat and C. Larbes, “A review of global maximum power point tracking techniques of photovoltaic system under partial shading conditions,” Renewable and Sustainable Energy Reviews, vol. 92, pp. 513–553, 2018. [Google Scholar]

17. V. Somasundaram, B. Jeevarathinam and P. Kasinathan, “An intellectual hybrid algorithm for optimal monitoring of power point in solar photovoltaic energy system-based grid network,” Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, vol. 43, no. 23, pp. 3045–3063, 2021. [Google Scholar]

18. M. S. Ngan and C. W. Tan, “Photovoltaic multiple peaks power tracking using particle swarm optimization with artificial neural network algorithm,” in Advances in Solar Photovoltaic Power Plants, Green Energy and Technology, Berlin, Heidelberg: Springer, pp. 107–138, 2016. [Google Scholar]

19. A. A. Kulaksız and R. Akkaya, “A genetic algorithm optimized ANN-based MPPT algorithm for a stand-alone PV system with induction motor drive,” Solar Energy, vol. 86, no. 9, pp. 2366–2375, 2012. [Google Scholar]

20. M. K. Karagöz and H. Demirel, “Novel MPPT method for PV arrays based on modified bat algorithm with partial shading capability,” International Journal of Computer Science and Network Security, vol. 12, no. 2, pp. 61–66, 2017. [Google Scholar]

21. M. Mao, L. Cui, Q. Zhang, K. Guo, L. Zhou et al., “Classification and summarization of solar photovoltaic MPPT techniques: A review based on traditional and intelligent control strategies,” Energy Reports, vol. 6, pp. 2352–4847, 2020. [Google Scholar]

22. A. O. Baba, G. Liu and X. Chen, “Classification and evaluation review of maximum power point tracking methods,” Sustainable Futures, vol. 2, pp. 1–28, 2020. [Google Scholar]

23. R. B. Roy, J. Cros, A. Nandi and T. Ahmed, “Maximum power tracking by neural network,” in Int. Conf. on Reliability, Infocom Technologies and Optimization, Noida, India, pp. 89–93, 2020. [Google Scholar]

24. M. M. Rahman and M. S. Islam, “PSO and ANN based hybrid MPPT algorithm for photovoltaic array under partial shading condition,” Engineering International, vol. 8, no. 1, pp. 9–24, 2020. [Google Scholar]

25. L. Chen and X. Wang, “Enhanced MPPT method based on ANN-assisted sequential monte–Carlo and quickest change detection,” IET Smart Grid, vol. 2, no. 4, pp. 635–44, 2019. [Google Scholar]

26. H. Shareef, A. H. Mutlag and A. Mohamed, “Random forest-based approach for maximum power point tracking of photovoltaic systems operating under actual environmental conditions,” Computational Intelligence and Neuroscience, vol. 2017, pp. 1–17, 2017. [Google Scholar]

27. A. Ab-BelKhair, J. Rahebi and A. Abdulhamed Mohamed Nureddin, “A study of deep neural network controller-based power quality improvement of hybrid PV/Wind systems by using smart inverter,” International Journal of Photoenergy, vol. 2020, pp. 1–22, 2020. [Google Scholar]

28. C. Fan, J. Zhu, H. Elahi, L. Yang and B. Li, “A hybridly optimized LSTM-based data flow prediction model for dependable online ticketing,” Wireless Communications and Mobile Computing, vol. 2021, pp. 1–13, 2021. [Google Scholar]

29. C. Kalogerakis, E. Koutroulis and M. G. Lagoudakis, “Global MPPT based on machine-learning for PV arrays operating under partial shading conditions,” Applied Sciences, vol. 10, no. 2, pp. 1–19, 2020. [Google Scholar]

30. G. B. Huang, Q. Y. Zhu and C. K. Siew, “Extreme learning machine: Theory and applications,” Neurocomputing, vol. 70, no. 1–3, pp. 489–501, 2006. [Google Scholar]

31. B. Wang, S. Huang, J. Qiu, Y. Liu and G. Wang, “Parallel online sequential extreme learning machine based on MapReduce,” Neurocomputing, vol. 149, Part A, pp. 224–232, 2015. [Google Scholar]

32. J. Fan, J. Fan, F. Liu, J. Qu and R. Li, “A novel machine learning method based approach for Li-ion battery prognostic and health management,” IEEE Access, vol. 7, pp. 160043–61, 2019. [Google Scholar]

33. Q. Luo, J. Li, Y. Zhou and L. Liao, “Using spotted hyena optimizer for training feedforward neural networks,” Cognitive Systems Research, vol. 65, pp. 1–6, 2021. [Google Scholar]

34. X. S. Yang and X. He, “Bat algorithm: Literature review and applications,” International Journal of Bio-Inspired Computation, vol. 5, no. 3, pp. 141–149, 2013. [Google Scholar]

35. H. Rezk, A. O. Mazen, M. R. Gomaa, M. A. Fathy, M. A. Abdelkareem et al., “A novel statistical performance evaluation of most modern optimization-based global MPPT techniques for partially shaded PV system,” Renewable and Sustainable Energy Reviews, vol. 115, pp. 109372–109400, 2019. [Google Scholar]

36. S. Malathy and R. Ramaprabha, “A Two-stage tracking algorithm for PV systems subjected to partial shading conditions,” International Journal of Renewable Energy Research, vol. 8, no. 4, pp. 1–8, 2018. [Google Scholar]

37. J. P. Ram, D. S. Pillai, D. Mathew, J. Ha and Y. J. Kim, “A simple, reliable and adaptive approach to estimate photovoltaic parameters using spotted hyena optimization: A framework intelligent to predict photovoltaic parameters for any meteorological change,” Solar Energy, vol. 236, pp. 480–498, 2022. [Google Scholar]

38. M. V. da Rocha, L. P. Sampaio and S. A. da Silva, “Comparative analysis of MPPT algorithms based on BAT algorithm for PV systems under partial shading condition,” Sustainable Energy Technologies and Assessments, vol. 40, pp. 1–14, 2020. [Google Scholar]