SNELM: SqueezeNet-Guided ELM for COVID-19 Recognition

1  Introduction

COVID-19 has caused 6.26 million deaths and 522.06 million confirmed cases till 17/May/2022. The polymerase chain reaction (PCR) can effectively detect its existence; however, the cluster of false-positive [1] perplexes clinicians. The chest computed tomography (CCT) [2] is another precise way to help clinicians to diagnose COVID-19 patients. Till July/2022, three vaccines are approved for use in UK, including Moderna, Oxford/AstraZeneca, and Pfizer/BioNTech.

In the recent few years, scholars proposed to novel artificial intelligence (AI)-based models for COVID-19 diagnosis. For examples, El-kenawy et al. [3] proposed an innovative feature selection and voting (FSV) classifier Wu [4] proposed a three-segment biogeography-based optimization (3SBBO) method for COVID-19 detection. Zhang [5] proposed a model combining a convolutional neural network (CNN) with stochastic pooling (SP). Their method is renamed CNNSP. Chen [6] merged gray-level co-occurrence matrix (GCM) and support vector machine (SVM) for COVID-19 classification. This method is named GCMSVM. Wang [7] proposed a wavelet entropy and Jaya (WEJ) algorithm. Pi [8] merged GCM with Schmitt neural network (SNN) for COVID-19 diagnosis. Their model is named GCMSNN. Wang [9] introduced self-adaptive particle swarm optimization (SaPSO) for COVID-19 detection. Ni et al. [10] proposed a deep learning approach (DLA) to characterize COVID-19. Wang et al. [11] developed a weakly supervised framework. Their model was named DeCovNet. Gafoor et al. [12] developed a deep learning model (DLM) to detect COVID-19 using chest X-ray.

Nevertheless, the above models still have room to improve in terms of their recognition performances, i.e., the accuracy. Inspired by the model in Özyurt et al. [13], we proposed SqueezeNet-guided ELM (SNELM), which combines traditional SqueezeNet (SN) with the extreme learning machine (ELM). Nevertheless, our SNELM is different from [13] in two ways. First, we do not use fuzzy C-means for super-resolution. Second, we choose the SN model with complex bypass, while [13] chooses the vanilla SN model. Our experiments show the effectiveness of this proposed SNELM model. In all, this study has several novel contributions:

a) The multiple-way data augmentation (MDA) is used to increase the size of the training set.

b) We propose the novel SNELM model to diagnose COVID-19.

c) SNELM model gives higher results than seven state-of-the-art models.

2  Dataset and Preprocessing

Two datasets (D1 and D2) are used since they can report the results more unbiasedly. The details of the two datasets can be found in [4,5]. Table 1 displays the descriptions of D1 and D2. Suppose n1 stands for the number of subjects, and n2 the number of CCT images. It is easy to observe that there are n2=296 images in D1 and n2=640 images in D2.

A five-step preprocessing is employed. The flowchart can be seen in Fig. 1a, in which the five steps are grayscaling, histogram stretching (HS), margin and text crop (MTC), downsampling (DS), and coloriazation. Here U stands for the dataset at each step. HS is used to enhance the contrast. Suppose U1={u1(k)} , we first need to calculate its lower bound u1L(k) and upper bound u1U(k) as:

{u1U(k)=maxx⁡maxy⁡u1(x,y|k)u1L(k)=minx⁡miny⁡u1(x,y|k), (1)

and the HSed image is defined as

u2(k)=u1(k)−u1L(k)u1U(k)−u1L(k). (2)

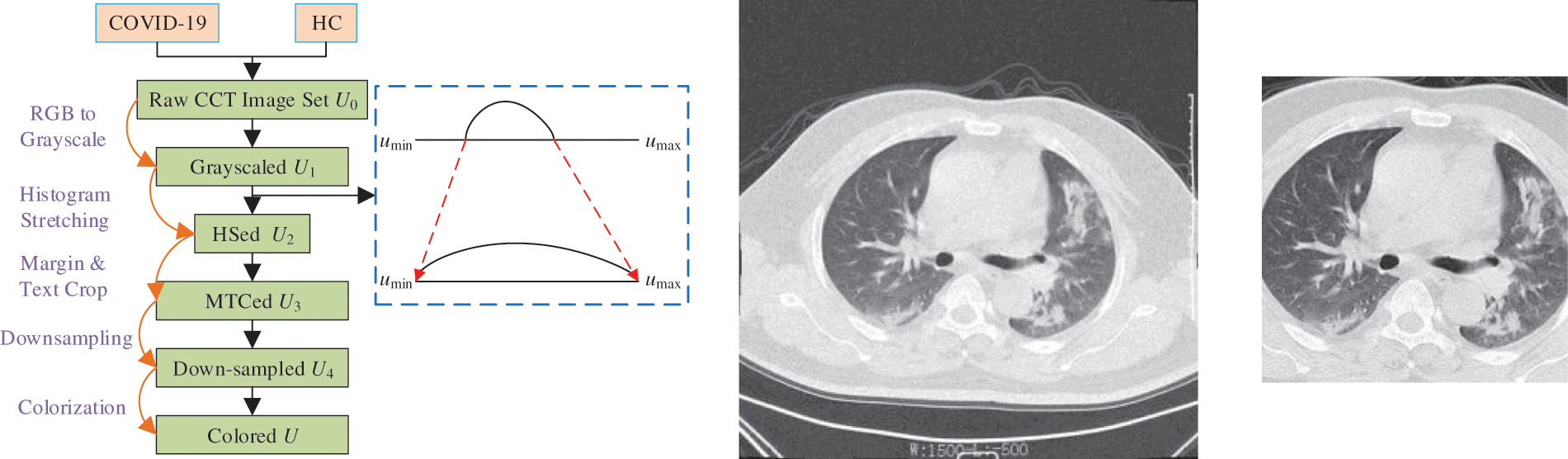
Figure 1: Preprocessing

The grayscale range of u2(k) is [umin,umax] . Figs. 1b and 1c show the raw COVID-19 and preprocessed images, respectively. The downsampled dataset is symbolized as U4={u4(k)} with the size of each image as (a1,a2) . The final grayscale image u4(k) is then stacked along channel direction to output the color image u(k) :

u(k)=fcatchannel[u4(k),u4(k),u4(k)], (3)

where fcatchannel denotes the catenation function along the channel direction. The size of u(k) is now a1×a2×3 .

3  Description of SNELM

3.1 Multiple-Way Data Augmentation

Table 2 itemizes the abbreviation and their meanings. Fig. 2 illustrates the schematic of MDA. Assume the original image is u(k) , then the horizontally mirrored image (HMI) is defined as uHMI(k) as

uHMI(x,y|k)=u(a1−x,y|k), (4)

where we do not take color channels into consideration. Then, all the b1 different data augmentation (DA) methods giDA,i=1,…,b1 are applied to both u(k) and uHMI(k) . Suppose each DA generates b2 new images. Finally, the whole generated images Λ(k) are defined as:

u(k)↦Λ(k)=fconimage{u(k)uHMI(k)g(1)DA[u(k)]⏟b2g(1)DA[uHMI(k)]⏟b2⋯⋯g(b1)DA[u(k)]⏟b2g(b1)DA[uHMI(k)]⏟b2}, (5)

where fconimage is the concatenation function along the image direction. The augmentation factor of MDA (AFMDA) is defined as:

b3=|Λ(k)|u(k)=2×b1×b2+2. (6)

Compared to normal individual DA methods, the MDA fuse the separate DA methods together and thus can yield better performances [14].

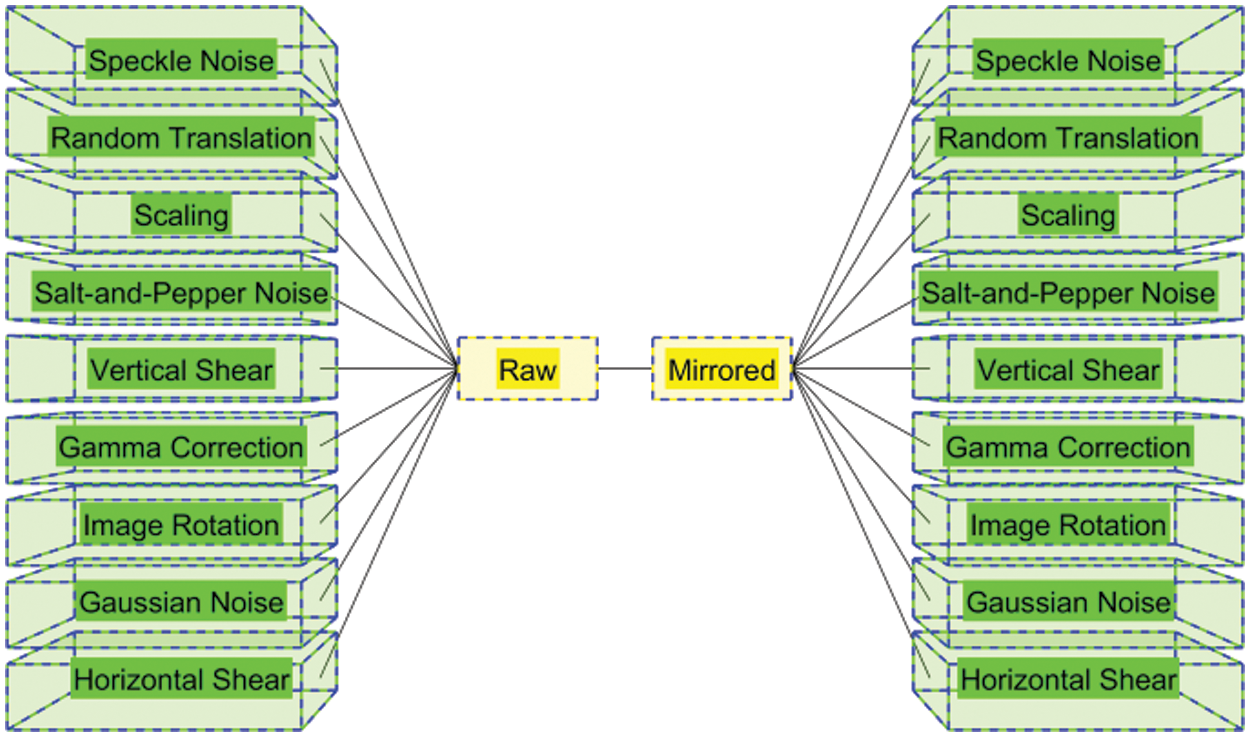
Figure 2: Schematic of MDA

3.2 Fire Module and SqueezeNet with Complex Bypass

SqueezeNet (SN) is chosen since it can achieve a 50× reduction in model size compared to AlexNet and maintain the same accuracy [15]. This lightweight SN can help make our final COVID-19 recognition model fast and still have sufficient accuracy.

The fire module (FM) is the core component in the N. It contains a squeeze layer (SL), which uses only 1×1 kernels, followed by an expand layer (EL), which contains several 1×1 and 3×3 kernels [16]. The structure of FM is shown in Fig. 3. Three tunable hyperparameters need to be tuned in an FM: s1×1 , e1×1 , and e3×3 , which stand for the number of 1×1 kernels in the SL, and the number of 1×1 and 3×3 kernels in the EL.

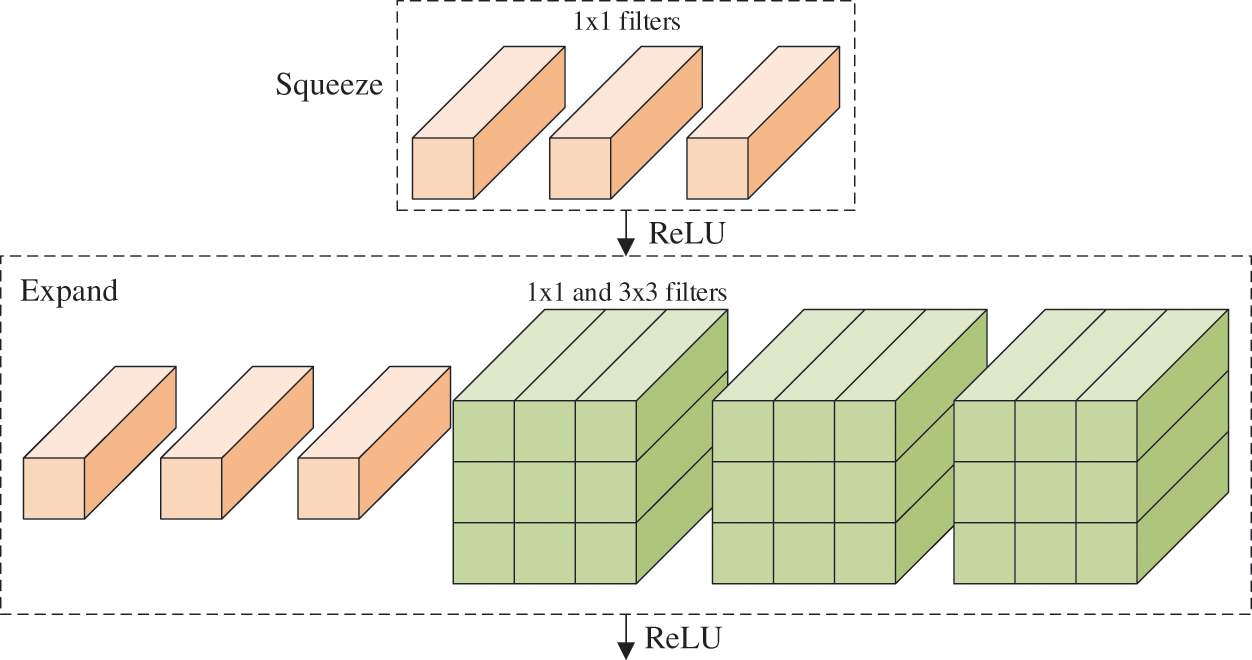
Figure 3: Structure of FM ( s1×1=3 , e1×1=3 , e3×3=3 )

Compared to ordinary convolutional neural network (CNN) architectures, the SN [17] has three main advantages: (i) replace traditional 3×3 kernels with 1×1 kernels. (ii) drop the number of input channels to 3×3 kernels using SLs. (iii) downsample late in SN, so the convolution layers have large activation maps [18].

There are different variants of SN. Özyurt et al. [13] used vanilla SN, while our SNELM use SN with complex bypass. Fig. 4 shows the flowchart, where we can observe not only simple bypass but also complex bypass are added between some FMs. If the “same-number-of-channel” requirement is met, a simple bypass is added. If that requirement is not met, a complex bypass is added. These bypasses can help improve the recognition performances, and their designs are similar to those in ResNet.

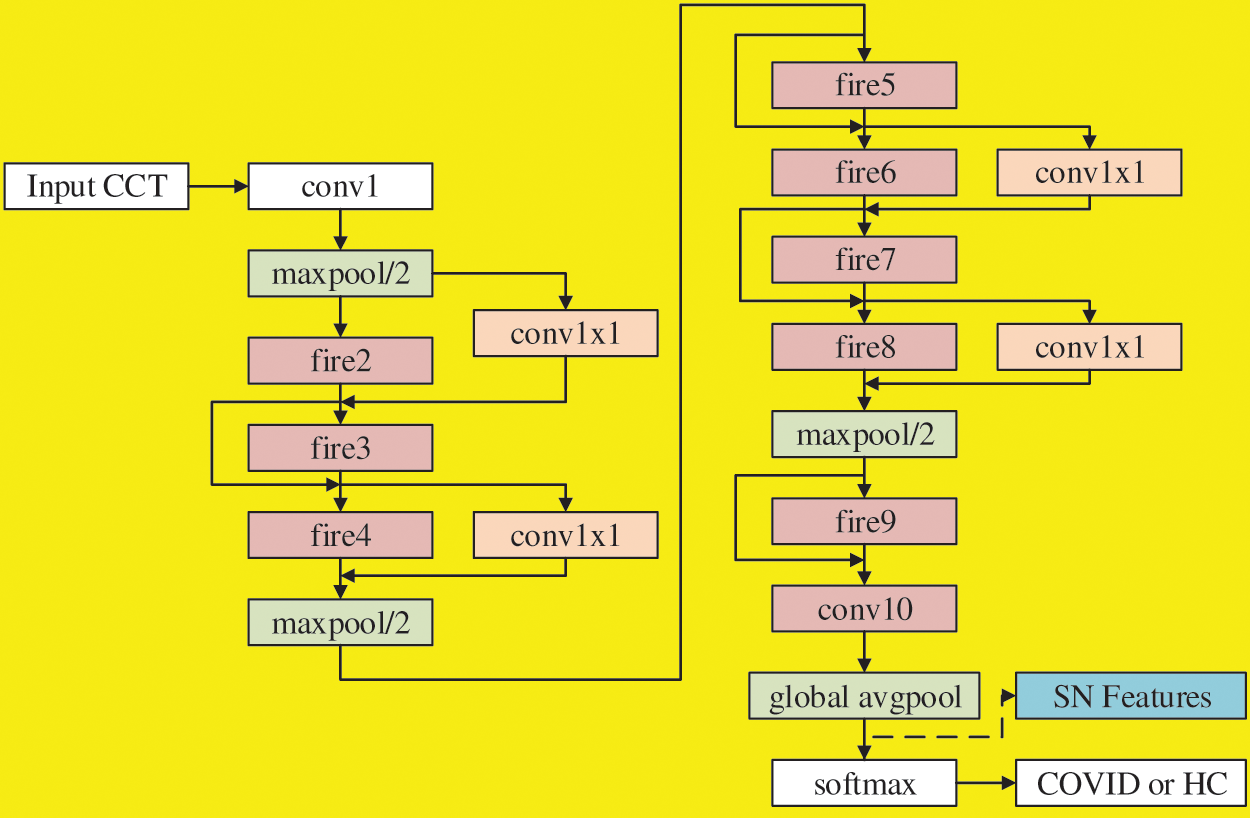
Figure 4: Flowchart of SN with simple bypass and complex bypass

3.3 SN-Guided ELM

The SN features after global avgpool (See Fig. 4) are used as the learnt features and passed to the extreme learning machine (ELM) [19] that features a very fast classifier. Besides, ELM is simple to use, has greater generalization performance, and is appropriate for several nonlinear kernel functions and activation functions. Its structure is a single hidden-layer feedforward network shown in Fig. 5.

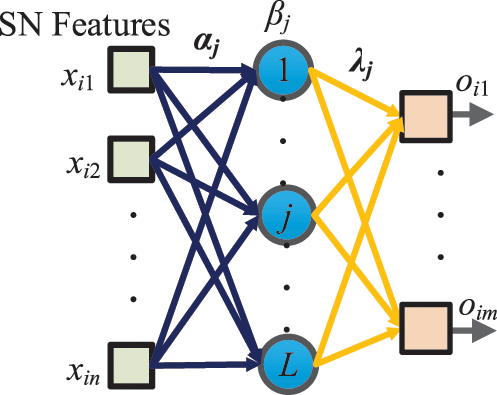
Figure 5: Schematic of SN-guided ELM

Let the i-th input sample be xi=(xi1,…,xin)T∈Rn,i=1,…,N . The output of an ELM with L hidden neurons is:

Oi=∑j=1Lλjh(αjxi+βj),i=1,…,N, (7)

where h stands for the activation function, αj=(αj1,αj2,…,αjn)T the input weight, βj the bias, Oi=(oi1,oi2,oi3,…oim)T the output of the model for the i -th input sample. Afterwards, the model is trained to yield

∑j=1L⁡λjh(αjxi+βj)=yi,i=1,…,N. (8)

Let us rephrase the above equation as

Mλ=Y, (9)

where

M(α1,…,αL,β1,…,βL,x1,…,xN)=[h(α1x1+β1)⋯h(αLx1+βL)⋮⋱⋮h(α1xN+β1)⋯h(αLxN+βL)]N×L, (10)

λ=[λ1T⋮λLT]L×m,Y=[y1T⋮yNT]N×m. (11)

It challenges the users to acquire the optimal αj , βj and λj . ELM can yield a solution quickly via the pseudo inverse:

λ=M†Y, (12)

where M† signifies the Moore-Penrose [20] of M . The pseudocode is shown in Algorithm 1.

3.4 Cross-Validation and Evaluation

T runs of I -fold cross-validation (CV) are carried out. Assume the test confusion matrix (TCM, symbolized as Θ ) over t -th run and i -th fold is:

Θ(t,i)=[θ11(t,i)θ12(t,i)θ21(t,i)θ22(t,i)], (13)

where i=1,…,I stands for the fold index, and t=1,…,T the run index. The (θ11,θ12,θ21,θ22) signify true positive, false negative, false positive, and true negative, respectively. At i -th trial, the i -th fold is employed as test, and the left folds {1,…,i−1,i+1,…,I} altogether are employed as training, as shown in Fig. 6, here one I -fold CV consists of I trials.

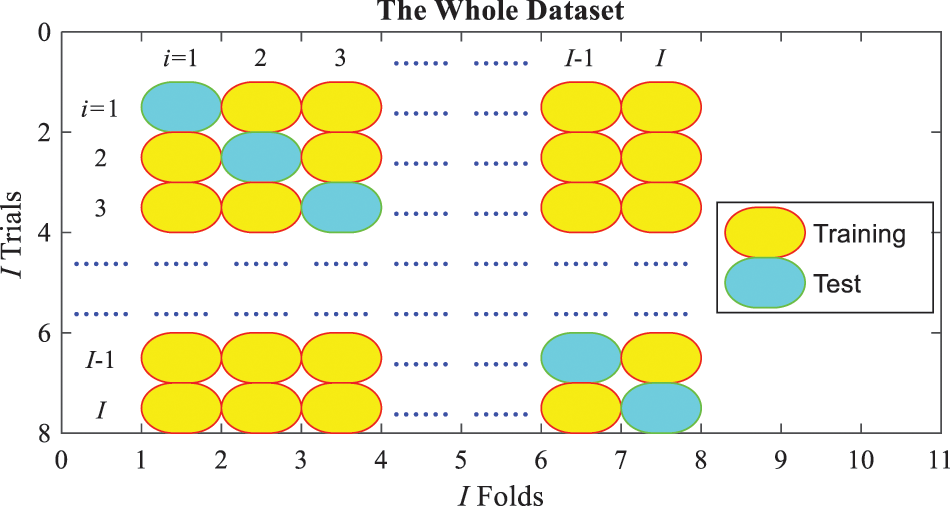
Figure 6: Schematic of one run of I -fold CV

Θ(t,i) is gauged based on the i -th fold, which is the test set. We afterward take their summation across altogether I trials, as shown in Fig. 6. The TCM at t -th run Θ(t) is attained as

Θ(t)=∑i=1IΘ(t,i). (14)

At t -th run, seven indicators κ→(t) based on the TCM are calculated and concatenated in a whole as Θ(t) :

Θ(t)↦κ→(t)={κm(t),m=1,…,7}, (15)

where the first four indicators mean: κ1 sensitivity, κ2 specificity, κ3 precision, and κ4 accuracy as:

{κ1(t)=θ11(t)θ11(t)+θ12(t)κ2(t)=θ22(t)θ22(t)+θ21(t)κ3(t)=θ11(t)θ11(t)+θ21(t)κ4(t)=θ11(t)+θ22(t)θ11(t)+θ12(t)+θ21(t)+θ22(t). (16)

κ5 is F1 score:

κ5(t)=2×κ3(t)×κ1(t)κ3(t)+κ1(t)=2×θ11(t)2×θ11(t)+θ12(t)+θ21(t), (17)

κ6 is Matthews correlation coefficient (MCC), which is a more reliable statistical rate that produces a high score only if the prediction obtained good results in all of the four entries in the TCM [21].

κ6(t)=θ11(t)×θ22(t)−θ21(t)×θ12(t)[θ11(t)+θ21(t)]×[θ11(t)+θ12(t)]×[θ22(t)+θ21(t)]×[θ22(t)+θ12(t)], (18)

and κ7 is the Fowlkes–Mallows index (FMI).

κ7(t)=θ11(t)θ11(t)+θ21(t)×θ11(t)θ11(t)+θ21(t) (19)

There are two indicators κ4 and κ6 using all the four basic measures (θ11,θ12,θ21,θ22) . This study finally chooses κ6 as the most important indicator due to its larger range ( −1≤κ6≤+1 ) than that of κ4 ( 0≤κ4≤1 ).

The previous process is for one run of I -fold CV. The experiment runs the I -fold CV T runs. After all runs, the mean and standard deviation (MSD) of all seven indicators κ→={κm(m=1,…,7)} are gauged over T runs.

{μ(κm)=1T×∑t=1Tκm(t)σ(τm)=1T−1×∑t=1T|κm(t)−μ(κm)|2,m=1,…,7, (20)

where μ signifies the mean value and σ the standard deviation. The values of MSD are recorded in the format of μ±σ .

4  Experiments, Results, and Discussions

4.1 Hyperparameter Setting

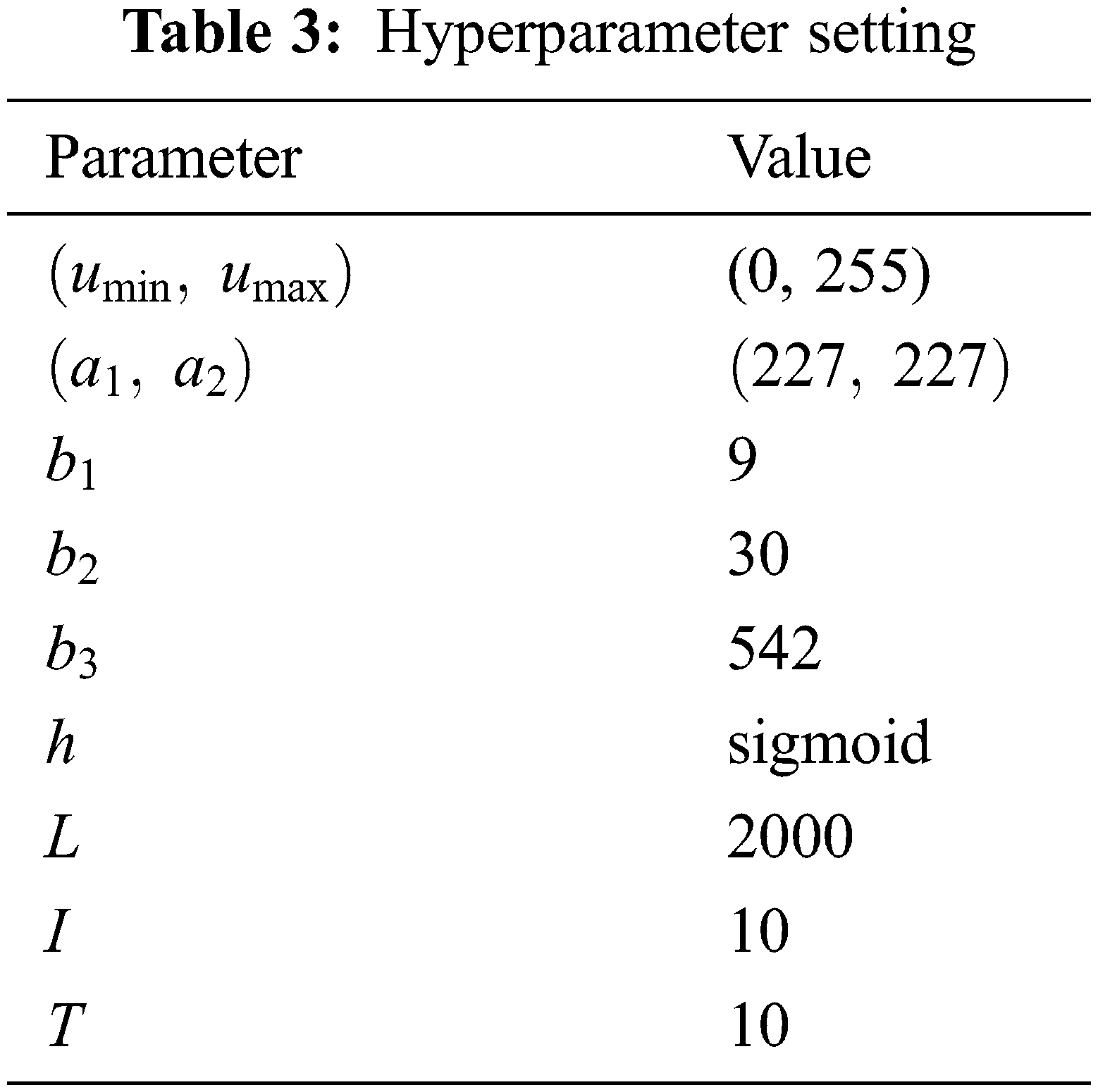
The hyperparameters are listed in Table 3. The minimum and maximum gray values of HSed images are (0,255) . The size of the downsampled image is 227×227 . We have in total b1=9 different DA methods on both raw image and HMI. Every DA produces b2=30 images. The AFMDA is b3=542 . Activation function in ELM is chosen the sigmoid function. The number of hidden neurons in ELM is set to L=2000 . We run ten runs of 10-fold CV to report the robust results.

4.2 Results of MDA

The MDA result of Fig. 1c is shown in Fig. 7, in which we can observe the nine DA results, i.e., speckle noise, random translation, scaling, salt-and-pepper noise, vertical shear, Gamma correction, rotation, Gaussian noise, and horizontal shear. Due to the space limit, the nine DA outcomes on HMI are not displayed. Fig. 7 indicates that the MDA can increase the diversity of the training set.

Figure 7: Result of MDA

Meanwhile, the AFMDA value b3=542 makes the training burden of our model 542 times as much as that of the model without MDA. Nevertheless, in the test stage, there is no need to apply MDA to the test images, so our model is the same quick as the model without MDA.

4.3 Results of Proposed SNELM Model

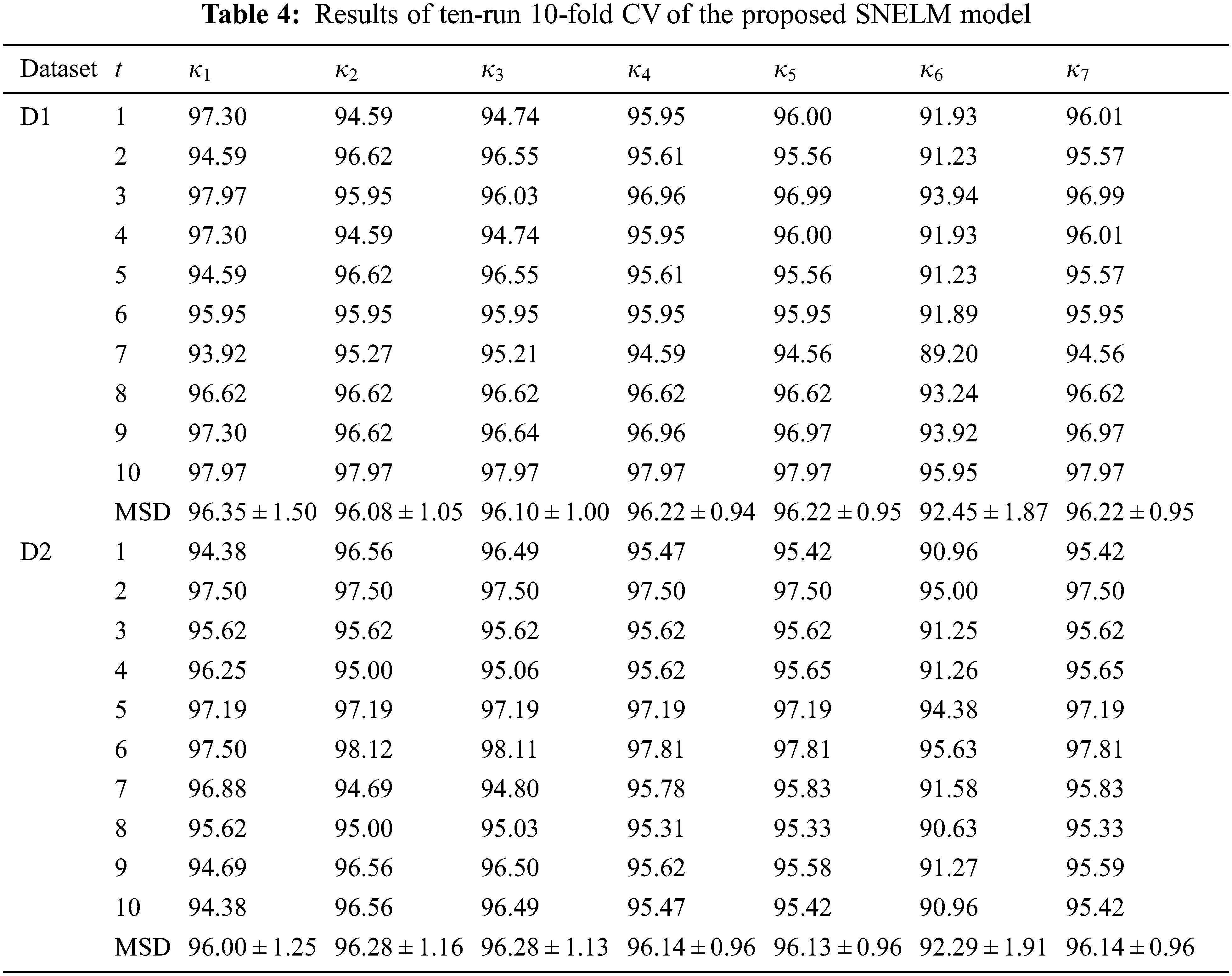
Table 4 displays the ten runs of 10-fold CV, where t = 1, 2, ..., 10 means the run index. For the dataset D1, SNELM attains a sensitivity of 96.35 ± 1.50%, a specificity of 96.08 ± 1.05%, a precision of 96.10 ± 1.00%, an accuracy of 96.22 ± 0.94%, an F1 score of 96.22 ± 0.95%, an MCC of 92.45 ± 1.87%, and an FMI of 96.22 ± 0.95%. For the dataset D2, SNELM attains a sensitivity of 96.00 ± 1.25%, a specificity of 96.28 ± 1.16%, a precision of 96.28 ± 1.13%, an accuracy of 96.14 ± 0.96%, an F1 score of 96.13 ± 0.96%, an MCC of 92.29 ± 1.91%, and an FMI of 96.14 ± 0.96%.

4.4 Confusion Matrix and ROC Curve

After combining the ten runs altogether, we can draw the overall TCMs and the ROC curves of the two datasets. The top row of Fig. 8 displays the TCM of two datasets. The bottom row of Fig. 8 displays their corresponding ROC curves. The AUC values of D1 and D2 are 0.9767 and 0.9776, respectively.

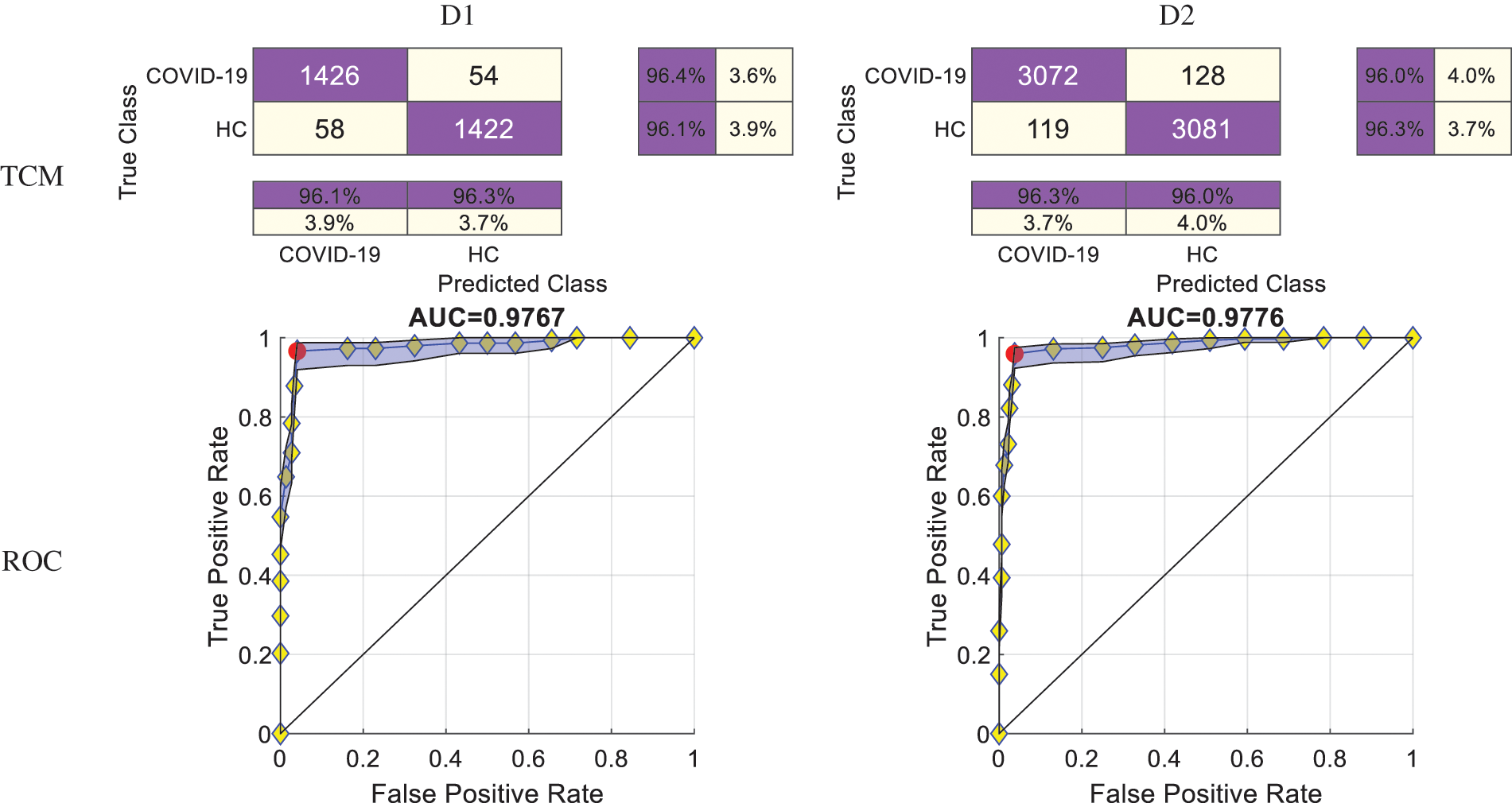
Figure 8: TCMs and ROC curves of two datasets

4.5 Comparison with State-of-the-Art Models

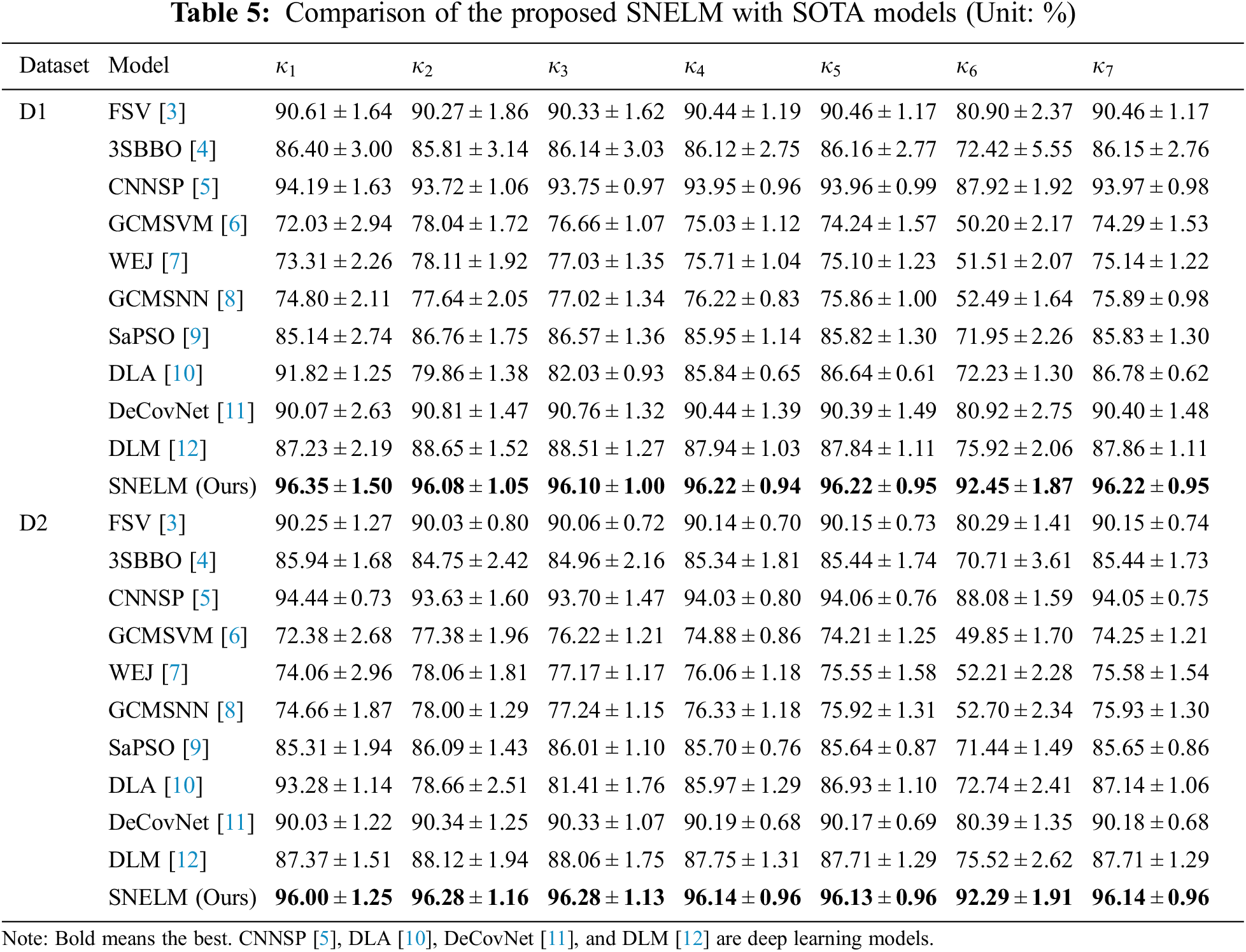
The SNELM model is compared with seven state-of-the-art COVID-19 recognition models over two datasets. The comparison models consist of FSV [3], 3SBBO [4], CNNSP [5], GCMSVM [6], WEJ [7], GCMSNN [8], SaPSO [9], DLA [10], DeCovNet [11], and DLM [12]. Particularly, CNNSP [5], DLA [10], DeCovNet [11], and DLM [12] are deep learning models. The results on two datasets are itemized in Table 5. As we can observe, the proposed SNELM outperforms other state-of-the-art models in both datasets.

Error bar (EB) can assist in observing the differences in the model’s performances. Fig. 9 displays the EB of different models over two datasets. It shows that the performance of this proposed SNELM model is higher than those of seven state-of-the-art models. The reason of the success of SNELM model may lie in three points: (i) MDA helps increase the size of training set significantly. (ii) The SN with complex bypass helps extract efficient features. (iii) ELM serves as an effective classifier.

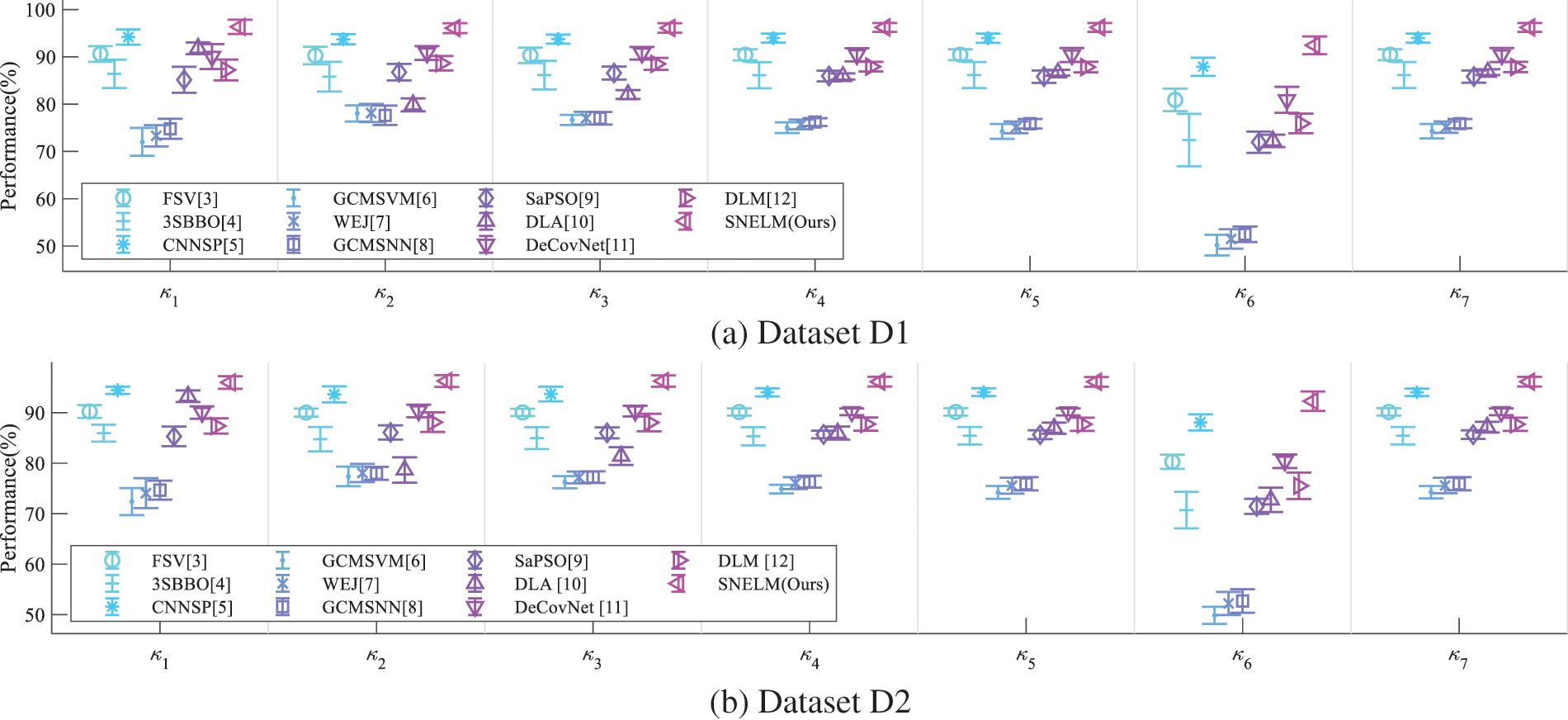
Figure 9: EBs of model comparison

5  Conclusions

This study proposes an innovative SNELM model for COVID-19 detection. The MDA is used to increase the size of the training set. The SN with complex bypass is employed to generate SN features. ELM is used as the classifier. This proposed SNELM model can produce higher results than seven state-of-the-art models.

There are three deficiencies of the proposed SNELM model: (i) Strict clinical validation is not tested. (ii) The SNELM model is a black box. (iii) Other chest-related infectious diseases are not considered.

In our future studies, our team first shall distribute the proposed SNELM model to the online cloud computing environment (such as Microsoft Azure or Amazon Web Services). Second, we intend to incorporate Gram-CAM into this model to make it explainable. Third, chest-related infectious diseases, such as tuberculosis or pneumonia, will be added to our task.

Funding Statement: This paper is partially supported by Medical Research Council Confidence in Concept Award, UK (MC_PC_17171); Royal Society International Exchanges Cost Share Award, UK (RP202G0230); British Heart Foundation Accelerator Award, UK (AA/18/3/34220); Hope Foundation for Cancer Research, UK (RM60G0680); Global Challenges Research Fund (GCRF), UK (P202PF11); Sino-UK Industrial Fund, UK (RP202G0289); LIAS Pioneering Partnerships award, UK (P202ED10); Data Science Enhancement Fund, UK (P202RE237).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  B. Joob and V. Wiwantikit, “COVID-19 pcr test, cluster of false positive and importance of quality control,” Clinical Laboratory, vol. 66, pp. 2147–2147, 2020. [Google Scholar]

 2.  S. S. Alotaibi and A. Elaraby, “Generalized exponential fuzzy entropy approach for automatic segmentation of chest ct with COVID-19 infection,” Complexity, vol. 2022, Article ID: 7541447, 2022. [Google Scholar]

 3.  E. S. M. El-kenawy, A. Ibrahim, S. Mirjalili, M. M. Eid and S. E. Hussein, “Novel feature selection and voting classifier algorithms for COVID-19 classification in ct images,” IEEE Access, vol. 8, pp. 179317–179335, 2020. [Google Scholar]

 4.  X. Wu, “Diagnosis of COVID-19 by wavelet renyi entropy and three-segment biogeography-based optimization,” International Journal of Computational Intelligence Systems, vol. 13, pp. 1332–1344, 2020. [Google Scholar]

 5.  Y. D. Zhang, “A seven-layer convolutional neural network for chest ct based COVID-19 diagnosis using stochastic pooling,” IEEE Sensors Journal, pp. 1–1, 2020, https://doi.org/10.1109/JSEN.2020.3025855 (Online First). [Google Scholar]

 6.  Y. Chen, “COVID-19 classification based on gray-level co-occurrence matrix and support vector machine,” In: K. C. Santosh and A. Joshi, (Eds.COVID-19: Prediction, Decision-Making, and its Impacts, Singapore: Springer, pp. 47–55, 2020. [Google Scholar]

 7.  W. Wang, “COVID-19 detection by wavelet entropy and jaya,” Lecture Notes in Computer Science, vol. 12836, pp. 499–508, 2021. [Google Scholar]

 8.  P. Pi, “Gray level co-occurrence matrix and schmitt neural network for COVID-19 diagnosis,” EAI Endorsed Transactions on e-Learning, vol. 7, pp. e3, 2021. [Google Scholar]

 9.  W. Wang, “COVID-19 detection by wavelet entropy and self-adaptive pso,” Lecture Notes in Computer Science, vol. 13258, pp. 125–135, 2022. [Google Scholar]

10. Q. Q. Ni, Z. Y. Sun, L. Qi, W. Chen, Y. Yang et al., “A deep learning approach to characterize 2019 coronavirus disease (COVID-19) pneumonia in chest ct images,” European Radiology, vol. 30, pp. 6517–6527, 2020. [Google Scholar]

11. X. G. Wang, X. B. Deng, Q. Fu, Q. Zhou, J. P. Feng et al., “A weakly-supervised framework for COVID-19 classification and lesion localization from chest ct,” IEEE Transactions on Medical Imaging, vol. 39, pp. 2615–2625, 2020. [Google Scholar]

12. S. A. Gafoor, N. Sampathila, M. Madhushankara and K. S. Swathi, “Deep learning model for detection of COVID-19 utilizing the chest x-ray images,” Cogent Engineering, vol. 9, Article ID: 2079221, 2022. [Google Scholar]

13. F. Özyurt, E. Sert and D. Avcı, “An expert system for brain tumor detection: Fuzzy c-means with super resolution and convolutional neural network with extreme learning machine,” Medical Hypotheses, vol. 134, pp. 109433, 2020. [Google Scholar]

14. V. Govindaraj, “Deep rank-based average pooling network for COVID-19 recognition,” Computers, Materials & Continua, vol. 70, pp. 2797–2813, 2022. [Google Scholar]

15. R. Y. Lin, Y. H. Xu, H. Ghani, M. H. Li and C. C. J. Kuo, “Demystify squeeze networks and go beyond,” in Conf. on Applications of Digital Image Processing XLIII, Bellingham, USA, pp. 11510, 2020. [Google Scholar]

16. A. Ullah, H. Elahi, Z. Y. Sun, A. Khatoon and I. Ahmad, “Comparative analysis of alexnet, resnet18 and squeezenet with diverse modification and arduous implementation,” Arabian Journal for Science and Engineering, vol. 47, pp. 2397–2417, 2022. [Google Scholar]

17. F. N. Iandola, S. Han, M. W. Moskewicz, K. Ashraf, W. J. Dally et al., “Squeezenet: Alexnet-level accuracy with 50x fewer parameters and <0.5 mb model size,” arXiv preprint arXiv:1602.07360, 2016. [Google Scholar]

18. L. S. Bernardo, R. Damasevicius, V. H. C. de Albuquerque and R. Maskeliunas, “A hybrid two-stage squeezenet and support vector machine system for Parkinson’s disease detection based on handwritten spiral patterns,” International Journal of Applied Mathematics and Computer Science, vol. 31, pp. 549–561, 2021. [Google Scholar]

19. S. Tummalapalli, L. Kumar, L. B. M. Neti and A. Krishna, “Detection of web service anti-patterns using weighted extreme learning machine,” Computer Standards & Interfaces, vol. 82, Article ID: 103621, 2022. [Google Scholar]

20. R. G. Moghadam, B. Yaghoubi, A. Rajabi, S. Shabanlou and M. A. Izadbakhsh, “Evaluation of discharge coefficient of triangular side orifices by using regularized extreme learning machine,” Applied Water Science, vol. 12, Article ID: 145, 2022. [Google Scholar]

21. D. Chicco and G. Jurman, “The advantages of the matthews correlation coefficient (mcc) over f1 score and accuracy in binary classification evaluation,” BMC Genomics, vol. 21, Article ID: 6, 2020. [Google Scholar]