Power Scheduling with Max User Comfort in Smart Home: Performance Analysis and Tradeoffs

1  Introduction

With the gradual expansion of the human population, electricity usage is increasing. Electricity consumption currently exceeds the capacity of traditional power systems [1]. Energy management is studied as one of the complex optimization issues in power control systems. The concept of a Smart Grid (SG) was proposed to meet this demand. In SG, Smart Meter (SM) is a conduit for information sharing among consumers and utilities. This data is then utilized to enhance smart homes’ energy efficiency. Various Demand-Side Management (DSM) solutions are proposed in the literature. In [2,3], to efficiently manage energy through a smart grid, such as ideal scheduling home efficient electric appliances, power dispatch and nature-inspired methods to solve an SG’s energy resource management problems.

In Energy Management System (EMS), the tactics such as load shifting, peak clipping and valley filling help consumers optimize their energy use patterns. That approach, sequentially, aids in achieving stability between supply and demand. Individuals are recommended to use these strategies to shift peak load to off-peak hours [4]. In [5] author argues that resolving grid stability issues is becoming more difficult with the rapid rise in energy demand. As the load demands of power users increase, demand and supply patterns become unbalanced. This eventually leads to load shedding. As a result, Demand Response (DR) is an efficient technique for energy customers to change their consumption patterns and receive rewards in exchange for a minor inconvenience. Price-based DR and Incentives-based DR programs are the two forms of DR. Some of the pricing rates available are Real-Time Pricing (RTP), Time of Use (ToU), Day-Ahead Pricing (DAP), Critical Peak Pricing (CPP), Inclination Block Rate (IBR).

Furthermore, among the pricing mentioned above assessing models, the most competent pricing scheme is RTP, which is intended for power markets [6]. The collective goals of power management in Singapore are to decrease power costs, user comfort, PAR, aggregated power consumption and integrate renewable energy sources. Several DSM strategies have been developed to attain the abovementioned goals in recent years. To reduce costs and energy usage, [7,8] use Mixed-Integer LP, convex programming, mixed-integer NLP and Non-integer Linear Programming. These approaches, on the other hand, are incapable of coping with a high number of items. Because of the shortcomings of the techniques mentioned above, various meta-heuristic optimization strategies for energy management trendy SG are introduced. The authors of [9,10] use a genetic algorithm to lower the Cost of power GA. Differential Evolution (DE) as well as swarm-based method, i.e., Ant Colony Optimization (ACO), is also employed to reduce power costs in addition to consumption [11]. In our study, we looked at rates of dynamic pricing that boost manipulators to swing Load among crowning hours. To reduce Peak Average Ratio (PAR) and electricity costs and increase user comfort, we used methods inspired by nature. We applied meta-heuristics methods; such as Grey Wolf Algorithm (GWA), Harmony Search Algorithm (HSA) and Hybrid HGWA (HSA and GWA) algorithms endure tested to understand in what way we can monitor and control the intelligent machines in many solo homes. HSA requires low mathematical and derivative knowledge requirements, startup configurations and the GWA optimization technique that mimics grey wolves’ searching and hunting behavior; by hybridizing these approaches, we enhanced the power scheduling and reduced the cost maximum.

1.1 Contributions

We proposed an energy-efficient framework for single and multi-dwellings. Our proposed approaches are compared against existing schemes using performance metrics, including Cost, PAR, Waiting time (User Comfort) and Load. On 12 appliances, the current and planned hybrid models were used to improve power usage for numerous homes. The proposed methods (HGWA) performed better than the existing mechanisms (ACO [11], MILP, ILP and NILP [12,13], respectively) proposed approach. An efficient way to schedule home appliances is with HGWA. Reduce the PAR to ensure the highest level of user comfort.

1.2 Paper Organization

The remainder of the article is structured. The background is discussed in Section 2. Relevant research is conferred in Section 3; Problem Statement is discussed in Sections 4 and 5 proposed system model is presented. Section 6 discusses the energy optimization measures we employ. Section 7 describes the Simulation and its results. Section 8 contains the Discussion and Significance, while Section 9 has the Conclusion and the Future Directions.

2  Related Work

Several optimization strategies have been proposed in recent years to boost SG significantly. Load management and cost minimization are the primary concerns in creating an optimal solution. Existing literature on the various optimization techniques is covered in this section. The effectiveness aims for a stable energy intake and avoids grid over-or under-utilization author uses a Multi-Objective Evolutionary (MOE) to solve these challenges [14]. The goal of this study is to save money on power by using efficient energy. The delay computation formula determines how long it takes for appliances to operate. Each Load is given priority in this paper. A high-priority device can prevent a low-priority appliance from running. The delay period of a small importance application is then increased by the time it has been waiting. The average latency of all appliances is calculated using a predefined function. The goal of this study is to decrease typical appliance wait times while lowering energy consumption costs. A skilled energy management system was proposed in [15]. The author focuses on supply chain management.

In [16], they provided an MG, day-ahead scheduling prototypical that considers the transmission network. The proposed work aims to reduce the entire PV operation generation costs, diesel generators (DG), wind turbines (WT), and batteries while considering power flow restrictions. According to [17], shutting off low-priority appliances reduces energy consumption, monetary Cost and PAR. Appliances are allocated priorities based on user preferences [18] suggested a GA-based optimization method for intelligent home cost reduction. The authors compare the new strategy to simulated annealing and greedy search techniques. In [19], describe a DSM model based on intelligent switches. Each appliance has a priority in this paradigm and every appliance operation is set individually with the help of a global positioning system. Our suggested system reduces total power consumption by 11.2 percent. Similarly, [20] describes a competent HSA for controlling energy storage scheduling employing renewable energy sources. The TOU pricing model is combined with a demand control policy. The author describes a heuristic strategy for scheduling smart appliances in residential areas [21]. The suggested technique is contrasted with the existing method based on computational and electricity costs. The computational time, on the other hand, is cut in half. In [22] author presents a unique scheduling model for residential appliances. The authors create a scheduling model based on MILP and heuristics.

The authors of [23] suggest an optimum power scheduling tactic for DR in a residential neighborhood. According to the results, the proposed scheduling tactic accomplishes a significant tradeoff between user comfort and the cost of electricity. The results show that the suggested GA-based model is produced in both circumstances. Describe an innovative scheduling technique based on an ideal stopping criterion [24]. The authors proposed dual scheduling algorithms. Simulation results demonstrate the proposed algorithms’ usefulness for comfort maximization and energy cost reduction. The authors of [25] also described Storage Models for renewable energy. They introduced upcoming days forecasting load technique based on ANN. The researchers predicted load demand load for the coming day using the previous day’s and present day’s energy consumption patterns. The proposed model condensed execution time by 38% and the precision of limiting quasi in historical load statistics supply curve was increased by 97%. The author in [26] proposes the SG energy efficiency enhancement prototype for intelligent manufacturing. To avoid reverberation peaks, the author suggests prioritizing induced energy management for load shifting [27]. A mathematical model for day-ahead load management is provided to reduce rebound peaks. For autonomous load shifting, however, meta-heuristic approaches are used. The proposed techniques save the most money while reducing rebound load surges during off-peak hours. The price of power on the open market is determined by customer behavior. Demand Response Programs (DRPs) that effectively educate power consumers are difficult to come by [28], suggesting a DRP model in which the most significant number of consumers are encouraged to create a plan for the DRP technique. The presented model differs from the demand electricity idea in that it lowers maximum energy consumption costs by enabling the most significant number of users to contribute to the DRP [29]. The simulation findings support the suggested model’s ability to lower energy costs and improve load valley fills.

Consumer decisions are mainly responsible for SG’s success. In [30], the author proposes conclusion support through energy management aimed at home applications. The projected finite machine assists in the selection of a suitable scenario based on the users’ preferences. According to the simulation results, the economic strategy reduces electricity costs by 18% [31]. According to available research, meta-heuristic methods are frequently utilized for optimization due to their capacity to quickly cope with large and complicated problems because of their self-curative, self-defense and self-association systems [32]. In [33], GWA, HSA, and anticipated HGWA are used to assess our tasks’ final goals. A new feature selection wrapper binary formula is based on an altered Whale Optimization Algorithm and the Sine Cosine Algorithm. This algorithm was linked to gathering peculiar properties and picking the best features [34]. ANOVA and Wilcoxon’s rank-sum tests are used in statistical analysis to propose and validate the Enhanced Ensemble Method for Solar Radiation [35]. They exhibit remarkable specificity and uniformity when comparing the proposed design issues to multi-objective optimization using particle swarms to high convergence. To address any related scheduling issues, Aquila Optimizer Premised PSO Swarm Intelligence is merged for IoT Scheduling Algorithm Application [36]. In this article, GWA, HSA, and anticipated HGWA are used to assess our tasks’ final goals.

3  Problem Statement

Furthermost commonly addressed topics in the literature on SG are cost minimization, PAR reduction, load balancing and consumer ease expansion. Aside from that, RES integration is a significant concern in the SG domain. [37] for example, convex programming reduces electricity costs, although execution time suffers. In [38], the author use MILP, ILP and NILP optimization strategies to address the cost reduction challenge. User comfort and RES integration, on the other hand, are overlooked. Correspondingly, in [9], MILP is used to discover the ideal energy-feasting pattern to decrease power cost while considering the integration of RES. However, the comfort of the user is ignored. All the above-given methods are incapable of handling a high number of appliances. Various meta-heuristic optimization methodologies are used to develop an effective HEMS to overcome this constraint. In [10], the authors employed GA to minimize the cost of electricity. Researchers in this study operated appliances with the same power rating for different households. Several households have appliances with varying power ratings. In [14] author uses the MOEA to fulfill their cost and user comfort goals, but PAR is ignored. For the scheduling problem, [15] suggests a mix of DE and HSA algorithms. The results indicate that this hybrid strategy reduces costs well. A new HSA is employed by [17,19]. Ant colony optimization is used to schedule priority-based energy storage systems. The writers tried to cut the electricity bill and PAR but failed to account for the usual wait times.

The majority of them accomplish low costs by sacrificing user comfort. It can, however, be minimized by moving the Load from high-load hours to low-load hours when the load demand is low. The existing rating mechanism influences power use and prices. According to our research, the suggested HEMS lowers power and PAR costs. We planned to use a hybrid approach termed HGWA, which combines HSA and GWA, to analyze the effectiveness of our HEMS. It combines the best aspects of both techniques. We consider numerous dwellings in our focused scenario. Each home has a variety of appliances. According to the nature of each appliance’s consumption pattern, it is divided into distinct classifications.

Our research took into account multiple homes and intelligent appliances. The following are the overall objectives of this project: Reduce your costs and PAR, Load balance, Determine the cost-benefit ratio between user comfort and cost and determine the most efficient schedule for household appliances.

4  Problem Formulation

The project’s primary goals are to lower PAR and electricity costs by optimizing energy use patterns. We use several knapsack problems to formulate our optimization problem (MKP). MKP is a combinative optimization problem that involves selecting the most acceptable object from an established of alternatives. Weight and value are two attributes that each item has. MKP’s goal is to choose valuable and light things with a total weight that does not exceed the knapsack’s full capacity. Our optimization challenge aims to save money on power by strategically positioning appliances in each time slot. Each appliance has two characteristics: its on/off status and power rating.

We use MKP to map our development problem as follows:

•   The number of appliances and things. Each appliance’s power rating and the weight of each object. The cost of an object at apiece interval of time value.

•   The number of knapsacks and the numeral of the interval of time. This optimization problem can be well-defined as:

min∑t=1T⁡(∑a=1APP⁡PApp X sv(t) X ya,t)       (1)

Subject to:

L(t)=Ein(t)+Eni(t)+Eb(t), (2)

L(t)≤βth, (3)

Lsch total=Luns total (4)

Csch total<Cuns total (5)

tα<t<tβ (6)

SV(t) ε [0,1] (7)

Eq. (1) shows the goal function, which aims to lower the daily cost as much as possible. Eq. (2) shows the total energy consumed by all appliances over a t-minute period. Eqs. (2)–(7) define the objective function limitations, with Eq. (2) indicating the total energy usage of all appliances for a given time interval denoted by t. Eq. (3) shows how energy use in a given time slot must be less than or equal to a predetermined threshold, lowering PAR. In Eq. (4), the power consumption constraint ensures that power utilization stays unchanged before and after scheduling. It also helps ensure that scheduling does not affect how long each appliance is in use. Correspondingly, Eq. (5) indicates that the entire cost of a planned load per day must be less than the total cost of an unprepared load per day. In Eq. (6), t represents the beginning of an appliance and t represents the end of an appliance (7) denotes the appliance’s current position, either 0 or 1. A 1 indicates that now the appliance is on, while a 0 means that it is off.

5  System Model

After considering highlighted problems, we have designed a proposed model discussed in detail in this section. The utility tariff is received by many households in a residential neighborhood, as indicated in Fig. 1. We present a HEMS aimed at scheduling a residential appliance to reduce electricity costs and PAR. Smart appliances, EMC and SM, are all included in a smart home. SM serves as a link between the utility and the consumer. EMC plans or schedules appliances based on the price signal supplied by the utility. Appliances submit data about their power use to EMC, which regulates them based on the signal price set by the utility. The utility sends pricing information to SM, who passes them through to EMC.

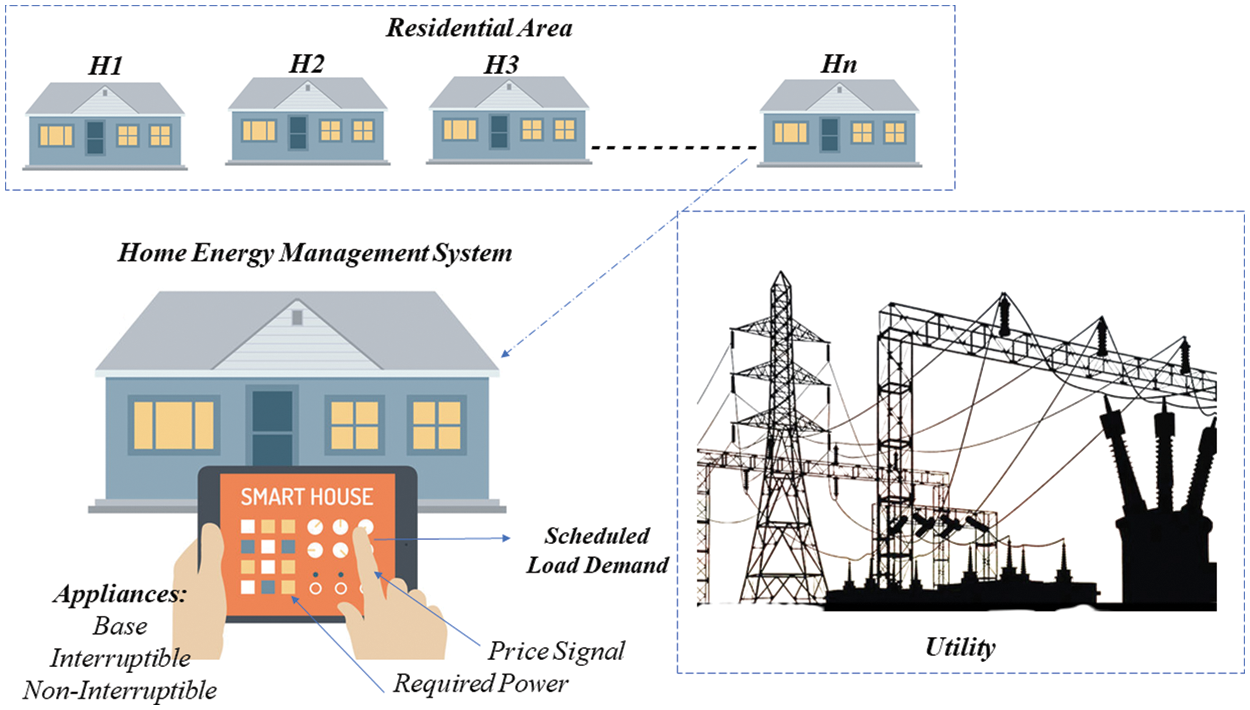
Figure 1: System model HEMS

Mean while, it gathers and delivers EMC energy data to the provider. Wireless networks like Z-wave and ZigBee, as well as conventional protocols, are used to connect utility and SM. Through a home area network, appliances, EMC and SM exchange data. This study looks at several residences, each of which has 12 appliances. We utilize the RTP tariff to calculate our electricity bills. A decision can be taken every 12 min in our circumstances. In other words, instead of 1 h, the scheduling horizon is 12 min. Single-day is alienated into 120 equivalent time slots, apiece of which is 12 min long. Because only a few appliances running for less than 60 min. When a day is alienated into 24 segments, a single hour is given to a device that only takes a limited time to work and the other time is unused since the schedule will not run-on machines that are not specified for that interval. As a result, choosing a time interlude of 12 min would save money on electricity while also improving the system's reliability. RTP pricing scheme is used. RTP is the competent pricing system for power markets among the abovementioned pricing methods [22]. To calculate electricity bills, we used RTP. Price indications in RTP might vary as frequently as hourly. Price signals fluctuate for different time slots in an RTP pricing scheme but remain constant within each time slot.

In the proposed system, users have single and multiple homes that contain various appliances that are classified into three types based on the usage time and the nature of the appliances: interruptible, non-interruptible and baseload appliances. These smart appliances are divided into groups based on their power usage patterns for scheduling purposes. The goal of our model seems to be to diminish the user’s PAR and electricity costs while taking UC into account as a waiting time. Table 1 includes the appliances’ energy ratings and working time (LOT) length.

For evaluation, we implemented three scenarios in a smart home with multiple appliances using HSA, GOW and hybrid HSA & GWA along with RTP tariff: The results are based on user comfort, PAR, power cost and energy consumption for 12 appliances.

Load Classification

Appliances are grouped based on their power usage or consumption patterns: base appliances, interruptible appliances (which can be interrupted during running) and non-interruptible appliances (once started, cannot be interrupted). Each category is described below:

Interruptible Appliances

These devices are similar to procrastinating appliances that can be used later. Its functionality might be disturbed if it is moved to another time period. Heavy loads are appliances having a power usage of more than 1.5 kWh that is interruptible. To meet the cost-cutting and PAR objectives, not more than two substantial additional loads are expected to function at a similar time. In this study, we deliberate electric radiators, water heaters and water pump to be heavy loads. If the electric radiator beside the water pump is turned on simultaneously, the water heater must also be turned off. ‘IN’ denotes the installation of interruptible appliances. The power used in ‘IN’ is represented by ‘Ein.’ The total power use in a single day is computed as follows for every interruptible appliance ‘in IN’ with a power evaluation of ‘in’:

Ein=T∑t=1∑in∈INρin×svin(t) (8)

where T stands for the total number of periods, svin (t) describes the state of an autonomously time-limited appliance at a given time slot ‘t’ and is expected to be as below:

sv in(t)={0    Appliance is off1     Appliance is on (9)

Non-Interruptible Appliances

A burst load appliance is another name for this sort of equipment. Such devices can be switched toward any time slot, but they must continue to run without interruption once they start. A washing machine and a textile dryer are two examples of such gadgets. ‘NI’ stands for non-interruptible appliances and ‘Eni’ stands for energy usage. If a non-interruptible appliance consumes a power assessment factor of ‘ni,’ whole power usage is computed as follows:

Eni=T∑t=1∑ni∈NIρni × svni(t), (10)

where svni(t) shows a representation of a particular time-limited appliance in the time slot ‘t.’ It can also be described as follows:

svni(t)={0    Appliance is off1     Appliance remains on (11)

Base Appliances

It is often known as a fixed appliance and cannot be managed. These appliances’ energy usage patterns and total operating time cannot be modified. When a user wants to switch on these appliances, they must be turned on. For example, a light, a fan, a television and a refrigerator. Base appliances are designated by the letter ‘B,’ while the letter ‘Eb represents their power consumption.’ The power usage of separately base appliance bB is ‘b’. The following formulation is used to compute total power consumption:

E b=T∑t=1∑b∈Bρb×svb(t) (12)

where T is the total number of periods donated, svb(t) denotes the state of an individually interruptible appliance in a given time slot; it is expected to be as follows:

Svb(t)={0ifapplianceisOFF&1applianceisON} (13)

6  Optimization Approaches

Traditional approaches such as MILP, ILP and MINLP can’t handle large numbers of appliances. Furthermore, because of their deterministic character, these strategies are computationally inefficient for real-time optimization. As a result, we are using the Metaheuristic techniques of HSA and GWA to fulfill our goals. The results of a combination of HSA and SBA are compared to those of regular HSA and GWA for the evaluation of User comfort, PAR and Cost. The following sub-sections talk about the meta-heuristic algorithms that were chosen.

6.1 Greywolf Algorithm

GWA mimics the grey wolf’s leadership hierarchy and hunting instincts. GWA’s social structure is divided into alpha, beta, Delta, and Omega levels [27]. Alpha is the best solution, compared to beta and delta, which comes in second and third solutions. The remainder is classified as omega. Hunting instructions, wolves surrounding the prey while hunting and finally attacking, we initialize and with some value in smart appliances and produce the population Np at random. Then, as shown in Eq. (16), calculate the target function to independently estimate each search agent's fitness. In Eq. (17), t represents the maximum number of iterations we performed. Eq. (10) can calculate coefficient vectors A Eq. (14) and C Eq. (15). XP symbolizes the prey position vector. The grey wolf situation vector is denoted by X. Eq. (18). Whereas r1 and r2 are arbitrary or random vectors in [0,1], the first three excellent solutions are stored. The remaining agents needed to update their respective locations by the positions of the most significant search agents, as specified in Eq. (19). As a result, we arrived at the best solution.

A=2a.r1.a (14)

C=2.r2 (15)

Obi=(EhourxPApp) (16)

D=|C.XP(t)−A.X(t)| (17)

X(t+1)=Xp(t)−A.D (18)

X(t+1)=(X1+X2+X3)/3 (19)

6.2 Harmony Search Algorithm

HSA is a form of metaheuristic based on the improvisational technique of jazz musicians. Music improvisation is a technique for enhancing musical harmony. We used three processes to create a new harmony: memory consideration, pitch change and simple random [31]. Eq. (20) is used to produce harmonious memory at random;

Xk,l=lk+rand_Func()⋅(Ul−ll) (20)

where xi, j is the jth element of primary harmony memory. The rand() method generates a random number between 0 and 1, where lj and Uj are lower and upper limits. The new harmony improvisation process begins after the successful formation of harmony memory. The PitchAdjustmentRate (PAR) and the HarmonyMemoryConsiderationRate (HMCR) are two control constraints or parameters that govern the development of new harmony. A random value is generated for each element of new harmony; if the resulting random number is smaller than the provided; HMCR, the value of that specific spot is picked from previously stored memory. If the generated random number is superior to the HMCR, the value is created at random within a preset range. The following Eq. (21) is used by [33] to construct a new harmony vector:

Vi,j={xrandj if randb()<HMCR lj+rand()⋅(Uj−lj)else, (21)

where xrandj is the jth harmonic memory element picked at random. Elements designated from the memory consideration stage are further adjusted based on the PA rate, as accomplished by Eq. (22), which is utilized in [35]:

Vk,m={vk,m±rand_func()⋅bwmifrand_func()<PAvk,melse, (22)

The arbitrary bandwidth is denoted by bw j. The New Harmony vector is formerly connected with the worst in harmonic memory. Change it in HM if New Harmony is improved than Worst Harmony. The process of improvisation continues till the finish conditions are satisfied. In our suggested scenario, each harmony characterizes a time and each harmony constituent represents an appliance. The number of appliances in use determines the length of the harmony. Each harmony has 12 bits because we're using 12 appliances. These bits have 0 or 1, with 0 indicating that the appliance is off and 1 suggesting that it is turned on. All HSA processes are depicted in Algorithm 2.

6.3 Ensembler of GWA and HSA

The hybrid approach is a combination of two methods in which the HAS fitness function is used to operate the initial operation of GWA. This section delves deeply into the proposed hybrid strategy. HSA generates a New Harmony vector in three processes, as mentioned in Section 6.2: memory consideration and pitch correction, random selection. The population is restructured in the harmony memory by comparing new and worst harmony vectors. In [36] found that recently generated memory isn’t always functioning since randomization might or not produce the most significant outcomes. Furthermore, a new search is performed in GWA through alpha, delta and beta wolf. The selection in GWA is made by modifying the positions of Beta, Alpha and Delta, but the selection in HSA is made entirely using HM members.

The hybridization of the HGWA technique is increasingly often used since it syndicates the best elements of existing methods, GWA and HSA, to boost performance. GOW-based search and attack mechanism and HSA-based selection technique are combined in HGWA. The HSA-based selection approach and the HSA-based selection strategy have been combined. Algorithm 3 illustrates the detailed processes of HGWA. Eq. (20) is used to build the early harmony memory in the proposed hybrid method. In a hybrid approach, GWA is used to find the best position or time to operate the appliance; this position generates a New Harmony vector. Algorithm 3 describes the crossover technique. The newly created vector is then compared to the worst vector to see if it may be replaced.

The proposed approach produces effective results for PAR and cost reduction. Algorithm 3 goes over the proposed HGWA in greater detail. The hybrid approach is evaluated using the results of waiting for time (User Comfort), PAR, Load and Electricity Cost. Three scenarios were investigated in our work to simulate and assess the outcomes of HSA, GWA and a combination of these techniques. Our approach focuses on minimizing PAR and cutting power costs while considering user comfort and waiting time. An optimization problem is distinct as the appliances are scheduled in various time slots to save money on electricity. The attributes allied with each appliance and the power rating are shown in Table 1 and calculated using Eq. (11). Eq. (23) is used to estimate electricity cost. PAR and Load are calculated using Eqs. (24) and (25), respectively.

Cost=∑t=124ERatehour∗PRateApp (23)

Load=PRateApp∗App (24)

PAR=max(Loads)Ave(Loads) (25)

7  Simulations and Results

This section goes into great detail about the simulation results. We use MATLAB simulations to assess the performance of GWA, HSA and the proposed HGWA approach. Furthermore, algorithms are evaluated based on the cost of electricity, energy consumed, the PAR and the user's comfort. We contemplate a single house and ten houses for simulation purposes, with each home including 12 appliances. Every house contains the same kind of appliances but with varying power ratings. Table 1 shows all types of appliances, power ratings and loT. The following sub-sections detail the simulation findings for our designed objectives.

7.1 Energy Consumption

The energy usage pattern for every slot after and before scheduling depicts in Fig. 2a. According to the findings, the proposed HGWA schedules load more efficiently to the desired goals. HGWA is designed to prevent peak production during any time of the day, generating fewer overall peaks than other strategies. The scheduling strategies’ load consumption pattern is comparatively optimal compared to unscheduled Loads. The suggested strategy improves the regular energy ingesting pattern by shifting most load commencement onto off-peak hours. Load shifting diminishes customer comfort while saving money. The more customers move their Load and accept changes in their energy consumption schedule, the greater the cost savings. Fig. 2b depicts the energy consumption patterns of ten homes. Our proposed technique outperformed the abovementioned techniques in terms of power consumption patterns.

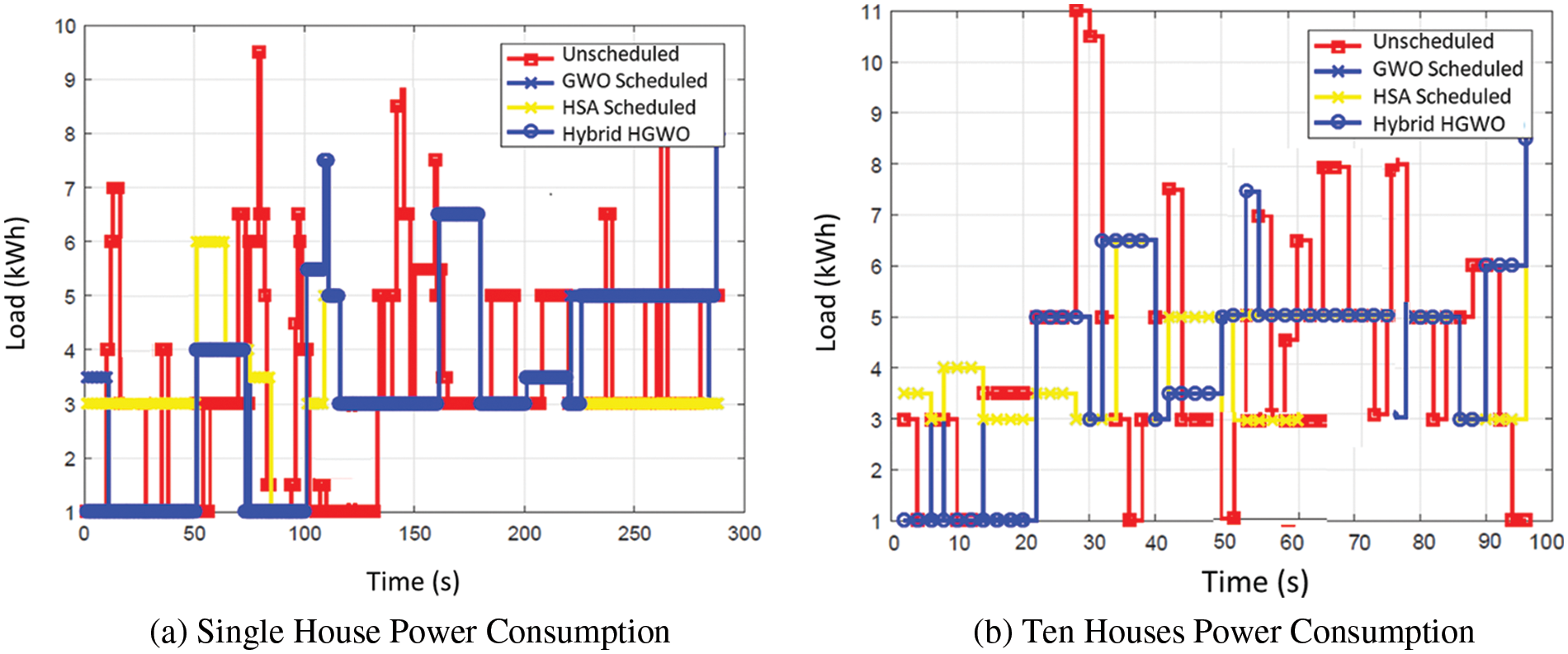
Figure 2: (a) Single house power consumption; (b) Ten houses power consumption

7.2 Cost

The cost of a single day for solo and ten houses depicts in Figs. 3a and 3b, respectively. The performance of the considered number of houses is assessed using the heuristic optimization approaches described in the labels. The entire cost of energy for a single residence using GWA, HSA and planned HGWA. For a single home, the proposed technique HGWA achieves the highest cost reduction of 2 percent, while GWA a and HSA achieve cost reductions of 1.7 and 1.5 percent, respectively. Overall, the proposed method outperformed the competition. In the case of ten houses, unscheduled costs are 2200.3, which is higher than 503.4 in GWA, 398.10 in HSA and 640.3 in HGWA. Similarly, all three strategies outperform unplanned costs. The suggested HGWA beats compared to the other techniques.

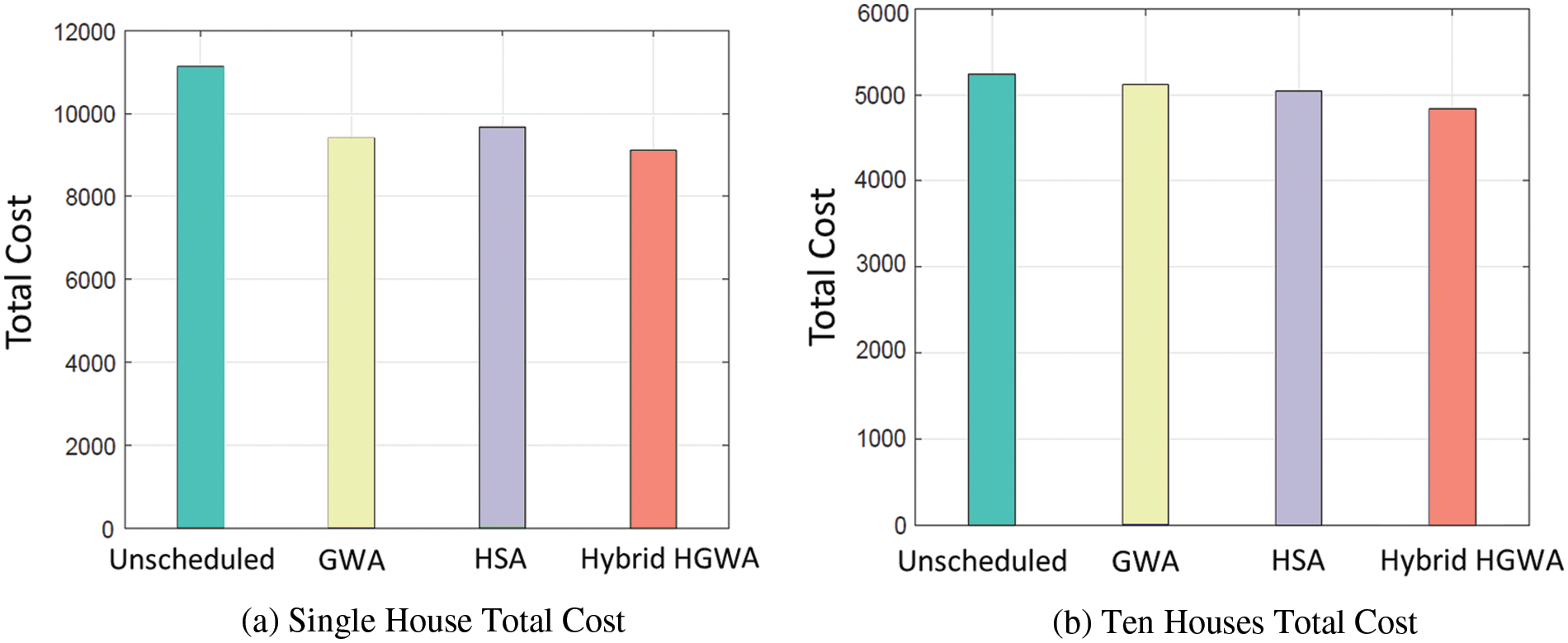
Figure 3: (a) Single house total cost (b) Ten houses total cost

7.3 PAR

Consumers and the utility both benefit from DSM. The lower PAR allows the utility to retain stability at a lower expense. Fig. 4 depicts the PAR performance of all connected techniques. Figs. 4a and 4b demonstrate that each method can reduce PAR, but the proposed HGWA can reduce PAR the most. Compared to the unplanned instance, the PAR of a single dwelling is lowered by 45.79 percent. GWA and HSA, on the other hand, reduce by 21.92% and 20.54 percent, respectively. The proposed hybrid approach delivers the lowest PAR possible. When the same procedures are used to calculate PAR for many residences, as shown in Fig. 4, our technique outperforms the others significantly. However, the remainder of the strategies performed admirably compared to the unplanned situation. Fig. 4b shows the PAR reduction in each case of ten houses.

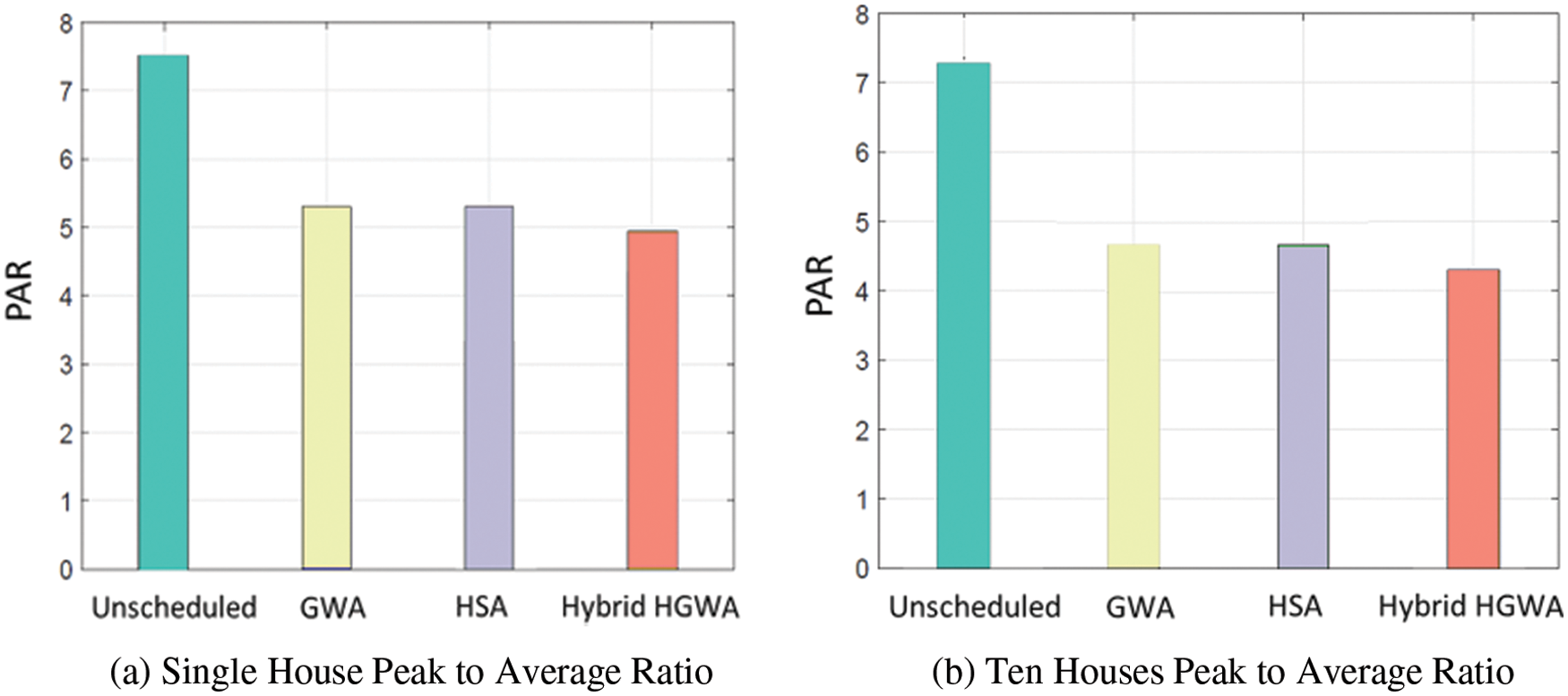
Figure 4: (a) Single house peak to average ratio (b) Ten houses peak to average ratio

7.4 User Comfort

The cost of power and the length of time spent waiting to affect user satisfaction. Waiting time is used to gauge user comfort in the planned job (i.e., how long the user waits for the appliances to switch on). To save money on power, users use their home appliances with an optimum scheduler. Users more concerned with their comfort level must make a budgetary compromise. Both cost and user comfort have a negative relationship. The average waiting time for all procedures is depicted in Fig. 5.

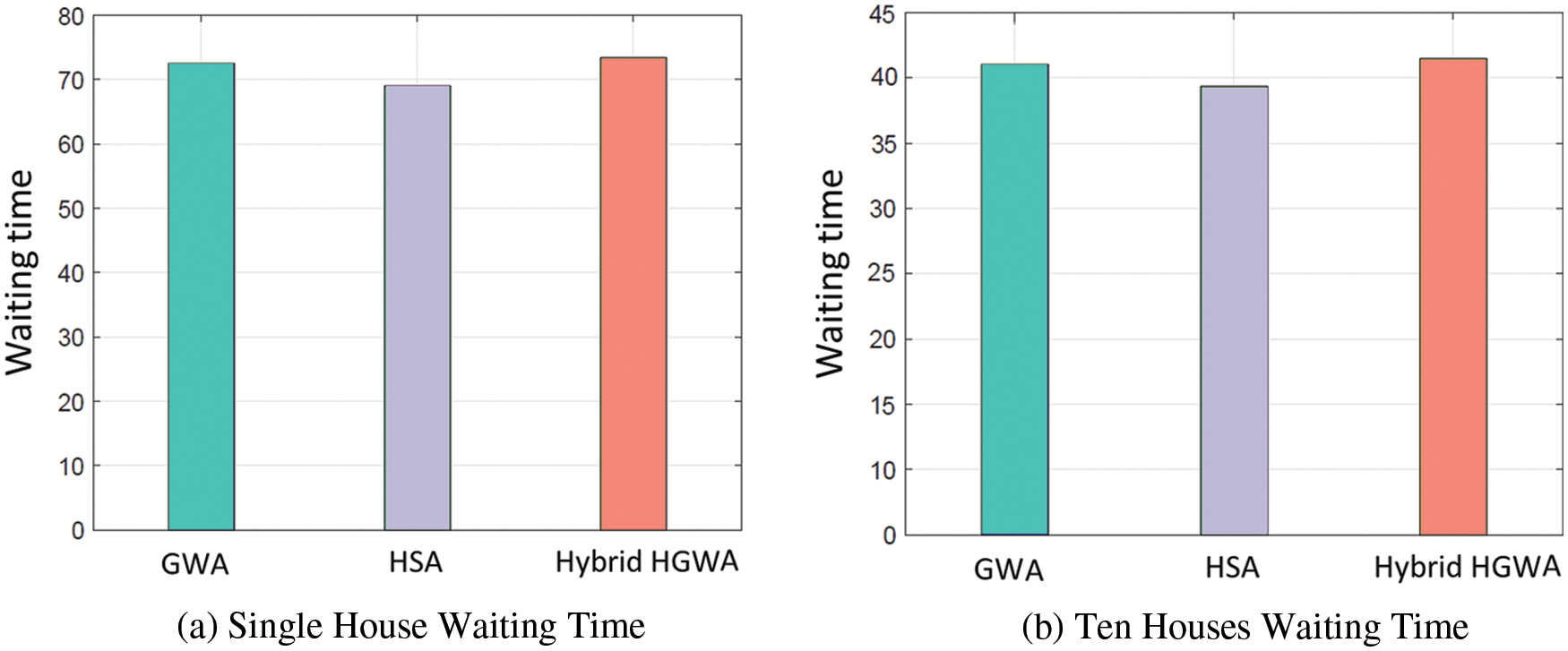
Figure 5: (a) Single house waiting time (b) Ten houses waiting time

In comparison with GWA and HGWA, HSA has the shortest waiting time. HGWA has the longest wait time of any technique. The reason is the tradeoff between cost, waiting time, and user comfort exists. If we need to reduce the cost, we will be compromised on user comfort. As depicted in Figs. 3a and 3b and Figs. 5a to 5b clear cost-waiting-time tradeoff. The proposed technique has the lowest cost, but in the HGWA example, the waiting time is the longest of all the methods. When these data are compared, it is evident that there is a tradeoff between cost also waiting time.

In summary of evaluation parameters, HGWA outperforms in terms of cost. GWA and HSA in terms of Waiting Time/User Comfort, whereas HSA beats GWA for PAR. The projected hybrid HGWA, on the other hand, beats the competition in terms of electricity cost and PAR. However, it compromised waiting time/ user comfort.

8  Conclusion

The performance of HEMS with RTP is explored in this work utilizing nature-inspired techniques, including HSA, GWA and the suggested HGWA. To demonstrate the proposed approach's efficacy, we run simulations for single and multiple residences. Each house has 12 smart appliances. Based on their energy-feasting patterns, these utilizations are divided into sub-categories. We look at similar appliances with various power ratings in each residence. User comfort, cost, and PAR are all considered while considering optimization options. The time the user has to wait determines their comfort level. Simulation results reveal the efficiency of our proposed method for PAR and cost reduction. The proposed method saves the most money, 2200.3 PKR, compared to 503.4 PKR in GWA, 398.10 PKR in HSA and 640.3 PKR in HGWA, for single and ten houses. The proposed approach outperformed as compared to HSA and GWA for PAR reduction. PAR for single-family homes in HGWA, GWA and HSA is reduced by 45.79 percent, 21.92 percent and 20.54 percent, respectively. Additionally, the proposed HGWA method outperformed the other methods in terms of Cost and PAR minimization, even though a cost-to-user comfort tradeoff is imperative to manage. In the future, we will examine the cost of reducing electricity usage by combining RES with a storage system.

Acknowledgement: The Research Groups Funding Program Grant Code Number (NU/RG/SERC/11/7) was used by the authors to receive funding for this work from the Deanship of Scientific Research, Najran University, Kingdom of Saudi Arabia.

Funding Statement: : The authors gratefully acknowledge the Deanship of Scientific Research at Najran University in the Kingdom of Saudi Arabia for funding this work through the Research Groups funding program with the Grant Code Number (NU/RG/SERC/11/7).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. S. Fazili and J. Grover, “Smart grid: A survey,” Smart Technologies for Energy and Environmental Sustainability, vol. 1, no. 1, pp. 147–159, 2022. [Google Scholar]

    2. S. Suraj and K. Senthil, “Demand side management: Demand response, intelligent energy systems and smart loads,” Journal of Electrical Engineering and Technology, vol. l, no. 10, pp. 17–23, 2019. [Google Scholar]

    3. F. A. Al Balas, W. Mardini, Y. Khamayseh and K. Dua’a Ah, “Improved appliance coordination scheme with waiting time in smart grids,” International Journal of Advanced Computer Science and Applications, vol. 7, no. 4, pp. 1–15, 2016. [Google Scholar]

    4. F. Rahim and A. Ipakchi, “Demand response as a market resource under the smart grid paradigm,” IEEE Transactions on Smart Grid, vol. 1, no. 1, pp. 82–88, 2010. [Google Scholar]

    5. M. B. Rasheed, N. Javaid, A. Ahmad, M. Awais, Z. A. Khan et al., “Priority and delay constrained demand side management in real-time price environment with a renewable energy source,” International Journal of Energy Research, vol. 40, no. 14, 2016. [Google Scholar]

    6. Y. Ozturk, D. Senthilkumar, S. Kumar and G. Lee, “An intelligent home energy management system to improve demand response,” IEEE Transactions on Smart Grid, vol. 4, no. 2, pp. 694–701, 2013. [Google Scholar]

    7. P. Yi, X. Dong, A. Iwayemi, C. Zhou and S. Li, “Real-time opportunistic scheduling for residential demand response,” IEEE Transactions on Smart Grid, vol. 4, no. 1, pp. 227–234, 2013. [Google Scholar]

    8. Z. Zhao, W. C. Lee, Y. Shin and K. B. Song, “An optimal power scheduling method for demand response in home energy management system,” IEEE Transaction on Smart Grid, vol. 4, no. 3, pp. 1391–1400, 2013. [Google Scholar]

    9. A. Molderink, V. Bakker, M. G. Bosman, J. L. Hurink and G. J. Smit, “Domestic energy management methodology for optimizing efficiency in smart grids,” 2009 IEEE Bucharest PowerTech, Bucharest, Romania, vol. 1, no. 1, pp. 1–7, 2009. [Google Scholar]

  10. K. M. Tsui and S. C. Chan, “Demand response optimization for smart home scheduling under real-time pricing,” IEEE Transactions on Smart Grid, vol. 3, no. 4, pp. 1812–1821, 2012. [Google Scholar]

  11. A. Arabali, M. Ghofrani, M. Etezadi-Amoli, M. S. Fadali and Y. Baghzouz, “Genetic algorithm based optimization approach for energy management,” IEEE Transactions on Power Delivery, vol. 28, no. 1, pp. 162–170, 2013. [Google Scholar]

  12. T. Logenthiran, D. Srinivasan and T. Z. Shun, “Demand side management in smart grid using heuristic optimization,” IEEE Transaction on Smart Grid, vol. 3, no. 3, pp. 1244–1252, 2012. [Google Scholar]

  13. S. G. Malla, J. M. R. Malla, P. Malla, S. Ramasamy, S. K. Doniparthi et al., “Coordinated power management and control of renewable energy sources based smart grid,” International Journal of Emerging Electric Power Systems, vol. 23, no. 2, pp. 261–276, 2022. [Google Scholar]

  14. S. S. Reddy, J. Y. Park and C. M. Jung, “Optimal operation of microgrid using hybrid differential evolution and harmony search algorithm,” Frontiers in Energy, vol. 10, no. 3, pp. 355–362, 2016. [Google Scholar]

  15. J. Zhang, Y. Wu, Y. Guo, B. Wang, H. Wang et al., “A hybrid harmony search algorithm with differential evolution for day ahead scheduling problem of a microgrid with consideration of power flow constraints,” Applied Energy, vol. 18, no. 3, pp. 791–804, 2016. [Google Scholar]

  16. M. Rastegar, M. F. Firuzabad and H. Zareipour, “Home energy management incorporating operational priority of appliances,” International Journal of Electrical Power and Energy Systems, vol. 7, no. 4, pp. 286–292, 2016. [Google Scholar]

  17. H. Miao, X. Huang and G. Chen, “A genetic evolutionary task scheduling method for energy efficiency in smart homes,” International Review of Electrical Engineering, vol. 7, no. 5, pp. 5897–5904, 2012. [Google Scholar]

  18. J. Mocnik, M. Gornik, B. Murovec and A. Zemva, “A concept to optimize power consumption in smart homes based on demand side management and using smart switches,” Electrotechnical Review, vol. 80, no. 5, pp. 217–221, 2013. [Google Scholar]

  19. Z. W. Geem and Y. Yoon, “Harmony search optimization of renewable energy charging with energy storage system,” International Journal of Electrical Power and Energy Systems, vol. 8, no. 6, pp. 120–126, 2017. [Google Scholar]

  20. B. Chreim, M. Esseghir and L. M. Boulahia, “LOSISH-load scheduling in smart homes based on demand response: Application to smart grids,” Applied Energy, vol. 323, no. 1, pp. 119606, 2022. [Google Scholar]

  21. A. Agnetis, G. D. Pascale, P. Detti and A. Vicino, “Load scheduling for household energy consumption optimization,” IEEE Transaction on Smart Grid, vol. 4, no. 4, pp. 2364–2373, 2013. [Google Scholar]

  22. M. B. Rasheed, N. Javaid, M. Awais, Z. A. Khan, U. Qasim et al., “Real-time information based energy management using customer preferences and dynamic pricing in smart homes,” Energies, vol. 9, no. 7, pp. 54–62, 2016. [Google Scholar]

  23. M. A. Khan, N. Javaid, A. Mahmood, Z. A. Khan and N. Alrajeh, “A generic demand side management model for smart grid,” International Journal of Energy Research, vol. 39, no. 7, pp. 954–964, 2015. [Google Scholar]

  24. W. Deng, W. Shang, X. Cai, H. Zhao, Y. Song et al., “An improved differential evolution algorithm and its application in the optimization problem,” Soft Computing, vol. 25, no. 7, pp. 5277–5298, 2022. [Google Scholar]

  25. W. Zijian, Y. Kaili, Y. Jiangxin, C. Yanlong and Y. Gan, “Energy efficiency oriented scheduling in smart manufacturing,” Journal of Ambient Intel Humanize Computer, vol. 10, no. 3, pp. 969–978, 2019. [Google Scholar]

  26. H. Jalili, S. E. Eslami, P. M. Moghaddam and P. Siano, “Modeling of demand response programs based on market elasticity concept,” Journal of Ambient Intelligence and Humanized Computing, vol. 10, no. 6, pp. 2265–2276, 2018. [Google Scholar]

  27. A. Khan, N. Javaid, A. Ahmad, M. Akbar, Z. A. Khan et al., “A priority induced demand side management system to mitigate rebound peaks using multiple knapsacks,” Journal of Ambient Intelligence and Humanized Computing, vol. 10, no. 4, pp. 1655–1678, 2019. [Google Scholar]

  28. W. Deng, J. Xu, X. Z. Gao and H. Zhao, “An enhanced MSIQDE algorithm with novel multiple strategies for global optimization problems,” IEEE Transactions on Systems, Man and Cybernetics: Systems, vol. 52, no. 3, pp. 1578–1587, 2022. [Google Scholar]

  29. S. Pierluigi, G. Giorgio, A. Mauro and P. Antonio, “Designing and testing decision support and energy management systems for smart homes,” Journal of Ambient Intelligence and Humanized Computing, vol. 4, no. 6, pp. 651–661, 2013. [Google Scholar]

  30. T. Sousa, H. Morais, Z. Vale, P. Faria and J. Soares, “Intelligent energy resource management considering vehicle-to-grid: A simulated annealing approach,” IEEE Transaction Smart Grid, vol. 3, no. 1, pp. 535–542, 2012. [Google Scholar]

  31. E. S. M. El-kenawy, F. Albalawi, S. A. Ward, S. S. Ghoneim, M. M. Eid et al., “Feature selection and classification of transformer faults based on novel meta-heuristic algorithm,” Mathematics, vol. 10, no. 17, pp. 3144, 2022. [Google Scholar]

  32. N. Khodadadi, L. Abualigah and S. Mirjalili, “Multi-objective stochastic paint optimizer (MOSPO),” Neural Computing and Applications, vol. 34, no. 18, pp. 1–24, 2022. [Google Scholar]

  33. E. S. M. El-Kenawy, S. Mirjalili, S. S. M. Ghoneim, M. M. Eid, M. El-Said et al., “Advanced ensemble model for solar radiation forecasting using sine cosine algorithm and newton’s laws,” IEEE Access, vol. 9, pp. 115750–115765, 2021. [Google Scholar]

  34. S. Sheng, P. Chen, Z. Chen, L. Wu and Y. Yao, “Deep reinforcement learning-based task scheduling in IoT edge computing,” Sensors, vol. 21, no. 5, pp. 1666, 2021. [Google Scholar]

  35. Y. Li, Z. Yang, G. Li, D. Zhao and W. Tian, “Optimal scheduling of an isolated microgrid with battery storage considering load and renewable generation uncertainties,” IEEE Transactions on Industrial Electronics, vol. 66, no. 2, pp. 1565–1575, 2018. [Google Scholar]

  36. Z. W. Geem, J. H. Kim and G. V. Loganathan, “A new heuristic optimization algorithm: Harmony search,” Simulation, vol. 76, no. 2, pp. 60–68, 2001. [Google Scholar]

  37. B. Liu, J. Kang, N. Jiang and Y. Jing, “Cost control of the transmission congestion management in electricity systems based on ant colony algorithm,” Energy Power Energies, vol. 3, no. 1, pp. 1–7, 2011. [Google Scholar]

  38. C. A. Hassan, J. Iqbal, N. Ayub, S. Hussain, R. Alroobaea et al., “Smart grid energy optimization and scheduling appliances priority for residential buildings through meta-heuristic hybrid approaches,” Energies, vol. 15, no. 5, pp. 1752, 2022. [Google Scholar]