An Improved Reptile Search Algorithm Based on Cauchy Mutation for Intrusion Detection

1  Introduction

Due to the increased internet usage rate caused by the widespread computer networks, security has become one of the most critical areas for research because of the threats and attacks on these networks, which are now more aggressive than before [1]. Several security technologies are employed to deal with and prevent attacks, such as firewalls, authentication, and encryption. Despite the powerful capabilities of these technologies, they have limitations in reaching the desired level of attack detection. ID system and intrusion prevention system can analyze data passing the networks in greater depth compared to other security systems, are used to overcome the issue of these technologies,.

With the increase in the number of attacks, cybersecurity companies focus on developing sensitive systems besides traditional security methods [2–4]. As a result, proactive cybersecurity systems such as network behavior analysis, threat analysis, and Machine learning (ML) are also developed. ID systems are frequently used technology that has become more sensitive to cyber threats. ID system is a software package that is responsible for detecting threats across the network or system.

In order to achieve optimal security requirements of a network, researchers have focused on the use of ML approaches to develop an ID system that can detect such types of attacks more accurately [5,6]. ML techniques gained special attention in ID in recent years because of their capabilities to classify hundreds of features into normal system behavior or attack attempt [7,8]. The primary purpose of Feature Selection (FS) as a technique is to select an Optimal Feature Subset (OFS) in a given dataset, thus, optimizing the learning process by the ML techniques.

Selecting OFS in a given dataset facilitates learning by ML techniques to achieve better prediction, and classification results for ID. Nature-inspired algorithms are mostly Meta-Heuristics (MH) optimization methods inspired by nature. They gained special attention from scholars in different applications due to their great potential to specify OFS. These methods are effective, and reliable gradient-free stochastic optimization techniques that have been successful in various numerical, and combinatorial optimization problems with diverse frameworks [9–11]. MH inspiration sources are broken down into three types [12]: swarm-based algorithms, evolutionary-based algorithms, and physics-based algorithms. Some of the more popular MH methods include Multi-Verse Optimizer (MVO) [13], Particle Swarm Optimization (PSO) [14], Genetic Algorithm (GA) [15], Salp Swarm Algorithm (SSA) [16], Whale Optimization Algorithm (WOA) [17], Gray Wolf Optimizer (GWO) [18], and Reptile Search Algorithm (RSA) [19].

MH algorithms can be combined to achieve better results for FS in different applications. The authors in [20] combined RSA with Remora Optimization Algorithm (ROA) for data clustering. In another work [21], RSA is combined with deep learning for ID. In [22], chaotic-map, and simulated annealing are used to improve RSA for FS in Medical field. In [23], the authors used Levy flight to improve the capability of the RSA for vehicle cruise control system design. In [24], ant colony optimization’s capability is boosted by RSA for churn prediction. In [25], the mean transition mechanism is used to improve RSA for constrained engineering problems. In [26], an enhanced GA based FS method, named GbFS, is presented to increase classification detection accuracy. In [27], the authors proposed a hybrid model based on the correlation feature selection (CFS) with three different search techniques: Best-first, greedy stepwise and GA for ID. In another work [28], the authors used Intelligent Water Drops (IWD) method to choose OFS in KDD-CUP99 dataset.

These methods use two principles that are characteristic in all optimization techniques, which are exploration and exploitation. In exploration, the algorithm tries to find different regions in the search area, while the second principle, exploitation, and the method searches around the obtained solution from the first phase to find the best solutions. In this paper, an improved version of RSA, named RSA-CM for ID is introduced. The RSA-CM combines the original RSA with CM to enhance the exploration capability and maintain a balance between exploration, and exploitation of the RSA. The main contributions of this work could be summarized as follows:

•   An improved version of RSA using CM named RSA-CM is introduced for ID.

•   CM strategy is used to boost the search mechanism of the RSA during the search process.

•   The RSA-CM is examined using five open access datasets for ID, and two popular engineering optimization problems.

•   The results confirm the efficacy of the RSA-CM compared to other MH methods and the engineering problems as well.

This paper is organized as follows: Section 2 provides a brief idea of RSA and CM, followed by a description of the developed method presented in Section 3. The experimental results, and statistical comparison with other FS methods are shown in Section 4, and Section 5 concludes this paper.

2  Method

2.1 Reptile Search Algorithm (RSA)

In 2022, Abualigah et al. [19] reported a MH method inspired by the hunting behavior of Crocodiles and is known as RSA. The method initializes the ith set of candidate OFS xi,j randomly as follows:

xi,j=rand∈U(0,1)∗(UBj−LBj)+LBji∈{1,…,N}andj∈{1,…,M}(1)

where LBj and UBj and are minimum, and maximum values of the jth feature, rand∈U(0,1) generates a random number from uniform distribution, N is a maximum number of sets of candidate OFS, and M is the total number of input features.

The crocodiles’ food search is implemented in RSA using two separate strategies namely, exploration and exploitation. For sequential implementation of these two strategies, the maximum number of iterations is split into four stages. In the first half of the total number of stages, the crocodile’s encircling behavior is implemented using the high and the belly walking movements of the crocodile to effectively explore the region. This stage can mathematically be written as:

xi,j(g+1)={[−ni,j(g)⋅γ⋅Bestj(g)]−[rand∈[1,N]⋅Ri,j(g)],g≤T4ES(g)⋅Bestj(g)⋅x(rand∈[1,N],j),g≤2T4andg>T4(2)

where, for gth iteration, ith candidate OFS, and  jth feature Bestj(g) is the best solution, ni,j is the hunting operator (Eq. (3)), and ES(g) is Evolutionary Sense (Eq. (7)) which reduces from 2 to −2 over the total number of iterations, and γ is set as 0.1 for controlling the exploration accuracy. The Ri,j, computed as in Eq. (6), reduces the search region, and rand∈[1,N] randomly selects one of the candidate OFS.

ni,j=Bestj(g)×Pi,j(3)

where Pi,j, calculated as in Eq. (4), is the normalized difference between the jth feature value of the ith candidate OFS and average value of the ith solution. It is calculated as:

Pi,j=θ+xi,j−μ(xi)Bestj(g)×(UBj−LBj)+ϵ(4)

where θ controls the sensitive of the exploration, and ϵ is a minimum floor value. It is defined as:

μ(xi)=1n∑j=1nxi,j(5)

Ri,j=Bestj(g)−x(rand∈[1,N],j)Bestj(g)+ϵ(6)

ES(g)=2×rand∈{−1,1}×(1−1T)(7)

where the value 2 acts as a multiplier to provide correlation values in the range [0, 2], and rand∈{−1,1} is a random integer between {−1, 1}.

Crocodiles’ hunting coordination and cooperation are implemented to exploit the search space. The exploitation stage can be mathematically represented as:

xi,j(g+1)={rand∈[−1,1]⋅Bestj(g)⋅Pi,j(g),g≤3T4andg>2T4[ϵ⋅Bestj(g)⋅ni,j(g)]−[rand∈[−1,1]⋅Ri,j(g)],g≤Tandg>3T4(8)

The algorithm terminates after T iterations while the performance of each set of candidate OFS is evaluated using a predefined Fitness Function (FF). The OFS is a candidate feature set with the smallest FF.

2.2 Cauchy Mutation (CM)

Several mutation operators are introduced in the literature to escape the problem of premature convergence and to improve the performance. Among them, CM shows a powerful capability due to its extended tail probability distribution function, which can enrich the performance, and prevent getting, stuck in any optimization method’s local optima.

CM is a continuous probability distribution having two parameters, where p0 indicates the location parameter and γ is the scale parameter used to determine the shape of the Cauchy distribution [29–31]. CM aims to solve the premature convergence problem and local stagnation problem of any optimization algorithm by taking controlled small steps. The Probability Distribution Function (PDF) of CM is defined as follows:

f(p:p0,γ)=1πγ[+(p−p0γ)2]=1π[γ(p−p0)2+γ2](9)

where γ is set to 1, p equals 0, and p0 is a random number between [0, 1]. The CM operator is calculated as:

γ=tan(π(p0−12))(10)

3  Proposed Method

In RSA, the exploration phase is performed by encircling the prey, and exploitation is done in the subsequent stages. However, this may result in the method suffering from premature convergence. Accordingly, CM is integrated into the RSA structure to escape from being trapped in local solutions by allowing RSA to jump, and visit new locations in the search space. This will help the RSA control, and balance the exploration, and exploitation abilities during the search process. The flowchart of the RSA-CM is provided in Fig. 1, and the pseudo-code is given in Algorithm 1.

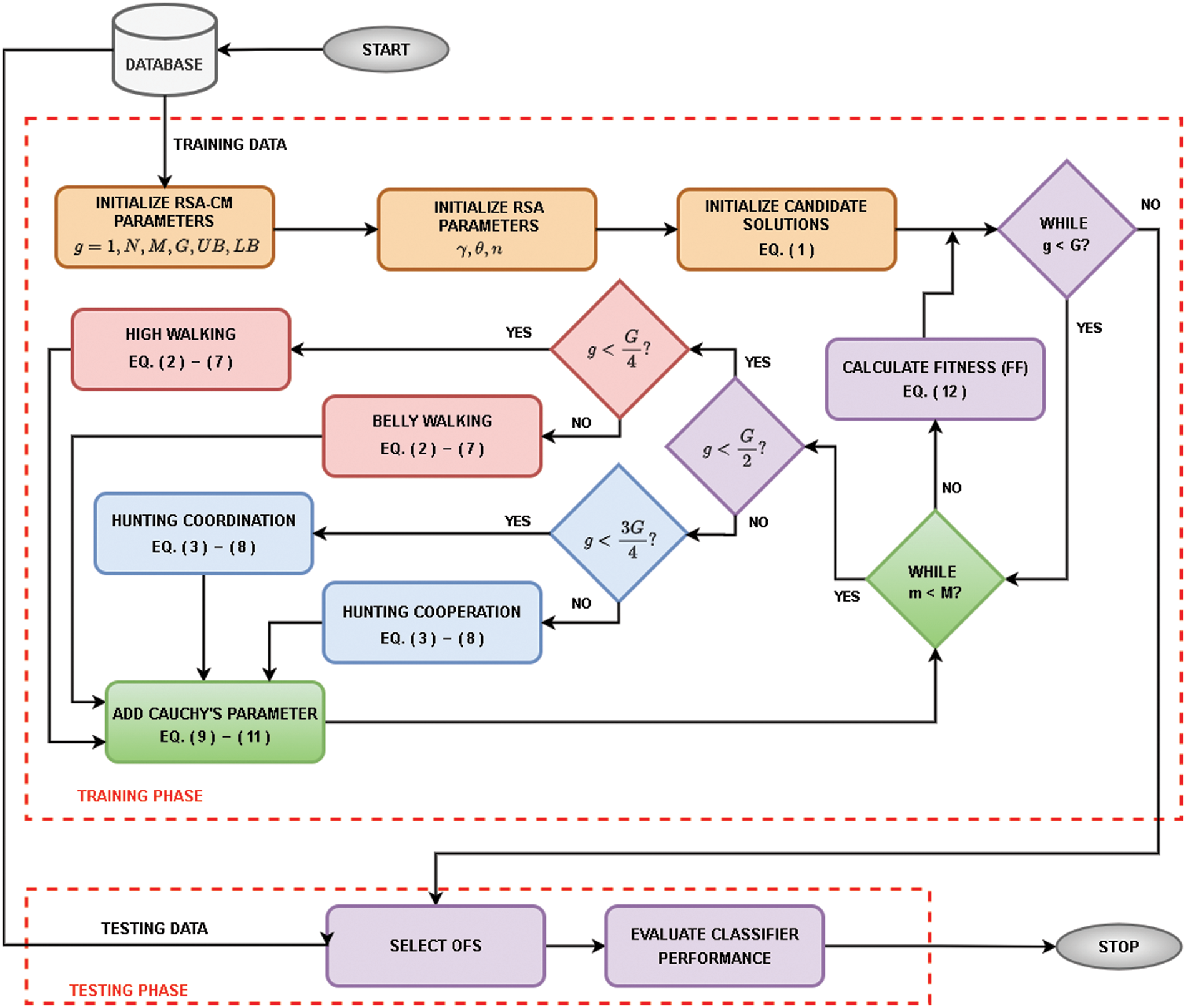
Figure 1: Flow diagram of the developed RSA-CM algorithm

For gth iteration and mth dimension, a Cauchy’s parameter (p), generated using Eqs. (9) and (10), is added to the best possible candidate solution of RSA (xbestRSA) as follows:

xbest,m(g)=xbest,mRSA(g)+pj(g)(11)

The performance of the updated solution is calculated using FF, as shown in Eq. (12). It uses a K-Nearest Neighbor (KNN) classifier with five neighbors, and a threshold value of 0.5 as recommended by [24,32]. The candidate OFS that has minimum features, and attains maximum accuracy attains smallest fitness.

FF(xi)=α×E+(α−1)×|OFSi|M(12)

where E is the classification error rate of the K-Nearest Neighbor (KNN) classifier with five neighbors, |OFSi| is the cardinality of optimum feature set and M is the cardinality of input feature set of the dataset, and α controls the relative importance of classification error and number of selected features. The value of α varies in the range of [0,1], and is set to 0.99 in this work [32].

4  Experimental Results and Discussion

The capability of the interdicted RSA-CM method to determine the OFS is assessed using five datasets for ID and comparing it with other FS methods: PSO [14], GWO [18], MVO [13], and RSA [19].

4.1 Experimental Setup

Python is used to implement all the methods used in this work and they are executed on a 3.13 GHz PC with 16 GB RAM and Windows 11 operating system. The parameter settings for all the methods are provided in Table 1. These methods are implemented based on their implementations in original work. For all methods, the population of 32 and the maximum iterations of 100 are selected empirically. Each algorithm is executed 20 times independently to obtain reliable analysis and convincing results.

4.2 Datasets Description

Five real datasets from ID applications are selected to assess RSA-CM efficiency. These datasets are widely used for ID [22,23] and they include KDD-CUP99, NSL-KDD, UNSW-NB15, CIC-IDS2017, and CIC-IDS2018. The main characteristics of those datasets are given in Table 2.

4.3 Evaluation Metrics

The quantitative evaluation measures employed to compare the proposed RSA-CM and the other MH methods are as follows:

•   Fitness values are used to compute the quality of the solution, which is used to guide the searching process by the RSA-CM method.

•   The number of OFS is used to illiterate RSA-CM’s ability to reduce number of features in a given dataset.

•   Accuracy (AC): It calculates the accuracy over the total number of runs and in this work number of runs is 20:

AC=TP+TNTP+TN+FN+FP(13)

Precision (P): It measures the actual positives which are actually positive:

P=TPTP+FP(14)

Recall (R): It measures the proportion of actual positives which are correctly identified:

R=TPTP+FN(15)

F-measure (F): is the harmonic mean of recall and precision measures and it is defined as:

F=2PRP+R(16)

where True Positive and (TP) and True Negative (TN) denote the samples of customers correctly detected as churner or not, while False Negative (FN) and False Positive (FP) represents the number of misclassified positive and negative cases, respectively.

4.4 Experimental Results and Discussion

To examine the efficacy of the RSA-CM as an FS method, the real-world datasets provided in Table 1 are used and compared against other MH methods.

Table 3 gives the results of the introduced RSA-CM and the other MH methods using mean and standard deviation (Std) of fitness. From Table 3, the RSA-CM got the lowest mean and Std values in four out of five datasets compared to other methods. The PSO method outperformed the other methods in the CIC-IDS2017 dataset.

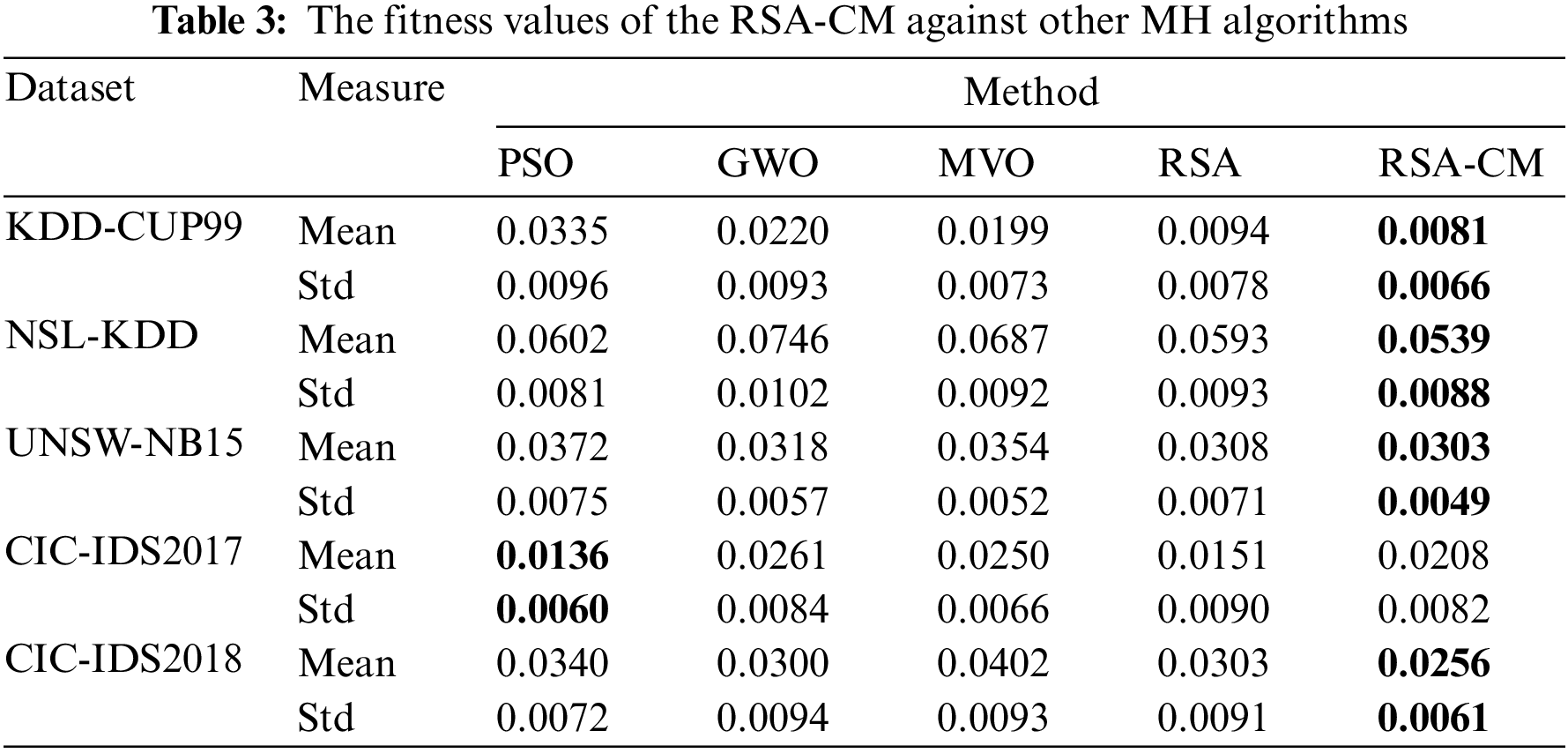
The results of the proposed RSA-CM and the other MH algorithms based on the mean and standard deviation (Std) of the number of optimum features selected by the corresponding MH algorithm are provided in Table 4. In Table 4, the RSA-CM selected the least-average OFS for three out of five datasets, while for KDD-CUP99, both RSA and RSA-CM selected the least number of features. In the case of CIC-IDS2017, PSO selected least OFS, followed by RSA, RSA-CM, MVO, and GWO. Similarly, Std of number of OFS is least for RSA-CM for three out of five datasets, indicating better stability. For UNSW-NB15, both MVO and RSA-CM show similar Std, while for CIC-IDS2018, RSA and RSA-CM show similar Std. In the case of CIC-IDS2017, PSO shows the least Std of number of OFS, followed by RSA-CM, GWO, MVO, and RSA.

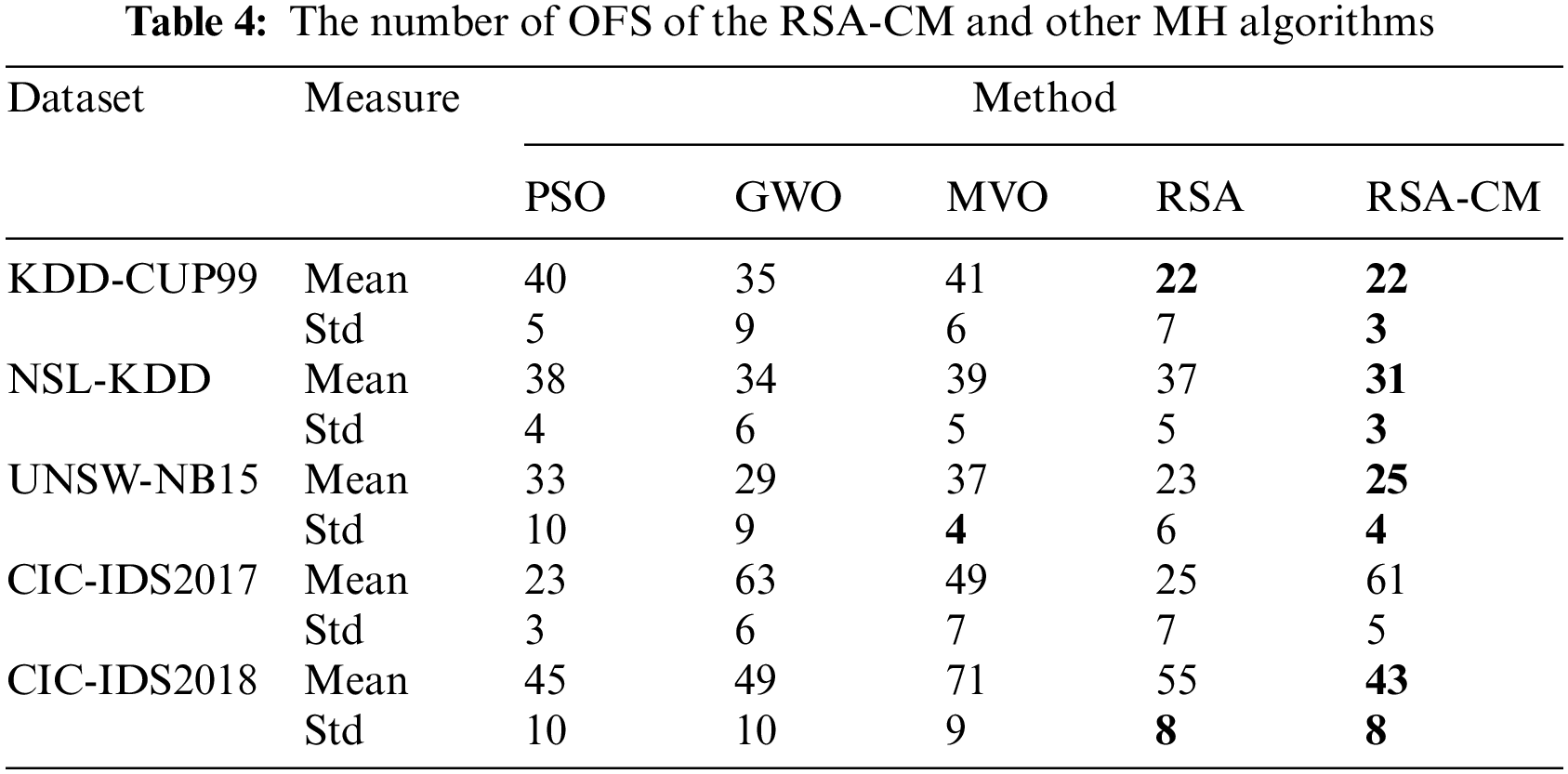
Table 5 compares different MH algorithms in terms of mean and Std of accuracy. The proposed RSA-CM shows highest mean accuracy for all five datasets. The Std of accuracy is least for the proposed RSA-CM for four out of five datasets indicating high stability of the trained model. In the case of KDD-CUP99, GWO achieves the least Std, followed by the proposed RSA-CM.

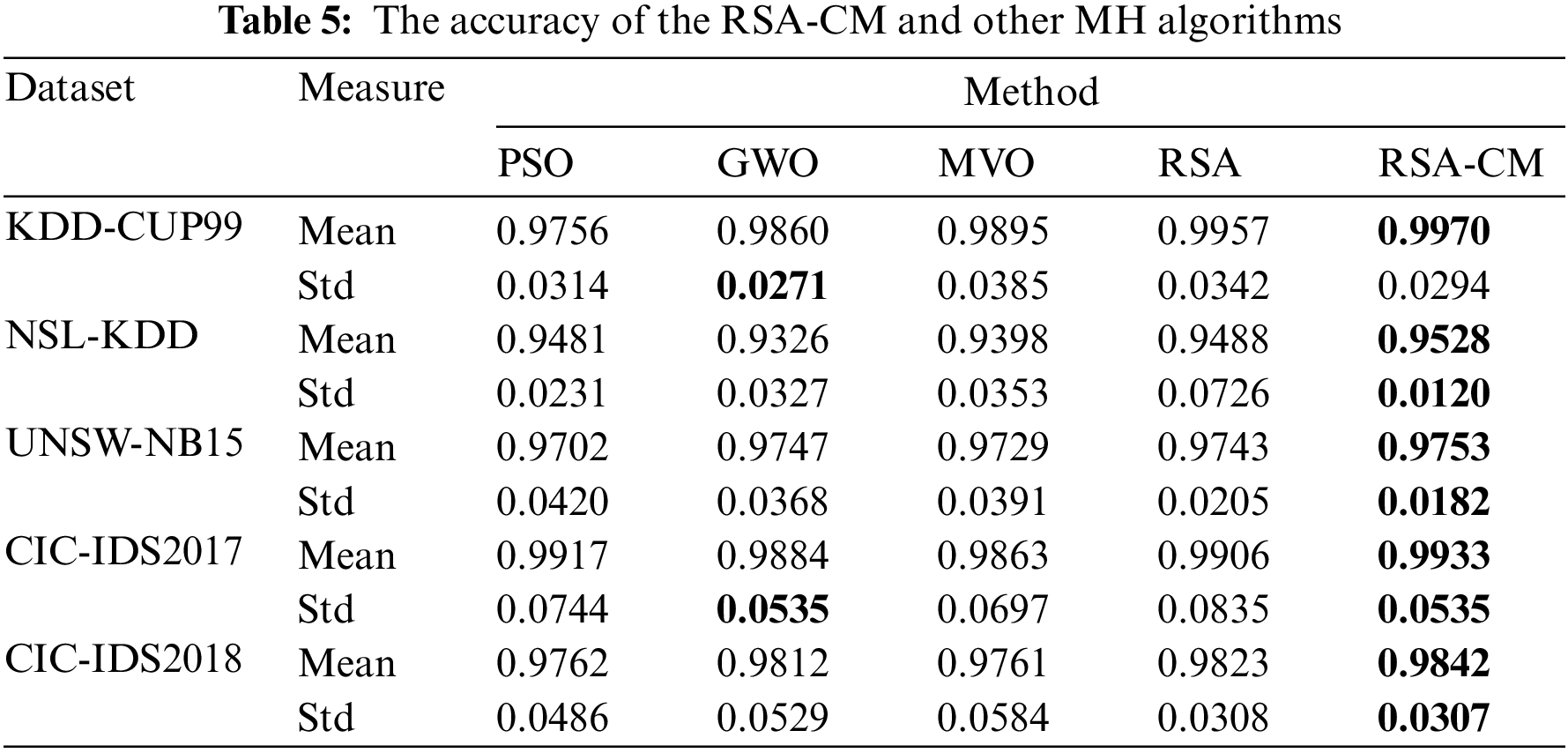
Table 6 compares MH algorithms in terms of mean and Std of precision. The proposed RSA-CM shows the highest mean precision for all five datasets. The Std of precision is least for the proposed RSA-CM for three out of five datasets, indicating consistency of the trained model in detecting the cyber-attacks. In the case of KDD-CUP99, GWO achieves the least Std followed by PSO, RSA-CM, RSA, and MVO. RSA achieves the least Std for CIC-IDS2017 followed by GWO, RSA-CM, PSO, and MVO.

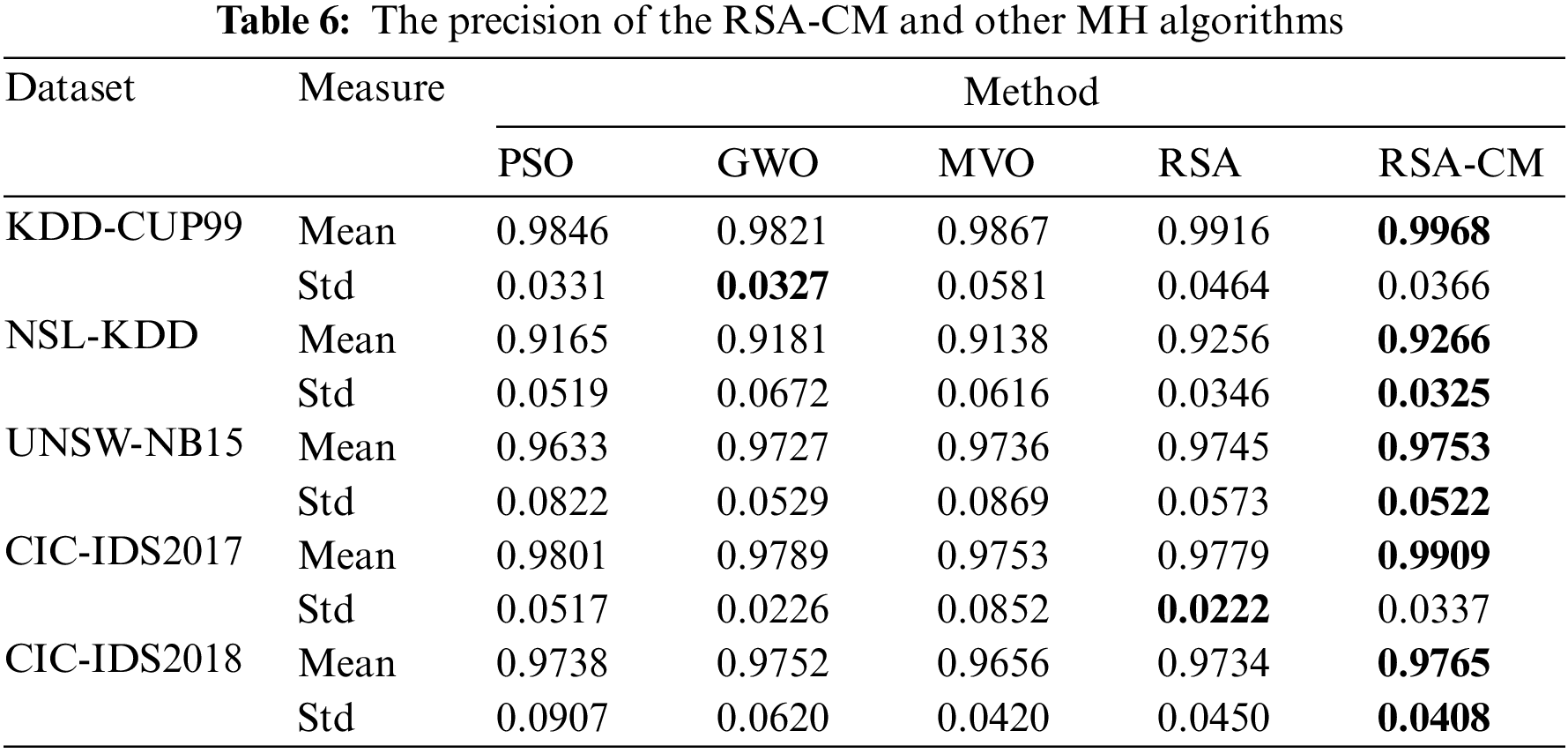
The mean and Std of recall for different MH algorithms are compared in Table 7. The proposed RSA-CM shows the highest mean recall for all five datasets, indicating that the trained model understands cyber-attacks well. The Std of recall is least for the proposed RSA-CM for three out of five datasets showing consistency of the model’s understanding and the actual pattern of the cyber-attacks. MVO and GWO achieve the least Std of recall for CIC-IDS2017 and CIC-IDS2018 datasets, respectively.

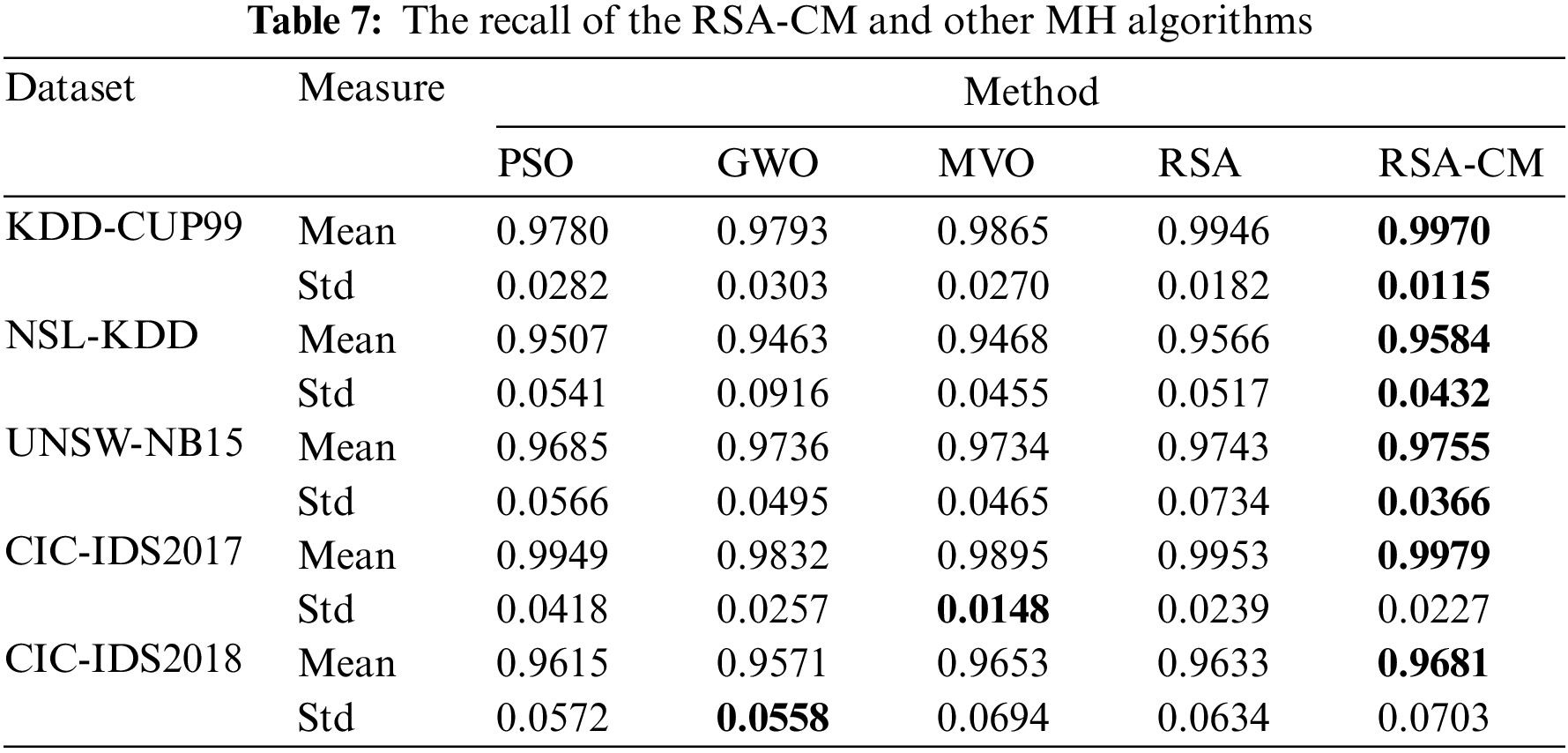
Table 8 compares different MH algorithms in terms of mean and Std of F1-score. The proposed RSA-CM shows the highest mean F1-score for all five datasets. The Std of F1-score is least for the proposed RSA-CM for two out of five datasets. In the case of KDD-CUP99 and CIC-IDS2018, GWO achieves the least Std followed by RSA-CM; in the case of UNSW-NB15, MVO achieves the least Std followed by RSA-CM.

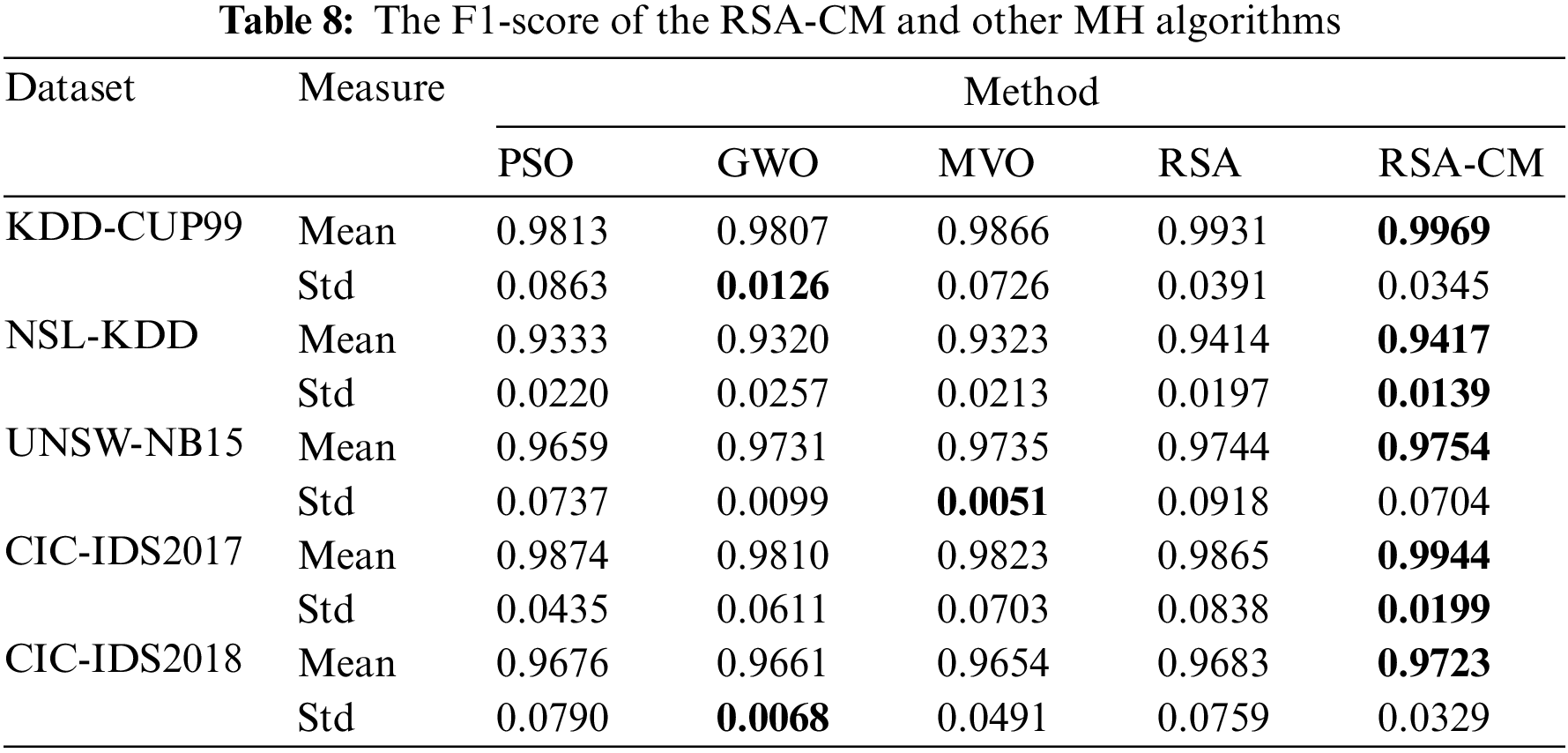
Comparative analysis of convergence of RSA-CM and different MH methods is shown in Fig. 2 after 20 independent runs for each method. In Fig. 2, the developed RSA-CM improves the convergence rate towards optimal solutions much better than the other MH algorithms in almost all the used datasets, which reflects the stability of the proposed RSA-CM as an FS method for ID.

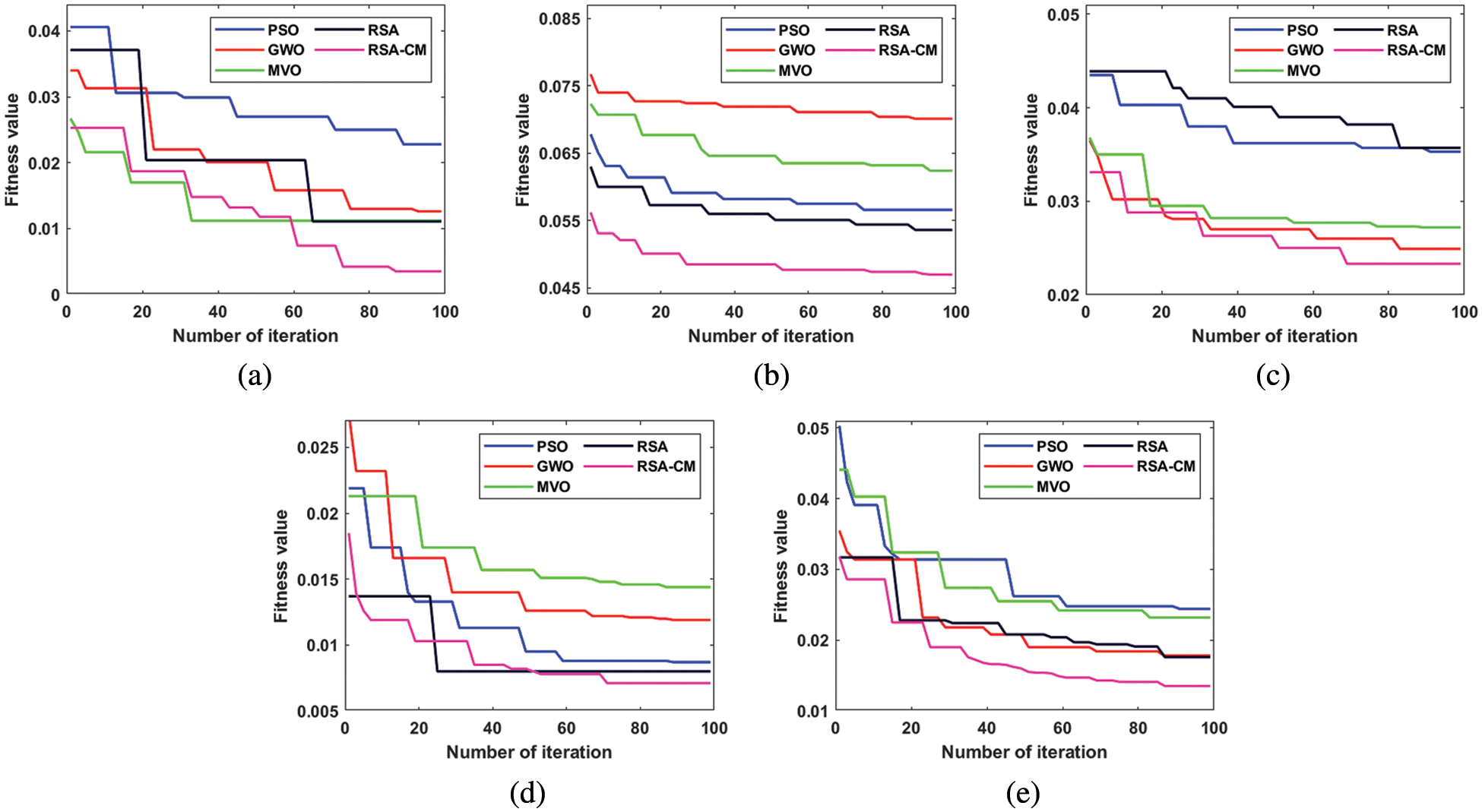
Figure 2: RSA-CM and the other MH methods convergence curves for (a) KDD-CUP99, (b) NSL-KDD, (c) UNSW-NB15, (d) CIC-IDS2017, and (e) CIC-IDS2018

Boxplot is used to visualize representations of data distribution of the results in terms of accuracy in three quartiles: lower, middle, and upper. A boxplot of all MH algorithms over five datasets is shown in Fig. 3. This figure shows that the median accuracy of RSA-CM is higher than other MH algorithms for all the five datasets, while upper accuracy is higher in four out of five datasets.

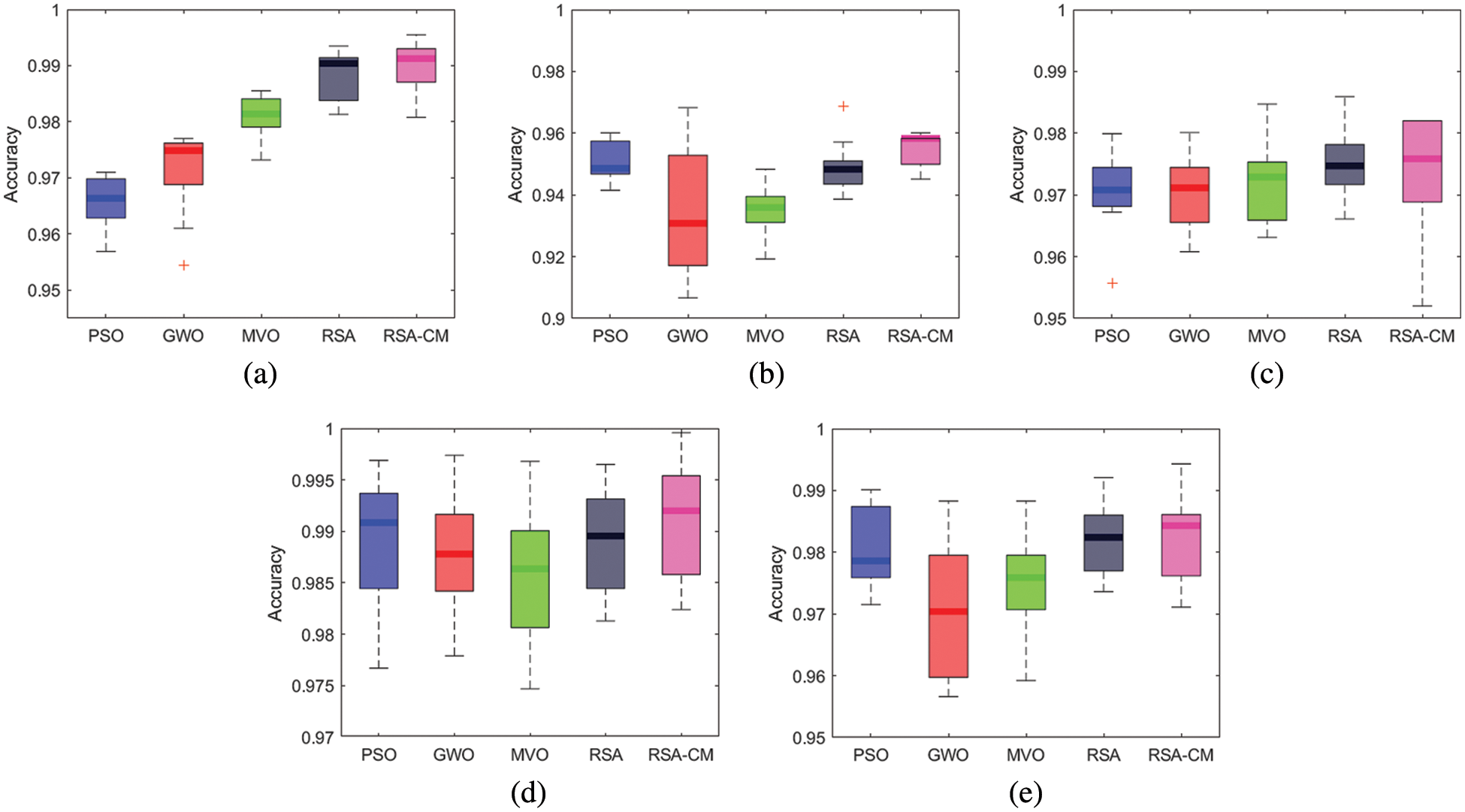
Figure 3: Boxplots of the RSA-CM and the other MH algorithms for (a) KDD-CUP99, (b) NSL-KDD, (c) UNSW-NB15, (d) CIC-IDS2017, and (e) CIC-IDS2018

4.5 Real-World Engineering Problems

The RSA-CM method is employed to solve two engineering problems with constraints, including Pressure Vessel Design (PVD) and Three-bar Truss Design, and the results are provided in this section.

4.5.1 Pressure Vessel Design (PVD)

In this problem, the PVD seeks to minimize the welding cost of the pressure vessel using the constraints on material and shipping. It consists of four variables, as illustrated in Fig. 4. These variables comprise Ts as the shell thickness, Th as the head thickness, R as the inner radius, and L as the cylindrical-section length. The objective function of the PVD can be represented as:

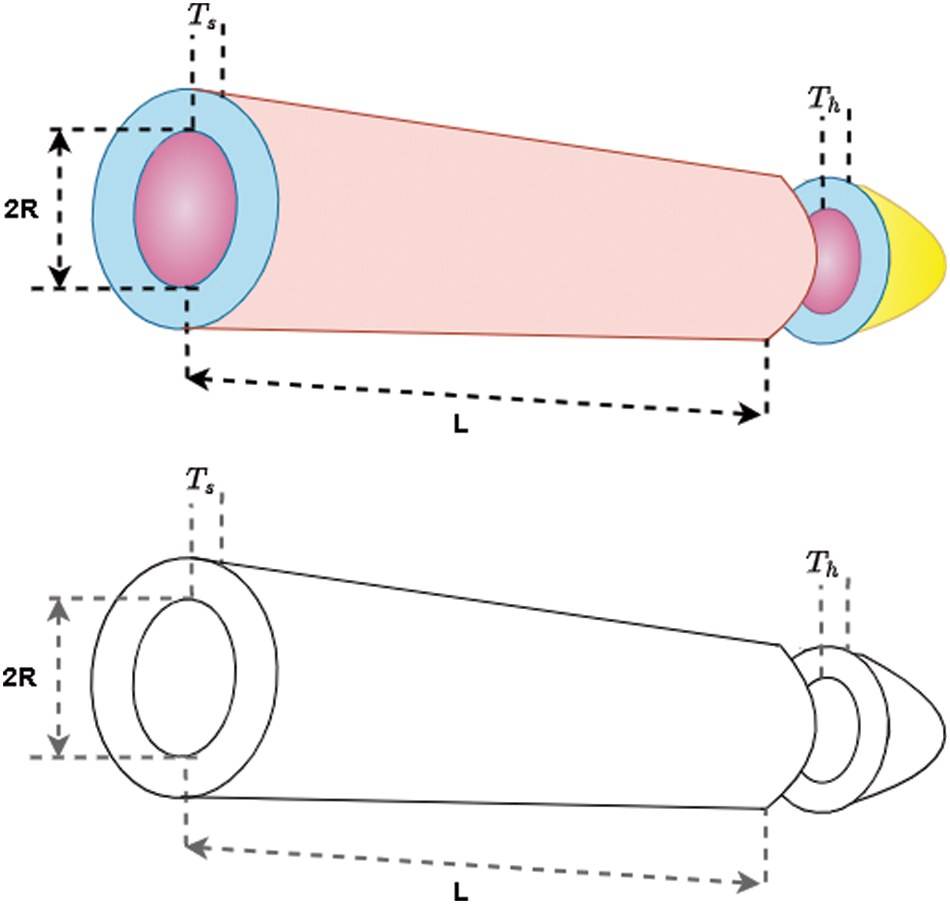
Figure 4: The PVD problem

Minimize

f(x)=0.6224x1x2x3+1.7781x2x32+3.1661x12x4+19.84x12x3(17)

Subject to

g1(x)=−x1+0.0193x3≤0,

g2(x)=−x3+0.00954x3≤0,

g3(x)=−πx32x4−43πx33+1,296,000≤0,

g4(x)=x4−240≤0,(18)

where (0≤xi≤100,i=1.2) and (10≤xi≤200,i=3.4).

Table 9 shows the welding cost for different methods used in this work. From this table, one can observe that the RSA-CM has the smallest weight of 2100.7202 compared to PSO, GWO, MVO and RSA, followed by the GWO with an optimal cost of 2101.866 and the PSO ranked last since it gained the highest optimal cost.

4.5.2 Three-Bar Truss Design (TBD)

A TBD’s optimal design seeks to reduce the structure weight subject to support total load acting vertically downward. The structural geometry of the problem is given in Fig. 5 and its objective function can be written as:

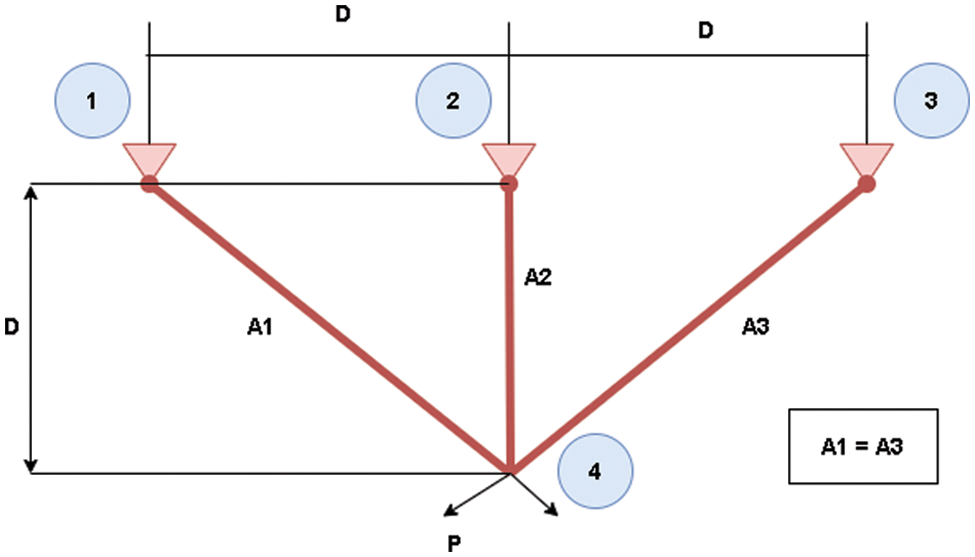
Figure 5: TBD problem

Minimize

f(x)=(22x1+x2)∗l(19)

Subject to

g1(x)=x1x1+x22x12+2x1x2P−σ≤0

g2(x)=x22x12+2x1x2P−σ≤0

g3(x)=12x2+x1P−σ≤0(20)

where l=100 cm,P=2 kN/cm2,σ=2 kN/cm2, 0≤xi≤1, and i=1.2.

The RSA-CM results for solving the problem of  TBD are provided in Table 10. From this table, the RSA-CM gives the best outcomes since it gained 317.3389, which is the smallest weight in comparison to other MH methods. Then GWO method ranked second while MVO ranked last for the problem of TBD.

4.6 Statistical Test

The Friedman test, a widely used non-parametric two-way analysis of variances by ranks [47], is performed to identify the significance of the performance evaluation measures on five datasets and five MH algorithms with 20 independent runs. The test assumes a null hypothesis (H0) as the equal performance of the comparative methods while the alternative hypothesis (H1) assumes the difference in the performance of the comparative MH algorithms. The highest rank for accuracy refers to the best algorithm as the larger value is preferred. On the other hand, the lowest rank is best for OFS and fitness as the smaller values are selected.

Table 11 shows average ranks for different MH algorithms with significance level α=0.05. The highest p-value calculated using Friedman’s test for all five datasets was 0.0166, which is less than α, indicating that the results are statistically significant. The proposed RSA-CM gained the best accuracy, OFS, and fitness value as compared to PSO, GWO, MVO, and RSA in three out of five datasets. In the case of CIC-IDS201, GWO achieved the best OFS and fitness, followed by the proposed RSA-CM. In the case of CIC-IDS2018, PSO performed the best OFS, but the proposed RSA-CM achieved the best accuracy and fitness value.

5  Conclusion and Future Work

Several security solutions based on ML have been developed in recent years, including ID systems. However, the existence of irrelevant or redundant data affects the performance of ML methods and their performance. Therefore, a novel FS method to improve the capability of the original RSA in exploration and exploitation using CM is presented. The CM is used to expand search capability of the RSA, which in turns prevent the RSA from getting stuck in local optima and improve its convergence speed. The developed RSA-CM efficiency is validated using five open-access datasets in the ID domain and two engineering problems. Its efficiency is also compared with PSO, GWO, MVO, and RSA methods. The results show that the RSA-CM performs better than the other methods on almost the datasets and the tested engineering problems in terms of several evaluation metrics used in this work. Moreover, Friedman test outcomes show that the proposed RSA-CM has the most significant results compared to other methods. These results make introduced RSA-CM superior to other comparative methods and more suitable to be used as a FS approach for the application of ID. In future work, we will attempt to use developed RSA-CM as an FS method in other applications such as text mining, image segmentation, and IoT.

Funding Statement: The author received no specific funding for this study.

Conflicts of Interest: The author declare that they have no conflicts of interest to report regarding the present study.

References

    1. I. H. Sarker, A. S. M. Kayes, S. Badsha, H. Alqahtani, P. Watters et al., “Cybersecurity data science: An overview from machine learning perspective,” Journal of Big Data, vol. 7, no. 1, pp. 1–29, 2020. [Google Scholar]

    2. E. Jaw and X. Wang, “Feature selection and ensemble-based intrusion detection system: An efficient and comprehensive approach,” Symmetry, vol. 13, no. 10, pp. 1764, 2021. [Google Scholar]

    3. H. Kure and S. Islam, “Cyber threat intelligence for improving cybersecurity and risk management in critical infrastructure,” Journal. Universal Computer Science, vol. 25, pp. 1478–1502, 2019. [Google Scholar]

    4. I. Lee, “Internet of Things (IoT) cybersecurity: Literature review and IoT cyber risk management,” Future Internet, vol. 12, no. 9, pp. 157, 2020. [Google Scholar]

    5. V. Ford and A. Siraj, “Applications of machine learning in cyber security,” in 27th Int. Conf. on Computing Application Industry & Engineering, Kota Kinabalu, Malaysia, pp. 1–6, 2014. [Google Scholar]

    6. A. Gupta, R. Gupta and G. Kukreja, “Cyber security using machine learning: Techniques and business applications,” Application Artificial Intelligence in Business Education & Healthcare, Studies Computer Intelligence, vol. 954, pp. 385–406, 2021. [Google Scholar]

    7. Z. Ahmad, A. Shahid Khan, C. Wai Shiang, J. Abdullah and F. Ahmad, “Network intrusion detection system: A systematic study of machine learning and deep learning approaches,” Transactions Emerging Telecommunication Technology, vol. 32, no. 1, pp. e4150, 2021. [Google Scholar]

    8. H. Liu and B. Lang, “Machine learning and deep learning methods for intrusion detection systems: A survey,” Applied. Sciences, vol. 9, no. 20, pp. 4396, 2019. [Google Scholar]

    9. M. Banaie-Dezfouli, M. H. Nadimi-Shahraki and Z. Beheshti, “R-GWO: Representative-based Grey wolf optimizer for solving engineering problems,” Applied Soft Computing, vol. 106, no. 4, pp. 107328, 2021. [Google Scholar]

  10. R. Khalid and N. Javaid, “A survey on hyperparameters optimization algorithms of forecasting models in smart grid,” Sustainable Cities & Society, vol. 61, no. 6, pp. 102275, 2020. [Google Scholar]

  11. L. Abualigah and A. Diabat, “A comprehensive survey of the Grasshopper optimization algorithm: Results, variants, and applications,” Neural Computing & Applications, vol. 32, no. 19, pp. 15533–15556, 2020. [Google Scholar]

  12. R. Khalid and N. Javaid, “A survey on hyperparameters optimization algorithms of forecasting models in smart grid,” Sustainable Cities & Society, vol. 61, no. 6, pp. 102275, 2020. [Google Scholar]

  13. S. Mirjalili, S. M. Mirjalili and A. Hatamlou, “Multi-verse optimizer: A nature-inspired algorithm for global optimization,” Neural Computing & Applications, vol. 27, no. 2, pp. 495–513, 2016. [Google Scholar]

  14. J. Kennedy and R. Eberhart, “Particle swarm optimization,” in Int. Conf. on Neural Networks, Perth, WA, Australia, pp. 1942–1948, 1995. [Google Scholar]

  15. J. H. Holland, “Genetic algorithms,” Scientific American, vol. 267, no. 1, pp. 66–73, 1992. [Google Scholar]

  16. S. Mirjalili, A. H. Gandomi, S. Z. Mirjalili, S. Saremi, H. Faris et al., “Salp swarm algorithm: A bio-inspired optimizer for engineering design problems,” Advances Engineering Software, vol. 114, pp. 163–191, 2017. [Google Scholar]

  17. S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Advances Engineering Software, vol. 95, no. 12, pp. 51–67, 2016. [Google Scholar]

  18. S. Mirjalili, S. M. Mirjalili and A. Lewis, “Grey wolf optimizer,” Advances Engineering Software, vol. 69, pp. 46–61, 2014. [Google Scholar]

  19. L. Abualigah, M. Abd Elaziz, P. Sumari, Z. W. Geem and A. H. Gandomi, “Reptile Search Algorithm (RSAA nature-inspired meta-heuristic optimizer,” Expert Systems with Applications, vol. 191, no. 11, pp. 116158, 2022. [Google Scholar]

  20. K. H. Almotairi and L. Abualigah, “Hybrid reptile search algorithm and remora optimization algorithm for optimization tasks and data clustering,” Symmetry, vol. 14, no. 3, pp. 116158, 2022. [Google Scholar]

  21. A. Dahou, M. Abd Elaziz, S. A. Chelloug, M. A. Awadallah, M. A. Al-Betar et al., “Intrusion detection system for IoT based on deep learning and modified reptile search algorithm,” Computer Intelligence Neuroscience, vol. 2022, no. 4, pp. 6473507, 2022. [Google Scholar]

  22. Z. Elgamal, A. Q. M. Sabri, M. Tubishat, D. Tbaishat, S. N. Makhadmeh et al., “Improved reptile search optimization algorithm using Chaotic map and Simulated annealing for feature selection in medical field,” IEEE Access, vol. 10, pp. 51428–51446, 2022. [Google Scholar]

  23. S. Ekinci and D. Izci, “Enhanced reptile search algorithm with Lévy flight for vehicle cruise control system design,” Evolutionary Intelligence, vol. 2022, pp. 1–13, 2022. [Google Scholar]

  24. I. Al-Shourbaji, N. Helian, Y. Sun, S. Alshathri and M. Abd Elaziz, “Boosting ant colony optimization with reptile search algorithm for churn prediction,” Mathematics, vol. 10, no. 7, pp. 1031, 2022. [Google Scholar]

  25. K. H. Almotairi and L. Abualigah, “Improved reptile search algorithm with novel mean transition mechanism for constrained industrial engineering problems,” Neural Computing Applications, vol. 2022, no. 20, pp. 1–21, 2022. [Google Scholar]

  26. Z. Halim, M. N. Yousaf, M. Waqas, M. Sulaiman, G. Abbas et al., “An effective genetic algorithm-based feature selection method for intrusion detection systems,” Computers & Security, vol. 110, no. 34, pp. 102448, 2021. [Google Scholar]

  27. M. H. Kamarudin, C. Maple and T. Watson, “Hybrid feature selection technique for intrusion detection system,” International Journal High Performance Computing & Networking, vol. 13, no. 2, pp. 232–240, 2019. [Google Scholar]

  28. N. Acharya and S. Singh, “An IWD-based feature selection method for intrusion detection system,” Soft Computing, vol. 22, no. 13, pp. 4407–4416, 2018. [Google Scholar]

  29. H. Wang, C. Li, Y. Liu and S. Zeng, “A hybrid particle swarm algorithm with Cauchy mutation,” in IEEE Swarm Intelligence Symp. Honolulu, HI, USA, pp. 356–360, 2007. [Google Scholar]

  30. A. Kollu and S. Vadlamudi, “Eagle strategy with Cauchy mutation particle swarm optimization for energy management in cloud computing,” International Journal Intelligent. Engineering & Systems, vol. 13, no. 6, pp. 42–51, 2020. [Google Scholar]

  31. M. P. Behera, A. Sarangi and S. Mishra, “Analysis of Gaussian and Cauchy mutations in k-means particle swarm optimization algorithm for data clustering,” Technical Advancements Machine Learning Healthcare, Studies Computer Intelligence, vol. 936, pp. 103–117, 2021. [Google Scholar]

  32. I. Al-Shourbaji, P. H. Kachare, S. Alshathri, S. Duraibi, B. Elnaim et al., “An efficient parallel reptile search algorithm and snake optimizer approach for feature selection,” Mathematics, vol. 10, no. 13, pp. 2351, 2022. [Google Scholar]

  33. M. Tavallaee, E. Bagheri, W. Lu and A. A. Ghorbani, “A detailed analysis of the KDD CUP 99 data set,” in IEEE Symp. Computer Intelligence Security & Defense Applications, Ottawa, ON, Canada, pp. 1–6, 2009. [Google Scholar]

  34. S. Sapre, P. Ahmadi and K. Islam, “A robust comparison of the KDDCup99 and NSL-KDD IoT network intrusion detection datasets through various machine learning algorithms,” ArXiv:1912.13204, 2019. [Google Scholar]

  35. N. Moustafa and J. Slay, “UNSW-NB15: A comprehensive data set for network intrusion detection systems,” in Int. Conf. on Military Communication & Information Systems, Canberra, ACT, Australia, pp. 1–6, 2015. [Google Scholar]

  36. I. Sharafaldin, A. H. Lashkari and A. A. Ghorbani, “Toward generating a new intrusion detection dataset and intrusion traffic characterization,” in Int. Conf. on Information Systems & Security, Libson, Portugal, pp. 108–116, 2018. [Google Scholar]