Social Engineering Attack-Defense Strategies Based on Reinforcement Learning

1  Introduction

With the continuous development of network technology, communication is not limited by traditional distance or the various social networks, e-mail, or network communication methods that satisfy daily needs for communication and entertainment. The internet is becoming increasingly important, and we cannot live without it. However, there are also nefarious actors lurking in the network; they attack by taking advantage of users’ psychological weaknesses and inducing them to disclose sensitive information [1].

In the second quarter of 2022, the APWG (Anti-Phishing Working Group) observed 1,097,811 phishing attacks, a new record, and this was the worst quarter for phishing ever followed by the APWG. The number of phishing attacks reported to the APWG has quadrupled since the beginning of 2020, when the APWG started to keep phishing attacks. A total of 68,000 to 94,000 episodes per month were followed by the APWG in early 2020 [2].

Unlike traditional cyber attacks, social engineering attacks mainly exploit the psychological weaknesses of the target to execute the attack, and Reference [3] designed a general architecture for social engineering attacks. The main features of the structure are attack preparation, attack implementation, and attack gain. In the preparation stage, information and relationships are collected for the target, usually using web crawlers, social network information collection, etc. A social engineering script design is carried out in the attack preparation stage for the social engineering targets. In the attack gain stage, all information obtained is evaluated and judged on whether the attack was successful [4].

Network security has recently received increased attention, especially for social engineering attack defense strategies research. Many studies have focused on reinforcement learning, some based on game theory [4–7]. However, there are two problems with these technical approaches. First, social engineering attacks exploit human vulnerabilities to deceive and trick users into revealing sensitive information. The traditional social engineering defense strategy does not consider user vulnerability, leading to ineffective defense strategies. Therefore, we need to design a new model considering user vulnerability. Second, social engineering attacks are real-time, requiring real-time reactions to the attacks to avoid serious harm. Current game theory and reinforcement learning-based defense strategy responses are delayed because of their high time complexity [8,9].

A summary of the related work on reinforcement learning applied to cybersecurity, game-learning programs, and secure game-theoretic modeling are shown in Table 1.

2  Definition of the Problem

Usually, when attackers engineer user attacks, this paper considers the attack method, attack technique, attack detection, etc., however, all of these factors must be identified through human judgment. Therefore, the threat comes from combining these attacks and interaction with people during attack reinforcement. Existing social engineering attack defense models ignore the role of human attributes, so this paper proposes a new quantitative approach that combines human characteristics to quantitatively evaluate each attack node using the standard notation in Table 2.

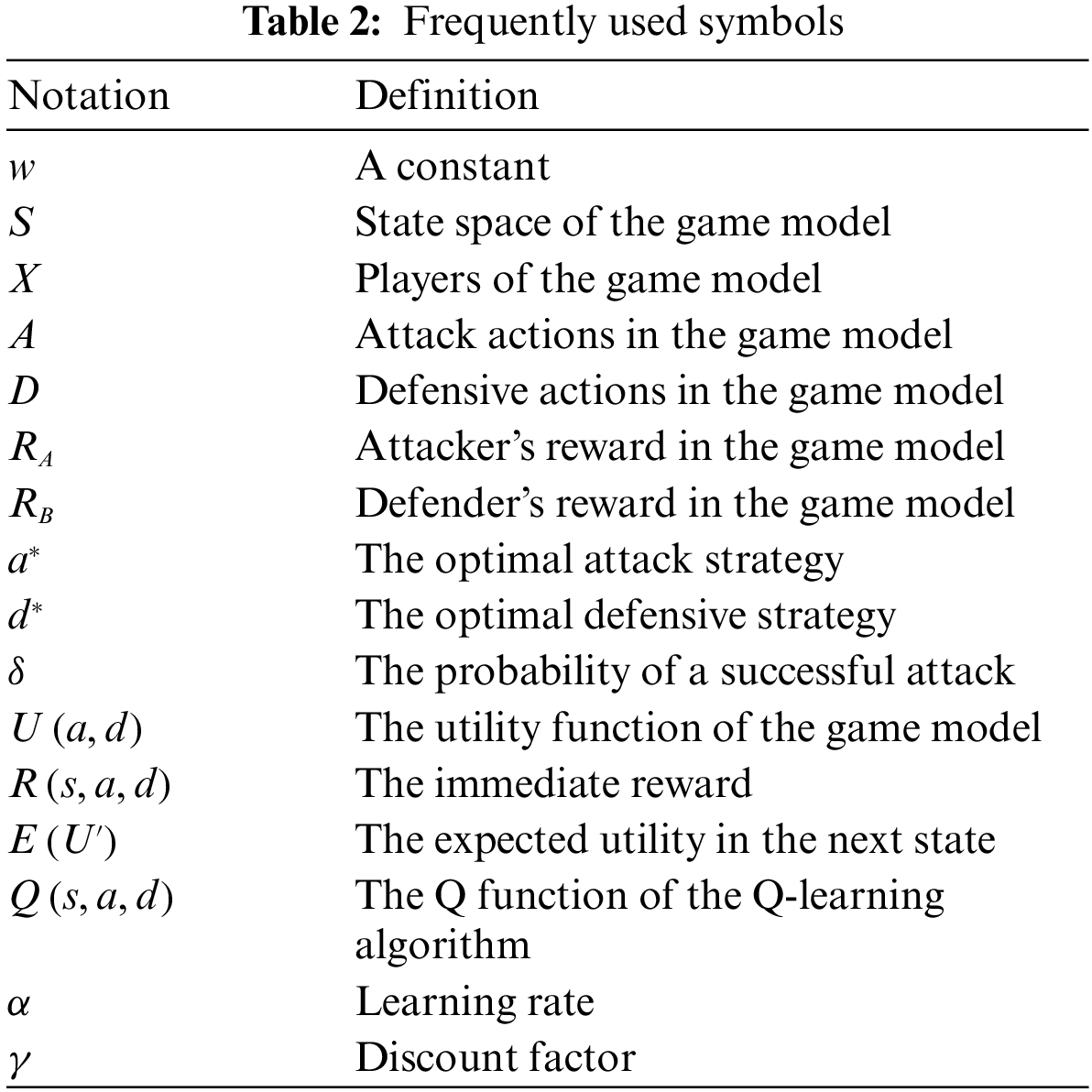
The attributes of the nodes are divided into two types: physical attributes and target attributes. A physical analysis mainly considers the impact size of the nodes in the entire system. Each node’s physical characteristics include the importance level of the node and the connection level in the node. The node’s target attributes mainly have the features of the target, security knowledge, character, and security awareness attributes. These attributes are directly related to the strength of the security defense.

Definition 1: The physical attributes mainly include the importance level and connection level of the node.

The importance level (IL) mainly indicates the node’s importance in the entire social engineering system. This importance level primarily three factors: the valid information that can be obtained, the impact on subsequent attacks, and whether trust is established [19].

The connection level (CL), which indicates the importance of the node’s associations in the social engineering system, is determined by the stage of the social engineering model in which the node is located and the number of other nodes connected to this node.

Definition 2: Target attributes (TA) mainly include defense technology, defense means, basic information of the target, security knowledge level, personality type, security awareness registration, and target cognitive paths [20]. The higher the target’s attributes value, the stronger its defense capability and the higher the node security. If the physical characteristics of the node are high, the assigned defense is enhanced accordingly [21].

The above values of the physical attributes and target attributes are set by the system administrator and mapped to a vector F, where fi denotes the result of the administrator’s evaluation of i using F. The ratings for the social engineering security system are divided into three primary levels: high, medium, and low. Therefore, we have F ∈ [1, 2, 3]. The attribute-based social engineering security metric (SESM) is defined as

SESM=w∗log2⁡(1+IL⋅CLTA)(1)

In the above equation, w is a constant. This constant is related to the state space and action space for the node: w=A+DS, where the greater the value of the SESM is, the higher the importance of the node, the greater the loss due to an attack, and the lower the node defense capability. The value of SESM indicates the target receiving the social engineering attacks and the impact of each node on itself. For the social engineering attacker, who mainly uses the vulnerability of the person at the node to implement the attacks, this paper defines a time-based function in the form of attack resource consumption, defense resource consumption, and loss recovery consumption.

Attack resource consumption (AR): the consumption of attack resources in the attack preparation phase, the attack implementation phase, target information collection, scripting, trust building, and other actions that consume time [22].

Defense resource (DR) consumption: resource consumption in resisting social engineering attacks; time consumed in preventing attackers from obtaining protected information, detecting attacks, and identifying attacks for information collection [23].

Loss recovery consumption (LR): the time consumed in recovering from the loss caused by the attack, such as replacing a secret key, changing a password, or taking other actions to protect one’s property and information [24].

3  Material and Methods

In the human vulnerability-based social engineering model, an attacker can use human vulnerabilities to perform social engineering attacks and obtain sensitive information. For the attacker, the greater the vulnerability found, the greater the harm and the greater the social engineering gain. Defense against social engineering focuses on the corresponding social engineering defenses for detected social engineering attacks. Ideally, the target has no exploitable vulnerabilities and is safe. However, in practice, the target attributes vary, the vulnerability performance ranges, the attacker can always find vulnerabilities to attack, and the defenses can lag and collapse when an attack occurs. The attacker and the defender are similar to the two sides of a game; the attacker tries to obtain the maximum reward, and the defender pursues the minimum loss. The two sides of the attacker and defender can be considered a stochastic game, and a stochastic game model can be used to analyze the best defense strategy for the defender. This paper design a new reward quantification method to quantify the role of vulnerability in the model, considering the properties of the target and the interaction between the vulnerability and the attack. The social engineering attack model is shown in Fig. 1 below.

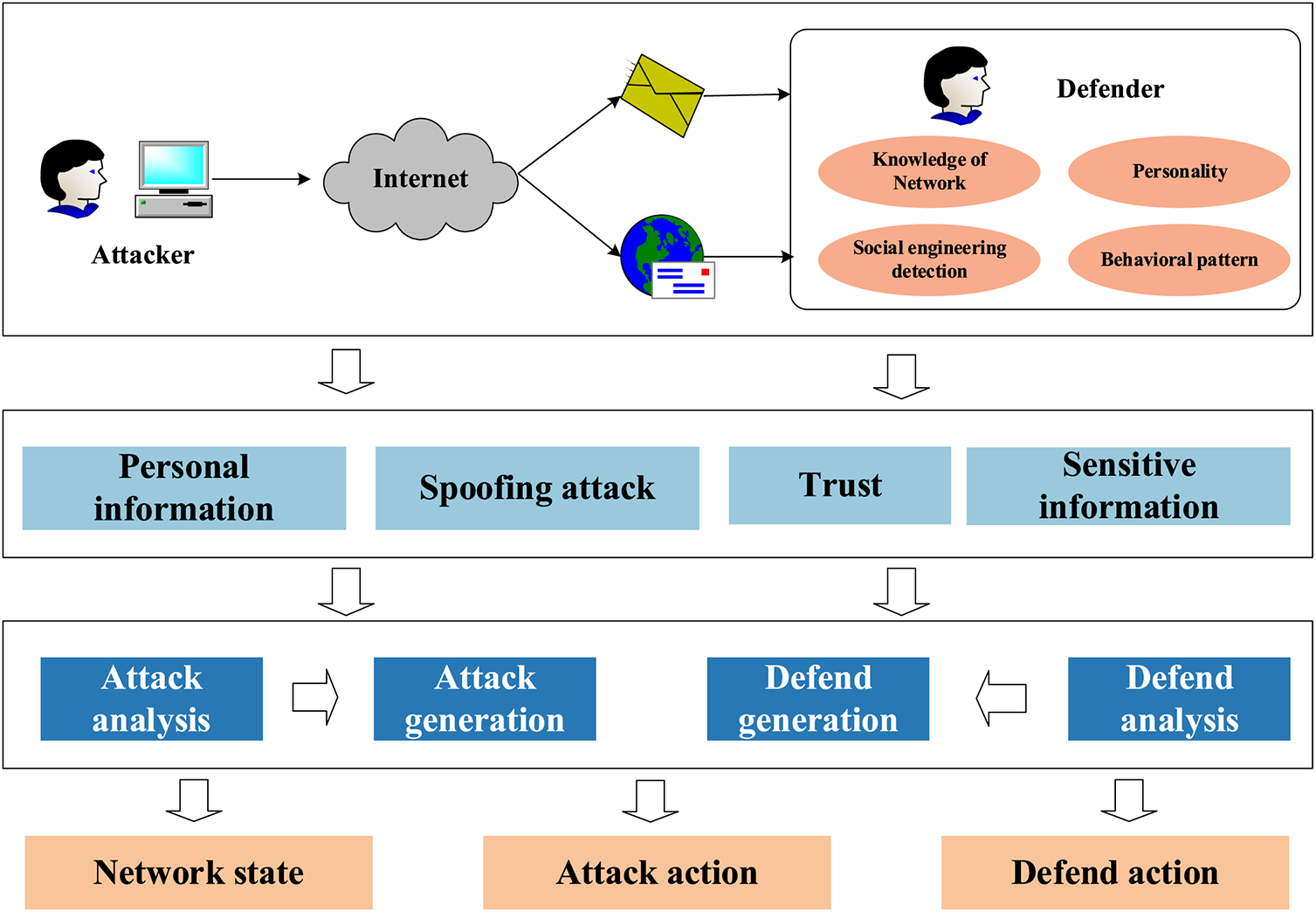
Figure 1: Social engineering attack model diagram

3.1 Basic Model

The structure of the social engineering system model is complex, with multiple stages. At each stage, the attacker does not have access to information about the entire system and takes random actions based on the information obtained at this stage. At the same time, neither the attacker nor the defender has access to the game information of the adversary or the gain of each action. This paper describes the game between the attacker and the defender in the social engineering system as a stochastic game model with incomplete information. The model is defined as follows.

G=⟨S,X,A,D,RA,RD⟩(2)

where S denotes the state set, X denotes the players involved in the game, A drepresents the attack action space, D drepresents the defense action space, RA denotes the attack gain, and RD denotes the defense gain. The players in the different states have corresponding sets of response actions; attackers have attack action sets, and defenders have defense action sets. The attackers and defenders have action sets that implement offensive and defensive games. The current state, attack action, and defense action result in a state change, and the attacker and the defender obtain live gains.

The attacker’s utility consists of the attack gain and the period of the next state, and it can be expressed as

UA(a,d)=R(s,a,d)+E(UA′)(3)

E(UA′) in the above equation represents the expectation of the next state, where R(s,a,d) represents the attacker’s attack gain, a represents the attack action and d represents the defense action. Then, the dynamic policy is defined as

(a,d)=[a1,d1,a1,d2,…,a1,dIa2,d1,a2,d2,…,a2,dI……⋱…aJ,d1,aJ,d2,…,aJ,dI](4)

In the above equation, (aj,di) denotes an action pair with attack action aj and defense action di in state s. In the game between the attacker and defender, the utility of the attacker is not only determined by the attack action but also depends on the defense action; then, the reward function is

R(s,a,d)=SESM⋅(δ⋅RT(a)+DT(d)−AT(a))(5)

Here, the SESM is an attribute-based social engineering security level indicator, and the SESM mainly reflects the node’s importance. δ indicates the success probability of the social engineering attack, and we analyze this probability by studying real social engineering attack cases. RT is the set of resources required to recover from social engineering attack action a. The response of the target is affected by the degree of the attack, where DT indicates the defense resource consumption of the attack action. In addition to the physical resource consumption, the target’s mental resource consumption must be considered. The effectiveness function U represents the interaction between the target vulnerability and the social engineering attack. The purpose of the defense is to reduce the loss from the social engineering attack, so we can assume that the attack gain of the optimal attacker is 0. The game between the attacker and the defender in the social engineering process is zero-sum [25].

By formalizing the representations of the social engineering attack participants, the entire defined social engineering attack process is constructed as a game model G, where the attacker seeks the maximum gain from the attack, and the defender aims to minimize the loss. This use a stochastic game model to construct the social engineering attack model. In this model, the different targets have different attributes, and the other attributes have different vulnerabilities. There are interactions between the target’s vulnerability and the social engineering attack, and finally, a stochastic game model of social engineering based on the attributes of the target is designed. The model optimization problem can be defined as follows.

Definition 3: Social engineering defense security decision optimization problem: Using quantified rewards as input, the social engineering defense security decision optimization problem is to find the optimal attack strategy a∗ and defense strategy d∗ for a∈A such that UA(a∗,d∗)=MaxUA(a,d∗) and for d∈D such that UD(a∗,d∗)=MaxUD(a∗,d).

The utility function in the entire social engineering system, mainly considering the interaction between the target vulnerability and attacker, is quantified by the attack utility function UA(a∗,d∗) and the defense utility function UD(a∗,d∗). The final social engineering defense security decision optimization objective is to solve the Nash equilibrium. Therefore, (a∗,d∗) is the optimal strategy for social engineering defense security decisions. The attacker’s optimal attack strategy is a∗ because this yields the maximum attack gain, and the defender’s optimal defense strategy is d∗ because this yields the minimum system loss.

3.2 Improved and Optimized Q-Learning Algorithm

In social engineering defense strategies, traditional approaches use Q-learning. This is because Q-learning algorithms converge quickly and can compute optimal policies. This method is widely used; however, as the system’s complexity increases, the system’s unstable and dynamic nature leads to an increase in the convergence time of the Q-learning method. Researchers have proposed relevant solutions combined with deep learning to improve the convergence speed of Q-learning algorithms. However, these solutions require a large amount of computation and often do not guarantee the algorithm’s convergence in computing the optimal policy. The traditional formulation of the Q algorithm can be expressed as

Q(s,a,d)=(1−α)Q(s,a,d)+α(R(s,a,d)+γV(s′)))(6)

where s’ is the next state, γ is the discount factor and the iterative learning rate can be denoted as α=1/(t+1)ω. R(s,a,d) denotes the gain under attack action a and defense action d, where V(s′) denotes the maximum expected Q value for the next state. V(s′) can be set as

V(s′)=maxminπ(s′)Q(s′,a′,d′)(7)

Theorem 1: The multi-attribute quantitative reinforcement learning model based on human weakness proposed in this paper is convergent, and the reward sequence {Q_t }_(t→∞) is the optimal rewards Q^*.

Proof:

According to Eqs. (6) and (7).

Q∗(s,a,d)=∑s′∈SP(s′∣s,a,d)(R(s,a,d)+α(maxminπ(s′)Q(s′,a′,d′)))=E[FtQ∗](8)

then it can be computed ∥FtQ−FtQ∗∥

∥FtQ−FtQ∗∥=mins,s′∈Smax|γπ(s)Q(s)−γπ(s′)Q∗(s′)|≤γ|π(s)Q(s)−π(s′)Q∗(s′)|(9)

In order to prove convergence, it is necessary to prove that the sequence {Qt}t→∞ is the most optimal strategy Q∗

|π(s)Q(s)−π(s′)Q∗(s′)|≤∥Q−Q∗∥(10)

According to π(s) and π(sʹ), we have

|π(s)Q(s)−π(s′)Q∗(s′)|=π(s′)Q(s′)−π(s′)Q∗(s)≤π(s′)Q(s′)−π(s′)Q∗(s)≤π(s′)∥Q(s)−Q∗(s′)∥=∥Q(s)−Q∗(s′)∥(11)

If π (s) Q (s) − π (s^ʹ) Q^* (s^') ≥ 0

|π(s)Q(s)−π(s′)Q∗(s′)|=π(s)Q(s)−π(s′)Q∗(s′)≤π(s)Q(s)−π(s)Q∗(s′)≤π(s)∥Q(s)−Q∗(s′)∥=∥Q(s)−Q∗(s′)∥.(12)

can get

∥FtQ−FtQ∗∥≤γ∣π(S)Q(s)−π(s′)Q∗(s′)≤γ∥Q−Q∗∥≤γ∥Q−Q∗∥+λt(13)

According to the above proof, the model is convergent, where t he sequence {Qt}t→∞ is the most optimal strategy Q∗. To speed up the computation of Q-learning, a parallel computation method is designed in this paper to implement the IQL algorithm. By setting up multiple learning processes, each of which is attacker-centric, and ensuring that all learning is performed independently, the computational complexity of IQL is lower than that of the QL algorithm, and it converges more easily.

The Q-value update mechanism is also optimized to further improve the computation speed. Different learning processes can be updated simultaneously in parallel for the current state of the Q-value. There is no need to update after learning. All Q-learning procedures are performed simultaneously and synchronously to update the values, using the updated Q-values to update the previous Q-values. This is faster and more effective; the algorithm is shown in Algorithm 1.

According to Algorithm 1, this paper quantifies two global q variables, QA and QD. The algorithm uses parallel computation by calculating multiple attackers’ learning processes at the same time, and all the computations constantly update the states of QA and QD. Therefore, the Q value can be guaranteed to be updated synchronously. For attacker j in the algorithm, the attacker performs an attack action aj, and the defender performs the corresponding defense action dj. Based on the attacker’s attack action and the defender’s defense action, an attack gain is obtained, and the state when the reward is oreceived A gain matrix GM is generated based on the states and rewards. A final gain and an optimal strategy are output by continuously cycling until all the attackers’ learning processes are completed.

4  Experimental Results and Analysis

In this chapter, we construct a simplenatural social engineering system and analyze the simulation results.

4.1 Experimental Setup

The social engineering system mainly simulates phishing attacks, and the ’ystem’s architecture is shown in Fig. 2. The whole structure includes the attack preparation, attack route, attack implementation, and attack gain stages. Attack preparation comprises collecting information from public resources, performing information system queries, collecting data from users, and writing scripts; attack target selection includes determining attack route nodes, such as phishing websites, phishing emails, and phishing SMSs; the attack implementation stage includes influencing the target, conducting psychological exploitation and script exploitation, assessing participant behavior, and building trust; and the attack gain stage mainly involves acquiring device permissions, obtaining sensitive information, and influencing target behavior.

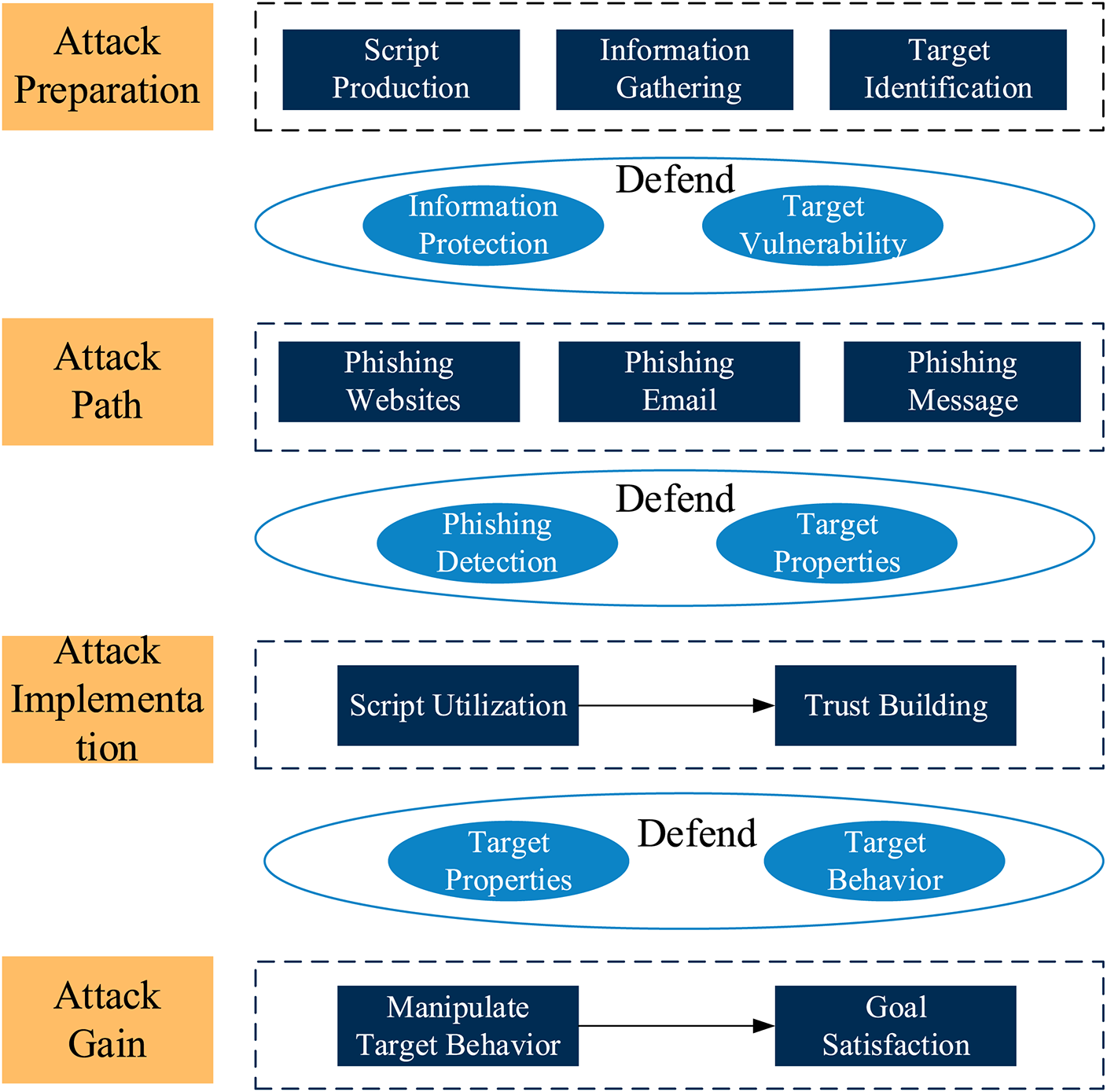
Figure 2: Experimental environment

The values of IL, CL, and TA for all nodes are shown in Table 3, where the three values of information search N1 are set to 2, 1, and 2; for the attack state N2, the three values are set to 1, 2, and 1; for gaining trust, N3, the three values are set to 2, 3, and 3; and for performing action N4, the three values are set to 3, 2, and 3.

The social engineering attacker, through the collection of target information, discovers the target attributes, finds the arget’s vulnerability, and executes an attack on the target, and the purpose of the attack is to obtain sensitive information or goods. The Common Attack Pattern Enumeration and Classification (CAPEC) database, developed and maintained by MITRE, records known cyber attack patterns [26]. The vulnerabilities are shown in Table 4.

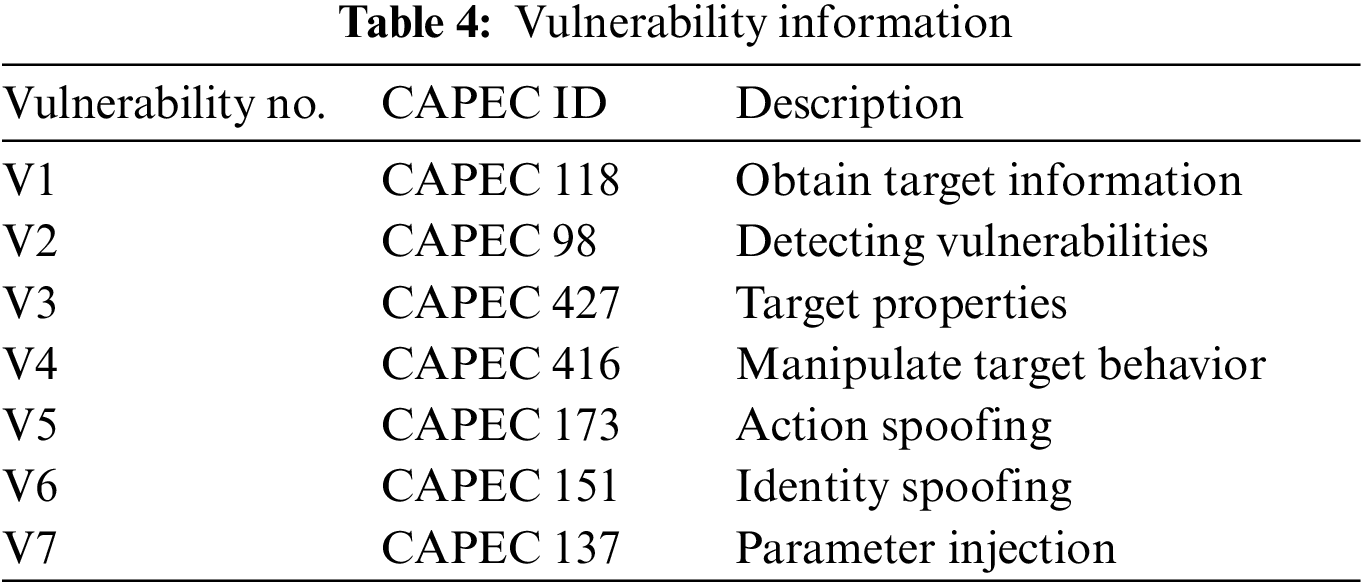
Table 5 lists all the states of the game; if the attacker discovers a vulnerability to an attack and exploits it, a state transition occurs. If the attacker does not find an attack state, the attacker takes no action. The attack actions are shown in Table 6, and the defense actions are shown in Table 7.

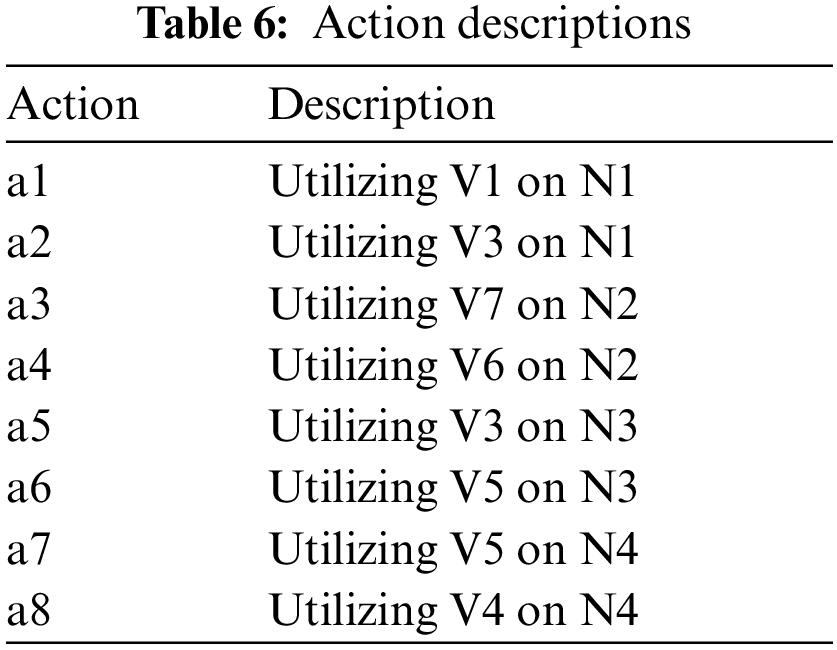
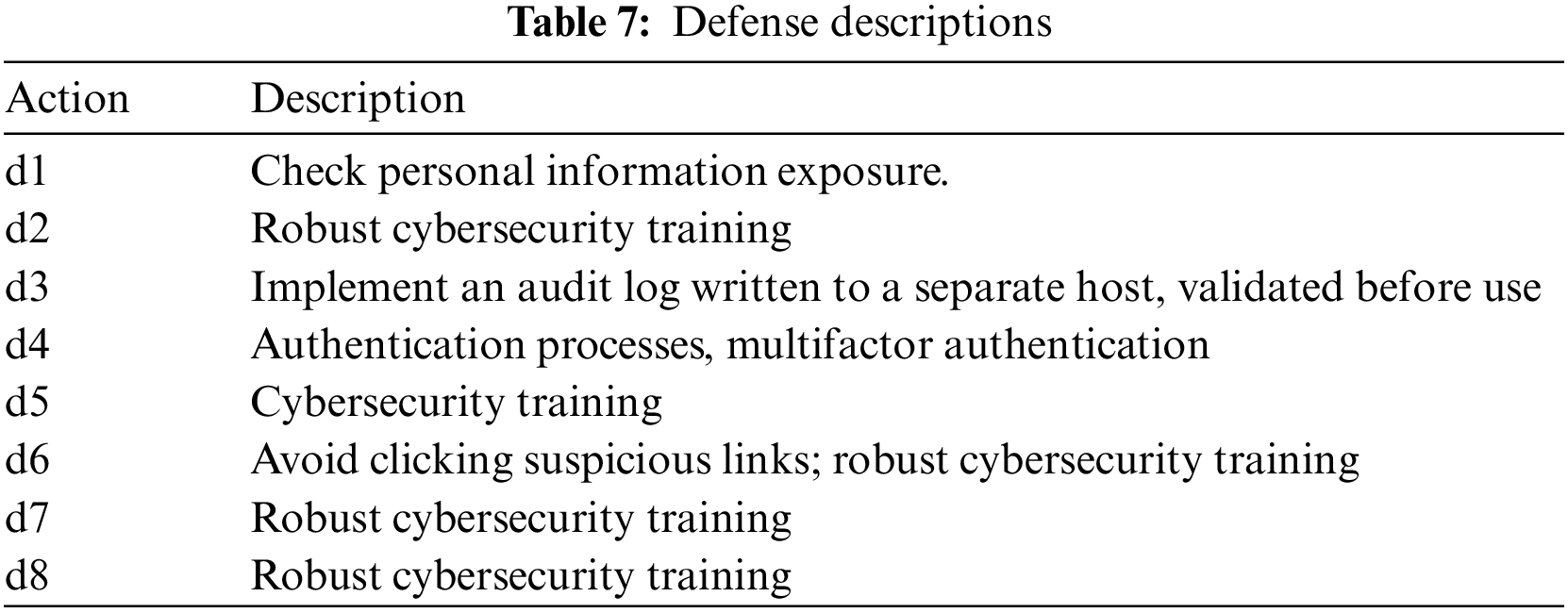
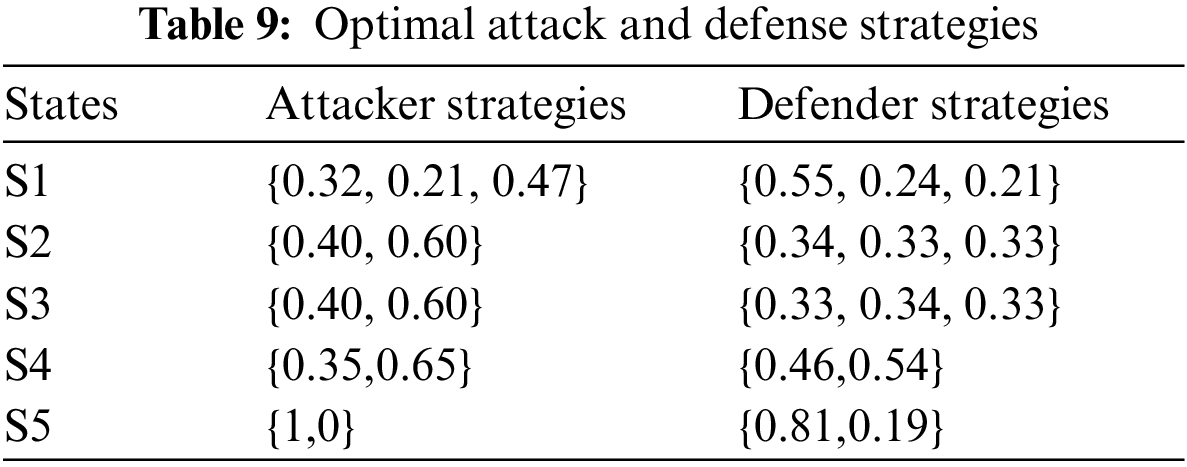
The corresponding sets of defense and attack strategies are shown in Table 9.

4.2 Experimental Analysis

In this paper, we introduce the concepts of players and strategies and construct a model of reinforcement learning using players and strategies with a custom nature. In the game model of this paper, there are two players, and each player learns a new strategy. Each player’s strategy is formulated according to the player’s current state and the actions taken. The player’s probability is updated by observing the opponent’s behavior and changing the action accordingly. The best behavioral strategy is finally acquired through reinforcement learning for maximum benefit. The model in this paper has five states, and the reward of each state is shown in Fig. 3. As shown, the stochastic game reaches a Nash equilibrium after 2300 iterations. Table 8 lists the average rewards for the five states. According to the table, the rewards of S1 and S2 are essentially the same.

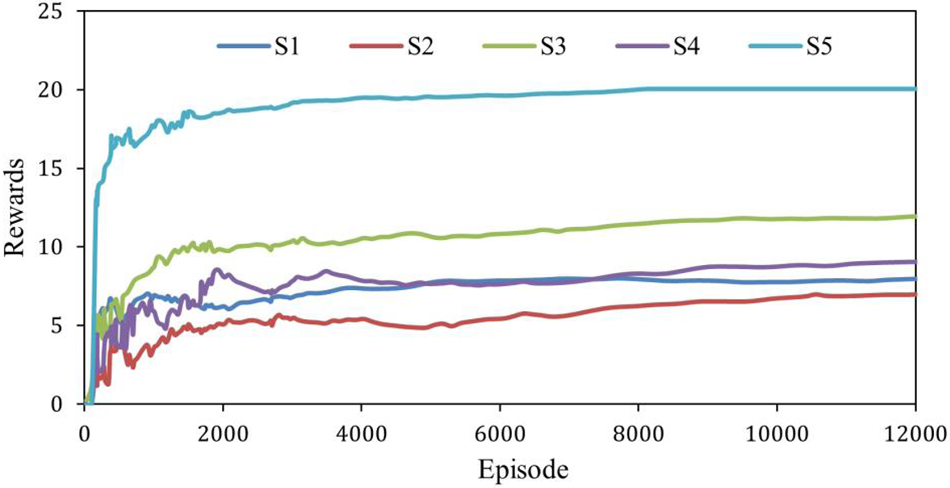
Figure 3: IQP process rewards in different states

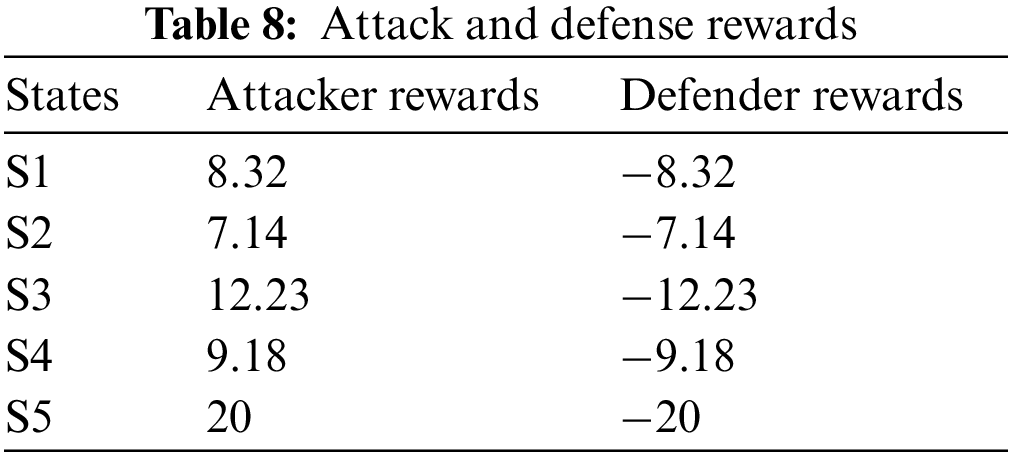
Table 9 lists the optimal strategies of the attackers and defenders in all states for each actual situation. It can be seen that in the initial stage of IQL, the probabilities of the players’ decisions are random. As the number of iterations of the overall tethered model increases, the agent can obtain information about the adversary, and the best defense strategies are finally accepted by using the solved game matrix. According to the IQL algorithm proposed in this paper, the optimal strategy for the attacker and the defender are solved. The implementation results show that the method proposed in this paper can effectively obtain the optimal defense strategies.

In this paper, we propose an improved Q-learning algorithm that utilizes parallel computing to improve the efficiency of the computation. We conducted experiments using 1, 10, 20, and 30 parallel learning states to verify the relationship between multiple parallel learning processes and decision-makingsimilar. The results are shown in Fig. 4. Increasing the number of learning processes within a specific range can effectively improve learning efficiency and lead to fast convergence. However, if 30 learning processes are set, the efficiency will be small, and the decision time will increase due to the overly complicated iterative process. The experiment shows that increasing the number of learning methods within a specific range can effectively reduce the strategy learning time, but using too many learning processes will increase the strategy learning time.

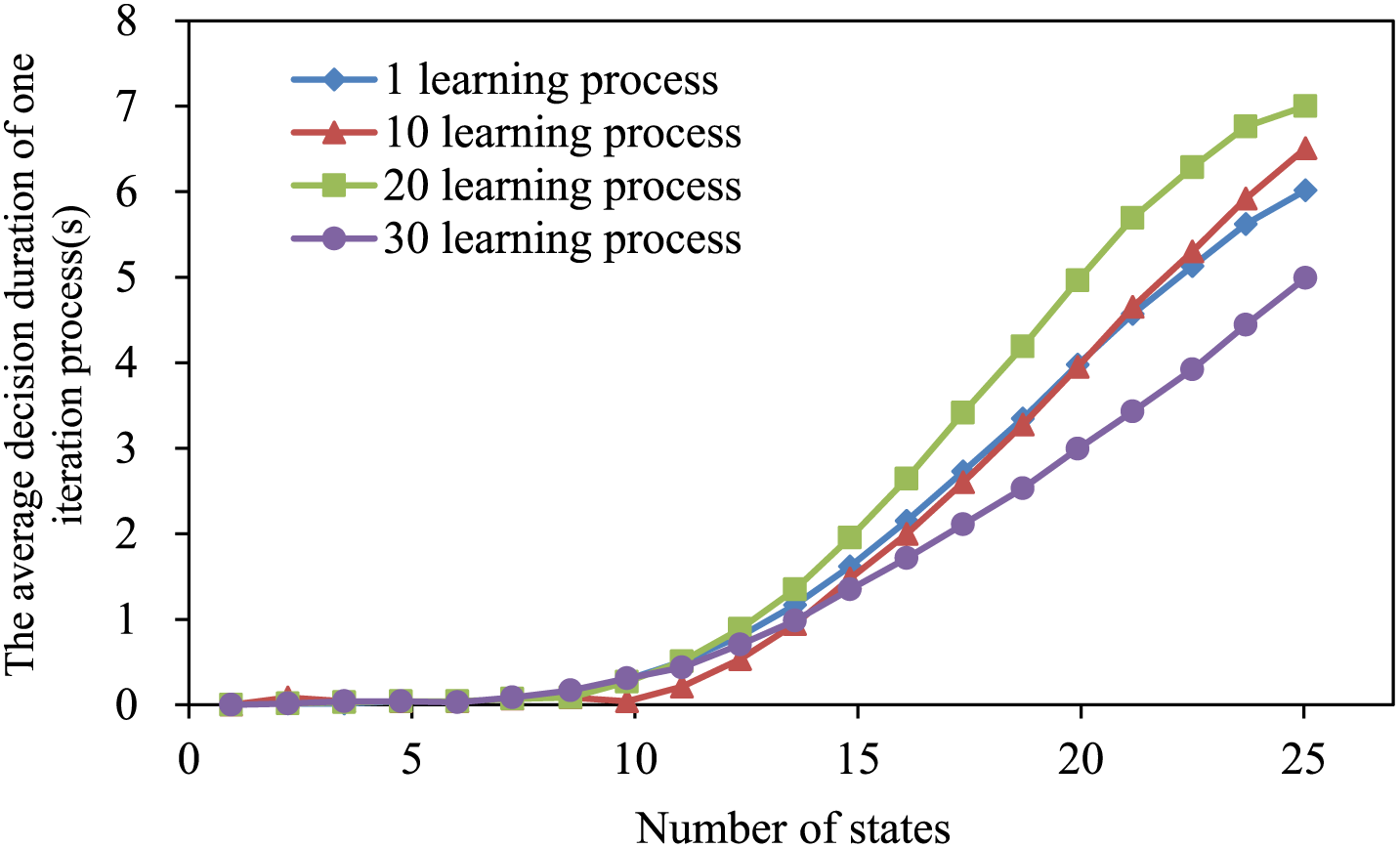
Figure 4: The decision duration of one iterative process for different numbers of learning processes

According to the literature survey, few studies apply game theory and reinforcement learning algorithms to the problem of social engineering defense strategy generation problem. Using different performance indicators and characteristics to compare and analyze the algorithm in this paper cannot prove the performance of the algorithm. Two commonly used reinforcement learning algorithms QL algorithm, and DQN algorithm [27], are used in this paper to compare and analyze the effectiveness and performance of the IQL algorithm proposed in this paper.

In this paper, the simulation experiment of social engineering defense strategy generation is carried out in the same network simulation environment, and the statistical analysis of the experimental data is carried out. The experimental results show that the simulation results obtained using Q-learning, DQN, and the algorithm in this paper in the social engineering random game scenario are shown in Fig. 5.

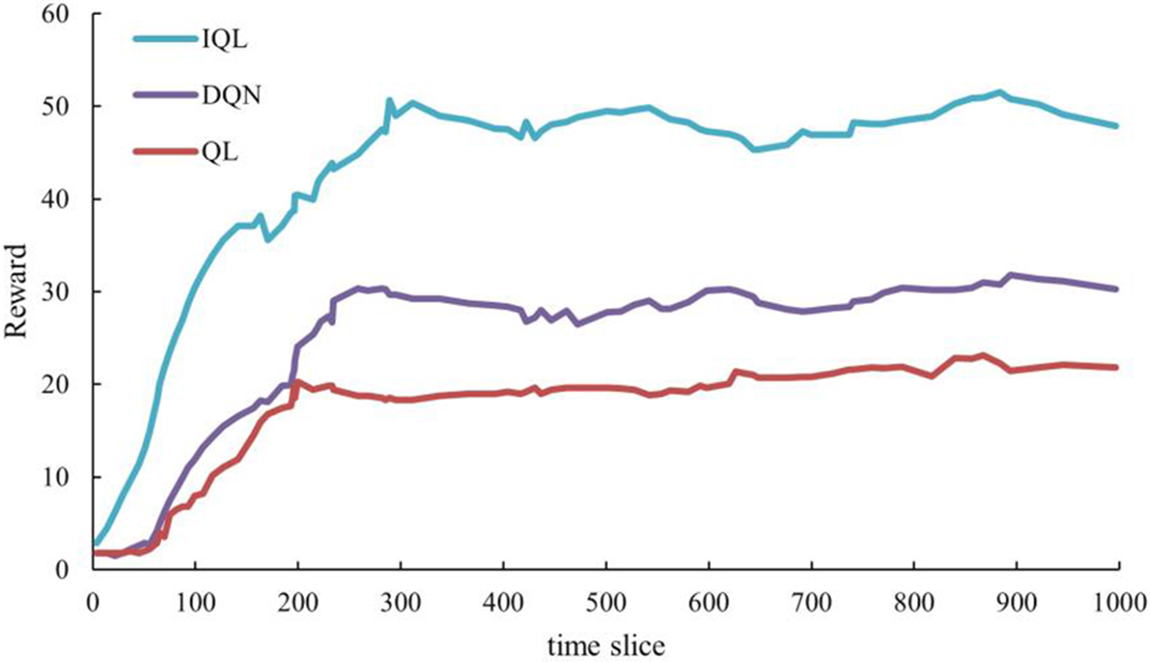
Figure 5: Comparison of simulation results obtained by using three different strategy-solving algorithms in social engineering attack-defense game

The above results show that in the social engineering random game scenario, the defender rewards obtained by the IQL solution are significantly greater than those obtained by the Q-Learning and DQN solutions. This experiment shows that defenders can reach their optimal defense strategy faster under the IQL reinforcement learning mechanism than other deep learning algorithms.

In a single iteration, the IQL algorithm can update different irrelevant states simultaneously, which can be considered an independent process. Therefore, the decision time of the IQL algorithm is always shorter than that of the QL algorithm. To prove this conclusion, we set up comparison experiments to calculate the policy learning time using the QL algorithm, the DQN algorithm, and the algorithm in this paper with different greedy values. The experimental results are shown in Fig. 6. The IQL algorithm has the shortest policy learning time for different greedy values. Under the condition ofe = 0.04, the IQL algorithm performs best on the minicamp testbed, with the highest number of states. QL runs for 15400 steps, DQN runs for 17400 steps, and IQL runs for only 14000.

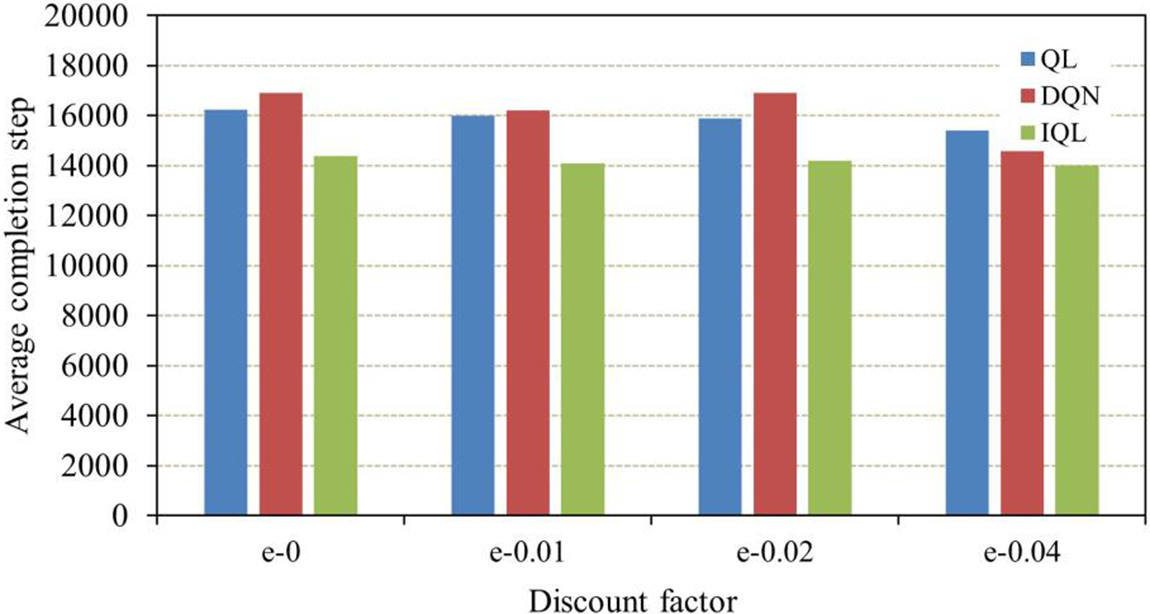
Figure 6: Average completion times of the QL, DQN, and IQL algorithms with different discount factors

This is because the more states there are in the iterative process, the more computation is required and the higher the computational complexity. In general, the best performing iteration over the least is when e-0.04, and the completion time of the IQL algorithm can be reduced by 9.1% and 19.4% compared to the DQN and QL algorithms. The calculation formula is as follows:

cab=(ta−tb)/ta

In the above equation, cab denotes the rate of reduction of consumption time of algorithm b over algorithm a, ta denotes the time consumed by algorithm a, and tb denotes the time consumed by algorithm b.

5  Conclusion

In this paper, we propose a reinforcement learning model based on game theory that can generate optimal social engineering defense strategies for social engineering attack models to enhance social engineering defenses and reduce losses. Since the traditional methods of social engineering defense strategy generation consider only the technical aspects of defense, humans are idealized and regarded as having consistent properties, which leads to an unsatisfactory defense strategy. Considering the interaction between target vulnerabilities and social engineering attacks, a quantification mechanism based on multiple target attributes is proposed. The attacker and defender are also modeled as a two-sided stochastic game. The optimal defense strategies of the defender are analyzed. To improve the real-time performance and effectiveness of the defense, a Q-learning algorithm based on the game is optimized, and a multistate independent parallel learning optimization method is proposed to improve the learning efficiency and to generate the optimal defense strategy quickly. According to the experimental simulation results, the average time needed to create the optimal policy is reduced by 12.5%~20% with the optimization method proposed in this paper compared with the QL and DQN algorithms. However, there are still some significant problems for the process in this paper; for example, the model construction could be more rough and sufficiently detailed for parallel task scheduling algorithm research, and the attack recovery method presented here could be improved.

Acknowledgement: Thanks are due to Kangfeng Zheng and Chunhua Wu for assistance with the experiments and to Xiujuan Wang and Bin Wu for valuable discussion. We are grateful for the assistance of the Beijing Natural Science Foundation (4202002).

Funding Statement: This research was funded by the Beijing Natural Science Foundation (4202002).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. APWG, Phishing Activity Trends Reports. 2022. [Online]. Available: https://apwg.org/trendsreports/ [Google Scholar]

2. Dmarcian, 2021 FBI Internet Crime Report. 2022. [Online]. Available: https://dmarcian.com/2021-fbi-internet-crime-report/ [Google Scholar]

3. K. Zheng, T. Wu, X. Wang, B. Wu and C. Wu, “A session and dialogue-based social engineering framework,” IEEE Access, vol. 7, pp. 67781–67794, 2019. [Google Scholar]

4. A. Yasin, L. Liu, T. Li, R. Fatima and W. Jianmin, “Improving software security awareness using a serious game,” IET Software, vol. 13, no. 2, pp. 159–169, 2019. [Google Scholar]

5. J. M. Hatfield, “Social engineering in cybersecurity: The evolution of a concept,” Computers & Security, vol. 73, pp. 102–113, 2018. [Google Scholar]

6. S. M. Albladi and G. R. S. Weir, “User characteristics that influence judgment of social engineering attacks in social networks,” Human-Centric Computing and Information Sciences, vol. 8, no. 1, pp. 5, 2018. [Google Scholar]

7. S. Seo and D. Kim, “SOD2G: A study on a social-engineering organizational defensive deception game framework through optimization of spatiotemporal MTD and decoy conflict,” Electronics, vol. 10, no. 23, pp. 3012, 2021. [Google Scholar]

8. Q. Zhu and T. Basar, “Game-theoretic methods for robustness, security, and resilience of cyberphysical control systems: Games-in-games principle for optimal cross-layer resilient control systems,” IEEE Control Systems Magazine, vol. 35, no. 1, pp. 46–65, 2015. [Google Scholar]

9. J. Pawlick, E. Colbert and Q. Zhu, “A game-theoretic taxonomy and survey of defensive deception for cybersecurity and privacy,” ACM Computing Surveys (CSUR), vol. 52, no. 4, pp. 1–28, 2019. [Google Scholar]

10. K. Zhong, Z. Yang, G. Xiao, X. Li, W. Yang et al., “An efficient parallel reinforcement learning approach to cross-layer defense mechanism in industrial control systems,” IEEE Transactions on Parallel and Distributed Systems, vol. 33, no. 11, pp. 2979–2990, 2022. [Google Scholar]

11. R. Elderman, L. J. J. Pater, A. S. Thie, M. M. Drugan and M. Wiering, “Adversarial reinforcement learning in a cyber security simulation,” in Proc. of the 8th Int. Conf. on Agents and Artificial Intelligence (ICAART), Rome, Italy, pp. 559–566, 2017. [Google Scholar]

12. K. Chung, C. A. Kamhoua, K. A. Kwiat, Z. T. Kalbarczyk and R. K. Iyer, “Game theory with learning for cyber security monitoring,” in Proc. of the 2016 IEEE 17th Int. Symp. on High Assurance Systems Engineering (HASE), Orlando, FL, USA, pp. 1–8, 2016. [Google Scholar]

13. K. Durkota, V. Lisy, B. Bošansky and C. Kiekintveld, “Optimal network security hardening using attack graph games,” in Proc. of the 24th Int. Conf. on Artificial Intelligence, Buenos Aires, Argentina, pp. 526–532, 2015. [Google Scholar]

14. K. Durkota, V. Lisý, B. Bošanský, C. Kiekintveld and M. Pěchouček, “Hardening networks against strategic attackers using attack graph games,” Computers & Security, vol. 87, pp. 101578, 2019. [Google Scholar]

15. A. Ridley, “Machine learning for autonomous cyber defense,” The Next Wave, vol. 22, no. 1, pp. 7–14, 2018. [Google Scholar]

16. M. L. Littman, “Markov games as a framework for multi-agent reinforcement learning,” in Proc. of the Eleventh Int. Conf. on Int. Conf. on Machine Learning, Rutgers University, New Brunswick, NJ, pp. 157–163, 1994. [Google Scholar]

17. J. Hu and M. P. Wellman, “Nash q-learning for general-sum stochastic games,” Journal of Machine Learning Research, vol. 4, pp. 1039–1069, 2003. [Google Scholar]

18. J. Heinrich and D. Silver, “Deep reinforcement learning from self-play in imperfect-information games,” arXiv preprint arXiv:1603.01121, 2016. [Google Scholar]

19. R. Yang, K. Zheng, B. Wu, D. Li, Z. Wang et al., “Predicting user susceptibility to phishing based on multidimensional features,” Computational Intelligence and Neuroscience, vol. 2022, pp. 7058972, 2022. [Google Scholar] [PubMed]

20. R. Yang, K. Zheng, B. Wu, C. Wu and X. Wang, “Prediction of phishing susceptibility based on a combination of static and dynamic features,” Mathematical Problems in Engineering, vol. 2022, pp. 2884769, 2022. [Google Scholar]

21. C. Liu, F. Tang, Y. Hu, K. Li, Z. Tang et al., “Distributed task migration optimization in MEC by extending multi-agent deep reinforcement learning approach,” IEEE Transactions on Parallel and Distributed Systems, vol. 32, no. 7, pp. 1603–1614, 2021. [Google Scholar]

22. F. Mouton, M. M. Malan, L. Leenen and H. S. Venter, “Social engineering attack framework,” in IEEE 2014 Information Security for South Africa, pp. 1–9, 2014. [Google Scholar]

23. A. Ghasempour, “Internet of things in smart grid: Architecture, applications, services, key technologies, and challenges,” Inventions, vol. 4, no. 1, pp. 22, 2019. [Google Scholar]

24. K. P. Mayfield, M. D. Petty, T. S. Whitaker, J. A. Bland and W. A. Cantrell, “Component-based implementation of cyberattack simulation models,” in Proc. of the 2019 ACM Southeast Conf., New York, NY, ACM, pp. 64–71, 2019. [Google Scholar]

25. M. S. Barnum, Common attack pattern enumeration and classification (CAPEC) schema. Department of Homeland Security, 2008. [Online]. Available:https://capec.mitre.org/ [Google Scholar]

26. R. Mitchell and R. Chen, “Modeling and analysis of attacks and counter defense mechanisms for cyber physical systems,” IEEE Transactions on Reliability, vol. 65, no. 1, pp. 350–358, 2015. [Google Scholar]

27. H. Van Hasselt, A. Guez and D. Silver, “Deep reinforcement learning with double q-learning,” in Proc. of the AAAI Conf. on Artificial Intelligence, Phoenix, Arizona, USA, pp. 2094–2100, 2016. [Google Scholar]