A Novel Hybrid Optimization Algorithm for Materialized View Selection from Data Warehouse Environments

1  Introduction

Generally, a view represents the set of query data. If the query data is occasionally updated in the base stable, it is known as a materialized view (MV). MVs are usually utilized frequently in environments where the data is accessed [1,2]. MVs are commonly used in data warehousing to decrease network load. Moreover, MVs are commonly utilized to improve query performances [3]. MV is a broadly utilized approach in data warehouses (DWs) to enhance the performance of analytical queries. The major issue of the MV process is memory space since it consumes a large amount of space, and another one is the maintenance cost of MVs [4,5]. An appropriate selection of views is important to respond faster to queries. MVs are generally smaller than DW and can give answers in less time for queries [6,7]. A DW responds to online queries with around a million reports in less time. The major challenge is decreasing online query processing time compared to the other approaches [8]. The views are chosen to improve the query process and decrease the cost. MVs aim to decrease the execution time of analytical queries posted next to a DW [9,10]. A DW is generally comprised of different views and responds to queries. The time consumption of responding to queries is reduced than the compared approaches through the view selection [11]. MV decreases the response time by reporting views instead of a whole table. The MV selection process enhances the efficiency of query processing performance [12]. The complex nature of analytical query processing and large data is the main reason for the high response time. The goal MV process is to decrease the processing time of analytical queries [13]. Current studies are focused on the automatic creation of data views and identifying the views. MVs are very effective in increasing the query process, and it is attractive in DW environments due to the query-intensive behavior of DW [14]. An MV is comprised of aggregated and pre-computed data. An optimal selection of views solves the non-deterministic polynomial-time (NP) hard issue. Appropriately, the way of choosing views is materialization. It can decrease the time consumption of query responses [15]. In existing randomized approaches [16], evolutionary and metaheuristic approaches [17] were used for MV selection. Here, randomized schemes select the set of views semi-optimally. Moreover, optimal view selection is performed with genetic algorithms [18], particle swarm optimization (PSO) [19], and greedy-based algorithms. The most common approaches utilized in MV selection are deterministic algorithms, randomized algorithmic approaches and constraint programming [20].

Contributions

The major contributions of the proposed methodology are described as follows:

• An optimal MV selection procedure is introduced in this work with the combination of   constraint handling and metaheuristic optimization-based selection steps.

• An effective ensemble constraint handling technique (ECHT) is presented to refine the   solutions and to enable the framework to select the most optimal set of views for  materialization.

• A combined approach is introduced in this work to select optimal MVs with minimized cost   functions. The proposed framework hybridizes the Ebola and coot optimization algorithms   to achieve the desired performance.

• The proposed methodology considered different cost-based fitness evaluations to reduce   the query response time. The proposed combination of approaches provides an optimal view   selection and lesser query response time.

The rest of the paper’s organization is summarized as follows; Section 2 describes the recent associated works, Section 3 provides a proper explanation of the proposed methodology, Section 4 illustrates the results and their discussion and Section 5 concludes the paper.

2  Related Work

To select the MVs optimally, Prakash et al. developed a multi-objective algorithm-based approach [21]. Optimal MV selection was performed using a non-Pareto-based genetic optimization approach. The multi-dimensional lattice view was generated for the finest chosen of MVs. The most important K-views were selected for the finest selection of MVs. The performance of query execution time was improved to the compared approaches. However, the performance of the proposed scheme can be improved by considering recent optimization approaches. Kharat et al. [22] designed a proficient query optimizer to enhance resource utilization in a distributed cloud environment. A large amount of resources needs a query optimizer to decrease the response time and increase the utilization of resources. The proposed innovative query optimization scheme enhanced the query processing with selected MVs.

Moreover, it decreased the payment overhead of customers. The performance of the presented approach can be improved by utilizing an improved combination of methodologies. A stochastic ranking (SR) based cuckoo search (CS) optimization was introduced by Gosain et al. [23] to attain an optimal selection of MVs. The optimal selection of MV improves the efficiency of the query process. Here, constraint handling was performed using the SR process, and CS optimization was utilized for view selection. The incorporation of both ranking and optimization schemes improved query processing. The combination of approaches solves the scalability and price of the query process. However, the MV selection process can be improved using recent approaches. Another optimal MV creation plan was established by Roy et al. [24]. Here, MV is created in the data space of non-binary space. Different weight values were considered for selecting the particular queries from many queries. The developed scheme creates the weight-based MV selection process to choose the views significantly. A new MV selection approach based on the proactive re-selection of MVs (ProRes) was designed by Mouna et al. [25]. Here, the RE-selection scheme was considered for an optimal selection of views. The online and offline features were considered for the analysis process. The threshold was selected for the optimal selection MVs. Afterwards, a scheduling scheme was considered for an optimal choice of views [26]. The performance efficiency of the system was improved, and improved approaches need to be used to improve the process of MV selection. Another approach for view selection based on game theory was introduced by Azgomi et al. [27], where a game was developed with two players to reduce the cost functions. The game theory-based MV selection (GTMV) approach was then tested on different synthetic and real-world datasets to prove its excellence.

Many MV selection approaches have recently followed deep learning and machine learning strategies to attain performance benefits. The literature analyzes some popular and effective learning strategies that can be incorporated to achieve the MV selection task. An advanced version of the extreme learning machine (ELM) was introduced by Wang et al. [28] to overcome the problem of sensitivity to neuron numbers. The model was named self-adaptive ELM (SaELM) and could select the optimal number of neurons for hidden layers, thereby forming the neural networks. One of the significances of the model was that the parameters were not needed to be adjusted during training. Wang et al. [29] developed an automatic architecture design methodology for CNN evolution. This methodology utilized monarch butterfly optimization (MBO) and an expressive neural function unit (NFU) based architecture to achieve the desired task. The NFU model integrated DenseNet, ResNet and GoogLeNet to enable a joint search of macro-architecture and depth of CNNs. A new and advanced deep learning-based malicious code detection approach was invented by Cui et al. [30] that converted the code into images for classification. The parameters of the CNN model were tuned using the bat algorithm to enable effective and accurate classification. This improved version of learning models can be incorporated in the future to select the views for materialization effectively.

Analyzing existing works is important for deliberating the necessity of MV selection. They focused on MV selection using different approaches. However, the existing approaches failed to get the query response in less time. Moreover, an effective MV selection approach is needed to improve the performance using MVs. Therefore, this work presented an optimal MV selection approach using an ensemble of constraint handling approaches and optimization approaches.

3  Proposed Methodology

The proposed model deals with the MV selection problem based on ECHT. The ensemble constraints are considered for optimizing the problem. The proposed model introduces a novel algorithm called the constrained hybrid Ebola with coot optimization (CHECO) algorithm for faster and optimal selection of queries from the DW. The proposed CHECO algorithm chooses the top views based on satisfaction of defined fitness. The schematic diagram of the proposed methodology is depicted in Fig. 1.

Figure 1: Schematic diagram of the proposed methodology

3.1 MV Processing Using Ensemble Constraint Handling Techniques (ECHT)

The constraint handling approaches enhance the MV selection process and provide the optimal solution. Here, ensemble constraint handling is attained by integrating the following constraints.

3.1.1 Self-Adaptive Penalty

In this step, two penalty types are united for each individual to identify non-viable individuals. The higher penalty value is considered for the infeasible views, and a lower penalty value is considered a feasible solution. Then, the threshold value is utilized for ranking the feasible and infeasible solutions, and thus optimal views are obtained. The ranking process of views is expressed in condition (1),

f(z)=dist(z)+Py(z)(1)

Here, f(z)signifies the fitness value, the distance measure is indicated as dist(z), and Py(z) signifies the penalty value.

3.1.2 Epsilon (ε)-Constraint

In this processing approach, constraints are handled by the ε parameter. The suitable ε value is important for an effective selection of views. The revised ε value is still the counter n reaches the control generation counter Km. If the counter n exceeds the Km, then ε is initialized as zero to attain the solution with no violation of constraints. It is expressed in condition (2),

ε(0)=w(Zt)(2)

ε(n)={ε(0)=(1−nKm)np,0<n<Km0,n≥Km(3)

Here, Zt represents the top tth individual and t=(0.05×np) represents the considered threshold limit of parameters Km∈[0.1Kmax,0.8Kmax]. The view selection using this constraint approach is optimal if the entire violation of views is lesser than ε(n).

3.1.3 Stochastic Ranking (SR)

The SR constraint handling scheme finds the finest feasible solution by balancing the penalty and objective function. It provides the ranks for each individual by comparing the two individuals according to the probability of individuals. If both provide optimal results, the individual with a lesser objective value is given the highest value. Moreover, if one has a non-viable result and the other has a viable outcome, the highest rank is given to the individual with a viable outcome.

3.2 Optimal Query Selection Using Constrained Hybrid Ebola with Coot Optimization (CHECO)

This section presents CHECO, a combination of Ebola [31] and coot [32] algorithms for a faster and optimal selection of queries from the DW. The Ebola and coot algorithms are chosen to select the optimal views, as these algorithms offer better convergence. Moreover, these algorithms are efficient in exploring the search space, and the search procedures of these algorithms are highly effective. Therefore, the search procedures of these two algorithms are combined in this work to attain optimal outcomes efficiently. The proposed hybrid optimization approach results in the optimal selection of views by navigating the search space and evaluating each individual’s fitness. The fitness function is evaluated for each iteration, and the solutions are compared to choose the most optimal solution. At first, arbitrarily create the index from all individuals. Then, fix the index as the current best and the global best. Subsequently, compute the fitness value based on the global and current best one. If the maximum iteration is not reached, there will be an optimal individual. The processing steps of the CHECO approach are described in subsequent subsections.

3.2.1 Random Initialization of Data

Arbitrary data search is performed on the arbitrarily initialized data in random directions to find the optimal data positions. At first, arbitrary populations are generated with the starting position being zero. The ranges of data with upper and lower boundaries are Uk and Lk respectively for the kth individual. The generated individuals are expressed as in [31],

Ik=Lk+R(0,1)×(Uk+Lk)(4)

The current best positions are identified and updated in time t, and it is expressed in condition (5) [31],

Ibest={Gbest,f(Cbest)<f(Gbest)Cbest,f(Cbest)≥f(Gbest)(5)

Here, Ibest represents the best solution, Gbest represents the global best, and Cbest represents the current best. The global and current best solutions are differentiated to decide the optimal solution.

3.2.2 Chain Movement

The mean positions of two views are considered in the chain movement process to update the position, and it is expressed in the subsequent condition (6) [32],

Cp(k)=0.5∗(Cp(k−1)−Cp(k))(6)

Here, Cp(k−1) signifies the current location of (k−1) view and Cp(k) signifies the current position of k view.

3.2.3 Adjusting the Position Based on Group Leaders

The views are updating their position and moving towards the optimal position. Here, the movement is based on the mean position of leaders. According to the mean position of leaders, all the views are updating their position. The movement is based on the expressed condition (7) [32],

L″=1+(k mod nL)(7)

Here, k represents the index number, nL represents the number of leaders, and L″ represents the index number of leader data. The computation of the next moving location depends on the leader is expressed in subsequent conditions (8) [32],

P(k)=PL(k)+2∗r1∗(k mod nL)(8)

Here, PL(k) represents the position of the leader, r1 represents an arbitrary number in the range [0,1] and * indicates the multiplication symbol.

3.2.4 Position Movement Towards the Optimal Location

The positions of individuals are updated to reach the optimal location. The optimal position update is expressed in subsequent conditions (9) [32],

LP(k)={W∗r3∗cos⁡(2rπ)∗(gbest−PL(k))+gbest,r4<0.5W∗r3∗cos⁡(2rπ)∗(gbest−PL(k))−gbest,r4≥0.5(9)

Here, gbest represents the attained finest position, r3, r4 represents the arbitrary number between the interval 0 to 1 and W is computed by the subsequent condition (10) [32].

W=2−CI∗(1I)(10)

Here, CI represents the current iteration and I represents the iteration. Condition (10) is updated in condition (9) and attains the optimal solution. The proposed hybrid optimization scheme attains the optimal MVs. The example diagram of MV selection is depicted in Fig. 2 [33].

Figure 2: Example diagram of MV selection

An optimal choice of views for materialization is necessary for a lesser processing time of queries. A DW is a huge data storehouse that supports query decision-making in an incorporated environment. A DW has many data records, and it is necessary to decrease the online query processing time. Furthermore, fitness is evaluated using condition (14) to update the optimal position.

3.2.5 Multi-Objective-Based Fitness Evaluation

In this section, different processing cost measures are considered for computing the performance of the developed system. Multiple objective functions are developed for the CHECO algorithm, and these objective values are analyzed for each individual view in every iteration. This helps the algorithm in attaining the most optimal solution.

Query Processing Cost

The processing cost is to access the views of queries that mention their execution frequency. It is expressed in subsequent conditions (11) [33],

Qpk=∑fq×Cakq(11)

Here, Qpk signifies the query processing cost, fq represents the frequency count of queries and Cakq signifies the accessing cost of k queries. The query processing cost is required to be minimized to indicate the optimal selection of MVs.

Maintenance Cost

It is the cost needed to restore the views whenever their respective base associations are restructured. The calculation of maintenance is expressed by the subsequent condition (12) [33],

Mck=∑uq×CaNq(12)

Here, Mck represents the maintenance cost, uq signifies the updated frequency of queries, and CaNq signifies the maintenance cost of view k for an updated base association N. It is aimed to minimize the maintenance cost to enhance the view selection procedure.

Response Cost

It is the cost used to respond to queries. The reduced response cost enhances the performance of the system. It is calculated in subsequent conditions (13) [33],

Rck=∑q∈QC(Mt)(13)

Here, C(Mt) represents the cost of query response with MVs and Rck represents the total response cost. The response cost is required to be minimized to indicate better performance. The fitness evaluation based on these cost estimations is represented in condition (14),

F(q)=Min(Qpk+Mck+Rck)(14)

Here, F(q) represents the evaluated fitness value, which should be lesser for optimally selected views. The reduction of different processing costs can improve the performance of the system. The proposed CHECO algorithm results in selecting Pareto-optimal solutions to enhance the overall selection process. The Pareto-optimal solutions are identified based on the compromise between the objectives of each solution. The major aim of MV selection is to decrease the weighted processing cost. If MVs are chosen optimally, they can answer queries accurately in less time. pseudocode of the CHECO approach is given in Algorithm 1.

The queries in the DW are selected using CHECO schemes for faster and optimal selection. Here, optimal MV selection is performed to respond to the queries in less time and processing cost.

4  Results and Discussion

This section evaluates the performance of the proposed MV selection using ensemble approaches. The performance of the presented methodology is examined with different existing schemes in terms of performance metrics like query processing cost, maintenance cost, total cost, execution time and maintenance cost. The existing approaches are Genetic algorithm based MV selection (GAMVS), PSO-based MV selection (PSOMVS), Ant-Colony optimization-based MV selection (ACOMVS), Coral reefs optimization-based MV selection (CROMVS) [33], PRoREs, PHAN [25], Evolutionary Algorithm (EA), SR based CS algorithm for MV selection (SRCSAMVS) [23] and YANG’s [25] algorithm. The efficacy of the proposed model for MVS is measured using the well-known TPC-H dataset [34].

4.1 Performance Metrics

In this section, different performance metrics are deliberated to validate the performance of the proposed approach. The metrics are described in subsequent subsections.

4.1.1 Execution Time

The processing time is taken to execute the number of queries in MV selection. It is computed by the subsequent condition (15),

Texe=tEnd−tinitial(15)

Here, Texe represents the execution time, tinitial represents the initial time and tEnd represents the ending time.

4.1.2 Query Processing Cost

It is the cost taken to process the queries in the proposed methodology. It is computed by expressed condition (11).

4.1.3 Maintenance Cost

It is the cost needed to restore the views whenever its respective base associations are restructured. The maintenance cost calculation is expressed by the subsequent condition (12).

4.1.4 Total Cost

It is the total cost of all the processes in MV, like query processing, query response and query maintenance cost. It is expressed in subsequent conditions (16),

T(cos⁡t)=∑CK(16)

Here, T(cos⁡t) represents the total cost and CK represents the consumed cost of each process.

4.2 Performance Analysis

This section analyses the performance of the presented methodology with different current approaches. The query process comparison of the proposed approach is analyzed in execution time is shown in Fig. 3.

Figure 3: Comparison of query processing

Fig. 3 illustrates the performance of the proposed methodology in some query MVs and dropped views for 1000 queries. Here, the execution time of the proposed scheme is lesser than the compared approaches. The proposed scheme takes lesser computational time than the compared approaches. Then the comparison analysis of the proposed scheme by various queries is depicted in Fig. 4 analyses the developed system for 1000 queries because of construction and query processing costs. The performance comparison proved that the proposed methodology attains enhanced performance compared to the ProRes, YANG and PHAN [25] approaches. Then, the total costs for varying numbers of queries are depicted in Fig. 5.

Figure 4: Comparison of the proposed approach by a varying number of queries

Figure 5: The comparison examination of total process cost

In Fig. 5, the comparison examination of total process cost is illustrated. It is analyzed using approaches such as EA and SRCSAMVS [23]. The cost analysis proved that the processing cost of the proposed scheme is much lesser than the compared approaches for varying numbers of queries 100, 200, 300, 400 and 500, respectively. Furthermore, the comparison analysis of query processing cost with existing approaches is depicted in Fig. 6. The proposed scheme’s query cost is compared with existing approaches like GAMVS, ACOMVS, PSOMVS, and CROMVS [33]. The query processing cost of the developed scheme is much lesser than other current methodologies. Then, the performance comparison of the total cost is depicted in Fig. 7.

Figure 6: Comparison analysis of query cost

Figure 7: Comparison of the total cost

Fig. 7 depicts the entire cost of the developed approach with existing approaches. Here, the total cost value of the proposed scheme is significantly lesser than the compared approaches. The comparison examination of different cost values is mentioned in Table 1.

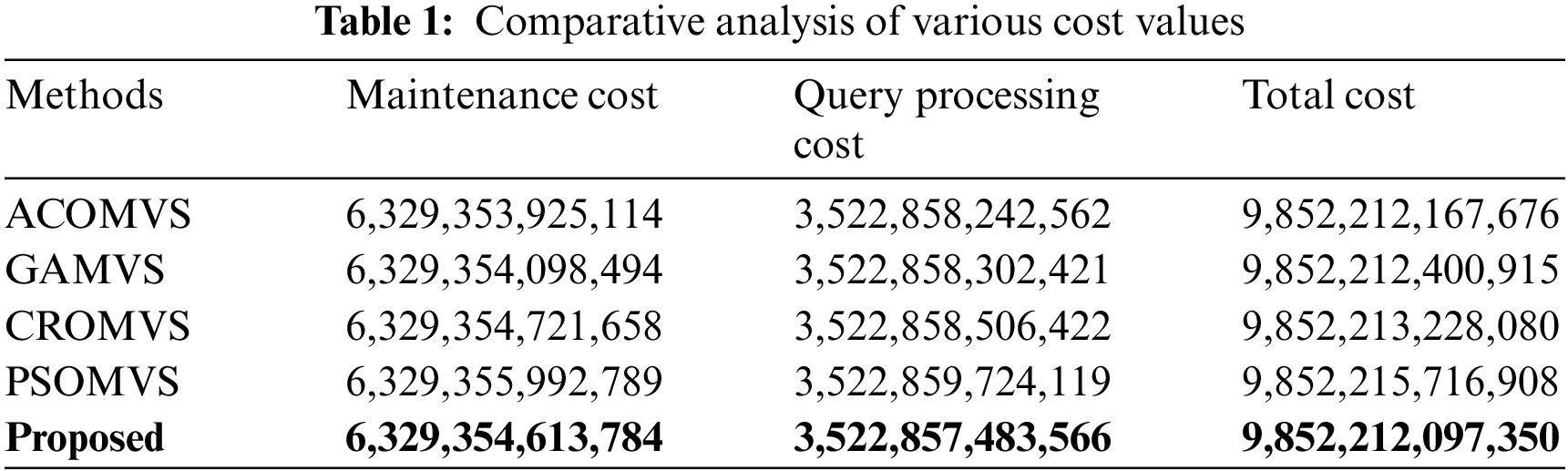
In Table 1, the comparisons of various cost values are mentioned. It mentions that the proposed scheme takes a lesser cost than the different compared approaches. The performance comparison of the total cost for varying dataset sizes is depicted in Fig. 8. In Fig. 8, the total cost of the developed scheme is examined with different current approaches for varying datasets illustrated. The performance of the developed methodology is improved to the compared approaches. The performance comparison is with the existing CROMVS, EGTMVS and GTMVS approaches. The performance comparison on total cost is much lesser than the compared approaches. Then, the performance comparison of maintenance costs is depicted in Fig. 9.

Figure 8: Comparison of the total cost for varying dataset size

Figure 9: Performance comparison of maintenance cost

In Fig. 9, the proposed approach’s maintenance cost is compared with existing approaches. Here, the proposed approach consumes lesser maintenance costs than the compared approaches like GAMVS, ACOMVS, CROMVS, and PSOMVS [33]. Similarly, the comparison analysis of maintenance costs for varying dataset sizes is depicted in Fig. 10 shows the performance comparison of maintenance costs by varying dataset sizes. The developed approach’s maintenance cost is reduced to current methodologies like CROMVS, EGTMVS, and GTMVS [33]. The maintenance cost values have been plotted by varying the dataset size from 0.25 to 1 Gb. In comparison, it has been identified that the proposed approach’s maintenance cost is much reduced than the other algorithms. It is due to the enhanced searching procedure in selecting optimal MVs. The performance comparison of execution time is provided in Table 2.

Figure 10: Maintenance cost for varying sizes of the dataset

In Table 2, the performance comparison of execution time is provided. From the comparison, it is observed that the execution time of the proposed algorithm is slightly higher than the other compared algorithms. When the dataset size is small, the execution time is higher for the proposed and GAMVS algorithms. Compared to the other algorithms, such as PSOMVS and CROMVS, the proposed algorithm resulted in higher execution times for different dataset sizes. This is because of the increased computations involved in the proposed algorithm. But, there is only a slighter increase in execution time that can be negligible compared to the performance outcomes obtained in processing and maintenance costs. Furthermore, the execution time comparison is depicted in Fig. 11.

Figure 11: Comparison of execution time

In Fig. 11, the performance analysis of execution time is examined. The proposed approach is compared with existing approaches like GAMVS, ACOMVS, CROMVS, and PSOMVS [33]. The proposed scheme takes lesser execution time than the compared approaches. The proposed approach provides significant enhancement in different performances than the compared approaches.

4.2.1 Evaluation of Statistical Analysis

In this section, the statistical analysis of the proposed methodology is evaluated. At first, the ANOVA test examines the exact difference between attained results and techniques. The ANOVA test is examined by varying dataset sizes and several queries. Therefore, different results are examined by using the ANOVA test. The TPC-H dataset is considered for the ANOVA test in the proposed work. The test analysis for some queries with the TPC-H dataset is mentioned in Table 3.

Table 3 provides the ANOVA test of execution time investigation based on the number of queries utilizing the TPC-H database. The significance level of confidence is set as η=0.05 to execute the ANOVA test. Furthermore, the analysis of the ANOVA test by varying dataset sizes is mentioned in Table 4.

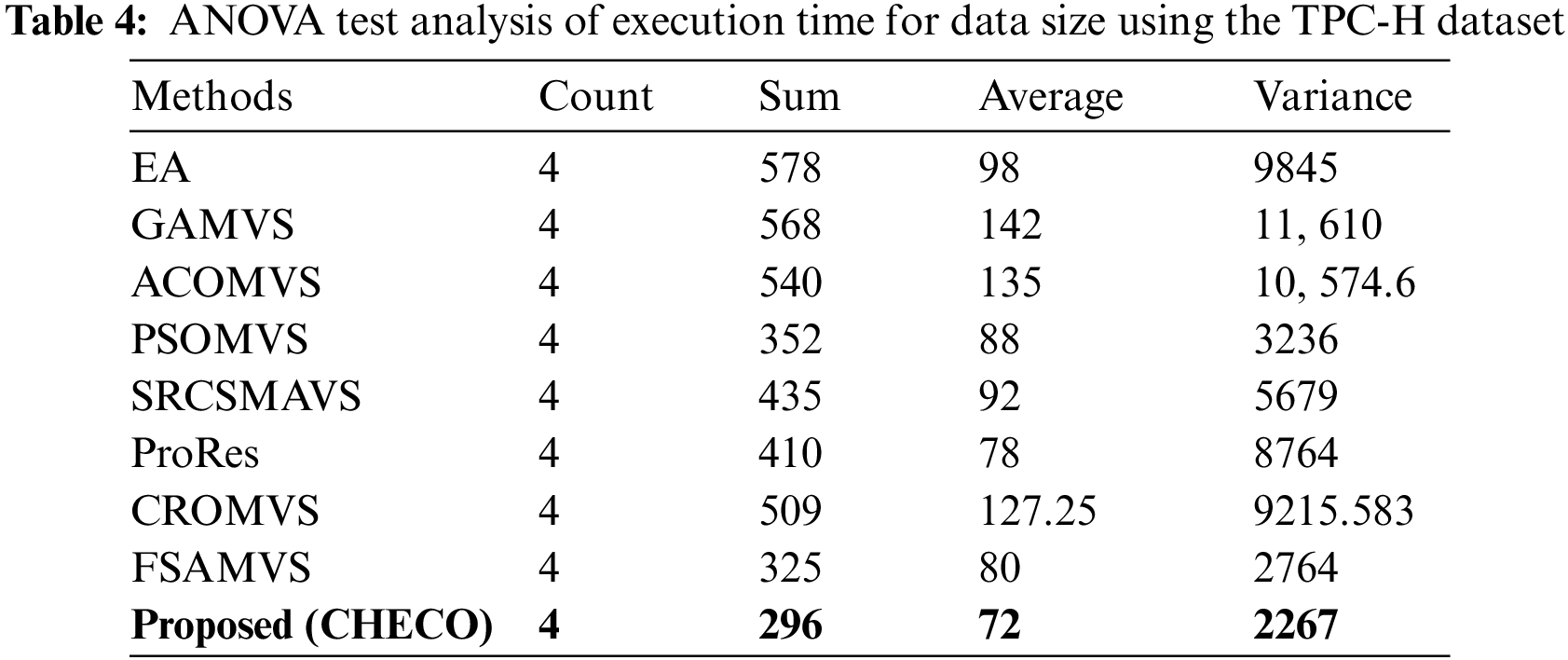
Table 4 provides the ANOVA test of time analysis based on the data size utilizing the TPC-H database. The strengths and weaknesses are computed and compared with existing approaches according to the data analysis. Table 5 provides the comparative strengths and weaknesses of the proposed and existing approaches.

Table 5 clearly illustrates the proposed approach applies to every application. The existing models are only suitable for some applications. Apart from the results obtained, a comparison is made with the recently published effective algorithms to describe the performance efficacy of the proposed method. The algorithm chosen includes self-adaptive spherical search (SASS) [35], sCMAgES [36] and EnCODE [37]. The results obtained are provided in Table 6.

4.3 Discussion

The overall analysis states that the proposed framework is more suitable and effective for solving the MV selection problem than the recent techniques. The proposed framework established a combined approach to choose the optimal MVs with reduced cost values. Moreover, the constraint handling scheme helped the framework to achieve the desired performance by fine-graining the solutions. The analysis of the proposed framework regarding cost functions proved that the model is more effective in choosing the MVs that can minimize the cost abruptly than the other state-of-the-art techniques. The time taken by the framework is slightly larger than the compared techniques for larger dataset size. This is because of the increased number of computations involved in the execution of the algorithm. Varying the dataset’s size impacts the framework’s overall computational efficiency. The significance of the framework is also proved through the statistical analysis conducted in the performance evaluation part. From the results obtained, it is clear that the methodology is statistically significant in selecting the optimal views than the compared techniques. The framework’s main advantage is that it can select the most optimal set of views despite the size of the dataset or the number of queries involved. Also, the framework can select cost-effective views more effectively than the recently introduced techniques.

Overall, the proposed framework leads to an effective contribution in selecting the most optimal MVs with minimized processing and maintenance costs to the customers. One of the main problems identified is with the overall computational efficiency of the framework. When the size of the dataset increases, the time is taken by the algorithm for execution increases resulting in computational complexity. Therefore, future works can be built to reduce the required computations, even combined algorithms.

A comparison with the previous works using the same dataset has been made, and the results are presented in Table 7. From the values, it is obvious that the proposed approach is highly advantageous in reducing the maintenance and query processing costs compared to the existing techniques. The best values obtained are highlighted in bold font. Compared to the other techniques, the proposed approach significantly reduces the cost values, whereas there is a slight increase in execution time. It is because of the additional computations involved in the proposed algorithm’s execution. However, the execution time of the proposed approach is nearly optimal and can be compromised with the performance improvement achieved in terms of costs.

5  Conclusion

This paper presented an optimal selection of MVs using an effective combination of ensemble approaches. At first, an ensemble combination of constraint-handling approaches is presented for an optimal selection of queries. Here, constraints like SR, epsilon, and self-adaptive penalty are considered for optimal selection views. Afterwards, hybrid Ebola and coot optimization is utilized for faster and optimal query selection in views. Here, fitness parameters like maintenance cost, query processing and response cost are considered to improve the performance. The performance of the developed MV selection is validated with different current approaches in terms of performance metrics like query processing cost, maintenance cost, total cost, execution time and maintenance cost. The overall analysis suggested that the performance of the proposed approach is more optimal and effective than the other approaches. The proposed approach also resulted in a query processing cost of 3,522,857,483,566 and a maintenance cost of 6,329,354,613,784, which is much more effective than the other algorithms. In the future, the MV selection can be improved using further enhanced processes, and it can be analyzed with many benchmark datasets.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Popuri Srinivasa Rao: Conceptualization, Methodology, Analyzing, Software Improvements, Writing—Original Draft Preparation, Supervision, Investigation, Resources, Data Curation. Aravapalli Rama Satish: Conceptualization, Methodology, Software, Validation, Formal Analysis, Review & Editing, Visualization, Supervision, Project Administration.

Availability of Data and Materials: TPC-H data warehouse. Available at http://www.tpc.org/tpcdocuments_current_versions/pdf/tpc-h_v2.17.1.pdf

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. R. Adnan and T. M. Abbas, “Materialized views quantum optimized picking for independent data marts quality,” Iraqi Journal of Information and Communications Technology, vol. 3, no. 1, pp. 26–39, 2020. [Google Scholar]

2. J. F. R. Gjengset, “Partial state in dataflow-based materialized views,” Ph.D. Dissertation, Massachusetts Institute of Technology, United States, 2021. [Google Scholar]

3. A. R. Raipurkar and M. B. Chandak, “Optimized execution method for queries with materialized views: Design and implementation,” Journal of Intelligent & Fuzzy Systems, vol. 41, no. 6, pp. 1–15, 2021. [Google Scholar]

4. M. K. Sohrabi and H. Azgomi, “Evolutionary game theory approach to materialized view selection in data warehouses,” Knowledge-Based Systems, vol. 163, no. 1, pp. 558–571, 2019. [Google Scholar]

5. A. Gosain and K. Sachdeva, “Random walk grey wolf optimizer algorithm for materialized view selection (RWGWOMVS),” in Novel Approaches to Information Systems Design, Haryana, India, IGI Global, pp. 101–122, 2020. [Google Scholar]

6. H. Azgomi and M. K. Sohrabi, “MR-MVPP: A map-reduce-based approach for creating MVPP in data warehouses for big data applications,” Information Sciences, vol. 570, no. 1, pp. 200–224, 2021. [Google Scholar]

7. S. S. Solanki, “Incremental maintenance of a materialized view in data warehousing: An effective approach,” Global Journal of Computer Science and Technology, vol. 18, pp. 11–16, 2018. [Google Scholar]

8. A. Verma, P. Bhattacharya, U. Bodkhe, A. Ladha and S. Tanwar, “Dams: Dynamic association for view materialization based on rule mining scheme,” in The Int. Conf. on Recent Innovations in Computing, Singapore, vol. 701, pp. 529–544, 2020. [Google Scholar]

9. M. Mohseni and M. K. Sohrabi, “MVPP-based materialized view selection in data warehouses using simulated annealing,” International Journal of Cooperative Information Systems, vol. 29, no. 3, pp. 2050001, 2020. [Google Scholar]

10. A. Gosain and K. Sachdeva, “Selection of materialized views using stochastic ranking based backtracking search optimization algorithm,” International Journal of System Assurance Engineering and Management, vol. 10, no. 4, pp. 801–810, 2019. [Google Scholar]

11. A. Gosain and H. Madaan, “Query prioritization for view selection,” in Progress in Intelligent Computing Techniques: Theory, Practice, and Applications, vol. 1. Singapore: Springer, pp. 403–410, 2018. [Google Scholar]

12. L. Ordonez-Ante, G. Van Seghbroeck, T. Wauters, B. Volckaert and F. De Turck, “A workload-driven approach for view selection in large dimensional datasets,” Journal of Network and Systems Management, vol. 28, no. 4, pp. 1161–1186, 2020. [Google Scholar]

13. Z. M. Fadhil, “Human behavior based particle swarm optimization for materialized view selection in data warehousing environment,” Periodicals of Engineering and Natural Sciences, vol. 8, no. 4, pp. 2367–2378, 2020. [Google Scholar]

14. L. Ordonez-Ante, G. Van Seghbroeck, T. Wauters, B. Volckaert and F. De Turck, “Automatic view selection for distributed dimensional Data,” in Int. Conf. on Internet of Things, Big Data and Security, Greece, pp. 17–28, 2019. [Google Scholar]

15. N. Berkani, L. Bellatreche and C. Ordonez, “ETL-aware materialized view selection in semantic data stream warehouses,” in 2018 12th Int. Conf. on Research Challenges in Information Science (RCIS), France, pp. 1–11, 2018. [Google Scholar]

16. F. Betouati and S. A. Rahal, “A scalable approach to model big and interacted queries for materialized view through data mining,” Multiagent and Grid Systems, vol. 15, no. 2, pp. 137–154, 2019. [Google Scholar]

17. S. Kumar and T. V. Vijay Kumar, “A novel quantum-inspired evolutionary view selection algorithm,” Sādhanā, vol. 43, no. 10, pp. 1–20, 2018. [Google Scholar]

18. Z. M. Yusoh, K. B. Gan and N. A. Emran, “Materialized view selection problem using genetic algorithm for manufacturing execution system,” Journal of Physics: Conference Series, vol. 1502, no. 1, pp. 012044, 2020. [Google Scholar]

19. A. Kumar and T. V. Kumar, “Materialized view selection using set based particle swarm optimization,” International Journal of Cognitive Informatics and Natural Intelligence (IJCINI), vol. 12, no. 3, pp. 18–39, 2018. [Google Scholar]

20. M. K. Sohrabi and V. Ghods, “materialized view selection for a data warehouse using frequent itemset mining,” Journal of Computers, vol. 11, no. 2, pp. 140–148, 2016. [Google Scholar]

21. J. Prakash and T. V. Kumar, “A multi-objective approach for materialized view selection,” in Research Anthology on Multi-Industry Uses of Genetic Programming and Algorithms, Hershey, PA, IGI Global, pp. 512–533, 2021. [Google Scholar]

22. V. Kharat and M. Shelar, “An efficient Query optimizer with materialized intermediate views in distributed and cloud environment,” Tehničkiglasnik, vol. 15, no. 1, pp. 105–111, 2021. [Google Scholar]

23. A. Gosain and K. Sachdeva, “Materialized view selection for query performance enhancement using stochastic ranking based cuckoo search algorithm,” International Journal of Reliability, Quality and Safety Engineering, vol. 27, no. 3, pp. 2050008, 2020. [Google Scholar]

24. S. Roy, B. Shit, S. Sen and A. Cortesi, “Construction and distribution of materialized views in non-binary data space,” Innovations in Systems and Software Engineering, vol. 17, no. 3, pp. 205–217, 2021. [Google Scholar]

25. M. C. Mouna, L. Bellatreche and N. Boustia, “ProRes: Proactive re-selection of materialized views,” Computer Science and Information Systems, vol. 19, no. 2, pp. 735–762, 2022. [Google Scholar]

26. M. K. Sohrabi and H. Azgomi, “TSGV: A table-like structure-based greedy method for materialized view selection in data warehouses,” Turkish Journal of Electrical Engineering and Computer Sciences, vol. 25, no. 4, pp. 3175–3187, 2017. [Google Scholar]

27. H. Azgomi and M. K. Sohrabi, “A game theory based framework for materialized view selection in data warehouses,” Engineering Applications of Artificial Intelligence, vol. 71, no. 1, pp. 125–137, 2018. [Google Scholar]

28. G. G. Wang, M. Lu, Y. Q. Dong and X. J. Zhao, “Self-adaptive extreme learning machine,” Neural Computing and Applications, vol. 27, no. 2, pp. 291–303, 2016. [Google Scholar]

29. Y. Wang, X. Qiao and G. G. Wang, “Architecture evolution of convolutional neural network using monarch butterfly optimization,” Journal of Ambient Intelligence and Humanized Computing, vol. 8, no. 6, pp. 1–15, 2022. [Google Scholar]

30. Z. Cui, F. Xue, X. Cai, Y. Cao, G. G. Wang et al., “Detection of malicious code variants based on deep learning,” IEEE Transactions on Industrial Informatics, vol. 14, no. 7, pp. 3187–3196, 2018. [Google Scholar]

31. O. N. Oyelade, A. E. S. Ezugwu, T. I. Mohamed and L. Abualigah, “Ebola optimization search algorithm: A new nature-inspired metaheuristic optimization algorithm,” IEEE Access, vol. 10, pp. 16150–16177, 2022. [Google Scholar]

32. I. Naruei and F. Keynia, “A new optimization method based on COOT bird natural life model,” Expert Systems with Applications, vol. 183, no. 2, pp. 115352, 2021. [Google Scholar]

33. H. Azgomi and M. K. Sohrabi, “A novel coral reefs optimization algorithm for materialized view selection in data warehouse environments,” Applied Intelligence, vol. 49, no. 11, pp. 3965–3989, 2019. [Google Scholar]

34. https://www.tpc.org/tpch/ [Google Scholar]

35. A. Kumar, S. Das and I. Zelinka, “A self-adaptive spherical search algorithm for real-world constrained optimization problems,” in Proc. of the 2020 Genetic and Evolutionary Computation Conf. Companion, United States, pp. 13–14, 2020. [Google Scholar]

36. A. Kumar, S. Das and I. Zelinka, “A modified covariance matrix adaptation evolution strategy for real-world constrained optimization problems,” in Proc. of the 2020 Genetic and Evolutionary Computation Conf. Companion, United States, pp. 11–12, 2020. [Google Scholar]

37. K. M. Sallam, S. M. Elsayed, R. K. Chakrabortty and M. J. Ryan, “Multi-operator differential evolution algorithm for solving real-world constrained optimization problems,” in 2020 IEEE Congress on Evolutionary Computation (CEC), UK, pp. 1–8, 2020. [Google Scholar]