Stability Analysis and Control of DC Distribution System with Electric Vehicles

1  Introduction

The medium/low voltage flexible DC power distribution system can flexibly accommodate new DC loads such as Electric Vehicles (EVs) and data centers [1], and efficiently accommodate grid-connected new energy. Due to the lack of strong inertial components and the high proportion of power electronic equipment access, compared with the AC power distribution system, the DC power distribution system has the characteristics of weaker damping and lower inertia, so its stability problem is more prominent [2].

In DC distribution network system, the connection between AC and DC systems is realized through the Voltage Source Converter (VSC): in the grid-connected operation state, the DC voltage control of AC/DC converter is adopted, while in standalone mode, VSC is out of operation, and the DC bus voltage is coordinated and controlled by the DC bus voltage control unit [3] of droop control. The main factors affecting the stability of the distribution system include: (a) source-side control dynamics and interaction between multiple sources [4]; (b) dynamic characteristics of loads [5] and interaction between multiple loads [6]; and (c) source/net/load interactions.

Aiming at the impact of source-side dynamic components on stability, reference [7] explored low-frequency oscillation of the DC system caused by the AC/DC converter, and found that the constant voltage control loop and DC capacitors have a significant impact on the low-frequency oscillation, while the simplification of loads constrained the medium/high frequency stability analysis [8]. For impacts of dynamic loads: negative resistance of CPL has been well researched [5], and interactions among loads have been investigated from the point of view of the modal interaction [9] and aggregated situation [6]. However, current studies tended to ignore dynamics of sources when focused on load interactions [6].

To determine whether DC distribution system is stable or not, reference [10] used Nyquist criterion to analyze the influence of DC line parameters, AC interconnection grid strength and other factors on system stability. A unified mathematical model under the distributed control strategy of DC system is established in reference [11], and a method for determining stability of DC system when the load changes is proposed. Yang et al. [12] studied low frequency oscillation caused by photovoltaic access to flexible DC power distribution system, analyzes the influence of photovoltaic operating point, control parameters and network parameters on oscillation, and points out that the increase of DC network impedance is beneficial to the stability of photovoltaic grid-connected system. Guo et al. [13] studied high frequency oscillation and instability problems in DC system and pointed out the low damping LC loop of converter interacts with the equivalent output impedance of the DC bus voltage control unit, which leads to high frequency oscillation and instability of the DC system. Zhang et al. [14] proposed a stability analysis method for AC-DC hybrid distribution system based on impedance matching, and conducted stability analysis for multi-terminal flexible interconnection devices using two modes of master-slave and droop control.

For stability of DC distribution network system considering the access of EV clusters, the work in this paper is as follows: (a) Firstly, the small disturbance stability model of distribution network system is established, and the broadband oscillation characteristic equation is derived; (b) for the low-frequency oscillation mode, the reduced-order form is derived by means of sensitivity analysis, and key factors are clarified to be the parameters of AC/DC converter; (c) for the high-frequency oscillation problem of distribution network, based on the idea of matrix similarity transformation, the impacts of topology, the number of dynamic loads are identified. Proper design of DC distribution network system could enlarge stable operation domain of system.

2  Model Establishment of DC Distribution System

The typical topology structure of DC distribution network includes radial structure, ring structure and multi-level busbar structure, etc. The DC distribution system in Fig. 1 adopted master-salve control is connected to utility grid via the AC/DC converter.

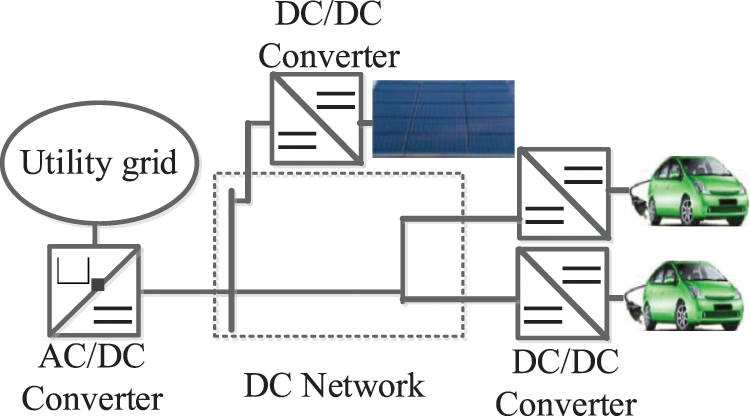
Figure 1: Configuration of the DC distribution system

2.1 AC/DC Converter Model

The AC/DC converter is connected to utility grid through the filter reactance, Xf, as shown in Fig. 2a. Cdc and Udc are the DC bus capacitance and its voltage, respectively. Idc and IDC are currents injected from distribution system and into AC/DC converter, respectively. Id + jIq and Ucd + jUcq are the output AC current and voltage, while Ud + jUq is the terminal AC voltage.

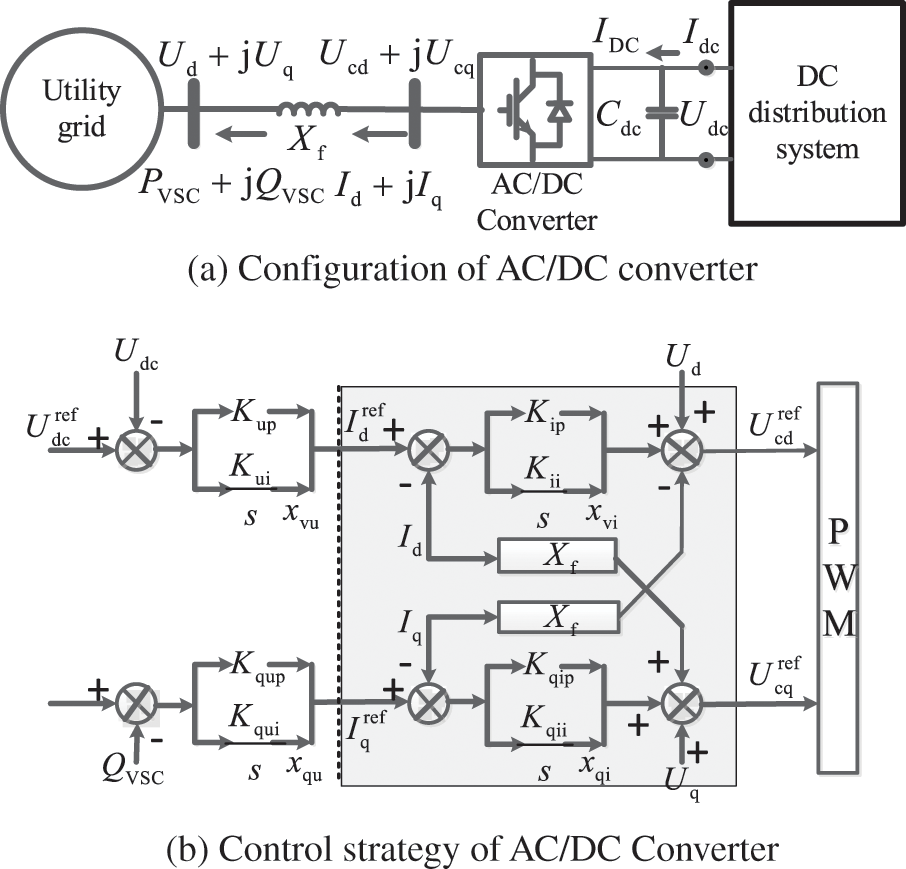
Figure 2: Diagram of AC/DC converter and control strategy

Denote PVSC + jQVSC as output power of AC/DC converter, and PDC = Udc * Idc is the power of DC distribution system. The DC voltage control of AC/DC converter is shown in Fig. 2b. Kup/Kui and Kqup/Kqui are the control parameters of outer loop, and Kip/Kii and Kqip/Kqii are parameters of inner loop. Denote xvu, xvi, xqu, xqi as output terms of integral loops. The linearization state-space model of AC/DC converter can be represented as:

sΔXVSC=AVSCΔXVSC+BVSCDCΔIdc+BVSCACΔUacΔIac=CVSCACΔXVSC+DVSCDCΔIdc+DVSCACΔUacΔUdc=CVSCDCΔXVSC(1)

while ∆ XVSC is the vector of state variables, ∆ Uac and ∆ Iac represent the input AC voltage and output currents respectively. Detailed model derivation can be found in reference [8], as presented in Eq. (A1) of Appendix A.

2.2 Single EV Load Model

Single dynamic load, EV, could be modeled as a six-order full model constant power load (CPL) or two-order reduced model CPL, based on taking dynamics of DC-DC converters into consideration or not. Considering the CPL oscillation mode associated with converter dynamics generally has good damping when classic converter parameters are used, the two-order CPL model [2] as shown in Fig. 3 are used. UdcL and IdcL are the node voltage and injected current, respectively. RdcL and LdcL are the line resistance and inductance of CPL. CFL and UFL are the filter capacitance and its voltage of DC/DC converter, while the load power is PTL = UFL * IF.

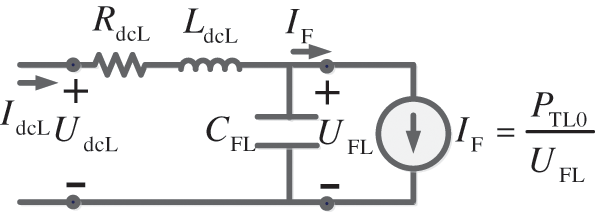
Figure 3: Model of the two-order CPL

The state-space model of the kth CPL can be presented as shown in Eq. (2). ∆ XCPLk is the vector of CPL state variables.

sΔXCPLk=ACPLkΔXCPLk+BCPLkΔUdcLkΔIdcLk=CCPLkΔXCPLk+DCPLkΔUdcLk(2)

2.3 DC Topology and Load Group Model

Based on the single model of CPL shown above, the model of aggregated loads can be derived. For instance, electrical bus charging station of N CPLs are integrated to DC network via a common coupling point (PCC) whose voltage is UPCC, PCC is connected to DC bus through a common transmission line of resistance R0 and inductance L0. For CPLs connected in parallel, the input voltage is derived as shown in Eq. (3a). For arbitrary topology of CPLs connection, ∆UdcLk is presented in Eq. (3b), while RNkk/LNkk is the total resistance/inductance from kth CPL to PCC, and RNij/LNij is resistance/inductance of the common line of ith and jth load to PCC.

ΔUdcLk=ΔUdc−(R0+sL0)∑j=1NΔIdcLj(3a)

ΔUdcLk=ΔUdc−(RNkk+sLNkk)ΔIdcLk−(R0+sL0)∑j=1NΔIdcLj−∑i=1i≠kN(RNki+sLNki)ΔIdcLi(3b)

ΔUL=ΔUdc−ZT(s)ΔIL=ΔUdc−(Z0(s)+ZN(s))ΔIL(3c)

Denote Z0(s)=(R0+sL0)E,ZN(s)=(RNij+sLNij)E, and E is a N-order full matrix with element 1, voltage-current relationship can be presented in Eq. (3c), while ΔUL=[ΔUdcL1⋯ΔUdcLN]T,ΔIL=[ΔIdcL1⋯ΔIdcLN]T,ΔUdc=ΔUdc∗[11⋯1]1∗NT.Thus, the model of single CPL and aggregated CPLs are:

sΔXCPLk=ACPLkΔXCPLk+BCPLkΔUdc−∑j=1NZTkj(s)BCPLjCCPLjΔXCPLjΔIdcLk=CCPLkΔXCPLk(4a)

sΔXL=ALΔXL+BLΔUdcΔIdc=−CLΔXL(4b)

while ΔXL=[ΔXCPL1ΔXCPL2⋯ΔXCPLN]T is the state vector of aggregated CPLs, detailed elements of Eqs. (4a) and (4b) are shown in Eqs. (A2) and (A3) of Appendix A.

2.4 Interconnection Model of Distribution Network System

Denote Xscr as the reactance of AC line between utility grid and the AC/DC converter, the dynamic model of AC side can be simplified into the form shown in Eq. (5a). The state-space model of utility grid and AC/DC converter is given in Eq. (5b). Thus, closed-loop state-space model of DC distribution system with aggregated CPLs can be derived as shown in Eq. (5c).

ΔUac=XscrEac(s)ΔIac;Eac(s)=[s/ω0−11s/ω0](5a)

sΔXS=ASΔXS+BSΔIdcΔUdc=CSΔXS(5b)

sΔX=AΔXs[ΔXSΔXL]=[AS−BSCLBLCSAL][ΔXSΔXL](5c)

Based on Eq. (5), it can be concluded that, the stability of DC distribution system is determined by three parts: (a) the open-loop stability of AC side, AS; (b) stability of aggregated loads, AL; and (c) interaction among load and source subsystem, BS CL/BL CS. Detailed elements of Eq. (5b) are listed in Eq. (A4).

3  Stability Analysis and Enhancement Measures of DC Distribution Network

To describe the stability issue in brief, taking the system in Fig. 4 as an example with CPLs connected in parallel connection.

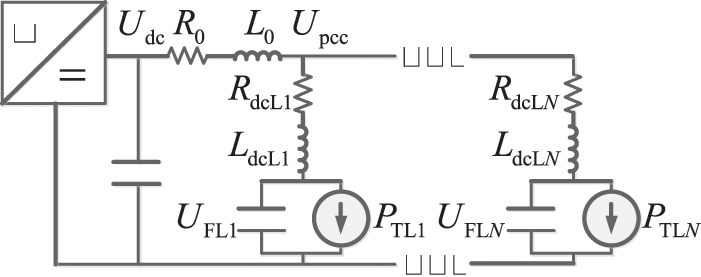
Figure 4: Equivalent circuit of the DC system with EVs

The dynamic equation of DC capacitance voltage is derived in Eq. (6a), while the term ∆xvu and ∆xqu present the impacts of AC/DC control loop on the stability of distribution system. The term Idc0 and ∆Idc represent the influences of stable state power flow and dynamics of loads, respectively. ∆Ud and ∆Uq are the impacts of dynamics of AC utility grid.

sCdcUdc0ΔUdc=(Idc0−Ud0Kup)ΔUdc−Ud0Δxvu−Uq01+KqupUd0Δxqu+Udc0ΔIdc+−Id0ΔUd−Iq0ΔUq(6a)

sCdcUdc0ΔUdc=(Idc0−Ud0Kup)ΔUdc−Ud0Δxvu+Udc0ΔIdc(6b)

AC/DC converter usually takes the d-axis orientation thus Uq0 ≈ 0, and utility grid can be modeled as an infinite bus thus ∆Ud = ∆Uq = 0, dynamic equation in Eq. (6a) can be simplified into the form shown in Eq. (6b), which is the low-frequency reduced-order characteristic equation. Detailed elements of Eq. (6b) are presented in Eq. (A5) of Appendix A.

3.1 Low-Frequency Stability Dominated by AC/DC Converter

Based on the dynamic relationship in Eq. (6b), when the dynamic of DC loads are ignored, ∆Idc = 0, the low-frequency characteristic is simplified into Eq. (7a), and the real part of the corresponding oscillation mode is derived in Eq. (7b).

CdcUdc0s2−(Idc0−Ud0Kup)s+Ud0Kui=0(7a)

real(λVSC)=(Idc0−Ud0Kup)/2CdcUdc0(7b)

It can be seen from Eq. (7b) the low-frequency oscillatory mode dominated by AC/DC converter is mainly affected by control parameter Kup, DC capacitance Cdc, power flow of the distribution system Idc0. The damping of low-frequency mode would be improved as Kup increased, be deteriorated when Cdc increased. And the total charging power addition would lead to the deterioration of system stability. To maintain low-frequency stable, the parameter conditions should make the inequality, real (λVSC) < 0, holds. The dynamics of DC current, ∆Idc, is determined by input impedance of CPLs, which are negative among low-frequency ranges, indicating that oscillatory estimation results shown in Eq. (7) are conservative.

3.2 High-Frequency Stability Dominated by Aggregated CPLs

The state-space model of the CPLs in parallel connection at PCC is derived as shown in Eq. (8a). And the voltage, ∆UFLk, is presented in Eq. (8b). Therefore, the state-space model of the aggregated CPLs is described by Eq. (8c).

{ΔUdc−(R0+sL0)∑k=1NΔIdcLk−(RdcLk+sLdcLk)ΔIdcLk=ΔUFLksCFLkΔUFLk=ΔIdcLk+PTLk0ΔUFLk/UFLk02(8a)

ΔUFLk=ΔUdc−R0∑i=1NCCPLkΔXCPLk−L0∑i=1NCCPLkACPLkΔXCPLk1+L0∑i=1NCCPLkBCPLk(8b)

AL=[ACPL1+AX1AX2⋯AXNAX1ACPL2+AX2⋯AXN⋮⋮⋱⋮AX1AX2⋯ACPLN+AXN]BL=[BX1BX2⋯BXN]T;CL=[CCPL1CCPL2⋯CCPLN](8c)

While,

AXk=−L0BCPLkCCPLkACPLk−R0BCPLkCCPLk(1+L0∑i=1NCCPLkBCPLk),BXk=BCPLk1+L0∑i=1NCCPLkBCPLk.

In order to further clarify the influencing factors of the stability characteristics of the CPL group, it could be assumed that the dynamics of N CPLs are the same. According to the principle of matrix similarity transformation [6], AL in Eq. (4b) can be diagonalized into the form as shown in Eq. (9).

TXALTX−1=[ACPL0⋯00ACPL⋯0⋮⋮⋱⋮00⋯ACPL+NAX](9)

While,

TX=[I−I0⋯00I−I⋯000I⋯0⋮⋮⋮⋱⋮III⋯I]N∗N ACPL+NAX=[PTL0CFLUFL021CFL−1LdcL+NL0N/LdcLLdcL+NL0(L0RdcL−LdcLR0)−RdcLLdcL],

AX=−1LdcL(LdcL+NL0)[00L0(L0RdcL−LdcLR0)]real(λCPL0)=12(PTL0CFLUFL02+N/LdcLLdcL+NL0(L0RdcL−LdcLR0)−RdcLLdcL).

Based on Eq. (9), it can be concluded the dynamic stability of CPL group is mainly affected by:(i) the open-loop stability characteristics of single CPL, ACPL; (ii) the interactions among CPLs, N * AX. The high-frequency dominant oscillation mode, λCPL0, is calculated based on matrix similarity transformation, and high-frequency stability is achieved when parameter conditions makes the inequality, real (λCPL0) < 0, holds. When CPLs dynamic models are not the same, Matrix Perturbation Theory based on state-space model [15] or differences among CPL input impedance based on impedance model [16] could be adopted.

The partial derivatives of the damping, in Eq. (10), of mode of ACPL + N * AX represent the impacts of crucial factors on high-frequency dominant oscillation mode: the number of CPL, N, has a negative influence and the parameter of common line, L0, plays an important role in stability operation.

∂∂Ntrace(ACPL+NAX)−2=L0LdcL/2(NL0+LdcL)2(R0L0−RdcLLdcL)(10a)

∂∂L0trace(ACPL+NAX)−2=−NRdcL2LdcLLdcL(LdcL+NL0)2(10b)

4  Study Case Analysis

Tested DC distribution network adopts the configuration shown in Fig. 4 with N0 = 5 CPLs in parallel connection. Typical parameters of distribution system in [17] are used.

4.1 Eigenvalue Analysis of DC Distribution System

Firstly, considering dynamic models of CPLs are the same. based on the state-space matrix A of the interconnected system in Eq. (5c), oscillation mode results of the distribution network system can be obtained, as shown in Table 1. According to the different frequency ranges, it can be roughly divided into two types: high-frequency oscillation modes and medium/low frequency oscillation modes.

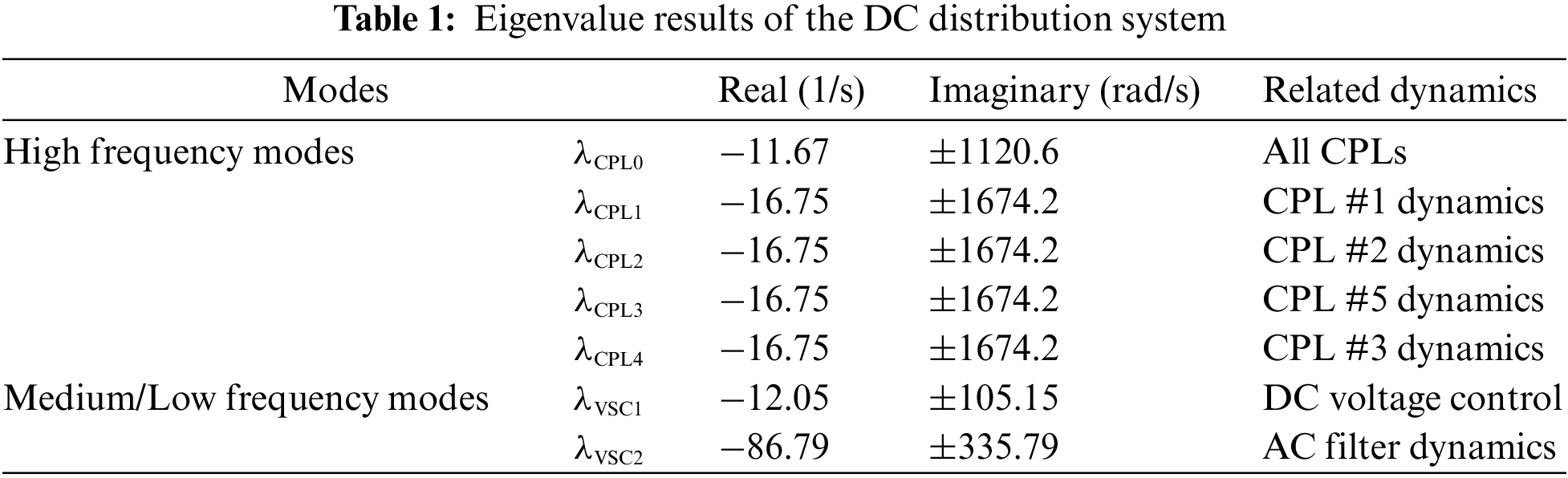
Analysis results of participation factors (PFs) of oscillation modes in Table 1 are shown in Fig. 5. Among them, the high-frequency oscillation modes are more related to load dynamics of CPLs. Mode λCPL0 is equally participated by five CPLs, and the matrix ACPL + N * AX in Eq. (9) represents the dynamic characteristics of load subsystem are affected by interaction among aggregated CPLs, which is the dominant oscillation mode in the high frequency range of DC distribution network. Mode λCPL1–λCPL4 represents interaction oscillation between N0 = 5 loads in the load cluster, related to matrix ACPL in Eq. (9), which are mainly affected by load parameters of single CPL. ∆ XVSC has low participation in mode λCPL1–λCPL4.

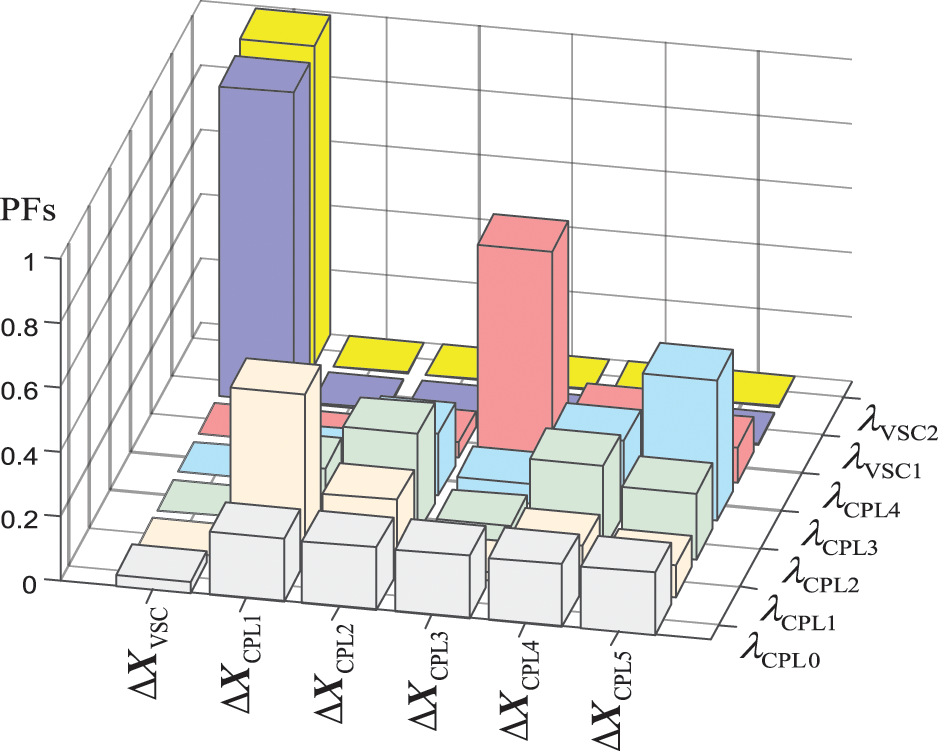
Figure 5: PFs calculation results of oscillation modes

The low-frequency mode λVSC1 is related to the dynamic characteristics of DC bus capacitor voltage Udc and the outer loop of constant voltage control of main station converter, and the low-frequency dynamic characteristics of DC distribution network are mainly affected by the converter parameters. λVSC2 is related to the filtering current dynamics of AC side of AC/DC converter, and usually has good damping under reasonable parameter configuration. It can be seen that the mode λVSC1 is the dominant oscillation mode in the middle/low frequency of the distribution network, which is less affected by the CPL dynamic loads, ∆ XCPL1–∆ XCPL5.

The calculation results in Table 1 show that the small-signal stability of DC distribution network system is mainly determined by DC side load in high frequency range and AC/DC converter station in middle/low frequency range. In the following chapter, the impact of system parameters and control parameters on the oscillation modes of different frequency ranges is explored according to the sensitivity analysis.

4.2 Eigenvalue Sensitivity Analysis of DC Distribution System

The sensitivity calculation results of mode λVSC1 and λVSC2 are listed in Table 2.

According to the calculation results of the oscillation mode sensitivity, it can be seen the low-frequency oscillation mode λVSC1 is mainly affected by the active power of the DC distribution side, the DC bus capacitor, and the proportional coefficient of the constant voltage control outer loop of the AC/DC converter. The increase of DC side charging power will reduce the damping of λVSC1 and has limited impacts on its oscillation frequency. The increase of DC-side bus capacitance will reduce the oscillation frequency while improving the damping of mode λVSC1; the increase of the proportional coefficient Kup of the voltage control outer loop in the control dynamic of the main station converter will improve the damping of mode λVSC1 and the integral coefficient Kui of the voltage control outer loop mainly affects the imaginary part of mode λVSC1. Affects of outer loop and AC side parameters of converter reactive power control on low-frequency oscillation mode is limited. Medium frequency oscillation mode λVSC2 is affected by AC side filter reactance Xf.

The results from Tables 1 to 2 show that the mode λVSC1 is the dominant mode in middle/low frequency range of DC distribution system, and its trajectory changes with the main parameters are shown in Fig. 6. The increase of charging power, DC capacitance, and the decrease of Kup would result in the deterioration of the damping of the dominant oscillation mode λVSC1, proving the correctness of reduced-order model in Eq. (7).

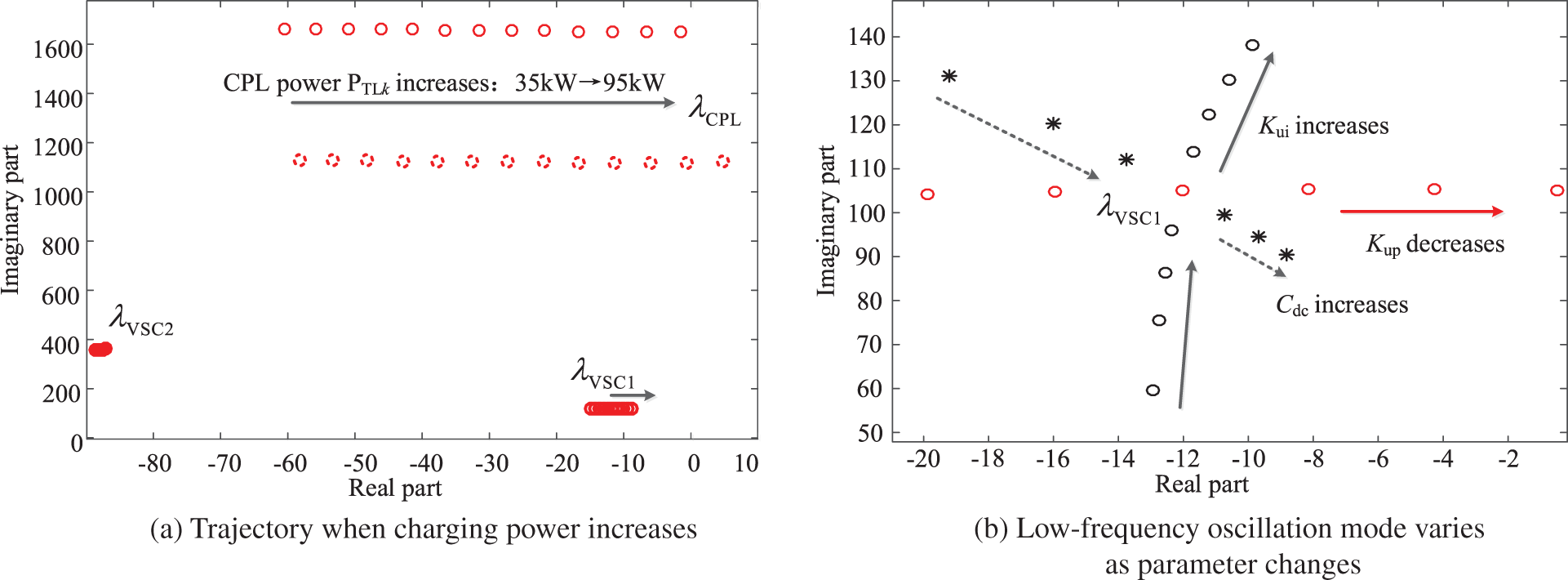
Figure 6: Trajectory of the low-frequency oscillation modes

For the high-frequency oscillation mode, λCPL0–λCPL4, the stability of aggregated CPLs is determined by open-loop dynamic characteristics of single CPL, ACPL, and interactions among CPLs, N * AX. The sensitivity calculation results of the dominant mode λCPL0 are listed in Table 3.

Mode λCPL0 is high-frequency dominant oscillation mode of DC distribution system, which is participated equally by every CPL as demonstrated in Fig. 5. The charging power and inductance of DC transmission line have most significant effect on deteriorating the damping of λCPL0. In order to clarify the influence of critical parameters, i.e., the number of CPLs and the topology, on high-frequency range mode, following cases are conducted.

Taking typical connection topology of charging EVs as an example: the parallel connection, ring-structure connection and series-connection are depicted as shown in Fig. 7a. And the trajectory of mode λCPL0 is shown in Fig. 7b as the number of CPLs, N, varies. It can be concluded high-frequency mode moves towards the right-half plane of the complex plane when N increases, and λCPL0 turns unstable under parallel connection when N = 12, proving increasing number of CPLs has negative impacts on high-frequency range stability of DC distribution network. The trajectories of different connection structure in Fig. 7b illustrate that connection types might influence the strength of interactions of aggregated CPLs, thus λCPL0 stay in the left-half of the complex plane though of poor damping.

Figure 7: Trajectory of the high-frequency oscillation modes

4.3 Simulation Results

For the low-frequency range stability: taking the impact of control parameter of voltage control outer loop of the AC/DC converter as examples. The initial number of CPLs is N0 = 5. The charging power of CPL#1 drops by 20% at 1 second, and the simulation results of DC bus voltage and the power of CPL#5 are presented in Figs. 8a and 8b, respectively. Three situations are compared: (i) Kup = 0.5; (ii) Kup = 1.5; (iii) Kup = 2.5. It can be seen that the increasing Kup helps improving the low-frequency dynamic characteristics of DC distribution system.

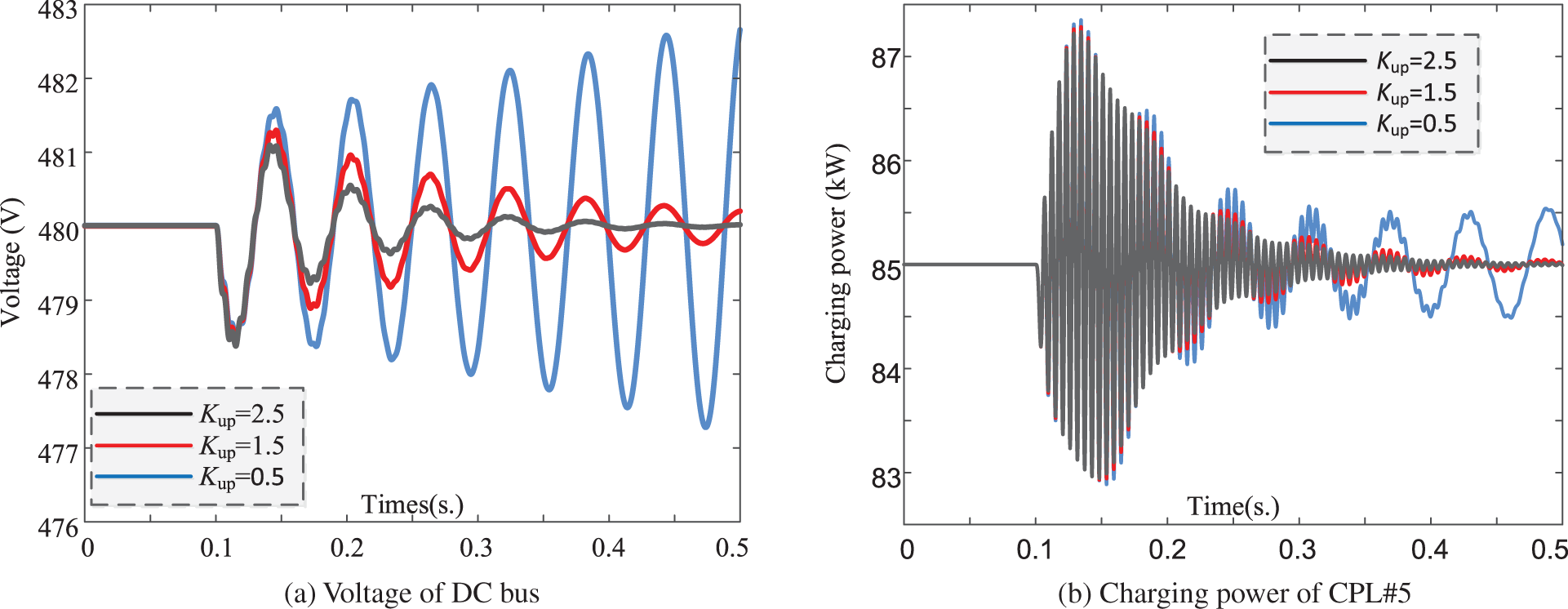
Figure 8: Simulation results of DC system (Low-frequency)

For the high-frequency range stability: taking DC system of topology type 1 for simulation conduction: simulation results in Figs. 9a and 9b are the DC bus voltage and active power of CPL#5, respectively. Two situations are compared: (i) N = 5; (ii) N = 12. Charging power of CPL#1 in test system drops by 20% at 1 s of simulation. It can be seen that DC distribution system turns unstable as number of aggregated CPLs increases, demonstrating the correctness of former analysis. Stability enhancement manner could be adopted based on two aspects: improving the damping of single CPL [5] or decreasing the strength of interactions among CPLs [6]. Detailed description about the effect of stability enhancement is omitted due to the length limitation of this paper. Simulations are conducted based on the full electromagnetic transient model built in MATLAB.

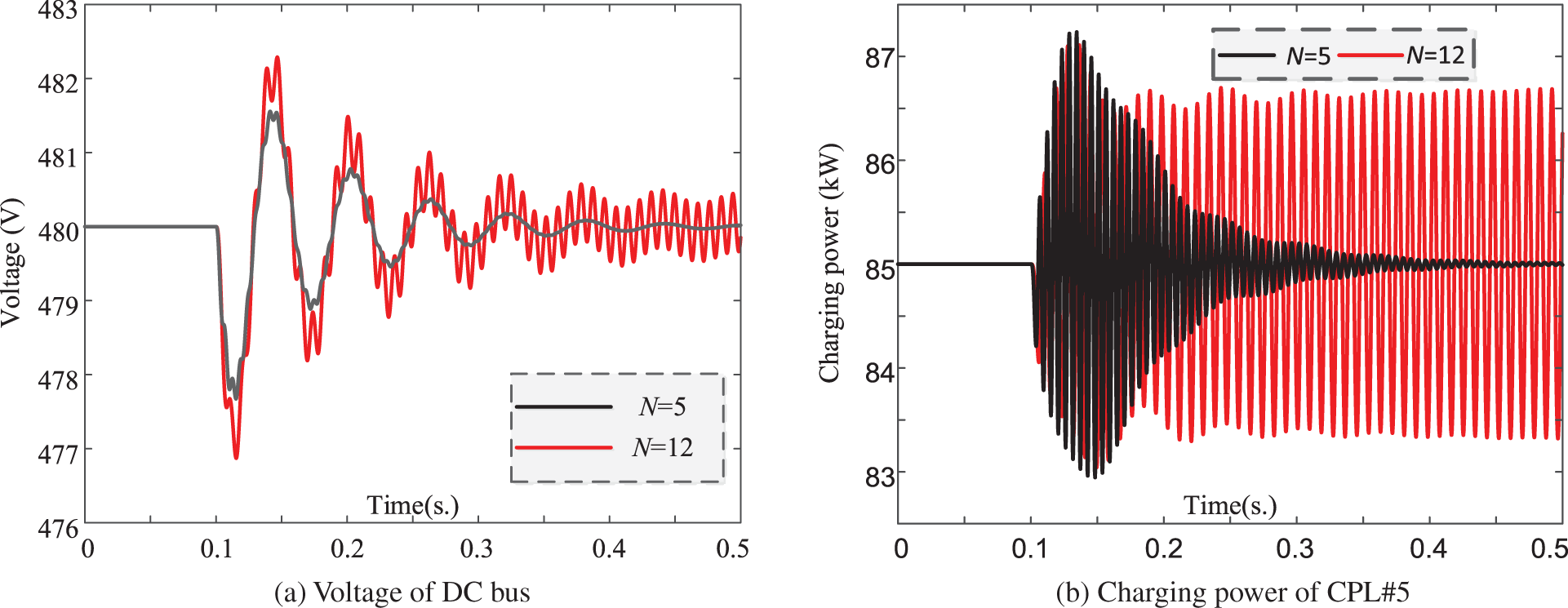
Figure 9: Simulation results of DC system (High-frequency)

5  Conclusion Research Prospect

This paper studies the broadband oscillation characteristics of DC distribution network by establishing the small-signal state-space model of VSC-based DC distribution system with aggregated loads. Main work and conclusions are as follows:

(1) Based on eigenvalue and participation factor analysis, the dominant oscillation mode in the flexible DC distribution network system is identified, and impacts of typical system parameters on dominant oscillation modes are analyzed. It is found that the low frequency oscillation mode of the distribution network is mainly affected by the dynamic effect of the AC/DC converter, and high frequency dominant mode is mainly influenced by interactions of aggregated dynamic loads. Eigenvalue analysis method could provide a clear mechanistic explanation on system oscillation, but its own limitations requires improved analysis method to be adopted in future research work.

(2) The oscillation characteristics of high frequency and low frequency ranges are analyzed, respectively, and reduced order simplified model of oscillation characteristics in different frequency ranges are derived. Influencing factors of oscillation in various frequency ranges of distribution system are analyzed.

(3) In this paper, the CPL model is assumed to be the same, which is only suitable for large-scale scenarios of electric bus charging stations. Future research will focus on extending the research to different application situations of distribution network. The load in this paper only discusses the typical constant power load represented by electric vehicles, and the coexistence of multiple dynamic loads should be considered in the future research. The DC distribution network studied in this paper adopts master-slave control strategy under grid-connected operation state. Future research will explore the stability mechanism analysis and control strategy under off-grid operation state and adopting peer control.

Funding Statement: This work was supported by the State Grid Shandong Electric Power Company Economic and Technical Research Institute Project (Grant No. SGSDJY00GPJS2100135).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Lee, J. Y., Kim, H. S., Jung, J. H. (2020). Enhanced dual-active-bridge DC-DC converter for balancing bipolar voltage level of DC distribution system. IEEE Transactions on Industrial Electronics, 67(12), 10399–10409. DOI 10.1109/TIE.2019.2959503. [Google Scholar] [CrossRef]

 2.  Tabari, M., Yazdani, A. (2014). Stability of a DC distribution system for power system integration of plug-in hybrid electric vehicles. IEEE Transactions on Smart Grid, 5(5), 2564–2573. DOI 10.1109/TSG.2014.2331558. [Google Scholar] [CrossRef]

 3.  Chen, D., Xu, L., Yu, J. (2017). Adaptive DC stabilizer with reduced DC fault current for active distribution power system application. IEEE Transactions on Power Systems, 32(2), 1430–1439. [Google Scholar]

 4.  Krismanto, A. U., Mithulananthan, N. (2018). Identification of modal interaction and small signal stability in autonomous microgrid operation. IET Generation Transmission & Distribution, 12(1), 247–257. DOI 10.1049/iet-gtd.2017.1219. [Google Scholar] [CrossRef]

 5.  Xu, Q., Jiang, W., Blaabjerg, F., Zhang, C., Zhang, X. et al. (2020). Backstepping control for large signal stability of high boost ratio interleaved converter interfaced DC microgrids with constant power loads. IEEE Transactions on Power Electronics, 35(5), 5397–5407. DOI 10.1109/TPEL.2019.2943889. [Google Scholar] [CrossRef]

 6.  Du, W., Zheng, K., Wang, H. F. (2019). Oscillation instability of a DC microgrid caused by aggregation of same constant power loads in parallel connection. IET Generation, Transmission & Distribution, 13(13), 2637–2645. DOI 10.1049/iet-gtd.2018.6940. [Google Scholar] [CrossRef]

 7.  Amin, M., Molinas, M. (2017). Small-signal stability assessment of power electronics based power systems: A discussion of impedance- and eigenvalue-based methods. IEEE Transactions on Industry Applications, 53(5), 5014–5030. DOI 10.1109/TIA.2017.2712692. [Google Scholar] [CrossRef]

 8.  Gao, F., Bozhko, S., Costabeber, A., Patel, C., Wheeler, P. et al. (2017). Comparative stability analysis of droop control approaches in voltage-source-converter-based DC microgrids. IEEE Transactions on Power Electronics, 32(3), 2395–2415. DOI 10.1109/TPEL.2016.2567780. [Google Scholar] [CrossRef]

 9.  Du, W., Zheng, K., Wang, H. F. (2020). Instability of a DC microgrid with constant power loads caused by modal proximity. IET Generation, Transmission & Distribution, 14(5), 774–785. DOI 10.1049/iet-gtd.2019.0696. [Google Scholar] [CrossRef]

10. Zhao, X., Peng, K., Zhang, X., Liu, J., Zhao, Y. et al. (2019). Research on influencing factors and improving methods for DC distribution system stability. The Journal of Engineering, 16(3), 2147–2153. DOI 10.1049/joe.2018.8557. [Google Scholar] [CrossRef]

11. Zhi, N., Zhang, H., Xiao, X., Yang, J. (2016). System-level stability analysis of DC microgrid with distributed control strategy. Proceedings of the CSEE, 36(2), 368–378. [Google Scholar]

12. Yang, X., Sun, Y., Wei, W. (2018). Power oscillation analysis of PV generators connected to DC distribution network. Proceedings of the CSEE, 38(23), 6814–6824. [Google Scholar]

13. Guo, L., Feng, Y., Li, X. (2016). Stability analysisi and research of active damping method for DC microgrids. Proceedings of the CSEE, 36(4), 927–963. [Google Scholar]

14. Zhang, X., Pei, W., Deng, W., Yu, T., Huang, R. (2017). Stability analysis of AC/DC distribution system with constant power loads. Proceedings of the CSEE, 37(19), 5572–5582. [Google Scholar]

15. Dong, W., Xin, H., Wu, D., Huang, L. (2019). Small signal stability analysis of multi-infeed power electronic systems based on grid strength assessment. IEEE Transactions on Power Systems, 34(2), 1393–1403. DOI 10.1109/TPWRS.2018.2875305. [Google Scholar] [CrossRef]

16. Zheng, K., Du, W., Wang, H. F. (2021). DC microgrid stability affected by aggregated constant power loads based on impedance method. Power System Technology, 45(1), 134–148. [Google Scholar]

17. Tabari, M., Yazdani, A. (2015). A mathematical model for stability analysis of a DC distribution system for power system integration of plug-in electric vehicles. IEEE Transactions on Vehicular Technology, 64(5), 1729–1738. DOI 10.1109/TVT.2014.2336854. [Google Scholar] [CrossRef]

Appendix A. Equations

AVSC=[Idc0−Ud0KupCdcUdc0−Ud0CdcUdc0−Uq0/(1+KqupUd0)CdcUdc0Kui00KquiUq0KupKquiUq0−KquiUd01+KqupUd0];(A1-1)

BVSCDC=[Udc0CdcUdc000];BVSCAC=[(Uq0KqupIq01+KqupUd0−Id0)CdcUdc0−(Uq0KqupId01+KqupUd0+Iq0)CdcUdc000−Iq0Kqui1+KqupUd0Id0Kqui1+KqupUd0];(A1-2)

CVSCAC=[Kup1000Kup1+KqupUd0];CVSCDC=[100];(A1-3)

DVSCDC=0;DVSCAC=[00−KqupIq01+KqupUd0KqupId01+KqupUd0](A1-4)

ACPL=[PTL0CFLUFL021CFL−1LdcL−RdcLLdcL];BCPL=[01LdcL];CCPL=[01];DCPL=0(A2)

AL=diag(ACPLk)−ZT(s)⊗diag(BCPLkCCPLk)[ACPL10⋯00ACPL2⋯0⋮⋮⋱⋮00⋯ACPLN]−[ZT11(s)BCPL1CCPL1ZT12(s)BCPL2CCPL2⋯ZT1N(s)BCPLNCCPLNZT21(s)BCPL1CCPL1ZT22(s)BCPL2CCPL2⋯ZT2N(s)BCPLNCCPLN⋮⋮⋱⋮ZTN1(s)BCPL1CCPL1ZTN2(s)BCPL2CCPL2⋯ZTNN(s)BCPLNCCPLN]BL=[BCPL1BCPL2⋯BCPLN]T;CL=[11⋯1]1∗N[CCPL1CCPL2⋯CCPLN]T(A3)

ΔXS=ΔXVSC;CS=CVSCDCAS=AVSC+BVSCACXscrEac(s)(I−DVSCACXscrEac(s))−1CVSCACBS=BVSCDC+BVSCACXscrEac(s)(I−DVSCACXscrEac(s))−1DVSCDC(A4)

CFL=diag(CFL1CFL2⋅⋅⋅CFLN)PTL=diag(PTL1/UFL12PTL2/UFL22⋅⋅⋅PTLN/UFLN2)LL=L0+LL;RL=R0+RL;L0=[L0L0⋯L0L0L0⋯L0⋮⋮⋱⋮L0L0⋯L0];LL=[LdcL10⋯00LdcL2⋯0⋮⋮⋱⋮00⋯LdcLN];R0=[R0R0⋯R0R0R0⋯R0⋮⋮⋱⋮R0R0⋯R0];RL=[RdcL10⋯00RdcL2⋯0⋮⋮⋱⋮00⋯RdcLN](A5)