Analysis of Additional Damping Control Strategy and Parameter Optimization for Improving Small Signal Stability of VSC-HVDC System

Nomenclature

1  Introduction

Voltage source converter based high voltage direct current transmission (VSC-HVDC) has the advantages of active and reactive power decoupling, low harmonic content and no commutation failure, and is widely used in long-distance large-capacity transmission [1–4].

However, with the development of DC transmission technology, the converter operation mode and control parts are advancing in the direction of complexity and diversification, which makes the interaction between AC and DC systems and different control parts more complex, and its related stability problems are gradually highlighted [5,6]. Therefore, the small signal model considering various factors is widely used to analyze its stability and provide some guidance for the planning and parameter design of VSC-HVDC projects [7–9].

VSC-HVDC is usually based on synchronous reference coordinate system for power control, which mainly includes current inner loop and voltage outer loop, and the reference phase is synchronized by obtaining the grid phase through the phase-locked loop (PLL), and the converter is modulated according to the reference quantity of the control system to realize the AC-DC conversion [10–12]. At present, a large amount of literature has studied its modeling. The literature [13] established a small-signal model to analyze its stability, and proposed an analytical criterion for system instability by studying the zero-pole distribution of the open/closed-loop transfer function of the linearized transfer function model. In the literature [14], a time-scale small-signal model of VSC DC voltage under weak grid was established to reveal the mechanism of the influence of phase-locked control and AC voltage control on DC voltage stability. However, the control parts are simplified in the above modeling analysis, and control parts such as filtering are not considered.

In this paper, based on the traditional control method, the state space model of VSC-HVDC system is established by considering the influence of additional filtering links, damping controller and AC-DC side interaction characteristics, and the accuracy of the established model is verified by comparing with the electromagnetic transient model of PSCAD/EMTDC. At the same time, this paper considers the impact on system stability when the AC-side grid operating conditions change, and optimizes the key control parameters for the AC-side operation mode that is prone to oscillations according to the analysis law to eliminate oscillations and improve the small-signal stability of the system.

2  Mathematical Modeling of VSC-HVDC System

2.1 System Structure and Working Principle of Converter

Fig. 1 shows the basic topology of the VSC-HVDC access to the AC system. The converter station is connected to the PCC point via the converter transformer and interconnected with the equivalent AC grid, where Vc, Vo and Vdc are the outlet voltage of the converter, the voltage at PCC and the DC bus voltage, Rc and Lc are the equivalent resistance and inductance of the AC side, Rg and Lg are the equivalent impedance of the AC system, and Vg is the voltage of the AC system.

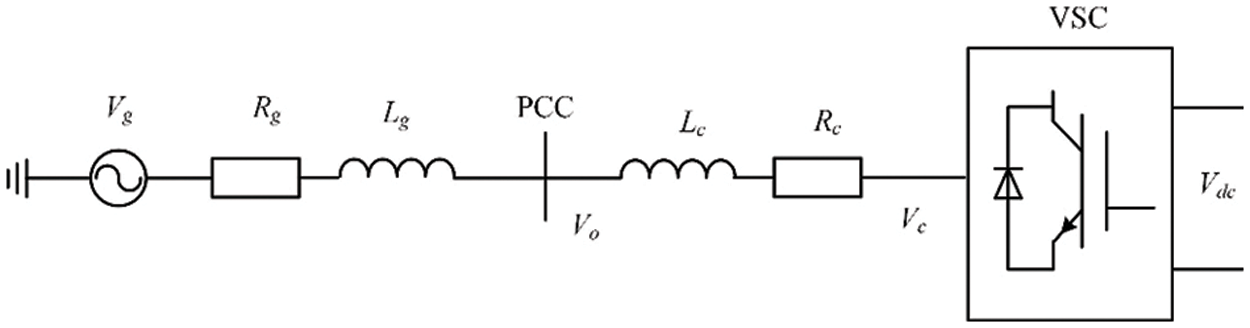
Figure 1: Schematic diagram of VSC-HVDC system structure

In order to realize active and reactive power decoupling, the dynamic process of the system is analyzed in the Synchronous Reference Frame (SRF), and the dynamic relationship of current on the AC side of the converter is:

{dicddt=ωbLcvcd−ωbLcvod−ωbRcLcicd+ωbωgicqdicqdt=ωbLcvcq−ωbLcvoq−ωbRcLcicq−ωbωgicd(1)

DC line model depicted is represented by a lumped π-equivalent scheme. The dynamic relationship of the DC side system parameters of the converter is:

{dvdcdt=ωbCdclineidcline−ωbCdclineidcCdc=Cdclink+Ccable 2(2)

where, ωb is the reference value of angular frequency, ωg is the identity value of grid frequency, Cdcline is the equivalent capacitance of DC line, Ccable is the capacitance of the cable, Cdc is the dc link capacitor, idcline is the current flowing through DC line, and idc is the DC current of converter station. Assume that the DC and AC power balance, then

idcvdc=icdvcd+icqvcq(3)

dvdcdt=ωbCdcidcline−ωb(icdvcd+icqvcq)Cdcvdc(4)

2.2 Design of Inner and Outer Loop Controller of Converter

The converter adopts the inner and outer loop control structure, and the outer loop controller is the power loop, which independently controls the active and reactive power components of the converter. The inner loop controller controls the D axis current component and the Q axis current component of the converter, respectively. The overall structure block diagram is shown in Fig. 2. In this paper, the active power and reactive power component control of the outer loop of the converter controller adopts the fixed active and reactive power control mode, and the actual measured values of active power and reactive power, Po and Qo, are expressed as:

{Po=vodiod+voqioqQo=voqiod−vodioq(5)

Figure 2: Overall structure block diagram of inner and outer loop controller of converter

In order to ensure the stability of the measured power value, the first-order inertial filter is used for filtering, and the equation of state of the filter is:

{dPfdt=−ωPQPf+ωPQPo=−ωPQPf+ωPQ(vodiod+voqioq)dQfdt=−ωPQQf+ωPQQo=−ωPQQf+ωPQ(voqiod−vodioq)(6)

where, ωPQ is the cut-off frequency of the filter. If the cut-off frequency is too low, the power signal of a specific frequency will not pass through, affecting the accuracy of the power signal. If the cut-off frequency is too high, the dynamic performance speed of the system will be limited, so the value of ωPQ needs to take the stability and dynamic performance requirements of the system into consideration [15,16]. The power deviation is obtained by Proportional Integral (PI) controller, idref and iqref is expressed as:

{idref=kpp(Pref−Pf)+kip∫(Pref−Pf)dt+ifdc=kpp(Pref−Pf)+kipηP+ifdciqref=−[kpp(Qref−Qf)+kip∫(Qref−Qf)dt]=−[kpp(Qref−Qf)+kipηQ](7)

where, ifdc is the reference voltage generated by the active DC damping controller, and its design process is shown in Section 2.3. The inner loop adopts constant current control mode, and the DQ component is decoupled by SRF and proportional integral controller, and the output voltage is expressed as:

{vcdref=kpc(idref−icd)+kicηcd−ωpLcicq+vod−vodfvcqref=kpc(iqref−icq)+kicηcq+ωpLcicd+voq−voqf(8)

where, kpc and kic are the parameters of the proportional integration link of PI controller, ωp is the angular frequency output by the phase-locked loop, vodf and voqf are the reference voltage generated by the active AC damping controller. See Section 2.3 for the design process, ηcd and ηcq are used to define the integral part of the current controller, which is expressed as:

{dηcddt=idref−icddηcqdt=iqref−icq(9)

2.3 Active AC Damping Controller

The active AC damping controller can suppress the LC oscillation in the system and improve the stability margin of the system [17–19]. As shown in Fig. 3, vodq passes through a first-order low-pass filter to isolate the high-frequency signal. The filtered signal ζdq is differentiated from the original signal and multiplied by gain kAD to obtain the oscillation component, and then its negative value is introduced into the reference voltage calculation link to achieve the effect of oscillation suppression. Its expression is shown in (10) and (11). Among them, the gain kAD is used to amplify the high-frequency error signal so that it can quickly eliminate the high-frequency components.

vodqf=kAD(−ζdq+vodq)(10)

{dζddt=−ωADζd+ωADvoddζqdt=−ωADζq+ωADvoq(11)

Figure 3: Active AC damping controller

2.4 Active DC Damping Controller

The active DC damping controller is used to suppress the oscillation of the converter, as shown in Fig. 4. Its principle is similar to that of the active AC damping controller. After extraction, the oscillation component is multiplied by the DC gain kADdc to obtain the reference current ifdc, as shown in (12).

ifdc=kADdc(−ζdc+vdc)(12)

where, ζdc is the filtered DC component, and its state space equation is:

dζdcdt=−ωADdcζdc+ωADdcvdc(13)

Figure 4: Active DC damping controller

2.5 Phase-Locked Loop

In order to accurately track the power grid phase, the design of PLL is based on the SRF [20], as shown in Fig. 5.

Figure 5: Phase-locked loop

The equation of state of the voltage component of DQ axis filtered by the low-pass filter is shown in (14), where ωlp is the cut-off frequency of the filter.

{dvpddt=−ωlpvpd+ωlpvoddvpqdt=−ωlpvpq+ωlpvoq(14)

Phase error of voltage component obtained by PI controller δωp is shown in (15) and (16), where kppll and kipll are the gains of the proportional and integral of the PI controller, εp representing the state of integrator.

δωp=kppllarctan⁡(vpqvpd)+kipllεp(15)

dεpdt=arctan⁡(vpqvpd)(16)

Therefore, the relationship between the output phase of the PLL and the phase of the power grid is:

dδθpdt=δωpωb=ωbkppllarctan⁡(vpqvpd)+ωbkipllεp(17)

3  State Space Equations Building

3.1 Model Structures

According to the derivation of the mathematical model in Chapter 2, the final formal representation of Eq. (1) is as follows (18)–(20):

dicddt=−ωbLckADvod−ωbLc(kpc+Rc)icd−ωb(kppllarctan⁡(vpqvpd)+kipllεp)icq+ωbLckicηcd+ωbLckADζd−ωbLckpckppPf+ωbLckpckADdc(vdc−ζdc)+ωbLckpckipηP+ωbLckpckppPref(18)

dicqdt=−ωbLckADvoq+ωb(kppllarctan⁡(vpqvpd)+kipllεp)icd−ωbLc(kpc+Rc)icq+ωbLckicηcq+ωbLckADζq+ωbLckpckppQf+ωbLckpckipηQ−ωbLckpckppQref(19)

dvdcdt=ωbCdcidcline−ωb(1−kAD)Cdcvdc(icdvod+icqvoq)+ωbkpcCdcvdc(icd2+icq2)−ωbkpckADdcCdcicd−ωbkicCdcvdc(icdηcd+icqηcq)−ωbkADCdcvdc(icdζd+icqφq)+ωbkpckppCdcvdc(icdPf−icqQf)+ωbkpckADdcCdcvdcicdζdc−ωbkpckipCdcvdc(icdζP+icqζQ)−ωbkpckppCdcvdc(icdPref−icqQref)(20)

The state space equation of the current controller's integrator is

{dηcddt=kppPref−kppPf+kipηP−kADdcζdc+kADdcvdc−icddηcqdt=−kppQref+kppQf+kipηQ−icq(21)

The state equation of reference voltage at PCC is

{dvoddt=ωbCoicd−ωbCoiod+ωbωgvoqdvoqdt=ωbCoicq−ωbCoioq−ωbωgvod(22)

The state equation of the current flowing to the power grid at PCC is

{dioddt=ωbLgvod−ωbLgv^gcos⁡(δθp)−ωbRgLgiod+ωbωgioqdioqdt=ωbLgvoq+ωbLgv^gsin⁡(δθp)−ωbωgiod−ωbRgLgioq(23)

To sum up, the small signal model of ac system and controller is

dΔXdt=AΔX+BΔU(24)

where, the state variable X and input variable U are

X=[vod;voq;icd;icq;ηcd;ηcq;iod;ioq;ζd;ζq;Pf;Qf;vpd;vpq;εp;δθp;vdc;idcline;ζdc;ηP;ηQ;]T(25)

U=[Pref ;Qref ;vdci;vg;ωg]T(26)

3.2 Model Validation

In order to verify the correctness and validity of the small-signal model of the VSC-HVDC system proposed in this paper, the proposed small-signal model can be implemented in MATLAB and compared with the detailed electromagnetic transient simulation results in PSCAD. Since PSCAD has good electromagnetic transient calculation capability, the accuracy of the small-signal model can be verified if the output of the small-signal model is similar to the model in PSCAD. The main circuit parameters are selected with reference to the parameters of China Yue-Hubei Project, and the system parameters are shown in Table 1.

At t=0, the initial conditions of system operation are set to active power reference Pref=1 pu and reactive power reference 0. At t=1s, Pref steps down from 1 to 0.95 pu, and at t=2s, Pref steps up from 0.95 to 1 pu. The response results of this process in MATLAB and PSCAD/EMTDC are shown in the Fig. 6. It can be seen from the figure that the established small signal model and the electromagnetic transient model have very similar response results, which confirms the correctness of the model.

Figure 6: Simulation comparison between electromagnetic transient model and small signal model

4  Analysis of Influence of Control Parameters on System Stability

In order to analyze the influence of control parameters on system stability, they are divided into three categories: (1) internal and external loop parameters; (2) Damper parameters; (3) PLL control parameters. The influences of these three types of parameters on stability are studied in the following paragraphs.

4.1 System Modal Analysis

Based on the established small signal model, the eigenvalues of the system can be obtained and the eigenvalues and participation factor analysis can be carried out to determine the main control parts affecting its stability [21–23]. In Table 2, the oscillation frequency, damping rate of all modes of the system and the state variables mainly related to each mode are given.

As shown in Table 2, the system has 21 characteristic roots, which can be divided into 14 groups, corresponding to 14 modes respectively. By analyzing each mode, it can be seen that λ2−3, λ4−5 and other modes have the lowest damping ratio, and λ15−16, λ19 and other modes are closest to the right half plane, so the corresponding modes of these pairs of characteristic roots are more likely to be unstable. Therefore, the influence of control parameters on these two types of modes is analyzed in the following part. Participation factor analysis of each mode can determine the main control parts that affect it. As shown in Table 2, λ2−3 and λ4−5 are mainly related to vod,voq,iod,ioq; λ15−16 is mainly related to ηcq,ηQ, that is, it is greatly affected by inner and outer loop parameters; λ19 is mainly related to εp, it is greatly affected by phase-locked loop.

4.2 Inner and Outer Loop Control Parameters

4.2.1 Current Control Loop Parameters

The proportional coefficient kpc and integral coefficient kic of the current loop are changed respectively to analyze the change trajectory of key characteristic roots affecting the system stability. In Fig. 7, (a), (b) represent the eigenvalue trajectory when kpc changes from 0.06 to 5, and (c) represents the eigenvalue trajectory when kic changes from 0.06 to 3. The blue dot in the figure represents the eigenvalue position with the smallest parameter within the adjustment range.

Figure 7: Influence of current control loop parameters on eigenvalues (a) The effect of kpc on the eigenvalues λ2–3, λ4–5 (b) The effect of kpc on the eigenvalues λ8–9, λ15–16, (c) The effect of kic on the eigenvalues

As shown in Figs. 7a and 7b, with the increase of kpc, the characteristic root λ15−16 moves to the right. The characteristic roots λ8−9, λ2−3 and λ4−5 move to the left and then to the right to a certain extent. When kpc is greater than 2.913, λ2−3 crosses the virtual axis and the system oscillates around the frequency of 903 Hz. When kpc is greater than 3.156, λ4−5 crosses the virtual axis and the system oscillates at about 703 Hz, resulting in system instability. It can be seen that increasing kpc will make λ2−3, λ4−5 close to the virtual axis quickly and cross over, becoming the dominant oscillation mode of the system. From the above conclusion, it can be seen that kpc has a great influence on the high frequency stability of the system, and its setting is not reasonable to make the system oscillate in the high frequency band.

As shown in Fig. 7c, with the increase of kic, λ8−9, λ15−16 and other characteristic roots all shift to the left, which improves the stability of the system.

4.2.2 Voltage Outer Loop Parameters

The proportional coefficient kpp and integral coefficient kip of the voltage loop are changed respectively, and the trajectories of the key characteristic roots affecting the system stability were analyzed. In Fig. 8, (a), (b) represent the eigenvalue trajectory when kpp changes from 1 to 35, and (c) represents the eigenvalue trajectory when kip changes from 10 to 200.

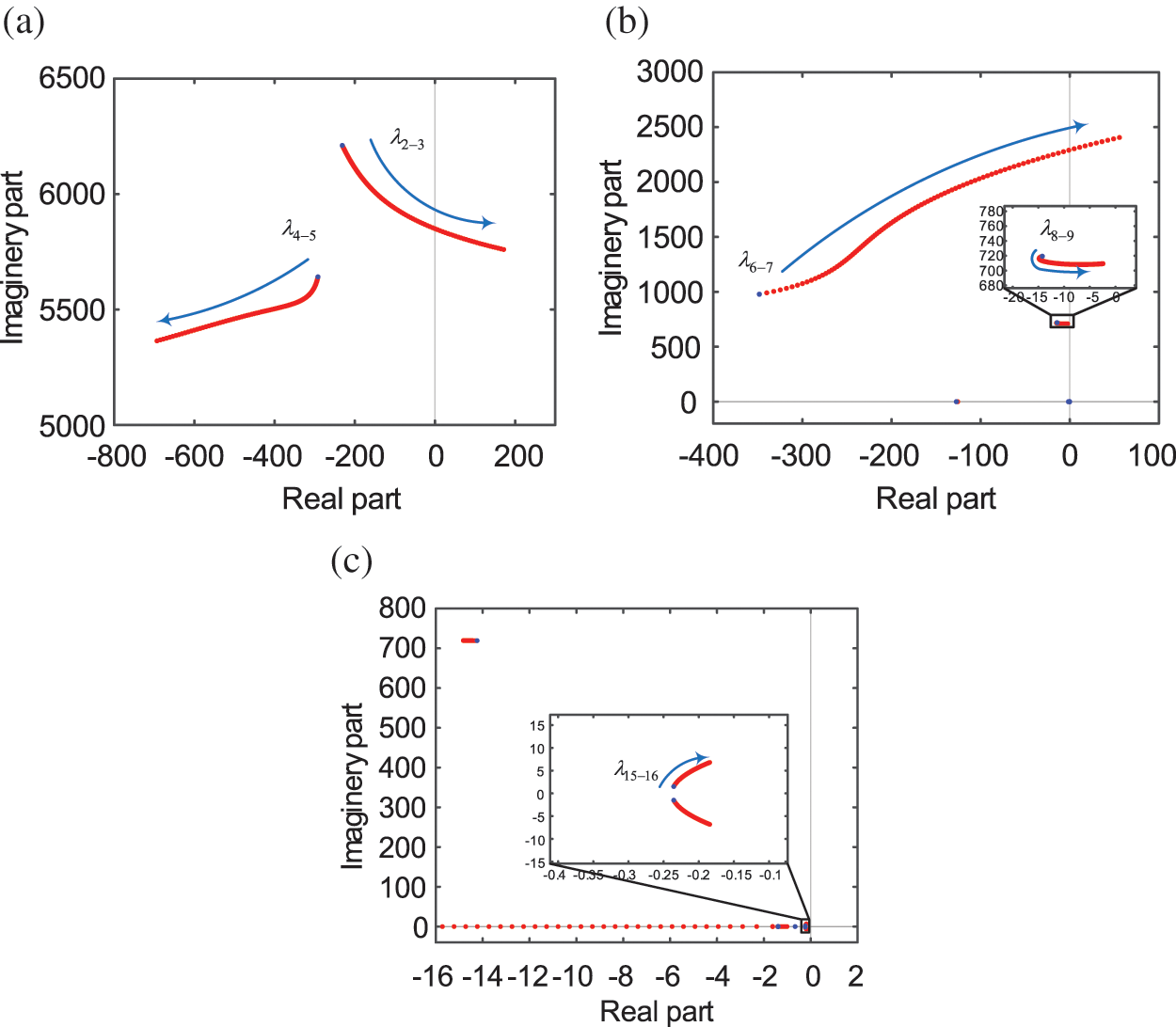
Figure 8: Influence of voltage outer loop parameters on eigenvalues (a) The effect of kpp on the eigenvalues λ2–3, λ4–5, (b) The effect of kpp on the eigenvalues λ6–7, λ8–9 (c) The effect of kip on the eigenvalues

As shown in Figs. 8a and 8b, with the increase of kpp, the characteristic root λ4−5 moves to the left. λ2−3 and λ6−7 have a great impact on system stability. When kpp is greater than 25.856, the real λ2−3 part changes from negative to positive, and the system oscillates around the frequency of 931 Hz. When kpp is greater than 31.863, the real part of λ6−7 also becomes positive, and the system will oscillate around the 365 Hz frequency. The characteristic root λ8−9 moves first left and then right. To prevent system oscillation, the value of kpp should not be too large. Same as the current control loop, the proportionality factor kpp is not set reasonably easy to trigger the system high frequency band oscillation.

As shown in Fig. 8c, with the increase of kip, the characteristic root λ8−9 moves to the left. The characteristic root λ15−16 moves slowly to the right, but has less influence on the stability than other parameters of the link.

4.2.3 Filter Parameter

By changing the filter parameter ωPQ, the trajectory of the key characteristic roots affecting the stability of the system is analyzed. Fig. 9 shows the track of eigenvalues when ωPQ changes from 400π to 1000π.

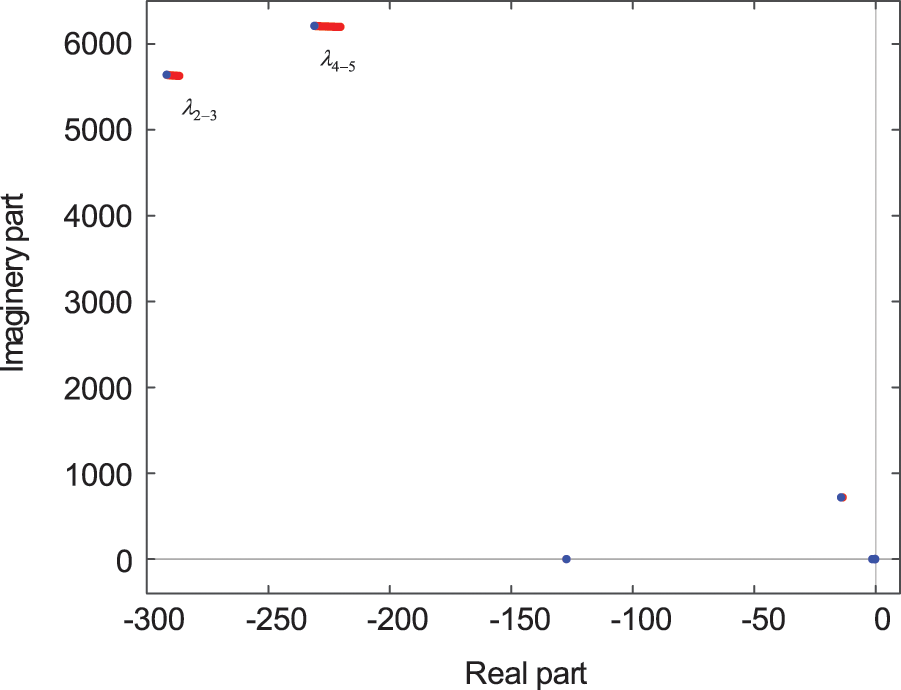
Figure 9: The effect of ωPQ on eigenvalues

As shown in Fig. 9, as ωPQ increases, the characteristic roots λ2−3 and λ4−5 move to the right. The other eigenvalues are basically unchanged.

4.3 Damper Parameter

4.3.1 Active AC Damping Controller Parameters

Change the gain kAD of the active AC damper gain and the filter cutoff frequency ωAD respectively to analyze the trajectory of the key characteristic roots that affect the system stability. In Fig. 10a, represents the eigenvalue trajectory when kAD changes from 1 to 150, and (b) represents the eigenvalue trajectory when ωAD changes from 400π to 1000π.

Figure 10: Influence of active AC damping controller parameters on eigenvalues (a) The effect of kAD on the eigenvalues (b) The effect of ωAD on the eigenvalues

As shown in Fig. 10a, with the increase of kAD, the characteristic roots λ2−3 and λ4−5 move to the left. The characteristic root λ8−9 moves to the right and crosses the virtual axis when kAD is greater than 20.934, and the system oscillates around the frequency of 114 Hz. Meanwhile, with the further increase of kAD, new unstable modes λ6−7 and λ11−12 appear. When kAD is greater than 54.54, the system will become unstable and the system will oscillate at about 28 Hz. The trajectory of λ6−7 is elliptical, and it is in the positive half axis in the range of 42.991 to 120.513. When kAD is greater than 120.513, the mode returns to the negative half axis. It can be seen that kAD is one of the key factors affecting the stability of the system.

As shown in Fig. 10b, with the increase of ωAD, λ2−3, λ4−5 and other characteristic roots move to the left. But it has no effect on the unstable mode near the virtual axis, i.e., it has less effect on the system stability.

4.3.2 Active DC Damping Controller Parameters

The gain kADdc of the active DC damper and the filter cutoff frequency ωADdc are changed respectively to analyze the trajectory of the key characteristic roots that affect the system stability. In Fig. 11, (a) represents the eigenvalue trajectory when kADdc changes from 1 to 100, and (b) represents the eigenvalue trajectory when ωADdc changes from 40π to 100π.

Figure 11: Influence of active DC damping controller parameters on eigenvalues (a) The effect of kAD, dc on the eigenvalues (b) The effect of ωAD,dc on the eigenvalues

As shown in Fig. 11a, with the increase of kADdc, the characteristic root λ8−9 moves to the left. The other characteristic roots are basically unchanged.

As shown in Fig. 11b, with the increase of ωADdc the characteristic root λ14 moves to the right. The other characteristic roots are basically unchanged. It can be seen that active DC damping controller have less influence on system stability than active AC damping controller.

4.4 PLL Control Parameters

The proportional coefficient kppll, the integral coefficient kipll and the filter cutoff frequency ωlp of the PLL are changed respectively to analyze the change trajectory of the key characteristic roots affecting the system stability. In Fig. 12, (a) represents the eigenvalue trajectory when kppll changes from 3 to 15, (b) represents the eigenvalue trajectory when kipll changes from 2 to 20, and (c) represents the eigenvalue trajectory when ωlp changes from 400π to 1000π.

Figure 12: Influence of phase locked loop parameters on eigenvalues (a) The effect of kppll on the eigenvalues (b) The effect of kipll on the eigenvalues (c) The effect of ωlp on the eigenvalues

As shown in Fig. 12a, as kppll increases, the characteristic root λ4−5 moves to the left. λ2−3 moves to the left for some distance and then to the right. λ6−7 becomes a new unstable mode. When kppll is greater than 13.403, the system oscillates at about 352 Hz frequency.

As shown in Fig. 12b, λ19 moves to the left as kipll increases. The other characteristic roots are basically unchanged.

As shown in Fig. 12c, with the increase of ωlp, the characteristic root λ2−3 and λ4−5 move to the left to a certain extent and then to the right for a small distance. The other characteristic roots are basically unchanged. In terms of the three PLL parameters mentioned above, kppll plays a major role in the system stability.

4.5 The Influence of Grid Impedance on Stability

The AC system to which the flexible DC transmission system is connected has multiple modes of operation, which have a large impact on the equivalent impedance on the AC side. The effect of the change in the operating conditions of the AC side of the system on the stability of the system is studied by changing the size of the equivalent inductance.

By changing the filter parameter Lg, the trajectory of the key characteristic roots affecting the stability of the system is analyzed. Fig. 13 shows the track of eigenvalues when Lg changes from 0.05 to 0.3 pu (corresponds to a change in SCR from 20 to 3.2).

Figure 13: The effect of Lg on eigenvalues

As shown in Fig. 13, as Lg increases, the characteristic roots λ2−3, λ4−5 and λ10 move to the left. λ11−12 and λ13 move to the right. The characteristic root λ6−7 moves to the right and crosses the virtual axis when Lg is greater than 0.186 pu, and the system oscillates around the frequency of 139 Hz.

4.6 Summary of Influence of Control Parameters on Stability

The analysis shows that the studied characteristic roots may move to the right half plane when the control parameters change, resulting in system instability. Further analysis shows that the rise of kpc, kpp, kAD and kppll will lead to a significant increase in the real root of key features of the system, resulting in system instability.

To demonstrate the effect of control parameter optimization on system stability improvement, the system oscillation phenomenon of 139 Hz occurs by changing the grid equivalent impedance and reducing the grid SCR. Now, the oscillation phenomenon caused by the change of grid strength is eliminated by optimizing the control parameters, and the time domain graph is plotted to illustrate the effect of optimization in this paper.

The red dots in the Fig. 14 indicate the distribution of the characteristic roots of the system before optimization. For this operating condition, the blue dots in the figure indicate the distribution of the characteristic roots after the optimization of the control parameters, and the pair of unstable characteristic roots is eliminated, making the system stable. Fig. 15 reflects the variation of active power variation and reactive power variation with time before and after optimization after applying a small disturbance of −5% step change to the active power reference value at 5 s under unstable operating conditions. The images illustrate that the oscillations due to the alternating current side impedance variations are well eliminated and the small-signal stability of the system is enhanced after the parameter optimization.

Figure 14: Distribution of each eigenvalue before and after adjustment

Figure 15: Active power and reactive power changes before and after optimization

5  Conclusion

This paper focuses on the small-signal stability of VSC-HVDC systems. Firstly, a small-signal model of the system considering additional filtering links, damping controller and AC-DC side interaction characteristics is established. Based on this, the oscillation modes of the system are calculated and the influence of the control parameters on the stability of the system in each frequency band is analyzed. The system stability is improved by optimizing the system control parameters for the grid strength changes caused by the changes in AC-side operating conditions, and the specific conclusions are as follows:

(1) The inner and outer loop PI control scale factors kpc, kpp, AC active damper gain kAD and PLL scale factor kppll are the key factors affecting the high frequency oscillation. Increasing the above parameters tends to reduce the stability of the system, and the high frequency oscillation of different frequencies may occur according to the variation rule of the root trajectory. Decreasing the inner and outer loop PI control scaling factors, AC active damper gain and PLL scaling factor can improve the system damping characteristics.

(2) For the system low frequency oscillation phenomenon, the AC active damper gain kAD plays a key role in the system low frequency oscillation, and its value is too large to make the system oscillate in the low frequency domain. The above control parameters can be adjusted to improve the damping characteristics of the system in each frequency band, which is conducive to improving the stability of the system in broadband.

(3) When the AC side of the grid due to fault caused by the change in operating conditions, resulting in system strength changes, may also cause system oscillations. As the AC grid strength decreases, the system small signal stability gradually decreases until destabilization. For this situation, the system stability of this condition can be improved and the oscillation phenomenon can be eliminated by optimizing the key control parameters of the destabilization characteristic root according to the change of the characteristic root trajectory. In the engineering design, it is necessary to consider whether the grid strength changes caused by a variety of possible current grid operating conditions will lead to broadband oscillation problems, and use this to adjust the control parameters.

Funding Statement: The authors thankfully acknowledge the support of the project supported by Research on the Oscillation Mechanism and Suppression Strategy of Yu-E MMC-HVDC Equipment and System (2021Yudian Technology 33#).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. Flourentzou, N., Agelidis, V. G., Demetriades, G. D. (2009). VSC-based HVDC power transmission systems: An overview. IEEE Transactions on Power Electronics, 24(3), 592–602. DOI 10.1109/TPEL.2008.2008441. [Google Scholar] [CrossRef]

    2. Wang, X., Blaabjerg, F. (2018). Harmonic stability in power electronic based power systems: Concept, modeling, and analysis. IEEE Transactions on Smart Grid, 10(3), 2858–2870. DOI 10.1109/TSG.2018.2812712. [Google Scholar] [CrossRef]

    3. Hannan, M. A., Hussin, I., Ker, P. J., Hoque, M. M., Hossain Lipu, M. S. et al. (2018). Advanced control strategies of VSC based HVDC transmission system: Issues and potential recommendations. IEEE Access, 6, 78352–78369. DOI 10.1109/ACCESS.2018.2885010. [Google Scholar] [CrossRef]

    4. Mochamad, R. F., Preece, R. (2020). Assessing the impact of VSC-HVDC on the interdependence of power system dynamic performance in uncertain mixed AC/DC systems. IEEE Transactions on Power Systems, 35(1), 63–74. DOI 10.1109/TPWRS.2019.2914318. [Google Scholar] [CrossRef]

    5. Zou, C., Hong, R. G., Xu, S., Yan, L., Bo, L. (2018). Analysis of resonance between a VSC-HVDC converter and the AC grid. IEEE Transactions on Power Electronics, 33(12), 10157–10168. DOI 10.1109/TPEL.2018.2809705. [Google Scholar] [CrossRef]

    6. Zhang, Y., Hong, C., Tu, L., Zhou, T., Yang, J. (2018). Research on high-frequency resonance mechanism and active harmonic suppression strategy of power systems with power electronics. International Conference on Power System Technology (POWERCON), pp. 2350–2356. Guangzhou, China. DOI 10.1109/POWERCON.2018.8601628. [Google Scholar] [CrossRef]

    7. Guo, C., Yang, S., Liu, W., Zhao, C., Hu, J. (2021). Small-signal stability enhancement approach for VSC-HVDC system under weak AC grid conditions based on single-input single-output transfer function model. IEEE Transactions on Power Delivery, 36(3), 1313–1323. DOI 10.1109/TPWRD.2020.3006485. [Google Scholar] [CrossRef]

    8. Huang, Y., Zhai, X., Hu, J., Liu, D., Lin, C. (2018). Modeling and stability analysis of VSC internal voltage in DC-link voltage control timescale. IEEE Journal of Emerging and Selected Topics in Power Electronics, 6(1), 16–28. DOI 10.1109/JESTPE.2017.2715224. [Google Scholar] [CrossRef]

    9. Arani, M. F. M., Mohamed, Y. A. I. (2017). Analysis and performance enhancement of vector-controlled VSC in HVDC links connected to very weak grids. IEEE Transactions on Power Systems, 32(1), 684–693. DOI 10.1109/TPWRS.2016.2540959. [Google Scholar] [CrossRef]

  10. Pinares, G., Bongiorno, M. (2016). Modeling and analysis of VSC-based HVDC systems for DC network stability studies. IEEE Transactions on Power Delivery, 31(2), 848–856. DOI 10.1109/TPWRD.2015.2455236. [Google Scholar] [CrossRef]

  11. Guan, M., Pan, W., Zhang, J., Hao, Q., Cheng, J. et al. (2015). Synchronous generator emulation control strategy for voltage source converter (VSC) stations. IEEE Transactions on Power Systems, 30(6), 3093–3101. DOI 10.1109/TPWRS.2014.2384498. [Google Scholar] [CrossRef]

  12. Li, H., Liu, C., Li, G., Iravani, R. (2017). An enhanced DC voltage droop-control for the VSC–HVDC grid. IEEE Transactions on Power Systems, 32(2), 1520–1527. DOI 10.1109/TPWRS.2016.2576901. [Google Scholar] [CrossRef]

  13. Xu, L., Sun, M., Xin, H., Song, X., Wang, C. (2019). Influence of power factor on small-signal stability of grid-connected converter systems. 2019 IEEE 8th International Conference on Advanced Power System Automation and Protection (APAP), pp. 878–882. Xi'an, China. DOI 10.1109/APAP47170.2019.9225181. [Google Scholar] [CrossRef]

  14. Ding, H., Fan, S., Zhou, J. Z., Zhang, Y., Gole, A. M. (2015). Parametric analysis of the stability of VSC-HVDC converters. 11th IET International Conference on AC and DC Power Transmission, pp. 1–6. Birmingham, UK. DOI 10.1049/cp.2015.0002. [Google Scholar] [CrossRef]

  15. Renedo, J., Garcia-Cerrada, A., Rouco, L., Sigrist, L. (2021). Coordinated design of supplementary controllers in VSC-HVDC multi-terminal systems to damp electromechanical oscillations. IEEE Transactions on Power Systems, 36(1), 712–721. DOI 10.1109/TPWRS.2020.3003281. [Google Scholar] [CrossRef]

  16. Du, C., Agneholm, E., Olsson, G. (2008). Comparison of different frequency controllers for a VSC-HVDC supplied system. IEEE Transactions on Power Delivery, 23(4), 2224–2232. DOI 10.1109/TPWRD.2008.921130. [Google Scholar] [CrossRef]

  17. Raza, A., Xu, D., Li, Y., Su, X., Williams, B. W. et al. (2016). Coordinated operation and control of VSC based multiterminal high voltage DC transmission systems. IEEE Transactions on Sustainable Energy, 7(1), 364–373. DOI 10.1109/TSTE.2015.2497340. [Google Scholar] [CrossRef]

  18. Safari Tirtashi, M. R., Samuelsson, O., Svensson, J., Pates, R. (2018). Impedance matching for VSC-HVDC damping controller gain selection. IEEE Transactions on Power Systems, 33(5), 5226–5235. DOI 10.1109/TPWRS.2018.2815153. [Google Scholar] [CrossRef]

  19. Du, W., Fu, Q., Wang, H. (2018). Subsynchronous oscillations caused by open-loop modal coupling between VSC-based HVDC line and power system. IEEE Transactions on Power Systems, 33(4), 3664–3677. DOI 10.1109/TPWRS.2017.2771764. [Google Scholar] [CrossRef]

  20. Zhou, J. Z., Ding, H., Fan, S., Zhang, Y., Gole, A. M. (2014). Impact of short-circuit ratio and phase-locked-loop parameters on the small-signal behavior of a VSC-HVDC converter. IEEE Transactions on Power Delivery, 29(5), 2287–2296. DOI 10.1109/TPWRD.2014.2330518. [Google Scholar] [CrossRef]

  21. Amin, M., Suul, J. A., D'Arco, S., Tedeschi, E., Molinas, M. (2015). Impact of state-space modelling fidelity on the small-signal dynamics of VSC-HVDC systems. 11th IET International Conference on AC and DC Power Transmission, pp. 1–11. Birmingham, UK. DOI 10.1049/cp.2015.0048. [Google Scholar] [CrossRef]

  22. Li, Y., Du, Z. (2022). Stabilizing condition of grid-connected VSC as affected by phase locked loop (PLL). IEEE Transactions on Power Delivery, 37(2), 1336–1339. DOI 10.1109/TPWRD.2021.3115976. [Google Scholar] [CrossRef]

  23. Urquidez, O. A., Xie, L. (2016). Singular value sensitivity based optimal control of embedded VSC-HVDC for steady-state voltage stability enhancement. IEEE Transactions on Power Systems, 31(1), 216–225. DOI 10.1109/TPWRS.2015.2393253. [Google Scholar] [CrossRef]