 Open Access
Open Access
ARTICLE
Research on Operation Optimization of Energy Storage Power Station and Integrated Energy Microgrid Alliance Based on Stackelberg Game
College of Mechanical and Control Engineering, Guilin University of Technology, Gulin, 541006, China
* Corresponding Author: Yu Zhang. Email:
Energy Engineering 2024, 121(5), 1209-1221. https://doi.org/10.32604/ee.2024.046141
Received 20 September 2023; Accepted 08 December 2023; Issue published 30 April 2024
Abstract
With the development of renewable energy technologies such as photovoltaics and wind power, it has become a research hotspot to improve the consumption rate of new energy and reduce energy costs through the deployment of energy storage. To solve the problem of the interests of different subjects in the operation of the energy storage power stations (ESS) and the integrated energy multi-microgrid alliance (IEMA), this paper proposes the optimization operation method of the energy storage power station and the IEMA based on the Stackelberg game. In the upper layer, ESS optimizes charging and discharging decisions through a dynamic pricing mechanism. In the lower layer, IEMA optimizes the output of various energy conversion coupled devices within the IEMA, as well as energy interaction and demand response (DR), based on the energy interaction prices provided by ESS. The results demonstrate that the optimization strategy proposed in this paper not only effectively balances the benefits of the IEMA and ESS but also enhances energy consumption rates and reduces IEMA energy costs.Graphic Abstract
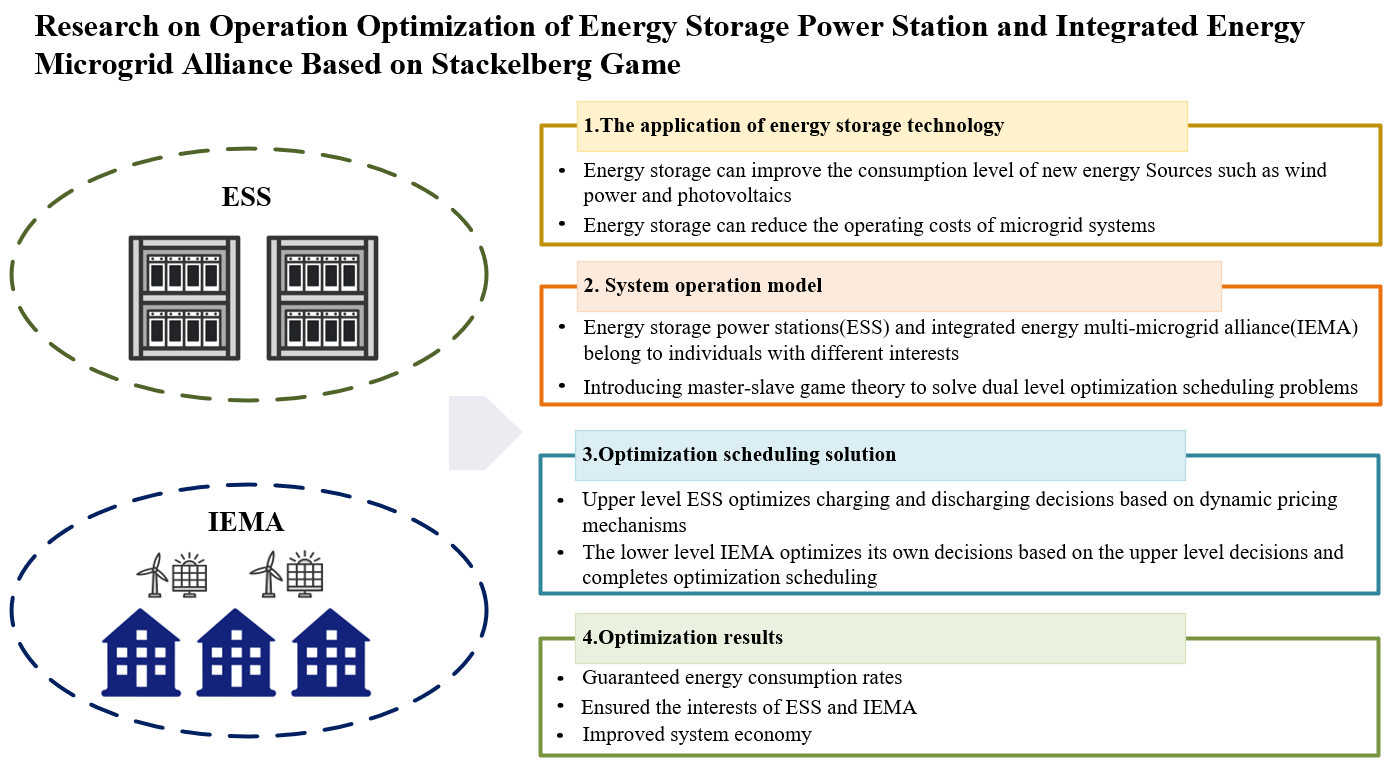
Keywords
With the excessive extraction of fossil fuels, non-renewable energy sources were gradually depleting. To develop clean and efficient energy sources and reduce environmental damage, a series of clean energy sources, such as wind power and photovoltaics, were being widely applied in microgrids (MG). However, the intermittent nature of new energy generation due to spatial constraints resulted in unstable output. Additionally, production and consumption characteristics variations led to a common phenomenon of wind and solar energy curtailment [1–4].
The use of DR and energy storage (ES) can effectively mitigate the instability of new energy generation. Reference [5] established an optimization scheduling model for microgrids, which used the fast charging and discharging characteristics of energy storage to smooth out the power fluctuations of new energy generation, thereby reducing wind and solar energy curtailment. The development of DR technology played a significant role in adjusting supply-demand dynamics and reducing peak load. Reference [6] constructed price-based and incentive-based DR models, significantly improving load characteristics within the scheduling cycle and enhancing system stability. The pursuit of energy efficiency and diverse user demands for integrated energy systems had catalyzed the development of integrated energy systems. In these systems, various heterogeneous energy flows were coupled, and energy complementarity relationships were complex. Furthermore, optimizing energy interactions in integrated energy systems was more challenging compared to single microgrid configurations. References [7,8], considering the coupling of electrical and thermal energy, established an optimization scheduling model for electric-thermal coupling systems to enhance energy utilization efficiency. Reference [9] proposed an energy management strategy for Multi-Microgrids (MMG) that took into account the energy coupling and exchange within MMG to enhance the integration of new energy sources and improve overall economic viability through mutual support and connectivity within the MMG network.
Although energy sharing within MMG and ES systems had indeed reduced wind and solar power curtailment to some extent in the past, standalone ES systems had suffered from high investment costs and low capacity utilization rates in the past. References [10,11] proposed establishing centralized ES services for communities and industrial parks in the past. By optimizing microgrid operators’ capacity construction, these references aimed to enhance the allocation of ES resources and achieve greater economic efficiency in the past. However, all of the above methods involved centralized optimization. The introduction of game theory could address decision-making and conflicts of interest among different entities. In reference [12], considering the interests of individual MG within the MMG energy sharing, a Nash equilibrium game approach was adopted to ensure the reduction of individual MG costs and alliance costs in the past. References [13,14] introduced a Stackelberg game into the electricity interaction between Microgrid operators (MGO) and user aggregators (US) to balance the interests of both parties in the past. This was achieved by reasonably guiding users’ Demand Response (DR) adjustments through electricity pricing in the past. References [15] constructed a game interaction framework between the DN and MG in the past. Through the dynamic pricing mechanism of the leader DN, they optimized strategies for MG and ES to accommodate peak and valley periods of new energy in the past. Reference [16] proposed guiding MG energy coupling and adjusting DR through the mode of ‘heat follows power’ and ‘power follows heat’ in the past. However, the above game studies only considered the conflict of interests between the energy supply side and demand side, often overlooking the interests of ES as a stakeholder in the past.
Building upon the aforementioned research and issues, this paper proposes an optimization operating strategy for ES serving an IEMA within a Stackelberg game framework. By seeking equilibrium solutions of the game model, it determines pricing strategies, ES response, various energy conversion and coupling device strategies within the ES, under the dynamic pricing mechanism of centralized ES. The objective is to enhance energy coupling, reduce wind and solar power curtailment, and improve system economic efficiency.
2.1 Energy Interaction Framework
The framework of the ESS and IEMA energy interaction model constructed in this paper is illustrated in Fig. 1. Considering that the demand response within each integrated energy sub-microgrid (IESM) may not align perfectly with the output of new energy devices, this paper proposes an energy interaction framework where multiple IESMs ally to facilitate energy sharing within the alliance. Simultaneously, ESS is employed to facilitate the assimilation of new energy within the comprehensive multi-microgrid alliance. This involves storing excess electricity generated by new energy sources and releasing it during peak demand periods or when there is a shortage of new energy electricity.
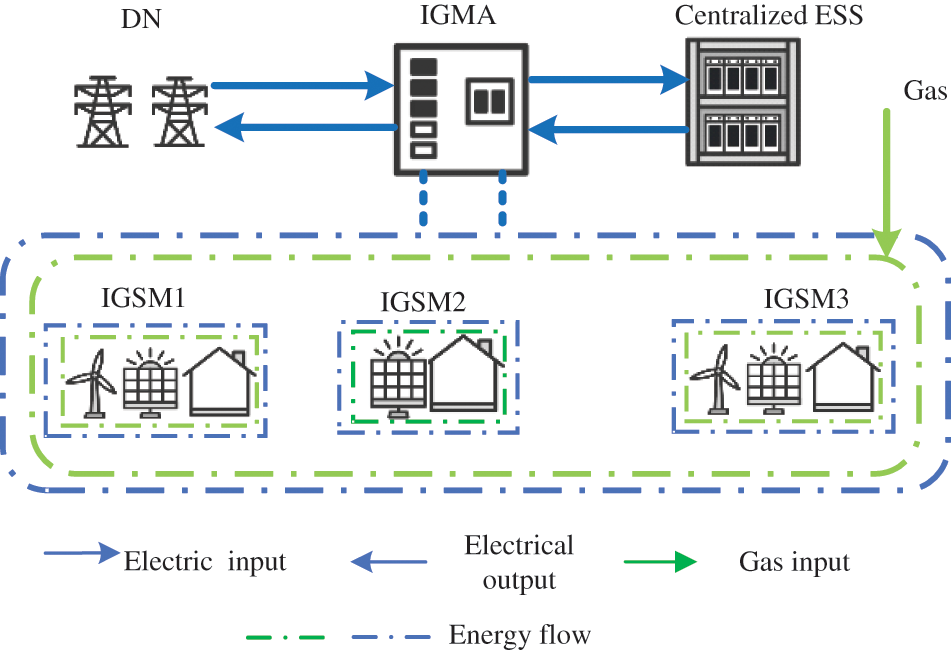
Figure 1: Energy interaction framework
Standalone ES systems have high investment costs and limited capacity at the sub-microgrid level. Their frequent interactions with the distribution grid and microgrids not only affect the lifespan of energy storage equipment [17] but also create pressure on the distribution grid. These factors collectively restrict the use of standalone energy storage devices. In this paper, a centralized energy storage station is used to provide energy storage services to the comprehensive multi-microgrid alliance. When there is surplus electricity within the alliance, it stores the excess energy, and when there is an electricity deficit within the alliance, it supplements the energy supply. This approach reduces wind and solar power curtailment, enhances the efficiency of energy storage equipment utilization, and improves overall system performance [18].
As the smallest unit of energy generation and consumption, the energy coupling situation within IESM is depicted in Fig. 2 [19]. In this paper, these IESMs are aggregated into an IEMA to promote energy assimilation and achieve efficient energy utilization. When IESMs have surplus energy, they contribute it to the alliance, and when there is an energy deficit, they obtain it from the alliance. Multiple IESMs entrust the alliance dispatch center and centralized energy storage stations for energy interactions. Furthermore, in cases of energy shortages within the alliance, IESM is allowed to purchase electricity from the distribution grid for supplementation.
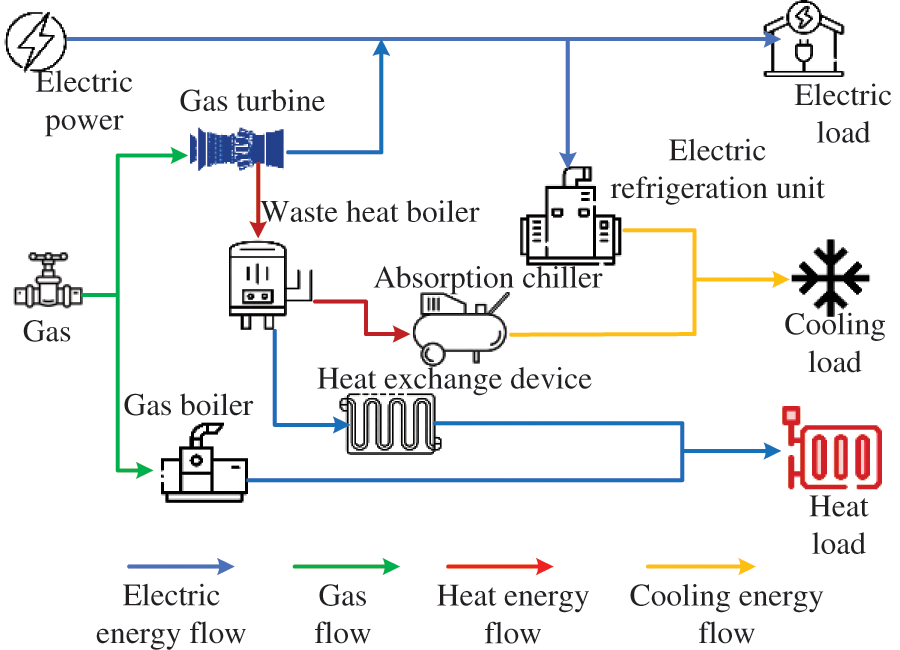
Figure 2: IEMA energy coupling
3.1 Optimization Model for EES
3.1.1 Benefit Function for ESS
The objective function of the ESS is to maximize revenue:
The equation
The equation
The charging and discharging power of the ESS should be within the range of the maximum charging and discharging power. Additionally, the current state of charge of the ESS is equal to the state of charge in the previous time step plus the charging or discharging power at the current time. The constraints that the ESS must satisfy during operation are:
In the equation,
3.2 Optimization Model for IEMA
3.2.1 Benefit Function for IEMA
IEMA’s objective function is to minimize operational costs:
In the equation,
The equation represents the unit volume price of natural gas,
Power balance constraint for electric power/thermal power/cooling power and equipment output balance constraint:
In the equation,
Based on the previously described operating modes of ESS and the energy interaction framework within IEMA, both ESS and the IEMA act as independent decision-making entities. The operational mode of ESS influences the energy coupling device conversion within various sub-microgrid systems of the IEMA and the DR of comprehensive energy users. From this, a model is constructed for ESS and the IEMA based on a Stackelberg game. The game model framework is illustrated in Fig. 3.
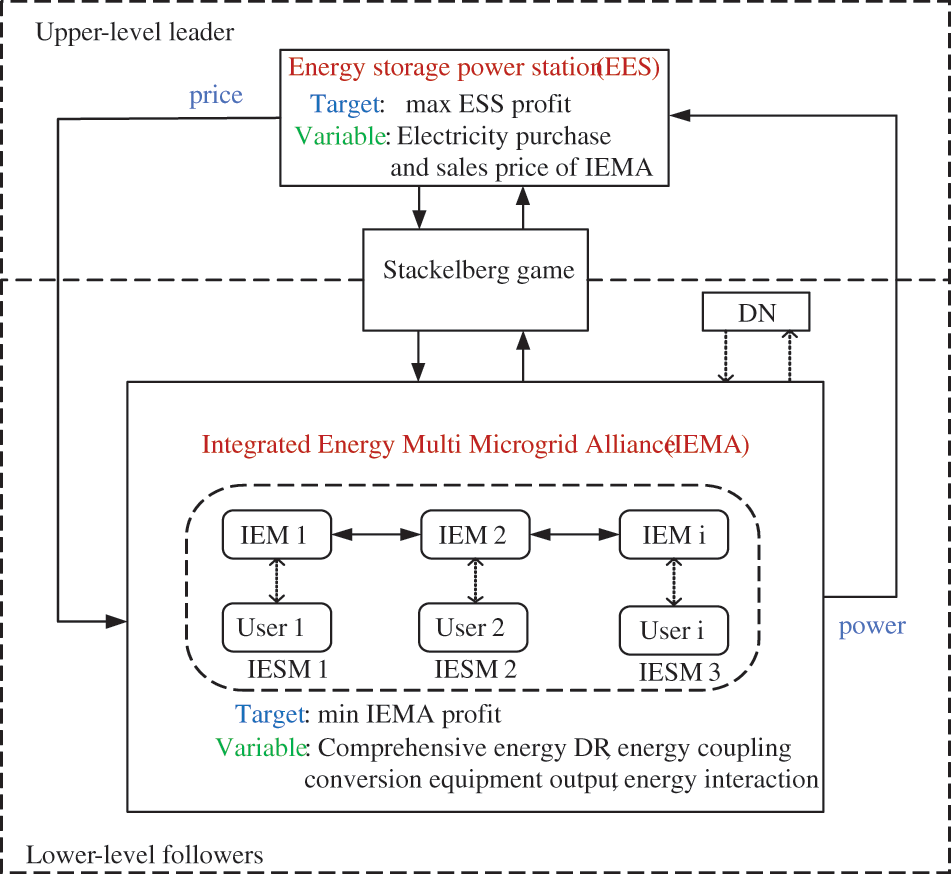
Figure 3: Stackelberg game model
The game model consists of three elements: participants
4.2 Stackelberg Game Model Solution Method
The optimization process for ESS and IEMA based on the Stackelberg Game in Fig. 4 is as follows.
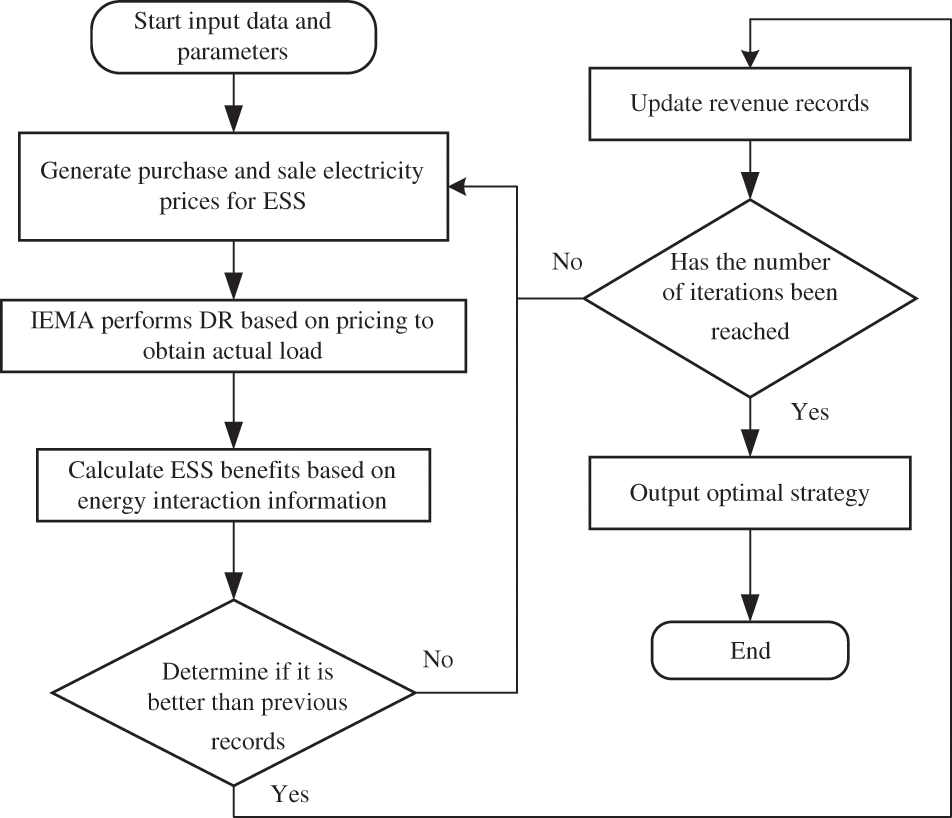
Figure 4: Optimize the solving process
The paper conducts a case study analysis using a comprehensive energy multi-microgrid alliance consisting of three integrated energy sub-microgrids as the selected case. The chosen reference day is in the spring season, with a scheduling period of 24 h. The integrated energy multi-microgrid system takes into account various forms of energy, including new and renewable energy sources. The maximum reducible integrated energy demand load for users can account for up to 15% of the demand load. The parameters for various energy-coupling devices for energy storage equipment and the integrated energy multi-microgrid alliance are detailed in Appendix A.
Case 1: IESM, which does not include independent energy storage equipment, operates independently, and any shortfall in electrical energy can be procured from the distribution.
Case 2: The IEMA incorporates energy interactions, and IESM achieves energy exchange by utilizing independent energy storage.
Case 3: The IEMA participates in centralized ESS services to achieve energy optimization scheduling.
Case 4: Based on the Stackelberg game, the IEMA participates in centralized ESS services to achieve energy optimization scheduling and integrated energy DR.
Fig. 5a shows the renewable energy consumption rate and the comparison of profits and costs among different stakeholders. This is generated by four different optimization methods applied to IES. In Example 1, only the comprehensive energy coupling situation in IESM is considered, and there is no energy storage device to absorb energy peaks and valleys, resulting in a renewable energy consumption rate of only 72.3%. In Example 2, a single energy storage device is considered for peak and valley consumption, although it improves the renewable energy consumption rate, However, the high investment cost of single energy storage equipment has increased the energy storage cost. In scenario 3, compared to scenario 2, adopting a centralized ESS improves energy storage capacity utilization, reduces investment and construction costs, and avoids inefficient energy storage. In Example 4, considering the integration of energy DR and granting priority decision-making rights to energy storage facilities, the energy coupling device output and energy interaction of the entire IEMA were reduced by 7500 yuan and 27900 yuan, respectively, compared to Cases 3 and 2. The cost of IESM was reduced by 11.2% and 42.2%, respectively. In Fig. 5b, adaptive particle swarm optimization and differential evolution algorithms were used to solve the optimization scheme of Example 4, respectively, The crossover and mutation of differential evolution algorithms can effectively avoid falling into local optima, which is beneficial for solving game equilibrium solutions.
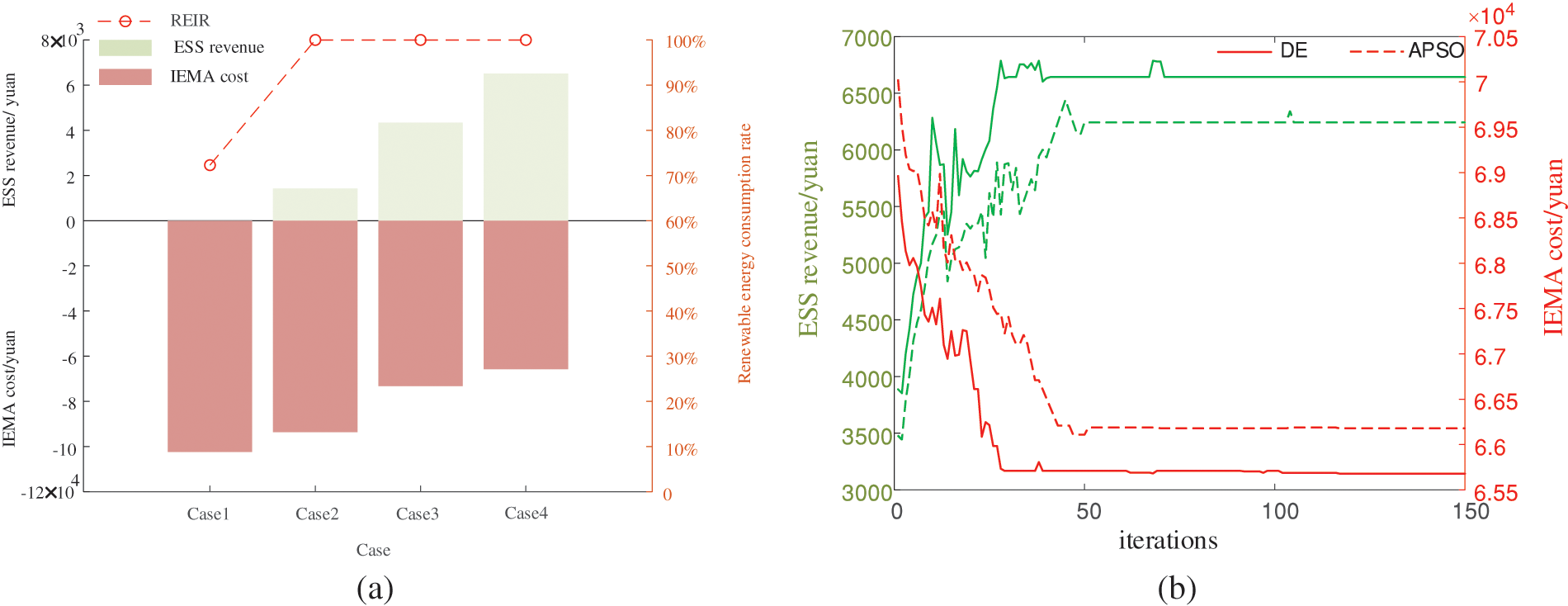
Figure 5: (a) Comparison of benefits of various cases. (b) Case 4 ESS revenue and IEMA cost optimization iteration curve
5.2 Stackelberg Game Optimization Decision
5.2.1 ESS Optimization Decision
In Case 4, the IEMA prioritizes internal energy interactions and stores the surplus energy in the centralized ESS. The ESS operator adjusts its own charge and discharge scheduling based on a dynamic pricing mechanism and information from IEMA devices’ output and energy interactions, as shown in Fig. 6. The charging time for the ESS is mainly concentrated between 10:00 and 14:00 when IEMA is in a surplus energy state. The energy storage facility purchases surplus electrical energy during this period, which increases the utilization of renewable energy and reduces wind and solar curtailment. Combining the wind and solar output with the load curve, it is evident that dynamic optimization led by the energy storage facility can effectively perform peak shaving and load-filling functions. As depicted in Fig. 7, during the period from 10:00 to 14:00, to encourage the IEMA to store surplus electrical energy in the energy storage facility, and thus increase the integration of renewable energy, the purchasing price of electricity from the ESS is relatively high. This incentivizes IEMA to sell electricity to the energy storage facility, aligning with IEMA’s interests.
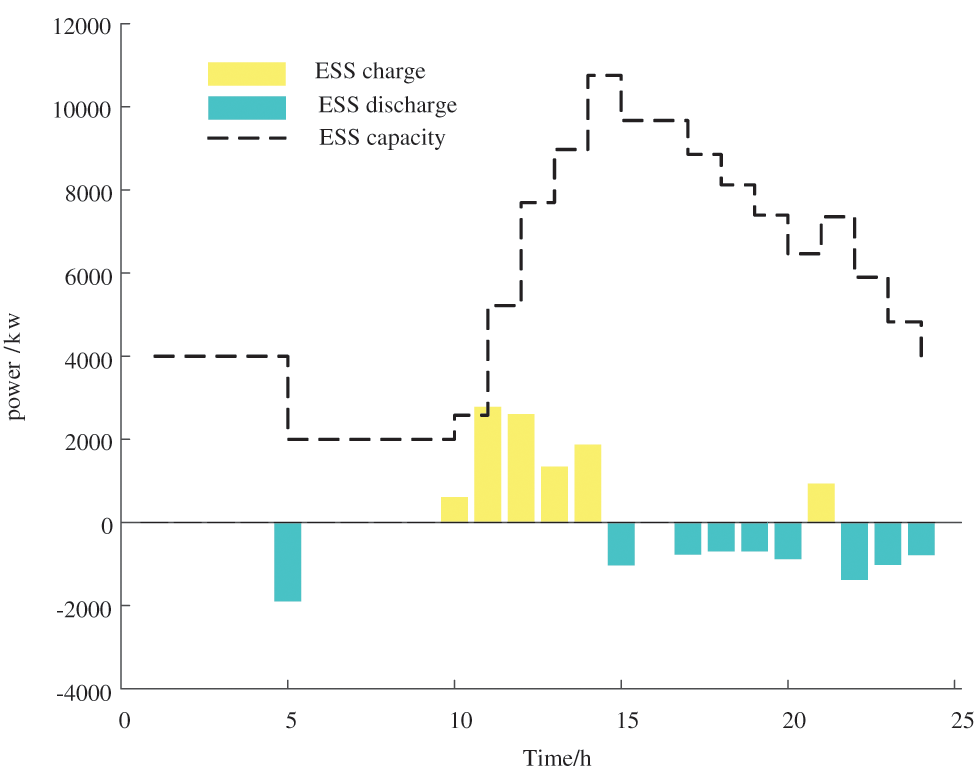
Figure 6: Ess charging and discharging strategy
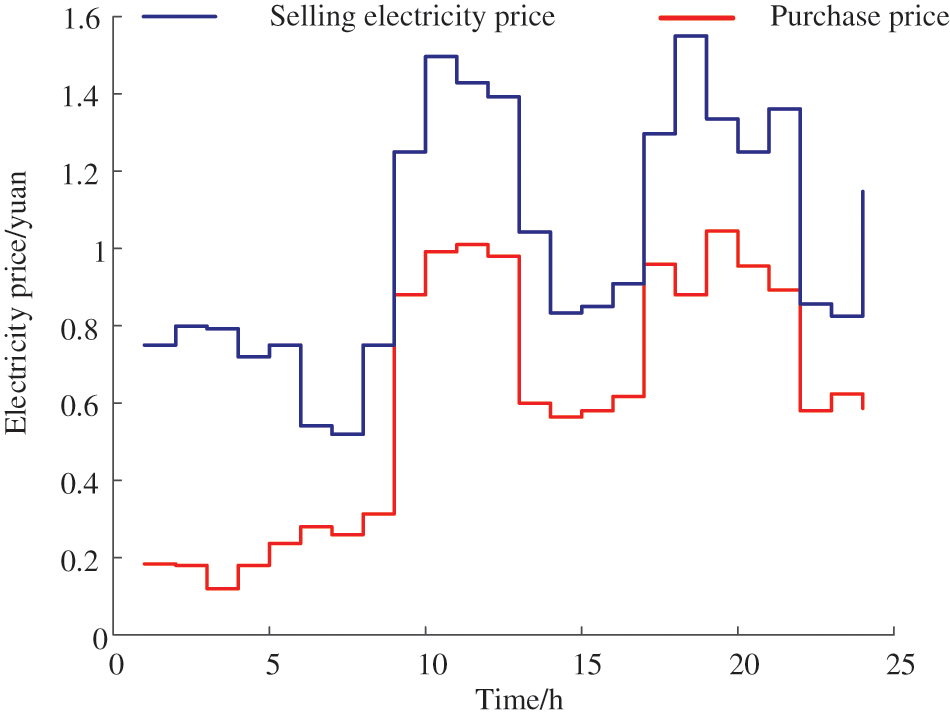
Figure 7: Optimization of ESS pricing strategy
5.2.2 IEMA Optimization Decision
As shown in Fig. 8, taking the demand response load of IESM 1 as an example, different demand reduction amounts are optimized at different times within the selected reference day. This is done from the perspective of appropriately reducing user energy demand to compensate for the drawbacks of unstable and intermittent renewable energy capacity:
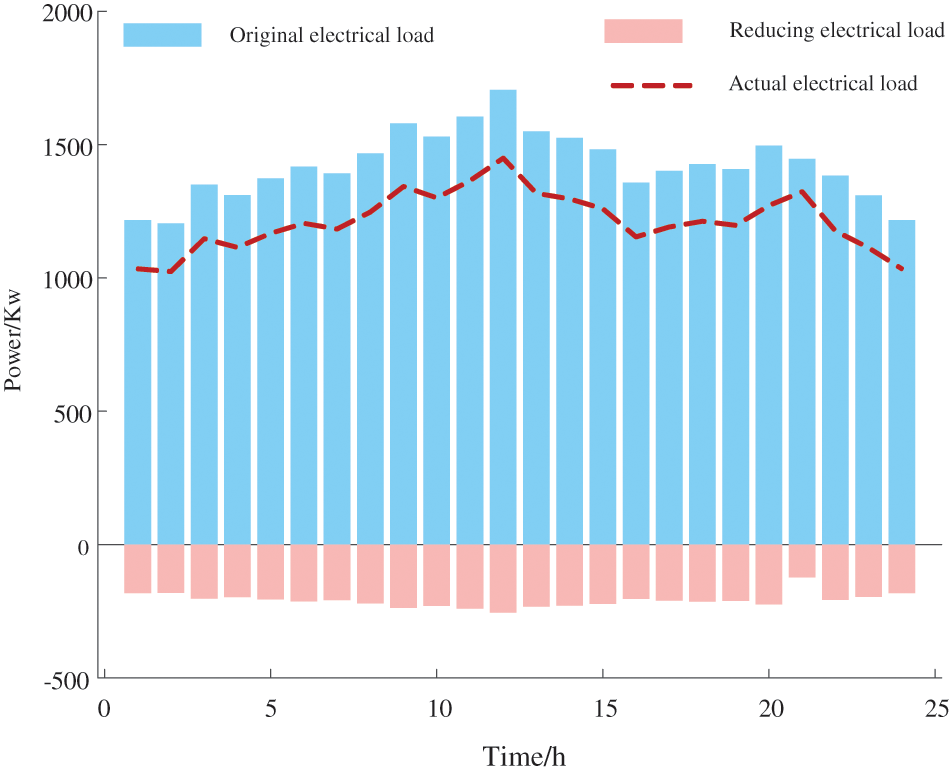
Figure 8: IESM 1 demand response
In Figs. 9a and 9c, IESM 1, as a multi-electric-type microgrid, contributes electricity to the alliance for most of the scheduling period on the reference day. However, at 4:00 and 6:00, the renewable energy output did not meet the load demand of sub-microgrid 1. Insufficient demand can be supplied by the surplus of the IEMA. At this time, IESM 3, which is closest to the alliance dispatch center, takes on the main task of purchasing additional electricity from the distribution grid. Additionally, at this time, the distribution grid price is lower than the energy storage station price, aligning with the interests of all stakeholders. The optimization strategy in Fig. 9b also aligns with the interests of IESM 2. In summary, surplus energy from the Integrated Energy Multi-Microgrid Alliance is stored in the centralized Energy Storage System (ESS), and the ESS is dispatched during periods of energy scarcity to meet the energy demands of the Integrated Energy Multi-Microgrid Alliance. The dynamic pricing of the ESS also aligns with the interests of the ESS operator.
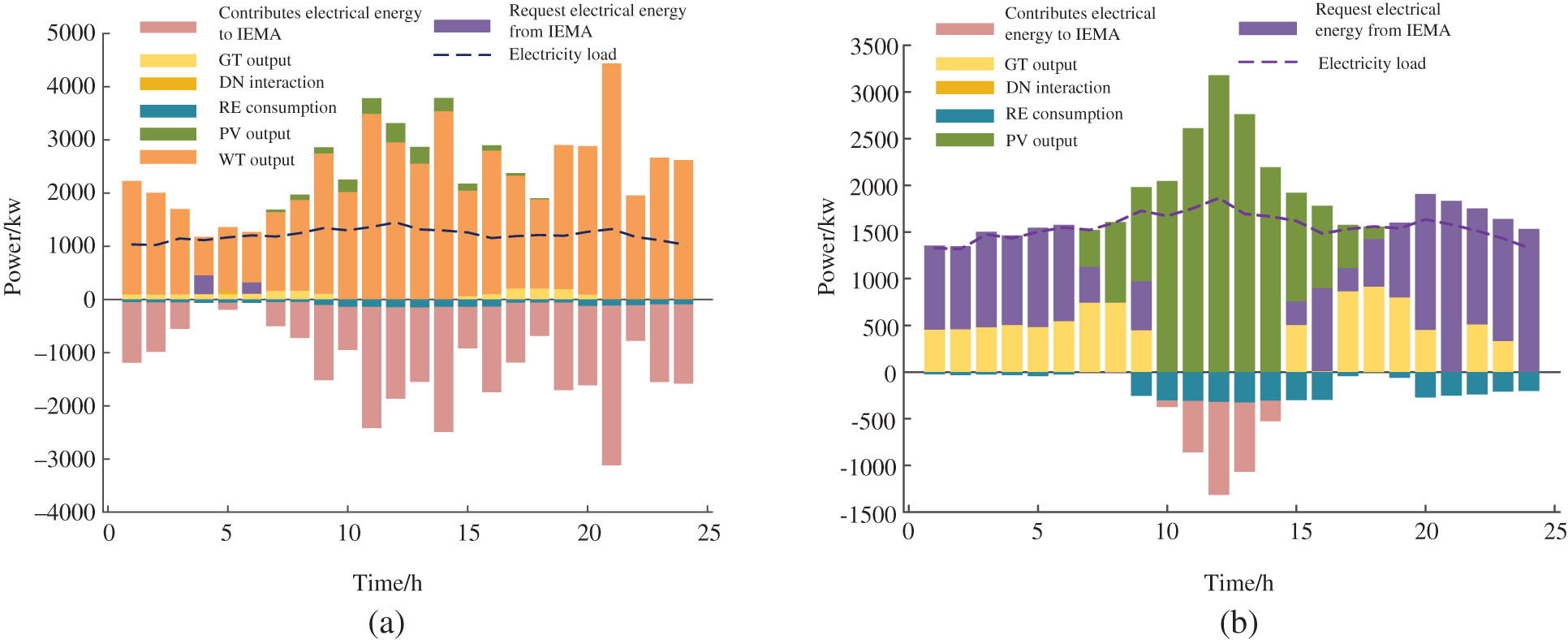
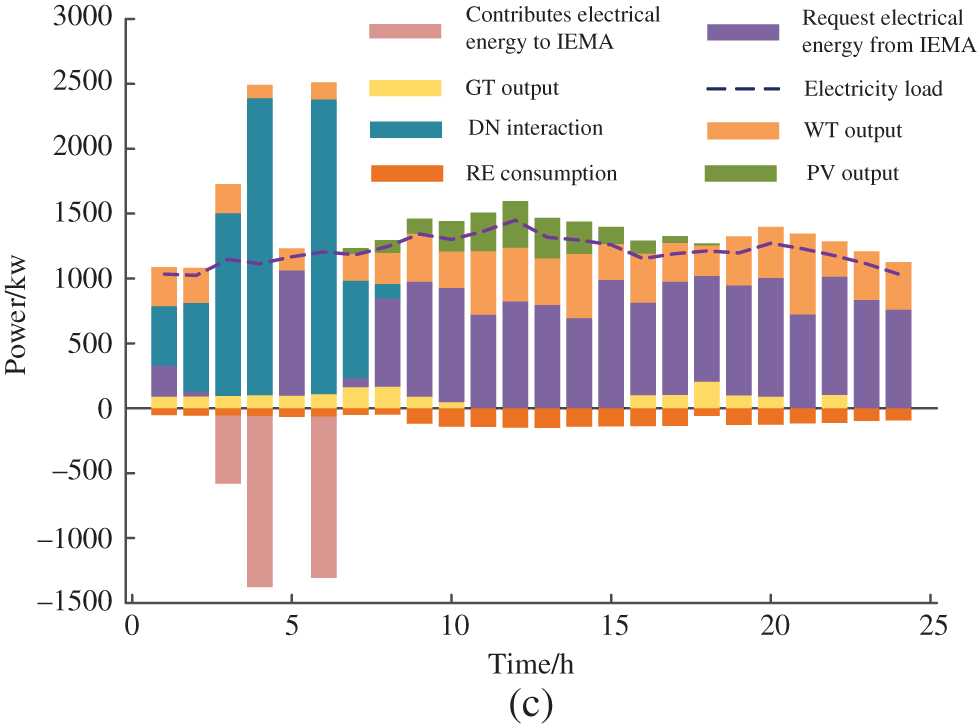
Figure 9: (a) IESM 1 optimization and scheduling results of electric energy. (b) IESM 2 optimization and scheduling results of electric energy. (c) IESM 3 optimization and scheduling results of electric energy
The first point: The energy optimization framework of the centralized energy storage power station and integrated energy microgrid alliance based on master-slave game proposed in this article takes into account the decision-making impact between ESS and IEMA under the consideration of elastic pricing mechanism, which is in line with the interests of multiple stakeholders. This article focuses on optimizing the operating mechanisms of IEMA and ESS. Through comparative analysis of four examples, the introduction of centralized energy storage stations and master-slave game operating mechanisms in the context of IEMA’s internal energy mutual assistance can strengthen the integration of renewable energy and peak valley regulation, encourage users to use energy reasonably, and achieve the goal of reducing energy costs. When solving the energy peak valley mode, it proposes the transfer of remaining electricity from energy storage stations and optimizes energy scheduling strategies based on master-slave game theory in the context of energy mutual assistance. In addition, ESS has the advantage of reducing investment costs. Compared to the mode of configuring energy storage for each integrated energy sub-grid, the initial construction investment cost of energy storage equipment is reduced through centralized energy storage power plants.
Secondly, the services of energy storage operators are conducive to IEMA’s new energy consumption and meeting its energy needs. Through dynamic pricing mechanisms, IEMA achieves low-cost energy consumption, while IEMA achieves comprehensive energy demand response and new energy consumption through electricity pricing and charging and discharging decisions. IEMA makes energy coupling and demand response decisions based on electricity prices and charging and discharging strategies. In the case analysis, compared to not using a game theory framework, the cost of IEMA decreased by 11.2%, and the revenue of ESS increased by 21%, which meets the demand for benefits.
The framework proposed in this article can accurately depict the interaction and cooperation mechanism between IEMA and ESS, which has certain reference significance for the research of energy co-economy and energy storage power station cooperation models. In the future, further research will be conducted based on factors such as source load uncertainty and hydrogen energy coupling utilization.
Acknowledgement: None.
Funding Statement: This work was supported by the Guangxi Science and Technology Major Special Project (Project Number GUIKEAA22067079-1).
Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Lianmin Li, Yu Zhang; data collection: Zhongxiang Li, Yuhu Wu; analysis and interpretation of results: Lianmin Li, Yu Zhang; draft manuscript preparation: Lianmin Li, Yu Zhang. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data used to support the findings of this study are available from the corresponding author upon request.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Shuai, Z., Sun, Y., Shen, Z. J., Tian, W., Tu, C. et al. (2016). Microgrid stability: Classification and a review. Renewable and Sustainable Energy Reviews, 58, 167–179. [Google Scholar]
2. Uddin, M., Romlie, M. F., Abdullah, M. F., Tan, C., Shafiullah, G. et al. (2020). A novel peak shaving algorithm for islanded microgrid using battery energy storage system. Energy, 196, 117084. [Google Scholar]
3. Xu, H., Meng, Z., Zhao, R., Wang, Y., Yan, Q. (2020). Optimal dispatching strategy of an electric-thermal-gas coupling microgrid considering consumer satisfaction. IEEE Access, 8, 173169–173176. [Google Scholar]
4. Maślak, G., Orłowski, P. (2022). Microgrid operation optimization using hybrid system modeling and switched model predictive control. Energies, 15(3), 833. [Google Scholar]
5. Talluri, G., Lozito, G. M., Grasso, F., Iturrino Garcia, C., Luchetta, A. (2021). Optimal battery energy storage system scheduling within renewable energy communities. Energies, 14(24), 8480. [Google Scholar]
6. Astriani, Y., Shafiullah, G. M., Shahnia, F. (2021). Incentive determination of a demand response program for microgrids. Applied Energy, 292, 116624. [Google Scholar]
7. Wu, J., De, G., Tan, Z., Li, Y. (2021). Study on bi-level multi-objective collaborative optimization model for integrated energy system considering source-load uncertainty. Energy Science & Engineering, 9(8), 1160–1179. [Google Scholar]
8. Gao, J., Yang, Y., Gao, F., Wu, H. (2022). Two-stage robust economic dispatch of regional integrated energy system considering source-load uncertainty based on carbon neutral vision. Energies, 15(4), 1596. [Google Scholar]
9. Kim, J. H., Moon, G. H., Joo, S. K., Oh, J. C. (2011). Development of demand response operation system for load aggregators. Transactions of the Korean Institute of Electrical Engineers, 60(12), 2221–2224. [Google Scholar]
10. Cui, S., Wang, Y. W., Liu, X. K., Wang, Z., Xiao, J. W. (2021). Economic storage sharing framework: Asymmetric bargaining-based energy cooperation. IEEE Transactions on Industrial Informatics, 17(11), 7489–7500. [Google Scholar]
11. Walker, A., Kwon, S. (2021). Analysis on impact of shared energy storage in residential community: Individual versus shared energy storage. Applied Energy, 282, 116172. [Google Scholar]
12. Liu, G., Jiang, T., Ollis, T. B., Zhang, X., Tomsovic, K. (2019). Distributed energy management for community microgrids considering network operational constraints and building thermal dynamics. Applied Energy, 239, 83–95. [Google Scholar]
13. Li, L., Cao, X., Zhang, S. (2022). Shared energy storage system for prosumers in a community: Investment decision, economic operation, and benefits allocation under a cost-effective way. Journal of Energy Storage, 50, 104710. [Google Scholar]
14. Erol, Ö., Filik, Ü. B. (2022). A Stackelberg game approach for energy sharing management of a microgrid providing flexibility to entities. Applied Energy, 316, 118944. [Google Scholar]
15. Wu, Q., Xie, Z., Li, Q., Ren, H., Yang, Y. (2022). Economic optimization method of multi-stakeholder in a multi-microgrid system based on Stackelberg game theory. Energy Reports, 8, 345–351. [Google Scholar]
16. Wei, M., Deng, Y., Long, M., Wang, Y., Li, Y. (2022). Transaction model based on Stackelberg game method for balancing supply and demand sides of multi-energy microgrid. Energies, 15(4), 1362. [Google Scholar]
17. Wang, J., Xu, Z., Sun, Y., Du, X., Mahfoud, R. J. et al. (2022). Optimal configuration and pricing strategies for electric-heat cloud energy storage: A Stackelberg game approach. Sustainable Energy Technologies and Assessments, 53, 102596. [Google Scholar]
18. Li, B., Yang, Q., Kamwa, I. (2023). A novel Stackelberg-game-based energy storage sharing scheme under demand charge. IEEE/CAA Journal of Automatica Sinica, 10(2), 462–473. [Google Scholar]
19. Wu, Q., Xie, Z., Ren, H., Li, Q., Yang, Y. (2022). Optimal trading strategies for multi-energy microgrid cluster considering demand response under different trading modes: A comparison study. Energy, 254, 124448. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools