The Role of Participant Distribution and Consumption Habits in the Optimization of PV Based Renewable Energy Communities

1  Introduction

The paradigm transition toward the electric power system in recent years has led to an increase in the integration of RESs [1–3]. As a result, decentralized RESs are becoming more prevalent, and local control offered by decentralized energy systems makes possible community-based energy production [4,5]. By bringing energy generation closer to customers, local decentralized energy resources minimize complexity, expenditure, and inefficiency when compared to centralized energy systems. Additionally, they promote energy independence, increase local resilience, and facilitate the transition to zero carbon emissions [6,7]. Moreover, decentralized energy systems give people more authority because they promote community involvement. These ECs share the objective of reducing energy use and encouraging active consumers to use energy more flexibly, which will lessen the heavy energy loads on the power grid [8]. Including local ECs and integrating local Distributed Renewable Energy sources appears to be an efficient strategy for managing the shift in the local energy landscape [9]. The European Union released the Clean Energy Package in response to the energy sector’s essential role in the climate crisis. The package emphasized the need for the energy market to be modernized to account for flexibility and that 32% of the energy mix should come from renewable energy sources by 2030.

The European Community is well-positioned to be a major player in creating a decentralized and more adaptable Energy Union where people have more influence. The concept of Renewable Energy Communities (RECs) and their creation, with a focus on RES usage, were introduced by the Clean Energy Package and, more significantly, the 2018/2001 Renewable Energy Directive (RED II). Meanwhile, the 2019/944 ED directives present the concept of CECs, which focus on electricity with the combined primary aim of delivering social, economic, and environmental benefits to their members [10]. RECs and self-consumers have become new players in the electricity market since they offer a multitude of chances to encourage community members’ active involvement. In local communities, the prosumers have an important role because of their capacity to generate energy instead of just being simple consumers. However, consumers are also fundamental because their presence in the community makes it possible to obtain the financial benefits that come from shared energy, which should be maximized to improve and encourage the decentralized system. Moreover, REC should include economically disadvantaged people to defeat energy poverty (social benefits).

Finding the ideal configuration is one of the biggest issues for the adoption of RECs. Researchers are working on this topic from different points of view [11,12]. For example, optimizing RES production and energy sharing management to support REC investment decisions was the focus in reference by the authors [13]. They suggested that this approach would be advantageous for deploying RES generation and ultimately lead to the decarbonization of electricity. Another study, developed by Lazzari et al. [14], tries to optimize participant targeting and solar shared energy allocation in RECs to achieve favorable results, such as cheap paybacks and high averted CO2 emissions for all participants. They considered both economic and environmental concerns. According to the Italian regulatory framework, Cutore et al. [15] proposed an optimization model for the ideal size and management of energy flow in RECs. The model accounted for the cost-effectiveness of the investment and performance assessment of energy, and it demonstrated the reduction of energy poverty and environmental impacts as well as the increase in economic benefits. The examination of energy sharing directives, management analysis of both the current and previous versions of these directives, and economic and environmental views were all worked on by Ceglia et al. [16]. When comparing the conventional design with the local self-consumption index of RES in the EC, it was seen that RECs allow for the avoidance of 39.5 t/y of CO2 emissions in EU countries. According to the Spanish regulatory framework, Gallego-Castillo et al. [17] conducted a regional analysis of the best self-consumption installations. The results show that the optimal installation size reduces costs for self-consumers across the region, both with and without compensation for extra energy. In their work on the RECs Model, Casalicchio et al. [18] concentrated on the operation, investment, and optimal Demand Side Management (DSM) as well as the assessment of a fairness index to determine the most advantageous distribution of benefits. They study different design typologies of energy communities (ECs) in European nations such as Portugal, accounting for different consumer types with heterogeneous profiles of electricity demand and willingness to participate, as well as multiple scenarios of technology deployment and electricity trading, such as collective self-consumption vs. peer-to-peer [19]. Alam et al. developed a model which optimizes prosumers participation with heterogenous energy sources in REC based on a stochastic algorithm with the target of costs minimization [20] and developed a model in which in a fixed size REC (constant numbers of prosumers and consumers) participants switch their role to find an optimal distribution [21]. There aren’t many research articles focusing on the work of optimizing the configuration of RECs based on the distribution of prosumers and consumers. Sassone et al. developed a model to find the optimal distribution of REC users but neglecting financial parameters such as net present value (NPV) or payback period or changes in REC’s energy consumption habits of users and variation in the size of the plant. Similarly, in [21], the authors did not consider the switch of participants’ habits, and the saturation of energy shared within the community if the number of consumers increases. This work addresses this gap and focuses on a mathematical model of a fixed number of REC participants to maximize the variation of profit in case of Photovoltaic based REC respect to the configuration in which the REC is not constituted. The optimal configuration is based on the distribution of the number of prosumers and consumers with different consumption habits considering the constraints from regulatory framework limitations. To maximize the profit, shared energy should increase, finding the best compromise between the energy demand and the energy sold to the grid.

In the work, the optimal distribution of users and the load profiles have been assessed, and computations for self-consumption, sold, and shared energies have been performed. The findings and results from the model indicate that there is a prosumer and consumer distribution configuration that could optimize the extra profit, and that this configuration is heavily influenced by the load profiles. Moreover, the financial sustainability of a plant is allowed by self-consumption, so it is inadvisable to use incentives for shared energy to create a giant photovoltaic plant if there is not enough prosumers’ energy demand. The overall work is organized into different sections: Section 2 discusses the mathematical model, Section 3 shows the outcomes of the models and discusses the findings from the numerical simulations, and Section 4 concludes the overall work carried out for this article.

2  RECs Mathematical Model and Formulation

The purpose of this model is to optimize photovoltaic-based REC by maximizing the extra profit due to the shared energy (Esh) compared to the case of the same configuration but without the REC advantages. In the model, REC’s efficiency η is defined as follows:

η=EshNc⋅Ed(1)

where:

-   Nc is the number of consumers

-   Ed is single REC user yearly energy demand for both types (prosumers and consumers)

-   Esh is the shared energy

As an example, the time evolution of the extra power of the REC in one day is shown in Fig. 1a–c at different η values along with three different load power profiles: 1 kW (a), 3 kW (b), and 5 kW (c). The extra power profile is the difference between the PV power production profile and the load of the prosumers (self-consumed energy). When η<0.32, all the extra power is shared during the day, while when η=0.44 the load profile is too low, and shared energy is not maximized. If the load profile increases, as in the case of η=0.19, the shared energy is maximized, but the total load of consumers is oversized concerning the size of the PV plant, and the benefits of shared for unit of load are lower. When REC efficiency decreases under the threshold 0.32, even if the shared energy is still maximized, due to a high number of consumers, the In fact if the number of consumers increases, even if the shared energy is still maximized, economic benefits will be shared among a higher number of users and for this reason each participant will receive a lower benefit. This suggests that there exists an optimal distribution of prosumers and consumers in REC and that it depends on the load profiles and the size of the PV plant. In this study, an optimization algorithm has been developed to find the optimal distribution of prosumers and consumers.

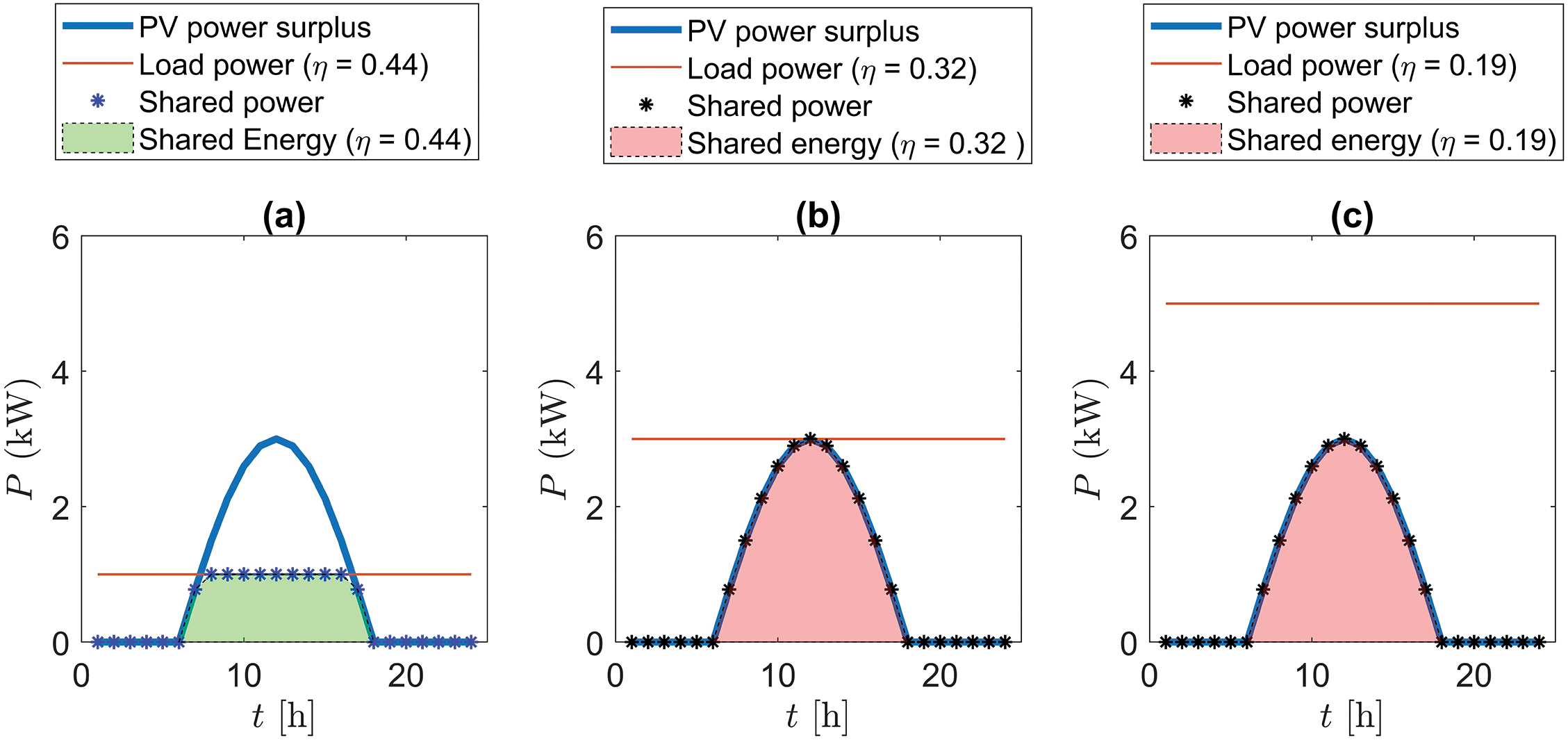
Figure 1: Time evolution of the extra power and the load in a representative day. Shared energy is highlighted in three different cases: load 1 kW (a), 3 kW (b), and 5 kW (c)

Fig. 2 shows a REC model sketch based on the number of prosumers and consumers. As discussed, REC is PV-based with a constraint of 1 MW total capacity. The load for both prosumers and consumers are supplied through the primary substation subtending to a geographic area. However, PV production for the prosumer is also considered with the same cabin and the same area in the REC. The owner of the PV plant can be a single prosumer (Pi) or can be the community pink box in Fig. 2.

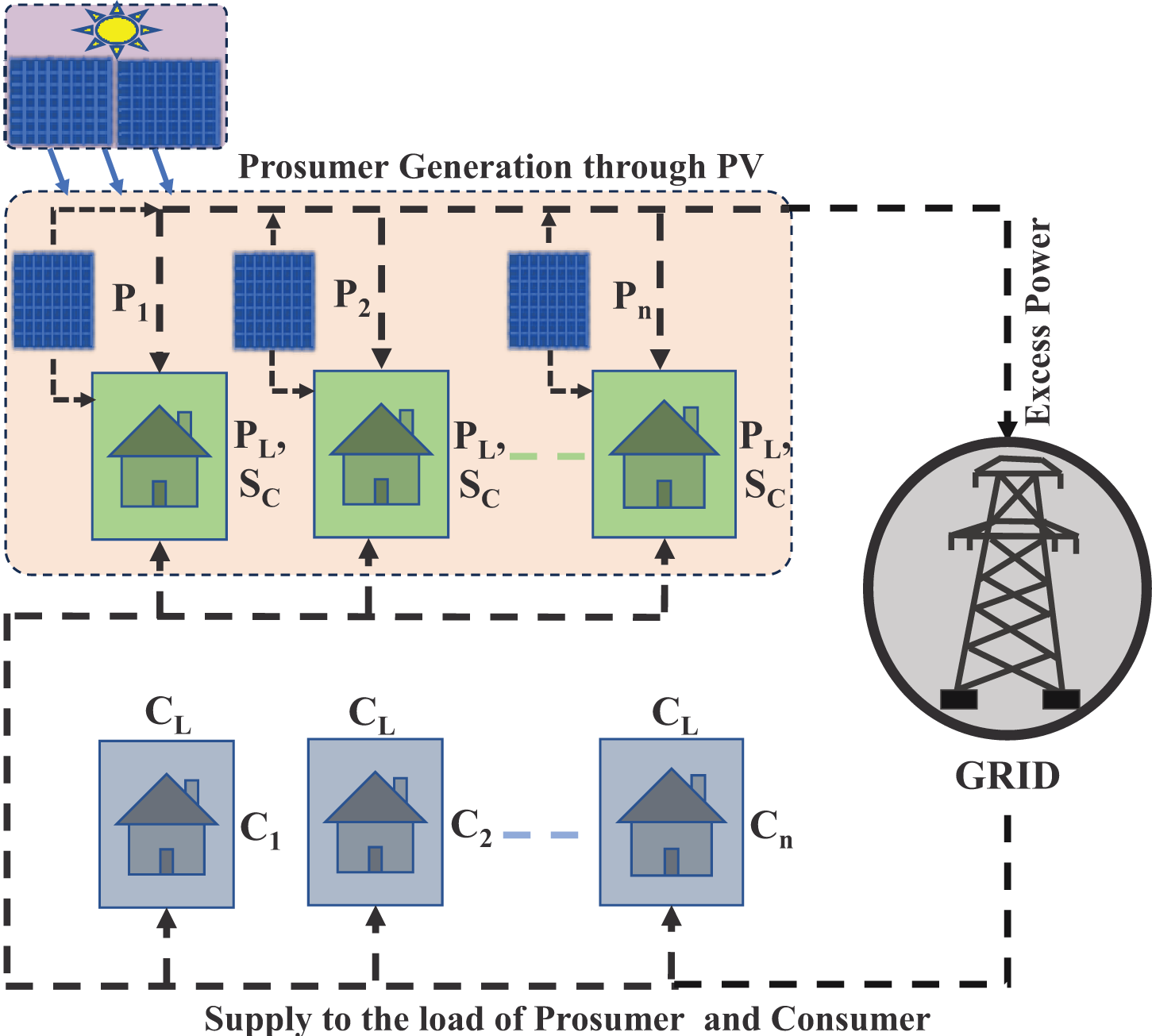
Figure 2: REC configuration sketch [21]

The mathematical model has been developed to simulate and optimize a REC composed by Np prosumers and Nc consumers as depicted in Fig. 2, by assuming the following hypothesis:

1.    The total number of prosumers and consumers are kept constant, Np+Nc=constant

2.    Prosumers and consumers energy demand (Ed) have the same hourly-based shape of the load profile (L). In the future, real data can be implemented by considering clustering of a large number of real data or by including a forecast model for the load data

3.    There is the opportunity for consumers to become prosumers and vice versa

4.    Participants can change their consumption habits

To find the best configuration of REC and to maximize the variation of Net Present Value (ΔProfit) as a function of user load profiles and distribution of consumers and prosumers, a multi-objective function has been introduced:

y=Esh(δ,Np,Nc)Esh,max(δ¯,Np¯,Nc¯)+η(δ,Np,Nc)(2)

where:

-   Esh is the yearly energy shared by the members of the community

-   δ=ElightEd is the ratio between the consumption of energy during the hours of light for the whole year (Elight) and Ed

-   Np is the number of prosumers

-   Esh,max represents the maximum energy that the community can share

The maximization of the function y is based on a 2-step optimization algorithm because y is maximized by finding the optimal value of δ and of Np which in turn is a function of δ. Both steps are based on the Trust Region Method Based on Interior Point Techniques for Nonlinear Programming developed by Byrd et al. [22]. The interior point techniques-based trust region approach solves nonlinear programming problems by combining the efficiency of interior point methods with the robustness of trust region methods. Step sizes are constrained using a trust region, and feasibility is guaranteed by adding a barrier function for inequality restrictions. Large-scale, constrained optimization problems benefit greatly from this method’s dependable convergence and good management of intricate feasible zones. By controlling restrictions like energy balance, grid capacity, and renewable generation limits while maximizing energy flow, resource allocation, and cost reduction, this method can be used in mathematical modeling for energy communities. Other optimization algorithms can be successfully considered, especially if the number of free parameters increases [23].

A primary substation subtending to a geographic area is used to construct the REC. The Italian regulatory framework (Decreto CER and GSE Technical Rules 2024) states that the maximum power allowed for the REC is 1 MW. The first hypothesis states that while the distribution of prosumers and consumers can fluctuate, allowing a consumer to become a prosumer and vice versa, the overall number of REC users is still fixed (Nt). To optimize profitability, the primary goal is to determine the optimal distribution of REC users (consumers and producers) and their optimal consumption habits (δ). Photovoltaic (PV) production can either partially or fully satisfy a portion of the prosumer load, which is represented by Eself (self-consumption. When PV generation exceeds demand, the excess power can be sold to the grid; if users need energy during that period (on an hourly basis), the difference between the excess and load energy is what’s referred to as shared energy.

Data on PV production for prosumers is sourced from PVGIS (Photovoltaic Geographical Information System) [24]. Prosumers can choose to produce their own Photovoltaic (PV) energy or use the common plant shown in Fig. 2; in this scenario, prosumers are owners of a single PV plant which supplies their own energy needs, and the surplus of energy is sold to the grid, or it could be shared into the community. The load for both prosumers and consumers were built by considering the same total yearly energy demand, Ed, and by generating a load profile as follows:

L=C⋅Pr(δ,h)(3)

where:

-Pr(δ,h) is a basic hourly load profile whose shape depends on the parameter δ

C=Ed∑h=18760Pr(δ,h)(4)

is a constant, and it is the ratio between the yearly energy demand and the basic load profile.

To evaluate the influence of load profile on a REC distribution, different load profiles with different values of δ were generated, as shown in Fig. 3. Higher values of δ means that prosumers and consumers are distributing their load during the daylight period, when the PV plants produce electric energy.

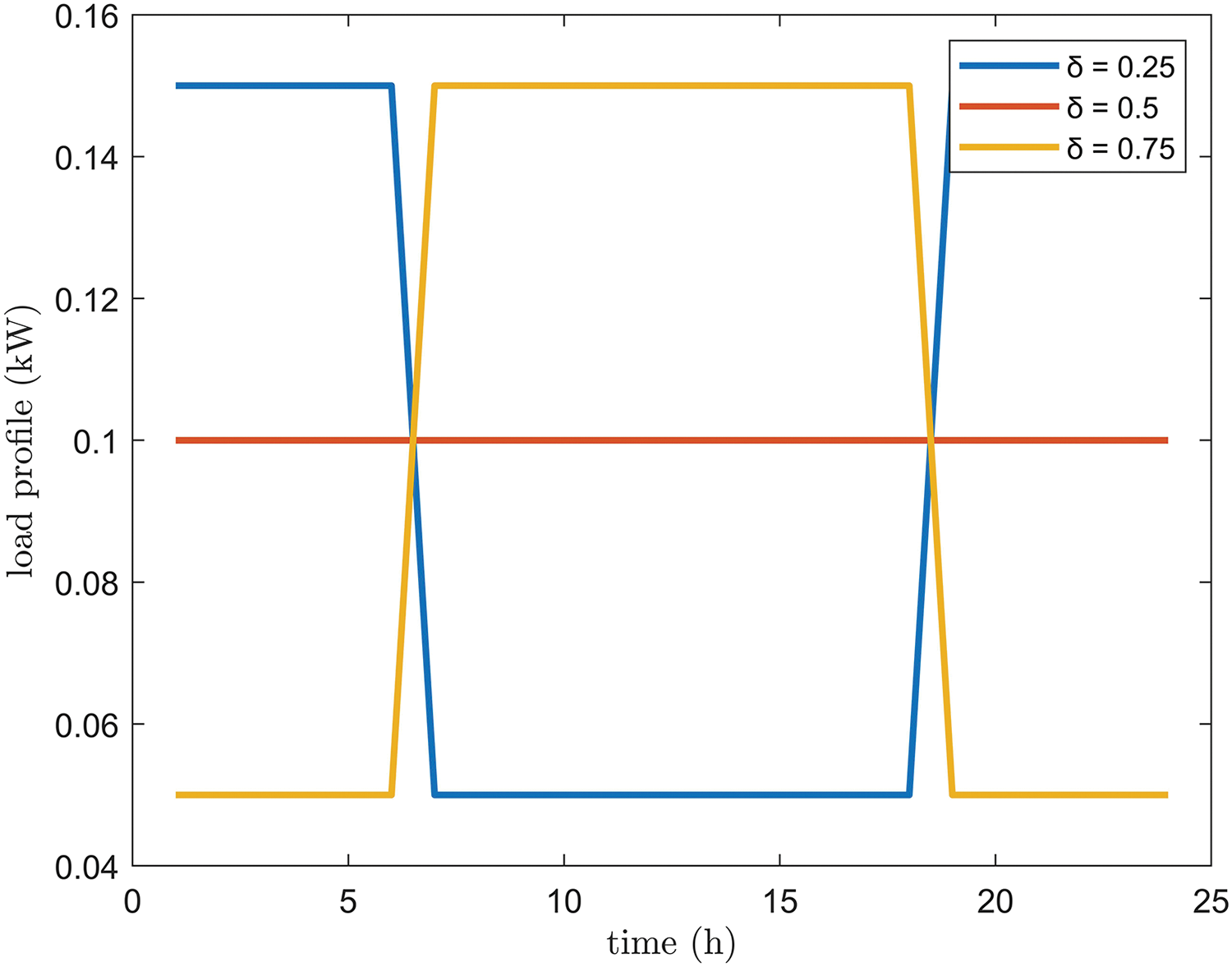
Figure 3: Effect of δ on the shape of the load profile

This model allows REC participants to change their role, which means that consumers could become prosumers or vice versa, but plant size cannot be increased if that means exceeding 1 MW, Moreover, it allows them to change their consumption habits by changing δ. The possibility of selling excess power to the grid and distributing it among REC members with additional financial incentives could boost profitability. If, at a certain time, consumers are consuming energy and prosumers sell the surplus of energy to the grid, this amount of energy is called energy shared (Esh) and generates more profit, thanks to the incentives given by Gestore dei Servizi Energetici (GSE) according to the Italian framework [25,26]. However, the benefits of REC are not only financial but also social and environmental. By assuming that all the prosumers have the same energy demand (Ed), it is important to design, for each prosumer, the size of the plant (individual nominal power Pn,i); in fact, different sizes of the PV plant will be evaluated to find which size maximizes the NPV after 20 years.

The hourly shared energy (Esh,h) is defined as the minimum value between the energy produced by the photovoltaic plant, which is not self-consumed by prosumers (it is the amount given to the national grid) and the hourly energy demand of all REC users (DE,h), it includes consumer energy demand and the part of prosumers’ energy demand that is not satisfied by their plant. Hourly shared energy can be evaluated as in the following equations:

Esh,h=min(Esold,h;DE,h)(5)

DE,h=∑i=1NpLres,ih+∑j=1NcLjh(6)

where:

-   i=1,…,Np is the index of the i-th prosumer

-   j=1,…,Nc is the index of the j-th consumer

-   h=1,…,8760 is the index of the h-th hour of the year

-   Esold,h is the surplus of energy produced by the photovoltaic plant and sold to the grid is calculated as follows:

Esold,h=max(∑i=1Np(PPVih(Pn,i)−Eself,ih);0)(7)

-   Eself,ih is the energy produced by the photovoltaic plant that is self-consumed by the prosumer

Eself,ih=min(PPVih,;Lih)(8)

-   Lih is the hourly energy load of prosumer

-   PPVih,(Pn,i) is the hourly energy production of the plant owned by one prosumer as a function of the size of the prosumer’s plant (Pn,i)

-   Lres,ih is the amount of Lih of prosumers, which it is not satisfied by PPVih,, it can be computed as follows:

Lres,ih=max(∑i=1Np(Lih−PPVih(Pn,i));0)(9)

In this case, there is no possibility for the surplus of energy of one prosumer to supply Lres,ih because all prosumers have the same energy demand, and all users have the same load profile.

If Eq. (5) is combined with (6)–(9), it is possible to obtain (10):

Esh,h=min(max(Y;0);∑j=1NcLjh−min(Y;0))(10)

Y=∑i=1NpPPVih−Lih(11)

According to the European Union framework, the constraint expressed in Eq. (12) must be satisfied:

Np⋅Pn<_1 MW(12)

Once the energy flows of the community have been evaluated, it is possible to calculate the NPV as it follows [27]:

NPV=∑n=0tCf(t)(1+r)t(13)

Cf,o=∑n=0t[CX+OX+RX]n(14)

Cf,i=∑n=0t(1−dc)⋅[CEsc+CEs+CEsh]n(15)

where:

-   Cf is the total cashflows

-   Cf,o are the cash outflows

-   Cf,i are the cash inflows

-   CX and OX are CAPEX and OPEX

-   RX is the rest of costs

-   CEsc is self-consumed energy cost

-   CEs is the sold energy cost

-   CEsh is the shared energy cost

-   dc is the degradation rate of the PV plant in percentage

-   r is the discount rate

-   t is the lifetime (year)

-   Cinv is the cost of replacement for the inverters after 10 years

The profitability has been computed as the difference between REC and without REC configurations and is computed as follows:

Δprofit=NPVREC−NPVNoREC(16)

Here,

Δprofit=∑t=120Csh⋅Esh+Cd⋅Eself−Cman(1+r)t(17)

where:

-   NPVREC is the NPV in case of REC

-   NPVNoREC is the NPV in case without REC

-   Δprofit is the difference between NPVREC and NPVNoREC, it means the extra profit due to REC realizations.

-   Csh is the amount of price given by GSE to incentivize shared energy in a REC as per Italian Framework (Decreto CER)

-   Cd is the amount of price given by GSE to incentivize distribution power loss avoided by Eself

-   Cman is the management cost in the case of REC (it is equal to 0 if there is no REC)

The data used to calculate NPV with the above set of equations are given in Table 1 [26–29].

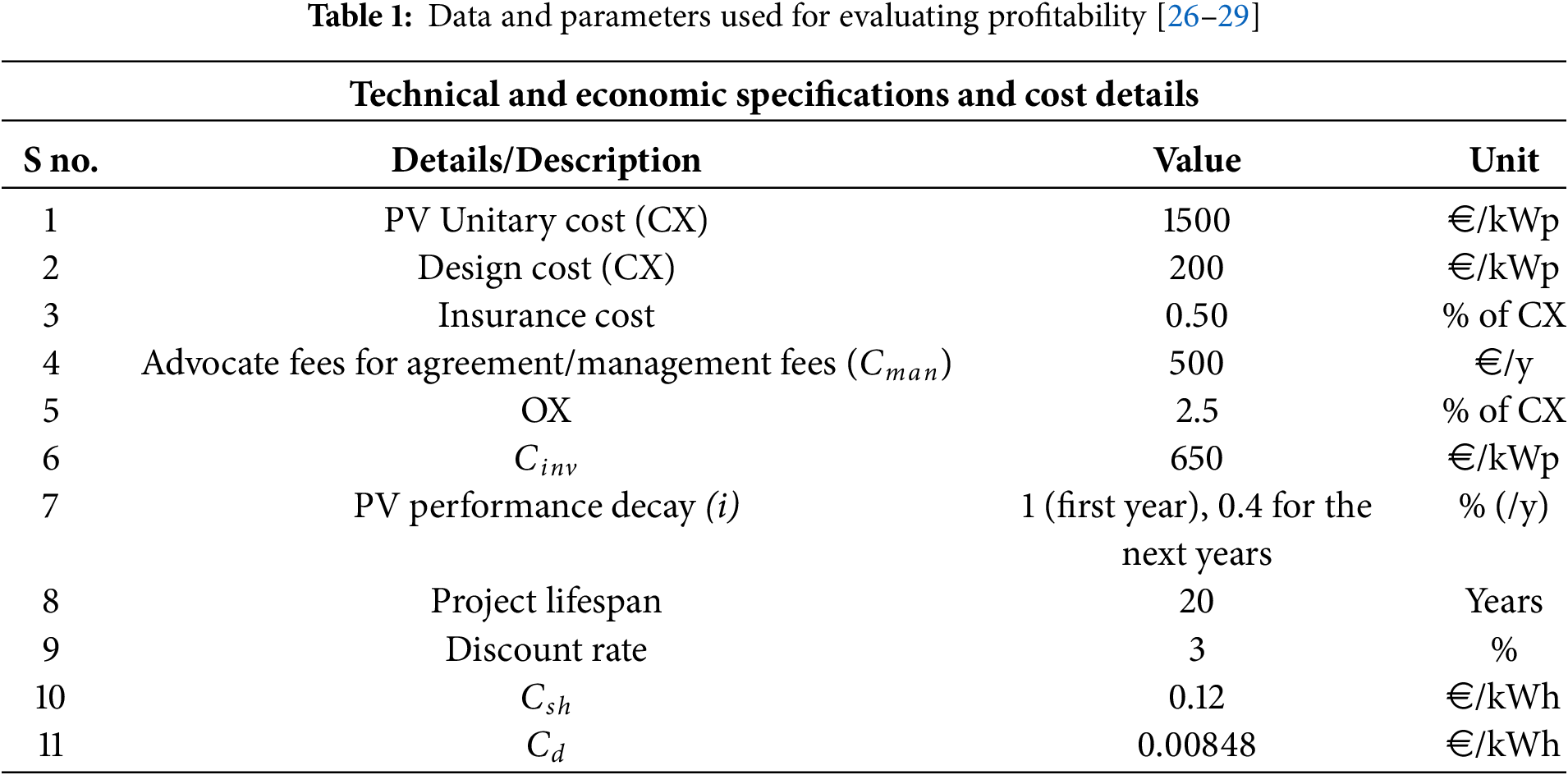
When a REC is constituted, the prosumers will gain a part of Δprofit due to the shared energy plus the money that they save from the bill by self-consuming PV energy, equal to CEsc⋅Eself and the money that they gain by selling the surplus of energy to the grid, equal to CEs⋅Esold.

The objective function y to be maximized in Eq. (2) depends on the number of prosumers, consumers, and on δ. Both shared energy Esh and efficiency η are functions of the parameter δ, but efficiency and shared energy reach their maximum for different values of δ and a competitive behavior arises between Esh and η when δ changes. When δ increases energy shared increases reaching a maximum value and start decreasing due to the higher self-consumption of prosumers. The optimization of the objective function y will be made by considering different sizes of the plant PPV and then NPV will be calculated if the PV plant is part of a REC and if it is not part of a REC.

3  Results and Discussions

A case study has been considered, a PV-based REC situated in Potenza (Southern Italy), composed of one-hundred users (Nt=100), with the possibility for the prosumers to become consumers and vice-versa. The yearly energy demand is equal to 2250 kWh per year for each user, moreover, the users can change their consumption habits, inducing a change in the parameter δ. The size of the plant is 1.25 kWp for each prosumer (Pn,i). Simulations have been performed over one year, considering the PV production profile on an hourly basis as taken by the PVGIS database.

Initially, different and fixed values of δ have been considered to analyze the effects of load profile to the system, and then δ was considered a variable of the function y as described in the previous section to show the competitive effects between the necessity of maximizing the extra profit of REC and the necessity of sharing energy efficiently. Fig. 4 shows the combined effect of the number of prosumers and δ on the optimum of shared energy. Results show that when δ increases, the surplus of energy decreases, and the optimal configuration is found with a lower number of consumers, which means a higher number of prosumers (Nt=Np+Nc=100). Vice versa, if δ decreases, the number of prosumers should decrease too due to a higher extra PV power. The number of consumers should increase. About shared energy there is a competitive effect, because if δ increases too much the maximum value of shared energy decreases with it, due to the lower surplus of energy, but if δ decreases too much, than then the total power installed for the REC decreases, because of the lower number of prosumers required to optimize the REC and then again, we have a lack of extra energy from prosumers.

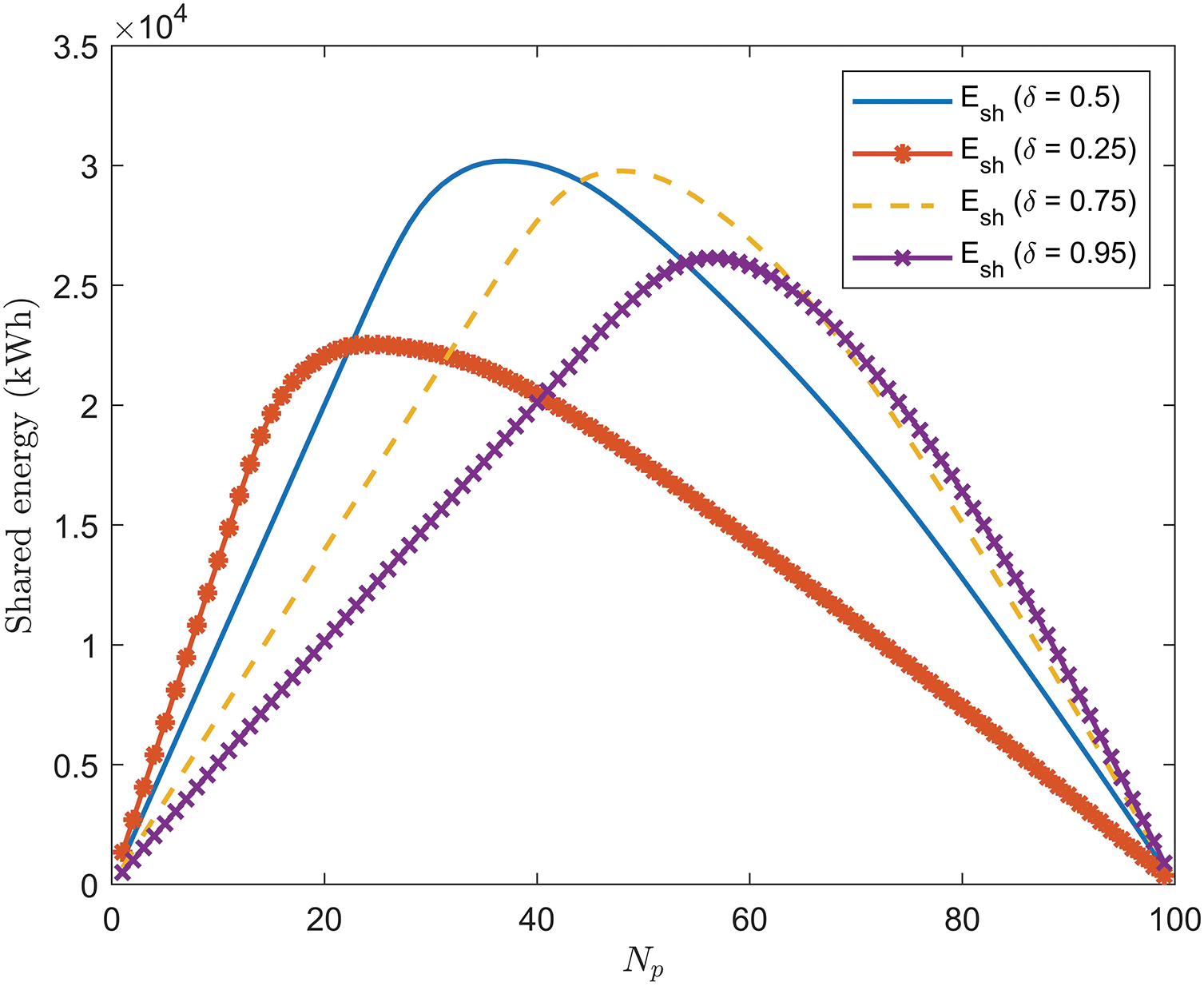
Figure 4: Shared energy in a REC at different values of δ and with Pn,i=1.25 kWp

According to this analysis, for each δ value exists an optimal distribution of consumers and prosumers, but among these maximum values, there is a combination of δ(δ¯=0.6) and users’ distribution that maximizes the shared energy, as shown in Fig. 5.

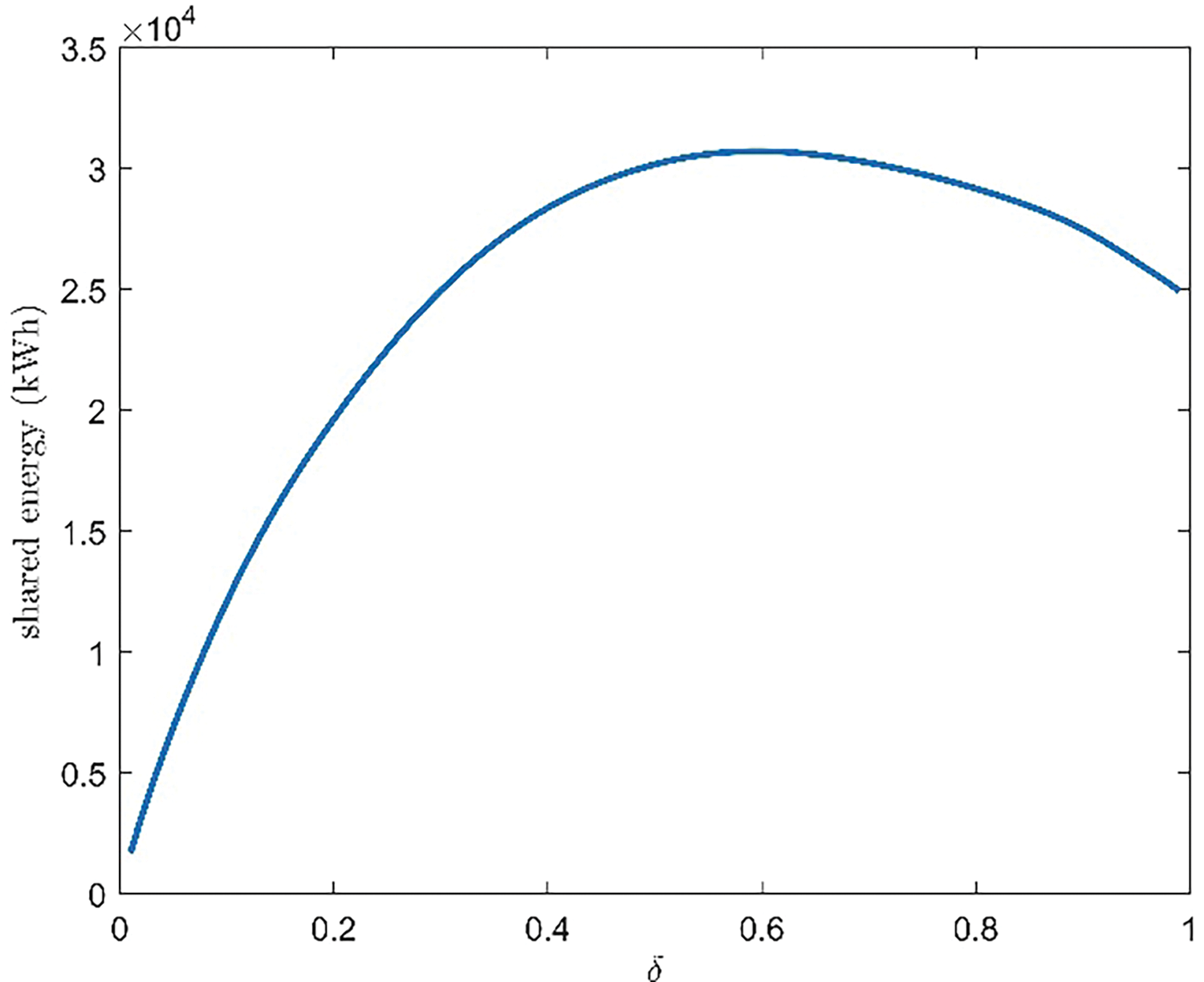
Figure 5: Variation of shared energy in a REC with Pn,i=1.25 kWp, as a function of δ

The value of δ¯=0.94 which maximize η is different from the value of δ¯=0.6 which maximize Esh as shown in Fig. 6.

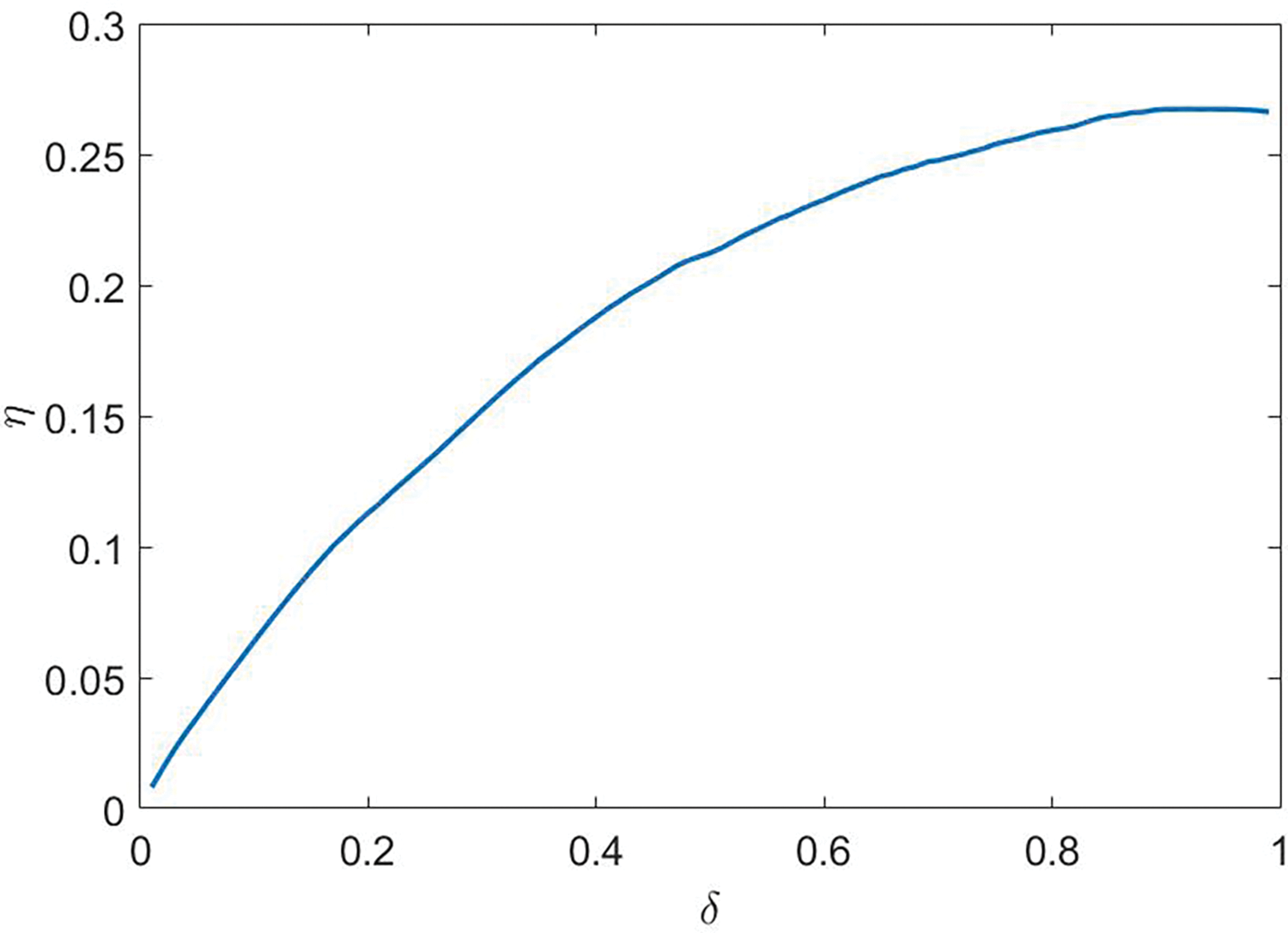
Figure 6: Variation of η, in a REC with Pn,i=1.25kWp, as a function of δ

Results show that there is an optimal value of δ, to reach a good compromise between extra profit and efficiency. Numerical simulations have been performed by considering the complete model in which y depends both on Np,δ. The results of the simulations are shown in Table 2, and the optimal configuration has been represented in Fig. 7, in which Np = 45 and Nc = 55.

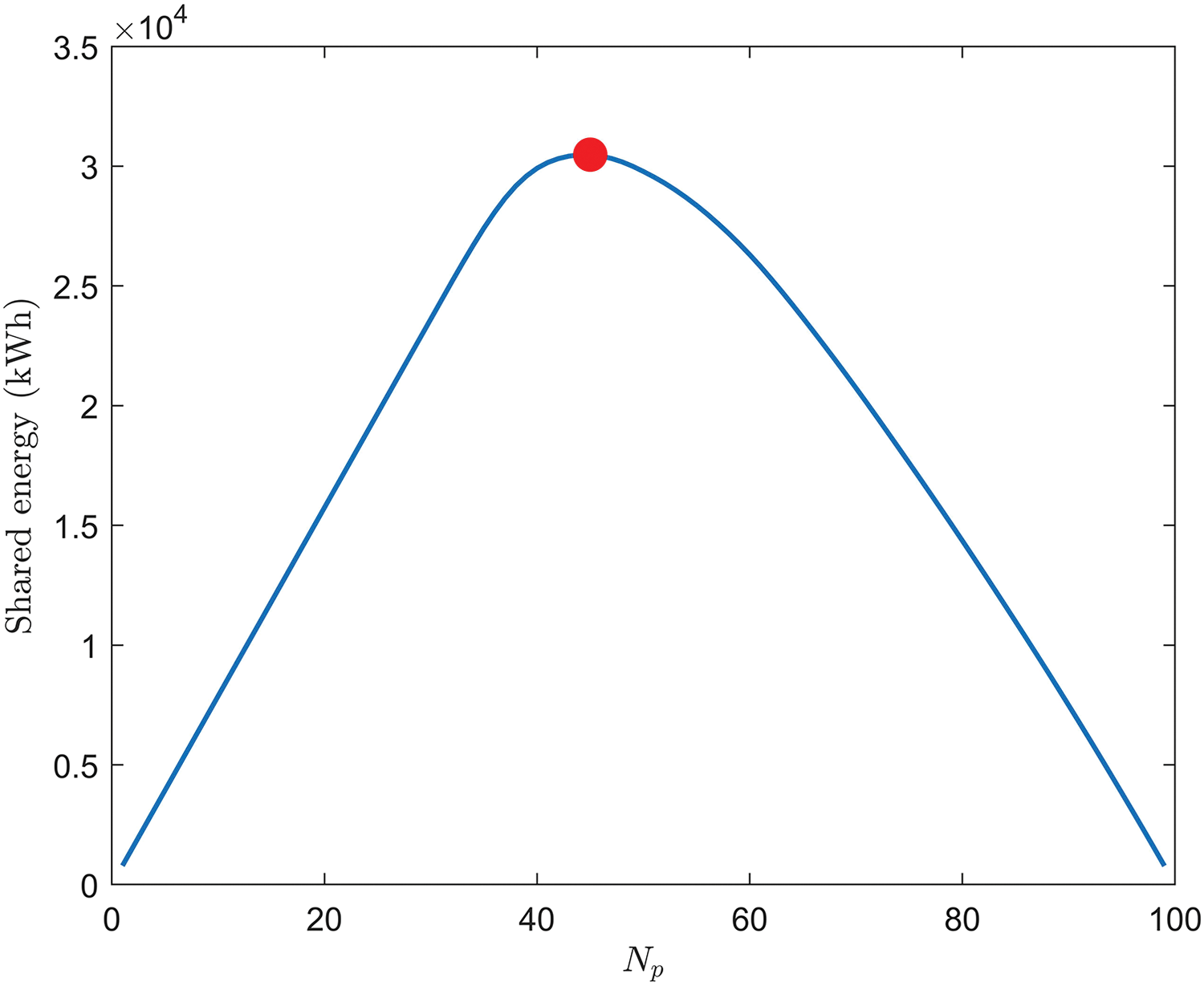
Figure 7: Optimal REC plot

From Table 2, it is shown that, maximizing y allows to share the 99.24% of Esh=30,713 kWh with an efficiency η=0.246. It is important to remember that the maximum efficiency, which is almost equal to 0.25, could be obtained if δ is equal to 0.94, so this kind of optimization gives a good compromise between maximum efficiency and maximum sharing.

As the optimal design of the REC is established, it is important to perform the financial analysis for this optimal case, in which each prosumer of the REC has his plant of 1.25 kWp (total capacity of 56.2 kWp by considering 45 prosumers as the best configuration). From the economic or financial analysis, it is computed that the Net present value (NPV) considering the lifetime of 20 years is equal to 2539€ in the case of REC. If the same participants do not want to join the REC, the NPV is computed as 2347€. The calculated payback period is equal to 7 years in the case of REC and 8 years without REC. So, it is convenient and better for the owner of the plant to be part of a REC as they can take benefits being part of REC.

Some results obtained with different δ values are reported. If for the same REC, the load profile is characterized by a higher value of δ (e.g., if δ = 0.9), the NPV increases in both cases, 3115€ with REC and 3013€ without REC, and the variation of NPV (ΔNPV) is equal to 101€ lower than 192€ obtained in the optimal case. Obviously if δ decreases NPV and ΔProfit decrease, so it is less convenient to create this kind of REC.

To highlight the importance of finding the optimal configuration, energy flows and shared energy for a random day from the spring season are shown for an REC with δ¯=0.6 and 1.25 kWp per prosumer as the size of the plant. In Fig. 8, it is shown that if there are few prosumers (Np = 15), there is not enough surplus of power to share with the community. If the number of prosumers is higher (Np = 90), as shown in Fig. 9, there is not enough consumers’ load for sharing the whole surplus of energy. However, in the case of the optimized REC, as shown in Fig. 10, with 45 prosumers and 55 consumers, it is well balanced by the load and energy sharing.

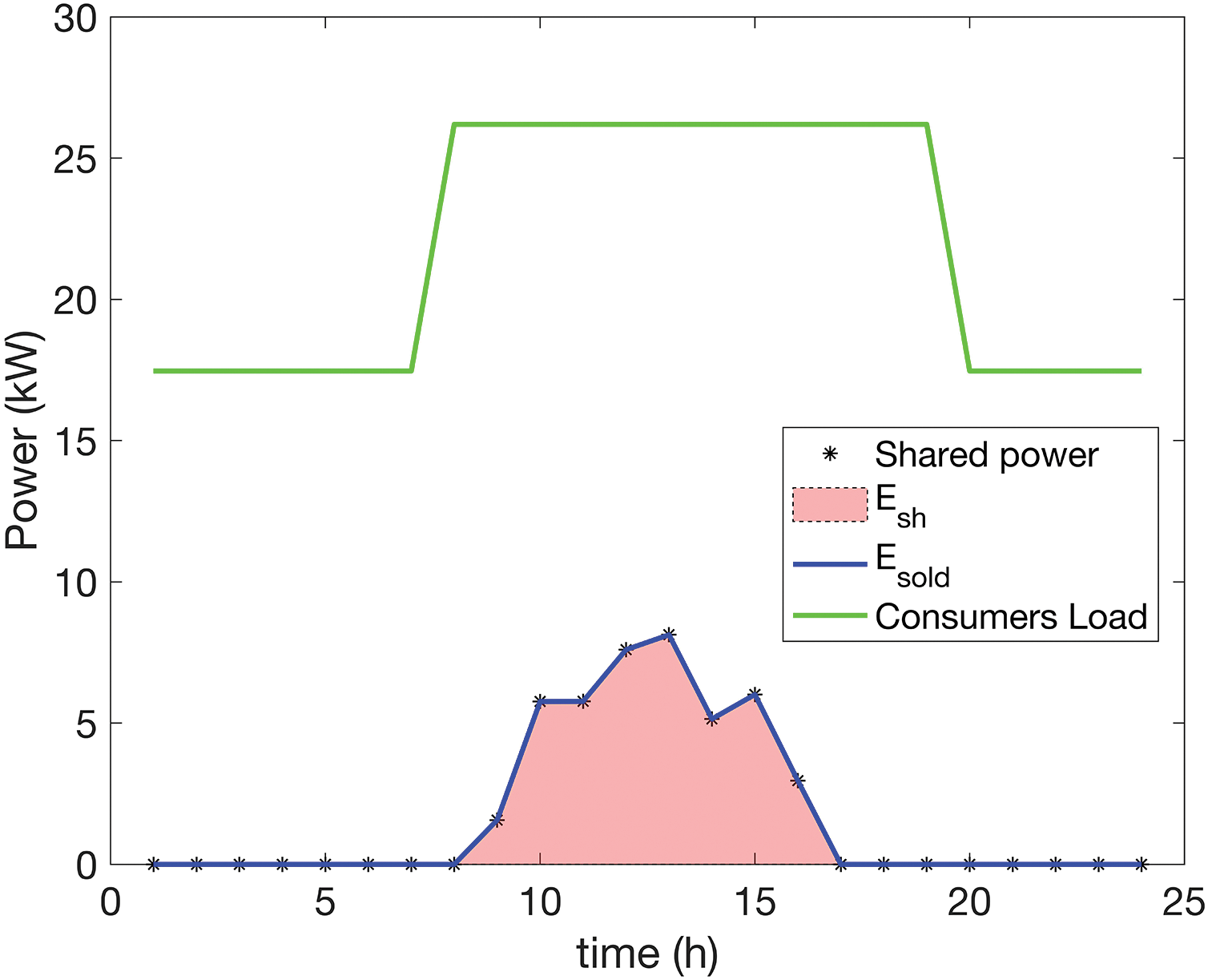
Figure 8: REC with 15 prosumers and 75 consumers

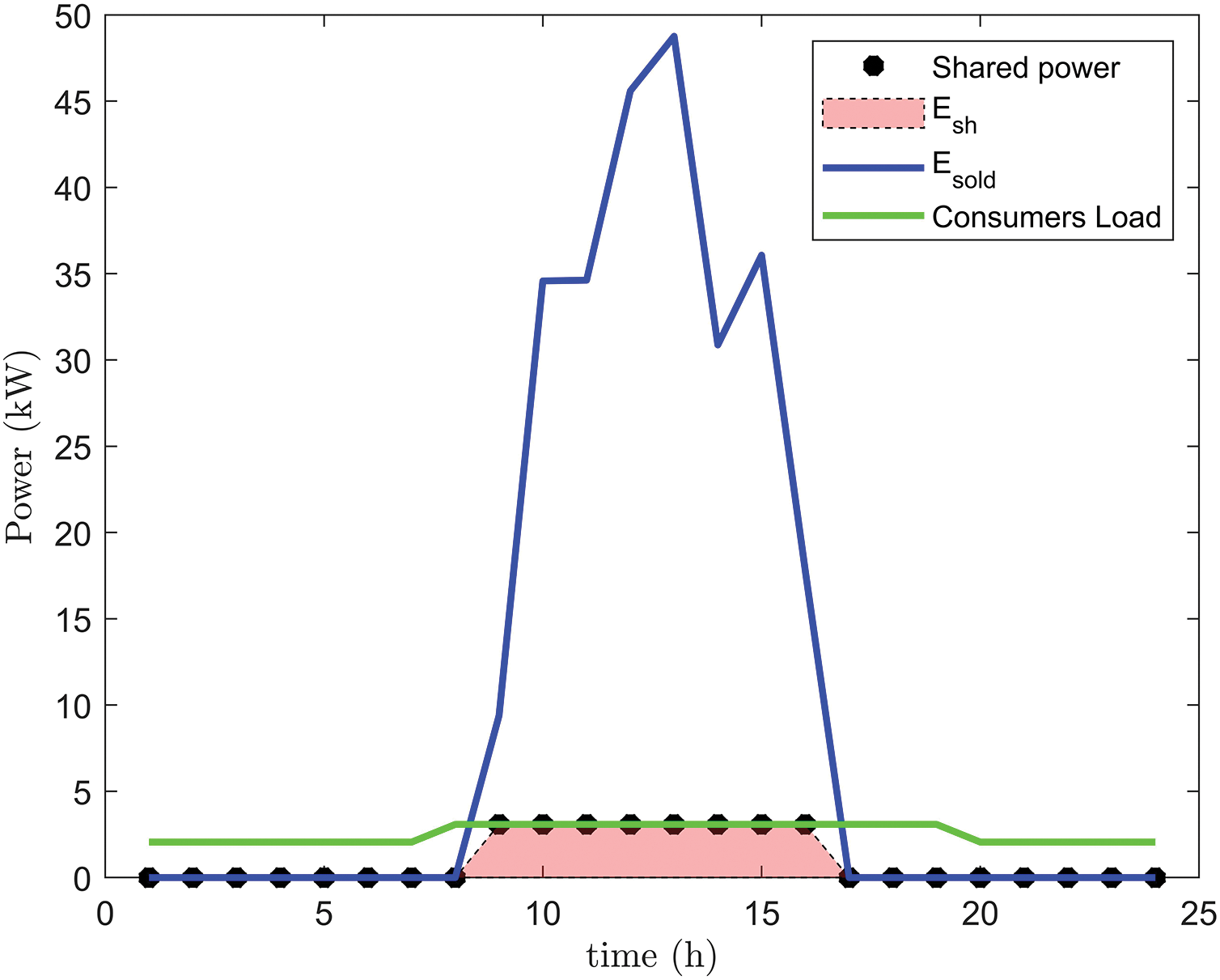
Figure 9: REC with 90 prosumers and 10 consumers

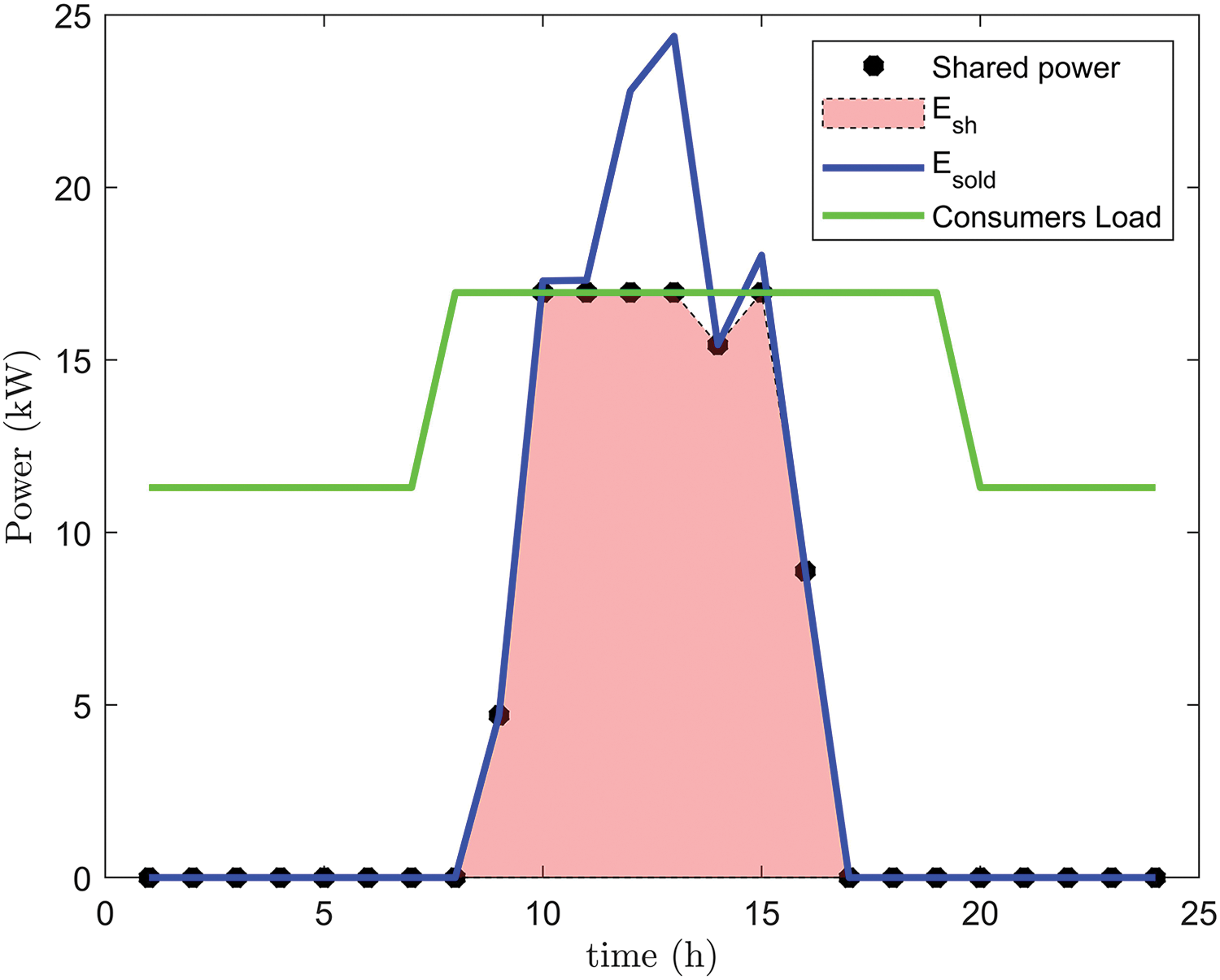
Figure 10: Optimal REC with 45 prosumers and 55 consumers

Finally, the effects of the variation of prosumers’ size of the plant have been considered to check if an optimal REC configuration exists as a function of Pn. By applying the optimization model, it was possible to calculate the size of the plant with the maximum NPV, as shown in Fig. 11. The optimal power is equal to 3 kWp for each user if a REC is established, while it is equal to 2 kWp without a REC. Those results confirm quantitatively that financial incentives do not allow the realization of an enormous PV plant if there are not enough prosumers’ yearly energy demand and self-consumed energy. Indeed, by increasing the size of the plant, shared energy increases, but at the same time, the costs of the plant become higher. Due to those two competitive contributions, the profit reaches a maximum configuration for an optimal size, which in this case study equals 3 kWp (Fig. 11).

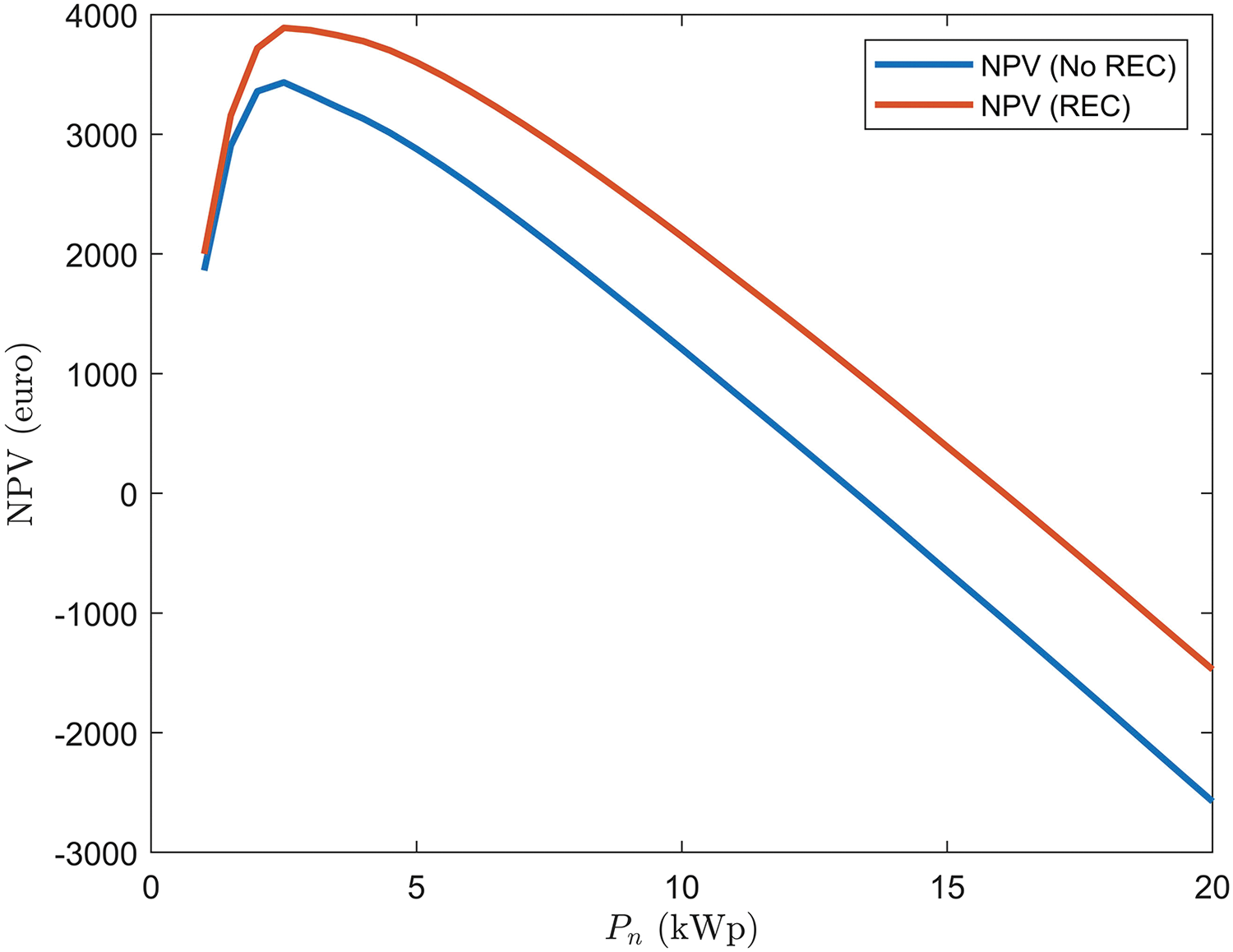
Figure 11: Results of financial analysis on REC with different sizes of the plant

If the size of the plant changes, by applying the optimization model, the optimal distribution of prosumers and consumers and the optimal value of δ change. The results are presented in Table 3 and Fig. 12 for further analysis.

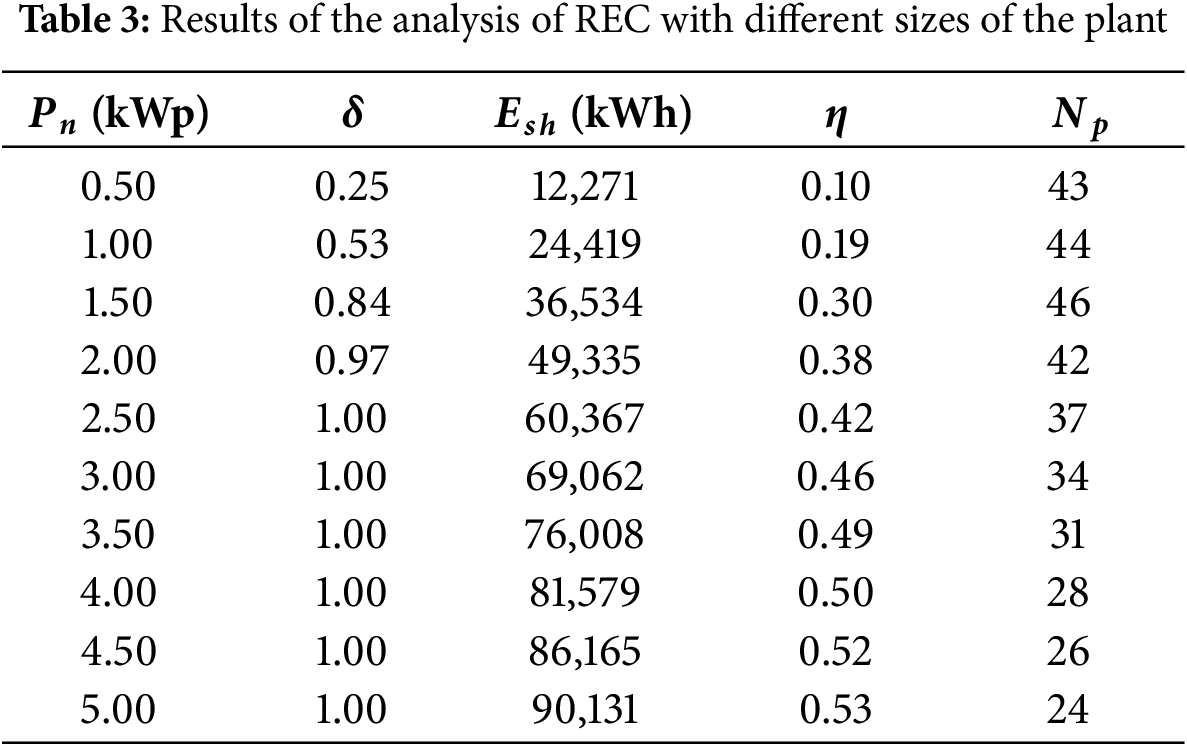
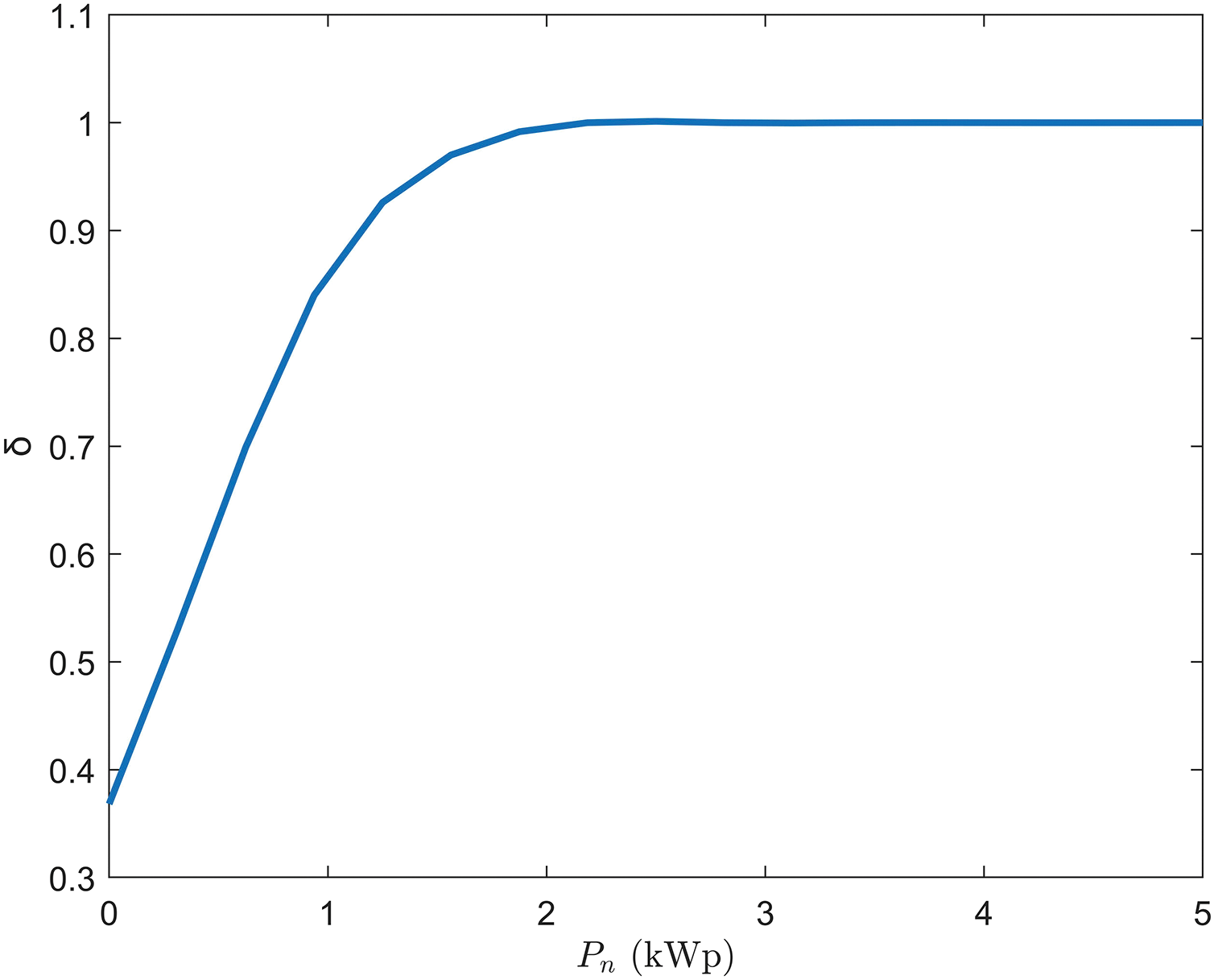
Figure 12: δ as a function of Pn

As shown in Table 3 and Fig. 12, it is not clear that the best REC users are those with δ=1. In the case of prosumers with a low size of the plant (Pn < 2.5), it is convenient to have δ<1, because otherwise, there would not be enough surplus energy to share with the community. while if Pn > 2.5, the plant is over-sized, so even if δ=1 and the prosumers self-consume all the energy that they can, there would be in any case a surplus of energy to be shared with the REC, which generates extra profit.

4  Conclusion and Future Work

Because of numerous benefits like social, economic, and environmental, RECs under the RED II guideline are becoming more popular in Europe. Numerous stakeholders, researchers, businesses, individuals, and public administration have been involved in this topic. Since citizen-owned production units have become more prevalent, RECs are governed by citizens, which include local RES generation, like solar, wind, biogas, and hydro. In RECs, self-consumption, sold, and shared energy are noteworthy because they offer individuals incentives and earnings. In this context, our work is focused on a mathematical model following the optimization for a REC based on load profile and user distribution in terms of the number of consumers and prosumers, by switching their role from consumer to prosumer or by changing their consumption profiles. The target of this model is to find the right compromise between two competitive effects: the need to share the maximum energy surplus given by prosumers to the community and the need to do that efficiently. Efficiency is important because with a large number of consumers, it would be possible to share the same amount of energy, but economically, it would be less convenient than in the case of fewer consumers. In the case of the closed community (the number of participants is constant) low value of efficiency means that REC’s plant is badly dimensioned because a greater size of the plant would be necessary to satisfy consumers’ needs or it could mean that there are unnecessary consumers in the community, that take money without a corresponding increase of shared energy.

The design and administration of a REC may benefit from this work, and it may also be beneficial in assessing the role shift from consumer to prosumer or vice versa or a change in user behavior regarding load profiles. Moreover, the findings of this work show that financial incentives as per the Italian framework do not allow to realize enormous PV plants if there is not enough prosumer yearly energy demand and self-consumption of energy, in fact by increasing the size of the plant energy shared increases, but so does the cost of the plant. Due to those two competitive effects, the optimal profit can be calculated as a function of PV size. Moreover, this model could be extended to consider different classes of participants based on plant size and energy demand. Class distribution could give a more detailed analysis of information to be adopted in the design optimization of a REC and a more realistic simulation of a REC. Finally, the role of the storage could be included to investigate the possible benefits in financial and technical aspects. Finally, forecasting models for solar PV and users’ electric load data should be considered to overcome the uncertainties using statistical data based on previous measurements.

Acknowledgement: All the authors thank RSE for the load data used in this work. Dr. Shoaib Ahmed also thanks the University of Salerno and the National Photovoltaic PhD program in Italy.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Antonio Sassone: Methodology, conceptualization, writing, and original draft preparation. Shoaib Ahmed: Drafting and reviewing critically the work for important intellectual content and data curation. Alessandro Ciocia: Improvements of simulations, interpretation of data, and critical review of the work for important intellectual content. Gabriele Malgaroli: Improvements of simulations, interpretation of data, and critical review of the work for important intellectual content. Antonio D’Angola: Methodology, conceptualization, and supervision. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study is available within the article.

Ethics Approval: Ethical approval was not required for this study as this is simulation-based work.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Nomenclature

References

1. Materi S, D’Angola A, Enescu D, Renna P. Reducing energy costs and CO2 emissions by production system energy flexibility through the integration of renewable energy. Prod Eng. 2021;15(5):667–81. doi:10.1007/s11740-021-01051-5. [Google Scholar] [CrossRef]

2. D’Agostino D, Mazzella S, Minelli F, Minichiello F. Obtaining the NZEB target by using photovoltaic systems on the roof for multi-storey buildings. Energy Build. 2022;267:112147. doi:10.1016/j.enbuild.2022.112147. [Google Scholar] [CrossRef]

3. Shaikh S, Katyara S, Majeed A, Khand ZH, Staszewski L, Shah M, et al. Holistic and scientific perspectives of energy sector in Pakistan: progression, challenges and opportunities. IEEE Access. 2020;8:227232–46. doi:10.1109/ACCESS.2020.3046310. [Google Scholar] [CrossRef]

4. Majeed Shaikh A, Fawad Shaikh M, Ahmed Shaikh S, Krichen M, Ali Rahimoon R, Qadir A. Comparative analysis of different MPPT techniques using boost converter for photovoltaic systems under dynamic shading conditions. Sustain Energy Technol Assess. 2023;57:103259. doi:10.1016/j.seta.2023.103259. [Google Scholar] [CrossRef]

5. Alstone P, Gershenson D, Kammen DM. Decentralized energy systems for clean electricity access. Nature Clim Change. 2015;5(4):305–14. doi:10.1038/nclimate2512. [Google Scholar] [CrossRef]

6. Liu WH, Alwi SRW, Hashim H, Muis ZA, Klemeš JJ, Rozali NEM, et al. Optimal design and sizing of integrated centralized and decentralized energy systems. Energy Proc. 2017;105:3733–40. doi:10.1016/j.egypro.2017.03.866. [Google Scholar] [CrossRef]

7. Ahmed S, Ali A, Ciocia A, D’Angola A. Technological elements behind the renewable energy community: current status, existing gap, necessity, and future perspective—overview. Energies. 2024;17(13):3100. doi:10.3390/en17133100. [Google Scholar] [CrossRef]

8. Minelli F, Ciriello I, Minichiello F, D’Agostino D. From net zero energy buildings to an energy sharing model—the role of NZEBs in renewable energy communities. Renew Energy. 2024;223:120110. doi:10.1016/j.renene.2024.120110. [Google Scholar] [CrossRef]

9. Mihailova D, Schubert I, Burger P, Fritz MMC. Exploring modes of sustainable value co-creation in renewable energy communities. J Clean Prod. 2022;330:129917. doi:10.1016/j.jclepro.2021.129917. [Google Scholar] [CrossRef]

10. Ahmed S, Ali A, D’Angola A. A review of renewable energy communities: concepts, scope, progress, challenges, and recommendations. Sustainability. 2024;16(5):1749. doi:10.3390/su16051749. [Google Scholar] [CrossRef]

11. Tostado-Véliz M, Rezaee Jordehi A, Icaza D, Mansouri SA, Jurado F. Optimal participation of prosumers in energy communities through a novel stochastic-robust day-ahead scheduling model. Int J Electr Power Energy Syst. 2023;147:108854. doi:10.1016/j.ijepes.2022.108854. [Google Scholar] [CrossRef]

12. Faria J, Marques C, Pombo J, Mariano S, do Rosário Calado M. Optimal sizing of renewable energy communities: a multiple swarms multi-objective particle swarm optimization approach. Energies. 2023;16(21):7227. doi:10.3390/en16217227. [Google Scholar] [CrossRef]

13. Sousa J, Lagarto J, Camus C, Viveiros C, Barata F, Silva P, et al. Renewable energy communities optimal design supported by an optimization model for investment in PV/wind capacity and renewable electricity sharing. Energy. 2023;283:128464. doi:10.1016/j.energy.2023.128464. [Google Scholar] [CrossRef]

14. Lazzari F, Mor G, Cipriano J, Solsona F, Chemisana D, Guericke D. Optimizing planning and operation of renewable energy communities with genetic algorithms. Appl Energy. 2023;338:120906. doi:10.1016/j.apenergy.2023.120906. [Google Scholar] [CrossRef]

15. Cutore E, Volpe R, Sgroi R, Fichera A. Energy management and sustainability assessment of renewable energy communities: the Italian context. Energy Convers Manage. 2023;278:116713. doi:10.1016/j.enconman.2023.116713. [Google Scholar] [CrossRef]

16. Ceglia F, Esposito P, Faraudello A, Marrasso E, Rossi P, Sasso M. An energy, environmental, management and economic analysis of energy efficient system towards renewable energy community: the case study of multi-purpose energy community. J Clean Prod. 2022;369:133269. doi:10.1016/j.jclepro.2022.133269. [Google Scholar] [CrossRef]

17. Gallego-Castillo C, Heleno M, Victoria M. Self-consumption for energy communities in Spain: a regional analysis under the new legal framework. Energy Policy. 2021;150:112144. doi:10.1016/j.enpol.2021.112144. [Google Scholar] [CrossRef]

18. Casalicchio V, Manzolini G, Prina MG, Moser D. From investment optimization to fair benefit distribution in renewable energy community modelling. Appl Energy. 2022;310:118447. doi:10.1016/j.apenergy.2021.118447. [Google Scholar] [CrossRef]

19. Belmar F, Baptista P, Neves D. Modelling renewable energy communities: assessing the impact of different configurations, technologies and types of participants. Energy Sustain Soc. 2023;13(1):18. doi:10.1186/s13705-023-00397-1. [Google Scholar] [CrossRef]

20. Alam SE, Shukla D. Optimal regulation of prosumers and consumers in smart energy communities. In: 2022 IEEE International Smart Cities Conference (ISC2); 2022 Sep 26–29; Pafos, Cyprus. p. 1–7. doi:10.1109/ISC255366.2022.9921890. [Google Scholar] [CrossRef]

21. Sassone A, Ahmed S, D’Angola A. A profit optimization model for renewable energy communities based on the distribution of participants. In: 2024 IEEE International Conference on Environment and Electrical Engineering and 2024 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe); 2024 Jun 17–20; Rome, Italy. p. 1–6. doi:10.1109/EEEIC/ICPSEurope61470.2024.10751093. [Google Scholar] [CrossRef]

22. Byrd RH, Gilbert JC, Nocedal J. A trust region method based on interior point techniques for nonlinear programming. Math Program. 2000;89(1):149–85. doi:10.1007/PL00011391. [Google Scholar] [CrossRef]

23. D’Agostino D, De Falco F, Minelli F, Minichiello F. New robust multi-criteria decision-making framework for thermal insulation of buildings under conflicting stakeholder interests. Appl Energy. 2024;376:124262. doi:10.1016/j.apenergy.2024.124262. [Google Scholar] [CrossRef]

24. D’Angola A, Zaffina R, Enescu D, Di Leo P, Fracastoro GV, Spertino F. Best compromise of net power gain in a cooled photovoltaic system. In: 2016 51st International Universities Power Engineering Conference (UPEC); 2016 Sep 6–9; Coimbra, Portugal. p. 1–6. doi:10.1109/UPEC.2016.8114086. [Google Scholar] [CrossRef]

25. Regole Operative CER. GSE; 2024. [Internet]. [cited 2025 Mar 17]. Available from: https://www.mase.gov.it/sites/default/files/ALLEGATO%201%20Regole%20operative%20CACER%20def.pdf. [Google Scholar]

26. Energy: MASE CER Decree. Ministry of the Environment and Energy Security; 2024. [Internet]. [cited 2025 Mar 17]. Available from: https://www.mase.gov.it/sites/default/files/DD_22_2024.pdf. [Google Scholar]

27. Chaudhry S, Surmann A, Kühnbach M, Pierie F. Renewable energy communities as modes of collective prosumership: a multi-disciplinary assessment part II—case study. Energies. 2022;15(23):8936. doi:10.3390/en15238936. [Google Scholar] [CrossRef]

28. Trevisan R, Ghiani E, Ruggeri S, Mocci S, De Tuglie E, Pilo F. Techno-economic analysis of port renewable energy communities. In: 2022 IEEE 21st Mediterranean Electrotechnical Conference (MELECON); 2022 Jun 14–16; Palermo, Italy. p. 1061–6. doi:10.1109/MELECON53508.2022.9843022. [Google Scholar] [CrossRef]

29. Cirone D, Bruno R, Bevilacqua P, Perrella S, Arcuri N. Techno-economic analysis of an energy community based on PV and electric storage systems in a small mountain locality of south Italy: a case study. Sustainability. 2022;14(21):13877. doi:10.3390/su142113877. [Google Scholar] [CrossRef]