 Open Access
Open Access
ARTICLE
Development of Micro Hydropower Systems in Amazonia Using Multiple Axial-Flow Turbines
1 Laboratory of Fluid Dynamics and Particulate, Federal University of Pará, Tucuruí, 68455-901, Brazil
2 School of Environmental and Sanitary Engineering, Federal University of Pará, Belém, 66075-110, Brazil
* Corresponding Author: André L. Amarante Mesquita. Email:
(This article belongs to the Special Issue: Selected Papers from the SDEWES 2024 Conference on Sustainable Development of Energy, Water and Environment Systems)
Energy Engineering 2025, 122(6), 2197-2213. https://doi.org/10.32604/ee.2025.064196
Received 08 February 2025; Accepted 23 April 2025; Issue published 29 May 2025
Abstract
Despite significant Brazilian social programs to expand energy access, approximately one million people in rural Amazonia still lack electricity. Moreover, the existing rural electricity grid in the region is inadequate for supporting efficient small-scale production systems due to both the poor quality and high cost of supplied energy. In parallel, traditional wooden bridges in the Amazon have been progressively replaced by more durable concrete structures in recent years. In this context, this study explores the application of very low-head hydropower installations in the Amazon, focusing on integrating axial-flow turbines beneath small concrete bridges. The methodology involves analyzing flow duration curves and key hydraulic parameters upstream and downstream to design a micro-hydropower system comprising two or more units, thereby maximizing annual energy generation. Additionally, the study assesses the applicability of the minimum pressure coefficient criterion to improve the efficiency of very low-head turbines. This design criterion is first validated against an existing experimental study featuring a propeller turbine with a simple curved plate blade. The proposed methodology is then applied to a case study involving a small dam-bridge with a head variation from 1.4 to 2.4 m and a flow rate ranging from 0.23 to 0.92 m3/s. The optimal configuration achieves an energy output of 26.2 MWh/year with an efficiency of up to 86%.Graphic Abstract
Keywords
Brazil possesses a vast and diverse electrical grid; however, remote regions of the Amazon remain underserved, with approximately 990,000 people still lacking access to electricity. Of these, 32% reside in isolated communities that depend on polluting fossil fuel generators [1,2]. Government initiatives such as Mais Luz para a Amazônia (MLA) aim to achieve universal energy access [3]. Yet, progress is hindered by geographic barriers, weak municipal governance, and deteriorating infrastructure, most notably the collapse of wooden bridges essential for transportation and maintenance [4,5].
Paradoxically, Amazon’s extensive hydrographic network holds significant yet underutilized potential for decentralized hydropower, a key driver of economic growth and social equity [3,6,7]. Previous studies have demonstrated the feasibility of run-of-river (ROR) turbines in Amazonian microgrids [8,9] and globally [10], with recent advancements further confirming the viability of Very Low Head Turbines (VLHTs) for sites with heads below 3 meters [11]. However, existing designs often overlook integration with critical infrastructure, notably the transition from wooden to concrete bridges [12] and fail to address the region’s hydrological variability [13] adequately.
Furthermore, standardized design criteria for VLHTs operating at high specific speeds (Ns > 180) remain underdeveloped, as prior work by Sutikno et al. [14] focused solely on airfoil-shaped blade profiles at lower Ns ranges (Ns = 102). Additionally, while hydrological optimization frameworks exist for sizing micro hydropower plants [15], they neglect turbine design parameters, creating a disconnect between flow duration curves and blade geometry selection. Finally, critical for rural Amazonia, cost-effective manufacturing is hindered by reliance on complex aerodynamic profiles [16] rather than simplified geometries compatible with local machining capabilities.
These conditions apply to the rural community of Janarí, within the Janarí district, approximately 70 km from its headquarters in the municipality of Goianésia do Pará, southeastern Pará, Amazon region, as shown in Fig. 1. The Água Preta creek runs through the Janari community. In one section of the creek, there is a wooden bridge that connects the two banks. The bridge is located at the coordinates 4°08′23″S 49°25′44″W. This wooden bridge is used to enter and leave the community and is used by both people and cars and trucks transporting local agricultural produce. The area around the bridge is mainly used for small-scale agriculture and livestock farming. There are also some small areas of virgin forest, especially near the Água Preta stream and especially in indigenous reserves.


Figure 1: Location of the Janari community and the small river Água Preta: (a) Overview map of Brazil showing the location of Janari, indicated with a marker (image from Google Maps); (b) Closer view of the Janari area, as indicated in (a), showing local geographical context (image from Google Maps); (c) Aerial photograph of a small portion of the area shown in (b), taken by the research team, featuring a bridge crossing the Água Preta stream
As Quintas et al. [9] discussed, this type of turbine arrangement has a negligible environmental impact. A small dam should be built integrated with the bridge. However, the water level upstream should be raised very little, which leads to small flooding areas.
The design of VLHTs is grounded in classical turbomachinery principles, including velocity triangles and the Cordier diagram [17], complemented by modern computational tools such as Computational Fluid Dynamics (CFD). A fundamental aspect of this approach is the minimum pressure coefficient criterion (Cpmin), which ensures optimal performance by maintaining a critical threshold on the blade’s suction side [18]. This coefficient is determined by:
where p is the static pressure on the blade cascade surface, p0 is the reference pressure, and w is the relative flow velocity. The criterion defines a minimum value for this coefficient on the suction side of the blade at the hub section.
The Cpmin is the lowest pressure coefficient on an airfoil’s suction side, typically negative due to upstream static pressure (p0). It is an aerodynamic loading criterion to identify cascades with low-profile losses (Fig. 2). An optimal operating interval exists between two negative thresholds, Cpsi (pressure coefficient inferior limit) and Cpss (superior limit). If Cpmin > Cpss, friction losses increase due to larger flow-exposed surfaces, though boundary layer separation risks decrease. Conversely, Cpmin < Cpsi reduces the friction area but raises the separation risks from higher pressure loading. Thus, maintaining Cpsi < Cpmin < Cpss balances these trade-offs. This interval is best determined by testing purpose-designed turbomachines.

Figure 2: Minimum pressure coefficient criterion
Using this criterion, Muis et al. [13] achieved 90% efficiency in a 2-kW axial turbine with a 1.2 m head. Recent studies have further explored diverse optimization strategies, including Ebhota and Inambao’s development of a low-cost four-blade turbine [19], Soesanto et al.’s elimination of tangential flow components to enhance efficiency [20], and Shukla and Parashar’s CFD-driven design of a 58.48 kW propeller turbine [21]. However, significant gaps remain in adapting these methodologies to Amazon’s unique hydrological and logistical constraints, where seasonal rainfall-runoff dynamics [22] and fabrication limitations necessitate robust yet simplified geometries.
To address the dual challenges of manufacturability and efficiency in resource-limited settings, this study adopts circular arc cascades—a geometry validated by decades of empirical research [23]. Pioneering work by Ikui et al. [23] established fundamental performance curves for the profiles, while subsequent efforts by Tezuka et al. [24] and Fagbenro [25] quantified pressure distribution and geometric effects on aerodynamic behavior. Bian et al. [26] expanded this knowledge by analyzing leading and trailing edge modifications, and Balla and Vad János [27] derived empirical formulas for lift and drag coefficients, enabling cost-effective optimization.
The proposed methodology integrates an enhanced Cordier diagram [28] with CFD simulations (using k − ω SST and k − ε turbulence models) [14,29] to balance hydraulic efficiency with fabrication simplicity. Key advances include:
• Defining a Cpmin range for circular arc cascades at Ns > 180, enabling locally manufacturable blades to achieve higher hydraulic efficiency.
• A hybrid dam-bridge-turbine system that synergizes hydrological optimization with infrastructure upgrades, leveraging planned bridge projects to reduce deployment costs.
This methodology allows high hydraulic efficiency even with low-cost, simplified blade geometries, effectively balancing performance and manufacturability. However, the ultimate goal of the proposed Cpmin methodology is to provide a guide to the designer using specific rotor blades so that he does not need to perform the CFD calculation, with continuous development of the work.
This approach maintains high performance even with simplified geometries, effectively harmonizing technical and practical demands. While the Cpmin methodology ultimately aims to eliminate CFD dependence through designer guidelines, current validation relies on simulations and experimental data from a tubular propeller turbine [30]. Applied to the Água Preta River (head: 1.4–2.4 m; flow: 0.23–0.92 m3/s [12]), the system achieves 26.2 MWh/year with seasonal robustness.
By prioritizing geometries that simplify manufacturing without compromising performance—an approach previously demonstrated in Sub-Saharan Africa [19] and further optimized via genetic algorithms [20]—this study contributes to bridge the gap between theoretical advancements and practical implementation, offering a scalable model for sustainable hydropower in rural Amazonia.
This study outlines the design procedures for multiple high-efficiency, very low-head axial turbines tailored explicitly for operation in hydroelectric power plants (HPPs) integrated into concrete bridges over small rivers in rural Amazonia.
Fig. 3 presents an overview of the research stages, which are detailed in the following sections, to better clarify how the proposed methodology will work.

Figure 3: Stages of the proposed methodology
2.2 Key Curve Analysis of the Selected Site
Portilho et al. [12] conducted measurements of the Água Preta Creek through field inspections to characterize its hydraulic behavior. Their study revealed significant flow variability and an exceptionally low hydraulic head at the site, challenges that are critical for designing sustainable energy solutions in such environments.
The flow duration curves in Fig. 4 illustrate these findings. These measurements directly informed the turbine flow rate definition and operational range analyzed in this study, which is detailed in the following section. By integrating their site-specific hydraulic data, we established realistic boundary conditions for turbine performance evaluation, ensuring alignment with the creek’s unique hydrological characteristics.
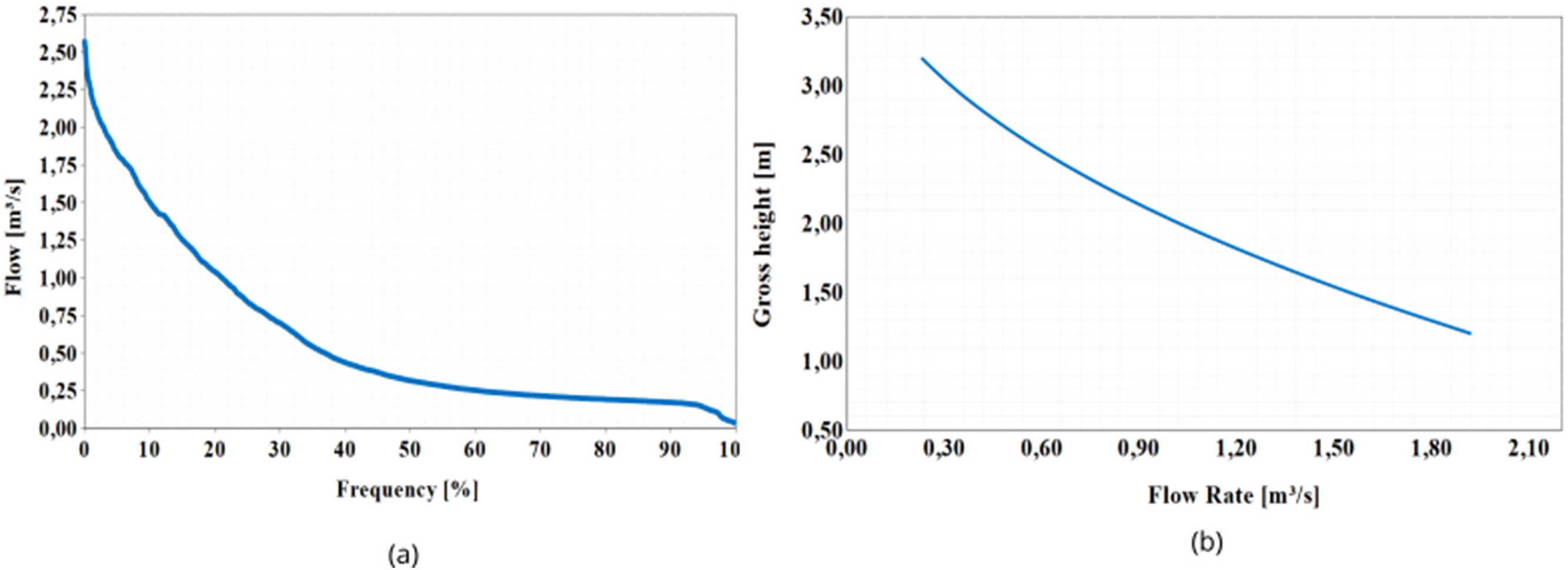
Figure 4: Hydrology of the small river Água Preta: (a) duration curve; (b) key curve
2.3 Definition of the Best Turbine Configuration
Considering the project site’s flow duration curve, the smaller turbine’s flow rate was set to Q95%, representing the flow rate exceeding 95% of the time. The flow rate for the larger turbine was determined based on the configuration that maximizes energy generation. Fig. 5 illustrates a schematic of two turbines operating in parallel, where Q1 (larger turbine), Q2 (smaller turbine), and Qt (total design flow) are defined, with Qt = Q1 + Q2. When the river flow exceeds the capacity of the smaller turbine (Q2) but remains below that of the larger turbine (Q1), the excess water is directed through the spillway. This approach, applied in the present study, aims to optimize the efficiency and sustainability of micro hydropower plants.
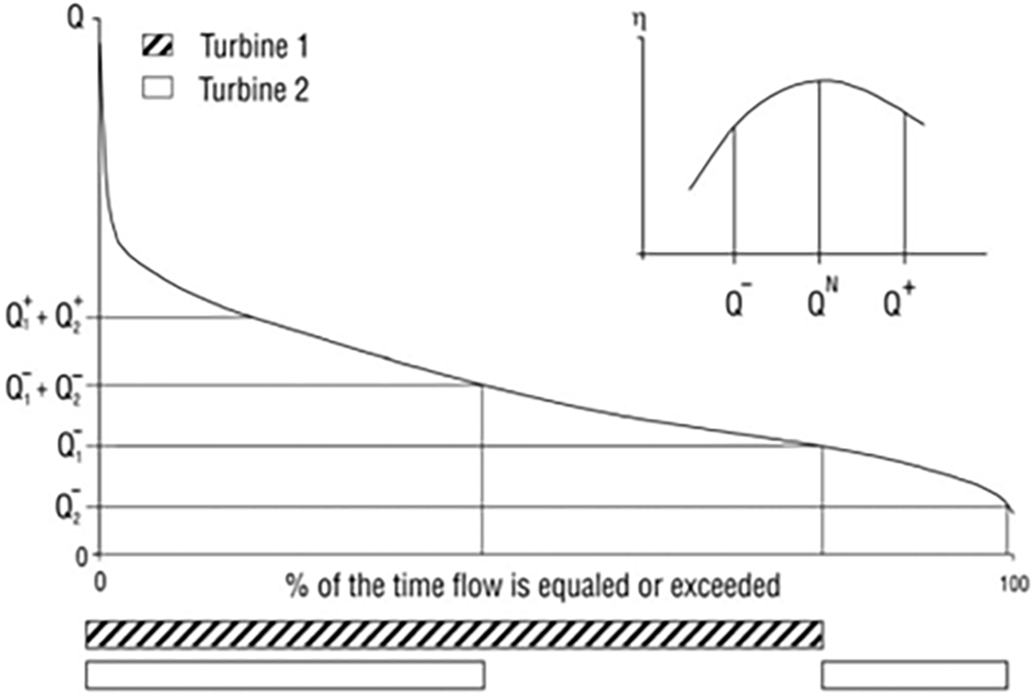
Figure 5: Operation scheme of the turbines. Adapted with permission from the reference [8]
An alternative to ultra-low-head axial turbines would be using pumps as turbines (PATs), given their lower installation costs when utilizing commercially available centrifugal pump components. However, PATs generally exhibit lower efficiency than ultra-low-head axial turbines, particularly in environments with significant seasonal flow variability and limited available energy. For low-head, high-flow-rate conditions, axial flow pumps (when repurposed as turbines) often operate far from their best efficiency point (BEP), requiring oversized or custom-designed units that significantly increase costs. This efficiency gap becomes even more pronounced under fluctuating hydrological conditions. Consequently, investing in developing site-specific turbines optimized for low-head, high-flow regimes, which balance hydraulic performance and fabrication simplicity, is a more advantageous approach. This strategy avoids the cost penalties of retrofitting pumps for off-design conditions while ensuring sustained efficiency across seasonal variations, as adopted in this study.
2.4 Turbine Design Using Cordier and Cpmin Criteria
The methodology for designing very low-head axial turbines was developed to maximize energy efficiency while minimizing implementation costs. The proposed approach integrates semi-empirical diagrams, computational simulations, and technical feasibility analyses. For the primary geometric parameters of the rotor, the Cordier diagram [28] was utilized to optimize the specific speed (Nq) and rotor diameter, ensuring compatibility with ultra-low-head conditions. This methodology was further refined using the empirical diagrams of Menny [31] and the correlations proposed by Quaranta [32] to determine the optimal rotational speed and define key parameters such as the number of blades and the hub-to-tip ratio.
The Cpmin represents the lowest pressure on the suction side at the blade’s hub section and is a critical parameter for assessing aerodynamic loading [14,18]. By incorporating both hydrodynamic and geometric factors, Cpmin provides a more comprehensive criterion than the lift coefficient. Cruz et al. [18] recommend a Cpmin range of −0.8 to −0.4, while Sutikno and Adam [14] suggests a range between −2.25 and −1.25 for designing blade cascades, particularly in sections near the rotor hub.
To validate the CFD methodology used in evaluating the performance of the selected turbines, experimental data from a tubular axial turbine (Fig. 6) with varying speed and flow conditions were utilized. The simulations were conducted using ANSYS CFX software within a single-phase model.
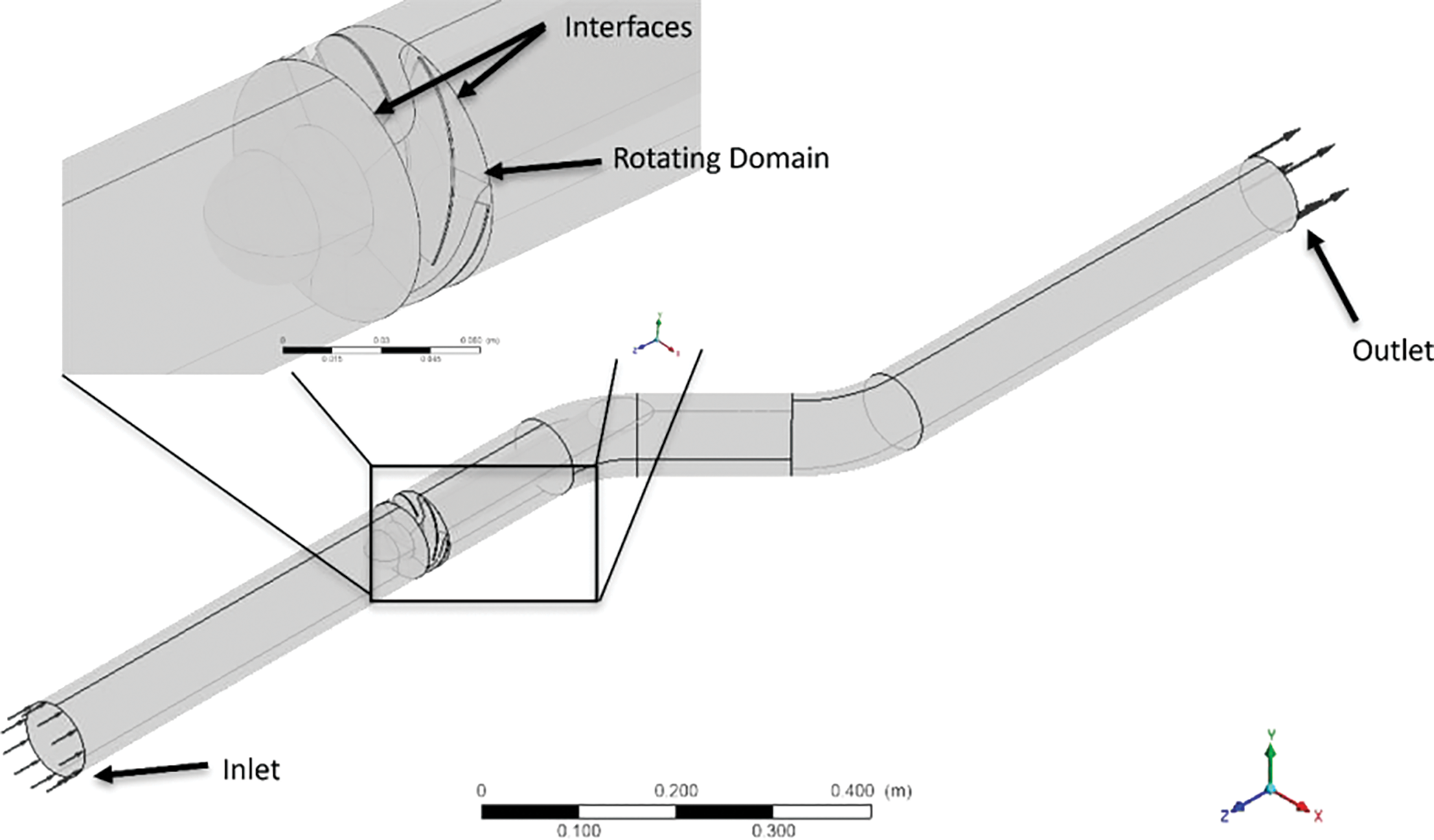
Figure 6: Turbine used for the validation of the CFD model
By employing three-dimensional viscous Navier-Stokes solvers, researchers can analyze complex flow separation patterns, identify sources of energy loss, and map loss distributions across components under design and off-design conditions. These methods rely on solving the continuity equation (Eq. (2)) and the Reynolds-Averaged Navier-Stokes (RANS) equations (Eq. (3)) to resolve critical flow characteristics. For incompressible flows with constant density, the continuity equation simplifies to:
where u is the velocity vector. The RANS equations, governing momentum conservation, are expressed as:
The numerical analysis employed the Shear Stress Transport (SST) k − ω turbulence model, a hybrid approach that combines the near-wall robustness of the k − ω model with the free-stream accuracy of k − ε. This model is particularly well-suited for capturing flow separation and adverse pressure gradients—key phenomena in low-head turbine operation, where boundary layer dynamics play a critical role in performance [33].
To enhance the accuracy of near-wall turbulence resolution, the computational mesh was refined in the boundary layer region, with the first-layer thickness calibrated to maintain a dimensionless wall distance (y+) ≤1 across all blade surfaces. A controlled expansion factor of 1.05 was also applied to adjacent layers, ensuring a smooth growth of prismatic elements while preserving gradient accuracy for the SST k − ω equations. A mesh independence study was performed (Fig. 7) to ensure the reliability of the numerical simulations.

Figure 7: Mesh independence study
Four mesh configurations, ranging from 3.4 to 5.6 million elements, were evaluated by monitoring key performance parameters: hydraulic efficiency (η) and head (H). The selected mesh, consisting of 4.1 million elements, exhibited less than 2% variations in η and H compared to the finest grid, meeting the Grid Convergence Index (GCI) criterion. Fig. 8 presents the hexahedral mesh for the cylindrical hub section, where localized refinement was applied to capture secondary flow structures and tip leakage effects accurately.

Figure 8: Mesh on the hub section of the rotor
The simulations employed a pressure-based transient solver with second-order spatial discretization to enhance numerical accuracy. The boundary conditions were defined as follows:
- Inlet: Mass flow rate ranging from 0.004 to 0.010 m3/s, with a turbulence intensity of 5%.
- Outlet: Static pressure set to atmospheric, with backflow stabilization enabled.
- Rotating Domain: A Moving Reference Frame (MRF) approach was applied to the turbine rotor, with angular velocities varying between 750 and 1500 RPM to cover the operational range. The interface between stationary and rotating domains utilized a frozen rotor approximation, which has been validated for steady-state performance prediction in turbomachinery.
3.1 Turbine Configuration and Flow Rate Specification
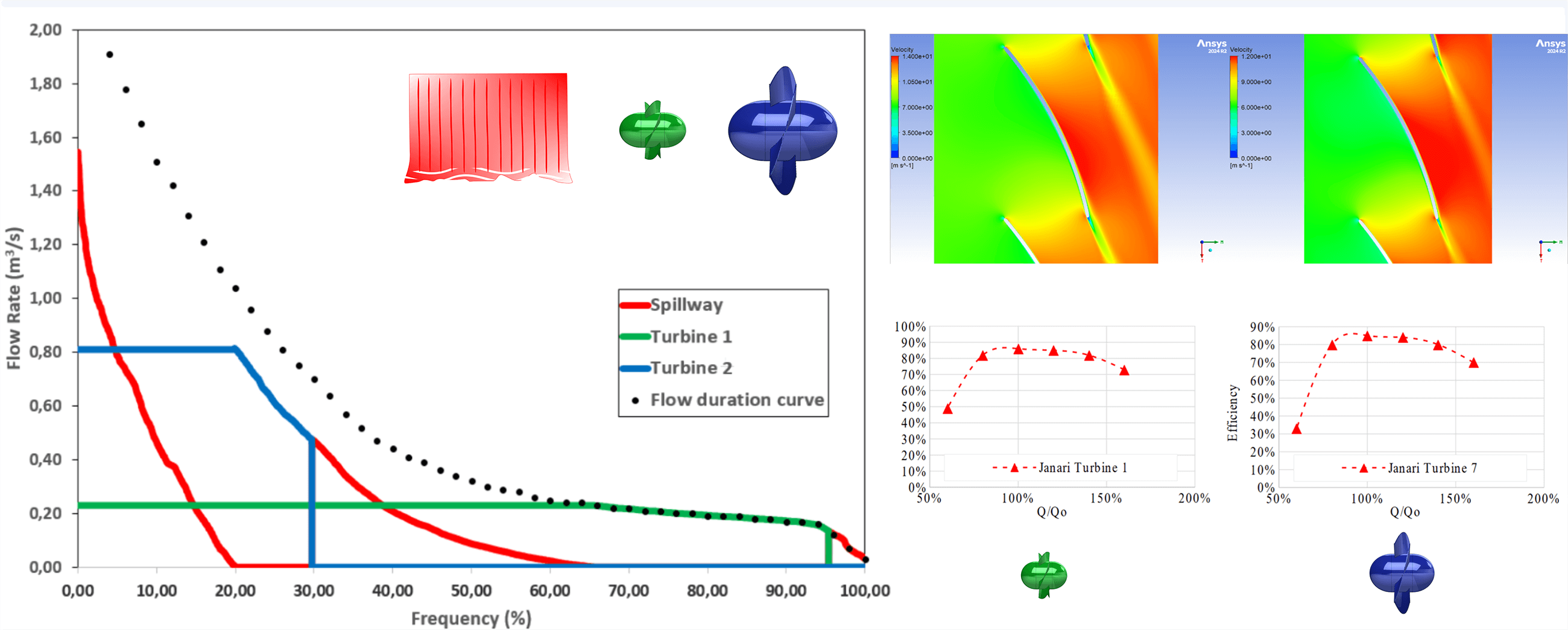
Eight potential turbine configurations were evaluated for their operational viability under the site’s hydraulic conditions based on an analysis of the key stream curves. Configurations 1 and 7 emerged as the most suitable options, selected for their alignment with the flow variability and energy generation criteria outlined in Table 1. The annual utilization rates for the selected configuration, illustrated in Fig. 9, further validate this selection, demonstrating how setups 1 and 7 optimize energy output while accommodating the site’s hydrological constraints.
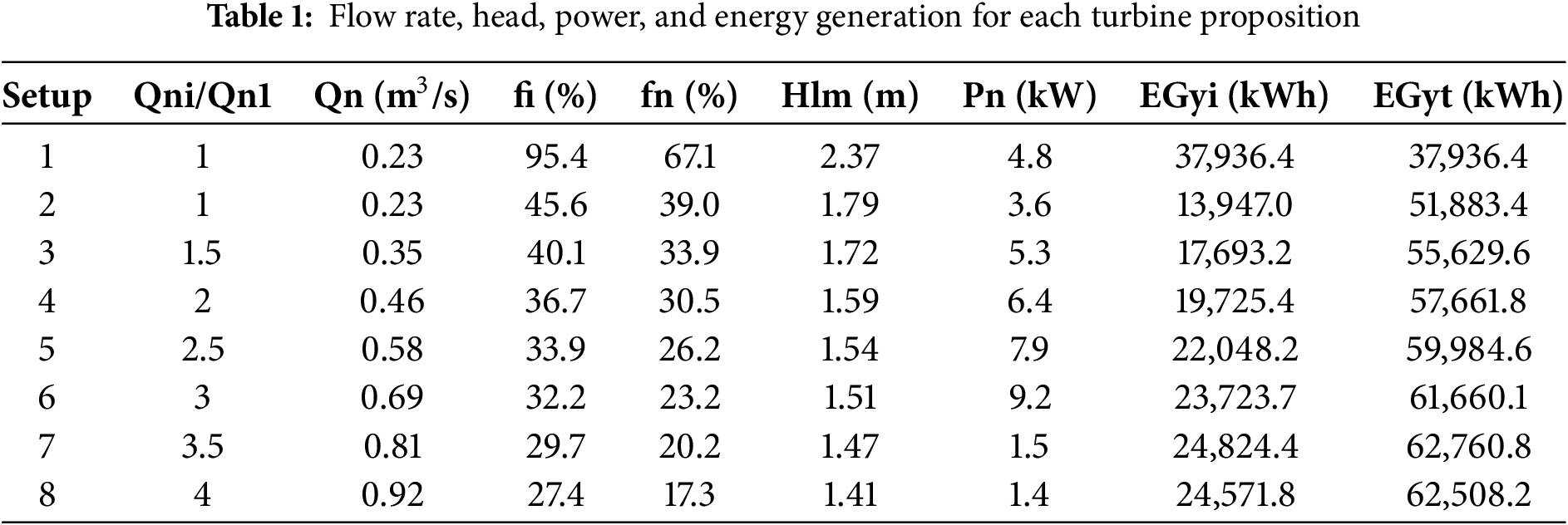
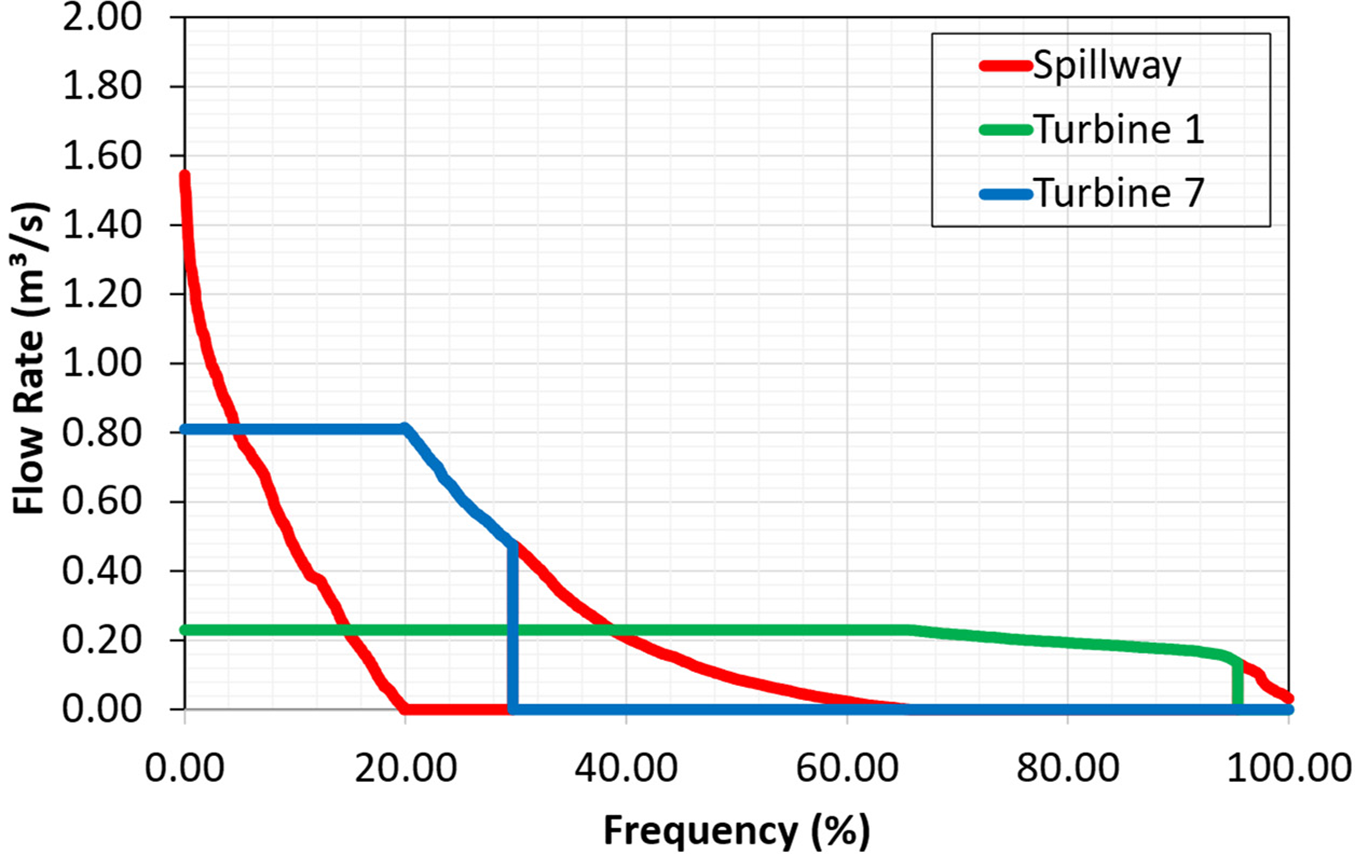
Figure 9: Frequency in % of the year for the proposed turbines
To validate the proposed CFD modeling approach, experimental and simulated results were compared. Post-processing analysis demonstrated a strong correlation between the CFD and experimental head-efficiency curves, as illustrated in Fig. 10. At the BEP, rotational speed of 750 rpm, deviations in efficiency and head were confined to 2.3%, affirming the model’s reliability for VLHT applications.

Figure 10: CFD and experimental results for the BEP rotation of 750 rpm
Following the validation of the numerical methodology, an updated turbine design was developed to operate under the same conditions as those used in the validation process. The optimal cascade configuration for energy generation was identified using the Cordier diagram and the minimum pressure coefficient criterion. Three configurations with varying pressure coefficient values were simulated to implement the minimum pressure coefficient criterion. Table 2 compares the reference turbine and the enhanced design derived from the Cordier diagram. Table 3 outlines the distinctions among the three turbines with differing pressure coefficient values.
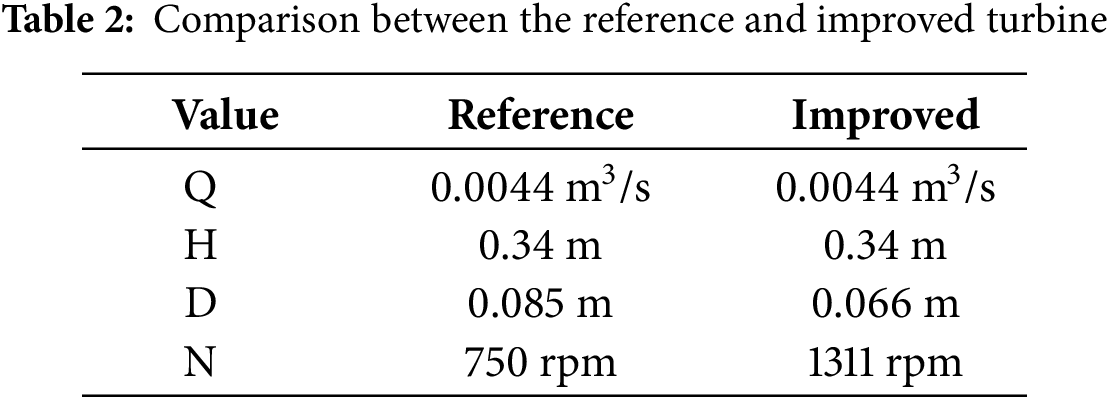
As shown in Table 3, a reduction in the pressure coefficient is anticipated to result in lower efficiency. This phenomenon can be attributed to the steeper pressure gradients that arise when the pressure coefficient is decreased, exacerbating flow separation and turbulence losses. Consequently, the efficiency of converting hydraulic energy into mechanical energy is diminished.
Fig. 11 illustrates the variations in flow patterns across the blades of the different turbine configurations. Building on the analysis performed for the reference machine, the turbines intended for installation on the bridge will be designed to adhere to the same criteria. The selected design will correspond to the configuration achieving the highest efficiency, and the results will be rigorously evaluated through CFD simulations.

Figure 11: Visualization of the flow on the three tested configurations: (a) Machine a, (b) Machine b, (c) Machine c
The flow characteristics across Machines a to c demonstrate a progressive increase in hydraulic loading, consistent with their geometric parameters. Machine A, which operates at the highest solidity (1.3), represents an optimized configuration for lower hydraulic loading. As the flow transitions to Machine c (l/t = 0.66), the loading intensifies, leading to steeper pressure gradients along the blade suction side. This trend is quantified by the Cpmin, which decreases from −0.78 (Machine a) to −2.65 (Machine c), indicating stronger adverse pressure gradients and an increased likelihood of boundary layer separation. These findings highlight a fundamental trade-off between energy transfer efficiency and aerodynamic stability in axial-flow cascades, underscoring the necessity for targeted optimization to ensure robust performance under variable riverine conditions.
3.3 Application of Methodology to the Case Study
Using the proposed methodology, two very high axial-flow hydraulic machines were explicitly developed at Janari Bridge. The turbines were designed to address the site’s unique hydraulic and geometric constraints, with Table 4 summarizing their key design parameters and operational specifications. Fig. 12 offers a detailed representation of the machines, highlighting their main dimensions.
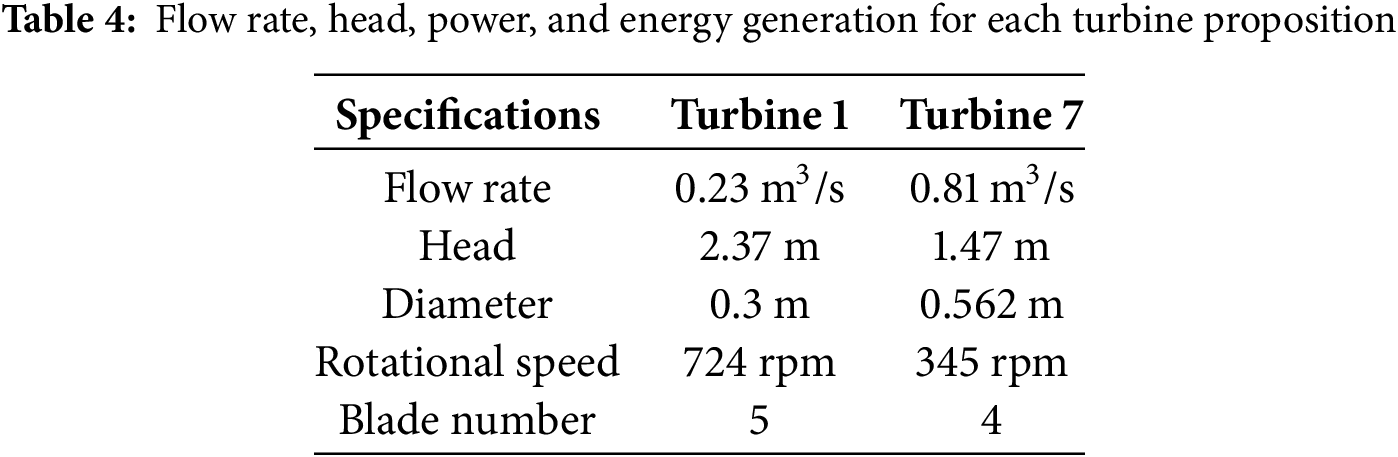

Figure 12: Turbines designed. (a)—T1 Lateral View. (b)—T1 Front View. (c)—T7 Lateral View. (d)—T7 Front View
Table 5 details the minimum pressure coefficient and the machine’s selected configuration. Fig. 13 visualizes the flow patterns on the cylindrical section of the blade hub for both machines.


Figure 13: Flow visualization for hub section: (a) Turbine 1; (b) Turbine 7
The flow visualization results (Fig. 14) reveal that both turbines exhibit similar configurations, despite differences in their efficiency. The Cpmin values for Turbine 1 (−0.9) and Turbine 7 (−1.1) indicate that Turbine 7 operates under slightly higher hydraulic loading than Turbine 1, aligning with the observed efficiency discrepancy. Turbine 1 achieves an efficiency of 85%, while Turbine 7 demonstrates a marginally higher efficiency of 87%. This enhanced performance in Turbine 7 may be attributed to its larger diameter and distinct blade configuration, which appear better suited to the flow conditions anticipated at the Janari Bridge. The performance of the turbines was evaluated across a range of flow rates, from 60% to 160% of the design flow rate. The results of these tests are presented in Fig. 14.

Figure 14: Efficiency of the designed turbines at different flow rates: (a) Turbine 1; (b) Turbine 7
Both turbines exhibit varying levels of efficiency across different flow rates, a characteristic common in hydropower systems operating under fluctuating water availability. While efficiency at higher flow rates (exceeding 100% of the design flow) demonstrates the turbines’ capacity to adapt to increased water volumes, efficiency losses become more pronounced at lower flow rates (below 100%), particularly for Turbine 7. This highlights the importance of optimizing turbine performance across various operational conditions.
Deploying multiple ultra-low-head turbines results in minimal flood areas, as one turbine operates nearly 100% of the time. As flow rates in the creek increase throughout the year, the second turbine activates as soon as the flow conditions permit. Consequently, water impoundment remains minimal for the majority of the time. To further regulate water levels, the turbine operation is complemented by a spillway. The spillway discharges excess water during periods when the flow is sufficient to operate the smaller turbine but insufficient to activate the larger one. Additionally, the spillway functions during peak flow periods, when both turbines’ combined operation cannot maintain upstream water levels below the maximum threshold suitable for bridge operations.
The Igarapé Preto is home to an aquatic fauna composed of small fish and amphibians. The spillway must be designed to facilitate the passage of these species downstream and upstream, ensuring minimal disruption to aquatic ecosystems. As a result, the environmental impact on fauna is expected to be low.
The enhanced methodology, integrating the Cordier diagram and the minimum pressure coefficient criterion with CFD simulations, proved highly effective in designing efficient low-head axial turbines. Crucially, this work advances VLHT design in two domains: First, we defined a Cpmin range of −1.1 < Cpmin < −0.9 for turbines operating at specific speeds above Ns > 180—a threshold critical for Amazonian micro-rivers, revealing a direct correlation between Cpmin and Ns absent in prior studies.
Second, the proposed dam-bridge-turbine system leverages the Amazon’s unique geography, where thousands of small rivers intersect rural roads, by integrating multiple turbines into concrete bridges. This approach transforms infrastructure liabilities into decentralized energy hubs, simultaneously addressing energy poverty and transportation risks.
The accuracy of the CFD simulations in predicting turbine behavior was validated using experimental data from a small turbine with circular arc blades, confirming the reliability of the numerical approach for performance evaluation. The turbines designed using this methodology demonstrated strong efficiency at the design flow rate. However, efficiency declined significantly at flow rates below the design point, underscoring the need for further optimization to enhance performance under such conditions.
Although the current designs omitted stators to reduce costs, future designs could incorporate stators to evaluate their impact on turbine behavior under off-design conditions. This would help determine whether potential improvements in energy generation justify the additional cost. Improved off-design performance is particularly critical given the significant seasonal flow variations in the Amazon basin. Additionally, a Levelized Cost of Energy (LCOE) analysis is essential to assess the economic viability of each turbine configuration, ensuring that the selected designs are both sustainable and cost-effective for long-term deployment. Future research will prioritize advanced transient simulation techniques, such as sliding mesh or transient rotor-stator methods, to resolve unsteady flow interactions and refine performance predictions under dynamic operating conditions.
This study establishes a comprehensive framework for future low-head turbine designs, demonstrating that integrating the enhanced Cordier diagram, minimum pressure coefficient criterion, and CFD simulations offers a systematic and reliable methodology for developing efficient and adaptable turbines. By correlating Cpmin to specific speed and synergizing energy-infrastructure solutions, this study contributes to conventional turbine design paradigms.
Acknowledgement: The authors express sincere gratitude for the technical support provided by the Federal University of Pará and the Laboratory of Fluid Dynamics and Particulates. Their assistance was invaluable in completing this study successfully.
Funding Statement: This research was funded by the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq), project number 408034/2022−0.
Author Contributions: The authors confirm contribution to the paper as follows: conceptualization, André L. Amarante Mesquita; methodology, André L. Amarante Mesquita and Cláudio J. C. Blanco; software, Rodolfo V. C. Ramalho and Manoel J. S. Sena; validation, Rodolfo V. C. Ramalho; formal analysis, Rodolfo V. C. Ramalho; investigation, André L. Amarante Mesquita and Davi E. S. Souza; resources, Davi E. S. Souza; data curation, Vitoria B. Portilho and Natália M. Graças; draft manuscript preparation, Rodolfo V. C. Ramalho; review and editing, Gilton C. A. Furtado and Manoel J. S. Sena; visualization, Rodolfo V. C. Ramalho; supervision, André L. Amarante Mesquita; project administration, André L. Amarante Mesquita. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data supporting this study’s findings are available from the Corresponding Author, André L. Amarante Mesquita, upon reasonable request.
Ethics Approval: Field data collection, including hydrological measurements and infrastructure inspections along the Água Preta River, adhered to environmental protection regulations outlined in Brazilian Law. No human participants or sensitive personal data were involved in this research. Community engagement activities, including consultations with residents of the Janarí district, followed the principles of free, prior, and informed consent (FPIC) as defined by the International Labour Organization’s Convention 169. All interactions were conducted in partnership with local authorities to ensure cultural respect and minimal ecological disruption.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
Nomenclature
| CFD | Computational Fluid Dynamics |
| VLHT | Very Low Head Turbine |
| SST | Shear Stress Transport |
| Cpmin | Minimum Pressure Coefficient |
| Cpsi | Inferior Pressure Coefficient Limit |
| Cpss | Superior Pressure Coefficient Limit |
| Qn | Flow Rate |
| f | Frequency |
| Hl | Liquid Head |
| Pn | Generated Power |
| EG | Generated Energy |
References
1. Silva Pereira J, Santos MAO, de Lima Bandeira F, Soares FIL, Vieira TA. Electrification in remote regions: an analysis of the more light for Amazon program. Energies. 2023;16(12):4663. doi:10.3390/en16124663. [Google Scholar] [CrossRef]
2. Electrical exclusion on the Legal Amazon: who is still without access to electricity? [Internet]. [cited 2024 Aug 7]. Available from: https://energiaeambiente.org.br/wp-content/uploads/2021/02/relatorio-amazonia-2021-bx.pdf. [Google Scholar]
3. Hampl N. Energy systems for Brazil’s Amazon: could renewable energy improve indigenous livelihoods and save forest ecosystems? Energy Res Soc Sci. 2024;112(5):103491. doi:10.1016/j.erss.2024.103491. [Google Scholar] [CrossRef]
4. Sánchez AS, Torres EA, Kalid RA. Renewable energy generation for the rural electrification of isolated communities in the Amazon Region. Renew Sustain Energy Rev. 2015;49(10):278–90. doi:10.1016/j.rser.2015.04.075. [Google Scholar] [CrossRef]
5. Lembi R, Lopez MC, Ramos KN, Johansen IC, da Silva LJS, Santos MRP, et al. Towards energy justice and energy sovereignty: participatory co-design of off-grid systems in the Brazilian Amazon. Energy Res Soc Sci. 2025;119(3):103858. doi:10.1016/j.erss.2024.103858. [Google Scholar] [CrossRef]
6. Chaudhari S, Brown E, Quispe-Abad R, Moran E, Müller N, Pokhrel Y. In-stream turbines for rethinking hydropower development in the Amazon basin. Nat Sustain. 2021;4(8):680–7. doi:10.1038/s41893-021-00712-8. [Google Scholar] [CrossRef]
7. Ponte GP, Calili RF, Souza RC. Energy generation in Brazilian isolated systems: challenges and proposals for increasing the share of renewables based on a multicriteria analysis. Energy Sustain Dev. 2021;61(1):74–88. doi:10.1016/j.esd.2020.12.007. [Google Scholar] [CrossRef]
8. Blanco CJC, Secretan Y, Mesquita ALA. Decision support system for micro-hydro power plants in the Amazon region under a sustainable development perspective. Energy Sustain Dev. 2008;12(3):25–33. doi:10.1016/S0973-0826(08)60435-4. [Google Scholar] [CrossRef]
9. Quintas MC, Blanco CJ, Amarante Mesquita AL. Analysis of two schemes using micro hydroelectric power (MHPs) in the Amazon with environmental sustainability, energy, and economic feasibility. Environ Dev Sustain. 2012;14(2):283–95. doi:10.1007/s10668-011-9322-8. [Google Scholar] [CrossRef]
10. Mardiyanto IR, Raharjo J, Utami S, Mursanto WB, Rahardjo AH. An Improvement in power quality and by-product of the run-off river micro hydro power plant. Energy Eng. 2023;120(6):1295–305. doi:10.32604/ee.2023.027756. [Google Scholar] [CrossRef]
11. Quaranta E, Bahreini A, Riasi A, Revelli R. Very Low Head Turbine for hydropower generation in existing hydraulic infrastructures: state of the art and future challenges. Sustain Energy Technol Assess. 2022;51(4):101924. doi:10.1016/j.seta.2021.101924. [Google Scholar] [CrossRef]
12. Portilho VB, José C, Blanco C, Ramalho RVC, Davi R, Sales E, et al. Integration of micro hydropower plants in a multipurpose bridge-dam in the rural Amazon. In: Proceedings of the 27th ABCM International Congress of Mechanical Engineering; 2023 Dec 4–8; Florianópolis, Brazil. doi:10.26678/ABCM.COBEM2023.COB2023-1569. [Google Scholar] [CrossRef]
13. Muis A, Sutikno P, Soewono A, Hartono F. Design optimization of axial hydraulic turbine for very low head application. Energy Proc. 2015;68:263–73. doi:10.1016/j.egypro.2015.03.255. [Google Scholar] [CrossRef]
14. Sutikno P, Adam IK. Design, simulation and experimental of the very low head turbine with minimum pressure and freevortex criterions. Int J Mech Mechatron Eng. 2011;11(1):9–16. [Google Scholar]
15. Anagnostopoulos JS, Papantonis DE. Optimal sizing of a run-of-river small hydropower plant. Energy Convers Manag. 2007;48(10):2663–70. doi:10.1016/j.enconman.2007.04.016. [Google Scholar] [CrossRef]
16. Hermanto A, Permana DI, Rusirawan D, Shantika T. Investigation of very low micro-hydro turbine: design, simulation and prototype xperimental. Int J Heat Technol. 2023;41(2):332–40. doi:10.18280/ijht.410206. [Google Scholar] [CrossRef]
17. Mohammadi M, Riasi A, Rezghi A. Design and performance optimization of a very low head turbine with high pitch angle based on two-dimensional optimization. J Braz Soc Mech Sci Eng. 2020;42(1):1–18. doi:10.1007/s40430-019-2084-1. [Google Scholar] [CrossRef]
18. Cruz AGBD, Mesquita ALA, Blanco CCJ. Minimum pressure coefficient criterion applied in axial-flow hydraulic turbines. J Braz Soc Mech Sci Eng. 2008;30(1):1–10. doi:10.1590/S1678-58782008000100005. [Google Scholar] [CrossRef]
19. Ebhota F, Inambao WS. Design basics of a small hydro turbine plant for capacity building in Sub-Saharan Africa. Afr J Sci Technol Innov Dev. 2016;8(1):111–20. doi:10.1080/20421338.2015.1128039. [Google Scholar] [CrossRef]
20. Soesanto QMB, Widiyanto P, Susatyo AEY. Cascade optimization of an axial-flow hydraulic turbine type propeller by a genetic algorithm. Int J Technol. 2019;10(1):200–11. doi:10.14716/ijtech.v10i1.1744. [Google Scholar] [CrossRef]
21. Shukla RS, Parashar C. Design of propeller turbine for micro hydro power station using CFD. Int J Sci Eng Sci. 2017;1(7):37–41. [Google Scholar]
22. Vinagre MVA, Blanco CJC, Mesquita ALA. A non-linear rainfall-runoff model with a sigmoid gain factor to simulate flow frequency distribution curves for Amazon catchments. J Hydro Hydromech. 2011;59(3):145–56. doi:10.2478/v10098-011-0012-x. [Google Scholar] [CrossRef]
23. Ikui T, Inoue M, Kaneko K. Two-dimensional cascade performance of circular-arc blades. In: Proceedings of the Tokyo Joint International Gas Turbine Conference and Products Show; Tokyo, Japan: JSME; 1971. p. 57–64. [Google Scholar]
24. Tezuka A, Sunada Y, Rinoie K. Surface pressure distributions on 4% circular arc airfoil at low Reynolds number. J Aircr. 2008;45(6):2164–67. doi:10.2514/1.35365. [Google Scholar] [CrossRef]
25. Fagbenro KA. Cascade effects on circular arc airfoils for windmill analysis [master’s thesis]. Calgary, AB, Canada: University of Calgary; 2013. 111 p. [Google Scholar]
26. Bian T, Shen X, Wang B, Feng J, Han QP. Numerical and experimental investigation of flow loss and flow structure of circular arc cambered plate blade cascade. Proc Inst Mech Eng A J Power Energy. 2019;233(8):961–73. doi:10.1177/0957650919846006. [Google Scholar] [CrossRef]
27. Balla E, Vad J. An empirical model to determine lift and drag coefficients of cambered plates at moderate Reynolds numbers. Proc Inst Mech Eng A J Power Energy. 2021;235(2):202–10. doi:10.1177/0957650920915317. [Google Scholar] [CrossRef]
28. Zhang Z. Improvement and extension of Cordier diagram for hydraulic turbines. Proc Inst Mech Eng A J Power Energy. 2022;236(7):1309–19. doi:10.1177/09576509221092282. [Google Scholar] [CrossRef]
29. Tackaberry B, Yuen A, Vertz J, Hartloper C, Sessarego M, Wong J, et al. Investigation of approach conditions for very low head (VLH) water turbine performance. In: Proceedings of the 23rd Canadian Congress of Applied Mechanics; 2011 Jun 5–9; Vancouver, BC, Canada. p. 698–701. [Google Scholar]
30. Samora I, Hasmatuchi V, Münch-Alligné C, Franca MJ, Schleiss AJ, Ramos HM. Experimental characterization of a five-blade tubular propeller turbine for pipe inline installation. Renew Energy. 2016;95(5):356–66. doi:10.1016/j.renene.2016.04.023. [Google Scholar] [CrossRef]
31. Menny K. Strömungsmaschinen: hydraulische und thermische Kraft- und Arbeitsmaschinen. 5th ed. Leipzig, Germany: Teubner; 2006. [Google Scholar]
32. Quaranta E. Optimal rotational speed of Kaplan and Francis turbines with focus on low-head hydropower applications and dataset collection. J Hydraul Eng. 2019;145(12):04019043. doi:10.1061/(ASCE)HY.1943-7900.0001643. [Google Scholar] [CrossRef]
33. Menter FR. Review of the shear-stress transport turbulence model experience from an industrial perspective. Int J Comput Fluid Dyn. 2009;23(4):305–16. doi:10.1080/10618560902773387. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools