Research on Post Evaluation of Mechanized Construction in Power Transmission and Transformation Projects with Game Theory and Fuzzy Grey Projection

1  Introduction

Currently, the international economic landscape is becoming increasingly complex, and there is significant downward pressure on the global economy. In recent years, China’s infrastructure sector has experienced rapid growth, and the structure of its power engineering business has gradually evolved from traditional infrastructure construction to a more diversified range of services, including production, operation, maintenance, and emergency repairs [1]. The central challenge now is how to shorten the construction timeline of power transmission and transformation projects under the dual carbon target, while ensuring environmental protection, on-site construction safety, and the economic benefits of the project. This issue has become an urgent topic that needs thorough investigation and resolution within the current power grid context. Consequently, the transformation of mechanized construction in power transmission and transformation projects is increasingly critical [2,3].

Compared to traditional manual construction, mechanized construction offers more diverse forms and is essential for achieving the long-term goals of mechanization replacement, automation reduction, and intelligent, unmanned construction in power transmission and transformation engineering [4,5]. On 7 February, 2023, the State Grid Corporation of China issued the “Implementation Opinions on Fully Promoting Mechanized Construction in Power Transmission and Transformation Engineering” (State Grid Infrastructure [2023] No. 6), emphasizing that mechanized construction represents a profound shift in the power grid construction method and is the only viable path to building an internationally competitive power grid [6]. This highlights the growing importance of mechanized construction in the industry.

However, current evaluations of mechanized construction’s economic benefits often rely solely on individual indicators such as project cycle time or cost savings. These evaluations fail to account for the impact of other factors like construction quality, safety, environmental effects, and subsequent maintenance on economic performance [7–9]. To explore the full economic and social benefits and provide theoretical guidance for the full life cycle of power transmission and transformation projects, a comprehensive and effective multi-index evaluation method is essential for the development of power grid engineering [10–12]. Thus, assessing comprehensive benefits and sustainability within the power system has become a key area of research [13,14].

In recent years, scholars have developed multi-index evaluation systems for mechanized construction in power transmission and transformation projects, considering factors such as economy, energy consumption, and environmental impact. Qin proposed a comprehensive evaluation model based on AHP and VPRS, determining the risk level of construction projects to conduct a thorough analysis of safety risks and providing guidance for safe project execution [15]. Li et al. created a TTP evaluation index system, considering technical, economic, and social benefits to assist in precise investment decisions for transmission construction projects [16]. Sun et al. recognized that investment in power transmission projects is both a profit-oriented and public service activity. They established a job evaluation index system and employed fuzzy hierarchical evaluation methods to develop a fuzzy comprehensive evaluation model for power transmission and transformation projects [17]. Yin and Hou analyzed ultra-high voltage transmission and transformation engineering, proposing a grey evaluation model for construction quality by combining subjective and objective weighting methods [18]. Zhou et al., aligning with China’s “dual carbon” strategic goals and the planning of new energy systems, created a comprehensive evaluation system based on the SMART principle for energy storage as a regulatory resource [19]. Liu et al. developed a system to evaluate the efficiency of multi-business integration in power grid projects, focusing on operational time and functional types [20].

For the successful construction and high-quality development of power transmission and transformation projects, mechanized construction must be applied throughout their life cycle. Post-evaluation plays a crucial role in advancing this development. However, most studies focus on only a few indicators, often neglecting social benefits, safety, and stability. Additionally, existing evaluation methods often struggle to balance subjectivity and objectivity, leading to less scientific and reasonable results. Therefore, this paper introduces several innovative aspects:

(1) This paper develops a comprehensive post-evaluation index system that spans the full life cycle of mechanized construction in power transmission and transformation projects. It includes the engineering planning, design stage, on-site construction stage, operation and maintenance stage, and shutdown disposal stage, with specific calculation methods for each index.

(2) A case study of a power transmission and transformation project in a certain location in China is used. Various data preprocessing methods are applied, and the AHP and entropy weight methods are employed to determine the weights of the indicators. Game theory is then used to optimize the combination of the two weights, determining the final indicator weights.

(3) The Fuzzy Grey Relational Projection (FGRP) method is used to comprehensively evaluate mechanized construction schemes for power transmission and transformation projects. Scheme 1, with a membership degree of 0.870945, performs the best in terms of sustainability. These results indicate that the proposed framework can scientifically guide decisions on mechanized construction plans, offering valuable insights for the sustainable development of diversified businesses in the future of mechanized power transmission and transformation projects.

In this paper, Section 2 introduces the post evaluation index system for the full life cycle of mechanized construction in power transmission and transformation projects. Section 3 outlines the comprehensive evaluation method based on game theory and fuzzy grey projection. Section 4 presents empirical analysis using real data. Section 5 concludes the paper.

2  Design of Post Evaluation Index System for the Full Life Cycle of Mechanized Construction in Power Transmission and Transformation Projects

2.1 Application of Mechanized Construction

Currently, mechanized construction has been widely applied throughout the entire life cycle of transmission and transformation projects, covering various stages such as project planning and design, on-site construction, operation and maintenance, and decommissioning and disposal.

2.1.1 Engineering Planning and Design Stage

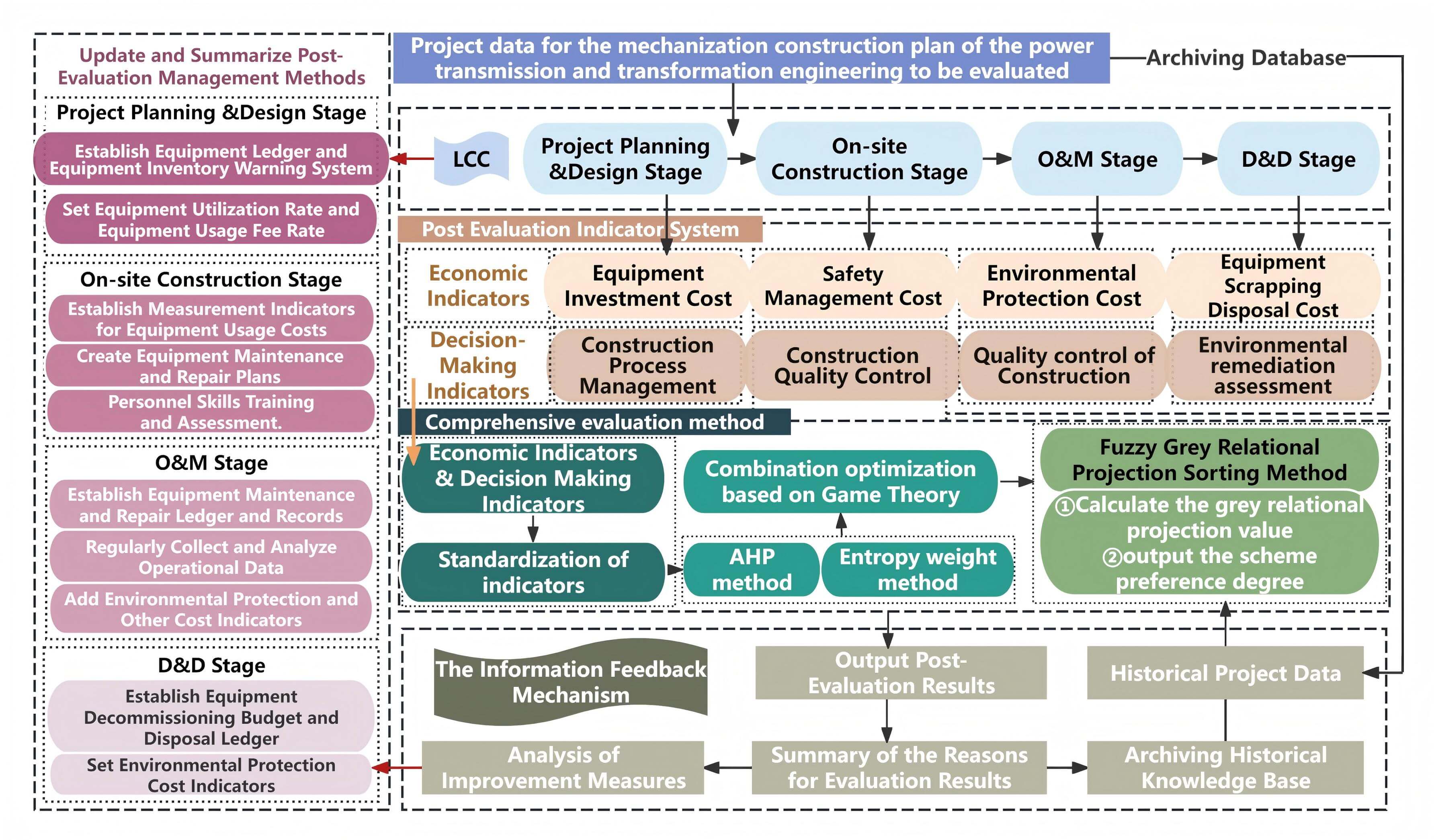
In the project planning and design stage, mechanized construction can assist engineers in the planning and design of transmission and transformation projects by using various software and simulation tools. For example, as shown in the Fig. 1 [20]:

Figure 1: Example of mechanized construction application in the project planning and design stage

2.1.2 On-Site Construction Stage

In the on-site construction stage, mechanized construction is widely applied to various construction tasks, such as foundation construction, line installation, equipment installation, and more. Specifically, as shown in Fig. 2.

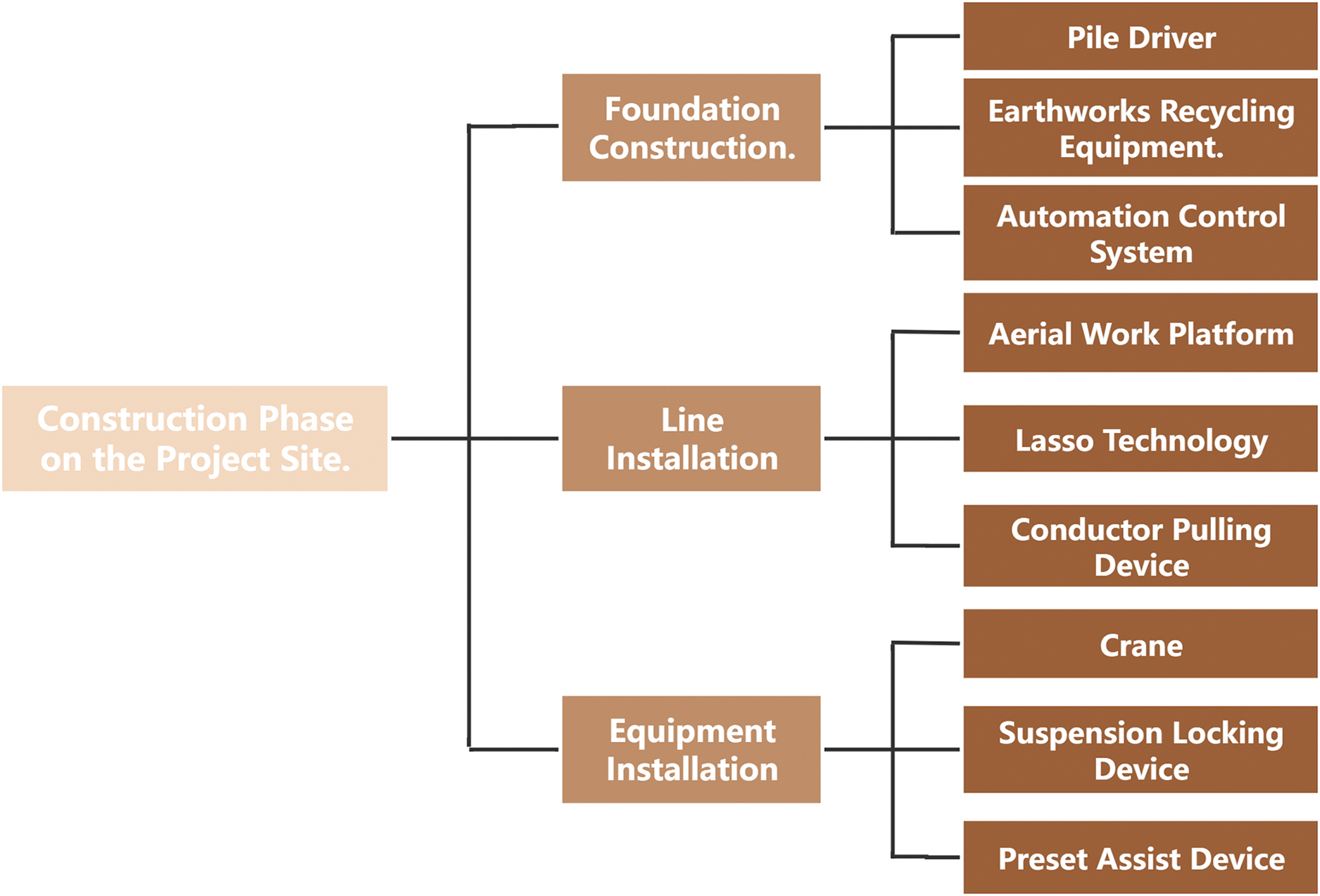
Figure 2: Example of mechanized construction application in the on-site construction stage

2.1.3 Operation and Maintenance Stage

In the operation and maintenance stage, mechanized construction for transmission and transformation projects is primarily applied to tasks such as inspections and patrols, equipment maintenance and repair, line inspections and maintenance, and more. Specifically, as shown in the Fig. 3.

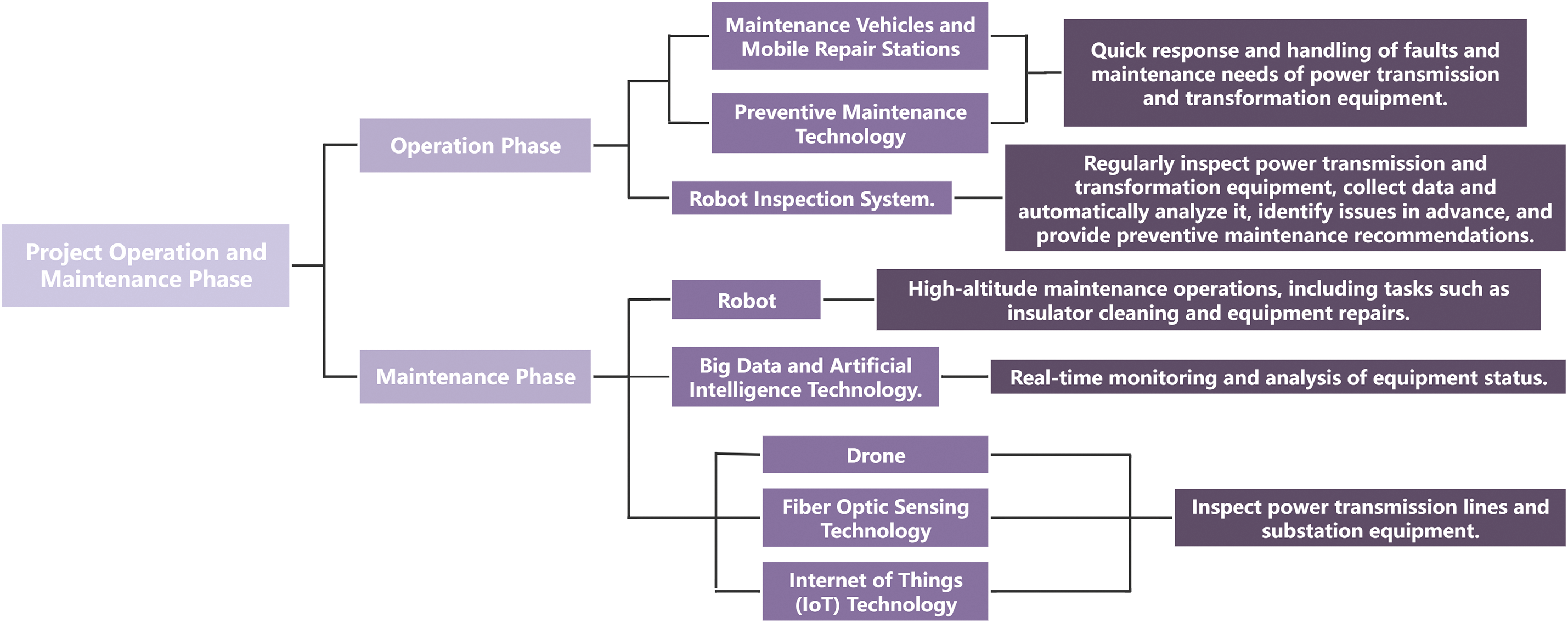
Figure 3: Example of mechanized construction application in the operation and maintenance stage

2.1.4 Decommissioning and Disposal Stage

In the decommissioning and disposal stage, mechanized construction for transmission and transformation projects is primarily applied to tasks such as equipment dismantling, facility cleaning, soil remediation, waste disposal, and more. Specifically, as shown in the Fig. 4.

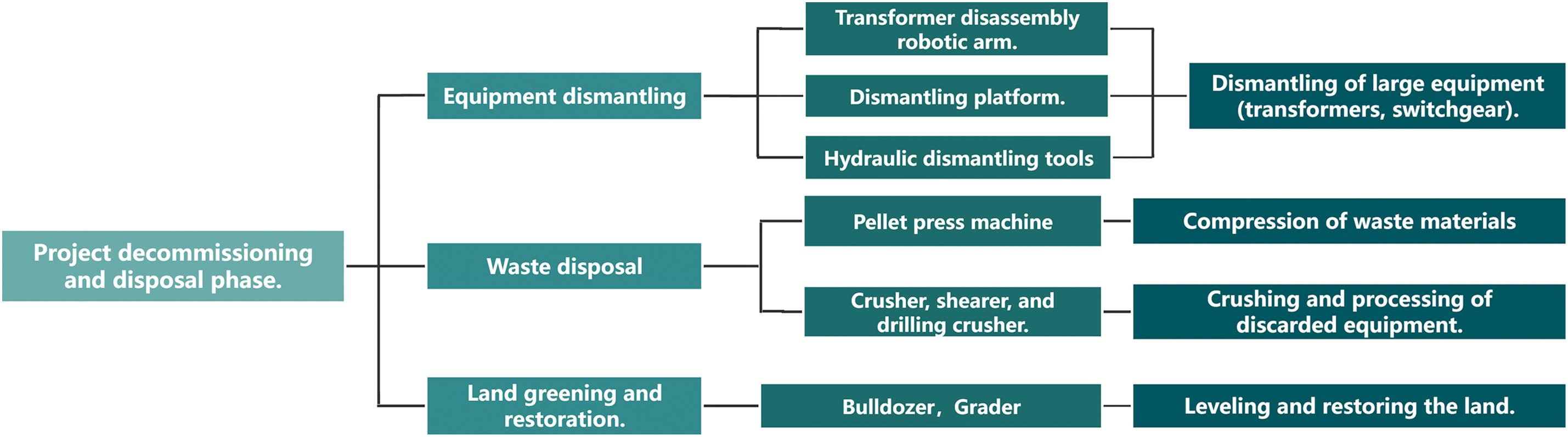
Figure 4: Example of mechanized construction application in the decommissioning and disposal stage

2.2 Establishing the Full Life Cycle Post-Evaluation Indicator System

This paper, centered around the full life cycle, breaks away from the traditional manual construction business model by making full use of mechanized construction. While ensuring effective operation and optimization of the project, it involves the planning, design, and analysis of each phase. With reference to the current post-evaluation indicator system for power transmission and transformation projects under the dual-carbon background, and considering the characteristics of mechanized construction, the paper outlines four stages: Engineering Planning and Design Stage, On-site Construction Stage, Operation and Maintenance Stage, and Decommissioning and Disposal Stage. It identifies the economic indicators (primarily reflecting the economic benefits of the project) and decision-making indicators (mainly reflecting the social, environmental, and technical benefits of the project) for each stage [21]. The mechanized construction post-evaluation indicator system for power transmission and transformation projects over the full life cycle is then constructed. The quantitative standards for economic indicators are based on engineering practices, with major valuation criteria such as labor costs, material costs (including fuel), and machinery costs (including operators). The quantitative standards for decision-making indicators are primarily determined through anonymous reviews by industry experts, and the final indicator system is shown in Table 1. The meanings of variables in Table 1 can be found in Table 2.

3  Comprehensive Evaluation Method

3.1 Standardization of Evaluation Indicators

Due to the differences in the evaluation effectiveness of different evaluation indicators on the overall goal, the obtained data is normalized and evaluated. Before standardization, a 5-level classification method was used to define the comment set for qualitative indicators, and the corresponding scores for each level are shown in Table 3.

When conducting a feasibility assessment of mechanized construction in power transmission and transformation projects, the number of evaluation objects i is m, and there are n evaluation indicators j in each object. The j-th indicator of the i-th evaluation object is denoted as Xij(i=1,2,3,…,m;j=1,2,3,…,n), forming the original matrix of the evaluation object. Eq. (1) is used to unify the original matrix of the evaluation object according to Eq. (2), and then normalized according to Eq. (3) to obtain the standardized data matrix B1=(bij∗)m×n, bij∗∈[0,1]:

X=[X11X12⋯X1nX21X22⋯X2n⋮⋮⋯⋮Xn1Xn2⋯Xnn](1)

bij=Xij−min(Xj)max(Xj)−min(Xj)(2)

In the formula, Xij is a decision-making indicator.

X=max(Xj)−Yijmax(Xj)−min(Xj)(3)

In the formula, Yij is a cost indicator.

bij∗=bij∗∑i=1mbij

3.2 Improving the Comprehensive Weighting Method Based on Game Theory

The subjective weighting method is greatly influenced by human factors and has a strong subjectivity, while the objective weighting method relies entirely on the inherent characteristics of the data and easily ignores the characteristics of the indicators. To solve the problems of subjective and objective weight calculation methods, the AHP+entropy weight method game theory weight determination method includes three parts. Firstly, the AHP method and entropy weight method are used to determine the indicator weights, and then the game theory idea is adopted to combine and optimize the subjective and objective weights to obtain the combined weight.

3.2.1 Analytic Hierarchy Process (AHP) Determines Subjective Weights

The Analytic Hierarchy Process (AHP) is a decision analysis method that combines qualitative and quantitative methods. It belongs to the subjective weight calculation method and can effectively solve multi criteria and multi-objective problems, achieving comprehensive treatment of qualitative and quantitative influencing factors. The method is simple and scientific, and is widely used in power generation technology optimization selection, project evaluation, plant site selection, power planning, load forecasting, and other aspects [22]. Subjective weighting of indicators through Analytic Hierarchy Process, combined with mathematical processing, increases credibility and makes them more logical [23].

1) Construct a judgment matrix. Using the 1-9 scale method to determine quantification, establish a corresponding positive and negative judgment matrix C=(cij)r×r for the post evaluation index system of the entire life cycle of mechanized construction in power transmission and transformation projects, and describe the importance of each index corresponding to the upper level index in the evaluation system.

2) Hierarchical single sorting and its consistency check. By solving the eigenvalues CW=λmaxW of matrix C, the eigenvector W is obtained, and after normalization, the weights of the indicators for the corresponding upper level indicators are obtained. The formula for calculating consistency index C1 is

CI=λmax−rr−1(4)

In the formula, λmax is the maximum eigenvalue of the judgment matrix; r is the number of indicators.

Calculate the value of the random consistency ratio CR=CIRI, where RI is the average random consistency index of the judgment matrix. When CR≤0.1, it is considered that the consistency of the judgment matrix is good, otherwise the relative importance values of the judgment matrix need to be adjusted.

3) Hierarchical sorting. By calculating layer by layer from left to right, the target layer weight W1=[v1,v2,…,vn]T of the evaluation system can be obtained.

3.2.2 Entropy Weight Method Determines Objective Weights

Entropy weighting method is an objective weighting method that calculates weights based on the discreteness of each evaluation index data itself. For evaluation indicators, the degree of dispersion can be determined by the entropy value. Therefore, information entropy can be used to calculate the weights of each indicator, providing a basis for comprehensive evaluation of multiple indicators. The specific steps of using entropy weight method for objective weighting are as follows:

1) Standardize the judgment matrix to eliminate the dimensionality of the original values of various indicators.

2) Calculate the entropy j of evaluation indicator Ej as

Ej=−1lnm∑i=1mPijlnPij(5)

In the formula, Pij=Vij∗/∑j=1nVij∗; m is the number of evaluation objects.

3) According to entropy calculation, the weight wj of the j-th evaluation index is

wj=1−Ejn−∑j=1nEj(6)

3.2.3 Combination Weight Based on Game Theory

Game theory is an important part of operations research, which assumes that each solution is the result of rational decision-making by decision-makers to safeguard their own interests [24]. This article applies the idea of game theory to calculate the final combination weight by combining the subjective and objective weights. The specific steps are as follows:

1) Let the basic weight set be: u={ui1,uk2,…,uin}, i=1,2,3…,l. l is the number of weight determination methods, and in this article, any linear combination of vectors with a value of 2 is

u=∑i=1laiuiT>0,i=1,2,3,…,l,(7)

In the formula, u is the comprehensive weight vector of l weight sets; ai is the weight coefficient.

2) According to game theory, ultimately minimizing the difference between u and ui, optimizing l weight vectors ai, that is

min||∑i=1laiuiT−ui||2 i=1,2,3,…,l.(8)

3) The linear differential equation system with the optimal first-order derivative condition of Eq. (8) is

[u1⋅u1Tu1⋅u2T⋯u1⋅ulTu2⋅u1Tu2⋅u2T⋯u2⋅ulT⋮⋮⋯⋮ul⋅u1Tul⋅u2T⋯ul⋅ulT][a1a2⋮al]=[u1⋅u1Tu2⋅u2T⋮ul⋅ulT](9)

By using Matlab to calculate (a1,a2,…,al) and then normalizing it, we can obtain

ai∗=ai/∑i=1la1i(10)

The comprehensive weight for obtaining the combination weighting in game theory is

u∗=∑i=1lai∗uiT(11)

3.3 Fuzzy Grey Relational Projection Sorting Method

1) Determine ideal and inferior mechanized construction plans. Let the ideal optimal solution be G0={1,1,…,1}; based on the smallest attribute value of each indicator processed by nondimensionalization, which is 0, the ideal inferior solution is obtained as G0−={0,0,…,0}.

2) Positive and negative weighted grey relational decision matrix. By calculation, the degree of correlation between each plan and the ideal plan can be obtained:

The grey correlation coefficient between scheme Gi and G0+={1,1,…,1} is

rij+=minnminm|b0j+−bij|+αmaxnmaxm|b0j+−bij||b0j+−bij|+αmaxnmaxm|b0j+−bij|(12)

The grey correlation coefficient between Scheme Gi and Scheme G0−={0,0,…,0} is

rij−=minnminm|b0j−−bij|+maxnmaxm|b0j−−bij||b0j−−bij|+αmaxnmaxm|b0j−−bij|(13)

Among them, α is the resolution coefficient used to adjust the size of the comparison environment, usually α = 0.5; b0j+ is the index value of the ideal optimal solution, b0j+=1, (j=1,2,…,n); b0j− is the index value of the ideal worst solution, b0j−=0,(j=1,2,…,n). Obviously, γ01+=γ02+=…=γ0n+=1, γ01−=γ02−=…=γ0n−=0.

Due to the varying importance of each evaluation indicator in the indicator system, the grey relational decision matrix is weighted. The weight wi of each indicator should meet the following requirements:

0≤wi≤1,∑j=1nwj=1,j=1,2,…,n(14)

Obtain positive and negative weighted grey relational decision matrix γw:

γw+=γww=[w1w2⋯wnw1γ11+w2γ12+⋯wnγn2+⋮⋮⋯⋮w1γn1+w2γn1+⋯wnγnm+],(15)

γw−=γ−w=[w1w2⋯wnw1γ11−w2γ12−⋯wnγn2−⋮⋮⋯⋮w1γn1−w2γn1−⋯wnγnm−],(16)

In the formula, the i-th row vector of γw+, γw− represents the weighted grey correlation between decision scheme Gi and positive and negative ideal plans at each point.

3) Grey correlation projection value. Consider each alternative solution as a row vector, and the gray correlation projection angle is the angle θi between each alternative solution Ai and the ideal solution A∗ [25]. The cosine of the angle is

cosθi=AiA∗||AiA∗||=∑j=1nfijwj2∑j=1nwj2∑j=1n(wjfij)2(17)

In the formula, i=1,2,…,m.

The projection Di of scheme Gi on ideal scheme G0 is

Di=|Gi¯|cosθi=Gi¯G0¯|G0¯|=∑j=1nγijwj2∑j=1nwj2(18)

In the formula, i=1,2,…,m.

Normalize the weights to obtain the grey relational projection weights:

μj=wj2∑j=1n(wj)2, j=1,2,…,n(19)

Di=∑j=1nγijμj, i=1,2,…,m(20)

Di reflects the degree of correlation between scheme Gi and ideal scheme G0. The larger scheme Di, the closer it is to the ideal scheme. Specifically, the grey correlation projection values of the ideal optimal solution and the ideal inferior solution on themselves are

D0+=∑j=1nγijμj=∑j=1nμj,i=1,2,…,m(21)

D0−=∑j=1nγijμj,i=1,2,…,m(22)

Obviously, D0+ = D0−. Let D0=D0+=D0− be, in essence, the modulus of the ideal solution after weighting.

4) Superior membership degree. If the degree of superiority of scheme Gi is ui, then its degree of inferiority to the ideal inferior scheme is 1−u. The generalized weighted distance between scheme F and the ideal superior scheme is defined as

Dgi+=ui(D0−D0+)(23)

Similarly, the generalized weighted distance between Scheme Gi and the ideal inferior scheme is defined as

Dgi−=(1−ui)(D0−D0+)(24)

According to the minimum sum of squares criterion, the objective function is

min{F(ui)=(Dgi+)2+(Dgi−)2}(25)

Obtained by ∂F(ui)∂ui=0

ui=11+(D0−Di+D0−Di−)(26)

The larger ui is, the greater the membership degree of scheme Gi to the ideal optimal scheme. By sorting each plan in descending order of ui, the order of superiority and inferiority of each plan can be obtained.

3.4 Information Feedback Mechanism

In order to fully utilize the full life cycle post evaluation system, ensure close connection between various links of mechanized construction in power transmission and transformation projects, and achieve information sharing among various departments, it is necessary to establish a supporting information feedback mechanism for post evaluation management of mechanized construction in power transmission and transformation projects. Firstly, establish an evaluation index system, analyze and compare the mechanization construction plans of power transmission and transformation projects in the historical database, and make decisions on the optimal plan. Secondly, analyze the relevant construction plans of the project to be evaluated and compare them again with the optimal plan in the experience database. The final optimal plan will be used for on-site implementation and form a case study to be included in the experience database; The eliminated plan will be analyzed for improvement space and measures. If improvements can be made, optimize and re plan; If improvement is not possible, summarize the lessons of failure and synchronize them into the experience library. The specific process is shown in Fig. 5.

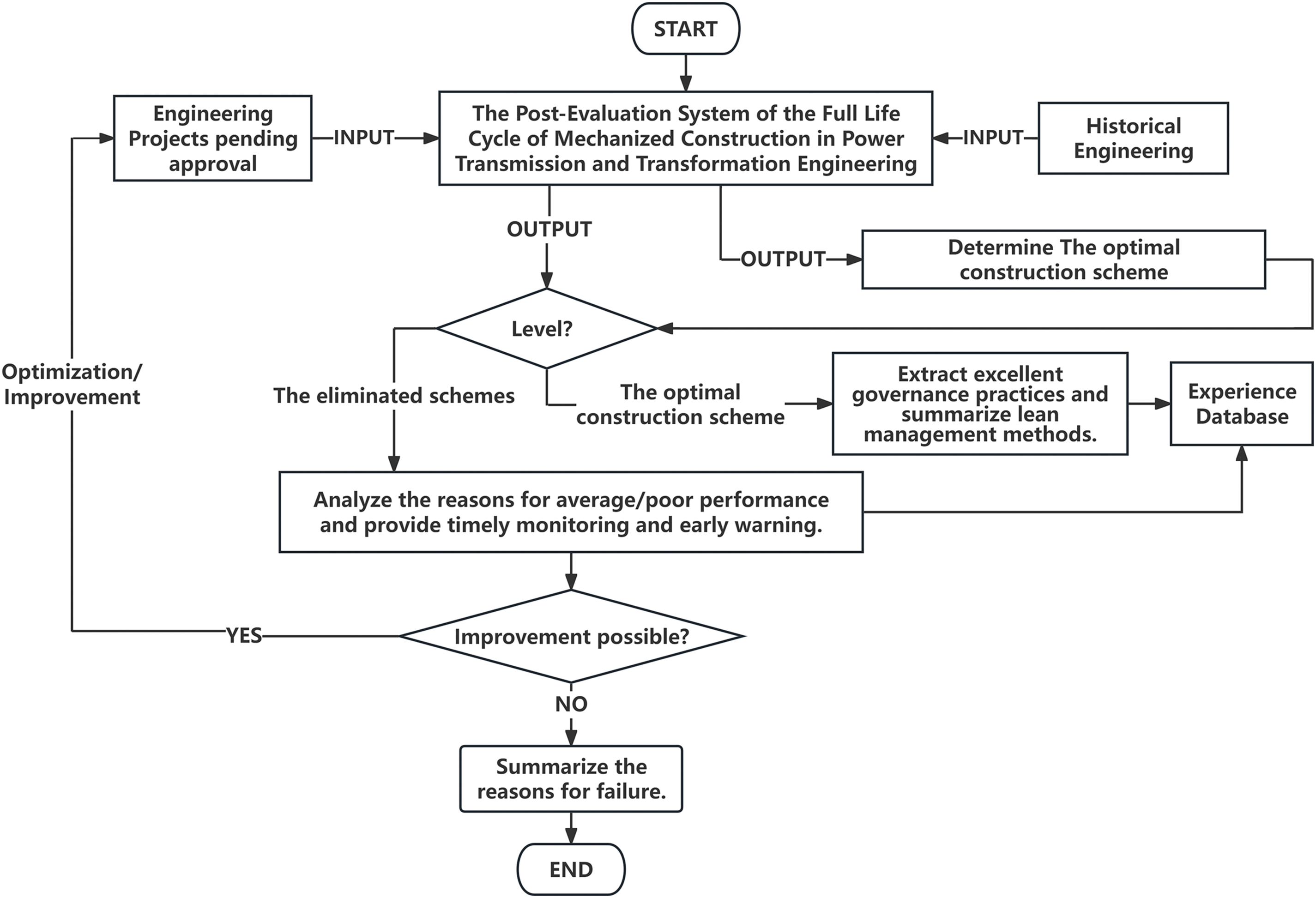
Figure 5: Process of the information feedback mechanism in the post-evaluation system for the full life cycle of mechanized construction in transmission and transformation projects

3.5 Post Evaluation of the Full Life Cycle of Mechanized Construction in Power Transmission and Transformation Projects

The post evaluation process for the full life cycle of mechanized construction in power transmission and transformation projects constructed in this article is shown in Fig. 6. Firstly, establish a post evaluation index system for the full life cycle of mechanized construction in power transmission and transformation projects. Use AHP and entropy weight method to determine the weights of the indicators, and optimize the subjective and objective weights using game theory to calculate the combined weights. Using the fuzzy grey relational projection sorting method to comprehensively evaluate the quality and efficiency of mechanized construction schemes for power transmission and transformation.

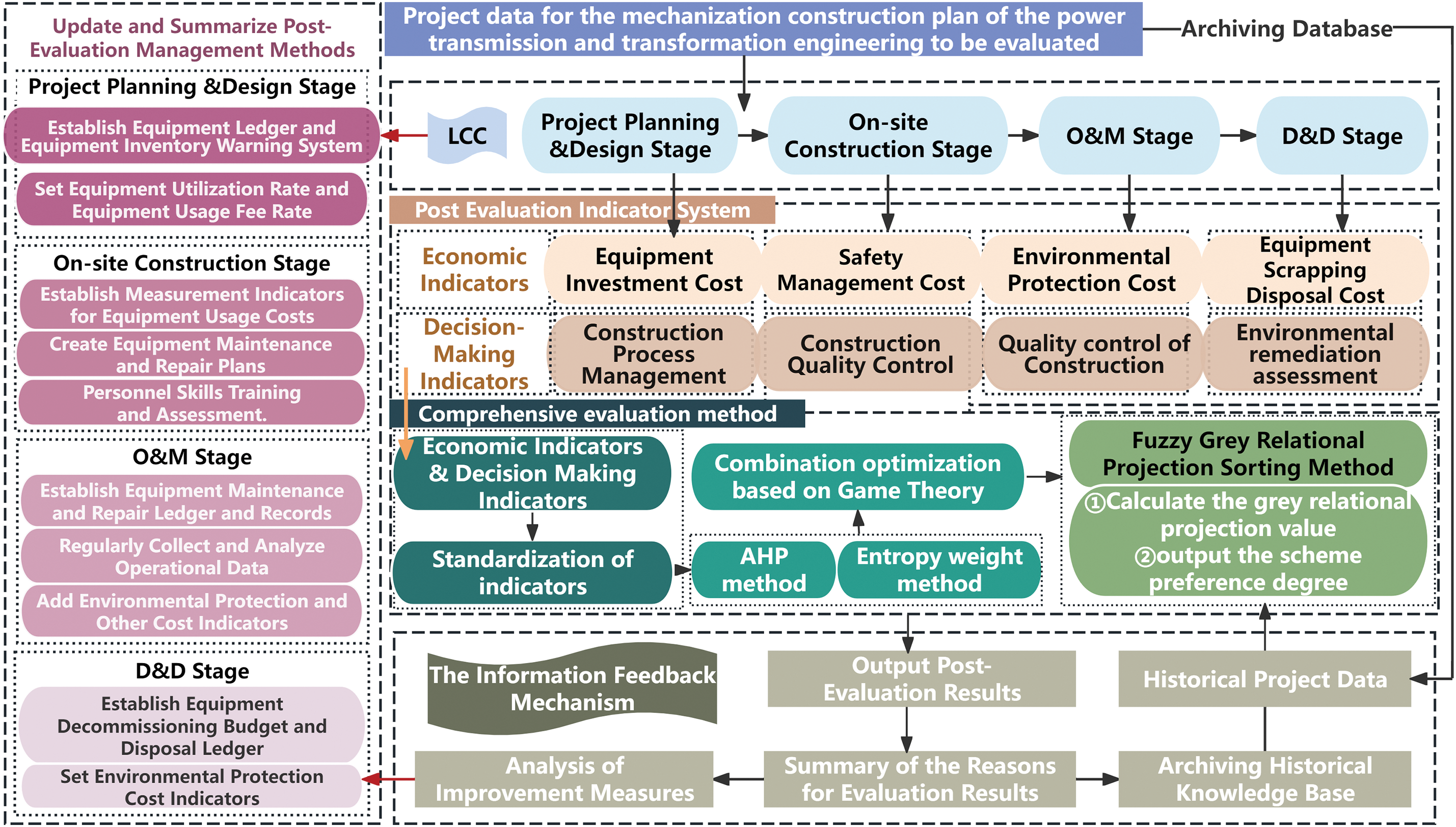
Figure 6: Post-evaluation system for the full life cycle of mechanized construction in power transmission and transformation projects

4  Example Analysis

4.1 Case Background

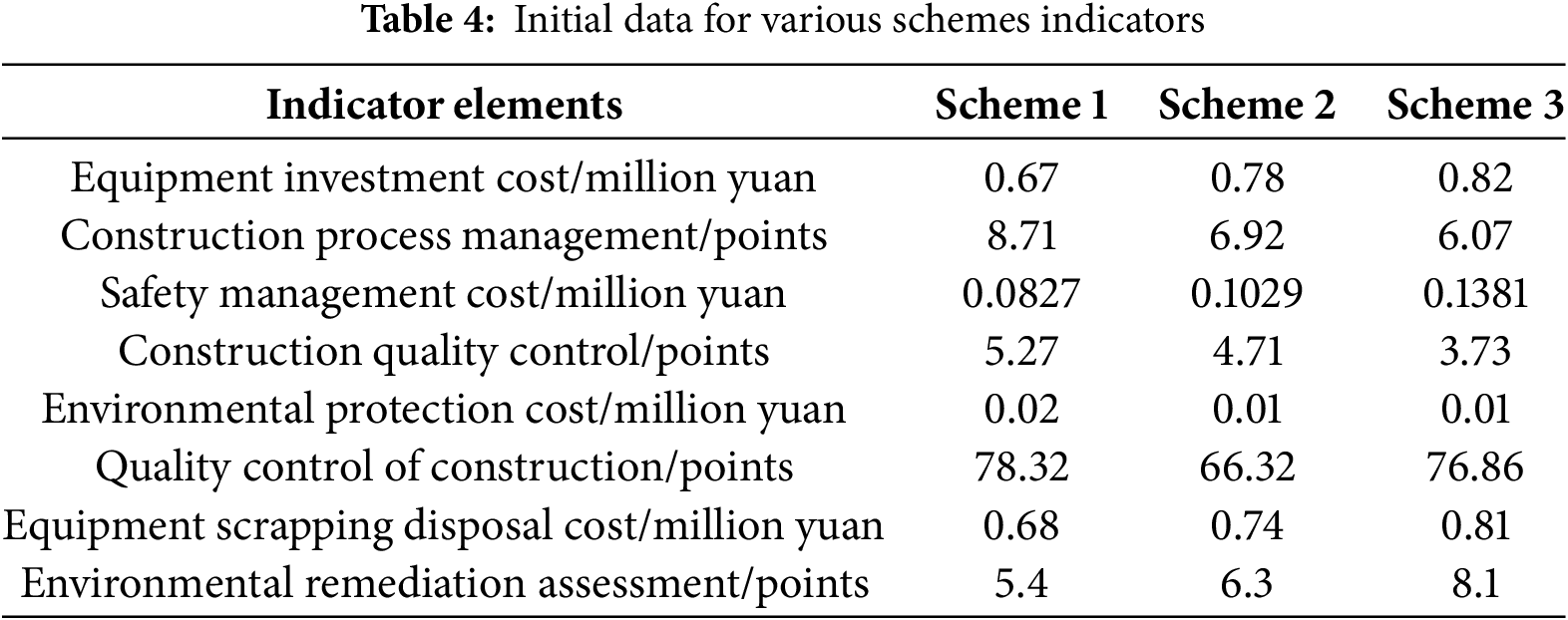
This article selects the 220 kV main transformer expansion project in Zhejiang Province to construct one main transformer with a capacity of 180 MVA; The main transformer is equipped with 3 × 8 Mvar and reactive power compensation capacitors; There are eight 10 kV outgoing lines. The project received initial design approval on 10 August 2024. The sustainability of three mechanized construction schemes for power transmission and transformation projects proposed by different contractors was evaluated using the method described in this article. The scheme data is detailed in Table 4.

4.2 Weight Determination

According to the indicator weight calculation method described in Section 3.2, combined with the importance of each indicator in the indicator system and the scoring of qualitative indicators by four relevant experts in the field, the subjective and objective weights of the sustainability evaluation indicators for the mechanized construction of the power transmission and transformation project are calculated through the AHP method and entropy weight method. The combination weight of the evaluation indicators is calculated using game theory. The subjective and objective weights and their combination weights of the secondary indicators are shown in Table 5, while the subjective and objective weights and their combination weights of the primary indicators are shown in Fig. 7. It can be seen that the weights of AHP indicators fluctuate greatly, and the reason for this is that they are easily influenced by the subjective opinions of various evaluation experts. The objective weights obtained by entropy weighting method, although relatively stable, cannot clearly reflect the differences between various indicators. In contrast, combination weights can simultaneously consider the will of decision-makers and the differences in indicator data, resulting in combination weights that fall between subjective and objective weights, making them more persuasive.

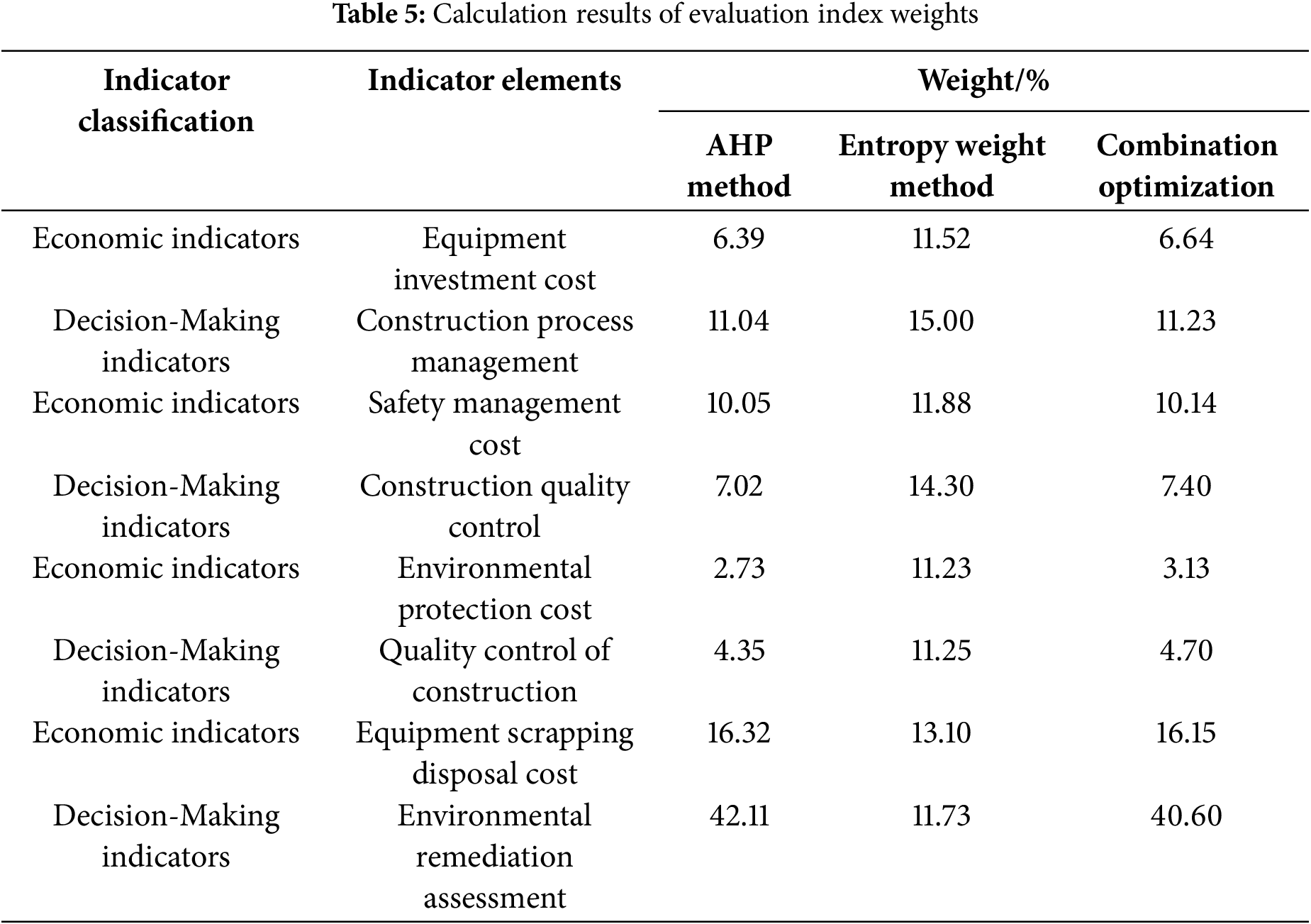
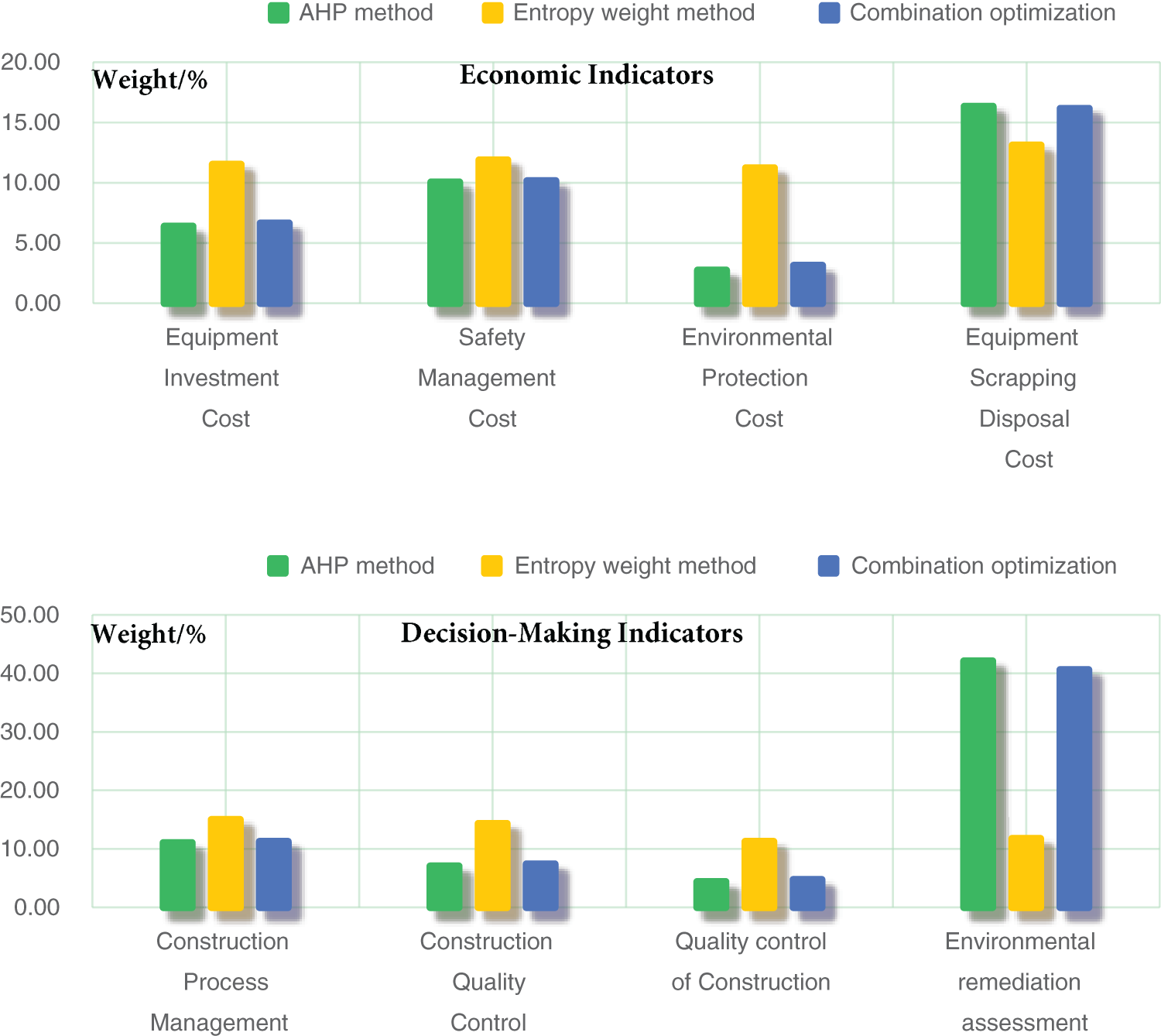
Figure 7: Post-evaluation system for the full life cycle of mechanized construction in power transmission and transformtion projects

4.3 Post-Evaluation Result Analysis

4.3.1 Engineering Quality Ranking

Based on the combined weight calculation results of the above indicators, the fuzzy grey correlation projection sorting method was used to analyze the three schemes, and the positive and negative grey correlation schemes values and membership degrees of each scheme were obtained, as shown in Table 6.

4.3.2 Post Evaluation Results of the Project

According to ui’s ranking of the three options, option u1>u2>u3 is obtained, so option 1 is the best. According to the comprehensive evaluation results, Scheme 1 performs the best in terms of sustainability. This plan prioritizes the use of economically efficient mechanized construction techniques, reasonably controls equipment investment and maintenance costs, and optimizes the allocation of safety management resources, significantly reducing the overall cost of the entire period while ensuring construction quality (with the highest Construction Quality Control index value). Although Scheme 3 performs well in the application of environmental protection technologies (such as outstanding environmental remediation assessment indicators), excessive reliance on high cost equipment leads to an increase in disposal costs, and there are significant fluctuations in construction quality control, resulting in an imbalance between overall benefits and investment. Although Scheme 2 has advantages in some environmental indicators, its construction management capability is weak (with the lowest Construction Process Management indicator value), and the stability of quality control is insufficient, making it difficult to achieve sustainable improvement of the entire life cycle benefits. Therefore, Scheme 1 has more comprehensive advantages in the coordinated optimization of economic benefits, construction quality, and safety management.

4.3.3 Application of Information Feedback Mechanism

Based on project data, the following two processes can be used to analyze the post evaluation system for the entire life cycle of mechanized construction in power transmission and transformation projects:

Process 1: Start → Evaluation Index System for the Whole Life Cycle of Mechanized Construction in power transmission and transformation projects → Evaluation Model for the Whole Life Cycle of Mechanized Construction in power transmission and transformation projects Based on Game Theory and Fuzzy Grey Projection → Substitute Historical Project Data into the Model → Decide on the Optimal Plan from Historical Project Data.

Process 2: Start → Evaluation index system for the full life cycle of mechanized construction in power transmission and transformation projects → Evaluation model for the full life cycle of mechanized construction in power transmission and transformation projects based on game theory and fuzzy grey projection → Substitute the construction plan of the project to be evaluated into the model → Output the results and compare them with the optimal plan in Process 1 to determine the optimal construction plan.

Taking the result of Section 4.3.2 as an example, the contracting party analyzed that the Safety Management Cost of the optimal construction plan 1 was relatively low, but it could achieve the best Construction Quality Control index among the three plans, which is worth learning from. Finally, this index was input into the experience database. For the eliminated construction plans 2 and 3, analyze that the indicators such as equipment investment cost and construction quality control in this plan need to be improved, and make revisions and improvements. Among them, in order to ensure the stable operation of power transmission and transformation, designated equipment must be used in project implementation. Therefore, indicators such as Equipment Investment Cost cannot be adjusted or corrected, and will be synchronously input into the experience database. If there are devices with higher cost-effectiveness in the next stage, this indicator will be further optimized and decided upon.

5  Conclusion and Outlook

1) The framework for mechanized construction of power transmission and transformation projects employs game theory to optimize the combination of subjective and objective weights, aiming to maximize collective interests. It also considers the grey and incomplete factors that influence the construction process, as well as the grey correlation between decision-making and economic indicators.

2) The mechanized construction plan for power transmission and transformation projects is evaluated to identify the optimal decision-making solution. Compared to traditional single-weighting methods, this model demonstrates greater applicability and decision sensitivity, offering a more efficient way to optimize construction plans tailored to the specific project.

3) The proposed mechanized construction framework for power transmission and transformation projects provides data-driven support and guidance for future power engineering construction planning. It also serves as a valuable reference for assessing the economic and social benefits of mechanized construction in these projects.

4) The current research primarily focuses on the routine aspects of mechanized construction in power transmission and transformation projects. Future studies can expand upon this work by incorporating factors such as the impact of electricity markets [26] and extreme weather [27].

Acknowledgement: We would like to express our sincere gratitude to Zhejiang Electric Transmission & Transformation Engineering Corporation for their invaluable support in data collection.

Funding Statement: This research received no external funding and was entirely supported by the author personally.

Availability of Data and Materials: The data used in this study are available from the corresponding author upon reasonable request.

Ethics Approval: This study was conducted in accordance with ethical standards. Informed consent was obtained from all participants (if applicable), and all data were collected and analyzed ethically and confidentially.

Conflicts of Interest: The author declares no conflicts of interest to report regarding the present study.

References

1. Zhang Y, Hua H. Carbon financial system construction under the background of dual-carbon targets: current situation, problems and suggestions. arXiv:2502.15807v1. 2025. [Google Scholar]

2. Ma Y, Mao P. Multiple benefits evaluation of mechanized construction of 110 kV transmission lines. In: The Proceedings of 2023 International Conference on Wireless Power Transfer (ICWPT2023). Singapore: Springer Nature Singapore; 2024. p. 669–78. doi:10.1007/978-981-97-0877-2_70. [Google Scholar] [CrossRef]

3. Liu X, Huang Y, Shi Y, Zheng Y. Thoughts on the transformation and development of mechanized and intelligent construction of pumped storage power stations under the dual carbon goal. J Phys Conf Ser. 2024;2752(1):012145. doi:10.1088/1742-6596/2752/1/012145. [Google Scholar] [CrossRef]

4. Zhu X, Ye M, Feng J, Ke Y, Wang Y, Chen C. Research on evaluation method of temporary road scheme in mechanized construction of transmission line. E3S Web Conf. 2024;520:04028. doi:10.1051/e3sconf/202452004028. [Google Scholar] [CrossRef]

5. Gao X, Wu J, Shi H, Wang R, Sun J, Li Y. A knowledge-enabled evaluation system for mechanized construction in power grid projects. In: 2024 4th International Conference on Energy, Power and Electrical Engineering (EPEE); 2024 Sep 20–22; Wuhan, China: IEEE; 2024. p. 1121–6. doi:10.1109/EPEE63731.2024.10875430. [Google Scholar] [CrossRef]

6. State Grid Corporation of China. State grid infrastructure [2023] No. 6. Beijing, China: State Grid Corporation of China; 2023. [Google Scholar]

7. Kayashima M, Noguchi Y. Toward the future of mechanized construction introduction and future prospects of mechanized constructions using digital information. Int J High Rise Build. 2022;11(2):16. [Google Scholar]

8. Liu Q, Liu F. Analysis on the key design points of the whole process mechanized construction of transmission lines. In: 2024 4th International Conference on New Energy and Power Engineering (ICNEPE); 2024 Nov 8–10; Guangzhou, China: IEEE; 2024. p. 391–8. doi:10.1109/ICNEPE64067.2024.10860612. [Google Scholar] [CrossRef]

9. Xie D, Guo T, Zhou F, Wu Y, Zhuan X. Optimization of mechanized construction scheme of overhead transmission line based on mechanization rate. In: 2020 39th Chinese Control Conference (CCC); 2020 Jul 27–29; Shenyang, China. IEEE; p. 1553–8. [Google Scholar]

10. Lyu Y, Luo Y, Jia Z, Fu S, Tang Y, Wang Q, et al. Benefit evaluation of HVAC and HVDC for offshore wind power transmission system under the multidimensional index. Electr Power Syst Res. 2024;237:111018. doi:10.1016/j.epsr.2024.111018. [Google Scholar] [CrossRef]

11. Li Z, Zhang W, He B, Xie L, Chen M, Li J, et al. A comprehensive life cycle assessment study of innovative bifacial photovoltaic applied on building. Energy. 2022;245:123212. doi:10.1016/j.energy.2022.123212. [Google Scholar] [CrossRef]

12. Du GEJ. Evaluation of power transmission and transformation projects using fuzzy multi-layer models. Int J Simul Syst Sci Technol. 2016. doi:10.5013/ijssst.a.17.47.21. [Google Scholar] [CrossRef]

13. Mejia-Giraldo D, Villarreal-Marimon J, Gu Y, He Y, Duan Z, Wang L. Sustainability and resiliency measures for long-term investment planning in integrated energy and transportation infrastructures. J Energy Eng. 2012;138(2):87–94. doi:10.1061/(asce)ey.1943-7897.0000067. [Google Scholar] [PubMed] [CrossRef]

14. Rahaman A, Noor KN, Abir TA, Rana S, Ali M. Design and analysis of sustainable green data center with hybrid energy sources. J Power Energy Eng. 2021;9(7):76–88. doi:10.4236/jpee.2021.97006. [Google Scholar] [CrossRef]

15. Qin W. Research on grey comprehensive evaluation of construction risk of power transmission and transformation based on AHP and VPRS. J Wuhan Univ Technol Inf Manag Eng. 2018;40(1):26–30,35. (In Chinese). [Google Scholar]

16. Li M, Wu W, Lin Y, Yan T, Huang P, Chen H. Decision-making model considering functional differences in transmission and transformation projects. In: 2020 5th Asia Conference on Power and Electrical Engineering (ACPEE); 2020 Jun 4–7; Chengdu, China. IEEE; 2020. p. 2124–30. doi:10.1109/acpee48638.2020.9136168. [Google Scholar] [CrossRef]

17. Sun HB, Zi JZ, Du DH, Cao XL, Zheng FY. Application of fuzzy comprehensive evaluation in post-evaluation of power transmission and transformation project. J Civil Archit Environ Eng. 2013;35(Z2):101–3. doi:10.1021/ic00205a025. [Google Scholar] [CrossRef]

18. Yin CG, Hou XL. Grey evaluation model for construction quality of UHV power transmission and transformation project based on combination weighting method. J Henan Univ Eng (Nat Sci Ed). 2017;3:53–9. [Google Scholar]

19. Zhou XG, Ling X, Chen WZ, Huang SH, Fu XQ. Research on the comprehensive evaluation index system of power grid considering energy storage. China Rural Water Hydropower. 2024;5:231–6. (In Chinese). doi:10.12396/znsd.231774. [Google Scholar] [CrossRef]

20. Liu Y, Zheng Y, Xin C. Multi-dimensional efficiency and benefit evaluation system of operation effect of power grid project cluster and corresponding application prospect. In: 2020 International Conference on Wireless Communications and Smart Grid (ICWCSG); 2020 Jun 12–14; Qingdao, China: IEEE; 2020. p. 292–5. doi:10.1109/icwcsg50807.2020.00069. [Google Scholar] [CrossRef]

21. Gao M. Research on the post-evaluation system of the entire life cycle of transmission and transformation engineering based on decision-making factors [Ph.D. dissertation]. Beijing, China: North China Electric Power University; 2021. doi:10.27140/d.cnki.ghbbu.2021.001589. [Google Scholar] [CrossRef]

22. Yao Y, Lian Z, Liu S, Hou Z. Hourly cooling load prediction by a combined forecasting model based on Analytic Hierarchy Process. Int J Therm Sci. 2004;43(11):1107–18. doi:10.1016/j.ijthermalsci.2004.02.009. [Google Scholar] [CrossRef]

23. Gao ZN, Zhou FH, Ge G, Jin YJ, Wang HL. Research on comprehensive evaluation of multi dimensional power market’s risks. Power Demand Side Manage. 2021;23(6):26–30. (In Chinese). [Google Scholar]

24. Jia M, Li M, Han S, Li Q. Research on the comprehensive evaluation system of rural power grids based on game theory combined weighting. J Electr Sci Technol. 2020;35(2):69–75. [Google Scholar]

25. Lu D, Xu C, Zhang L, Wang L. Comprehensive risk assessment method for power grids based on game theory weighting and grey relational projection. J Saf Sci Technol. 2019;15(9):170–5. doi:10.1088/1755-1315/453/1/012068. [Google Scholar] [CrossRef]

26. Xiao D, Chen H. Stochastic up to congestion bidding strategy in the nodal electricity markets considering risk management. IEEE Access. 2020;8:202428–38. doi:10.1109/access.2020.3015025. [Google Scholar] [CrossRef]

27. Zhang W, Shao C, Hu B, Xie K, Siano P, Li M, et al. Transmission defense hardening against typhoon disasters under decision-dependent uncertainty. IEEE Trans Power Syst. 2023;38(3):2653–65. doi:10.1109/TPWRS.2022.3194307. [Google Scholar] [CrossRef]