 Open Access
Open Access
ARTICLE
Buoyancy Effects in the Peristaltic Flow of a Prandtl-Eyring Nanofluid with Slip Boundaries
Department of Mathematics, Shaheed Benazir Bhutto Women University, Peshawar, 25000, Pakistan
* Corresponding Author: Hina Zahir. Email:
(This article belongs to the Special Issue: Electro- magnetohydrodynamic Nanoliquid Flow and Heat Transfer)
Fluid Dynamics & Materials Processing 2023, 19(6), 1507-1519. https://doi.org/10.32604/fdmp.2023.022520
Received 14 March 2022; Accepted 22 July 2022; Issue published 30 January 2023
Abstract
The interaction of nanoparticles with a peristaltic flow is analyzed considering a Prandtl-Eyring fluid under various conditions, such as the presence of a heat source/sink and slip effects in channels with a curvature. This problem has extensive background links with various fields in medical science such as chemotherapy and more in general nanotechnology. A similarity transformation is used to turn the original balance equations into a set of ordinary differential equations, which are then integrated numerically. The investigation reveals that nanofluids have valuable thermal capabilitises.Keywords
It is a fact that peristalsis appears in the stomach, esophagus, and intestines. Movement of the bolus into the digestive tract, transport of ovum, chyme, and spermatozoa in the reproductive tract represent peristaltic motion. Owing to its significance, several investigators have considered this phenomenon in articles. Nadeem et al. [1] analyzed peristalsis with sinusoidal walls in a duct. Further Ali et al. [2] discussed the thermodynamics of nonlinear convection in peristalsis. Gangavathi et al. [3] studied the peristaltic pumping in a porous medium. Narla et al. [4] investigated wave propagation by considering the peristaltic motion of spermatozoa. In straight microchannel, Waheed et al. [5] indicates heat stream in electromotive biofluid flow which involves the peristalsis. The peristaltic flow of viscoelastic fluid with the Hartmann boundary layer effect is investigated by Ali et al. [6]. Akram and Rashid discussed the peristaltic flow of Rabinowitsch and Williamson fluid respectively (see [7,8]). An experimental approach is discussed by Mirzaei et al. [9] in dialysis machines of peristaltic slug flows. Saleem et al. [10] and Akram et al. [11] also studied peristaltic flow in different channels.
In the heat transfer process, when free and forced convection both takes part, it is then known as mixed convection. In several technological and scientific fields such as biology, geology chemical processes, astrophysics, etc., this effect is utilized. The importance of peristalsis with convective heat exchange cannot be underestimated as it has several examples, i.e., in translocation of water in tall trees, solar ponds, dynamic of lakes, diffusion of nutrients out of blood, lubrication and drying technologies, oxygenation, hemodialysis, and nuclear reactors. Also due to, its vast usage different researchers work on it. Akbar et al. [12] found irreversibility rate with taking mixed convective effect. Mixed Marangoni flow of copper hybrid and aluminum oxide nanofluid is discussed by Li et al. [13]. Song et al. also discussed mixed convection in rotating and inclined channels respectively (see [14,15]).
Nanomaterial is a mixture of nanoparticles and base fluid. Nanomaterials hold great significance in textile fiber production, cooling of fluid in nuclear reactors, reservoirs of petroleum, cancer therapy, and surgical processes. This phenomenon was first studied by Choi et al. [16]. Hayat et al. [17] considered this phenomenon for the peristaltic flow of fourth-grade fluid. Bashir et al. [18] considered magnetic flux and Fourier/Ficks theories on effects in the peristaltic motion of Carreau-Yasuda nanofluid. Zahid et al. [19] showed informative results by taking hybrid nanofluid with entropy effect. Thermal analysis in curved microchannels via nanofluids is investigated by Akram et al. [20]. Further research in this context can be seen through refs. [21–29].
The present investigation aims to venture further into the regime of peristaltic transport of nanofluids with base material satisfying rheological characteristics. A curved channel curve is considered for the description of a more realistic situation. Peristaltic transport of Prandtl-Eyring nanofluid (as this fluid consideration is significant for various applications in biomedicine and engineering) in a curved channel is examined subject to mixed convection, radiation, and heat generation/absorption. Unlike the traditional attempts, the partial slip features for temperature, velocity, and concentration are implemented. Governing flow problem is simulated numerically. The physical interpretation is arranged and some conclusions are pointed out.
Here peristaltic transport of Prandtl--Eyring nanofluid in the curved channel is examined. The coordinate system
where
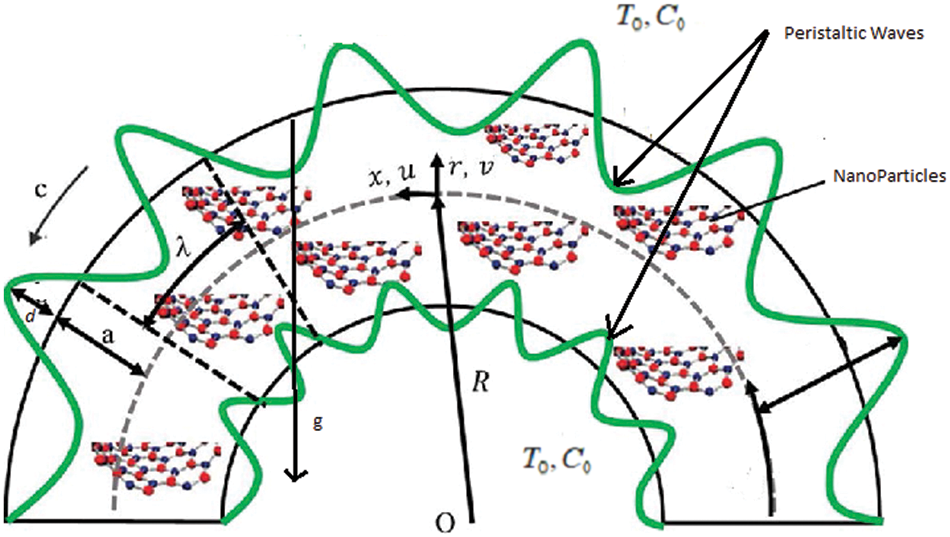
Figure 1: Schematic representation of the electroosmotically modulated peristaltic propulsion in the curved microchannel
Governing equations can be formulated under the considered assumptions (see [5,8,10]):
Continuity Equation:
Momentum Equations:
Heat Equation:
Concentration Equation:
Prandtl fluid’s stress tensor is given by
In the above equations velocity field is represented by
Velocity, temperature, and concentration slip boundary conditions are given by
Compliant Wall Condition:
Here boundary slip, elastic parameter, damping, and mass/area are denoted by
We use
And applying long wavelength and small Reynolds number approximations one obtains
Here
Non-dimensional conditions are
Non-dimensional stress component is
in which
The rate of heat transfer coefficient Z can be defined as
In the above-mentioned descriptions, the system of non-linear coupled equations is derived whose exact solutions are difficult to obtain by solving explicitly. However, during the last few decades, the advancement of techniques come up with more effective ways to solve non-linear problems. Thus present problem can be tackled by the NDSolve routine of Mathematica which is a built-in solver of the mathematical software. Such a technique is useful for choosing a suitable algorithm automatically and it will track errors from provided maximum to minimum range. Further, it provides graphical illustrations directly and intricated solution expressions are avoided.
The behavior of the obtained solutions is visualized by plotting the graphs for different flow properties such as velocity, thermal distribution, heat transfer coefficient, etc., in the given section.
In this subsection graphs of velocity for various parameters of interest are plotted. The influence of the curvature parameter on the velocity profile u is shown in Fig. 2. For larger k the velocity has dual behavior. In the lower half of the channel u decays while velocity is increased in the upper half of the channel. Because of the non-symmetry of velocity about the center line in a curved channel. In Fig. 3 increasing behavior of fluid velocity is observed for a rise in the wall parameters
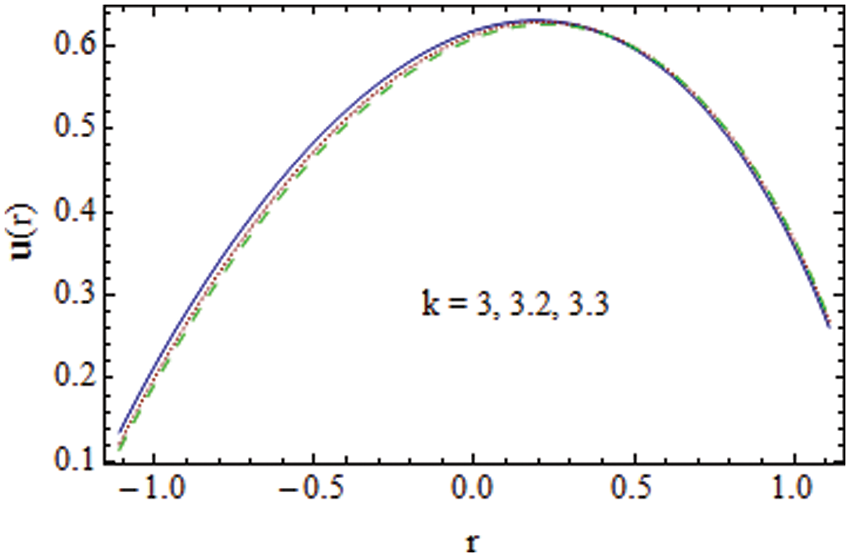
Figure 2:
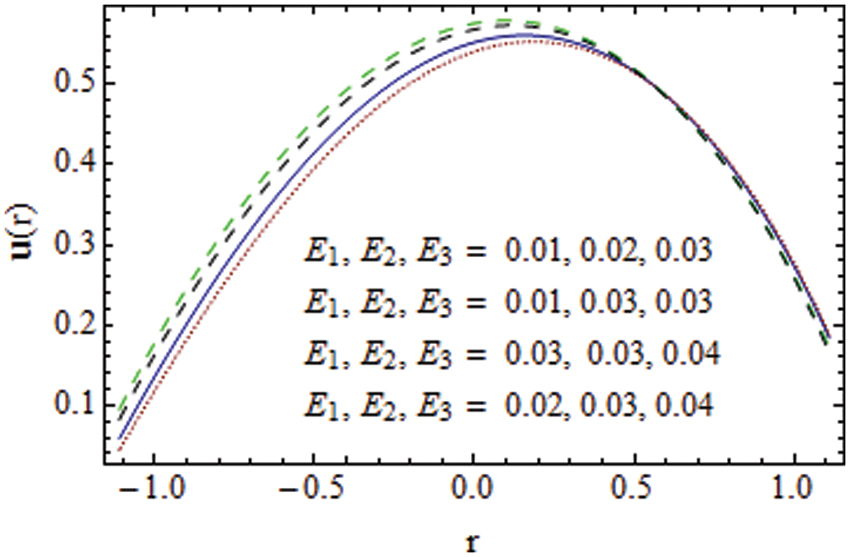
Figure 3:
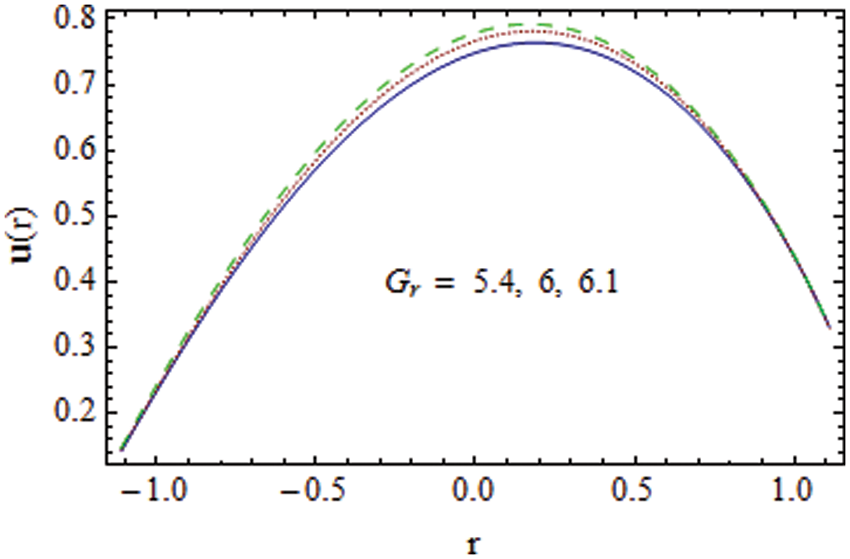
Figure 4:
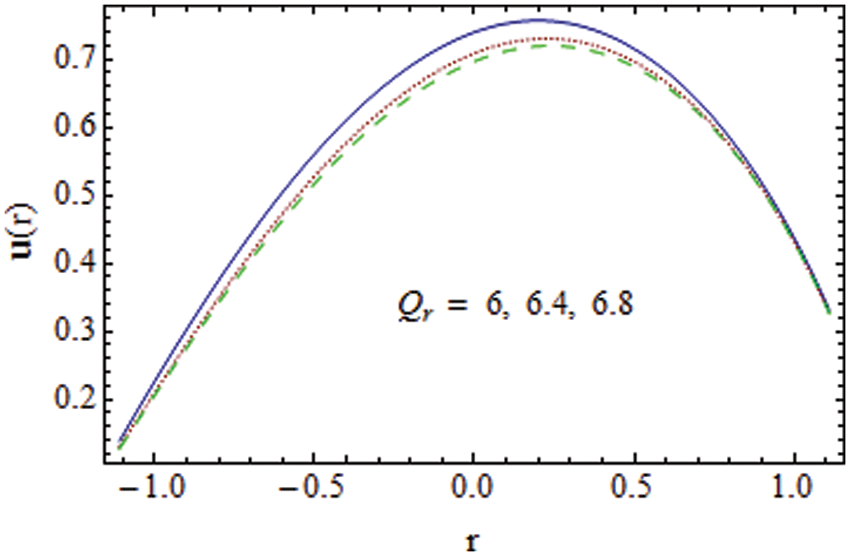
Figure 5:
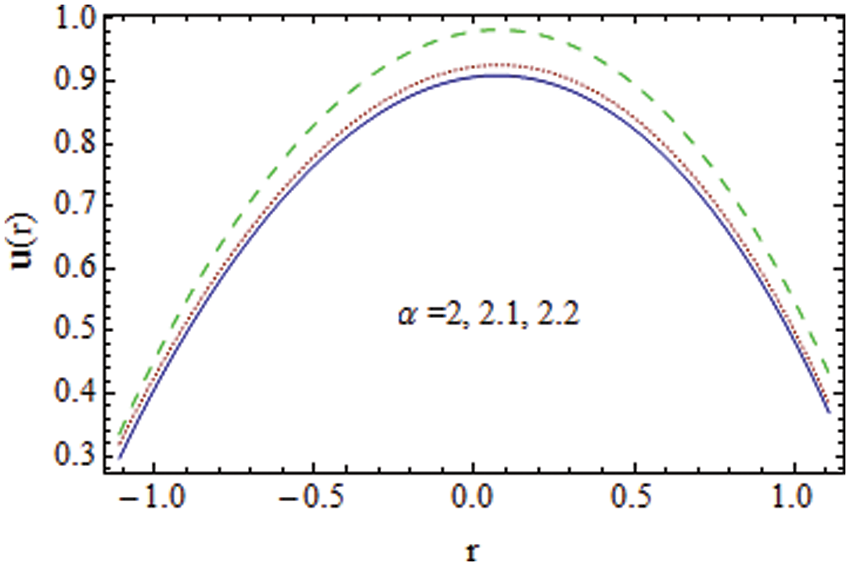
Figure 6:

Figure 7:
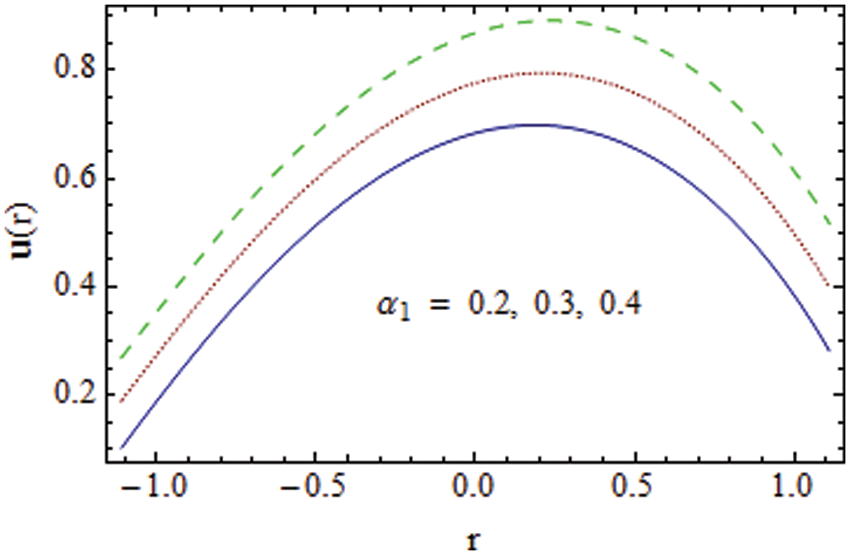
Figure 8:
Increasing behavior of thermal slip
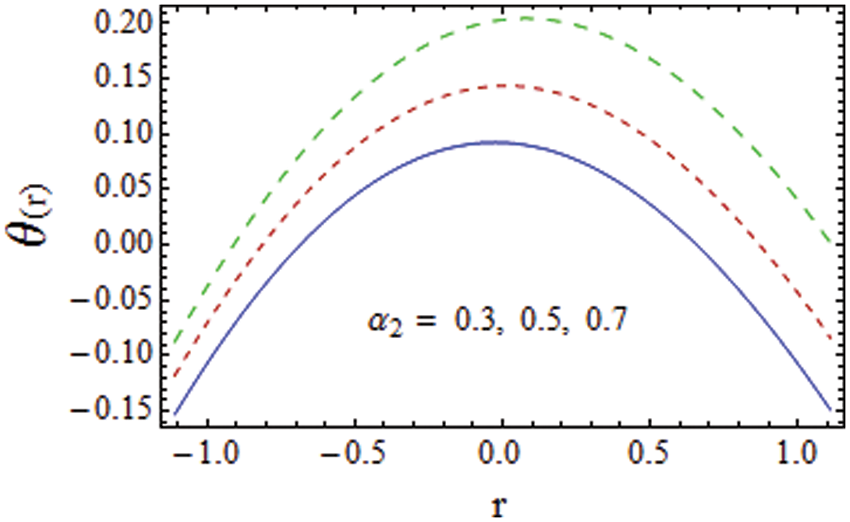
Figure 9:
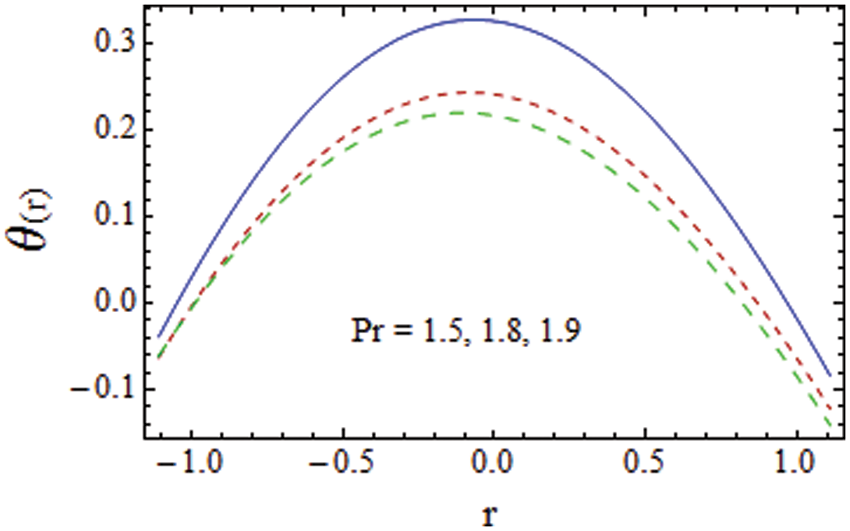
Figure 10:
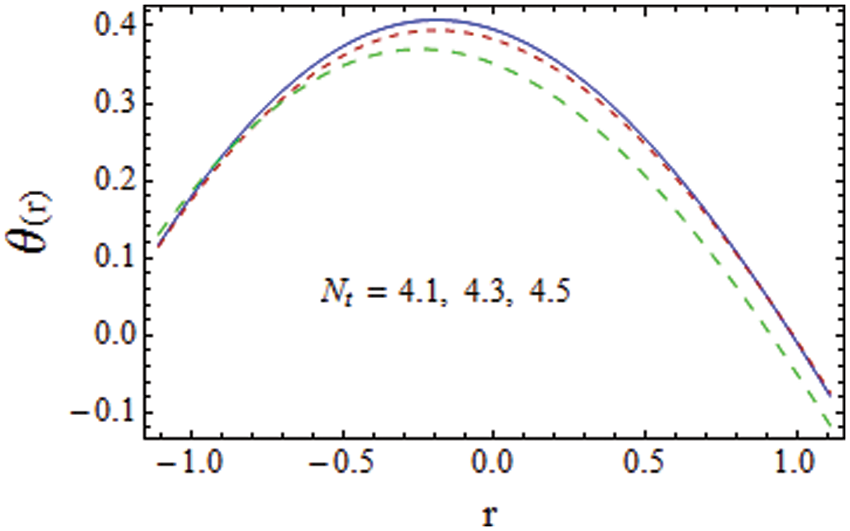
Figure 11:
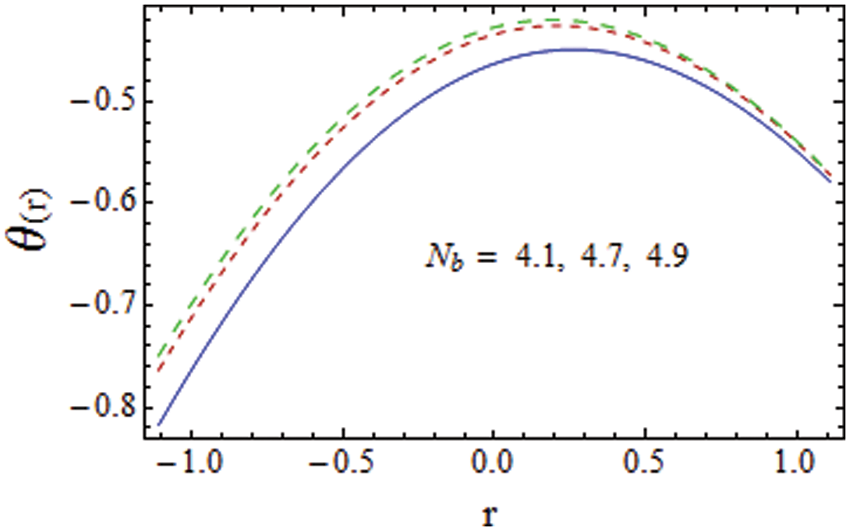
Figure 12:
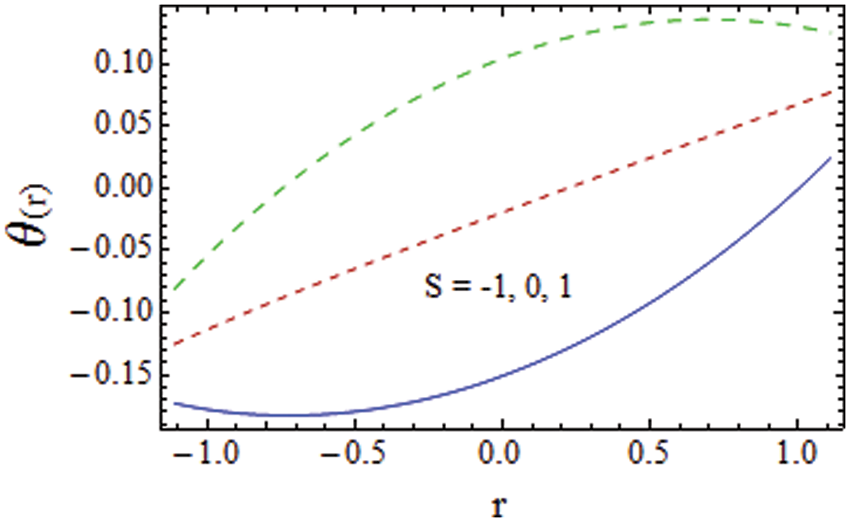
Figure 13:
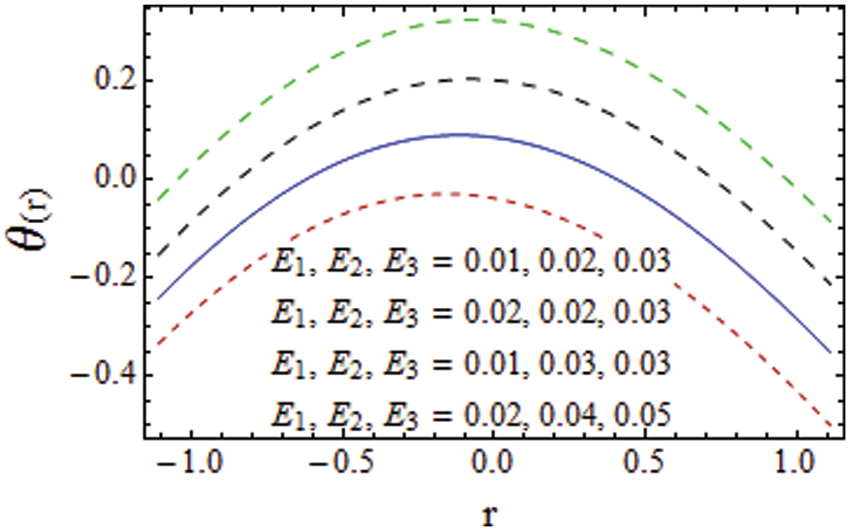
Figure 14: I E1, E2, E3 on the thermal field
The impact of various parameters on heat transfer coefficient Z is discussed in this section through Figs. 15–17. By increasing Brownian diffusion
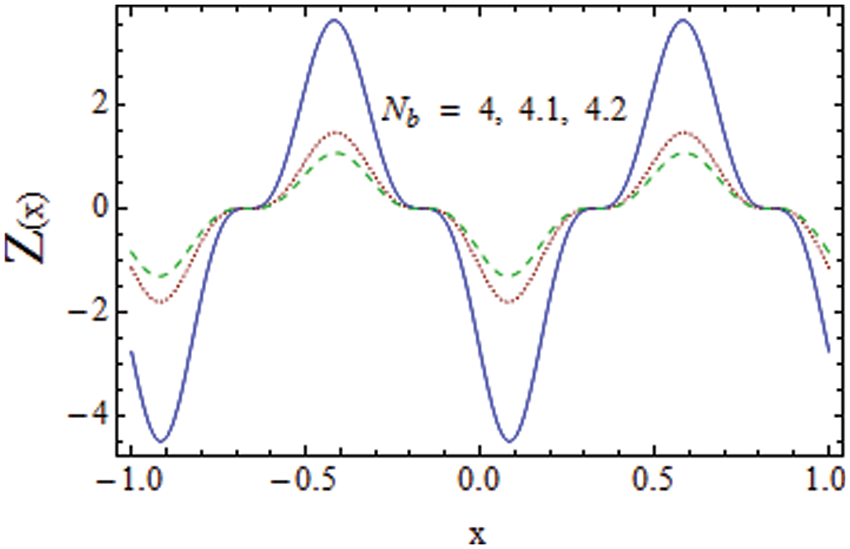
Figure 15:
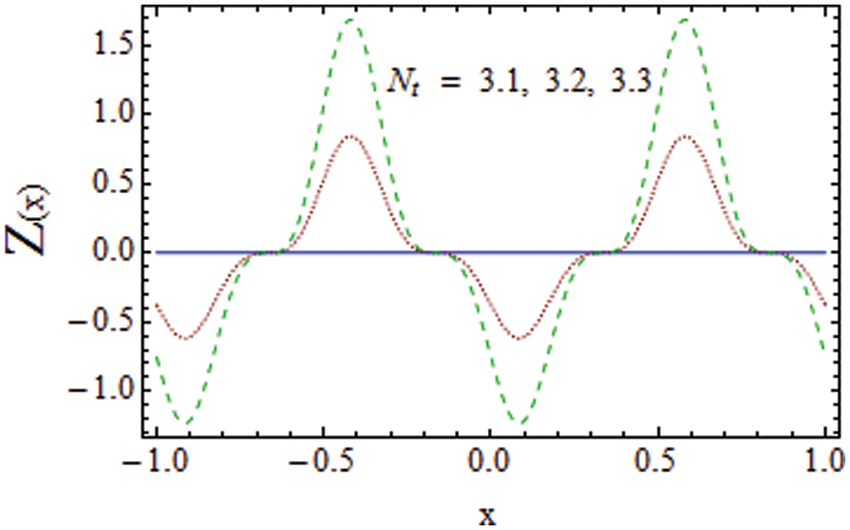
Figure 16:
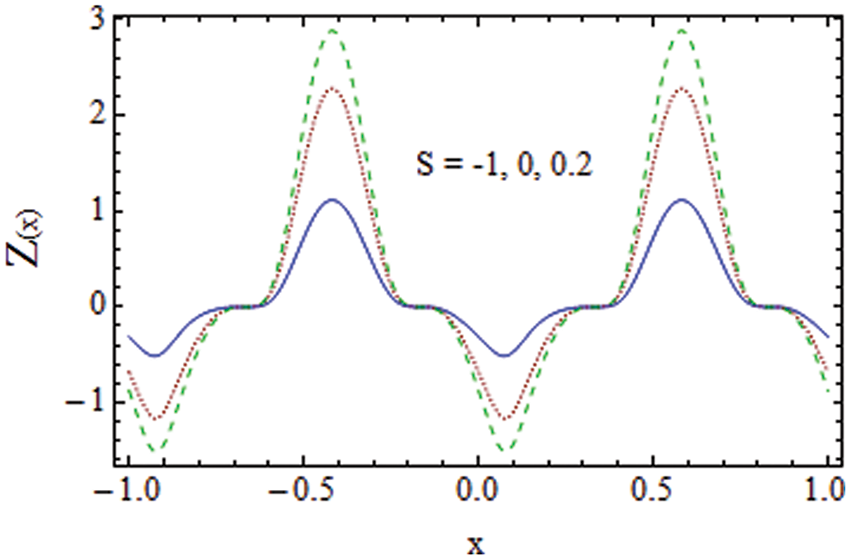
Figure 17: S on heat transfer coefficient
Effects of involved parameters on
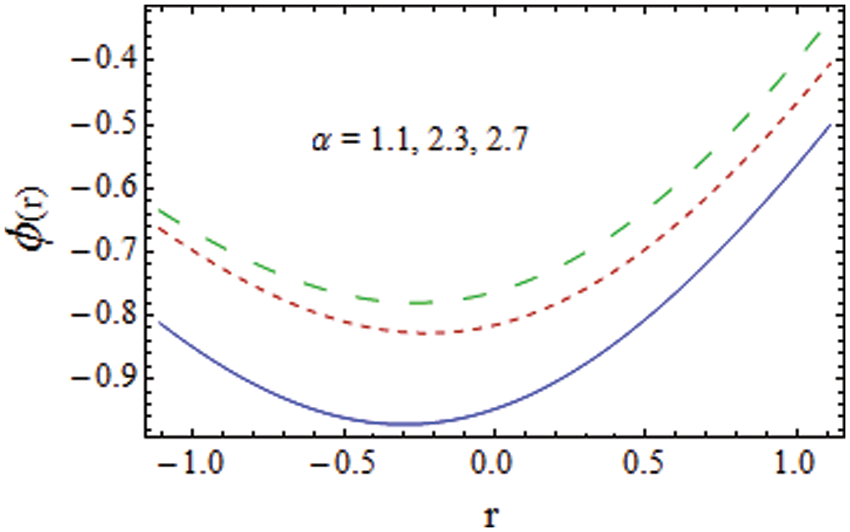
Figure 18: Impact of
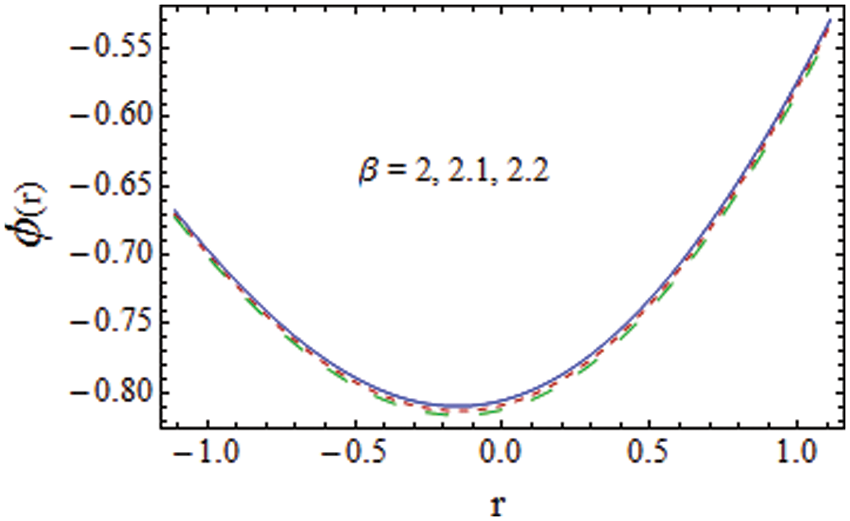
Figure 19: Impact of
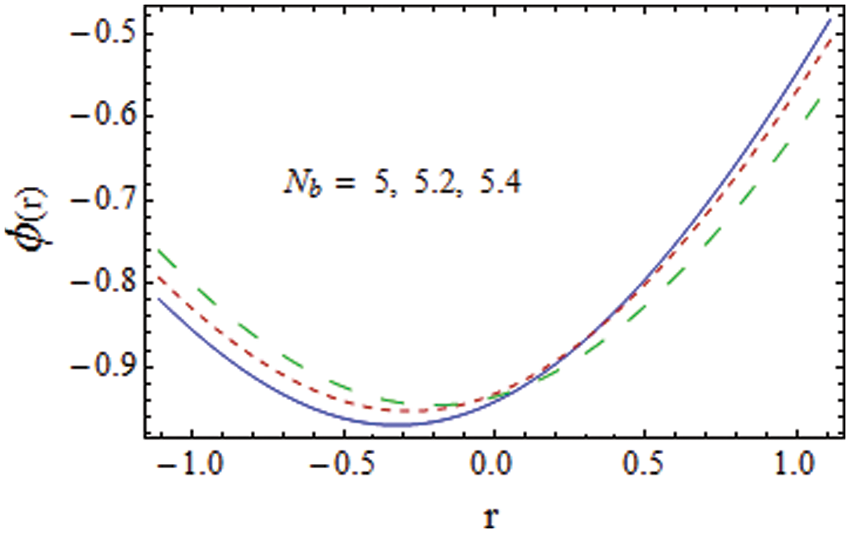
Figure 20: Impact of
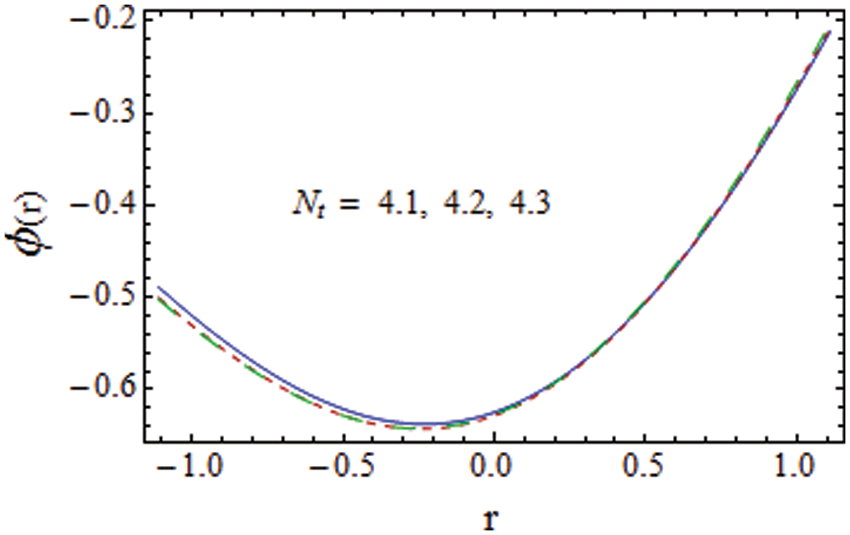
Figure 21: Impact of
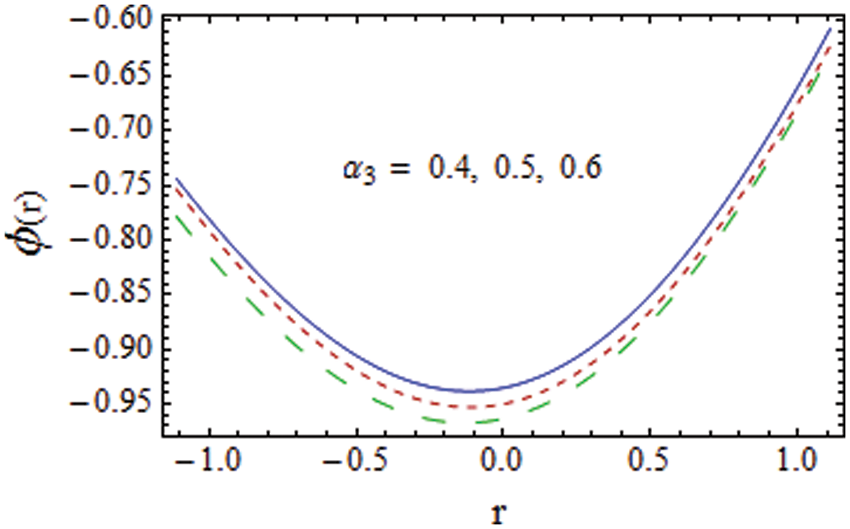
Figure 22: Impact of
Fig. 23 examines the impact of k on temperature. Here bolus size decays and the number of circulation increases for larger
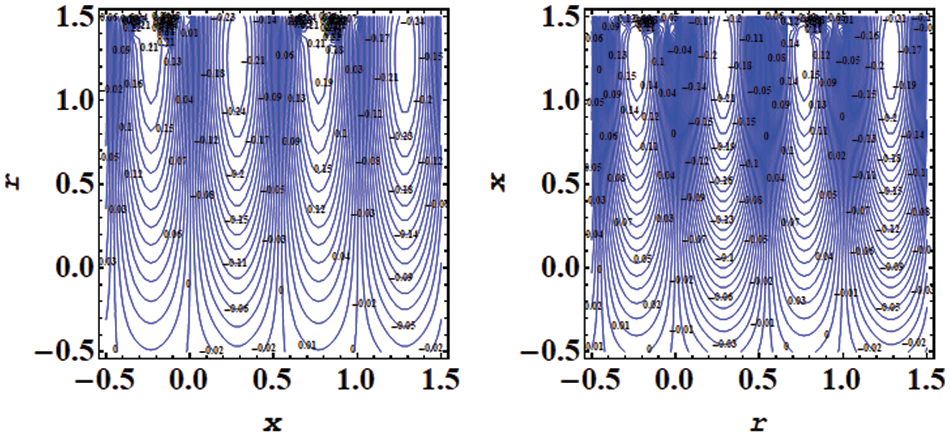
Figure 23: Impact of streamlines for various values of
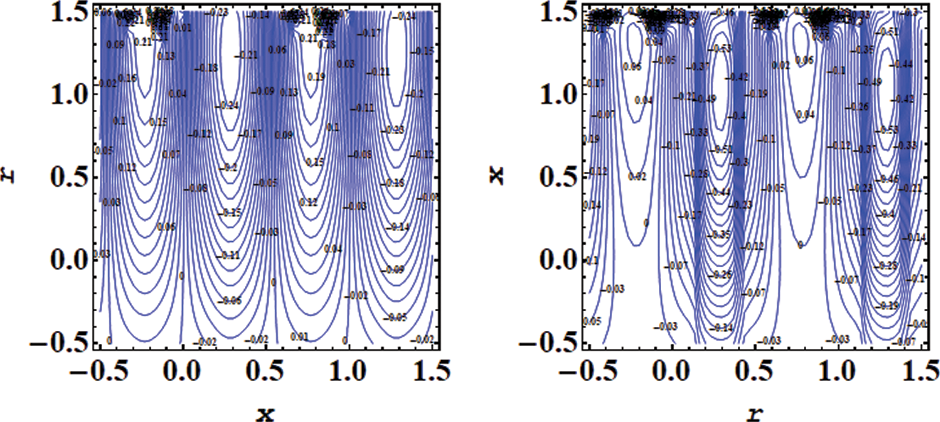
Figure 24: Impact of streamlines for various values of
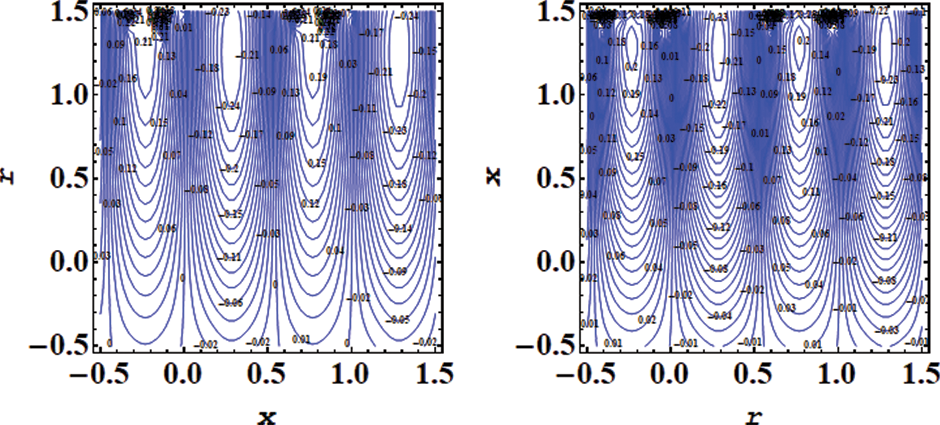
Figure 25: Impact of streamlines for various values of
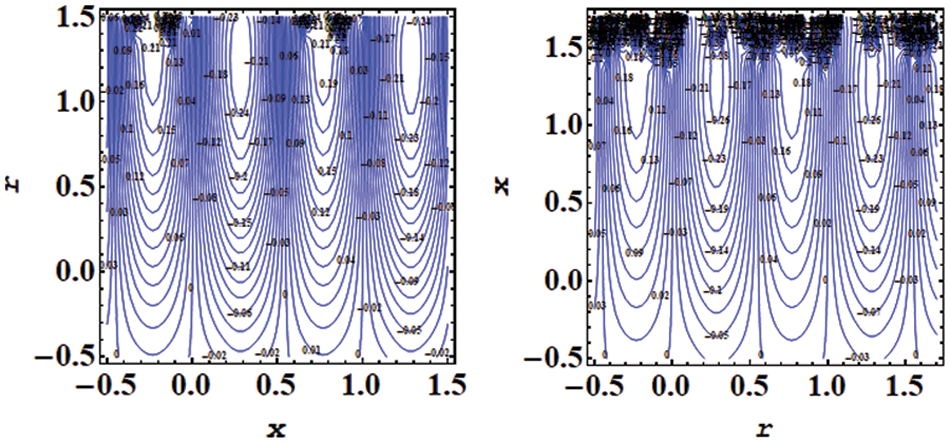
Figure 26: Impact of streamlines for various values of
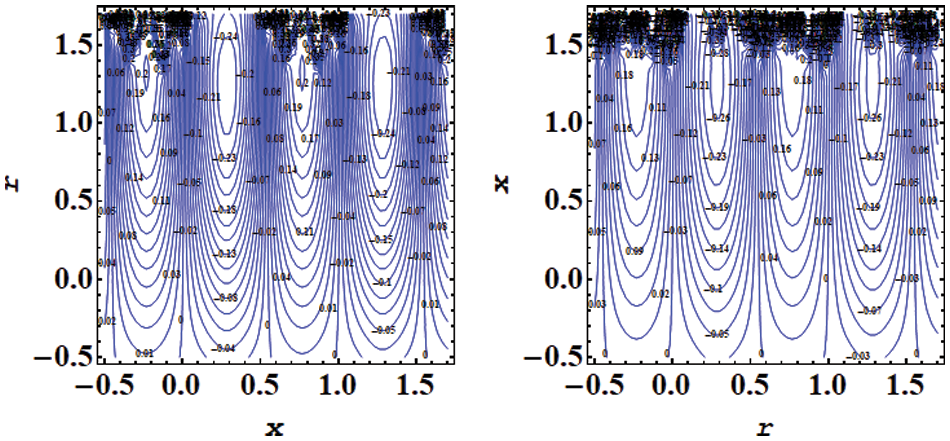
Figure 27: Impact of streamlines for various values of
Here an investigation is being carried out on the peristaltic flow of Prandtl fluid in the presence of mixed convection across a curved channel and the influence of heat source/sink is also accounted. The following key features of the analysis are worth mentioning:
• Fluid parameters tend to increase velocity.
• The opposite behavior is noticed for Grashof numbers
• Similar behavior is observed for thermophoresis and Brownian motion on temperature and concentration.
• Velocity and temperature show enhancement for wall parameters whereas temperature decays for damping parameters.
• For a larger heat source/sink, the temperature and heat transfer coefficient rises.
• Heat transfer for thermophoresis and Brownian motion parameters has an opposite response.
• Outcomes of slip parameters on velocity and temperature are similar.
Funding Statement: The author received no specific funding for this study.
Conflicts of Interest: The author declares that they have no conflicts of interest to report regarding the present study.
References
1. Nadeem, S., Akhtar, S., Alharbi, F. M., Saleem, S., Issakhov, A. (2022). Analysis of heat and mass transfer on the peristaltic flow in a duct with sinusoidal walls: Exact solutions of coupled PDEs. Alexandria Engineering Journal, 61(5), 4107–4117. DOI 10.1016/j.aej.2021.08.087. [Google Scholar] [CrossRef]
2. Ali, Z., Qasim, M., Ashraf, M. U. (2021). Thermodynamic analysis of nonlinear convection in peristaltic flow. International Communication in Heat and Mass Transfer, 129, 105686. DOI 10.1016/j.icheatmasstransfer.2021.105686. [Google Scholar] [CrossRef]
3. Gangavathi, P., Jyothi, S., Subba Reddy, M. V., Yogeswara Reddy, P. (2021). Slip and hall effects on the peristaltic flow of a jeffrey fluid through a porous medium in an inclined channel. Materialstoday Procedures. DOI 10.1016/j.matpr.2021.05.696. [Google Scholar] [CrossRef]
4. Narla, V. K., Tripathi, D. (2020). Entropy and energy analysis on peristaltic pumping in a curved narrow channel. Heat Transfer, 49(6), 3357–3373. DOI 10.1002/htj.21777. [Google Scholar] [CrossRef]
5. Waheed, S., Lu, D. C., Tripathi, D. (2021). Heat stream in electroosmotic bio-fluid flow in straight microchannel via peristalsis. International Communications in Heat and Mass Transfer, 123, 105180. DOI 10.1016/j.icheatmasstransfer.2021.105180. [Google Scholar] [CrossRef]
6. Ali, A., Awais, M., Al-Zubaidi, A., Saleem, S., Marwat, D. N. K. (2022). Hartmann boundary layer in peristaltic flow for viscoelastic fluid: Existence. Ain Shams Engineering Journal, 13(2), 101555. DOI 10.1016/j.asej.2021.08.001. [Google Scholar] [CrossRef]
7. Akram, J., Akbar, N. S., Tripathi, D. (2021). Entropy generation in electroosmotically aided peristaltic pumping of MoS2 rabinowitsch nanofluid. Fluid Dynamics Research, 54(1), 015507. DOI 10.1088/1873-7005/ac4e7b. [Google Scholar] [CrossRef]
8. Rashid, M., Ansar, K., Nadeem, S. (2020). Effects of induced magnetic field for peristaltic flow of williamson fluid in a curved channel. Physica A: Statistical Mechanics and its Applications, 553, 123979. DOI 10.1016/j.physa.2019.123979. [Google Scholar] [CrossRef]
9. Mirzaei, M., Parrany, M. (2021). An experimental study on real–time analysis of two-phase peristaltic slug flows in dialysis machines. Flow Measurement and Instrumentation, 79, 101941. DOI 10.1016/j.flowmeasinst.2021.101941. [Google Scholar] [CrossRef]
10. Saleem, A., Akhtar, S., Alharbi, F. M., Nadeem, S., Ghalambaz, M. et al. (2020). Physical aspects of peristaltic flow of hybrid nanofluid inside a curved tube having a ciliated wall. Results in Physics, 19, 103431. DOI 10.1016/j.rinp.2020.103431. [Google Scholar] [CrossRef]
11. Akram, S., Saleem, N., Umair, M. Y., Munawar, S. (2021). Impact of partial slip and lateral walls on peristaltic transport of a couple stress fluid in a rectangular duct. Science Progress, 104(2), 1–17. DOI 10.1177/00368504211013632. [Google Scholar] [CrossRef]
12. Akbar, Y., Abbasi, F. M., Zahid, U. M., Shehzad, S. A. (2021). Effectiveness of heat and mass transfer on mixed convective peristaltic motion of nanofluid with irreversibility rate. Communications in Theoretical Physics, 73(10), 105004. DOI 10.1088/1572-9494/ac10bf. [Google Scholar] [CrossRef]
13. Li, X. L., Khan, M., Punith Gowda, R. J., Ali, A., Shahid, F. et al. (2021). Dynamics of aluminum oxide and copper hybrid nanofluid in nonlinear mixed marangoni convective flow with entropy generation: Applications to renewable energy. Chinese Journal of Physics, 73(1), 275–287. DOI 10.1016/j.cjph.2021.06.004. [Google Scholar] [CrossRef]
14. Song, Y. Q., Khan, S. A., Imran, M., Waqas, H., Khan, S. U. et al. (2021). Applications of modified darcy law and nonlinear thermal radiation in bioconvection flow of micropolar nanofluid over an off centered rotating disk. Alexandria Engineering Journal, 60(5), 4607–4618. DOI 10.1016/j.aej.2021.03.053. [Google Scholar] [CrossRef]
15. Vedavathi, N., Dharmaiah, G., Abdul Gaffar, S., Venkatadri, K. (2021). Entropy analysis of nanofluid magnetohydrodynamic convection flow past an inclined surface: A numerical review. Heat Transfer, 50, 5996–6021. DOI 10.1002/htj.22159. [Google Scholar] [CrossRef]
16. Choi, S. U., Eastman, J. A. (1995). Enhancing thermal conductivity of the fluids with nanoparticles. ASME International Mechanical Engineering Congress & Expositions, vol. 231, pp. 99–105. Argonne. [Google Scholar]
17. Hayat, T., Nisar, Z., Alsaedi, A. (2020). Impacts of slip in radiative MHD peristaltic flow of fourth-grade nanomaterial with chemical reaction. International Communication in Heat and Mass Transfer, 119, 104976. [Google Scholar]
18. Bashir, S., Ramzan, M., Chung, J. D., Chu, Y. M., Kadry, S. (2021). Analyzing the impact of induced magnetic flux and fourier’s and fick’s theories on the carreau-yasuda nanofluid flow. Science Report, 9230. DOI 10.1038/s41598-021-87831-6. [Google Scholar] [CrossRef]
19. Zahid, U. M., Akbar, Y., Abbasi, F. M. (2020). Entropy generation analysis for peristaltically driven flow of hybrid nanofluid. Chinese Journal of Physics, 67, 330–348. DOI 10.1016/j.cjph.2020.07.009. [Google Scholar] [CrossRef]
20. Akram, J., Akbar, N. S., Tripathi, D. (2021). Thermal analysis on MHD flow of ethylene glycol-based BNNTs nanofluids via peristaltically induced electroosmotic pumping in a curved microchannel. Arabian Journal for Science and Engineering, 47, 7487–7503. DOI 10.1007/s13369-021-06173-7. [Google Scholar] [CrossRef]
21. Narla, V. K., Tripathi, D., AnwarBég, O. (2020). Electro-osmotic nanofluid flow in a curved microchannel. Chinese Journal of Physics, 67, 544–558. DOI 10.1016/j.cjph.2020.08.010. [Google Scholar] [CrossRef]
22. Aldabesh, A., Khan, S. U., Habib, D., Waqas, H., Tilili, A. et al. (2020). Unsteady transient slip flow of williamson nanofluid containing gyrotactic microorganism and activation energy. Alexandria Engineering Journal, 59(6), 4315–4328. DOI 10.1016/j.aej.2020.07.036. [Google Scholar] [CrossRef]
23. Ali, B., Thumma, T., Habib, D., Salamat, N., Riaz, S. (2022). Finite element analysis on transient MHD 3D rotating flow of Maxwell and tangent hyperbolic nanofluid past a bidirectional stretching sheet with cattaneo christov heat flux model. Thermal Science and Engineering Progress, 28, 101089. DOI 10.1016/j.tsep.2021.101089. [Google Scholar] [CrossRef]
24. Ali, B., Siddique, I., Ahmadian, A., Senu, N., Ali, L. et al. (2022). Significance of lorentz and coriolis forces on dynamics of water-based silver tiny particles via finite element simulation. Ain Shams Engineering Journal, 13(2), 101572. DOI 10.1016/j.asej.2021.08.014. [Google Scholar] [CrossRef]
25. Ali, B., Siddique, I., Khan, I., Masood, B., Hussain, S. (2021). Magnetic dipole and thermal radiation effects on hybrid base micropolar CNTs flow over a stretching sheet: Finite element method approach. Results in Physics, 25, 104145. DOI 10.1016/j.rinp.2021.104145. [Google Scholar] [CrossRef]
26. Tamizharasi, P., Vijayaragavan, R., Magesh, A. (2021). Heat and mass transfer analysis of the peristaltic driven flow of a nanofluid in an asymmetric channel. PDEs Applied Mathematics, 4, 100087. DOI 10.1016/j.padiff.2021.100087. [Google Scholar] [CrossRef]
27. McCash, L. B., Akhtar, S., Nadeem, S., Saleem, S. (2021). Entropy analysis of the peristaltic flow of hybrid nanofluid inside an elliptic duct with sinusoidally advancing boundaries. Entropy, 23, 732. DOI 10.3390/e23060732. [Google Scholar] [CrossRef]
28. Ahmed, B., Hayat, T., Alsaedi, A., Abbasi, F. M. (2020). Entropy generation analysis for peristaltic motion of carreau–Yasuda nanomaterial. Physica Scripta, 95(5), 055804. DOI 10.1088/1402-4896/ab4550. [Google Scholar] [CrossRef]
29. Nisar, Z., Hayat, T., Alsaedi, A., Ahmad, B. (2022). Significance of activation energy in radiative peristaltic transport of eyring-powell nanofluid. International Communications in Heat and Mass Transfer, 116, 104655. DOI 10.1016/j.icheatmasstransfer.2020.104655. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools