 Open Access
Open Access
ARTICLE
Influence of the Inclination Angle on Mixed Convection and Heat Transfer in a “T” Shaped Double Enclosure
1 Polymer Physics and Critical Phenomena Laboratory, Department of Physics, Faculty of Sciences of Ben M’Sik, Hassan II University, Casablanca, Morocco
2 Laboratory of Control and Mechanical Characterization of Materials and Structures, National Higher School of Electricity and Mechanics, Hassan II University, Casablanca, Morocco
3 Laboratory of Electrical Systems and Telecommunications, Department of Applied Physics, FST, Hassan 1st University, Settat, Morocco
4 Laboratory of Engineering Industrial Management and Innovation, FST, Hassan 1st University, Settat, Morocco
* Corresponding Author: M’Barka Mourabit. Email:
Fluid Dynamics & Materials Processing 2023, 19(7), 1753-1774. https://doi.org/10.32604/fdmp.2023.025739
Received 28 July 2022; Accepted 08 November 2022; Issue published 08 March 2023
Abstract
The effect of the tilt angle on mixed convection and related heat transfer in a “T” shaped double enclosure with four heated obstacles on the bottom surface is numerically investigated. The considered obstacles are constantly kept at a relatively high (fixed) temperature, while the cavity’s upper wall is cooled. The finite volume approach is used to solve the mass, momentum, and energy equations with the SIMPLEC algorithm being exploited to deal with the pressure-velocity coupling. Emphasis is put on the influence of the tilt angle on the solution symmetry, flow structure, and heat exchange through the walls. The following parameters and related ranges are considered: Rayleigh number 104 ≤ Ra ≤ 5.105, tilt angle 0° ≤
Graphic Abstract
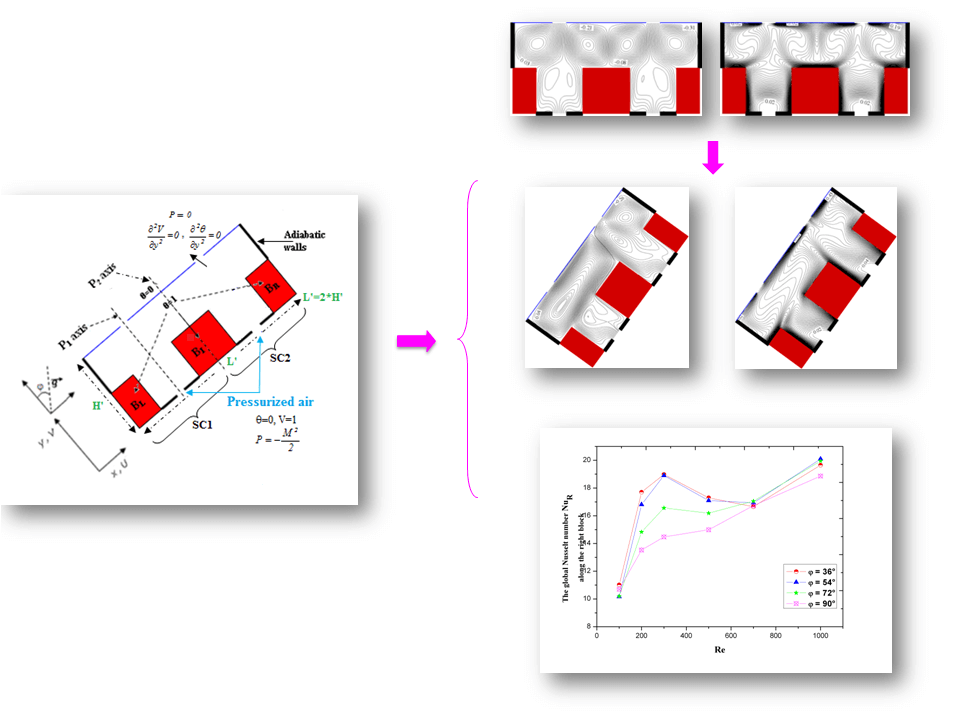
Keywords
Nomenclature
| A | Aspect ratio of calculation domain (A = L′/H′ = 2) |
| B | Dimensionless block height (B = h′/H′ = 0.5) |
| C | Dimensionless openings diameter (C = l′/H′ = 0.15) |
| D | Dimensionless space between blocks (D = d′/H′ = 0.5) |
| d′ | Space between adjacent blocks (m) |
| | Action of external volume forces |
| p | Dimensional pressure |
| P | Dimensionless fluid pressure (Pm/(ρU02)) |
| Pm | Driving pressure (p+ρgy) |
| H′ | Cavity height (m) |
| h′ | Blocks height (m) |
| L′ | Horizontal length of calculation domain (m) |
| M | Mass flow rate |
| l′ | Opening diameter (m) |
| g | Acceleration due to gravity (m/s²) |
| NuL | Global Nusselt number along the planes of the left block |
| NuI | Global Nusselt number along the planes of the intermediate block |
| NuR | Global Nusselt number along the planes of the right block |
| θ | Dimensionless temperature (T − TC)/(TH − TC) |
| T | Temperature of the fluid |
| ΔT | Temperature difference (TH − TC) |
| U0 | Characteristic velocity of the forced flow |
| (x, y) | Dimensionless Cartesian coordinates in the two directions (x, y) = (x′, y′)/H′ |
| (u, v) | Velocities |
| (U, V) | Dimensionless velocities (U, V) = (u, v)/U0 |
| Greek Symbols | |
| µ | Thermal diffusivity (m²s−1) |
| ρ | Volumetric coefficient of thermal expansion (K−1) |
| | Inclination angle of the cavity |
| λ | Thermal conductivity (Wm−1K−1) |
| λv | Second coefficient of viscosity |
| ν | Cinematic viscosity (m²s−1) |
| ρ | Fluid density (kg/m3) |
| Ψ | Dimensionless stream function, ψ = ψ′/α |
| Ω | Dimensionless vorticity Ω = Ω′H′2/α |
| Subscripts | |
| H | Heated wall |
| C | Cold wall |
| m | Iteration number |
| Non-Dimensional Numbers | |
| Pr | Prandtl number (Pr = ν/α) |
| Re | Reynolds number (Re = U0 × H′/ν) |
| Ra | Rayleigh number (Ra = gβΔTH′3/(αν)) |
| Gr | Grashof number (Gr = gβΔTH’3/ν2) |
| Ri | Richardson number (Ri = Gr/Re2) |
| Abbreviations | |
| The following abbreviations are used in this manuscript: | |
| ICF | Intra Cellular Flow |
| ECF | Extra Cellular Flow |
| FF | Forced Flow |
| UCLF | Uni Cellular Left Flow |
| SC1 | Simple Cavity 1 |
| SC2 | Simple Cavity 2 |
| OL | Open Lines |
Heat transfer by natural, mixed or forced convection in horizontal, vertical or inclined channels has received significant interest during the last four decades due to its application in various fields, namely solar collectors, heat exchangers and in particular, the cooling of electronic systems.
One of the disadvantages of electronic boards is that they generate a lot of heat when they are running. This is due to a variety of factors, including the advancement of electronic devices such as vacuum tubes, transistors, and integrated circuits, as well as the development of chips that are used in millions of devices. As a result, various studies on cooling of electronic devices, notably heat transfer by free, mixed, or forced convection in a channel containing heated blocks, or heat-generating blocks, that simulate electronic components, have been published [1–3].
The thermal management of electronic equipment has become a contentious issue. As a result, numerous researchers are interested in studying convective heat transfer in horizontal, vertical, or inclined channels. Bhowmik et al. [4] used water to conduct studies on the single-phase transient free convection heat transfer from four simulated electronic chips in-line. They discovered that the experimental results for steady-state forced and free convection correspond well with those reported in the open literature. Madhusudhana Rao et al. [5] presented a numerical investigation to explore two-dimensional, laminar, natural, forced, and mixed convective heat transfer from projecting volumic heat sources joined to vertical substrates generating a series of channels. The governing equations were discretized on a staggered mesh using a control volume technique. They discovered that, for a certain Grashof number, the natural convection generated velocity component in the presence of mixed convection reduces with rising Reynolds number owing to the well ventilation of the devices. Boutina et al. [6] modeled numerically laminar mixed convection in an inclined channel with two heat sources that represent electronic components. The mathematical model was solved using the finite volume method. According to the findings, increasing the Reynolds number and the separation distance can improve the cooling of electronic devices within the channel. Heat transfer decreases as the size of the heat sources grows larger.
A review of the literature reveals multiple studies on convection in cavities of various forms. Bilgen et al. [7] studied free convection in an enclosed square hollow with two airing openings on the right vertical surface and heaters on the left vertical surface. They discovered that heat transfer grows in terms of the Rayleigh number, heater size, and number of discrete heaters. Sharif [8] used a numerical simulation to investigate laminar mixed convection processes in shallow 2D rectangular enclosures at three distinct Richardson values. The governing equations were solved using the commercial code FLUENT. Flow behavior differed amongst the three different flow regimes. They confirmed that the average Nusselt number rises in proportion to cavity inclination.
Many researches on convective heat transport in “T” shaped cavities, with varying boundary conditions, have been reported [9–12]. Najam et al. [10] numerically analyzed mixed convection in a horizontal channel with heated obstacles on the lower surface. They discovered that there is a crucial Re over which the Rayleigh Bénard cells are dragged downhill by the forced flow. The movement of the cells can be observed even when the stream is overpowered by typical convection. Even when the stream is governed by natural convection, the displacement of the cells can be observed.
However, few numerical studies on inclined “T” type cavities have been conducted [13,14]. Amraqui et al. [14] numerically investigated coupled laminar convection and surface radiation inside a tilted “T” shaped enclosure for the impact of the tilt angle φ in the presence and absence of the radiation. They discovered that as the inclination angle increases, heat transfer and mass flow rate drop.
Several articles on heat transfer have recently been published. Ghalambaz et al. [15] examined natural convection heat transfer of a suspension of Nano–Encapsulated Phase Change Materials (NEPCMs) in a tilted porous enclosure using a simulation. The finite element approach was used to find the solution of the ruling equations. According to the findings, the best heat transfer performance appears at a non–dimensional fusion temperature of 0.5 and an inclination angle of 42°. They also stated that lowering the Stefan number promotes heat exchange.
On the other hand, some authors have used different methods to solve the equations that govern the heat transfer problem, like Das [16] that have numerically examined the estimation of parameters in a 2D-transient conduction-radiation heat transfer problem. They estimated the boundary emissivity, the scattering albedo and the conduction-radiation parameters by the lattice Boltzmann method and the finite volume method in combination with the genetic algorithm. The association of these three methods precisely foretells the unknown parameters. In 2011, Das [17] has numerically solved the Navier-Stockes equations to simultaneously estimate the Reynolds number, the length, and the width of the cavity by using the combination of the simplex search method and the finite difference method. They have found a good estimation of these variables.
Moreso, Mishra et al. [18] have numerically studied heat transfer by transient conduction-radiation in a 1-D concentric cylindrical participating medium. The governing equations are solved by using the conjunction of the lattice Boltzmann method (LBM) and the finite volume method (FVM), and the combination of the finite difference method (FDM) with the finite volume method. In addition, they have studied the impact of many parameters, like the conduction-radiation parameter, the scattering albedo, the extinction coefficient, and the radius ratio on temperature distributions in the medium. A good agreement was found by comparing the results of the LBM-FVM and those of the FDM-FVM. A numerical investigation of heat transfer by transient conduction-radiation was conducted by Das et al. [19]. They have estimated such parameters, as the boundary emissivity, the scattering albedo and the conduction–radiation parameter by using the combination of the LBM, the FVM and the generic algorithm. The temperature field obtained in the direct method is used in the inverse method for simultaneous estimation of unknown parameters using the LBM–FVM and the GA. They have obtained that the LBM–FVM–GA conjunction correctly forecasts the unknowns.
Other researchers have been interested in ventilating with many inlets, such as Bioswas et al. [20] who have studied mixed convection in a grooved channel with injection. It is found that injection, Reynolds number and the Richardson number enhance heat transport inside this channel. Chakravarty et al. [21] numerically examined the influence of a ventilation method and, the furnishing side injection of cold fluid by the face of the enclosure, on heat management by using the thermal non-equilibrium approach. A novel method was evinced by Bioswas et al. [22] in order to enhance heat transfer in thermal enclosures assuming aspiration. It was reported that the heat transfer was ameliorated in all three enclosures owing to aspiration. Bioswas et al. [23] also numerically investigated the docket of aspiration to raise magneto-hydrodynamic (MHD) convection (heat transfer) in protruded heater enclosure. Likewise, Bioswas et al. [24] numerically analyzed the boosting of convective heat transfer in a lid-driven porous cavity by dint of free aspiration. The investigation depicts that the aspiration can impressively improve heat transfer without pumping.
Recently, a numerical study of heat transfer by Rayleigh Bénard convection in a “T” form cavity with water-based CNT–aluminum oxide hybrid nanofluid has been analyzed by Almeshaal et al. [25]. Their results show that the control parameters have effects on the heat transfer inside this cavity.
In 2019, Yousefzadeh et al. [26] numerically modeled the mixed convection in an open square enclosure holding a circular heat source. They reported that the hot zone location has an impact on heat transfer and the temperature gradient. Further, Xiong et al. [27] have examined the emphasis of the variables Richardson number, Reynolds number, Hartmann number, and cold circular obstacle on the heat transfer inside a lid driven triangular cavity containing a circular block and filled with a Newtonian MHD fluid. The ruling equations were solved by the finite element method. They found that the Ri, Gr and Re all influence heat transfer.
The inclination’s effect on mixed convection within a “T” form double enclosure has not received much attention in the analysis of heat exchange in repeating geometries. Thus, the proposed research is required, because it aims to treat the ventilation of a tilted double geometry containing electronic components. It also arouses curiosity and pays attention to the numerical examination of convective heat transfer in a “T” shaped double enclosure with two inlets, two outlets, and four heated obstacles arranged on its bottom surface. The top surface is kept cold, whereas the vertical and bottom walls are adiabatic. To ventilate the double cavity, an air jet is introduced through two entry ports. The effect of tilt angle on solution symmetry, flow structure, isothermal lines, and heat transmission is examined.
The schematic representation indicated in Fig. 1 is a “T” form double cavity with four apertures and four heated obstacles put on its bottom surface and is maintained at a fixed temperature θH. At θC < θH, the top surface is cold. The bottom and vertical walls are both adiabatic. For B = 0.5, the blocks’ altitude remains constant.
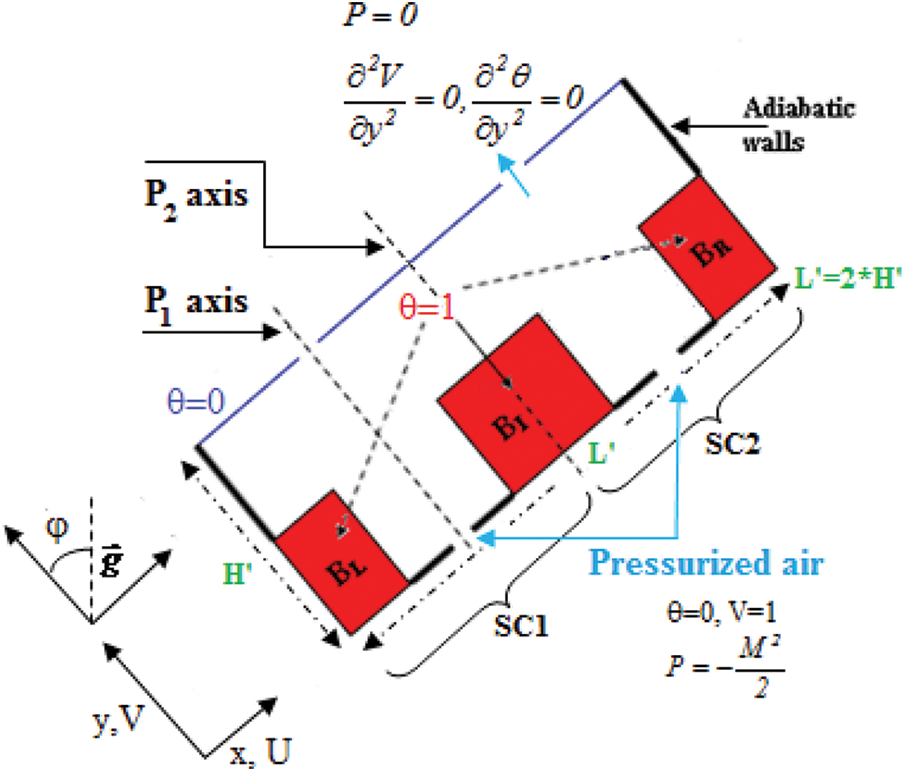
Figure 1: Schematic representation of the problem
3 Physical Problem and Governing Equations
The configuration represented in Fig. 1 is considered. It is a “T” form double enclosure which contains four apertures and 4 heated obstacles fixed on its bottom surface and is maintained at a constant temperature θH. The top surface is cold at θC < θH. The vertical surface and also the bottom surface are adiabatic. The altitude of the obstacles is constant for B = 0.5.
In order to solve the Navier-Stockes equations, the fluid is assumed to be bidimensional, laminar, Newtonian and incompressible. The approximation of Boussinesq is validated, the viscous dissipation is negligible and the fluid properties are constant.
The fundamental dimensional equations of this problem can generally be written in the following simplified form:
Continuity equation:
Momentum equation:
Energy equation:
The Boussinesq assumption consists in simplifying the equation of the state of the fluid by linearizing the expression of ρ according to the variations of the temperature T as follows:
where:
TC designates the reference temperature, ρ0 is the density of the fluid at TC and p is the fluid pressure.
β defines the expansion coefficient at a constant pressure by:
Taking into account the assumptions adopted, the dimensional governing equations become:
We seek to highlight the similarity parameters. For an incompressible fluid, taking as the base scale the height of the cavity H′, the fluid velocity U0, the temperature difference TH − TC and the pressure scale ρU02. The dimensionless quantities are then defined as follows:

On one hand, the non-dimensional equations that rules the issue are as follows:
Continuity
Momentum
Energy
where the non-dimensional numbers are as follows:
Prandtl number
Rayleigh number
Grashof number
Richardson number
Gr/Re2 is the mixed convection parameter, the parameter
Then again, the global Nusselt numbers along the heated obstacles NuL, NuI and NuR will be determined to evaluate the heat exchange between the air jet and the obstacles of the enclosure. Respectively, the average Nusselt number along the active surfaces of the enclosure is:
The global Nusselt number on the left obstacle surfaces is:
The global Nusselt number on the intermediate obstacle surfaces is:
The global Nusselt number on the right obstacle surfaces is:
The dynamic and thermal boundary conditions associated to the problem Eqs. (9)–(12) are given by:
• At the obstacles
• At the top wall
For y = 1; 0 ≤ x ≤ 0.425; 0.575 ≤ x ≤ 1.425 and 1.575 ≤ x ≤ 2
• At the entrance openings
For y = 0; 0.425 ≤ x ≤ 0.575 and 1.425 ≤ x ≤ 1.575
• At the portions of the bottom surface separating the apertures and the obstacles
For y = 0; 0.25 ≤ x ≤ 0.425; 0.575 ≤ x ≤ 0.75; 1.25 ≤ x ≤ 1.425 and 1.575 ≤ x ≤ 1.75
• At the adiabatic vertical walls
For B ≤ y ≤ 1; x = 0 and x = 2
• At the evacuation openings
For y = 1; 0.425 ≤ x ≤ 0.575 and 1.425 ≤ x ≤ 1.575
The finite volume approach was utilized to find the solutions of the ruling equations of continuity, momentum, and energy. To discretize the convective elements of the transport equation, Leonard et al. adopted the (Quadratic Upstream Interpolation for Convective Kinetics) Quick schema, which is of third order in precision [28]. The (SIMPLE Consistent) SIMPLEC technique is utilized to tackle the velocity-pressure coupling, according to van Doormaal et al. [29]. This technique improves on the SIMPLE algorithm for predicting incompressible fluid flows. It includes several of changes that simplify implementation while also lowering solution costs, as illustrated in Fig. 2. This study takes into account time steps among 10−4 and 10−3.
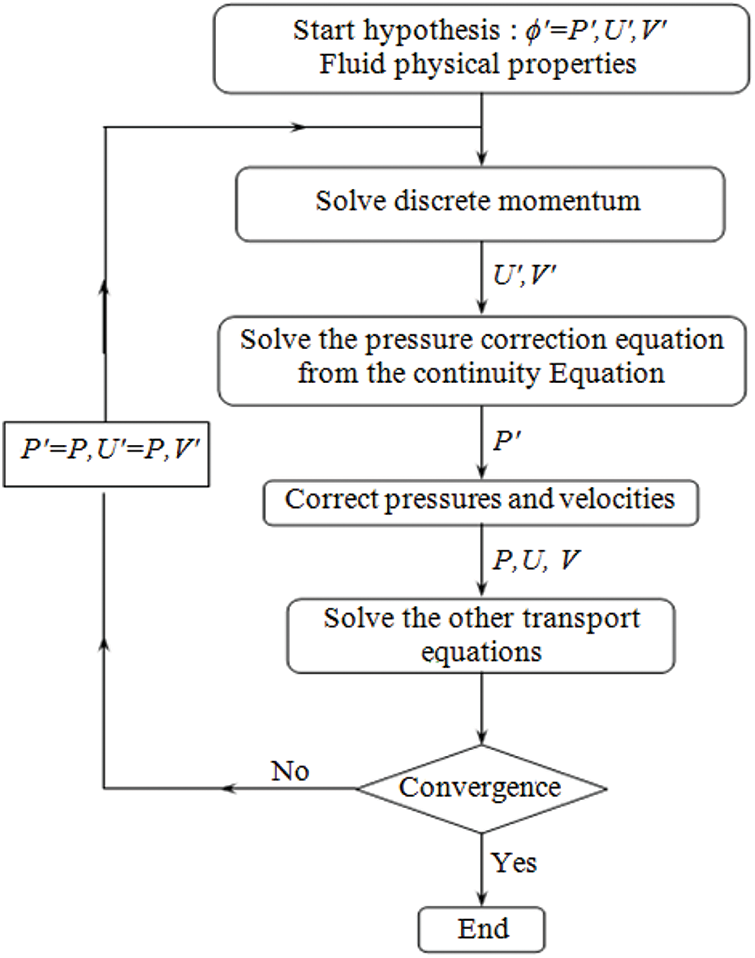
Figure 2: Representative diagram of the SIMPLE algorithm
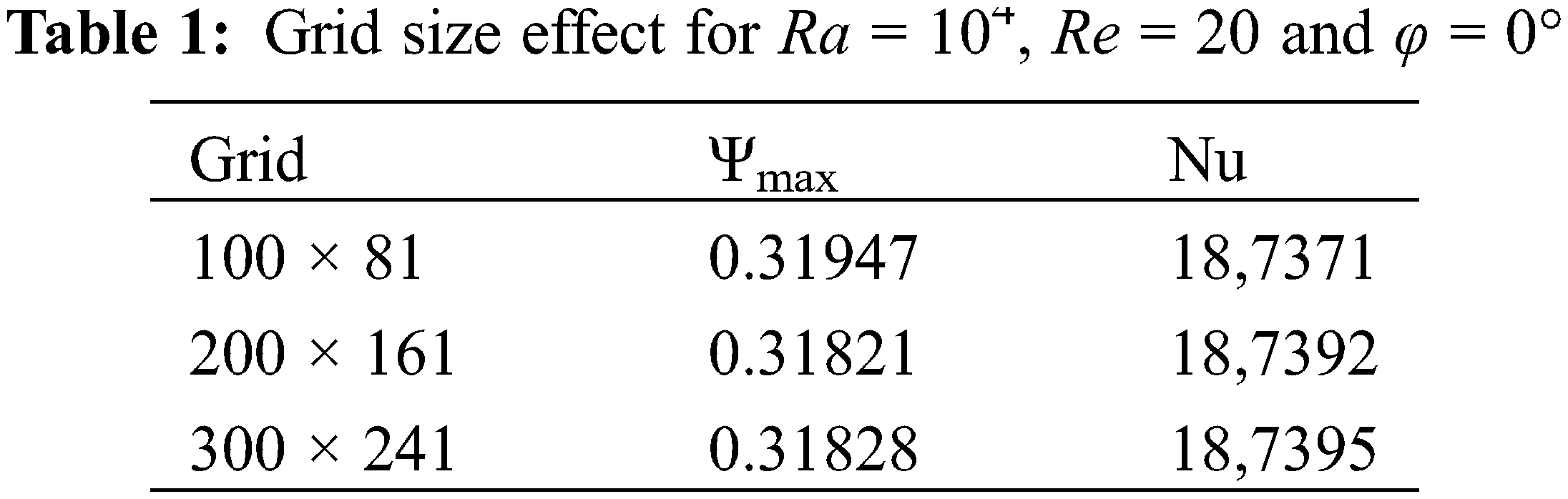
The effect of the mesh on the accuracy of the numerical solution was analyzed by comparing the present results in terms of the maximum stream function Ψmax of mixed convection with Rayleigh number Ra = 104, Prandtl number Pr = 0.72, Reynolds number Re = 20 and the inclination angle
It was observed that for Ra = 104, the variations of the stream function Ψmax are very small especially for the grid sizes 200 × 161 and 300 × 241, as presented in Table 1. Moreso, the computation of the average Nusselt number becomes substantive when passing from a grid of 200 × 161 to 300 × 241. Then, the sensitivity of the results to the mesh is negligible from the grid of 200 × 161. Thus, the mesh of 200 × 161 was selected to describe the details of heat transfer by mixed convection, in the studied geometry, namely the flow structure and the temperature field.
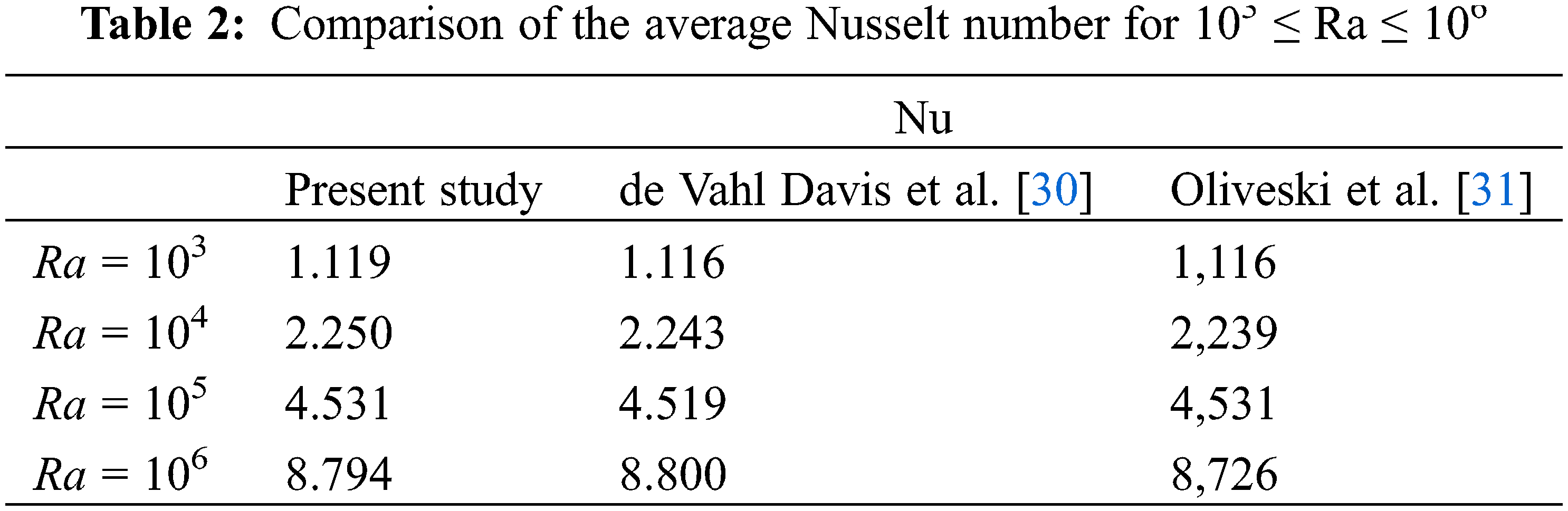
To validate our code, a comparison of the current study’s results with those found for natural convection flows inside a differentially heated cavity, has been done, de Vahl Davis et al. [30] and Oliveski et al. [31]. The average Nusselt number was computed for various Rayleigh numbers (103 ≤ Ra ≤ 106). Table 2 compares our findings to those reported in [30] and demonstrates a high degree of consistency.
In addition, our results were compared with those presented by de Vahl Davis et al. [32]. It was noted that for Rayleigh number Ra = 106, the obtained results in terms of flow fields and thermal fields, reveal a good agreement between the present results and those of the reference [28], as shown in Fig. 3.
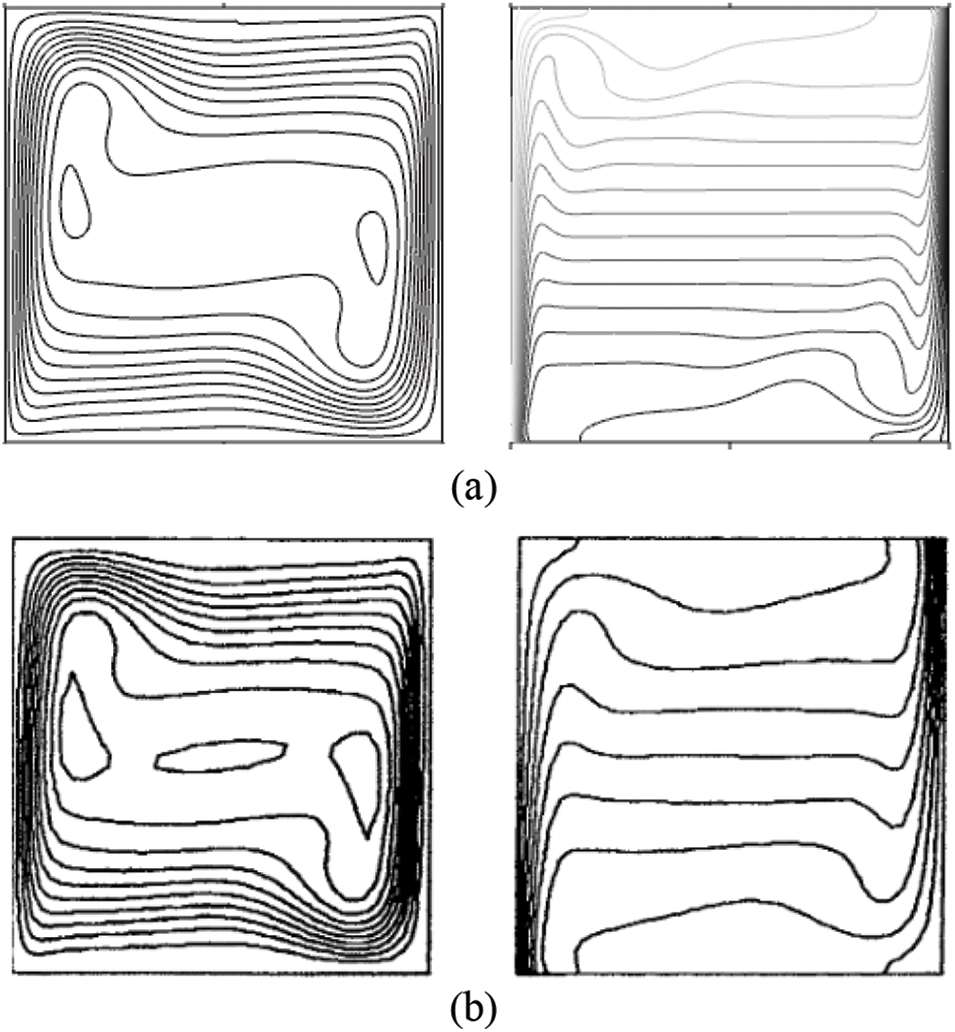
Figure 3: Comparison between the present streamlines and isotherms (a) and those of de Vahl Davis et al. [32] (b), of a square cavity
The steady-state results were achieved when the following criterion is verified for the Nusselt number:
Furthermore, the results of the mixed convection phenomenon were reproduced in a lid driven cavity by Iwatsu et al. [33], Cheng [34], and Dahani et al. [35], for Gr = {100; 104; 106} and 100 ≤ Re ≤ 1000 as presented in Table 3 and illustrated in Fig. 4. It was found that the changing of the Nusselt number agrees with those of the reference [33–35]. Besides, the outcomes as flow fields and temperature distributions are similar to those of Iwatsu [33].
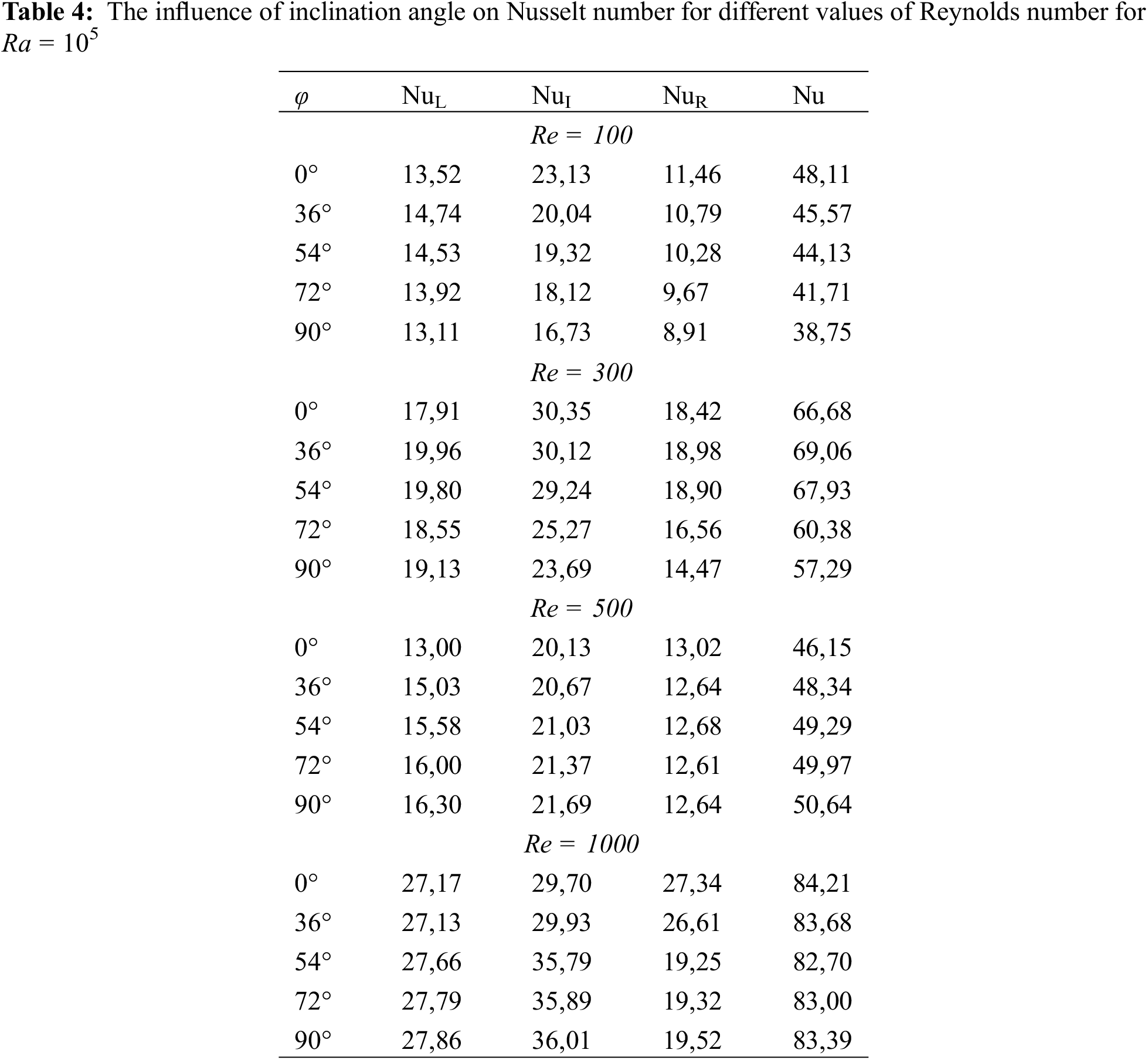

Figure 4: Comparison between the present streamlines and isotherms (a) and those of Iwatsu et al. [33] (b), of a lid driven cavity
Changing Re and
4.1 Flow Structure and Isothermal Lines
A previous investigation was already studied by Mourabit et al. [37]. In this section, the solutions are symmetric as compared to the P2 axis, passing by the middle of the double cavity, for all cases not inclined (
For Re = 300,
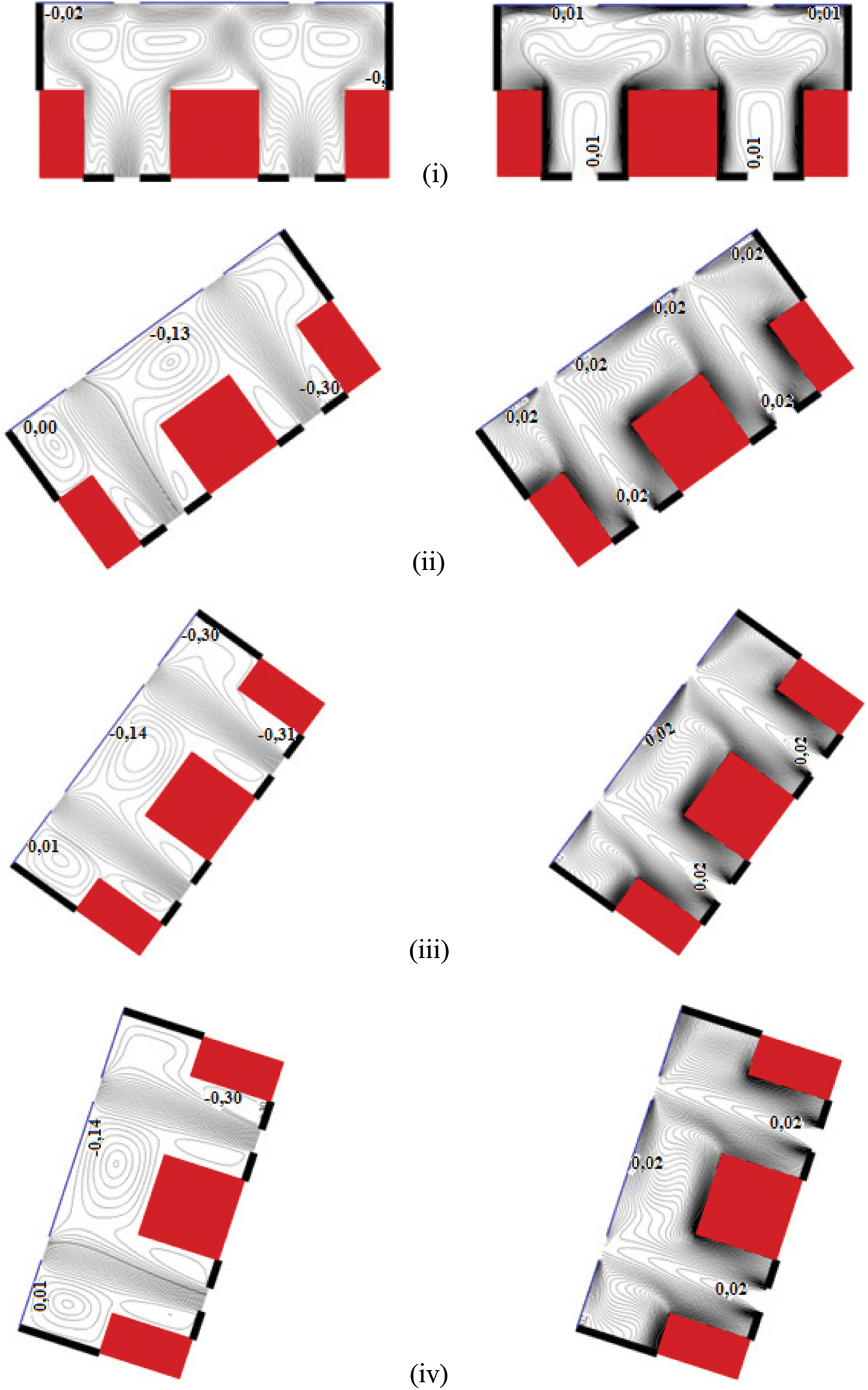
Figure 5: Flow and temperature fields of Reynolds number Re = 300, Rayleigh number Ra = 105 for different values of
When we incline the double enclosure Re = 300,
By raising
It is also observed that the open lines are intensive. The corresponding isothermal lines show that the lower parts of the vertical active walls are badly cooled because of the recirculation cells. The horizontal wall of the left block BL is more cooled than the other horizontal ones.
By raising the Rayleigh number to 5.105, the flow field is found to be symmetric in regard to P2 axis for all cases not inclined (
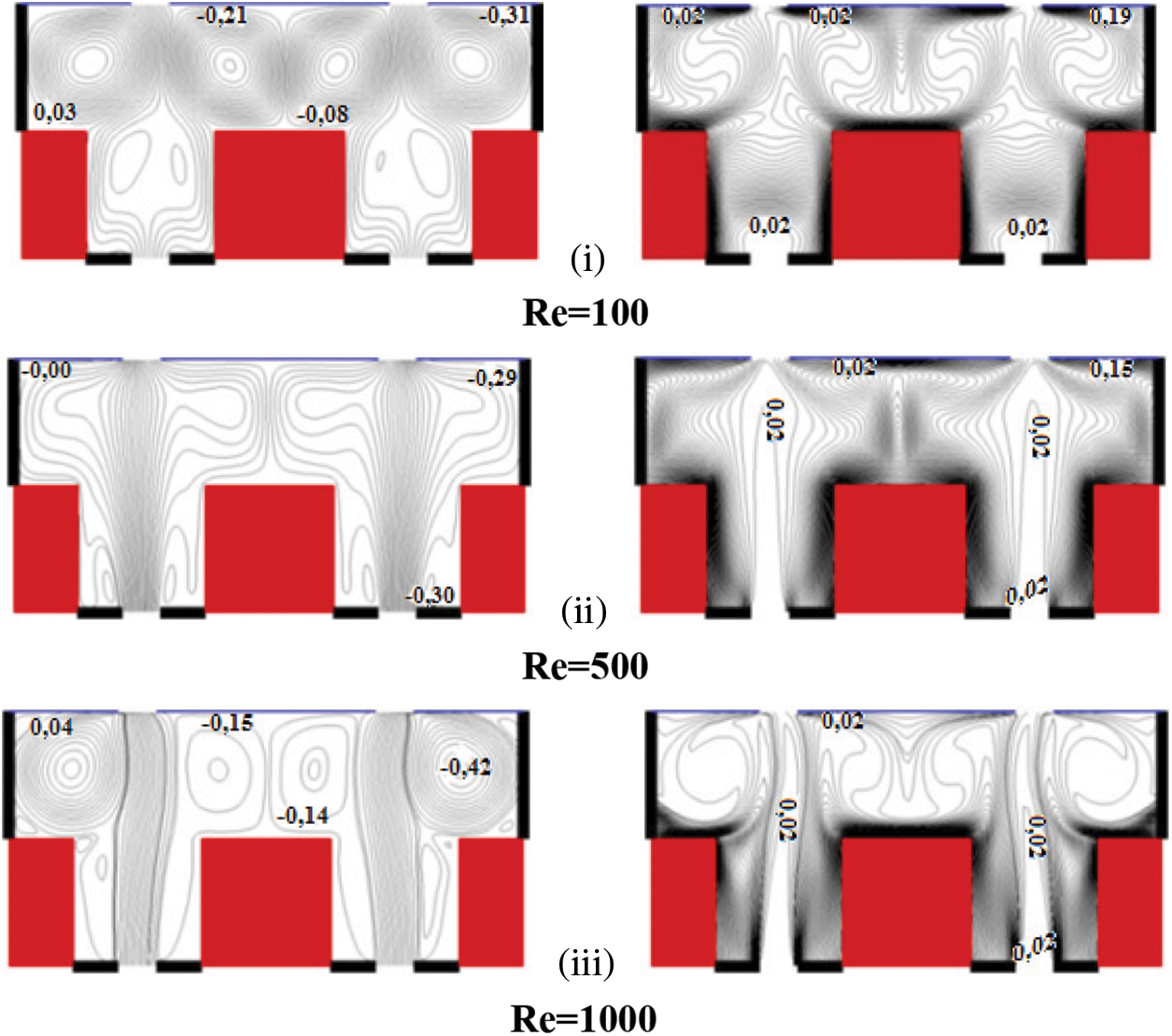
Figure 6: Flow and temperature fields for Rayleigh number Ra = 5.105; tilt angle
Fig. 6iii indicates the onset of four new convective cells that mix the recirculation ones. It also shows that the size of the convection cell above the right obstacle is decreased. The corresponding thermal fields confirm that there is an effective cooling of all horizontal active surfaces. The vertical ones are found to be poorly ventilated as the air jet exits the micro-cavities and fills the upper part of the double cavity.
By raising the tilt angle to 54° (Re = 100) as seen in Fig. 7i, the result continues to be asymmetric in comparison to the P2 axis. The type of this solution is a combination of the UCLF and ECF types. Fig. 7i shows the appearance of a big convective cell taking all the space of SC1 and the remaining space above BI. Likewise, the rest of SC2 is filled by the Open Lines (OL) that surround the recirculation cells. The matching isotherms show that BL’s horizontal faces are more ventilated than the other horizontal ones. Moreso, they show good ventilation of the vertical active walls of BL and BI (SC2) and bad ventilation of the other vertical surfaces. The recirculation cells cause the flow inside the micro cavities to be slanted.
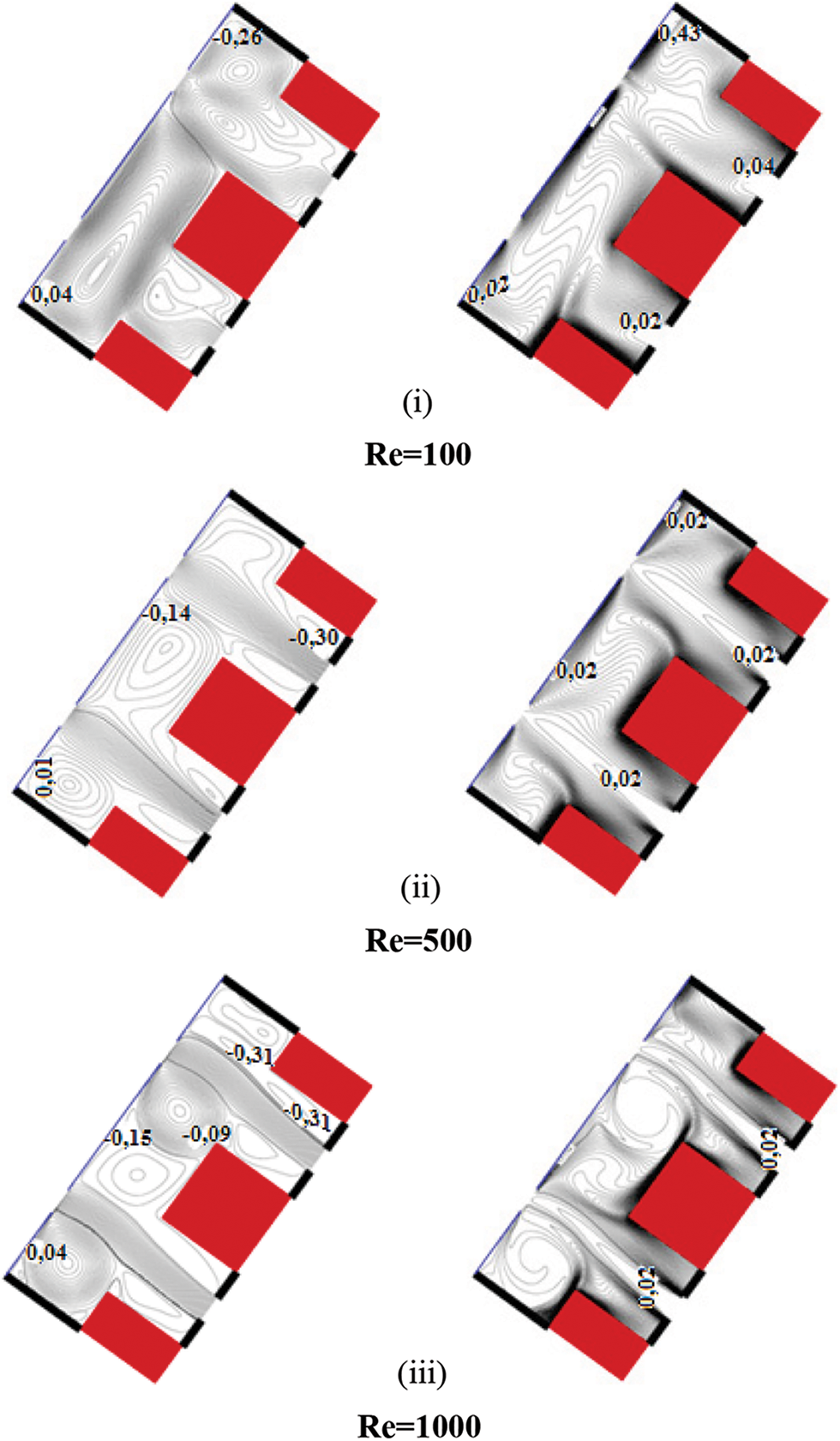
Figure 7: Flow and temperature fields for Rayleigh number Ra = 5.105; tilt angle
For Re = 500,
By increasing the tilt angle to 72°, at Re =100 as shown in Fig. 8i, the solution is observed to be asymmetric and its type is a combination of the UCLF and ECF types. The presence of a big convective cell taking all the space of SC1 and the remaining space above BI is observed. In the SC2 domain, two convective cells are bordered by opening lines. The air jet increases, decreases, then increases again (because the fluid is heavy (Re = 100)). The related temperature distributions show that all the horizontal active walls are well ventilated because of the convection cells. The upper parts of the vertical active surfaces are badly ventilated due to the low intensity of the air jet (Re = 100). At Re = 500,
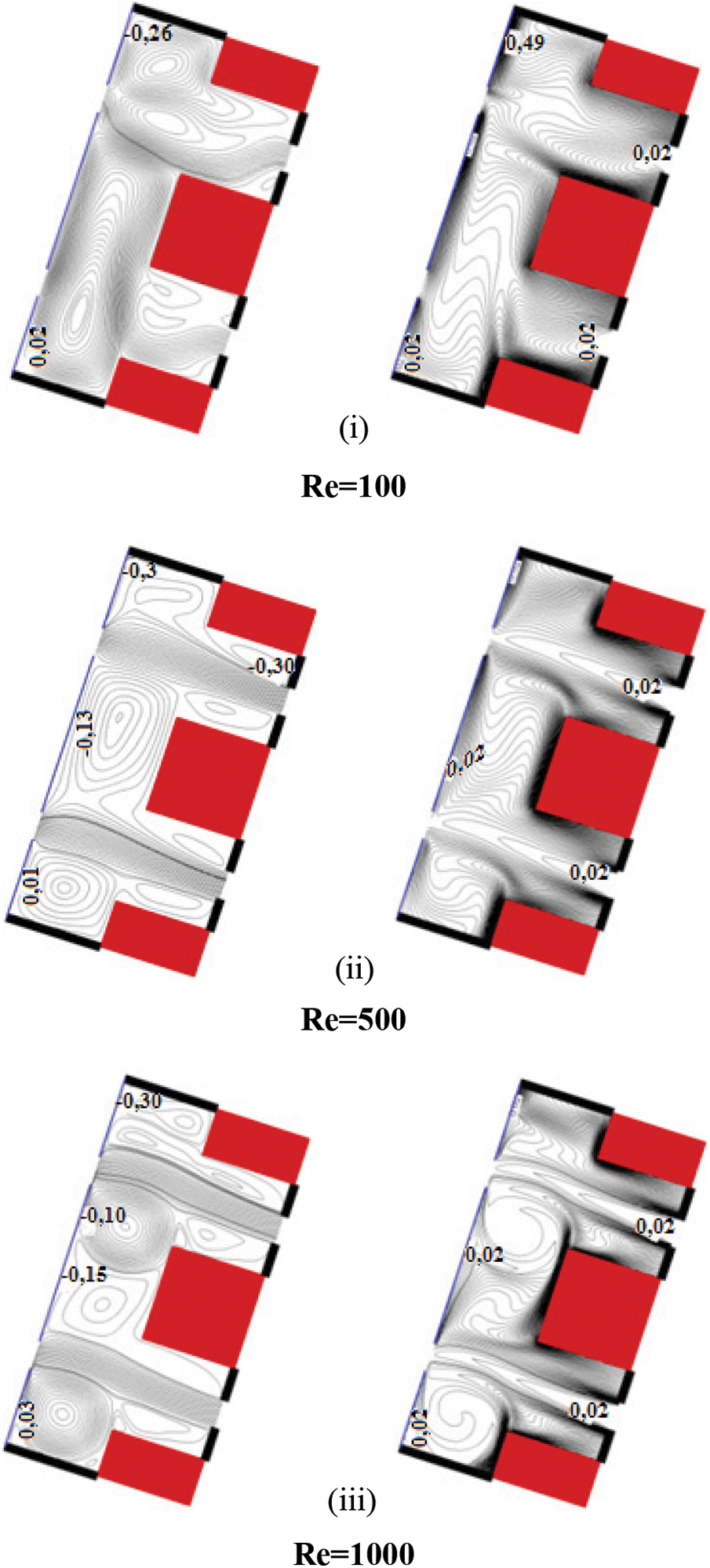
Figure 8: Flow and temperature fields for Rayleigh number Ra = 5.105; tilt angle
Figs. 9 and 10 illustrate the global Nusselt numbers along the heated obstacles NuL, NuI, and NuR evolutions with Re depending on Reynolds number 100 ≤ Re ≤ 1000 and for inclination angles ranging from 0° to 90° (105 ≤ Ra ≤ 5.105).
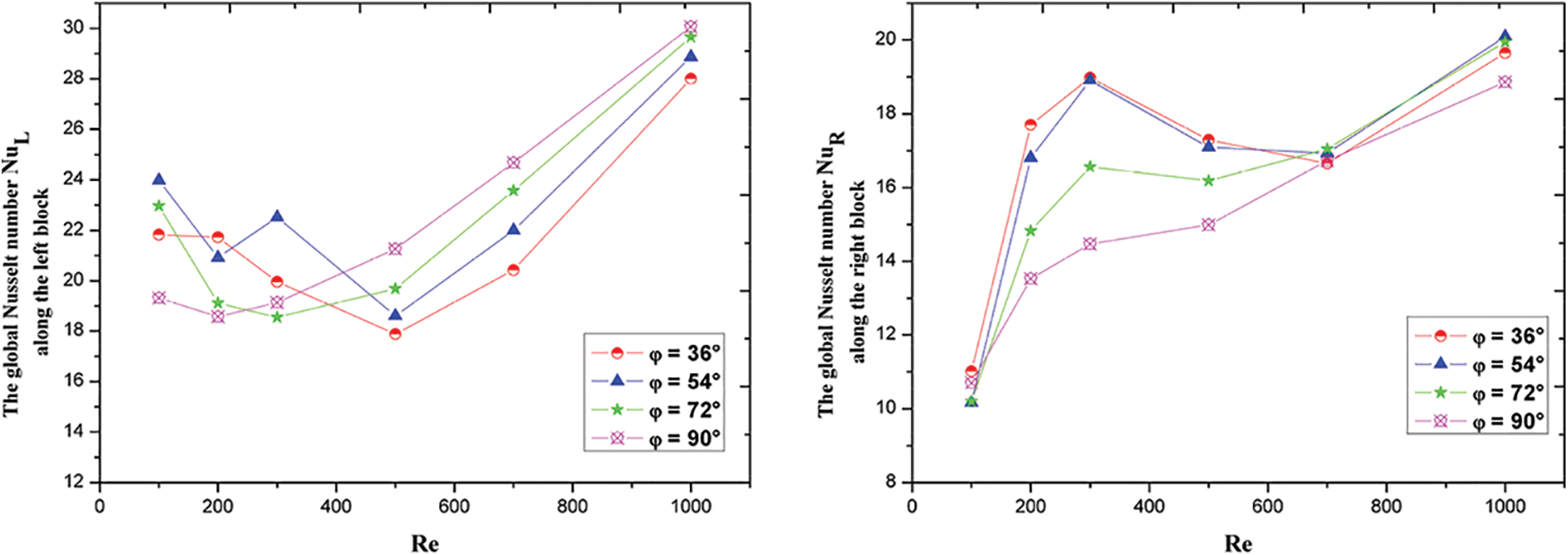
Figure 9: The variations of NuL and NuR as function of Reynolds for various values of
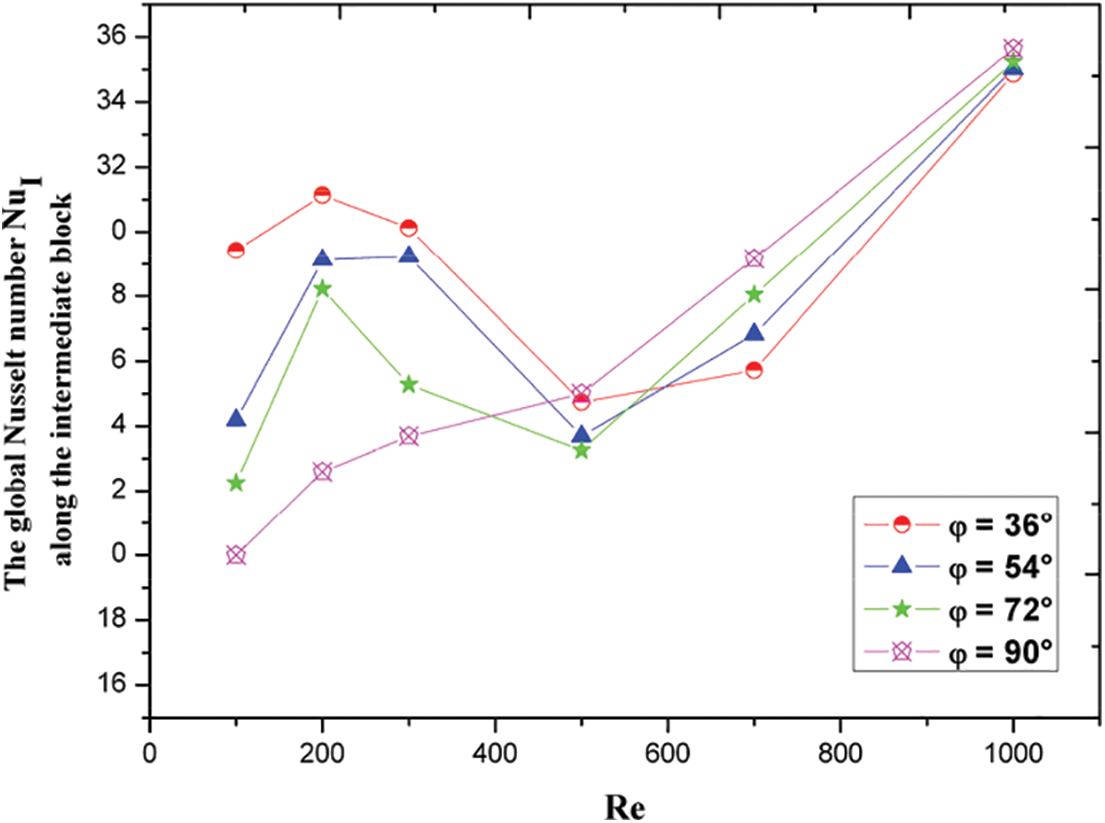
Figure 10: Variation of NuI as function of Reynolds number Re for various values of
It is noticed that for Reynolds number ranging from 100 to 300, the heat transfer rate decreases with the tilt angle
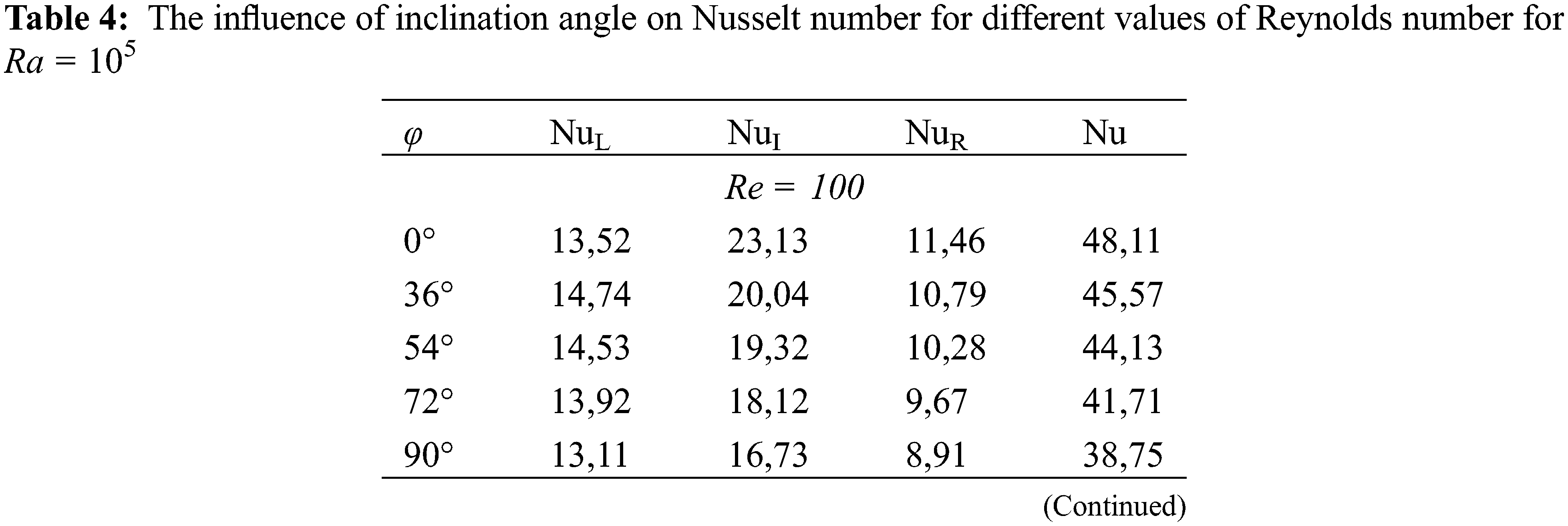
But, for Re = 500, it is observed that the tilt is in favor of the cooling of the double enclosure: there is a good heat exchange inside this cavity, the forced flow is installed in Table 4.
Likewise, when Re is equal to 1000, it is noted that the heat transfer is nearly constant inside the double cavity, Table 4 while, the intermediate obstacle exchanges heat with the rest of this cavity very well. The tilt is not in favor of the ventilation of the right block because, the effective heat transfer is installed in the middle of the double cavity (around the principal axis).
In this case, as illustrated in Fig. 9, the global Nusselt number NuL on the left obstacle’s surfaces descends to a minimum with the Reynolds number and it ascends afterward in the area of the installation of the forced flow.
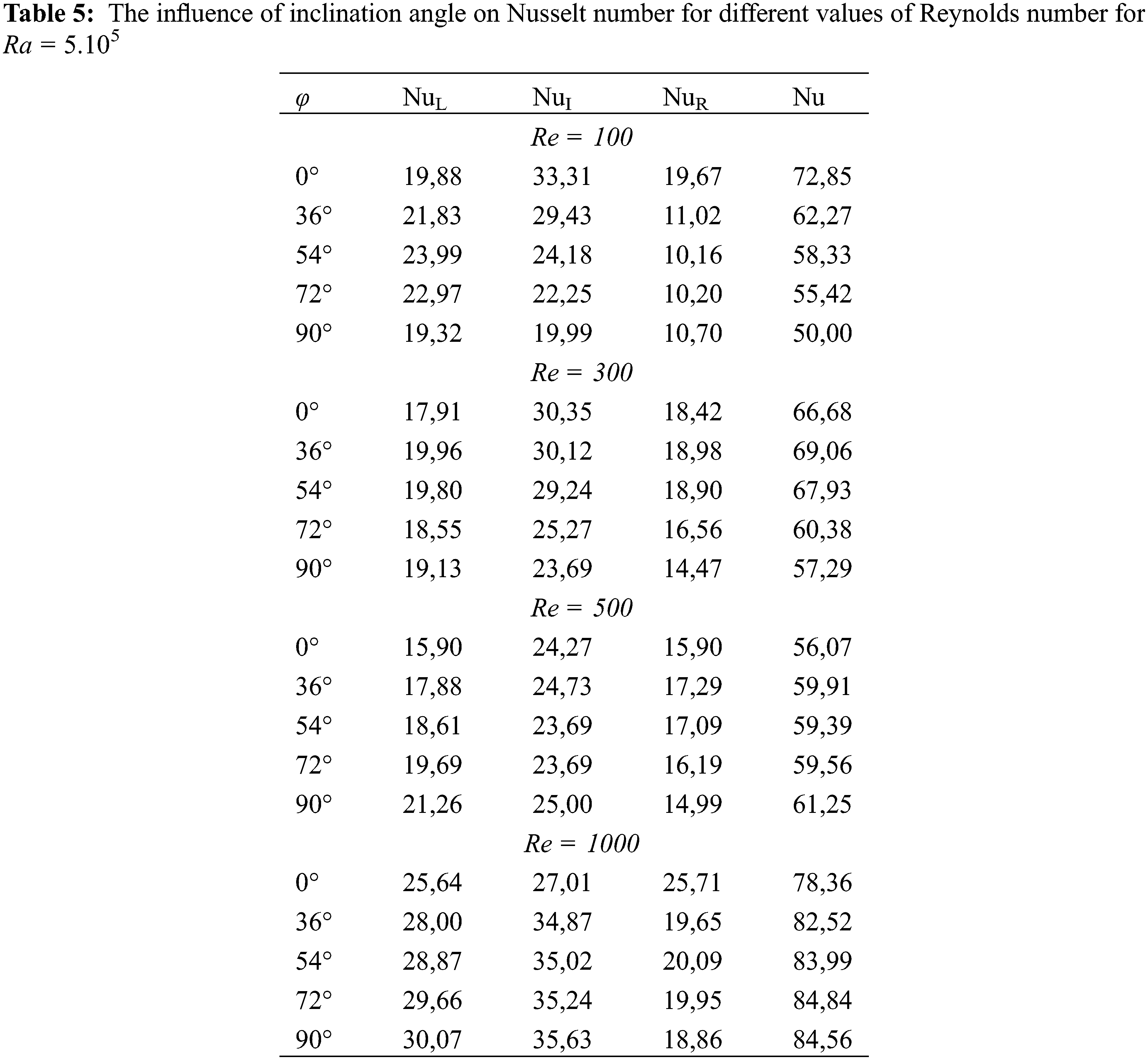
It alters in a roughly identical manner for all inclination degrees ranging from 36° to 90°. However, it is noted that the global Nusselt number NuR on the right obstacle surfaces rises slowly in general to a maximum with the Reynolds number Re (Fig. 9), drops steadily for 200 ≤ Re ≤ 300, and then rises slowly with 300 ≤ Re ≤ 500. After that it rocketed for 500 ≤ Re ≤ 1000 for the entire range of variation of the inclination angle between 36° and 90°. There was a steady rise for the variation of NuI with Re for 100 ≤ Re ≤ 200, then there was a slow drop for the variation of NuI with Re (200 ≤ Re ≤ 300) after which there was a sharp increase in the variation of NuI with Re for 300 ≤ Re ≤ 1000 as shown in Fig. 10. Moreso, it is observed that the mean Nusselt number reduces with the inclination angle for 100 ≤ Re ≤ 300, as shown in Table 5, but, for 500 ≤ Re ≤ 1000, it is noted that the heat transfer increases with
In this investigation, the heat transfer by mixed convection in a “T” shaped double enclosure containing four heated obstacles and subjected to a vertical jet was numerically analyzed. The emphasis of tilt angle on solution symmetry, flow structure, isotherms, and Nusselt number variation is investigated. The obtained results showed the existence of various solutions sorts (ICF, ECF, FF, UCLF, and a combination of these solutions) by varying Re and φ.
Besides, it is found that the symmetry of the solution regarding the P2 axis is respected for all cases not inclined for the values of Re between 100 and 1000. Further, the symmetry of the solution as compared to the P1 axis is respected for cases not inclined for lower values of Re ranging from 100 to 300. It is also found that the inclination has more significant effects on the symmetry of the results for Re smaller than 700 (Re < 700) while the rise of the parameter Re (Re = 1000) correlates to the conservation of the solution type even if the double cavity is inclined. The solution symmetry ICF supports the cooling of the horizontal active surfaces of the heated blocks. It is noted that for Re = 100, the upper parts of the vertical active surfaces are poorly ventilated due to the low intensity of the air jet. Furthermore, for raised Reynolds number 500 ≤ Re ≤ 1000, the outcomes shows that the horizontal fronts of the obstacles BL and BI are better cooled than that of BR. The heat transfer inside the “T” form double enclosure is greatly influenced by the inclination angle. In addition, the flow and thermal fields evinced an important communication between the two sub cavities SC1 and SC2.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: Conceptualization, M.Mo., M.Me, S.F., S.M., H.R. and E.S.; methodology, M.Mo., M.Me, S.F., S.M., H.R. and E.S.; software, M.Mo., M.Me, S.M., H.R. and E.S.; validation, M.Mo., M.Me, S.F., S.M., H.R. and E.S.; formal analysis, M.Mo., M.Me, S.M., H.R. and E.S.; investigation, M.Mo., M.Me, S.M. and E.S.; data curation, M.Mo. and M.Me.; writing–original draft preparation, M.Mo., M.Me, S.M., H.R. and E.S.; writing–review and editing, M.Mo., M.Me, S.F, S.M., H.R. and E.S.; visualization, M.Mo., M.Me, S.F., S.M., H.R. and E.S.; supervision, M.Mo., M.Me, S.M., H.R. and E.S. All authors have read and agreed to the published version of the manuscript.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Choi, S. H., Shin, S., Cho, Y. I. (1993). The effects of the Reynolds number and width ratio on the flow distribution in manifolds of liquid cooling modules for electronic packaging. International Communications in Heat and Mass Transfer, 20(5), 607–617. https://doi.org/10.1016/0735-1933(93)90073-5 [Google Scholar] [CrossRef]
2. Florio, L. A., Harnoy, A. (2007). Combination technique for improving natural convection cooling in electronics. International Journal of Thermal Sciences, 46(1), 76–92. https://doi.org/10.1016/j.ijthermalsci.2006.03.007 [Google Scholar] [CrossRef]
3. Tseng, Y. S., Fu, H. H., Hung, T. C., Pei, B. S. (2007). An optimal parametric design to improve chip cooling. Journal of Applied Thermal Engineering, 27(11–12), 1823–1831. https://doi.org/10.1016/j.applthermaleng.2007.01.012 [Google Scholar] [CrossRef]
4. Bhowmik, H., Tou, K. W. (2005). Experimental study of transient natural convection heat transfer from simulated electronic chips. Experimental Thermal and Fluid Science, 29(4), 485–492. https://doi.org/10.1016/j.expthermflusci.2004.06.003 [Google Scholar] [CrossRef]
5. Madhusudhana Rao, G., Narasimham, G. S. V. L. (2007). Laminar conjugate mixed convection in a vertical channel with heat generating components. International Journal of Heat and Mass Transfer, 50(17–18), 3561–3574. https://doi.org/10.1016/j.ijheatmasstransfer.2006.12.030 [Google Scholar] [CrossRef]
6. Boutina, L., Bessaïh, R. (2011). Numerical simulation of mixed convection air-cooling of electronic components mounted in an inclined channel. Applied Thermal Engineering, 31(11–12), 2052–2062. https://doi.org/10.1016/j.applthermaleng.2011.03.021 [Google Scholar] [CrossRef]
7. Bilgen, E., Balkaya, A. (2008). Natural convection on discrete heaters in a square enclosure with ventilation ports. International Journal of Heat and Fluid Flow, 29(4), 1182–1189. https://doi.org/10.1016/j.ijheatfluidflow.2008.01.013 [Google Scholar] [CrossRef]
8. Sharif, M. A. R. (2007). Laminar mixed convection in shallow inclined driven cavities with hot moving lid on top and cooled from bottom. Journal of Applied and Thermal Engineering, 27(5–6), 1036–1042. https://doi.org/10.1016/j.applthermaleng.2006.07.035 [Google Scholar] [CrossRef]
9. Amahmid, A., Hasnaoui, M., Vasseur, P. (1997). Multiplicité des solutions en convection naturelle dans une géométrie répétitive. International Journal of Heat and Mass Transfer, 41(16), 3805–3818. [Google Scholar]
10. Najam, M., Amahmid, A., Hasnaoui, M., El Alami, M. (2003). Unsteady mixed convection in a horizontal channel with rectangular blocks periodically distributed on its lower wall. International Journal of Heat and Fluid Flow, 24(5), 726–735. https://doi.org/10.1016/S0142-727X(03)00063-8 [Google Scholar] [CrossRef]
11. Mouhtadi, D., Amahmid, A., Hasnaoui, M., Bennacer, R. (2012). Natural convection in a horizontal channel provided with heat generating blocks: Discussion of the isothermal blocks validity. Energy Conversion and Management, 53(1), 45–54. https://doi.org/10.1016/j.enconman.2011.08.006 [Google Scholar] [CrossRef]
12. Hatami, M., Zhou, J., Geng, J., Song, D., Jing, D. (2017). Optimization of a lid-driven T-shaped porous cavity to improve the nanofluids mixed convection heat transfer. Journal of Molecular Liquids, 231(9), 620–631. https://doi.org/10.1016/j.molliq.2017.02.048 [Google Scholar] [CrossRef]
13. Rouijaa, H., El Alami, M., Semma, E. A., Najam, M. (2011). Natural convection in a inclined T-shaped cavity. Fluid Dynamics & Material Processing, 7, 57–70. https://doi.org/10.3970/fdmp.2011.007.057 [Google Scholar] [CrossRef]
14. Amraqui, S., Mezrhab, A., Abid, C. (2010). Computation of coupled surface radiation and natural convection in an inclined «T» form cavity. Energy Conversion and Management, 51, 505–517. [Google Scholar]
15. Ghalambaz, M., Mehryan, S. A. M., Zahmatkesh, I., Chamkha, A. (2020). Free convection heat transfer analysis of a suspension of nano-encapsulated phase change materials (NEPCMs) in an inclined porous cavity. International Journal of Thermal Sciences, 157(3), 106503. https://doi.org/10.1016/j.ijthermalsci.2020.106503 [Google Scholar] [CrossRef]
16. Das, R. (2012). A simulated annealing-based inverse computational fluid dynamics model for unknown parameter estimation in fluid flow problem. International Journal of Computational Fluid Dynamics, 26(9–10), 499–513. https://doi.org/10.1080/10618562.2011.632375 [Google Scholar] [CrossRef]
17. Das, R. (2012). Inverse analysis of Navier–Stokes equations using simplex search method. Inverse Problems in Science and Engineering, 20(4), 445–462. https://doi.org/10.1080/17415977.2011.629046 [Google Scholar] [CrossRef]
18. Mishra, S. C., Kim, M. Y., Das, R., Ajith, M., Uppaluri, R. (2009). Lattice Boltzmann method of the analysis of transient conduction-radiation problems in a cylindrical medium. Numerical Heat Transfer, 56(1), 42–59. https://doi.org/10.1080/10407780903107162 [Google Scholar] [CrossRef]
19. Das, R., Mishra, S. C., Ajith, M., Uppaluri, R. (2008). An inverse analysis of a transient 2-D conduction-radiation problem using the lattice Boltzmann method and the finite volume method coupled with the genetic algorithm. Journal of Quantitative Spectroscopy & Radiative Transfer, 109(11), 2060–2077. https://doi.org/10.1016/j.jqsrt.2008.01.011 [Google Scholar] [CrossRef]
20. Bioswas, N., Mahapatra, P., Manna, N. (2015). Mixed convection heat transfer in a grooved channel with injection. Numerical Heat Transfer, 68(6), 663–685. https://doi.org/10.1080/10407782.2014.994411 [Google Scholar] [CrossRef]
21. Chakravarty, A., Biswas, N., Ghosh, K., Manna, N., Mukhopadhyay, A. et al. (2021). Impact of side injection on heat removal from truncated conical heat-generating porous bed: Thermal non-equilibrium approach. Journal of Thermal Analysis and Calorimetry, 143(5), 3741–3760. https://doi.org/10.1007/s10973-020-09295-6 [Google Scholar] [CrossRef]
22. Bioswas, N., Chamkha, A., Manna, N. (2020). Energy-saving method of heat transfer enhancement during magneto-thermal convection in typical thermal cavities adopting aspiration. Applied Sciences, 2(11), 1911. [Google Scholar]
23. Bioswas, N., Manna, N. (2017). Enhanced convective heat transfer in lid-driven porous cavity with aspiration. International Journal Heat and Mass Transfer, 114(15), 430–452. https://doi.org/10.1016/j.ijheatmasstransfer.2017.06.078 [Google Scholar] [CrossRef]
24. Bioswas, N., Manna, N., Datta, A., Mandal, D., Benim, A. (2020). Role of aspiration to enhance MHD convection in protruded heater cavity. Progress in Computational Fluid Dynamics, 20(6), 363–378. https://doi.org/10.1504/PCFD.2020.111408 [Google Scholar] [CrossRef]
25. Almeshaal, M. A., Kalidasan, K., Askri, F., Velkennedy, R., Alsagri, A. S. et al. (2020). Three-dimensional analysis on natural convection inside a T-shaped cavity with water-based CNT-aluminum oxide hybrid nanofluid. Journal of Thermal Analysis and Calorimetry, 139(3), 2089–2098. https://doi.org/10.1007/s10973-019-08533-w [Google Scholar] [CrossRef]
26. Yousefzadeh, S., Rajabi, H., Ghajari, N., Sarafraz, M. M., Akbari, O. A. et al. (2020). Numerical investigation of mixed convection heat transfer behavior of nanofluid in a cavity with different heat transfer areas. Journal of Thermal Analysis and Calorimetry, 140(6), 2779–2803. https://doi.org/10.1007/s10973-019-09018-6 [Google Scholar] [CrossRef]
27. Xiong, P. Y., Hamid, A., Iqbal, K., Irfan, M., Khan, M. (2021). Numerical simulation of mixed convection flow and heat transfer in the lid-driven triangular cavity with different obstacle configurations. International Communications in Heat and Mass Transfer, 123, 105202. https://doi.org/10.1016/j.icheatmasstransfer.2021.105202 [Google Scholar] [CrossRef]
28. Léonard, B. P. (1979). A stable and accurate convective modeling procedure based on quadratic upstream interpolation. Computer Methods Applied Mechanics and Engineering, 19(1), 59–98. https://doi.org/10.1016/0045-7825(79)90034-3 [Google Scholar] [CrossRef]
29. van Doormaal, J. P., Raithby, G. D. (1984). Enhancements of the SIMPLE method for predicting incompressible fluid flows. Numerical Heat Transfer, 7(2), 147–163. [Google Scholar]
30. de Vahl Davis, G., Jones, I. P. (1983). Natural convection in a square cavity: A comparison exercise. International Journal for Numerical Methods in Fluids, 3(3), 227–248. [Google Scholar]
31. Oliveski, R. D. C., Macagnan, M. H., Copetti, J. B. (2009). Entropy generation and natural convection in rectangular cavities. Applied Thermal Engineering, 29(8–9), 1417–1425. https://doi.org/10.1016/j.applthermaleng.2008.07.012 [Google Scholar] [CrossRef]
32. de Vahl Davis, G. (1983). Natural convection of air in a square cavity a benchmark numerical solution. International Journal for Numerical Methods in Fluids, 3(3), 249–264. [Google Scholar]
33. Iwatsu, R., Hyun, J. M., Kuwahara, K. (1993). Mixed convection in a driven cavity with a stable vertical temperature gradient. International Journal Heat and Fluid Flow, 36(6), 1601–1608. https://doi.org/10.1016/S0017-9310(05)80069-9 [Google Scholar] [CrossRef]
34. Cheng, T. (2011). Characteristics of mixed convection heat transfer in a lid-driven square cavity with various Richardson and Prandtl numbers. International Journal of Thermal Sciences, 50(2), 197–205. https://doi.org/10.1016/j.ijthermalsci.2010.09.012 [Google Scholar] [CrossRef]
35. Dahani, Y., Hasnaoui, M., Amahmid, A., Hasnaoui, S. (2022). A multiple-relaxation-time lattice Boltzmann analysis of coupled mixed convection and radiation effect in a tilted two-sided lid-driven enclosure. Chemical Physics Letters, 791(9–10), 139386. https://doi.org/10.1016/j.cplett.2022.139386 [Google Scholar] [CrossRef]
36. Najam, M., El Alami, M., Oubarra, A. (2004). Heat transfer in a “T” form cavity with heated rectangular blocks submitted to a vertical jet: The block gap effect on multiple solutions. Energy Conversion and Management, 45(1), 113–125. https://doi.org/10.1016/S0196-8904(03)00126-2 [Google Scholar] [CrossRef]
37. Mourabit, M., Rouijaa, H., Semma, E. A., El Alami, M., Najam et al. (2014). A mixed convection and heat transfer in a T form cavity: Effect of inclination angle. Fluid Dynamics & Material Processing, 10(3), 395–415. https://doi.org/10.3970/fdmp.2014.010.395 [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools