Chemically Radiative MHD Flow of a Micropolar Nanofluid over a Stretching/Shrinking Sheet with a Heat Source or Sink

Nomenclature

1  Introduction

Nanoparticles are particles with a size of less than 100 nanometers. They can be made through nanotechnology-based procedures. When nanoparticles are added to a base fluid, they can form a stable suspension and enhance the thermal properties of the fluid. This is because the nanoparticles increase the surface area of the fluid, which allows for more efficient heat transfer. Nanofluids have been shown to have much better heat absorbing and heat transfer properties than traditional working fluids. This makes them promising candidates for a variety of applications, such as electronics, communication, and computational systems, optical devices, and thermal management. In recent years, research into nanofluids has attracted considerable interest due to their extraordinary potential applications. The use of nanoparticles for heat transfer enhancement was first proposed by Choi et al. [1]. Nanoparticles are mostly oxides, metals, and carbides. They are characterized by Brownian agitation over gravity-induced settling. Stable nanofluids are possible if the particles are adequately tiny (usually smaller than 100 nm). As nanoparticles boost fluid heat transfer, they could cool vehicles like cars, while nanophase powders’ high relative surface areas, also aid in heat transfer. Several mechanisms explain nanofluids’ enhanced heat transfer. Pak et al. [2] found that suspended particles caused nanofluids increased heat transfer coefficients. Xuan et al. [3] hypothesized that nanoparticle mobility created turbulence and facilitated heat transfer. Sheikholeslami et al. [4] studied the role of magnetic force on ferrofluid flow and entropy generation through a permeable space. Khan [5] investigated a new way to model human blood flow in nanofluids using Atangana-Baleanu fractional derivatives. Kumar et al. [6,7] and Ibrahim et al. [8] reported on their research into the heat transfer performance of nanofluids prepared with different metal oxide nanoparticles suspended in various common fluids. The investigation of the impact of chemical reactions on hybrid nanofluid in the absence and presence of magnetic field are reported by Sajid et al. [9] and Bejawada et al. [10]. Rani et al. [11] studied the nanoparticle shape effect on a hybrid nanofluid under a transverse magnetic field.

Micropolar fluids are a type of fluid characterized by their microstructure. They fall into the category of fluids with a non-symmetric stress tensor, which we will refer to as polar fluids. These micropolar fluids can also represent systems where rigid, randomly oriented (or spherical) particles are suspended within a viscous medium, with the deformation of these particles being disregarded. This extension of the concept constitutes a noteworthy expansion of the traditional Navier-Stokes model, offering new avenues for potential applications. The model of micropolar fluids particularly compelling and robust is that it serves as both a significant and straightforward extension of the classical Navier-Stokes model. This dual nature enhances its attractiveness and utility in various scientific and engineering contexts. The micropolar fluids were defined by Erignen [12]. In his work, Eringen [13] provided an extensive exploration of motion and micromotions within the theory. He also presents empirical support for the recently introduced micro-deformation rate tensors, a crucial element in formulating the constitutive equations essential for describing a basic microfluidic system. Ariman et al. [14] brought a comprehensive review of micropolar fluids and their practical applications. Lukaszewicz [15] delved into the study of boundary layer flow involving micropolar fluids around a semi-infinite plate. For an in-depth understanding of the fundamental principles of micropolar fluids, consult the works authored by Eringen [16]. In the boundary layer theory, Malga et al. [17] studied the unsteady boundary layer of natural convection flow over an infinite accelerated vertical porous plate with suction, considering viscous dissipation. Guram et al. [18] studied the flow of micropolar fluids in two cases: the plane flow and the axially symmetric flow. In both cases, the fluid was in contact with an infinite plate. In the plane flow case, the fluid tended to potential flow at infinity, meaning that the velocity field approached a constant value as the distance from the plate increased. In the axially symmetric flow case, the fluid also tended to potential flow at infinity, but there was a stagnation point on the plate, where the velocity field was zero. Jena et al. [19] discussed the thermo-micropolar fluid free convective boundary layer flow across a non-isothermal vertical flat plate. Gorla [20] investigated the micropolar boundary layer flow nearby a stagnation point on a rotating wall. Further, many investigations have been done for new geometries on micropolar fluids [21–23].

The Fluid flow caused by stretching/shrinking sheet has become an extremely interesting topic over the past decade due to its many industrial uses. Numerous researchers have investigated the dynamics of boundary layer flow and heat transfer over sheet subjected to linear or non-linear stretching or shrinking. The study of micropolar nanofluid flow over these sheets has gained increasing attention in the realm of fluid mechanics. Micropolar nanofluids can be used to improve the quality of glass fibres by reducing defects and increasing strength. Miklavčič et al. [24] explored the flow over a shrinking sheet through viscous medium along suction near the boundary layer. In this paper, authors studied the characteristics of the flow, and the rate of heat and mass transfer over shrinking sheet and this results were inspired to many others to investigate the fluid flow over shrinking sheet rather than stretching sheet. Zaimi et al. [25] developed a model on nanofluid flow over stretching/shrinking sheet in presence of bio-organisms types of particles. Wang [26] studied a model on thin film of liquid metals of an exponential shrinking and stretching sheet, in this proposed model they found that the unique solutions for a stretching sheet are contrasted to the non-unique solutions for a shrinking sheet in a study of the effects of solid volume fraction on fluid flow and heat transfer characteristics. The details of boundary layer flows over shrinking sheets have been examined by different researchers, each with their own unique perspective. For instance, Fang [27] delved into the flow over shrinking sheet with power-law surface velocity, heat and mass transfer. Building upon this, Fang et al. [28] offered a systematic closed-form resolution for the viscous flow over shrinking porous sheet subjected to suction. Meanwhile, Fang et al. [29] explored unsteady 2D free convective flow contains viscous over shrinking sheet by mass suction. In a further study, Bhattacharyya [30] investigated exponentially shrinking sheet with microstructural fluid flow, taking into account radiation effects. Roja et al. [31] proposed the effects of thermophoresis and radiation on a micropolar fluid through a porous medium with variable heat and mass flux. Dawar et al. [32] studied the chemical reaction impact on micropolar nanofluid flow with velocity slips and variable heat source/sink. Micropolar hybrid nanofluid flow over a flat surface subject to mixed convection and thermal reaction was studied by Lone et al. [33]. Nanofluid flow over stretching sheets has been studied by several researchers using a variety of theoretical approaches [34–36].

MHD is the study of how fluids and magnetic fields can interact to produce a variety of phenomena, such as plasma confinement, magnetic propulsion, and dynamo action. The study of magnetohydrodynamic (MHD) flow on boundary layers over continuous stretching/shrinking sheets has gained significant attention in recent years due to its many applications in industrial manufacturing processes. This research is still ongoing, but it has the potential to make significant contributions to the efficiency and safety of these processes. The effects of MHD flow on different geometries have been investigated by many researchers [37–39].

Inspired by the previous studies and the importance of heat and mass transfer (HMT) over a stretching/shrinking sheet in various applications of magnetic micropolar-nanomaterials, we are currently working on a study that investigates a novel theoretical approach to the flow behavior of a micropolar nanofluid over a stretching or shrinking sheet in the presence of a transverse magnetic field and thermal effects. The study will take into account various physical aspects, such as chemical reactions, heat generation/absorption, thermal and mass convection. The findings will be well-analyzed using both graphical illustrations and tabular representations.

A review of the literature shows that no previous study has investigated the numerical treatment for creeping the flow through a stretching and shrinking sheet with a magnetic field of micropolar nanofluid model, taking into account the efficiency of thermal radiation, heat source/sink, and chemical reaction. This study aims to fill this gap by providing a comprehensive understanding of the non-Newtonian transport of magnetic field of nanofluid model.

The findings of this study are also relevant to electromagnetic micro-scale pumps that mimic real working fluids and use non-Newtonian micropolar mechanisms. These pumps have the potential to be used in bio-inspired transportable intravenous dripping systems for medical procedures in the 21st century, as they avoid contamination problems, require less maintenance, and have better longevity and efficiency. The current study is discussed in the following sections: Section 2 presents the mathematical aspects of the non-Newtonian model for two-dimensional flow involving nanofluid motion patterns characteristics. Sections 3 and 4 present the conceptual framework and a graphical interpretation of the acquired data, respectively. Section 5 summarizes the problems and possible conclusions that can be drawn from the study.

2  Physical and Mathematical Model

The continuation of a transverse magnetic field in a two-dimensional (2D) flow of a micropolar fluid of nanoparticles with heat and mass transfer over a stretching or shrinking surface was investigated. Both chemical (first-order homogeneous) reactions and thermal radiation were considered. The flow was restricted to the section (y > 0) of the coordinate system, as shown in Figs. 1a and 1b. A strong magnetic field, B0, was applied perpendicular to the flow. The induced magnetic field was ignored because the magnetic Reynolds number was relatively constant. The velocity distribution was assumed to be parabolic, as shown in Figs. 1a and 1b. Physically, the values of a > 0 indicated a stretching sheet, whereas a < 0 indicated a shrinking sheet. The temperature and concentration profiles at the sheet and at infinity were assumed to be constant, as Tw, Cw, T∞ , and C∞ , respectively. The associated micropolar nanofluid flow approximations were expressed as given by other researchers [40,41], and are written as follows:

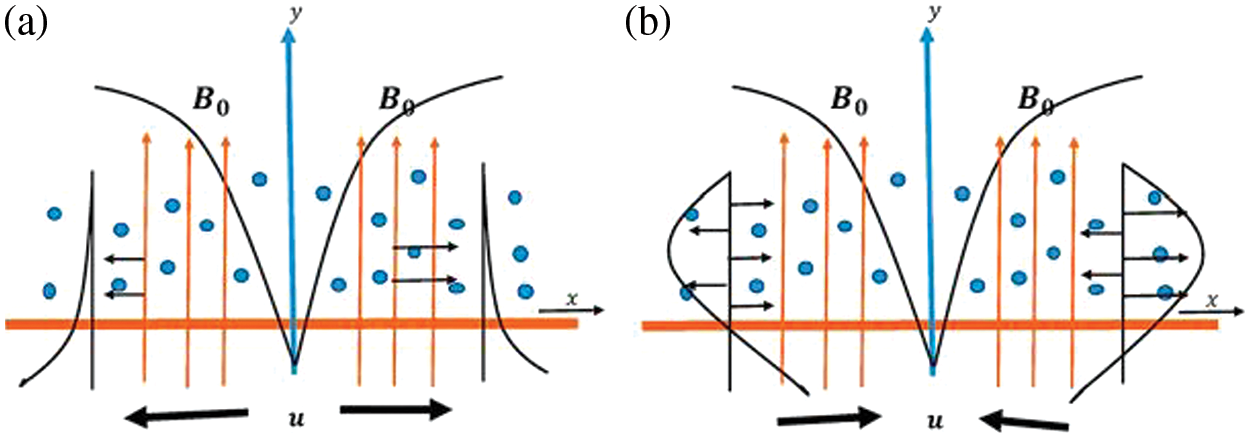
Figure 1: (a): Physical sketch for stretching case (a > 0). (b): Physical sketch for shrinking case (a < 0)

(i) Continuity equation:

∂u∂x+∂u∂y=0 (1)

(ii) Momentum equation:

u∂u∂x+v∂u∂y=(v+kρ)∂2u∂y2+kρ∂N∂y−σB02uρf−gβ(T∞−T)−gβ∗(C∞−C) (2)

(iii) Angular momentum equation:

u∂N∂x+v∂N∂y=γρj∂2N∂y2−kρj(2N+∂u∂y) (3)

(iv) Energy equation:

u∂T∂x+v∂T∂y=kρc∂2T∂y2−1ρc∂qr∂x+Q0(T−T∞)+τ[DB∂T∂y∂C∂y+DTT∞(∂T∂y)2] (4)

(v) Nanoparticle volume fraction equation:

u∂C∂x+v∂C∂y=DB∂2C∂y2+DTT∞∂2T∂y2−K0(C−C∞) (5)

The term can be expressed clearly as follows, using the Roseland approximation (Brewster [42]).

qr=−4σ13k1∂T4∂y (6)

The coefficient of mean absorption is here represented by k1 , and the Stefan-Boltzmann constant is represented by σ1 .

Assuming that the temperature difference within the flow can be expressed as a linear combination of the temperature, we can expand T4as a Taylor series about T∞, as follows:

T4≅4T∞3T−3T∞4 (7)

Here neglecting higher order terms beyond the first degree. Using (6) and (7) in (3), we obtain

u∂T∂x+v∂T∂y=α∂2T∂y2+16σT∞33ρcpk1∂2T∂y2−Q0(T∞−T)+τ{DB∂T∂y∂ϕ∂y+(DTD∞)[(∂T∂x)2+(∂T∂y)2]} (8)

The equivalent boundary conditions are defined as follows, based on the requirements of the problem [40].

v=vw,u=U0(x)=−ax,N=−m∂u∂y,T=Tw,C=Cwaty=0v→0,u→0,T→T∞,N→0,C→C∞asy→∞ (9)

Here, vw < 0 assumes negative values for mass suction and vw > 0 positive values for mass injection. It is important to highlight that the constant m lies within the range of 0 to 1. In this context, when m is set to 0, it represents a scenario characterized by strong concentration, where N equals 0, signifying that particles within the concentration remain immobile near the wall surface. Conversely, when m is equal to 1/2, it signifies the disappearance of the anti-symmetric component of the stress tensor, indicating weaker concentrations. Finally, when m is set to 1, it is employed for the modeling of turbulent boundary layer flow.

The spin gradient viscosity (γ) is proposed to be defined as follows (Fauzi et al. [40]):

γ=(μ+k/2)j=μ(1+K/2) j (10)

In the above context, the material constraint is represented by K=k/μ . This statement was made to ensure that the equation field can accurately predict the behavior of a system in cases where the influence of the microstructure is negligible and the total spin N can be simplified to the angular velocity.

Based on the premises outlined by Fauzi et al. [40], the free stream velocity and the velocity associated with suction/injection were assumed to be:

U0(x)=ax and V=−(av)1/2fw (11)

Here, a > 0 denotes the initial stretching rate, fw > 0 indicates transpiration (suction), fw < 0 indicates injection, and fw = 0 corresponds to the scenario of an impermeable plate surface.

To non-dimensionalize the governing equations, we make the following suitable substitutions (Fauzi et al. [40]):

N=xa(a/v)1/2h(η),θ(η)=T−T∞Tw−T∞,η=y(a/v)1/2,ϕ(η)=C−C∞Cw−C∞,ψ=(av)1/2xf(η). (12)

here η is the similarity variable and ψ is the stream function defined as

v=−∂ψ∂x & u=∂ψ∂y (13)

It is clear that Eq. (1) is identically satisfied. When Eq. (12) is used in Eqs. (2), (3), (5), and (8), along with the boundary conditions in Eq. (9), we have:

(K+1)f′′′+f′′f−(f′)2−Mf′+Kg′+Grxθ+Gcxϕ=0 (14)

(K/2+1)g′′+fg′−f′g−K(f′′+2g)=0 (15)

(43R+1)θ′′+Pr(θ′f+Nbθ′ϕ′+θ′2Nt)+Prβθ=0 (16)

ϕ′′+Lefϕ′+NtNbθ′′−LeKrϕ=0 (17)

The boundary conditions at the transformed domain are as follows:

f(0)=0.0,f′(0)=1.0,g(0)=−mf′′(0),θ(0)=1.0,ϕ(0)=1.0f′(∞)=0.0,g(∞)=0.0,θ(∞)=0.0,ϕ(∞)=0.0. (18)

where the prime notation signifies differentiation with respect to η and

Gr=βgρ(Tw−T∞)aU0(Grashofnumber),Gc=β∗gρ(Cw−C∞)aU0(ModifiedGrashofnumber),M=σB02ρa(Magneticfieldparameter),Le=vDB(Lewisnumber),Pr=vα(Prandtlnumber),Nb=τDB(Cw−C∞)ν(Brownianmotionparameter),Nt=τDT(Cw−C∞)vT∞(thermophoresisparameter),R=4σT∞3kk∗(radiativeparameter,δ=Q0vak(heatsource/sin⁡kparameter),Kr=K0a(chemicalreactionvalue) (19)

To provide a comprehensive analysis of the flow, this study not only provides solutions for velocity, microrotation, temperature, and concentration, but also solutions for shear stress at the plates. Additionally, it includes dimensional coefficients for mass and heat transfer rates at the plates, which are quantified by the local Sherwood and local Nusselt numbers.

The skin resistance (friction) Cf, local Nusselt numeral Nu, and local Sherwood numeral Sh are defined as Fauzi et al. [40]:

Cf=τwρfu02((μnf+κ)∂u∂y+κN)y=0,Mw=1ρfxu02((μnf+κ2) j)(∂N∂y)y=0Nu=qwxkf(T−T∞)(knf+16σ∗T∞33k∗),Sh=xqmDB(C−C∞) (20)

where τw , qw and qm represent the skin resistance (friction), surface heat flux, and surface mass flux, respectively, defined by [40]

τw=μ(∂u∂y)y=0,qw=−k∂T∂y|y=0 and qm=−Db∂C∂y|y=0 (21)

Substituting (21) into (20) we obtain,

Cfx=Rex1/2Cf=(μnfμf+(1−m)K)f′′(0),Cfy=Rex1/2Mw=(μnfμf+K2)g′(0), (22)

Nux=Rex1/2Nu=−(knfkf+43R)θ′(0), (23)

Shx=Rex1/2Sh=−ϕ′(0). (24)

where Rex=U0x/ν is the Reynolds number.

3  Numerical Procedure

It is difficult to obtain an analytical solution to the reduced set of coupled similarity Eqs. (14)–(17) with boundary condition (18). Therefore, we numerically solved the equations using the mathematical software Mathematica 11 and the Runge-Kutta-Fehlberg integration scheme, which is a fourth-fifth-order method. Mathematica 11 has been rigorously tested for its accuracy and stability, and it has been used to solve a variety of nonlinear problems.

In this study, we assumed that the solution approaches a specific value as η→∞, such as η6 , so that the boundary conditions are asymptotically satisfied. The step size Δη = 0.01 was used throughout the computation. The numerical results for the skin-resistance (friction) coefficient, couple stress coefficient, local Nusselt number, and local Sherwood number are presented in Tables 1 and 2 for different parameters. The flowchart provides a visual representation of the numerical procedure for solving the problem Fig. 2.

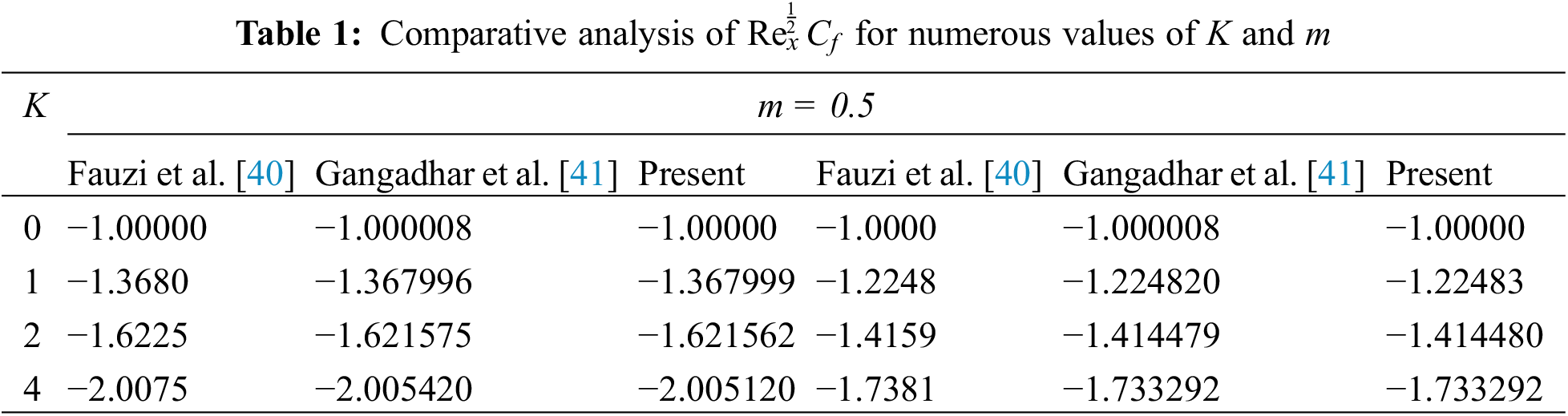
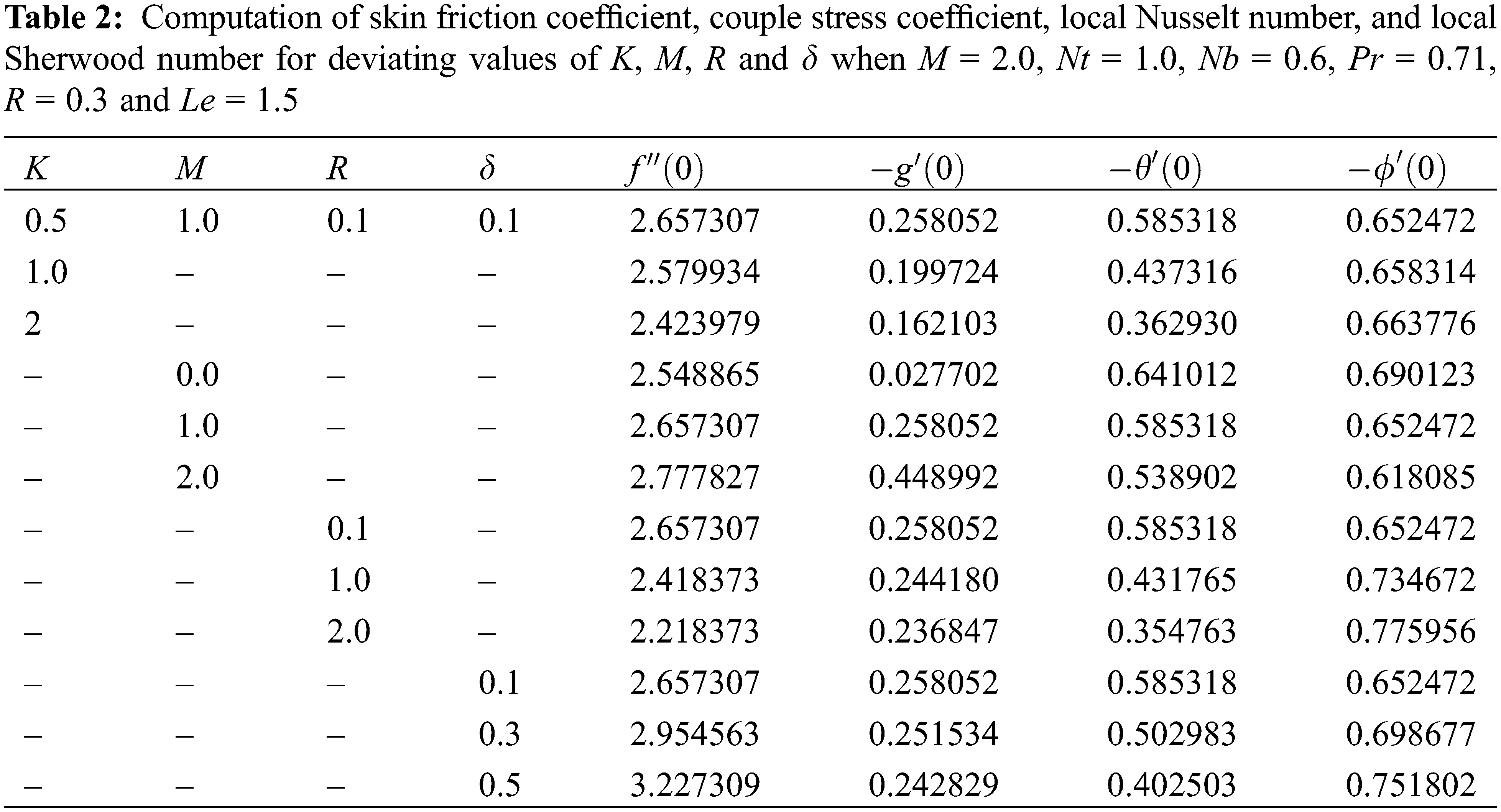
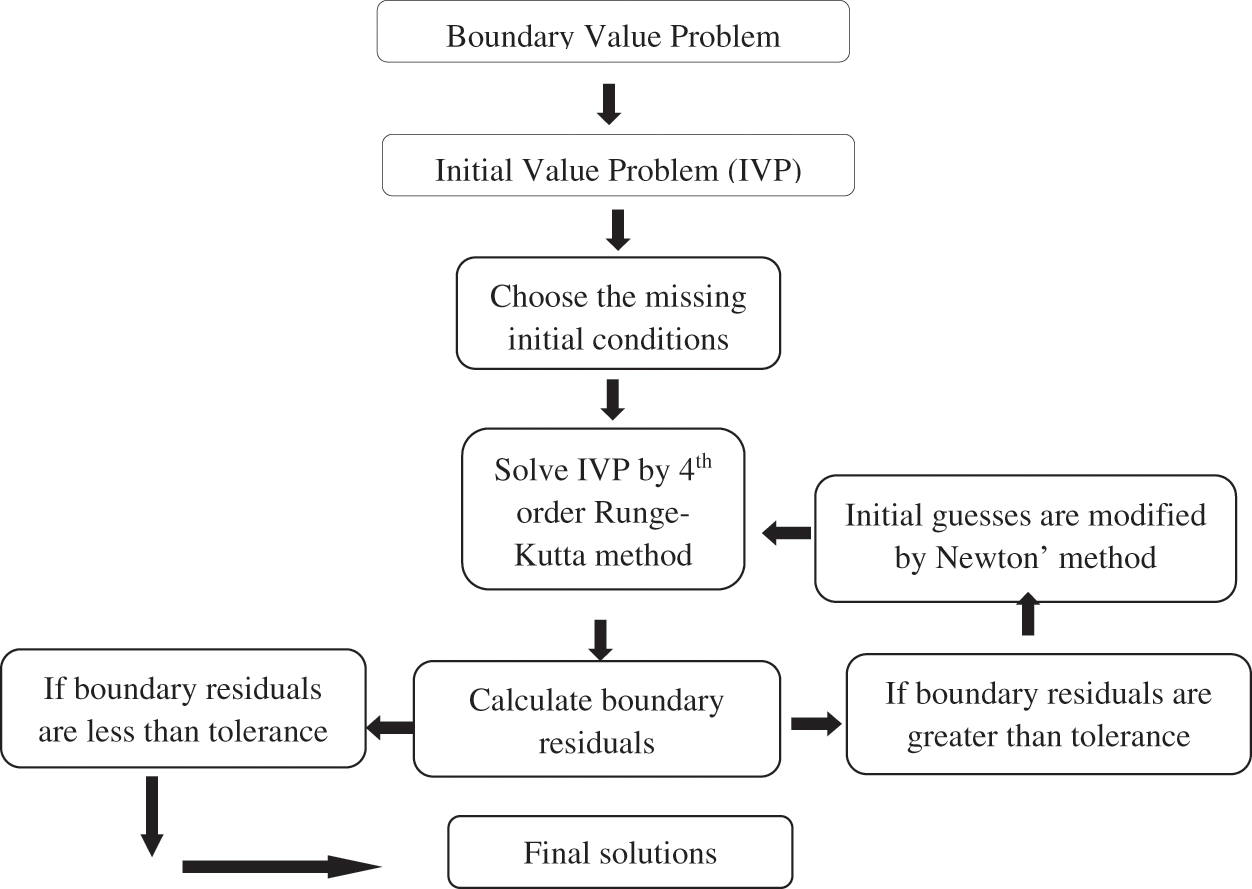
Figure 2: Flow chart

4  Results and Discussion

A mathematical framework has been developed to investigate the combined effects of thermal and mass convection, as well as variable electrical conductivity, on a two-dimensional stretching/shrinking MHD micropolar nanofluid flow. The flow variables in Figs. 3–9 were analyzed in this section by examining numerical results that were processed using Mathematica symbolic software. The effects of important electromagnetic and hydrodynamic parameters on the flow variables were investigated. It is important to note that all of the derived figures use the same parameter values: K = 0.1, M = 1.0, Gr = 1.0, Gc = 1.0, Le = 1.3, Nb = 0.5, Nt = 0.8, Pr = 0.71, R = 0.1, and Kr = 0.1. These values are used consistently throughout the study, except for minor variations in specific figures and tables.

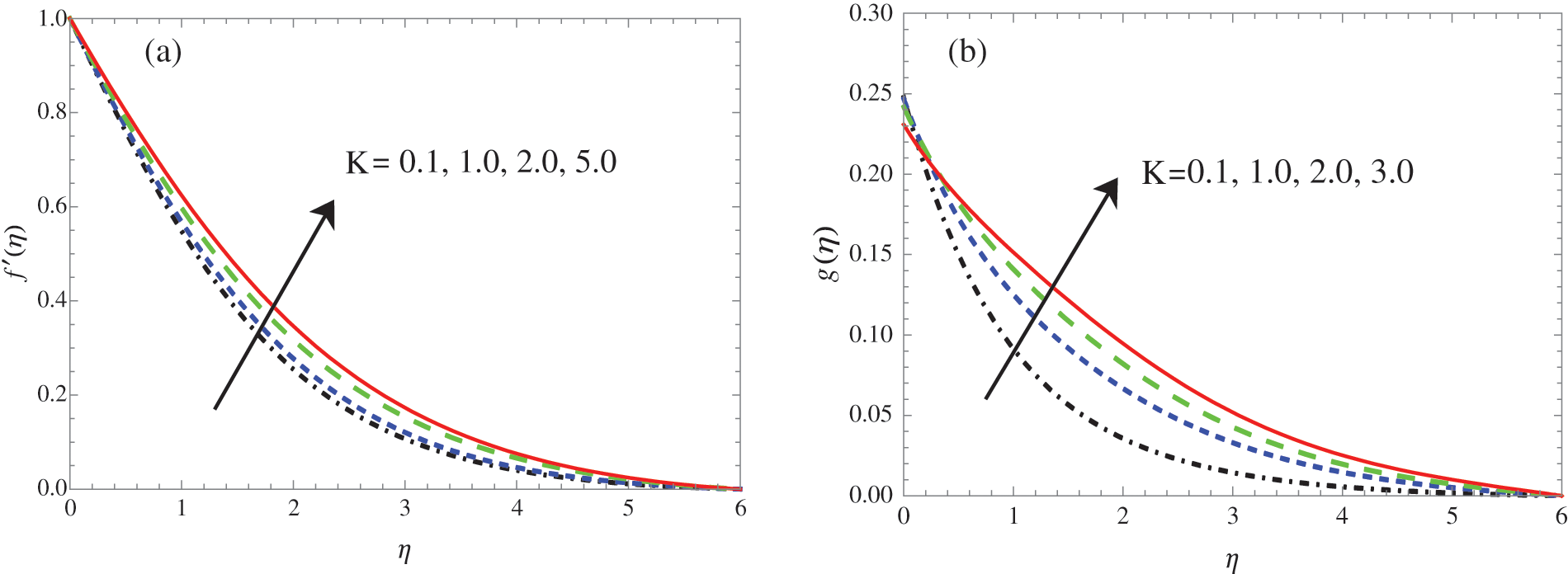
Figure 3: Variation of f′(η) and g(η) for deviating values of K

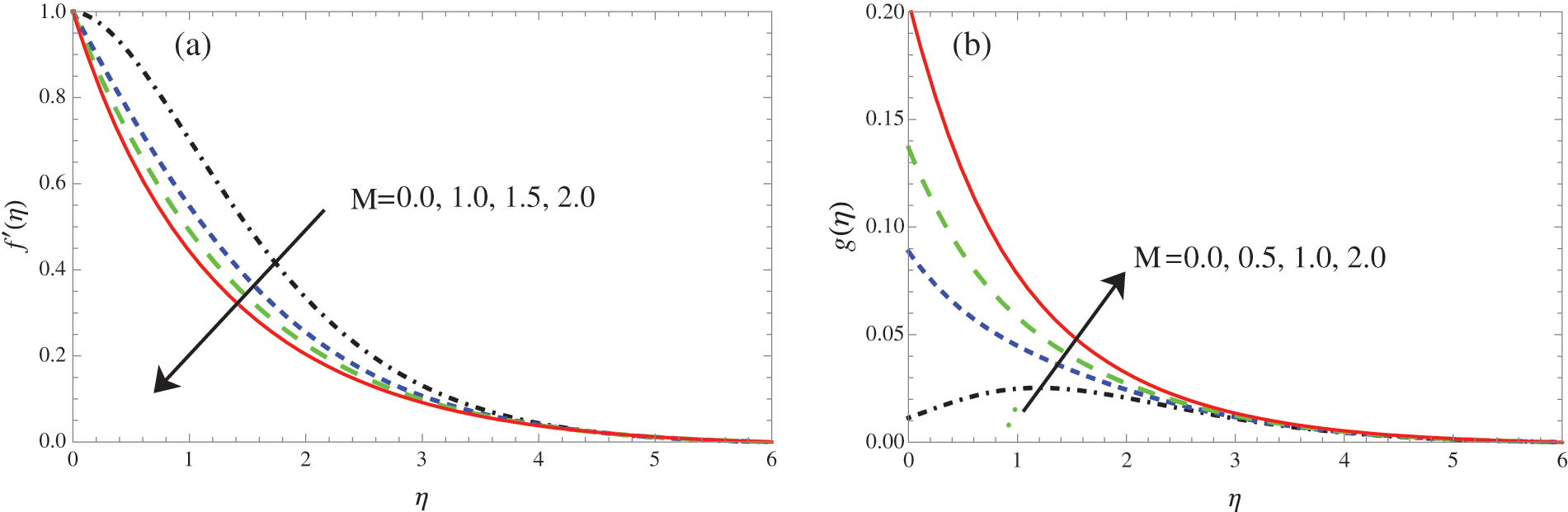
Figure 4: Variation of f′(η) and g(η) for deviating values of M

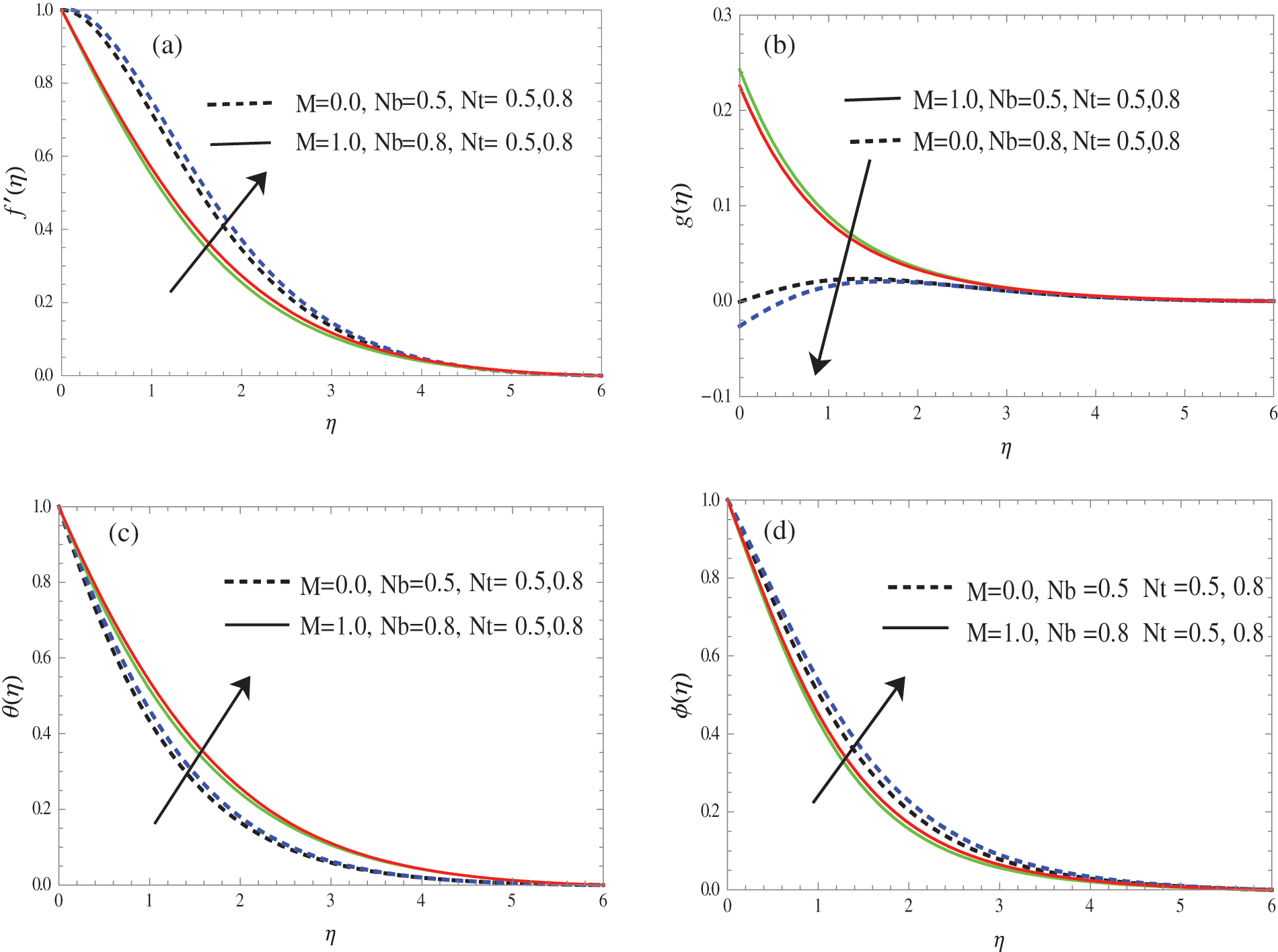
Figure 5: Variation of f′(η) , g(η) , θ(η) and ϕ(η) for deviating values of M, Nb and Nt

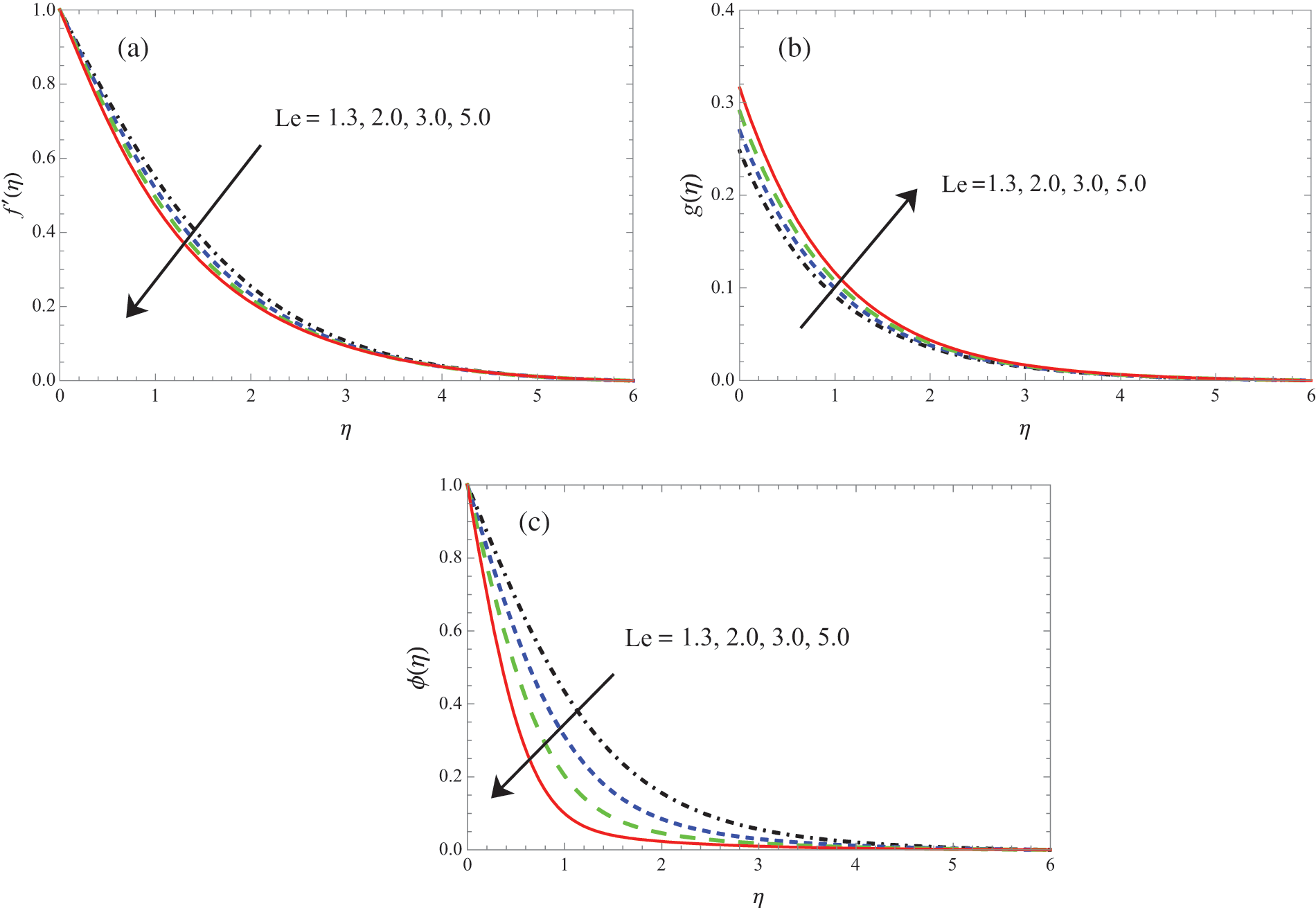
Figure 6: Variation of f′(η) , g(η) , and ϕ(η) for deviating values of Le

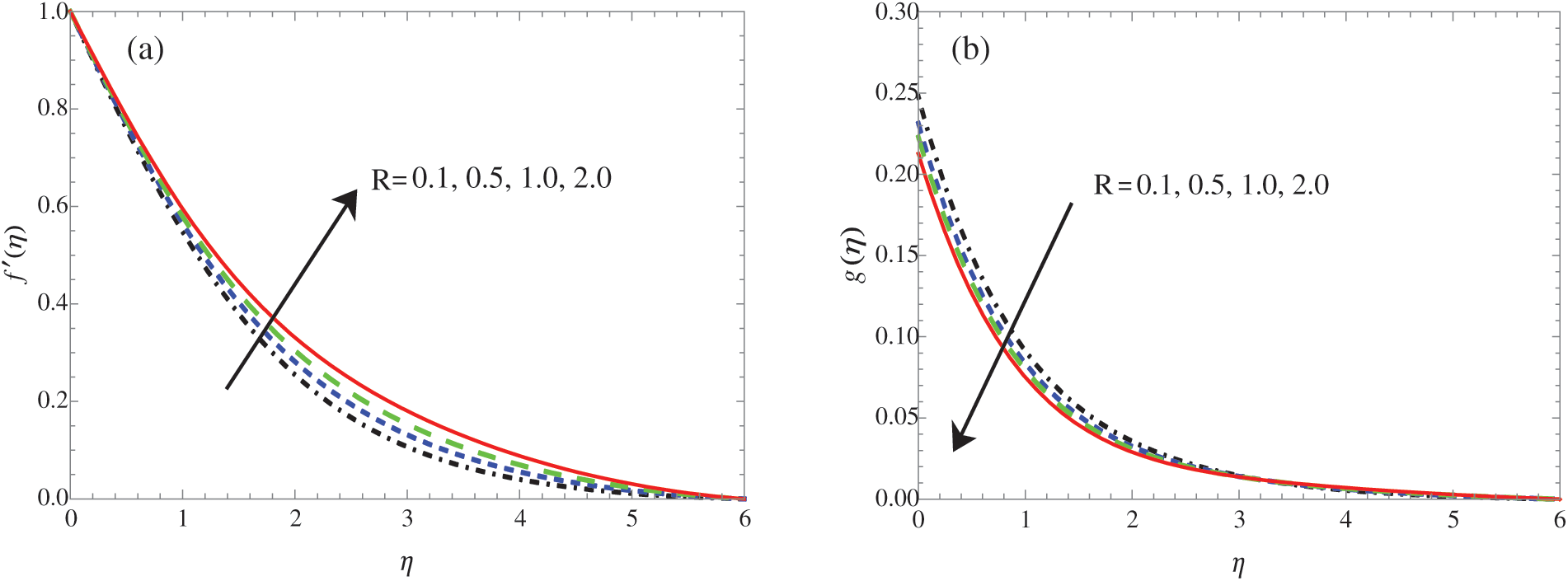
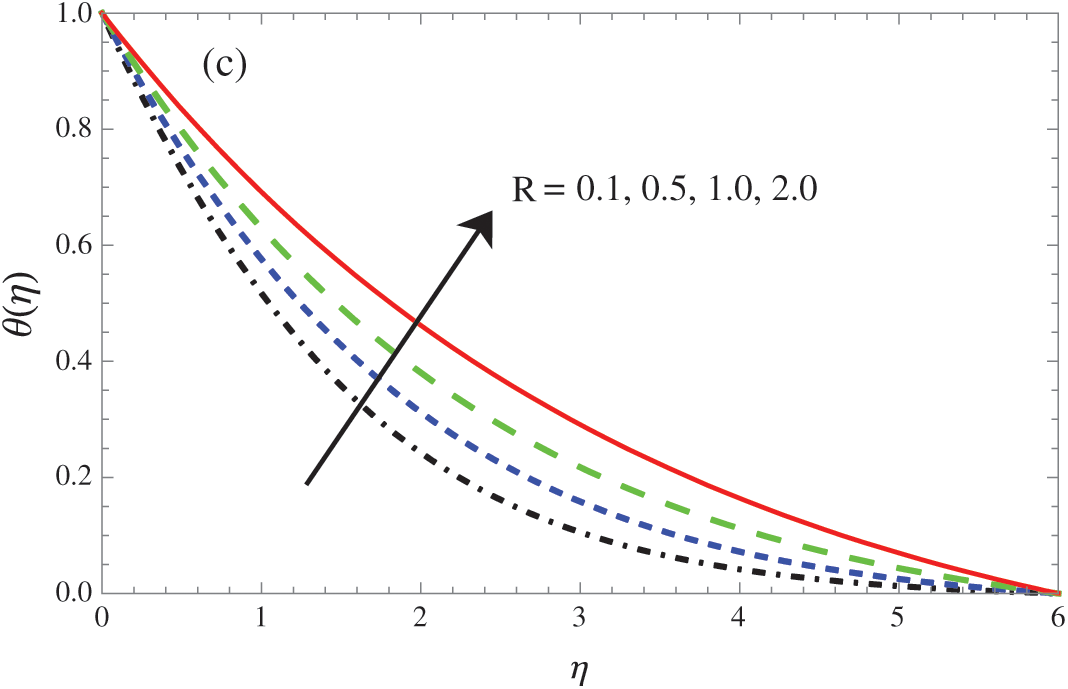
Figure 7: Variation of f′(η) , g(η) , and θ(η) for deviating values of R

Figure 8: Variation of f′(η) , g(η) , and θ(η) for deviating values of δ

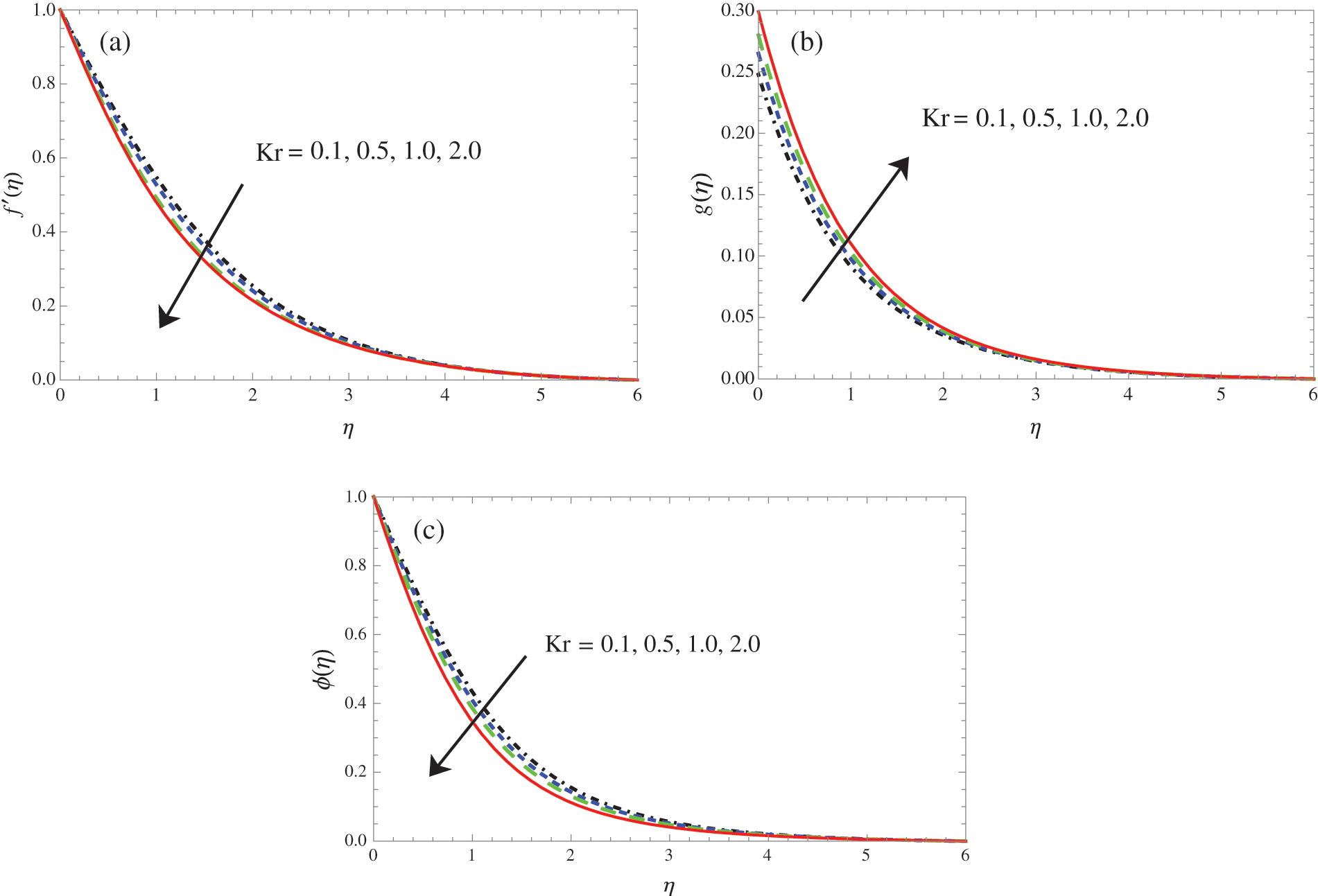
Figure 9: Variation of f′(η) , g(η) , and ϕ(η) for deviating values of Kr

The calculated values are used in Figs. 3–9 to investigate the effects of the governing parameters on the flow velocity, microrotation, temperature, and nanoparticle concentration profiles. The governing parameters include the material parameters K, magnetic field parameter M, Brownian motion parameter Nb, thermophoresis parameter Nt, Lewis number Le, radiation parameter R, and chemical (first order homogeneous) reaction parameter Kr.

Figs. 3a and 3b show the effects of changing the coupling parameter K on the velocity and microrotation fields. As K increases, the velocity increases. The results also show that the distance from the plate affects the frequency of microrotation. The microrotation is reduced closer to the plate and increased at greater distances from the plate.

The impact of the field of magnetic parameter M was seen via the action of the Lorentz force in Figs. 4a and 4b. The Lorentz force is a force that acts on a moving charged particle in a magnetic field. When an electrically conductive fluid flow under the influence of an external magnetic field, the Lorentz force acts in the opposite direction of the flow, slowing it down. The stronger the magnetic field, the greater the Lorentz force. The slowing down of the flow is directly proportional to the Lorentz force. In the study, the researchers found that the Lorentz force had a significant impact on the flow of the fluid. As the magnetic parameter M was increased, the flow velocity profiles were reduced. This was most evident in the middle of the plate, where the flow velocity was highest. The Lorentz force also caused the microrotation patterns in the fluid to increase. Additionally, the magnetic parameters thinned the motion boundary layer and thickened the angular motion boundary layer which was observed in Fig. 4b. The findings of this study have important implications for the understanding of fluid flow in magnetic fields. The Lorentz force can be used to control the flow of fluids, and this could be used for a variety of applications, such as in microfluidics, chemical engineering, and plasma physics.

The influences of the Brownian motion parameter Nb and thermophoretic parameter Nt on velocity, angular velocity, temperature, and concentration distribution are shown in Figs. 5a–5d. The temperature distributions increased as both Nb and Nt increased, while the velocity profiles decreased as Nb and Nt increased. However, the concentration profiles are decreased as Nb increased and the opposite effect was observed for Nt.

As shown in Figs. 6a–6c, the Lewis number Le affects the distribution of velocity, temperature, and nanoparticle concentration. The velocity and temperature distributions become less uniform as Le increases. This is because Le is the ratio of thermal diffusivity to mass diffusivity, and it determines how easily heat and mass are transferred in a fluid. Therefore, Le is one of the most important factors in characterizing fluid flow with simultaneous heat and mass transfer.

Figs. 7a–7c show the effects of the radiation parameter R on the velocity, microrotation, and temperature fields. As R increases, the velocity distribution becomes more uniform across the boundary layer. The microrotation profiles also increase with R. The temperature profiles also increase with R. The increase in R leads to a decrease in the mean absorption coefficient ke . This means that the divergence of the radiative heat flux increases, which in turn increases the thickness of the thermal boundary layer. As a result, the fluid temperature increases significantly and the proportion of radiative heat transfer increases.

The flow (velocity), microrotation, and temperature summaries for several values of the heat absorption/generation parameter δ are displayed in Figs. 8a–8c, respectively. As the heat source parameter was raised to higher levels, it was evident that the rate of motion accelerated. The results also revealed that as the heat source parameter was raised, the microrotation profiles also rose in along with it. When the heat generation parameter was raised, the resulting temperature profiles are shown in Fig. 8c.

The patterns of translational flow (velocity), microrotation, and nanoparticle concentration change for deviating values of the Kr parameter in the chemical (first-order homogeneous) process are shown in Figs. 9a–9c. Visual inspection of data reveals that as the value of the chemical (first-order homogeneous) reaction parameter Kr was increased, the microrotation distribution grew, while the flow (velocity) distribution over the boundary layer decreased. The concentration profiles of nanoparticles are shown to vary for deviating Kr values in Fig. 9c. As Kr increased, the concentration profiles of the nanoparticles reduced.

To validate the accuracy of the numerical method used in this study, we compare our results with the available studies of Fauzi et al. [40] and Gangadhar et al. [41]. The comparisons are presented in Table 1 for different values of K when m = 0.0 and m = 0.5. It is evident that our results are in good agreement with the previous studies for each value of K. Tables 2 and 3 are presented to analyze the variation of skin friction coefficient, local Nusselt number, and local Sherwood number for different values of the dimensionless parameters.

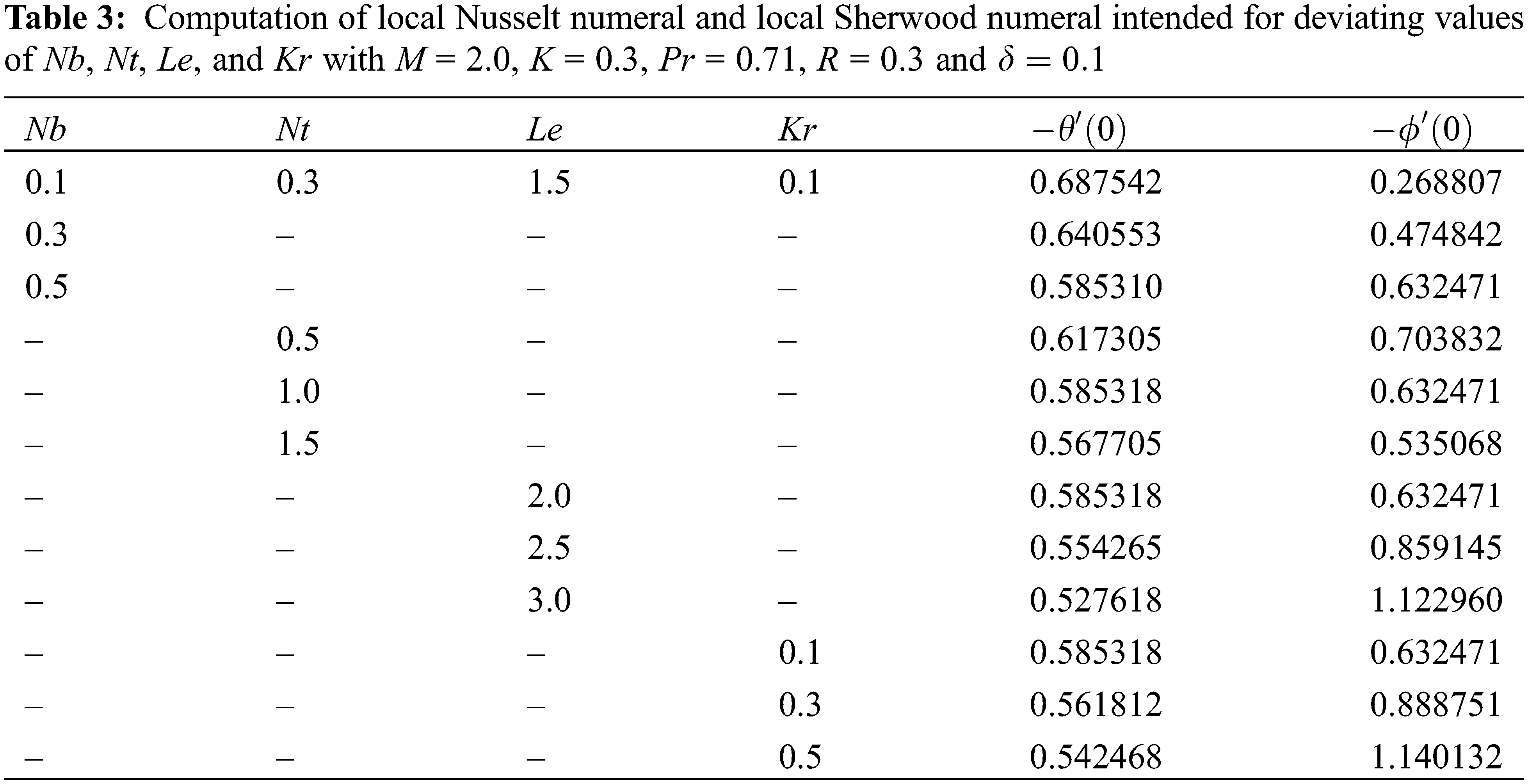
Tables 2–3 show the skin friction coefficient, couple stress coefficient, local Nusselt number, and local Sherwood number for different values of K, M, R, δ , Nb, Nt, Le, and Kr. The skin friction coefficient increased as the values of M and δ increased. However, the increase in the skin friction coefficient decreased when K and R values increased. The couple stress coefficient was inversely proportional to the function of K, R, and δ . The Nusselt number decreased as the values of K, M, R, δ , Nb, Nt, Le, and Kr increased. The Sherwood number increased as the values of K, R, δ , Nb, Nt, Le, and Kr increased, but decreased as the value of M increased.

5  Conclusion

We used a similarity function to investigate the effects of thermal radiation and chemical reaction on MHD free convection flow of micropolar nanofluid across a stretching/shrinking sheet in the presence of a heat source. We obtained the features of the flow, heat transfer, and mass transfer, as well as their rate of flow (skin-friction), rate of heat transfer (local Nusselt number), and rate of mass transfer (local Sherwood number). Here are some of the most significant findings of our study:

     i)  The Brownian motion parameter Nb increased the boundary layer temperature, but decreased the concentration profiles.

    ii)  As the nonlinear stretching sheet/shrinking sheet parameter n increased, the boundary layer flow profile decreased.

   iii)  The concentration of the fluid decreased as the Lewis number Le increased.

    iv)  The fluid concentration and temperature profiles both increased as the thermophoretic parameter Nt increased. The mass transport rate at the surface was positively correlated with the Lewis number and chemical reaction parameter.

The study opens up new avenues for future research. By examining the effects of hybrid nanoparticles and other physical parameters on the flow and thermal behavior of fluids, we can better understand how to control and optimize these processes. This knowledge could be used to develop new and improved technologies in a variety of fields.

The investigation of the flow mechanics throughout an exponential stretching/shrinking regime provides a framework for scientific and practical applications utilizing electric fluids as they may shed more light on how oil and gas move through a reservoir in an oil or gas field, the movement of subsurface water, and the effectiveness of deviating filtration and purification processes. Possible applications in nuclear engineering include advances in heat shifter design, glass fiber outlining, and combined reactor cooling.

Acknowledgement: We are very much thankful to learned reviewers for their useful suggestions for the improvement in the quality of our manuscript.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The majority of the article was prepared by P. Roja, and T. Sankar Reddy, however, S.M. Ibrahim, and G. Lorenzini developed the model, provided computational suggestions, and proofread it. The final manuscript was read and approved by all authors.

Availability of Data and Materials: All code and materials used in the study are available from the corresponding author upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Choi, S. U., Eastman, J. A. (1995). Enhancing thermal conductivity of fluids with nanoparticles. International Mechanical Engineering Congress and Exhibition, pp. 12–17. San Francisco, USA. [Google Scholar]

2. Pak, B. C., Cho, Y. I. (1998). Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles. Experimental Heat Transfer, 11(2), 151–170. [Google Scholar]

3. Xuan, Y., Li, Q. (2003). Investigation on convective heat transfer and flow features of nanofluids. Journal of Heat Transfer, 125(1), 151–155. [Google Scholar]

4. Sheikholeslami, M., Arabkoohsar, A., Khan, I., Shafee, A., Li, Z. (2019). Impact of Lorentz forces on Fe3O4-water ferrofluid entropy and exergy treatment within a permeable semi annulus. Journal of Cleaner Production, 221(5), 885–898. [Google Scholar]

5. Khan, I. (2019). New idea of Atangana and Baleanu fractional derivatives to human blood flow in nanofluids. Chaos, 29(1), 013121. [Google Scholar] [PubMed]

6. Kumar, P. V., Sunitha, C., Ibrahim, S. M., Lorenzini, G. (2023). Outlining the slip effects on MHD casson nanofluid flow over a permeable stretching sheet in the existence of variable wall thickness. Journal of Engineering Thermophysics, 32(1), 69–88. [Google Scholar]

7. Kumar, P. V., Sunitha, C., Lorenzini, G., Ibrahim, S. M. (2022). A study of thermally radiant williamson nanofluid over an exponentially elongating sheet with chemical reaction via homotopy analysis method. CFD Letters, 14(5), 68–86. [Google Scholar]

8. Ibrahim, S. M., Shehzad, S. A., Mabood, F., Badruddin, I. A., Ambreen, T. (2023). Hydromagnetic CuO-H2O nanofluid transportation through irreversibility analysis. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, 237(3), 872–880. [Google Scholar]

9. Sajid, T., Ayub, A., Shah, S. Z. H., Jamshed, W., Eid, M. R. et al. (2022). Trace of chemical reactions accompanied with arrhenius energy on ternary hybridity nanofluid past a wedge. Symmetry, 14(9), 1850. [Google Scholar]

10. Bejawada, S. G., Jamshed, W., Safdar, R., Reddy, Y. D., Alanazi, M. et al. (2022). Chemical reactive and viscous dissipative flow of magneto nanofluid via natural convection by employing Galerkin finite element technique. Coatings, 12(2), 151. [Google Scholar]

11. Rani, S., Al–Sharifi, H. A. M., Zannon, M. S., Hussanan, A., Ullah, Z. (2023). Nanoparticle shape effect on a sodium-alginate based Cu-nanofluid under a transverse magnetic field. Fluid Dynamics & Materials Processing, 19(7), 1975–1996. https://doi.org/10.32604/fdmp.2023.025224 [Google Scholar] [CrossRef]

12. Eringen, A. C. (1966). Theory of micropolar fluids. Journal of Mathematics and Mechanics, 16(1), 1–18. [Google Scholar]

13. Eringen, A. C. (1972). Theory of thermomicrofluids. Journal of Mathematical Analysis and Applications, 38(2), 480–496. [Google Scholar]

14. Ariman, T., Turk, M. A., Sylvester, N. D. (1973). Microcontinuum fluid mechanics—A review. International Journal of Engineering Science, 11(8), 905–930. [Google Scholar]

15. Lukaszewicz, G. (1999). Micropolar fluids: Theory and applications. Basel: Springer Science & Business Media. [Google Scholar]

16. Eringen, A. C. (2001). Microcontinuum field theories. II: FIuent media. New York: Springer. [Google Scholar]

17. Malga, B. S., Kishan, N. (2013). Viscous dissipation effects on unsteady free convection and mass transfer flow of micropolar fluid embedded in a porous media with chemical reaction. Elixir Applied Mathematics, 63, 18569–18578. [Google Scholar]

18. Guram, G. S., Smith, A. C. (1980). Stagnation flows of micropolar fluids with strong and weak interactions. Computers & Mathematics with Applications, 6(2), 213–233. [Google Scholar]

19. Jena, S. K., Mathur, M. N. (1981). Similarity solutions for laminar free convection flow of a thermomicropolar fluid past a non-isothermal vertical flat plate. International Journal of Engineering Science, 19(11), 1431–1439. [Google Scholar]

20. Gorla, R. S. R. (1983). Micropolar boundary layer flow at a stagnation point on a moving wall. International Journal of Engineering Science, 21(1), 25–33. [Google Scholar]

21. Izadi, M., Shahivand, I., Mehryan, S. A., Hasan, M. S., Lorenzini, G. (2020). Magneto-hydrodynamic flow of micropolar nanofluid containing motile microorganisms passing over a vertical stretching sheet with magnetic field dependent viscosity. Journal of Engineering Thermophysics, 29(4), 632–656. [Google Scholar]

22. Goud, B. S., Reddy, Y. D., Alshehri, N. A., Jamshed, W., Safdar, R. et al. (2022). Numerical case study of chemical reaction impact on MHD micropolar fluid flow past over a vertical riga plate. Materials, 15(12), 4060. [Google Scholar] [PubMed]

23. Mahabaleshwar, U. S., Vishalakshi, A. B., Hatami, M. (2022). MHD micropolar fluid flow over a stretching/shrinking sheet with dissipation of energy and stress work considering mass transpiration and thermal radiation. International Communications in Heat and Mass Transfer, 133(32), 105966. [Google Scholar]

24. Miklavčič, M., Wang, C. (2006). Viscous flow due to a shrinking sheet. Quarterly of Applied Mathematics, 64(2), 283–290. [Google Scholar]

25. Zaimi, K., Ishak, A., Pop, I. (2014). Stagnation-point flow toward a stretching/shrinking sheet in a nanofluid containing both nanoparticles and gyrotactic microorganisms. Journal of Heat and Mass Transfer, 136(4), 041705. [Google Scholar]

26. Wang, C. Y. (1990). Liquid film on an unsteady stretching surface. Quarterly of Applied Mathematics, 48(4), 601–610. [Google Scholar]

27. Fang, T. (2008). Boundary layer flow over a shrinking sheet with power-law velocity. International Journal of Heat and Mass Transfer, 51(25–26), 5838–5843. [Google Scholar]

28. Fang, T., Zhang, J. (2009). Closed-form exact solutions of MHD viscous flow over a shrinking sheet. Communications in Nonlinear Science and Numerical Simulation, 14(7), 2853–2857. [Google Scholar]

29. Fang, T. G., Zhang, J., Yao, S. S. (2009). Viscous flow over an unsteady shrinking sheet with mass transfer. Chinese Physics Letters, 26(1), 014703. [Google Scholar]

30. Bhattacharyya, K. (2011). Boundary layer flow and heat transfer over an exponentially shrinking sheet. Chinese Physics Letters, 28(7), 074701. [Google Scholar]

31. Roja, P., Sankar Reddy, T., Ibrahim, S. M., Lorenzini, G., Sidik, N. A. C. (2022). The effect of thermophoresis on MHD stream of a micropolar liquid through a porous medium with variable heat and mass flux and thermal radiation. CFD Letters, 14(4), 118–136. [Google Scholar]

32. Dawar, A., Shah, Z., Kumam, P. (2020). Chemically reactive MHD micropolar nanofluid flow with velocity slips and variable heat source/sink. Scientific Reports, 10(1), 20926. [Google Scholar] [PubMed]

33. Lone, S. A., Alyami, M. A., Saeed, A. (2022). MHD micropolar hybrid nanofluid flow over a flat surface subject to mixed convection and thermal radiation. Scientific Reports, 12(1), 17283. [Google Scholar] [PubMed]

34. Ibrahim, S. M., Kumar, P. V., Lorenzini, G. (2023). Influence of thermophoresis and brownian motion of nanoparticles on radiative chemically-reacting MHD hiemenz flow over a nonlinear stretching sheet with heat generation. Fluid Dynamics & Materials Processing, 19(4), 855–868. https://doi.org/10.32604/fdmp.2022.019796 [Google Scholar] [CrossRef]

35. Kausar, M. S., Al-Sharifi, H., Hussanan, A., Mamat, M. (2023). The effects of thermal radiation and viscous dissipation on the stagnation point flow of a micropolar fluid over a permeable stretching sheet in the presence of porous dissipation. Fluid Dynamics & Materials Processing, 19(1), 61–81. https://doi.org/10.32604/fdmp.2023.021590 [Google Scholar] [CrossRef]

36. Patel, H. R., Mittal, A. S., Darji, R. R. (2019). MHD flow of micropolar nanofluid over a stretching/shrinking sheet considering radiation. International Communications in Heat and Mass Transfer, 108, 104322. [Google Scholar]

37. Khan, W. A., Rashad, A. M., EL-Kabeir, S. M. M., EL-Hakiem, A. M. A. (2020). Framing the MHD micropolar-nanofluid flow in natural convection heat transfer over a radiative truncated cone. Processes, 8(4), 379–388. [Google Scholar]

38. Alam, N., Poddar, S., Karim, M. E., Hasan, M. S., Lorenzini, G. (2021). Transient MHD radiative fluid flow over an inclined porous plate with thermal and mass diffusion: An EFDM numerical approach. Mathematical Modelling of Engineering Problems, 8(5), 739–749. [Google Scholar]

39. Khan, U., Zaib, A., Ishak, A., Waini, I., Pop, I. et al. (2023). Stagnation point flow of a water-based graphene-oxide over a stretching/shrinking sheet under an induced magnetic field with homogeneous-heterogeneous chemical reaction. Journal of Magnetism and Magnetic Materials, 565, 170287. [Google Scholar]

40. Fauzi, E., Ahmad, S., Pop, I. (2014). Flow over a permeable stretching sheet in micropolar nanofluids with suction. AIP Conference Proceedings, 1605, 428–433. [Google Scholar]

41. Gangadhar, K., Kannan, T., Jayalakshmi, P. (2017). Magnetohydrodynamic micropolar nanofluid past a permeable stretching/shrinking sheet with newtonian heating. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 39(11), 4379–4391. [Google Scholar]

42. Brewster, M. Q. (1992). Thermal radiative transfer and properties. New York: John Wiley and Sons. [Google Scholar]