Inertial-Wave Regime of Averaged Thermal Convection in a Rotating Vertical Flat Layer

1  Introduction

Studies of thermal convection in rotating cavities, both experimental and numerical, are an important task for the development of fundamental and applied aspects of convective fluid motion [1,2].

Various phenomena associated with the effect of vibrations on hydrodynamic systems [3], led to the formation of a separate section—vibrational thermal convection [3,4]. Vibrational thermal convection employs the averaging method for the equations of thermal convection in the Boussinesq approximation [4]. This method is founded upon the partitioning of all variables in the equations of motion and heat and mass transfer into two categories [4]: “slow”, representing smoothly changing variables that are averaged over the period of oscillations, and “fast”, denoting oscillating variables with a frequency equal to that of the external influence.

The convective processes occurring under vibration conditions are determined by the interaction of temperature fields and pulsation velocity fields. The equations of averaged (vibrational) thermal convection obtained by the averaging method along with the Rayleigh Ra=gβΘh3/νχ and Prandtl Pr=ν/χ numbers contain an additional term with a lifting force characterized by a vibrational analogue of the Rayleigh number Rav=(bΩoscβΘh)2/2νχ. Here h is characteristic cavity size, b and Ωosc are amplitude and cyclic frequency of the cavity’s translational vibrations. The remaining designations are generally accepted.

The case of the influence of linear translational vibrations on a non-isothermal liquid was studied in detail in [3]. The equations of vibrational thermal convection in oscillating force fields of elliptical polarization were derived in [5]. In the case of circular polarization vibration, in rotating inertial force fields, the control parameter Rav has the same form. For a flat layer, the fundamental difference lies in the degeneration of the solution in the direction. In particular, vibro-convective structures have the form of cells arranged in a hexagonal order, motionless relative to the cavity.

The description developed in [5] proved to be effective in describing thermal vibrational convection in rotating systems [6]. We apply the term “Thermo-vibrational convection” to the averaged convection caused by oscillations under the action of gravity in a non-isothermal fluid inside a cavity rotating around a horizontal axis. Note that there are no vibrations, but the mechanisms are similar, at this, the averaged convection is characterized by a modified vibrational parameter Rv. One particular instance is that of averaged thermal convection excited in a cavity uniformly rotating in an external static force field. In the context of a liquid rotating around a horizontal axis within a gravitational field, gravitational acceleration g can be considered to play the role of vibration acceleration bΩosc2. In this instance, the oscillations of the non-isothermal liquid are initiated by a stationary field, thereby exhibiting the characteristics of tidal oscillations. It is important that despite the absence of vibrations, the equations of averaged convection are similar to the equations of vibrational convection [5]. This formulation corresponds to a special case when the rotation velocity of the force field in a non-inertial system coincides in magnitude with the rotation velocity of the cavity and is opposite in direction. The dimensionless oscillation frequency takes the value ω=Ωosc/Ωrot=−1, and a modified dimensionless control vibration parameter is introduced Rv=(gβΘh)2/2νχΩrot2 [6]. Another defining parameter is the dimensionless rotation velocity ωrot=Ωroth2/ν, which determines the influence of the Coriolis force on convective (averaged) structures. This parameter is analogous to the well-known Taylor number Ta≡4Ωrot2h4/ν2 [7].

The phenomenon of “vibrational” thermal convection (averaged convection) has been the subject of extensive experimental and theoretical investigation in a range of cavity geometries. The experimental study was started with the case of a vertical flat layer with boundaries of different temperatures, performing uniform rotation around a horizontal axis oriented perpendicular to the plane of the layer [8]. This was subsequently developed in a series of works, as referenced [9]. The experiments [9] conducted on relatively thin layers with a circular boundary and a large aspect ratio a=R/h, where R is a radius of the outer boundary of the layer with a thickness h, showed the emergence of vibrational thermal convection in the form of a system of convective cells arranged in a hexagonal order (Fig. 1a).

Figure 1: Photos of convective cells in a layer of thickness h=1.0 cm in the supercritical region of vibrational convection—a; and toroidal structures in the subthreshold region—b. A view from the cold border. At the centers of the convective cells (a), the fluid moves from the hot boundary towards the observer

The observations [8,9] showed that up to the excitation threshold of cellular vibrational thermal convection, toroidal convective vortex flows were evident in the vicinity of the outer lateral boundary (Fig. 1b). Presumably, these flows are caused by inertial waves [10]. It is known that in a rotating liquid, the development of specific wave mode with inertial effects [10], associated with the action of the Coriolis force—is possible. The region of such waves existence is limited by the value of the dimensionless frequency of cavity oscillations ω<2.

Studies of such wave processes in an isothermal setting are carried out quite widely [11–16] since it is a relevant task in connection with geophysical applications. Inertial waves and specific “inertial modes”—resonant conditions for mode with inertial and wave characteristics—have been studied in cavities of varying geometries: spherical [17–20], cylindrical [21–24], in axisymmetric cylindrical layers with parallel boundaries [25], and a case where one of the cylindrical layer boundaries has a conical shape [26,27]. A detailed overview of these studies can be found in [28]. It should be noted that inertial modes have been primarily investigated from a theoretical perspective.

With regard to rotating non-isothermal systems, the occurrence of inertial waves has been documented in experimental studies, particularly in liquids exhibiting internal heat generation [29]. In a rotating cylindrical layer, in the case of heating the layer both from the inside and from the outside, the existence of convective flows in the form of toroidal vortices located in the subthreshold region of averaged convection was discovered. It was shown that these flows arise in a non-threshold manner, have a relatively low intensity and are generated by inertial waves propagating in the layer.

In previous studies [8,9], thermovibrational convection in rotating systems was investigated. Earlier, only hypotheses were proposed regarding the existence of a region for inertial wave propagation. When thermovibrational convection is excited by oscillations of an external force field at a frequency ω=1, inertial modes can exist in a rotating cavity. This study presents, for the first time, a theoretical model focusing on the development of inertial modes in a layer. The studies are carried out in a vertical flat layer with a circular lateral boundary, rotating around a horizontal axis of symmetry (Fig. 2). The boundaries of the layer have different temperatures, the rotation velocity and temperature drop vary. The paper provides a velocity field in a cross-section (Fig. 3), demonstrating that the development of toroidal structures in the layer is associated with the excitation of standing inertial waves (inertial modes).

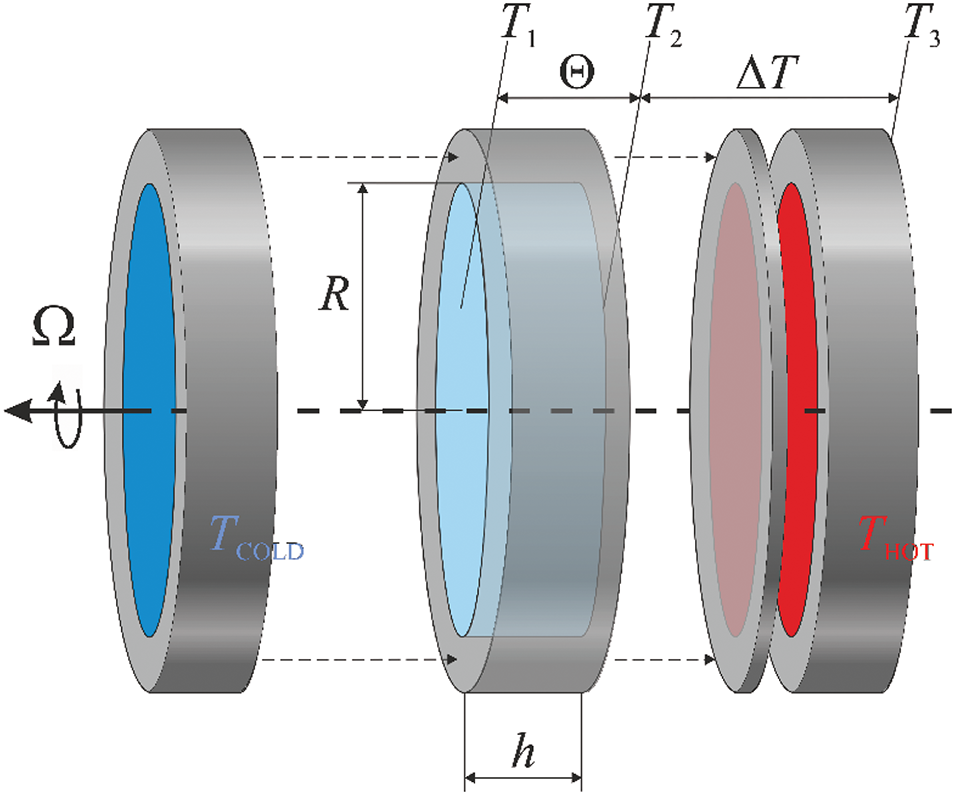
Figure 2: Cuvette elements

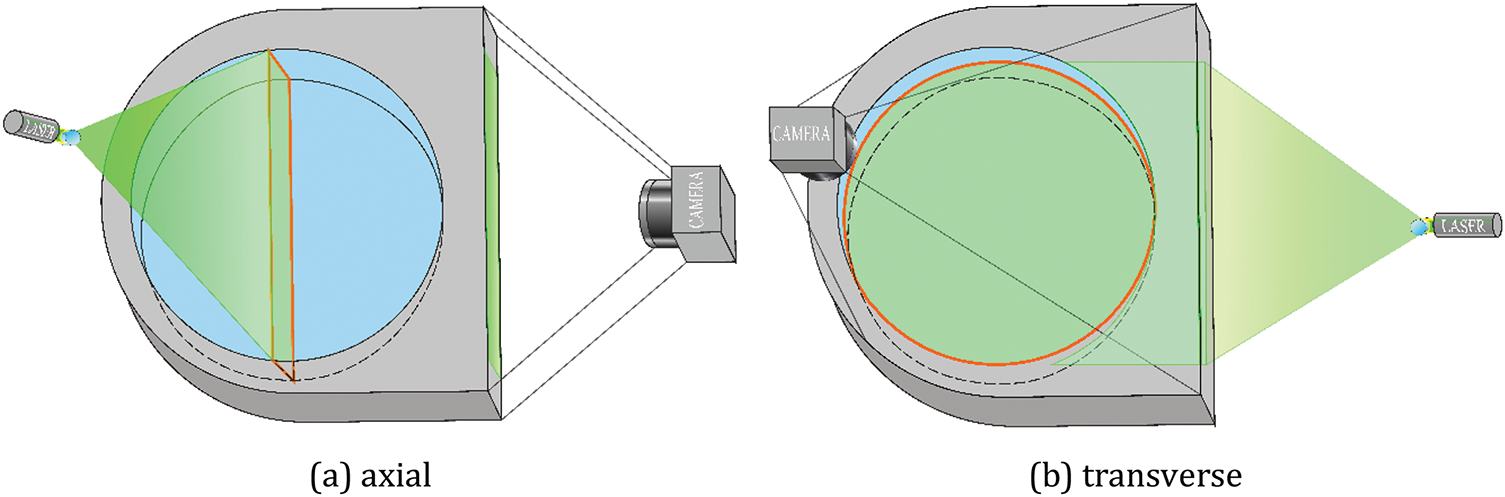
Figure 3: Schemes of axial and transverse sections of a flat layer by a laser knife. The orange lines indicate the area captured by the camera

In practical applications, the problem under consideration involves studying the dynamics of non-isothermal systems rotating around a horizontal axis. In rotating containers (in particular, a flat layer), fluid oscillations can lead to the generation of inertial waves. In our geometry, the flow takes the form of toroidal structures. In the case of a different geometry, the flow will also adopt a toroidal shape, but its location relative to the rotation axis will differ [29]. The transformation of toroidal structures into thermovibrational cells in industry can be utilized to optimize mixing, heating, and cooling processes, resulting in cost reduction and improved product quality.

2  Experimental Techniques

The working layer (Fig. 2) is a cavity formed between two heat exchangers. A ring gasket made of heat-insulating material limits the working cavity along the perimeter. The heat exchanger (Tcold), designed for the observation of convective structures is made of organic glass with glass flat boundaries. Another heat exchanger (Thot) is made of aluminum. The working fluid is distilled water. The annular gasket and heat exchangers with flat boundaries create a closed cylindrical cavity with specified geometric parameters: layer thickness h and radius R. The flat boundaries of the heat exchangers act as the layer boundaries. The temperature of the heat exchangers is maintained constant by pumping thermostatic liquid, which is supplied from the thermostats. The hydraulic collector ensures the uninterrupted circulation of liquid from the jet thermostats in the heat exchangers of the cuvette, fixed on a rotating platform. During the experiment, the temperature is measured with precision 0.1∘C. Temperature control at the cavity boundaries is carried out using temperature sensors (resistance thermometers). The signal from the sensors is transmitted to the computer via the measuring module “Termodat-13IK” using an electric collector. The rotation of the platform is controlled by a stepper motor, enabling precise adjustment of the angular rotation velocity with an accuracy of 0.06 rad/s.

Experimental methodology. The cuvette is filled with distillate water and positioned on the platform of the laboratory stand. Then the stepper motor sets the platform with the cuvette fixed to it in relatively fast motion. The rotation speed was varied discretely with a sequential decrease, with a step size of 0.05 rps. The step size did not affect the process of inertial wave generation in the fluid layer. At each stage of the experiment, a waiting period of approximately 10 min was maintained to ensure the stabilization of the system’s thermal regime. The focus of the study was on the rotation frequency range of 0.5–1.5 rps. At lower rotation frequencies, the amplitude of fluid oscillations over the period significantly increases, leading to a weakening of the inertial wave regime. The temperature sensors transmit the real-time temperature data of the flat boundaries of heat exchangers (Fig. 2) to the PC. Based on the temperature difference between the layer boundaries Θ and the temperature drop ΔT on the heat flux sensor, the Nusselt number Nu is calculated to characterize the heat transfer. It is the ratio of the temperature difference across the heat flux sensor to the temperature difference under molecular heat transfer conditions ΔT0 at the same value of Θ measured in the absence of rotation with the horizontal layer heated from above. Proceeding to the subsequent phase of the experiment entails a reduction in the rotation velocity of the cavity. This reduction is continued stepwise until the cuvette reaches a complete stop. The excitation threshold of the averaged convection is determined by plotting the Nusselt number in relation to the rotation velocity (Fig. 4).

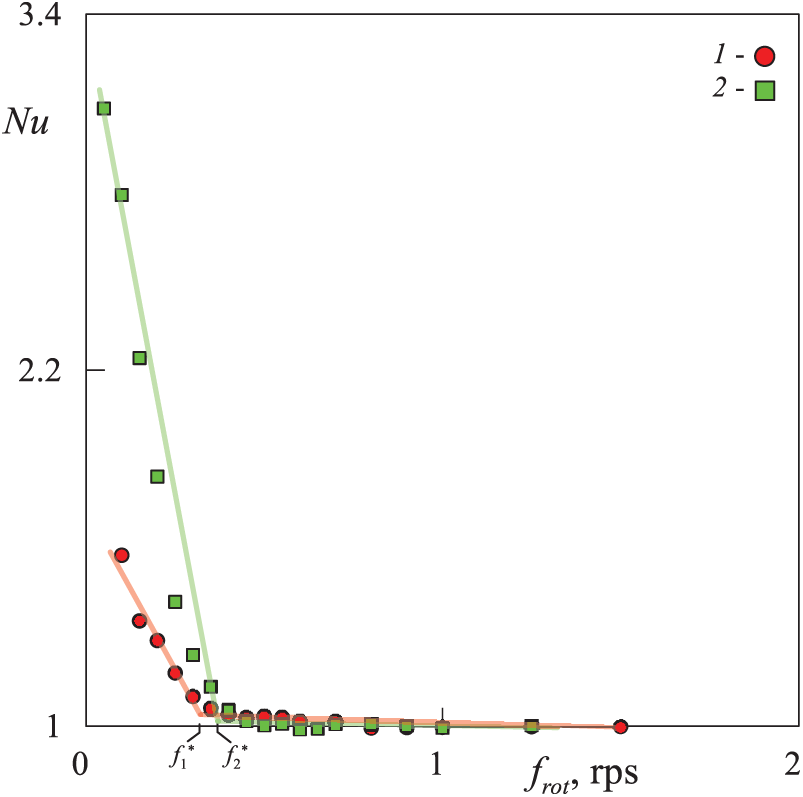
Figure 4: Heat transfer curves in the layers of different thicknesses. Symbol 1—h=1.0 cm, Θ=8.4°C; symbol 2—h=2.0 cm, Θ=6.0°C

Methodology of the velocity fields measuring is based on the utilisation of the tracer particles. Light-scattering Resin Amberlite particles with a size of 50 microns are introduced into the working fluid to visualize its motion. The particle density of approximately 1.05 g/cm3 is close to that of the working fluid, allowing them to move with the fluid. During the experiment, particle motion is recorded by a high-speed camera, specifically a Sony RX0 II, in the area illuminated by a laser sheet. A green line laser module with a wavelength of 520 nm and a Powell lens type is used as the laser sheet. The tracer particles upon entering the plane of the laser knife scatter the light, and the high-speed camera record allows for the analysis of the particles movement. The resulting image of particle movement provides a comprehensive representation of the flow velocities within the plane of the laser knife. In the experiment, the velocity field is analyzed in two sections: the axial (Fig. 3a) and the transverse (Fig. 3b) ones.

The digital correlation of successive images enables the construction of two-dimensional maps of velocity fields. The PIV method provides detailed spatio-temporal data on the flow in a rotating cavity.

3  Experimental Results

3.1 Measurement of Heat Transfer

Let us consider the case of uniform rotation of a liquid flat layer about a horizontal axis. The temperatures at the layer boundaries are maintained constant. During the experiment, the rotation velocity is gradually changed from high (frot=1.5 rps) to the minimum value (frot=0.05 rps). Fig. 4 shows the heat transfer curves—change in Nusselt number depending on the cavity rotation velocity for two-layer thicknesses. The heat transfer crisis corresponds to the excitation of averaged thermovibrational convection in the form of cells [6,8] in a layer.

At relatively high rotation velocities, the liquid is in a state that is close to the mechanical equilibrium Nu=1 (centrifugal convection is weak). In the subthreshold region of thermo-vibrational convection, with a decrease in the rotation velocity, there is a gradual (smooth) increase in heat transfer caused by the formation and intensification of toroidal structures in the layer. At the threshold of vibrational convection, the average flow assumes the form of hexagonal cells [6,8]. The heat transfer is determined by the action of the thermo-vibrational mechanism of convection. In the supercritical region, an increase in heat transfer occurs due to an increase in the size and intensity of cellular structures. A further decrease in the rotation velocity leads to the transformation of the cells into the vortex structures moving in the plane of the layer. The formed vortex structures, drifting in the plane of the layer, undergo a periodic change in intensity, whereby they “die out” and then reform.

The objective is to ascertain the threshold for averaged thermal convection on a plane Nu,frot. This is achieved by identifying the point of intersection between two lines representing distinct convective modes. The threshold values f1∗ and f2∗, obtained in experiments with the layers of different thicknesses (symbols 1 and 2) are close.

The heat transfer crisis corresponds to the excitation of averaged thermovibrational convection in the form of cells in a layer, which leads to a change in the temperature field. In previous work, the author used a technique to visualize the cell structure using an infrared camera, with the cells arranged in a hexagonal pattern.

3.2 Mean Velocity Field

Let us consider the velocity field averaged over the rotation period in the subthreshold region of thermovibrational convection. The averaged velocity field in the cross section of the laser knife is shown in Fig. 5 for several values of the rotation velocity. The observation of the velocity field is carried out from the side of the cold layer boundary. The layer rotates uniformly clockwise (Fig. 1). The arrows show the velocity field in the middle of the layer. The color indicates the vorticity in the laser sheet plane, where red corresponds to cyclonic liquid motion and blue to anticyclonic motion. The vector arrows illustrate the direction and magnitude of local flow velocities, highlighting the presence of vortex structures or characteristic convection cells, which indicate the development of thermal convection in a closed system.

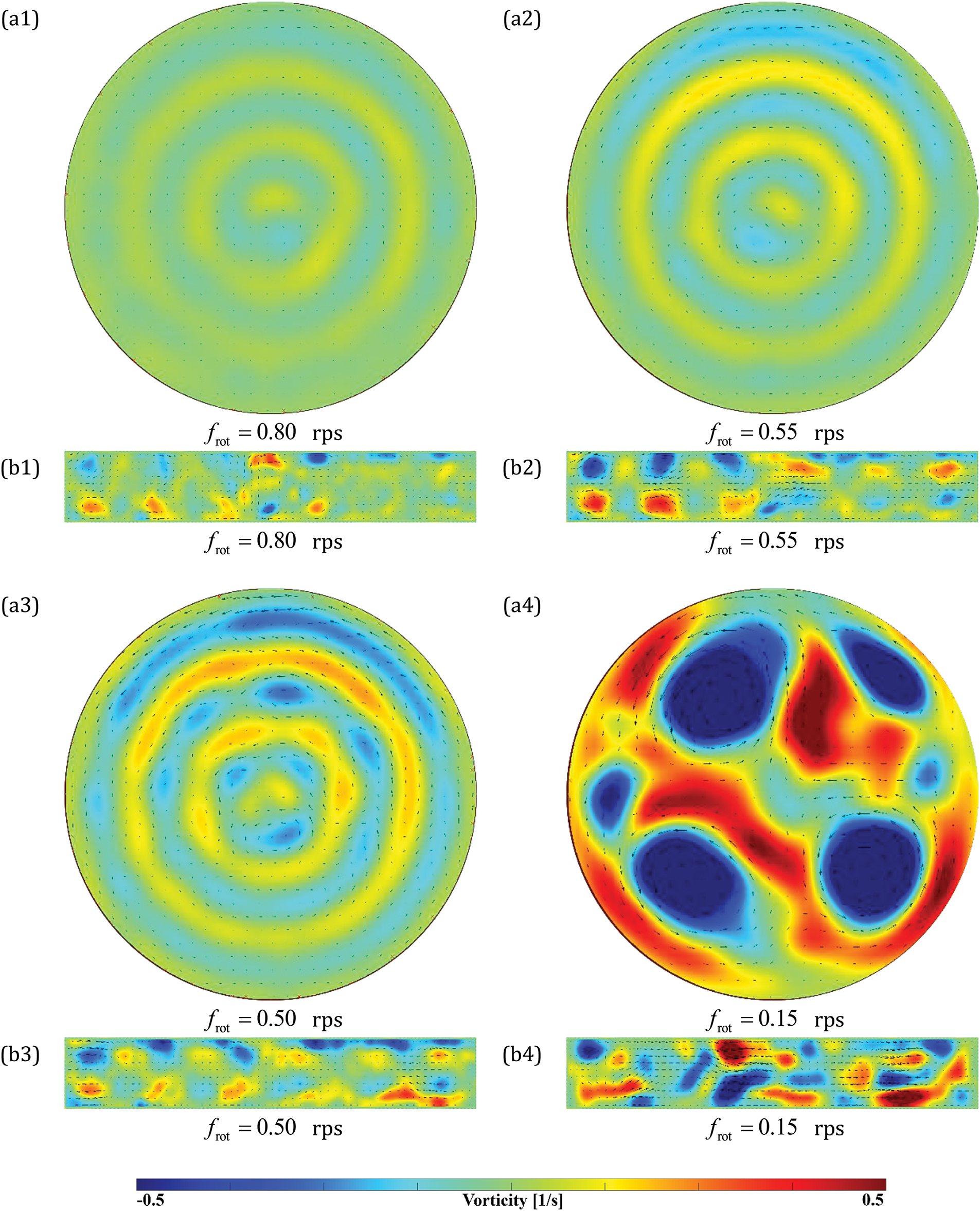
Figure 5: Averaged (over the rotation period) velocity field in the transverse (upper row) and axial sections (lower row) depending on the rotation velocity of the cavity. h=2.0 cm, Θ=6.0°C

The velocity fields depicted in the transverse sections (Fig. 5a) are to be considered as corresponding to those observed in the axial sections (Fig. 5b). The lower boundary of the picture of the velocity field obtained in the axial section has a higher temperature. In the pictures with axial sections, the axis of rotation is directed downwards.

At rotation velocity within the range of 1–2 rps the system is in a quasi-stationary state, and convective structures are absent. The decrease in the rotation velocity down to 0.8 rps leads to the formation of toroidal structures of low intensity (Fig. 5a1), and the heat transfer is close to the molecular one (Fig. 4). Below it will be shown that the generation of toroidal structures occurs due to the development of inertial waves [11]. In this case, the liquid in the layer performs weak oscillations, which are insufficient to induce a significant flow. In the axial section, one can see the appearance of small vortices near the flat boundaries of the cavity (Fig. 5b1).

A further reduction in rotation velocity increases the intensity of the toroidal structures (Fig. 5a2). The average flow in the diametrical section demonstrates a developed system of vortices (Fig. 5b2). Between the flat boundaries of the cavity there are pairs of vortices with opposite swirls. Three pairs of vortices are observed in the radial direction (Fig. 5b2), which is consistent with the presence of three toroidal structures in the cross-section of the laser knife (Fig. 5a2).

As the rotation velocity is reduced, the emergence of thermo-vibrational cells is observed (Fig. 5a3). The size of these cells is coordinated with the characteristic dimensions of toroidal structures (Fig. 5a2). The formation of the cells indicates that a further decrease in the rotation velocity will lead to the formation of averaged thermovibrational convection in the form of hexagonal cells filling the entire cavity. The typical appearance of thermovibrational cells is shown in Fig. 1a. The development of the cells is accompanied by a heat transfer crisis.

A further reduction of the rotation velocity results in the transformation of thermovibrational cells into the vortex structures. The structures observed in the supercritical region of thermovibrational convection are large-sized vortices. The strictly defined radial positions of the structures imposed by inertial waves are disrupted; the vortices shift along the plane of the layer and reorganize among themselves over the period of rotation. The vortex structures drift in both radial and azimuthal directions. Thermovibrational cells presented in Fig. 5a4 have the anticyclonic swirl and drift in the direction opposite to the cavity rotation. This development and transformation of large anticyclonic vortices merits further study, as it may facilitate a more detailed understanding of the processes associated with the movement of the Earth’s liquid shell.

Let us investigate the velocity field in both the transverse and axial sections in a layer of a smaller thickness h=1.0 cm. In Fig. 6, there is the averaged velocity field for several values of rotation velocity. With a decrease in the rotation velocity, the formation of convective structures in experiments with a smaller layer thickness occurs in a way similar to that in the layer h=2.0 cm. The heat transfer curves also look similar.

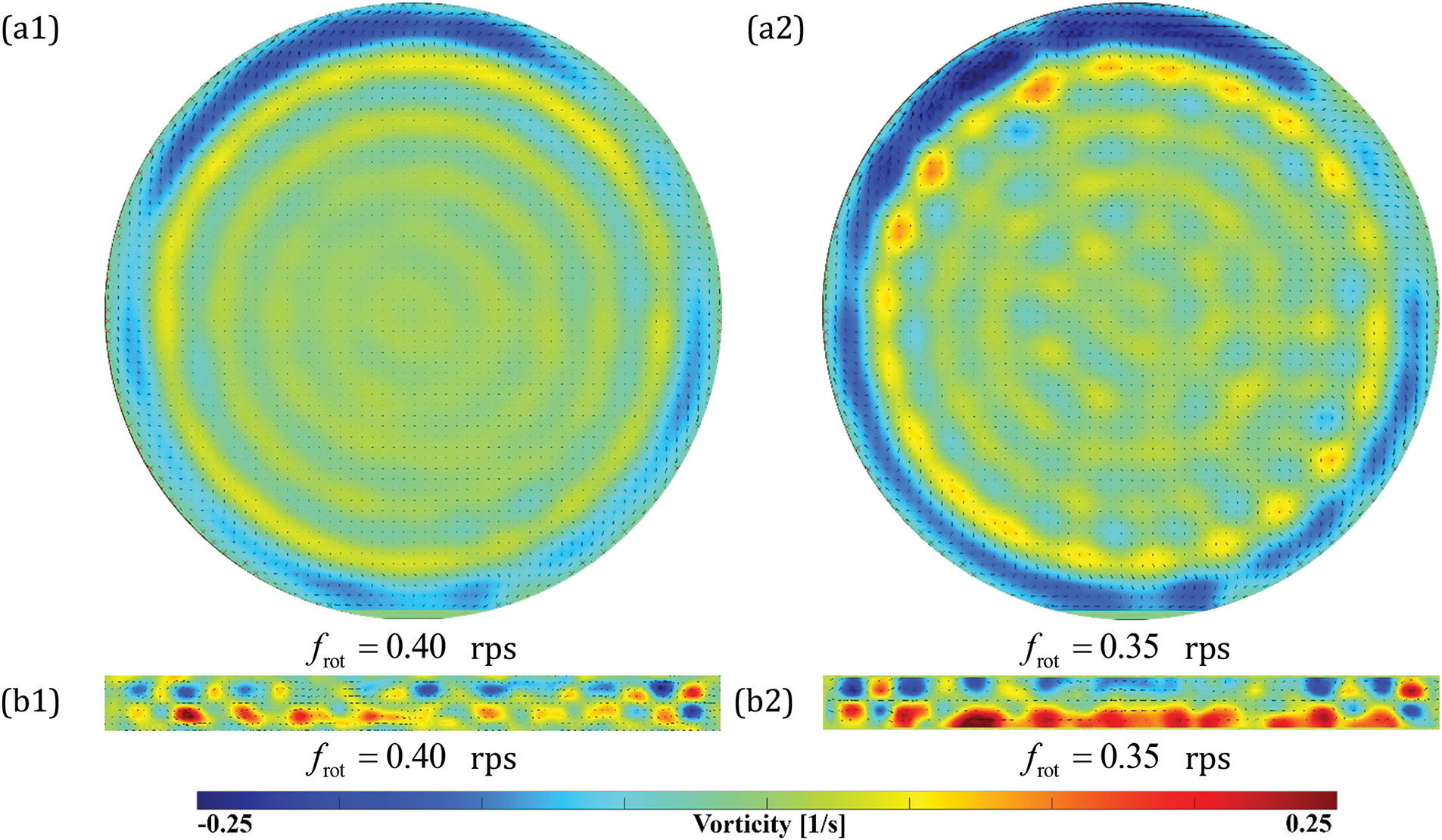
Figure 6: Averaged (over the rotation period) velocity fields obtained in the transverse and axial section of the laser knife for a layer of thickness h=1.0 cm, Θ=8.4°C

A decrease in the layer thickness leads to an increase in the number of toroidal convective structures in the plane of the layer. The size of the thermovibrational cells formed against the background of toroidal structures is observed to decrease.

3.3 Analysis of the Instantaneous Velocity Field

With the rotation of the cavity, the plane of the laser knife (stationary in the cavity reference frame) changes its position relative to the direction of the gravity field. Fig. 7 shows the transformation of the instantaneous velocity field in a rotating system. The instantaneous velocity field obtained at a certain position of the laser knife plane relative to the gravity field is supplemented by a schematic representation of the cavity in the laboratory reference frame.

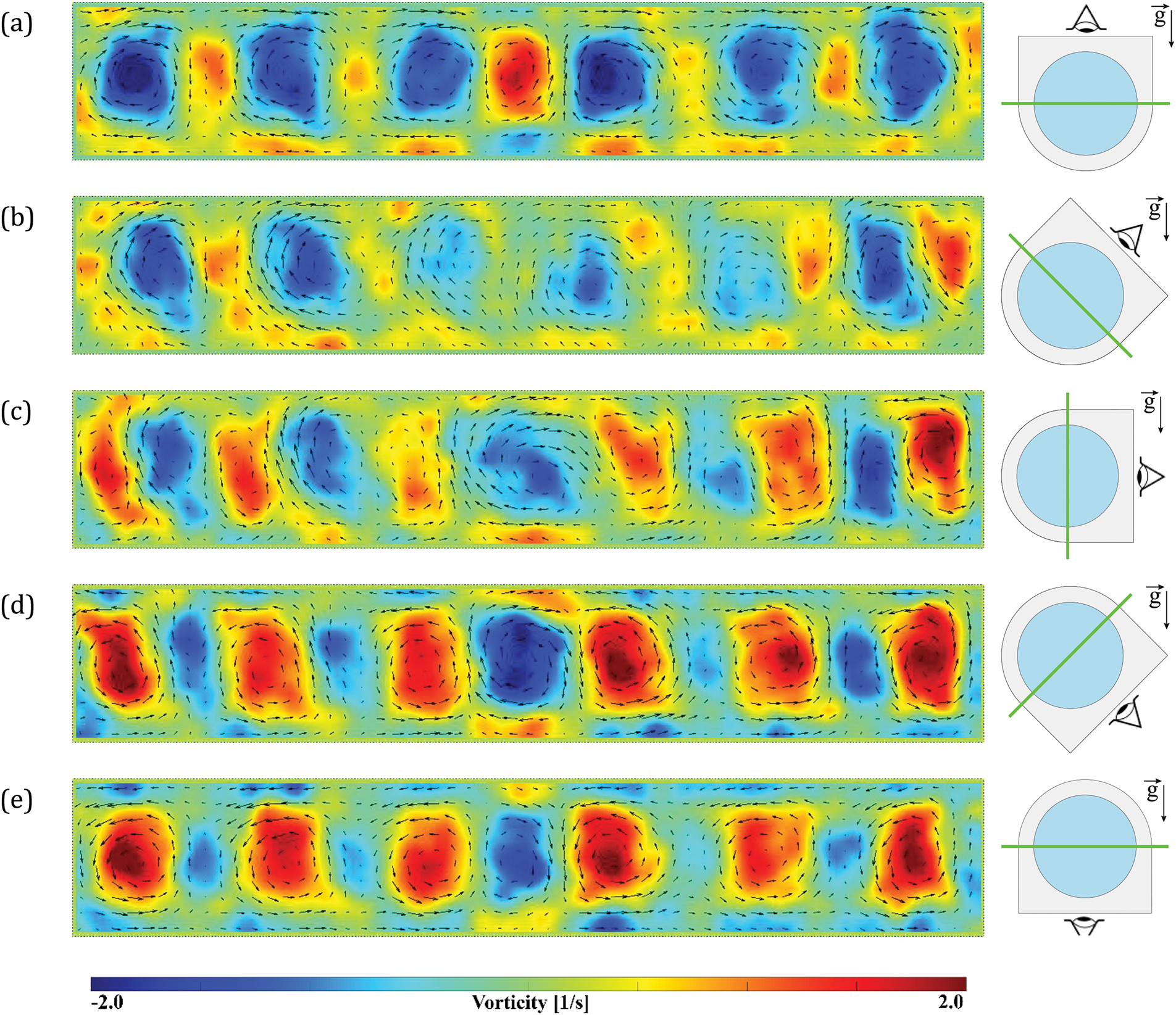
Figure 7: Instantaneous velocity field (center) in different phases of the cavity position relative to the direction of the gravity field (diagram on the right). The lower boundary of the velocity field images is hot, the upper one is cold. Experimental parameters: h=2.0 cm, frot=0.55 rps, Θ=6.0°C. The angle between the normal vector to the cutting plane and the gravitational acceleration vector: (a) α = 0°, (b) α = 45°, (c) α = 90°, (d) α = 135°, (e) α = 180°

Let us analyze the instantaneous velocity field in the axial section for half of the period of the cavity rotation. The velocity field (Fig. 7) is obtained in the subthreshold region of averaged cellular vibrational convection. In this case, the influence of the vibrational mechanism of convection is minimal, and the velocity field reflects only the combination of gravitational and inertial-wave mechanisms action.

In the phase when the laser knife plane is perpendicular to the gravity field (horizontal in the laboratory frame), the velocity field is a regular system of single-twist vortices (Fig. 7a). In this case, the gravitational component of the velocity field is responsible for the formation of the flow structure. Changing the direction of vortex structures when rotating the layer by 180 degrees (Fig. 7e) is explained by the fact that the vortex structures remain stationary in the laboratory reference frame. Since the measurements of the velocity fields (Fig. 3a) are carried out in a rotating system, the observer sees the same system of vortices in Fig. 7a and e, but from different sides.

When the cavity rotates and the angle of the laser knife changes, an observer can see the transition from a system of vortices of one twist to a system of cells of an inertial-wave nature (Fig. 7c,d). A cell is a pair of vortices of different directions. There are 6 pairs in the diametrical section. Their shape indicates that in this phase, the gravity field, which forms a global motion in the cavity (Fig. 7a) appears in the perpendicular direction. In this case, the velocity vector is directed perpendicular to the plane of the laser knife (Fig. 7c), when the plane of the knife is located vertically. As a result, a periodic system of vorticity of opposing signs is formed. In the plane of the layer, toroidal structures of opposite signs of vorticity are observed in the amount of three pairs (Fig. 5a2).

Furthermore, the average velocity field in the axial section (Fig. 8) will be considered. The field was obtained by averaging over several periods of the cavity rotation when a significant contribution of the oscillating components of the velocities associated with gravitational and inertial-wave harmonic oscillations of the liquid is eliminated.

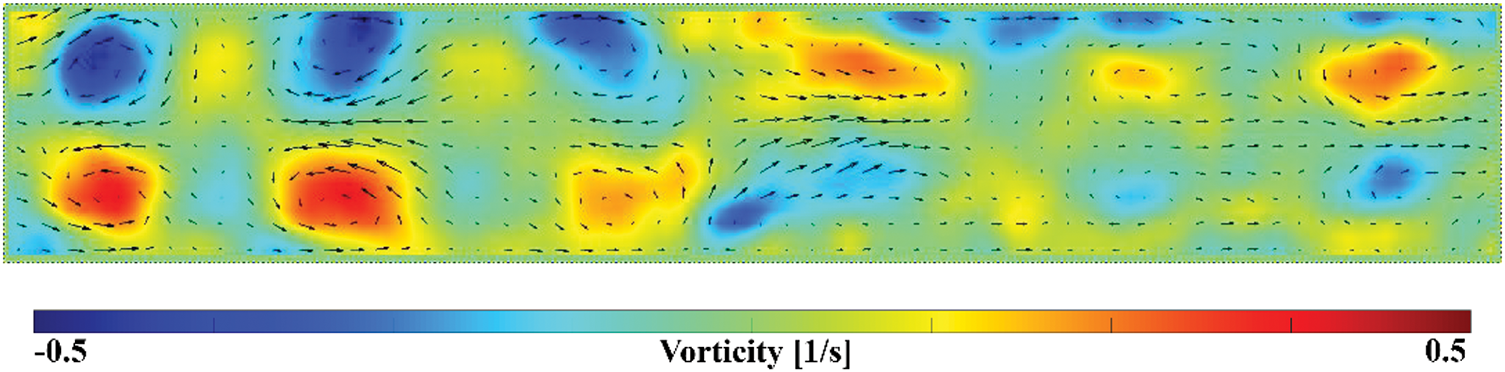
Figure 8: Averaged velocity field in the layer

While the instantaneous velocity field in a rotating system characterizes the sum of all terms (Fig. 7), averaging over the rotation period (or over several whole periods) allows us to isolate exclusively the time-averaged component of the velocity, i.e., the averaged motion caused by the oscillations of the fluid (Fig. 8).

It can be assumed that the generator of these averaged flows is inertial waves, and the averaged motion is generated in the Stokes boundary layers. In the experiments, the thickness of the Stokes layer is δ=2ν/Ωrot≈0.8 mm. These flows are related to the phenomenon of “steady streaming” and they are generated according to the Schlichting mechanism [30].

3.4 Dimensionless Control Parameters

The vibration effects generated by oscillations of gravity in a rotating layer are determined by the dimensionless rotation velocity ωrot and the modified vibration parameter Rv [6]. The dimensionless rotation velocity on the one hand characterizes the action of the Coriolis force, on the other hand—the ratio of the layer thickness to the Stokes layer thickness. When the layer is arranged vertically (the axis is in a horizontal position), the temperature gradient is directed horizontally. The static component of the field in the cavity is absent, the value of the gravitational Rayleigh number Ra=0.

The structure of averaged convection and heat transfer in a layer of a given geometry and at a certain value of the Prandtl number are completely determined by two independent parameters: the dimensionless rotation frequency and the vibration parameter Rv (Fig. 9). In this study, the value of the Prandtl number is taken as Pr=4.8. At the same time, the Prandtl number, as well as the shape of the cavity, can play an important role in terms of the generation of inertial waves, their structure and contribution to averaged convection and heat transfer. This makes the further study of its role an important task.

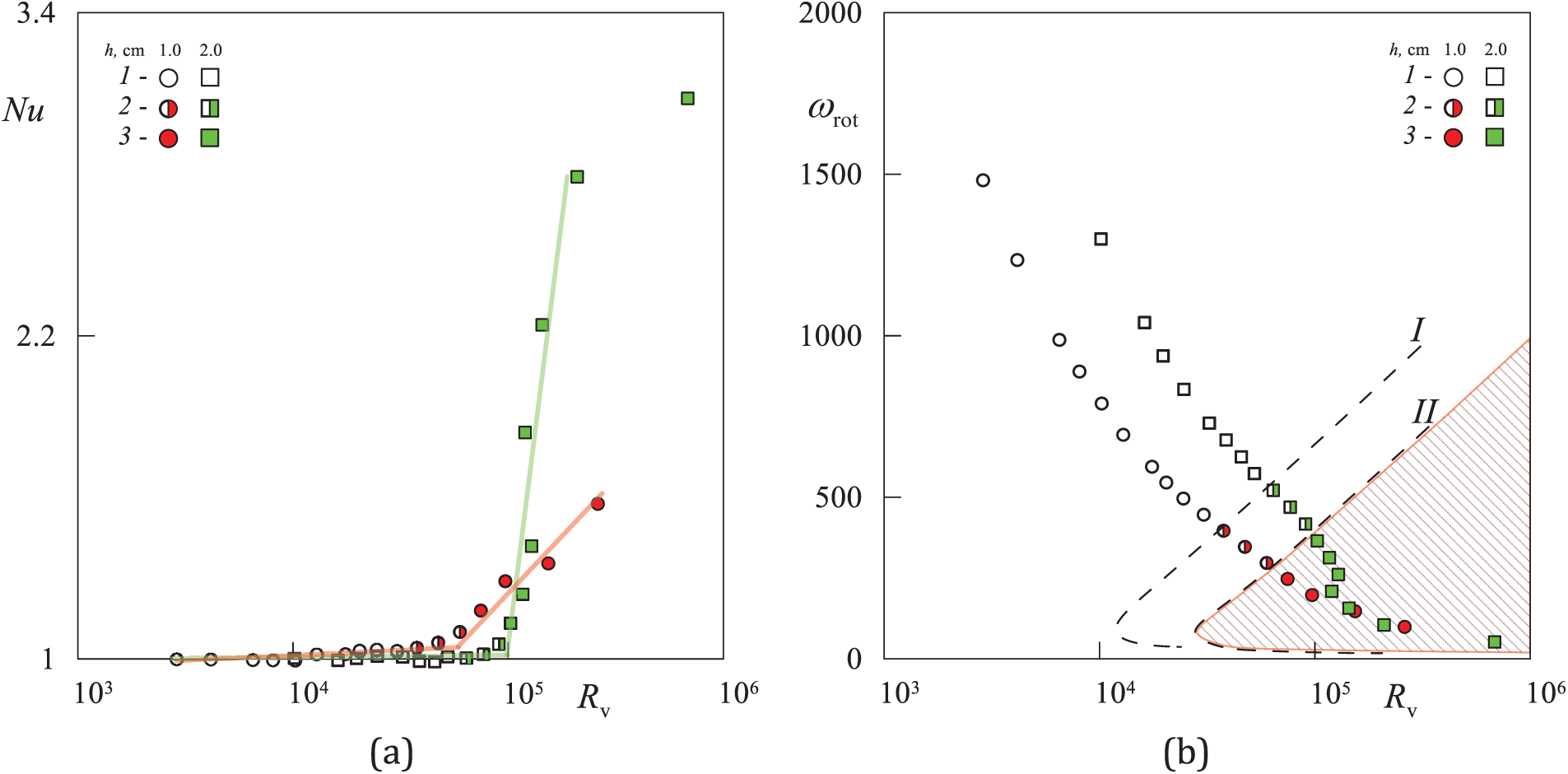
Figure 9: Heat transfer curves on the plane of the control parameter Rv (a) and the corresponding map of the averaged convection modes (b)

Let us consider heat transfer on the plane of dimensionless parameters Nu,Rv (Fig. 9a). In the area of heat conduction mode Nu=1 (symbols 1). As the rotation velocity decreases, the vibration parameter value increases. A weak increase in heat transfer is characterized by the development of toroidal structures (symbols 2), generated by inertial waves in the layer. With a further decrease in the rotation velocity, against the background of developed toroidal convective structures, the formation of hexagonal cells of the correct order is observed (symbols 3). An increase in the value of the vibration parameter is accompanied by an increase in the intensity of heat transfer. The threshold of averaged convection is determined by a sharp increase in heat transfer. The threshold value of the vibration parameter increases slightly with increasing layer thickness.

This problem has been considered previously [8,9]. The boundary of toroidal vortices occurrence (dashed line I) was obtained in the plane of control parameters ωrot,Rv (Fig. 9b) without analyzing the reasons of the structures generation. The boundary of averaged vibrational convection excitation is represented by curve II. In the low-velocity range (ωrot<100), with decreasing ωrot the experimental threshold of stability Rv increases sharply [8]. The change in the dependency on the plane ωrot,Rv in the low-frequency range is explained by the fact that the averaged effects are generated by high-frequency oscillating fields.

The following modes are shown on this mode map using different symbols: symbols 1—the region of mechanical quasi-equilibrium, symbols 2—development of the flow in the form of toroidal structures, symbols 3—the case of the averaged convection excitation. The progression of a single experiment (at the fixed values of Θ and h) is shown in different colors for two layer thicknesses, h=1.0 cm and h=2.0 cm. A decrease in the rotation velocity is accompanied by an increase in the value of the modified vibration parameter. The effect of rotation on thermovibrational convection is comparable to the effect of rotation on Rayleigh convection—with an increase in the dimensionless rotation velocity ωrot the threshold value of Rv increases.

Conducting experiments on a layer of a given thickness while varying parameters (Θ,frot) within a certain range confines the study to a specific region of the dimensionless parameters Ra,Rv and ωrot. This region cannot be significantly expanded without transitioning from the investigated convection regime to a different one.

The current experiment was conducted in a flat layer, considered as a limiting case of cavity geometry. In the study by Vjatkin et al. [29], another limiting case was examined, where the cavity is an annulus with boundaries maintained at different temperatures. This configuration leads to specific oscillatory modes in which inertial waves develop. A key aspect of the generation and propagation of inertial waves is the dependence of the observed effects on the aspect ratio, which characterizes the ratio of the layer’s radius to its thickness. Future research is planned to investigate the influence of the aspect ratio on the inertial waves and averaged convection in a cavity rotating around a horizontal axis.

4  Discussion

Inertial waves are defined as wave oscillations that occur in rotating fluids under the influence of the Coriolis force, which leads to stable oscillatory processes. The theoretical description of inertial waves, given in [10], allows one to calculate the parameters of the inertial mode arising in a closed rotating cavity: m—radial, n—axial, and k—azimuthal wave numbers.

In the problem of a rotating cylindrical flat layer of a given geometry a=R/h, it is pertinent to consider the structure and natural frequencies of inertial oscillations of liquid–inertial modes. In [27], the solutions were found for the inertial modes neglecting viscous forces (small Ekman numbers) and in the approximation of small oscillation amplitude (small Rossby numbers). The solution obtained in [27] for pressure during the excitation of liquid inertial oscillations with a dimensionless frequency ω=Ωosc/Ωrot in a rotating cylindrical layer of liquid is presented here. If we consider the pressure disturbance in a liquid in a rotating cylindrical layer in the form P=F(r)eikθcos⁡nπz, then for the function F(r) the next equation is obtained in [27].

r2∂2F∂r2+r∂F∂r+[(4/ω2−1)n2π2r2−k2]F=0.(1)

In this context, the unit of distance measurement is the length of the cavity h. Introducing a radial variable x=σr, where σ≡nπ(4/ω2)−1, the Eq. (1) is reduced to the Bessel equation, the solution of which has the form

F(x)=A(Jk(x)+BYk(x)).(2)

Here, Jk(x) and Yk(x) are the Bessel functions of the first and second kinds. The resulting solution must satisfy the boundary conditions

x∂F/∂x+k(σ/πn)2+1)F=0(3)

on the cylindrical boundary of the liquid layer x=σr. Note that r—dimensionless radius of the outer boundary of the liquid layer, the unit of measurement is the thickness of the cavity h. In the solution of the equation, the Bessel function of the second kind is absent. These boundary conditions permit the calculation of the m-th eigenvalue of the mode with azimuthal wave number k and axial wave number n denoted by ωmnk. Here ωmnk is the dimensionless frequency of the wave, with a unit of measurement equal to the frequency of the cavity rotation.

In the case under consideration, a wave in a rotating system with a non-isothermal liquid is excited by a gravity field directed perpendicular to the rotation axis, rotating in the cavity reference frame with the rotation velocity of the cavity itself, but in the opposite direction. It should be expected that the resonance condition is met by a wave with a frequency |ωmnk|=1 and azimuthal wave number k=1. Determination of the conditions for resonant excitation of inertial modes for a cavity of a given relative length a=R/h is reduced to solving Eq. (1) taking into account Eq. (3). It follows from the solution that for the relative length of the liquid layer a=3.33, the resonance conditions are met when m=6 at k=1 and n=1.

In the experiment R=7.0 cm, h=2.0 cm, the ratio of the layer radius to the layer thickness is a=R/h=7.0/2.0=3.5. As it can be seen from Fig. 7c, the radial wave number value m=6, obtained in the experiment, corresponds to the theoretical condition of resonance at the value of the wave number m=6 eigenwave mode with azimuthal wave number k=1 and axial wave number n=1. The spatial period of the structures discovered in the experiment is consistent with the calculated value.

A comparison of the theoretical data on the number of vortex structures in the radial direction with experimental results on the plane of parameters m,a (Fig. 10) reveals a high degree of correlation. The solid line is the theoretical curve of the radial value number m depending on the geometry of the cavity a, for the case k=1, n=1. The colored symbols show the experimental results obtained in this work at different layer thicknesses. The experimental data and theoretical curve are in good agreement.

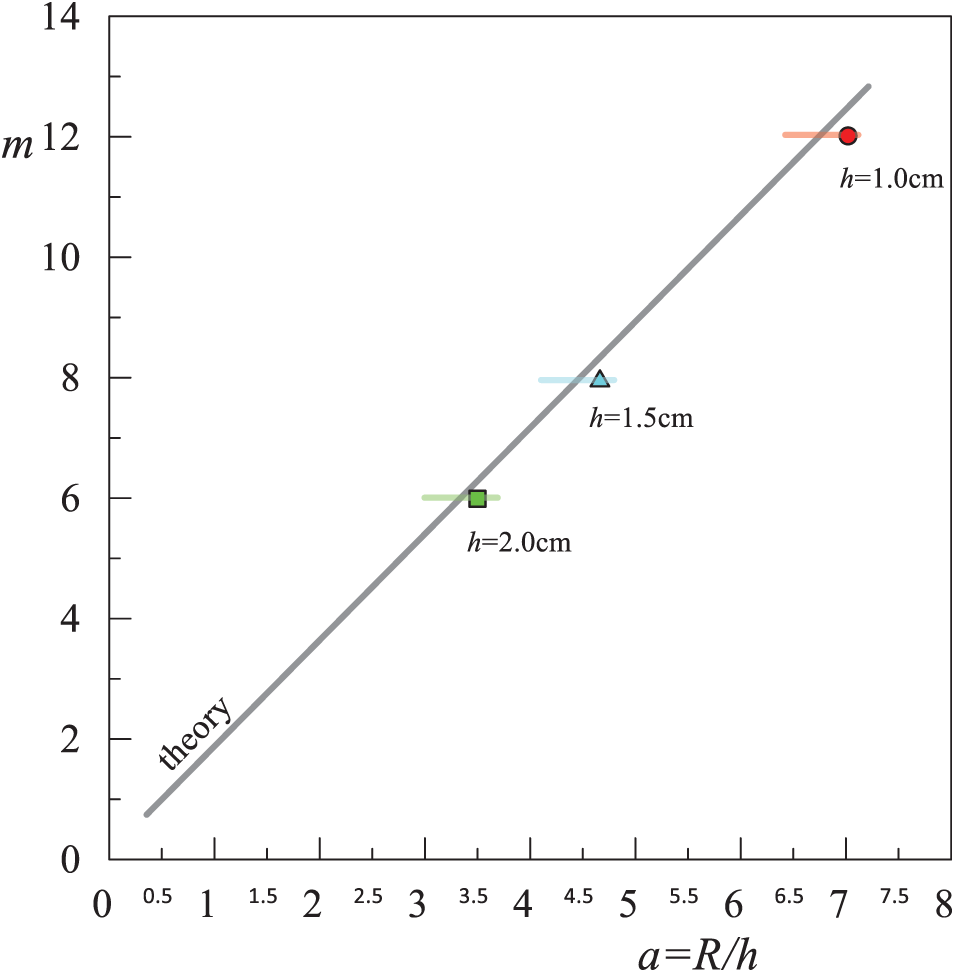
Figure 10: Dependence of the radial wave number m on the geometry of the cavity a. Solid line—theory, symbols—experiment

It is assumed that certain values of m may correspond to the aspect ratio a values within a certain interval (Fig. 10, colored lines). Changing the aspect ratio of the cavity leads to a change in the number of vortex structures in the layer; under resonance conditions, the number m takes the integer values.

An analysis of the instantaneous velocity field (Fig. 7) and the theoretical calculations of the inertial mode (Fig. 10) shows that for a frequency |ωmnk|=1 when n=1, k=1 the selected geometry a=3.5 meets the condition of the resonant excitation of the mode m=6. In this case, an oscillatory mode is excited in space, which is a system of toroidal rolls localized between pressure nodes and performing the rotation coordinated with each other. An important feature is that the movement in each toroidal roll changes with an angle according to the harmonic law, that is, in the laboratory coordinate system on different sides of the axis of rotation, the toroidal rolls rotate in opposite directions. From the condition |ωmnk|=1 it follows that the desired wave and the phase of its oscillations remain unchanged in the laboratory reference frame.

5  Conclusion

The averaged thermal convection in a flat layer rotating around a horizontal axis was experimentally investigated. The attention was paid to the inertial-wave regime of thermal convection. The study was conducted using the PIV method in transverse and axial sections. The analysis of the instantaneous velocity field shows that the emergence of toroidal structures in the subthreshold region of averaged convection occurs during the excitation of inertial modes of fluid oscillations (standing inertial waves). In this case, the entire wave system remains stationary in the laboratory system since the wave propagates in the rotating cavity with an azimuthal velocity equal to the rotation velocity of the cavity (in the opposite direction).

It has been established that the wavelength of the toroidal structure is determined by the radial component of the wave number of the inertial mode for the liquid layer of a given geometry. The spatial period of the radially located vortex structures has been theoretically determined depending on the aspect ratio. The results of experiments with the cavities of different geometries are consistent with the results of theoretical analysis performed in the approximation of low viscosity of the liquid and high rotation velocity (in the limit of small values of the Ekman and Rossby numbers).

The performed studies shed light on the inertial-wave nature of specific averaged convective flows excited in rotating cavities with a non-isothermal liquid. The experiments performed are limited by the cavity shape (flat layer) and a certain value of the Prandtl number. Taking into account that the issues of heat transfer in rotating systems (under the action of various aggravating factors) are the object of attention [31–33], a detailed study of a new, relatively simple to implement mechanism—averaged thermal convection in a cavity rotating uniformly around a horizontal axis—is an urgent task. The results can inform the design of rotating systems [34] where thermal management is critical, such as in turbines, reactors, or space applications, by leveraging the predictable behavior of inertial-wave-driven convection.

The goal of further research is to clarify the mechanisms of generation of averaged flows by inertial waves, as well as to study the effect of the Prandtl number and the cavity shape (aspect number) on the structure and intensity of averaged thermo-convective flows under conditions of inertial-wave oscillations of the liquid.

Acknowledgement: The authors express their gratitude to the Ministry of Education of the Russian Federation for supporting scientific research.

Funding Statement: This research is funded by the Ministry of Education of the Russian Federation within the framework of a state assignment, number 1023032300071-6-2.3.1.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Victor Kozlov and Kirill Rysin; data collection: Kirill Rysin; analysis and interpretation of results: Alexei Vjatkin and Victor Kozlov; draft manuscript preparation: Kirill Rysin, Victor Kozlov and Alexei Vjatkin. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data are included in this published article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Nomenclature

References

1. Lappa M. Thermal convection: patterns, evolution and stability. Hoboken, NJ, USA: Wiley; 2009. [Google Scholar]

2. Lappa M. Rotating thermal flows in natural and industrial processes. Hoboken, NJ, USA: Wiley; 2012. [Google Scholar]

3. Gershuni GZ, Lyubimov DV. Thermal vibrational convection. New York, NY, USA: Wiley; 1998. [Google Scholar]

4. Zen’kovskaya SM, Simonenko IB. Influence of high-frequency vibration on the onset of convection. Izv Akad Nauk SSSR, Mekh Zhidk Gaza. 1966;5:51–5. [Google Scholar]

5. Kozlov VG. Vibrational convection in a cavity undergoing spatial pendulum oscillations. Heat Transfer Sov Res. 1991;23:999–1008. [Google Scholar]

6. Kozlov VG. Thermal vibrational convection in rotating cavities. Fluid Dyn. 2004;39(1):3–11. doi:10.1023/B:FLUI.0000024806.35710.e7. [Google Scholar] [CrossRef]

7. Gershuni GZ, Zhukovitskii EM. Convective stability of incompressible fluids. Hoboken, NJ, USA: Wiley; 1976. [Google Scholar]

8. Kozlov VG, Ivanova AA, Rylova VV. Thermal convection in a plane layer rotating about a horizontal axis. Fluid Dyn. 2003;38(1):9–17. doi:10.1023/A:1023374625749. [Google Scholar] [CrossRef]

9. Vjatkin AA, Ivanova AA, Kozlov VG, Rysin KY. Effect of the tangential component of a force field on convection in a rotating plane layer. Izv Atmos Ocean Phys. 2017;53(2):187–94. doi:10.1134/S000143381702013X. [Google Scholar] [CrossRef]

10. Greenspan HP. The theory of rotating fluids. Cambridge, UK: Cambridge University Press; 1968. [Google Scholar]

11. McComas CH, Bretherton FP. Resonant interaction of oceanic internal waves. J Geophys Res. 1977;82(9):1397–412. doi:10.1029/JC082i009p01397. [Google Scholar] [CrossRef]

12. Bardsley OP, Davidson PA. Inertial-Alfvén waves as columnar helices in planetary cores. J Fluid Mech. 2016;805:R2. doi:10.1017/jfm.2016.577. [Google Scholar] [CrossRef]

13. Le Reun T, Favier B, Barker AJ, Le Bars M. Inertial wave turbulence driven by elliptical instability. Phys Rev Lett. 2017;119(3):034502. doi:10.1103/PhysRevLett.119.034502. [Google Scholar] [PubMed] [CrossRef]

14. Gerick F, Jault D, Noir J. Fast quasi-geostrophic magneto-coriolis modes in the earth’s core. Geophys Res Lett. 2021;48(4):e2020GL090803. doi:10.1029/2020GL090803. [Google Scholar] [CrossRef]

15. Xu W, Uwe Harlander U. Inertial mode interactions in a rotating tilted cylindrical annulus with free surface. Phys Rev Fluids. 2020;5(9):094801. doi:10.1103/PhysRevFluids.5.094801. [Google Scholar] [CrossRef]

16. Gizon L, Cameron R, Bekki Y, Birch A, Bogart R, Brun A, et al. Solar inertial modes: observations, identification, and diagnostic promise. Astron Astrophys. 2021;652:L6. doi:10.1051/0004-6361/202141462. [Google Scholar] [CrossRef]

17. Wang J, Wang Y, Chai Q. Free vibration analysis of a spinning functionally graded spherical-cylindrical–conical shell with general boundary conditions in a thermal environment. Thin-Walled Struct. 2022;180:109768. doi:10.1016/j.tws.2022.109768. [Google Scholar] [CrossRef]

18. Dintrans B, Rieutord M, Valdettaro L. Gravito-inertial waves in a rotating stratified sphere or spherical shell. J Fluid Mech. 1999;398:271–97. doi:10.1017/S0022112099006308. [Google Scholar] [CrossRef]

19. Rieutord M, Georgeot B, Valdettaro L. Inertial waves in a rotating spherical shell: attractors and asymptotic spectrum. J Fluid Mech. 2001;435:103–44. doi:10.1017/S0022112001003718. [Google Scholar] [CrossRef]

20. He J, Favier B, Rieutord M, Le Dizès S. Internal shear layers in librating spherical shells: the case of attractors. J Fluid Mech. 2023;974:A3. doi:10.1017/jfm.2023.761. [Google Scholar] [CrossRef]

21. Subbotin S, Dyakova V. Inertial waves and steady flows in a liquid filled librating cylinder. Microgravity Sci Technol. 2018;30:383–92. doi:10.1007/s12217-018-9621-x. [Google Scholar] [CrossRef]

22. Sauret A. Mean zonal flow generated by azimuthal harmonic forcing in a rotating cylinder. Fluid Dyn Res. 2015;47(3):035506. doi:10.1088/0169-5983/47/3/035506. [Google Scholar] [CrossRef]

23. Shiryaeva M, Subbotina M, Subbotin S. Linear and non-linear dynamics of inertial waves in a rotating cylinder with antiparallel inclined ends. Fluid Dyn Mater Proc. 2024;20(4):787–802. doi:10.32604/fdmp.2024.048165. [Google Scholar] [CrossRef]

24. Subbotin S. Steady circulation induced by inertial modes in a librating cylinder. Phys Rev Fluids. 2022;5(1):014804. doi:10.1103/PhysRevFluids.5.014804. [Google Scholar] [CrossRef]

25. Subbotin S, Shiryaeva M. Inertial wave beam path in a non-uniformly rotating cylinder with sloping ends. Microgravity Sci Technol. 2023;35(3):32. doi:10.1007/s12217-023-10054-z. [Google Scholar] [CrossRef]

26. Maas LRM. Wave focusing and ensuing mean flow due to symmetry breaking in rotating fluids. J Fluid Mech. 2001;437:13–28. doi:10.1017/S0022112001004074. [Google Scholar] [CrossRef]

27. Borcia ID, Harlander U. Inertial waves in a rotating annulus with inclined inner cylinder: Comparing the spectrum of wave attractor frequency bands and the eigenspectrum in the limit of zero inclination. Theor Comput Fluid Dyn. 2013;27(3-4):397–413. doi:10.1007/s00162-012-0278-6. [Google Scholar] [CrossRef]

28. Le Bars M, Cébron D, Le Gal P. Flows driven by libration, precession, and tides. Annu Rev Fluid Mech. 2015;47(1):163–93. doi:10.1146/annurev-fluid-010814-014556. [Google Scholar] [CrossRef]

29. Vjatkin A, Petukhov S, Kozlov V. Experimental study of thermal convection and heat transfer in rotating horizontal annulus. Fluid Dyn Mater Proc. 2024;20(11):2475–88. doi:10.32604/fdmp.2024.052377. [Google Scholar] [CrossRef]

30. Schlichting G. Theory of a boundary layer. Moscow: Science; 1974. [Google Scholar]

31. Arshad M, Hassan A. A numerical study on the hybrid nanofluid flow between a permeable rotating system. Eur Phys J Plus. 2022;137:1126. doi:10.1140/epjp/s13360-022-03313-2. [Google Scholar] [CrossRef]

32. Riahi M, Choujaa MH, Rajy S, Aniss S. Primary bifurcation mechanism, heat transfer and bicriticality in time temperature-modulated Rayleigh-Bénard convection in a Hele-Shaw cell. Int J Heat Mass Transf. 2024;223:125264. doi:10.1016/j.ijheatmasstransfer.2024.125264. [Google Scholar] [CrossRef]

33. Vasiliev A, Sukhanovskii A, Popova E. Influence of bottom inclination on the flow structure in a rotating convective layer. Fluid Dyn Mater Proc. 2024;20(4):739–48. doi:10.32604/fdmp.2024.048092. [Google Scholar] [CrossRef]

34. Meunier P. Geoinspired soft mixers. J Fluid Mech. 2020;903:A15. doi:10.1017/jfm.2020.634. [Google Scholar] [CrossRef]