Open Access

ARTICLE

Shallow Water Waves with Surface Tension by Laplace–Adomian Decomposition

Oswaldo González-Gaxiola¹, Yakup Yildirim^2,3,4, Luminita Moraru^5,6, Anjan Biswas^7,8,9,10,*

1 Applied Mathematics and Systems Department, Universidad Autónoma Metropolitana-Cuajimalpa, Vasco de Quiroga 4871, Mexico City, 05348, Mexico
2 Department of Computer Engineering, Biruni University, Istanbul, 34010, Turkey
3 Mathematics Research Center, Near East University, Nicosia, 99138, Cyprus
4 Faculty of Arts and Sciences, University of Kyrenia, Kyrenia, 99320, Cyprus
5 Faculty of Sciences and Environment, Department of Chemistry, Physics and Environment, Dunarea de Jos University of Galati, 47 Domneasca Street, Galati, 800008, Romania
6 Department of Physics, Sefako Makgatho Health Sciences University, Medunsa, Pretoria, 0204, South Africa
7 Department of Mathematics and Physics, Grambling State University, Grambling, LA 71245-2715, USA
8 Department of Physics and Electronics, Khazar University, Baku, AZ1096, Azerbaijan
9 Department of Applied Sciences, Cross-Border Faculty of Humanities, Economics and Engineering, Dunarea de Jos University of Galati, 111 Domneasca Street, Galati, 800201, Romania
10 Department of Mathematics and Applied Mathematics, Sefako Makgatho Health Sciences University, Medunsa, Pretoria, 0204, South Africa

* Corresponding Author: Anjan Biswas. Email:

(This article belongs to the Special Issue: Recent Advancements in Wave Dynamics Models for Fluids: Analytical and Numerical Approaches)

Fluid Dynamics & Materials Processing 2025, 21(9), 2273-2287. https://doi.org/10.32604/fdmp.2025.067959

Received 17 May 2025; Accepted 01 September 2025; Issue published 30 September 2025

Abstract

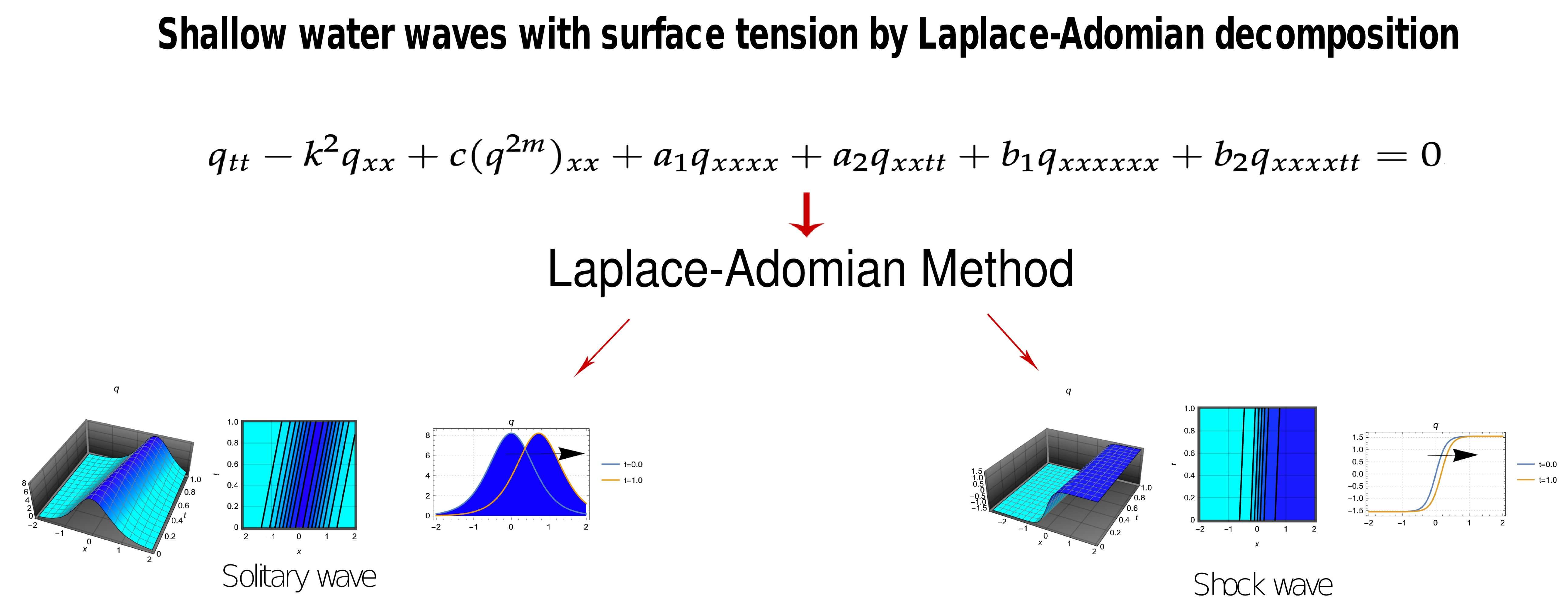
This study presents a numerical investigation of shallow water wave dynamics with particular emphasis on the role of surface tension. In the absence of surface tension, shallow water waves are primarily driven by gravity and are well described by the classical Boussinesq equation, which incorporates fourth-order dispersion. Under this framework, solitary and shock waves arise through the balance of nonlinearity and gravity-induced dispersion, producing waveforms whose propagation speed, amplitude, and width depend largely on depth and initial disturbance. The resulting dynamics are comparatively smoother, with solitary waves maintaining coherent structures and shock waves displaying gradual transitions. When surface tension is incorporated, however, the dynamics become significantly richer. Surface tension introduces additional sixth-order dispersive terms into the governing equation, extending the classical model to the sixth-order Boussinesq equation. This higher-order dispersion modifies the balance between nonlinearity and dispersion, leading to sharper solitary wave profiles, altered shock structures, and a stronger sensitivity of wave stability to parametric variations. Surface tension effects also change the scaling laws for wave amplitude and velocity, producing conditions where solitary waves can narrow while maintaining large amplitudes, or where shock fronts steepen more rapidly compared to the tension-free case. These differences highlight how capillary forces, though often neglected in macroscopic wave studies, play a fundamental role in shaping dynamics at smaller scales or in systems with strong fluid–interface interactions. The analysis in this work is carried out using the Laplace-Adomian Decomposition Method (LADM), chosen for its efficiency and accuracy in solving high-order nonlinear partial differential equations. The numerical scheme successfully recovers both solitary and shock wave solutions under the sixth-order model, with error analysis confirming remarkably low numerical deviations. These results underscore the robustness of the method while demonstrating the profound contrast between shallow water wave dynamics without and with surface tension.

---

Graphic Abstract

---

Keywords

---