Heat Transfer Characteristics for Solar Energy Aspect on the Flow of Tangent Hyperbolic Hybrid Nanofluid over a Sensor Wedge and Stagnation Point Surface

1  Introduction

The study of non-Newtonian fluids has been one of the most significant developments in recent decades. As a result, the thermophysical characteristics of non-Newtonian fluids have attracted considerable interest. Numerical solutions have received significant attention in the literature due to their numerous commercial and technical applications. It should be noted that shear thinning is a recognized behavior for non-Newtonian fluids such as pseudoplastic, where viscosity increases with an increase in shear rate. On the other hand, shear thickening is defined for non-Newtonian fluids like dilatant, where viscosity decreases as shear rates increase [1]. This has led to the development of numerous non-Newtonian fluid models, including the Sisko, Carreau fluid, Williamson, Cross, Maxwell, Casson, and Micropolar models [2–8].

The tangent hyperbolic fluid model accurately describes the characteristics of shear thinning fluids. It explains how a fluid will respond to both very low and very high shear rates. The tangent hyperbolic model falls under the category of rate type fluids, and the concept being considered exhibits simultaneous characteristics of retarded time and relaxation time. Malik et al. [9] investigated the magnetohydrodynamics of a hyperbolic tangent fluid model through an extended cylinder using the Keller box method. Their study demonstrated a reduction in the velocity of the hyperbolic tangent fluid when influenced by the Lorentz force. Hayat et al. [10] examined the influence of endoscopic effects on the induced magnetic field in peristaltic movement of hyperbolic tangent nanofluid. The findings revealed that both slip mechanisms contribute to an increase in the temperature of the hyperbolic tangent nanofluid. Ali et al. [11] analyzed the transient MHD-3-D rotating flow of Maxwell/Tangent hyperbolic nanofluid on a bidirectional stretching surface using FEM analysis and the non-Fourier heat flux model. The research findings demonstrated that several physical parameters, such as the magnetic parameter, Brownian motion, rotational parameter, thermophoresis, and unsteady parameter, have a significant influence on the temperature distribution. Seid et al. [12] found that the concentration of nanoparticles can be improved by increasing the Soret effect, wall suction, wall friction, magnetic field, porosity, and constructive chemical reaction. Conversely, decreasing the magnetic field or increasing the thermal Grashof number enhances the rate of heat transfer. Walelign et al. [13] found that the heat transfer rate can be enhanced by increasing the buoyancy ratio, chemical reaction, or heat sink. This transfer can also be facilitated by decreasing the dissipation parameter, reciprocal of the Prandtl number, or porosity of the medium.

In recent decades, engineers and scientists have been drawn to the exploration of boundary layer flows across surfaces due to their wide range of applications in manufacturing and engineering processes. These processes include metal and aerodynamic extrusion of elastic sheets, MHD generators, artificial fibers, cooling of electronic chips, hot rolling wire drawing, chemical processing equipment, paper-making, glass fiber manufacture, and crystal expansion [14]. Crane [15] was the first to utilize an analytical solution to study the boundary layer flow over a linearly stretched sheet of an incompressible viscous fluid in 1970. Jamshed et al. [16] examined heat transmission by employing a hybrid nanofluid over an inside curved solar-powered accumulator to enhance the analysis of solar airplane wings in the presence of non-Fourier heat flux and porous media. They found that thermal transfer efficiency increases in aircraft wings when thermal radiation amplification and varied thermal conduction parameters are present. Sheikholeslami et al. [17] reviewed solar flat plate collectors and photovoltaic systems under the influence of nanofluids. Waqas et al. [18] investigated the MHD convective heat transfer with slip flow of Jeffrey nanofluid over a stretched surface, considering activation energy, radiation from the sun, and viscous incompressible effects.

The location where the local velocity of a fluid is zero is referred to as the stagnation point. The static pressure at a stagnation point in fluid flow is called the pitot pressure or stagnation pressure (see Fox [19]). In incompressible flow, the sum of dynamic pressure and static pressure (i.e., total pressure) is equal to the stagnation pressure. Many researchers have contributed to the understanding of heat transfer dynamics in stagnant flow in different scenarios due to its widespread applications in manufacturing and engineering. Fay et al. [20] revealed that the stagnation point is ineffective in heat transfer due to the non-equilibrium position of the boundary layer, and they pointed out that the wall behaves as a catalyst near the stagnation point, with the Lewis number closer to unity. The stagnation region exhibits the highest heat transfer rate, mass decomposition rate, and pressure. Bhatti et al. [21] proposed a strategy combining the Successive-linearization-method with the Chebyshev-spectral-collocation-method to find the solution for stagnation point flow over a nonlinear porous extending sheet problem, as it is accurate and convergent iteratively. Rashidi et al. [22] presented a Pade approximation to solve the hydromagnetic Hiemenz flow over a flat plate along with the stagnation point. Abbas et al. [23] used the Casson rheological fluid model to discuss heat transfer near the stagnation point of a flat surface. The study of stagnation point flow has made significant progress in recent times, particularly in aerodynamics, where it has been explored in edge flows over submarines, airplanes, rockets, and oil tankers. The Langmuir type probe, which has a small collection electrode, can be applied to various potentials, and corresponding collection flows can be measured, making it suitable for static plasma conditions. Such probes are commonly used in plasma jets where high-speed flows are produced.

Previous studies have not simultaneously considered the combined effects of hybrid nanofluid flow, Riga wedge, and a stagnation point. In this research article, we aim to address this gap by investigating the steady-state, incompressible, two-dimensional forced convective magnetized boundary layer fluid flow of kerosine hybrid nanofluid over a wedge and stagnation magnetic sensor (Riga Plate) surface. The novelty of our study lies in including the effects of thermal radiation and viscous dissipation, which have been overlooked in previous investigations of Riga plate electromagnetic actuator flows. Additionally, we incorporate the use of tangent hyperbolic non-Newtonian fluid, which has also been neglected in prior Riga plate studies. To obtain numerical solutions, we develop a computational approach using the Runge-Kutta-Fehlberg (RKF) method with shooting techniques while ensuring that the conservation equations are appropriately transformed under physically realistic conditions at the wall (sensor surface) and in the free stream. This study presents a generalized mathematical model for Riga plate flows, incorporating the effects of thermal radiation and viscous dissipation. We analyze the flow of a hyperbolic tangent nanofluid containing magnesium oxide (MgO) and silver (Ag) over a wedge and stagnation point when linear thermal radiation is present. Moreover, the aforementioned research revealed that no investigation has been done so far on the effects of thermal radiation on two various geometries when a hybrid nanofluid is used, despite the numerous applications of hybrid nanofluids in engineering [24–26]. The system of flow and temperature transport equations is transformed into an ordinary differential system using appropriate self-similarity transformations, which is then solved using the bvp4c solver in MATLAB. Graphs and tables are used to describe the computed results.

2  Formulation of the Problem

Fig. 1 illustrates the schematic perspective of two distinct geometries. We consider the steady two-dimensional incompressible time-independent forced convective magnesium oxide-silver/kerosene hybrid nanofluid in the presence of a thermal radiation over two diverse geometries which is presented in Fig. 2. It is significant to note that the stagnation point and wedge surfaces are regarded as Riga plates. Table 1 gives an expression of the base fluid’s and nanoparticles’ thermo-characteristics. The free stream velocity, denoted by the formula u∞=bxm, is constant b. As [1/((2/β1)−1)], the Hartree pressure gradient m may be written. The temperatures of the ambient fluid and wall are represented by T∞ and Tw, correspondingly. This study investigates the laminar, time-independent, incompressible forced convective flow of a blood nanofluid. The rheological behavior of the nanofluid is characterized by adopting the tangent hyperbolic model, which is specifically chosen to accurately describe the rheological properties of Kerosine Nanofluid. To comprehensively analyze the energy equation, the effects of viscous dissipation and thermal radiation are taken into consideration. The governing equations of the system are modeled using the well-established nanofluid model proposed by Tiwari and Das. The nonlinear differential equations governing this problem are derived based on the problem assumptions and the effective terms for the flow through the desired geometries as mentioned in [25–32].

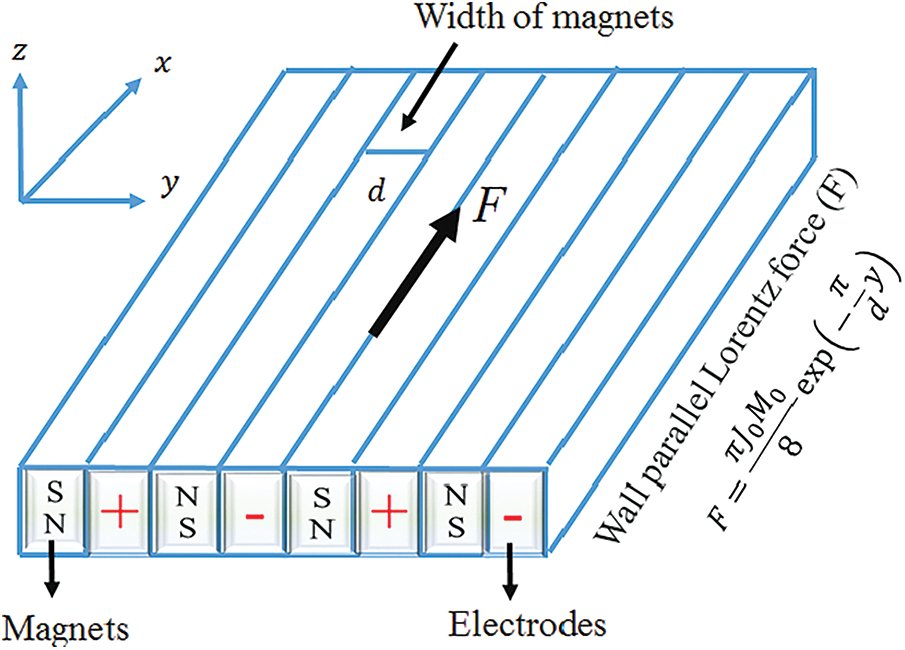
Figure 1: Schematic diagram of a sensor surface

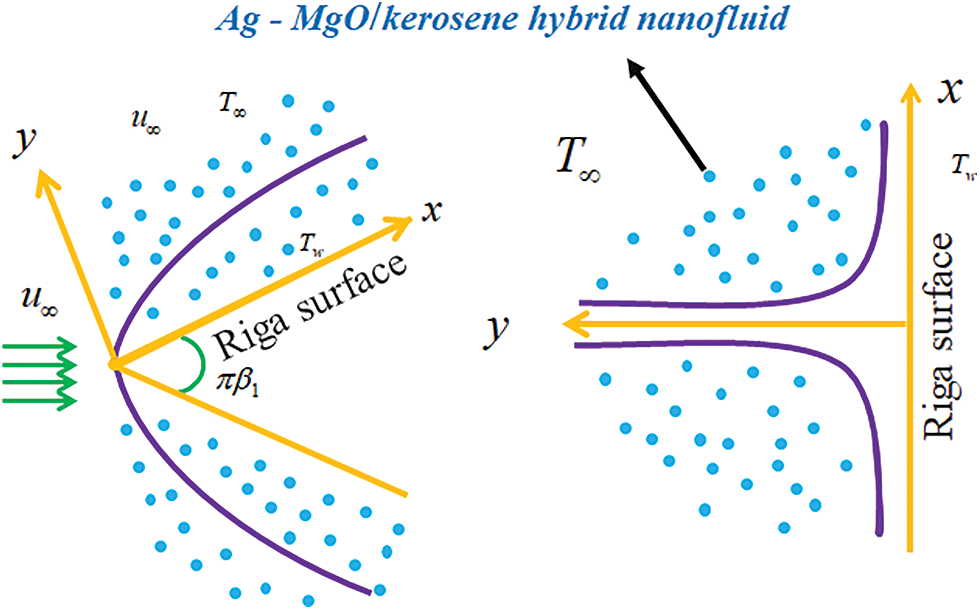
Figure 2: Flow configuration

The proper boundary circumstances are [29,31] and [33].

{u=0,v=0,T=Tw aty=0u=u∞,T→T∞, asy→∞(4)

A parameter λ is given by Lin et al. [33] which is used to apply for any fluid Prandtl number.

λ=δRe, where Re=u∞xνf is Reynolds number, δ=Pr(1+Pr)n, where n=16 and Pr is Prandtl number for wedge and stagnation of flat plate.

The similarity transformation follows the work of [33]

{η=λ(yx),u=κxmf′(η)(1+Pr)2n(α*x)[m+12f(η)+m−12ηf′(η)]f(η)=ψ(x,y)λα*,T=T∞+(Tw−T∞)θ(η)(5)

By using Eq. (5), the Eqs. (2)–(4) are converted in the form

Prf‴(1−na+nawef‴Pr(1+Pr)2n)((1−Φ1)2.5(1−Φ2)2.5)((1−Φ2)[(1−Φ1)ρf+Φ1ρs1]+Φ2ρs2)+(m+12)ff″+m((1+Pr)4n−(f′)2)+MH(1+Pr)4n((1−Φ2)[Φ1ρs1+(1−Φ1)ρf]+Φ2ρs2)×exp[−ηαH(1+Pr)nPr]=0}(6)

θ″(κhnf+43Rd)((1−ϕ2)[(1−ϕ1)(ρCp)f+ϕ1(ρCp)s1]+ϕ2(ρCp)s2)+(m+12)fθ′+PrEc(f″)2[(1−na)+naf″WePr2(1+Pr)3n](1+Pr)4n((1−ϕ1)2.5(1−ϕ2)2.5)((1−ϕ2)[(1−ϕ1)ρf+ϕ1ρs1]+ϕ2ρs2)=0}(7)

With boundary circumstances

{f(η)=f′(η)=0,θ=1, atη=0.f′(η)=(1+Pr)2n,θ(η)→0,asη→∞(8)

The skin friction coefficient and Nusselt number are engineering-related metrics that are described as:

Cf∗Re1/2=2f″(0)Pr(1−ϕ1)2.5(1−ϕ2)2.5(1+Pr)Nu∗Re1/2δ−1=−κhnfκf(1+43Rd)θ′(0)(9)

3  Numerical Solution

The 4th order RK technique has been used to solve the dimensionless Eqs. (6) and (7) and associated boundary conditions (8) by using this strategy, the boundary value problem (BVP) is changed into an initial value issue (IVP). In the literature [29–32], there is some discussion of certain investigations into partial differential equations.

Zi+1¯−Zi¯h=q025216+q214082565+q321974109−q415(10)

Zi+1¯−Zi¯h=q016135+q2665612825+q32856156430−q4950+q5255(11)

where the approximate solutions in the fourth and fifth orders, respectively, are (10) and (11).

{q0f=xm¯+zm¯q1f=xm¯+h4,zm¯+hq04q2f=xm¯+3h8,zm¯+3hq032+9hq132q3f=xm¯+12h13,zm¯+1932hq02197−7200hq12197+7296hq22197q4f=xm¯+h,zm¯+439hq0216−8hq1+3860hq2513−845hq34104q4f=xm¯+h2,zm¯−8hq027+2hq1−3544hq22565+1859hq34104−11hq440(12)

The newly listed set of variables below are used in the computation:

f=b1,f′=b2,f″=b3,f‴=b1,f′=b1′,θ=b4,θ′=b5,θ″=b5′(13)

Prb1′(1−na+naWeb3Pr(1+Pr)2n)((1−Φ1)2.5(1−Φ2)2.5)((1−Φ2)[(1−Φ1)ρf+Φ1ρs1]+Φ2ρs2)+(m+12)b1b3+m((1+Pr)4n−(f′)2)+MH(1+Pr)4n((1−Φ2)[(1−Φ1)ρf+Φ1ρs1]+Φ2ρs2)×exp[ηαH(1+Pr)nPr]=0}(14)

b5′(khnf+43Rd)((1−Φ2)[(1−Φ1)(ρCp)f+Φ1(ρCp)s1]+Φ2(ρCp)s2)+(m+12)b1b5+PrEc(b3)2[(1−na)+nafnwePr2(1+Pr)3n](1+Pr)4n((1−Φ1)2.5(1−Φ2)2.5)((1−Φ2)[(1−Φ1)ρf+Φ1ρs1]+Φ2ρs2)=0}(15)

With boundary conditions

b1(η)=b2(η)=0,b4=1,atη=0b2(η)=(1+Pr)2n,b2(η)→0,asη→∞(16)

The convergence criteria is specified at ten-decimal 1 × 10−10 places precision and the step size in the numerical solution is fixed at 0.001 (η = 0:001). In addition, good beginning hypotheses are necessary to find a better solution. Shampine et al. [32] provided a thorough explanation of this solver’s processes. The references [28,29] and [33] provided several numerical methods for resolving nonlinear differential equations. It is crucial to transform higher-order ODEs into first-order ODEs before applying this technique. The comparison between the initial solution on Nu and Maple (dsolve included by the midway) for various magnesium oxide nanoparticle volume fraction values is shown in Table 2 compares the current findings with those from Lin et al. [33] and dsolve (Maple) results for the solution without ϕ1,ϕ2,Ec,MH. It can be shown that there is considerable agreement between the current findings, dsolve (Maple), and Lin et al.’s [33] results.

4  Graphical Description

The objective of this division is to illustrate the hyperbolic tangent flow of Magnesium oxide (MgO) and Silver (Ag)/Kerosene hybrid nanofluid with thermal radiation. In this portion, the physical importance of momentum and thermal aspects of key parameters, such as Hartman number (MH=0.2,0.4,0.6,0.8), power-law-index (nk=0.1,0.2,0.3,0.4), Weissenberg number (We=0.0,1.0,1.5,2.0), Nanoparticle volume fraction (ϕ2=0.0,0.01,0.02,0.03), thermal radiation (Rd=0.0,1.0,2.0,3.0), Eckert number (EC=0.1,0.2,0.3,0.4) and Nanoparticle volume fraction of hybrid (ϕ2=0.0,0.01,0.03,0.05) on MgO-Ag/Kerosene based hyperbolic tangent hybrid nanofluid velocities (f′), temperature (θ), skin friction (Cf∗)and Nusselt number (Nu∗) are visualized and elaborately discussed. Under specific boundary circumstances, the dimensional version of the flow and transport equations are resolved using the Bvp4c with MATALB solver. Solid and dotted lines, respectively, depict the features of the wedge and stagnation point over the hyperbolic tangent. The comparison findings show a high level of agreement, which is shown in Table 2. This shows that the accuracy of the numerical simulation’s outcomes.

Figs. 3 and 4 exhibit the wedge and stagnation on velocity (f′) and temperature (θ) are examined for Hartman number parameter (MH=0.2,0.4,0.6,0.8) through numerical investigation. Fig. 3 reveals that improving Hartman number (MH) tend to intensification the (f′). When compared to stagnation, it is found that wedge has more significant influence. Fig. 4 describes how the velocity profile (θ) gets influenced for the variations in magnetic field parameter (MH). It is observed that (θ) reductions for augmenting the (MH) parameters.

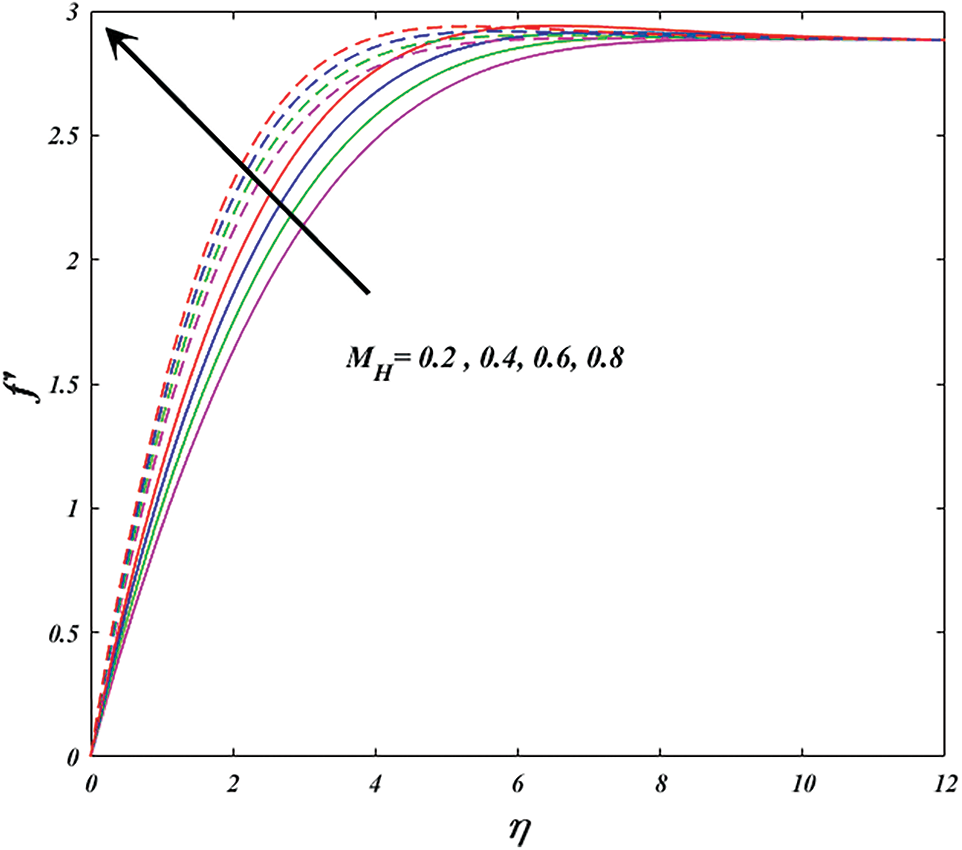
Figure 3: Variation of MH on f′

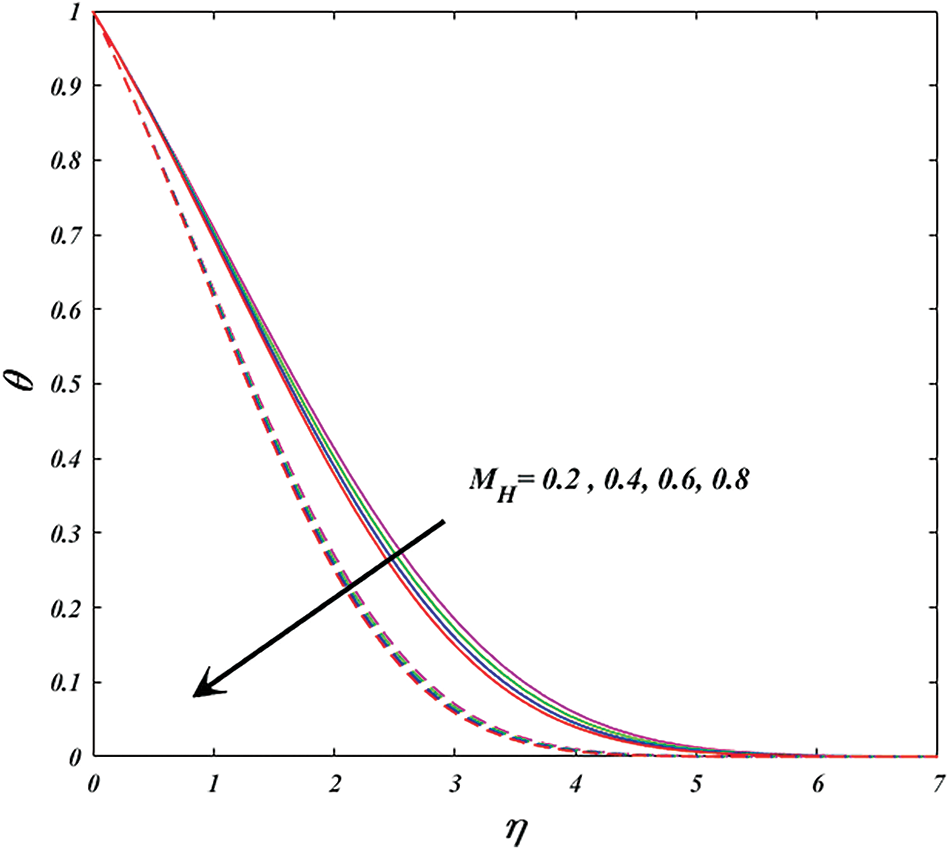
Figure 4: Variation of MH on θ

Physically, varying magnetic parameter values result in Lorentz force deviation, which increases the resistance of the transport phenomenon. In comparison to the wedge, the significant has stronger effects. Figs. 5 and 6 are plotted for investigating the consequence of active aspect on power-law-index (nk=0.1,0.2,0.3,0.4) in the (f′) and temperature θ(η). Fig. 5 illustrates how the thermal radiation parameter (nk) influence on temperature (f′) changes. According to this graph, the (f′) is growths by increasing values in the (nk). Fig. 6 shows the behavior of (nk) on temperature θ(η) is portrayed. It has been determined that temperature θ(η) decreases for increased (nk) values. Figs. 7 and 8 describe distinctions in the (f′) and θ(η) influenced by the Weissenberg number (We=0.0,1.0,1.5,2.0). Fig. 7 illustrates how the Weissenberg number (We) influence on (f′) changes in wedge and stagnation, correspondingly. It is observed that the (f′) enlargement by improving the (We). In general, the Weissenberg number is defined as the ratio between the relaxation time of fluid stress and the specific process time. The figure illustrates that as the Weissenberg number increases, the thickness of the tangent hyperbolic fluid decreases. Fig. 8 illustrates how the (We) influence on temperature θ(η) changes. According to this graph, the temperature θ(η) is growths by increasing values in the (We). Observations reveal that elevated values of the Weissenberg number lead to an augmentation in the relaxation time of the tangent hyperbolic fluid. Consequently, as the Weissenberg number increases, there is a corresponding rise in this temperature for cases involving a wedge, and stagnation point.

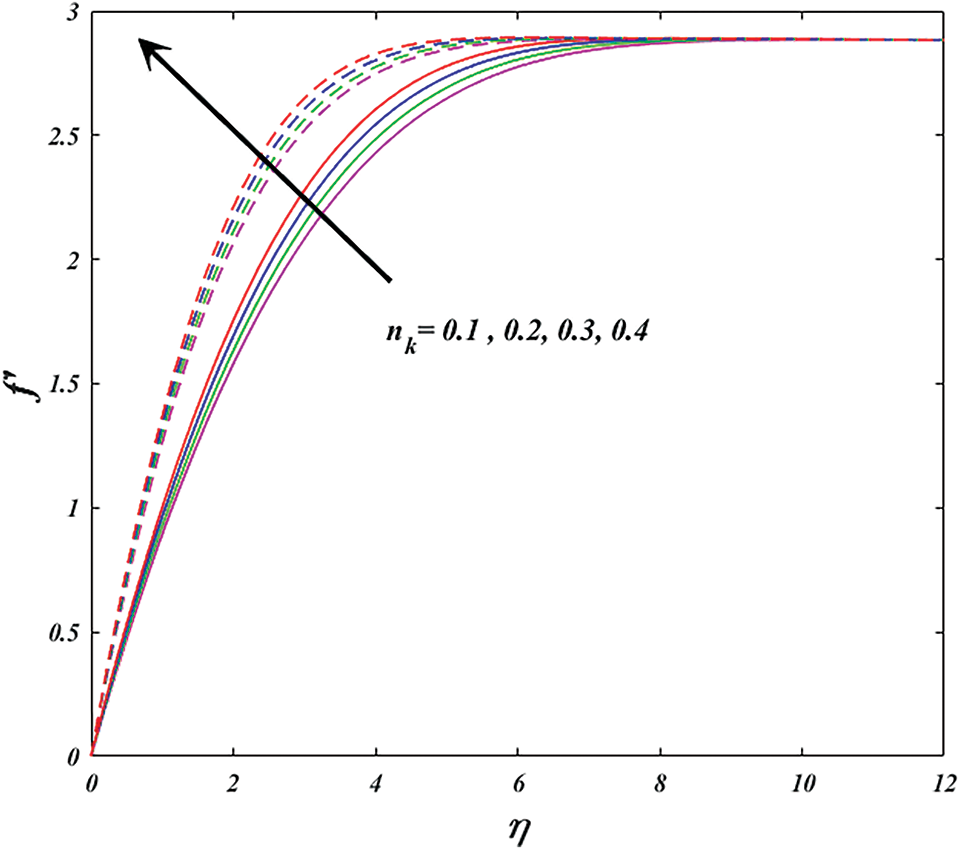
Figure 5: Variation of nk on f′

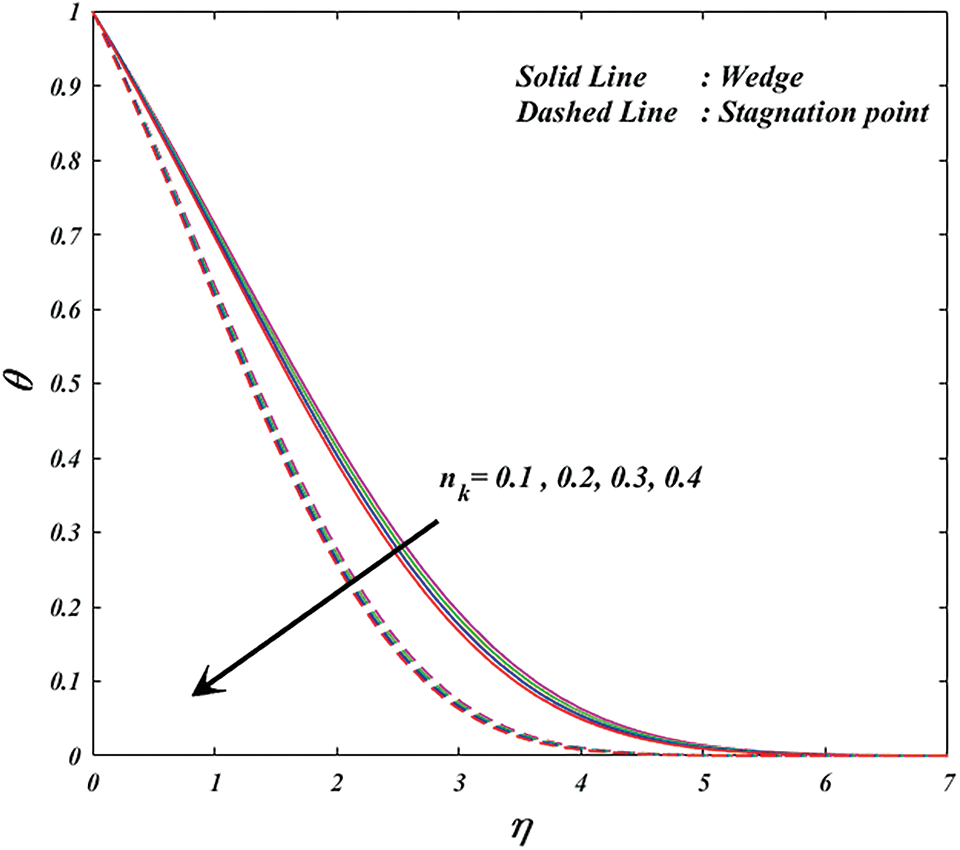
Figure 6: Variation of nk on θ

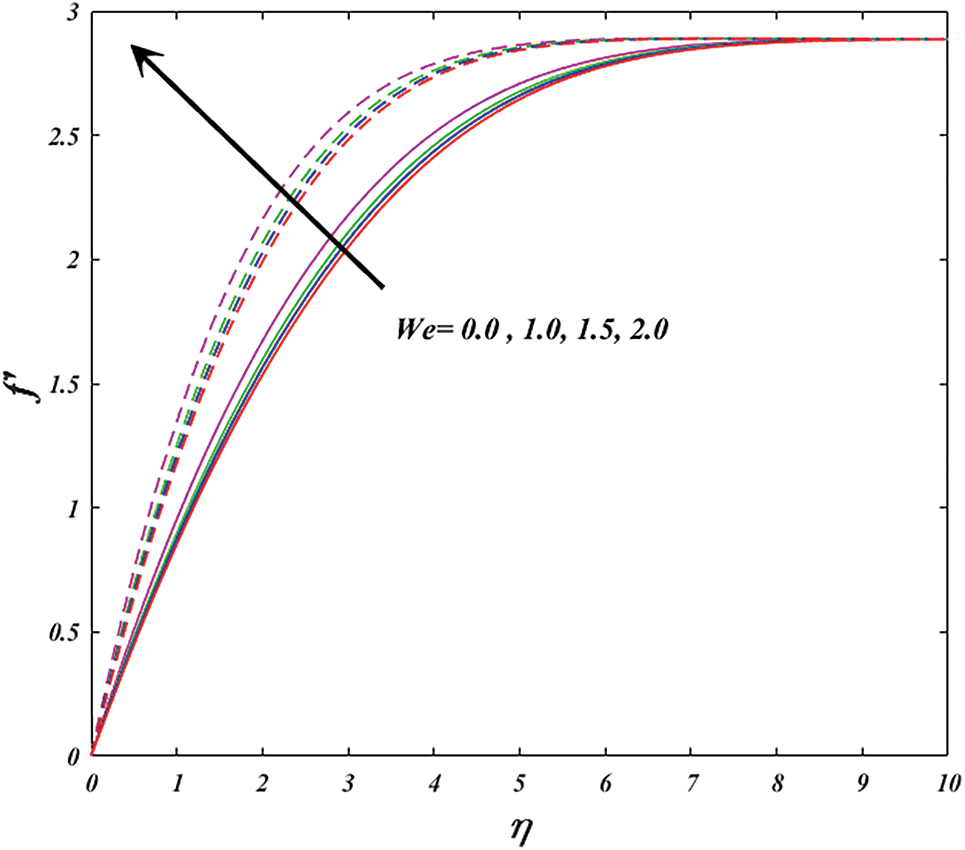
Figure 7: Variation of We on f′

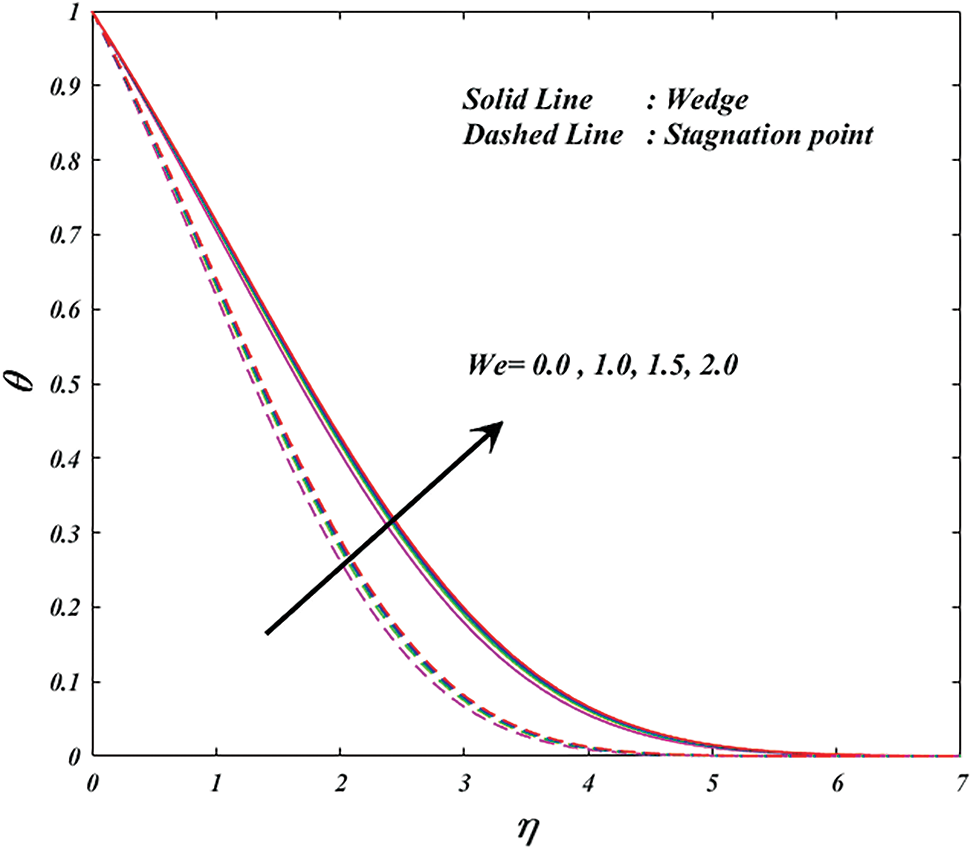
Figure 8: Variation of We on θ

Figs. 9 and 10 explore the changes of nanoparticle volume fraction (ϕ2=0,0.01,0.02,0.03) on velocity (f′) and temperature θ(η) in the case of wedge and stagnation. Fig. 9 describes how the (f′) profile gets influenced for the variations in (ϕ2). It is observed that (f′) diminutions for boosting the (ϕ2). The thermal conductivity of hybrid nanofluid is enhanced with an increase in the volume fraction of nanoparticles. This increase in thermal conductivity promotes the clustering of nanoparticles due to the lower viscosity of the base fluid. Consequently, the clustering of nanoparticles creates interference channels that facilitate the spreading of thermal energy. Due to this reason, the hybrid nanofluid temperature rises over a wedge and stagnation point.

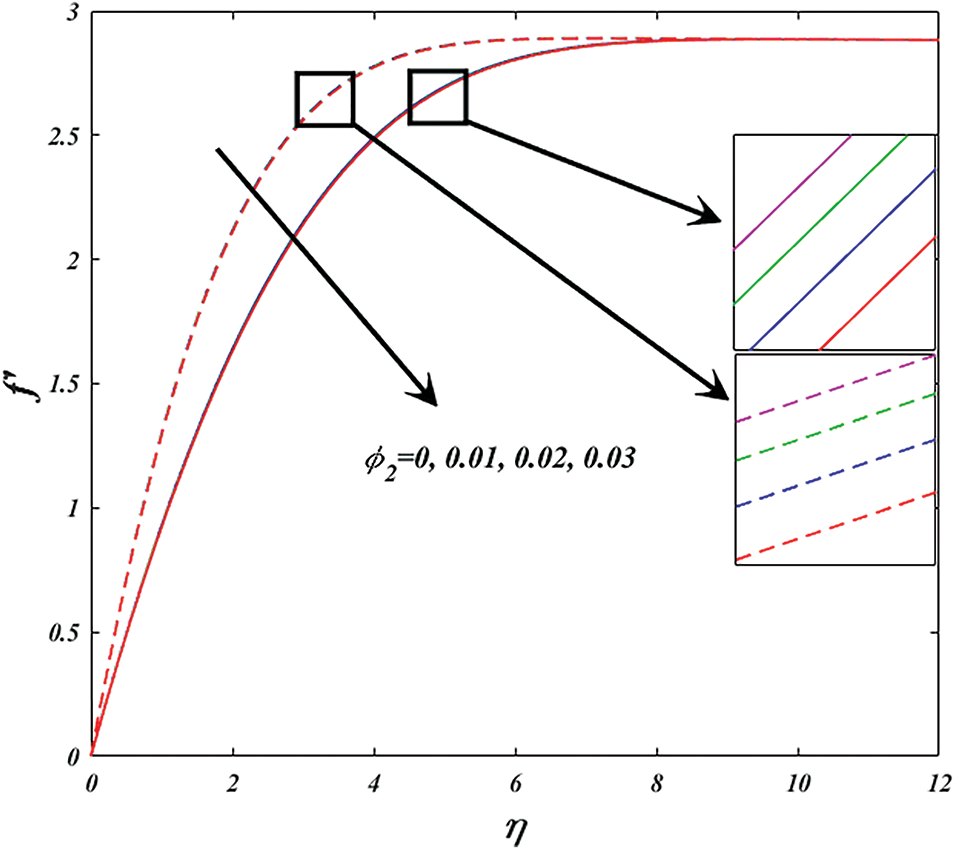
Figure 9: Variation of ϕ2 on f′

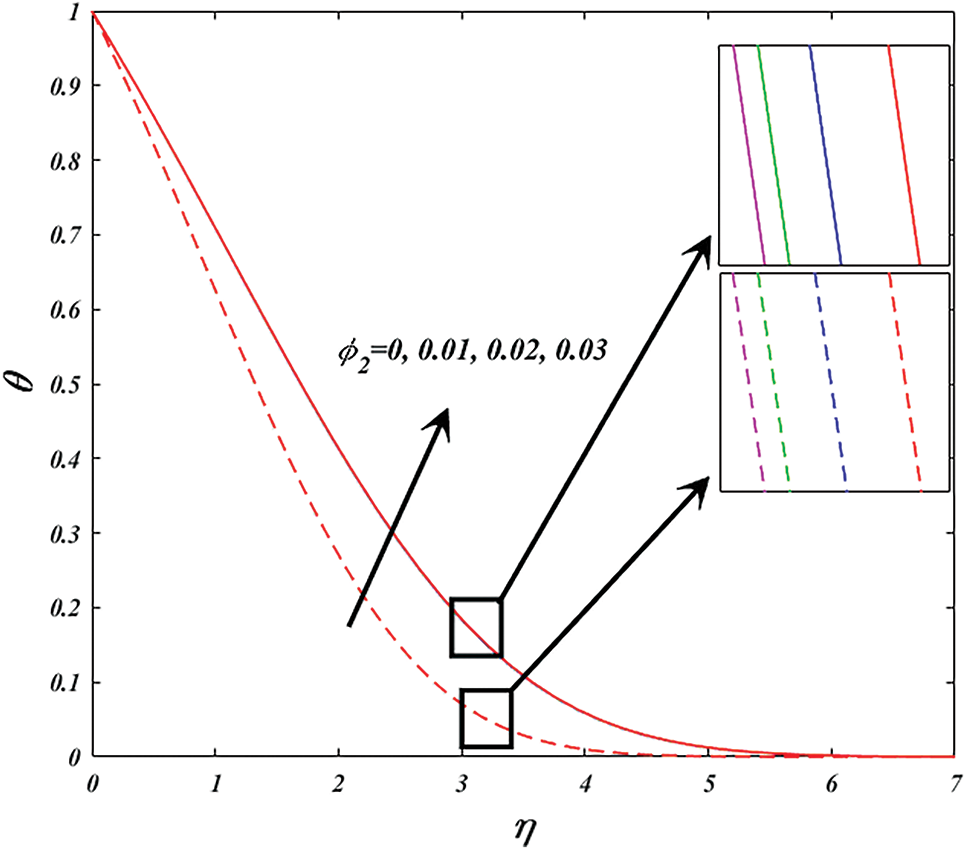
Figure 10: Variation of ϕ2 on θ

Fig. 11 illustrates how the thermal radiation parameter (Rd=0.0,1.0,2.0,3.0) influence on temperature θ(η) changes. According to this graph, the temperature θ(η) is growths by increasing values in the (Rd). Physically, higher thermal radiation characteristics are connected with higher temperatures and thicker thermal boundary layers. Fig. 12 illustrates how the Eckert number (Ec=0.1,0.2,0.3,0.4) influence on temperature θ(η) changes. According to this graph, the temperature is improved by rising values in the (Ec).

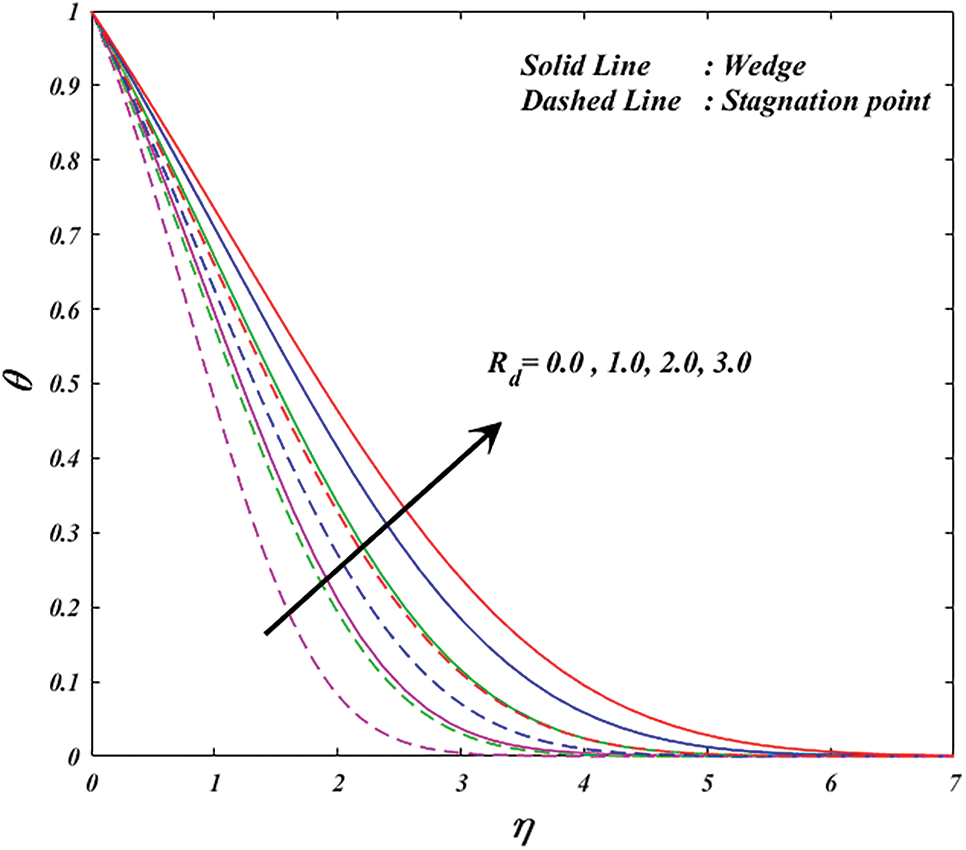
Figure 11: Variation of Rd on θ

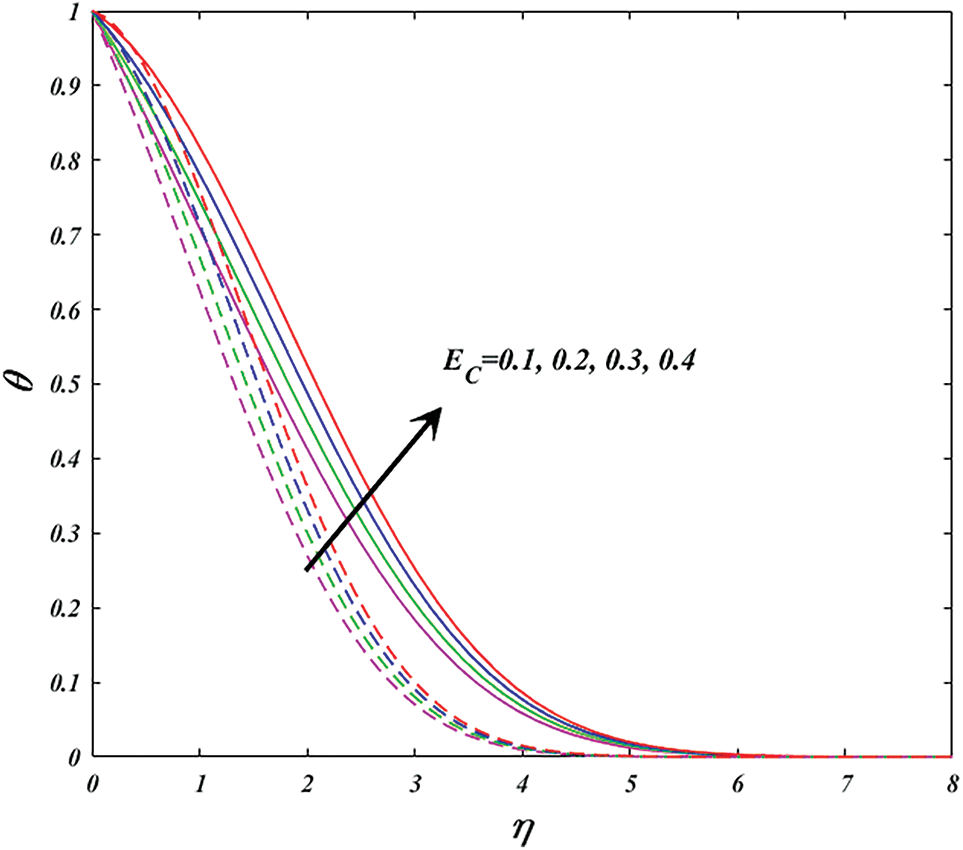
Figure 12: Variation of EC on θ

Physically, the higher (Ec) produce more kinetic energy, causing particles to collide more frequently and dissipate energy. Fig. 13 reveals the impact of Weissenberg number (We) and Hartman number (MH) on skin friction (Cf∗). It is recognized that the (Cf∗) improves for greater values of (We) and (MH) parameters. The role of volume fraction (ϕ1+ϕ2) and power-law-index (nk) parameters on skin friction (Cf∗) is illustrated in Fig. 14. According to this graph, these factors enhance by the skin friction for wedge and stagnation. The changes in Weissenberg number (We) and Eckert number (Ec) parameters on the heat transfer rate (Nu∗) is depicted in Fig. 15. From this figure, both parameters reduced the (Nu∗) for wedge and stagnation, respectively. The changes in thermal radiation (Rd) and Eckert number (Ec) parameters on the heat transfer rate (Nu∗) is depicted in Fig. 16. From this figure, both parameters intensification the (Nu∗) for wedge and stagnation, respectively. The role of volume fraction (ϕ1+ϕ2) and thermal radiation (Rd) parameters on heat transfer rate (Nu∗) is illustrated in Fig. 17. According to this graph, these factors enhance by the (Nu∗) for wedge and stagnation. Fig. 18 reveals the impact of power law index (nk) and Hartman number (MH) on heat transfer rate (Nu∗). It is recognized that the (Nu∗) improves for greater values of (nk) and (MH) parameters.

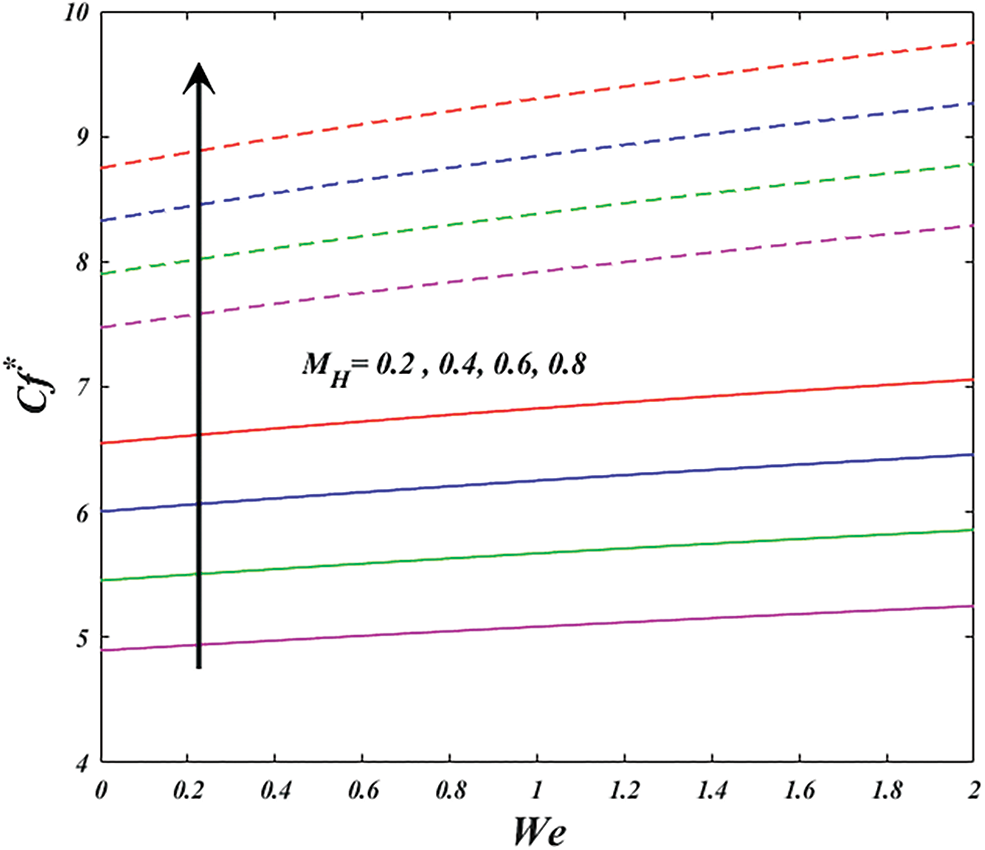
Figure 13: Variation of MH & We on Cf∗

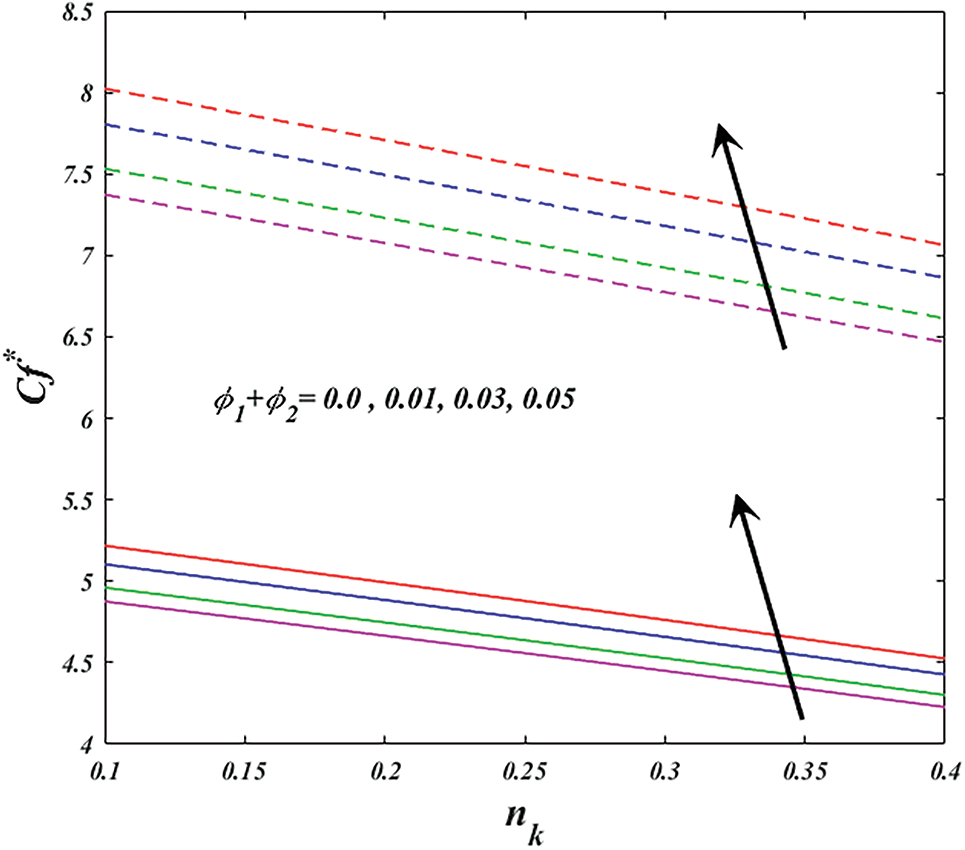
Figure 14: Variation of ϕ1+ϕ2 & nk on Cf∗

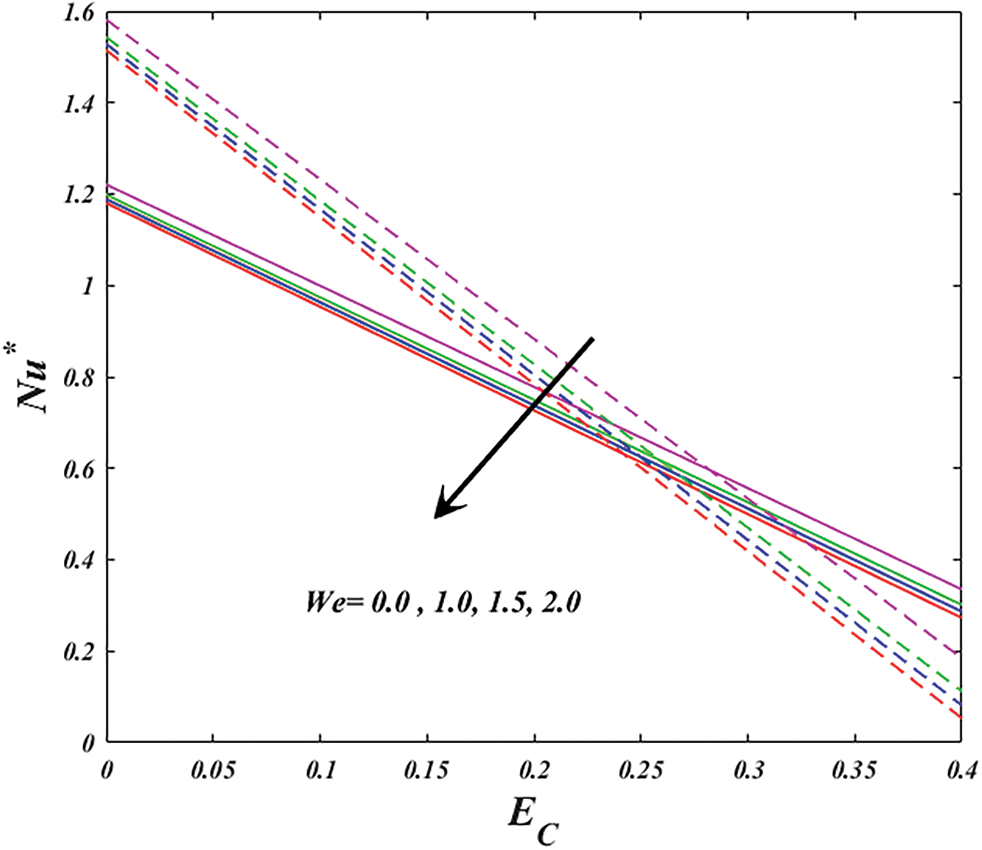
Figure 15: Variation of We & Ec on Nu∗

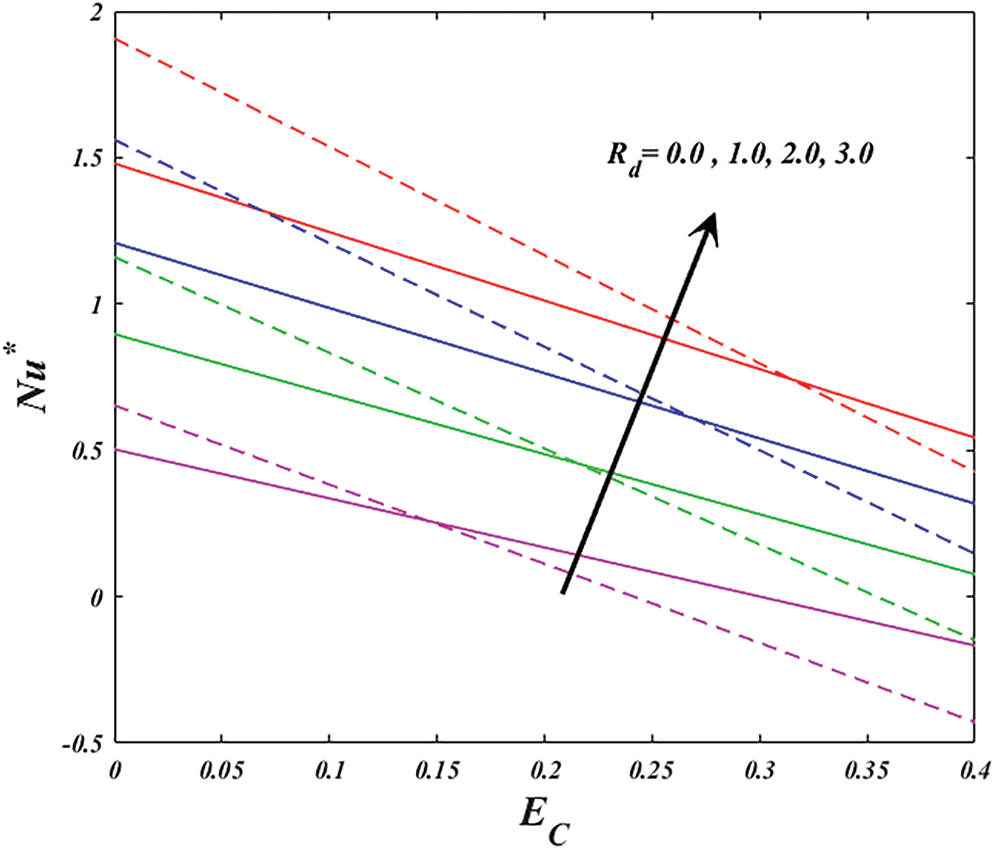
Figure 16: Variation of Rd & Ec on Nu∗

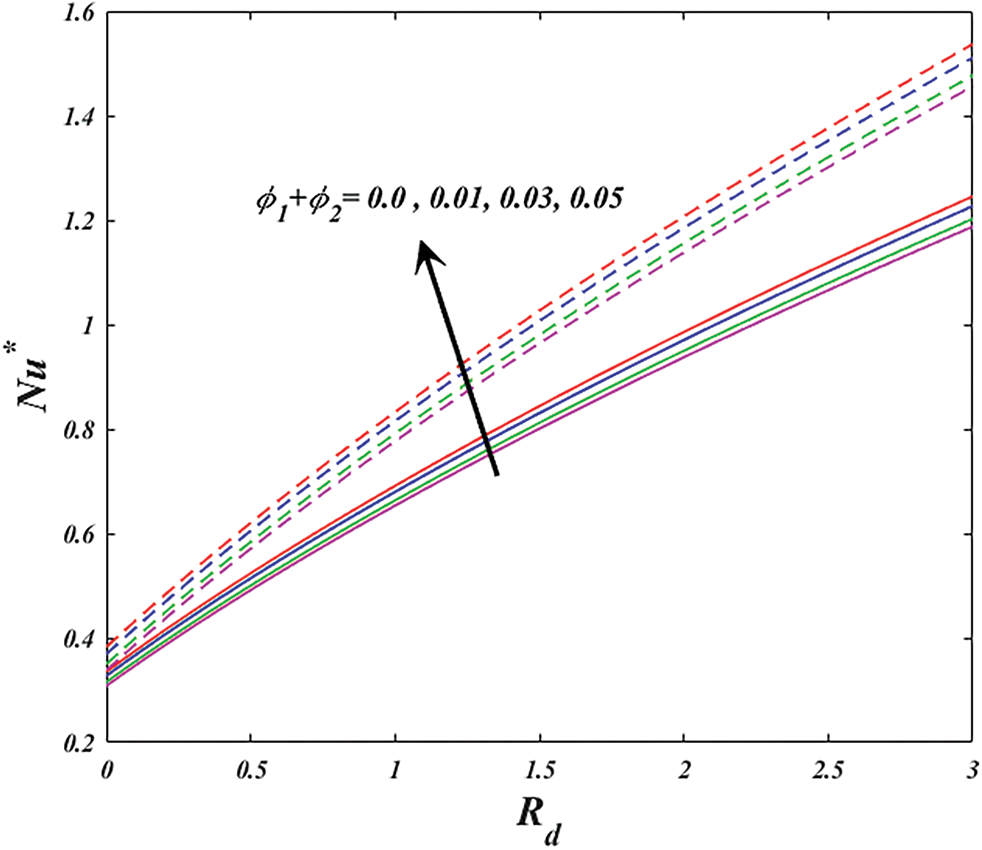
Figure 17: Variation of ϕ1+ϕ2 & Rd on Nu∗

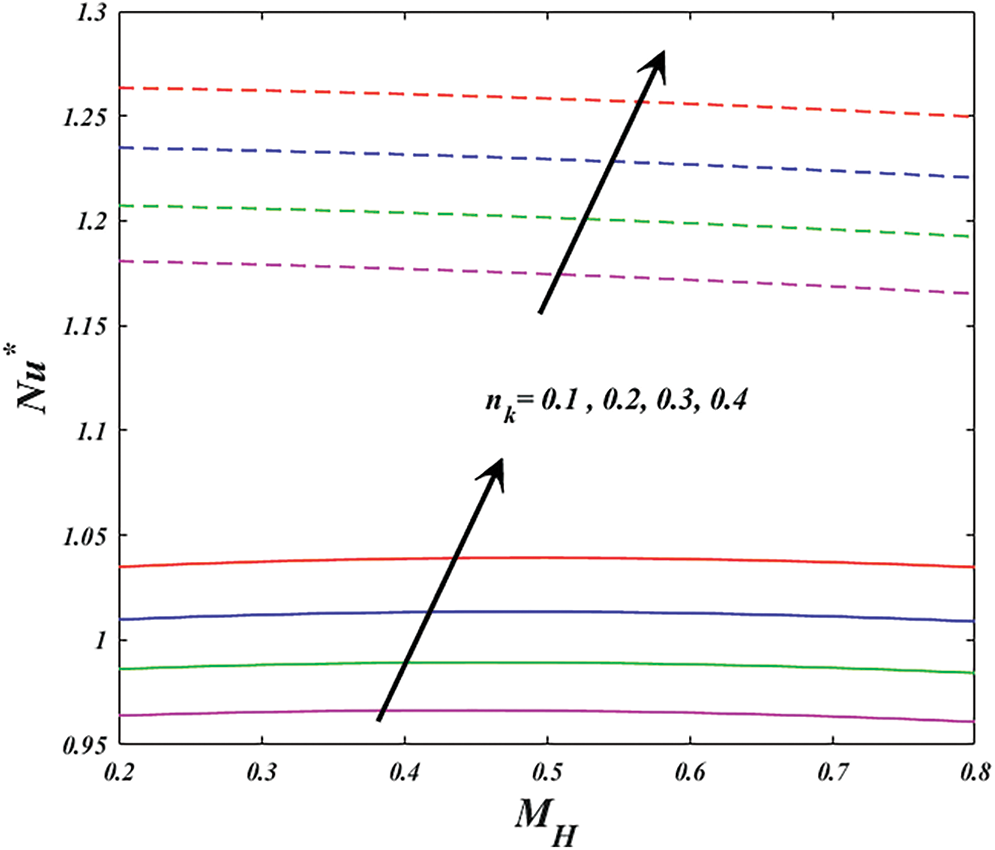
Figure 18: Variation of MH & nk on Nu∗

5  Conclusions

This study aims to determine the hyperbolic tangent flow of Magnesium oxide (MgO) and Silver (Ag)/Kerosene hybrid nanofluid over a wedge and stagnation with the influence of a linear thermal radiation. The main goal of this research is to depict the Kerosene-based Magnesium oxide and silver nanoparticle flow properties after the mechanism has been filled with hybrid nanofluids. The influence of distinctive factors like Hartman number, power law index, Weissenberg number, Nanoparticle volume fraction, thermal radiation, Eckert number and Nanoparticle volume fraction of hybrid parameters on hyperbolic tangent flow over a wedge and stagnation. The results are shown through two-dimensional graphs and tables. The following significant findings emerged from this investigation:

•   Improving Hartman number tend to intensification the velocity but temperature is decreases.

•   The velocity is growths but it is declarations in temperature by increasing values in the power law index parameter.

•   The velocity profile and temperature in the wedge and stagnation are both improved by higher values of the Weissenberg number, respectively.

•   The temperature profiles for the both the cases increase when the silver nanoparticles volume fraction intensifications.

•   Thermal radiation and Eckert number both parameters intensification the heat transfer rate for wedge and stagnation, respectively.

•   This study indicates that the heat transfer rate in the fluid flow over a stagnation point case is 14.0346% higher compared to the flow over a wedge case.

•   Incorporating hybrid nanoparticles into the base fluid leads to an increase in the heat transfer rate by 8.92% for the wedge case and 13.26% for the stagnation point case.

•   The heat transfer rate over a Riga stagnation point surface exhibits a significant increase of 191.86% when thermal radiation is considered. Similarly, for the Riga wedge surface, the heat transfer rate experiences a substantial increase of 194.39% due to the inclusion of thermal radiation.

The current investigation has uncovered fascinating flow phenomena observed in the boundary layer flows of Riga electromagnetic plate actuators. However, the focus of this study has been limited to the analysis of boundary layer flows over wedges and stagnation points. To broaden our understanding, future studies could explore the implementation of Eringen’s micropolar model to account for non-Newtonian effects. Additionally, it would be valuable to investigate these effects across three distinct geometries incorporating high thermal conductivity nanoparticles like graphene and diamond. The findings of these future studies will be communicated in the near future.

Acknowledgement: Authors would like to express their gratitude for the reviewer’s valuable comments and suggestions.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: A. H. A & N. A. A; data collection: A. H. A & N. A. A; analysis and interpretation of results: A. H. A & N. A. A; draft manuscript preparation: A. H. A & N. A. A. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data used or analyzed during the current study available from the corresponding author on reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Animasaun, I. L., Shah, N. A., Wakif, A., Mahanthesh, B., Sivaraj, R. et al. (2022). Ratio of momentum diffusivity to thermal diffusivity, 1st edition. New York, Boca Raton: Chapman and Hall/CRC. [Google Scholar]

2. Reddy, C. S., Naikoti, K., Rashidi, M. M. (2017). MHD flow and heat transfer characteristics of williamson nanofluid over a stretching sheet with variable thickness and variable thermal conductivity. Transactions of A Razmadze Mathematical Institute, 171(2), 195–211. [Google Scholar]

3. Nadeem, S., Zaheer, S., Fang, T. (2011). Effects of thermal radiation on the boundary layer flow of a jeffrey fluid over an exponentially stretching surface. Numerical Algorithms, 57(2), 187–205. [Google Scholar]

4. Bhatti, M. M., Abbas, T., Rashidi, M. M., Ali, M. E. S., Yang, Z. (2016). Entropy generation on MHD eyring-powell nanofluid through a permeable stretching surface. Entropy, 18(6), 1–14. [Google Scholar]

5. Shah, F., Khan, S. A., Al-Khaled, K., Khan, M., Khan, S. et al. (2022). Impact of entropy optimized Darcy-Forchheimer flow in MnZnFe2 and NiZnFe2O4 hybrid nanofluid towards a curved surface. Zamm-Journal of Applied Mathematics and Mechanics/Zeitschrift fur Angewandte Mathematik and Mechanik, 102(3). [Google Scholar]

6. Abbasi, A., Al-Khaled, K., Zouidi, F., Khan, S., Khan, M. et al. (2022). Blood-based electro-osmotic flow of non-newtonian nanofluid (curreau-Yasuda) in a tapered channel with entropy generation. Zamm-Journal of Applied Mathematics and Mechanics/Zeitschrift fur Angewandte Mathematik and Mechanik, 103(5). [Google Scholar]

7. Alhussain, Z. A., Tassaddiq, A. (2022). Thin film blood based Casson hybrid nanofluid flow with variable viscosity. Arabian Journal for Science & Engineering, 47(1), 1087–1094. [Google Scholar]

8. Hussain, A., Malik, M. Y., Bilal, S., Awais, M., Salahuddin, T. (2017). Computational analysis of magnetohydrodynamic sisko fluid flow over a stretching cylinder in the presence of viscous dissipation and temperature dependent thermal conductivity. Results in Physics, 7, 139–146. [Google Scholar]

9. Malik, M. Y., Salahuddin, T., Hussain, A., Bilal, S. (2015). MHD flow of tangent hyperbolic fluid over a stretching cylinder: Using keller box method. Journal of Magnetism and Magnetic Materials, 395, 271–276. [Google Scholar]

10. Hayat, T., Aslam, N., Alsaedi, A., Rafiq, M. (2017). Endoscopic effect in MHD peristaltic activity of hyperbolic tangent nanofluid: A numerical study. International Journal of Heat and Mass Transfer, 115, 1033–1042. [Google Scholar]

11. Ali, B., Thumma, T., Habib, D., Salamat, N., Riaz, S. (2022). Finite element analysis on transient MHD 3D rotating flow of maxwell and tangent hyperbolic nanofluid past a bidirectional stretching sheet with cattaneo christov heat flux model. Thermal Science Engineering and Progress, 28, 101089. [Google Scholar]

12. Seid, E., Haile, E., Walelign, T. (2022). Multiple slip, Soret and Dufour effects in fluid flow near a vertical stretching sheet in the presence of magnetic particles. International Journal of Thermofluids, 13, 100136. [Google Scholar]

13. Walelign, T., Haile, E., Kebede, T., Awgichew, G. (2021). Heat and mass transfer in stagnation point flow of maxwell nanofluid towards a vertical stretching sheet with effect of induced magnetic field. Mathematical Problems in Engineering, 2021, 6610099. [Google Scholar]

14. Metwally, A. S. M., Khalid, A., Khan, A. A., Iskakova, K., Gorji, M. R. et al. (2022). Radiation consequences on sutterby fluid over a curved surface. Journal of Engineering Thermophysics, 31(2), 315–327. [Google Scholar]

15. Crane, L. J. (1970). Flow past a stretching plate. Zeitschrift für Angewandte Mathematik und Physik ZAMP, 21(4), 645–647. [Google Scholar]

16. Jamshed, W., Nisar, K. S., Ibrahim, R. W., Shahzad, F., Eid, M. R. (2021). Thermal expansion optimization in solar aircraft using tangent hyperbolic hybrid nanofluid: A solar thermal application. Journal of Materials Research and Technology, 14, 985–1006. [Google Scholar]

17. Sheikholeslami, M., Farshad, S. A., Ebrahimpour, Z., Said, Z. (2021). Recent progress on flat plate solar collectors and photovoltaic systems in the presence of nanofluid: A review. Journal of Cleaner Production, 293, 126119. [Google Scholar]

18. Waqas, H., Kamran, T., Imran, M., Muhammad, T. (2022). MHD bioconvectional flow of jeffrey nanofluid with motile microorganisms over a stretching sheet: Solar radiation applications. Waves in Random and Complex Media, 2022(1), 1–30. [Google Scholar]

19. Fox, J. A. (1974). An introduction to engineering fluid mechanics. UK: Macmillan Education. [Google Scholar]

20. Fay, J. A., Riddell, F. R. (1958). Theory of stagnation point heat transfer in dissociated air. Journal of the Aeronautical Sciences, 25(2), 73–85. [Google Scholar]

21. Bhatti, M. M., Abbas, M. A., Rashidi, M. M. (2018). A robust numerical method for solving stagnation point flow over a permeable shrinking sheet under the influence of MHD. Applied Mathematics and Computation, 316, 381–389. [Google Scholar]

22. Rashidi, M. M., Erfani, E. (2011). A new analytical study of MHD stagnation-point flow in porous media with heat transfer. Computers & Fluids, 40(1), 172–178. https://doi.org/10.1016/j.compfluid.2010.08.021 [Google Scholar] [CrossRef]

23. Abbas, Z., Sheikh, M., Motsa, S. S. (2016). Numerical solution of binary chemical reaction on stagnation point flow of Casson fluid over a stretching/shrinking sheet with thermal radiation. Energy, 95, 12–20. [Google Scholar]

24. Muntazir, R. M. A., Mushtaq, M., Jabeen, K. (2021). A numerical study of MHD carreau nanofluid flow with gyrotactic microorganisms over a plate, wedge, and stagnation point. Mathematical Problems in Engineering, 2021, 5520780. [Google Scholar]

25. Raju, C. S. K., Ahammad, N. A., Sajjan, K., Shah, N. A., Yook, S. J. et al. (2022). Nonlinear movements of axisymmetric ternary hybrid nanofluids in a thermally radiated expanding or contracting permeable darcy walls with different shapes and densities: Simple linear regression. International Communications in Heat and Mass Transfer, 135, 106110. [Google Scholar]

26. Kavya, S., Nagendramma, V., Ahammad, N. A., Ahmad, S., Raju, C. S. K. et al. (2022). Magnetic-hybrid nanoparticles with stretching/shrinking cylinder in a suspension of MoS4 and copper nanoparticles. International Communications in Heat and Mass Transfer, 136, 106150. [Google Scholar]

27. Khan, U., Zaib, A., Ishak, A., Waini, I., Madhukesh, J. K. et al. (2022). Impact of buoyancy and stagnation-point flow of water conveying Ag-MgO hybrid nanoparticles in a vertical contracting/expanding Riga wedge. Symmetry, 14(7), 1312. [Google Scholar]

28. Basha, H. T., Sivaraj, R., Subramanyam Reddy, A., Chamkha, A. J. (2019). SWCNH/diamond-ethylene glycol nanofluid flow over a wedge, plate and stagnation point with induced magnetic field and nonlinear radiation-solar energy application. The European Physical Journal Special Topics, 228, 2531–2551. [Google Scholar]

29. Basha, H. T., Sivaraj, R. (2021). Numerical simulation of blood nanofluid flow over three different geometries by means of gyrotactic microorganisms: Applications to the flow in a circulatory system. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 235(2), 441–460. [Google Scholar]

30. Mohapatra, D. K., Mishra, S., Jena, S. (2019). Cu-water and Cu-kerosene micropolar nanofluid flow over a permeable stretching sheet. Heat Transfer—Asian Research, 48(6), 2478–2496. [Google Scholar]

31. Basha, H. T., Sivaraj, R., Animasaun, I. L. (2020). Stability analysis on Ag-MgO/water hybrid nanofluid flow over an extending/contracting Riga wedge and stagnation point. Computational Thermal Sciences: An International Journal, 12(6), 491–508. [Google Scholar]

32. Shampine, L. F., Gladwell, I., Thompson, S. (2003). Solving ODEs with MATLAB. Cambridge: Cambridge University Press. [Google Scholar]

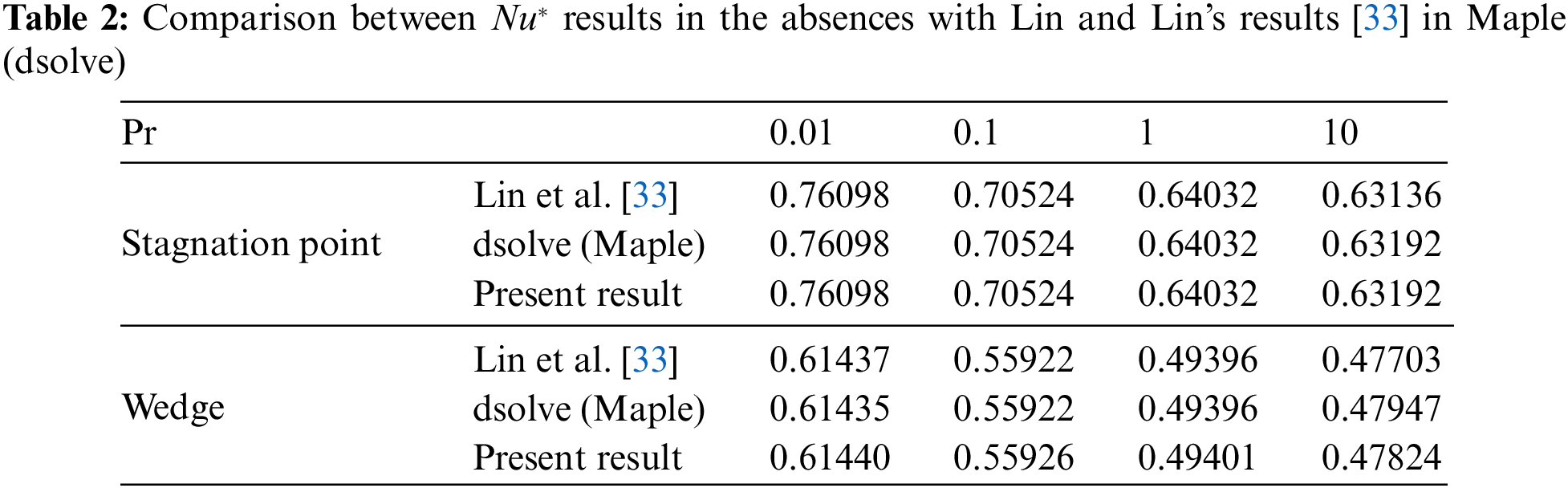
33. Lin, H. T., Lin, L. K. (1987). Similarity solutions for laminar forced convection heat transfer from wedges to fluids of any prandtl number. International Journal of Heat and Mass Transfer, 30(6), 1111–1118. [Google Scholar]