Thermal Radiation Effects on 2D Stagnation Point Flow of a Heated Stretchable Sheet with Variable Viscosity and MHD in a Porous Medium

Nomenclature

1  Introduction

Due to its potential applications in a number of sectors, including nanofluidic devices, drug delivery, and biomedical engineering, the stagnation point flow of nanomaterials with natural convection and variable fluid properties is a developing field that has drawn more attention nowadays. The thermal and physical characteristics of the fluid, such as viscosity, density, and thermal conductivity, have a significant impact on how nanomaterials behave at stagnation points. This study intends to examine the hydrodynamic flow of nanomaterials at stagnation point x=0 with natural convection and variable fluid characteristics. The results of this study could have important implications for the design of nanofluidic devices and other applications where the behavior of nanomaterials at stagnation points is critical. Choi et al. [1] investigated the results of incorporating nanoparticles into fluids to increase their thermal conductivity. A theoretical analysis of the behavior of a nanofluid flow over a vertical plate under the effect of natural convection was reported by Kuznetsov et al. [2]. In a non-Darcy porous medium saturated with a nanofluid, Shaw et al. [3] investigated dual solutions for homogeneous-heterogeneous reactions over an elastic sheet. Their research sheds light on the effects of various parameters, including chemical reaction and non-Darcy effects on the flow of the nanofluid.

Magnetohydrodynamics (MHD) is a field of physics and engineering that studies the dynamics of electrically conducting fluids in the presence of magnetic fields. In MHD fluid flow, the fluid is influenced by electromagnetic fields, which can lead to interesting and complex phenomena such as the generation of electric fields and currents, the formation of magnetic structures, and the suppression of turbulence. MHD fluid flow has many practical applications in engineering, such as in plasma confinement for nuclear fusion, in the design of electric generators, and in the study of space weather. Roberts [4] and Davidson [5] served as introductory texts on Magnetohydrodynamics (MHD), providing basic concepts, principles, and applications of MHD in various fields of science and engineering. Qamar et al. [6] investigated the influence of variable electromagnetohydrodynamic (EMHD) on the motion of fluid over a porous elastic sheet. A hybrid nanofluid’s magnetohydrodynamic stagnation point flow was studied by Anuar et al. in [7], along with the associated ODEs that were numerically solved using dual solutions. Zainal et al. [8] provided numerical solution of non-axisymmetric Homann impinging flow of hybrid nanofluid. Nadeem et al. [9] numerically analyzed the impact of different parameters on heat transfer and skin friction coefficient in the two-dimensional stagnation point flow of nanofluid over a curved surface. For the Newtonian magnetohydrodynamic fluid flow across an unsteady stretched sheet with thermal radiation, variable heat flux, and variable viscosity/conductivity, Megahed et al. [10] employed a shooting approach to solve the ordinary differential equations. Ali et al. [11] developed a mathematical model of 2D stagnation point flow over incorporated Newtonian heating.

Modeling nonlinear thermal radiation in fluid flow involves the use of complex mathematical models and numerical methods to obtain accurate predictions of the temperature field. The nonlinearity can significantly affect the temperature distribution in the fluid and has important implications for heat transfer in various engineering applications. In their study, Bouslimi et al. [12] studied the Williamson fluid under the influence of thermal radiation and electromagnetic force flowing in a porous material. According to Bilal et al. [13] the effects of nonlinear thermal radiation on the Darcy-Forchheimer flow of a magnetohydrodynamic Williamson nanofluid with entropy optimization are examined. Mixed convection micropolar fluid flow in a porous material with a magnetic field and boundary condition of convective type by Patel et al. [14], used similarity transformations and the Homotopy analysis approach to solve the governing equations with non-linear thermal radiation. To investigate the combined impact of various parameters on the Eyring-Powell nanofluid under the influence of MHD flow of through an elastic sheet, Reddy et al. [15] did an analysis. The findings were shown graphically and statistically. Kumar et al. [16] provided a detailed analysis of the Casson nanofluid in a vertical channel containing pores with the effect of MHD and thermal radiation.

The concept of the porous medium has gained significant attention in nowadays due to its numerous applications in scientific fields. A porous medium refers to a material with interconnected voids or spaces that allow fluid to pass through it. The presence of porous media in fluid flow systems often results in changes to the fluid’s physical properties, including its viscosity. Understanding the impact of porous media on viscosity is crucial in designing and optimizing fluid flow systems for various applications. In this research paper, we aim to investigate the effects of porous media on fluid viscosity and explore its implications in practical applications. McWhirter et al. [17] presented experimental findings on magnetohydrodynamic flows in porous media, and shed light on the interaction between fluid flow, magnetic fields, and porous media. A mathematical model was developed by Bhatti et al. [18] for electromagnetic blood flow with coagulation, magnetohydrodynamics, and Hall current in an annular vessel with a porous medium, solved analytically for fluid and particle phase with the homotopy perturbation method. Reddy et al. [19] investigated the effect of MHD flow over a porous medium, obtained numerical solutions using the Keller-box method, and identified the flow features and their behavior under different parameters.

Bioconvection is a process where microorganisms are introduced into a fluid, causing the upper surface to become thicker and unstable, leading to the tumbling of microorganisms toward the ground. This process has numerous applications in various fields, such as pharmaceuticals, culture purification, microfluidics, mass transfer enhancement, oil recovery, and enzyme biosensors, and is currently a subject of ongoing research [20]. The flow of nanofluids comprising nanomaterials and motile microorganisms through a porous elastic wedge with Nield boundary through a porous matrix was the subject of research by Hussain et al. [21]. Muhammad et al. [22] examined the effects of activation energy, magnetic field, and other physical variables, as well as motile microorganisms, on the characteristics of Jeffrey nanofluid flow on a three-dimensional surface. Numerical analysis of a nanofluid flow via an elastic surface containing gyrotactic microorganisms was performed by [23–25]. The study by Dawar et al. [26] compared the results of magnetized and non-magnetized Casson fluids through a stretching cylinder.

The research questions and innovatives explored in this research are as follows:

•   How does the viscoelastic parameter K influence the flow characteristics and boundary layer behavior of the fluid near the heated sheet?

•   How does the magnetic parameter M influence fluid velocity and transfer rate of heat?

•   What is the relationship between the bioconvection Lewis number Lb and the density number in the context of bioconvection phenomena?

In the literature, the effects of gyrotactic microorganisms in two dimensional (2D) flow stagnates at x=0 over an extended stretchable surface are limited. In this study, these effects for two-dimensional stagnation point flow [11] at x=0 over an extended heated stretchable sheet are being investigated by considering factors such as nonlinear thermal radiation, MHD, porous medium, and variable viscosity. The governing PDEs will be transformed into ODEs using a similarity transformation and then numerically tackled using the bvp4c method in MATLAB [27–31]. The resulting solutions will be plotted in two-dimensional graphics to illustrate the models’ complexity at various fluid parameter values.

The paper is structured into several sections, starting with the mathematical model of the problem in the Section 2, followed by a discussion of the numerical approach in the Section 3. The Section 4 presents the findings and a conclusion is drawn in the Section 5.

2  Mathematical Modeling

Consider a two-dimensional viscoelastic nano-fluid flow stagnates at x=0 containing gyrotactic microorganisms across an heated elastic sheet, taking into account that magnetic field applied vertical in direction to the surface, as well as Joule heating and viscous dissipation. At the stagnation point (0,0), two equal and opposing forces stretching the surface with velocities uw=ax and u∞=bx. To ignore the impact of the induced magnetic field, the magnetic Reynolds number must be very low. The momentum equation has the following form after the boundary layer approximation [11].

∂u∂x+∂v∂y=0,(1)

uux+vvy=u∞(u∞)x−σeB02(u−u∞)ρf+1ρf(μuy)y−μρfk(u−u∞)+k0(uuxyy+uxuyy+νuxxx−uyuxy),(2)

and the corresponding boundary conditions are

u=uw(x)=ax,v=0,wheny=0,u→u∞(x)=bx,wheny→∞,(3)

where (u,v),u∞,uw(x),νf,σe,k0, and ρf represent the fluid velocities, free stream velocity, velocity of the sheet, kinematic viscosity, electrical conductivity, viscoelastic parameter, and fluid density, respectively.

In (2), the fluid viscosity μ is assumed to vary with temperature as follows:

μ=μ∞e−αθ,(4)

A similarity transformation is employed as follows [11]:

η=−aνfu=axf′(η),v=−aνff(η),(5)

We get the following ODE with boundary conditions as

ff″−f′2+K(2f′f″−ff″−f″2)+(M+e−αθδ)(λ−f′)+λ2+e−αθ(f‴−αθ′f″)=0,(6)

f(0)=0,f′(0)=1,f′(∞)=λ.(7)

Here, the viscoelastic parameter is defined as K=ak0νf, while the external magnetic source is represented by M=σeB02aρf. Additionally, the local Darcy number is given by δ=μ∞ρfka, the viscosity parameter is defined as α, the ratio parameter is denoted by λ=ba denotes the ratio parameter and α represents the dimensionless viscosity parameter.

2.1 Energy Equation

The energy equation in fluids describes the conservation of energy in fluid flow, accounting for thermal energy transfer due to conduction, convection, and radiation. It is an important equation in fluid dynamics and is commonly used in the analysis of heat transfer problems. After boundary layer approximation, the energy equation [11] takes the following form:

uTx+vTy=μfρfcp(uy)2−σeB02(u−u∞)(ρc)f+τ(DBTyCy+DTT∞(Ty)2)−Q0(T−Tf)(ρcp)f+1(ρc)f(K(T)Ty)y=0,(8)

and the corresponding boundary conditions are

−K∂T∂y=[T−Tf]h1,wheny=0,T=T∞,wheny→∞,(9)

where Tf refers to the fluid’s temperature, kinematic viscosity is represented by νf, σe represents the electrical conductivity, ρf is the fluid’s density, Q0 is the heat source parameter, DB denotes brownian diffusion, u∞ is the velocity of the free stream, k0 refers to the viscoelastic parameter, and B0 represents the magnetic parameter. In (8), the thermal conductivity K(T) is written as follows:

K(T)=K∞(1+εθ),(10)

Using the following similarity transformation [11] in Eq. (8):

η=−aνf,θ(η)=T−T∞Tf−T∞,u=axf′,v=−aνff,(11)

We get

(1+ε)θ+εθ′2+Pr(fθ′+Ecf″2+MEc(λ−f′)2+Nbθ′ϕ′+Ntθ′2+γθ)=0,(12)

θ′(0)=−γ1[1−θ(0)],θ(∞)=0.(13)

The ratio parameter is denoted by λ=ba, which is equal to the ratio of b to a. The Eckert number, denoted by Ec, is defined as uw2cpf(Tf−T∞), where u is the velocity, w is the enthalpy, specific heat is represented by cp the temperature of fluid is assigned as Tf and the free stream temperature is T∞. The Brownian motion parameter, Nb=τDB(Cw−C∞)νf, and the thermophoresis parameter, Nt=τDT(Tf−T∞)νfT∞. The local heat source/sink parameter is given by γ=Q0B02a(ρcp)f. The Prandt number is denoted by Pr=μ0cpK∞, while γ1 is the thermal number and is defined as νfa(hk).

2.2 Mass Transfer Equation

The mass transfer equation in fluid mechanics describes the transport of a chemical species, such as mass or concentration, in a fluid. It is a fundamental equation that governs a variety of processes, including heat transfer, chemical reactions, and diffusion. After boundary layer approximation, the mass transfer equation [11] takes the following form:

uCx+vCy=DBCyy+(DTT∞)Tyy(14)

and the corresponding boundary conditions are

−DBCy=[C−Cf]h2,wheny=0,C=C∞(x),wheny→∞,(15)

where C the concentration, DB is the diffusion coefficient, T is the temperature, the thermal diffusivity DT, the Brownian diffusion DB, and T∞ is the free-stream temperature.

The following similarity transformation [11] in Eq. (14):

η=−aνf,ϕ(η)=C−C∞Cf−C∞,u=axf′,v=−aνff,(16)

We get the following ODE with boundary conditions as

ϕ″+(NtNb)ϕ″+Pr Lefϕ′=0,(17)

ϕ′(0)=−γ2(1−ϕ(0)),ϕ(∞)=0.(18)

where Nt and Nb are the Brownian motion and thermophoresis parameters, respectively, the Prandtl number Pr, the concentration Biot number γ2, and the Lewis number Le based on the thermal diffusion coefficient.

2.3 Gyrotactic Microorganisms

The gyrotactic microorganisms equation in fluids describes the movement and behavior of microorganisms in response to fluid flows and gravitational forces. This equation is important in understanding the dynamics of aquatic ecosystems and the biogeochemical cycling of nutrients. The gyrotactic microorganism concentration equation [23] is expressed below:

uNx+vNy+bWc(Cf−C∞)(NCy)y=DmNyy,(19)

and the corresponding boundary conditions are

−DmNy=[N−Nf]h3,wheny=0,N=N∞,wheny→∞,(20)

where Dm is the diffusivity of microorganism, h3 is the microorganisms transfer coefficients and N∞ is the ambient microorganism concentration. Using the following similarity transformation [23] in Eq. (19):

η=−aνf,χ(η)=N−N∞Nf−N∞,u=axf′(η),v=−aνff(η),(21)

we get

χ″+Lb(fχ′)−Pe[ϕ″(χ+Ω)+χ′ϕ′]=0,(22)

χ′(0)=γ3(1−χ(0)),χ(∞)=0.(23)

where Lb=kρcpDm represents the bioconvection Lewis number, Pe=bWcDm the bioconvection Peclet number, and Ω=N∞N∞−N0 the concentration difference parameter.

2.4 Physical Quantities

Skin friction coefficient, Nusselt number, Sherwood number and Density number are defined below:

Cf=τwρuw2,Nux=xqwK(Tf−T0),Shx=xjwDB(Cf−C0),Dnx=xqnDm(Nf−N0),(24)

where

τw=[μfuy+k0ρf(uuxy+vuyy+2uxuy)]y=0,qw=−k(Ty)y=0,jw=−DB(Cy)y=0,qn=−Dm(Ny)y=0,(25)

Now, the dimensionless forms are defined below:

CfxRex=f″(0)+K(3f′(0)f″(0)−f(0)f‴(0)),NuxRex−12=−θ′(0),ShxRex−12=−ϕ′(0),DnxRex−12=−χ′(0).(26)

where Rex=uwxν represents the Reynolds number.

3  Solution Methodology

The governing equations given by Eqs. (6), (12), (17), (22) with boundary conditions specified in Eqs. (7), (13), (18), (23), respectively, were solved numerically using the built-in MATLAB function bvp4c. The bvp4c finite difference solver relies on the three-stage Lobatto IIIa collocation formula, ensuring a C1-continuous solution that uniformly maintains fourth-order accuracy throughout the integration interval. To manage errors and select an appropriate mesh, the solver employs the residual of the continuous solution. The integration interval is subdivided into smaller subintervals using a mesh of data points. The solver then tackles a comprehensive system of algebraic equations formed by combining boundary conditions and collocation requirements across these subintervals. Error assessment is carried out for each subinterval, and if the computed solution does not meet the predefined tolerance criteria, the solver iteratively adjusts the mesh. To initiate this iterative process, initial approximations of the solution at the mesh points are required. Achieving asymptotic behavior entails configuring the solution tolerance rate to be as stringent as 10−6. Consequently, the solver continues its iterations until the solution reaches a level of accuracy where the relative error falls within 10−6. The aforementioned equations converted into a first-order system of ODEs before applying this method as

y1=f,y2=f′,y3=f″,y4=θ,y5=θ′,y6=ϕ,y7=ϕ′,y8=χ,y9=χ′,(27)

To get the numerical answer, a new set of variables is defined in MATLAB as the following:

y1′=f′,y2′=f″,y3′=f‴=eαy4[−y1y3+y22−K(2y2y3−y1y3−y32)−(M+e−αy4δ)(λ−y2) −λ2+e−αy4αy5y3],(28)

y4′=θ′,y5′=θ″=11+εy4[−εy52−Pr(y1y5+Ecy32+MEc(λ−y2)2+Nby5y7+Nty52+γy4)],(29)

y6′=ϕ′,y7′=ϕ″=−LePry1y7−NtNby5′,(30)

y8′=χ′,y9′=χ″=−Lby1y9+Pe[y7′(y8+Ω)+y9y7],(31)

The boundary conditions are written in boundary value residual form, as required by bvp4c, as shown below:

y0(1)=0,y0(2)−1=0,y0(5)+γ1(1−y0(4))=0,y0(7)+γ2(1−y0(6)=0,y0(9)+γ3(1−y0(8)=0,y∞(2)−λ=0,y∞(4)=0,y∞(6)=0,y∞(8)=0.(32)

The physical quantities converted as below:

CfxRex=y3(0)+K(3y2(0)y3(0)−y3′(0)y1(0)),NuxRex−12=−y5(0),ShxRex−12=−y7(0),DnxRex−12=−y9(0).(33)

4  Numerical Results and Discussion

The numerical results from our work and research questions are thoroughly discussed in this section, along with their physical importance and applicability to a wider range of fluid dynamics and heat transport problems. Our findings cover a wide range of flow and transport processes in a porous viscoelastic fluid-saturated medium affected by magnetic fields, heat effects, and microorganism dynamics.

For different values of the ratio parameter λ, the value of the skin friction coefficient is calculated as mentioned in Table 1. To validate our findings, results are compared with the previous research.

Multiple tables show the outcomes of our numerical calculations. Tables 2–5 present the skin friction coefficient, local Nusselt number, local Sherwood number, and local density number of motile microorganisms, in that order. Skin friction coefficient parameter is vital for describing the drag force applied by the fluid to a solid surface and is used in many different engineering applications. Skin friction is observed to increase with increases in the ratio parameter λ, whereas declines are observed with increases in the viscosity parameter α, the local Darcy number δ, and the magnetic number M. The viscoelastic parameter K influences the flow characteristics near the heated sheet by affecting the boundary layer behavior. An increase in K leads to a reduction in the thickness of the velocity boundary layer region. This results in a decrease in fluid velocity near the solid surface. Additionally, the presence of the magnetic field in the presence of a porous surface significantly increases fluid velocity. It is observed that, on the specific value of M, fluid velocity can increase by approximately 25% to 45%. This suggests that magnetic effects play a crucial role in enhancing fluid motion under these conditions.

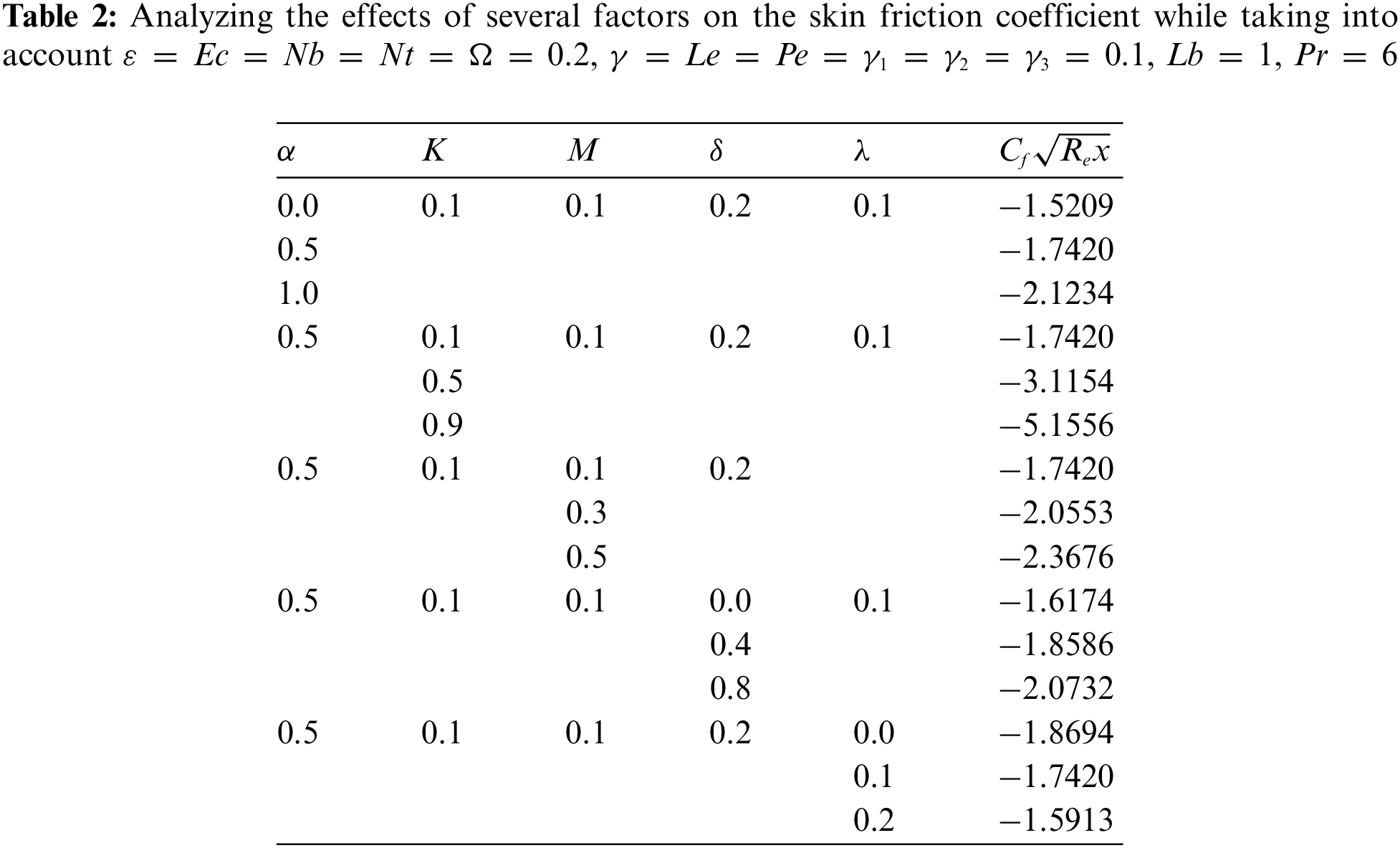
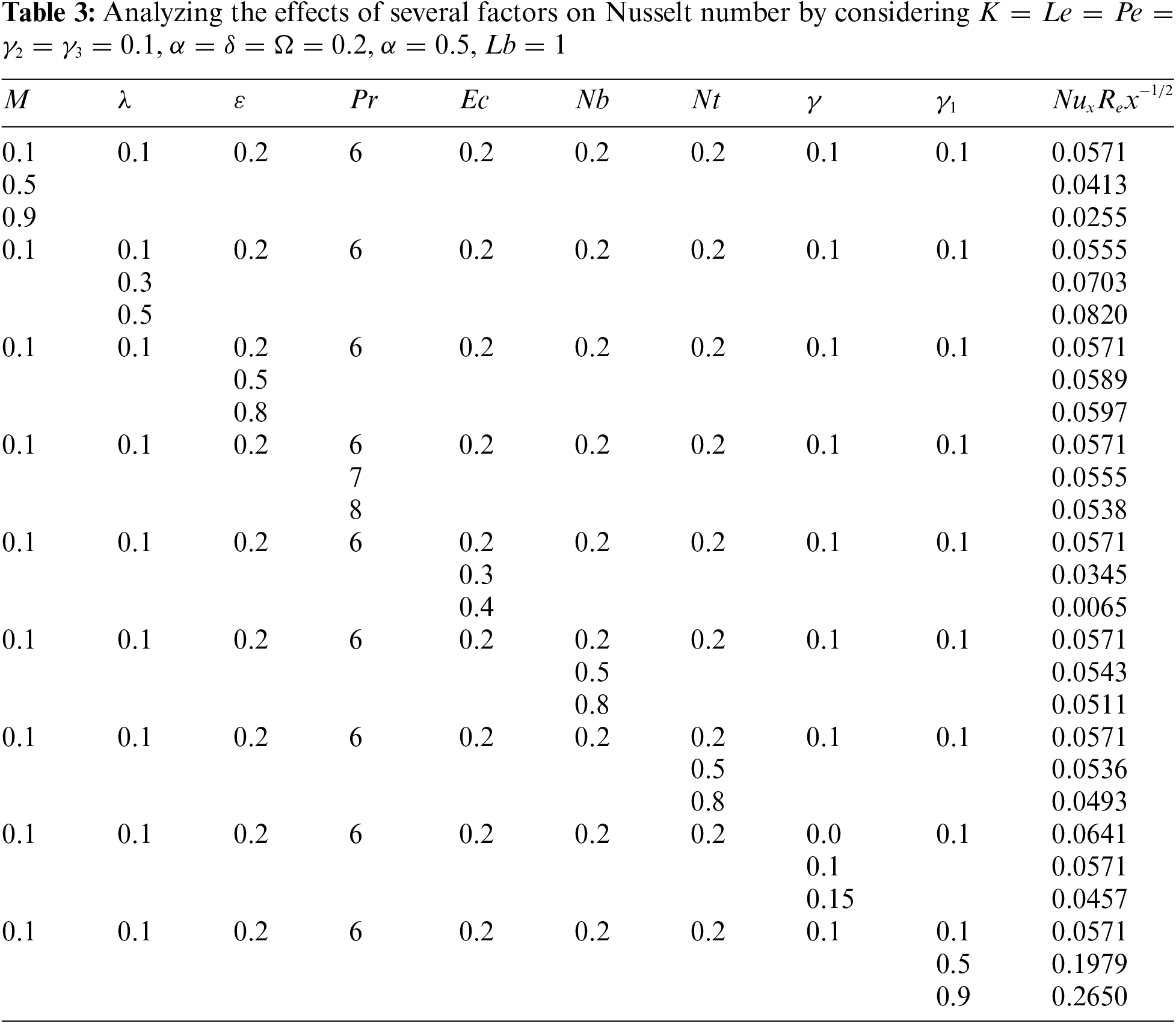
The convective heat transfer at a solid-fluid interface is represented by the local Nusselt number. It exhibits a decreasing trend with M the magnetic parameter, Ec the Eckert number, Nb the Brownian motion parameter, Nt the thermophoresis parameter, and the local heat source/sink parameter γ but rises with the ratio parameter λ, thermal conductivity parameter ε and thermal number γ1. Furthermore, with an increase in the Prandtl number Pr, we have seen a notable improvement of about 6% in fluid thermal conductivity.

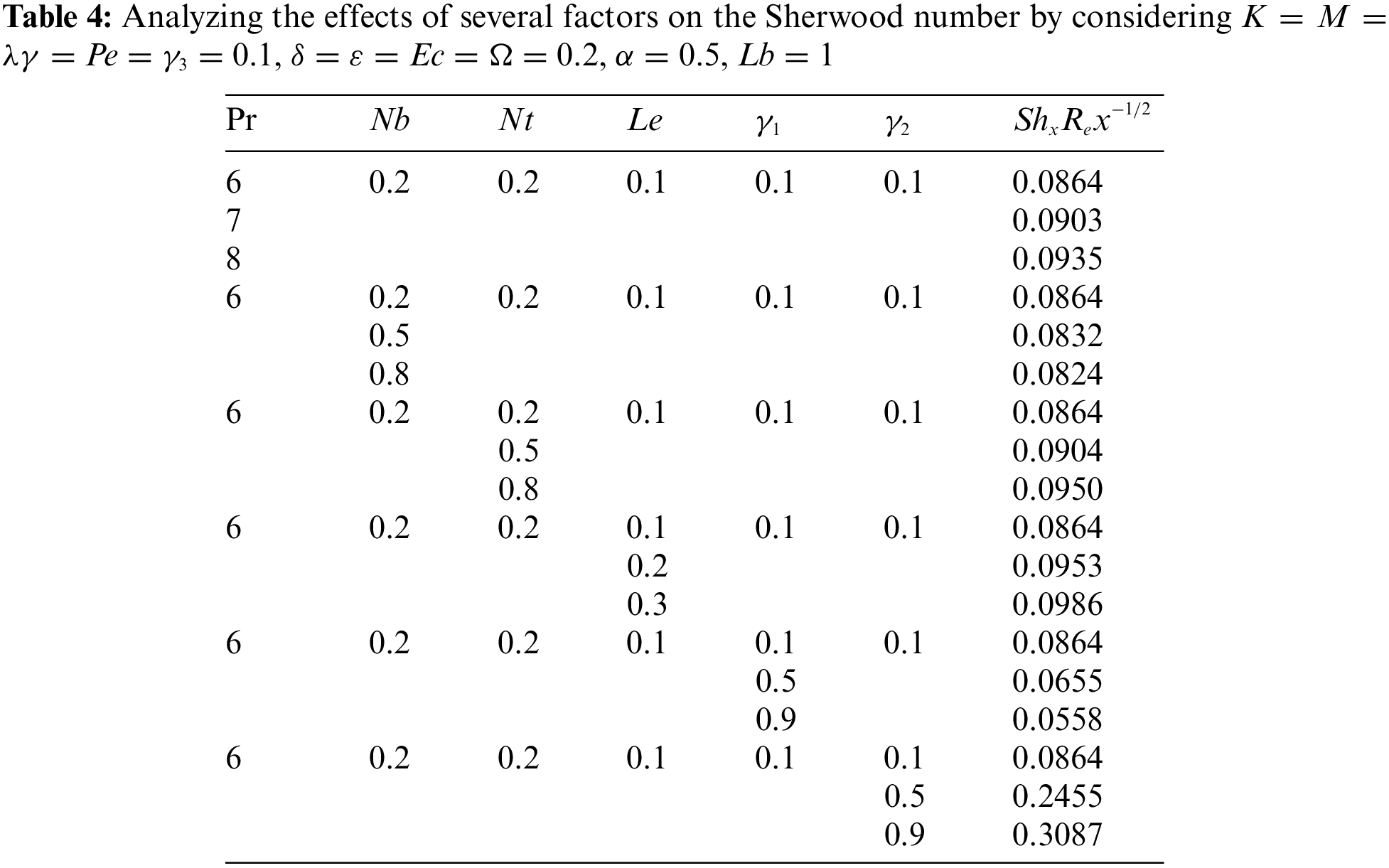
The convective mass transfer is represented by the local Sherwood number. For local Sherwood number, it is observed that it rises with Pr the Prandtl number, Le the Lewis number, Nt the thermophoresis parameter, and the concentration Biot number, but drops with Nb and γ1.

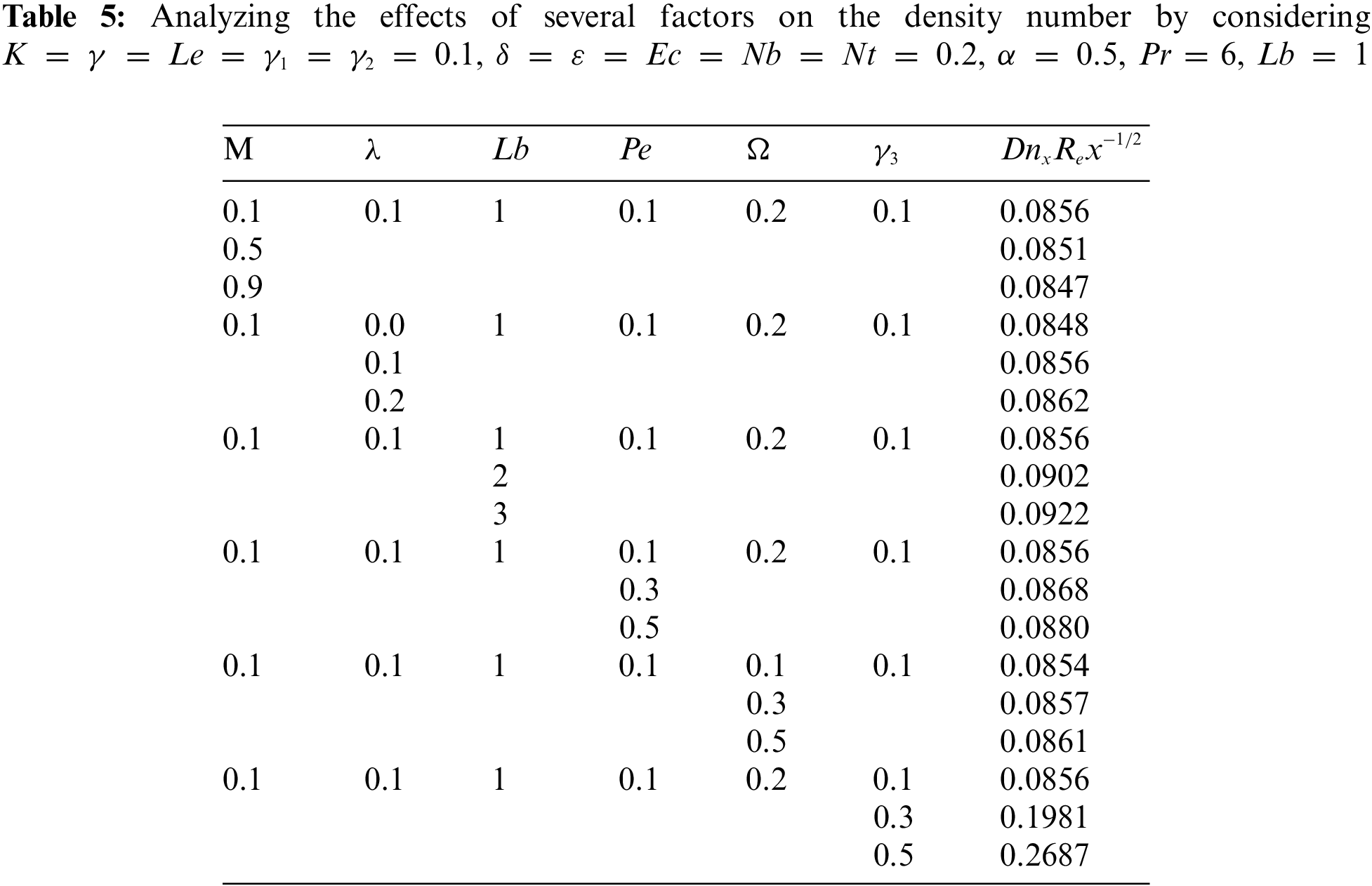
Finally, the local density number describes how the density of mobile microorganisms varies in the fluid. The behavior of this parameter has ramifications for environmental and biotechnological applications and is essential to understanding biological convection processes. It grows with λ, Lb, Pe, γ3, and ω, but decreases with the magnetic number M. So, the diffusibility of microorganisms tends to increase for all the parameters considered in the study, except for the magnetic parameter M.

Fig. 1 presents the diagrammatic depiction of the flow model. Figs. 2–5 present the velocity profile under varying conditions of the viscosity parameter α, magnetic number M, local Darcy number δ, and ratio parameter λ. Except for λ, it is shown that the fluid velocity drops as α, M, and δ rise. On the other hand, a rise in the value of lambda causes an increase in fluid velocity.

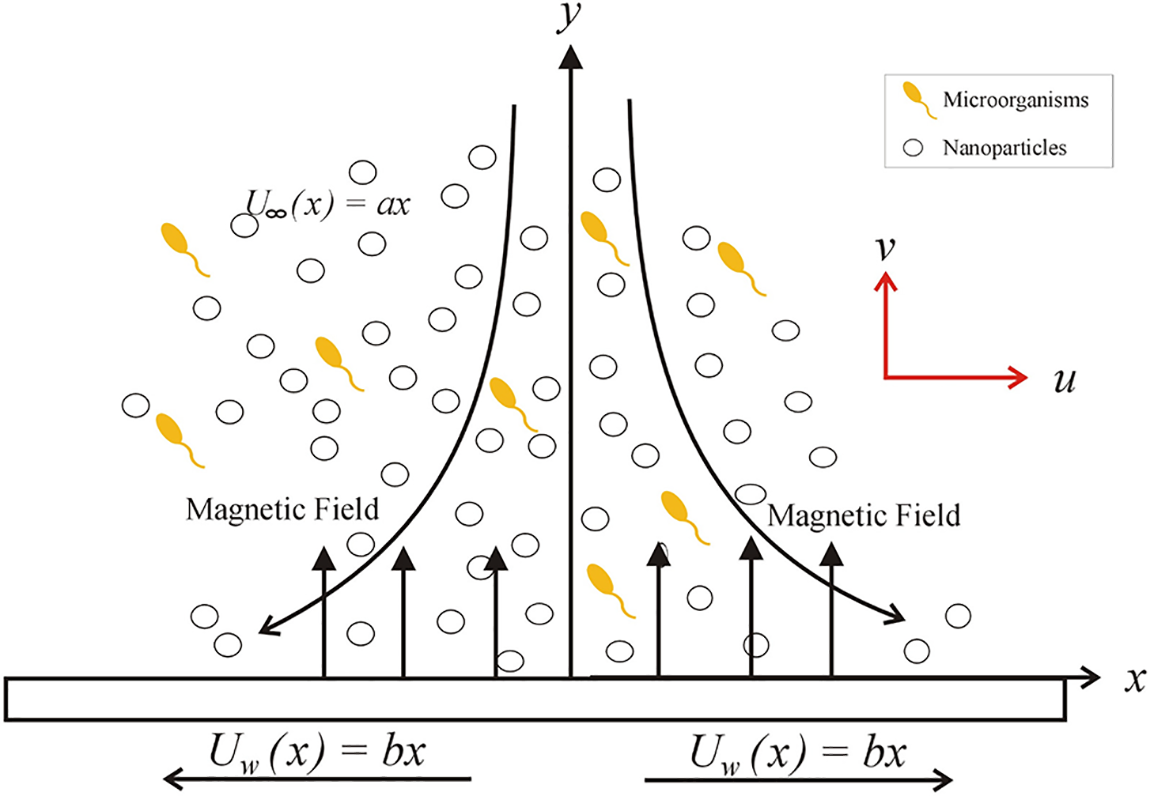
Figure 1: A diagrammatic depiction of the flow model

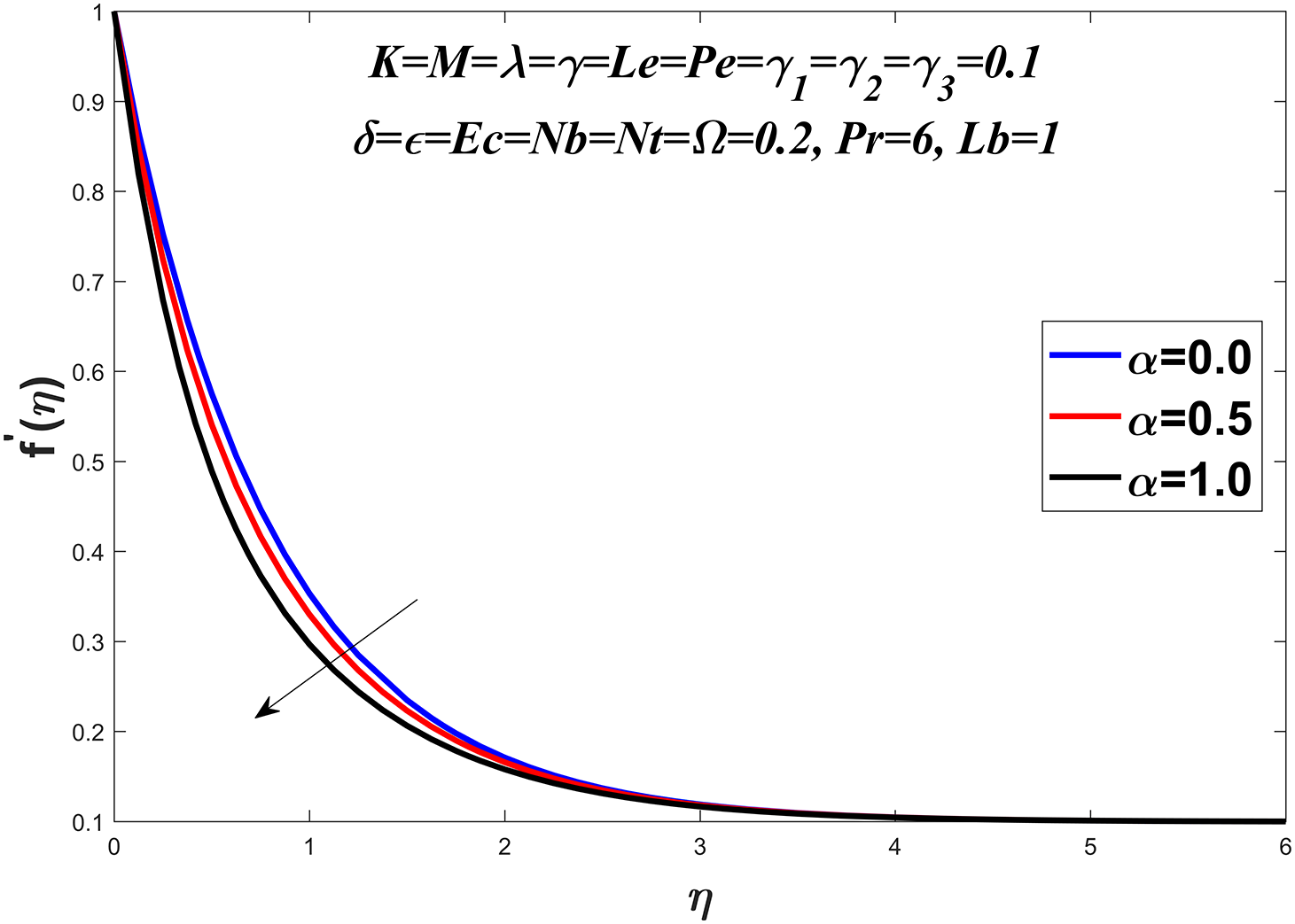
Figure 2: f′(η) against α

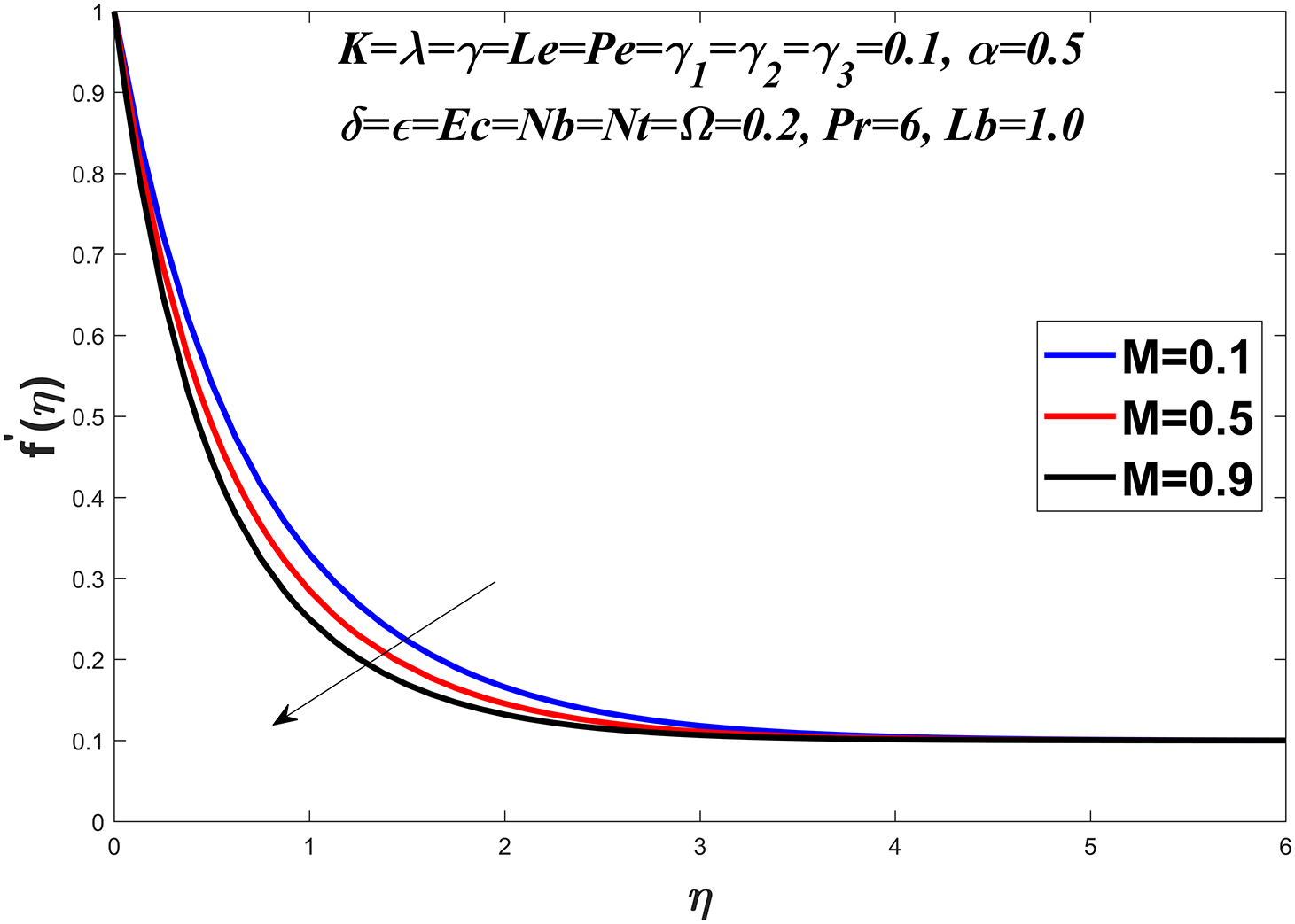
Figure 3: f′(η) against M

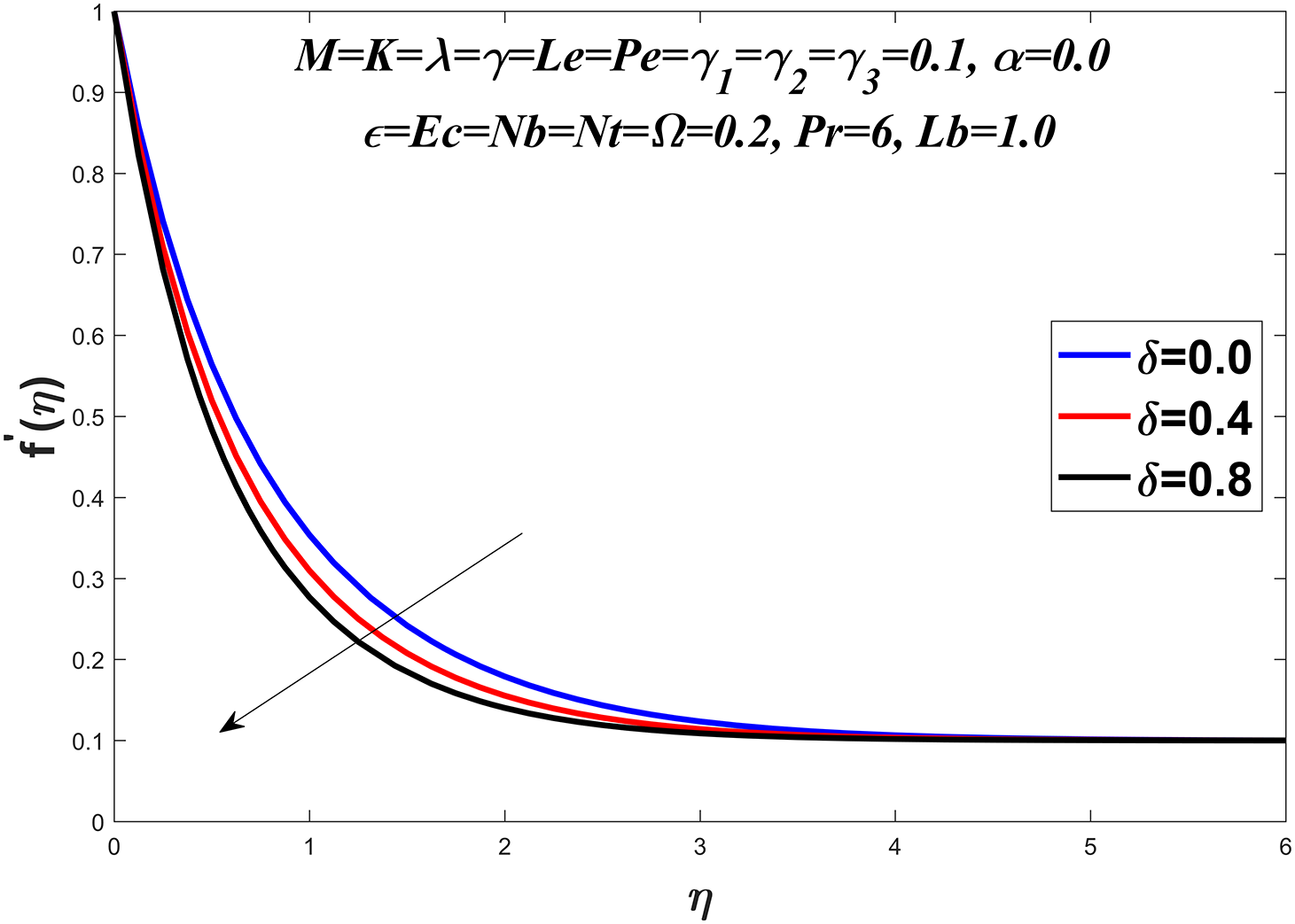
Figure 4: f′(η) against δ

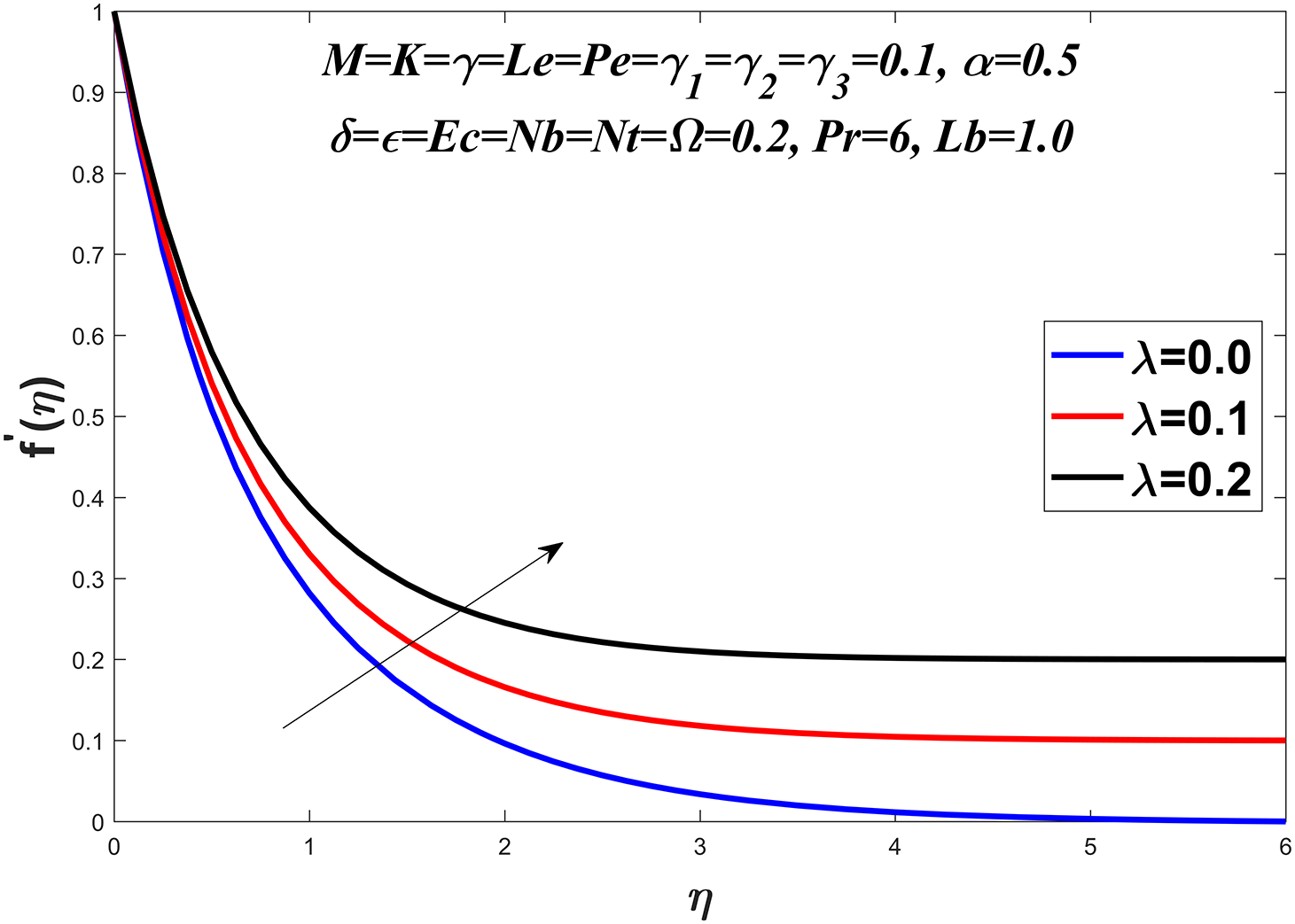
Figure 5: f′(η) against λ

The temperature profile is shown in Figs. 6–13 by considering a range of values for the Prandtl number Pr, the ratio parameter λ, the thermal conductivity parameter ε, and the Eckert number Ec, the Brownian motion parameter Nb, the thermophoresis parameter Nt, the thermal number γ1, and the magnetic number M. The temperature profile is affected by changes in the thermal conductivity parameter ε, as seen in Fig. 8. It was discovered that increasing the thermal conductivity parameter gave greater heat to neighboring liquid particles. Figs. 9–13 depict the effect of the Eckert number Ec, Brownian motion parameter Nb, thermophoresis parameter Nt, thermal number γ1, and magnetic number M on the temperature profile. The temperature profile grow as Ec, Nb, Nt, γ1, and M increased.

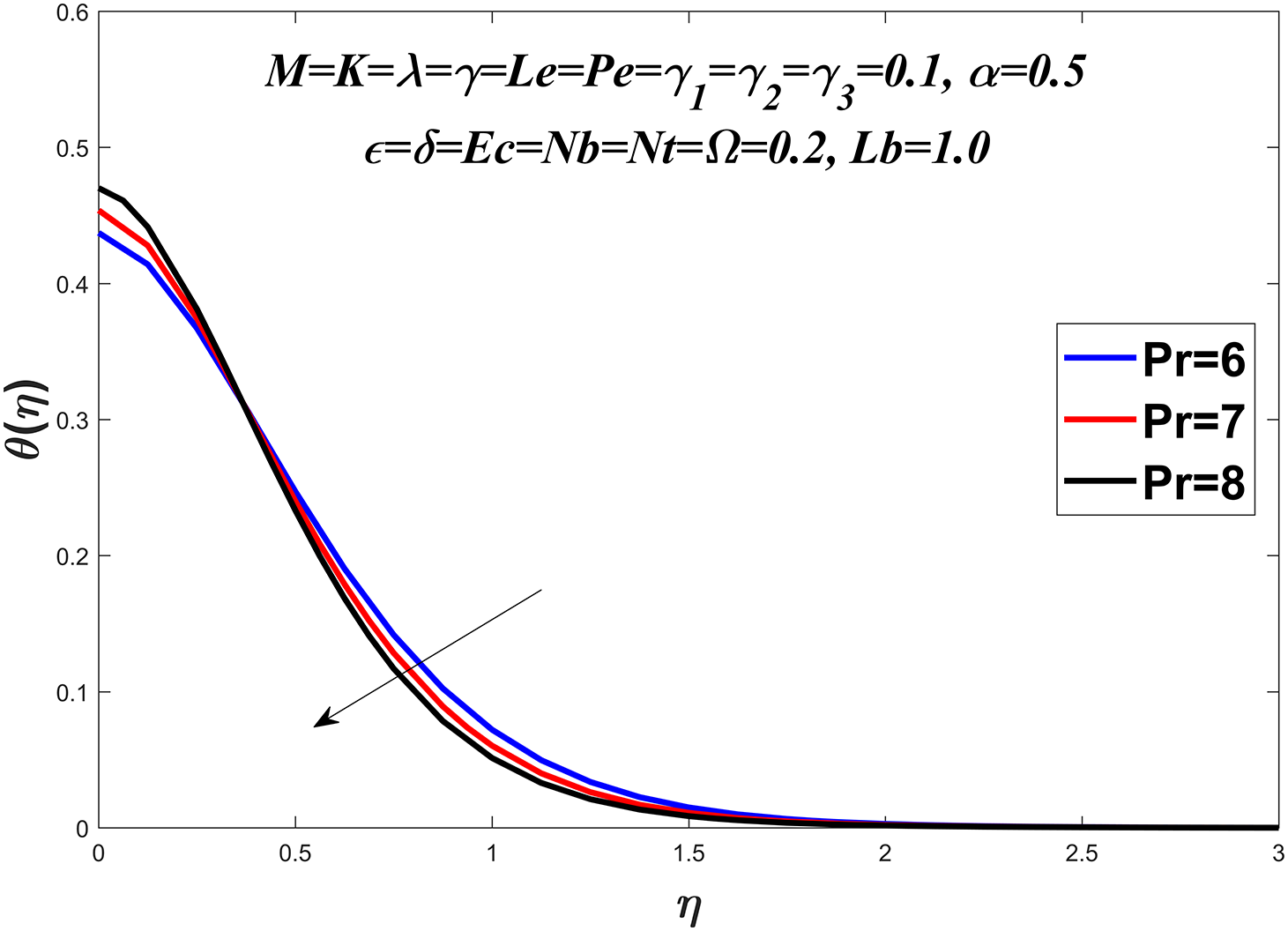
Figure 6: Temperature profile against Pr

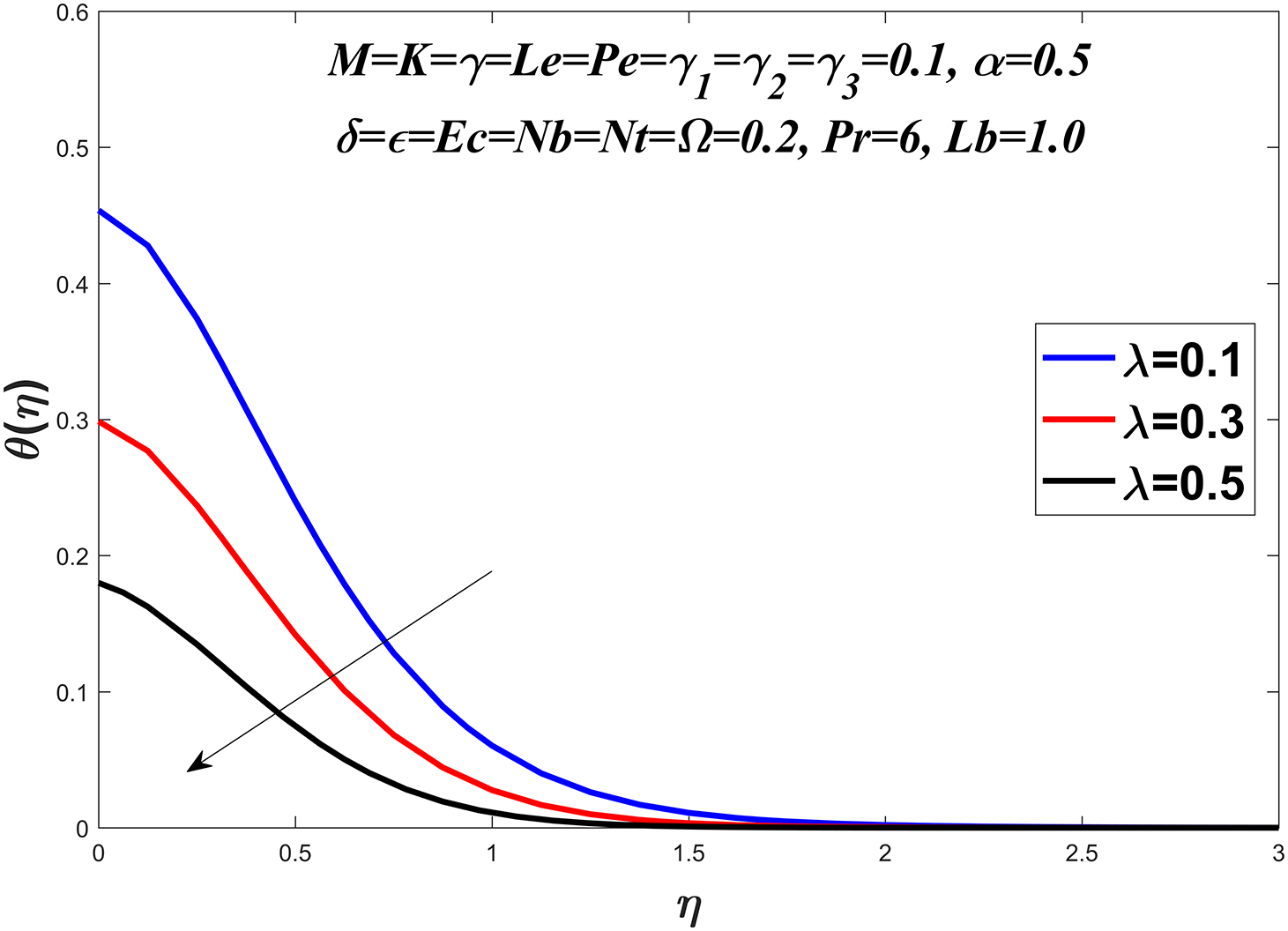
Figure 7: Temperature profile against λ

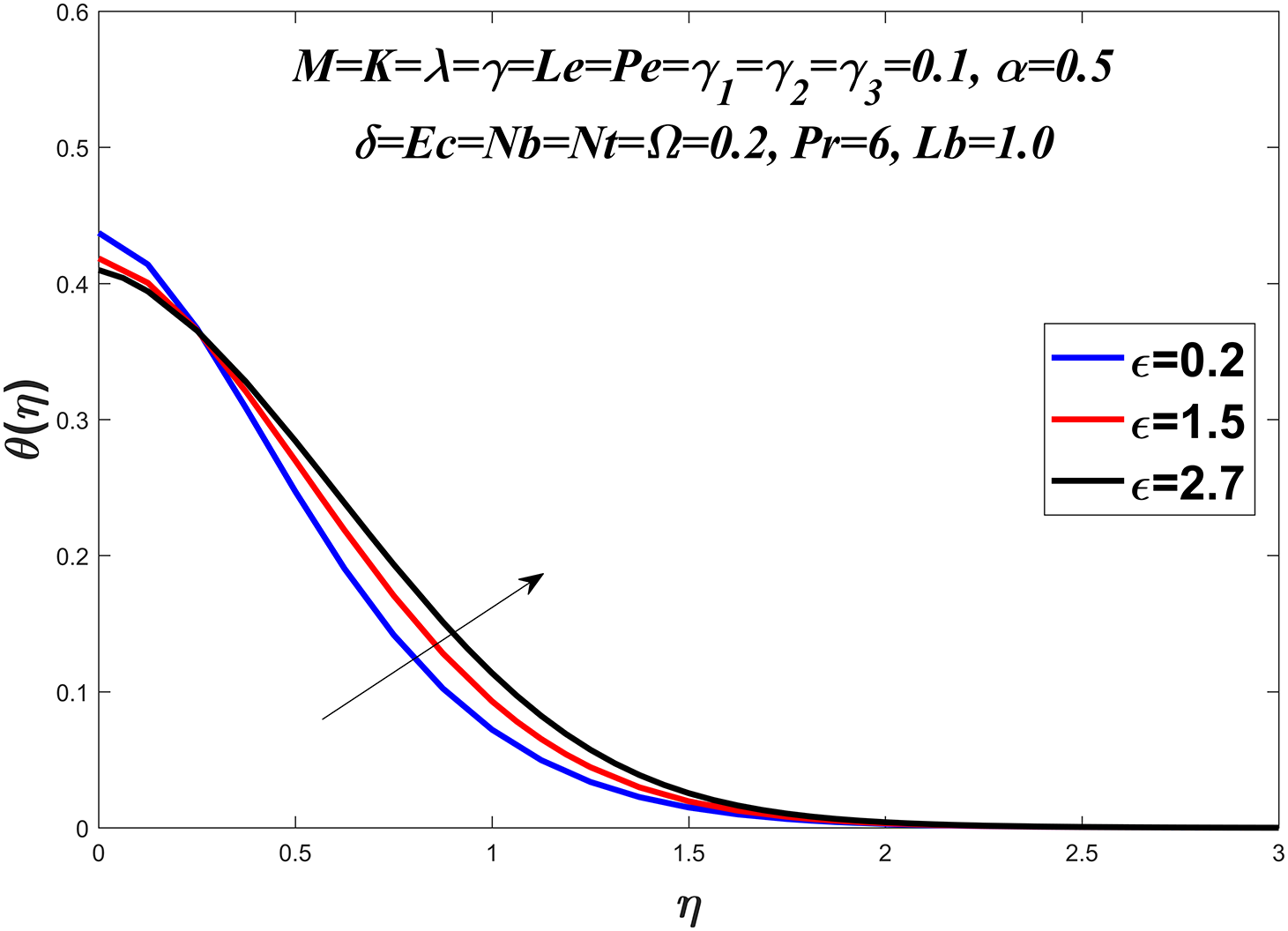
Figure 8: Temperature profile against ε

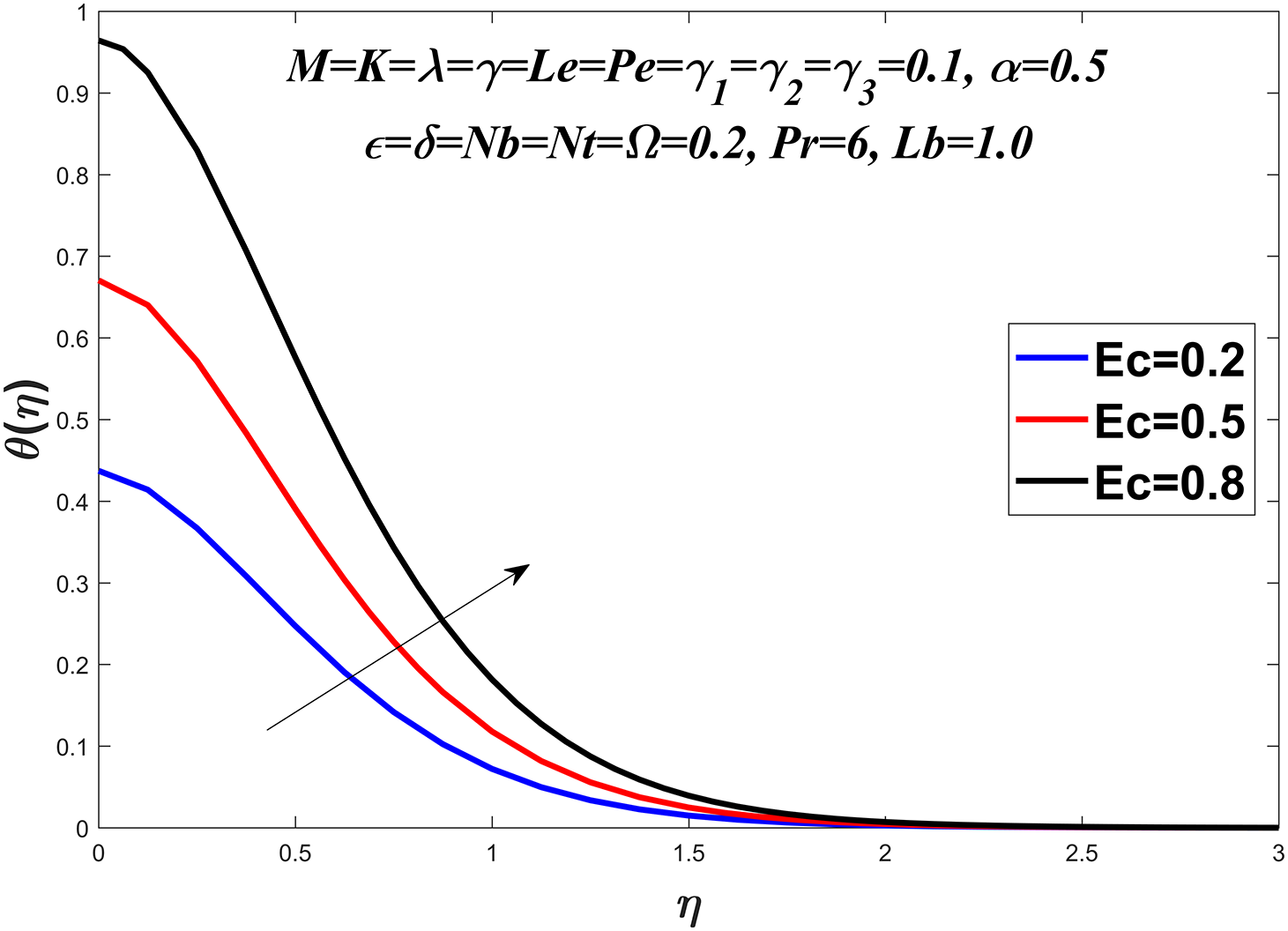
Figure 9: Temperature profile against Ec

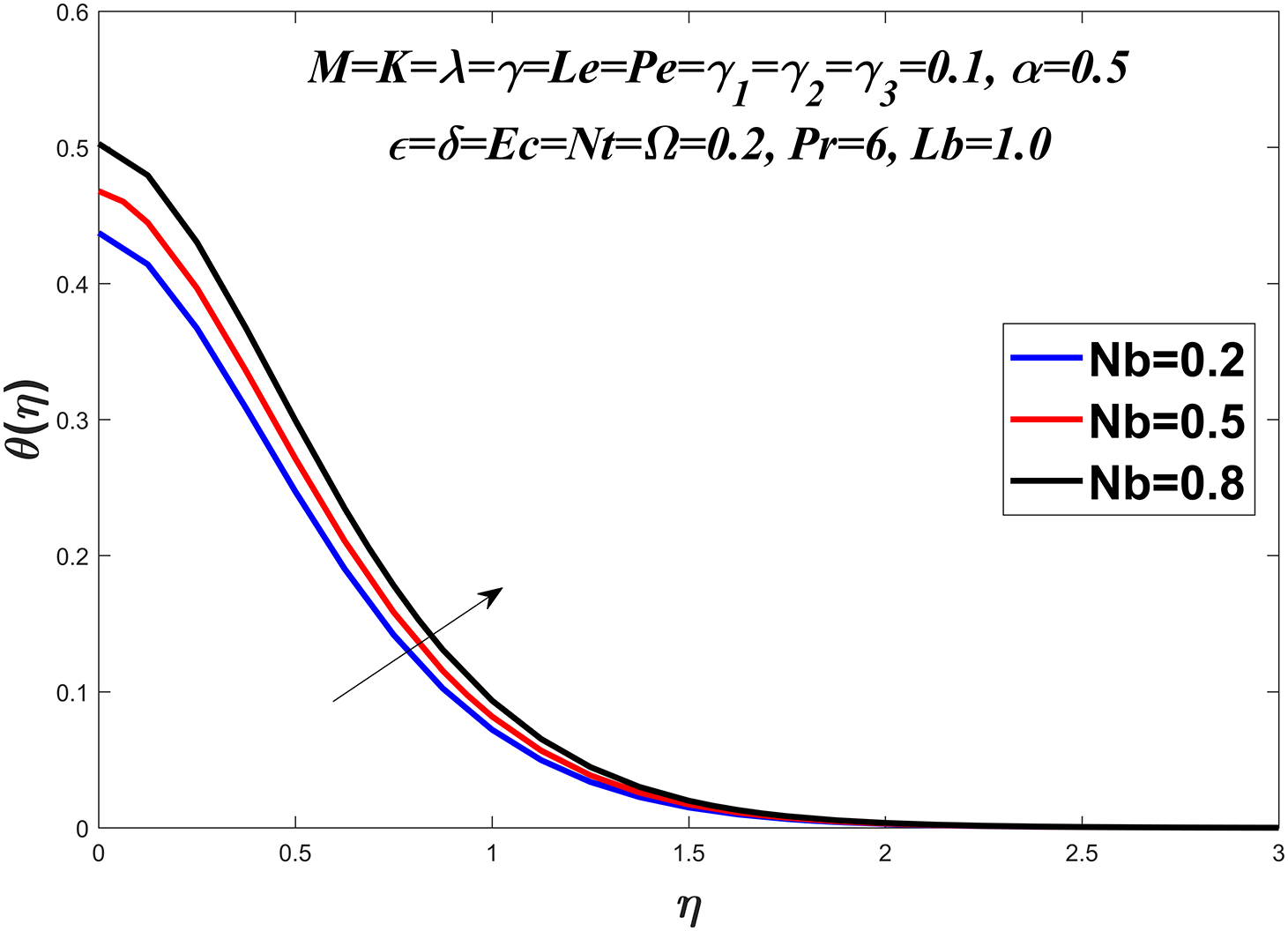
Figure 10: Temperature profile against Nb

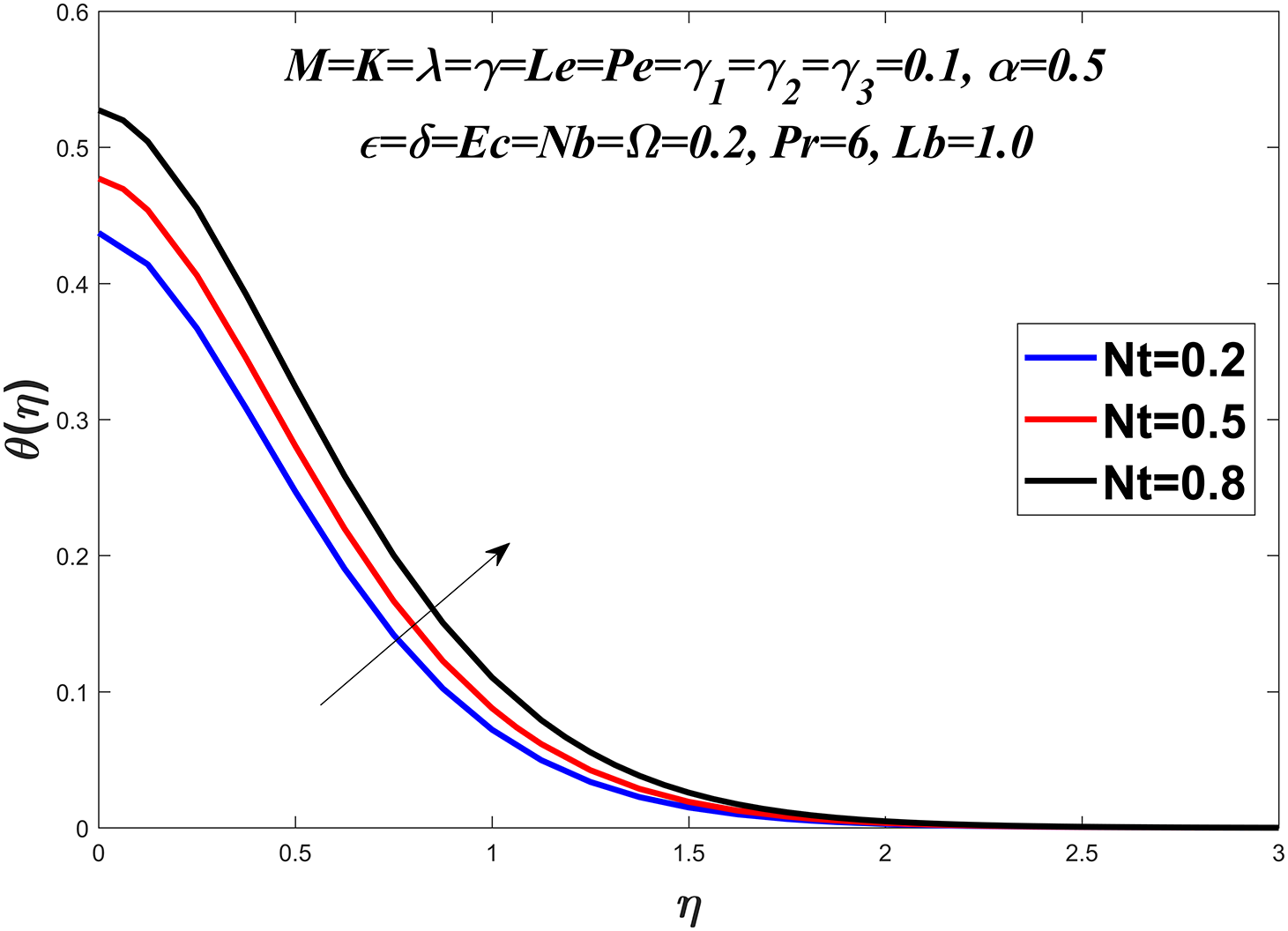
Figure 11: Temperature profile against Nt

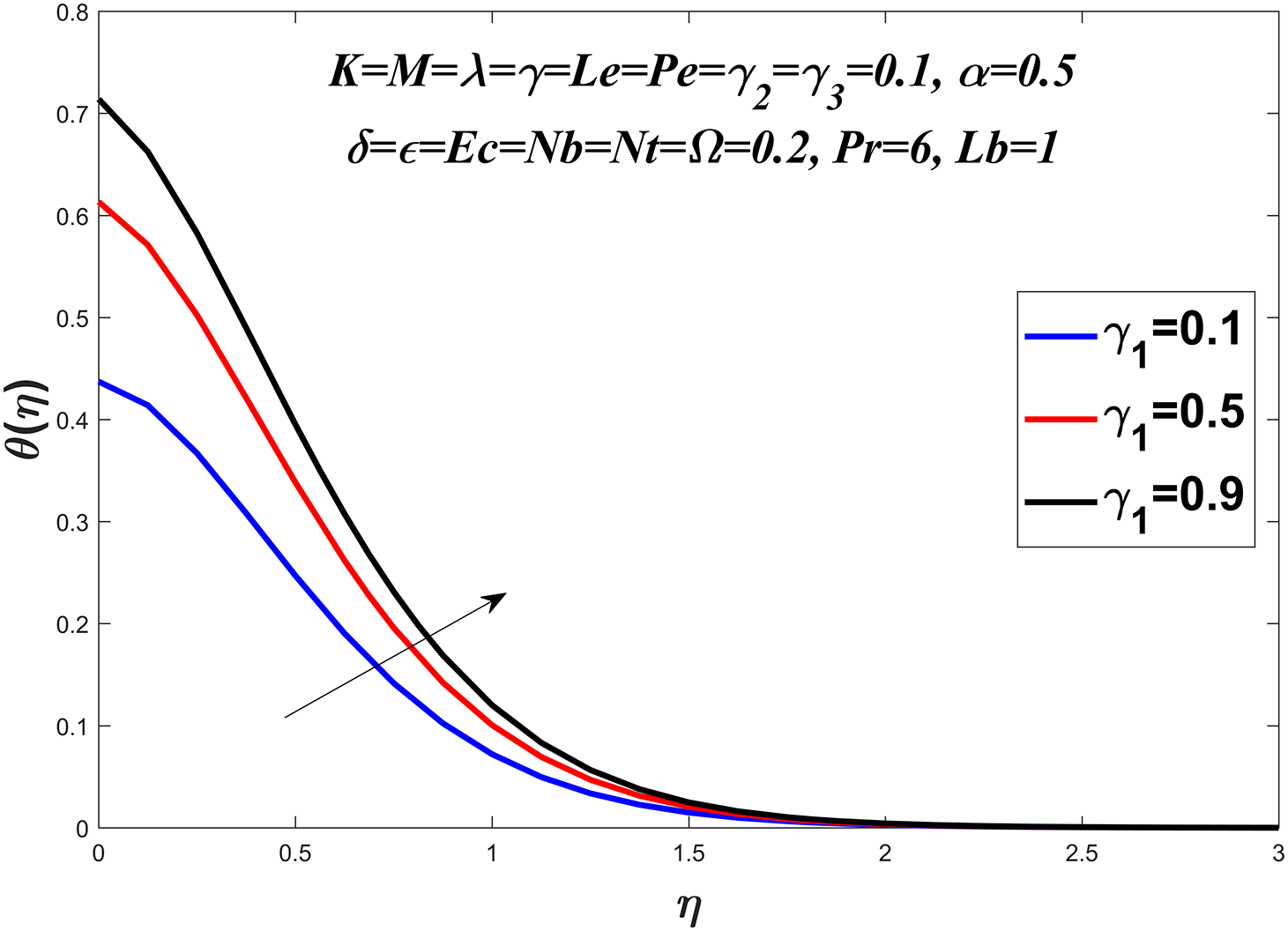
Figure 12: Temperature profile against γ1

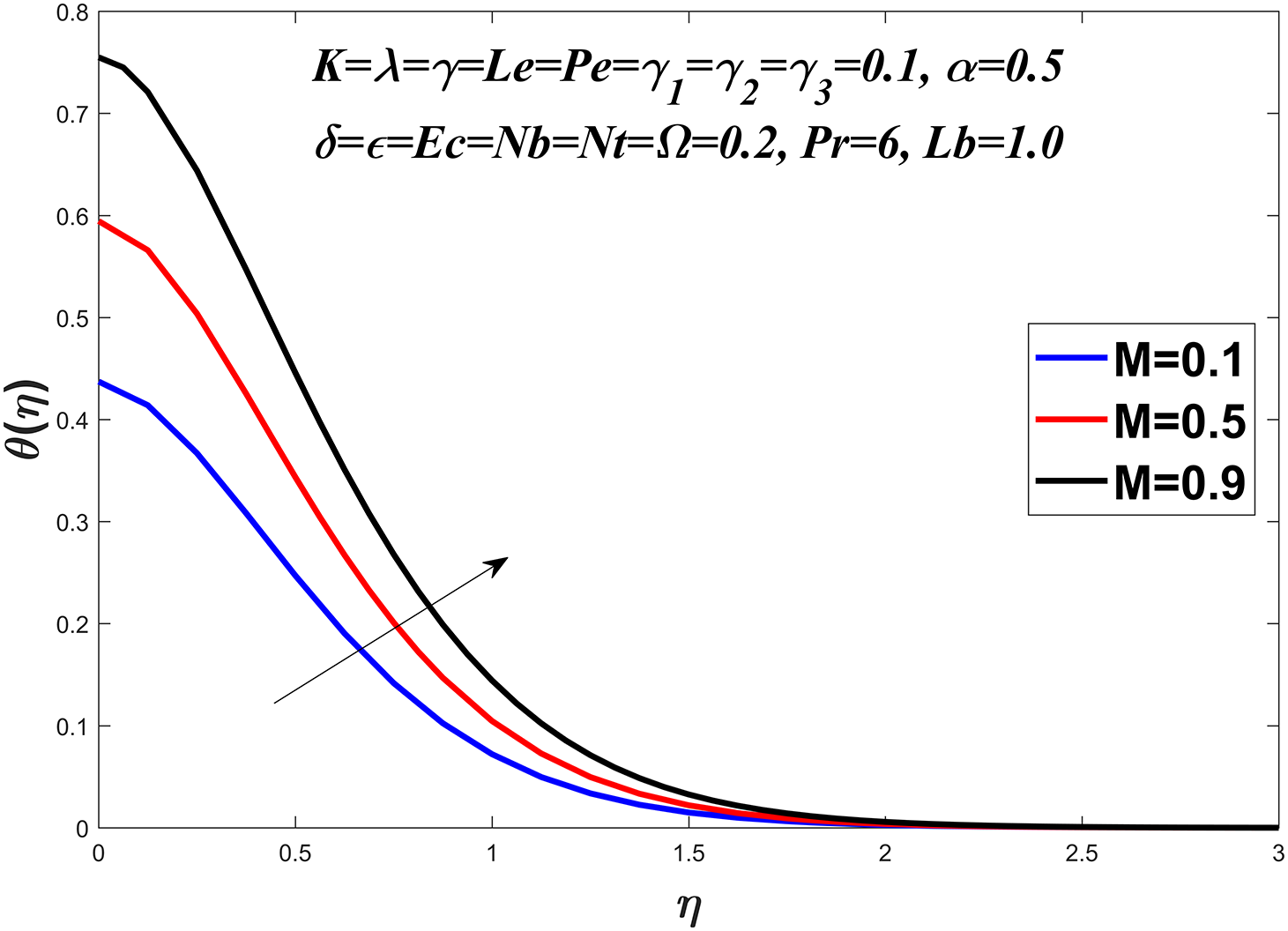
Figure 13: Temperature profile against M

Figs. 14 to 19 explore the concentration profile for various values of the Prandtl number Pr, the thermophoresis parameters Nb, the Brownian motion parameter Nt, the Lewis number Le, the thermal number γ1, and the concentration Biot number γ2. In Fig. 14, a decrease in the concentration field is observed when Pr goes from 6 to 8. Fig. 15 depicts the effect of the thermophoresis parameter Nb on the concentration profile, demonstrating that the concentration profile decreases as Nb increases. Fig. 16, on the other hand, demonstrates that the concentration field grows in response to Nt. Changes in the Lewis number Le are shown to have an impact on the concentration profile in Fig. 17. A drop in the concentration profile is shown to be accompanied by an increase in Le. Additionally, the thermal number γ1 and the concentration Biot number γ2 vary for various parameter values, as shown in Figs. 18 and 19. The concentration boundary layer expands in both cases.

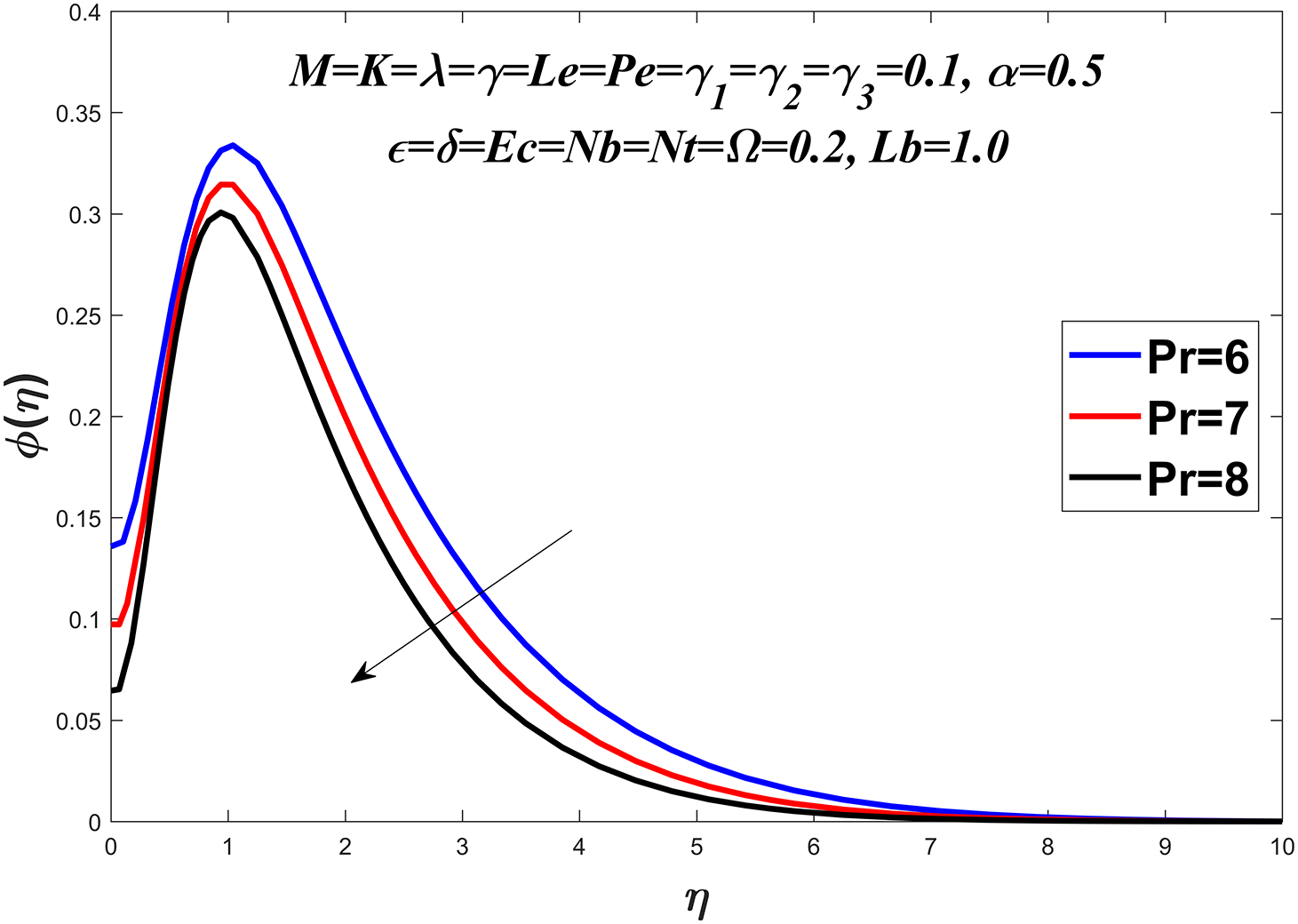
Figure 14: Concentration profile against Pr

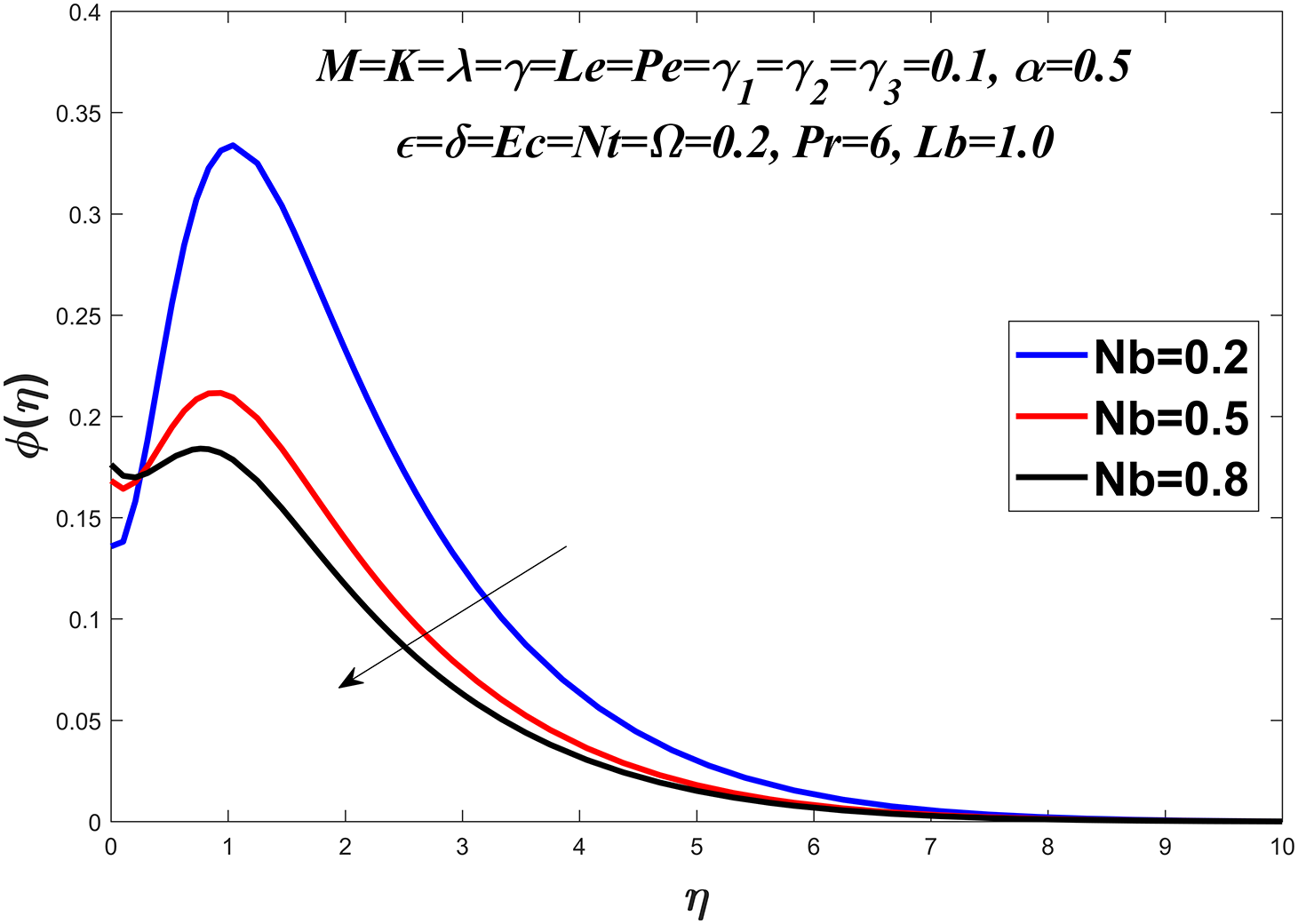
Figure 15: Concentration profile against Nb

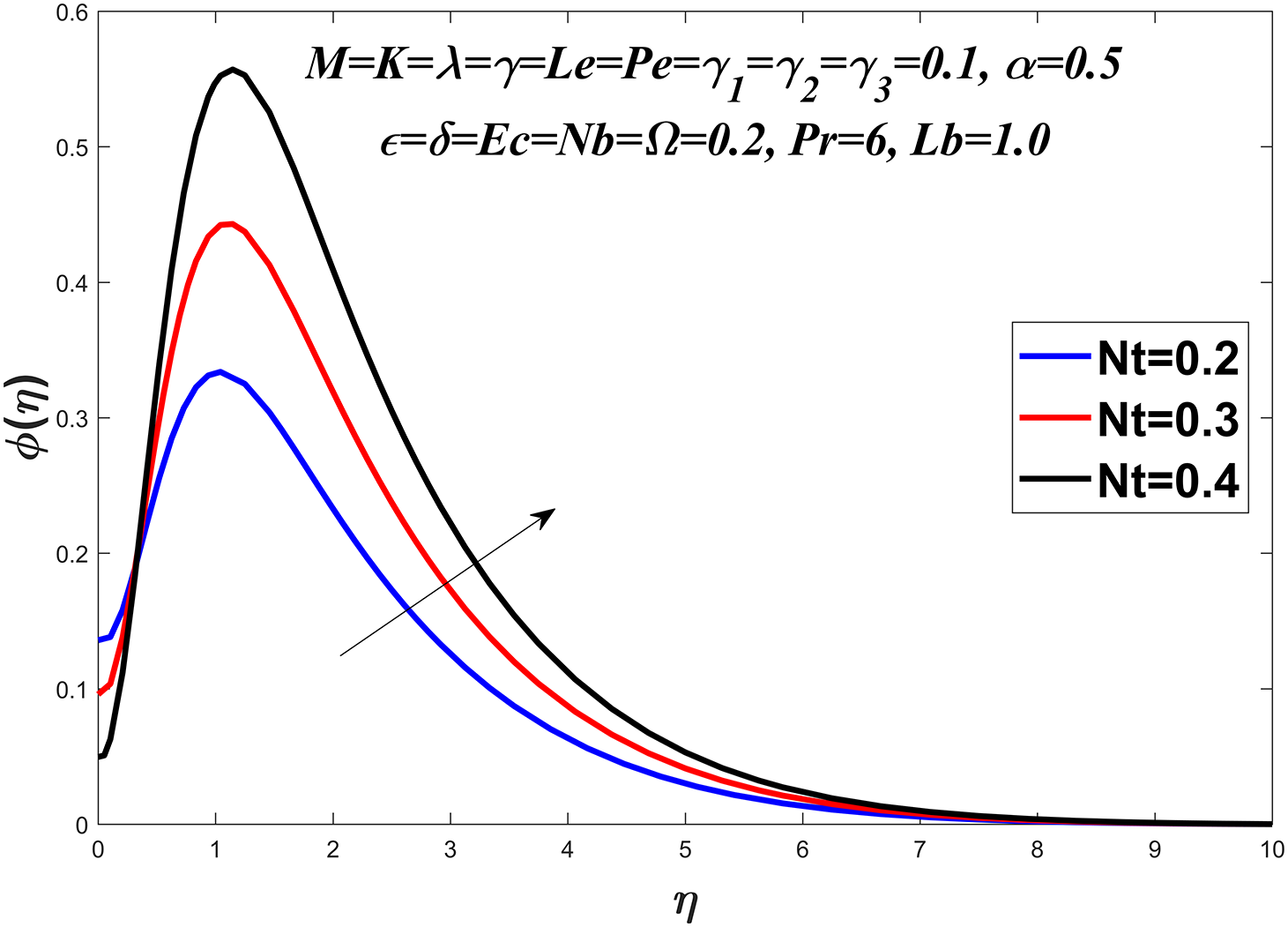
Figure 16: Concentration profile against Nt

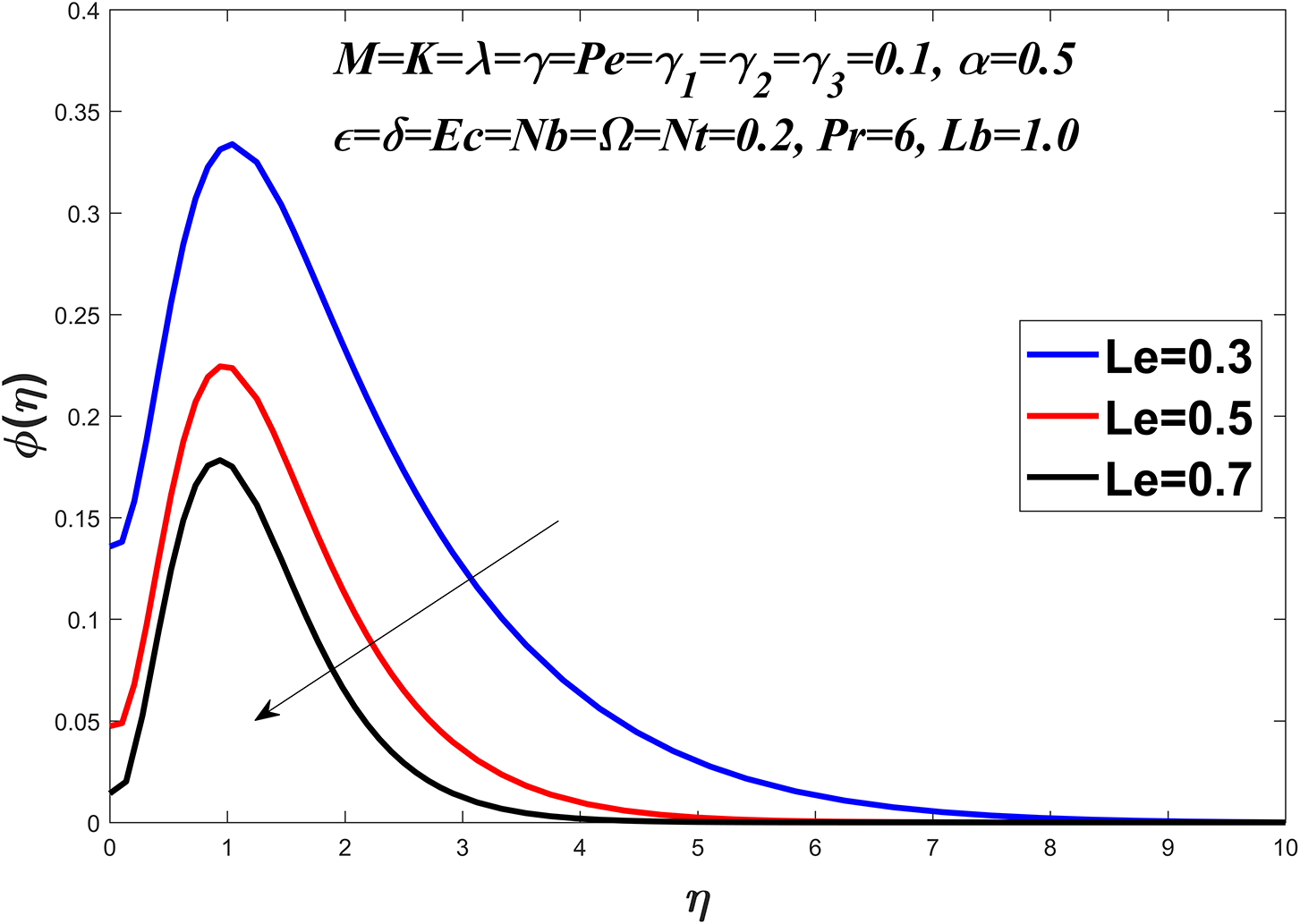
Figure 17: Concentration profile against Le

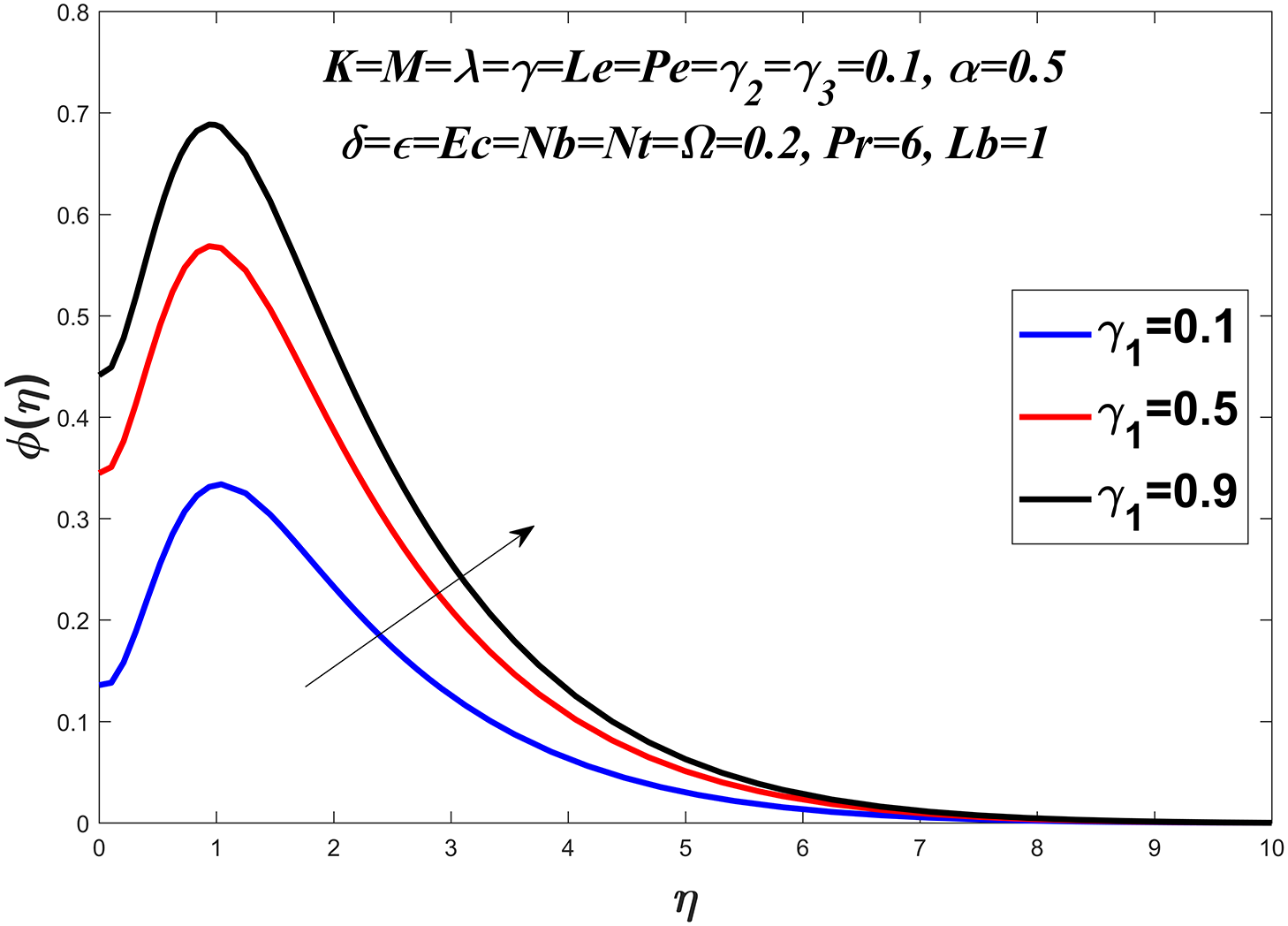
Figure 18: Concentration profile against γ1

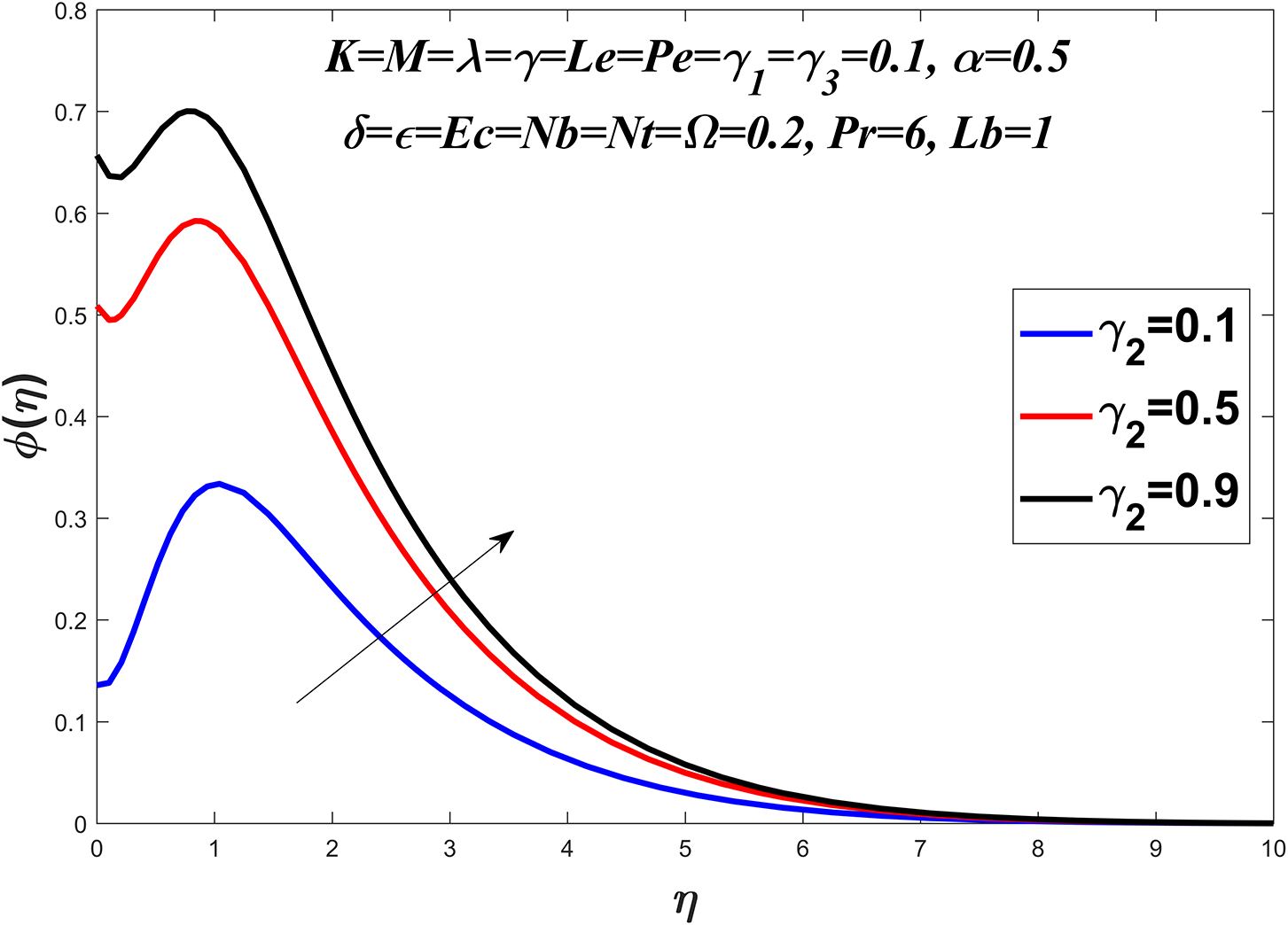
Figure 19: Concentration profile against γ2

Figs. 20 to 23 show the microorganism profile for various values of the bio-convection Lewis number Lb, concentration difference parameter Ω, magnetic number M, and density number γ3. It is seen that the motile density profile falls for Lb and Ω but grows for all other parameters, showing that the diffusivity of microorganisms increases for M and γ3.

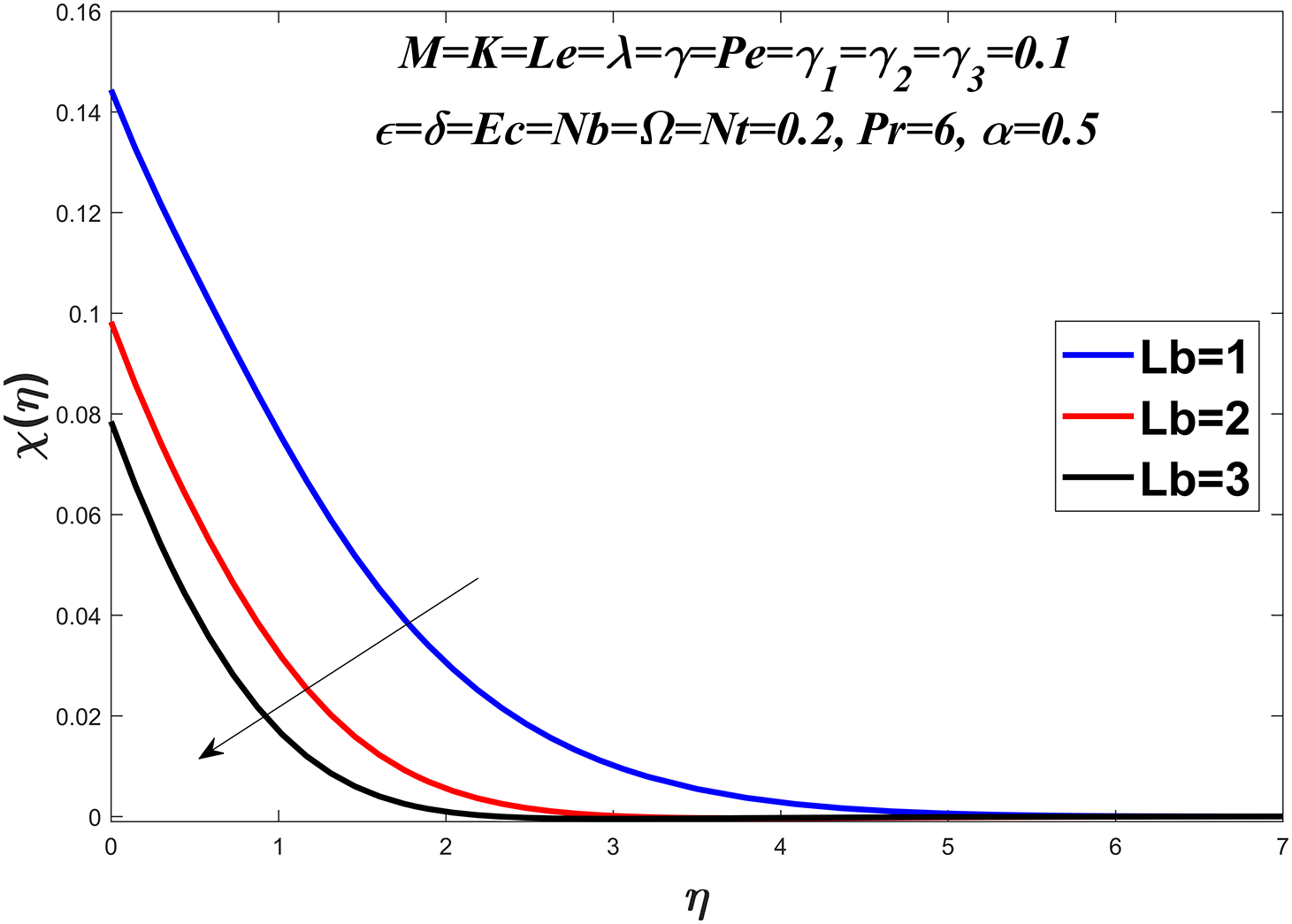
Figure 20: Microorganisms profile against Lb

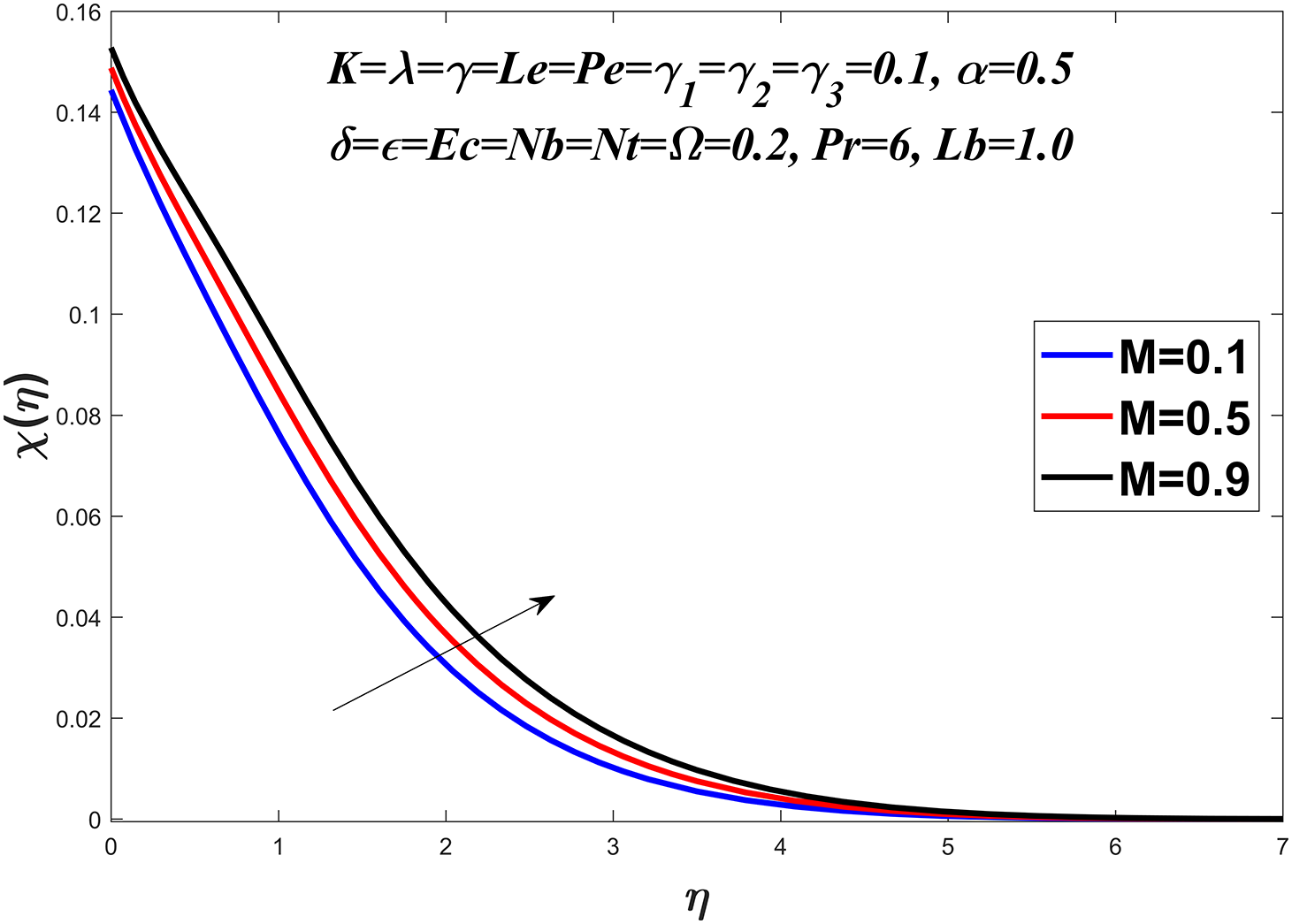
Figure 21: Microorganisms profile against M

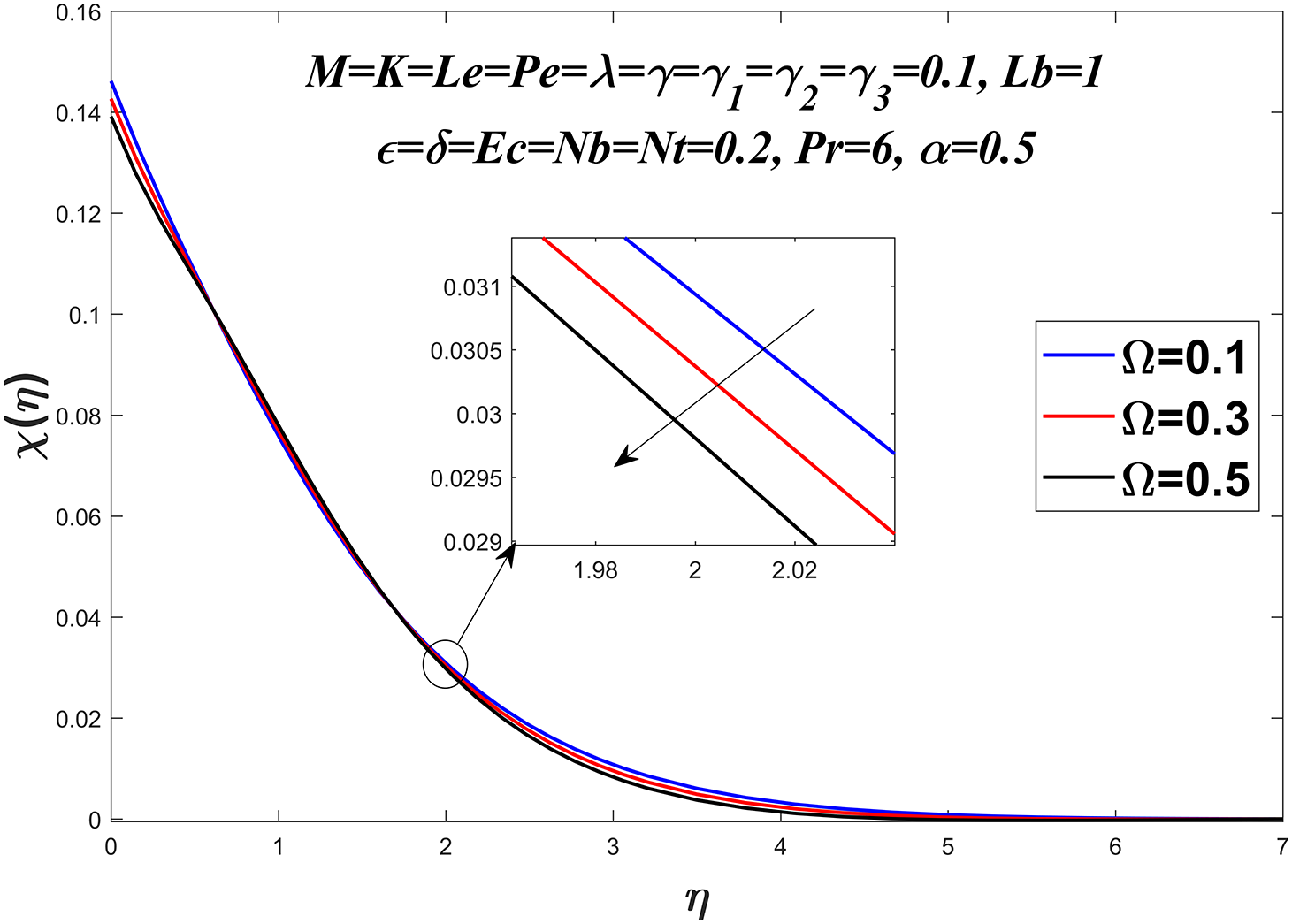
Figure 22: Microorganisms profile against Ω

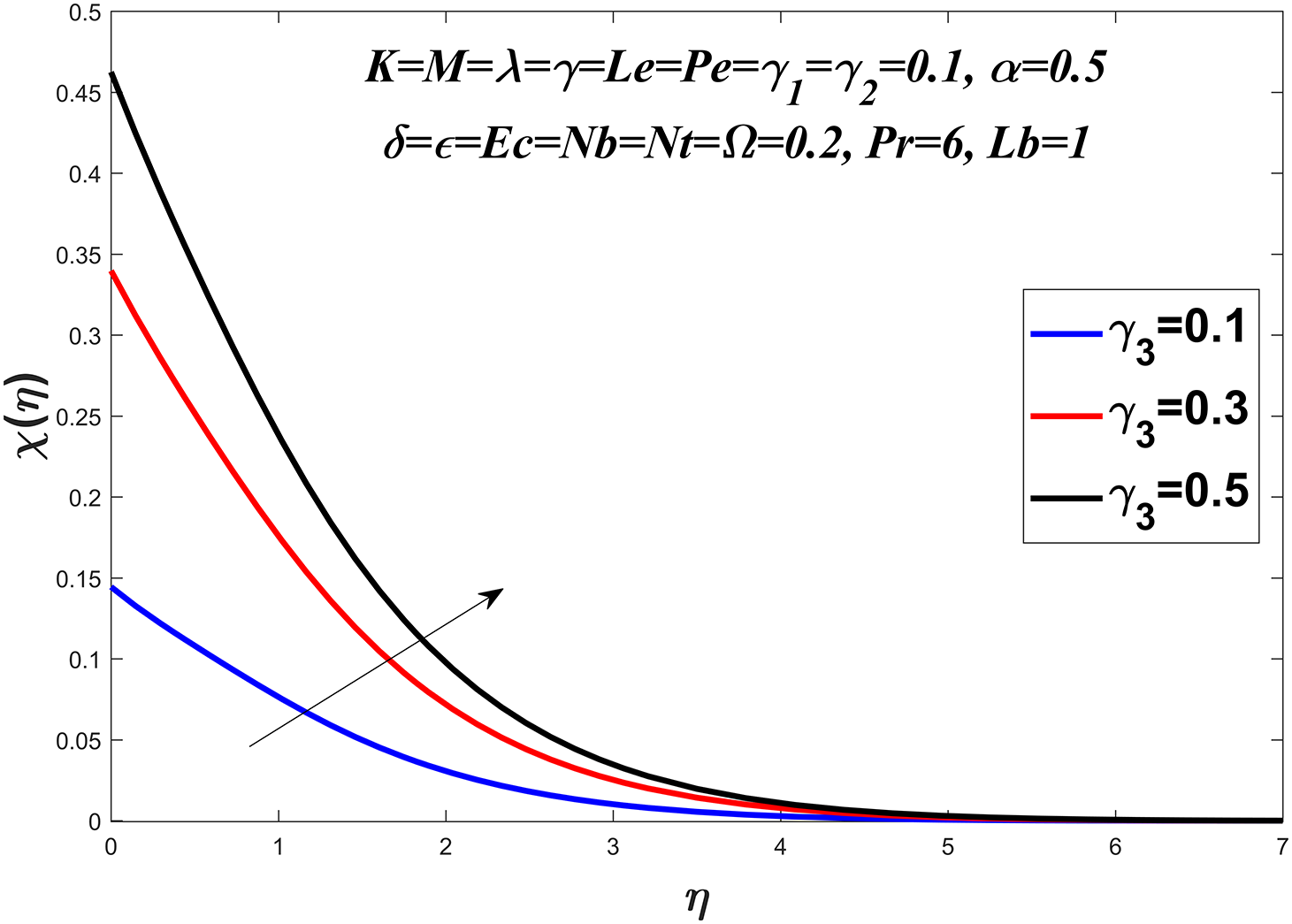
Figure 23: Microorganisms profile against γ3

In summary, our numerical findings illuminate the intricate interactions between different factors in fluid dynamics, heat transfer, mass transfer, and microorganism dynamics. Engineering, environmental science, and biotechnology can all benefit from these discoveries. For better performance and efficiency, fluid systems can be designed and optimized using the observed trends and dependencies.

Our findings serve as the foundation for more advanced research in this subject. These fundamental ideas, we feel, are critical for building a comprehensive understanding of the phenomena under investigation. Future research can build on these foundations to investigate more complex scenarios and solve specific engineering problems.

5  Conclusion

This paper gives the following conclusions based on the analysis and discussion of the results after conducting study on the two-dimensional flow stagnates at x=0 over an extended heated elastic sheet under radiative heat transfer with nonlinear characteristics, variable viscosity, and MHD in a porous medium. Moreover, we extend our analysis by considering convective boundary conditions and introducing the gyrotactic microorganisms equation to capture microorganism behavior influenced by fluid flow.

1.    Various parameters such as λ, α, K, M, and δ influence the skin friction coefficient. An increase in λ causes the fluid speed to decrease, whereas an increase in α, K, M, or δ causes it to increase. Our investigations reveal that, contingent upon the magnetic parameter M, the presence of a porous medium leads to a substantial enhancement in fluid velocity, ranging between approximately 25% and 45%.

2.    Fluid temperature is affected by parameters such as M, Ec, Nb, Nt, γ, λ, Pr, ε, and γ1. An increase in M, Ec, Nb, Nt, or γ causes a reduction in fluid temperature, whereas a rise in λ, ε, or γ1 causes an increase. An increase in the Prandtl number (Pr) results in a noticeable improvement of around 6% in fluid thermal conductivity.

3.    The concentration boundary layer thickness is determined by parameters such as Pr, Nb, Le, γ2, Nt, and γ1. An increase in Pr, Nt, Le, or γ2 causes the concentration boundary layer thickness to grow, whereas an increase in Nb or γ1 causes it to drop.

4.    The local density number is influenced by parameters such as λ, Lb, Pe, γ3, Ω, and M. An increase in λ, Lb, Pe, γ3, or Ω leads to an increase in the local density number, while an increase in M results in a decrease.

These findings provide insight into the behavior of fluid flow under various physical conditions and can be used to optimize industrial processes. The mathematical modeling approach used in this study can be applied to other related problems to gain a better understanding of fluid dynamics in various industrial applications.

Acknowledgement: The authors extend their sincere gratitude to the reviewers for their helpful suggestions, which significantly enhanced the quality and presentation of this paper.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Conceptualization, M.A.U.R. (Muhammad Abaid Ur Rehman) and M.A.F. (Muhammad Asif Farooq); methodology, M.A.U.R.; software, M.A.U.R.; validation, M.A.U.R. and M.A.F.; formal analysis, M.A.U.R. and A.H.M. (Ahmed M Hassan); investigation, M.A.U.R. and M.A.F.; resources, A.H.M., M.A.F.; data curation, M.A.U.R.; writing original draft preparation, M.A.U.R.; writing review and editing, M.A.U.R. and A.H.M.; visualization, M.A.U.R., A.H.M. and M.A.F.; supervision, M.A.F.; funding acquisition, A.H.M. All authors have read and agreed to the published version of the manuscript.

Availability of Data and Materials: The data generated in this study can be made available by corresponding author following a request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Choi, S., Eastman, J. (1995). Enhancing thermal conductivity of fluids with nanoparticles. 1995 International Mechanical Engineering Congress and Exhibition, vol. 231, pp. 91–105. San Francisco, CA, USA. [Google Scholar]

2. Kuznetsov, A. V., Nield, D. A. (2010). Natural convective boundary-layer flow of a nanofluid past a vertical plate. International Journal of Thermal Sciences, 49(2), 243–247. [Google Scholar]

3. Shaw, S., RamReddy, C., Murthy, P. V. S. N., Sibanda, P. (2016). Dual solutions for homogeneous-heterogeneous reactions on stagnation point flow over a stretching/shrinking sheet in a non-darcy porous medium saturated with a nanofluid. Journal of Nanofluids, 5(3), 408–415. [Google Scholar]

4. Roberts, P. H. (1967). An introduction to magnetohydrodynamics. London: Longmans. [Google Scholar]

5. Davidson, P. A. (2002). An introduction to magnetohydrodynamics. Cambridge: Cambridge University Press. [Google Scholar]

6. Qamar, I., Farooq, M. A., Irfan, M., Mushtaq, A. (2022). Insight into the dynamics of electro-magneto-hydrodynamic fluid flow past a sheet using the galerkin finite element method: Effects of variable magnetic and electric fields. Frontiers in Physics, 10, 1002462. [Google Scholar]

7. Anuar, N. S., Bachok, N., Pop, I. (2020). Cu-Al2O3/water hybrid nanofluid stagnation point flow past MHD stretching/shrinking sheet in presence of homogeneous-heterogeneous and convective boundary conditions. Mathematics, 8(8), 1237. [Google Scholar]

8. Zainal, N. A., Nazar, R., Naganthran, K., Pop, I. (2020). Unsteady three-dimensional MHD non-axisymmetric homann stagnation point flow of a hybrid nanofluid with stability analysis. Mathematics, 8(5), 784. [Google Scholar]

9. Nadeem, S., Khan, M. R., Khan, A. U. (2019). MHD stagnation point flow of viscous nanofluid over a curved surface. Physica Scripta, 94(11), 115207. [Google Scholar]

10. Megahed, A. M., Ghoneim, N. I., Reddy, M. G., El-Khatib, M. (2021). Magnetohydrodynamic fluid flow due to an unsteady stretching sheet with thermal radiation, porous medium, and variable heat flux. Advances in Astronomy, 2021, 1–9. [Google Scholar]

11. Ali, B., AlBaidani, M. M., Jubair, S., Ganie, A. H., Abdelmohsen, S. A. (2023). Computational framework of hydrodynamic stagnation point flow of nanomaterials with natural convection configured by a heated stretching sheet. ZAMM-Journal of Applied Mathematics and Mechanics/Zeitschrift für Angewandte Mathematik und Mechanik, 2023, e202200542. [Google Scholar]

12. Bouslimi, J., Omri, M., Mohamed, R. A., Mahmoud, K. H., Abo-Dahab, S. M. et al. (2021). MHD williamson nanofluid flow over a stretching sheet through a porous medium under effects of joule heating, nonlinear thermal radiation, heat generation/absorption, and chemical reaction. Advances in Mathematical Physics, 2021, 1–16. [Google Scholar]

13. Bilal, M., Ramzan, M., Mehmood, Y., Kbiri Alaoui, M., Chinram, R. (2021). An entropy optimization study of non-darcian magnetohydrodynamic williamson nanofluid with nonlinear thermal radiation over a stratified sheet. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, 235(6), 1883–1894. [Google Scholar]

14. Patel, H. R., Singh, R. (2019). Thermophoresis, brownian motion and non-linear thermal radiation effects on mixed convection MHD micropolar fluid flow due to nonlinear stretched sheet in porous medium with viscous dissipation, joule heating and convective boundary condition. International Communications in Heat and Mass Transfer, 107, 68–92. [Google Scholar]

15. Reddy, S. R. R., Reddy, P. B. A., Bhattacharyya, K. (2019). Effect of nonlinear thermal radiation on 3D magneto slip flow of eyring-powell nanofluid flow over a slendering sheet with binary chemical reaction and arrhenius activation energy. Advanced Powder Technology, 30(12), 3203–3213. [Google Scholar]

16. Kumar, C. K., Srinivas, S., Reddy, A. S. (2020). MHD pulsating flow of casson nanofluid in a vertical porous space with thermal radiation and joule heating. Journal of Mechanics, 36(4), 535–549. [Google Scholar]

17. McWhirter, J. D., Crawford, M. E., Klein, D. E. (1998). Magnetohydrodynamic flows in porous media ii: Experimental results. Fusion Technology, 34(3P1), 187–197. [Google Scholar]

18. Bhatti, M. M., Zeeshan, A., Ellahi, R., Bég, O. A., Kadir, A. (2019). Effects of coagulation on the two-phase peristaltic pumping of magnetized prandtl biofluid through an endoscopic annular geometry containing a porous medium. Chinese Journal of Physics, 58, 222–234. [Google Scholar]

19. Reddy, N. N., Rao, V. S., Reddy, B. R. (2021). Chemical reaction impact on MHD natural convection flow through porous medium past an exponentially stretching sheet in presence of heat source/sink and viscous dissipation. Case Studies in Thermal Engineering, 25, 100879. [Google Scholar]

20. Sajid, T., Sagheer, M., Hussain, S., Shahzad, F. (2020). Impact of double-diffusive convection and motile gyrotactic microorganisms on magnetohydrodynamics bioconvection tangent hyperbolic nanofluid. Open Physics, 18(1), 74–88. [Google Scholar]

21. Hussain, S., Ahmad, F., Ayed, H., Malik, M. Y., Waqas, H. et al. (2021). Combined magnetic and porosity effects on flow of time-dependent tangent hyperbolic fluid with nanoparticles and motile gyrotactic microorganism past a wedge with second-order slip. Case Studies in Thermal Engineering, 26, 100962. [Google Scholar]

22. Muhammad, T., Waqas, H., Manzoor, U., Farooq, U., Rizvi, Z. F. (2022). On doubly stratified bioconvective transport of jeffrey nanofluid with gyrotactic motile microorganisms. Alexandria Engineering Journal, 61(2), 1571–1583. [Google Scholar]

23. Ferdows, M., Reddy, M. G., Sun, S., Alzahrani, F. (2019). Two-dimensional gyrotactic microorganisms flow of hydromagnetic power law nanofluid past an elongated sheet. Advances in Mechanical Engineering, 11(11), 1687814019881252. [Google Scholar]

24. Elbashbeshy, E. M., Asker, H. G., Nagy, B. (2022). The effects of heat generation absorption on boundary layer flow of a nanofluid containing gyrotactic microorganisms over an inclined stretching cylinder. Ain Shams Engineering Journal, 13(5), 101690. [Google Scholar]

25. Hosseini, Z. S., Abidi, A., Mohammadi, S., Mehryan, S. A. M., Hulme, C. (2021). A fully resolved computational fluid dynamics study of the boundary layer flow of an aqueous nanoliquid comprising gyrotactic microorganisms over a stretching sheet: The validity of conventional similarity models. Mathematics, 9(21), 2655. [Google Scholar]

26. Dawar, A., Shah, Z., Alshehri, H. M., Islam, S., Kumam, P. (2021). Magnetized and non-magnetized casson fluid flow with gyrotactic microorganisms over a stratified stretching cylinder. Scientific Reports, 11(1), 16376. [Google Scholar] [PubMed]

27. Irfan, M., Farooq, M. A., Iqra, T. (2020). A new computational technique design for emhd nanofluid flow over a variable thickness surface with variable liquid characteristics. Frontiers in Physics, 8, 66. [Google Scholar]

28. Farooq, M. A., Salahuddin, A., Mushtaq, A., Razzaq, M. (2021). A simplified finite difference method (SFDM) solution via tridiagonal matrix algorithm for MHD radiating nanofluid flow over a slippery sheet submerged in a permeable medium. Mathematical Problems in Engineering, 2021, 1–17. [Google Scholar]

29. Ahmadpour, A., Sadeghy, K. (2013). Swirling flow of bingham fluids above a rotating disk: An exact solution. Journal of Non-Newtonian Fluid Mechanics, 197, 41–47. [Google Scholar]

30. Rafiq, T., Mustafa, M., Farooq, M. A. (2020). Modeling heat transfer in fluid flow near a decelerating rotating disk with variable fluid properties. International Communications in Heat and Mass Transfer, 116, 104673. [Google Scholar]

31. Hayat, T., Ali, S., Farooq, M. A., Alsaedi, A. (2015). On comparison of series and numerical solutions for flow of eyring-powell fluid with newtonian heating and internal heat generation/absorption. PLoS One, 10(9), e0129613. [Google Scholar] [PubMed]