Experimental Study of the Effect of Water Salinity on the Parameters of an Equilibrium Droplet Cluster Levitating over a Water Layer

Nomenclature

1  Introduction

The present experimental work continues the study of levitating droplet clusters for potential laboratory investigations of biochemical processes in micron-sized droplets. The use of small droplets as microreactors suggested in [1] is very promising due to the expected acceleration of organic reactions with decreasing droplet size [2–4]. For chemical experiments, it is desirable to use droplets levitating in the air and not in contact with any surfaces. Various methods of obtaining such droplets are known, but the most promising are acoustic levitation of individual droplets, as well as equilibrium droplets forming stable clusters levitating above the surface of the evaporating liquid. Note that the Leidenfrost effect [5–7] and thermophoresis [8,9] cannot be used because, in both cases, the substrate is generally too hot.

A large number of publications have been devoted to acoustic levitation of droplets, in particular, the works [10–14]. In some cases, the authors managed to observe some chemical and biochemical processes in isolated droplets. However, in acoustic levitation, the droplets usually change their shape. A significant disadvantage of this method is also that the droplet size decreases due to evaporation. The latter does not allow working with droplets of constant size. On the contrary, the condensational growth of droplets in clusters can be suppressed and it is possible to work with equilibrium droplets of constant size for as long as necessary.

Self-assembled droplet clusters that levitate over a heated liquid have been studied for about two decades since the discovery of this amazing phenomenon [15–17]. Droplet clusters have also been considered by researchers who have worked mainly on problems related to cooling in microelectronics [18,19]. We prefer to start with a brief description of the physical conditions of droplet cluster formation. It is known that only randomly moving small droplets are observed over an almost uniformly heated water surface [20,21]. The transition to a pronounced localized water heating leads to intense evaporation and the observed upward gas flow of water vapor and entrained air. Water droplets condense out of the vapor as the upstream cools. Some droplets grow by condensation of vapor and gravity brings them closer to the water layer. These droplets collect in the central zone of the flow, where the pressure is lower, and form a droplet cluster. Our studies have shown that electrostatic forces between charged droplets and even a layer of water are also present, but the structure and behavior of the droplet cluster are usually determined by the aerodynamic interaction between the gas flow and the droplets [22].

Unfortunately, the droplets of the cluster grow rather fast and less than a minute after the beginning of the cluster formation it coalesces with the water layer. Of course, it is impossible to conduct biochemical studies in the droplets of this natural cluster and it was necessary to somehow suppress the condensational growth of droplets. This was done by heating the droplets by low-power near-infrared radiation [23]. We also tried to modulate the water heating power to “renew” the droplets [24]. However, this method was not as effective as infrared irradiation of droplet clusters. Note that a long-term infrared stabilization of clusters containing the droplets of pure water was rather accurately described by a quantitative theoretical model [25].

It has recently been found that a cluster of pure water droplets can spontaneously stabilize even without infrared irradiation. This is reached by adding a little salt (NaCl) to the water layer under the cluster [26]. The theoretical analysis of the problem showed that this effect is related to the formation of a steady-state salt concentration profile in the water layer. However, it is not enough to add salt to the water layer to stabilize clusters containing droplets of different solutions, and the infrared heating of droplet clusters remains the main method for obtaining equilibrium droplets [27]. Small infrared volumetric heating of droplets leads to an increase in their temperature and some increase in water evaporation. It was experimentally shown that this is sufficient to suppress the condensational growth of the cluster droplets.

The objective of the present study is to find experimentally a combination of two methods (changing the salt content of the water layer and infrared heating) to stabilize levitating clusters containing saltwater droplets. The use of salt water brings us closer to the practically important case where the droplets contain water-soluble but not evaporating biological substances. It is also important to separate the effects of salinity of water droplets and water under the cluster into a combined heat and mass transfer problem involving evaporation, condensation and salt diffusion in water.

2  Experimental Procedure

The method of droplet cluster generation used in our earlier works is unsuitable for obtaining clusters of droplets of different chemical compositions. A fundamentally new engineering solution with independent generation of primary droplets, which are fed into the zone above the locally heated surface of water or aqueous solution, was required. The incoming droplets increase in size due to the normal process of water vapor condensation, but the vapor inflow can also be controlled independently by changing the composition of the solution under the cluster. In other words, there is a new possibility to influence the growth of cluster droplets.

Fig. 1 shows a schematic of a modern droplet cluster generation module. The schematic shows the most important elements of the laboratory setup: the piezoelectric dispenser 1, the layer of water or aqueous solution 2, the laser beam for local heating of the water layer 3, and the conventional image of infrared radiation from miniature sources 4. A similar experimental setup was also used in recent papers [26,27]. The setup used has been continuously improved, mainly during the last two years. The modern modification of the laboratory setup has no analogues.

Figure 1: Schematic view of the droplet cluster generation module

An advanced “printing” procedure for the initial droplet clusters was used. A piezoelectric dispenser (MicroFab Technologies, Inc., USA) generated three droplet jets with different sizes of droplets. The selected droplets are fed into the hermetic working volume. At the bottom of this volume is a cuvette with a thin layer of salt water and a small amount of surfactant to suppress thermocapillary flow. The central part of the cuvette is heated by a laser beam through an opaque substrate, resulting in a maximum liquid surface temperature, Tmax, of 60°C to 85°C. The temperature range of the present study is much wider than in our recent works. It now includes temperatures typical of the habitat of a large group of extremophile microorganisms, which are of interest for studying their behavior in levitating droplets [28–30]. At the cuvette’s periphery, the working solution’s temperature is maintained at 10°C. The droplet cluster levitates in an upward flow of humid air over the hot liquid surface, and the initial droplet size, d0, increases due to the condensation of water vapor. The water surface temperature in the area of cluster localization is monitored by a pyrometric sensor CTL-CF1-C3 (Micro-Epsilon, USA). The operating wavelength range of the pyrometer from 8 to 14 μm allows measuring the surface temperature of the water layer with an accuracy of about 0.1°C. In the upper part of the working volume, miniature infrared sources EK-8520 (Helioworks, USA) are located. The infrared heating of droplets suppresses their condensational growth and ensures the formation of droplets of equilibrium size. In a series of the discussed experiments, the total radiative flux to the cluster droplets was constant and equal to qrad=1.24 mW/mm2. Thus, the infrared heating was kept constant and we focused on the effect of the second way of stabilizing the cluster–increasing the salt concentration in the water layer under the cluster. The cluster image was recorded using an AXIO Zoom.V16 stereomicroscope (Zeiss, Germany) equipped with a camera EDGE 5.5C (PCO, Germany). Computer processing of the images allows the size of the cluster droplets to be monitored during the experiment. The created computer code processes a series of consecutive frames with the image of the cluster, identifying the droplets (each droplet is assigned an individual number) and determining the diameter of each droplet and the coordinates of its center frame by frame. Depending on the specific task, it is possible to record both the change of parameters of a selected droplet and the averaged parameters of a selected group of droplets. In this work, the averaging was performed over the entire cluster.

In the experiments, the initial salt concentration in the solution from which the cluster was printed, C0=9 g/l, was not changed, but the salt concentration in the water layer, Clayer, was varied. The salt concentration, which is suitable for infrared stabilization of clusters from droplets of isotonic biological and medical solutions [31], was determined. In the main series of experiments, three Clayer values were considered: 2, 4, and 6 g/l (the estimated error was ±0.05 g/l).

In a preliminary stage of the work, the possibility of obtaining a cluster of equilibrium droplets without infrared irradiation was examined, as it was successive for clusters of pure water droplets. Unfortunately, clusters of saltwater droplets did not stabilize even when the concentration of salt in the water layer was much higher than that in the droplets. It turned out that in the region of local heating of the working solution, the salt concentration increases monotonically at high values of both parameters: Tmax and Clayer. This is explained by a high rate of water evaporation and very low diffusivity of salt in water [32,33]. As a result, growing salt crystals are formed on the layer surface. Even at a low initial salt concentration and small Tmax, the increase in the local surface salt concentration led to a decrease in the size of the equilibrium cluster droplets within a few minutes. This undesirable effect was eliminated by selecting the minimum necessary pumping rate of the working solution of 0.1 ± 0.01 g/min, at which the slow flow of liquid does not affect the temperature field in the layer.

In the experiments, a cluster of a small number of droplets was initially printed at Tmax=65∘C, then a pause of 300 s was allowed for the cluster to stabilize completely, and a series of 100 frames was recorded. The surface temperature of the water layer under the cluster was then increased by 5∘C, paused again and a new series of frames was recorded. The experiment was continued similarly until Tmax=85∘C, and then this temperature was decreased to 60∘C in the same way. The laser heating power was then reduced until the cluster lost its stability and the droplets coalesced into the water layer.

3  Experimental Results

Fig. 2a shows the experimental dependence of the average diameter of cluster droplets, d, on the surface temperature of the layer of salt water. These results were obtained using the procedure described above. The experiment was conducted at Clayer=4±0.05 g/l. The curves d(Tmax) for both the heating and cooling stages of the experiment are very close to each other. The latter can be seen as a confirmation of the applicability of the chosen pumping procedure. The divergence of the forward and backward branches of the experimental curve in Fig. 2a makes it possible to obtain an estimate of the error in measuring the equilibrium droplet diameter. The resulting error of about 0.7 μm is comparable to the pixel size of the droplet image.

Figure 2: (a) Variation of diameters of equilibrium droplets during slow water heating (1) and subsequent cooling (2); (b) The images of the equilibrium cluster at different temperatures

It is of interest to observe clusters of droplets of initially different sizes and consequently with different amounts of salt. For example, the cluster shown in Fig. 3 consisted of group 1 of three upper droplets having initial diameter d0,1=16.4 μm, group 2 of three middle and one lower droplet with d0,2=24 μm and the largest droplet (lower right) with diameter d0,3=26.3 μm. The estimated error in these values was ±0.5 μm. Note that the Bond number for these water droplets is about 10−5. This means that all droplets are perfectly spherical. It turns out that the diameters of all droplets increase similarly with temperature. As a result, the ratio of droplet sizes from different groups remained approximately constant when the temperature Tmax increases from 60∘C to 85∘C.

Figure 3: Effect of water temperature under the cluster on equilibrium droplet size

As might be expected, the droplet size of the equilibrium cluster increases with increasing water temperature Tmax and decreasing water salinity Clayer, whereas the salinity of the droplets decreases. The experimentally found dependencies of d(Tmax,Clayer) and Cdrop(Tmax,Clayer) at fixed values of C0=9 g/l and d0=24 μm are presented in Fig. 4. The choice of the initial salt concentration C0 is because this concentration is typical for biological isotonic solutions. The value of d0 is the initial diameter of the most of the generated droplets.

Figure 4: The diagrams for (a) the average diameter of the equilibrium droplets and (b) the concentration of salt in these droplets

Interestingly, the dependences of d(Tmax) at various values of Clayer are similar to each other. Of course, this similarity also holds for the Cdrop(Tmax). This remarkable feature, which is convenient for estimating parameters of equilibrium/stabilized clusters, is shown in Fig. 5, where the values d¯=d(Tmax)/d(60∘C) and C¯drop=Cdrop(Tmax)/Cdrop(60∘C) obtained at constant values of Clayer are connected by straight lines. The small effect of the Clayer appears to be within the measurement error.

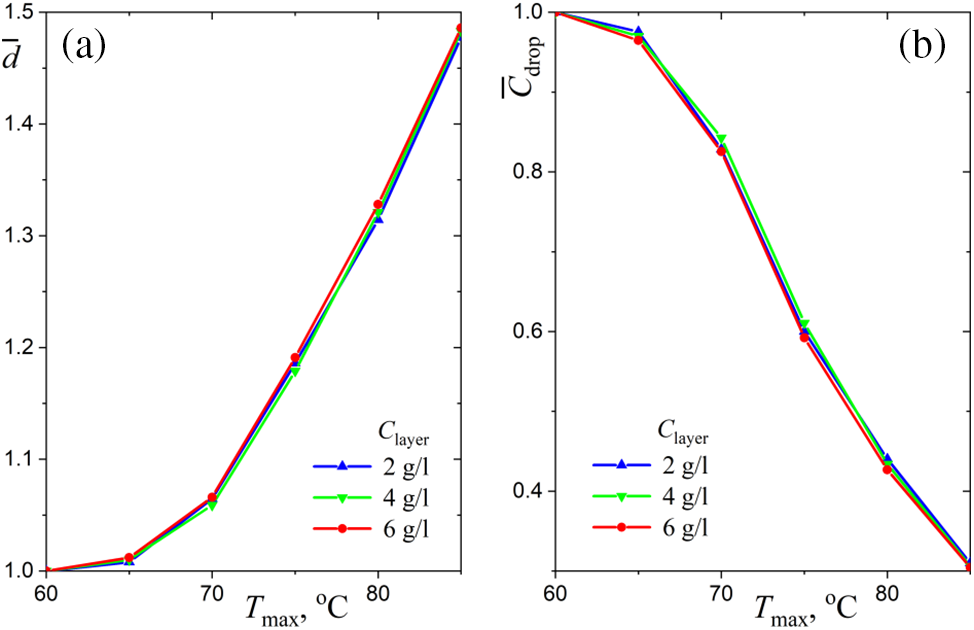
Figure 5: Temperature dependencies of equilibrium droplet parameters for different values of water layer salinity: (a) normalized diameter, (b) normalized droplet salinity

The curves in Fig. 5b are a direct consequence of the dependencies shown in Fig. 5a:

C¯drop(Tmax)=1/[d¯(Tmax)]3.(1)

The cubic relationship (1) is a consequence of the fact that the amount of salt in the droplet is constant and the salt concentration decreases as the droplet grows due to condensation of water vapor. It is sufficient to understand the features of the functions d¯(Tmax). The water surface temperature is a strong parameter of the problem. In the temperature range in question, according to Fig. 5a, the value of d¯ is approximately proportional to the square of the temperature difference (Tmax−60∘C). At the same time, experiments have shown that the monotonic decrease of d¯ with increasing Clayer is almost linear and insensitive to the water temperature. A similar conclusion can be drawn from the saltwater evaporation model. Therefore, the coincidence of the curves d¯(Tmax) at different values of Clayer was expected.

In contrast to [27], the experiments in this work cover a much wider range of water surface temperature (up to 85∘C rather than 70∘C). In addition, the dissolution of salt in the water layer under the cluster allowed us to obtain stable clusters of saltwater droplets levitating over the entire temperature range. Moreover, varying the salinity of the water layer provided a considerable amount of data on the variation of the equilibrium droplet parameters. This extensive information makes it possible to carry out a thermophysical analysis of a general problem of levitating droplet clusters under fixed infrared heating.

4  Analysis of Thermal Processes Responsible for Stabilization of Droplet Clusters

In [25], a computational model was proposed to calculate the parameters of droplet clusters stabilized by infrared radiation and calculations were performed for droplets of different sizes that formed the initial levitating cluster. These droplets acquire the same constant temperature and they become nearly identical. It was shown that the numerical results are in good agreement with experimental data. This model, which works perfectly for a small droplet cluster levitating over a layer of pure water, is based on solving a system of coupled differential equations for the variable temperature and size of individual droplets in combination with the previously developed kinetic model of evaporation taking into account the Knudsen layer on the droplet surface [34,35]. The volumetric absorption of infrared radiation in semitransparent water droplets was calculated by Mie theory which gives a rigorous analytical solution to the scattering problem for single spherical particles [36–40]. The independent absorption and scattering of the external infrared radiation by single droplets of the cluster can be considered because the droplets are much larger than the radiation wavelength and they are relatively far from each other [41,42]. It should be noted that the distances between the droplets in the so-called “small droplet cluster” with which we worked in the discussed study do not affect the heat and mass transfer conditions for individual droplets [17,25].

For the convenience of potential readers, the main equations used to determine the parameters of the equilibrium droplets in the cluster are reproduced below. The mass rates of condensation and evaporation are equal to each other for equilibrium droplets, and these processes do not contribute to the energy balance, which can be written as the equality of the absorbed radiative flux and convective heat losses:

0.75Q¯aqrad,1=3kair(Teq−Tair)/aeq,(2)

where qrad,1 is the integral (over the spectrum) incident radiative flux on a water droplet of radius aeq from infrared sources, Teq is the equilibrium temperature of the droplet, Tair and kair are the temperature and thermal conductivity of a humid air outside the boundary layer on the droplet surface, and Q¯a is the spectrally averaged droplet efficiency factor of absorption calculated as follows:

Q¯a(a)=∫λ1λ2Qa(λ,a)Ib(λ,Tb)dλ/∫λ1λ2Ib(λ,Tb)dλ.(3)

Here Qa is the efficiency factor of scattering of a spherical particle introduced in Mie theory and Ib is the Planck function at temperature Tb=1223 K of infrared emitters. This temperature determines a choice of λ1 and λ2 in the calculations. Note that there is a monotonic increase of Q¯a with increasing droplet radius, which is explained by the increase of the optical thickness of semitransparent droplets.

It is assumed that Tair is equal to the surface temperature of the water layer, Tmax. This assumption is realistic because the levitation height of the cluster is very small [43]. In this case, Eq. (2) is sufficient to obtain the value of Teq for each value of aeq:

Teq=Tmax+aeq4kairQ¯aqrad,1.(4)

In turn, the equality of the mass rates of condensation and evaporation leads to a simple expression for relative air humidity derived from the kinetic model of evaporation [25]:

φair=psat(Teq)/psat(Tmax),(5)

where psat(T) is the saturation pressure of water vapor [44]:

lg⁡psat(T)=4.6543−1435.264/(T−64.848),(6)

where T is measured in Kelvin and psat is obtained in bar (105 Pa).

Unfortunately, Eqs. (4) and (5) cannot be used to determine the important value of the equilibrium radius of water droplets. Therefore, it is necessary to numerically solve the following Cauchy problem for the current temperature and radius of small isothermal droplets:

ρwcwdTdt=3a(Q¯aqrad,14+m˙L−kairT−Taira),T(0)=T0,(7)

ρwdadt=m˙, a(0)=a0,(8)

where ρw and cw are the density and specific capacity of water, m˙ is the resultant mass rate of water vapor in the direction of the droplet due to condensation and evaporation, L is the latent heat of evaporation. Of course, the coupled Eqs. (7) and (8) should be completed by the evaporation model. This model takes into account the kinetic processes in the Knudsen layer at the droplet surface, as discussed in the early monograph [45] and then confirmed by experimental studies. The mass flow rate of water vapor is determined by the following equation, which is true at arbitrary humidity of ambient air [35,46]:

m˙=DpairaRair(Tair,φair)Tairln1−ψ(T,φK)φK1−ψ(Tair,φair)φair,ψ(T,φ)=psat(T)pairMvapMair(T,φ),(9)

where D is the diffusion coefficient of water vapor in air, Rair is the gas constant for the humid air, pair is the atmospheric pressure, Mvap and Mair are the molecular masses of water vapor and humid air, and φK is the relative humidity at the Knudsen layer boundary determined from the mass balance equation:

fevpsat(T)2πRvapT(φK−1)=DpairaRair(Tair,φair)Tairln1−ψ(T,φK)φK1−ψ(Tair,φair)φair.(10)

The known equations for the molecular mass and gas constant of humid air are:

Mair(T,φ)=RRair(T,φ),Rair(T,φ)=Rair,01−φ(1−MvapMair,0)psat(T)pair,(11)

where the values Rair,0 and Mair,0 are calculated for the dry air and R=8314 J/(kmol K) is the universal gas constant. The dimensionless coefficient fev in Eq. (10) was introduced in [34,45] to avoid time-consuming numerical ssolutionsfor the coupled Boltzmann kinetic equations. Strictly speaking, this coefficient is a function on the problem parameters. However, a constant value of fev=0.0024 can be used for water droplets in air [46]. The above model with the recommended coefficient was validated by comparing calculations and the experimental data of [47] for water droplets evaporating in ambient air. The model with the constant value of fev is sufficiently accurate in the range of parameters of the problem under consideration.

In [27], an attempt was made to modify this model to calculate the possible stabilization of a cluster of saltwater droplets. The difference between the calculations and the experimental data turned out to be significant even when taking into account nonuniform salt concentration in the asymmetrically heated water droplet. This is probably due to the formation of salt microcrystals near the surface of the droplet heated by infrared radiation. Computational modeling of the more general problem, when the salt is also dissolved in the water layer under the cluster, is very difficult. Therefore, we limited ourselves to a physical comparison of a series of calculations according to the model of [25] with new experimental data. It will be shown below that such an analysis makes it possible to separate the effect of the salt in the water layer from the effect due to the presence of salt in the cluster droplets. A comparison of the results of numerical calculations for pure water (both in droplets and in the water layer) and experimental data for saline water is presented in Fig. 6. The error bars are marked on the experimental curves.

Figure 6: Dependencies of equilibrium droplet diameters on water layer surface temperature. Comparison of calculations for a cluster of pure water droplets over a pure water layer with experiments for saltwater clusters over the water layer of various salt concentrations

As the salt concentration in the water layer decreases, the diameter of the equilibrium saltwater droplets increases significantly. It can be seen that for water with a very low salt concentration, as for pure water, the saline droplets grow to a much larger size than pure water droplets. This is explained by a much smaller evaporation of water from the surface of the salt droplets at the same condensation rate of water vapor from the surrounding humid air.

The temperature dependences compared are also significantly different. For pure water, the dependence d(Tmax) is linear (black curve in Fig. 6), while in the experiments with saline water, the normalized droplet diameter d¯ is proportional to the square of the water layer temperature Tmax (color curves in Fig. 6). Obviously, the latter dependence is not related to the properties of levitating droplets but depends on the parameters of the upward flow of humid air. In other words, the nature of the nonlinear temperature dependence of the equilibrium droplet size is completely determined by the change in the evaporation rate of the saltwater layer with increasing temperature.

Thus, we are able to separate two effects of salt water: one of them is related only to hindered evaporation of water from the salt droplets and the other is exclusively to the specific change of mass evaporation rate of salt water layer with temperature. This result makes it possible to consider separately two independent problems of heat and mass transfer: (1) the formation of a zone of increased salt concentration at the droplet surface (probably, at the irradiated upper surface) and (2) heat transfer and salt diffusion in the evaporating layer of saline water. According to the authors, the above analysis is of methodological importance for structuring the complex problem of heat transfer and diffusion in a multicomponent evaporating liquid and condensed droplets.

5  Conclusions

Laboratory experiments showed that the infrared heating of the cluster, in combination with a properly selected salt concentration in the water layer under the cluster, is sufficient to stabilize droplet clusters of saline water droplets. The equilibrium droplets were obtained in the most important ranges of droplet size and water salinity. Pumping the working solution into the water layer at a flow rate of 0.1 g/min is shown for the first time to prevent an abnormal increase in the surface salt concentration and is sufficient for the reliable long-term operation of the laboratory setup.

Universal quantitative dependencies for the main parameters of equilibrium saltwater droplets were obtained. With the help of this relationship, it is easy to predict the necessary salt concentration in the water layer to produce nearly identical levitating droplets of the desired size. The new experimental results can be seen as the next step toward using levitating droplets as microreactors for in-depth laboratory studies of biochemical processes.

A physical analysis of experimental results on diameters of equilibrium saltwater droplets with the use of additional numerical calculations makes it possible to separate the effects related to the salinity of the water layer under the droplet cluster from the effects related to the reduction of water evaporation from the droplets. The results obtained helped to better understand the influence of the chemical composition of the water layer and cluster droplets on the conditions for obtaining equilibrium droplets. This experience is expected to be useful when working with solutions used in medicine and agriculture. Note that the methods developed in experiments with simple binary systems like saline water can be applied to multicomponent systems. For example, these methods allow one to study the parameters for chemical plant protection products including the growth or evaporation times of aerosol droplets.

Acknowledgement: The authors are grateful to the Russian Science Foundation (Project No. 24-29-00303) for the financial support of the present study.

Funding Statement: This study was financially supported by the Russian Science Foundation (Project No. 24-29-00303: https://rscf.ru/project/24-29-00303/). The grant was received by A.A.F.

Author Contributions: The authors confirm contribution to the paper as follows: study conception: A.A.F., L.A.D.; experimental design and procedure: A.A.F.; computer processing the experimental data: E.E.K.; physical analysis: A.A.F., L.A.D.; computational model and calculations: L.A.D., draft manuscript preparation: A.A.F., L.A.D. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: No data was used for the research described in the article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Fedorets, A. A., Bormashenko, E., Dombrovsky, L. A., Nosonovsky, M. (2019). Droplet clusters: Nature-inspired biological reactors and aerosols. Philosophical Transactions of the Royal Society A, 377, 2019012. https://doi.org/10.1098/rsta.2019.0121 [Google Scholar] [PubMed] [CrossRef]

2. Wei, Z., Li, Y., Cooks, R. G., Yan, X. (2020). Accelerated reaction kinetics in microdroplets: Overview and recent developments. Annual Review of Physical Chemistry, 71, 31–51. https://doi.org/10.1146/annurev-physchem-121319-110654 [Google Scholar] [PubMed] [CrossRef]

3. Zhang, Z., Apsokardu, M. J., Kerecman, D. E., Achtenhagen, M., Johnston, M. V. (2021). Reaction kinetics of organic aerosol studied by droplet assisted ionization: Enhanced reactivity in droplets relative to bulk solution. Journal of the American Society of Mass Spectrometry, 32(1), 46–54. https://doi.org/10.1021/jasms.0c00057 [Google Scholar] [PubMed] [CrossRef]

4. Li, K., Gong, K., Liu, J., Ohnoutek, L., Ao, J. et al. (2022). Significantly accelerated photochemical and photocatalytic reactions in microdroplets. Cell Reports Physical Science, 3(6), 100917. https://doi.org/10.1016/j.xcrp.2022.100917 [Google Scholar] [CrossRef]

5. Hashmi, A., Xu, Y., Coder, B., Osborne, P. A., Spafford, J. et al. (2012). Leidenfrost levitation: Beyond droplets. Scientific Reports, 2, 797. https://doi.org/10.1038/srep00797 [Google Scholar] [PubMed] [CrossRef]

6. Panchanathan, D., Bourrianne, P., Nicollier, N., Chottratanapituk, A., Varanasi, K. K. et al. (2021). Levitation of fizzy drops. Science Advances, 7(28), eabf0888. https://doi.org/10.1126/sciadv.abf0888 [Google Scholar] [PubMed] [CrossRef]

7. Sobac, B., Maquet, L., Duchesne, A., Machrafi, H., Rednikov, A. et al. (2020). Self-induced flows enhance the levitation of Leidenfrost drops on liquid baths. Physical Review Fluids, 5, 62701(R). https://doi.org/10.1103/PhysRevFluids.5.062701 [Google Scholar] [CrossRef]

8. Kelling, T., Wurm, G. (2009). Self-sustained levitation of dust aggregate ensembles by temperature-gradient-induced overpressures. Physical Review Letters, 103, 215502. https://doi.org/10.1103/PhysRevLett.103.215502 [Google Scholar] [PubMed] [CrossRef]

9. Roy, P. K., Legchenkova, I., Dombrovsky, L. A., Levashov, V. Y., Binks, B. P. et al. (2022). Thermophoretic levitation of powders at atmospheric pressure. Advanced Powder Technology, 33(3), 103497. https://doi.org/10.1016/j.apt.2022.103497 [Google Scholar] [CrossRef]

10. Yarin, A. L., Brenn, G., Karstner, O., Rensink, D., Tropea, C. (1999). Evaporation of acoustically levitating droplets. Journal of Fluid Mechanics, 399, 151–204. https://doi.org/10.1017/S0022112099006266 [Google Scholar] [CrossRef]

11. Zang, D., Yu, Y., Chen, Z., Li, X., Wu, H. et al. (2017). Acoustic levitation of liquid drops: Dynamics, manipulation and phase transition. Advances in Colloid and Interface Science, 243, 77–85. https://doi.org/10.1016/j.cis.2017.03.003 [Google Scholar] [PubMed] [CrossRef]

12. Contreras, V., Valencia, R., Peralta, J., Sobral, H., Meneses-Nava, M. A. et al. (2018). Chemical elemental analysis of single acoustic-levitated water droplets by laser-induced breakdown spectroscopy. Optics Letters, 43(10), 2260–2263. https://doi.org/10.1364/OL.43.002260 [Google Scholar] [PubMed] [CrossRef]

13. Maruyama, Y., Hasegawa, K. (2020). Evaporation and drying kinetics of water-NaCl droplets via acoustic levitation. RSC Advances, 10(4), 1870–1877. https://doi.org/10.1039/c9ra09395h [Google Scholar] [PubMed] [CrossRef]

14. Honda, K., Fujiwara, K., Hasegawa, K., Kaneko, A., Abe, Y. (2023). Coalescence and mixing dynamics of droplets in acoustic levitation by selective colour imaging and measurement. Scientific Reports, 13, 19590. https://doi.org/10.1038/s41598-023-46008-z [Google Scholar] [PubMed] [CrossRef]

15. Fedorets, A. A. (2004). Droplet cluster. JETP Letters, 79(8), 372–374. https://doi.org/10.1134/1.1772434 [Google Scholar] [CrossRef]

16. Fedorets, A. A., Dombrovsky, L. A. (2023). Levitating droplet clusters: From the discovery to potential applications. Academia Engineering, 1, 1–5. https://doi.org/10.20935/AcadEng6093 [Google Scholar] [CrossRef]

17. Fedorets, A. A., Dombrovsky, L. A., Bormashenko, E., Nosonovsky, M. (2023). Levitating droplet clusters. New York: Begell House. https://doi.org/10.1615/978-1-56700-532-5.0 [Google Scholar] [CrossRef]

18. Zaitsev, D. V., Kirichenko, D. P., Ajaev, V. S., Kabov, O. A. (2017). Levitation and self-organization of liquid microdroplets over dry heated substrates. Physical Review Letters, 119(9), 94503. https://doi.org/10.1103/PhysRevLett.119.094503 [Google Scholar] [PubMed] [CrossRef]

19. Zaitsev, D. V., Kirichenko, D. P., Shatekova, A. I., Ajaev, V. S., Kabov, O. A. (2018). Experimental and theoretical studies of ordered arrays of microdroplets levitating over liquid and solid surfaces. Soft Matter, 6(3), 219–230. https://doi.org/10.1615/InterfacPhenomHeatTransfer.2019029816 [Google Scholar] [CrossRef]

20. Schaefer, V. J. (1971). Observations of an early morning cup of coffee. Amer Scientist, 59(5), 534–535. [Google Scholar]

21. Ienna, F., Yoo, H., Pollack, G. H. (2012). Spatially resolved evaporative patterns from water. Soft Matter, 8(47), 11850–11856. https://doi.org/10.1039/C2SM26497H [Google Scholar] [CrossRef]

22. Fedorets, A. A., Dombrovsky, L. A., Gabyshev, D. N., Bormashenko, E., Nosonovsky, M. (2020). Effect of external electric field on dynamics of levitating water droplets. International Journal of Thermal Sciences, 153, 106375. https://doi.org/10.1016/j.ijthermalsci.2020.106375 [Google Scholar] [CrossRef]

23. Dombrovsky, L. A., Fedorets, A. A., Medvedev, D. N. (2016). The use of infrared irradiation to stabilize levitating clusters of water droplets. Infrared Physics and Technology, 75, 124–132. https://doi.org/10.1016/j.infrared.2015.12.020 [Google Scholar] [CrossRef]

24. Fedorets, A. A., Aktaev, N. E., Dombrovsky, L. A. (2018). Suppression of the condensational growth of droplets of a levitating cluster using the modulation of the laser heating power. International Journal of Heat and Mass Transfer, 127A, 660–664. https://doi.org/10.1016/j.ijheatmasstransfer.2018.07.055 [Google Scholar] [CrossRef]

25. Dombrovsky, L. A., Fedorets, A. A., Levashov, V. Y., Kryukov, A. P., Bormashenko, E. et al. (2020). Stable cluster of identical water droplets formed under the infrared irradiation: Experimental study and theoretical modeling. International Journal of Heat and Mass Transfer, 161, 120255. https://doi.org/10.1016/j.ijheatmasstransfer.2020.120255 [Google Scholar] [CrossRef]

26. Fedorets, A. A., Shcherbakov, D. V., Levashov, V. Y., Dombrovsky, L. A. (2022). Self-stabilization of droplet clusters levitating over heated salt water. International Journal of Thermal Sciences, 182, 107822. https://doi.org/10.1016/j.ijthermalsci.2022.107822 [Google Scholar] [CrossRef]

27. Fedorets, A. A., Medvedev, D. N., Levashov, V. Y., Dombrovsky, L. A. (2023). Stabilization of levitating clusters containing saltwater droplets. International Journal of Thermal Sciences, 188, 108222. https://doi.org/10.1016/j.ijthermalsci.2023.108222 [Google Scholar] [CrossRef]

28. Pikuta, E. V., Hoover, R. B., Tang, J. (2007). Microbial extremophiles and the limits of life. Critical Reviews in Microbiology, 33(3), 183–209. https://doi.org/10.1080/10408410701451948 [Google Scholar] [PubMed] [CrossRef]

29. Merino, N., Aronson, H. S., Bojanova, D. P., Feyhl-Buska, J., Wong, M. L. et al. (2019). Living at the extremes: Extremophiles and the limits of life in a planetary context. Frontiers in Microbiology, 10, 780. https://doi.org/10.3389/fmicb.2019.00780 [Google Scholar] [PubMed] [CrossRef]

30. Zhu, D., Adebisi, W. A., Ahmad, F., Sethupathy, S., Danso, B. et al. (2020). Recent development of extremophilic bacteria and their application in biorefinery. Frontiers in Bioengineering and Biotechnology, 8, 483. https://doi.org/10.3388/fbioe.2020.00483 [Google Scholar] [CrossRef]

31. Savva, M. (2019). Isotonic solutions. In: Pharmaceutical calculations. Switzerland, Cham: Springer Nature. [Google Scholar]

32. Fell, C. J. D., Hutchison, Y. P. (1971). Diffusion coefficients for sodium and potassium chlorides in water at elevated temperatures. Journal of Chemical and Engineering Data, 16(4), 427–429. https://doi.org/10.1021/je60051a005 [Google Scholar] [CrossRef]

33. Hamann, C. H., Hamnett, A., Vielstich, W. (2007). Electrochemistry. Second Edition. Weinheim, Germany: Wiley-VCH. [Google Scholar]

34. Kryukov, A. P., Levashov, V. Y., Shishkova, I. N. (2009). Evaporation in mixture of vapor and gas mixture. International Journal of Heat and Mass Transfer, 52(23–24), 5585–5590. https://doi.org/10.1016/j.ijheatmasstransfer.2009.06.021 [Google Scholar] [CrossRef]

35. Levashov, V. Y., Kryukov, A. P. (2017). Numerical simulation of water droplet evaporation into vapor-gas medium. Colloid Journal, 79(5), 647–653. https://doi.org/10.1134/S1061933X1705009X [Google Scholar] [CrossRef]

36. Van de Hulst, H. C. (1981). Light scattering by small particles. New York: Dover Publ. [Google Scholar]

37. Bohren, C. F., Huffman, D. R. (1998). Absorption and scattering of light by small particles. New York: Wiley. https://doi.org/10.1002/9783527618156 [Google Scholar] [CrossRef]

38. Mishchenko, M. I., Travis, L. D., Lacis, A. A. (2002). Scattering, absorption, and emission of light by small particles. Cambridge: Cambridge University Press. [Google Scholar]

39. Dombrovsky, L. A., Baillis, D. (2010). Thermal radiation in disperse systems: An engineering approach. New York: Begell House. [Google Scholar]

40. Hergert, W., Wriedt, T. (2012). The Mie theory: Basics and applications. Berlin: Springer. [Google Scholar]

41. Mishchenko, M. I. (2014). Electromagnetic scattering by particles and particle groups: An introduction. Cambridge, UK: Cambridge University Press. [Google Scholar]

42. Mishchenko, M. I. (2018). “Independent” and “dependent” scattering by particles in a multi-particle group. OSA Continuum, 1(1), 243–260. https://doi.org/10.1364/OSAC.1.000243 [Google Scholar] [CrossRef]

43. Fedorets, A. A., Kolmakov, E. E., Dombrovsky, L. A. (2024). A new method for precise optical measurements of the sub-micron height of levitation of droplet clusters. Particuology, 87, 173–178. https://doi.org/10.1016/j.partic.2023.08.005 [Google Scholar] [CrossRef]

44. Stull, D. R. (1947). Vapor pressure of pure substances. Organic and inorganic compounds. Industrial and Engineering Chemistry, 39(4), 517–550. https://doi.org/10.1021/ie50448a022 [Google Scholar] [CrossRef]

45. Fuchs, N. A. (1959). Evaporation and droplet growth in gaseous media. London: Pergamon Press. [Google Scholar]

46. Levashov, V. Y., Kryukov, A. P., Shishkova, I. N. (2018). Influence of the noncondensable component on the characteristics of temperature change and the intensity of water droplet evaporation. International Journal of Heat and Mass Transfer, 127B, 115–122. https://doi.org/10.1016/j.ijheatmasstransfer.2018.07.069 [Google Scholar] [CrossRef]

47. Borodulin, V. Y., Letushko, V. N., Nizovtsev, A. N., Sterlyagov, A. N. (2017). Determination of parameters of heat and mass transfer in evaporating drops. International Journal of Heat and Mass Transfer, 109, 609–618. [Google Scholar]