Thermal Assessment of a Differentially Heated Nanofluid-Filled Cavity Containing an Obstacle

Nomenclature

1  Introduction

The adoption of nanofluids in industrial and engineering fields has recently attracted much attention because of their superior thermal properties, such as superior thermal conductivity, higher thermal capacity, and reduced viscosity compared to base fluids. These particular thermal properties of nanofluids make them promising candidates for a broad range of cooling and storage applications, such as thermal management of electronic devices, energy conversion and storage systems, and solar energy systems [1–3]. Recent studies point to the significant potential of nanofluids in improving heat transfer efficiency and thermal management in a variety of applications. Hybrid nanofluids, which combine different nanoparticles, have proved particularly effective in solar collectors and thermal storage systems, offering efficient thermal storage even in diverse thermal environments [4]. Based on this point, the nanofluids integration into energy storage systems can lead to significant improvements in thermal efficiency and energy recovery, paving the way for more sustainable and efficient energy solutions. In addition, nanofluids have proved effective in addressing the challenges of heat dissipation in electronic cooling systems, positioning them as key contributors to advanced cooling technologies. All these aspects discussed prove the versatile application of nanofluids in the industrial, energy, and technological fields [5–9].

Mohebbi et al. [10] investigated the effect of roughness within a cavity on heat transfer quality using a nanofluid. They found that roughness presence disrupts the flow pattern, but only at high heat levels. While roughness does not affect heat transfer to any great extent at lower heat levels. In this context, the best arrangement of roughness elements is to place them only on the hot wall, thus maintaining good heat transfer, benefiting from the cooling effect of the roughened surface. Adding nanoparticles to the fluid slightly improves heat transfer at high heat levels. Overall, roughness is considered a significant tool for managing heat transfer in cavities, but its effectiveness depends on the heat level and how it is arranged. They also studied numerically the impact of the nanofluid on the thermal exchange evolution in an Γ-shaped cavity containing a heated rectangular block. The numerical results show that adding nanoparticles to the fluid improves heat transfer based on specific Targets. It depended on the position of the obstacle, with the left-hand side of the cavity being the most effective. Overall, nanofluids and appropriate positioning of the obstacle improve heat transfer in such geometries. Ma et al. [11] studied the utilization of nanofluids in a triangular corrugated-wall solar collector. They found that the nanoparticle’s addition and wall design impact heat transfer. It is observed that the nanoparticles’ participation in the fluid can enhance the heat transfer rate but by a reasonable percentage. In contrast, the increase in the nanoparticle reduces the heat transfer efficiency.

Ghazanfari et al. [12] analyzed the impact of Al₂O₃ nanofluids and twisted tubes on shell-and-tube heat exchanger performance. The findings demonstrated that the utilization of twisted tubes enhances heat transfer by 25% and that the incorporation of a 20% Al2O3 nanofluid augments efficiency by up to 78% while reducing pressure drop by 40% in comparison to conventional smooth tubes. These findings emphasized the potential of twisted tube designs and nanofluids for optimizing heat exchanger efficiency in applications such as nuclear energy and Heating, Ventilation, and Air Conditioning (HVAC) systems. They also investigate the potential for enhancing heat transfer in heat exchangers through the use of twisted tubes in conjunction with nanofluids, including Al2O3, Cu, CuO, and TiO2 [13]. The results of this investigation indicate that smaller pitch lengths and higher nanoparticle concentrations improve heat transfer performance, with Cu-based nanofluids achieving high thermal efficiency with an increase in pressure drop. In contrast, Al2O3 shows a balance of high thermal efficiency with a reduced pressure drop, offering valuable insights for optimizing heat exchanger designs.

Walelign et al. [14] presented an analytical investigation into the influence of varying parameters on the transport rates of a nanofluid in proximity to a cylindrical surface. The optimal homotropy analysis method was employed to examine the effects of magnetic fields, porosity, and thermos-diffusion on heat, mass, and momentum transfer rates. The findings indicate that magnetic fields and thermal radiation enhance heat transfer, whereas increased porosity or Dufour effects tend to reduce it. These insights are valuable for optimizing cooling and heating in industrial processes involving cylindrical surfaces, such as material processing and energy systems. They also investigated the heat and mass transfer dynamics in a micropolar nanofluid flow influenced by hydromagnetic effects over an inclined stretching sheet [15]. Likewise, this research is also based on the homotopy analysis method to model fluid transport rates under various physical influences, including micro-polarity, magnetic fields, buoyancy forces, and cross-diffusion effects. It focused on the examination of critical transport properties, such as linear and angular momentum, as well as heat and mass transfer rates, by calculating the Nusselt and Sherwood numbers. The results demonstrated significant interactions between the fluid’s microstructure and external forces, offering valuable insights for optimizing industrial processes involving nanofluids.

Recently, the numerical method based on the lattice Boltzmann method (LBM) has been applied to analyze the thermal pattern of nanofluid effects in different geometries [16–18]. These analyses provided precise results in pursuit of the nanofluid’s flow and its thermal behavior, which proved its capacity to get the same results as experimental examinations. Rahimi et al. [19] performed a numerical investigation of thermal transfer by natural convection in a hollow L-shaped cavity filled with nanofluid, entropy generation analysis using the LBM method. The numerical results show that the average Nusselt number and total entropy generation increase by increasing the Rayleigh number while the Bejan number decreases. They concluded from these results that the design of this system can be significant for thermal management for heat exchangers. Zhou et al. [20] studied natural convection heat transfer and entropy generation in a cavity filled with liquid nanoscale fluids (copper, diamond, or carbon nanotubes). They found that increasing the Grashof number and volume fraction of nanoparticles improved heat transfer and entropy production. It is concluded that carbon nanotube (CNT) based fluids perform best in terms of heat transfer but also generate the most entropy. This suggests that the choice of optimal fluid depends on specific needs. CNT-based fluids maximize heat transfer while minimizing temperature, while copper-based fluids are more energy-efficient for general use. Ahrar et al. [21] conducted a numerical study about heat transfer and entropy production in a nanofluid-filled cavity under the influence of a magnetic field. The results proved that raising the magnetic field strength reduced thermal exchange and entropy production. However, increasing fluid flow through a specific magnetic field angle could improve heat transfer without significantly raising the entropy generation. This suggests that magnetic field angle could be a valuable strategy for controlling heat transfer in nanofluid systems.

The results of the aforementioned studies and others demonstrated that nanofluids significantly enhance heat transfer efficiency [22–24]. Moreover, it plays a pivotal role in thermal management, contributing effectively to both energy storage systems and heat dissipation processes in cooling technologies [25,26]. Hence, the elevate of these enhancements depends on taking into consideration many factors such as nanoparticle concentration, base fluid properties, and operating conditions in different geometries. These aspects led us to a more in-depth study of typical applications, especially the cavities problem. The choice of studying the natural convection of nanofluids in a square cavity was adopted to comprehensively evaluate their performance and to observe the hydrodynamic and thermal behavior of nanofluids. This includes analyzing the impact of the base fluid and nanoparticles as a function of Rayleigh number and studying the effect of introducing an obstacle on thermal performance inside the cavity.

The present research focuses on thermal exchange evaluation and nanofluid behavior within a rectangular cavity with and without obstacles. Various parametric examinations were performed to analyze the heat transfer rate, such as Rayleigh number, nanoparticle volume fraction, based-fluid nature, and position and size of the obstacle. These parametric studies highlight the significance of nanofluid adoption for thermal systems, which provided valuable insights, especially for cooling systems for electronic devices.

2  Numerical Method

The lattice Boltzmann method is a revolutionary advance in fluid flow simulation and the modeling of thermal phenomena for different complex geometries. The LBM method, in contrast to conventional approaches, is based on the simulation of fluid flow at a specific level, which is the mesoscopic level. This feature guarantees precise results, enabling it to stand out for different situations like boundaries and interactions between fluid particles are complicated. The LBM method has several distinctive features, such as a linear particle displacement mode in velocity space and the ability to reproduce closely the Navier-Stokes equations for incompressible fluids [27]. In this study, The LBM numerical method will be utilized to investigate the thermal exchange and nanofluid flow within a differentially heated cavity. The LBM equations have been utilized to describe the fluid flow and heat transfer phenomena using the D2Q9 and D2Q5 models, respectively. These models were applied to discretize the domain of fluid flow velocity and thermal transfer [28].

2.1 Lattice Boltzmann Equation for Fluid Flow

The lattice Boltzmann method enables precise numerical simulation of fluid dynamics in contrast to conventional numerical methodologies. This approach characterizes the fluid as a unit of cohesive particles, departing from the conventional practice of individually specifying each particle or the entirety of the fluid assembly [29]. A defining feature of this method is its equation, which articulates a collective distribution function (denoted as fi) for the fluid particles. Additionally, the lattice Boltzmann equation delineates two distinct expressions, namely the propagation and the collision terms, as elucidated in the subsequent equation [30]:

fi(r+ei×Δt,t+Δt)=−1τv[fi(r,t)−fieq(r,t)]+ΔtFi,i=0,8(1)

where τv represents the relaxation time for the flow fields, and Fi is the buoyancy force presented as follows [30]:

Fi=3ωiρgβΔTei(2)

The discretization model used in this study is the D2Q9 model, which characterizes the lattice Boltzmann equation in two-dimensional space with nine discrete velocity directions. This model improves the accuracy of the numerical simulation, contributing to the method’s effectiveness in addressing complex fluid flow phenomena [31].

The discrete particle velocities ei in the D2Q9 model are defined as follows [30]:

ei={0i=0(cos⁡[(i−1)π2],sin⁡[(i−1)π2])i=1,42(cos⁡[(i−5)π2+π4],sin⁡[(i−5)π2+π4])ci=5,8(3)

The equilibrium distribution function fieq in the D2Q9 model can be derived as follows [30]:

fieq(r,t)=ρωi[1+ei.ucs2+12(ei.u)2cs4−12u.ucs2](4)

cs2 denotes the speed of sound determined by cs=1/3, and the quantity ωi is the weight coefficients, which are presented in the D2Q9 model by the following expression [32]:

ωi{49i=019i=1,4136i=5,8(5)

After the numerical calculation of the lattice Boltzmann equation, the macroscopic variables, specifically density ρ and momentum ρu, are calculated through the following expressions [30]:

ρ=∑i8fi(6)

u=1ρ∑i8fiei(7)

2.2 Lattice Boltzmann Equation for Thermal Process

The lattice Boltzmann equation utility not only comprises fluid flow behavior but also reliably simulates the thermal dynamics of fluids. The D2Q5 model, strategically designed for thermal analysis, was used to discretize the thermal lattice Boltzmann equation with five distinct thermal directions, emphasizing the detailed representation of thermal properties within the fluid. This equation can be defined as follows [30]:

gi(r+ei×Δt,t+Δt)=−1τc(gi(r,t)−gieq(r,t)),i=0,4(8)

where τc is the relaxation time for the temperature fields.

The equilibrium distribution functions for temperature gieq in the D2Q5 model are derived as follows [30]:

gieq(r,t)=ωiT[1+ei.ucs2](9)

The quantity ωi denotes the weight factors for the D2Q5 model, which are given by [30]:

ωi{26i=016i=1,4(10)

After the computational process of the thermal lattice Boltzmann equation, the macroscopic temperature is calculated using the following expression [30]:

T=∑i4gi(11)

3  Mathematical Formulation for Nanofluid Conception

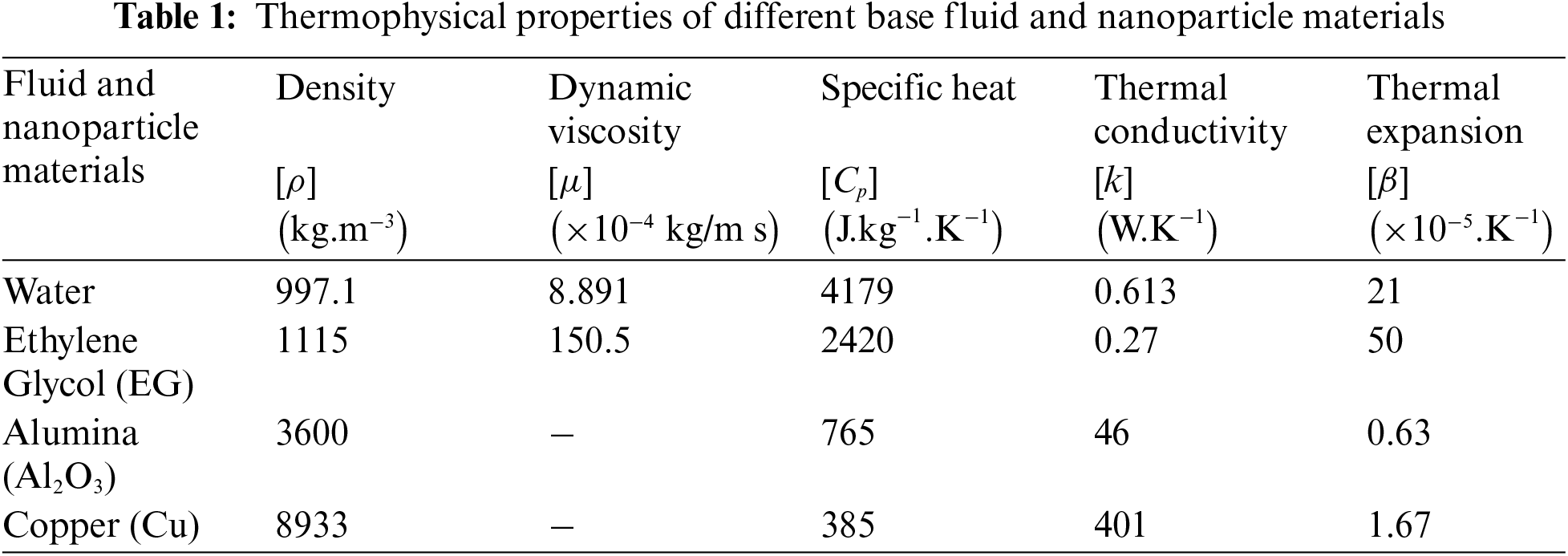
To simulate the flow of a nanofluid using the lattice Boltzmann method, it is necessary to modify the thermophysical characteristics. Due to the minute size and low concentration of nanoparticles in suspension, the mixture of solid and liquid phases is considered to be a homogeneous single-phase fluid [33]. Water is generally used as the base fluid and different types of nanoparticles are included in it [34].

To determine the effective thermo-physical properties of a nanofluid, several formulae exist in the literature, which can differ significantly. The present study focuses on examining the impact of uncertainties in the thermal conductivity and effective viscosity of the nanofluid. In this regard, the following formulae have been selected to determine the thermo-physical properties of the nanofluid [35].

Density [33–35]:

ρnf=(1−ϕ)ρf+ϕρp(12)

Coefficient of thermal expansion [36]:

βnf=(1−ϕ)βf+ϕβp(13)

Specific heat [36]:

Cnf=1ρnf[(1−ϕ)ρfCf+ϕρfCp](14)

Thermal conductivity [36]:

Knf=Kf[2Kf+Kp−2ϕ(Kf−Kp)2Kf+Kp+2ϕ(Kf−Kp)](15)

Dynamic viscosity [36]:

μnf=μf(1−ϕ)−2.5(16)

To examine the rate of heat transfer between the nanofluid and the heated walls, the local and average Nusselt number in the hot wall (Nu and Nu¯, respectively) were calculated using the following expressions [37]:

Nu=HKnfKf∂T∂x(17)

Nu¯=1H∫0HNudx(18)

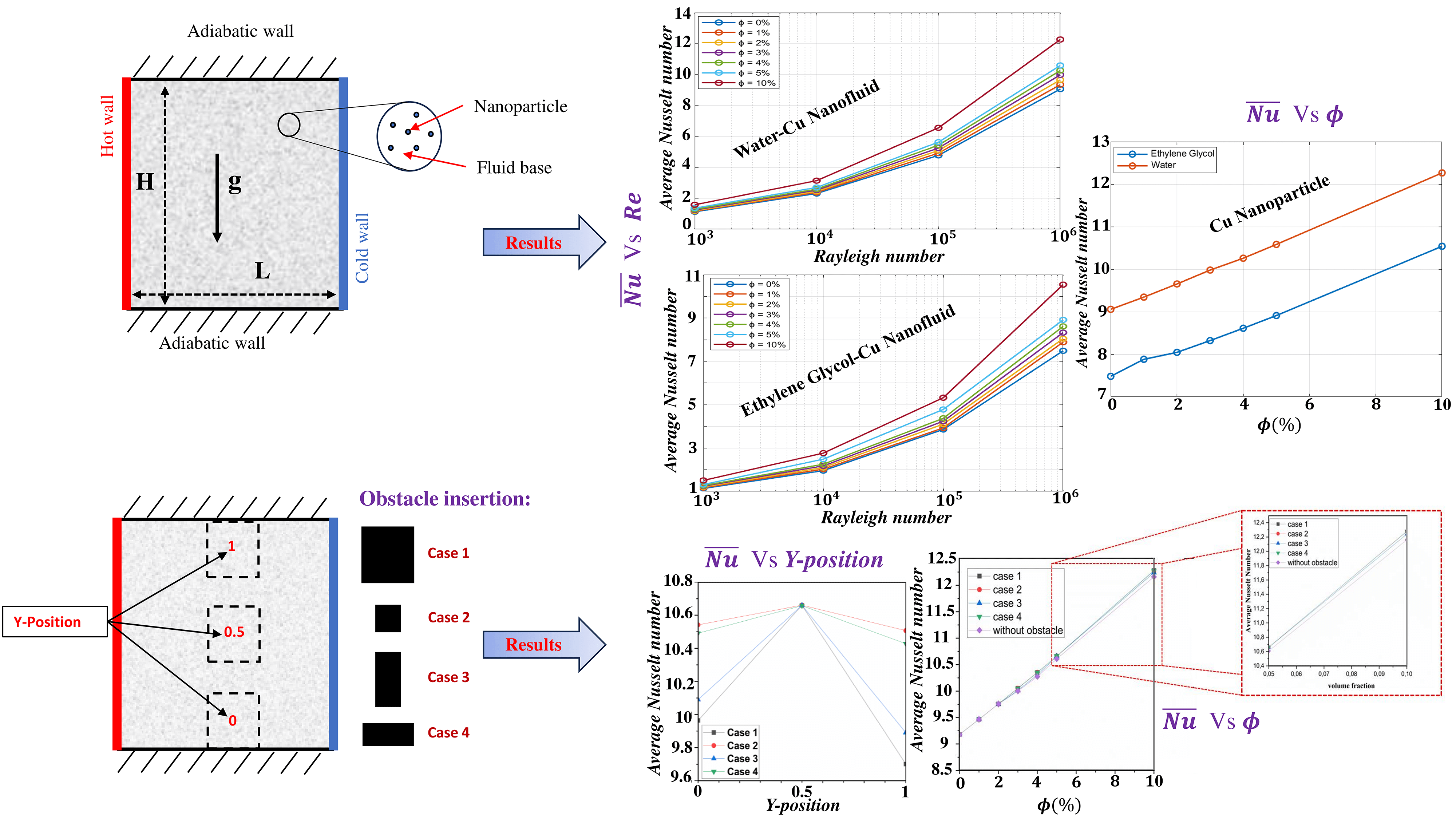
4  Statement of Studied Geometry

The cavity under study, filled with nanofluid, has the same length L, and height H, as shown in Fig. 1. In addition, its walls were defined as domain limits by applying the bounce-back boundary conditions [38]. This sort of boundary condition is realized by setting the incoming distribution as equal to the outgoing distribution after interacting with the wall and bouncing back into the flow region. Mathematically, this condition is represented as follows [39]:

fi(x,y)=fi¯(x,y)(19)

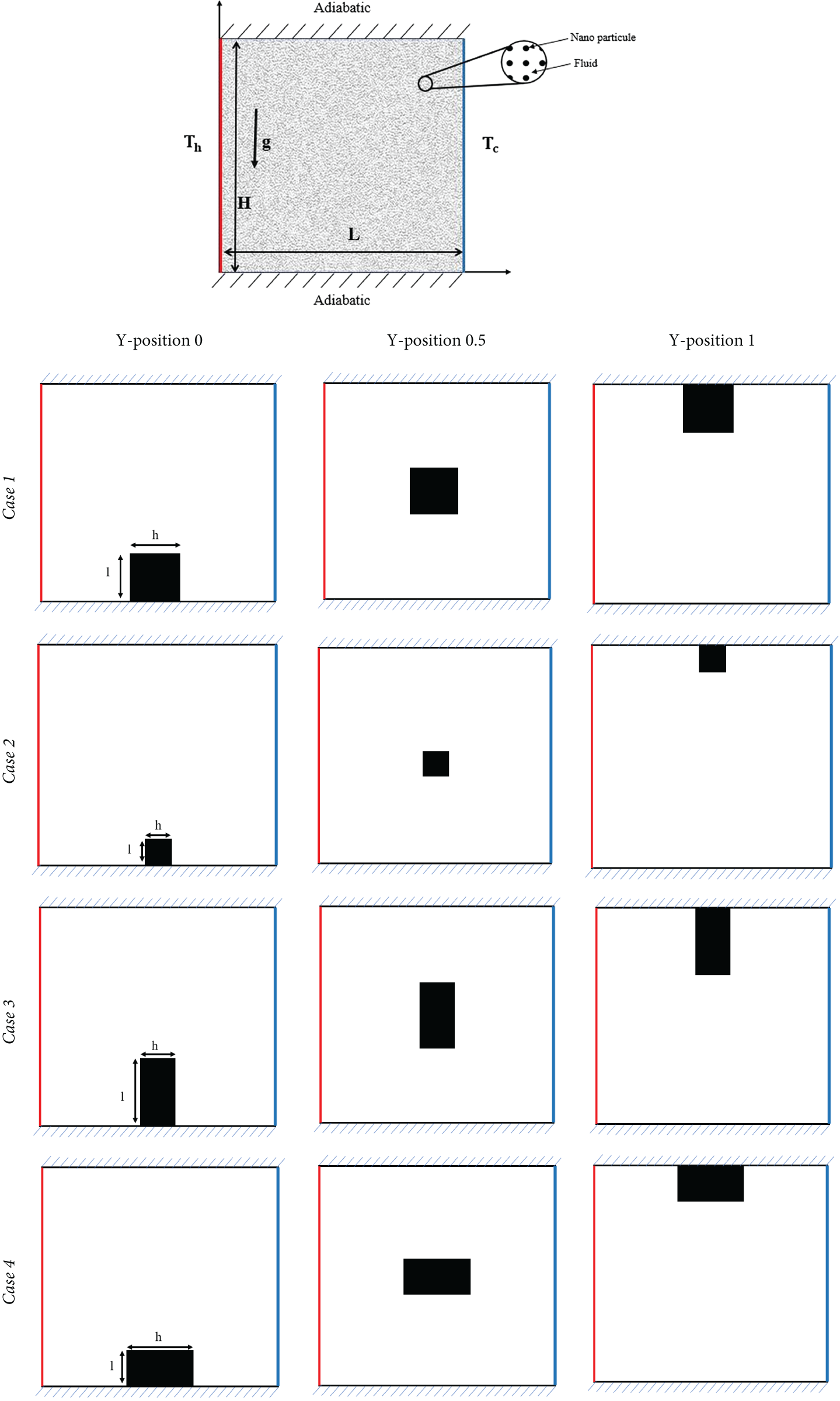
Figure 1: Geometries structure under study

The quantities of fi and fi¯ denote the pre- and post-collision distribution functions, respectively, and i represents the lattice velocity direction.

Concerning the obstacle contained in the cavity, its position and dimensions study is carried out, where the bounce-back boundary conditions are used to describe this obstacle for four different cases (see Fig. 1).

For the thermal specifics of the system under study, the upper and lower cavity walls are considered insulated by applying the Neumann boundary condition for the expression obtained by a heat flux equal to zero [39]:

gi(x,y)=gi¯(x,y)(20)

The right and left walls are maintained at cold (Tc=−0.5) and hot (Th=0.5) dimensionless temperatures, respectively (see Fig. 1). The conditions used to describe the wall temperature can be expressed in a general form [30]:

gi(x,y)=Tw(ωi+ωi¯)−gi¯(x,y)(21)

Nanofluids used for the present study have been formulated utilizing either water or ethylene glycol as the fluid basis, incorporating nanoparticles such as copper or alumina (see Table 1). The thermophysical characteristics of nanoparticles dispersed in the base fluid are critical factors in enhancing the heat transfer quality.

5  Numerical Results and Discussion

The present study aims to analyze the nanofluid’s flow behavior and heat transfer rate employing the LBM-SRT method. The primary investigations focus on model validation, mesh independence, the effects of nanoparticle type, Rayleigh number, and fluid base on heat exchange and heat transfer rates. The purpose of the study is to better understand the hydrodynamic and thermal effects of nanofluids and their essential role in improving heat transfer to find ideal solutions for optimizing cooling performance.

5.1 Validation Model

Numerical validation is an essential aspect of computational research, as it verifies the numerical accuracy of models. This process involves a rigorous examination of model predictions with experimental or theoretical data, ensuring alignment and reinforcing the model’s credibility. By demonstrating agreement with established knowledge, validation inspires confidence in the model’s ability to accurately represent real-world phenomena. This essential step protects against inaccuracies and strengthens the scientific basis of research.

Table 2 displays the average Nusselt number values obtained using the LBM-SRT method which is compared with previous research for different Rayleigh numbers. The results suggest that the mean Nusselt number values obtained in the present study are marginally higher than those reported in the other studies, especially for lower Rayleigh numbers (see Table 2). Despite these slight differences, one can observe an excellent agreement between the present study and previous studies [22,36,40]. This indicates that the results of the present study are reliable and consistent with previous research.

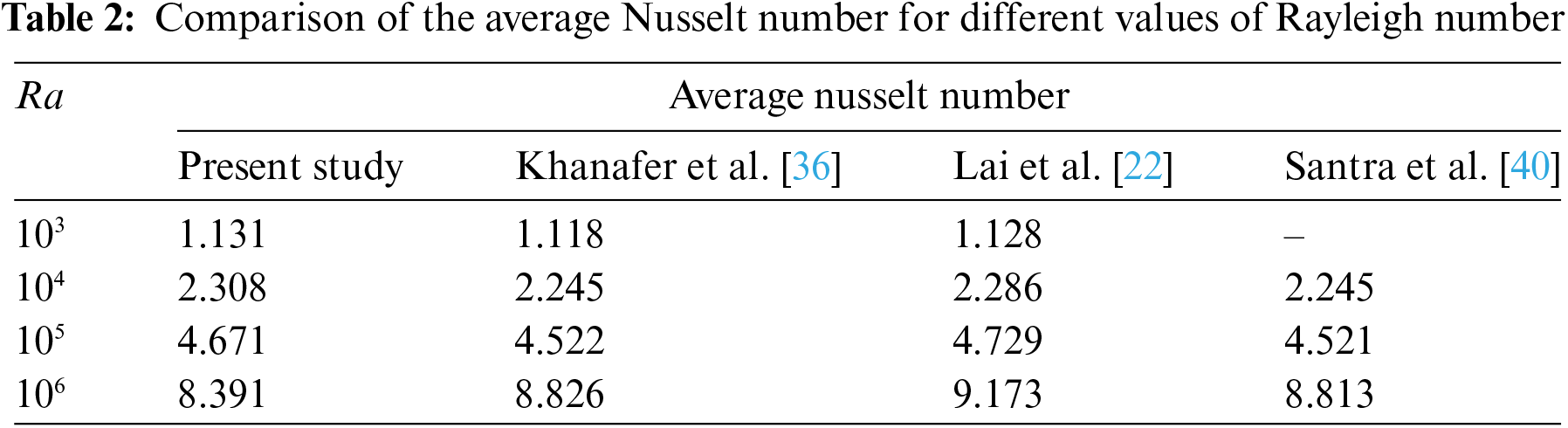
To further validate the results presented in Table 2, we also calculated the root mean square error (RMSE) and mean absolute error (MAE) to make a quantitative comparison with the results reported by Khanafer et al. [36]. The analysis yielded a mean absolute error of 0.165 and a mean square error of 0.232, indicating a high level of consistency between our study and the reference results.

Fig. 2 displays the average Nusselt number calculated using the LBM-SRT method and previous research for different Grashof numbers and nanoparticle volume fractions. The results reveal excellent consistency between the current study and those reported by Khanfar et al. [36].

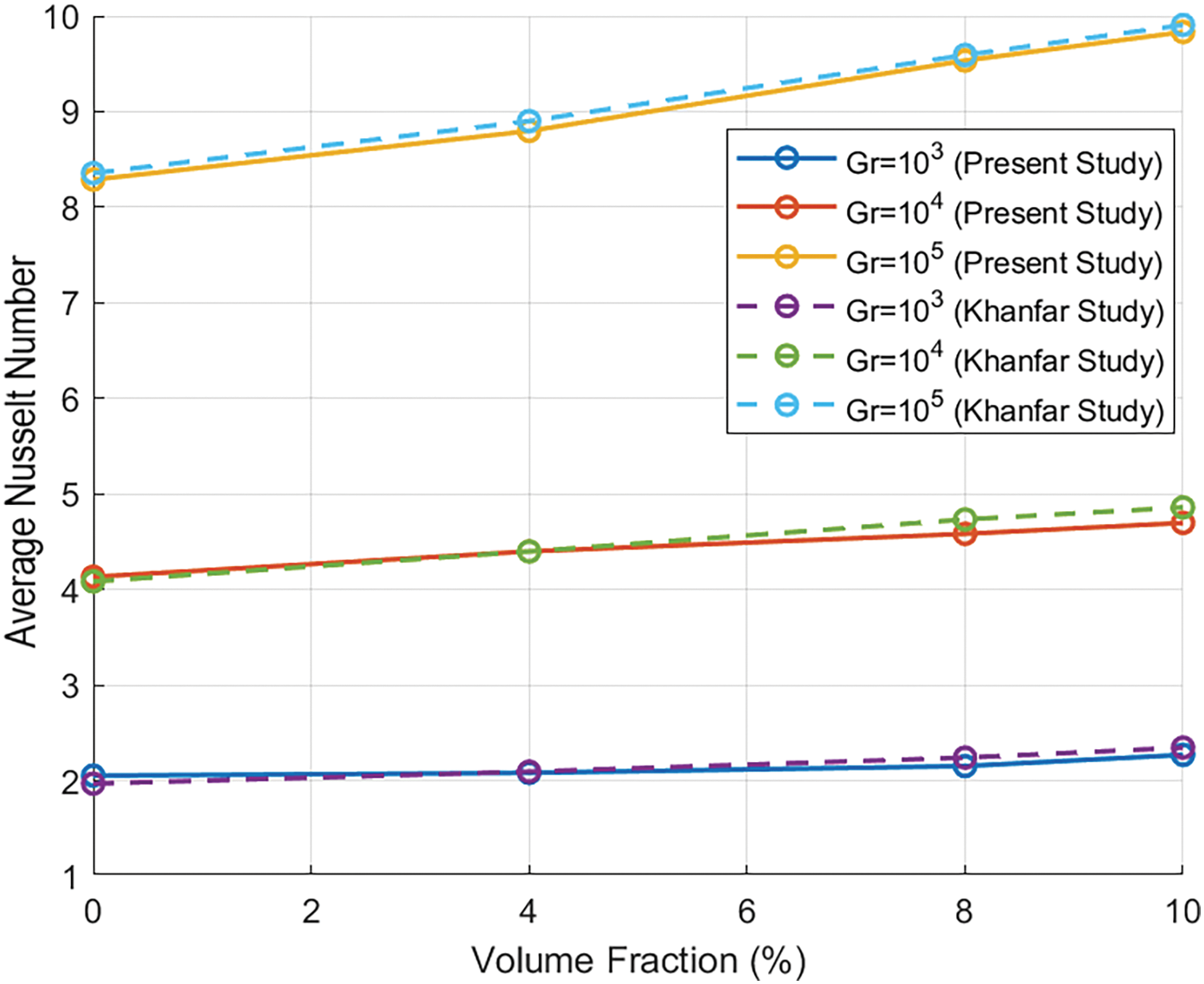
Figure 2: Comparison of the average Nusselt number for different values of Grashof number and volume fraction [36]

Fig. 3 shows a comparison between the temperature profile obtained with the LBM-SRT method and that obtained by Khanafer et al. [36]. The temperature profiles show a good consistency, demonstrating the reliability of our numerical approach. Based on these validation and comparison studies, it can be concluded that the adopted method is reliable and consistent for studying the problem of nanofluid flow and heat transfer for different geometries.

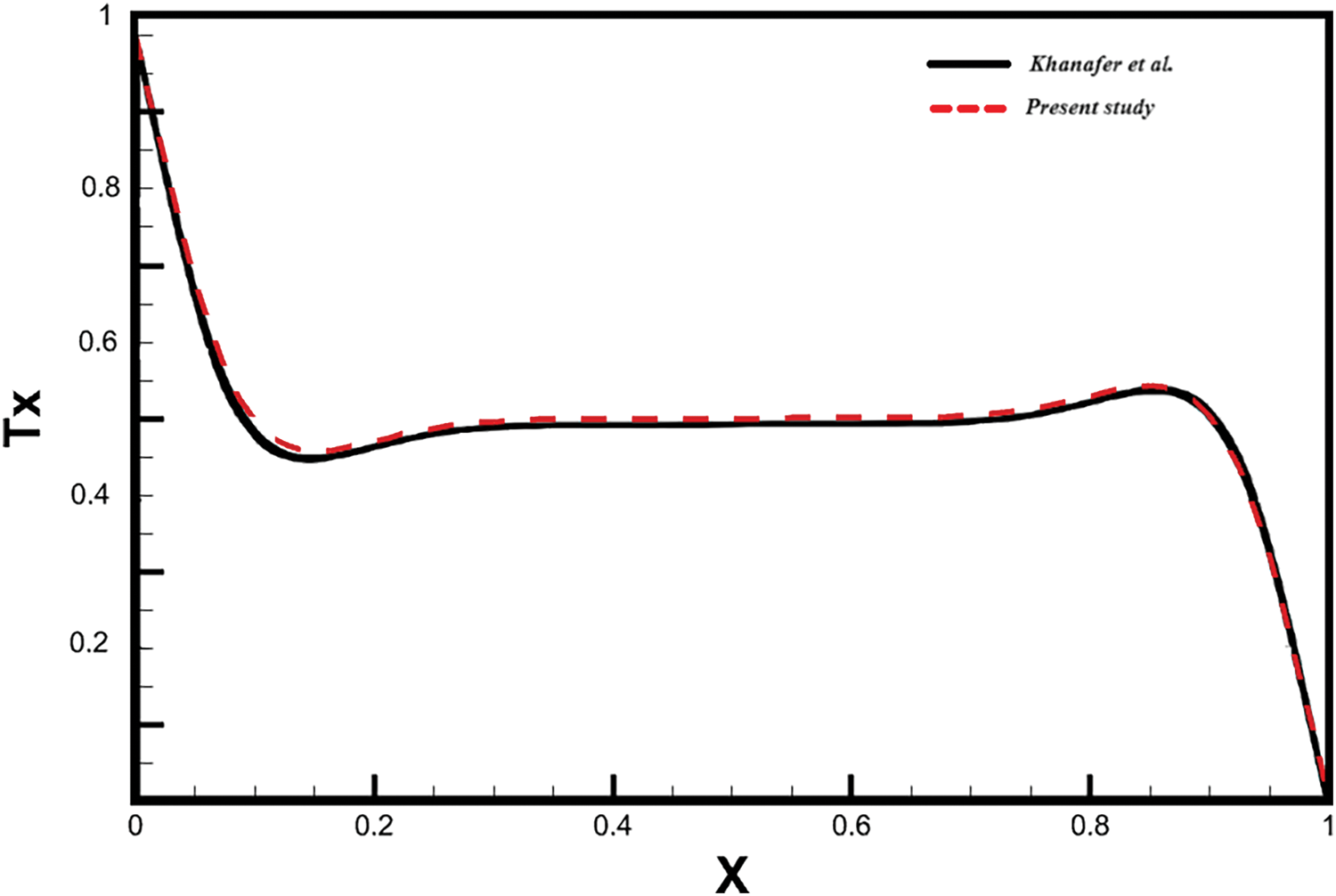
Figure 3: Temperature profiles at mid-sections of the cavity for Gr=105, Pr=6.2, and ϕ=5% [36]

5.2 Mesh Independency Study

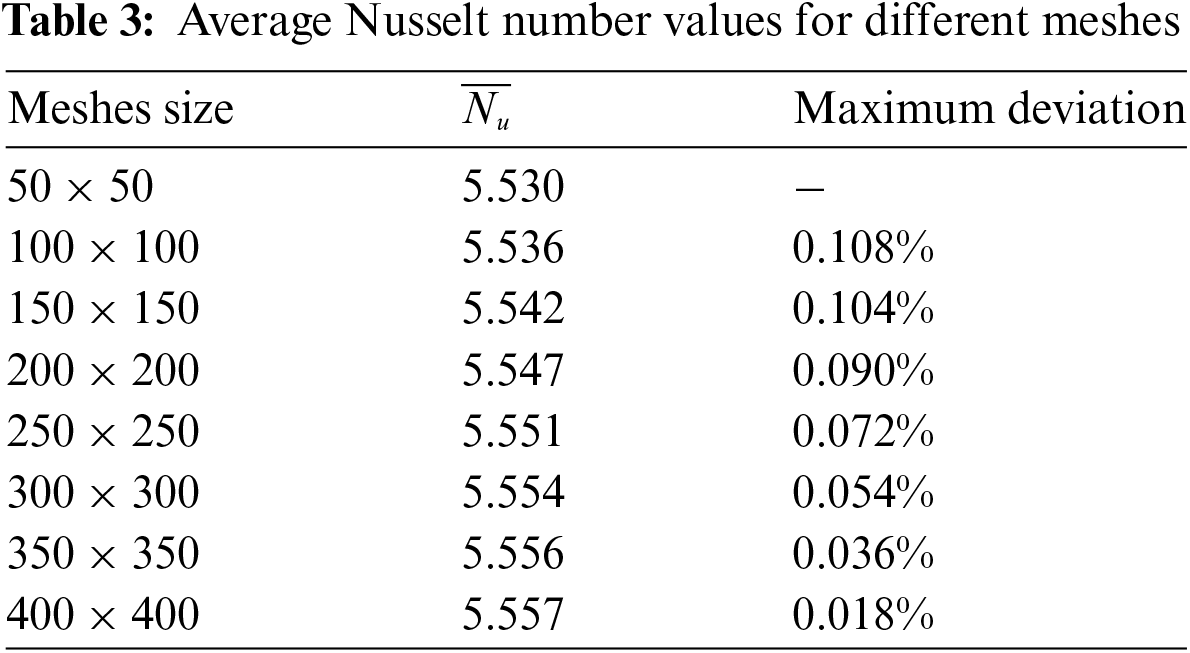
Mesh study is considered an essential tool for verifying the independence between numerical results and the mesh used. This analysis also focuses on determining the optimum mesh size for numerical simulations, balancing computation time and accuracy.

Table 3 illustrates the average Nusselt number for various mesh sizes. It can be seen that the Nu¯ values increase with mesh size up to a specific limit, after which the Nu¯ results become relatively constant, indicating that simulation accuracy improves with larger mesh sizes. In this study, the 100×100 mesh was chosen as the optimal mesh size for all simulations because of its low maximum deviation compared to other mesh sizes. Furthermore, this mesh size offers a good balance between accuracy and computational cost.

Regarding numerical stability criteria, we have computed the evolution of the average Nusselt number as a function of the number of iterations for a Rayleigh number equal to 106 and a nanoparticle volume fraction equal to 10% (see Fig. 4). During the initial stages of the numerical calculation, the average Nusselt number undergoes a pronounced fluctuation, reaching a maximum value of around 180 during the transient phase and then establishing stable patterns. As the number of iterations increases, the fluctuations decrease and the Nusselt number approaches a stable value of around 12. This stability is observed from the 200,000th iteration onwards, proving that the system has achieved numerical stability under these conditions. These results validate the numerical setup, including grid resolution, and the correct implementation of the boundary conditions, guaranteeing accurate predictions of heat transfer characteristics and nanofluid flow behavior under the given parameters.

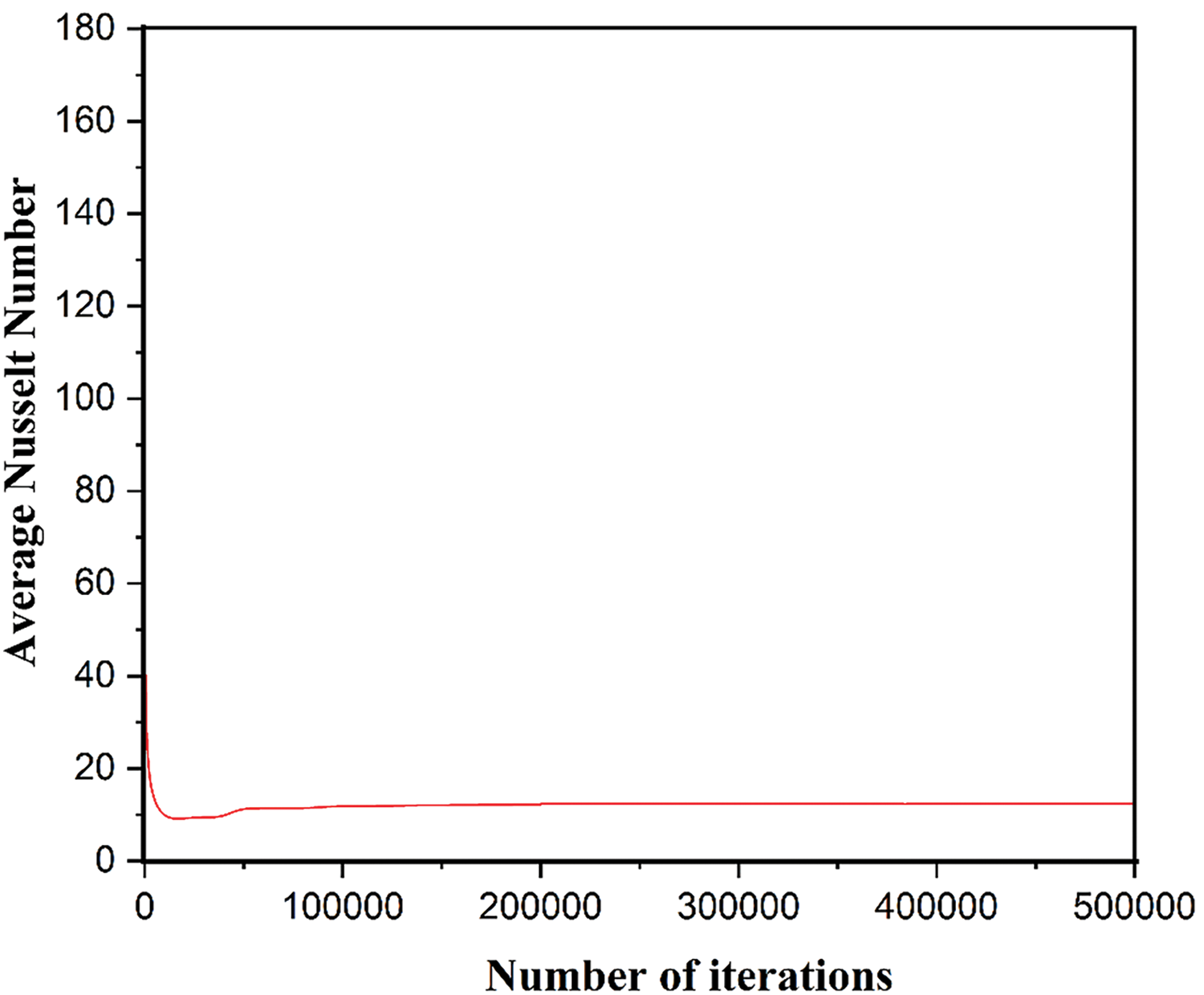
Figure 4: Average Nusselt number vs. iteration number for Ra=106 and ϕ=10%

5.3 Effect of the Nanoparticle Type and Rayleigh Number on the Thermal Exchange

The effect of nanoparticle kind and Rayleigh number has been examined in this section to track the evolution of thermal transfer and flow behavior. Fig. 5 illustrates the streamlines and isotherms for water and water-Cu with different nanoparticle volume fractions (ϕ=5% and ϕ=10%) at various Rayleigh numbers (Ra). At low Ra values, the fluid flow is dominated by viscous forces, and a central vortex dominates the flow. On the other hand, as Ra increases, buoyancy-induced flow becomes more important, and the shape of vortices may change due to thermal diffusion. These remarks can also be deduced for water-Cu with different volume fractions (see Fig. 5).

Figure 5: Comparison of streamlines and isotherms for different Rayleigh numbers: water (black-lines), water-Cu with ϕ = 5% (red-lines), and water-Cu with ϕ = 10% (blue-lines)

Adding copper nanoparticles to the water increases the strength of the streamlines, resulting in the deformation of the center vortex and higher velocities at the cavity center when going from low Ra to high Ra. It can be seen that the isotherms are affected by the thermal diffusion of the nanofluid, and higher volume fractions may lead to changes in the vertical stratification of isotherms (see Fig. 5).

The analysis of the average Nusselt number was conducted for a variety of nanoparticles to pursue the heat transfer evolution inside the cavity. Fig. 6 shows the average Nusselt number as a function of the Rayleigh number for two different nanoparticles, alumina (Al2O3) and copper (Cu), dispersed with various volume fractions (ϕ) in pure water. It can be observed that the Nu¯ values increase with volume fraction and Rayleigh number for both nanoparticles used, indicating an improvement in heat transfer. This improvement in heat transfer is due to the thermal properties of the nanoparticles used, which are characterized by high thermal conductivity.

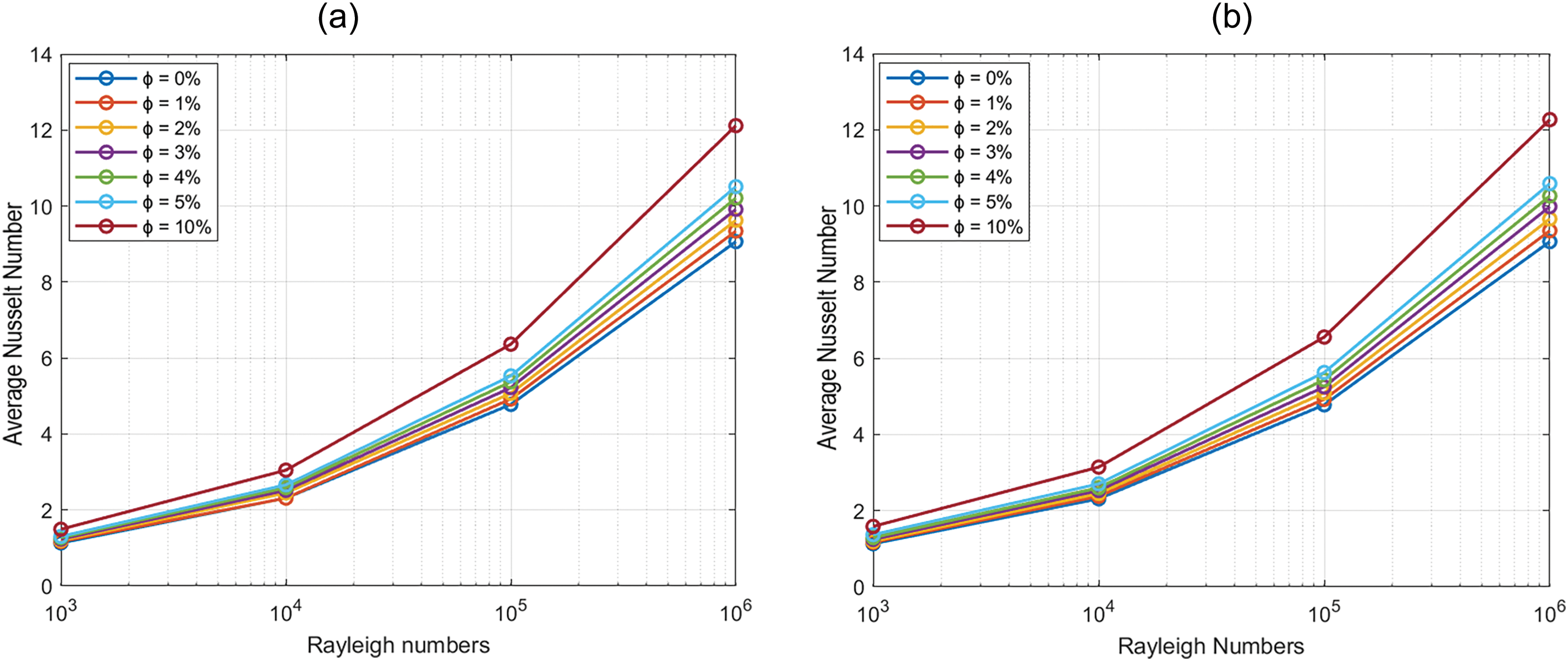
Figure 6: Evolution of average Nusselt number for different Rayleigh numbers and volume fractions (ϕ): (a) water-Cu, (b) water-Al2O3

Comparing the introduction of nanoparticles (Cu and Al2O3) into pure water, it is observed that at low Rayleigh numbers (Ra = 103), the improvement in heat transfer is approximately 1% higher for the water-Cu nanofluid than for the water-Al2O3 nanofluid. This result is attributed to the predominance of conductive heat transfer at low Rayleigh numbers, where the superior thermal conductivity of copper nanoparticles enhances thermal performance. Conversely, at higher Rayleigh numbers (Ra = 106), where natural convection becomes the dominant heat transfer mechanism, the performance difference between the two nanofluids becomes negligible, with only a 0.24% improvement for the Cu-water nanofluid. This indicates that when convective heat transfer becomes the dominant mechanism, the influence of nanoparticle thermal conductivity on overall heat transfer diminishes.

The following study focuses on a comparison of the evolution of the average Nusselt number as a function of volume fraction for two different nanoparticles (Cu and Al2O3) for the same base fluid (pure water) and a Rayleigh number equal to 106. The results observed in Fig. 7 show that the switch of nanoparticles dispersed in pure water exhibits slightly elevated average Nusselt number values for different volume fractions, where the use of Cu nanoparticles showed an enhancement in heat transfer rate compared to Al2O3 nanoparticles, with an average difference of around 0.08%–1.22%.

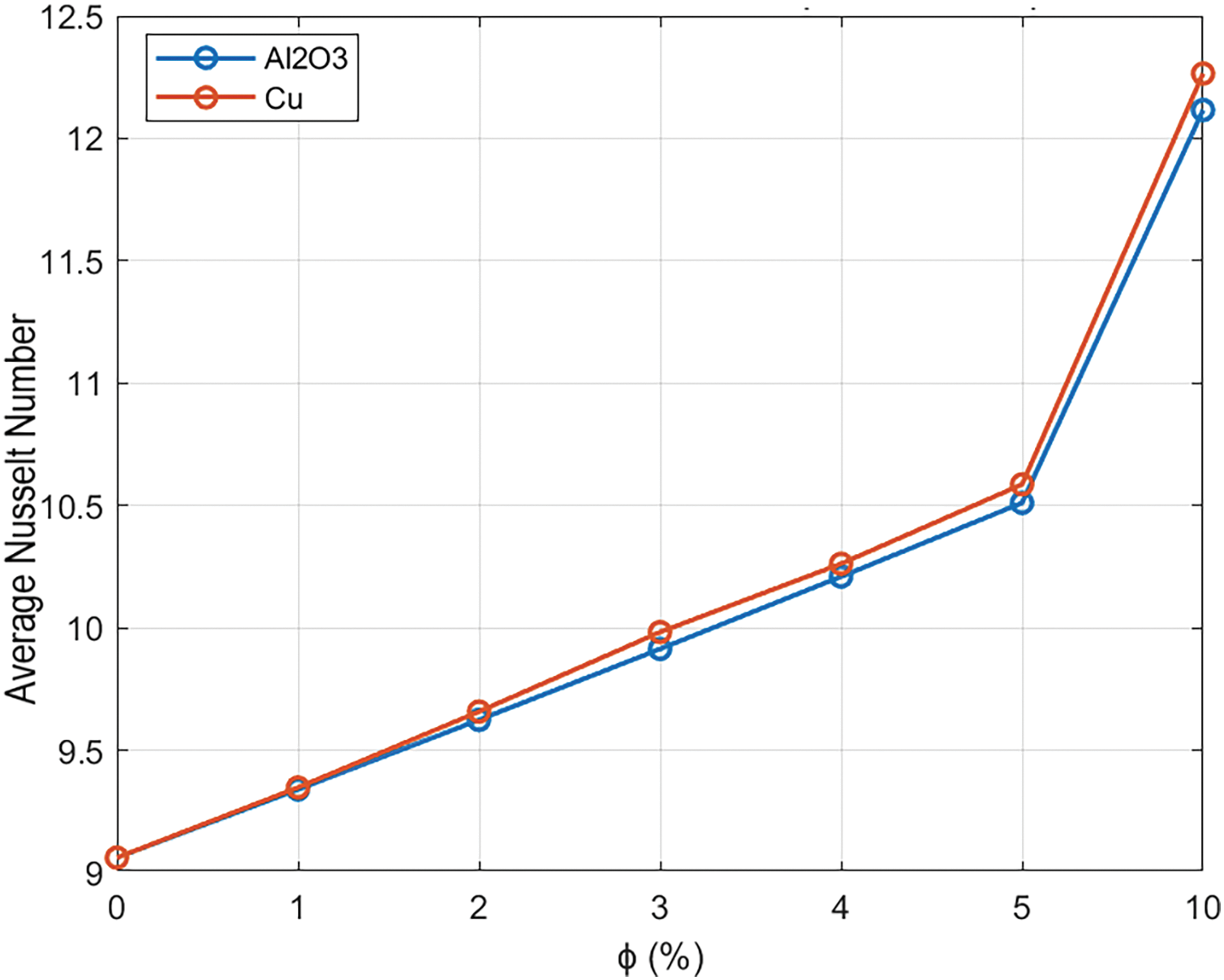
Figure 7: Effect of Cu and Al2O3 nanoparticles on the evolution of average Nusselt number for different volume fractions (ϕ) at Ra=106

5.4 Effect of the Fluid Basis and Rayleigh Number on the Heat Transfer Rate

This section examines the evolution of heat transfer quality for different types of fluid (water or ethylene glycol) when copper nanoparticles are incorporated. Fig. 8 demonstrates the average Nusselt number evolution under the effect of the volume fraction of copper nanoparticles for water and ethylene glycol. It can be seen that an increase in the volume fraction of nanoparticles leads to an augmentation of the average Nusselt number for both water-Cu and EG-Cu for several values of the Rayleigh number.

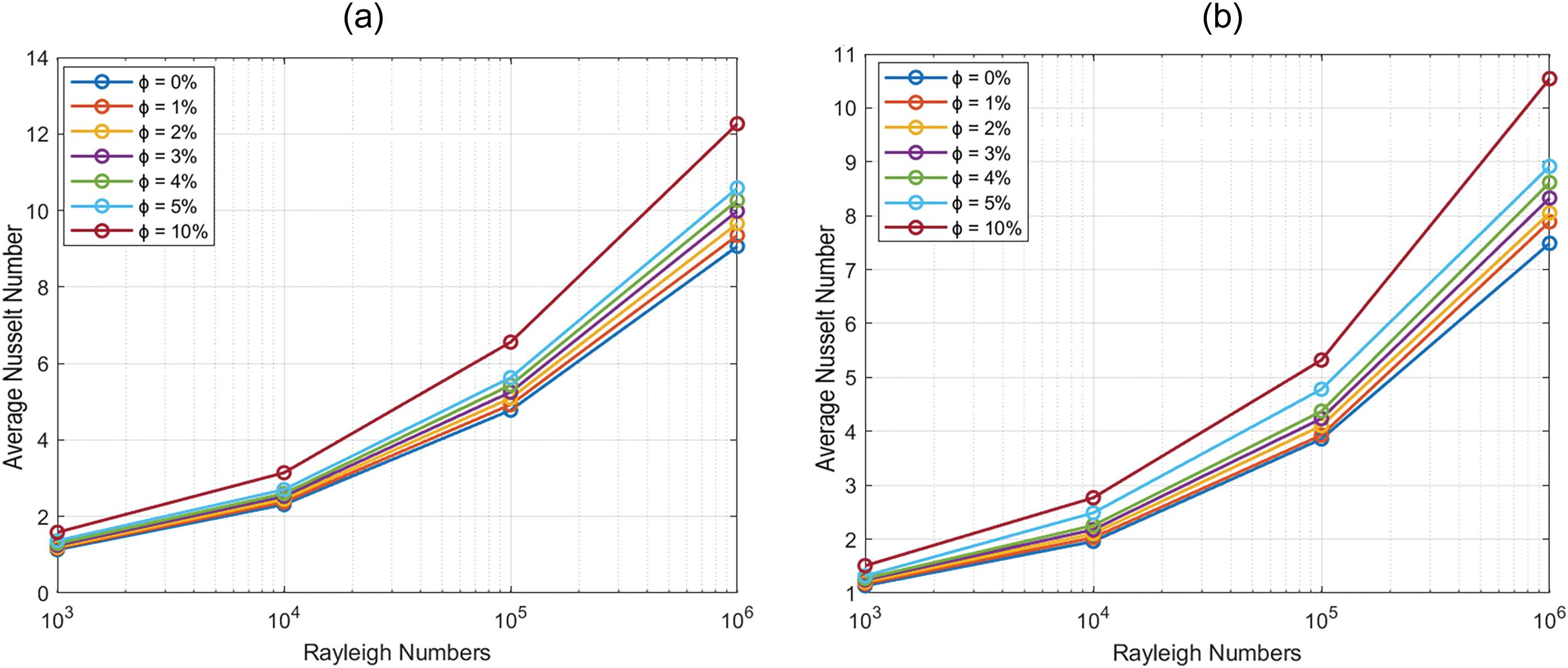
Figure 8: Evolution of average Nusselt number for different Rayleigh numbers and volume fractions (ϕ): (a) water-Cu, (b) ethylene glycol-Cu

Assessment of heat transfer quality was also studied to compare the influence of changing the fluid basis for different nanoparticle volume fraction values at Ra=106. Fig. 9 reveals that the average Nusselt number values for water-Cu exceed the values obtained for EG-Cu by around 14%–17%  for different volume fractions. These disparities are due to the thermal properties of water vs. ethylene glycol, specifically the thermal conductivity and specific heat capacity. Consequently, the water-Cu nanofluid use offers better convective thermal exchange performance than the EG-Cu nanofluid under similar thermal conditions.

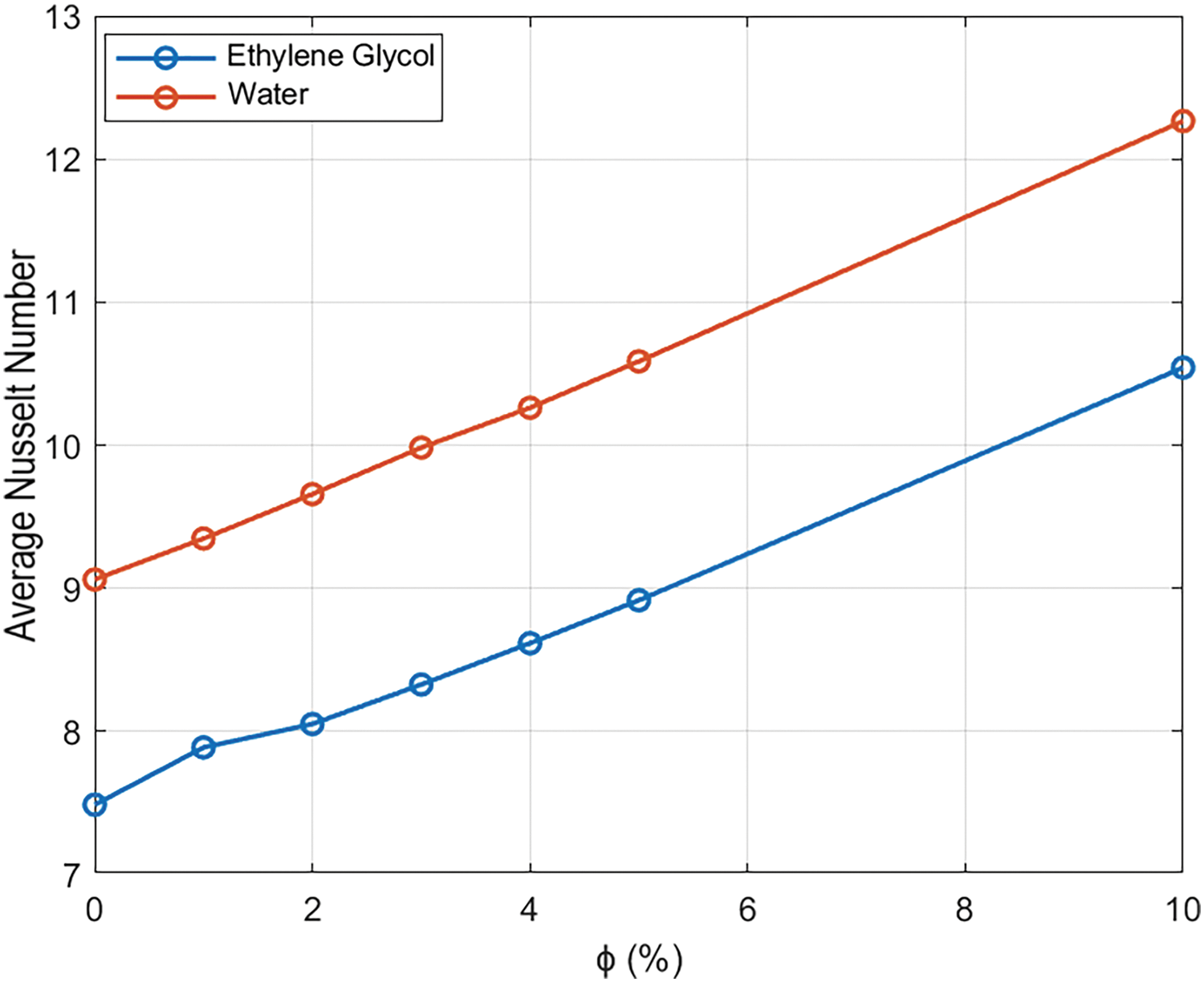
Figure 9: Fluid type impact on the evolution of average Nusselt number for different volume fractions (ϕ) at Ra=106

5.5 Impact of an Obstacle Dimension and Position on Nanofluid Behavior and Thermal Exchange Quality

The study of the obstacle effect inside a differentially heated cavity containing the water-Cu nanofluid was conducted with a volume fraction equal to 5% and a Rayleigh number equal to 106. This study aims to evaluate the effect of obstacle size and positioning on heat transfer enhancement along the hot cavity wall. Four cases were studied in which the obstacle dimensions vary according to three positions (see Fig. 1): the first position is located at the cavity base (Y-position 0), the second position is situated at the cavity center (Y-position 0.5), and the third position is at the cavity ceiling (Y-position 1).

Fig. 10 shows the obstacle effect on the streamlines of the water-Cu nanofluid. It can be seen that the presence of the obstacle within the cavity changes the shape and intensity of the streamlines, especially when the obstacle is oversized (Case 1) or when it is positioned in mid-cavity (Y-position 0.5). It can also be seen that positioning the obstacle at the base of the cavity (Y-position 0) gives symmetrical streamlines in comparison with positioning the obstacle at the cavity ceiling (Y-position 1). While the rotating vortex has become composed of two inner vortices due to Y-position 0.5.

Figure 10: Streamlines of water-Cu nanofluid for various cases at Ra=106 and ϕ=5% 

Concerning the thermal field, Fig. 11 displays the effect of obstacle size and positioning on the temperature lines for Ra=106 and ϕ=5%. It can be noted that the presence of the obstacle at Y-position 0 and Y-position 1 influences the thermal behavior of the nanofluid, where the isotherms’ stratification becomes less pronounced. In contrast, the isotherms retain their stratification when the obstacle is at Y-position 0.5. It can be interpreted that when the obstacle is situated at the base of the cavity, it will prevent cold nanofluid flow toward the hot wall of the cavity. Likewise, the obstacle positioning at the top of the cavity will prevent hot nanofluid flow toward the cold wall of the cavity.

Figure 11: Isotherms of water-Cu nanofluid for various cases at Ra=106 and ϕ=5% 

After investigating the effect of the obstacle on the behavior of the nanofluid flow and the evolution of the thermal pattern, the remainder of this study will focus on evaluating the quality of heat transfer near the hot cavity wall and highlighting the best scenarios for improving heat transfer with the presence of the obstacle.

Fig. 12 shows the evolution of the average Nusselt number vs. obstacle position for the four cases studied earlier. It can be noted that the best scenario in which the Nu¯ registers high values was obtained for Case 2, followed by Cases 4, 3, and 1. The substantial increase in the average Nusselt number in Case 2 can be attributed to the diminutive dimensions of the obstacle, making its influence negligible compared to the other cases. This matter underlines the minimal impact of the obstacle on heat transfer in this scenario. Consequently, there is a notable improvement in the heat transfer rate by an average of 5% at Y-positions 0 and 1 for Case 2 compared to other cases. This superior thermal performance in Case 2 is explained by the reduced dimensions of the obstacle, which does not block the nanofluid flow toward the hot and cold walls. As a result, heat exchange performance is higher than in the other cases. In contrast, the larger obstacle in Case 1 impedes the flow, resulting in lower thermal performance.

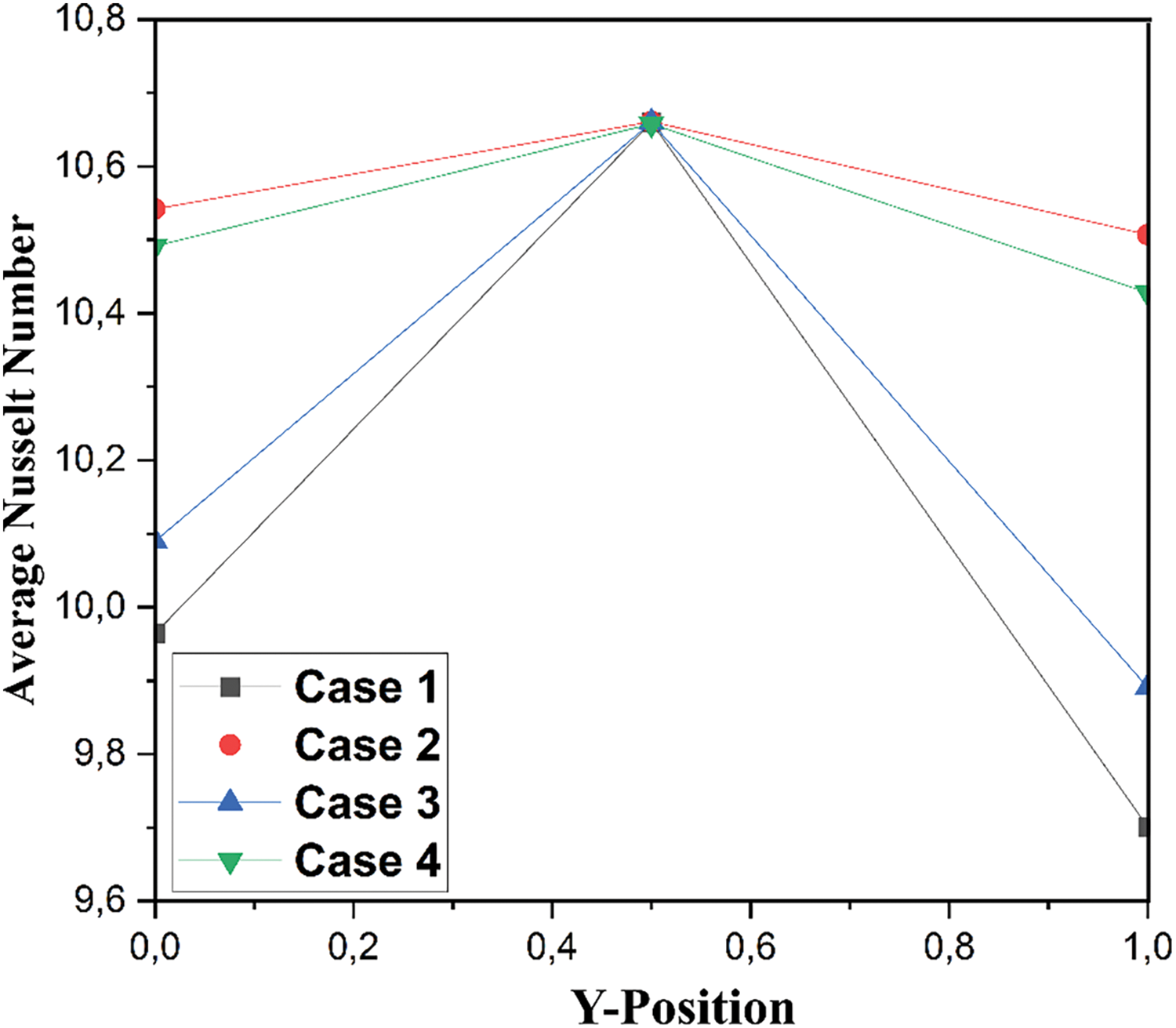
Figure 12: Evolution of the average Nusselt number for various cases with three different positions of the obstacle for Ra=106 and ϕ=5% 

Regarding the positional impact of the obstacle, it is noteworthy that the Nu¯ exhibits substantial values at the mid-cavity position (Y-position 0.5). Consequently, regardless of the case, optimal placement of the obstacle to enhancing heat transfer efficiency occurs at the mid-cavity (see Fig. 12). This improvement is particularly pronounced in Case 2, where the heat transfer quality reached around 1.5%−9.7%. These results suggest that optimizing the dimensions and positioning of obstacles can lead to more efficient thermal management in practical applications, such as cooling systems, by balancing flow disturbance and heat transfer performance.

Performance evaluation of heat transfer where the obstacle is in the mid-cavity has been carried out in this part to prove the best scenarios offering significant improvement. Fig. 13 presents the Nu¯ evolution as a function of nanoparticle volume faction at a fixed Rayleigh number (Ra=106). At low-volume fractions (1% and 2%), the thermal performance in all cases is almost identical. This indicates that the geometry and position of obstacles do not influence thermal exchange quality. At a volume fraction equal to 3%–5%, the discrepancies between the cases and the configuration without obstacles become slightly pronounced. For example, at a volume fraction of 3%, the average Nusselt numbers for all cases exhibit a medium degree of convergence, indicating that the influence of the obstacle designs and position become slightly observed on heat transfer under these conditions. At higher volume fractions, especially at 10%, Case 2 has the highest heat transfer efficiency compared with the other cases and the configuration without obstacles. To illustrate, Case 2 shows a 0.98% improvement over the configuration without obstacles and marginal deviations from other cases. These deviations can be attributed to the geometry and positioning of the obstacle, which affects flow patterns and thermal gradients inside the cavity. It can be deduced that Case 2 shows a significant improvement in heat transfer rate over the other cases.

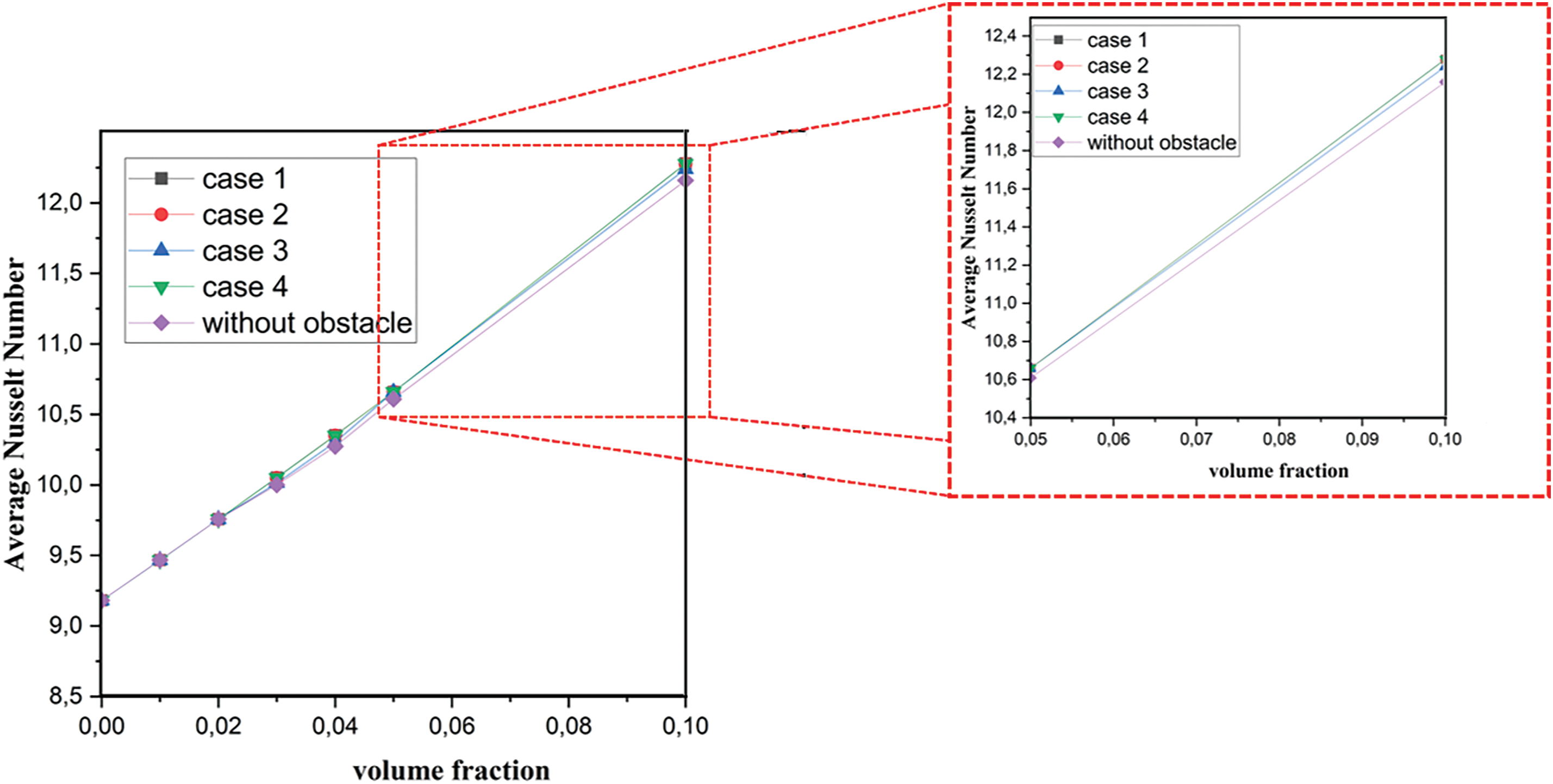
Figure 13: Impact of the obstacle presence at the mid-cavity on the evolution of the average Nusselt number for different volume fractions of nanoparticles at Ra=106

6  Conclusion

The current research focuses on the numerical study of the thermal assessment of a differentially heated nanofluid-filled cavity with and without an obstacle. The lattice Boltzmann method associated with single relaxation time was used to analyze the heat transfer and nanofluid flow in various scenarios to find the best benchmark that enhances the heat transfer quality. This numerical approach was compared and validated with previous studies to verify the validity and consistency of the used approach compared with other methods. The numerical comparisons show a good agreement, making the LBM-SRT method a good tool for studying the problem of heat transfer and nanofluid flow with high precision. Several parameters were examined in this research to evaluate the heat transfer inside the nanofluid-filled cavity, such as the type and volume fraction of nanoparticles, Rayleigh number, type of fluid basis, and the position and dimension of the obstacle inside the cavity. Key findings and potential optimization strategies can be summarized as follows:

–   The increase in Rayleigh number increases the buoyancy force, where the vortices’ structure changes due to thermal diffusion. These remarks can also be deduced for all nanofluids studied with different volume fractions. As a result, this increase in Ra enhances heat transfer efficiency for all configurations studied.

–   The use of nanoparticles with higher thermal conductivity induces a slight augmentation of the heat transfer quality, where the Cu nanoparticles use showed an enhancement compared to Al2O3 nanoparticles, with an average difference of around 0.08%–1.22%.

–   The Increases in nanoparticle concentration generally led to improved heat transfer for all nanoparticles used.

–   Water-Cu nanofluids present better heat transfer performance than ethylene glycol-Cu nanofluids under similar conditions with an improvement of around 14%–17%.

–   The presence of obstacles at either the bottom or top of the cavity results in a decline in the overall heat transfer rate for all cases. However, there is a notable improvement in the heat transfer rate by an average of 5% at Y-positions 0 and 1 for Case 2 compared to other cases.

–   The obstacle presence at the mid-cavity improves the heat exchange rate by around 1.5%−9.7%.

These results have important implications for engineering and industrial applications, especially for the improvement of thermal management systems. The optimized obstacle design and strategic placement demonstrated in this study can be directly applied to improve the efficiency of cooling systems, thermal energy storage units, and heat exchangers. Such advances are particularly relevant to industries requiring precise temperature control, including renewable energy systems, electronics cooling, ventilation, and air-conditioning technologies, thus contributing to improved performance and energy sustainability.

This study provides valuable insights into convective heat transfer in nanofluid-filled cavities but is subject to certain limitations. The analysis is limited to Three nanofluid types (water-Cu, ethylene glycole-Cu, and water-Al2O3), fixed obstacle geometries, and equilibrium conditions. In future work, we aim to address these limitations by exploring other nanofluids, including hybrid and biological options, analyzing the effects of different obstacle shapes and orientations, and incorporating transient heat transfer behaviors. In addition, we intend to extend the study to more complex systems and investigate advanced applications, such as heat sinks and immersion cooling technologies, to enhance the practical applicability of the results.

Acknowledgement: The authors would like to express their gratitude for the invitation to submit this paper to FHMT-Frontiers in Heat and Mass Transfer. We also extend our sincere appreciation to the reviewers for their constructive feedback, which greatly enhanced the quality of this article.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Abdelilah Makaoui, El Bachir Lahmer, Jaouad Benhamou; data collection: Abdelilah Makaoui; analysis and interpretation of results: El Bachir Lahmer, Jaouad Benhamou, Mohammed Amine Moussaoui, Ahmed Mezrhab; draft manuscript preparation: Abdelilah Makaoui, El Bachir Lahmer, Mohammed Amine Moussaoui. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Aglawe KR, Yadav RK, Thool SB. Preparation, applications and challenges of nanofluids in electronic cooling: a systematic review. Mater Today: Proc. 2020;43(1):366–72. doi:10.1016/j.matpr.2020.11.679. [Google Scholar] [CrossRef]

2. Saidina DS, Abdullah MZ, Hussin M. Metal oxide nanofluids in electronic cooling: a review. J Mater Sci: Mater Electr. 2020;31(6):4381–98. doi:10.1007/s10854-020-03020-7. [Google Scholar] [CrossRef]

3. Nobrega G, de Souza RR, Gonçalves IM, Moita AS, Ribeiro JE, Lima RA. Recent developments on the thermal properties, stability and applications of nanofluids in machining, solar energy and biomedicine. Appl Sci. 2022;12(3):1115. doi:10.3390/app12031115. [Google Scholar] [CrossRef]

4. Croitoru C, Bode F, Calotă R, Berville C, Georgescu M. Harnessing nanomaterials for enhanced energy efficiency in transpired solar collectors: a review of their integration in phase-change materials. Energies. 2024;17(5):1239. doi:10.3390/en17051239. [Google Scholar] [CrossRef]

5. Moita A, Moreira A, Pereira J. Nanofluids for the next generation thermal management of electronics: a review. Symmetry. 2021;13(8):1362. doi:10.3390/sym13081362. [Google Scholar] [CrossRef]

6. Wang Y, Zou C, Li W, Zou Y, Huang H. Improving stability and thermal properties of TiO2 nanofluids by supramolecular modification: high energy efficiency heat transfer medium for data center cooling system. Int J Heat Mass Transf. 2020;156:119735. doi:10.1016/j.ijheatmasstransfer.2020.119735. [Google Scholar] [CrossRef]

7. Nasrin R, Hasanuzzaman M, Rahim NA. Effect of nanofluids on heat transfer and cooling system of the photovoltaic/thermal performance. Int J Numer Methods Heat Fluid Flow. 2019;29(6):1920–46. doi:10.1108/HFF-04-2018-0174. [Google Scholar] [CrossRef]

8. Okonkwo EC, Wole-Osho I, Almanassra IW, Abdullatif YM, Al-Ansari T. An updated review of nanofluids in various heat transfer devices. J Therm Anal Calorim. 2021;145(6):2817–72. doi:10.1007/s10973-020-09760-2. [Google Scholar] [CrossRef]

9. Yasmin H, Giwa SO, Noor S, Sharifpur M. Experimental exploration of hybrid nanofluids as energy-efficient fluids in solar and thermal energy storage applications. Nanomaterials. 2023;13(2):278. doi:10.3390/nano13020278. [Google Scholar] [PubMed] [CrossRef]

Mohebbi R, Izadi M, Sajjadi H, Delouei AA, Sheremet MA. Examining of nanofluid natural convection heat transfer in a Γ-shaped enclosure including a rectangular hot obstacle using the lattice Boltzmann method. Phys A Stat Mech Appl. 2019;526:120831. doi:10.1016/j.physa.2019.04.067. [Google Scholar] [CrossRef]

11. Ma Y, Rashidi MM, Mohebbi R, Yang Z. Nanofluid natural convection in a corrugated solar power plant using the hybrid LBM-TVD method. Energy. 2020;199(6):117402. doi:10.1016/j.energy.2020.117402. [Google Scholar] [CrossRef]

12. Ghazanfari V, Imani M, Shadman MM, Amini Y, Zahakifar F. Numerical study on the thermal performance of the shell and tube heat exchanger using twisted tubes and Al2O3 nanoparticles. Prog Nucl Energy. 2023;155:104526. doi:10.1016/j.pnucene.2022.104526. [Google Scholar] [CrossRef]

13. Ghazanfari V, Taheri A, Amini Y, Mansourzade F. Enhancing heat transfer in a heat exchanger: CFD study of twisted tube and nanofluid (Al2O3, Cu, CuO, and TiO2) effects. Case Stud Therm Eng. 2024;53(12):103864. doi:10.1016/j.csite.2023.103864. [Google Scholar] [CrossRef]

14. Walelign T. Rates of heat, mass and momentum transfer in a magnetic nanofluid near cylindrical surface with velocity slip and convective heat transfer. Heliyon. 2024;10(6):e27675. doi:10.1016/j.heliyon.2024.e27675. [Google Scholar] [PubMed] [CrossRef]

15. Walelign T, Seid E. Mathematical model analysis for hydromagnetic flow of micropolar nanofluid with heat and mass transfer over inclined surface. Int J Thermofluids. 2024;21(3):100541. doi:10.1016/j.ijft.2023.100541. [Google Scholar] [CrossRef]

16. Naseri Nia S, Rabiei F, Rashidi MM, Kwang TM. Lattice Boltzmann simulation of natural convection heat transfer of a nanofluid in a L-shape enclosure with a baffle. Results Phys. 2020;19(12):103413. doi:10.1016/j.rinp.2020.103413. [Google Scholar] [CrossRef]

17. Matori A, Mohebbi R, Hashemi Z, Ma Y. Lattice Boltzmann study of multi-walled carbon nanotube (MWCNT)-Fe3O4/water hybrid nanofluids natural convection heat transfer in a Π-shaped cavity equipped by hot obstacle. J Therm Anal Calorim. 2019;136(6):2495–508. doi:10.1007/s10973-018-7881-8. [Google Scholar] [CrossRef]

18. Nazarafkan H, Mehmandoust B, Toghraie D, Karimipour A. Numerical study of natural convection of nanofluid in a semi-circular cavity with lattice Boltzmann method. Int J Numer Methods Heat Fluid Flow. 2020;30(5):2625–37. doi:10.1108/HFF-11-2018-0686. [Google Scholar] [CrossRef]

19. Rahimi A, Kasaeipoor A, Malekshah EH, Amiri A. Natural convection analysis employing entropy generation and heatline visualization in a hollow L-shaped cavity filled with nanofluid using lattice Boltzmann method- experimental thermo-physical properties. Phys E Low-Dimensional Syst Nanostructures. 2018;97(5):82–97. doi:10.1016/j.physe.2017.10.004. [Google Scholar] [CrossRef]

20. Zhou X, Jiang Y, Li X, Cheng K, Huai X, Zhang X, et al. Numerical investigation of heat transfer enhancement and entropy generation of natural convection in a cavity containing nano liquid-metal fluid. Int Commun Heat Mass Transf. 2019;106(1):46–54. doi:10.1016/j.icheatmasstransfer.2019.05.003. [Google Scholar] [CrossRef]

21. Ahrar AJ, Djavareshkian MH, Ahrar AR. Numerical simulation of Al2O3-water nanofluid heat transfer and entropy generation in a cavity using a novel TVD hybrid LB method under the influence of an external magnetic field source. Therm Sci Eng Prog. 2019;14(3805):100416. doi:10.1016/j.tsep.2019.100416. [Google Scholar] [CrossRef]

22. Lai FH, Yang YT. Lattice Boltzmann simulation of natural convection heat transfer of Al2O3/water nanofluids in a square enclosure. Int J Therm Sci. 2011;50(10):1930–41. doi:10.1016/j.ijthermalsci.2011.04.015. [Google Scholar] [CrossRef]

23. Ruan H, Xie H, Wang J, Liao J, Sun L, Gao M, et al. Numerical investigation and comparative analysis of nanofluid cooling enhancement for TEG and TEC systems. Case Stud Therm Eng. 2021;27:101331. doi:10.1016/j.csite.2021.101331. [Google Scholar] [CrossRef]

24. Pandey GK, Sikha SS, Thakur A, Yarlagadda SS, Thatikonda SS, Baiju Suja B, et al. Thermal mapping and heat transfer analysis of an induction motor of an electric vehicle using nanofluids as a cooling medium. Sustainability. 2023;15(10):8124. doi:10.3390/su15108124. [Google Scholar] [CrossRef]

25. Pambudi NA, Sarifudin A, Firdaus RA, Ulfa DK, Gandidi IM, Romadhon R. The immersion cooling technology: current and future development in energy saving. Alex Eng J. 2022;61(12):9509–27. doi:10.1016/j.aej.2022.02.059. [Google Scholar] [CrossRef]

26. Almeshaal MA, Altohamy AA. Experimental analysis of a photovoltaic thermal collector using phase change materials and copper oxide nanofluid. J Energy Storage. 2024;93:112265. doi:10.1016/j.est.2024.112265. [Google Scholar] [CrossRef]

27. Sukop MC, Thorne DT. Lattice Boltzmann modeling: an introduction for geoscientists and engineers. Heidelberg: Springer-Verlag; 2006. doi:10.1007/978-3-540-27982-2. [Google Scholar] [CrossRef]

28. Wahba MA, Abdelrahman AA, El-Sahlamy NM, Rabbo MFA. Double SRT thermal lattice boltzmann method for simulating natural convection of low prandtl number fluids. Int J Eng Sci. 2017;6(12):21–35. [Google Scholar]

29. Chen S, Doolen GD. Lattice boltzmann method for fluid flows. Annu Rev Fluid Mech. 1998;30(1):329–64. doi:10.1146/annurev.fluid.30.1.329. [Google Scholar] [CrossRef]

30. Mohamad AA. Lattice boltzmann method: fundamentals and engineering applications with computer codes. 2nd ed. London: Springer-Verlag; 2019. doi:10.1007/978-1-4471-7423-3. [Google Scholar] [CrossRef]

31. Li H, Lu X, Fang H, Qian Y. Force evaluations in lattice Boltzmann simulations with moving boundaries in two dimensions. Phys Rev E. 2004;70(2):026701. doi:10.1103/PhysRevE.70.026701. [Google Scholar] [PubMed] [CrossRef]

32. McCracken ME, Abraham J. Lattice Boltzmann methods for binary mixtures with different molecular weights. Phys Rev E-Stat Nonlinear, Soft Matter Phys. 2005;71(4):046704. doi:10.1103/PhysRevE.71.046704. [Google Scholar] [PubMed] [CrossRef]

33. Albojamal A, Vafai K. Analysis of single phase, discrete and mixture models, in predicting nanofluid transport. Int J Heat Mass Transf. 2017;114(13–14):225–37. doi:10.1016/j.ijheatmasstransfer.2017.06.030. [Google Scholar] [CrossRef]

34. Bayat AE, Jalalat Moghanloo P, Piroozian A, Rafati R. Experimental investigation of rheological and filtration properties of water-based drilling fluids in presence of various nanoparticles. Colloids Surfaces A Physicochem Eng Asp. 2018;555(1):256–63. doi:10.1016/j.colsurfa.2018.07.001. [Google Scholar] [CrossRef]

35. Tongkratoke A, Pramuanjaroenkij A, Chaengbamrung A, Kakaç S. Numerical study of nanofluid heat transfer enhancement with mixing thermal conductivity models. Comput Therm Sci. 2014;6(1):1–12. doi:10.1615/ComputThermalScien.2013006287. [Google Scholar] [CrossRef]

36. Khanafer K, Vafai K, Lightstone M. Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids. Int J Heat Mass Transf. 2003;46(19):3639–53. doi:10.1016/S0017-9310(03)00156-X. [Google Scholar] [CrossRef]

37. Lahmer EB, Benhamou J, Elouazzani MA, Moussaoui MA, Mezrhab A. Heat transfer enhancement of a microchannel cooler with V-shaped partitions. Int J Thermofluids. 2023;20:100450. doi:10.1016/j.ijft.2023.100450. [Google Scholar] [CrossRef]

38. Zou Q, He X. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Phys Fluids. 1997;9(6):1591–8. doi:10.1063/1.869307. [Google Scholar] [CrossRef]

39. Lahmer EB, Benhamou J, Admi Y, Moussaoui MA, Jami M, Mezrhab A, et al. Assessment of conjugate and convective heat transfer performance over a partitioned channel within backward-facing step using the lattice Boltzmann method. J Enhanc Heat Transf. 2022;29(3):51–77. doi:10.1615/JEnhHeatTransf.2022040357. [Google Scholar] [CrossRef]

40. Santra AK, Sen S, Chakraborty N. Study of heat transfer augmentation in a differentially heated square cavity using copper-water nanofluid. Int J Therm Sci. 2008;47(9):1113–22. doi:10.1016/j.ijthermalsci.2007.10.005. [Google Scholar] [CrossRef]